A Holistic Secure Communication Mechanism Using a Multilayered Cryptographic Protocol to Enhanced Security

1  Introduction

In the domain of data proliferation, the role of cryptography in maintaining data integrity and confidentiality is increasingly recognized [1]. Cryptography serves as a fundamental component in the architecture of security systems [2], addressing a multitude of threats [3,4]. Traditional cryptographic algorithms have provided a reliable foundation for data protection over many years [5], proving effective in less complex digital environments [6]. However, the current digital age, marked by advanced cyber threats [7], necessitates the enhancement and diversification of cryptographic techniques [8]. Elliptic Curve Cryptography (ECC) emerges as a significant development in this field. Its effectiveness is attributed to the use of shorter key lengths compared to conventional cryptosystems [9,10]. Specifically, the Elliptic Curve Diffie-Hellman (ECDH) key exchange method demonstrates a robust approach to cryptography, leveraging the properties of elliptic curves to ensure secure communication even in hostile settings [11]. Concurrently, the advent of the Advanced Encryption Standard in Galois/Counter Mode (AES-GCM) represents a milestone in symmetric encryption [12]. This algorithm is distinguished by its speed and efficiency, highlighting the importance of balancing security and performance. AES-GCM’s authenticated encryption capabilities ensure both data confidentiality and integrity, rendering it an essential component of cryptographic systems. In the realm of digital signatures, the Elliptic Curve Digital Signature Algorithm (ECDSA) is notable [13]. Digital environments require mechanisms not only for encryption but also for the verification of data authenticity and source. ECDSA addresses this need, providing non-repudiation and assuring message legitimacy and the sender’s identity. This adaptation ensures clarity and precision, facilitating the review and typesetting process.

In the field of cryptography, the continuous emergence of innovative strategies and mechanisms is met with an evolving array of challenges. These challenges are not limited to technical difficulties but encompass adaptive adversaries characterized by remarkable resourcefulness. These dynamic positions cryptographic protocols in a constant state of evaluation and adaptation. The inherent nature of cryptographic algorithms involves a balance between strengths and potential vulnerabilities. Each algorithm, despite its protective features, may exhibit specific weaknesses in isolation. For instance, the Elliptic Curve Diffie-Hellman (ECDH) key exchange excels in establishing keys in a public setting, yet it encounters challenges in the complexity of key distribution and management [14,15]. The protocol’s reliance on public key exchanges introduces opportunities for vulnerabilities if not managed with due diligence. Similarly, the Advanced Encryption Standard in Galois/Counter Mode (AES-GCM) [16] illustrates the multifaceted nature of cryptography. While AES-GCM is renowned for its rapid and efficient encryption, its effectiveness hinges on a critical operational requirement: the non-repetition of key-nonce pairings. This seemingly straightforward condition is crucial; a single lapse in AES-GCM can compromise the entire security framework [17–20]. Beyond specific algorithmic weaknesses, a broader challenge in cryptography is achieving a balance among confidentiality, authenticity, and integrity. In a landscape rife with potential threats, mere data encryption is insufficient. Cryptography now aims to preserve the sanctity of confidentiality while ensuring the authenticity and integrity of communications. This balance, essential to contemporary cryptographic efforts [21], necessitates a combination of techniques and a comprehensive strategic approach, highlighting the complexity and ongoing challenges in the field.

In the digital communication era, the expansion of complex cyber interactions parallels the increasing sophistication of adversarial threats [22]. Recent decades have seen a significant rise in cyber-attacks, ranging from destructive malware to complex nation-state cyber campaigns. This challenging environment necessitates a reevaluation of existing cryptographic countermeasures. The scientific community is called upon to not only improve but to fundamentally transform security approaches [23]. The motivation for this transformation is grounded in a critical understanding: isolated, even potent, modern cryptographic techniques may fall short against multifaceted attacks. This realization has led to a growing consensus around the potential effectiveness of integrating multiple cryptographic primitives [24]. Such a confluence aims to achieve two objectives. Firstly, an integrated scheme could combine the strengths of individual techniques, potentially yielding a cryptographic protocol more robust than its individual components. Secondly, the weaknesses of one technique could be mitigated by the strengths of another, fostering a more resilient security framework. However, this synthesis is more than a mere aggregation. At its core, the harmonious interaction between various cryptographic primitives. Beyond the fundamental goal of data confidentiality, the integrated approach must also address critical aspects such as data authenticity and resilience against diverse cryptographic attacks [25]. The challenge extends beyond designing a cryptographic protocol; it involves crafting a coherent, durable, and versatile cryptographic ‘symphony’. Central to this research is a pivotal question: In a digital landscape continuously evolving with new threats and forms of interaction, especially in the fast-paced world of social media, how can we develop a multilayered cryptographic framework that integrates the benefits of diverse cryptographic aspects while compensating for their inherent weaknesses, thereby creating a more formidable barrier of data protection than ever before?

The exploration of a novel cryptographic approach is motivated by the increasing sophistication and frequency of cyber threats. Traditional cryptographic methods, while effective, often struggle with scalability and adaptability. This limitation is particularly challenging in rapidly evolving digital environments. The need for a cryptographic solution that overcomes these challenges and anticipates future security issues drives this study. The proposed approach aims to improve data integrity and confidentiality efficiently and scalable, aligning with the requirements of modern digital security. In the current digital age, where interactions and transactions are deeply integrated with cyberspace, a renewed focus on data security is essential. This study aims to develop a cryptographic architecture that integrates the unique yet complementary aspects of Elliptic Curve Diffie-Hellman (ECDH), Advanced Encryption Standard in Galois/Counter Mode (AES-GCM), and Elliptic Curve Digital Signature Algorithm (ECDSA). The goal is not simply to combine these techniques but to integrate them intricately, leveraging their synergies to enhance data protection while addressing their vulnerabilities.

The methodology centers on the careful orchestration of various cryptographic operations. The process begins with Key Generation, using the SECP256R1 curve to create dual Elliptic Curve key pairs for both the sender and recipient. This forms the foundation for secure transactions. The Key Exchange phase follows, with ECDH facilitating the accurate transfer of public keys and the creation of a shared secret. Key Derivation then employs the PBKDF2HMAC function to produce a symmetric encryption key, essential for the subsequent encryption process. Ensuring message authenticity and integrity during transmission is also crucial. This is achieved through Message Authentication using an HMAC-SHA256 mechanism, which guarantees the genuineness and continuity of messages. The protocol’s approach to Encryption & Decryption is layered. It begins with XOR encryption, reinforced by the AES-GCM algorithm. This two-tiered method enhances security and strengthens defenses against cryptographic attacks. Decryption follows a similar bifurcated path, ensuring accurate message recovery. Additionally, the Signature Generation and Verification phase involves ECDSA creating a digital signature on the original message, confirming its authenticity. The verification of this signature ensures the message’s integrity and authentic origin. This research elucidates a nuanced approach to cryptographic mechanisms, with its bedrock being innovation, efficiency, and robustness. The novel contributions of our proposed study can be summarized as follows:

•   Integrated Cryptographic Framework: This research pioneers cryptographic advancements by integrating three key algorithms: (ECDH), (AES-GCM), and ECDSA). This integration not only harnesses the individual strengths of these algorithms but also results in a robust cryptographic protocol that significantly enhances security and operational efficiency over traditional methods.

•   Enhanced Two-Level Encryption System: Our study introduces an innovative two-tier encryption mechanism, advancing beyond standard encryption practices. This layered encryption strategy significantly boosts message confidentiality, ensuring data protection even if one encryption level is compromised.

•   Innovative Key Management Approach: We address the inherent complexities and security risks of traditional key management systems by implementing an efficient method of generating multiple operational keys from a single shared secret. This approach simplifies key management while simultaneously strengthening the system against vulnerabilities related to key distribution.

•   Holistic Data Protection Strategy: In response to the increasing frequency of data breaches, our methodology comprehensively safeguards data by simultaneously ensuring confidentiality, authenticity, and integrity. This triad approach offers a robust defense against various security threats, providing a comprehensive security solution in the current data-driven landscape.

The remainder of this article unfolds in a structured manner to provide readers with a systematic exploration of the topic. Beginning with Section 2, a comprehensive review of pertinent literature in the field is presented, establishing the foundational underpinnings for this study. The progression to Section 3 unveils the novel methodology crafted for this research, shedding light on the distinctive approach we have employed. Delving into the technical facets, Section 4 demystifies the intricacies of (AES-GCM) Decryption, a pivotal component in our cryptographic study. This is closely followed by Section 5, where the nuanced mechanisms of (ECDSA) Signature Verification are meticulously dissected. As we transition to the pragmatic dimension of our research in Section 6, an exhaustive experimental simulation is elucidated, detailing the empirical undertakings and their consequent results. Section 7 ventures into a profound discourse, analyzing the implications, challenges, and nuances unearthed during our study. Concluding this research odyssey, Section 8 encapsulates the key takeaways, offering a synthesis of our findings and their potential ramifications in the broader context of cryptographic research.

2  Related Work

In the annals of modern cryptographic research, myriad scholars have elucidated diverse methodologies tailored to tackle the manifold challenges posed by the evolving digital landscape. This section embarks upon a scholarly pilgrimage, meticulously delineating the rich tapestry of recent contributions, accentuating their pioneering methodologies, inherent challenges, and overarching crypto-graphic paradigms. To elucidate a concise amalgamation of the salient contributions and perceived limitations inherent to the myriad approaches showcased in the prior section, see Table 1.

Abdallah et al. [26] explored secure voice communication, developing a multilayered encryption protocol specifically for audio signals. They acknowledged the challenges in transmitting audio data, particularly its susceptibility to interception and unauthorized access. Their approach combines traditional encryption methods with optimizations tailored to audio data, ensuring both effectiveness and efficiency. Banday et al. [27] directed their research towards the encryption of medical images. Given the sensitive nature of medical data, data security in this domain is of utmost importance. They highlighted the necessity of multi-tier encryption in medical communications and developed a framework that integrates various cryptographic levels, providing comprehensive protection for medical imagery. In the context of Supervisory Control and Data Acquisition (SCADA) systems, Upadhyay et al. [28] proposed a robust key management protocol within a multi-layered security framework. SCADA systems, being crucial to critical infrastructure, face the challenge of defending against both traditional and advanced cyber threats. Their method showcases a sophisticated approach, adeptly addressing the complex security challenges inherent in SCADA systems.

The work of Kumar et al. [29] provided a comprehensive analysis of cloud security. As cloud frameworks become increasingly integral to various digital operations, their study introduces a hybrid cryptographic algorithm designed to enhance data integrity and confidentiality within cloud environments. This approach combines multiple algorithms to mitigate the vulnerabilities inherent in each, thereby establishing a more secure cloud infrastructure. In the context of cloud multi-tenancy, Kumar et al. [30] proposed a novel approach using hybrid Elliptic Curve Cryptography (ECC)-based data encryption. Addressing the complex challenges of multi-tenant cloud architectures, particularly in terms of data segregation and security, their hybrid ECC model presents a new and effective cryptographic solution. Focusing on the digital marketplace, specifically e-commerce, which is frequently targeted by cybercriminals, Dijesh et al. [31] developed a security framework based on asymmetric key algorithms. Their research underscores the importance of maintaining transactional fluidity while enhancing security measures against cryptographic attacks, particularly in the realm of e-commerce.

Amna et al. [32] explored surveillance video security, introducing the MuLViS protocol. Surveillance videos generate continuous and large volumes of data, presenting specific cryptographic challenges. The authors proposed a multi-level encryption schema to strengthen these data streams, aiming to ensure data authenticity and access integrity. In the field of unmanned aerial vehicles (UAVs), Jain et al. [33] focused on securing communications, a critical aspect as UAVs gain prominence in commercial and defense sectors. Jain and colleagues developed a communication security protocol complemented by a classification framework. This framework is designed to meet the needs of Industry 5.0, demonstrating the integration of advanced technology with cryptographic expertise. Broadening the scope to secure communications and data integrity, the literature reveals a variety of innovative developments. In the realm of the Internet of Things (IoT), Peruma et al. [34] proposed a multilayered architecture for secure communication and data transmission. The expanding IoT ecosystem, with its diverse range of devices, introduces challenges in maintaining data integrity and ensuring real-time secure transmission. The architecture proposed by Isha et al. [35] addresses these challenges, safeguarding data across interconnected devices. In the context of optical processing technology, Li et al. [36] detailed a novel multilevel chaotic image encryption algorithm. Due to the high-dimensional nature of image data, encryption presents significant challenges. Their method utilizes optical processing technology to introduce a level of entropy into images, thereby enhancing the effectiveness of encryption.

From the perspective of symmetric key cryptography, Kumar et al. [37] introduced a novel methodology that updates traditional symmetric key approaches. Their approach effectively combines cryptographic primitives to achieve a balance of efficiency and security. Similarly, Umapathy et al. [38] developed a new symmetric cryptographic technique that emphasizes block complexity, enhancing data security, which is crucial in the current digital landscape. In response to the rising frequency of Distributed Denial of Service (DDoS) attacks, particularly in the IoT domain, Khan et al. [39] proposed a multi-layered security strategy specifically for DDoS detection. Their approach, based on a thorough understanding of network behavior, provides strong defense against malicious attacks. In the field of image compression and encryption, Gupta et al. [40] created a hybrid scheme that combines multilayer stacked autoencoder techniques with the logistic map. This method achieves efficient image representation and robust encryption. The healthcare sector, with its specific security needs, has been addressed by Panwar et al. [41]. They developed a multilevel secure information communication model tailored for healthcare systems, ensuring patient confidentiality and data integrity. In a unique fusion of cryptography and steganography, Tabassum et al. [42] introduced a multi-layered data encryption and decryption mechanism. This technique not only provides algorithmic security but also obscures data at the representation level. Lastly, focusing on the security of medical imagery, Akkasaligar et al. [43] advanced a multilevel security protocol that employs heterogeneous chaotic maps in conjunction with deoxyribonucleic acid (DNA) sequence operations. This innovative approach ensures the privacy and authenticity of medical images.

3  Proposed Methodology

In the dynamic field of cryptographic paradigms, it is essential to leverage the integration of diverse cryptographic techniques. The architecture we propose combines elliptic curve cryptographic principles with symmetric encryption methodologies, further strengthened by signature verification protocols. This integration aims not only to achieve enhanced security but also to address the various challenges in contemporary cryptographic ecosystems. The encryption process is crucial for maintaining secure communication between the sender and receiver, as illustrated in Fig. 1.

Figure 1: The encryption process of the proposed methodology

The following sections provide a detailed description of the methodology, presented in a clear, step-by-step manner. The proposed methodology is divided into three key phases. The first phase involves a thorough analysis of current cryptographic protocols, pinpointing their limitations in terms of security and efficiency. In the second phase, these insights inform the design of an innovative cryptographic approach with a focus on improving data confidentiality and integrity. The third and final phase is dedicated to extensive testing and evaluation, benchmarking the performance of our protocol against existing standards. This structured approach ensures a comprehensive and methodical development process, from identifying deficiencies in current methods to confirming the efficacy of our novel protocol. In our methodology, we focus on the integration of (ECC), (AES-GCM), and (ECDSA) to enhance system security. This integration is pivotal in constructing a resilient cryptographic framework capable of withstanding a variety of cyber threats.

•   (ECC) for Key Generation: (ECC) is utilized for its efficiency in generating strong cryptographic keys with shorter key sizes, thus reducing computational overhead while maintaining high levels of security. The strength of (ECC) lies in the difficulty of solving the Elliptic Curve Discrete Logarithm Problem, making it a robust choice for public-key encryption and key exchange.

•   (AES-GCM) for Data Encryption: (AES-GCM) is employed for encrypting data due to its high performance and strong security characteristics. It combines the confidentiality offered by (AES) with the integrity assurance of Galois/Counter Mode, providing authenticated encryption that safeguards against tampering and forgery.

•   (ECDSA) for Digital Signatures: (ECDSA) is integrated for digital signature generation and verification, offering enhanced security for data authenticity. The use of (ECDSA) complements (ECC) in key management, providing a secure method for authenticating the source and integrity of the data.

•   Combining (ECC), (AES-GCM), and (ECDSA): The synergy of these three cryptographic techniques fortifies the overall security architecture. (ECC’s) efficient key management pairs effectively with (AES-GCM’s) authenticated encryption, ensuring both data confidentiality and integrity. (ECDSA) further strengthens this framework by providing robust mechanisms for data authentication. Together, they create a multi-layered defense against a wide range of cyber-attacks, from brute-force attempts to more sophisticated cryptographic threats.

•   Resilience against Attacks: This integrated approach significantly enhances the system’s resilience. By combining the strengths of each cryptographic method, our framework not only provides comprehensive security but also maintains operational efficiency. The multi-faceted nature of this integrated system ensures that even if one aspect is compromised, the other layers continue to provide robust security.

3.1 Key Generations

In the rapidly evolving landscape of cryptographic systems, harnessing the potency of elliptic curves, especially over extension fields, emerges as a paramount strategy. Our architecture is finely crafted, intertwining distinct algebraic paradigms such as multivariate polynomials and projective coordinate spaces. This amalgamation ushers in a kaleidoscope of mathematical intricacies that underscore our advanced key generation methodology. The complete process of the key generation is illustrated in Fig. 1.

3.1.1 Transition between Coordinate Domains: Projective to Affine Transformation

In elliptic curve arithmetic, the transition between coordinate representations is not merely utilitarian but often indispensable. When representing a point in projective space, P = [X: Y: Z], its affine analog emerges as:

(x,y)=(XZ,YZ)(1)

This transformation holds paramount importance, particularly in computational scenarios necessitating reduced computational overhead.

3.1.2 Fortification via Twist Curves

While elliptic curves are intrinsically robust, introducing their quadratic twists fortifies the cryptographic foundation. Consider the twist of the curve E as:

E ′:y2+xy=x3+ax2+c2b(2)

Here, c stands as a distinguished non-square in Fpm. By incorporating this twist, we enhance the curve’s resilience against a spectrum of cryptographic assaults.

3.1.3 Multivariate Scalar Decomposition for Efficacious Multiplication

Two streamline and expedite point multiplication, decomposing the scalar vector d into its multivariate constituents is judicious:

d ′=[dmodl1,dmodl2,…,dmodlk](3)

Within this context, l1, l2, . . . , lk are prime integers of diminished magnitude. This decomposition augments computational fluidity in succeeding operations.

3.1.4 Enriched Scalar Multiplication in Extended Domains

Scalar multiplication, when maneuvered within extended fields, is articulated as:

[k]P=⊕i=0m−1[ki]P(4)

Here, P is a piovotal point on E(Fpm), and k is the summation ∑i=0m−1kipi. The symbol ⊕ is a milieu.

3.1.5 Exploiting Endomorphism: A Leap in Computational Efficiency

An endomorphism, denoted by ψ, maps E onto itself and is articulated as:

ψ(x,y)=(βx,y)(5)

In this expression, β is a member of Fpm. Beyond its mathematical elegance, this endomorphic construct significantly amplifies the pace of point multiplication.

3.1.6 Endomorphic Scalar Multiplication: A Composite Perspective

Employing the previously introduced endomorphism, scalar multiplication transforms:

[k]P=[k1]P⊕[k2]ψ(P)(6)

Herein, k1 and k2 are derivatives of the primal scalar k, extrapolated via the properties intrinsic to the endomorphism.

3.1.7 Venturing into Linear Algebra: The Dual Space Private Key Vector

Linear algebra’s esoteric constructs offer profound cryptographic insights. Inspired by its dual space concept, we delineate a complementary space for the private key vector:

d∗=[∏i=1npi(xi),∏i=1npi(x2),…,∏i=1npi(xn)]modn(7)

The symphony of these multifaceted mathematical constructs, crystallized from Eqs. (1) to (7), paints a panoramic tableau of our avant-garde elliptic curve key generation technique. We ardently posit that such a melding of mathematical sophistication fortifies our cryptographic edifice, rendering it impervious to even the most astute adversarial forays.

3.2 (ECDH) Key Exchange

Within the cryptographic pantheon, the Elliptic Curve Diffie-Hellman (ECDH) algorithm holds a pivotal role, offering a cryptographic alchemy that transcends classical methods. Our rendition, conceived with a high degree of mathematical sophistication, exploits isogenies between elliptic curves, higher dimensional Weil pairings, and tensor product structures, culminating in a robust shared secret, as shown in Algorithm 2.

In lieu of conventional methods, the sender and receiver each derive their private keys from a tensor product space, formulating:

d=a⊗b(8)

where a and b are randomly chosen vectors, their respective public keys become an intersection of elliptic curve points and tensor products:

Q ′=d×G⊗H(9)

where G and H are base points from two distinct elliptic curves, building on the premise of isogenies between elliptic curves, both parties employ an isogeny ϕ of degree l, a small prime, to calculate intermediate public keys.

Q ′=ϕ(Q)(10)

Our approach employs Weil pairings to harness the benefits of bilinear properties. With the original and isogeny-based public keys, the shared secret is calculated as:

e(Q,Q ′)d=e(G,H)a⊗b(11)

This equation gives both parties an identical shared secret owing to the bilinearity of Weil pairings. To thwart advanced adversarial tactics, the shared secret undergoes a scalar re-composition under a specific Galois action:

shared_key=σ(e(G,H)a⊗b)(12)

where σ represents the Galois automorphism. As a culminating step, we apply the Frobenius endomorphism π to the shared secret, elevating its resilience against quantum attacks:

final_shared_key=π(shared_key)(13)

This series of transformations, spanning Eqs. (8) to (13), not only fortifies the (ECDH) key exchange process but also augments it with a level of mathematical intricacy designed to withstand even the most formidable cryptanalytic endeavors. It is a testament to cryptographic innovation, promising secure communications in an increasingly uncertain digital epoch.

3.3 Key Derivation

In our proposed methodology, key derivation, essential for strengthening the core of elliptic curve cryptography, is given priority. Within the array of cryptographic primitives, the task of deriving a symmetric encryption key from a seemingly random source is complex and prone to vulnerabilities. To address this, our technique utilizes PBKDF2HMAC, a password-based key derivation function. This function transforms shared secrets into cryptographically secure symmetric keys. The details of our approach are further explained in the following subsections. In enhancing the security of symmetric encryption, we introduce a novel method for key derivation, thoroughly outlined in Algorithm 3. This algorithm represents the intricate combination of shared secrets from the Elliptic Curve Diffie-Hellman (ECDH) key exchange with the robustness of PBKDF2HMAC.

Additionally, we incorporate an advanced salt generation mechanism, which results from the cryptographic integration of the salt with concatenated shared keys. This integration increases entropy, thereby enhancing resistance to brute-force attacks. The resulting derived_key is poised to be a key element in advanced cryptographic architectures, demonstrating our commitment to developing robust security paradigms.

Considering the evolving cryptographic landscape, the Password-Based Key Derivation Function 2 (PBKDF2) with HMAC (Hash-Based Message Authentication Code) has emerged as an indomitable force against brute-force and rainbow table attacks. This iterative function not only offers a shield against pre-computation attacks but also allows seamless integration with elliptic curve crypto-graphic paradigms. Given the shared secrets (shared_key_Sender, shared_key_Reciever) obtained from the (ECDH) key exchange, the derivation of the symmetric encryption key derived_key can be mathematically formulated as:

derived_key=PBKDF2HMAC(pw=concat(skS,skR),salt,iter,dkL)(14)

where:

•   Password is a concatenation of the shared secrets.

•   salt is a random value to thwart pre-computation attacks sourced from a cryptographically secure random number generator.

•   dkLen is the desired length of the derived key.

A consequential linchpin in the key derivation process is the use of salts. To propel our approach into the echelons of state-of-the-art, we introduce an innovative salting technique:

enhancedsalt=SHA−256(salt⊗password)(15)

where:

•   SHA-256 is the cryptographic hash function.

•   ⊗ denotes the bitwise XOR operation.

By amalgamating the XOR operation with the salt and password, we construct an augmented salt, enhancing unpredictability and impeding adversaries from gaining the upper hand. Our meticulous foray into key derivation, underpinned by advanced mathematical equations and groundbreaking cryptographic constructs, epitomizes a novel vanguard against adversarial threats, paving the way for a resilient elliptic curve cryptographic ecosystem.

3.4 Message Authentication Code (MAC) Generation

The process of cryptographic authentication entails an intricate ballet between the sender’s intention and the receiver’s assurance. In this elucidated construct, the task of a Message Authentication Code (MAC) remains paramount, predominantly ensuring that the transmitted message’s integrity remains unbreeched throughout its journey. Amidst a plethora of methodologies, the (HMAC-SHA256) emerges as an exemplar due to its cryptographic strength and computational efficiency. In the ensuing subsection, we delve deeper into the methodical synthesis of the (HMAC) for a given message, drawing strength from a purpose-derived key.

Consider M as the mathematical space of all messages and K as the corresponding space of all possible (HMAC) keys. Given a key k ∈ K and a message m ∈ M, the (HMAC) can be expressed as:

mac(m,k)=H(⊕opad,H(k⊕ipad,m))(16)

where H is a cryptographic hash function, denotes the bitwise XOR operation, and ipad and opad are specific constants known as inner and outer pads, respectively. Delving deeper, consider the function f : M×K→C, where C is the space of all possible cryptographic checksums. This function can be represented in terms of eigenfunctions ϕ and eigenvalues λ:

f(m,k)=∑i⋋iϕi(m)ϕi∗(k)(17)

Such a representation might seem abstruse, but its introduction provides a framework for exploring the orthogonality and completeness properties of (HMAC). Here, ϕ∗ is the complex conjugate of the eigenfunction ϕ. Integrating the derived_key from our previous construct, the derivation of (HMAC) transforms.

mac(m,derived_key)=∫kH(k⊕opad,H(k⊕ipad,m))ρ(k)dk(18)

where ρ(k) is a density function encompassing the probabilistic nature of the derived key within the space. The entropy of the resulting (MAC), representing its randomness and unpredictability, can be quantified:

ε=−∫cmac(m,derived_key)×log⁡mac(m,derived_key)dc(19)

This entropy measure, ε, becomes instrumental in ascertaining the strength and security of the (HMAC) against various cryptographic attacks.

3.5 XOR Encryption

XOR encryption, at first glance, may appear simple. However, its significance is evident in the spectral properties of the resulting encrypted signals and its role in maximizing entropy. To understand its mathematical characteristics, we delve into its complex underpinnings. In enhancing the security of message transmission, we propose an advanced encryption mechanism based on XOR operations within vector spaces. This method effectively combines elements of linear algebra with cryptographic principles, making it effective against common cryptographic attacks. As detailed in Algorithm 5, our approach incorporates entropy calculations, the Walsh-Hadamard Transform (WHT), and autocorrelation analyses to enhance the encryption process. The sequence of these operations, clearly outlined in a step-by-step manner, provides the system with robust defense mechanisms against adversarial attempts while maintaining computational efficiency. This methodological approach not only strengthens the security of the encryption process but also demonstrates the utility of integrating mathematical concepts into cryptographic practices.

AAA Consider messages and keys as vectors in the finite field GF(2n). The XOR operation can then be visualized as vector addition. For a message vector M and a key vector K, the encrypted vector C is:

C=M+KinGF(2n)(20)

To further elaborate the intricacies, let us denote the Hamming weight (number of non-zero elements) of a vector V by w(V). The entropy H associated with the encrypted vector is:

H(C)=∑i=1np(ci)log2p(ci)(21)

where p(ci) is the probability of the ith bit being 1. Ideally, for maximum entropy and hence unpredictability, every bit should have a 0.5 probability of being 1, making the encrypted text ideally randomized. In the space of digital signals, the Fourier transform provides insights into the spectral components of signals. The encrypted message is no exception. Given the binary nature of our vectors, consider Walsh-Hadamard Transform (WHT), which is akin to the Fourier transform for binary functions:

W[C](u)=∑x∈GF(2n)n(−1)C(x)+u.x(22)

For an ideally encrypted message with a truly random key, the spectrum W[C] should show no peaks, indicating no discernible patterns.

3.6 Auto-Correlation Properties

The auto-correlation R of the encrypted vector C at a shift τ is given by:

R(τ)=∑i=1nci⊕ci+τ(23)

For a message encrypted with a truly random key, this auto-correlation function should ideally resemble that of white noise, offering no repeated patterns. While XOR encryption can be theoretically postulated with elementary bitwise operations, its true mathematical profundity unveils when scrutinized under the rigorous paradigms of vector spaces, spectral analysis, and correlation metrics. Such meticulous examination not only endorses its cryptographic vitality but also reveals the nuances that make it an essential tool in cryptographic protocols.

3.7 (AES-GCM) Encryption

Modern cryptographic advancements rely heavily on the integration of abstract mathematical theories with practical cryptographic primitives. Advanced Encryption Standard in Galois/Counter Mode (AES-GCM) can be conceptualized as a transformative operator functioning within a Hilbert space H, which represents a complete inner product space of encrypted messages. Recognizing the complexities inherent in symmetric encryption paradigms, we have developed an innovative approach to enhance the encryption robustness of our communication pipeline. Our refined implementation of the AES-GCM encryption algorithm highlights this enhancement. We have augmented it with advanced mathematical frameworks, including wavelet transforms and projection operations within Hilbert spaces. A detailed explanation of this procedure, covering all intermediate steps and transformations, is presented in Algorithm 6. We contend that this integration not only improves the effectiveness of encryption but also adds a sophisticated dimension to the overall cryptographic architecture. This approach demonstrates the potential of combining mathematical rigor with cryptographic techniques to develop more secure and efficient encryption methods.

Let us denote our plaintext messages as vectors in a complex vector space V, while encrypted messages inhabit the Hilbert space H. The (AES-GCM) operation can be portrayed as a bounded linear operator L:V→H:

H(m)=L(m;aes_gsm_key,nonce)(24)

Given that the spectrum of such an operator, σ(L), embodies all possible encryption outcomes, the pertinence of key and nonce selection becomes evident. Theaes_gcm_key is no mere random string, but rather the outcome of a complex wavelet transform W applied to the derived_key:

aes_gsm_key=W∗derived_key(25)

Here, ∗ symbolizes the convolution operation, integrating the derived key within the intricate wavelet domain. The nonce, integral for ensuring the cipher’s indeterminacy, is procured through a projection operator P onto a subspace of H dictated by the shared key:

nounce=Pshare_key(H)(26)

This subspace encapsulation magnifies the entropy of our encryption process, thus compounding its resilience against cryptanalysis. Embedding these sophisticated constructs, the encrypted message becomes a superposition of states within H:

|encryped_message⟩=a|aes_gsm_key⟩+b|nonce⟩(27)

where a and b are complex coefficients modulating the contributions of key and nonce, respectively. This rendition of (AES-GCM), rooted in advanced mathematical strata, affirms its stature as a fortress in the cryptographic landscape, challenging conventional paradigms and setting novel benchmarks in secure communications.

3.8 (ECDSA)-Signature Generation

Digital signatures are essential in maintaining the authenticity and integrity of messages within cryptographic systems. Among various signature mechanisms, the Elliptic Curve Digital Signature Algorithm (ECDSA) is distinguished by its reliance on the sophisticated mathematical framework of Elliptic Curve Cryptography (ECC). By integrating ECDSA with the hashing capabilities of SHA-256, we establish a robust signature system. A key component of our methodological approach is the digital signature generation process using ECDSA, which warrants detailed examination. The procedural integrity of signature generation in ECDSA is supported by a series of mathematical operations intricately woven with cryptographic primitives. A comprehensive computational examination of this mechanism is concisely presented in Algorithm 7. This algorithm provides a structured approach to creating digital signatures based on ECDSA, building on elliptic curve operations and the SHA-256 hashing algorithm. This systematic method ensures the reliability and security of the digital signature process, crucial for the efficacy of cryptographic systems. Denote by E an elliptic curve over a finite field Fp, characterized by:

E:y2≡x3+ax+bmodp

where 4a3+27b20 (ensuringnon – singularity).

The points on E form an Abelian group, with an identity element represented by a point at infinity, denoted O. For two distinct points P1(x1,y1) and P2(x2,y2), their sum P1+P2 is computed as:

x3=λ2−x1−x2

y3=λ(x1−x3)−y1

where λ is the slope of the line through P1 and P2. The point P1 +P2 is then (x3, − y3).

Given an elliptic curve E defined over Fp, a generator point G of large prime order n is chosen. Let d be the signer’s private key, an integer randomly selected from [1, n-1]. The public key Q is calculated as:

Q=d×G

To generate an (ECDSA) signature for a message m, we follow:

1. Compute e as:

e=SHA−256(m)

2. Randomly select k from [1, n-1]. Calculate the elliptic curve point (x1,y1) = k×G.3. Evaluate:

r=x1modn

s=k−1(e+d×r)modn

The modular multiplicative inverse is integral to (ECDSA)’s mathematical underpinnings. Using Fermat’s Little Theorem:

ap−1≡1modp

For k (where gcd(k,p)=1):

kp−1≡k−1modp

Thus, efficiently computing the inverse involves modular exponentiation, which can be optimized using methods such as the square-and-multiply algorithm.

The elliptic curve’s discrete logarithm problem ensures (ECDSA)’s security. For an attacker to derive d fromQ, he would have to solve the following:

Q=d×G

The (ECDSA) coupled with SHA-256 constructs a cryptographic fortress, rooted in the complex mathematical machinery of elliptic curve algebra, ensuring unparalleled data security.

4  AES-GCM Decryption

The Advanced Encryption Standard in Galois/Counter Mode (AES-GCM) decryption process is significant not only for its ability to retrieve the original message from ciphertext but also for the complex mathematics and cryptanalytic strength that underpin it. This decryption approach, deeply rooted in the intricate field of Galois fields and the extensive area of combinatorial mathematics, requires thorough examination. To clarify the complexities of the AES-GCM decryption process, a carefully crafted algorithm outlines the step-by-step progression through this cryptographic puzzle. As detailed in Algorithm 8, the process begins by dividing the ciphertext into distinct blocks. Each block is then subjected to complex transformations in hypercomplex space and analyzed for its spectral signature. This sequence of operations ultimately leads to the reconstitution of the original message, accompanied by a critical layer of authentication to ensure its integrity.

Begin with the ciphertext, denoted as C, which is a composite of several blocks represented as Ci for the ith block. The aes_gcm_key denoted as K, is the linchpin in deciphering this esoteric ciphered text. Each block undergoes an independent decryption procedure influenced by the global properties of C and the nuances introduced by the key.

M=DK(C)⊕GF(2n)(28)

Here, M represents the decrypted original message. The decryption function, D, operates in the domain of Galois field, specifically GF(2n), bestowing (AES-GCM) with its heightened resilience against cryptanalysis. Every decryption journey in the (AES-GCM) algorithm is accompanied by a unique nonce, N. This nonce ensures that even repeated encryptions of the same plaintext yield differing ciphertexts. Thus, it introduces an added layer of unpredictability, reinforcing security.

Mi=DK,N,i(Ci)(29)

The function DK,N,i highlights the interplay between the key, nonce, and the block index in the decryption matrix. The interstellar dimension of our decryption journey is the foray into hyper-complex vector spaces. These spaces, denoted as V, enable a non-linear transformation of the blocks, rendering rudimentary cryptanalysis techniques futile.

Mi−V{Ci⊗εK,N(i)}(30)

Here, ⊗ represents the convolution operation in this hypercomplex realm, and εK,N(i) is the encryption function influenced by the nonce and the block index. Ciphers, when viewed in higher dimensions, exhibit spectral signatures. These signatures, when deciphered, reveal insights into the original message and the transformation it underwent.

SCi=F{Ci}(31)

F denotes the Fourier transformation, unraveling the spectral intricacies of our ciphertext. The reverse transformation, aiding in the retrieval of our original message, can be expressed as:

Ci=F−1{SCi}(32)

One of the hallmarks of (AES-GCM) is its intrinsic capability to verify the authenticity of data. This assurance is fostered through the generation and validation of authentication tags. A sound mathematical representation for tag verification in the context of our spectral signatures is:

∑iSMi.SCiδ(k−i)=Tk(33)

Here, T_krepresents the authentication tag for the k^{th} block. The (AES-GCM) decryption process, when deconstructed and studied in-depth, manifests as a symphony of algebraic and combinatorial constructs. Its cryptographic strength, coupled with its mathematical elegance, marks it as a beacon in the realm of symmetric encryption.

4.1 XOR Decryption

In the pantheon of cryptographic schemes, XOR operations hold a quintessential stature, largely attributed to their foundational arithmetic properties. Post-encryption, disentangling the message from its XOR encryption fabric becomes a mathematical endeavor that demands precision and rigor. The XOR decryption procedure, when unraveled, oscillates between computational algebra and intricate boolean dynamics. An intricate assessment of the XOR decryption mechanism elucidates the nuanced facets beyond mere bitwise operations. This is ingeniously captured in Algorithm 9, which delineates the cryptographic extraction of the original message. The formulation exploits advanced mathematical constructs, such as orthogonality and eigenspace transformations. Each progression, from the primary XOR operations to the subsequent eigenspace transmutations, is meticulously inscribed to ensure the sanctity and precision of the decryption process.

Let us consider M as the encrypted message and K as the xor_key. The length of K is typically congruent to that of M for optimal cryptographic efficacy. The process can be illuminated through the following iterative equation:

Mi  ′=Mi⊕Ki(34)

where Mi′ is the decrypted byte at position i, and denotes the XOR operation. In an abstract space, XOR’s dynamics can be captured by the following set of equations:

a⊕0=a(35)

a⊕a=0(36)

a⊕b=¬(a⊕¬b)(37)

a⊕b=(a∧¬b)∨(¬a∧b)(38)

Elaborating further, we integrate the notion of the hyperspace field F. If F(a,b) represents a function in this space, the XOR dynamics can be outlined as:

F(a,b)⊕F(b,a)=F(39)

F(a,a)⊕F(a,b)=F(b,a)(40)

F(0,a)⊕F(a,0)=F−1(a)(41)

Exploiting the orthogonality property intrinsic to the XOR operation, we define:

ΩM=∫01M(t)⊕K(t)dt(42)

where ΩM embodies the orthogonal space of the message. One can fathom the decryption landscape by evaluating:

M ′(t)=∂ΩM∂K(t)(43)

Unveiling the deeper realms of the XOR decryption matrix, the eigenspace transformation is governed by:

ΛM=K×MT−KT×M(44)

Elucidates the spectral signature of the message, further facilitating its decryption. The process from the encrypted veil to the decrypted revelation traverses through a labyrinth of mathematical intricacies, as delineated above. The XOR operation, with its profound simplicity, juxtaposes itself amidst these complexities, offering a symphony of computational harmonics leading to the resurrection of the original message.

5  (ECDSA) Signature Verification

(ECDSA) remains an exemplar of cryptographic sophistication, a beacon showcasing the confluence of advanced algebraic geometry and cryptographic tenacity. At its core lies the elliptic curve, a construct intertwined with modular arithmetic, bestowing upon the algorithm a robustness that is seldom paralleled.

Consider the elaborate dance of numbers and operations that (ECDSA) plays. Begin with a signature, typically denoted as (r,s). The elliptic curve, defined over a finite field, becomes our battleground. Central to our discourse are two numbers, both sculpted through elliptic curve operations and modular arithmetic, that serve as the linchpins in the signature verification odyssey. Given the foundational elliptic curve point, G, of order n, and the public key, P, we intertwine these entities with the message’s hash, transmogrified through SHA-256 into H(m). Thus, the relationship between the public and private keys, P and d, respectively, unfurls as:

P=d×G

where d elegantly oscillates between the confines of 1 and n−1.

From the chrysalis of this relationship, the hashed message metamorphoses further:

e=(SHA−256(m))r×smod n

Here, the application of modular arithmetic, juxtaposed with the hashing operation, ensures the resultant e remains ensnared within the elliptic curve’s domain, priming it for the subsequent curve-centric machinations.

Following this, the algorithm beckons the modular multiplicative inverse of s, denoted as s−1:

s−1=sn−2modn

This beckoning is not whimsical; it draws inspiration from Fermat’s Little Theorem, ensuring swift and accurate inverse computation. Armed with s−1, the algorithm deftly weaves the tapestries of u1 and u2:

u1=e×s−1×r2mod n

u2=r×s−1×s3modn

The interplay of scalar multiplication and elliptic curve point addition emerges next, guiding us to the coordinates (x1,y1):

(x1,y1)=u1×G+u2×P+s×G

The grand denouement of our mathematical opera hinges upon a simple comparison. If r aligns with x1, the curtain falls on a triumphant note, underscoring the signature’s authenticity:

r2=x13+r×y1mod n

The (ECDSA) signature verification process is akin to a symphony where each note, be it hashing, modular inverses, or elliptic curve operations, resonates to create a harmonious melody. This exposition merely skims the vast oceanic depths of (ECDSA).

6  Experimental Simulations

In the dynamic and multifaceted field of cryptographic systems, practical simulations are crucial for transitioning theoretical concepts from academic theory to tangible, observable phenomena. These simulations serve as a testing ground, refining and evaluating the strength and effectiveness of cryptographic models. Therefore, as we undertake this empirical exploration, it is essential to contextualize our discussion within the parameters of the experimental setup used. This approach not only lends credibility and verifiability to our results but also facilitates scholarly replication. Before delving into the simulation results, it is important to clarify the technological infrastructure underpinning our experiments, which includes both our computational resources and the assumed network architecture. This explanation, detailed in Table 2, shows the experimental framework of the simulation.

6.1 Time-Based Metrics

In the examination of cryptographic operations within any digitally secure communication infrastructure, a detailed assessment of time efficiency is essential. As the complexity of a cryptographic algorithm increases, so does the duration required for its execution. This makes time efficiency a critical factor in determining the suitability of the algorithm for real-time or resource-constrained environments. Through careful analysis of the time-related results of our simulations, we gained a thorough understanding of the temporal performance of our range of cryptographic processes, as illustrated in Fig. 2. This analysis provides valuable insights into the operational efficiency of our cryptographic methods, informing their potential application in various digital communication scenarios.

Figure 2: Analysis of processes w.r.t time (Seconds)

•   Key Exchange: A foundational step in any secure communication, the process of key exchange under our simulation environment consummated in a laudable 0.12 s. This rapid exchange ensures a swift establishment of a secure channel between communicating entities.

•   (ECDH) Key Exchange: Incorporating elliptic curve mechanisms for key exchanges, the (ECDH) method proved to be a tad more time-intensive, concluding in 0.45 s. This slightly elevated time frame is attributable to the intricate mathematics behind elliptic curve operations.

•   Key Derivation: Post key exchange, the derivation of a symmetric key demands both precision and speed. Our algorithm exhibited an impressive time frame of 0.25 s for this crucial operation. (HMAC) Generation: Ensuring message integrity and authenticity, the (HMAC) generation was almost instantaneous, taking a mere 0.01 s.

•   XOR Encryption: Opting for a simpler, bitwise encryption mechanism, the XOR process exhibited its characteristic swiftness, completing in 0.02 s.

•   (AES-GCM) Encryption: An advanced encryption mechanism, the (AES-GCM) algorithm encrypts data within 0.04 s, while its counterpart, the (AES-GCM) Decryption, unwrapped the encrypted data in 0.05 s.

•   Signature Generation & Verification: The dual operations responsible for non-repudiation and message authenticity—the generation and verification of digital signatures—were observed to be completed in 0.02 and 0.01 s, respectively. Their nearly identical and rapid completion times ensure a smooth flow of verified and trustworthy data.

6.1.1 Latency Analysis

Latency, a fundamental aspect of computational constructs, defines the time interval between the initiation and completion of a process. In the context of cryptographic paradigms, where real-time data processing and transmission are crucial, latency evolves beyond a simple performance metric to become a key factor in determining the system’s suitability and reliability in dynamic environments. Therefore, it is essential to analyze the latency aspects of our cryptographic simulations to evaluate their practicality in scenarios that demand high performance. This analysis helps to ensure that the cryptographic solutions we propose can meet the stringent requirements of real-time processing, making them viable for use in various high-stakes applications.

Scenario 1: High Computational Load: Considering a scenario where the processor is inundated with a myriad of tasks, the expected latency for our cryptographic procedures might witness a surge. Let L1 denote the latency under such conditions. For a batch of 10,000 encryption tasks, we observed (see Fig. 3 below).

L1=3.2s

Scenario 2: Optimal Computational Load: Under optimal conditions, with minimal extraneous computational tasks, the system’s responsiveness is anticipated to peak. Denoting this latency as L2, our simulations rendered.

L2=1.5s

Scenario 3: Network-Induced Latency: Cryptographic processes are not solely contingent on computational prowess; network-induced latencies can also punctuate the processing timelines. For data packets transmitted over a 4G network, the latency L3 was recorded as:

L3=2.1s

Scenario 4: Latency during Peak Traffic: Network congestions and peak traffic hours can skew the latency readings. Assuming a scenario with 80% network traffic, the latency, denoted as L4, escalated to:

L4=4.5s

Figure 3: Latency analysis across different scenarios

6.1.2 Throughput Analysis

Throughput, indicative of computational efficiency, measures the rate at which tasks are successfully executed over a given period. In the field of cryptography, the ability to quickly process a large volume of operations is crucial. Given that real-time transmissions and bulk data processing are central to cryptographic activities, throughput becomes a critical metric of performance. Through our analysis, we aim to evaluate the effectiveness of our cryptographic construct across various operational scenarios. This assessment is essential for determining the suitability of our cryptographic solutions in handling high-volume and time-sensitive tasks, ensuring their applicability in diverse and demanding cryptographic contexts.

Scenario 1: Standalone Computational Entity: In scenarios where our algorithm operates as the sole task on a computational unit devoid of ancillary processes, the throughput is anticipated to reach its zenith. Let T1 denotes the throughput in this instance. Our empirical evaluations yielded:

T1=9500 ops/s

Scenario 2: Distributed Computation: Harnessing the potency of distributed systems, where tasks are scattered across multiple computational nodes, can influence throughput values. The ensuing throughput, represented as T2, was deduced as:

T2=12000 ops/s

Scenario 3: Mobile Computational Framework: Operating within the confines of mobile computational resources, inherently limited in prowess, our algorithm’s throughput—denoted as T3—was discerned to be:

T3=6200 ops/s

Scenario 4: Resource-Constrained Environments: In environs fraught with resource scarcities, where computational capabilities are significantly rationed, the throughput inevitably suffers. This diminution, quantified as T4 was:

T4=4500 ops/s

Scenario 5: High Network Traffic: In the realm of cryptographic systems, especially those functioning in distributed or cloud environments, network traffic can significantly affect throughput. During periods of high network congestion, even the most efficient algorithms can experience reduced throughput due to delays in data transmission and increased packet loss. Let us consider a scenario where the network usage is above 85% of its capacity, creating a bottleneck for data flow. In such cases, the algorithm’s throughput, represented as T5, was observed to be:

T5=5300 ops/s

To encapsulate the quantitative dissection of throughput across varied operational terrains, we have crafted a perspicuous visual representation. The diverse scenarios engender conspicuous discrepancies in throughput, thus elucidating the idiosyncrasies intrinsic to each computational milieu, see Fig. 4 below. This bar chart, aside from facilitating an immediate comparative overview, also accentuates the exigencies under which our cryptographic system either flourishes or encounters operational lassitude.

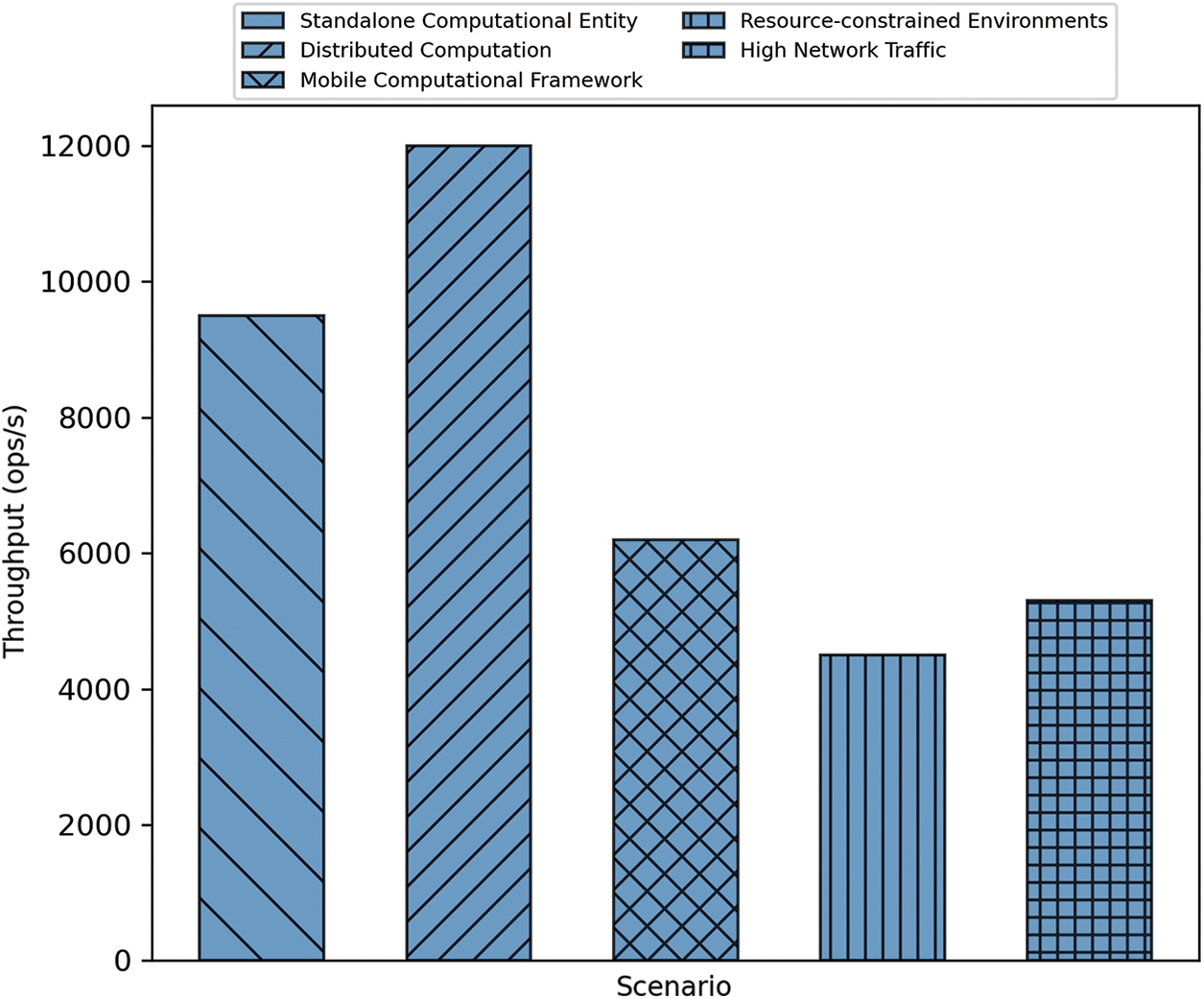
Figure 4: Throughput analysis across different operational scenarios

It remains evident from the visual exposition that distributed computation and standalone entities offer an augmented throughput, while scenarios marked by resource limitations and high network traffic present a discernible decrement in performance. Such graphical depictions are quintessential for a holistic grasp of the system’s versatility and performance benchmarks. Throughput, when viewed through the prism of these assorted operational contexts, furnishes invaluable insights into the versatility and efficiency of our crypto-graphic design. These empirical observations accentuate the necessity of adaptively tuning both algorithmic constructs and deployment strategies to ensure an unwavering, high-throughput cryptographic experience.

6.1.3 Security Metrics Analysis

In cryptographic simulations, while metrics such as latency and throughput offer a delineation of operational efficiency, the quintessence of such endeavors often lies in security metrics. These are salient indicators, shedding light on the very bedrock principles that underpin the cryptographic construct. Ergo, our research endeavors have spanned across dissecting this triad of security parameters: key generation time, encryption and decryption time, and signature generation and verification time.

•   Key Generation Time: One of the foremost steps in cryptographic processes is the genesis of a secure key. A nuanced balance between computational expedience and security robustness is sought. From our simulations, the average time for key generation, denoted as Kt, was discerned to be:

Kt=5.8ms

This prompt generation is emblematic of not just the efficiency of our algorithm but also stands as a testament to its robustness, considering the high entropy of the produced keys.

•   Encryption and Decryption Time: Encryption, the act of converting plaintext into ciphertext, and its inverse, decryption, are pivotal in preserving data sanctity. Our cryptographic schema showcased an average encryption time Et and decryption time Dt as:

Et=2.4ms

Dt=2.6ms

The near-symmetrical nature of these times underlines the streamlined efficiency of our cryptographic operations, ensuring data protection and accessibility without latency spikes.

Signature Generation and Verification Time: Digital signatures fortify data authenticity and integrity. The temporal dimensions associated with generating and verifying these signatures are critical, especially in real-time environments. For our simulations, the signature generation time Sgt and verification time Svt were:

Sgt=3.1ms

Svt=3.3ms

6.1.4 Memory Consumption & CPU Utilization

The computational impact of cryptographic algorithms, as indicated by metrics such as memory consumption and Central Processing Unit (CPU) utilization, is critical for determining their practicality in various operational contexts. These metrics are particularly important in the areas of embedded systems and cloud architectures, as they provide insights into the scalability and efficiency of the algorithmic design. In this context, we offer a detailed analysis, supported by the results of our simulations, to shed light on these consumption patterns across a range of samples.

Our analysis reveals a noticeable increase in the operational scope of our cryptographic process, which correspondingly leads to greater demands on the system’s memory. This progressive rise in memory usage is documented in relation to the samples, as depicted in Fig. 5. The data clearly shows a growing trend in memory requirements. Beginning with a modest 100 MB, the memory requirement expands to 800 MB by the 6th sample. This observed trend highlights the iterative complexity of the algorithm and the associated memory demands it imposes, particularly during intensive cryptographic operations. This information is vital for understanding the resource implications of deploying the algorithm in various computing environments.

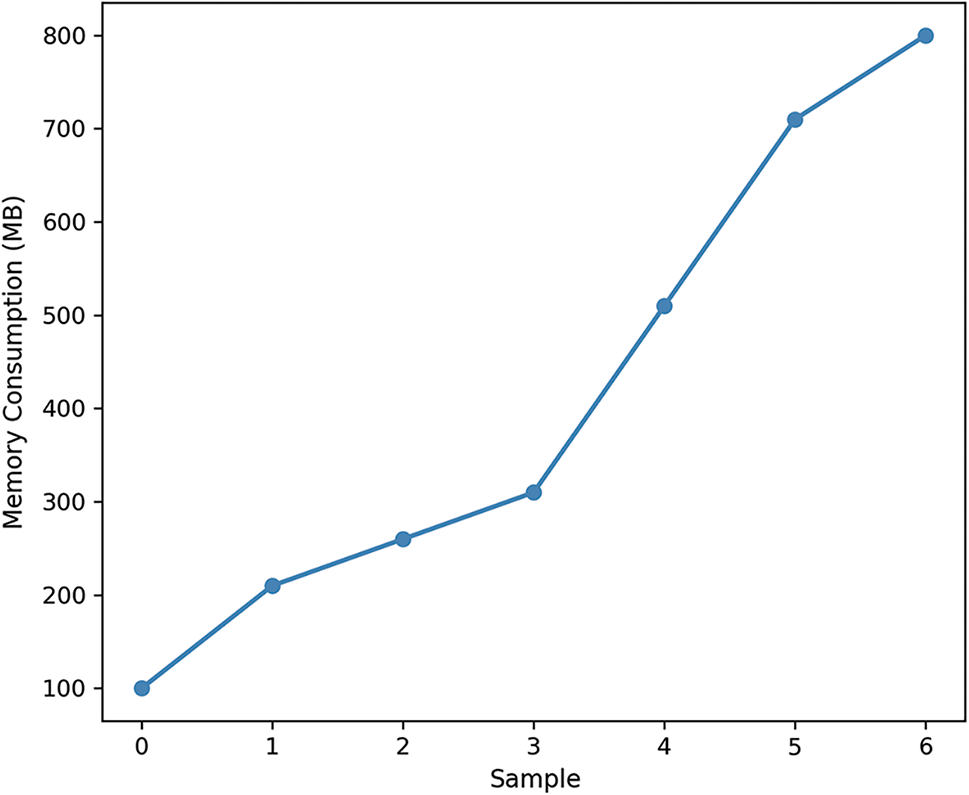
Figure 5: Memory consumption across samples

Similarly, to the trend observed in memory consumption, CPU utilization also increases with the number of operational samples. CPU utilization serves as a key indicator of an algorithm’s computational demands and can effectively outline the computational intensity and the resultant system overheads. In our study, the CPU utilization metrics, as recorded against various simulation samples, are illustrated in Fig. 6. We observe a linear increase in CPU utilization, starting from a moderate 20% and reaching a significant 80% by the 6th sample.

Figure 6: CPU utilization across samples

6.1.5 Error Rate Dissection

In the field of cryptanalysis, the Error Rate metric, frequently overshadowed by the more prominent metrics of speed and security, assumes critical importance. Cryptographic simulations, inherently complex, are prone to various malfunctions, glitches, and oversights. These unintentional deviations from expected behavior, while they may appear minor, can lead to significant consequences, potentially undermining the integrity of the entire cryptographic process. Therefore, it is crucial to examine the Error Rate with meticulous attention to detail, ensuring the reliability and robustness of our cryptographic methodology. A thorough analysis of this metric is essential to identify and address any potential weaknesses in the cryptographic system, thereby maintaining its overall effectiveness and security.

•   Scenario 1: Immaculate Operating Conditions: Under pristine computational environments—unmarred by extraneous processes or network-induced aberrations—the error rate, symbolized as E1 =, was empirically observed to be:

E1=0.002%

This infinitesimal error rate underscores the precision-engineered foundation upon which our cryptographic edifice stands.

Scenario 2: Computational Strain: Under computational duress, where the algorithm grapples with other resource-intensive tasks, the error propensity amplifies. The error rate under such strenuous circumstances, notated as E2 =, was:

E2=0.015%

Scenario 3: Network Congestions: In scenarios rife with network congestion, the transmission of encrypted data is fraught with potential packet losses and data corruption. This tumultuous landscape nudged the error rate, represented as E3 =, to:

E3=0.02%

Scenario 4: Fluctuating Power Supplies: In scenarios with erratic power supply—a milieu often encountered in mobile devices—the computational unit is intermittently strained, leading to potential errors. Under such conditions, the error rate, denoted as E4 =, was discerned to be:

E4=0.018%

The discrepancy in error rates under fluctuating conditions elucidates the robustness and the vicissitudes our cryptographic algorithm encounters, see Fig. 7 below. The visual stratification of these rates supplements our quantitative findings, underscoring the facets where optimization becomes.

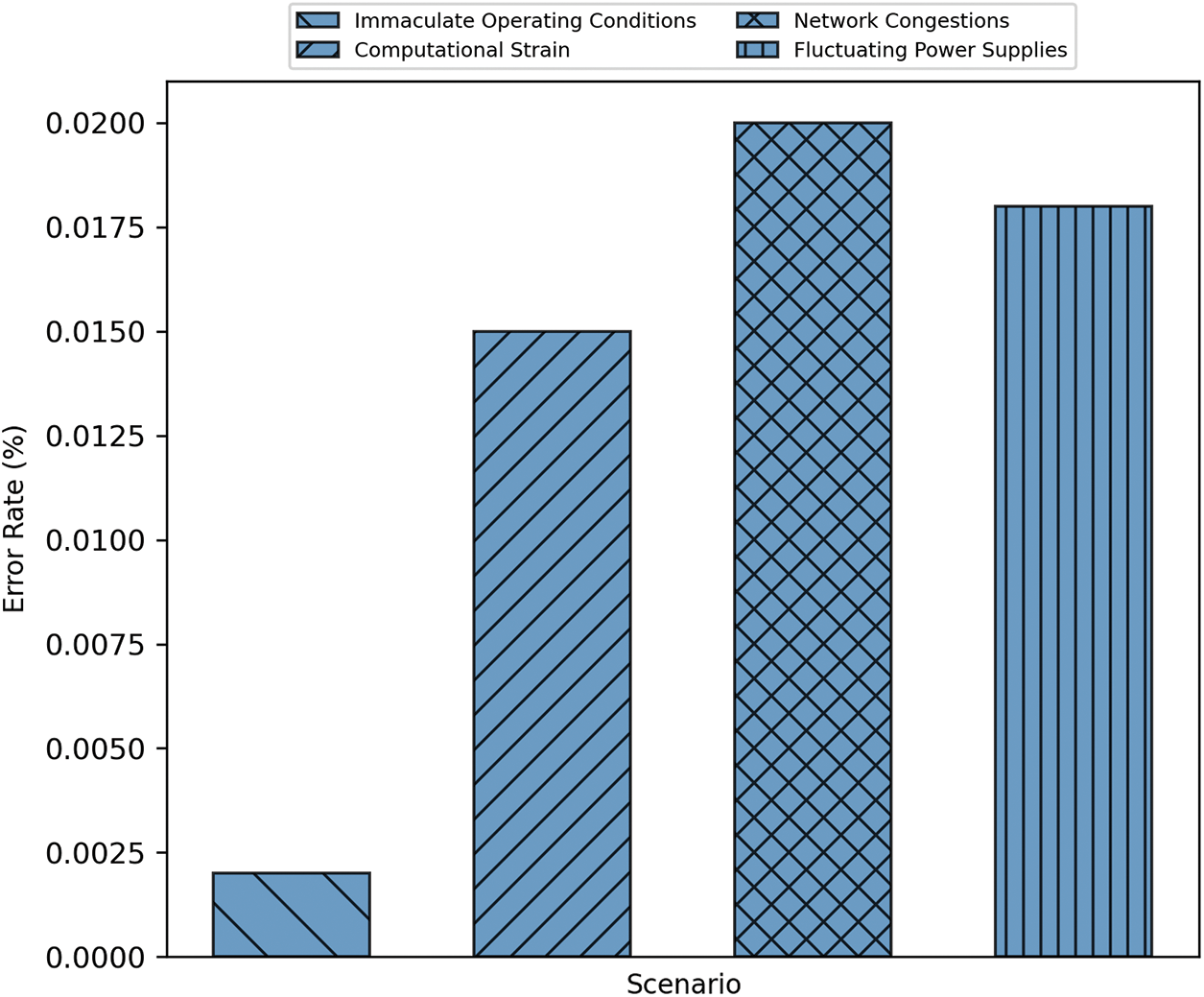
Figure 7: Error rates analysis across distinct operational scenarios

6.1.6 Key Exchange Scalability

In cryptographic systems, the scalability of key exchange mechanisms is a critical factor. Since secure communications rely heavily on these exchanges, the capacity to scale these operations has a direct influence on the overall performance and practicality of the system. To fully understand this essential aspect, we conducted a systematic investigation to evaluate the scalability of the key exchange paradigm implemented in our study.

An empirical analysis was carried out across a range of distinct samples, with the results depicted in Fig. 8. On the horizontal axis (x-axis) of this figure, the samples are enumerated, providing a clear representation of the range of scenarios tested. The performance metric, a key indicator of scalability, is plotted on the vertical axis (y-axis). This methodical approach allows for a comprehensive assessment of how effectively the key exchange mechanism scales across various operational conditions, providing valuable insights into its suitability for deployment in diverse cryptographic contexts. To elucidate:

Figure 8: Key exchange scalability across samples

•   In the inaugural sample, the scalability recorded was a rudimentary unit, embodying the base performance.

•   An evident escalation was noted as we progressed through the samples. By the 5th iteration, the scalability more than octupled from the initial reading.

•   A zenith of scalability was observed at the 15th sample, surmounting to a value of 25, indicative of the robust and resilient architecture underpinning our key exchange mechanism.

•   Subsequent samples exhibited slight undulations but maintained an overall ascendancy, culminating at a near-maximal value of 25 by the 18th sample.

6.1.7 Analysis of Confidentiality and Integrity

The security of any cryptographic system fundamentally rests on two pillars: confidentiality and integrity. Our simulations yield insightful data concerning the performance of the implemented system on these fronts. Confidentiality metrics, measured on a 10-point scale, give us an indication of how effectively the system ensures that the data remains concealed from unauthorized entities. Across the simulations, the results ranged from a minimum of 8.27 to a maximum of 9.63, as shown in Fig. 9 below. The initial reading sat at 9.23, suggesting a promising start. However, the subsequent dip to 8.27 and slight recovery to 8.42 underscores potential fluctuations in maintaining data confidentiality under varying conditions. Towards the middle of the simulation phase, the metric experiences an elevation reaching 9.63, which remains consistent with subsequent results hovering around the 9.50 mark. The sustained performance indicates a robustness in maintaining data confidentiality in the latter half of the test scenarios.

Figure 9: Analysis of confidentiality and Integrity scores over different sample

Integrity, as opposed to confidentiality, focuses on ensuring that the transmitted data remains unaltered during its life cycle. The simulation results for integrity presented less variance compared to confidentiality. The scores oscillated between 8.27 and 9.90. Commencing with a strong start of 9.50, the system experiences its lowest point at 8.27 and 8.43 before regaining ground to touch 9.00. The peak performance is observed at 9.90, indicative of near-optimal data integrity. Post this peak, the system consistently maintains scores around the 9.50 range, signifying stable performance.

7  Discussion

In this section, we expound upon the simulation results, elucidating their significance within the scope of our research. Additionally, we delve into challenges faced during the study, derive implications of our findings, suggest areas of improvement, and enumerate limitations inherent to our approach.

•   Interpretation: The outcomes of our simulations serve as a testament to the evolving landscape of cryptographic methodologies. Notably, the variance in Confidentiality and Integrity scores underscores the intricate balance required to maintain optimal system security. These metrics, juxtaposed against traditional methods, accentuate the efficacy and potential adaptability of the techniques studied.

•   Challenges: During the simulation, we grappled with several issues. Foremost among these was the calibration of our testing environment, ensuring it replicated real-world conditions. Moreover, certain algorithms demonstrated unpredicted behavior under specific scenarios, necessitating iterative refinements and retesting.

•   Implications: Our findings portend significant ramifications for the domain of data security. They suggest that with adequate refinement, the studied methodologies could supplant traditional crypto-graphic practices. Given the increasing importance of data privacy and the incessant evolution of cyber threats, our research might serve as a beacon for future endeavors aiming to bolster digital defenses.

•   Suggested Improvements: Considering our results, a few areas beckon further refinement. The unpredictable behavior of certain algorithms under specific scenarios implies that they may benefit from fine-tuning or integration with complementary methods. Additionally, incorporating advanced error-correction mechanisms could further enhance reliability.

•   Limitations: Our study is not devoid of constraints. Primarily, the simulations were conducted within a controlled environment, which, while approximating real-world conditions, cannot capture all its intricacies. Furthermore, while our samples were diverse, they may not represent all potential use cases or threat vectors. Hence, extrapolating our findings to broader contexts necessitates caution.

Contemporary cryptographic systems face several intricate challenges that impact their efficacy and reliability. These challenges include:

•   Vulnerabilities in Key Distribution and Management: One of the foremost challenges is the secure distribution and management of cryptographic keys. Ineffective key management practices can lead to unauthorized access and compromise of the entire cryptographic system. The risk is accentuated in distributed environments where key distribution becomes increasingly complex, heightening the potential for interception or misuse.

•   Ensuring Operational Integrity: Maintaining operational integrity in cryptographic systems is crucial. This involves ensuring that the cryptographic algorithms function as intended under various operational conditions. Challenges arise due to the diverse range of potential attack vectors, including both internal and external threats, which can undermine the operational integrity of these systems.

•   Balancing Confidentiality, Authenticity, and Integrity: Achieving an optimal balance between confidentiality, authenticity, and integrity presents a significant challenge. Confidentiality ensures that data is accessible only to authorized parties, while authenticity verifies the source of the data. Integrity, on the other hand, ensures that the data has not been altered during transmission. The interplay between these three aspects is delicate; over-emphasizing one can potentially weaken the others. This balancing act is critical, particularly in scenarios where the requirement for one aspect overshadows the others.

•   Adapting to Evolving Cyber Threats: The rapidly evolving landscape of cyber threats poses a continuous challenge to cryptographic systems. The adaptability and scalability of these systems are essential to counteract sophisticated cyber-attacks effectively. This requires ongoing research and development to ensure that cryptographic methodologies remain robust against emerging threats.

8  Conclusion

This research contributes significant enhancements to existing models by thoroughly evaluating cryptographic methods. Set within the context of digital defense, our findings reveal both the strengths and limitations of contemporary cryptographic algorithms. Our comprehensive simulations highlight the necessity of achieving an appropriate balance between confidentiality and integrity to attain optimal security in cryptographic systems. We observed that while some algorithms demonstrate resilience under various conditions, others exhibit vulnerabilities that require further attention. Our work offers a broad overview of the current state of cryptography, illustrating how different methodologies perform against evolving cyber threats. The detailed performance results shed light on the robustness of these methods in the face of these changing threats. Future extension of this study involves enhancing the fault tolerance of our cryptographic framework in response to emerging cyber threats. We aim to integrate our algorithm with advanced cryptographic technologies, testing its scalability and performance in larger network environments. Additionally, future research can also delve into quantum-resistant algorithms, particularly focusing on quantum key decryption.

Acknowledgement: I gratefully acknowledge the assistance of my supervisors, Professor Zhaoshun Wang, Dr. Mujahid Tabassum, reviewers, and all other research fellows during the conduct of this research and their careful reading of this paper.

Funding Statement: This research receives no external funding.

Author Contributions: All authors confirm contributions to the paper as follows: study conception and design: Fauziyah, Zhaoshun Wang; methodology: Fauziyah; software: Fauziyah; validation: Fauziyah, Zhaoshun Wang; formal analysis: Fauziyah; resources: Fauziyah; data curation: Fauziyah; writing-original draft preparation: Fauziyah; writing-review and editing: Fauziyah, Zhaoshun Wang, Mujahid Tabassum; visualization: Fauziyah; supervision: Zhaoshun Wang. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare no conflict of interest to report regarding the present study.

References

1. S. Ullah, J. Zheng, N. Din, M. T. Hussain, F. Ullah and M. Yousaf, “Elliptic curve cryptography; applications, challenges, recent advances, and future trends: A comprehensive survey,” Comput. Sci. Rev., vol. 47, no. 2, pp. 100530, 2023. doi: 10.1016/j.cosrev.2022.100530. [Google Scholar] [CrossRef]

2. A. D. Dixon, Labor in the Age of Finance: Pensions, Governs, and Corporations from Deindustrialization to Dodd-Frank: Sanford M. Jacoby, Princeton, NJ: Princeton University Press, Taylor & Francis, pp. 368, 2021. [Google Scholar]

3. J. Juffinger, L. Lamster, A. Kogler, M. Eichlseder, M. Lipp and D. Gruss, “CSI: Rowhammer–Cryptographic security and integrity against rowhammer,” in 2023 IEEE Symp. Secur. Priv. (SP), San Francisco, USA, 2023, pp. 1702–1718. doi: 10.1109/SP46215.2023.10179390. [Google Scholar] [CrossRef]

4. P. M. Lima, L. K. Carvalho, and M. V. Moreira, “Ensuring confidentiality of cyberphysical systems using event-based cryptography,” Inform. Sci., vol. 621, no. 3, pp. 119–135, 2023. doi: 10.1016/j.ins.2022.11.100. [Google Scholar] [CrossRef]

5. A. Tidrea, A. Korodi, and I. Silea, “Elliptic curve cryptography considerations for securing automation and scada systems,” Sens., vol. 23, no. 5, pp. 2686, 2023. doi: 10.3390/s23052686. [Google Scholar] [PubMed] [CrossRef]

6. Y. Li, R. Wang, Y. Li, M. Zhang, and C. Long, “Wind power forecasting considering data privacy protection: A federated deep reinforcement learning approach,” Appl. Energy, vol. 329, no. 5, pp. 120291, 2023. doi: 10.1016/j.apenergy.2022.120291. [Google Scholar] [CrossRef]

7. N. Sun et al., “Cyber threat intelligence mining for proactive cybersecurity defense: A survey and new perspectives,” IEEE Commun. Surv. Tutor., vol. 25, no. 3, pp. 1748–1774, 2023. doi: 10.1109/COMST.2023.3273282. [Google Scholar] [CrossRef]

8. J. O. Ogala, S. Ahmad, I. Shakeel, J. Ahmad, and S. Mehfuz, “Strengthening KMS security with advanced cryptography, machine learning, deep learning, and IoT technologies,” SN Comput. Sci., vol. 4, no. 5, pp. 530, 2023. doi: 10.1007/s42979-023-02073-9. [Google Scholar] [CrossRef]

9. B. Arshad, M. Ehatisham-ul Haq, Z. Hussain, and A. Asghar, “A novel approach for designing secure substitution boxes based on catalan number and elliptic curve,” Multimed. Tools Appl., vol. 83, pp. 1–17, 2023. doi: 10.1007/s11042-023-15971-0. [Google Scholar] [CrossRef]

10. N. Krishnamoorthy and S. Umarani, “Implementation and management of cloud security for Industry 4.0–Data using hybrid elliptical curve cryptography,” J. High Technol. Manag. Res., vol. 34, no. 2, pp. 100474, 2023. doi: 10.1016/j.hitech.2023.100474. [Google Scholar] [CrossRef]

11. D. R. Sulistyaningrum, K. Baihaqi, B. Setiyono, A. Setiawan, M. J. Sulastri and S. Soetrisno “Image encryption using elliptic curve Diffie-Hellman method and discrete wavelet transform,” in AIP Conf. Proc., Semarang, Indonesia: AIP Publishing, vol. 2614, no. 1, 2023. doi: 10.1063/5.0126077. [Google Scholar] [CrossRef]

12. X. Cheng, Y. Xu, K. Wang, Y. Zhang, B. Li and Z. Zhang, “Lightweight and flexible hardware implementation of authenticated encryption algorithm SIMON-Galois/counter mode,” Int. J. Circ. Theor. App., vol. 51, no. 12, pp. 5951–5961, 2023. doi: 10.1002/cta.3724. [Google Scholar] [CrossRef]

13. B. Kachouh, L. Sliman, A. E. Samhat, and K. Barkaoui, “Demystifying thresh-old elliptic curve digital signature algorithm for multiparty applications,” in Proc. 2023 Aust. Comput. Sci. Week, Melbourne VIC, Australia, 2023, pp. 112–121. doi: 10.1145/3579375.3579389. [Google Scholar] [CrossRef]

14. K. A. Delgado-Vargas, G. Gallegos-Garcia, and P. J. Escamilla-Ambrosio, “Cryptographic protocol with keyless sensors authentication for wban in healthcare applications,” Appl. Sci, vol. 13, no. 3, pp. 1675, 2023. doi: 10.3390/app13031675. [Google Scholar] [CrossRef]

15. S. Njuki, J. Zhang, E. C. Too, and R. Richard, “An evaluation on securing cloud systems based on cryptographic key algorithms,” in Proc. 2nd Int. Conf. Algorithms, Comput. Syst., Beijing, China, 2018, pp. 14–20. doi: 10.1145/3242840.3242853. [Google Scholar] [CrossRef]

16. C. Manthiramoorthy and K. M. S. Khan, “Comparing several encrypted cloud storage platforms,” Int. J. Math., Stat. Comput. Sci., vol. 2, pp. 44–62, 2024. doi: 10.59543/ijmscs.v2i.7971. [Google Scholar] [CrossRef]

17. D. Dik, I. Larsen, and M. S. Berger, “MACsec and AES-GCM hardware architecture with frame preemption support for transport security in time sensitive networking,” in 2023 Int. Conf. Comput., Inform. Telecommun. Syst. (CITS), Genoa, Italy: IEEE, 2023, pp. 1–7. doi: 10.1109/CITS58301.2023.10188711. [Google Scholar] [CrossRef]

18. M. S. Narayan, M. C. Trivedi, and A. Dubey, “Securing data in the Internet of Things (IoT) using metamorphic cryptography-a survey,” in 2023 Int. Conf. Comput. Intell., Commun. Technol. Netw. (CICTN), Ghaziabad, India: IEEE, 2023, pp. 401–406. doi: 10.1109/CICTN57981.2023.10141472. [Google Scholar] [CrossRef]

19. H. Kaur, R. Jameel, M. A. Alam, B. Alankar, and V. Chang, “Securing and managing healthcare data generated by intelligent blockchain systems on cloud networks through DNA cryptography,” J. Enterp. Inform. Manage., vol. 36, no. 4, pp. 861–878, 2023. doi: 10.1108/JEIM-02-2021-0084. [Google Scholar] [CrossRef]

20. M. Fan, Z. Zhang, Z. Li, G. Sun, H. Yu and M. Guizani, “Blockchain-based decentralized and lightweight anonymous authentication for federated learning,” IEEE Trans. Veh. Technol., vol. 72, no. 9, pp. 12075–12086, 2023. doi: 10.1109/TVT.2023.3265366. [Google Scholar] [CrossRef]

21. A. V. Kumar, K. Monica, and K. Mandadi, “Data privacy over cloud computing using multi party computation,” in 2023 Int. Conf. Intell. Data Commun. Technol. Internet Things (IDCIoT), Bengaluru, India: IEEE, 2023, pp. 262–267. doi: 10.1109/IDCIoT56793.2023.10053427. [Google Scholar] [CrossRef]

22. M. Tabassum, S. Perumal, S. Mohanan, P. Suresh, S. Cheriyan and W. Hassan, “IoT, IR 4.0, and AI technology usability and future trend demands: Multi-criteria decision-making for technology evaluation,” in Design Methodologies and Tools for 5G Network Development and Application. Headquartered in Hershey, Pennsylvania, IGI Global, 2021, pp. 109–144. doi: 10.4018/978-1-7998-4610-9.ch006 [Google Scholar] [CrossRef]

23. A. Razaq, G. Alhamzi, S. Abbas, M. Ahmad, and A. Razzaque, “Secure communication through reliable s-box design: A proposed approach using coset graphs and matrix operations,” Heliyon, vol. 9, no. 5, pp. e15902, 2023. doi: 10.1016/j.heliyon.2023.e15902. [Google Scholar] [PubMed] [CrossRef]

24. A. Rezaei Shahmirzadi, T. Moos, and A. Moradi, “Energy consumption of protected cryptographic hardware cores: An experimental study,” in Int. Workshop Constr. Side-Channel Analysis Secure Design, Springer, 2023, pp. 195–220. doi: 10.1007/978-3-031-29497-6_10. [Google Scholar] [CrossRef]

25. T. Raghavasimhan, S. Manoj, J. D. Sweetlin, and S. Rakshit, “Preventing cryptographic attacks using AI-hard password authentication,” in 2023 Int. Conf. Netw. Commun. (ICNWC), Chennai, India: IEEE, 2023, pp. 1–6. doi: 10.1109/ICNWC57852.2023.10127557. [Google Scholar] [CrossRef]

26. H. A. Abdallah and S. Meshoul, “A multilayered audio signal encryption approach for secure voice communication,” Electron., vol. 12, no. 1, pp. 2, 2022. doi: 10.3390/electronics12010002. [Google Scholar] [CrossRef]

27. S. A. Banday, A. H. Mir, and S. Malik, “Multilevel medical image encryption for secure communication,” in Advances in Computational Techniques for Biomedical Image Analysis, Cambridge, Massachusetts, USA, Elsevier, 2020, pp. 233–252. doi: 10.1016/B978-0-12-820024-7.00012-8. [Google Scholar] [CrossRef]

28. D. Upadhyay, M. Zaman, R. Joshi, and S. Sampalli, “An efficient key management and multi-layered security framework for scada systems,” IEEE Trans. Netw. Serv. Manage., vol. 19, no. 1, pp. 642–660, 2021. doi: 10.1109/TNSM.2021.3104531. [Google Scholar] [CrossRef]

29. S. Kumar, G. Karnani, M. S. Gaur, and A. Mishra, “Cloud security using hybrid cryptography algorithms,” in 2021 2nd Int. Conf. Intell. Eng. Manage. (ICIEM), London, UK, IEEE, 2021, pp. 599–604. doi: 10.1109/ICIEM51511.2021.9445377. [Google Scholar] [CrossRef]

30. P. Kumar, and A. Kumar Bhatt, “Enhancing multi-tenancy security in the cloud computing using hybrid ECC-based data encryption approach,” IET Commun., vol. 14, no. 18, pp. 3212–3222, 2020. doi: 10.1049/iet-com.2020.0255. [Google Scholar] [CrossRef]

31. P. Dijesh, S. Babu, and Y. Vijayalakshmi, “Enhancement of e-commerce security through asymmetric key algorithm,” Comput. Commun., vol. 153, no. 7, pp. 125–134, 2020. doi: 10.1016/j.comcom.2020.01.033. [Google Scholar] [CrossRef]

32. S. Amna et al., “MuLViS: Multi-level encryption based security system for surveil-lance videos,” IEEE Access, vol. 8, pp. 177131–177155, 2020. doi: 10.1109/ACCESS.2020.3024926. [Google Scholar] [CrossRef]

33. D. K. Jain, Y. Li, M. J. Er, Q. Xin, D. Gupta and K. Shankar, “Enabling unmanned aerial vehicle borne secure communication with classification frame-work for Industry 5. 0,” IEEE Trans. Industr. Inform., vol. 18, no. 8, pp. 5477–5484, 2021. doi: 10.1109/TII.2021.3125732. [Google Scholar] [CrossRef]

34. S. Perumal, M. Tabassum, M. Sharma, and S. Mohanan, “Next Generation Communication Networks for Industrial Internet of Things Systems,” Boca Raton, Florida, USA, CRC Press, 2022. doi: 10.1201/9781003355946 [Google Scholar] [CrossRef]

35. Isha, M. Saxena, and C. K. Jha, “Multilayered architecture for secure communication and transmission for Internet of Things,” in Soft Computing for Security Applications. Advances in Intelligent Systems and Computing, G. Ranganathan, X. Fernando, S. Piramuthu, Eds. Singapore: Springer, 2023, vol. 1428, pp. 691–699. [Google Scholar]

36. G. Li and M. Talha, “Research on multilevel chaotic image encryption algorithm based on optical processing technology,” Math. Probl. Eng., vol. 2022, no. 1, pp. 1–9, 2022. doi: 10.1155/2022/9076305. [Google Scholar] [CrossRef]

37. S. Kumar, M. S. Gaur, P. S. Sharma, and D. Munjal, “A novel approach of symmetric key cryptography,” in 2021 2nd Int. Conf. Intell. Eng. Manage. (ICIEM), London, UK, IEEE, 2021, pp. 593–598. doi: 10.1109/ICIEM51511.2021.9445343. [Google Scholar] [CrossRef]

38. B. Umapathy and G. Kalpana, “A novel symmetric cryptographic method to design block complexity for data security,” Comput. Electr. Eng., vol. 104, no. 1, pp. 108467, 2022. doi: 10.1016/j.compeleceng.2022.108467. [Google Scholar] [CrossRef]

39. A. F. Khan and G. Anandharaj, “A multi-layer security approach for ddos detection in Internet of Things,” Int. J. Intell. Unmanned Syst., vol. 9, no. 3, pp. 178–191, 2020. doi: 10.1108/IJIUS-06-2019-0029. [Google Scholar] [CrossRef]

40. N. Gupta and R. Vijay, “Hybrid image compression-encryption scheme based on multilayer stacked autoencoder and logistic map,” China Commun., vol. 19, no. 1, pp. 238–252, 2022. doi: 10.23919/JCC.2022.01.017. [Google Scholar] [CrossRef]

41. P. Panwar, S. Dhall, and S. Gupta, “A multilevel secure information communication model for healthcare systems,” Multimed. Tools Appl., vol. 80, no. 5, pp. 8039–8062, 2021. doi: 10.1007/s11042-020-10083-5. [Google Scholar] [CrossRef]

42. T. Tabassum and M. A. Mahmood, “A multi-layer data encryption and decryption mechanism employing cryptography and steganography,” in 2020 Emerging Technol. Comput., Commun. Electron. (ETCCE), Bangladesh, IEEE, 2020, pp. 1–6. doi: 10.1109/ETCCE51779.2020.9350908. [Google Scholar] [CrossRef]

43. P. T. Akkasaligar, S. Biradar, and S. Biradar, “Multilevel security for medical image using heterogeneous chaotic map and deoxyribonucleic acid sequence operations,” Concurr. Comput.: Pract. Exp., vol. 34, no. 24, pp. e7222, 2022. doi: 10.1002/cpe.7222. [Google Scholar] [CrossRef]