Prediction of Bandwidth of Metamaterial Antenna Using Pearson Kernel-Based Techniques

1  Introduction

Numerous studies in several disciplines have focused on metamaterials. Metamaterial antennas are another example of how metamaterials are used to enhance their performance. The loss of radiation and factor of quality of an electromagnetic antenna is influenced by its size. Compact antennas with increased gain and bandwidth can be produced using the metamaterial. Their electrical dimension should be as small as possible, and their directivity should be improved. The bandwidth constraints of small antennas can be overcome via metamaterial antennas. The influence of metamaterial on the antenna’s parameters, such as its bandwidth and gain, is estimated using simulation software. With a supplement to simulation software, Machine Learning (ML) techniques might be employed to predict antenna properties. Using the best ML models, the models in [1,2] attempt to forecast the bandwidth and gain of the metamaterial antenna. Since metamaterial antenna has peculiar features, it is being widely researched in the literature. These characteristics improve the capabilities of the source element and its industrial participation [3]. Computational electromagnetics is a branch of science and engineering that gives rise to metamaterial antennas. The foundation of computational electromagnetics is computation and technique optimization for antenna design. The purpose of this integration is to improve the metaheuristics that aid their search process, which eventually enhances the resilience, convergence rate, and solution quality. Additionally, there are several methods created to address the various optimization difficulties [4]. The capacity to establish an underlying link between the system input parameters and the envisioned results is the most significant advantage of ML-aided electromagnetics and as a result, the amount of computation required in experimental [5]. To address its significant complexity and computational cost, the use of ML in metamaterial antenna construction is a viable strategy [6]. A collaborative design for antenna selection was presented in [7]. Two deep learning models were also suggested, which will forecast the chosen antennas and predict hybrid beamformers. K-Nearest Neighbor (KNN) and Support Vector Machine (SVM) were used in a multiclass categorization of the Multiple-Input, Multiple-Output (MIMO) system-based antenna selection [8].

In [6], Artificial Neural Network (ANN) was used to identify the antennas having the lowest Signal-to-Noise Ratio (SNR) between users. For predicting a secure-based antenna on the wiretap medium, the authors of [9] combined naive Bayes and SVM into a hybrid machine learning algorithm. SVM was used in multiuser communication networks with multiple antennas. The SVM-based antenna scheduling system was proposed by the authors. The authors created a support vector regression model in [10] that was trained using information gathered to create the feed for a rectangular patch antenna, employing a microwave simulator. The foundation of ensemble ML is the combination of many ML techniques such as KNN, SVM, and ANN [11]. Using the average of the output readings to estimate an output is the fundamental idea behind ensemble learning which is used in certain approaches. Even though several approaches exist in the literature, there is a need for better normalization techniques, dimension reduction techniques, and optimization techniques for choosing the parameters of the neural networks used in the classification. This research will result in the following goals:

•   Founding a novel approach based on applying Pearson Kernel as the universal kernel for finding the bandwidth of the metamaterial antenna.

•   Founding a novel hypersphere-based normalization to normalize the values of the dataset attributes.

•   Developing a novel dimensionality reduction technique based on Pearson kernel for reducing the dimensions of the attributes.

•   Developing a Pearson-kernel-based bat optimization algorithm for the optimization of the parameters of Convolutional Neural Network (CNN).

•   Evaluating how well the suggested model predicts the metamaterial antenna’s bandwidth in comparison to the most recent ML models.

Small antenna bandwidth restrictions can be overcome with metamaterial antennas. Recently, ML algorithms have been used in the literature to predict antenna parameters. To determine the optimal simulated antenna parameters, manual experimentation can be replaced by machine learning. The model that is employed will have the biggest impact on the accuracy of the predictions. This paper presents a novel approach based on the Pearson kernel as a standard kernel for forecasting the bandwidth of the metamaterial antenna. This paper proposes a novel hypersphere-based normalization technique to normalize the values of the dataset attributes along with a dimensionality reduction method based on the Pearson kernel. This work also presents an algorithm for CNN parameter optimization based on improved Bat Algorithm-based Optimization with Pearson Mutation (BAO-PM). The remainder of the paper is divided into the following sections. The associated work is defined in Section 2. The proposed work is defined in Section 3. The results are reported in Section 4, and the conclusion is covered in Section 5.

2  Related Work

It was suggested in [12] to optimize the Frequency Selective Surface (FSS)-based filtering antenna with a lesser computational complexity. Signals at a certain frequency are enhanced and filtered by the Filtenna. The complex relationships and large number of factors that impact scattering reactions make it difficult to construct Filtenna FSS components. The authors develop a precise representation of unit cell activity using customized multilayered perceptron (M2LP), a deep learning technique that results in enhanced optimization. To speed up antenna tuning, Pietrenko-Dabrowska et al. [13,14] proposed a technique that restricts antenna response intensity upgrades. The predicted antenna properties change when traveling across the one-dimensional linear sub-space represented by these axes. Local optimization is used to reduce the computational expenses for full-wave Expectation-Maximization (EM) computations employed in the optimization of antenna. The outcomes demonstrate a 70% acceleration over benchmark methods without compromising quality. Many antenna layouts and faster variants of trusted sector procedures are used to test the strategy.

Reflectarray (RA) problems with design have been discussed in [15]. RAs have benefits over conventional antenna arrays but have limited losses and bandwidth. For precise transistor dispersion and noise factor simulation using ANN, a Fully Adaptable Regression Method (FARM) was put into practice [16]. To correlate inputs and network design, a tree Parzen predictor recognizes all elements of the network and handles tasks of processing in the FARM approach. When the original design is close to the optimum, gradient-based EM-driven circuit closure procedures perform effectively. A subpar local optimum may be reached by the method of search if the original layout is not ideal. The computational expense of simulation-based refinement is high. A novel approach to parameter tweaking via variable-resolution EM systems was suggested by some studies [17]. Table 1 gives a short survey of the existing optimization techniques.

The dimensional problem, which affects conventional metamodeling techniques, prevents them from functioning while dealing with nonlinear antenna features over an extensive spectrum of network parameters. This problem can be solved by performance-driven design systems, which creates models based on performance of antenna data instead of geometric parameters [23,24]. The antenna structure in the work by the author in [25] has twelve unit Meta Surface cells. To maximize performance, the antenna structure is simulated using the Computer Simulation Technology Microwave Studio (CST MWS) package, which includes all design methodologies. The High-Frequency Structure Simulator (HFSS) software package is utilized to validate the ideal antenna design through numerical testing. This gain bandwidth product of the system was excellent. Through metasurface (MTS), the antenna bandwidth is enhanced. CNN is used to study the design process parametrically. As a result, the CNN is an effective tool for parameter prediction. The proposed work can also be applied to such antenna structures for improved performance. In the proposed work, a unique method for predicting the metamaterial antenna’s bandwidth is developed using the Pearson Kernel (PK) as the global kernel. To normalize the values of the properties of the dataset, a unique hypersphere-based normalization is also developed. It normalizes and eliminates data overlapping by mapping the characteristics onto the surface of a hypersphere. The Pearson kernel is proposed as a novel kernel that achieves good performance over all the existing kernels in literature. It is used in kernel-based Principal Component Analysis (PCA) as Pearson Kernel-based Supervised PCA (PKSPCA) in the proposed technique. Then a Pearson mutation-based Bat optimization algorithm is also proposed for optimizing the weights of CNN that helps in achieving good accuracy compared to existing techniques. The proposed optimization algorithm uses Pearson mutation which helps in faster convergence. The results signify the improved act of the proposed technique.

3  Proposed Methodology

Low-profile microstrip antennas are used in high-performance aircraft, spacecraft, satellite, and missile applications where aerodynamic profile, size, weight, performance, and ease of installation are constraints. Wireless connections and mobile communication are examples of civilian applications. Particular arrangements of unit cells with unusual electrical characteristics are known as metamaterials. These materials have characteristics not found in the natural world. The magnetic permeability and electrical permissivity are negatives as a result of these dispositions. As a result, there is negative refraction, which alters the expected behavior of electromagnetic radiation. A dataset having results of electromagnetic simulations of metamaterial antennas is used in the proposed work. Fig. 1 displays the general layout of the proposed technique. The method begins by putting together a dataset for the metamaterial antenna and using simulation tools to capture the design parameters, as seen in the image. Before training the recommended deep network, preprocessing is an essential step that must be carried out because the dataset may contain some records of the design parameters with incorrect or null values. After preprocessing is complete, the dataset is divided into the train, validation, and test sets to be used to train the deep network. The CNN can be used to predict the ideal values of antenna parameters once it has been trained; in our case, it is utilized to forecast the bandwidth of the metamaterial antenna. The unique properties of the metamaterial allow antenna designers to create antennas with unique features, in contrast to the conventional material used in antenna design. In addition to applying one or more metamaterial layers to the antenna substrate, specific design parameters can be set to enhance the performance of antennas that use metamaterial. A Split Ring Resonator (SRR) unit cell for a metamaterial antenna is shown in Fig. 2 and is defined by the dataset used in this study. SRR is represented by two rings with a space in between. SRR is significant because it allows the bandwidth of the metamaterial antenna and mutual coupling to be reduced. The y-axis represents the Perfect Magnetic Conductor (PMC) of the metamaterial antenna on the radiation box’s surface.

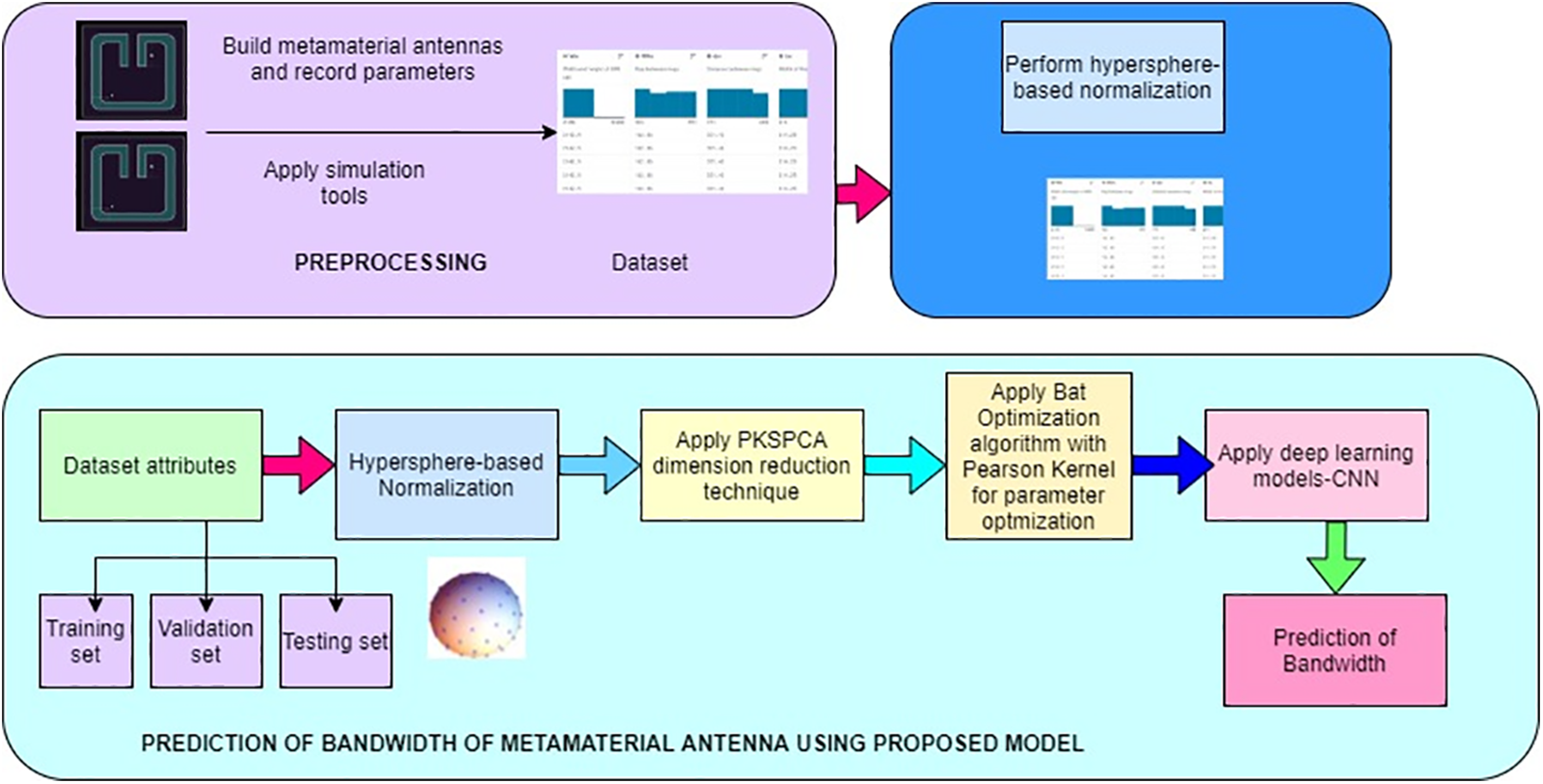
Figure 1: Overall architecture for prediction of bandwidth

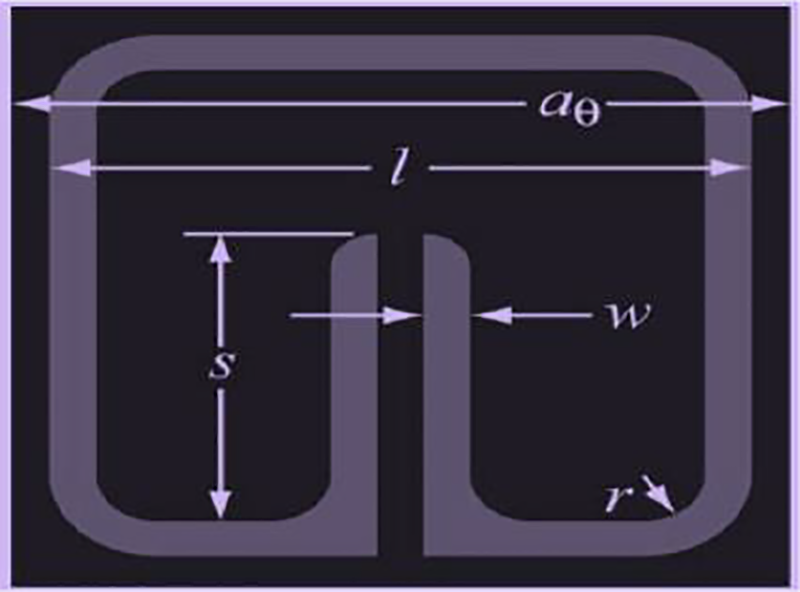
Figure 2: Shape of the split ring resonator. The parameters of the lattice in-plane are aθ = az = 10/3 mm. The ring has a square shape, with a trace width w of 0.2 mm and an edge length l of 3 mm. The substrate is Duroid 5870, which has a thickness of 381 μm and a loss tangent of td = 0.0012 at 10 GHz (Ɛ = 2.33). The thickness of the Cu film used to pattern the SRRs is 17 μm. The length of the split s and the radius of the corners r are the two geometric parameters that are adjusted to adjust the split ring resonator. The imaginary parts of εz and μr, respectively, yielded values of 0.002 and 0.006. The inner cylinder is 1 and the outer cylinder is 10

3.1 Dataset

The dataset used in this study contains 10 attributes that are used to define the design parameters of metamaterial antenna. On Kaggle [26] (Metamaterial Antennas | Kaggle), this dataset is accessible in tabular form with predefined rows and columns. This dataset contains 572 rows (records), 10 columns (parameters), and the following values: antenna gain, voltage standing wave ratio, return loss, gap amid rings, width of rings, distance amid rings, bandwidth, antenna patch, and distance among split-ring resonator cells in the array. Table 2 displays these parameters along with the accompanying symbols. In this study, nine of these factors are used to forecast the bandwidth of a metamaterial antenna. The correlation matrix, which determines the correlation between the attributes of the dataset for study, is displayed in Fig. 3. Fig. 3 clearly shows the substantial correlation between bandwidth and both Ya and Xa. Less strongly correlated are the bandwidth, Wm, and Tm.

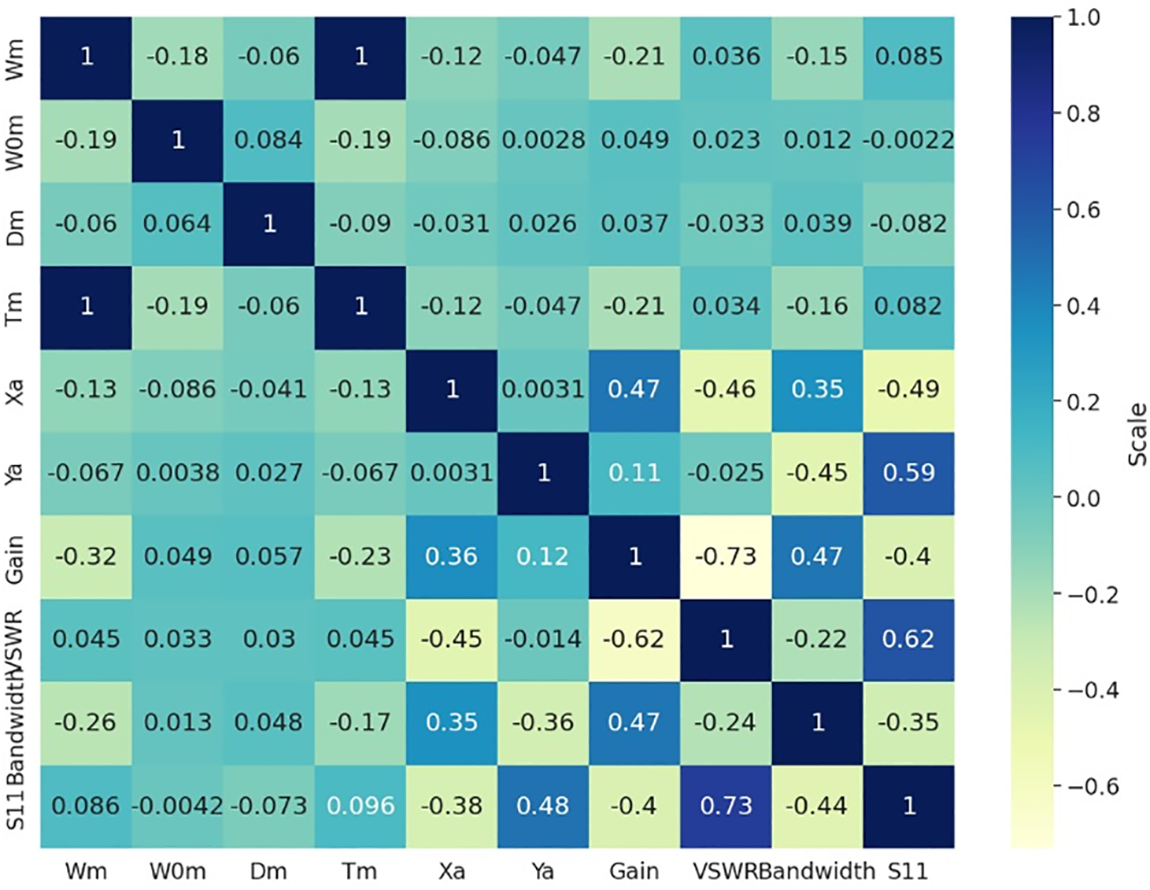
Figure 3: Correlation measure of the design parameters

3.2 Data Preprocessing

A set of preparation chores must be completed before using machine learning techniques on the provided dataset. Additionally, the efficacy of machine learning algorithms is typically impacted by the range of the features of the dataset. Scaling and normalizing all of the characteristics of the dataset is the second step in the preparation phase. Because these features fall within the same range of values, machine learning may treat them similarly. This study uses hypersphere-based normalization to scale the features and bring them within the range of the hypersphere.

3.3 Novel Hypersphere-Based Normalization Method

The proposed study uses the hypersphere-based normalization technique, which, unlike other normalization techniques, achieves effective normalization without overlapping. It also enhances the numerical characteristics of the kernel matrix by reducing the effect of other transformation variables on the features. Since the distances among the features projected onto the Hypersphere are relative to their original distances, these points are mapped to be scattered over the hypersphere without any overlaps. As a result, the proposed study uses the hypersphere-based normalization technique, which, unlike other normalization techniques, achieves effective normalization without overlapping.

The inner products between the data points have to be smooth to be mapped onto the Hypersphere. According to Boumal et al. [27], the smooth inner product is computed using the Conjugate Gradient solver of the Matlab Toolbox for Optimization on Manifolds (MANOPT) tool. By making the feature space a Riemannian manifold, the optimization problem is solved. Fig. 4 explains the algorithm used for hypersphere-based normalization of the features in the dataset. The algorithm is said to be complete when the inner product variable is smooth or when the specified tolerance criterion is satisfied. After initially traveling in the direction of d0=Δa0, the algorithm moves in the direction of tm. The globally convergent Conjugate Gradient technique is used to design the algorithm for changing the feature space to build a smooth inner product. When the inner product variable is nearly uniform or the stated tolerance condition is met, the algorithm is considered to have finished. The smoothing of the inner products scatters the properties of the new dataset over the closed hypersphere surface. The properties of the normalized attributes in the dataset are contained within a predetermined range. The normalized attributes are then made available for CNN classification. The next section explains the novel dimensionality reduction technique used for reducing the dimensions of the features.

Figure 4: Correlation measure of the design parameters

3.4 The Proposed Pearson Kernel-Based Dimensionality Reduction Technique

The properties of the compact dataset are represented using Pearson Kernel-Based Supervised Principal Component Analysis (PKSPCA), which eliminates both redundant features including noise, and yields the greatest performance. The proposed innovative PKSPCA assists in cutting down on calculation time significantly [28]. A new Pearson kernel, which aids in achieving a superior act compared to the other kernels such as linear, polynomial, and Gaussian, is projected in the proposed approach. Here, M is the space for the answer variable and N is the attribute space:

M=[m1,m2…mN]T(1)

N=[n1,n2…nN]T(2)

D={(m1,n1),(m2,n2),(m3,n3)…(m4,n4)}(3)

If F and G are discrete Reproducing Kernel Hilbert Spaces (RKHS), which comprise all endlessly limited real-valued functions of M and N, the empirical Hilbert Schmidt independence criterion (HSIC) can be determined as follows:

HSICem(D,F,G)=(A−1)2Tr(KSLS)(4)

Tr (•) stands for the trace of a square matrix, while K and L are the kernel matrices of F and G based on the kernel functions k() and l(), respectively.

Kij=k(xi,xj)andLij=l(yi,yj)(5)

S is referred to as the mean subtraction matrix and has the formula S=I−eeTA, where I is the identity matrix with order A and e denotes a column vector of order A. The dependency between UTX and Y are being maximized in the subspace UTX. The HSIC measures the interdependence between X and Y and is used to maximize Tr(KSLS) to solve the optimization problem. Here,

K=(UTX)T(UTX)(6)

UTU=I(7)

The optimization problem now becomes as UmaxTr(UTXSLSXTU) and UTU=I. In the PKSPCA X is substituted by Ф(X) and U = Ф(X)α. Therefore, the objective function is given as follows:

UmaxTr(αTK∗SLSK∗α)(8)

where K∗ and L are the proposed Pearson general kernel-generated kernel matrices of order N. The proposed Pearson function is employed as the universal Pearson kernel [11]. As a result, the Pearson kernel can be used across all datasets rather than alternative state-of-the-art kernels being tested. The time required for choosing the kernels and performing the computations is decreased by the proposed PKSPCA.

1[1+(‖xki−xlj‖22(1ω)−12/σ)2]ω(9)

The solution to the optimization issue is the B eigenvectors of (K∗SLSK∗,K∗) based on the first B eigenvalues. The kernel matrices K∗ and L concerning X and Y are computed using a Pearson kernel, where k is the function of the kernel. Analytically expressing the response to the objective function results in F of order BA, the newly created low-dimensional space. As a result, the following may be said about the low dimensional features (DF), that the PKSPCA gathered from the samples:

DF =α^TK∗(10)

The CNN then predicts the bandwidth using a lower dimensional attribute space.

3.5 Classification Using Optimized CNN with Pearson Mutation-Based Bat Optimization

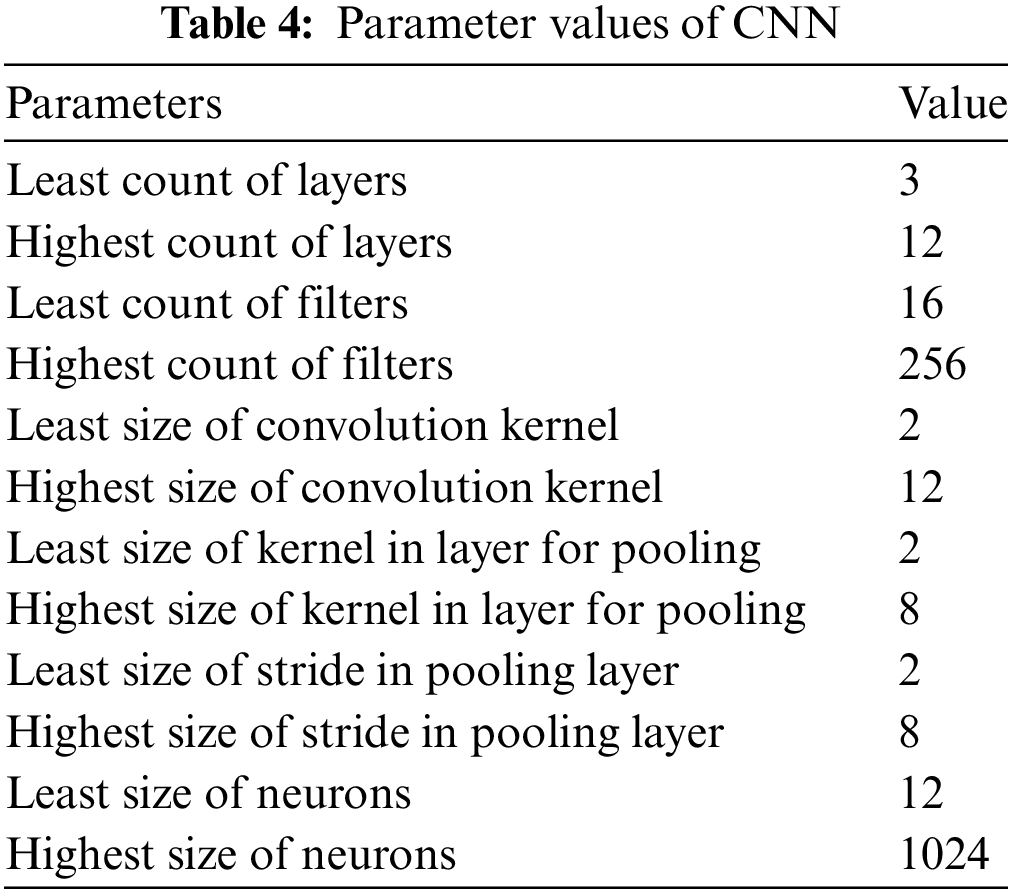
CNN employs a non-linear function called the Fully Connected layer [29]. The model uses the Softmax approach to predict the bandwidth over numerous epochs. The Rectified Linear Activation Unit (ReLU) compares the input with the value 0 as part of its operation. The dimension of the feature maps is decreased by pooling layers. The streamlined features in the feature map are produced by the pooling layer. The accuracy discovered via CNN is employed as the fitness function when employing the Bat algorithm-based optimization [30] for tuning the CNN parameters. Fig. 5 depicts the algorithm used to identify the optimized values for parameters. The best value, in contrast to other values, necessitates the mutation operator moving forward. The various parameters used in CNN are given in Tables 3 and 4.

Figure 5: The algorithm for BAO_PM

4  Results and Discussion

To illustrate the performance of the suggested methodology, the dataset is divided into three subsets: the train, validation, and test sets. The training subset has a ratio of 80% to 20%, while the testing subset is 20% smaller. The training subset is 25% smaller than the validation subset. The proposed deep network is trained by setting the network parameters to random values at the beginning. After that, using the guided BAO-PM, some iterations are performed to find the best values for these parameters. During training, the network seeks to develop its antenna bandwidth prediction skills. The performance of the trained network is assessed using the Mean Square Error (MSE) metric. Here is the formula for this measure.

MSE=1n∑i=1n(Yi−Yi∗)2(11)

where n is the total number of samples in the evaluation set, and Yi and Yi∗ stand for the antenna’s expected bandwidth and actual values, respectively.

Table 5 only displays the best results from testing different kernels in the suggested work for dimension reduction. The collection of values {210,29,…,2−9,2−10} is used to select the Radial Basis Function(RBF) kernel parameter σ. The grid search method is coupled with cross-validation on the samples used as the training set. Then, for the Pearson kernel in the proposed study, σ is selected from the set {210,29,…,2−9,2−10} and ω is selected from the set {20,21…,210}. The set of parameters that maximizes classification accuracy is the ideal set for the test set. Once the deep network has been trained, the test set is utilized to evaluate the robustness of the trained model [24,25]. The results signify that the Pearson kernel achieves higher accuracy when used for dimension reduction compared to the other kernels. The quantile-quantile (QQ) plot are displayed in Fig. 6. The diagonal line connecting the expected and actual residuals is fit by the distribution of the QQ plot’s points, as seen in the image. The predicted and actual values of the parameters are mapped out in a QQ plot. The mapping in this figure roughly fits a straight line, highlighting the efficiency of the suggested algorithm. This fitting verifies how well the proposed model predicts the bandwidth. The residuals and homoscedasticity of the prediction outcomes using the suggested Pearson kernel-based model are shown in the plots in Figs. 7 and 8. The residual error values are near zero, as shown in the figure, confirming the efficacy of the suggested technique. A homoscedasticity plot can also help determine whether the independent variables have the same error term, which can be determined from the plot values. The Receiver Operating Characteristics (ROC) of the suggested approach are also displayed in the plots of Fig. 9. These principles highlight how efficient the suggested strategy is.

Figure 6: QQ plot

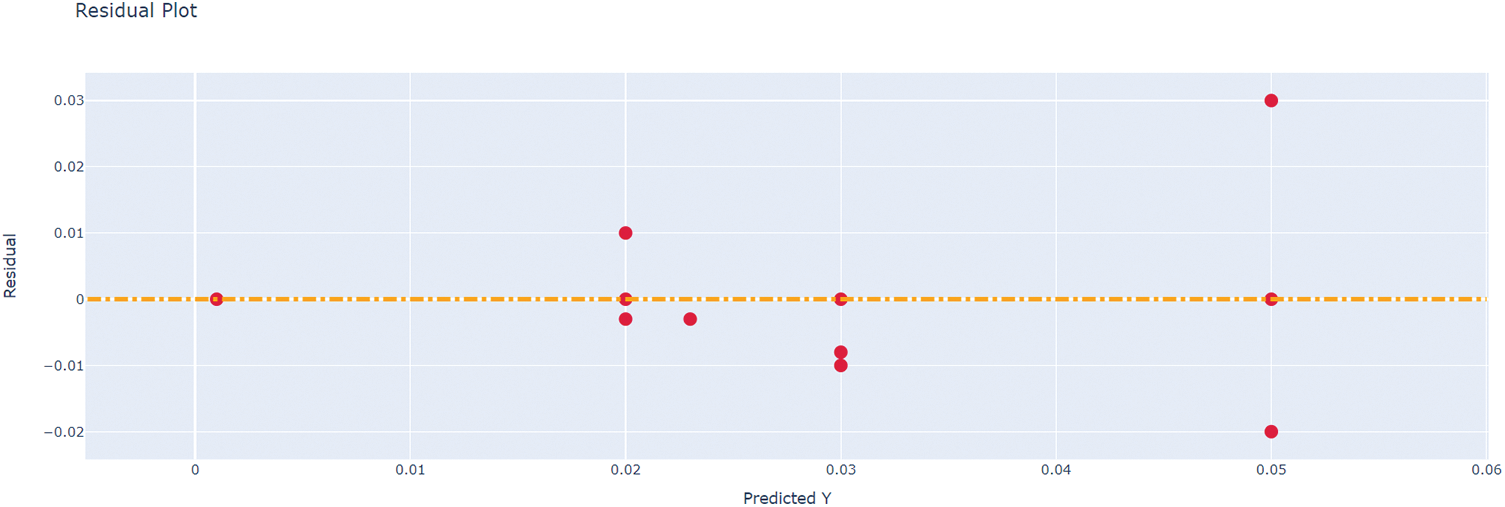
Figure 7: Residual plot

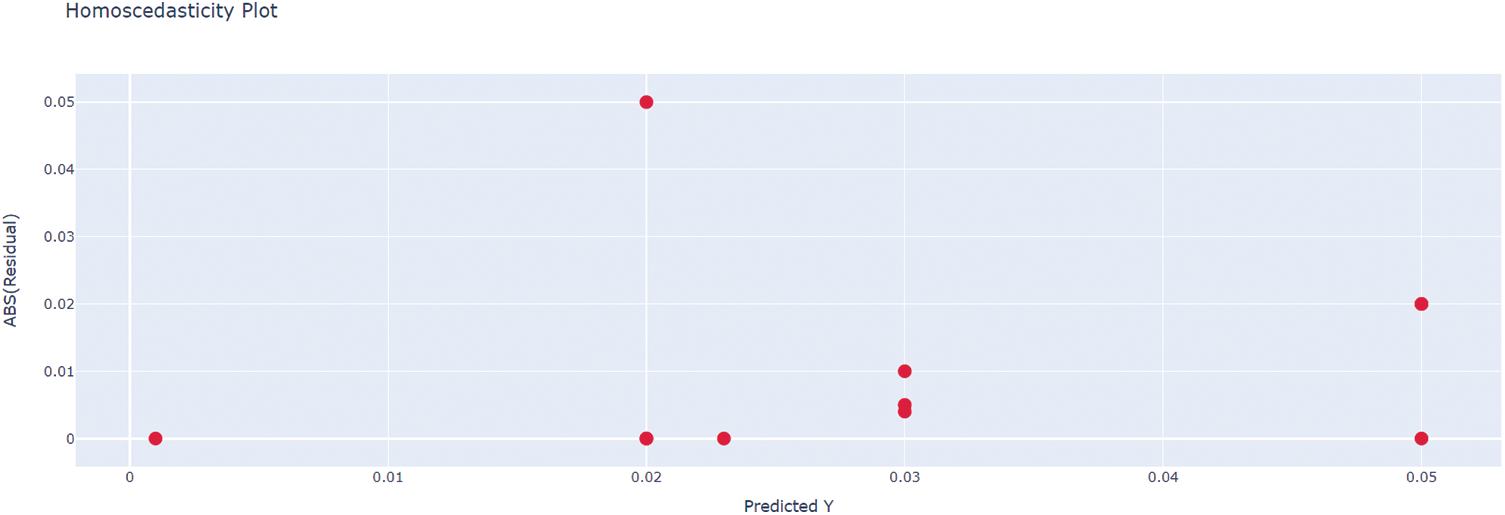
Figure 8: Homoscedasticity plot

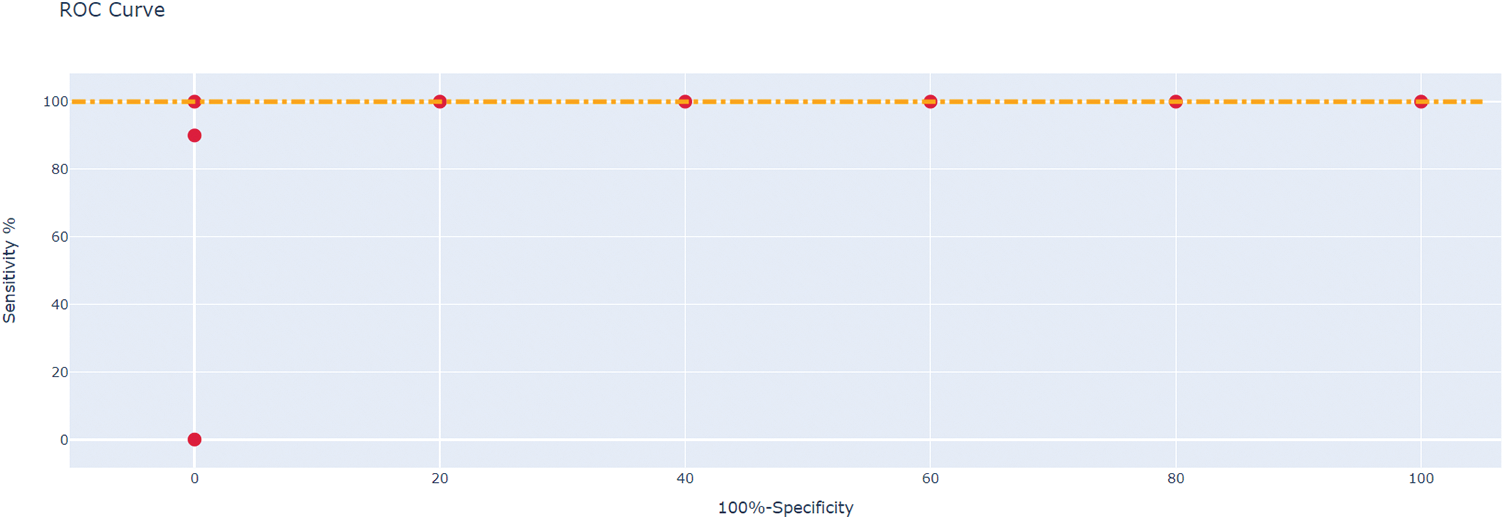
Figure 9: ROC curve

The evaluation of the model using different classifiers based on the metamaterial antenna test set is shown in Table 6. The findings obtained by the suggested model are represented in Table 6. These results are superior to those of the three rival methodologies Multilayer Perceptron (MLP), K-Nearest Neighbor (KNN), and Long Short Term Memory (LSTM) [30–38]. The table includes a list of additional evaluation criteria, the measured values of which are significantly higher than what the other models achieve. These measurements include the Mean Absolute Percentage Error (MAPE), Mean Absolute Error (MAE), Mean Bias Error (MBE), Coefficient of Determination (R2), Determine Agreement (WI), Nash Sutcliffe Efficiency (NSE), the Relative Root Mean Square Error (RRMSE), Pearson’s correlation coefficient (R), and the Root Mean Square Error (RMSE). Table 7 also contains the descriptive statistics of the recommended strategy over 20 runs.

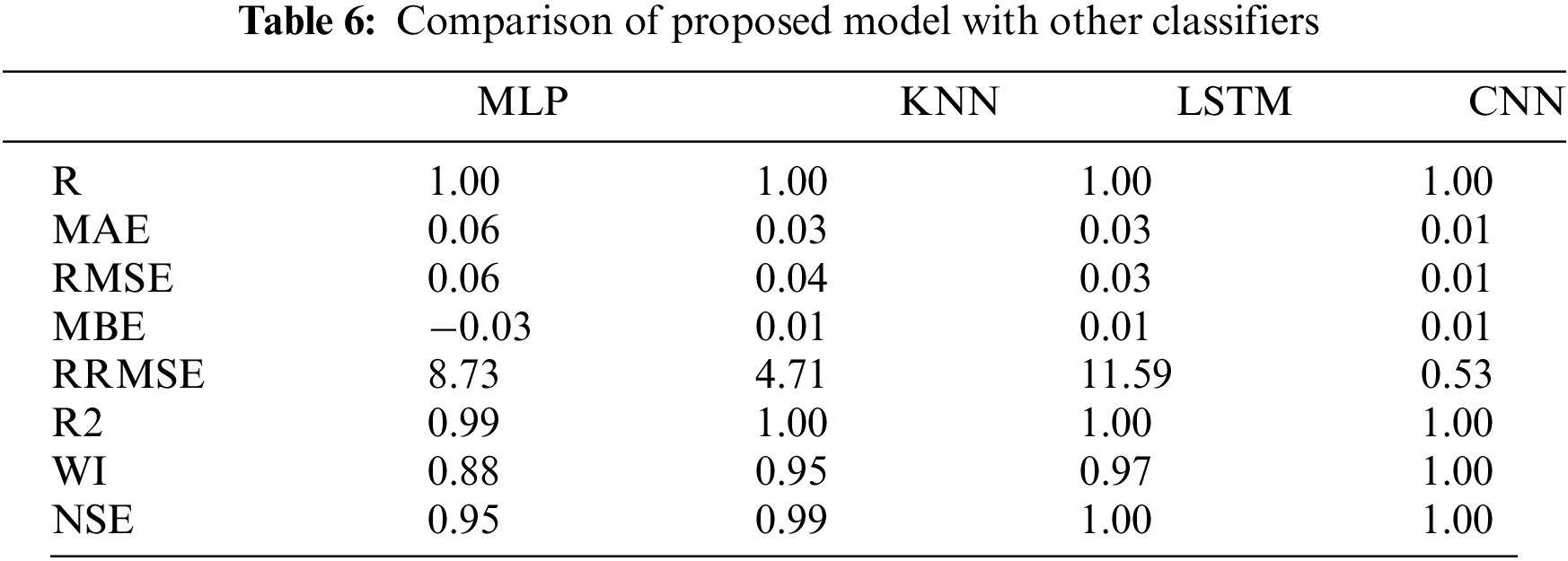
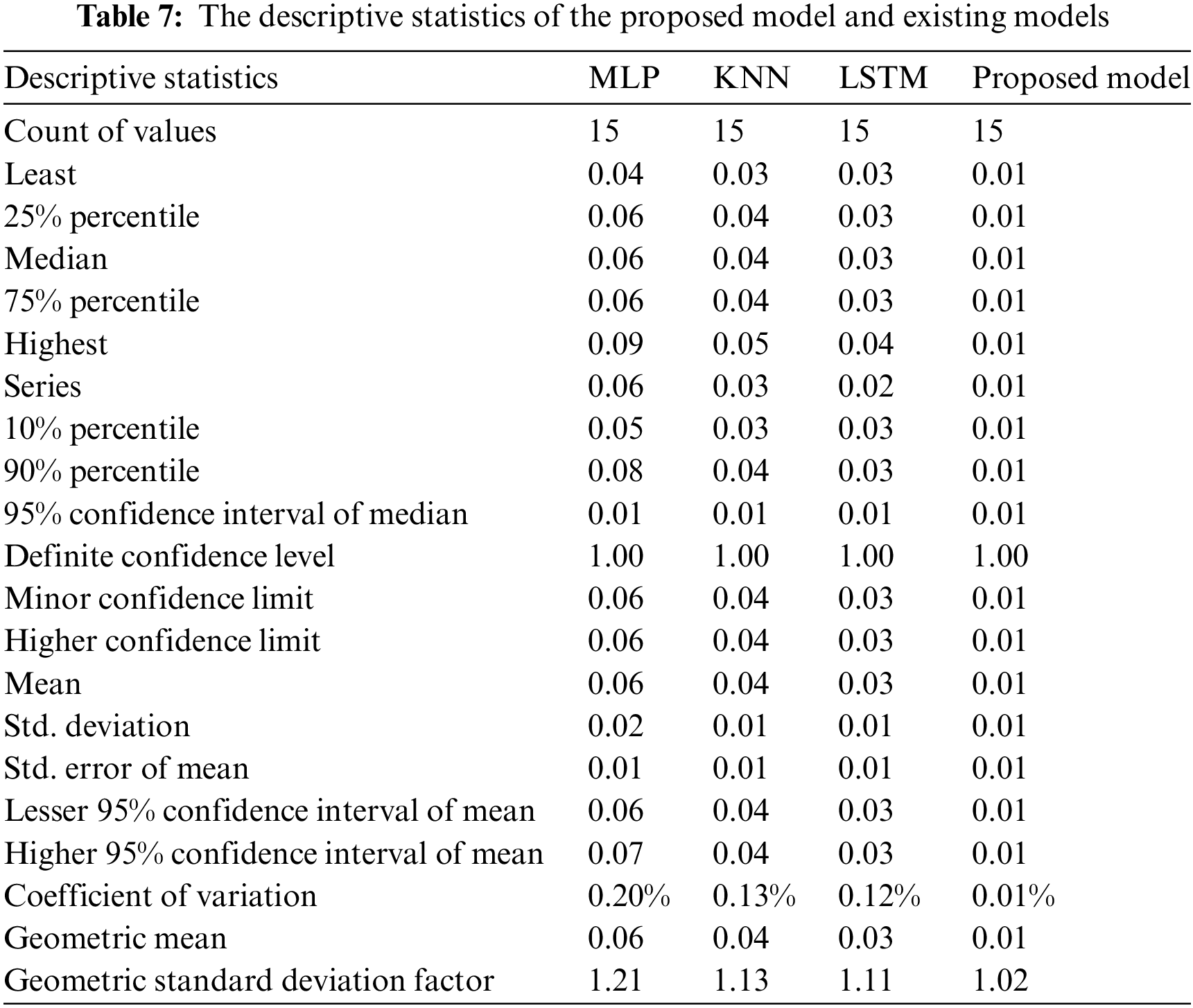
When compared to the similar values estimated from the outcomes obtained by the other ways, as indicated in the table, the calculated values of these statistics utilizing the suggested approach are reassuring. These numbers represent the effectiveness and superiority of the suggested model in estimating the bandwidth of the metamaterial antenna. The suggested strategy and the other approaches are statistically significant, as in the table. Here an additional test is done using the two-tailed t-test between each of the two algorithms to unequivocally demonstrate the superiority of the suggested method. Table 8 presents the test results for 21 samples at the 0.05 significance level. If the p-value of less than 0.05 indicates that the algorithm is significant. The measured p-value in Table 8 satisfies the condition and indicates their significance. Nonetheless, the suggested method was able to attain the least amount of difference between the tested models, demonstrating the superiority of the suggested algorithm and bolstering its increased statistical significance. Figs. 10a–10c illustrate the RMSE plots for different optimization algorithms, dimension reduction techniques (Principal Component Analysis (PCA), Linear Discriminant Analysis (LDA), Fisher Linear Discriminant Analysis (FLDA)), and normalization techniques [39] used in the proposed work. The RMSE plots show improved performance for the proposed BAO-PM, PKSPCA, and hypersphere-based normalization techniques in the proposed work. When compared to the other approaches, the suggested strategy yields the lowest discrepancy values over the test set, as the table illustrates. The remaining results, which are shown in the figures and tables, demonstrate the stability of the suggested method for estimating the bandwidth. Among the corresponding predictions made using the other feature selection algorithms, most of the predicted values in this figure have the lowest RMSE values. The majority of the obtained RMSE values fall between (0.002) to (0.004), surpassing the results attained by the other algorithms.

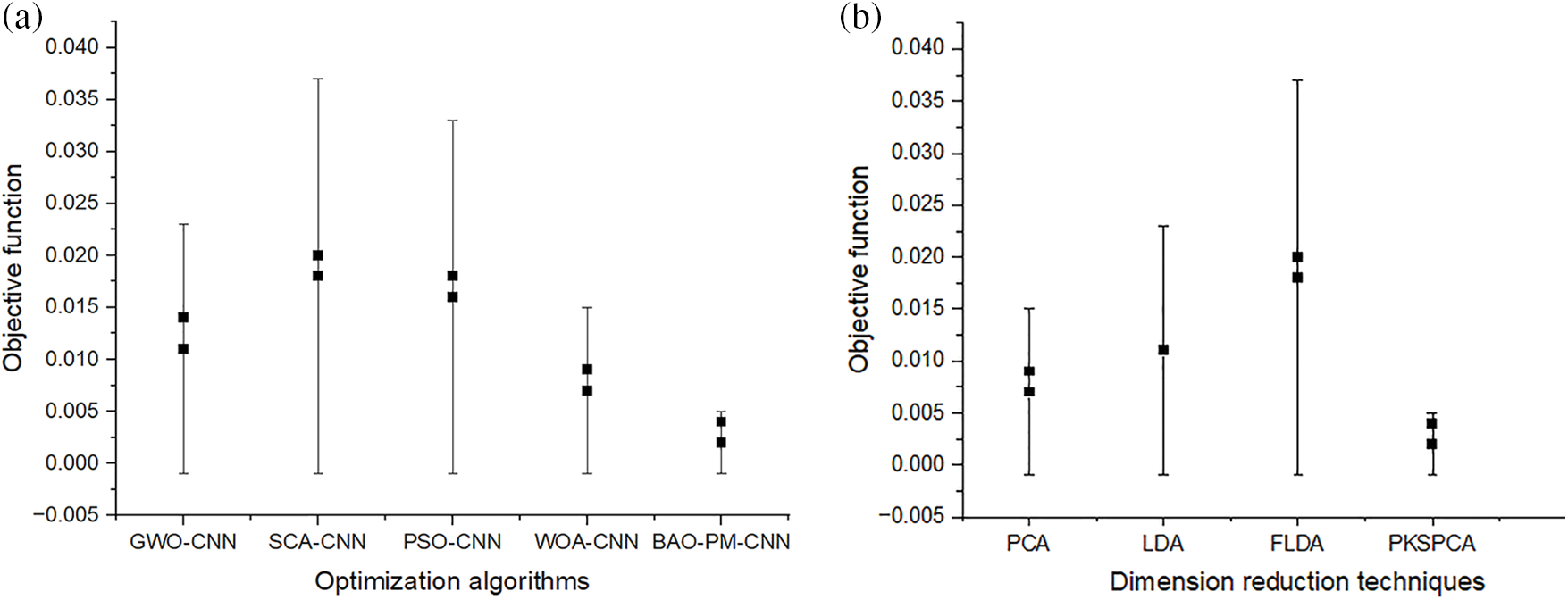
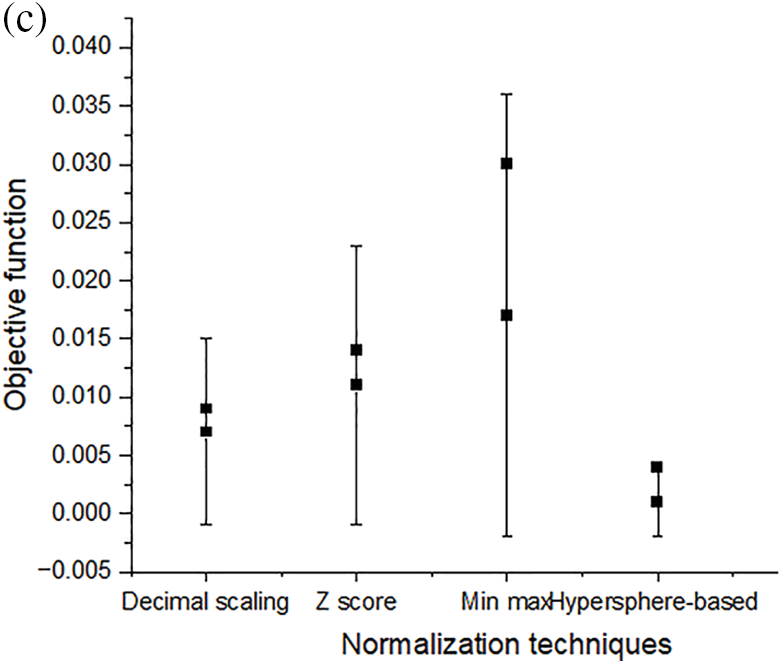
Figure 10: (a) RMSE plot of different optimization algorithms in the proposed model. (b) RMSE plot of different dimension reduction techniques in the proposed model. (c) RMSE plot of different normalization techniques in the proposed model

5  Conclusion

In this research, a unique CNN-based approach is presented for forecasting the parameters of metamaterial antenna. Based on a set of design criteria, the suggested approach can precisely estimate the bandwidth of metamaterial antennas. The Pearson Kernel shows superior results when compared to the other kernels while it is used for dimension reduction in the proposed work as seen in the results. The actual and anticipated bandwidths were examined in this investigation to emphasize and confirm the robustness of the suggested strategy. To demonstrate the superiority of the suggested algorithm, the results produced were also compared to those of other optimization algorithms. Prospects for this research in the future include evaluating the suggested algorithm in different antenna structures [25] and other optimization scenarios across various fields. The future directions include using the suggested method on more different kinds of microstrip antennas and combining it with ensemble models to improve predictions of antenna design parameters.

Acknowledgement: We thank Vellore Institute of Technology for supporting us with the APC.

Funding Statement: This research received no external funding.

Author Contributions: Investigation, software, writing, original draft preparation and validation: Sherly Alphonse. Writing-review & editing: Abinaya S. and Sourabh Paul. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: R. Machado, Metamaterial Antennas. 2019. [Online]. Available: https://www.kaggle.com/datasets/renanmav/metamaterial-antennas/.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. N. K. Grady et al., “Terahertz metamaterials for linear polarization conversion and anomalous refraction,” Science, vol. 340, no. 6138, pp. 1304–1307, 2013. doi: 10.1126/science.1235399 [Google Scholar] [PubMed] [CrossRef]

2. J. Shabanpour, S. Beyraghi, F. Ghorbani, and H. Oraizi, “Implementation of conformal digital metasurfaces for THz polarimetric sensing,” arXiv preprint arXiv:2101.02298, 2021. [Google Scholar]

3. J. Shabanpour, “Full manipulation of the power intensity pattern in a large space-time digital metasurface: From arbitrary multibeam generation to harmonic beam steering scheme,” Ann. Phys., vol. 532, no. 10, pp. 2000321, 2020. doi: 10.1002/andp.202000321 [Google Scholar] [CrossRef]

4. M. El Sayed et al., “Al-biruni earth radius (BER) metaheuristic search optimization algorithm,” Comput. Syst. Sci. Eng., vol. 45, no. 2, pp. 1917–1934, 2023. doi: 10.32604/csse.2023.032497 [Google Scholar] [PubMed] [CrossRef]

5. H. Sun, X. Chen, Q. Shi, M. Hong, X. Fu and N. D. Sidiropoulos, “Learning to optimize: Training deep neural networks for interference management,” IEEE Trans. Signal Process., vol. 66, no. 20, pp. 5438–5453, 2018. doi: 10.1109/TSP.2018.2866382 [Google Scholar] [CrossRef]

6. M. S. Ibrahim, A. S. Zamzam, X. Fu, and N. D. Sidiropoulos, “Learning-based antenna selection for multicasting,” in Proc. of the 2018 IEEE 19th Int. Workshop Signal Process. Adv. Wirel. Commun. (SPAWC), Kalamata, Greece, 2018, pp. 25–28. [Google Scholar]

7. A. M. Elbir and K. V. Mishra, “Joint antenna selection and hybrid beamformer design using unquantized and quantized deep learning networks,” IEEE Trans. Wirel. Commun., vol. 19, no. 3, pp. 1677–1688, 2020. doi: 10.1109/TWC.2019.2956146 [Google Scholar] [CrossRef]

8. J. Joung, “Machine learning-based antenna selection in wireless communications,” IEEE Commun. Lett., vol. 20, no. 11, pp. 2241–2244, 2016. doi: 10.1109/LCOMM.2016.2594776 [Google Scholar] [CrossRef]

9. P. Bardalai, H. Neog, P. E. Dutta, N. Medhi, and S. K. Deka, “Throughput prediction in smart healthcare network using machine learning approaches,” in 2022 IEEE 19th India Council Int. Conf. (INDICONKochi, India, Nov 24, 2022, pp. 1–6. doi: 10.1109/INDICON56171.2022.10040160 [Google Scholar] [CrossRef]

10. S. Ulker, “Support vector regression analysis for the design of feed in a rectangular patch antenna,” in Proc. of the 2019 3rd Int. Symp. on Multidisp. Studies Innov. Technol. (ISMSIT), Ankara, Turkey, 2019, pp. 11–13. [Google Scholar]

11. B. Üstün, W. J. Melssen, and L. M. Buydens, “Facilitating the application of support vector regression by using a universal Pearson VII function based kernel,” Chemom. Intell. Lab. Syst., vol. 81, no. 1, pp. 29–40, 2006. doi: 10.1016/j.chemolab.2005.09.003 [Google Scholar] [CrossRef]

12. P. Mahouti, A. Belen, O. Tari, M. A. Belen, S. Karahan and S. Koziel, “Data-driven surrogate-assisted optimization of metamaterial-based filtenna using deep learning,” Electronics, vol. 12, no. 7, pp. 1584, 2023. doi: 10.3390/electronics12071584 [Google Scholar] [CrossRef]

13. A. Pietrenko-Dabrowska and S. Koziel, “Rapid antenna optimization with restricted sensitivity updates by automated dominant direction identification,” Knowl.-Based Syst., vol. 268, no. 2, pp. 110453, 2023. doi: 10.1016/j.knosys.2023.110453 [Google Scholar] [CrossRef]

14. S. Koziel and A. Pietrenko-Dabrowska, “Improved-Efficacy EM-driven optimization of antenna structures using adaptive design specifications and variable-resolution models,” IEEE Trans. Antennas Propag., vol. 71, no. 2, pp. 1863–1874, 2023. doi: 10.1109/TAP.2023.3234167 [Google Scholar] [CrossRef]

15. S. Koziel, M. A. Belen, A. Çali¸skan, and P. Mahouti, “Rapid design of 3D reflectarray antennas by inverse surrogate modeling and regularization,” IEEE Access, vol. 11, pp. 24175–24184, 2023. doi: 10.1109/ACCESS.2023.3254204 [Google Scholar] [CrossRef]

16. N. Calik, F. Güne, S. Koziel, A. Pietrenko-Dabrowska, M. A. Belen and P. Mahouti, “Deep-learning-based precise characterization of microwave transistors using fully-automated regression surrogates,” Sci. Rep., vol. 13, no. 1, pp. 1445, 2023. doi: 10.1038/s41598-023-28639-4 [Google Scholar] [PubMed] [CrossRef]

17. S. Koziel, A. Pietrenko-Dabrowska, and A. G. Raef, “Knowledge-based expedited parameter tuning of microwave passives by means of design requirement management and variable-resolution EM simulations,” Sci. Rep., vol. 13, no. 1, pp. 334, 2023. doi: 10.1038/s41598-023-27532-4 [Google Scholar] [PubMed] [CrossRef]

18. S. Mirjalili, S. M. Mirjalili, and A. Lewis, “Grey wolf optimizer,” Adv. Eng. Softw., vol. 69, pp. 46–61, 2014. doi: 10.1016/j.advengsoft.2013.12.007 [Google Scholar] [CrossRef]

19. M. M. Eid, E. S. El-kenawy, and A. Ibrahim, “A binary sine cosine-modified whale optimization algorithm for feature selection,” in 2021 National Computing Colleges Conference (NCCC), Taif, Saudi Arabia, 2021, pp. 1–6. doi: 10.1109/NCCC49330.2021.9428794 [Google Scholar] [CrossRef]

20. R. Bello, Y. Gomez, A. Nowe, and M. M. Garcia, “Two-step particle swarm optimization to solve the feature selection problem,” in Seventh Int. Conf. Intell. Syst. Design Appl. (ISDA 2007), Rio de Janeiro, Brazil, 2007, pp. 691–696. doi: 10.1109/ISDA.2007.101 [Google Scholar] [CrossRef]

21. H. M. Mohammed, S. U. Umar, and T. A. Rashid, “A systematic and meta-analysis survey of whale optimization algorithm,” Comput. Intell. Neurosci., vol. 2019, no. 1, pp. 1–25, 2019. doi: 10.1155/2019/8718571 [Google Scholar] [PubMed] [CrossRef]

22. J. H. Holland, “Genetic algorithms,” Sci. Am., vol. 267, no. 1, pp. 66–73, 1992. doi: 10.1038/scientificamerican0792-66 [Google Scholar] [CrossRef]

23. R. Storn and K. Price, “Differential evolution_A simple and efficient heuristic for global optimization over continuous spaces,” J. Glob. Optim., vol. 11, no. 4, pp. 341–359, 1997. doi: 10.1023/A:1008202821328 [Google Scholar] [CrossRef]

24. A. Pietrenko-Dabrowska, S. Koziel, and L. Golunski, “Two-stage variable-fidelity modeling of antennas with domain confinement,” Sci. Rep., vol. 12, no. 1, pp. 17275, 2022. doi: 10.1038/s41598-022-20495-y [Google Scholar] [PubMed] [CrossRef]

25. M. H. Jwair and T. A. Elwi, “Metasurface antenna circuitry for 5G communication networks,” Infocommunications J., vol. 15, no. 2, pp. 2–7, 2023. doi: 10.36244/ICJ.2023.2.1 [Google Scholar] [CrossRef]

26. R. Machado, “Metamaterial antennas,” 2019. Accessed: Jun. 06, 2023. [Online]. Available: https://www.kaggle.com/datasets/renanmav/metamaterial-antennas [Google Scholar]

27. N. Boumal, B. Mishra, P. A. Absil, and R. Sepulchre, “Manopt, a Matlab toolbox for optimization on manifolds,” J. Mach. Learn. Res., vol. 15, no. 1, pp. 1455–1459, 2014. [Google Scholar]

28. A. Maćkiewicz and W. Ratajczak, “Principal components analysis (PCA),” Comput. Geosci., vol. 19, no. 3, pp. 303–342, 1993. doi: 10.1016/0098-3004(93)90090-R [Google Scholar] [CrossRef]

29. Z. Wang, X. Xiao, Y. Pang, and W. Su, “Non-invasive, intelligent, and continuous monitoring of human blood glucose with UWB dual-antenna and cascade CNN,” Meas. Sci. Technol., vol. 34, no. 9, pp. 095702, 2023. doi: 10.1088/1361-6501/acd138 [Google Scholar] [CrossRef]

30. J. Bi, H. Yuan, J. Zhai, M. Zhou, and H. V. Poor, “Self-adaptive bat algorithm with genetic operations,” IEEE/CAA J. Autom. Sin., vol. 9, no. 7, pp. 1284–1294, 2022. doi: 10.1109/JAS.2022.105695 [Google Scholar] [CrossRef]

31. D. Khafaga et al., “Improved prediction of metamaterial antenna bandwidth using adaptive optimization of LSTM,” Comput. Mater. Contin., vol. 73, no. 1, pp. 865–881, 2022. doi: 10.32604/cmc.2022.028550 [Google Scholar] [PubMed] [CrossRef]

32. J. Lan, X. Bu, Y. Meng, and Y. Li, “Sound insulation mechanism and prediction of membrane-type acoustic metamaterial with multi-state anti-resonances by weighted-kNN,” Appl. Phys. Express, vol. 16, no. 8, pp. 085501, 2023. doi: 10.35848/1882-0786/acf184 [Google Scholar] [PubMed] [CrossRef]

33. H. Wen, J. Yu, G. Pan, X. Chen, S. Zhang and S. Xu, “A hybrid CNN-LSTM architecture for high accurate edge-assisted bandwidth prediction,” IEEE Wireless Commun. Lett., vol. 11, no. 12, pp. 2640–2644, 2022. doi: 10.1109/LWC.2022.3213017 [Google Scholar] [CrossRef]

34. A. Ibrahim, H. Abutarboush, A. Mohamed, M. Fouad, and E. El-Kenawy, “An optimized ensemble model for prediction the bandwidth of metamaterial antenna,” Comput. Mater. Contin., vol. 71, no. 1, pp. 199–213, 2022. doi: 10.32604/cmc.2022.021886 [Google Scholar] [PubMed] [CrossRef]

35. N. Kurniawati, D. N. Putri, and Y. K. Ningsih, “Random forest regression for predicting metamaterial antenna parameters,” in 2020 2nd Int. Conf. on Ind. Electr. Electron. (ICIEE), Lombok, Indonesia, 2020, pp. 174–178. doi: 10.1109/ICIEE49813.2020.9276899 [Google Scholar] [CrossRef]

36. R. W. Ziolkowski, P. Jin, and C. C. Lin, “Metamaterial-inspired engineering of antennas,” in Proc. IEEE, vol. 99, no. 10, pp. 1720–1731, 2010. doi: 10.1109/JPROC.2010.2091610 [Google Scholar] [CrossRef]

37. A. A. Abdelhamid and S. R. Alotaibi, “Optimized two-level ensemble model for predicting the parameters of metamaterial antenna,” Comput. Mater. Contin., vol. 73, no. 1, pp. 917–933, 2022. doi: 10.32604/cmc.2022.027653 [Google Scholar] [PubMed] [CrossRef]

38. A. H. Alharbi et al., “Improved dipper-throated optimization for forecasting metamaterial design bandwidth for engineering applications,” Biomimetics, vol. 8, no. 2, pp. 241, 2023. doi: 10.3390/biomimetics8020241 [Google Scholar] [PubMed] [CrossRef]

39. M. Yadav, G. S. Chandel, and R. Gupta, “Review of image classification techniques based on LDA, PCA and genetic algorithm,” Int. J. Eng. Sci. Res. Technol., vol. 3, no. 2, 2014. Accessed: Jun. 23, 2023. [Online]. Available: https://europub.co.uk/articles/nbspreview-of-image-classification-techniques-based-on-lda-pca-and-genetic-algorithm-A-100880 [Google Scholar]