Enhanced Differentiable Architecture Search Based on Asymptotic Regularization

1  Introduction

Differentiable neural network architecture search updates the architecture optimization process via the gradient descent method, achieving a more efficient architecture search, and the quick and low-cost benefits have facilitated many researchers in studying the automated search for neural network architectures. In recent years, differentiable neural network architecture search has been extensively applied to various fields, for instance, computer vision [1–3], natural language processing [4,5], bioinformatics [6,7], and speech recognition [8,9]. Although differentiable architecture search (DARTS) [10] has achieved remarkable results in various tasks, there are still issues that remain to be overcome by researchers, thereby searching for superior neural network architectures for different missions on different datasets. The search process of differentiable neural network architecture search is to search for a neural network architecture with high performance in a predefined search space by using a performance evaluation strategy to guide a gradient-based search strategy. Therefore, the design of the search space, optimization of the search strategy, and improvement of the performance evaluation strategy have become critical factors affecting the performance of the architecture search. In this paper, we will also optimize the architecture search method in each of these three aspects to improve the performance of architecture search.

The design of the search space includes the selection of operations and the complexity of the search space, both of which have a profound bearing on the search results. The search space contains all possible candidate neural network architectures, if poorly designed, it can increase the complexity of the search process, causing it to miss the optimal solution and converge to suboptimal solutions. At the same time, an overly large or complex search space can make the search process very difficult and time-consuming. The choice of operations in the search space directly determines the size and quality of the search space and also decides the composition of the final generated neural network architecture. More rational operation choices can make the search process more likely to find a neural network architecture with better performance. Nakai et al. [11] proposed an attention search space containing multiple attention modules and concatenated it with the original search space of DARTS and selected an operation from two different search spaces on each edge of the cell. The introduction of attention modules in each edge makes architecture search more stable, albeit with a relative increase in time consumption. Hundt et al. [12] proposed a new HyperCuboid search space, which enables more efficient architecture search in the new search space through a gridded search method and more unified search operations, but they introduced a lot of extra parameters that need to be set manually. Therefore, controlling the complexity of the search space and finding a balance between computational efficiency and search quality is vitally important. Especially in practical problems, effectively reducing the complexity of the search space while maintaining search quality is a highly challenging task.

Search methods based on the gradient search strategy relax the discrete search space into a continuous one, making the search space differentiable. Therefore, the optimization process can be updated through gradient descent, significantly improving search efficiency. Among the gradient-based architecture search methods, Liu et al. [10] proposed a differentiable search method, which describes the architecture search process as a bi-level planning problem, in which the external optimization problem of the architecture parameters is limited by the internal optimization problem of the network parameters and the two optimization problems affect each other. Solving bi-level programming problems is usually arduous because it is challenging to find an analytical solution for the inner optimization problem. Hence, the thought process for solving the architecture search problem has shifted. By fixing the architecture parameters in the outer layer optimization, we optimize the network parameters in the inner layer and obtain an approximate solution of the inner objective function. Then, with the inner network parameters fixed, the approximate solution is substituted into the outer optimization problem to optimize the architecture parameters, obtaining an approximate solution of the outer objective function. Finally, repeat the above process for alternate updates, stop the search when the loop abort condition is satisfied at which point the optimal neural network architecture is derived.

Xu et al. [13] sampled parts of the cell’s intermediate nodes, reducing computation with equal probability by adjusting sampling probability, while proposing edge normalization to reduce operation selection bias. Chen et al. [14] introduced an asymptotic search concept, gradually increasing the cell count to make the network depth during the architecture search stage gradually approach that during the architecture evaluation stage, thereby reducing the depth disparity between the two stages. They also proposed two search space regularization methods to alleviate architecture overfitting issues. However, none of the above methods consider that in the process of architecture search based on two-layer optimization, the error brought by the gradient approximation of the network parameter optimization will be superimposed on the architecture parameter solution problem, resulting in the accumulation of the error in the iterative process and thus causing the architecture search to converge to a suboptimal architecture. While single-level optimization problem [15–17] avoid this issue and accelerate search speed, their instability can lead to the overfitting problem of architecture parameters and result in the architecture converging to a meaningless neural network architecture full of skip connections. Therefore, how to conduct gradient-based neural network architecture search more precisely, quickly, and stably is still a problem to be solved.

The efficiency of performance evaluation strategies also directly affects the time required for the architecture search process, and its accuracy and reliability are crucial to the performance of the final search architecture. If the performance evaluation strategy can more accurately reflect the architecture performance, the architecture search process will search for better network architectures. Meanwhile, a more reliable performance evaluation strategy will enable the searched architecture to be more widely applicable to different datasets. In addition, the evaluation strategy needs to have a better balance between computational cost and architecture performance, and the ideal result is to search for higher-performance neural network architectures using less computational cost. Therefore, we need to consider various constraints such as resource limitations and search goals to comprehensively design the performance evaluation strategy and adjust the variation process of some hyper-parameters in the architecture training process, making the architecture search process more reasonable and efficient.

To further optimize the design of the search space, improve the stability of the architectural search process, and enhance the rationality of the performance evaluation strategy, this paper proposes a faster and more efficient differentiable architecture search method (AllegroNAS). Firstly, a more efficient search space is proposed by designing two new convolutional modules. Compared with the original convolutional blocks, these new ones feature different numbers of layers and output channel counts within the convolutional block. Then, more uniform convolutional blocks are generated based on different kernel sizes, replacing the convolutional blocks in the original DARTS method, which enhances the complexity of the search space composition, thereby improving the performance of the architecture search. Secondly, to reduce the error caused by gradient approximation in the architecture update process, an asymptotic architecture parameter regularization method is proposed to mitigate the issues present in single-level and bi-level optimization, leading to the architecture search process converging to a more optimal neural network architecture. Next, a new learning rate annealing method, namely natural exponential cosine learning rate annealing, is proposed to accelerate the neural network search process. It accelerates the decay of the learning rate in the early stage, thus reducing the time interval for validation accuracy improvement, enabling the architecture search process to unfold more rapidly and stably with a more appropriate learning rate. In addition, data augmentation is used to further improve the precision of the architecture search, and convolutional blocks are replaced with group convolutions to reduce the number of parameters in the search process. Finally, the feasibility of the proposed method is verified through extensive experiments. Experimental results show that this method can achieve a faster and more efficient search process, and the neural network architecture searched is competitive with other methods. In summary, the main contributions of this paper are as follows:

1) We propose a more efficient search space by introducing two new convolutional modules, AllegroDilConv and AllegroSepConv, to increase the complexity of the search space and speed up the search, resulting in a more efficient architecture search.

2) We propose a natural exponential cosine learning rate annealing method to rationalize the learning rate of the neural network architecture training process, thereby accelerating the search process and improving its stability.

3) We propose a more stable asymptotic optimization process by regularizing the architecture parameters in stages, bringing architecture parameters closer to the optimal target, and enhancing the robustness of the architecture search process.

4) To enhance the performance of architecture search, group convolution is introduced to reduce the search cost and speed up the search process, and data augmentation is employed to improve the reliability of architecture performance evaluation.

5) We propose a faster and more efficient method for differentiable architecture search (AllegroNAS) and conduct extensive experiments on several publicly available datasets to prove the effectiveness of the proposed method.

2  Related Work

Neural networks are the most fundamental building blocks in deep learning. In the past few decades, manually designed neural network architectures, such as ResNet [18], DenseNet [19], and SENet [20], have achieved remarkable results. However, designing these architectures manually depends on the profound knowledge and extensive practical experience of experts, and due to the need for designing different neural network architectures for diverse tasks and environments, manually designed neural networks tend to have significant limitations. To solve the bottleneck of manually designing neural network architecture and reduce the burden of the architecture design, the automatic neural architecture search (NAS) was born. In 2017, Zoph et al. [21,22] used a reinforcement learning-based search strategy to kick-start a new era in architecture search. They proposed modularizing the entire neural network, making the architecture search process based on cell search and simplifying the search task. However, it still required spending several days on 500 GPUs to search for the final neural network architecture.

Subsequently, many researchers introduced evolutionary algorithms to enhance search performance. Liu et al. [23] proposed to integrate the architecture search process with the topology to reduce the computational cost by hierarchical representation, completing the experiment in 1.5 days on 200 GPUs. Liu et al. [24] introduced a proxy model to assist architecture search, making the architecture search process based on model complexity. Real et al. [25] introduced an age property based on the evolutionary algorithm to make the architecture search more biased towards the selection of younger offspring neural network architectures. The architecture search process based on the evolutionary algorithm requires retraining each sub-network architecture during each iteration, which consumes a considerable amount of time. Later, to improve the search efficiency and reduce the computational resources required in the architecture search process, Pham et al. [26] proposed using a weight-sharing strategy. They represented the search space as a topology, enabling different sub-network architectures to share some weights and simultaneously update multiple sub-architectures in each training step, significantly reducing the time and resources needed for training and evaluating the network. Inspired by the weight-sharing strategy, Liu et al. [10] proposed a differentiable weight-sharing neural network architecture search method. They made the discrete search space continuous, making the search space differentiable, and substantially reduced computational cost by updating network parameters through gradient descent. However, the error of gradient approximation gradually accumulates in each iteration, leading to the search process eventually converging in the wrong direction, which is most intuitively exhibited by the fact that the final architecture is loaded with meaningless operations, such as skip connections.

Although the DARTS method offers researchers a new avenue to overcome resource constraints in architecture search, its instability issues remain to be solved. Some researchers have shown through experiments that the architectures generated by random search [27,28] can even be comparable or superior to those generated by the DARTS method. While random search also produces some performance-comparable neural network architectures, the immense search space requires substantial time if relying solely on randomness, and there is no theory to confirm the correctness of this randomness. However, this finding has prompted people to start addressing the problems present in the DARTS method through different means. The enhancement of gradient-based neural network architecture search method performance mainly falls into two categories: explicit and implicit solutions. Explicit solutions primarily involve early stopping strategies based on various conditions, altering operations in the search space, pruning the search space, and asymptotic search methods. In contrast, implicit solutions primarily include changing the parameter update methods during architecture search, applying different regularization methods on architectural parameters, and employing more accurate gradient approximation methods.

Hao et al. [29] proposed adding an attention mechanism module in cell architecture to strengthen information interaction between intermediate nodes, thus enhancing the ability to select superior neural network architectures. Wang et al. [30] proposed a multi-group channel-level parallel sampling method that reduced competition between groups of channels and combined this with the SE attention module to stabilize the architecture search process and alleviate overfitting problems. Chu et al. [31] proposed to keep the individual operations in the search space to be selected more fairly by using a 0-1 loss function, enabling the architecture search process to break away from the erroneous loop biased towards selecting skip connections. Liang et al. [32] proposed an early stopping strategy based on the DARTS method, which directly limits the possibility of choosing non-parameter operations during the search process. If the non-parameter operations in the searched architecture exceed the set value, the search is stopped. This explicit early termination strategy prevents performance collapse issues found in the DARTS method. Chu et al. [33] proposed the adoption of auxiliary skip connections to directly mitigate performance collapse issues in architecture search, improving the robustness of architecture search without increasing the computational burden. Yu et al. [34] proposed a joint training approach where, without the aid of any teacher model and through introspective distillation, the evaluation network is cyclically feedback into architecture search. This approach brings the final generated network closer to the target and effectively extends to applications in object detection and semantic segmentation tasks. Dong et al. [35] simultaneously learned a differentiable sampler during the architecture search. Using the learned sampler, they achieved a fair sampling of sub-architectures in the search space, avoiding competition between operations and reducing the architecture search time. However, all of the above methods increase the human intervention or network architecture complexity to different extents and fail to fundamentally solve the problem of performance collapse in differentiable architecture search, while directly stopping the search process manually will cause the final generated network architecture to become a sub-optimal one.

In the implicit methods, Hsieh et al. [15] used the Mean-shift method to smooth sharp minima, enabling gradient descent to converge to flatter minima, and thus improving the robustness and generalization of architecture search. Ye et al. [16] proposed a new regularization approach to regularize Beta parameters by the architecture parameters normalized via the softmax function, which has stabilized the architecture search process while reducing the dependence of the architecture search on hyperparameters and datasets. Bi et al. [17] proposed a new gradient approximation that re-solves the second-order approximation process in the DARTS method. This more precise gradient approximation method reduced the estimation error of architecture parameters, thereby reducing the optimization gap between the supernet in the search space and the final generated subnet. He et al. [36] proposed a hybrid objective function that combines the utilization of a model-size-based search strategy and an early-stopping strategy to improve the final architecture performance. However, neither of the above implicit methods considered dynamic regularization in the architecture search, which makes the architecture search process more stable. Based on the above work, this paper proposes a search method that combines explicit and implicit approaches to improve each of the three aspects: search space, search strategy, and performance evaluation strategy. By using the search strategy of asymptotic regularization in a more efficient search space, analyzing the change of parameters in the architecture evaluation process, and designing a more reasonable performance evaluation strategy, we achieve a more stable and efficient architecture search method.

3  Method

3.1 Review of DARTS

The DARTS method [10] describes the cell as a directed acyclic graph that contains N intermediate nodes, each node represents a different layer of the feature map, and each edge in the directed acyclic graph includes all the operations in the search space, so there are as many operations in the search space as there are connections between every two nodes. The search space in the DARTS method contains eight operations in total, and the specific flow chart is shown in Fig. 1.

Figure 1: DARTS flowchart

DARTS describes the search process as a bi-level optimization problem, denoted as

minαℑval(ω∗(α),α)s.t.ω∗(α)=arg minωℑtrain(ω,α)(1)

where α and ω denote the architecture parameters and network parameters to be optimized, respectively, ℑtrainand ℑval denote the training set loss and validation set loss, respectively. Then, by a one-step approximation method, it can be derived

∇αℑval(ω∗(α),α)≈∇αℑval(ω−ℓω∇ωℜtrain(ω,α),α)(2)

where ℓ denotes the learning rate. Then the finite difference approximation is used to finally obtain

∇αℑval(ω∗(α),α) ≈∇αℑval(ω−ℓω∇ωℑtrain(ω,α),α) =∇αℑval(ω∗,α)−ℓω∇ω,α2ℑtrain(ω,α)⋅∇ω∗ℑval(ω∗,α) ≈∇αℑval(ω∗,α)−ℓω⋅∇αℑtrain(ω1,α)−∇αℑtrain(ω2,α)2σ(3)

where

ω∗(α)≈ω−ℓω∇ωℑtrain(ω,α), σ=0.01/‖∇ω∗ℑval(ω∗,α)‖2ω1=ω+σ∇ω∗ℑval(ω∗,α), ω2=ω−σ∇ω∗ℑval(ω∗,α)

The architecture parameters and network parameters are continuously updated iteratively through the above process, and then the optimal neural network architecture is generated based on human-defined search termination conditions.

3.2 Allegro Search Space

As can be observed from Fig. 1, the composition of the search space in the DARTS method is relatively simple, it only has some basic operations such as convolution and pooling. However, the design of the architecture search space is crucial to the architecture search process, and the selection of operations in the search space is a critical step in the design of the search space. The models generated by different operations have different compositions and computational complexities, directly affecting the performance of the final architecture. An appropriate increase in operation complexity will improve the performance of the final architecture. For this reason, we propose a new efficient search space called Allegro search space. In the search space, we propose two convolutional modules, AllegroSepConv and AllegroDilConv, and the composition diagram of the two modules is shown in Fig. 2.

Figure 2: Comparison of the convolution module in Allegro search space and DARTS search space

First, we can see from Fig. 2 that AllegroSepConv changes the number of output channels after the first layer of convolution compared to the original depth-separable convolution, allowing the network to handle more operations in higher dimensions, process more feature maps earlier, and improve the expressiveness of the model while retaining more essential information. Secondly, AllegroDilConv deepens the number of convolution layers compared to the original inflated convolution. Adding additional convolution layers allows the network to become deeper, and a deeper network provides stronger model representation, which helps capture more complex features and patterns, and also helps to be able to compete more fairly with each other during the search process with the AllegroSepConv module. Finally, we form our final Allegro search space by varying the size of the convolutional kernels, and the operational composition of the search space is as follows:

3.3 Asymptotic Regularization

In gradient-based architecture search methods, whether the optimization problem is solved by bi-level optimization or single-level optimization, the massive discrepancy in the quantities of architecture parameters and network parameters poses a challenge for the search algorithm to optimize them equitably. In dual-level optimization, since the architecture parameters are built upon the approximations of the network parameters, it leads to a continuous accumulation of gradient errors, eventually deviating from the true gradient. Moreover, due to its computational complexity, the search process becomes incredibly slow. In contrast, single-level optimization simplifies the optimization problem compared to dual-level optimization, hence speeding up the search process. However, it tends to overfit the architecture parameters, making the search process highly unstable.

To this end, this paper proposes an asymptotic architecture parameter regularization method that uses the gradient of the loss function on the training set as the regularization term of the architecture parameters. Then changes the architecture regularization size according to the growth of the search epoch, making the architecture search process more robust.

We add the gradient of the loss function ∇αℑtrain(ω∗,α) on the training set to the architecture update process and derive

α=α−ℓα(∇αℑval(ω∗,α)+χ⋅∇αℑtrain(ω∗,α))(4)

where χ is the asymptotic coefficient. The subsequent calculation steps are as follows:

α =α−ℓα(∇αℑval(ω∗,α)+χ⋅∇αℑtrain(ω∗,α)) ≈α−ℓα(∇αℑval(ω−ℓω∇ωℑtrain(ω,α),α)+χ⋅∇αℑtrain(ω−ℓω∇ωℑtrain(ω,α),α)) =α−ℓα(−ℓω∇ω,α2ℑtrain(ω,α)⋅ℑ1[ℑval(ω−ℓω∇ωℑtrain(ω,α),α)] +1⋅ℑ2[ℑval(ω−ℓω∇ωℑtrain(ω,α),α)] −χ⋅ℓω∇ω,α2ℑtrain(ω,α)⋅ℑ1[ℑtrain(ω−ℓω∇ωℑtrain(ω,α),α)]+1⋅χ⋅ℑ2[ℑtrain(ω−ℓω∇ωℑtrain(ω,α),α)]) =α−ℓα(∇αℑval(ω∗,α)−ℓω∇ω,α2ℑtrain(ω,α)⋅∇ω∗ℑval(ω∗,α)+χ⋅∇αℑtrain(ω∗,α)−χ⋅ℓω∇ω,α2ℑtrain(ω,α)⋅∇ω∗ℑtrain(ω∗,α)) ≈α−ℓα(∇αℑval(ω∗,α)−ℓω⋅∇αℑtrain(ω1,α)−∇αℑtrain(ω2,α)2σval+χ⋅∇αℑtrain(ω∗,α)−χ⋅ℓω⋅∇αℑtrain(ω3,α)−∇αℑtrain(ω4,α)2σtrain)(5)

where ℑ1 and ℑ2 denote the partial derivatives of the first and second terms of the loss function, respectively, and

ω1=ω+σval∇ω∗ℑval(ω∗,α), ω2=ω−σval∇ω∗ℑval(ω∗,α)ω3=ω+σtrain∇ω∗ℑtrain(ω∗,α), ω4=ω−σtrain∇ω∗ℑtrain(ω∗,α)σval=0.01/‖∇ω∗ℑval(ω∗,α)‖2, σtrain=0.01/‖∇ω∗ℑtrain(ω∗,α)‖2

Then we gradually change the asymptotic coefficients according to the different stages of the search, the rules of changing are as follows:

χ=χmax−χminH ⋅τ(6)

where H , τ, χmax and χmin denote the set total epoch, the current training epoch, the maximum values of the asymptotic coefficients and the minimum values of the asymptotic coefficients, respectively. We dynamically adjust the asymptotic coefficients according to Eq. (6) to make the model fit the training data as well as possible at the early stage of training, while at the later stage of training, we try to avoid the occurrence of the model overfitting problem, so we gradually and appropriately increase the size of the canonical term dynamically.

3.4 Natural Exponential Cosine Annealing

We search for the optimal architecture in the Allegro search space by an asymptotic regularization search method and then train the optimal architecture. The parameter variations of the training process are shown in Fig. 3a, where the percentage represents the time of architecture improvement as a percentage of the overall evaluation time. It can be seen through Fig. 3a that in the middle and late stages of architecture training, the time interval for model accuracy improvement also increases gradually. The reason for this phenomenon is the use of cosine learning rate annealing in the DARTS method, which is a learning rate adjustment strategy commonly used in training neural network models by adjusting the learning rate during the training process through the properties of the cosine function. The formula is expressed as follows:

ℓt=ℓmin+12⋅(ℓmax−ℓmin)(1+cos(πτE))(7)

where, ℓmax and ℓmin are the maximum and minimum values of the learning rate, τ and E are the current epoch and total number of epochs, respectively. Although cosine annealing has a broad application, it can be seen in Fig. 3a, it is not suitable for the architecture training process in this paper. Using cosine learning rate annealing to train the architecture, the learning rate decays slowly in the early stage, followed by a rapid decay in the middle stage, and then changes to a slow decay in the later stage. The unbalanced learning rate decay results in an unstable model training process, and the accuracy curve in the convergence process shakes more, ultimately reducing the final result of architecture training and the efficiency of training architectures. Therefore, this paper redefines the natural exponential learning rate decay as follows:

ℓt=ℓmin+1e−1(ℓmax−ℓmin)(e12⋅(ℓmax−ℓmin)(1+cos⁡(πτE))−1)(8)

Figure 3: Comparison of cosine annealing and natural exponential cosine annealing

By using the natural exponential learning rate described above to adjust the learning rate variation, the training process decays more rapidly in the early stages and maintains a relatively low learning rate in the later stages, thus improving the architecture search efficiency. The parameter variations of the training process using the natural exponential cosine annealing method for training the architecture are shown in Fig. 3b.

3.5 Auxiliary Augmentation

After achieving a more stable architecture training process, we consider how to enhance the final performance of architecture training. There are many auxiliary methods for enhancing architecture search performance, each providing varying degrees of performance gain, for instance, data augmentation, knowledge distillation, network pruning, early stopping strategy, and more. To further enhance the performance of architecture search, we utilized two auxiliary methods in this study: data augmentation and group convolution.

3.5.1 Data Augmentation

Data augmentation [37] is a technique that expands the volume of data by creating altered versions of the original data. This technique modifies the original data through various transformations, such as translation, rotation, scaling, flipping, noise addition, etc. Data augmentation helps the model generalize to novel, unseen data, mitigating overfitting, and thereby improving model performance. In architecture search, data augmentation enables the identified model to perform better when encountering diverse data. Hence, we utilized data augmentation to enhance the performance of the architecture search.

3.5.2 Group Convolution

In standard convolution, all input channels convolve with each filter. Group convolution, a variant, divides the input channels into several groups, with each filter convolving with one group of channels. This significantly reduces the computational load and model parameters, making the model more efficient and scalable. Therefore, we replaced standard convolution with group convolution, maintaining performance while reducing model complexity, making the search process more efficient, and reducing the computational cost.

By leveraging the above two auxiliary tools, the architecture search process has minimized the occurrence of overfitting, improved model generalization capability, and enhanced search efficiency. In summary, we propose a faster and more effective gradient-based neural network architecture search method (AllegroNAS), which identifies competitive neural network architectures against other SOTA methods by utilizing a more stable architecture search method in a more effective search space. The more intuitive process diagram of the AllegroNAS method is shown in Fig. 4.

Figure 4: AllegroNAS Flowchart

3.6 Relationship to Prior Work

AttDARTS [11] and SharpDARTS [12] methods also propose a new search space based on the DARTS search space, but our approach is more efficient and less computationally intensive compared to them.

MS-DARTS [15] and β-DARTS [16] methods propose a regularization based on single-level optimization, different from them we adopt an asymptotic mixed-level regularization method, which allows us to dynamically change the regularization terms during the architectural search process, thus improving the search efficiency.

In addition, our method employs natural exponential cosine annealing and auxiliary augmentation, which makes the architecture more stable during training, compared to all other gradient-based methods. A detailed comparison with other methods is shown in Table 1.

4  Experiments

4.1 Datasets

We perform architectural searches on the CIFAR10 dataset and then perform architectural evaluation on the CIFAR10, CIFAR100, and ImageNet-ILSVRC2012 datasets. The CIFAR10 dataset has a total of 60,000 color images, which consists of 50,000 training set images and 10,000 test set images. The dataset contains ten categories, each category consists of five thousand images from the training set and one thousand images from the test set, each with a resolution size of 32×32. The CIFAR10 dataset does not contain a huge number of images but has a rich training set, so it was chosen to perform the architecture search process on this dataset. The CIFAR100 dataset is similar to the CIFAR10 dataset in composition, and it also contains 60,000 color images with a resolution size of 32×32 color images. Each subcategory contains 600 images, of which 500 are training set images and 100 are test set images. The ImageNet-ILSVRC2012 dataset is a subset of the ImageNet dataset, where the training set contains 1.3 million color images, the validation set contains 50,000 color images, and both the training and validation sets include 1000 categories. All the experiments in this paper are conducted through a single NVIDIA V100 GPU.

4.2 Ablation Experiment

According to our experiments if H or E is set too small, the search process converges very slowly and this search process takes a lot of time. If H  or E is set too large, the network architecture searched is full of nonparametric operations, which makes the final network architecture searched meaningless. If the range of χ is set too large, it will make the search process underfitting, conversely, it will not prevent overfitting and will not improve the stability of the architecture search process. Therefore, after experimentation, in the architecture search phase, we set H, χmax, χmin, and E to 25, 0.1, 0, and 90, respectively, and all other settings are the same as those of the DARTS method. The optimal architecture searched by the AllegroNAS method is shown in Fig. 5.

Figure 5: Optimal network architecture diagrams

To validate the methods proposed within this paper in Subsections 3.2 to 3.5, we conduct ablation experiments on the searched optimal architectures, and the experimental results are shown in Table 2, where Ours_1 denotes architecture search using only the asymptotic architecture parameter regularization proposed in this paper, Ours_2 denotes Ours_1 + the Allegro search space proposed in this paper, and Ours_3 denotes Ours_2 + auxiliary enhancement. Firstly, we can find through Table 2 that the architecture accuracy of Ours_1 is higher than that of the DARTS method, and the architecture accuracy of the neural network architectures searched by the AllegroNAS method is still higher than that of DARTS method even without using the AllegroConv, auxiliary enhancement, and natural exponential cosine annealing, which proves the effectiveness of the asymptotic architecture parameter regularization proposed in this paper. The AllegroNAS method can search neural network architectures with higher performance with a more stable search process.

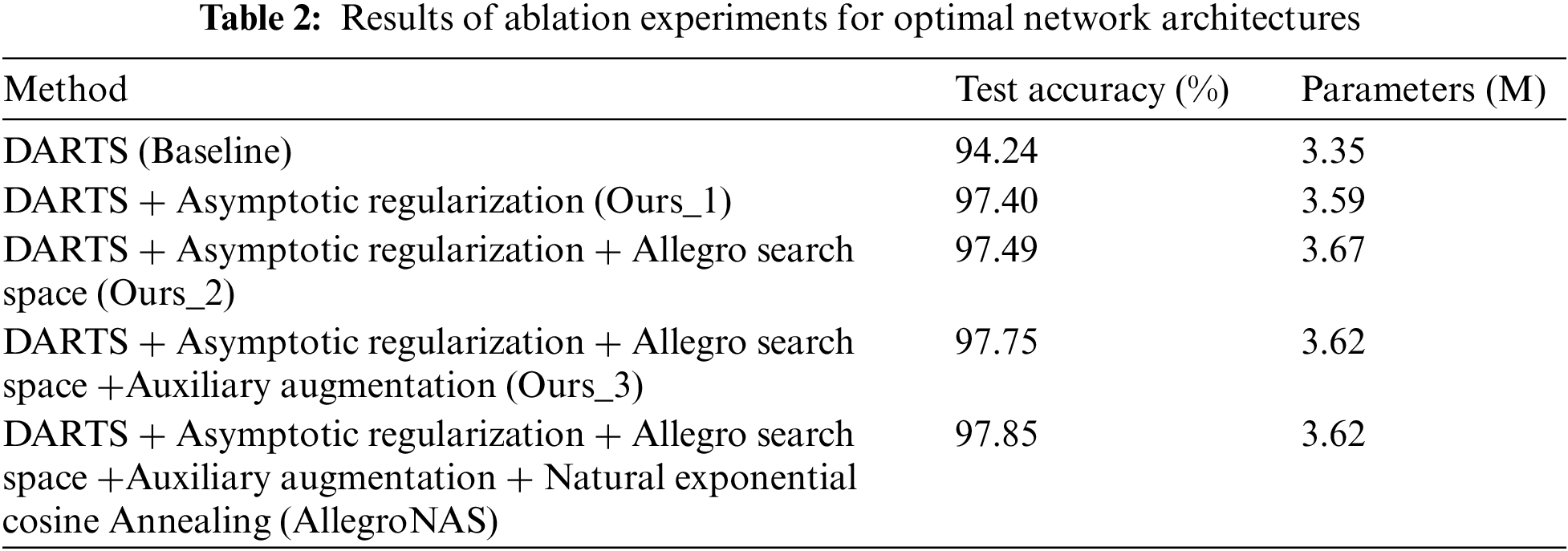
Secondly, Ours_2 accuracy is higher than DARTS and Ours_1, thus proving the effectiveness of the Allegro convolution module proposed in this paper. Then, Ours_3 accuracy is higher than DARTS, Ours_1, and Ours_2, verifying the feasibility of the auxiliary enhancement method proposed in this paper. In addition, the final architecture searched by the AllegroNAS method contains more operations compared to the DARTS method, such as the convolution operation with a convolution kernel size of 5 and the average pooling operation. The fact that the AllegroNAS method did not prefer the skip_connect operation more than the DARTS method also gives further evidence that the AllegroNAS method has higher stability.

Finally, AllegroNAS shows a further improvement in accuracy relative to DARTS, Ours_1, Ours_2, and Ours_3. In addition, after using the natural exponential cosine annealing method proposed in this paper, we can see that the number of blue percentage points greater than line = 3% in Fig. 3b is significantly reduced, and the distribution of the blue points is closer to the bottom, proving the feasibility of our proposed natural exponential cosine annealing method. Meanwhile, through Fig. 3c, we can see that in the middle stage of the architecture search, the difference between each epoch of the training process that used the natural exponential cosine annealing method is significantly smaller than that of the training process that did not use it (the area in pink is obviously smaller than the area in green), the validation accuracy curve in yellow is also a bit flatter, the process of accuracy enhancement is more stable, and thus further validates the importance of the natural exponential cosine annealing method. In summary, the AllegroNAS method improves the accuracy from 97.24%, which is difficult to further improve, to 97.85% relative to the DARTS method within the acceptable range of 0.27 M increase in the number of covariates, which realizes a significant improvement in the accuracy, and also fully proves the reliability of the AllegroNAS method proposed in this paper.

4.3 Architecture Evaluation

In the architecture evaluation phase, the parameter settings are the same as the DARTS method. First, on the CIFAR10 dataset, we retrain the best neural network architecture searched in the architecture search phase for 600 epochs and compare it with other methods. The comparison results are shown in Table 3. As can be seen from Table 3, the AllegroNAS method achieves a test error of 2.15% with 3.62 M parameters, which is significantly better than the other methods. Although the method of this paper is not dominant in the search time, it dramatically reduces the test error without increasing the number of parameters, which also proves the effectiveness of the method of this paper.

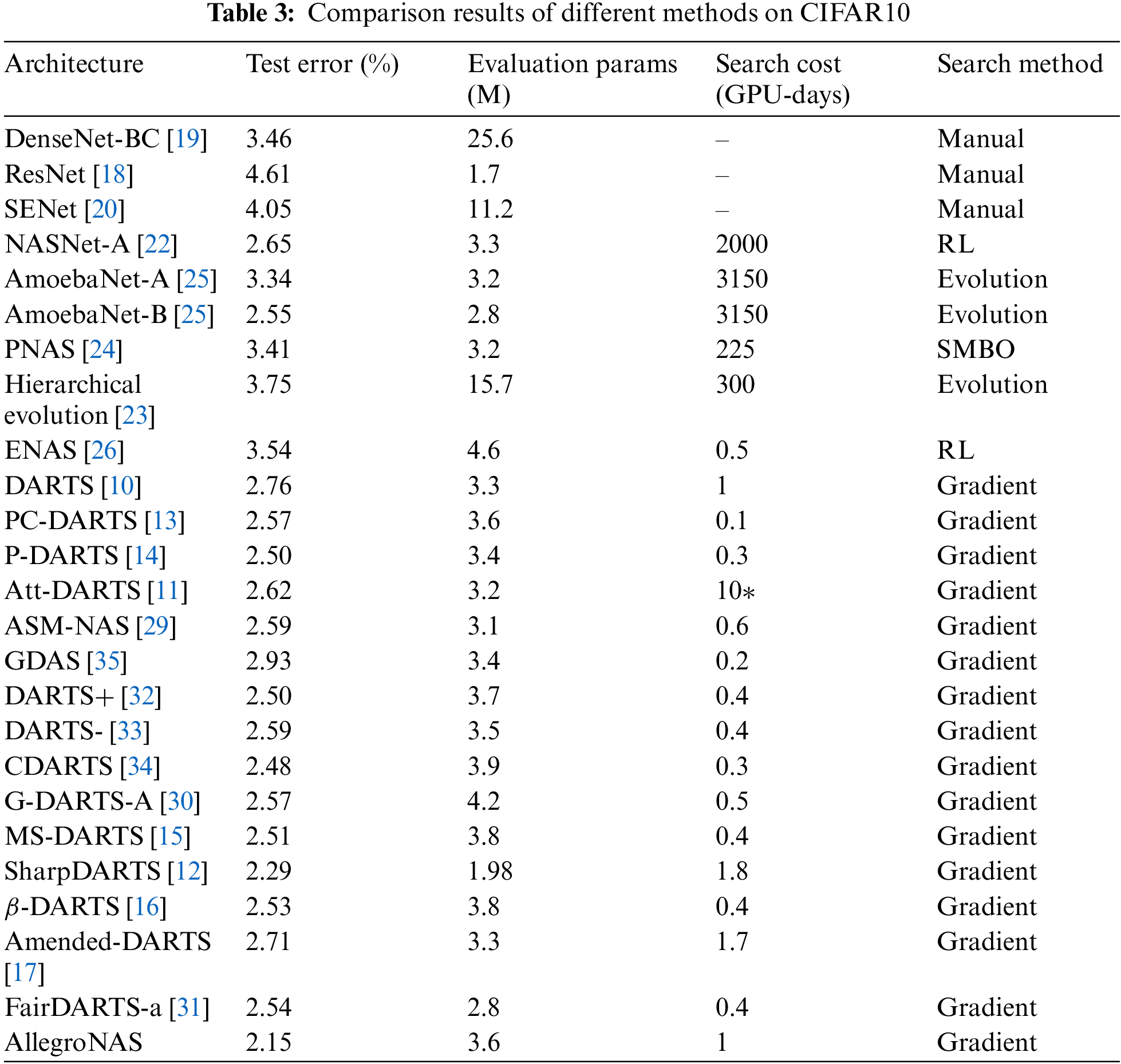
To prove that the best neural network architecture searched by the method in this paper is extensible, we migrate the best architectures searched on the CIFAR10 dataset to the CIFAR100 dataset for retraining and compare them with the other SOTA methods. The comparison results are shown in Table 4. As can be seen from Table 4, the AllegroNAS method achieves 14.92% test error with 3.67M parameters, and the AllegroNAS method also performs well on the CIFAR100 dataset, outperforming other SOTA methods. Although the AllegroNAS method yielded a slightly higher number of parameters than the DARTS, P-DARTS, GDAS, ASM-NAS, DARTS-, and ATT-DARTS methods, the method of this paper has a significant improvement in accuracy.

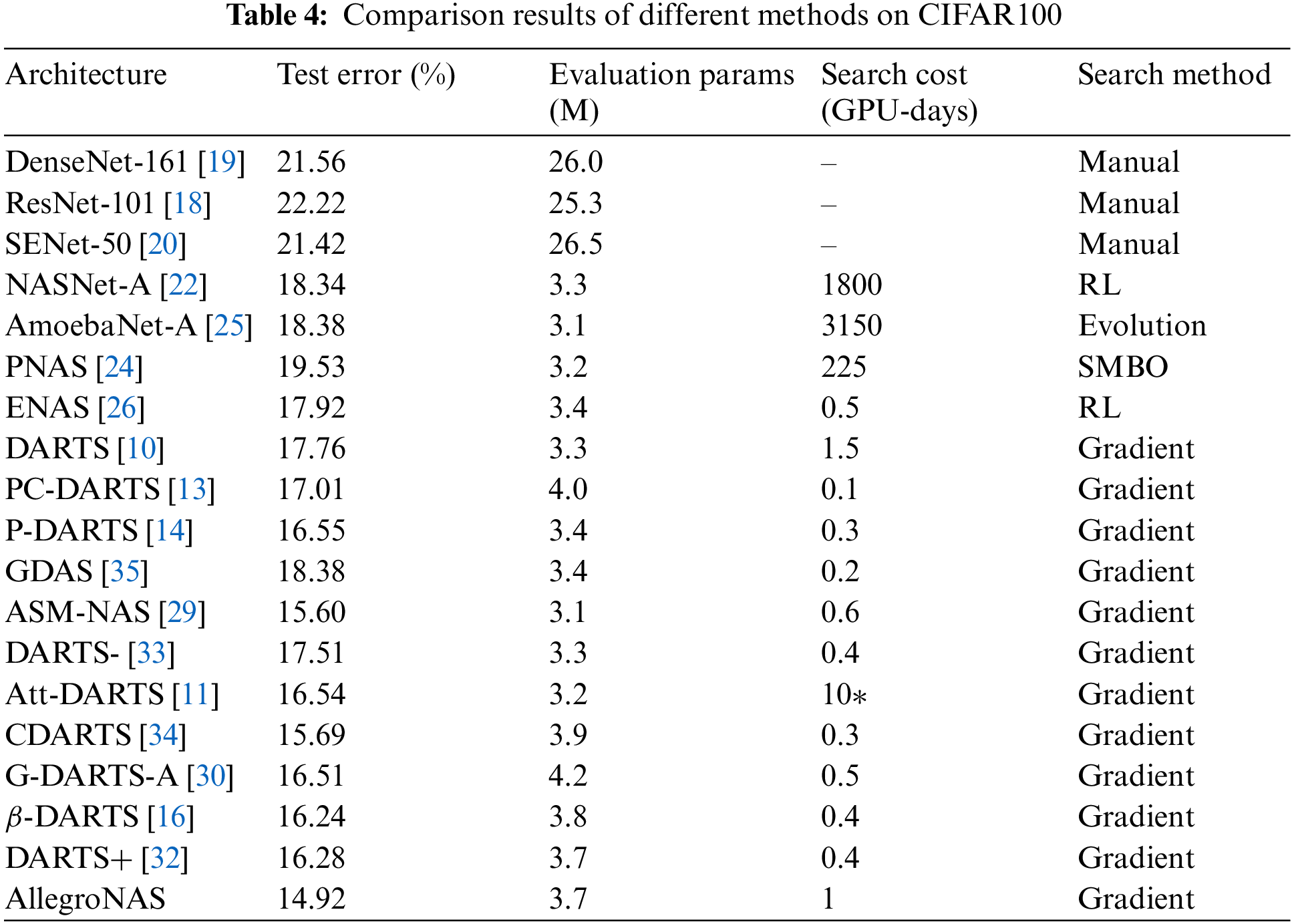
To further prove the effectiveness of the method in this paper, we extend it to a larger ImageNet dataset for architectural evaluation, and to make a fair comparison, the parameter settings of the AllegroNAS method are the same as those of the DARTS method. The results of its evaluation are shown in Table 5 in comparison with other SOTA methods. Table 5 shows that the AllegroNAS method achieves 25.4% Top1 test error and 8.1% Top5% test error with 5.08M parameters. First, the AllegroNAS method outperforms manually designed neural networks and is superior to NAS-Net and AmoebaNet. Compared to other gradient-based architecture search methods, the AllegroNAS method significantly outperforms PNAS, DARTS, Att-DARTS, ASM-NAS, GDAS, and FairDARTS. PC-DARTS, β-DARTS, and Amended-DARTS methods have higher parameters than the AllegroNAS method despite having slightly higher accuracy than the AllegroNAS method.

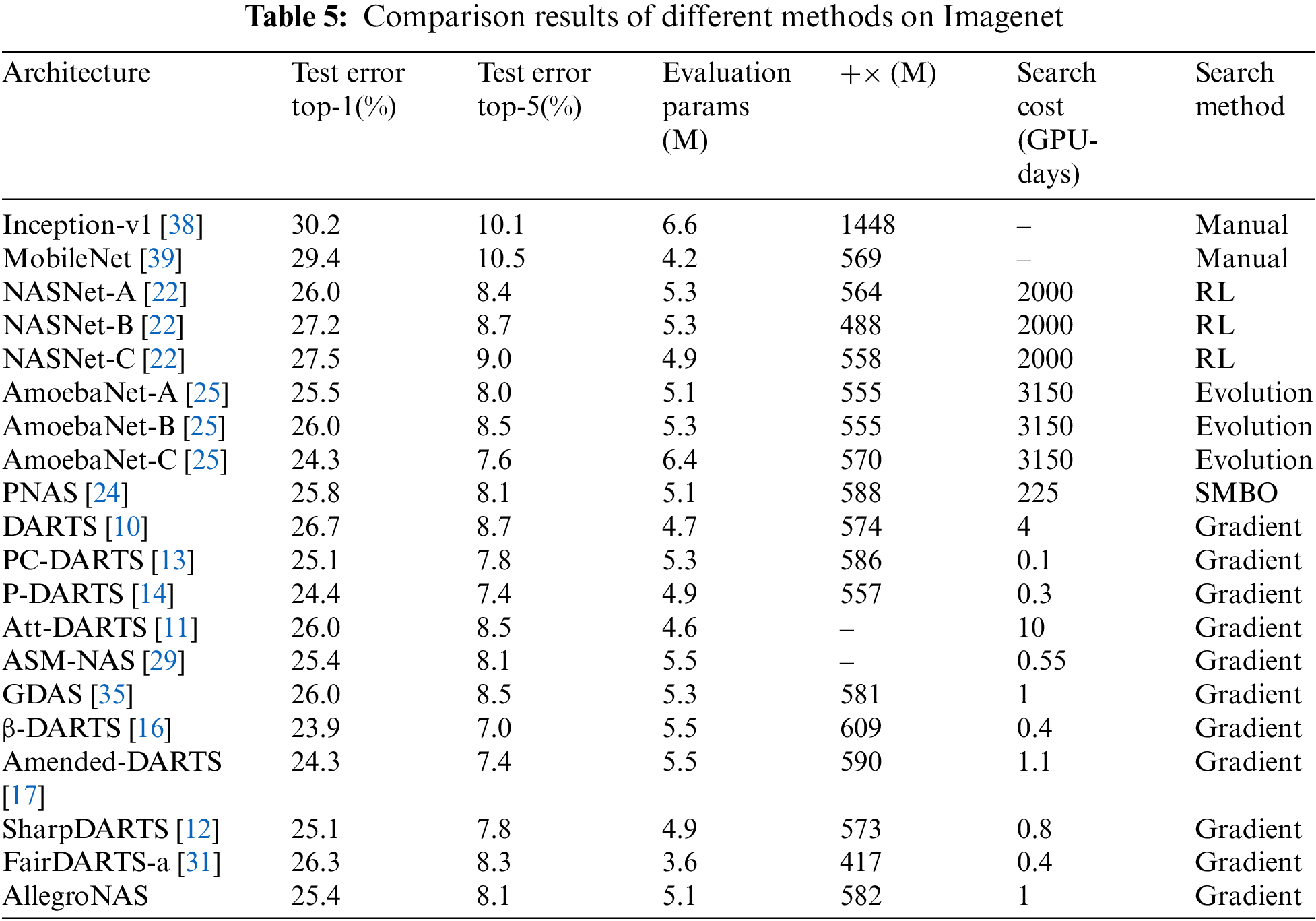
In summary, the AllegroNAS method proposed in this paper is superior to the vast majority of methods, and it also proves that the AllegroNAS method can be extended well to larger datasets, and the AllegroNAS method has strong competitiveness. In addition, although the method in this paper does not have an advantage in search time, compared with other methods, the AllegroNAS method does not add other artificial methods to scale down the search cost, such as partial sampling in the PC-DARTS method or early stopping strategy in the DARTS+ method, etc., therefore the number of parameters that need to be artificially set by the method in this paper is also less compared with other methods. In the future, we will also continue to study how to optimize a better balance between accuracy, number of parameters, and search time. To show the comparison results more intuitively, we plotted the comparison results, and the results are shown in Fig. 6.

Figure 6: Comparison of results on the three datasets

5  Conlusions

This paper presents a faster and more effective neural network architecture search method, AllegroNAS. Firstly, we propose an Allegro search space enriched by introducing two new convolutional modules, AllegroSepConv and AllegroDilConv. The two new convolutional modules enable operations in the search space to obtain more feature information and provide more possibilities for the architectures discovered during the architecture search. Secondly, we adopt an asymptotic optimization process by dynamically adjusting the size of regularization parameters to bring the search process closer to the search target, thereby enhancing the robustness of the architecture search. Furthermore, we introduce a faster natural exponential cosine learning rate annealing method, which rationalizes the architecture training process. In addition, to improve the architecture search performance, we utilize data augmentation and group convolutions, which further enhance search performance and reduce computational costs. Finally, through extensive experiments on different datasets, we demonstrate that the final architecture searched by the method in this paper exhibits a competitive architecture performance with SOTA in image classification tasks. The method in this paper is not dominant in terms of the number of parameters and search time, and in future work, we will continue to investigate how to optimize these two parameters while maintaining accuracy.

Acknowledgement: We thank all the members who have contributed to this work with us.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grant 61305001 and the Natural Science Foundation of Heilongjiang Province of China under Grant F201222.

Author Contributions: Conceptualization: Cong Jin, Yuanjian Chen; Methodology: Cong Jin; Formal analysis: Cong Jin, Jinjie Huang, Yuqing Gong; Writing—original draft preparation: Cong Jin; Writing—review and editing: Jinjie Huang, Cong Jin; Software resources: Jinjie Huang. All authors read and approved the final manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in Pytorch repository at https://pytorch.org/vision/stable/datasets.html. The data that support the findings of this study are openly available at https://image-net.org.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Zhang, W. Jing, J. Lin, N. Fang, W. Wei et al., “Automatic design and architecture search of neural network for semantic segmentation in remote sensing images,” Sensors, vol. 20, no. 18, pp. 5292, 2020. [Google Scholar] [PubMed]

2. C. Wang, X. Wang, Y. Wang, S. Hu, H. Chen et al., “FastDARTSDet: Fast differentiable architecture joint search on backbone and FPN for object detection,” Applied Sciences, vol. 12, no. 20, pp. 10530, 2022. [Google Scholar]

3. Z. Zhang, Y. Shan and J. Yuan, “Multi-level cell progressive differentiable architecture search to improve image classification accuracy,” Journal of Signal Processing Systems, vol. 93, pp. 689–699, 2021. [Google Scholar]

4. Q. Wan, L. Wu and Z. Yu, “Dual-cell differentiable architecture search for language modeling,” Journal of Intelligent & Fuzzy Systems, vol. 41, no. 2, pp. 3985–3992, 2021. [Google Scholar]

5. Q. Du, N. Xu, Y. Li, T. Xiao and J. Zhu, “Topology-sensitive neural architecture search for language modeling,” IEEE Access, vol. 9, pp. 107416–107423, 2021. [Google Scholar]

6. Q. Li, X. Wu and T. Liu, “Differentiable neural architecture search for optimal spatial/temporal brain function network decomposition,” Medical Image Analysis, vol. 69, pp. 101974, 2021. [Google Scholar] [PubMed]

7. L. Hu, Q. Liu, J. Zhang, F. Jiang, Y. Liu et al., “A-DARTS: Attention-guided differentiable architecture search for lung nodule classification,” Journal of Electronic Imaging, vol. 30, no. 1, pp. 013012, 2021. [Google Scholar]

8. Y. Liu, T. Li, P. Zhang and Y. Yan, “SFA: Searching faster architectures for end-to-end automatic speech recognition models,” Computer Speech & Language, vol. 81, pp. 101500, 2023. [Google Scholar]

9. S. Hu, X. Xie, M. Cui, J. Deng, S. Liu et al., “Neural architecture search for LF-MMI trained time delay neural networks,” IEEE/ACM Transactions on Audio, Speech, and Language Processing, vol. 30, pp. 1093–1107, 2022. [Google Scholar]

10. H. Liu, K. Simonyan and Y. Yang, “Darts: Differentiable architecture search,” arXiv preprint arXiv: 1806.09055, 2018. [Google Scholar]

11. K. Nakai, T. Matsubara and K. Uehara, “Neural architecture search for convolutional neural networks with attention,” IEICE TRANSACTIONS on Information and Systems, vol. 104, no. 2, pp. 312–321, 2021. [Google Scholar]

12. A. Hundt, V. Jain and G. D. Hager, “sharpDARTS: Faster and more accurate differentiable architecture search,” arXiv preprint arXiv:1903.09900, 2019. [Google Scholar]

13. Y. Xu, L. Xie, X. Zhang, X. Chen, G. J. Qi et al., “PC-DARTS: Partial channel connections for memory-efficient architecture search,” arXiv preprint arXiv:1907.05737, 2019. [Google Scholar]

14. X. Chen, L. Xie, J. Wu and Q. Tian, “Progressive differentiable architecture search: Bridging the depth gap between search and evaluation,” in Proc. of ICCV, Seoul, South Korea, pp. 1294–1303, 2019. [Google Scholar]

15. J. W. Hsieh, M. C. Chang, P. Y. Chen, S. Santra, C. H. Chou et al., “MS-DARTS: Mean-shift based differentiable architecture search,” arXiv preprint arXiv:2108.09996, 2021. [Google Scholar]

16. P. Ye, B. Li, Y. Li, T. Chen, J. Fan et al., “β-DARTS: Beta-decay regularization for differentiable architecture search,” in Proc. of CVPR, New Orleans, LA, USA, pp. 10864–10873, 2022. [Google Scholar]

17. K. Bi, C. Hu, L. Xie, X. Chen, L. Wei et al., “Stabilizing darts with amended gradient estimation on architectural parameters,” arXiv preprint arXiv:1910.11831, 2019. [Google Scholar]

18. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. of CVPR, Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]

19. G. Huang, Z. Liu, L. van der Maaten and K. Q. Weinberger, “Densely connected convolutional networks,” in Proc. of CVPR, Honolulu, HI, USA, pp. 4700–4708, 2017. [Google Scholar]

20. J. Hu, L. Shen and G. Sun, “Squeeze-and-excitation networks,” in Proc. of CVPR, Salt Lake City, UT, USA, pp. 7132–7141, 2018. [Google Scholar]

21. B. Zoph and Q. V. Le, “Neural architecture search with reinforcement learning,” arXiv preprint arXiv: 1611.01578, 2016. [Google Scholar]

22. B. Zoph, V. Vasudevan, J. Shlens and Q. V. Le, “Learning transferable architectures for scalable image recognition,” in Proc. of CVPR, Salt Lake City, UT, USA, pp. 8697–8710, 2018. [Google Scholar]

23. H. Liu, K. Simonyan, O. Vinyals, C. Fernando and K. Kavukcuoglu, “Hierarchical representations for efficient architecture search,” arXiv preprint arXiv:1711.00436, 2017. [Google Scholar]

24. C. Liu, B. Zoph, M. Neumann, J. Shlens, W. Hua et al., “Progressive neural architecture search,” in Proc. of ECCV, Munich, Germany, pp. 19–34, 2018. [Google Scholar]

25. E. Real, A. Aggarwal, Y. Huang and Q. V. Le, “Regularized evolution for image classifier architecture search,” Proc. of AAAI, vol. 33, no. 1, pp. 4780–4789, 2019. [Google Scholar]

26. H. Pham, M. Guan, B. Zoph, Q. Le and J. Dean, “Efficient neural architecture search via parameters sharing,” in Proc. of ICML, Stockholm, Sweden, pp. 4095–4104, 2018. [Google Scholar]

27. P. Liashchynskyi and P. Liashchynskyi, “Grid search, random search, genetic algorithm: A big comparison for NAS,” arXiv preprint arXiv:1912.06059, 2019. [Google Scholar]

28. L. Li and A. Talwalkar, “Random search and reproducibility for neural architecture search,” in Proc. of AAAI, New York, NY, USA, pp. 367–377, 2020. [Google Scholar]

29. J. Hao and W. Zhu, “Architecture self-attention mechanism: Nonlinear optimization for neural architecture search,” Journal of Nonlinear and Variational Analysis, vol. 5, pp. 119–140, 2021. [Google Scholar]

30. Z. Wang, W. Zhang and Z. Wang, “G-DARTS-A: Groups of channel parallel sampling with attention, 2020,” arXiv preprint arXiv:2010.08360, 2020. [Google Scholar]

31. X. Chu, T. Zhou, B. Zhang and J. Li, “Fair DARTS: Eliminating unfair advantages in differentiable architecture search,” in Proc. of ECCV, pp. 465–480, 2020. [Google Scholar]

32. H. Liang, S. Zhang, J. Sun, X. He, W. Huang et al., “DARTS+: Improved differentiable architecture search with early stopping,” arXiv preprint arXiv:1909.06035, 2019. [Google Scholar]

33. X. Chu, X. Wang, B. Zhang, S. Lu, X. Wei et al., “DARTS-: Robustly stepping out of performance collapse without indicators,” arXiv preprint arXiv:2009.01027, 2020. [Google Scholar]

34. H. Yu, H. Peng, Y. Huang, J. Fu, H. Du et al., “Cyclic differentiable architecture search,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 45, no. 1, pp. 211–228, 2022. [Google Scholar] [PubMed]

35. X. Dong and Y. Yang, “Searching for a robust neural architecture in four gpu hours,” in Proc. of CVPR, Long Beach, CA, USA, pp. 1761–1770, 2019. [Google Scholar]

36. C. He, H. Ye, L. Shen and T. Zhang, “MiLeNAS: Efficient neural architecture search via mixed-level reformulation,” in Proc. of CVPR, pp. 11993–12002, 2020. [Google Scholar]

37. E. D. Cubuk, B. Zoph, D. Mane, V. Vasudevan and Q. V. Le, “Autoaugment: Learning augmentation strategies from data,” in Proc. of CVPR, Long Beach, CA, USA, pp. 113–123, 2019. [Google Scholar]

38. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed et al., “Going deeper with convolutions,” in Proc. of CVPR, Boston, MA, USA, pp. 1–9, 2015. [Google Scholar]

39. A. G. Howard, M. Zhu, B. Chen, D. Kalenichenko, W. Wang et al., “Mobilenets: Efficient convolutional neural networks for mobile vision applications,” arXiv preprint arXiv:1704.04861, 2017. [Google Scholar]