Color Image Compression and Encryption Algorithm Based on 2D Compressed Sensing and Hyperchaotic System

1  Introduction

Owing to the advent of the big data era and multimedia technology, digital color images are applied in every field of people’s lives with the advantages of high resolution and intuitive expression. However, there are also many security risks in image transmission while being convenient [1]. Therefore, many scholars have been attracted to studying more secure encryption schemes in this field. At present, techniques for text encryption have become increasingly mature within the information encryption domain [2]. However, with the emergence of digital color images, simple text encryption methods are no longer sufficient. With the improvement of technology, the means of attackers are also becoming increasingly sophisticated. In today’s world, establishing a reliable and efficient encryption technique has become crucial [3].

American meteorologist E. Lorenz originally put up the idea of chaos in 1963. Unpredictability, unrepeatability, and nonrepeating ability define its behavior [4,5]. Consequently, numerous properties of chaotic systems apply to cryptography [6]. It has also aroused great interest in the last few decades [7]. Among the often employed chaotic systems are 1D chaotic systems [8], 2D chaotic systems [9], Multiple-dimensional chaotic systems, and hyperchaotic systems. In [10], a new chaotic system made up of two chaotic systems was used as an image encryption scheme. A new algorithm combining optics has been proposed by Liu et al. in [11]. In [12], a joint scrambling and diffusion scheme was proposed by Li et al. Reference [13] proposed a unique SCCM system that is 1D. Additionally, it provided a random DNA operation and SCCM-based image encryption technique. The scheme’s strong encryption effect is confirmed by the experiment. Compared to high-dimensional chaotic systems, the nonlinear behavior of the hyperchaotic systems is more intricate and unpredictable [14]. These characteristics show that applying a hyperchaotic system to image encryption will enhance system security [15].

Due to the rapid development of compressed sensing (CS) technology [16], its application in image processing has attracted the attention of many scholars. CS can compress and encrypt the image simultaneously, so digital image processing using CS technology has become a new research hotspot [17,18]. It is highly concerned in many fields, like computer vision and wireless communication. Gong et al. proposed an advanced algorithm for compressing and encrypting images [19]. Arnold transformation is used to arrange the image’s original, and then CS compresses and encrypts the resulting image. Subsequently, Zhang et al. proposed a cryptographic technique combining double random phase encoding with compressed sensing [20]. The scheme combines two images into one by encrypting and compressing them, increasing the difficulty of the algorithm. The scheme’s efficacy and sophisticated nature are demonstrated by the experimental results. In [21], Chai et al. offered a block compression and multi-objective optimization-based image encrypting system. In [22], this research proposed a unique data transfer paradigm that combines a hybrid cloud with semi-tensor product compression sensing. The efficiency and security of this approach are shown by the results of the simulation. Currently, most CS cryptographic algorithms are used to process gray images [23], so effectively compressing and encrypting color images is a problem worth studying.

This paper presents a novel approach for image encryption that leverages 2D CS, the 4D hyperchaotic system, and the joint permutation diffusion (JPD) approach to address this issue. There are three stages to this paper’s encryption algorithm. Firstly, generating initial values of hyperchaotic systems using the RSA algorithm. The system creates the matrix and chaotic sequence required for encryption. The Lorenz hyperchaotic system is prepared for the scrambling operation. Secondly, in the CS part, a grayscale mapping strategy is to process images and 2D CS to compress and quantify the mapped image. Among them, the 4D hyperchaotic system generates one measurement matrix, and the other is generated randomly, greatly increasing randomness. Finally, the encryption part encrypts the processed image using scrambling and spreading algorithms simultaneously. The decryption process consists of two distinct phases. The first step during the decryption process involves performing the inverse operation of JPD. Then, the 2DPG-ED algorithm decrypts the ciphertext image. Simulation experiments and performance analysis have demonstrated the effectiveness of the algorithm presented in this paper, showcasing its resilience against common attacks. After comparative analysis, the proposed algorithm has better encryption performance and less distortion ratio.

The remainder of this work is comprised of the following sections. Section 2 provides an overview of the preliminary work. Section 3 provides a detailed description of the proposed encryption scheme. Section 4 describes the experimental simulation results and analysis. Section 5 serves as the conclusion in the end.

2  Preliminary Work

2.1 The 4D Hyperchaotic System

A novel and extremely intricate 4D hyperchaotic system was suggested by [24]. Its definition is using the equation below:

x^=a(y−x−w)+byz,y^=c(4x+y)−xz,z^=dx−ez+xy,w^=rx+f(3yz+y2),(1)

here, a = 80, b = 45, c = 22, d = 5, e = 21, f = 8 and 60 ≤ r ≤ 322.

The system’s motion characteristics are represented by the Lyapunov exponent. For chaotic systems, they require at least one Lyapunov exponent to be positive. The system is said to be hyperchaotic when at least two of the exponents are positive. When r = 100, the Lyapunov exponents are LE1 = 25.6206, LE2 = 11.2401, LE3 = 1.717e−5, LE4 = −115.0336. Therefore, system Eq. (1) is in a state of hyperchaos. Fig. 1 depicts its hyperchaotic attractor when the initial condition is (0, 0.5, 0.5, 0.5).

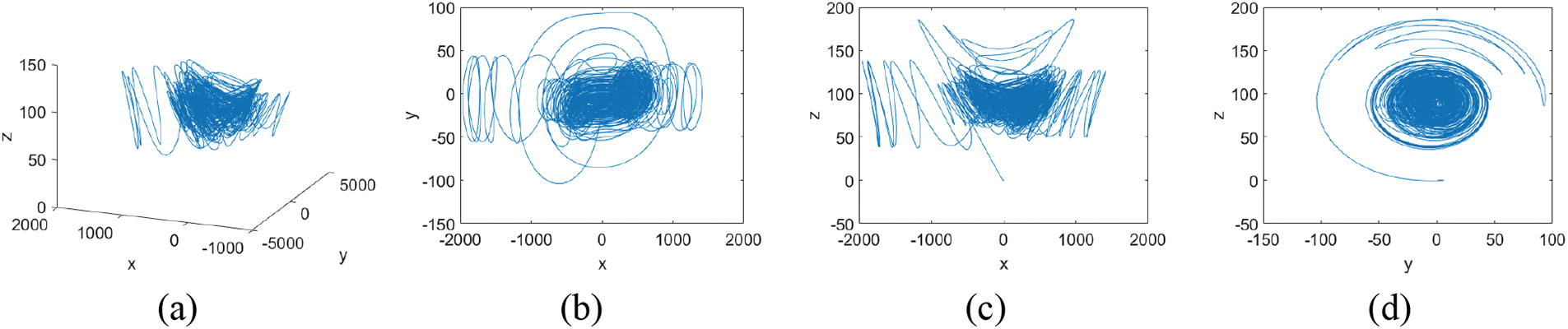
Figure 1: The system (1)’s hyperchaotic attractor at r = 100. The projections are as follows: (a) in x−y−z, (b) in x−y, (c) in x−z, and (d) in y−z

2.2 RSA Algorithm

In 1977, Rivest, Shamir, and Adleman proposed the public-key cryptography known as RSA. It is an asymmetric cryptographic algorithm [25]. It can be used to encrypt and digitally sign data, and for encryption and decoding, the system requires two distinct keys. The most extensively researched algorithm for public-key cryptography is the RSA algorithm. It has been put forth for almost 30 years and has also faced criticism on several occasions. The process of generating ciphertext using the RSA algorithm is shown in Fig. 2.

Figure 2: RSA algorithm

2.3 2D CS

In the process of sampling the signal, the signal compression is completed simultaneously by the CS theory; therefore, many image compression and encryption techniques employ CS theory [26]. For 2D CS, consider an N×N image P, in sparse form, which can be expressed as: β=ΨPΨT, β is a sparse representation of the P, Ψ is an N×N orthogonal base. Two measurement matrices: Φ1 and Φ2. They are needed for the 2D image P sampling and compression processes. The dimension of both matrices is M×N(M<N). Y’s measurement value is represented as a M×M matrix. It can be expressed as: Y=Φ1PΦ2T, where Φ1 and Φ2 meet the Restricted Isometry Property (RIP). Furthermore, by figuring out the following equation: min‖β‖0s.t.Y=Φ1PΦ2T, where ‖β‖0 is the l0 norm of β, we may precisely recreate P from Y.

An orthogonal matching pursuit algorithm is the primary CS reconstruction method [27], a reconstruction algorithm based on smooth l0 norm [28], a base tracking algorithm, gradient projection for sparse reconstruction [29], etc. The reconstruction algorithm in this paper adopts the 2DPG-ED method [30]. Under the premise of fast signal reconstruction, the algorithm ensures the quality of the image reconstruction by keeping the image information.

3  The Proposed Encryption Scheme

3.1 Encryption Process

Fig. 3 depicts the encryption processing flowchart; a further discussion of the procedure will follow:

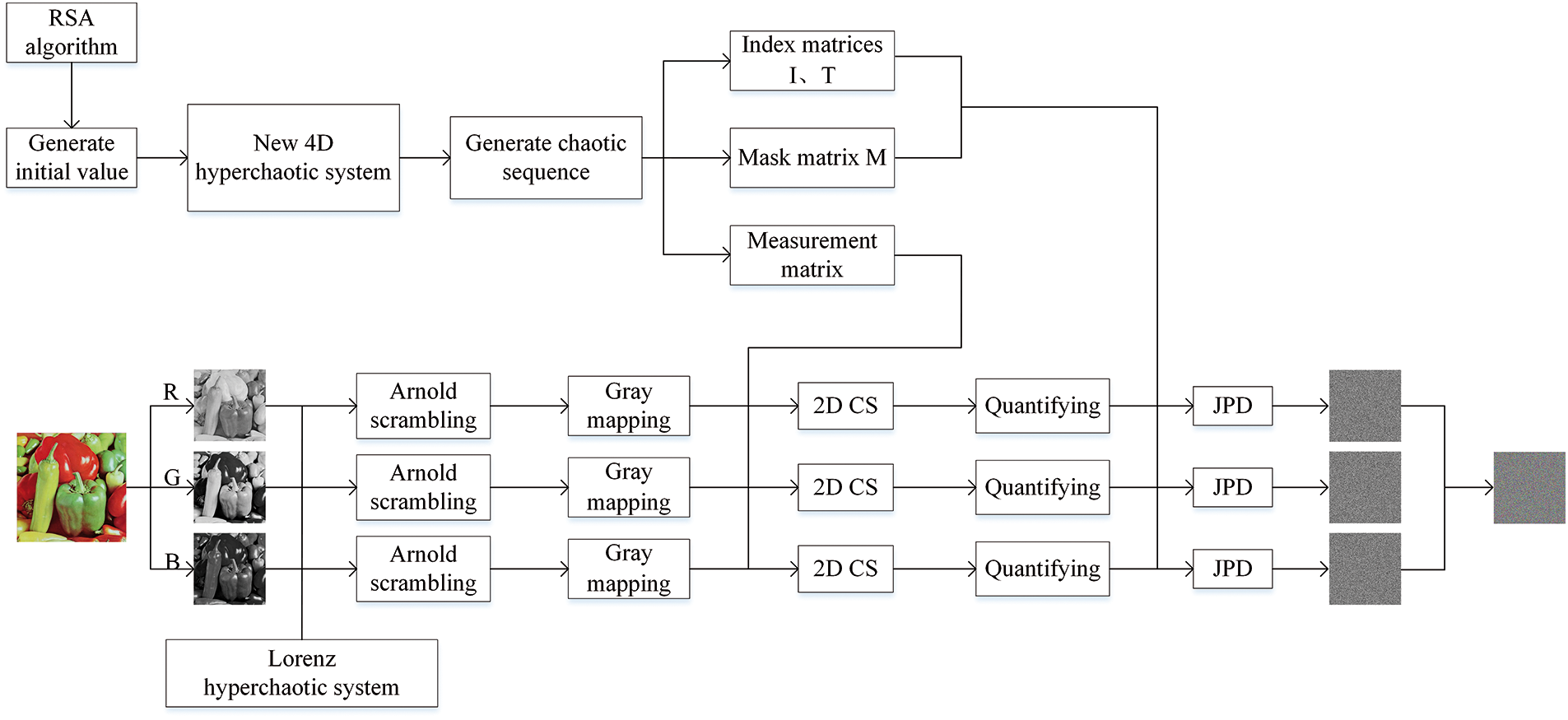
Figure 3: The procedure flow chart for the image encryption

Step 1: Generate initial values for the hyperchaotic system Eq. (1). At random, four large positive integers (m1,m2,m3,m4) are chosen. According to Fig. 2, then the public key (e, n) will be used for the computation of ci=miemodn, i = 1, 2, 3, 4. Using Eq. (2), the initial value of the 4D hyperchaotic system is computed as the final step.

x0=sqrt(log⁡(c1+m1)),y0=sqrt(log⁡(c2+m2)),z0=sqrt(log⁡(c3+m3)),w0=sqrt(log⁡(c4+m4)).(2)

Step 2: Generate a chaotic sequence. Based on the initial values Eq. (2), the system Eq. (1) generates a sufficiently long sequence iteratively. In the jth iteration, it is possible to obtain four status values rj={xj,yj,zj,wj}. Upon completing the iteration, by joining all the rj(j=1,2,⋯,n), it can obtain the hyperchaotic sequence S. It is shown in the Eq. (3).

S={r1,r2,⋯,rn}={x1,y1,z1,w1,⋯,xn,yn,zn,wn}={r1,r2,r3,r4,⋯,r4n−3,r4n−2,r4n−1,r4n}.(3)

Step 3: Generate mask matrix M and index matrices I, T. The chaotic sequences are utilized to select four sequences at random, r1, r2, r3, and r4, which are then arranged in ascending order to generate si1, si2, si3, and si4. Matrices I, T and M, specifically, they are described as follows: I(i,j)=si1(mod(i+si2(j)−1,w)+1), T(i,j)=si3(mod(i+si4(j)−1,w)+1). Next, a sequence r5 is chosen at random, and M=reshape(mod(((r5−⌊r5⌋)×232),256),[h,w]), to obtain matrix M, here, w denotes the image’s width and h its height.

Step 4: Generate the measurement matrix. First, remove the first 3001 items from the chaotic sequence S to obtain better randomness. The chaotic sequence S is standardized through formulas, and the measurement matrix Phi1 is obtained. A slight disturbance Pe is added to x every 1000 iterations to make it more complex. Then, assume that Phi2 are random matrices of size M×N.

Phi1=[S1SM+1⋯SM(N−1)S2SM+2⋯SM(N−1)+1⋮⋮⋱⋮SMS2M⋯SMN].(4)

Step 5: The optimized Arnold transformation. The pseudo-random numbers a and b are obtained using the Lorenz hyperchaotic system. The matrix of images is transformed into a vector A’ in one dimension. Obtaining an updated coordinate position (p’, q’), perform the scrambling operation at any given point coordinate location (1, j) of the vector A’ to acquire the image U. Its representation is shown in Eq. (5).

[p ′q ′]=[1abab+1][1j].(5)

Step 6: Mapping of the grey values of the scrambled image to the range −128 to 128 using a grey mapping strategy, which can be the form of the following: Uξ=U−F, where F is a template matrix with entries all of 128, Uξ is a mapping of U, and U represents the encrypted image from the above steps.

Step 7: Make use of the measurement matrix that was produced in Step 4. Another measurement matrix is produced at random. To sample the mapping of the confused image, 2D CS is applied. Yξ=AUξBT=AUBT−AFBT=Y−YF, where A is Phi1 and B is Phi2, Y, Yξ and YF denote 2D measurements of U, Uξ and F.

Step 8: To get the bitstream, put Yξ into the scalar quantization (SQ) encoder.

Step 9: Conduct JPD operations on preprocessed images. Give an ordinary image with a channel P. Using the matrix generated in Step 3, perform joint permutation, and diffusion operations. The following Eq. (6) can be used to explain it. It is split up into three sections. Finally, the ciphertext image C is acquired.

CIi,j,j={mod(Mi,j⊕(PTj,Ii,j,Ii,j+PIh,w,w),F),ifi=1,j=1mod(Mi,j⊕(PTj,Ii,j,Ii,j+CIi−1,w,w),F),ifi≠1,j=1mod(Mi,j⊕(PTj,Ii,j,Ii,j+CIi,j−1,j−1),F),ifj≠1,(6)

here, i and j denote the matrix’s positions.

3.2 Decryption and Reconstruction Algorithm

As depicted in Fig. 4, decryption corresponds to the reverse process of encryption. In particular, original images are reconstructed using the 2DPG-ED reconstruction technique in the decryption process.

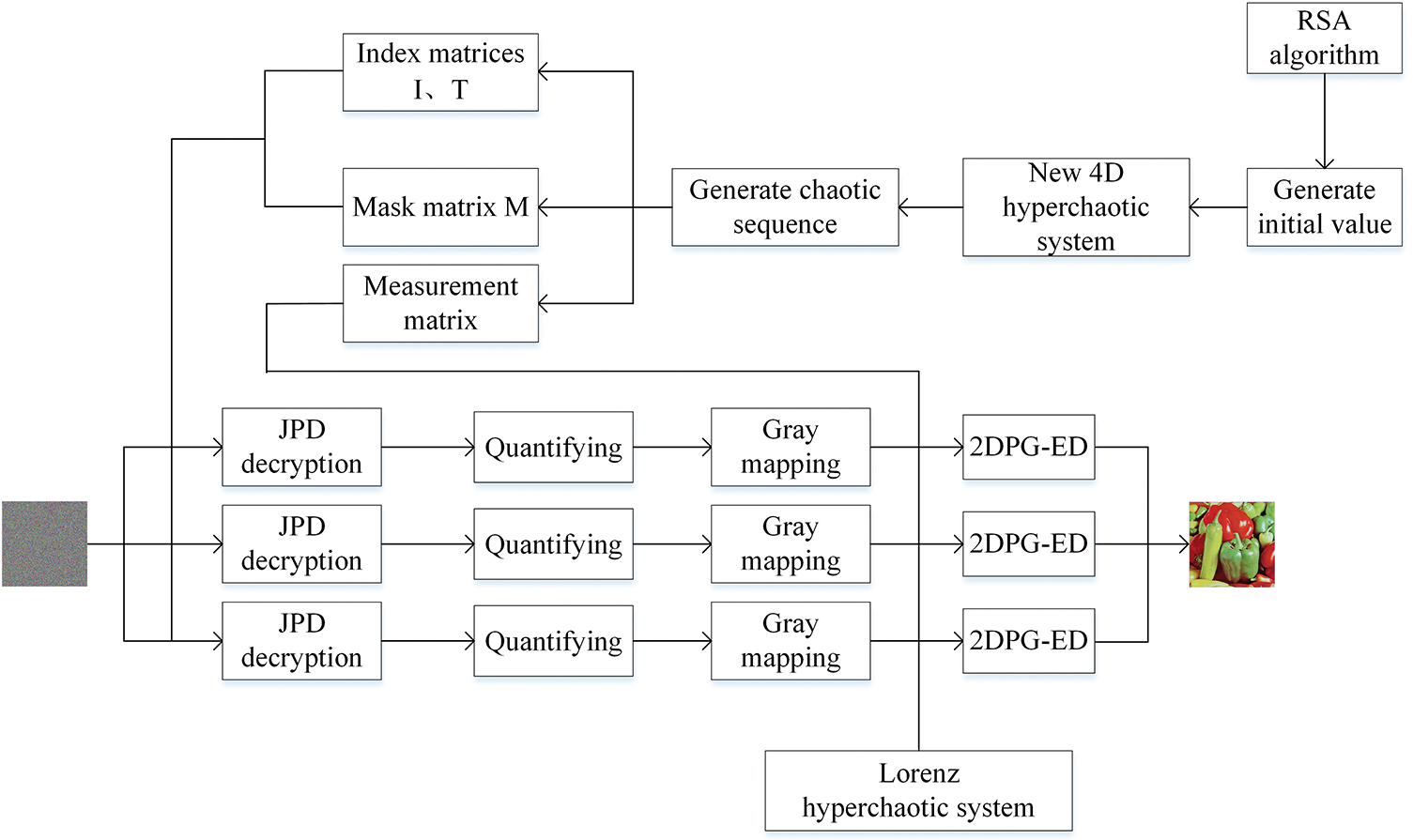
Figure 4: The procedure flow chart for the image decryption

Step 1: For ciphertext image C, the combined scrambling and diffusion procedures are reversed. The JPD decryption algorithm can be described by formulas using the index matrices I and T generated in Step 3 of 3.1, and the mask matrix M.

DTj,Ii,j,Ii,j={mod(Mi,j⊕(CIi,j,j−DIh,w,w),F),ifi=1,j=1mod(Mi,j⊕(CIi,j,j−DIi−1,w,w),F),ifi≠1,j=1mod(Mi,j⊕(CIi,j,j−CIi,j−1,j−1),F),ifj≠1.(7)

Step 2: Estimating the Yξ, referred to as Y^ξ, can be restored on the side of the decoder using inverse quantization. After that, we can use the formula to get Y’s estimate: Y^=Y^ξ+YF.

Step 3: To decode the final color image P, the 2DPG-ED algorithm rebuilds the image.

4  Simulation Results and Analysis

In this study, simulation tests on a 64-bit machine are accomplished using Matlab R2016a. The Lorenz hyperchaotic system’s starting value is as follows: x0 = 1.1, y0 = 2.2, z0 = 3.3, and w0 = 4.4. Within the trial, test images of the size 256×256 and 512×512 are selected for evaluation. Assuming that universality remains, the compression ratio in the compression sensing process is set to 0.9.

4.1 Evaluation of Encryption and Decryption Effects

The test images include 256×256 color images: House, Tree, and 512×512 color images: Lena, Baboon, and Black. It should be noted that due to the limited space of the paper, the size of the above two types of color images presented in this paper is the same. However, in the actual simulation experiment, the pixels of these two types of images are different. Fig. 5 shows the experimental results. There is no observable information about the original image in the concealed image. The size of the image is different in the compressed encrypted version and the original. The visual differences between the original and restored images are not very noticeable.

Figure 5: The experimental simulation results are obtained by using the scheme in this paper, where the original images are situated in the first row, compressed encrypted images are in the second row, and reconstructed images are in the third row

4.2 Statistic Analysis

Typically, two statistical qualities used in statistical analysis: histogram analysis and correlation analysis. These statistical properties can be used to assess the efficacy of encryption techniques.

4.2.1 Histogram Analysis

Histogram analysis is a useful tool for evaluating the security and effectiveness of encryption schemes. Attackers who use statistical analysis to break passwords do so by examining the statistical trends in both plaintext and ciphertext. To resist statistical attacks, the histogram of the encrypted images should exhibit a uniform appearance. Fig. 6 makes it evident that a clear statistical rule is displayed in the plaintext image histogram. However, the ciphertext image histogram is uniform, and it is impossible to get any information from it. Experiments have shown that the encryption algorithm has strong anti-histogram statistical performance.

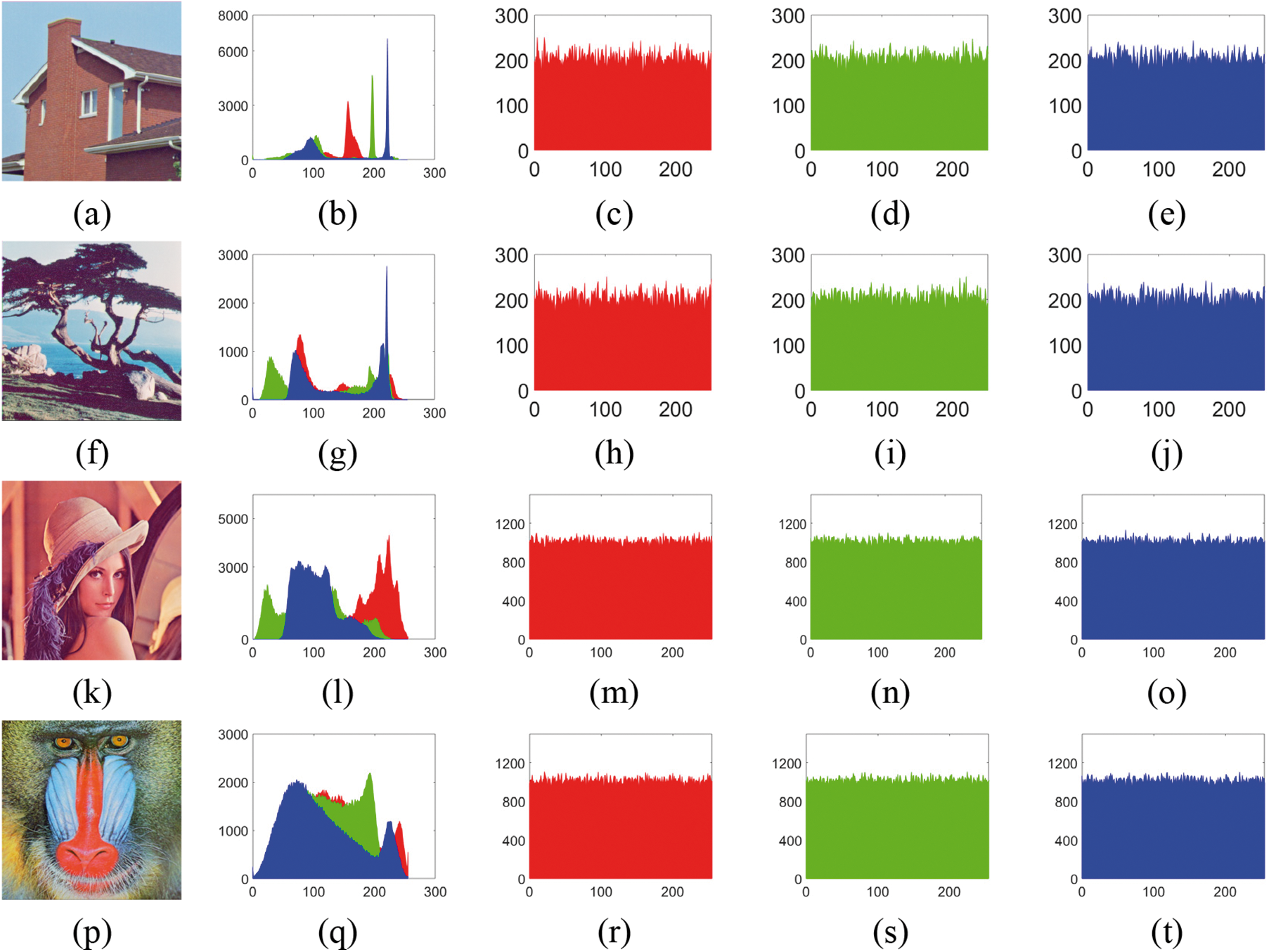
Figure 6: Histogram analysis, where (a), (f), (k), and (p) are original images, (b), (g), (l), and (q) are histograms of original images, the remaining images are the three channels histograms of the encrypted images R, G, and B

4.2.2 Correlation Analysis

Strong correlations exist between neighboring pixels in plaintext images; a pixel often leaks information about the pixels that surround it. So, to avoid statistical attacks, these strong correlations must be broken. It can be computed using the formula that follows.

Cor(X)=(∑i=1m(xi−E(x))(yi−E(y)))/∑i=1m(xi−E(x))2∑i=1m(yi−E(y))2,

here, xi and yi represent two pixels chosen at random from the test images, and m is 5000 pairs.

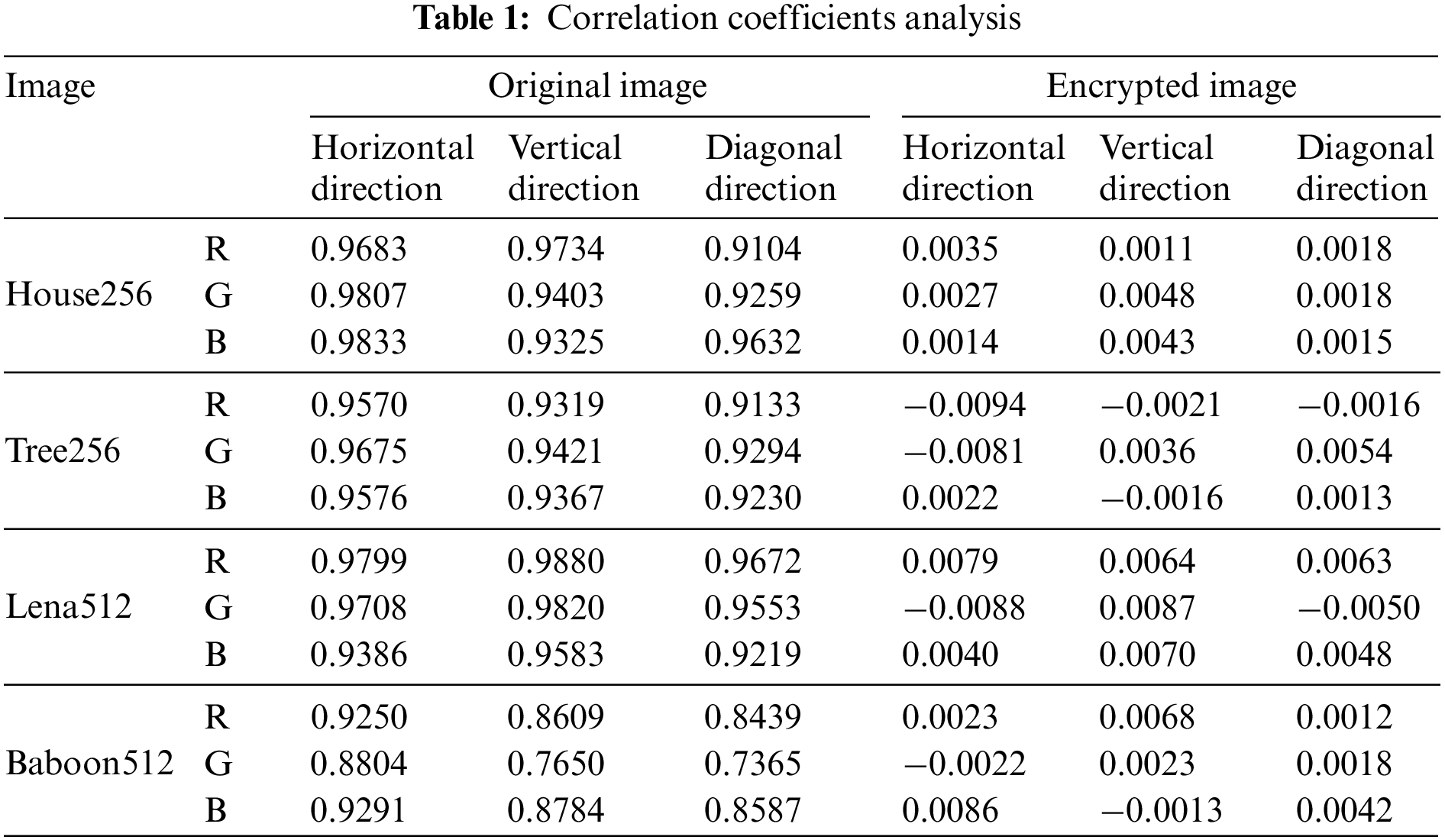
According to Fig. 7, the pixels in the original image are strongly associated with each other. However, in encrypted images, pixel distribution is uniform and uncorrelated. Table 1 gives the correlations between images in ciphertext and plaintext. When calculating correlations, all pixels in images are involved. From Table 1, we observe that the correlation coefficients of the original images are all nearly to 1, indicating strong correlations in the original images. On the other hand, all of the ciphertext images have very low correlations that are almost equal to 0.

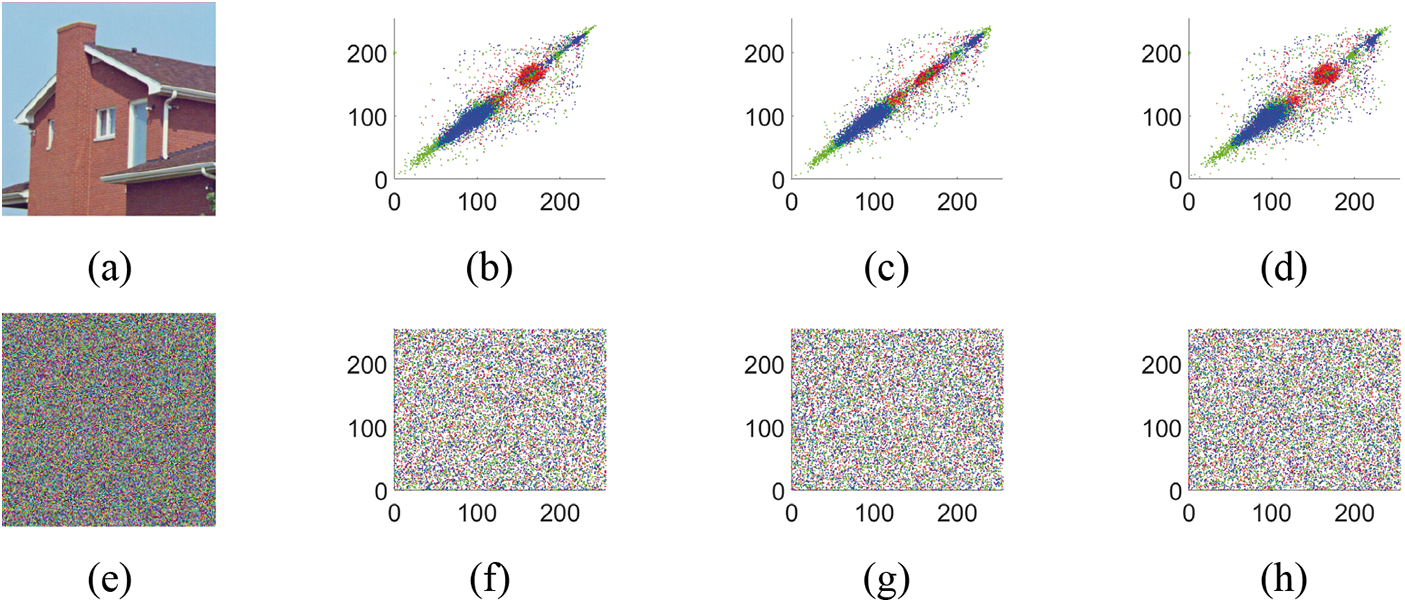
Figure 7: Correlation analysis. The last three columns represent the horizontal, vertical, and diagonal correlations of plaintext and ciphertext images, which correspond to the matching values in the first column

4.3 Information Entropy Analysis

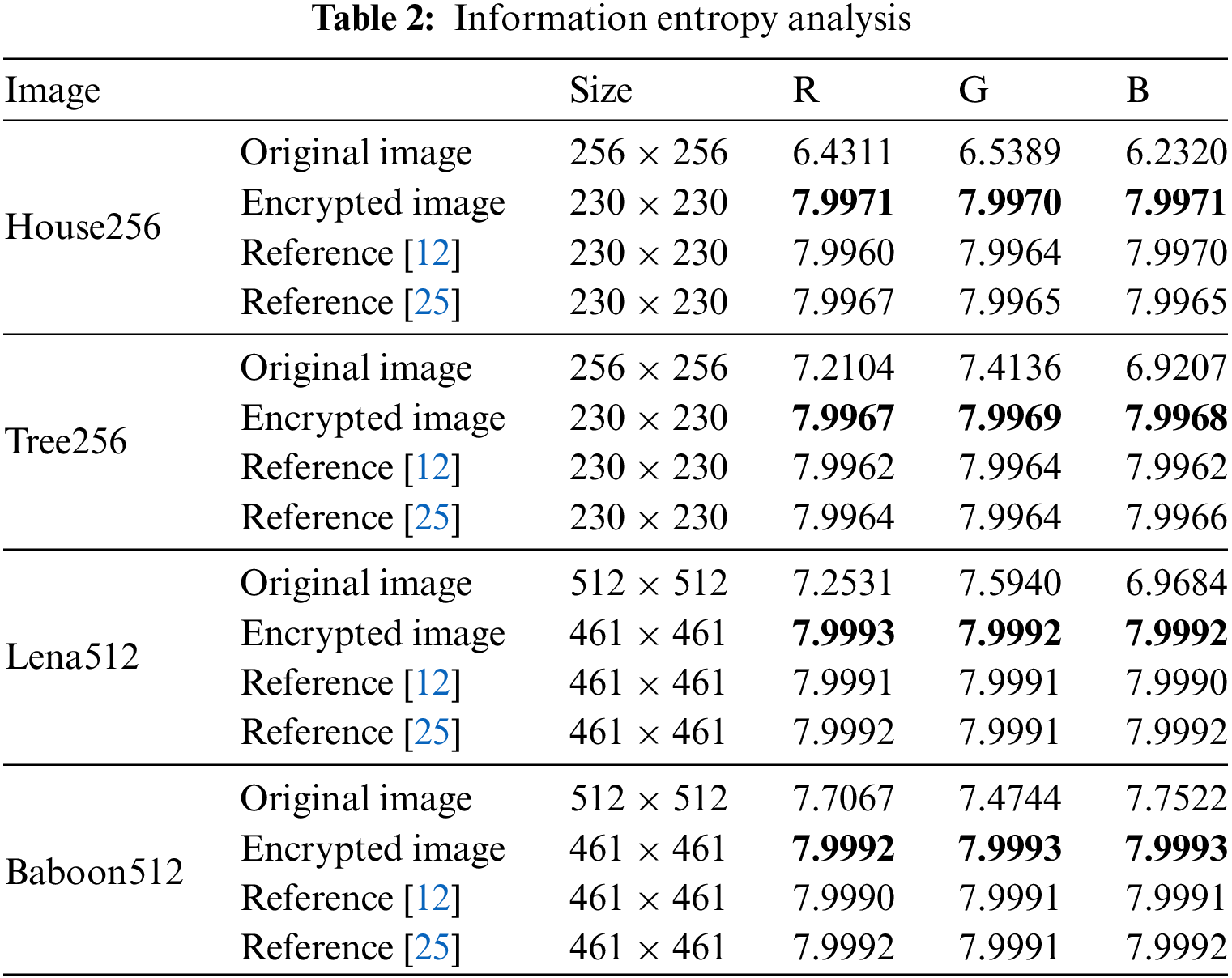
In the field of image encryption, information entropy analysis is the process of calculating and analyzing the entropy of encrypted images. It can evaluate the confidentiality and randomness of the image achieved by an encryption algorithm. The theoretical value of the encrypted picture for color image intensities ranging from 0 to 255 is 8. The computation formula that is employed is H(X)=−∑i=0Lp(i)log2⁡p(i), here, L denotes the total number of grey levels in the image, and P(i) represents the probability or likelihood of the occurrence of a specific grey value i.

In Table 2, the values of three channels of color test images are all around 7.997. However, the same images are used for testing in the [12], and all ciphertext images have a lower information entropy than the encryption method used in this paper. Therefore, entropy attacks can be resisted with this encryption scheme.

4.4 Analysis of Resisting Differential Attacks

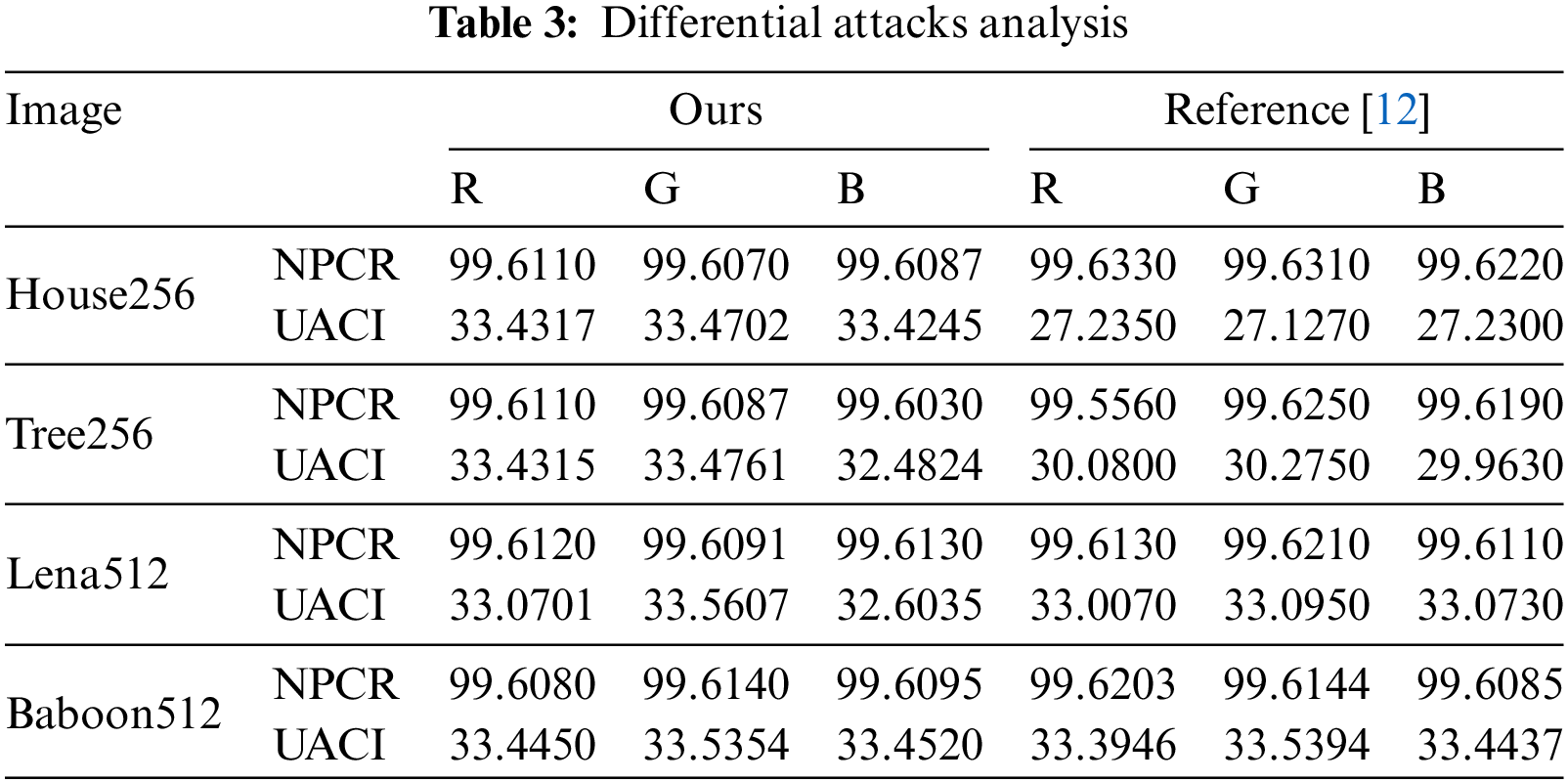
Differential attacks analyze the differences between pairings of plaintext and the matching ciphertext to deduce the encryption algorithm’s key or internal structure.

The two metrics used to assess the difference between two images are the Unified Average Changing Intensity (UACI) and the Number of Pixels Change Rate (NPCR). The calculation formulas are NPCR=∑ijD(i,j)/(M×N)×100% and UACI=∑ij|c1(i,j)−c2(i,j)|/255/(M×N)×100%, here, M and N stand for the rows and columns of images. Then, the theoretical value for NPCR is 99.6094%. The theoretical value for UACI is 33.4635%. Table 3 confirms that the encryption scheme’s NPCR and UACI calculation results are nearly to theoretical standard values, proving the algorithm’s robustness against attacks based on differences.

4.5 Key Analysis

4.5.1 Key Space Analysis

The key space refers to the complete set of possible values that a cryptographic key can take. Its size has a direct impact on the password system’s security. In the algorithm of this paper, two hyperchaotic systems make up the key space. Even if only one iteration is performed, the precision of the computation is 10−15, and the key space in this paper can reach 1015×1015×1015×1015×1015×1015×1015×1015=10120. As stated by [31], this cryptosystem is theoretically resistant to violence when the key space is greater than 2100. As a result, this algorithm is capable of withstanding strong attacks.

4.5.2 Key Sensitivity Analysis

In an ideal encryption system, with the correct key, it is possible to recover ordinary images completely, and any little alteration to the key will produce entirely different decoded images. In the experiment, we used one of the keys x0 + 10−14. The decrypted result is shown in Fig. 8. We cannot see any information objects from it. Therefore, we can deduce that this article’s encryption algorithm key is so sensitive that even little adjustments to the key will not be able to restore the original image.

Figure 8: Key sensitivity analysis

4.6 Robustness Analysis

4.6.1 Anti-Cropping Attack

Certain portions of an image will inevitably sustain damage during processing, transmission, and storage. A strong encryption method ought to be capable of resisting cropping attacks. To simulate the process of image destruction, we cropped the ciphertext image, as illustrated in Fig. 9.

Figure 9: Anti-cropping attack analysis. (a)–(d) show cropped images with 1/16 and 1/4 of different sizes of ciphertext cropped, and (e)–(h) display the reconstructed images that match the ciphertext image that was attacked with the cropping techniques. The experimental simulation findings illustrate that the majority of the initial image information remains intact in the encoded and reconstructed ciphertext image despite the cropping attack. This suggests that the approach may provide a degree of resistance against cropping attacks

Figs. 9a–9d show cropped images with 1/16 and 1/4 of different sizes of ciphertext cropped, and Figs. 9e–9h display the reconstructed images that match the ciphertext image that was attacked with the cropping techniques. The experimental simulation findings illustrate that the majority of the initial image information remains intact in the encoded and reconstructed ciphertext image despite the cropping attack. This suggests that the approach may provide a degree of resistance against cropping attacks.

4.6.2 Anti-Noise Attack

The encryption system ought to be able to fend off malicious noise attacks directed at the encrypted image. Therefore, as an example, let us consider adding salt and pepper noise. We conducted a simulation experiment as displayed in Fig. 10.

Figure 10: Anti-noise attack analysis

Figs. 10a–10c illustrate the images depicting salt and pepper noise with concentrations of 0.001, 0.05, and 0.1, respectively. Additionally, Figs. 10d–10f present the reconstructed images that match the noise-affected ciphertext images. The experimental results indicate that the restored image can reveal information associated with the original image, suggesting that this approach can withstand noise attacks.

4.7 Compression Performance Analysis

The compression performance is assessed through the use of Peak Signal-to-Noise Ratio (PSNR) and Structural Similarity Index Measure (SSIM) values. PSNR is one of the indicators for measuring image quality. In domains like image compression, it is often used to measure signal reconstruction quality. Mean Square Error (MSE), which is MSE=1M×N∑i=0M−1∑j=0N−1[P(i,j)−I(i,j)]2, here, P represents the original image of size, whereas I denotes a noisy image. Then, PSNR is based on the definition of MSE. PSNR can be defined as: PSNR=10×log10⁡(2552/MSE).

SSIM is defined as SSIM(x,y)=((2μxμy+C1)(2σxy+C2))/((μx2+μy2+C1)(σx2+σy2+C2)). Usually, SSIM with a range of values above 0.9 is considered an image of high quality.

As shown in the experimental results in Table 4, as an example, three channels of color images are used in this section. A higher PSNR value indicates a lower level of image distortion, resulting in a reconstructed image that closely resembles the original. As the compression ratio (CR) decreases, the reconstruction effect becomes worse, but important information can still be distinguished from it.

4.8 Running Time Analysis

The results of these evaluations are presented in Table 5, demonstrating that the encryption and decryption time differs according to the size of the images. The reconstruction time is often longer than the encryption time owing to this paper’s combination of compressed sensing. Compared to [12] and [25], the combination of CS technology with the scheme in this paper results in a shorter encryption time. However, the decryption time is longer due to the extended duration required by the reconstruction algorithm. After comprehensive consideration, our algorithm has a slight advantage.

4.9 Ablation Experiment Analysis

This part of this paper underwent ablation experiments and was divided into five parts, and the effectiveness of each part is evaluated as follows:

(1) Only Arnold scrambling of images is carried out. Image scrambling plays a role in hiding and protecting image information, which can be encrypted and transmitted and used as a pre-processing of image processing.

(2) Only JPD encryption of images is carried out. When combined with a hyperchaotic system, they are indeed commonly employed as encryption methods.

(3) Only CS. Using the CS algorithm to process the image can compress and encrypt the image simultaneously.

(4) Arnold scrambling and JPD operations are carried out. The encryption performance is improved when the two image processing techniques are combined.

(5) The scheme of this paper. The combination of the encryption method and compression method makes image encryption more perfect.

Specifically, take a color picture of House with a size of 256×256 as an example. Table 6 includes the correlation coefficient, with the horizontal value taken as an example. Simulation experiments have demonstrated the effectiveness of the solution in this paper, which combines chaotic encryption with CS.

From Table 6, schemes (1)–(4) do not have as good of an encrypting effect as the one suggested in this study. Although some schemes have short encryption and decryption times, the encryption effect is poor. Image encryption should not only look at the time but also need to combine ciphertext image performance. Consequently, the experiment proves the effectiveness of the scheme.

5  Conclusions

This work introduces a technique for color image compression and encryption that combines the hyperchaotic system with 2D CS. Firstly, this algorithm scrambles the original image. Subsequently, the scrambled image is compressed and encrypted simultaneously. Finally, for the sake of encryption security, the compressed and encrypted images are double-encrypted to achieve the ciphertext image. While decrypting, a reasonable image reconstruction algorithm is adopted to improve the reconstruction effect and reduce computational complexity. Experimental results show that it effectively resists several common attacks. Compared with existing advanced image encryption schemes, the proposed in this paper outperforms other schemes in performance and attack resistance. The validity of the encryption scheme has been verified. However, the decryption time is long, and we must improve it in our future work.

Acknowledgement: The editors and anonymous referees whose comments and recommendations have helped to improve this work are greatly appreciated by the authors. The authors would like to express their gratitude for the guidance and support provided by the research group.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China under Grants 71571091, 71771112, the State Key Laboratory of Synthetical Automation for Process Industries Fundamental Research Funds under Grant PAL-N201801, and the Excellent Talent Training Project of University of Science and Technology Liaoning under Grant 2019RC05.

Author Contributions: The following contributions to the work are confirmed by the authors: study conception and design: Zhiqing Dong, Zhao Zhang; gathering of data: Zhiqing Dong; analysis and interpretation of results: Zhiqing Dong, Hongyan Zhou; draft manuscript preparation: Zhiqing Dong, Zhao Zhang, Hongyan Zhou, Xuebo Chen. All authors have thoroughly reviewed the results and have provided their approval for the manuscript in its final form.

Availability of Data and Materials: Data and materials are available upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Liang, H. Peng, L. Li, F. Tong, S. Bao and L. Wang, “A secure and effective image encryption scheme by combining parallel compressed sensing with secret sharing scheme,” J. Inf. Secur. Appl., vol. 75, pp. 103487, 2023. doi: 10.1016/j.jisa.2023.103487. [Google Scholar] [CrossRef]

2. Y. Tao, W. Cui, and Z. Zhang, “Spatiotemporal chaos in multiple dynamically coupled map lattices and its application in a novel image encryption algorithm,” J. Inf. Secur. Appl., vol. 55, pp. 102650, 2020. doi: 10.1016/j.jisa.2020.102650. [Google Scholar] [CrossRef]

3. C. Xu, D. Li, K. Guo, Z. Yin, and Z. Guo, “Computational ghost imaging with key-patterns for image encryption,” Opt. Commun., vol. 537, pp. 129190, 2023. doi: 10.1016/j.optcom.2022.129190. [Google Scholar] [CrossRef]

4. E. Gokcay and H. Tora, “A novel data encryption method using an interlaced chaotic transform,” Expert. Syst. Appl., vol. 237, pp. 121494, 2024. doi: 10.1016/j.eswa.2023.121494. [Google Scholar] [CrossRef]

5. X. Y. Wang, L. Feng, and H. Y. Zhao, “Fast image encryption algorithm based on parallel computing system,” Inf. Sci., vol. 486, pp. 340–358, 2019. doi: 10.1016/j.ins.2019.02.049. [Google Scholar] [CrossRef]

6. A. Mehmood, A. Shafique, S. A. Chaudhry, M. Alawida, A. N. Khan, and N. Kumar, “A time-efficient and noise-resistant cryptosystem based on discrete wavelet transform and chaos theory: An application in image encryption,” J. Inf. Secur. Appl., vol. 78, pp. 103590, 2023. doi: 10.1016/j.jisa.2023.103590. [Google Scholar] [CrossRef]

7. M. Tang, G. Zeng, Y. Yang, and J. Chen, “A hyperchaotic image encryption scheme based on the triple dislocation of the Liu and Lorenz system,” Optik, vol. 261, pp. 169133, 2022. doi: 10.1016/j.ijleo.2022.169133. [Google Scholar] [CrossRef]

8. M. J. Wang, M. Y. An, X. A. Zhang, and H. H. C. Iu, “Feedback control-based parallel memristor-coupled sine map and its hardware implementation,” IEEE Trans. Circuits Syst. II Express Briefs, vol. 70, pp. 4251–4255, 2023. doi: 10.1109/TCSII.2023.3293109. [Google Scholar] [CrossRef]

9. J. Y. Wang, X. H. Song, H. Q. Wang, and A. A. Abd El-Latif, “Applicable image security based on new hyperchaotic system,” Symmetry, vol. 13, no. 12, pp. 2290, 2021. doi: 10.3390/sym13122290. [Google Scholar] [CrossRef]

10. Y. Zhou, L. Bao, and C. L. P. Chen, “A new 1D chaotic system for image encryption,” Signal Process, vol. 97, pp. 172–182, 2014. doi: 10.1016/j.sigpro.2013.10.034. [Google Scholar] [CrossRef]

11. Y. Liu, Z. Jiang, X. Xu, F. Zhang, and J. Xu, “Optical image encryption algorithm based on hyper-chaos and public-key cryptography,” Opt. Laser Technol., vol. 127, pp. 106171, 2020. doi: 10.1016/j.optlastec.2020.106171. [Google Scholar] [CrossRef]

12. T. Li, J. Shi, and D. Zhang, “Color image encryption based on joint permutation and diffusion,” J. Electron. Imaging, vol. 30, pp. 013008, 2021. doi: 10.1117/1.JEI.30.1.013008. [Google Scholar] [CrossRef]

13. Q. Liang and C. X. Zhu, “A new one-dimensional chaotic map for image encryption scheme based on random DNA coding,” Opt. Laser Technol., vol. 160, pp. 109033, 2023. doi: 10.1016/j.optlastec.2022.109033. [Google Scholar] [CrossRef]

14. W. Dong, Q. Li, Y. Tang, M. Hu, and R. Zeng, “A robust and multi chaotic DNA image encryption with pixel-value pseudorandom substitution scheme,” Opt. Commun., vol. 499, pp. 127211, 2021. doi: 10.1016/j.optcom.2021.127211. [Google Scholar] [CrossRef]

15. C. Zhu, “A novel image encryption scheme based on improved hyperchaotic sequences,” Opt. Commun., vol. 285, pp. 29–37, 2012. doi: 10.1016/j.optcom.2011.08.079. [Google Scholar] [CrossRef]

16. D. L. Donoho, “Compressed sensing,” IEEE Trans. Inf. Theory, vol. 52, pp. 1289–1306, 2006. doi: 10.1109/TIT.2006.871582. [Google Scholar] [CrossRef]

17. Y. Xiao, L. Jiang, and Z. Wang, “Convergence of compressed sensing encryption and deep network recovery in RoF system,” Opt. Commun., vol. 548, pp. 129835, 2023. doi: 10.1016/j.optcom.2023.129835. [Google Scholar] [CrossRef]

18. J. Cai, A. Wen, P. Li, H. Zhuo, W. Zhang, and Y. Y. Dong, “Instantaneous photonic frequency measurement based on compressive sensing,” Opt. Commun., vol. 530, pp. 129189, 2023. doi: 10.1016/j.optcom.2022.129189. [Google Scholar] [CrossRef]

19. L. Gong, K. Qiu, C. Deng, and N. Zhou, “An image compression and encryption algorithm based on chaotic system and compressive sensing,” Opt. Laser Technol., vol. 115, pp. 257–267, 2019. doi: 10.1016/j.optlastec.2019.01.039. [Google Scholar] [CrossRef]

20. R. Zhang and D. Xiao, “Double image encryption scheme based on compressive sensing and double random phase encoding,” Mathematics, vol. 10, pp. 1242, 2022. doi: 10.3390/math10081242. [Google Scholar] [CrossRef]

21. X. Chai, J. Fu, Z. Gan, Y. Lu, and Y. Zhang, “An image encryption scheme based on multi-objective optimization and block compressed sensing,” Nonlinear Dyn., vol. 108, pp. 2671–2704, 2022. doi: 10.1007/s11071-022-07328-3. [Google Scholar] [CrossRef]

22. X. L. Chai, J. Y. Fu, Z. H. Gan, Y. Lu, Y. S. Zhang and D. J. Han, “Exploiting Semi-tensor product compressed sensing and hybrid cloud for secure medical image transmission,” IEEE Int. Things J., vol. 10, pp. 7380–7392, 2023. doi: 10.1109/JIOT.2022.3228781. [Google Scholar] [CrossRef]

23. Y. Chen, C. Zhang, M. Cui, Y. Luo, T. Wu and X. Liang, “Joint compressed sensing and JPEG coding based secure compression scheme in OFDM-PON,” Opt. Commun., vol. 510, pp. 127901, 2022. doi: 10.1016/j.optcom.2022.127901. [Google Scholar] [CrossRef]

24. L. Chen, S. Tang, Q. Li, and S. Zhong, “A new 4D hyperchaotic system with high complexity,” Math. Comput. Simulat., vol. 146, pp. 44–56, 2018. doi: 10.1016/j.matcom.2017.10.002. [Google Scholar] [CrossRef]

25. R. Lin and S. Li, “An image encryption scheme based on lorenz hyperchaotic system and RSA algorithm,” Secur. Commun. Netw., vol. 2021, pp. 1–18, 2021. doi: 10.1155/2021/5586959. [Google Scholar] [CrossRef]

26. D. Huo et al., “A visually meaningful double-image encryption scheme using 2D compressive sensing and multi-rule DNA encoding,” Complex Intell. Syst., vol. 9, pp. 4783–4803, 2023. doi: 10.1007/s40747-023-00989-6. [Google Scholar] [CrossRef]

27. M. Imaduddin, Farikhin, and S. Hariyanto, “Analysis of orthogonal matching pursuit using orthogonal bases on digital image,” J. Phys. Conf. Ser., vol. 1776, pp. 012053, 2021. doi: 10.1088/1742-6596/1776/1/012053. [Google Scholar] [CrossRef]

28. J. H. Liu, S. K. Xu, X. Z. Gao, and X. Li, “Compressive radar imaging methods based on fast smoothed L0 algorithm,” Proc. Eng., vol. 29, pp. 2209–2213, 2012. doi: 10.1016/j.proeng.2012.01.289. [Google Scholar] [CrossRef]

29. M. A. T. Figueiredo, R. D. Nowak, and S. J. Wright, “Gradient Projection for sparse reconstruction: Application to compressed sensing and other inverse problems,” IEEE J. Sel. Top. Signal Process., vol. 1, pp. 586–597, 2008. doi: 10.1109/JSTSP.2007.910281. [Google Scholar] [CrossRef]

30. B. Zhang, D. Xiao, and Y. Xiang, “Robust coding of encrypted images via 2D compressed sensing,” IEEE Trans. Multimedia, vol. 22, pp. 2656–2671, 2020. doi: 10.1109/TMM.2020.3014489. [Google Scholar] [CrossRef]

31. R. Montero-Canela, E. Zambrano-Serrano, E. I. Tamariz-Flores, J. M. Munoz-Pacheco, and R. Torrealba-Melendez, “Fractional chaos based-cryptosystem for generating encryption keys in Ad Hoc networks,” Ad Hoc Netw., vol. 97, pp. 102005, 2020. doi: 10.1016/j.adhoc.2019.102005. [Google Scholar] [CrossRef]