Multi-Objective Equilibrium Optimizer for Feature Selection in High-Dimensional English Speech Emotion Recognition

1  Introduction

Speech communication has two channels, the explicit channel which carries linguistic content, and the implicit channel which contains speakers’ paralinguistic information (gender, dialect, emotion, and stress) [1]. Speech emotion recognition (SER) is a technology that extracts features from speech signals to judge human emotions [2]. It is used in various applications such as call center services to understand customers’ responses, vehicle services to gauge drivers’ psychological states and prevent accidents, and medical services to detect various diseases in patients. The process of SER includes pre-processing, feature extraction, and emotion classification [3]. The key focus of SER is extracting and selecting appropriate features, as their quality determines the final performance of emotion recognition.

Commonly used features in SER contain spectral features, sound quality features, intonation features, and corresponding statistical features like maximum, average, range, and variance [4]. Spectral features elucidate the relationship between vocal motion and vocal channel changes and involve cepstral features and linear spectral features. Sound quality features describe the vibration characteristics of sound and the clarity and recognition of speech.

Scholars have suggested numerous effective emotional features. However, they often possess high dimensions and exhibit substantial redundancy. When employing high-dimensional features directly in emotion analysis, it will impact recognition accuracy and prolong the model’s training time. Hence, it is crucial to extract meaningful and informative features for automatic emotion recognition. The presence of irrelevant features diminishes correct classification. Consequently, feature selection methods are employed to reduce the feature set’s size and computational burden. Filter and wrapper approaches represent two common feature selection techniques [5]. Filter approaches evaluate feature subsets based on data’s inherent properties. Wrapper approaches depend on the classifier’s performance, but they have a high computation time. Assuming that n is the number of features, then there will be 2n feature subsets. It is an NP-hard issue to find the optimal feature subset [6–8].

Metaheuristic algorithms, known for their randomness and global search ability, can discover approximate optimal solutions within limited computation time [9–11], and they are widely used in wrapper-based feature selection. Equilibrium optimizer (EO) is a new metaheuristic algorithm introduced in 2020. It draws inspiration from control volume mass balance used in various fields to comprehend dynamic conditions. EO stands out for its simplicity, rapid processing, and excellent ability to find the best solutions among different possibilities. It has demonstrated effectiveness in solving complex problems. Luo et al. utilized the crowding distance to keep the Pareto front well-distributed [12], and they employed dynamic coefficients to fine-tune exploration and exploitation. An equilibrium pool strategy, inspired by the slime mold’s cooperative foraging, enhances the algorithm’s ability to find better solutions. Abdel-Basset et al. proposed a method to enhance EO’s exploration and exploitation abilities [13]. Initially, the exploration factor is high, but it decreases with each iteration. At the same time, the exploitation factor increases to help the algorithm find the best solution efficiently. They also introduce improvement-based reference points to make sure that the algorithm converges well. Because the original EO algorithm uses fixed control settings, it cannot speed up the process of exploration and exploitation. Therefore, Abdel-Basset et al. suggested two improved versions [14]. The first version introduces mathematical equations that change as the number of iterations increases, while the second version adjusts solutions that dominate more gently while applying more significant changes to less dominant solutions. Premkumar et al. utilized the crowding distance mechanism to find a balance between exploration and exploitation [15]. The non-dominated sorting strategy promotes population diversity, which is especially for multi-objective optimization. Chalabi et al. employed an external archive to track the best solutions found [16]. Pareto dominance identifies the most promising solutions from the candidate population, and e-dominance guides the search to balance exploration and exploitation.

Drawing from the aforementioned research, we find that existing EO algorithms for feature selection primarily balance exploration and exploitation. However, they may not fully consider the importance of features and their impact on the EO algorithm’s performance, especially for high-dimensional multi-objective feature selection. In this study, we investigate the recognition of high-dimensional speech emotion with feature selection. This paper’s main contributions are summarized as follows:

1. Propose a system for multi-objective speech emotion recognition.

2. Propose a hybrid filter-wrapper algorithm for high-dimensional feature selection.

3. Propose a multi-objective approach to rank features.

4. Propose a multi-objective EO that improves the initialization, equilibrium pool, and update positions of EO.

5. Validate the suggested algorithm in the application of English SER.

The structure of this paper is organized as follows. Section 2 introduces the related works of SER. Section 3 describes the details of the proposed system. The experimental results with discussions are presented in Section 4, and the conclusions are provided in Section 5.

2  Related Works

SER determines the emotions of speakers by analyzing their speech signals. This assists us in predicting their mental and emotional state. The primary research in the field of single- and multi-objective SER will be presented in this section.

Huang et al. explored acoustic space division information and speech content [17]. First, the comparison of different methods confirms the importance of partitioning information and reveals a novel insight that the number of partitions plays a greater impact on valence than arousal prediction. Second, the phoneme specificity analysis of speech features illustrates that the emotional information of speech is less than the partition information, and it is more crucial for arousal than valence. In [18], Farooq et al. studied the advantages of deep convolutional neural networks (DCNNs) for SER. Pre-trained networks are utilized to extract emotional features, and a correlation-based feature selection algorithm selects the most useful features for SER.

Sun et al. brought a SER system through using genetic algorithm (GA) and decision tree (DT) [19]. To comprehensively express emotional content, acoustic features are first obtianed at the frame-level from speech signals. Next, five statistical variables of these features are obtained at the utterance-level. The Fisher criterion chooses high-performance features. Finally, the proposed SER model is built with the fusion features in which GA finds the weights in an adaptive manner. Mao et al. introduced a hierarchical SER architecture based on an enhanced DT [20]. Emotions that have less confusion are classified at the top level of the DT. GA selects the remaining features for classification and synchronously optimizes the parameters of the support vector machine (SVM). Little consideration is given to the interaction among features generated from the same audio, which may result in unnecessary redundancy and high computational cost. Liu et al. suggested a feature selection algorithm based on Fisher and correlation analysis [21], which effectively eliminates redundant features. To further enhance the accuracy of feature subsets, an emotion recognition approach based on extreme learning machine recognizes different emotions according to confusion.

Apart from recognizing accuracy, some studies have also focused on recognizing emotion faster, optimizing the parameters of classifiers, and making the process more unified. Brester et al. developed a new way to select the best features using cooperative multi-objective GA [22]. It saves computation time due to parallel work and the possibility of combining subsample exchange techniques. Furthermore, the method is effectively used as a pre-processing stage combined with ensemble classifiers. Daneshfar et al. brought an improved SER system [23]. Mel-scale frequency cepstral coefficient (MFCC), variance distortionless response (PMVDR), and perceptual linear predictive cepstral coefficient (PLPC) extract hybrid high-dimensional features from speech signals and glottal waveform signals, and prosodic features are derived from the fundamental frequency. A modified quantum particle swarm optimization algorithm (QPSO) selects the optimal features for classification and optimizes the parameters of the Gaussian mixture model. Li et al. explored a sophisticated approach to recognizing human emotions using multiple sources of information [24]. They utilize deep neural networks to process and analyze this data, and they employ a multi-objective optimization approach to design a more effective emotion recognition system. Yildirim et al. evaluated the performance of NSGA-II and cuckoo search (CS) in SER [25]. Furthermore, they propose improved metaheuristic algorithms for feature selection. Their results present that the proposed methods achieve acceptable classification performance while significantly reducing the number of selected features.

3  Methodology

The proposed system contains pre-processing, feature extraction, feature selection, and predicting the class of speech emotions.

3.1 Pre-Processing

Pre-processing plays an important part in improving the performance of SER models. In speech and audio signal analysis, framing, and windowing are necessary pre-process processes. They serve to enhance signal quality, extract relevant features, and reduce noise and variability, thus enabling more accurate emotion classification.

3.2 Feature Extraction

In our research, we use a toolkit called OpenSmile to collect specific acoustic features from speech data. These features are commonly used and recognized in computational paralinguistics at INTERSPEECH 2010 [26,27]. We managed to extract a total of 1582 features using this toolkit, and the detailed information is presented in Table 1.

3.3 Multi-Objective Equilibrium Optimizer for Feature Selection

Fig. 1 is the proposed algorithm’s flowchart. We regard the ranking of features as a multi-objective task. First, we utilize the information gain and Fisher Score to rank features and then divide them into multiple rankings according to the non-dominated sorting. Third, unlike metaheuristic algorithms, the initialization of individuals is generated with this ranking, and multi-objective functions are calculated for each individual. Fourth, the equilibrium pool guides individuals to update their positions. Finally, a novel position repair scheme is adopted to remove duplicate solutions.

Figure 1: The proposed algorithm’s flowchart

3.3.1 Filter Approaches

1. Fisher Score

Fisher Score is a statistical method that quantifies the ability of a feature to distinguish among different classes in a dataset [28]. Suppose nj represents the sample size in the j-th class, and (σji)2 and uji denote the variance and average of the i-th feature of the j-th class. The following equation determines the Fisher Score of the i-th feature:

Fi=∑ij=1Nnj(uji−ui)∑j=1Nnj(σji)2(1)

where N means the number of sample classes.

The Fisher Score measures the discriminative ability of a feature. A higher value indicates a greater likelihood of being selected for the final feature set. Specifically, if a feature is discriminative, it should have a small variance within the same class and a large variance across different classes.

2. Information Gain

Information gain measures the contribution of a specific feature to understanding a dataset or making predictions [29]. The conditional entropy H(X|Y) of a random variable Y is calculated as:

H(X|Y)=H(X,Y)−H(Y)(2)

where H(Y) is the information entropy of Y, and H(X,Y) means the joint entropy of X and Y.

H(Y)=−∑yp(y)log⁡p(y)(3)

H(X,Y)=−∑x∑yp(x,y)log⁡p (x,y)(4)

where p(y) is the probability distribution of Y, and p(x,y) indicates the joint probability distribution of X and Y.

Information gain is defined as follows:

I(X;Y)=H(X)−H(X|Y)=H(Y)−H(Y|X)(5)

Information gain helps us identify which features are the most informative and should be considered when building models. To reduce uncertainty and improve prediction accuracy, features that have higher information gain are more valuable.

3.3.2 Multi-Objective Ranking

Filter methods produce different rankings. Although various approaches, such as technique for order preference by similarity to an ideal solution (TOPSIS), can provide a comprehensive ranking, they may lose some feature evaluations. To better convey the importance of each feature, we employ the non-dominated sorting and treat each filter method as an objective to rank these features. Features in the same ranking layer are considered equally important, and Algorithm 1 describes the ranking process.

3.3.3 Multi-Objective Equilibrium Optimizer

1. Initialization

The randomness of the initial population results in features having the same selected probability, which is not conducive to expanding population diversity and enhancing the algorithmic efficiency. Therefore, we introduce a new initialization method based on the ranking of features, as shown in Algorithm 2.

The algorithm’s classification accuracy is quickly improved by high-ranking features with a large probability of being selected. Low-ranking features also have the opportunity to participate in subsequent operations to improve the algorithmic efficiency and classification performance.

2. Equilibrium pool

In the original EO, the equilibrium pool is used to store the four best solutions ever found. These solutions guide all individuals to move. In multi-objective EO, if the number of Pareto solutions exceeds four, they form the equilibrium pool. Otherwise, the equilibrium pool is constructed by the solutions of Pareto front ranks 1 and 2, as shown in Fig. 2.

Figure 2: Pareto front rank

3. Update positions

Eq. (6) defines the position update of the binary equilibrium optimizer. We adopt the transfer function to implement binarization, which provides a mechanism for changing the algorithm’s continuous search space into binary decision space.

Xlk(t+1)={Xlk(t)if(S(value)>rand)1−Xlk(t)else(6)

where Xlk implies the position of l at the k-th dimension, and t means the iteration. S is the transfer function, and it is calculated as follows:

S(value)=11+e−value(7)

value=(Xl(t)−Xeq(t))F(t)+G(t)λ(1−F(t))(8)

F(t)=sign(r−0.5)[e−λn(t)−1](9)

n(t)=(1−tMax_iter)(2tMax_iter)(10)

GCP={0.5r1 if(r2≥GP)0else(11)

G0(t)=GCP∗(Xeq(t)−Xi(t))(12)

G(t)=G0(t)∗F(t)(13)

where r1 and r2 are randomly selected from [0,1].

4. Repairing duplicate solutions

By merging the previous population (P) with the current population (Q), we can significantly maintain diversity and promote convergence. However, there may be individuals with duplicate positions. To prevent the loss of population diversity and conserve computing resources, we introduce a position repairing scheme, as depicted in Algorithm 3.

This scheme tries to explore feasible solutions in more unkown space. It expands population diversity but reduces the probability of low-ranking features being selected.

5. Objective function

Multi-objective feature selection mainly involves two objectives, minimizing the number of selected features and minimizing prediction error. Without loss of generality, its mathematical model is depicted as follows:

minF(x)=[f1(x),f2(x)]subject tof1(x)=number(x)f2(x)=1−accuracy(x)(14)

where f1 represents the selected number of feature sets (x) and f2 means the recognition error of x.

3.4 Classifiers

We utilize K-nearest neighbor (KNN) and random forest (RF) to build prediction models, and then we judge the models’ performance using K-fold cross validation. KNN does not need to understand the distribution of data, and it typically performs better in small datasets. RF provides strong generalization performance by integrating multiple decision trees. SVM is sensitive to missing data, while there are no universal solutions for nonlinear problems. Moreover, it is difficult to find a suitable kernel function. Due to the small size of emotional corpus datasets, we employ KNN and RF as classifiers to compare recognition algorithms more comprehensively. In this study, the K is set to 5.

K-fold cross validation separates a dataset into K folds. A classification model is trained and evaluated for K times, and it employs a different fold as a testing dataset and the other folds as a training dataset each time. After all K iterations, the performance indicators (like accuracy, precision, or recall) from each fold are averaged to offer an overall evaluation of the model’s effectiveness. In this study, we define K as 10.

4  Experimental Results and Analysis

4.1 Data Preparation

The proposed model is trained and evaluated with four different datasets, eNTERFACE05, ryerson audio-visual database of emotional speech and song (RAVDESS), surrey audio-visual expressed emotion (SAVEE), and Toronto emotional speech set (TESS).

1. eNTERFACE05

The dataset contains recordings of participants who are asked to perform specific tasks while displaying a range of emotions [30]. It includes anger, disgust, happiness, surprise, fear, sadness, and neutral expressions.

2. RAVDESS

RAVDESS contains recordings of 24 professional actors, evenly divided between 12 males and 12 females, from various backgrounds [31]. These actors portray different emotional states, such as calm, sad, happy, angry, surprised, fearful, and disgusted.

3. SAVEE

SAVEE is a specialized collection of audio and visual recordings designed for research in emotion recognition, speech analysis, and related fields [32]. It includes recordings of a male actor portraying different emotional states, such as surprise, anger, happiness, disgust, fear, and sadness.

4. TESS

TESS offers a variety of emotions, including disgust, fear, anger, sadness, happiness, pleasantness, and surprise. Every emotion is characterized by several actors, adding variability to the dataset.

4.2 Employed Algorithms

The recognition performance is compared with MEO [14], MQPSO [23], NSGA-II [25], and MBEO, and Table 2 describes the key parameters of the algorithms. The algorithms are designed to run 20 times and have a maximum of 100 iterations. The population size is 20. Wilcoxon rank sum and Frideman test are applied to show whether there exists any difference in the acquired experimental results.

4.3 Experimental Results

4.3.1 The Results Based on KNN

1. Hypervolume

Table 3 presents the HV values of the algorithms where MEAN and STD are the mean and variance of HV. The HV values of MBEO are 0.1145, 0.2502, 0.3220, and 0.6085, respectively. These values are better than the HV values of MEO, indicating that the proposed method improves the multi-objective solution ability of EO. In eNTERFACE05, the values of MEO and MBPSO are both 0, and their solutions do not constitute the final Pareto solutions. The algorithms perform best in TESS, followed by SAVEE, RAVDESS, and eNTERFACE05. The Wilcoxon rank sum shows that they do not exhibit similar statistical data, and MEO, MBPSO, NSGA-II, and MBEO perform well on 0, 0, 1, and 3 datasets, respectively. The average ranks of the algorithms are 3.75, 3.25, 1.75, and 1.25, and the P-value is less than 0.05. Experimental data, the Wilcoxon rank sum, and the Frideman test reveal the excellent performance of MBEO.

2. Inverted generational distance

Table 4 displays the results of the algorithms. The IGD values of MBEO in the four datasets are 0.0335, 0.0987, 0.0817, and 0.0994, which are smaller than the values of other algorithms. MBEO is superior to the comparison algorithms. Since the Pareto optimal solutions of IGD are composed of Pareto solutions for all solutions, it indicates that the solutions of MBEO are the closest to the Pareto solutions. Conversely, the values of MEO and MQPSO are large, and they only have a small number of solutions forming the final Pareto solutions. The Frideman test shows that MBEO performs best, followed by NSGA-II, MEO, and MQPSO. The Wilcoxon rank sum confirms that MQPSO, MEO, and NSGA-II do not have similar experimental statistical data with MBEO. Table 4 demonstrates the superiority of MBEO.

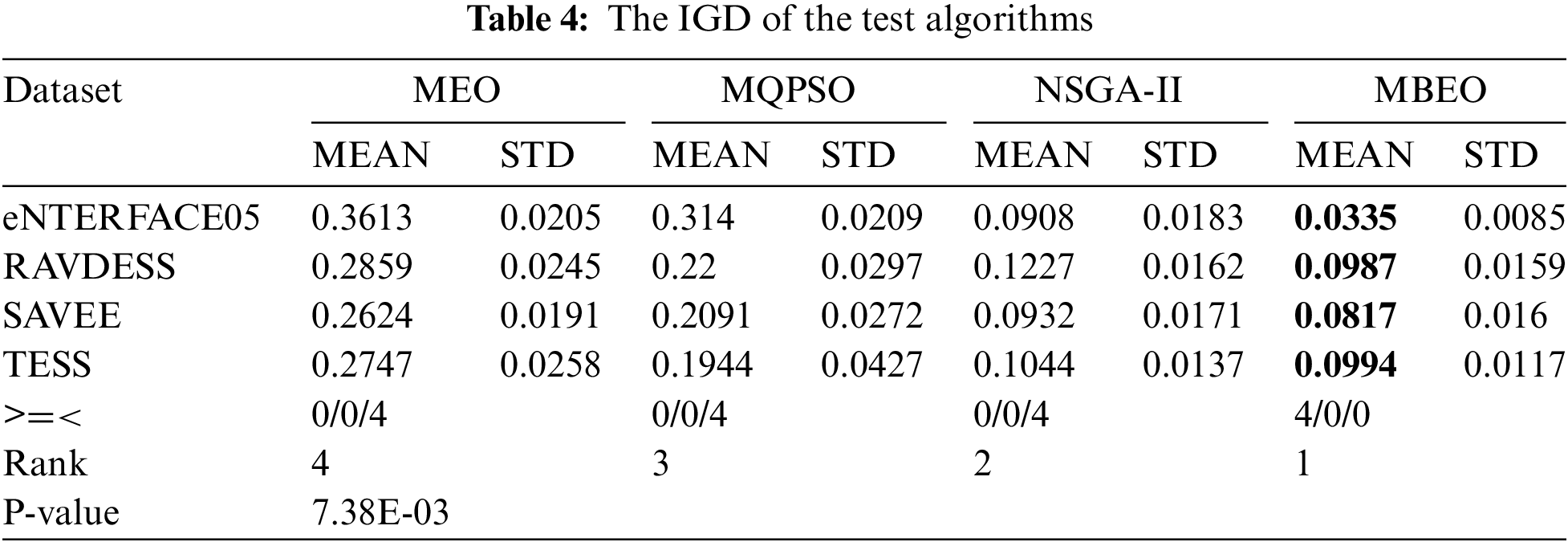
3. Pareto solutions

The non-dominated solutions produced by the algorithms after they run 20 times make up the final Pareto solutions, and Fig. 3 presents the Pareto solutions acquired by the test algorithms.

Figure 3: Pareto solutions found by the test algorithms

In eNTERFACE05, the solutions of MBEO are in low dimension, while the results of MEO and MQPSO fall in medium dimension. NSGA-II finds two feasible solutions in the low dimension, and it has the optimal solutions in the medium dimension. However, the accuracy of the algorithms is below 50%. In RAVDESS, MBEO achieves solutions in low dimensions. The solutions of MEO, MQPSO, and NSGA-II concentrate in the middle dimension, while the accuracy of NSGA-II is higher than that of MEO and MQPSO. In SAVEE, the solutions of MBEO are in the low dimension, while MEO and MQPSO distribute in the middle dimension. The solutions of NSGA-II span low and medium dimensions. In TESS, the algorithms obtain accuracy better than the value in eNTERFACE05, SAVEE, and RAVDESS, and MBEO achieves low recognition error using a small number of features. MEO, MQPSO, and NSGA-II concentrate on the mid-dimensional feature space, and the classification accuracy of NSGA-II outperforms other algorithms.

It can be observed from Fig. 3 that MBEO outperforms other algorithms in the Pareto front of RAVDESS and TESS. MBEO is capable of effectively capturing the intricate and diverse patterns linked to various emotions in RAVDESS and TESS. MBEO achieves high recognition using small features. The proposed algorithm can adapt to the characteristics of the datasets, which results in more robust and accurate emotion recognition in various conditions.

Table 5 is the execution time of the algorithms. It clearly shows that MBEO excels in running efficiency, and its average time on the four datasets is 195.9695, 467.9148, 209.8765, and 1191.9062. The time is smaller than those of the other algorithms. For KNN, its time complexity is O(M * F * F) where M and F represent the numbers of samples and selected features. MBEO focuses on using the top-ranking features for recognition. Although low-ranking features will supplement classification, it finally employs fewer features to complete the classification. MEO, MQPSO, and NSGA-II search for the best recognition results using all available features, so MBEO requires less running time than MEO, MQPSO, and NSGA-II.

4.3.2 The Results Based on RF

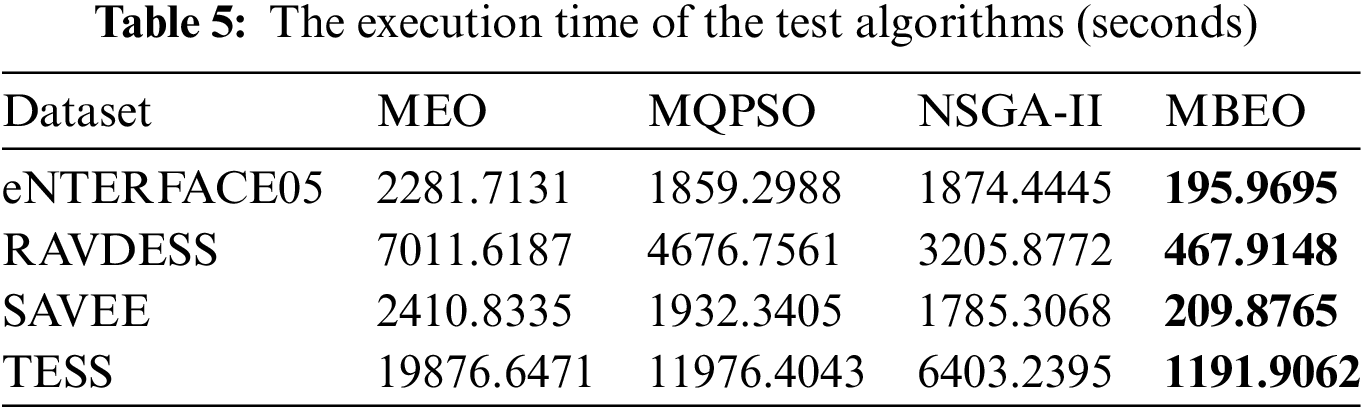
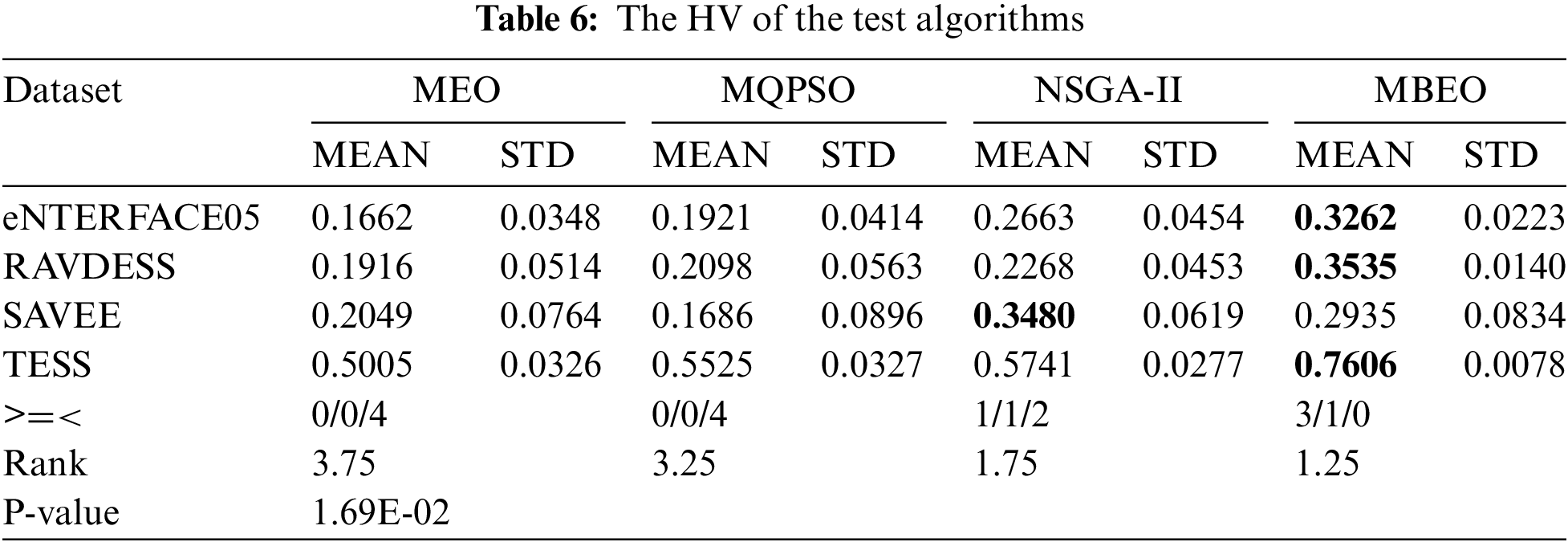
1. Hypervolume

Table 6 presents the HV values of the test algorithms. Specifically, the values of MBEO in eNTERFACE05, RAVDESS, and TESS are 0.3262, 0.3535, and 0.7606, and they are better than other algorithms. In SAVEE, NSGA-II exhibits a better HV value than MEO, MQPSO, and MBEO. The Wilcoxon rank sum demonstrates that they exhibit good performance on 0, 0, 2, and 4 emotion datasets, respectively, and MBEO and NSGA-II have similar statistics in eNTERFACE05 and SAVEE. The average ranks of MEO, MQPSO, NSGA-II and MBEO are 3.75, 3.25, 1.75, and 1.25, and the P-value is 1.26E-02. Table 6 evidences that MBEO outperforms MEO, MQPSO, and NSGA-II on HV.

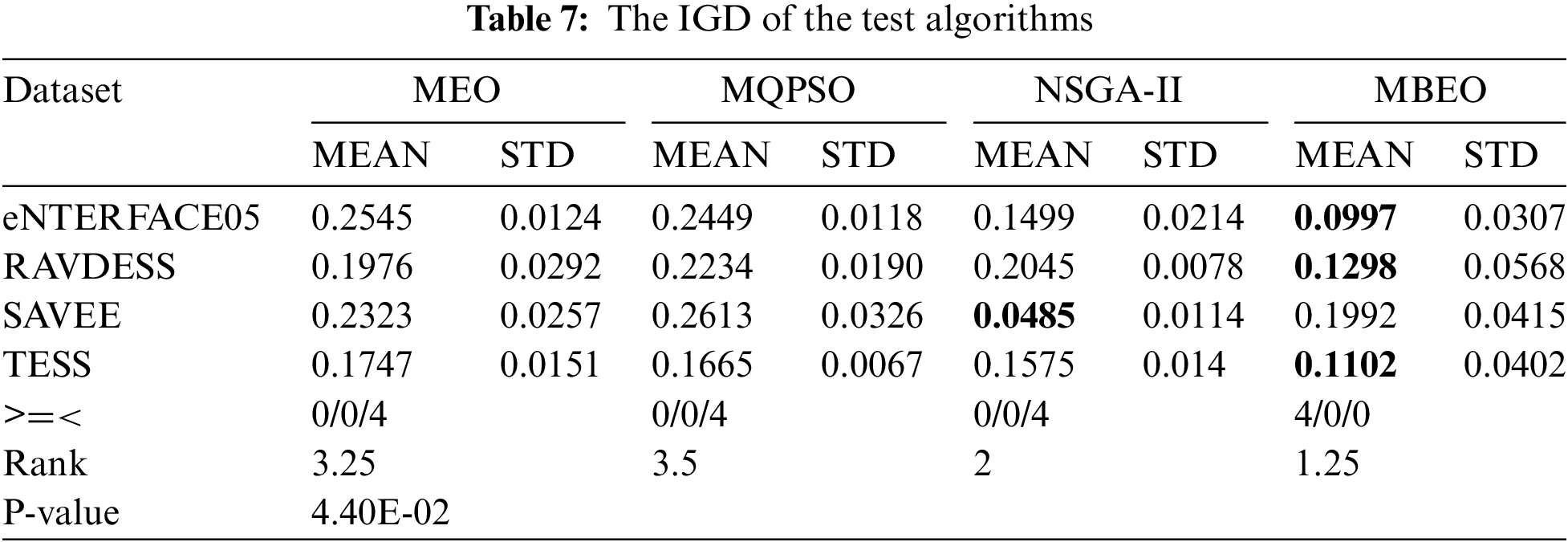
2. Inverted generational distance

Table 7 presents the results of the test algorithms on IGD, along with their non-parametric statistical analysis. MBEO demonstrates excellent performance in eNTERFACE05, RAVDESS, and TESS, while NSGA-II outperforms other algorithms in SAVEE. Based on the Wilcoxon rank sum, it is observed that MBEO and NSGA-II have compare experimental results in eNTERFACE05 and TESS, while MEO and MQPSO do not show statistical similarity with MBEO and NSGA-II. The Frideman test reveals that the average rank of MBEO is the lowest (1.25), followed by NSGA-II (2), MEO (3.25), and MQPSO (3.5). Experimental data, the Wilcoxon rank sum, and the Frideman test prove that MBEO is superior to other algorithms on IGD, and MBEO has exceptional multi-objective performance.

3. Pareto solutions

Fig. 4 displays the Pareto solutions obtained by the algorithms using the RF classifier.

Figure 4: Pareto solutions found by the test algorithms

The Pareto solutions obtained by the multi-objective algorithms on RF are similar to those acquired on KNN. In eNTERFACE05, the solutions of MBEO and MQPSO are distributed in low and medium dimensions. The outcomes of NSGA-II exist in the low and medium dimensions, while the solutions of MEO primarily occupy in middle and high dimensions. The highest recognition accuracy of the algorithms is 60%, while MBEO can achieve this with a small number of features. In RAVDESS, the solutions of MBEO concentrate in the low dimension, while the results of MQPSO and NSGA-II span in the middle dimension. MEO’s solutions are located in middle and high dimensions. Remarkably, MBEO achieves high recognition accuracy by using a few features. In SAVEE, MBEO shows outstanding performance in the low dimension, but the solutions of NSGA-II and MQPSO are found in the middle dimension. The solutions of MEO tend to reside in medium and high dimensions. In TESS, the algorithms receive excellent experimental results, and their accuracy exceeds 90%. The solutions of MBEO mainly cluster in the low-dimensional feature space, but it still obtains an optimal solution in the middle dimension. The solutions of NSGA-II and MQPSO are in the middle dimension, while MEO’s solutions are in the medium and high dimensions.

Table 8 displays the execution time of the algorithms. It indicates that the algorithms require more time for RF than for KNN, because the time complexity of RF, O(T * (M * F * logM)) where T represents the number of decision tress, is higher than KNN. Nevertheless, MBEO still exhibits a shorter running time compared to other algorithms, and MBEO uses fewer features for emotion recognition. When the number of samples remains constant, fewer features result in a more efficient algorithm. Since there are a lot of samples in TESS, the algorithms spend a significant amount of time processing.

From Figs. 3 and 4, it can be seen that MBEO uses 10%–30% of features to complete emotion recognition. Among these features, MBEO often chooses MFCCs, loudness, and line spectral pair frequencies. However, through the multi-objective feature ranking, it is found that MFCCs, differential jitter, and shimmer are the most important features that affect emotion classification. The reasons for the inconsistency are that the filter methods only analyze the intrinsic characteristics of features, and they are unable to truly evaluate their impact on classification. This also indicates that when recognizing high-dimensional emotions, the influence of low-ranking features cannot be ignored, and it is necessary to comprehensively evaluate features.

4.3.3 Discussion

1. Analysis of the values of K in KNN

If K is too small, a prediction model will become too specific and fail to generalize well. The model achieves high accuracy on a training set but has poor predictions for new datasets. As a result, we are likely to obtain an overfitted model. If K is too large, a prediction model becomes too general and cannot accurately predict data points in training and test sets. In KNN, the value of K is usually an odd number, and we analyze its impact on the performance of MBEO using the values of 3, 5, and 9. Table 9 presents the analysis based on the Wilcoxon rank sum where MBEO-3, MBEO-5, and MBEO-9 mean that the values of K are set to 3, 5, and 9 in KNN, respectively.

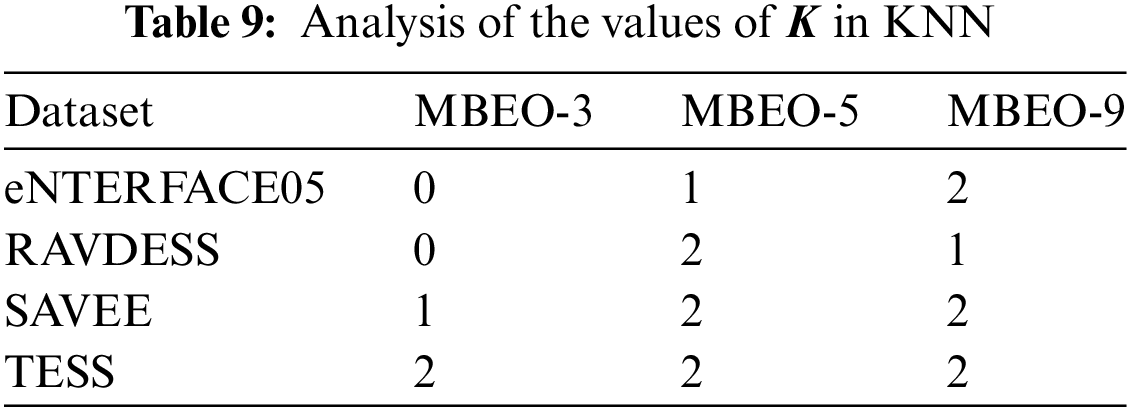
In eNTERFACE05, MBEO-9 is superior to MBEO-3 and MBEO-5, but MBEO-5 has similar data with MBEO-9 on HV. In RAVDESS, MBEO-5 and MBEO-9 are better than the comparison algorithms on IGD and HV, respectively, while they have similar experimental results on HV. In SAVEE, MBEO-5 and MBEO-9 perform well on IGD and HV, respectively. The algorithms cannot distinguish on HV, and MBEO-5 and MBEO-9 have a statistical similarity on IGD. In TESS, MBEO-5 and MBEO-9 obtain optimal solutions on IGD and HV, respectively, but the algorithms have the same data distribution on HV and IGD. From the above analysis, it can be seen that MBEO-5 and MBEO-9 have the best experimental results in the emotion datasets. K affects the performance of KNN, and KNN runs fast when K is small. Therefore, we utilize 5 as the value of K in this paper.

2. Analysis of the experiments with 3D convolutional neural network

Recently, reference [33] used a 3D convolutional neural network (CNN) for emotion recognition and achieved great accuracy with 1000 extracted features. We employ this architecture and the 1582 features obtained in Section 3.2 to explore emotion recognition with the MBEO algorithm. Since MBEO is a multi-objective algorithm, we compare the maximum accuracy of the obtained Pareto solutions with 3D CNN. Table 10 displays their experimental results.

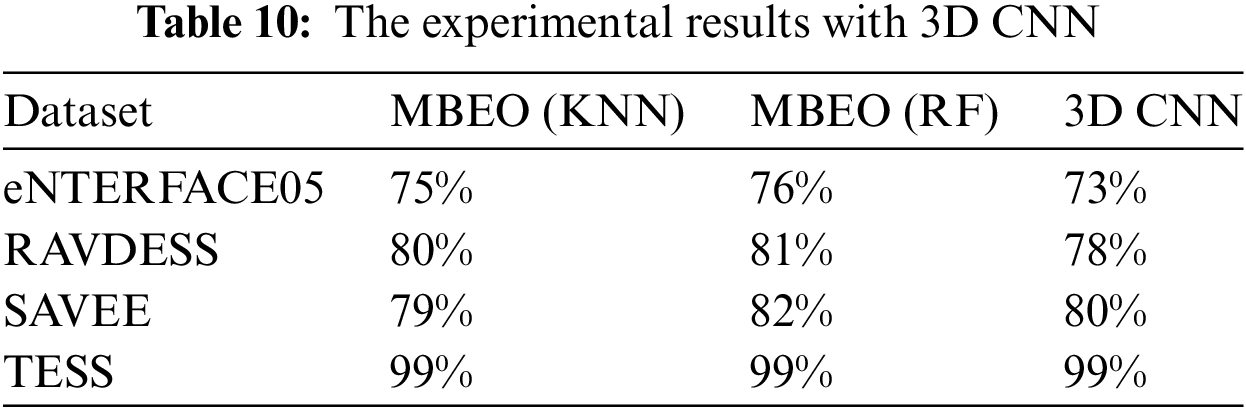
3D CNN demonstrates excellent recognition ability in eNTERFACE05, RAVDESS, SAVEE, and TESS. Furthermore, by using our proposed feature selection algorithm, MBEO improves the accuracy of emotion recognition. In eNTERFACE05 and RAVDESS, MBEO is superior to 3D CNN. In SAVEE, MBEO’s performance on KNN is not as good as 3D CNN, but it performs well on RF. MBEO and 3D CNN effectively capture the nuances of speech signals in TESS, so they have high accuracy. The above discussion shows that MBEO exhibits outstanding performance both when using features obtained only through OpenSmile and when using features obtained through the deep learning framework. The algorithm is robust.

5  Conclusions

This paper proposes a novel algorithm for multi-objective high-dimensional speech emotion recognition. The primary objectives are to identify the most suitable emotion recognition model and to extract the most valuable features for emotional representation. Furthermore, we utilize the emotional information carried by features to minimize both recognition errors and the number of features. We employ the OpenSmile tool to extract 1582 features from speech signals. The proposed algorithm uses filter methods to rank these features completed in a multi-objective task, and the features have different rankings. An improved EO implements wrapper-based feature selection. The algorithm outperforms the compared algorithms on KNN and RF with four common English datasets. The HV, IGD, and Pareto solutions of the algorithms on the RF classifier are better than their experimental results on the KNN classifier. As part of our future work, we try to extract more features from speech signals to validate the effectiveness of the proposed algorithm and improve recognition accuracy.

Acknowledgement: The authors would like to thank the editors and reviewers for their valuable work.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: L. Yue, P. Hu; data collection: P. Hu; analysis and interpretation of results: L. Yue, S. -C. Chu; draft manuscript preparation: L. Yue, J. -S. Pan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data generated or analysed during this study are included in this article and are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. A. Uddin, M. S. U. Chowdury, M. U. Khandaker, N. Tamam, and A. Sulieman, “The efficacy of deep learning-based mixed model for speech emotion recognition,” Comput. Mater. Contin., vol. 74, no. 1, pp. 1709–1722, 2023. doi: https://doi.org/10.32604/cmc.2023.031177. [Google Scholar] [CrossRef]

2. P. Gong, J. Liu, Z. Wu, B. Han, Y. K. Wang and H. He, “A multi-level circulant cross-modal transformer for multimodal speech emotion recognition,” Comput. Mater. Contin., vol. 74, no. 2, pp. 4203–4220, 2023. doi: https://doi.org/10.32604/cmc.2023.028291. [Google Scholar] [CrossRef]

3. S. Kumar et al., “Multilayer neural network based speech emotion recognition for smart assistance,” Comput. Mater. Contin., vol. 74, no. 1, pp. 1523–1540, 2023. doi: https://doi.org/10.32604/cmc.2023.028631. [Google Scholar] [CrossRef]

4. S. Kwon, “1D-CNN: Speech emotion recognition system using a stacked network with dilated CNN features,” Comput, Mater. Contin., vol. 67, no. 3, pp. 4039–4059, 2021. doi: https://doi.org/10.32604/cmc.2021.015070. [Google Scholar] [CrossRef]

5. N. Talpur, S. J. Abdulkadir, M. H. Hasan, H. Alhussian, and A. Alwadain, “A novel wrapper-based optimization algorithm for the feature selection and classification,” Comput. Mater. Contin., vol. 74, no. 3, pp. 5799–5820, 2023. doi: https://doi.org/10.32604/cmc.2023.034025. [Google Scholar] [CrossRef]

6. Y. Bi, B. Xue, and M. Zhang, “Multi-objective genetic programming for feature learning in face recognition,” Appl. Soft Comput., vol. 103, pp. 107152, 2021. doi: https://doi.org/10.1016/j.asoc.2021.107152. [Google Scholar] [CrossRef]

7. C. E. da Silva Santos, R. C. Sampaio, L. dos Santos Coelho, G. A. Bestard, and C. H. Llanos, “Multi-objective adaptive differential evolution for SVM/SVR hyperparameters selection,” Pattern Recognit., vol. 110, pp. 107649, 2021. doi: https://doi.org/10.1016/j.patcog.2020.107649. [Google Scholar] [CrossRef]

8. L. Ma, M. Huang, S. Yang, R. Wang, and X. Wang, “An adaptive localized decision variable analysis approach to large-scale multiobjective and many-objective optimization,” IEEE Trans. Cybern., vol. 52, no. 7, pp. 6684–6696, 2021. doi: https://doi.org/10.1109/tcyb.2020.3041212. [Google Scholar] [PubMed] [CrossRef]

9. J. S. Pan, L. G. Zhang, R. B. Wang, V. Snášel, and S. C. Chu, “Gannet optimization algorithm: A new metaheuristic algorithm for solving engineering optimization problems,” Math. Comput. Simul., vol. 202, pp. 343–373, 2022. doi: https://doi.org/10.1016/j.matcom.2022.06.007. [Google Scholar] [CrossRef]

10. X. Xue, R. Shanmugam, S. Palanisamy, O. I. Khalaf, D. Selvaraj and G. M. Abdulsahib, “A hybrid cross layer with harris-hawk-optimization-based efficient routing for wireless sensor networks,” Symmetry, vol. 15, pp. 438, 2023. doi: https://doi.org/10.3390/sym15020438. [Google Scholar] [CrossRef]

11. X. Xue and W. Liu, “Integrating heterogeneous ontologies in Asian languages through compact genetic algorithm with annealing re-sample inheritance mechanism,” ACM Trans. Asian Low-Resour. Lang. Inform. Process., vol. 22, pp. 1–21, 2023. doi: https://doi.org/10.1145/3519298. [Google Scholar] [CrossRef]

12. Q. Luo, S. Yin, G. Zhou, W. Meng, Y. Zhao and Y. Zhou, “Multi-objective equilibrium optimizer slime mould algorithm and its application in solving engineering problems,” Struct. Multidiscipl. Optim., vol. 66, pp. 114, 2023. doi: https://doi.org/10.1007/s00158-023-03568-y. [Google Scholar] [CrossRef]

13. M. Abdel-Basset, R. Mohamed, and M. Abouhawwash, “Balanced multi-objective optimization algorithm using improvement based reference points approach,” Swarm Evol. Comput., vol. 60, pp. 100791, 2021. doi: https://doi.org/10.1016/j.swevo.2020.100791. [Google Scholar] [CrossRef]

14. M. Abdel-Basset, R. Mohamed, S. Mirjalili, R. K. Chakrabortty, and M. J. Ryan, “MOEO-EED: A multi-objective equilibrium optimizer with exploration-exploitation dominance strategy,” Knowl.-Based Syst., vol. 214, pp. 106717, 2021. doi: https://doi.org/10.1016/j.knosys.2020.106717. [Google Scholar] [CrossRef]

15. M. Premkumar, P. Jangir, R. Sowmya, H. H. Alhelou, S. Mirjalili and D. S. Kumar, “Multi-objective equilibrium optimizer: Framework and development for solving multi-objective optimization problems,” J. Comput. Des. Eng., vol. 9, pp. 24–50, 2022. doi: https://doi.org/10.1093/jcde/qwab065. [Google Scholar] [CrossRef]

16. N. E. Chalabi, A. Attia, A. Bouziane, M. Hassaballah, A. Alanazi and A. Binbusayyis, “An archive-guided equilibrium optimizer based on epsilon dominance for multi-objective optimization problems,” Math., vol. 11, pp. 2680, 2023. doi: https://doi.org/10.3390/math11122680. [Google Scholar] [CrossRef]

17. Z. Huang and J. Epps, “An investigation of partition-based and phonetically-aware acoustic features for continuous emotion prediction from speech,” IEEE Trans. Affect. Comput., vol. 11, pp. 653–668, 2018. doi: https://doi.org/10.1109/taffc.2018.2821135. [Google Scholar] [CrossRef]

18. M. Farooq, F. Hussain, N. K. Baloch, F. R. Raja, H. Yu and Y. B. Zikria, “Impact of feature selection algorithm on speech emotion recognition using deep convolutional neural network,” Sens., vol. 20, no. 21, pp. 6008, 2020. doi: https://doi.org/10.3390/s20216008. [Google Scholar] [PubMed] [CrossRef]

19. L. Sun, Q. Li, S. Fu, and P. Li, “Speech emotion recognition based on genetic algorithm-decision tree fusion of deep and acoustic features,” ETRI J., vol. 44, pp. 462–475, 2022. doi: https://doi.org/10.4218/etrij.2020-0458. [Google Scholar] [CrossRef]

20. Q. Mao, X. Wang, and Y. Zhan, “Speech emotion recognition method based on improved decision tree and layered feature selection,” Int. J. Hum. Robot., vol. 7, pp. 245–261, 2010. doi: https://doi.org/10.1142/s0219843610002088. [Google Scholar] [CrossRef]

21. Z. T. Liu, M. Wu, W. H. Cao, J. W. Mao, J. P. Xu and G. Z. Tan, “Speech emotion recognition based on feature selection and extreme learning machine decision tree,” Neurocomput., vol. 273, pp. 271–280, 2018. doi: https://doi.org/10.1016/j.neucom.2017.07.050. [Google Scholar] [CrossRef]

22. C. Brester, E. Semenkin, and M. Sidorov, “Multi-objective heuristic feature selection for speech-based multilingual emotion recognition,” J. Artif. Intell. Soft Comput. Res., vol. 6, pp. 243–253, 2016. doi: https://doi.org/10.1515/jaiscr-2016-0018. [Google Scholar] [CrossRef]

23. F. Daneshfar and S. J. Kabudian, “Speech emotion recognition using discriminative dimension reduction by employing a modified quantum-behaved particle swarm optimization algorithm,” Multimed. Tools. Appl., vol. 79, pp. 1261–1289, 2020. doi: https://doi.org/10.1007/s11042-019-08222-8. [Google Scholar] [CrossRef]

24. M. Li et al., “Multimodal emotion recognition model based on a deep neural network with multiobjective optimization,” Wirel. Commun. Mob. Comput., vol. 2021, pp. 1–10, 2021. doi: https://doi.org/10.1155/2021/6971100. [Google Scholar] [CrossRef]

25. S. Yildirim, Y. Kaya, and F. Kılıç, “A modified feature selection method based on metaheuristic algorithms for speech emotion recognition,” Appl. Acoust., vol. 173, pp. 107721, 2021. doi: https://doi.org/10.1016/j.apacoust.2020.107721. [Google Scholar] [CrossRef]

26. L. Yue, P. Hu, S. C. Chu, and J. S. Pan, “Multi-objective gray wolf optimizer with cost-sensitive feature selection for predicting students’ academic performance in college english,” Math., vol. 11, no. 15, pp. 3396, 2023. doi: https://doi.org/10.3390/math11153396. [Google Scholar] [CrossRef]

27. T. Özseven, “A novel feature selection method for speech emotion recognition,” Appl. Acoust., vol. 146, pp. 320–326, 2019. doi: https://doi.org/10.1016/j.apacoust.2018.11.028. [Google Scholar] [CrossRef]

28. N. Janardhan and N. Kumaresh, “Improving depression prediction accuracy using fisher score-based feature selection and dynamic ensemble selection approach based on acoustic features of speech,” Trait. du Signal, vol. 38, no. 1, pp. 87–107, 2022. doi: https://doi.org/10.18280/ts.390109. [Google Scholar] [CrossRef]

29. S. R. Bandela and T. K. Kumar, “Unsupervised feature selection and NMF de-noising for robust speech emotion recognition,” Appl. Acoust., vol. 172, pp. 107645, 2021. doi: https://doi.org/10.1016/j.apacoust.2020.107645. [Google Scholar] [CrossRef]

30. L. Chen, K. Wang, M. Li, M. Wu, W. Pderycz and K. Hirota, “K-means clustering-based kernel canonical correlation analysis for multimodal emotion recognition in human-robot interaction,” IEEE Trans. Ind. Electron., vol. 70, no. 1, pp. 1016–1024, 2022. doi: https://doi.org/10.1109/tie.2022.3150097. [Google Scholar] [CrossRef]

31. S. K. Hazra, R. R. Ema, S. M. Galib, S. Kabir, and N. Adnan, “Emotion recognition of human speech using deep learning method and MFCC features,” Radioelectro. Comput. Syst., vol. 4, pp. 161–172, 2022. doi: https://doi.org/10.32620/reks.2022.4.13. [Google Scholar] [CrossRef]

32. M. Sharafi, M. Yazdchi, R. Rasti, and F. Nasimi, “A novel spatio-temporal convolutional neural framework for multimodal emotion recognition,” IEEE Trans. Ind. Electron., vol. 78, pp. 103970, 2022. doi: https://doi.org/10.1016/j.bspc.2022.103970. [Google Scholar] [CrossRef]

33. M. R. Falahzadeh, E. Z. Farsa, A. Harimi, A. Ahmadi, and A. Abraham, “3D convolutional Neural network for speech emotion recognition with its realization on intel CPU and NVIDIA GPU,” IEEE Access, vol. 10, pp. 112460–112471, 2022. doi: https://doi.org/10.1109/access.2022.3217226. [Google Scholar] [CrossRef]