A Post-Quantum Cross-Domain Authentication Scheme Based on Multi-Chain Architecture

1  Introduction

With the acceleration of informatization, the volume of data on the network is increasing exponentially, and how to securely and efficiently share data has become an urgent issue. Blockchain technology offers an excellent solution to this problem. Due to its decentralized, tamper-proof, and traceable characteristics, it has gained favor among many researchers in data sharing [1–5] and data protection [6–8]. In IoT scenarios, the introduction of blockchain enables many entities from different industries to jointly participate in data management, which improve the data reliability and shareability. Since different participants may maintain multiple blockchains, there is a requirement to enable the exchange of asset and value data among different blockchains within multi-chain environments.

Cross-chain technology plays a vital role in achieving interoperability among different blockchains, which primarily encompasses notary technology, side chain/relay technology, distributed private key control, and hashed time-locked contract (HTLC). However, notary technology exhibits a strong centralized feature, rendering the entire system non-distributed. Side chain/relay technology necessitates the introduction of a blockchain cross-chain network, which can be challenging to implement. Distributed private key control technology can result in transaction delays, significantly increasing communication consumption. On the other hand, HTLC, originally derived from the lightning network [9], offers a straightforward implementation, quick response, and the ability to facilitate asset exchanges between different blockchains without the involvement of an additional party. This characteristic has garnered substantial attention from researchers. Mohanty et al. [10] introduced a secure payment channel protocol, named New Hashed Time-Locked Contract (n-HTLC), which does not require the sender to send messages to each intermediate user along the payment route. In 2022, Shamili et al. [11] proposed an off-chain hash time lock commitment called the Federation Payment Tree (FPT), which employed a payment channel to provide a zero-knowledge hash lock commitment and allowed interaction between parties without a consensus protocol. Monika et al. [12] proposed a swap scheme between blockchains through HTLC and calculated the time-lock equations based on the confirmation time of the probabilistic blockchain. To address the inefficiencies associated with multiple participants exchanging tokens between blockchains simultaneously, Barbàra et al. [13] introduced MP-HTLC, demonstrating that the number of transactions remains independent of the number of participants on the UTXO blockchain. Subsequently, Wadhwa et al. [14] proposed a lightweight HTLC scheme called He-HTLC, which is inert to stimulus manipulation attacks and has excellent security.

In real-world scenarios, asset exchanges may involve entities located in different trust domains. Blockchain nodes from a foreign domain can access entities only after passing identity authentication by the authentication server in the local domain. This setup prevents blockchain nodes from different domains from interacting directly. To address these challenges, cross-domain authentication has emerged, enabling identity authentication of entities in distinct trust domains through various cryptographic primitives and facilitating session key negotiation to ensure entity identity credibility and communication confidentiality. Existing cross-domain authentication schemes primarily fall into three categories: based on symmetric cryptography, public key infrastructure (PKI), and identity cryptography. Numerous researchers have developed cross-domain authentication schemes using these cryptographic primitives. For instance, Sirbu et al. [15] proposed a cross-domain authentication scheme using public key cryptography to encrypt identity information. Liu et al. [16] integrated the ElGamal algorithm into a cross-domain authentication protocol, enabling key negotiation between participants. Zhang et al. [17] established a cross-domain authentication protocol based on PKI architecture by introducing an elliptic curve digital signature algorithm. Furthermore, identity-based cross-domain authentication schemes have gained prominence due to their ability to effectively reduce certificate management overhead, and several identity-based cross-domain authentication protocols have been developed. Peng [18] introduced an identity-based multi-trust domain authentication model, analyzing the security and anonymity of the identity authentication process. Luo et al. [19] implemented an identity-based cross-domain authentication scheme incorporating an elliptic curve signature, thereby achieving user identity anonymity. More recently, Wei et al. [20] applied blockchain certificate authority (BCCA) in each domain as nodes in consortium blockchain to realize cross-domain authentication. Zhou et al. [21] proposed an authentication scheme employing identity-based encryption and secret sharing, suitable for deployment on public channels within virtual enterprises. In the Industrial Internet of Things (IIoT), Cui et al. [22] introduced an anonymous cross-domain authentication scheme, which improves authentication efficiency while meeting traceability, scalability, forward privacy, and identity anonymity requirements.

In the aforementioned scenario, cross-domain identity authentication of blockchain nodes is an indispensable component before performing cross-chain asset exchange based on HTLC between blockchains located in different trusted domains. As is widely recognized, the reliability of cross-domain authentication schemes primarily depends on the security of cryptographic algorithms. However, the advent of quantum computers has introduced a significant threat to traditional cryptography, as the Shor algorithm [23] can solve the discrete logarithm problem in probabilistic polynomial time (PPT). This poses a grave challenge to the security of traditional cryptographic methods, and the trustworthiness of cross-domain authentication schemes is no longer assured. Researchers have delved into the post-quantum cryptography as a response to this threat. Among these endeavors, lattice-based cryptography has emerged as the leading post-quantum cryptographic algorithm due to its rapid operational efficiency. Various researchers have devised lattice-based cryptosystems to withstand quantum computing attacks. For instance, Rückert [24] created the first identity-based signature using lattice techniques, which exhibited strong unforgeability in the standard model. In 2014, Tian et al. [25] developed an innovative identity-based signature scheme over lattice, with security grounded in the SIS hardness assumption. In this scheme, we apply lattice-based cryptography to construct a cross-domain identity authentication scheme with post-quantum security, realize the cross-domain identity authentication of access nodes in the multi-chain architecture, and utilize the hashed time-locked contract to complete the cross-chain asset exchange between domains.

To sum up, the contribution of our paper is described as follows:

(1) This paper constructs a post-quantum secure cross-domain identity authentication scheme based on the multi-chain architecture, improves the traditional cross-domain authentication and applies the cross-chain technology based on HTLC, to achieve the identity authentication of cross-domain access nodes in the multi-chain architecture and the cross-chain asset exchange of nodes in different trust domains.

(2) This paper designs the hiding and recovery of the identity index based on lattice cryptography and introduces the identity-based signature on lattice in [25], which is used for the authentication server to check the identity of nodes, ensures the security and reliability of the cross-domain authentication process, and can resist quantum computing attacks.

(3) In security analysis, the IND-CPA of the identity index and the unforgeability of signature can be reduced to Learning With Errors (LWE) and Short Integer Solution (SIS) assumption, respectively. This scheme is efficient in terms of operation number and time consumption of the user and authentication server compared with other cross-domain authentication schemes through the comparison analysis.

2  Preliminary

2.1 Lattice

Definition 1 (Lattice): Given A=(a1|a2|…|am)∈Zn×m is a n×m-dimension matrix containing n linearly independent vectors a1,a2,…,am∈Zn. The n-dimension lattice Λ is generated by A, expressed as:

Λ(A)={y∈Zn|y=Ac=∑i=1mciai,c∈Zm},(1)

where A is called the basis of Λ.

Definition 2 (Full-rank integer lattice): Given a matrix A∈Zn×m, where q is a prime, m and n is a positive integer, define the full-rank lattice generated by A:

Λq⊥(A)={e∈Zm|Ae=0(modq)}(2)

Λq(A)={y∈Zm|∃s∈Zn,ATs=y(modq)}(3)

2.2 Discrete Gaussian Distribution

Definition 3 (Discrete Gaussian distribution): For the Gaussian parameter σ>0 and the center c, the Gaussian distribution on Λ⊂Zn is defined as: ∀x∈Λ,ρσ,c(x)=exp⁡(−π⋅‖x−c‖2σ2). The discrete Gaussian distribution on Λ is defined as: ∀y∈Λ,DΛ,σ,c(y)=ρσ,c(y)ρσ,c(Λ), where ρσ,c(Λ)=∑x∈Λρσ,c(x).

2.3 Hardness Assumption on Lattice

Definition 4 (LWE assumption): Given a prime q, positive integer m and n, a matrix A∈Zqn×m, a vector v∈Zqn, a noise vector e←χ, and then search a vector z∈Zqm such that v=Az+e.

Definition 5 (SIS and ISIS assumption): Given a prime q, positive integer m and n, a matrix A∈Zqn×m, a parameter β, and then search for a vector z∈Zqm∖0 such that Az=0 and ‖z‖≤β. The above assumption can be extended to inhomogeneous versions, given a prime q, positive integer m and n, a matrix A∈Zqn×m, a parameter β, a vector u∈Zqn, and then search for a vector z∈Zqm∖0 such that Az=u and ‖z‖≤β.

2.4 The Trapdoor and Sampling Lemma on Lattice

Lemma 1 (TrapGen) [26] Given an odd integer q≥3, and m=⌈6nlog⁡q⌉, there exists a PPT algorithm TrapGen(q,n) that calculates a matrix A statically closed the uniform distribution on Zqn×m, and a matrix B∈Zm×m which is a basis of Λq⊥(A), such that ‖B‖≤O(nlog⁡q) and ‖B~‖≤O(nlog⁡q).

Lemma 2 (SamplePre) [27] Given an integer q≥2, a matrix A∈Zqn×m, a matrix B∈Zm×m which is a basis of Λq⊥(A), and a vector v∈Zqn. There exists a PPT algorithm SamplePre(A,B,v,σ) that calculates a vector x∈Zm statically closed DΛqv(A),σm such that Ax=vmodq.

Lemma 3 (SampleMat) [25] Given a prime q≥2, an integer k≥2, a matrix A∈Zqn×m, a basis B∈Zm×m of Λq⊥(A), and a matrix V=(v1,v2,…,vk)∈Zqn×k. There exists a PPT algorithm SampleMat(A,B,V,σ) that calculates a matrix S∈Zqm×k statically closed DΛqv1(A),σm×DΛqv2(A),σm×⋯×DΛqvk(A),σm such that AS=Vmodq.

2.5 Rejection Sampling

To output a signature independent of the secret key, we introduce the Rejection Sampling technique. Let k is the secret key of the signer, y is selected from a random distribution, s is the candidate signature computed by y adding to the function of k, f is the distribution of outputted signature, g is the distribution of candidate signature. For all x and M>0, if f(x)≤Mg(x), the candidate signature is outputted with probability f(s)Mg(s). According to [28], the expected number of times to generate a valid signature is M.

3  System Model and Security Model

3.1 System Model

Fig. 1 shows the specific process of our scheme by taking the entity interaction between two domains as an example. In this example, we assume that domain A is the local domain and domain B is the external domain. The entities of each domain include an authentication server, private key generation center, and blockchain. The functions of each entity are as follows:

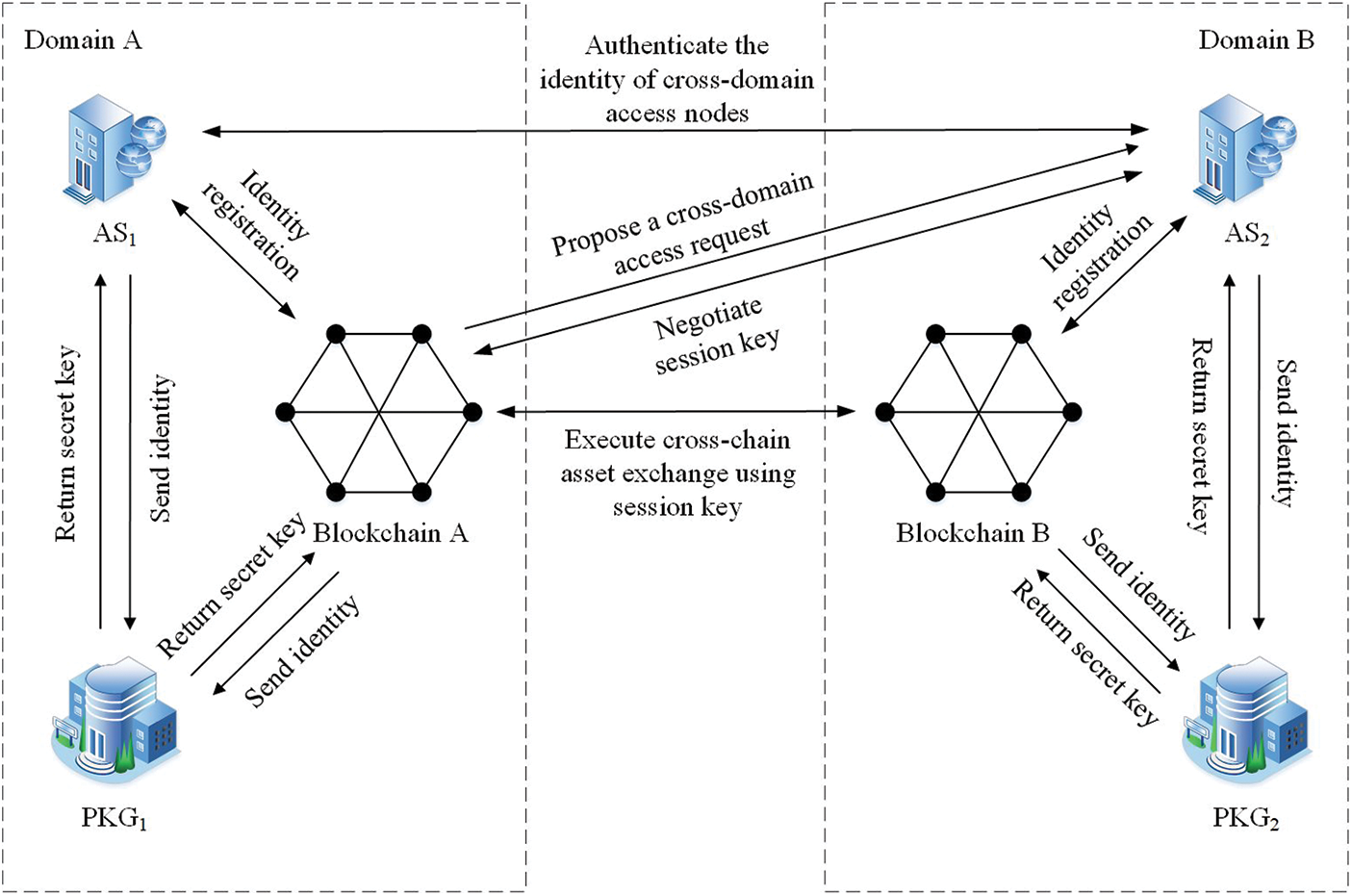
Figure 1: System architecture

(1) Authentication server (AS): AS is responsible for the identity registration and identity authentication of the blockchain nodes in the local domain, and maintains the identity list of the local domain. AS has its identity information that is exposed to each domain. The private key can be obtained from the private key generation center of the local domain. When an access request is made by a node in the foreign domain, the AS will send a request for assistance to the foreign AS. When the local AS receives the assistance authentication request from the foreign domain, it will authenticate the identity of the local node and return the authentication results to the foreign AS. In this scheme, the authentication server of domain A is referred to as AS1, and the authentication server of domain B is referred to as AS2.

(2) Private key generation center (PKG): PKG is responsible for generating the private key of the local AS and blockchain node. After receiving the identity information of the AS or blockchain node, the private key corresponding to this identity information is calculated and returned. In this scheme, the private key generation center of domain A is called PKG1 for short, and the private key generation center of domain B is called PKG2.

(3) Blockchain: Blockchain is a decentralized network composed of many nodes, and this scheme adopts a consortium blockchain based on Hyperledger Fabric. The blockchain node has its identity information. It can obtain the private key from PKG of the local domain, complete the identity registration with the local AS, submit a cross-domain access request to the foreign AS, and exchange cross-chain assets based on HTLC with the foreign blockchain node after the identity authentication is successful. Smart contracts can automatically execute function codes and provide interfaces and function encapsulation for HTLC. In this scheme, the blockchain of domain A is referred to as blockchain A, and the blockchain of domain B is referred to as blockchain B.

3.2 Security Model

The IND-CPA secure of a post-quantum secure cross-domain identity authentication scheme is defined as a series of games between challenger C and adversary A as follows:

(1) Setup: Challenger C executes the System initialization algorithm and generates public parameters pp to send to adversary A.

(2) Phase 1: In this phase, adversary A can conduct H2 and private key inquiries with challenger C, and C visits the H2 query oracle Private key query oracle and returns the results to A.

H2 query: Adversary A queries H2(IDi) corresponding to identity IDi for i-th query, while challenger C maintains the query list L and calculates H2(IDi) to return to A.

Private key query: Adversary A queries skIDi corresponding to identity IDi for i-th query, while challenger C maintains the query list L and calculates skIDi to return to A.

(3) Challenge: Adversary A selects IID0,IID1∈{0,1}m and sends it to challenger C. Then, C selects ξ∈{0,1} and calculates (R0∗,R1∗) corresponding to IIDξ. Finally, C sends (R0∗,R1∗) to A.

(4) Phase 2: Adversary A acquires the private key except Q∗ through calling the Private key query oracle.

(5) Guess: After receiving (R0∗,R1∗), adversary A selects a bit ξ∗∈{0,1}, and wins this game if ξ∗=ξ.

Moreover, the advantage of adversary A breaking our scheme is defined as:

AdvAIND-CPA(pp)=|Pr[ξ∗=ξ]−12|.(4)

Definition 6 (The IND-CPA security of a post-quantum secure cross-domain identity authentication scheme): Assuming that a post-quantum secure cross-domain identity authentication scheme is IND-CPA secure, if and only if the advantage AdvAIND-CPA(pp) is negligible for any PPT adversary A.

4  Our Proposed Scheme

Assume that domain A is the local domain and domain B is the external domain. Node AN1 of blockchain A makes a cross-domain access request to domain B and wants to exchange cross-chain assets with node BN1 of blockchain B. Moreover, AS1 and AS2 are honest and credible, and there is a secure and confidential channel between them. The specific process of our scheme is described as follows.

4.1 System Initialization

This section is responsible for creating the functions required for cross-chain in the blockchain smart contract, and setting the public parameters in the cross-domain process.

(1) Blockchain initialization: Blockchain in each domain deploys smart contracts and creates corresponding functions for cross-chain asset exchange of nodes. Smart contracts can automatically execute the created functions without human intervention.

(2) Parameter initialization: Set parameters m,n satisfying m>5nlog⁡q, where q is a prime and q≥3. Then, the TrapGen algorithm is called to generate the matrix A∈Zqn×m and the basis B∈Zqm×m of lattice Λ(A) such that ‖B~‖≤O(nlog⁡q), which B will be saved by PKG of each domain as the master key. Finally, four security hash functions H1:Zqn×{0,1}∗→{−1,0,1}m, H2:{0,1}∗→Zqn×m, H3:{0,1}∗×Zm×m→{0,1}m, and H4:{0,1}m→{0,1}κ are selected, which κ is the length of the session key. Then, the public parameter is set to pp={A,H1,H2,H3,H4}.

4.2 Private Key Generation

In this section, PKG generates private keys for authentication servers and blockchain nodes.

(1) The private key generation of AS: AS1 in domain A generates its own identity IDAS1∈{0,1}∗, exposes it to the AS entities in all domains, and sends it to PKG1. PKG1 runs the SampleMat(A,B,H2(IDAS1),σ) algorithm to obtain the private key skAS1∈Zm×m such that A⋅skAS1=H2(IDAS1) and ‖skAS1‖≤σm. Then, PKG1 returns skAS1 to AS1. AS1 can verify the correctness after receiving it through A⋅skAS1=?H2(IDAS1). Similarly, AS2 in domain B can also interact with PKG2 to generate its private key.

(2) The private key generation of blockchain nodes: AN1 of domain A blockchain generates its own identity IDAN1∈{0,1}∗ and sends it to PKG1. PKG1 runs the SampleMat(A,B,H2(IDAN1),σ) algorithm to obtain the private key skAN1∈Zm×m such that A⋅skAN1=H2(IDAN1) and ‖skAN1‖≤σm. Then, PKG1 returns skAN1 to AN1. AN1 can verify the correctness after receiving it through A⋅skAN1=?H2(IDAN1). Similarly, BN1 of domain B blockchain can also interact with PKG2 to generate its private key.

4.3 Registration

In this section, the blockchain nodes in each domain interact with AS in the local domain to generate the identity index and add it to the identity list.

(1) Calculating identity index: AS1 maintains an identity list LA=[ ] in domain A. AN1 calculates the identity index IAN1=H3(IDAN1,skAN1), and sends the registration request to AS1.

(2) Adding the identity list: AS1 adds the identity IDAN1 and index IAN1 to the identity list LA=[{IDAN1,I AN1}], and then returns the successful registration message of node AN1.

Similarly, domain B blockchain node BN1 can also interact with AS2 and register identity.

4.4 Identity Authentication

In this section, the blockchain node in the local domain makes a cross-domain request and sends it to the foreign domain AS. The foreign domain AS requests the local domain AS to assist in authenticating the node’s identity and negotiating the session key.

(1) AN1 randomly selects vector s∈Zqn and noise vector x∈χm, and calculates R0=ATs+x, R1=H2(IDAS1)Ts+x+IAN1⋅⌊q2⌋. Then, AN1 selects the current time T1 and sends a cross-domain request message mAN1→AS2={IDAS1,R0,R1,IDBN1,Cross-chain Asset Exchange,SHA256,T1} to AS2 in domain B. Among them, Cross-chain Asset Exchange means that the purpose of AN1 accessing BN1 is to exchange assets in the cross-chain scenarios, and SHA256 means that the hash function used in HTLC during the cross-chain asset exchange process is the SHA-256 algorithm.

(2) After AS2 in domain B receives the cross-domain request from AN1 in domain A, if T1 is timely, AS2 selects the current time T2 and generates the assistance request message mAS2→AS1={IDAS1,R0,R1,T1,IDAS2,T2}. Then, AS2 randomly selects the vector r1←Dσm, calculates hAS2=H1(Ar1,mAS2→AS1), zAS2=skAS2hAS2+r1, and generates the signature sigAS2 = (hAS2, zAS2) of the message mAS2->AS1 with probability min (1,...). After that, {mAS2→AS1,sigAS2} is sent to AS1, indicating that AS1 needs to assist in authenticating the identity of AN1.

(3) After AS1 receives the message {mAS2→AS1,sigAS2}, if T2 is timely, executes the signature verification algorithm. If hAS2=H1(AzAS2−H2(IDAS2)hAS2,mAS2→AS1) and ‖zAS2‖≤2σm, AS1 has successfully authenticated AS2’s identity. Secondly, AS1 extracts R0 and R1 from mAS2→AS1, calculates the vector R1−skAS1TR0, and compares the absolute value of each component minus ⌊q2⌋ with q4 to recover the identity index IAN1′. At this time, AS1 traverses the elements in the identity list LA. If IAN1=IAN1′, AS1 will complete the identity authentication of AN1. Then, AS1 calculates the session key kAN1=H4(IAN1), selects the current time T3, generates the assistance authentication message mAS1→AS2={IDAS1,IDAS2,T2,kAN1,T3}, randomly selects the vector r2←Dσm, calculates hAS1=H1(Ar2,mAS1→AS2), zAS1=skAS1hAS1+r2, and generates the signature sigAS1 = (hAS1, zAS1) of the message mAS1->AS2 with probability min (1,...). Finally, AS1 sends {mAS1→AS2,sigAS1} to AS2 in domain B through a secure and confidential channel, indicating that AS1 has assisted AS2 in completing the identity authentication of AN1.

(4) AS2 in domain B receives the message {mAS1→AS2,sigAS1} from AS1. If T3 is timely, the signature verification algorithm will be executed. If hAS1=H1(AzAS1−H2(IDAS1)hAS1,mAS1→AS2) and ‖zAS1‖≤2σm, the signature verification is passed, indicating that AS2 has successfully authenticated the identities of AS1 and AN1. Then, AS2 adds {IDAN1,⋅} to the identity list LB in domain B, which allows AN1 to access nodes in domain B. At the same time, AS2 sends the session key kAN1 and cross-chain information {IDBN1,Cross-chain Asset Exchange,SHA256} to blockchain B, selects the current time T4, uses the session key kAN1 to encrypt the authentication success message, and sends it to AN1 in domain A.

4.5 Cross-Chain Asset Exchange

After the cross-domain access request is allowed, the blockchain nodes in the local domain and the foreign domain conduct cross-chain asset exchange between domains based on HTLC.

(1) Cross-chain preparation: After receiving the message mAS2→AN1 from AS2, AN1 calculates the session key kAN1=H4(IAN1) and decrypts mAS2→AN1. If T4 is timely, AN1 knows that the identity authentication is successful and can exchange cross-chain assets with BN1. At the same time, after receiving the message {IDBN1,Cross-chain Asset Exchange,SHA256} from AS2, BN1 is ready for asset exchange.

(2) Cross-chain asset exchange between domains: As shown in Fig. 2, firstly, AN1 generates h randomly, calculates its hash value H=SHA256(h), and sends it to BN1 through the cross-domain channel. Secondly, AN1 selects the time t1 and uses the hash value H and time t1 to lock the asset a to be exchanged, and BN1 selects the time t2 such that t2<t1, uses the hash value H and time t2 to lock the asset b to be exchanged. Then, AN1 calls the smart contract interface of blockchain B across domains and uses random values h to unlock asset b. At this time, BN1 obtains the h from the contract of blockchain B and calls the smart contract interface of blockchain A across domains to unlock the asset a. If AN1 and BN1 unlock the assets within the specified time, the cross-chain asset exchange is successful, and the smart contracts of blockchain A and B send the asset a and b to BN1 and AN1 respectively through the cross-domain channel.

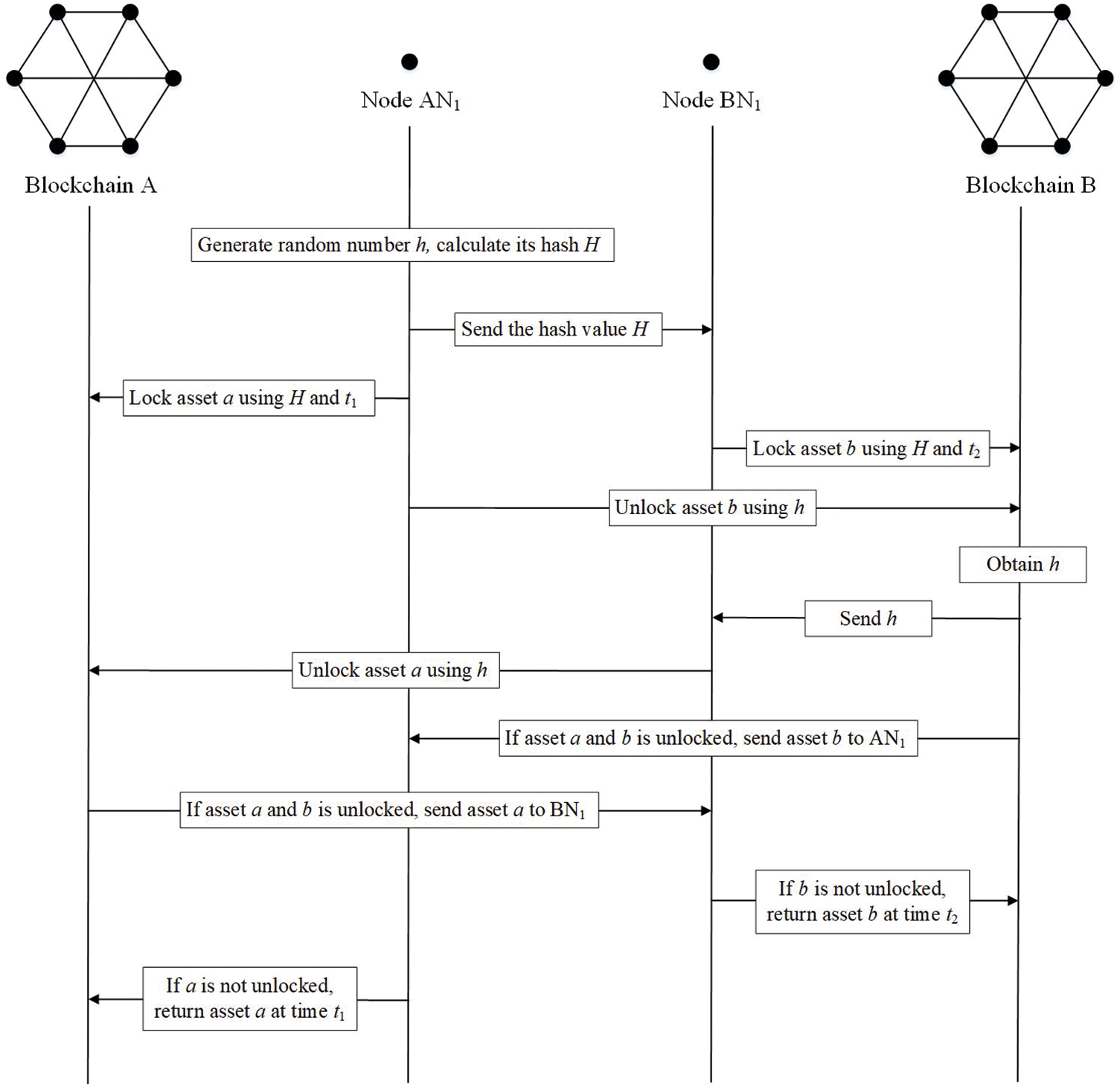
Figure 2: The cross-chain asset exchange process of our scheme

(3) Timeout asset return: As shown in Fig. 2, if one of the two nodes fails to unlock the assets within the specified time, the smart contract will return the assets to the nodes in the respective domain.

5  Security Analysis

5.1 Correctness

In this paper, the correctness of the cross-domain identity authentication scheme depends on the correctness of signature verification and identity index recovery described in Eqs. (5) and (6), respectively.

The correctness of signature verification:

AzAS−H2(IDAS)hAS=A(skAShAS+r)−H2(IDAS)hAS=H2(IDAS)hAS+Ar−H2(IDAS)hAS=Ar(5)

For example, AS1 receives the message mAS2→AS1 and the signature sigAS2=(hAS2,zAS2) sent by AS2, calculates H1(AzAS2−H2(IDAS2)hAS2,mAS2→AS1)=H1(Ar,mAS2→AS1), and compares it with hAS2 to verify the correctness of the signature.

The correctness of identity index recovery:

R1−skASTR0=H2(IDAS)Ts+x+IAN⌊q2⌋−skAST(ATs+x)=H2(IDAS)Ts+x+IAN⌊q2⌋−H2(IDAS)Ts−skASTx=IAN⌊q2⌋+x−skASTx⏟noise(6)

As described in [27], each component of the vector x−skASTx is less than q5. Consequently, each bit of the identity index IAN can be recovered correctly.

5.2 The Unforgeability of the Signature Process

Theorem 1 Assuming that an adversary A can break the unforgeability of the signature process in polynomial time, a challenger C is executing a PPT algorithm that can break the SIS assumption.

Analysis: To sign the cross-domain message in our scheme, we introduce the identity-based signature algorithm from lattice in [25]. The detailed proof of Theorem 4 in [25] has demonstrated that this algorithm can achieve the unforgeability under adaptive chosen message and identity attacks in the random oracle model, which can be reduced to SIS assumption.

Consequently, the signature process in our scheme is unforgeable and post-quantum secure to ensure the authenticity and credibility of identity in quantum computing circumstances.

5.3 The IND-CPA of the Hiding and Recovery of Identity Index

Theorem 2 Assuming that adversary A can break the IND-CPA security of the hiding and recovery of identity index in polynomial time, challenger C is executing a PPT algorithm that can break the LWE assumption.

Proof: Let adversary A have a non-negligible advantage ε to break the IND-CPA security of the hiding and recovery of identity index. For i=0,1,…,m, ui∈Zqn and x←χ, challenger C maintains a series of LWE instances, named (ui,R0,i) such that R0,i=uiTs+x. After that, challenger C and adversary A interact according to the IND-CPA game described in Section 3.2.

(1) Setup: Challenger C executes TrapGen algorithm in System initialization to obtain the matrix A=(u1,u2,…,um) and basis B∈Zqm×m of Λ(A), and defines H1:Zqn×{0,1}∗→{−1,0,1}m, H2:{0,1}∗→Zqn×m, H3:{0,1}∗×Zm×m→{0,1}m, and H4:{0,1}m→{0,1}κ. Then, C sends the public parameters pp={A,H1,H2,H3,H4} to adversary A.

(2) Phase 1: In this phase, adversary A can conduct H2 and private key inquiries with challenger C, and C visits the H2 query oracle Private key query oracle and returns the results to A.

H2 query: Let QH2 be the maximum number of adversary A queries to H2, and challenger C maintains a query list L. The steps for adversary A to query the H2 query oracle are as follows. Firstly, C selects Q∗∈{1,2,…,QH2} and computes a tuple {Qi,IDi,H2(IDi),skIDi} for i-th query Qi. If {Qi,IDi,H2(IDi),skIDi} is in the query list L, C returns H2(IDi) to A. If {Qi,IDi,H2(IDi),skIDi} is not in L and Q∗≠Qi, C executes the SampleMat(A,B,H2(IDi),σ) algorithm to obtain the private key skIDi∈Zm×m such that A⋅skIDi=H2(IDi) and ‖skIDi‖≤σm, returns H2(IDi) to A, and then supplements {Qi,IDi,H2(IDi),skIDi} to L. If {Qi,IDi,H2(IDi),skIDi} is not in L and Q∗=Qi, C defines H2(IDi)=(u0,u0,…,u0) to return to A, selects skIDi at random, and supplements {Qi,IDi,H2(IDi),skIDi} to L.

Private key query: Adversary A selects IDi to query the corresponding private key. After that, challenger C retrieves IDi in the query list L. If IDi is not found, C calls H2 query to add {Qi,IDi,H2(IDi),skIDi} to L. Otherwise, if Q∗≠Qi, C returns skIDi to A. If Q∗=Qi, C aborts this process.

(3) Challenge: Adversary A constructs IID0,IID1∈{0,1}m corresponding to ID0,ID1 which cannot be queried in Phase 1 and sends them to challenger C. Then, C selects ξ∈{0,1}, and calculates: R0∗=(R0,1,R0,2,…,R0,m)T and R1∗=(R0,0,R0,0,…,R0,0)T+IIDξ⋅⌊q2⌋. On the other hand, C samples (R0∗,R1∗) from Zqn×Zq randomly. Finally, C sends (R0∗,R1∗) to A.

(4) Phase 2: Adversary A acquires the private key through calling the Private key query, and cannot query about the private keys corresponding to ID0 and ID1.

(5) Guess: After receiving (R0∗,R1∗), adversary A selects a bit ξ∗∈{0,1}. If ξ∗=ξ, A wins this game.

Analysis: If (ui,R0,i) is a solution of LWE assumption, (R0∗,R1∗) is calculated as follows:

R0∗=(R0,1,R0,2,…,R0,m)T=(u1Ts+x,u2Ts+x,…,umTs+x)T=ATs+x(7)

R1∗=(R0,0,R0,0,…,R0,0)T+IIDξ⋅⌊q2⌋=(u0Ts+x,u0Ts+x,…,u0Ts+x)T+IIDξ⋅⌊q2⌋=(u0,u0,…,u0)Ts+x+IIDξ⋅⌊q2⌋(8)

Obviously, (R0∗,R1∗) is valid, and for adversary A, the probability that adversary A outputs ξ∗=ξ is Pr[ξ∗=ξ]=12+ε. If (R0∗,R1∗) is selected randomly, the probability that A outputs ξ∗=ξ is Pr[ξ∗=ξ]=12. Consequently, the advantage that adversary A makes correct judgment is:

AdvAIND-CPA(pp)=|Pr[ξ∗=ξ]−12|=|12⋅(12+ε)+12⋅12−12|=ε2.(9)

Considering the successful execution of the IND-CPA game, the advantage of solving the LWE assumption is (1−1QH2)⋅AdvAIND-CPA(pp)=QH2−12QH2⋅ε, which is negligible for adversary A.

To sum up, the hiding and recovery of the identity index in our scheme has IND-CPA security, making the cross-domain identity authentication process secure and reliable in quantum scenarios.

6  Comparison Analysis

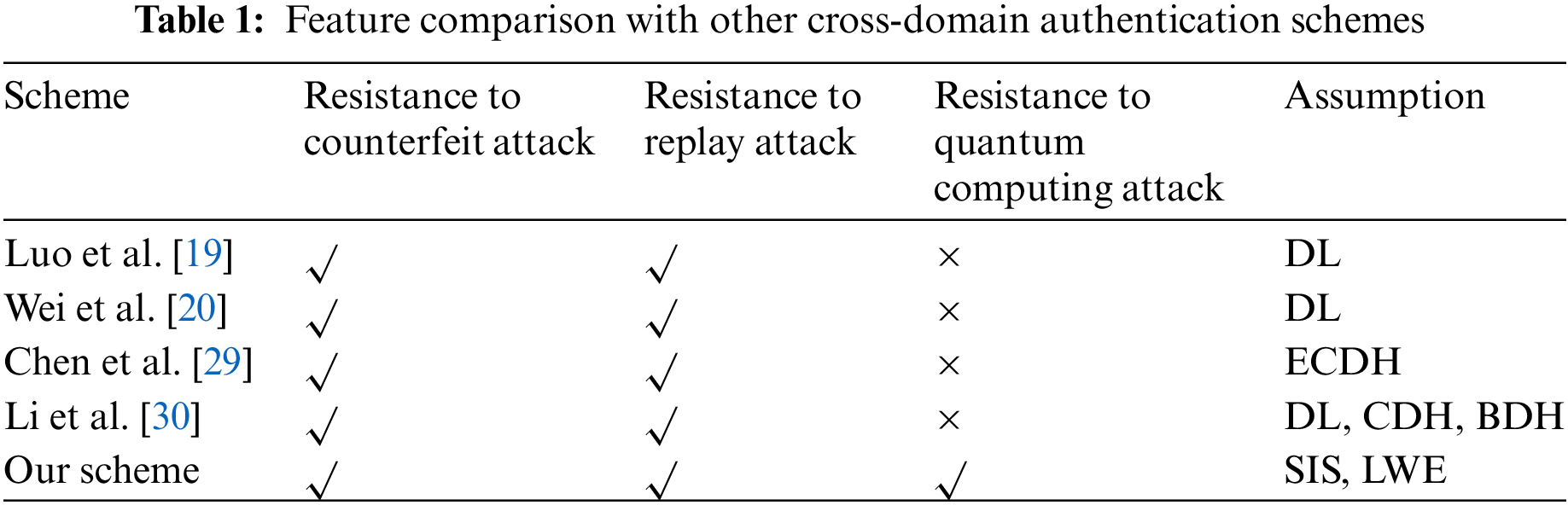
Table 1 compares the security features of references [19,20,29,30] and our scheme. Resistance to counterfeit attacks means that the authentication server in each domain can verify the identity of the node and the authentication server in the foreign domain to avoid the attack of the fake user on the system. Resistance to replay attacks means that the message is verified to be timely by introducing a timestamp in the message to avoid the replay attack of the attacker. Post-quantum computing attacks refer to a cross-domain authentication scheme based on post-quantum cryptography to avoid quantum computing attacks launched by attackers equipped with quantum computers. To sum up, the lattice-based cross-domain authentication scheme proposed in our paper meets the above three security characteristics, and the unforgeability of signature and the IND-CPA security of identity index is reduced to SIS and LWE assumptions, respectively.

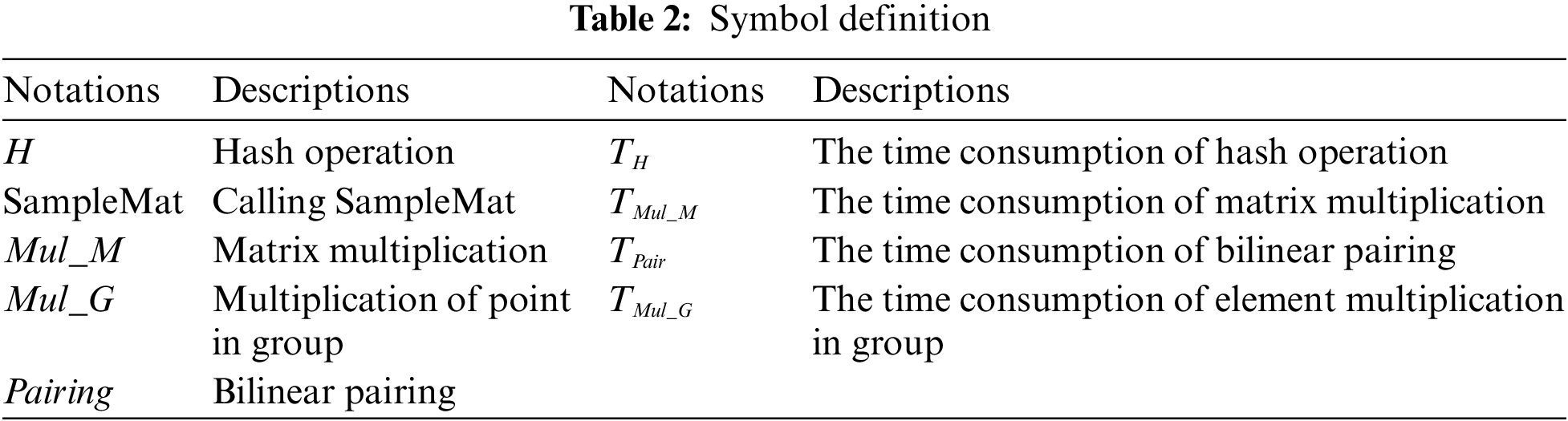
In Table 2, many notations in our scheme are defined. Table 3 defines the symbol and meaning of the operation, and compares the operation number of the key generation, signature process, and verification process of our scheme with [19,20,29]. It is evident that our scheme has fewer operation number than [19,20] and [29] in the aforementioned three areas. After that, Table 4 compares this scheme with [20] and [30] in terms of the user and authentication server time consumption. Our scheme realizes cross-domain identity authentication through the interaction of authentication servers in the local domain and the foreign domain. Therefore, the time consumption of the authentication server is divided into the local domain authentication server (AS1) and the foreign domain authentication server (AS2). Obviously, the operation designed in our scheme is mainly the multiplication of matrices, and its efficiency is much higher than the pairing operation on groups in [20] and [30].

7  Conclusion

To solve the problem of entity authentication between domains, we propose a post-quantum cross-domain authentication scheme by designing the transmission and recovery process of the identity index based on lattice cryptography and introducing the identity-based signature from lattice in our scheme. In addition, we apply HTLC to realize the cross-chain asset exchange between blockchain nodes in different trust domains. Moreover, security analysis shows that our scheme meets the correctness, unforgeability of signatures, and IND-CPA security for identity index under quantum computing. Finally, comparison analysis shows that our scheme can resist counterfeit attacks and replay attacks, and is more efficient in terms of operation number and time consumption of the user and authentication server compared to many schemes based on traditional cryptography.

Acknowledgement: All authors would like to thank the anonymous reviewers for their constructive suggestions, which improve the quality of this work.

Funding Statement: This work was supported by the Defense Industrial Technology Development Program (Grant No. JCKY2021208B036).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yi-Bo Cao, Xiu-Bo Chen; security proofs: Yi-Bo Cao, Gang Xu; analysis and interpretation of results: Yi-Bo Cao, Si-Yi Chen; draft manuscript preparation: Yun-Feng He, Lu-Xi Liu, Yin-Mei Che, Xiao Wang, Ke Xiao. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. Feng, B. Liu, Z. Guo, K. Yu, Z. Qin and K. R. Choo, “Blockchain-based cross-domain authentication for intelligent 5G enabled internet of drones,” IEEE Internet Things J., vol. 9, no. 8, pp. 6224–6238, 2021. [Google Scholar]

2. Z. Zhou, Y. Tian, J. Xiong, J. Ma, and C. Peng, “Blockchain-enabled secure and trusted federated data sharing in IIoT,” IEEE Trans. Industr. Inform., vol. 19, no. 5, pp. 6669–6681, 2023. [Google Scholar]

3. T. Wu et al., “Blockchain-based anonymous data sharing with accountability for Internet of Things,” IEEE Internet Things J., vol. 10, no. 6, pp. 5461–5475, 2022. [Google Scholar]

4. Y. Xie, X. Chen, and Y. Yang, “A new lattice-based blind ring signature for completely anonymous blockchain transaction systems,” Secur. Commun. Netw., vol. 2022, pp. 4052029, 2022. [Google Scholar]

5. X. Chen, S. Xu, T. Qin, Y. Cui, S. Gao and W. Kong, “AQ-ABS: Anti-quantum attribute-based signature for EMRs sharing with blockchain,” in Proc. 2022 IEEE Wireless Commun. and Netw. Conf. (WCNC), 2022, pp. 1176–1181. [Google Scholar]

6. W. Liang et al., “PDPChain: A consortium blockchain-based privacy protection scheme for personal data,” IEEE Trans. Reliab., vol. 72, no. 2, pp. 586–598, 2023. [Google Scholar]

7. S. Xu, X. Chen, and Y. He, “EVchain: An anonymous blockchain-based system for charging-connected electric vehicles,” Tsinghua Sci. Technol., vol. 26, no. 6, pp. 845–856, 2021. [Google Scholar]

8. Y. Cheng, S. Xu, M. Zang, S. Jiang, and Y. Zhang, “Secure authentication scheme for VANET based on blockchain,” in Proc. 2021 7th Int. Conf. Comput. Commun. (ICCC), 2021, pp. 1526–1531. [Google Scholar]

9. J. Poon and T. Dryja, The Bitcoin Lightning Network: Scalable Off-Chain Instant Payments, Canada: 1Bitcoin Inc., 2016. [Google Scholar]

10. S. K. Mohanty and S. Tripathy, “n-HTLC: Neo hashed time-lock commitment to defend against wormhole attack in payment channel networks,” Comput. Secur., vol. 106, pp. 102291, 2021. [Google Scholar]

11. P. Shamili and B. Muruganantham, “Federation payment tree: An improved payment channel for scaling and efficient zk-hash time lock commitment framework in blockchain technology,” Concurr. Eng., vol. 30, no. 4, pp. 317–324, 2022. [Google Scholar]

12. Monika, R. Bhatia, A. Jain, and B. Singh, “Hash time locked contract based asset exchange solution for probabilistic public blockchains,” Cluster Comput., vol. 25, no. 6, pp. 4189–4201, 2022. [Google Scholar]

13. F. Barbàra and C. Schifanella, “MP-HTLC: Enabling blockchain interoperability through a multiparty implementation of the hash time-lock contract,” Concurr. Computa.: Pract. Exp., vol. 35, no. 9, pp. e7656, 2023. [Google Scholar]

14. S. Wadhwa, J. Stöter, F. Zhang, and K. Nayak, “He-HTLC: Revisiting incentives in HTLC,” Cryptol. ePrint Arch., 2022. [Google Scholar]

15. M. A. Sirbu and J. Chuang, “Distributed authentication in kerberos using public key cryptography,” in Proc. SNDSS’97, 1997, pp. 134–141. [Google Scholar]

16. K. Liu, S. Qing, and Y. Meng, “An improved way on kerberos protocol based on public-key algorithms,” J. Softw., vol. 12, no. 6, pp. 872–877, 2001. [Google Scholar]

17. W. Zhang, X. Wang, and M. K. Khan, “A virtual bridge certificate authority-based cross-domain authentication mechanism for distributed collaborative manufacturing systems,” Secur. Commun. Netw., vol. 8, no. 6, pp. 937–951, 2015. [Google Scholar]

18. H. Peng, “An identity-based authentication model for multi-domain,” Chinese J. Comput., vol. 29, no. 8, pp. 1271, 2006 (In Chinese). [Google Scholar]

19. C. Luo, S. Huo and H. Xing, “Identity-based cross-domain authentication scheme in pervasive computing environments,” J. China Ins. Commun., vol. 32, no. 9, pp. 111–115+122, 2011 (In Chinese). [Google Scholar]

20. S. Wei, S. Li and J. Wang, “A cross-domain authentication protocol by identity-based cryptography on consortium blockchain,” Chinese J. Comput., vol. 44, no. 5, pp. 908–920, 2021 (In Chinese). [Google Scholar]

21. X. Zhou, F. Miao and Y. Xiong, “A certificate authority domain-based cross-domain authentication scheme for virtual enterprise using identity based encryption,” in Proc. 2021 7th Int. Conf. Big Data Comput. Commun. (BigCom), 2021, pp. 144–149. [Google Scholar]

22. J. Cui, N. Liu, Q. Zhang, D. He, C. Gu and H. Zhong, “Efficient and anonymous cross-domain authentication for IIoT based on blockchain,” IEEE Trans. Netw. Sci. Eng., vol. 10, no. 2, pp. 899–910, 2022. [Google Scholar]

23. P. W. Shor, “Polynomial time algorithms for discrete logarithms and factoring on a quantum computer,” in Proc. Algorithmic Number Theory: First Int. Symp., NY, USA, 1994, pp. 289–289. [Google Scholar]

24. M. Rückert, “Strongly unforgeable signatures and hierarchical identity-based signatures from lattices without random oracles,” in Proc. Post-Quantum Cryptogr.: Third Int. Workshop, PQCrypto 2010, Darmstadt, Germany, 2010, pp. 182–200. [Google Scholar]

25. M. Tian and L. Huang, “Efficient identity-based signature from lattices,” in Proc. ICT Syst. Secur. Privacy Protection: 29th IFIPTC 11 Int. Conf., SEC 2014, Marrakech, Morocco, 2014, pp. 321–329. [Google Scholar]

26. J. Alwen and C. Peikert, “Generating shorter bases for hard random lattices,” Theor. Comput. Syst., vol. 48, pp. 535–553, 2011. [Google Scholar]

27. C. Gentry, C. Peikert, and V. Vaikuntanathan, “Trapdoors for hard lattices and new cryptographic constructions,” in Proc. the Fortieth Annual ACM Symp. Theory Comput., 2008, pp. 197–206. [Google Scholar]

28. J. Von Neumann, “Various techniques used in connection with random digits,” J. Research Nat. Bur. Stand. Appl. Math. Series, vol. 12, pp. 36–38, 1951. [Google Scholar]

29. Y. Chen, C. Zhong, C. Zhou, L. Xue and H. Huang, “Design of cross-domain authentication scheme based on medical consortium chain,” Comput. Sci., vol. 49, no. 6, pp. 537–543, 2022. [Google Scholar]

30. Y. Li, W. Chen, Z. Cai, and Y. Fang, “CAKA: A novel certificateless-based cross-domain authenticated key agreement protocol for wireless mesh nsetworks,” Wirel. Netw., vol. 22, pp. 2523–2535, 2016. [Google Scholar]