Dynamic Routing of Multiple QoS-Required Flows in Cloud-Edge Autonomous Multi-Domain Data Center Networks

1  Introduction

In the future 6G era, more and more autonomous networks [1–3] are appearing. Autonomous networks are networks that operate with little or no manual participation. The cloud-edge autonomous multi-domain data center networks (DCNs) are composed of interconnected multi-domain DCNs which are required to perform better in the dynamic environment, including but not restricted to self-operation, self-healing, and self-optimization capabilities. However, as the volume of services for emerging Internet applications grows, which will increase the amount of data that needs to be transmitted for each scheduling/routing information exchange in the inter-data center network, it further enhances the diverse needs to fulfill the network QoS.

Traffic engineering (TE) is an essential tool that optimizes network scheduling/routing to improve network QoS performance and resource utilization. Multi-domain TE is about optimizing the performance and network utilization of different types of data flows for different network domains. In cloud-edge autonomous multi-domain DCNs, there is a trade-off between maximizing network utility and performance-centric fairness for inter-data center (inter-DC) links since the multi-domain DCNs are collaborating and competing with each other. Most of the conventional TE solutions for semi-autonomous/autonomous networks have used heuristic algorithms for resource allocation. By resolving the multi-commodity flows (MCFs) at each cycle, the Software-Driven Wide Area Network (SWAN) [4] maximizes the combined throughput of all flows. SWAN iterates from the allocation of lower rate flows and freezes the flow constrained by the link capacity at each step, thus achieving approximate max-min fairness. However, the QoS guarantees for flows with higher bandwidth requirements are restricted due to insufficient consideration of the bandwidth demand differences of various flows. Dong et al. [5] proposed TINA, which describes all transmissions in fair competition with each other as an El Farol game and allocates a probability to each transfer to maximize the utility in each transmission while ensuring that the traffic load on the link avoids congestion and conflicts under a certain threshold. However, the game process requires the game elements to be knowable and rational, which is often not the case in real network environments. In 2015 researchers at Google designed the Bandwidth-Efficient (BwE) data Backup System [6], in terms of network utility, which enables operators to construct intricate (non-linear) bandwidth functions to roughly evaluate the utility of the network. In terms of fairness, BwE determines the global max-min fairness through a concentrated multipath fair allocation algorithm (MPFA). However, due to the high inherent complexity of the multi-domain DCNs problem, the optimization model is typically difficult to solve and takes a long time. This paper studys cloud-edge autonomous multi-domain DCNs with dynamically changing traffic patterns and network environment parameters. In the conventional approaches described above, the network state is often underutilized for scheduling and routing.

In recent years, machine learning (ML) and deep reinforcement learning (DRL) have proven to be feasible and effective solutions for the autonomous control and management of complex systems. Some attempts have been made to improve routing decisions by using ML techniques, however, multi-domain routing is usually hypothetical and it increases the signaling overhead. Deep Reinforcement Learning Congestion Control (DRL-CC) [7] uses a single agent for dynamic and coordinated congestion management of all active Multipath Transmission Control Protocol (MPTCP) flows to the end hosts to enhance overall utility. DRL-CC also introduces proportional fairness, which achieves a tradeoff between utility and fairness. However, proportional fairness does not isolate well the business needs of different types of flows and can introduce interference. Zhang et al. [8] proposed Congestion-Free Routing with Reinforcement Learning (CFR-RL) intending to reduce the network’s maximum link consumption. CFR-RL establishes and resolves a straightforward linear programming optimization problem to identify each traffic matrix that has chosen a few key flows, which is subsequently rerouted to balance the network link utilization to achieve approximate fairness. However, since the Linear Programming (LP) solution space is large, it imposes a large computational overhead. Geng et al. [9] outlined a data-driven approach for the multi-domain TE problem that employs several agents for deep reinforcement learning in a unique way. Among them, TE’s goal is to maximize edge usage across the network. However, the evaluation of fairness is neglected. Our objective is to investigate the tradeoff between maximizing network utility and flows performance-centric fairness of inter-DC links in cloud-edge autonomous multi-domain DCNs from a new perspective, but there is little literature on this topic.

6G networks are expected to deliver higher data rates, lower latency, wider coverage, and greater reliability. This high-performance network environment has prompted the deployment of multi-domain data center networks with cloud-edge collaboration. In real-world deployments, this architecture faces several challenges and considerations:

Practical Challenges: (1) Heterogeneity: 6G networks may include a variety of devices (e.g., smartphones, IoT devices, drones, etc.) and multiple network technologies. This heterogeneity complicates unified resource management and optimization. (2) Resource constraints: Edge devices may be limited in terms of computation, storage and energy, and these devices need to work effectively with cloud resources. (3) Dynamics: The connectivity of devices, the needs of users and the conditions of the network may be dynamically changing, which requires real-time resource allocation and scheduling strategies.

Notes: (1) Resource allocation strategy: Considering the heterogeneity and dynamics of cloud-edge, a flexible and adaptive resource allocation strategy is needed. (2) QoS: Ensure that QoS requirements for different applications and services can be met during design and deployment. (3) Cross-domain collaboration: In a multi-domain environment, policies and protocols need to be developed to ensure collaboration and cooperation between different domains.

This article devises a reinforcement learning-based cloud-edge autonomous multi-domain data center networks architecture to meet the QoS requirements for various types of flows in a highly dynamic and interacting multi-domain network environment. The main contributions are as follows:

(1) To formalize the bandwidth fair allocation problem for different types of flows, this paper proposes a reward-based maximized variable elastic social welfare function (VESWF), which is a two-stage function incorporating proportional fairness and α-fairness.

(2) The essence of bandwidth fair allocation is to achieve a reasonable allocation and utilization of network resources for different types of flows that compete with each other, thus improving bandwidth utilization. In this paper, the bandwidth fair allocation is determined by the reward function which is used to evaluate the bandwidth resources. Different attributes of optimization (peak traffic demand and fluctuations in traffic demand) are taken into account according to the relevant measures of fairness and utility, and the corresponding reward function is used.

(3) For the scenario of the cloud-edge multi-domain data center networks, this paper describes the structure of the Long Short-Term Memory (LSTM)+Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithm, by improving the reinforcement learning experience pool and introducing an adaptive mechanism, thus speeding up the convergence of the model.

(4) After extensive simulation experiments, our LSTM+MADDPG algorithm outperforms other reinforcement learning algorithms, with a 14.6% improvement in delay convergence speed and at least 18.2% later packet loss onset. The rest of this paper is organized as follows. This article conducts the research for the related works in Section 2. Section 3 presents the background and motivation.

Section 4 describes the problem and the optimization objective this paper has investigated. Section 5 is an introduction to the LSTM+MADDPG algorithm. Section 6 depicts the experimental setup and the analysis of the experimental results. Finally, this article concludes the paper in Section 7.

2  Related Work

The dynamic routing problem for cloud-edge autonomous multi-domain data center networks that are explored in this paper includes the following research topics.

Multi-domain network traffic engineering: Multi-domain orchestration enables service providers to collaborate with other domains in the further provision of services in a federated environment. Reference [10] examined the service federation problem’s access control, which used the R-learning and Q-learning algorithms to maximize discounted rewards and maximize average rewards, respectively. Reference [11] studied the problem of Service Function Chains (SFCs) embedding in multi-domain networks. With very little information shared between Internet network operators and not much collaboration to improve routing decisions, reference [12] proposed a novel cooperative multi-domain routing system that effectively directed incoming flows through various domains, assuring their bandwidth and latency requirements and increasing overall network usage.

Flows performance-centric fairness: Fairness in flows performance implies that more types of flows are transmitted in parallel. Reference [13] introduced a fairness coefficient to provide network administrators with a flexible means of achieving utility and fairness maximization goals. To manage networks with multiple independent domains, it becomes possible for the distributed control plane to have a flat design. In reference [14], a distributed traffic engineering algorithm DisTE was designed for the traffic engineering problem on the flat control plane, to prevent policy conflicts between several controllers and a completely distributed arbitration system is used to deliver a fair max-min bandwidth allocation for traffic to maximize resource utilization. Considering the throughput and fairness trade-off in Network Function Virtualization (NFV) service chains between various network flows, reference [15] investigated a fair-aware flow scheduling problem that takes into account resource allocation and rate control for network utility maximization. To balance this trade-off, a low-complexity online distributed algorithm built on the Lyapunov optimization framework was presented to manage this trade-off. It allowed for the creation of arbitrary optimal utilities at various fairness levels by modifying the fairness deviation parameters.

Reinforcement learning for network traffic optimization: DRL is a promising method for effectively resolving issues with routing and traffic optimization that are pertinent to self-driving networks. Almasan et al. [16] integrated Graph Neural Networks (GNNs) into DRL agents and devised specific action spaces to achieve generalization. GNNs were created with the specific purpose of capturing useful data about the links’ relationships with one another and the traffic flowing through the network topology structure. Reference [17] developed intelligent TE algorithms for Software-Defined Wide Area Networks (SD-WAN) to provide service flows with certain QoS over the broadband Internet using software-defined capabilities. The performance of the baseline TE algorithm was first evaluated. Then, different deep- Reinforcement Learning (deep-RL) algorithms were implemented to overcome the limitations of the baseline approach. Liu et al. [18] proposed a new DRL-based routing Scheme, DRL-R, which used different images with resource reorganized pixels to represent the states of DRLs and actions representation at the path level. DRL agents deployed on Software-Defined Networking (SDN) controllers adaptively make reasonable routing decisions based on the network state, coordinating the optimal allocation of caches and bandwidth for traffic. Liu et al. [19] proposed DRL-OR, an online routing algorithm based on multi-intelligence deep reinforcement learning. Each routing node is controlled by a DRL agent, which quickly selects the best next hop for an upcoming flow request. To achieve energy efficiency goals in DCNs, Wang et al. [20] predicted traffic demand in DCNs using LSTM networks and tailored DRL algorithms to solve the MCF problem. To deal with user heterogeneity in terms of multi-dimensional characteristics of applications (including delay tolerance/sensitivity), reference [21] designed an incentive mechanism between edge servers and users using multi-dimensional contract theory modeling. In addition, the incentive mechanism realized users’ joint computational task offloading and uplink transmission power allocation through a Stackelberg game between users and edge servers. Guo et al. [22] proposed a federated learning framework in Digital Twin for Mobile Networks (DTMN), which is responsible for constructing virtual twin models for DTMN. To enhance the reliability of DTMN models trained by federated learning algorithms, they designed a method to assess the trust level of users participating in federated learning, which considered multiple behavioral attributes of the participants and the temporal correlation of the behavioral data. This paper gives a summary of DRL-based network traffic optimization in Table 1. These references are categorized into four aspects: art approaches, techniques, tools, and limitations.

LSTM+MADDPG is a pragmatic and challenging solution compared to existing works. The LSTM+MADDPG algorithm is not only considered to maximize the network utility but also to take into account the performance-centric fairness of flows for improving the overall performance of dynamic routing.

3  Background

As the number of various types of flows in mobile terminal devices and their QoS demands continue to expand, it has imposed a huge workload on the already congested cloud backbone network. Mobile Edge Computing (MEC) is a new approach to reducing the burden on the backbone network by immersing resources such as computing/storage into the edge network. Therefore, the future 6G network will need to be supported by cloud-edge automated multi-domain DCNs with distributed and centralized interoperability.

This paper describes the main framework of the cloud-edge automated DCNs. The network functional architecture of the cloud-edge automated DCNs is a hierarchical convergence, as demonstrated in Fig. 1, which contains the global autonomous layer and domain autonomous layers.

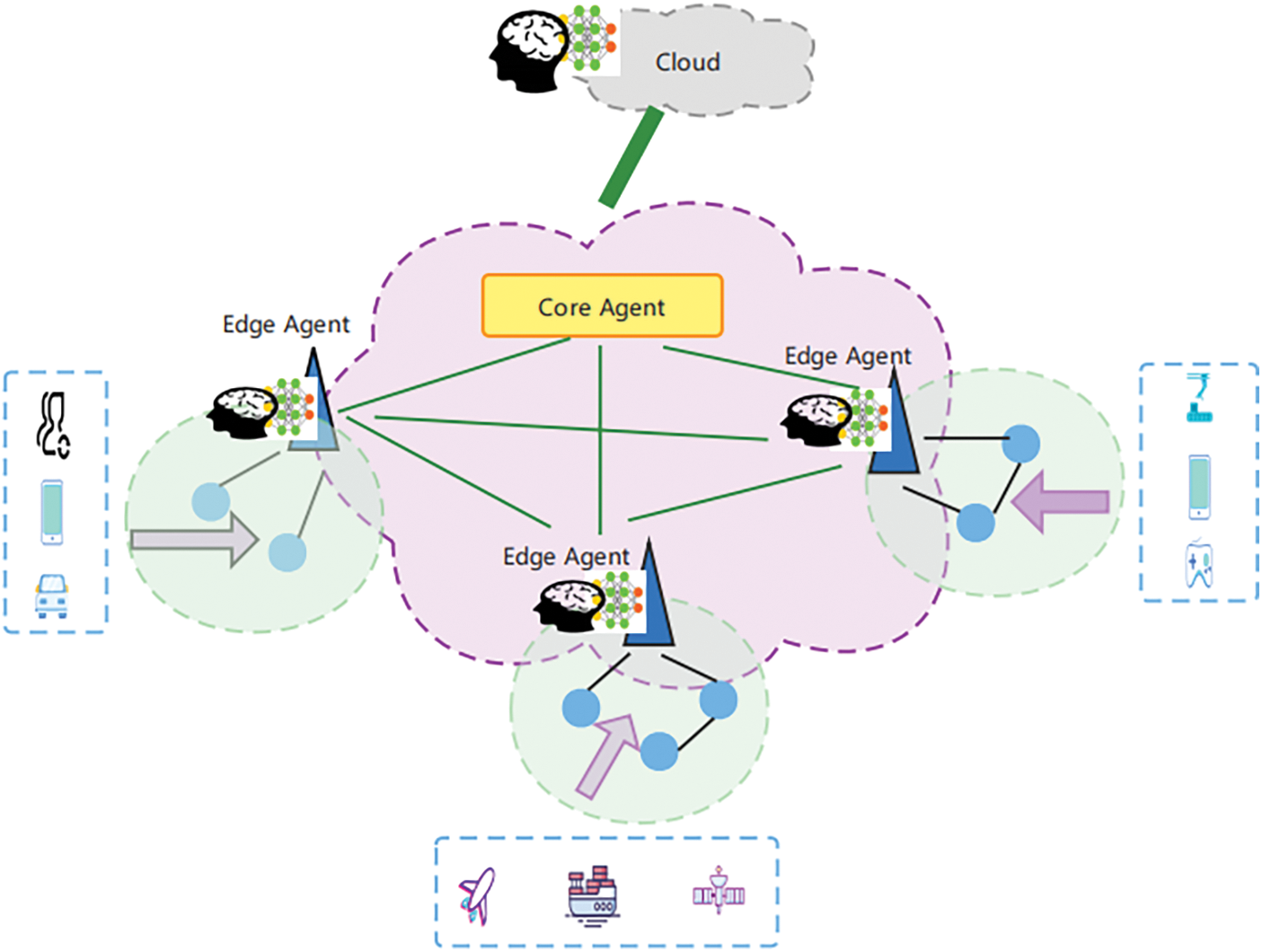
Figure 1: Framework of cloud-edge autonomous data center networks

1) Global autonomous layer: It is an autonomous pivot with centralized control function, which can complete the pivotal control and autonomous traffic scheduling of global coordination. The global autonomous layer cooperates with the flexible and fast-edge autonomous layer to constitute a distributed and hierarchical control system.

2) Edge autonomous layer: It refers to autonomous functions that are deployed on various distributed edge DCNs and cooperate with the autonomous pivot to compose Artificial Intelligence (AI) DCN systems. The edge autonomous layer provides fast on-demand autonomy services for multiple types of flows generated by a large number of edge devices through distributed AI algorithms that work together with the autonomous pivot to complete the autonomous function of DCNs. Moreover, under the control of the autonomous pivot, various edge DCNs can interact with each other to achieve distributed autonomous collaboration in specific scenarios.

4  Problem Statement

How to tradeoff maximizing network utility and flow performance-centric fairness in cloud-edge multi-domain data center networks is the primary issue which is needed to be addressed in this paper. Multiple types of flows are included in cloud-edge autonomous multi-domain DCNs, nevertheless, various types of flows have different network performance requirements. Flow performance-centric fairness is a concept in the networking field, especially in traffic management and resource allocation. It is primarily concerned with ensuring that each data flow in a network has fair access to the resources for which it is intended, rather than focusing only on per-user or per-connection. How strictly should this paper define the concept of flow performance-centric fairness? As available bandwidth resources are allocated to different types of flows, good or bad flow performance is reflected in the length of time it takes to complete a flow transmission. The time that is required to complete the traffic transmission of a flow is called the flow completion time (FCT). To achieve the best performance with the shortest FCT, the guiding principle of flow performance-centric fairness is that the inverse of the FCT is proportional to the weight of the bandwidth contended by the flow.

4.1 Problem Parameters

Cloud-edge multi-domain networks are complex systems of interconnected multi-domain data center networks that need to exhibit higher performance in dynamic environments, including, but not limited to, the ability to operate autonomously, self-heal, and self-optimize. In cloud-edge multi-domain data center networks, there are data flows with different QoS requirements, such as elephant flows and mice flows. Each network domain is usually managed by a single network operator, however, there is limited information sharing among different network operators and little collaboration among different network domains to improve routing decisions and enhance the overall performance of large-scale multi-domain networks. Dynamic routing optimization of network resources in cloud-edge multi-domain networks refers to the real-time and automated optimization of routing decisions for network traffic in a multi-domain network environment to ensure effective utilization of network resources, maximize performance, and satisfy different applications and user requirements. This optimization typically requires consideration of multiple domains, including cloud data centers, edge computing devices, and other network domains. Overall, dynamic routing optimization of network resources in the cloud-edge multi-domain network aims to ensure optimal utilization of network resources, improve network performance, and satisfy different applications and user demands through automated, real-time, and resource-aware approaches to cope with the complexity and dynamics in multi-domain network environments.

Assume a network that is constituted of multiple network domains. In general, the directed graph G(V,E) is employed to model the entire cloud-edge multi-domain DCNs, where V is represented as the set of all network nodes (routers/switches) and E is used for denoting the set of all edges. Each edge e(v,v ′)∈E has the capacity ce(v,v ′), which denotes the maximum throughput from node v to the neighboring node v ′ through this edge. The directed subgraph Gm(Vm,Em) is taken to indicate the network domain m. Assuming ∪mVm=V as well as Vm∩Vm ′≠ϕ (m domain and m′ domain will have intersection), and that Em={e(vm,vm  ′)|vm∈Vm}. There may be several mutually inverse edges between two adjacent domains, and the end-point nodes of these mutually inverse edges are the boundary nodes of domains.

Each flow f=(srcf,desf,Df,tsf,td1f,td2f) is represented by a six-tuple, where srcf and desf are source DC and destination DC, respectively, Df is traffic volume, tsf is the start time, and (td1f,td2f) represents soft deadline and hard deadline. The flow has no utility loss when the transmission is completed before td1f, the utility gradually degrades after td1f, and the utility is 0 at the moment of td2f. Note that if td1f=td2f, it means a hard deadline. Our goal is to maximize the network’s overall utility while meeting the FTC of different types of flows, each with specific QoS demands.

Let bfv,v ′ denotes the bandwidth allocated to the link ⟨v,v ′⟩ of flow f (⟨v,v ′⟩∈E) and Dfv,v ′ represents the traffic volume of flow f from source srcf to destination desf routed on link ⟨v,v ′⟩(srcf,desf∈V, srcf≠desf), then Dfv,v ′bfv,v ′ is employed to indicate the FCT of flow f on link ⟨v,v ′⟩. tf=max∑v∈V∑v′∈VDfv,v ′bfv,v ′ is denoted as the FCT of flow f, i.e., the sum of the FCTs of all links on the slowest path of flow f during the communication phase. Each flow f is associated with a weight wf. The performance of flow f is denoted as 1tf, indicating that the shorter the FCT, the better the performance.

4.2 Objectives

This paper is now ready to illustrate the problem of maximum network utility while maintaining flows performance-centric weighted fairness:

maxU(1)

subject to:

∑v∈V∑v ′∈Vbfv,v ′Dfv,v ′=wf∑fwf⋅cv,v ′⋅U,(∀f∈F)(2)

bv,v ′=∑fs,d∈Fσv,v ′s,d⋅Dfs,d⋅Xfv,v ′+bv,v ′¯(3)

bv,v ′≤cv,v ′⋅U(v,v ′:⟨v,v ′⟩∈E)(4)

Among them, Table 2 describes and defines the relevant parameters. Constraint (2) indicates weighted flow performance-centric fairness. Constraint (3) indicates that the allocated bandwidth on link ⟨v,v ′⟩ is contributed by the explicit routing and the default traffic volume of already allocated bandwidth. Constraint (4) is the link utilization constraint.

4.3 Variable Elastic Social Welfare Function

The social welfare function (SWF) is an important component of the study of welfare economics, which tries to point out the objectives pursued by society, while some factors should be under consideration. This paper considers the need to deal with the utilities (welfare) of these different flows when there are conflicting utilities between them.

The accurate choice of SWF depends on the specific problem that is trying to be addressed. This article proposes the Variable Elastic Social Welfare Function (VESWF), which makes a trade-off between fairness and utility, i.e., optimizing the SWF for a given fairness is equivalent to choosing the feasible solution with the best trade-off among the Pareto-optimal feasible solutions. Specifically, it allows considering several different defined reward functions to formulate bandwidth allocation problems for mice and elephant flows based on maximizing VESWFGα(r), where r(u,F(⋅))∈R+n is used to represent the reward obtained by assigning bandwidth u (utility) to flow f and F(⋅)∈Rn is employed to represent the distribution of flows generated according to the a-priori model.

The generalized SWF, which is defined as follows:

Gw(u)=∑f∈[D]wfuf↑(5)

where w∈[0,1]D is weight vector and u↑ is the vector derived by sorting the components of u incrementally. However, in order to ensure that the obtained solution is fair, the weights w are required to be strictly decreasing (i.e., Pareto optimal and fair). Another expression of SWF can be re-written as below:

G(u)=∑f∈[D]U(uf)(6)

where U : R→R is rigorously incremental as well as strictly concave. Among them, VESWF is a variant of SWF, and VESWF involves proportional fairness and α-fairness, as follows:

Gα(u)={∑f=1Fuf1−α1−αforα⩾0,α≠1∑f=1Flog⁡(uf)forα=1(7)

The function Gα(u) yields allocation based on flows performance-centric fairness. At the same time, it demonstrates that the welfare function is degrading with rising resources and the parameter α controls the rate of the degrading welfare function [23]. When α→∞ it has converged to the max-min fairness [24].

4.4 Solution Overview

In the cloud-edge automated multi-domain DCNs bandwidth resource allocation problem, the E-agent in each edge network domain needs to collaborate to find a policy πθii that maximizes the global utility. Based on the concept of VESWF, our problem can be simply formulated as:

maxθGα(J(θ))(8)

where θ is the set of all E-agent i corresponding to the policy parameter θi and Jf(θ)=Eθ[∑tγtrf,t] is the sum of the expected discounted rewards for flow f.

This paper has adopted the Deep Deterministic Policy Gradients (DDPG) approach for policy gradient learning of multi-domain E-gents in continuous action space. More specifically, considering a game with E-agents in all domains where the policies are parameterized by θ={θ1,…,θN}, and let uθ={uθ1,…,uθN} be continuous deterministic policies. Then this paper cans find an optimal deterministic policy (uθ) concerning the global RL objective:

J(uθ)=EX,a∼D[Quθ(X,a)|a=uθ(o)](9)

By performing gradient ascent concerning the following gradient:

▽θiJ(uθi)=EX,a∼D[▽θiuθi(oi)▽aiQiu(X,a)|ai=uθi(oi)](10)

Here Qiu(X,a) is a concentrated action-value function that treats all E-agents actions a=(a1,…,aN) as input, X=(o1,…,oN) is regarded as status information, and outputs the Q-value of E-agent i. Since each Qiu learned individually, the reward structure of the E-agent is arbitrarily combined and can be competing for conflicting rewards in a contending environment. Furthermore, the empirical replay buffer 𝒟 is composed of the tuple (X,X ′,a1,…,aN,r1,…rN), which records all E-agents’ experiences. This paper can achieve policy gradient estimates of policy parameter θi per E-agent i in multi-domain DCNs:

▽θiJ(uθi)=EX,a∼D[∑i=1mi▽θiuθi(oi)▽aiQiu(X,a)|ai=uθi(oi)](11)

As compared to the policy gradient in Eq. (10), in Eq. (11) if the variable mi is 1 indicating that domain i is selected, otherwise it is 0.

The action-value function Qiu is updated as follows:

ℒ(θi)=EX,a,r,X ′[(Qiu(X,a)−y)2]y=ri+γQiu ′(X ′,a ′)∣aj ′=uj ′(oj)(12)

where u ′={uθ1 ′,…,uθN ′} is used to denote the set of target policies and θi ′ is used to denote the delay parameter. In this paper, agents learn in a decentralized manner, each performing DDPG updates separately.

5  LSTM+MADDPG

This section proposes the innovative dynamic routing algorithm LSTM+MADDPG for cloud-edge autonomous DCNs, which can learn both the local reward of peak traffic demand and the global reward of traffic demand distribution. Since LSTM can handle time serial data, this paper introduces this structure to MADDPG to further improve the performance of multi-agent routing and bandwidth allocation.

5.1 System Overview

The cloud-edge automated DCN architecture based on deep reinforcement learning is illustrated in Fig. 2, which involves five components as described below.

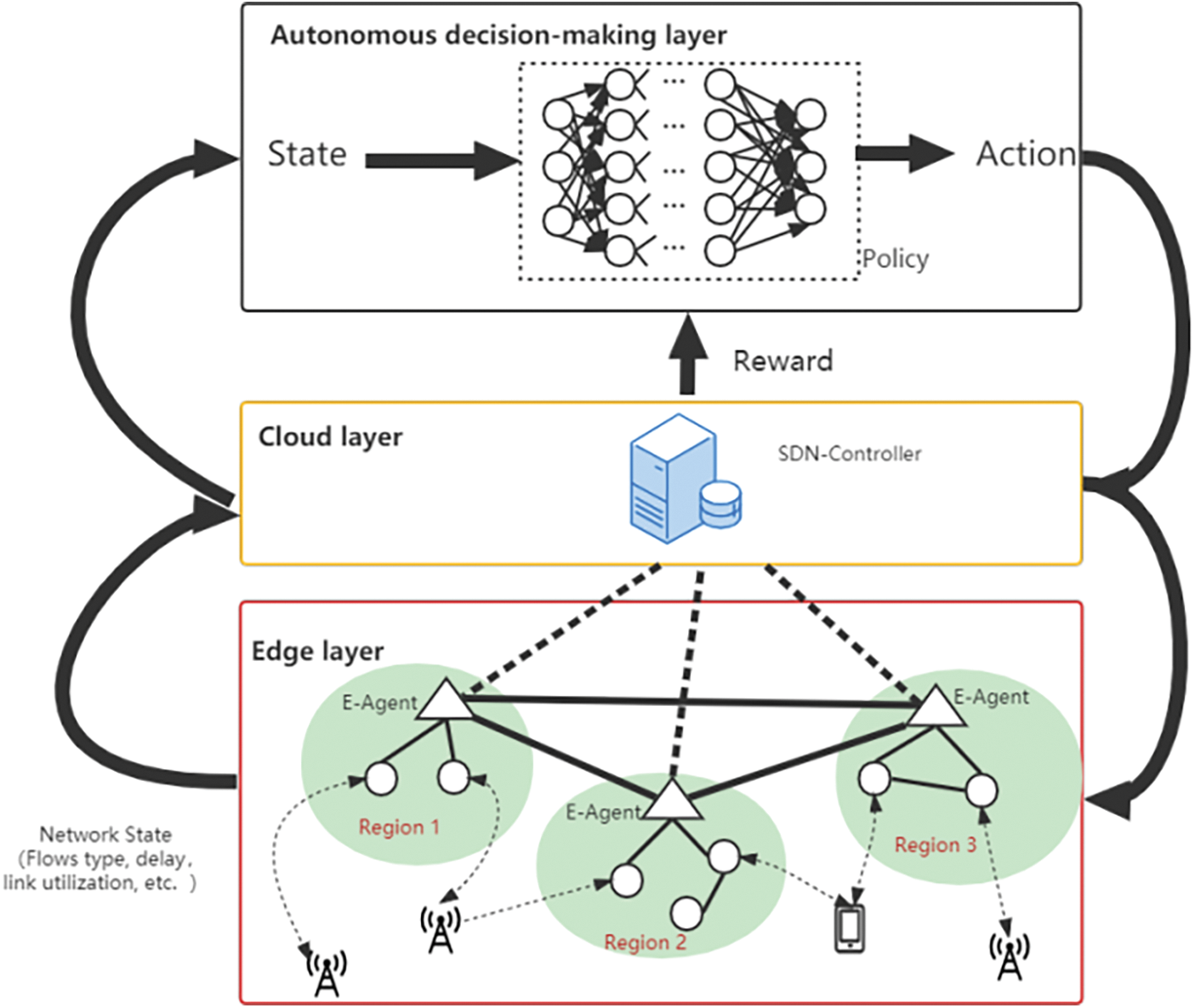
Figure 2: Deep reinforcement learning-based SDN cloud-edge automated DCNs architecture

Environment: According to the architecture in Fig. 2, the SDN-based multi-domain DCNs environment is composed of three parts: an SDN-enabled cloud-edge collaborative network, edge device providers, and clients. In the SDN-based cloud-edge automated DCNs, the SDN controller in the cloud layer controls the E-agent of each domain in the edge layer and deploys traffic control policies. The E-agent in each edge domain is responsible for managing the edge DCs in its domain, and E-agents in different edge domains can communicate with each other. The edge DCs collect and deliver different service data separately. In addition, the edge device providers offer clients 5G or 6G services, such as video, and so on.

E-Agent: There are multiple edge network domains in the edge layer, and each edge network domain generates an E-agent which dynamically and confederate controls the various types of flows on the edge DCs in that domain, to maximize network utility while guaranteeing flows performance-centric fairness. The cloud layer collects state information (global latency, throughput, traffic demand, etc.) of all E-agents and reports it to the autonomous decision layer for training. After completing the training, the autonomous decision layer deploys the well-trained model to the E-agents, and each E-agent i only requires the local observational information (single edge network domain delay, throughput, traffic demand, etc.) of the domain in which E-agent i is located and then makes the optimal decision.

State: As input to E-agents, which needs to capture the critical state of the network environment. Formally, this paper denotes st=[st1,…,sti,…,stN] as the set of observations of the E-agents in N edge domains at iteration step t. sti=[Dti,uti,lti,wti,gti] is the state of edge domain i at time t, where Dti indicates the Traffic Matrix (TM) in edge domain i at time t, uti denotes the link utilization of each link in the edge network domain i at time t, lti is used to indicate the transmission delay between each DC nodes pair in edge network domain i at time t, wti is used to indicate congestion rate per link in the edge network domain i at time t and gti denotes the goodput of each link in the edge network domain i at time t, respectively. This article assumes that goodput is the valid throughput, which is only counted for packets that are received successfully.

Define the set of all packets as P. For each packet pi that is transmitted in edge network domain i, a packet will be routed from the source DC k into edge network domain i at time t and diverted from destination DC j out of edge network domain i at time t. Assuming that the total number of DCs in edge network domain i is M, and all DCs can be transferred in and out of edge network domain i at time t, then the total number of all source-destination DC pairs is M × M. If Dti is defined as a TM of M × M dimensions, where each element dti,kj is the total traffic demand transmitted from source DC k to destination node j in edge domain i at time t, as follows:

Dti=[dti,11⋯dti,1M⋮⋱⋮dti,M1⋯dti,MM](13)

Formally, This article indicates dti,kj as the set of precomputed forwarding paths between source DC k and destination DC j at time t in edge network domain i. Let Dti be the traffic vector of E-agent on edge network domain i at time t, as follows:

dti,kj=|dti,kj|×[dt,pi,kj]p∈Pti,kj,j≠k,j,k∈Vm(14)

where dt,pi,kj∈[0,1] indicates the fraction of traffic amount delivered from source DC k to destination DC j on path p at time t in edge network domain i, as follows:

∑p∈Pti,kjdt,pi,kj=1,∀j,k∈Vm,j≠k(15)

Action: The objective of E-agents is to translate the state space into the action space and to determine an optimum traffic scheduling decision. Concerning the multi-domain DCNs traffic scheduling, an action includes two components: the selected path and the bandwidth adaption for all types of flows. Unlike traditional flow scheduling strategies, probability-based scheduling does not assign metrics to each link but assigns weights to each link. Define the link weight corresponding to DC k and any neighboring DC j in the edge network domain i at time t as wti,kj, then for a given DC k with M neighboring DCs have a weight vector Wti,k=[wti,k1,wti,k2,…,wti,kM]. Let ati=[Wti,1,Wti,2,…,Wti,M] as the set of all link weights at time t in edge domain i, then at=[at1,…,ati,…,atN] is used to denote the action set of all E-agents in the multi-domain DCNs at time t.

Reward: Based on the state of the network at the current moment and the actions taken by the E-agent, the E-agent will receive feedback on the network metrics at the next moment as a reward, which can be set as a function of different metrics according to different network optimization requirements. Let Uti(f)=[uti(f),v,v ′]∈RM×M is the bandwidth allocation matrix for flow f in edge network domain i at time t, consisting of all possible bandwidth allocations (BAs) for flow f (i.e., uti(f),v,v ′ is used to indicate the assigned bandwidth for flow f on link ⟨v,v ′⟩ at time t in edge network domain i). Since civ,v ′ is the capacity of link ⟨v,v ′⟩ in edge network domain i, then 0⩽uti(f),v,v ′⩽civ,v ′, for all flows and bandwidth allocations (i.e., when BA=civ,v ′ indicates the link is completely idle, and when BA = 0 indicates the link is congested). Maximize Gα(u(r)) as our optimization objective, where r=[r1,…,rF]∈R is used to denote the rewards obtained when assigning utility u=[u1,…,uF]∈U to flows. R and U are used to denote the set of rewards and the set of utilities, respectively. Thus, the flows performance-centric fairness is given by πr(α)∈argmaxr∈RGα(u(r)), from which the α-fairness allocation πr(α)=u∈U can be obtained.

This paper investigates two reward functions. Reward matrix Rti(f)=[rti(f),v,v ′]∈RM×M is computed depending on the reward function r(⋅) that scores the possible BAs according to the flows’ preferences. r(u,maxf) is used to denote the first reward function, which is depended on the assigned utility u and the peak traffic demand maxf∈RF of the flow, as expressed below:

rti(f),v,v ′(uti(f),v,v ′,maxi(f))={uti(f),v,v ′maxi(f)0<uti(f),v,v ′≤maxi(f)εotherwise(16)

where maxi(f) is used to represent the peak traffic demand for flow i (i.e., depending on the fluctuations i(f)∼Fi(⋅), and ε is used to indicate a score for BAs that are less preferred by the flow. r(u,f,ξ) is used to denote the second reward function, which relies on the quantity of assigned utility u, where f=[f1,…,fn] is used to denote the fluctuation matrix of the traffic demand, which relies on the traffic demand distribution F=[F1(⋅),…,Fn(⋅)], with the f∼F. The parameter ξ is defined as the degree of tolerance for unserved traffic in all flows, as follows:

rti(f),v,v ′(uti(f),v,v ′,i(f),ξ)={δti(f),v,v ′+|minv ′δti(f),v,v ′||maxv ′δti(f),v,v ′|+|minv ′δti(f),v,v ′|uti(f),v,v ′,(−)>ξεuti(f),v,v ′,(−)≤ξ(17)

where

δti(f),v,v ′=uti(f),v,v ′,(+)−uti(f),v,v ′,(−)(18)

is the difference between average excess utilities uti(f),v,v ′,(+) and average unserved traffic uti(f),v,v ′,(−) of flow f in edge domain i at time t, when allocated uti(f),v,v ′ utilities, given by:

uti(f),v,v ′,(+)=1T∑t|uti(f),v,v ′⩾i(ft)(uti(f),v,v ′−i(ft))(19)

uti(f),v,v ′,(−)=1T∑t|uti(f),v,v ′<i(ft)|(uti(f),v,v ′−i(ft))|(20)

where

i(ft)∼Fi(⋅),∀t=1,…,T(21)

Hence, u+ and u− are evaluated according to T traffic demand fluctuations (Eq. (21)) around u, quantifying the expected flow over- and under-provisioning effects of BA u.

5.2 Deep Reinforcement Learning Formulation For MADDPG

LSTM+MADDPG adopts a centralized training and decentralized execution architecture, as can be seen in Fig. 3. The LSTM+MADDPG is multiple actor-critic architecture, in which the actor-network of each agent obtains the local observed state information during training, while the critic network of the agent obtains its observed state information and additional information (usually the actions of other agents) for centralized global training. When the model is well-trained, it only needs the actor to interact with the environment to acquire the optimal action decision.

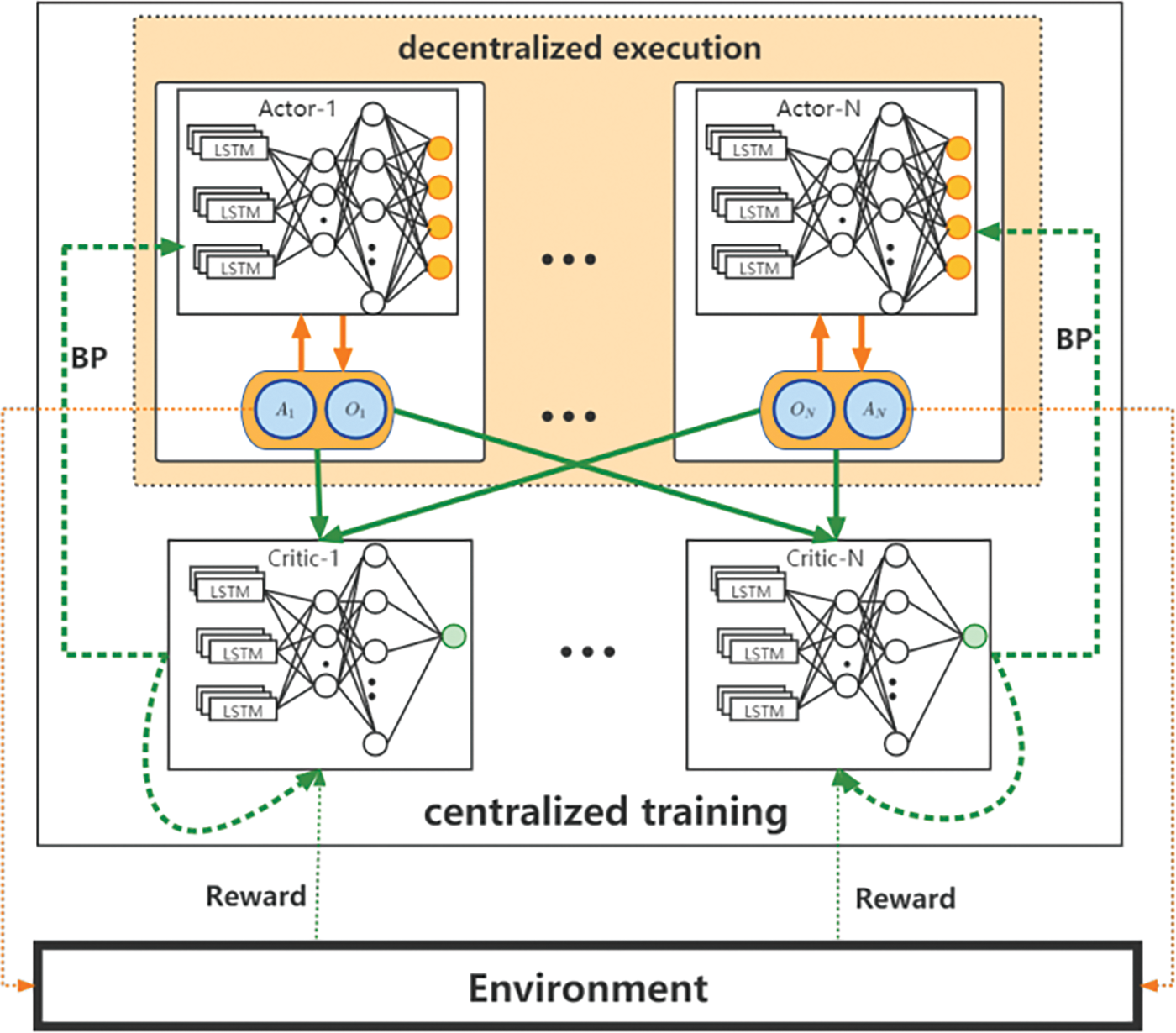
Figure 3: The overall approach of LSTM-MADDPG

Note that in multi-domain DCN scenarios, the network state often varies over time and changes with significant temporal correlation. Moreover, LSTM has achieved excellent results in processing and predicting data that exhibit significant temporal correlation [4]. This paper introduces an LSTM layer based on Multi-Agent Deep Deterministic Policy Gradient (MADDPG), which is referred to as LSTM+MADDPG described in Algorithm 1. Firstly, the actor actor-i generates actions ai according to their observation oi and interacts with the environment. Secondly, the centralized critics estimate the Q-value Critic-i based on the observations and actions of all agents. Finally, after receiving feedback rewards from the environment, the actors and critics are trained jointly using back propagation (BP) based on Eqs. (11) and (12). Assuming that all agents have the same observation and action space, the time complexity of the LSTM+MADDPG algorithm is denoted by O(n2(od+ad)). Where n is the number of agents, and od and ad indicate the dimensions of the observation and action space, respectively.

Among them, the recurrent neural network LSTM is added to the actor-network and the critic-network. Since the agents cannot communicate, the LSTM+MADDPG model fetches only a single frame in each time slot. The MADDPG adds the LSTM to memorize the last communication received from the other agents (the effect of the action on the reward). The actor-network and the critic-network are denoted by hat and hct for historical information, respectively. A single agent chooses an action based on the previous state hit, i.e., ait=πi φi(hit), at the same time the Q function becomes Qiθi(hct,at) (where hct={hc,1t,hc,2t,…,hc,Mt}). Among them, the loss function L(θi) in the critic network can be expressed as:

L(θi)=Ehct,at[(Qiθi(hct,at)−yit)2](22)

where

yit=rit+γQiθi ′(hct+1,π1ϕ1 ′(ha,1t+1),…,πMϕM ′(ha,Mt+1))(23)

the objective function can be expressed as:

J(ϕi)=Ehct,at[Qiθi(hct+1,π1ϕ1(ha,1t+1),…,πMϕM(ha,Mt+1))|ai=πiϕi(ha,it)](24)

In each training step, the critic and actor networks are updated by randomly sampled episodes from the replay buffer, with the target critic and actor-network parameters denoted by θ ′ and ϕ ′, respectively, and the target network using soft updates.

When this paper uses LSTM in combination with MADDPG, the hyperparameters affect not only the underlying learning process but also the processing of timing information. From the perspective of network architecture and algorithmic workflow, hyperparameters affect the algorithm as follows.

Network architecture perspective: 1) the number of hidden units of the LSTM directly determines the capacity and capability of the LSTM, i.e., the complexity of the timing information it can capture and memorize. Too few hidden units may not adequately capture the timing dependencies of the environment, while too many hidden units may lead to overfitting. 2) LSTM with multiple layers can help the model capture more complex timing patterns, but it also increases computational complexity. Increasing the number of layers may improve the performance of the model, but it may also lead to slower training and overfitting. 3) The width and depth of the neural network (the parts other than LSTM) determine the overall capacity of the model. A network that is too small may not capture all the necessary information, while a network that is too large may lead to overfitting and unstable training.

Algorithmic workflow perspective: 1) The learning rate directly determines the magnitude of weight updates. Too high a learning rate may lead to unstable training, while too low a learning rate may make the training process slow. 2) Discount factor (γ) determines the importance of future rewards in the current decision. A low γ value causes the agent to care more about short-term rewards, while a high γ value causes the agent to be more long-term. 3) Experience playback size determines how much the model can learn from historical data. A small buffer may lead to frequent data overwriting, while a large buffer can provide richer learning experiences.

The non-stationarity of the environment brought on by changes in the agents’ tactics is a persistent issue in multi-agent reinforcement learning. In particular, in an environment where multiple types of flows compete for network bandwidth, by overfitting the behavior of its rival E-agents, the E-agent can create a powerful policy, but such policies are undesirable since they are brittle and are susceptible to failure when rival E-agents alter their tactics. This paper trains a set of K distinct sub-policies to produce multi-agent policies that are more resistant to competing agents’ policy modifications. This paper assigns each agent a specific sub-policy to carry out at the beginning of each episode at random. At each episode, this paper arbitrarily selects a specific sub-policy to execute for each agent. Assume that policy uθi is the set of K different sub-policies and sub-policy k is denoted by uθi(k). For agent i, this paper is then maximizing the ensemble objective: Je(θi)=Ek∼unif(1,K)[∑t=0∞γtrti], where unif(1,K) denotes the set of sub-policy indexes, k denotes the sub-policy index. The corresponding policy gradient (Eq. (11)) can be rewritten as:

▽θiJe(uθi)=1KEX,a∼Di(k)[∑i=1mi▽θiuθi(k)(oi)▽aiQiu(X,a)|ai=uθi(k)(oi)](25)

6  Performance Evaluation

This section firstly describes the set-up of a simulation scenario for a cloud-edge autonomous data center network, then the LSTM+MADDPG algorithm is evaluated in comparison with existing routing algorithms based on reinforcement learning, and the experimental results are analyzed and summarized.

6.1 Experiment Setup

This paper has built a cloud-edge autonomous data center network using Ryu [25] and Mininet [26] on a Core i7, 3.4 GHz CPU, and 16 GB RAM server. In addition, the experimental simulation environment ultimately deploys the Ubuntu 20.04 operating system, and the specific reinforcement learning algorithms are implemented in PyTorch. Mininet is used to build a virtual network topology, generating network flows and collecting statistics according to scripts; Ryu controller is the controller in the SDN architecture, which implements and activates the routing actions of the agents by installing OpenFlow flow rules into the network devices.

The LSTM+MADDPG algorithm that we propose in this paper is based on the PPO algorithm, and the flow requests are randomly generated based on the real flow matrices measured in the literature [27]. In particular, when the probability of selecting a source-destination DC pair is proportional to the real traffic between that source-destination DC pair. The source code of this paper is available online at https://github.com/zsy32/LSTM-MADDPG. Our experiments use a network topology derived from a real-world network called GEANT [28], a larger network topology with 23 nodes and 37 bi-directional links, where each link has a different transmission capacity. In particular, the majority of the links have a data rate of 10 Mbps. The flow requests generated by the simulation experiments are based on a traffic matrix containing four types of flows (type 0: delay-sensitive, type 1: throughput-sensitive, type 2: delay-throughput-sensitive and type 3: delay-packet loss-sensitive, respectively).

The Mininet simulation platform collects statistics on delay, throughput ratio, and packet loss ratio for various types of network flows. This paper compares LSTM+MADDPG with three other schemes: Deep Reinforcement Learning with Optimal Routing (DRL-OR), Asynchronous Advantage Actor-Critic (A3C) and MADDPG. Furthermore, this article analyzes the impact of the LSTM network on the loss functions of the actor and critic network. DRL-OR is a multi-agent PPO algorithm that takes into account the behaviors and states of other agents during training, but during execution each agent still operates independently and does not take into account the interoperability of the different agents. A3C uses multiple parallel work processes to update a sharing neural network, which allows it to train quickly and stably, avoiding the need for empirical playback. However, since A3C does not use experience replay, it may be less responsive to continuously changing environments that require learning from experience. MADDPG is based on DDPG, which take into account the interactions of multiple agents, allowing each agent to update its strategy taking into account the strategies of the other agents, which contributes to better coordination and competition. Our propose LSTM+MADDPG algorithm combines LSTM with MADDPG, implying that in a multi-agent environment, each agent not only uses MADDPG for strategy learning but also uses LSTM to capture and take into account the temporal dependence of its observation sequence.

6.2 Evaluation with Current Methods

1) Delay: The delay is defined as the time that it takes for a packet to be transported in a topological network from the source node to the destination node. As the number of switches or routers involved in packet transmission increases, the delay in the network is decreased as the time slot increases due to multipath routing. Figs. 4a–4d show the delay variation for the four types of flows, this paper finds that the delay converges faster in Fig. 4a compared to the other types of flows. Since tpye 0 is a delay-sensitive type of flow, the final delay of each algorithm converges to about 5 ms. DRL-ORL, MADDPG and A3C converge 14.6%, 3.2% and 11.2% later respectively compared to LSTM+MADDPG. Furthermore, this paper finds that the delays for all types of flows are relatively small with the LSTM+MADDPG algorithm, and the change of delay with increasing time slots is not very significant (it tends to be stable). The lower latency of MADDPG and LSTM+MADDPG compared to the other two schemes means that lower latency is available for each agent.

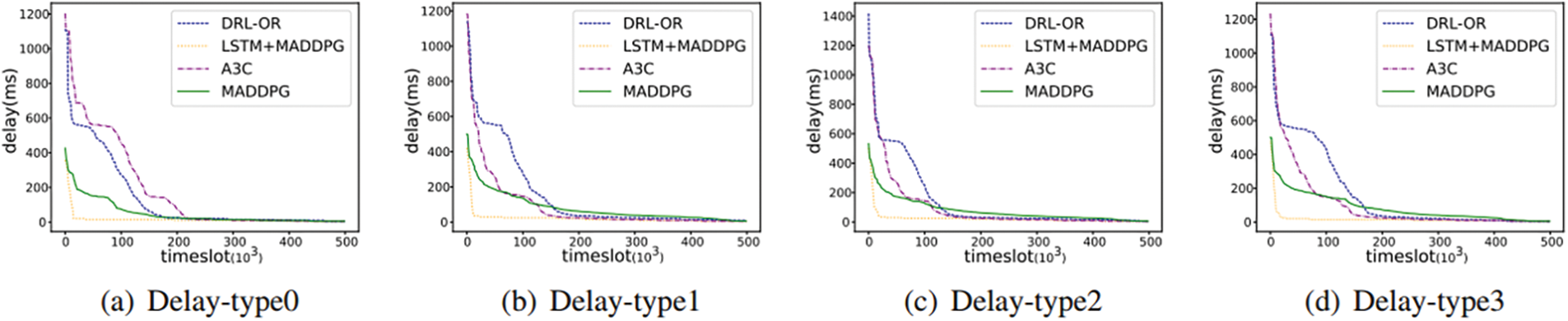
Figure 4: Comparison of the delay of different algorithms in GEANT topology

2) Throughput Ratio: The throughput ratio is the percentage of the remaining available bandwidth offered to the data flows between two nodes in a network topology at a given moment. Namely, the maximum rate that a network device can accept in the absence of packet loss. As shown in Figs. 5a–5d, the throughput ratio gradually increments as the time slot increases, eventually converging to a throughput ratio close to 100%. For lightly loaded scenarios, the bandwidth used by the links under the DRL-OR, MADDPG and A3C algorithms may not reach the upper limit of bandwidth resources, but the routing policy learned by the LSTM+MADDPG algorithm selects the path with a higher remaining available bandwidth for final routing. As a result, LSTM+MADDPG has a higher throughput ratio than other algorithms at the same time slot. In Fig. 5b, type 1 is the throughput-sensitive flows, and the LSTM+MADDPG algorithm is more sensitive to changes in throughput than applied to other types of flows, showing a later convergence to nearly 100% throughput.

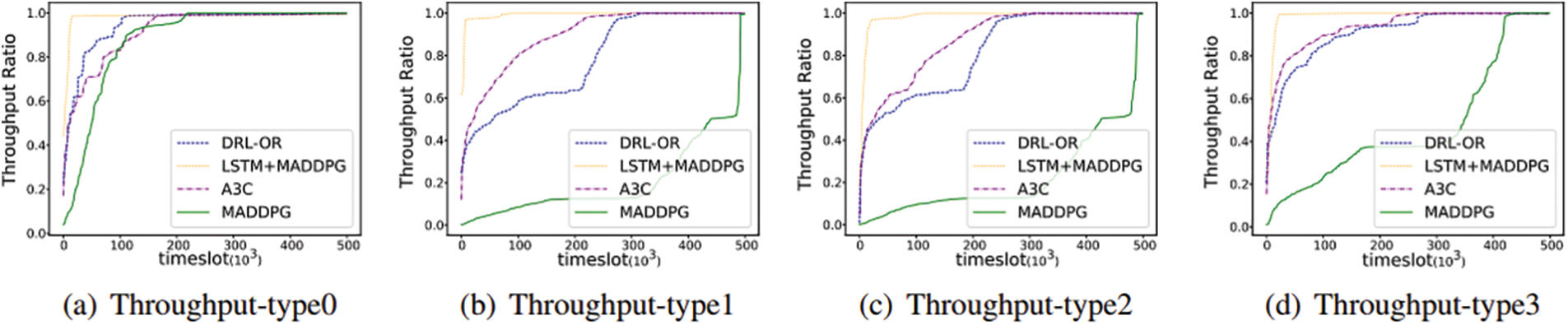
Figure 5: Comparison of the throughput ratio of different algorithms in GEANT topology

3) Packet Loss Ratio: Data is transmitted in a topological network in individual packets, and the packet loss ratio is the proportion of packets that are lost to the total amount of packets transmitted. As shown in Figs. 6a–6d, the packet loss ratio increases as the time slot grows. The packet loss rate of each algorithm is close to zero in the light load scenario, and the variation of the packet loss rate of each algorithm is different in the heavy load scenario. For example, in Fig. 6a, DRL-OR, A3C and MADDPG start dropping packets 7.4%, 18.2% and 16.4% earlier than LSTM+MADDPG, respectively. Furthermore, this paper finds that the proposed LSTM+MADDPG algorithm is suitable for all types of flows, with a packet loss rate close to 0% even in heavy load scenarios.

Figure 6: Comparison of the loss ratio of different algorithms in GEANT topology

4) Reward: The reward is seen as a metric for the outcome of the action, further enabling agents to perceive the relevant network state to the environment. In DRL, the agent performs one action as well as receives the reward according to the corresponding network policy. The trend of global reward about various types of flows under different algorithms is illustrated in Fig. 7. The reward for the DRL OR, A3C and LSTM+MADDPG algorithms fluctuates smoothly with the increasing time slot, with the mean values of reward for the DRL OR, A3C and LSTM+MADDPG algorithms being −1.36, −1.91 and 8.78. The results for positive rewards are more inclined to accrue those rewards, while the results for negative rewards are more inclined to terminate as soon as possible to avoid being penalized all the time. Therefore, our proposed LSTM+MADDPG algorithm can achieve more positive rewards compared to other algorithms.

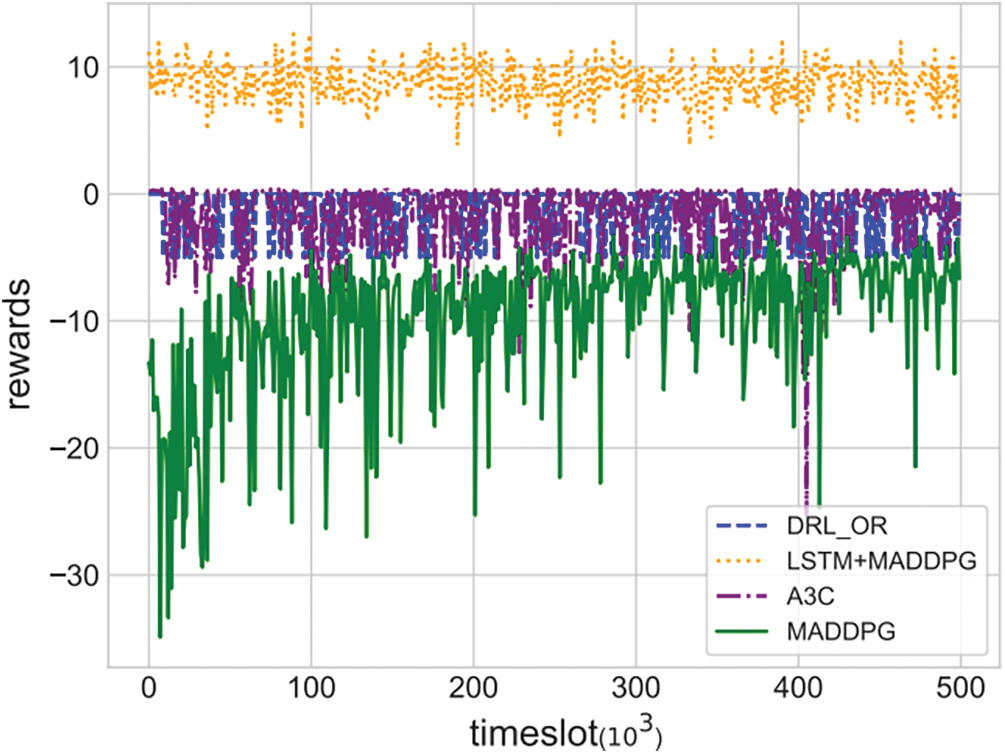
Figure 7: The variation of rewards over time for different algorithms

7  Conclusion

This paper establishes the latest cloud-edge autonomous multi-domain data center network architecture for routing multiple types of flows, specifically, the network architecture that the paper has designed incorporates a global autonomous layer and a regional autonomous layer. In addition, this paper proposes that maximizing network utility is used as an optimization objective while ensuring performance-centric weighted fairness for flows. Based on this, the paper targets the problem of how to improve the convergence speed of the model as well as the performance of the algorithm, this paper specifically designs the LSTM+MADDPG algorithm, which uses the agent’s observation of continuous time as input to the policy network and allows the LSTM layer to process hidden temporal messages. Finally, extensive simulation results demonstrate that our proposed approach outperforms the latest reinforcement learning algorithms. In conclusion, although MADDPG+LSTM provides a powerful mechanism to process time series data in a multiagent environment, several optimizations and adaptations are required to effectively apply this technique in large-scale multi-domain data center network. Because MADDPG relies on a centralized learning process, information from all agents is required, which can lead to significant communication overheads. In future large-scale multi-domain data center network, this article will considers optimizing the communication strategy between agents to reduce the communication burden by aggregating information or prioritizing the transmission of critical information.

Acknowledgement: Not applicable.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Shiyan Zhang: Conceptualization of this study, Methodology, Software. Ruohan Xu: Data curation, Writing-original draft preparation. Zhangbo Xu: Writing-original draft preparation. Cenhua Yu: Writing-original draft preparation. Yuyang Jiang: Writing-original draft preparation. Yuting Zhao: Writing-original draft preparation. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Not applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. K. Samriya, M. Kumar, M. Ganzha, M. Paprzycki, M. Bolanowski et al., “An energy aware clustering scheme for 5G-enabled edge computing based IoMT framework,” in Int. Conf. on Computational Science (ICCS), London, UK, pp. 169–176, 2022. [Google Scholar]

2. M. Kumar, A. Kishor, J. Abawajy, P. Agarwal, A. Singh et al., “An autonomic resource provisioning and scheduling framework for cloud platforms,” IEEE Transactions on Sustainable Computing, vol. 7, no. 2, pp. 386–399, 2022. [Google Scholar]

3. D. Kalka, S. C. Sharma and M. Kumar, “A secure IoT applications allocation framework for integrated fog-cloud environment,” Journal of Grid Computing, vol. 20, no. 1, pp. 1–23, 2022. [Google Scholar]

4. C. Y. Hong, S. Kandula, R. Mahajan, M. Zhang, V. Gill et al., “Achieving high utilization with software-driven WAN,” in Proc. of the ACM Special Interest Group on Data Communication (SIGCOMM) Conf., Hong Kong, China, pp. 15–26, 2013. [Google Scholar]

5. X. Dong, W. Li, X. Zhou, K. Li and H. Qi, “TINA: A fair inter-datacenter transmission mechanism with deadline guarantee,” in IEEE Int. Conf. on Computer Communications (INFOCOM), Toronto, ON, Canada, pp. 2017–2025, 2022. [Google Scholar]

6. K. Alok, S. Jain, U. Naik, A. Raghuraman, N. Kasinadhuni et al., “BwE: Flexible, hierarchical bandwidth allocation for WAN distributed computing,” in Proc. of the ACM Special Interest Group on Data Communication (SIGCOMM), London, UK, pp. 1–14, 2015. [Google Scholar]

7. Z. Xu, J. Tang, C. Yin, Y. Wang and G. Xue, “Experience-driven congestion control: When multi-path TCP meets deep reinforcement learning,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 6, pp. 1325–1336, 2019. [Google Scholar]

8. J. Zhang, M. Ye, Z. Guo, C. Y. Yen and H. J. Chao, “CFR-RL: Traffic engineering with reinforcement learning in SDN,” IEEE Journal on Selected Areas in Communications, vol. 38, no. 10, pp. 2249–2259, 2020. [Google Scholar]

9. N. Geng, T. Lan, V. Aggarwal, Y. Yang and M. Xu, “A multi-agent reinforcement learning perspective on distributed traffic engineering,” in Proc. of 2020 IEEE 28th Int. Conf. on Network Protocols (ICNP), Madrid, Spain, pp. 1–11, 2020. [Google Scholar]

10. Bakhshi, Bahador, J. M. Bafalluy and J. Baranda, “R-learning-based admission control for service federation in multi-domain 5G networks,” in Proc. of IEEE Global Communications Conf. (GLOBECOM), Madrid, Spain, pp. 1–6, 2021. [Google Scholar]

11. R. Lin, S. Yu, S. Luo, X. Zhang, J. Wang et al., “Column generation based service function chaining embedding in multi-domain networks,” IEEE Transactions on Cloud Computing, vol. 11, no. 1, pp. 185–199, 2021. [Google Scholar]

12. T. Moufakir, M. F. Zhani, A. Gherbi and O. Bouachir, “Collaborative multi-domain routing in SDN environments,” Journal of Network and Systems Management, vol. 30, no. 1, pp. 1–23, 2022. [Google Scholar]

13. W. Hu, J. Liu, T. Huang and Y. Liu, “A completion time-based flow scheduling for inter-data center traffic optimization,” IEEE Access, vol. 6, pp. 26181–26193, 2018. [Google Scholar]

14. L. Zhao, J. Hua, Y. Liu, W. Qu, S. Zhang et al., “Distributed traffic engineering for multi-domain software defined networks,” in Proc. of 2019 IEEE 39th Int. Conf. on Distributed Computing Systems (ICDCS), Dallas, TX, USA, pp. 492–502, 2019. [Google Scholar]

15. L. Gu, D. Zeng, S. Tao, S. Guo, H. Jin et al., “Fairness-aware dynamic rate control and flow scheduling for network utility maximization in network service chain,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 5, pp. 1059–1071, 2019. [Google Scholar]

16. P. Almasan, J. S. Varela, K. Rusek, P. B. Ros, A. C. Aparicio et al., “Deep reinforcement learning meets graph neural networks: Exploring a routing optimization use case,” Computer Communications, vol. 196, pp. 184–194, 2022. [Google Scholar]

17. S. Troia, F. Sapienza, L. Varé and G. Maier, “On deep reinforcement learning for traffic engineering in sd-wan,” IEEE Journal on Selected Areas in Communications, vol. 39, no. 7, pp. 2198–2212, 2020. [Google Scholar]

18. W. X. Liu, J. Cai, Q. C. Chen and Y. Wang, “DRL-R: Deep reinforcement learning approach for intelligent routing in software-defined data-center networks,” Journal of Network and Computer Applications, vol. 177, pp. 102865–102881, 2021. [Google Scholar]

19. C. Liu, M. Xu, Y. Yang and N. Geng, “DRL-OR: Deep reinforcement learning-based online routing for multi-type service requirements,” in IEEE Int. Conf. on Computer Communications (INFOCOM), Virginia Tech, USA, pp. 1–10, 2021. [Google Scholar]

20. Y. Wang, Y. Li, T. Wang and G. Liu, “Towards an energy-efficient data center network based on deep reinforcement learning,” Computer Networks, vol. 210, pp. 108939–108949, 2022. [Google Scholar]

21. M. Diamanti, P. Charatsaris, E. E. Tsiropoulou and S. Papavassiliou, “Incentive mechanism and resource allocation for edge-fog networks driven by multi-dimensional contract and game theories,” IEEE Open Journal of the Communications Society, vol. 3, pp. 435–452, 2022. [Google Scholar]

22. J. Guo, Z. Liu, S. Tian, F. Huang, J. Li et al., “TFL-DT: A trust evaluation scheme for federated learning in digital twin for mobile networks,” IEEE Journal on Selected Areas in Communications, vol. 41, pp. 3548–3560, 2023. [Google Scholar]

23. A. Rahmattalabi, S. Jabbari, H. Lakkaraju, P. Vayanos, M. Izenberg et al., “Fair influence maximization: A welfare optimization approach,” in The Thirty-Fifth AAAI Conf. on Artificial Intelligence (AAAI), pp. 11630–11638, 2021. [Google Scholar]

24. T. Panayiotou and G. Ellinas, “Fair resource allocation in optical networks under tidal traffic,” in IEEE Global Communications Conf. (GLOBECOM), Taipei, Taiwan, pp. 1–6, 2020. [Google Scholar]

25. Ryu, “A component-based software defined networking framework-ryu,” GitHub, 2020. [Online]. Available: https://github.com/osrg/ryu (accessed on 01/01/2020). [Google Scholar]

26. B. Lantz, B. Heller and N. McKeown, “A network in a laptop: Rapid prototyping for software-defined networks,” in Proc. of ACM SIGCOMM Workshop on Hot Topics in Networks, New York, NY, USA, pp. 1–6, 2010. [Google Scholar]

27. I. Kostrikov, “Pytorch implementations of reinforcement learning algorithms,” GitHub, 2018. [Online]. Available: https://github.com/ikostrikov/pytorch-a2c-ppo-acktr-gail (accessed on 01/01/2018). [Google Scholar]

28. S. Uhlig, B. Quoitin, J. Lepropre and S. Balon, “Providing public intradomain traffic matrices to the research community,” ACM SIGCOMM Computer Communication Review, vol. 36, no. 1, pp. 83–86, 2006. [Google Scholar]