Weighted Forwarding in Graph Convolution Networks for Recommendation Information Systems

1  Introduction

We are surrounded by a lot of information on the Internet and Recommendation Information Systems (RIS) help us quickly find our desired content. RIS, which is employed in various domains such as e-commerce, entertainment, and social media, is used on platforms such as YouTube, Netflix, and Amazon to provide users with desired content. The RIS analyzes users’ preferences and behavioral patterns to suggest content tailored to them, offering users new opportunities for discovery, which increases their loyalty to the content platform. Continuously providing users with relevant and intriguing content encourages them to spend more time on the platform, thereby enhancing its profitability.

Various approaches have been employed to effectively construct an RIS. The Collaborative Filtering (CF) approach [1] provides recommendations between users and items by calculating the similarity between users or items based on past user evaluations. However, the CF-based RIS model, which only uses user-item interaction data, such as user purchase records, for recommendations, has performance limitations. In addition, as the number of users increases, the computation required to determine the similarity between users increases, leading to a scalability problem. Recently, RIS models utilizing Graph Convolution Network (GCN) algorithms have been actively investigated to overcome these problems. However, the GCN algorithm updates the embeddings by combining information from adjacent nodes across multiple layers. As the network continuously averages information from adjacent nodes, the local features become diluted. Consequently, all nodes in the GCN algorithm converge to embeddings with similar features. This causes the learned network not to recognize local differences but to reflect overall features, leading to the embedding value vanishing problem where information becomes generalized and disappears. This reduces the diversity of recommendations and degrades performance [2–9]. The problem of disappearing embedding values occurs in models that use embedding layers in the deep learning training process, such as recommendation systems. These layers convert raw data (e.g., words or user/item IDs) into vectors of real numbers, where each element represents a learned feature. Although these vectors are essential for capturing meaningful relationships between inputs, several problems arise during the learning process. The loss of the gradient can halt the effective updating of the model weights (and hence embeddings). This causes the model to struggle to learn effective embeddings for all items or users and runs the risk of the model becoming too complex or not capturing enough information. In addition, embeddings from different inputs can converge to similar vectors, thereby losing the ability to distinguish between different data points. To address these issues in this study, we propose the Weighted Forwarding method for the GCN (WF-GCN). It multiplies the weights with an embedding value obtained from the learning of the previous layer and forwards them to the next layer during the hop hierarchy learning process of the GCN algorithm. Therefore, the proposed method suppresses the disappearance of embedded values and learns more hop hierarchies, even with fewer hop layers in GCN-based RIS models. In addition, RIS based on the GCN algorithm, LightGCN algorithm, an improvement algorithm of NGCF, is widely used as a backbone network in subsequent research, and the proposed method is applicable to all algorithms based on the LightGCN algorithm.

To verify the proposed method, mathematical statistics and dimensionality reduction techniques were used to analyze the reasons for the performance improvement of the WF-GCN algorithm, and the stability of various forms of neural networks was analyzed by mathematical methods in studies such as references [10,11].

2  Related Work

Traditional RIS using the CF approach can be broadly divided into two methods: the memory-based (or user-based) method, which identifies a group of users similar to the active user, from the entire user-item database, and the model-based method, applying machine learning algorithms based on Bayesian networks, clustering, and rule-based techniques to create a model of user ratings and then recommends content based on this model. The CF approach generates recommendation content on the premise that new users will also like products that similar users have liked in the past, based on the existing users’ database. Approaches based on CF include tapestry [1], Bayesian networks based on decision trees [12], clustering that groups similar users [13], and graph-based techniques that represent users as nodes and similarities between users as edges [14]. However, neither CF nor Matrix Factorization (MF) approaches can integrate and utilize various contextual information, such as user evaluation records of items, user session information, and item category information.

Recent proposals have incorporated Deep Learning (DL) techniques that utilize user experience data to better capture the correlation between users and items, and overcome the limitations of traditional CF and MF approaches. The Graph Neural Network (GNN) algorithm [15] is a commonly used DL model for RIS. Specifically, a particular form of the GNN algorithm, the GCN, is widely used in RIS owing to its highly suitable architecture for implementing RIS. The GCN succinctly aggregates a graph’s node and its surrounding information through convolutional operations, facilitating the learning and optimization of GCN-based RIS models. The GCN algorithm can effectively reflect the complex interactions between users and items specializing in processing data from graph architectures. To reflect these interactions, the GCN algorithm can integrate additional information about the relationship between users and items (such as user gender, age, and item category), thereby overcoming the limitations of traditional MF and CF approaches, which struggle to fully reflect the intricate interactions between users and items.

The GCN-based RIS model aggregates information from nodes and their surroundings to produce high-dimensional embeddings that effectively reflect the intricate features of users and items. Examining the process step-by-step, the GCN-based RIS model initially represents the interactions between users and items as graphs, showing the different relationships between them. Therefore, the derived graph-based modeling results were learned using the GCN algorithm, which ultimately determined the embedding values for the users and items. The RIS model then calculates preference scores between users and items using the determined user and item embedding values and based on these scores, it effectively recommends content. The GCN algorithm can easily represent information for new users or items in a graph architecture, alleviating the cold-start problem compared with pure CF or MF approaches. Additionally, with active research on various graph architectures and algorithms, the GCN algorithm possesses flexibility, allowing its application across diverse recommendation scenarios [16–18].

In RIS, algorithms such as LightGCN [19], Self-supervised Graph Learning (SGL) [20], and Simple Graph Contrastive Learning (SimGCL) [21] have demonstrated impressive performance. LightGCN, a simplified version of the CF-based Neural Graph Collaborative Filtering (NGCF) [22], streamlines the GCN by removing feature transformation, non-linear activation, and self-connection from the GCN propagation layer, thereby simplifying the complex weight learning process. LightGCN strengthens the interactions between nodes by utilizing an interaction graph between users and items. Consequently, it generates node embeddings using only the connection information between users and items, thereby enhancing recommendation performance. Instead of the weight learning of the GCN algorithm, LightGCN creates node embeddings using the interaction graph between nodes, thereby significantly reducing the learning and inference times. With its simple and fast architecture, LightGCN can deliver high performance in various recommendation scenarios with minimal learning, making it highly valuable for large-scale RIS.

SGL is an application of the self-supervised learning model to the LightGCN algorithm, utilizing relationships with other nodes in the graph for reconstruction through Structure Reconstruction (SR). Using SR, SGL randomly removes nodes or edges from the graph and reconstructs them, thereby augmenting the learning data. Augmented data can undergo graph learning using self-supervised learning, without separate labeling. Therefore, the SGL has the advantage of learning through unlabeled graphs.

SGL, which augments the graph to increase the learning data, requires significant resources and time for learning. The SimGCL method was proposed to overcome these constraints and achieve efficient learning with fewer resources and less time. SimGCL accurately learns solely through contrastive learning in the learning process of graph neural networks without augmenting the learning data. It uses a contrastive loss function to group similar samples and performs contrastive learning to distinguish between the grouped samples. Consequently, it improves accuracy and diversity by applying only contrastive learning to LightGCN without graph augmentation in the GCN-based RIS model.

These GCN-based RIS models demonstrate impressive performance across various content recommendation services. However, GCN algorithms are used in the RIS face embedding value vanishing problem, in which the embedding value converges to a significantly small value during learning. Therefore, this paper proposes a WF-GCN algorithm that multiplies the embedding value with a weight before the propagation rule and forwards it to the next layer, thereby alleviating the embedding value vanishing problem. The proposed method does not increase the complexity of the algorithm because it does not apply new learning methods or data augmentation to the existing algorithm, but rather reduces the learning time of the existing algorithm. This allows us to overcome the problems that occur in the learning process of GCN algorithms. In addition, the proposed method has the advantage of being applicable to various algorithms such as SGL and SimGCL that use the LightGCN algorithm as a backbone network.

3  Proposed Method

3.1 Learning and Inference Process for the General GCN Algorithm

Fig. 1 illustrates the generalized learning architecture of the general GCN algorithm applied to RIS. As shown in the figure, the general GCN algorithm initially generates a value through a matrix of user-item behavior records during the early stages of learning. The created initial layer, known as shallow embedding, is represented as eu(0) and ei(0) is used for learning. In the subsequent layers, it propagates according to the embedding propagation rule (Eq. (1)). Here, a hop signifies the distance between nodes in a graph, and the layers in the GCN algorithm aggregate the information from surrounding nodes. Therefore, as the propagation rule progresses, after passing through one, two, and N layers, it aggregates information from the 1-hop neighbor of the target node to the 2-hop neighbor and up to the N-hop.

Figure 1: Learning and inference process for a general GCN algorithm

𝒩u and 𝒩i denote the connected nodes of users u and item i, respectively. By normalizing, the symmetric normalization term (=1/|𝒩u||𝒩i|), ensures that the embedding value does not increase excessively during the convolution operation. eu(k) is the embedding of user u at the kth layer and ei(k) is the embedding of item i in the kth layer. The previous embedding values of the neighbors of user u and item i are summed with the normalized weight to obtain the embedding value of the k+1th layer, which includes the kth hop in the graph.

The general GCN algorithm sums the embeddings from each layer according to the propagation rule to obtain the final embedding vector for the users and items (as shown in Eq. (2)). Here, k represents the index of the layer and ak denotes the importance of embedding from the kth layer. In GCN-based RIS models, which commonly use LightGCN, SGL and SimGCL, ak is set to 1/(k+1).

eu(k+1)=∑i∈𝒩u1|𝒩u||𝒩i|ei(k);ei(k+1)=∑i∈𝒩i1|𝒩i||𝒩u|eu(k)(1)

eu=∑k=0nαkeu(k);ei=∑k=0nαkei(k)(2)

y^ui=euTei(3)

In a general GCN algorithm, the embedding for each layer is calculated according to the propagation rule from the initial layer, and the embedding values of each layer are weighted and summarized to compute the final embedding values eu for users and ei for items. The preference score y^ui between user u and item i is calculated by taking the inner product of eu and ei as shown in Eq. (3). The traditional general GCN algorithm maintains the self-connected effect of graph convolution by summing the embedding values derived from the previous hop layer, thereby inducing a comprehensive representation. However, the general GCN algorithm faces an embedding value-vanishing problem by predicting using only the last layer. The last layer is the sum and division of the embeddings of all the layers, where the embedding value diminishes as it passes through each layer.

3.2 Proposed Learning and Inference Process with the WF-GCN Algorithm

In Section 3.1, where the general GCN algorithm is described, a statistical analysis of each layer’s embedding value and the final embedding layer value revealed that the average value of the final embedding layer was 4.14×10−7 indicating that the overall embedding value was learned locally, leading to the embedding value vanishing problem. Consequently, the traditional general GCN algorithm robustly learns only the item features that users consistently view, undermining the intrinsic purpose of the RIS, which is to discover new and highly relevant content that users may not have encountered through other means, thereby reducing the probability of such discoveries.

Fig. 2 illustrates the architecture of the learning process (WF-GCN algorithm) proposed in this study to overcome the problem of disappearing embedded values. The proposed architecture obtains a more sharpened embedding value (eu ′(k+1),ei ′(k+1)) by transmitting a value, which is the result of multiplying a specific weight by the node embedding value, to the next layer as described in Eq. (4).

Figure 2: Proposed learning and inference process with WF-GCN algorithm

Using the embeddings obtained from Eq. (4), the proposed method attempted to overcome the problem of embedding loss by assigning weights to each embedding transfer layer, and the results of the experiment confirmed that the average value of the final embedding layer significantly increased to 3.19×10−2 through the WF-GCN algorithm. Using this method, the performance of the existing recommendation information system was improved, and the cause of the increase in recommendation performance was identified through various analyses. Eq. (5) represents performing the weighted sum as before with sharpened embedding values, while Eq. (6) represents calculating the score via the inner product of the embeddings of users and items calculated through the weighted sum process.

eu ′(k+1)=wk∑i∈𝒩u1|𝒩u||𝒩i|ei ′(k);ei ′(k+1)=wk∑i∈𝒩i1|𝒩i||𝒩u|eu ′(k)(4)

eu ′=∑k=0nαkeu ′(k);ei ′=∑k=0nαkei ′(k)(5)

y^ui ′=eu ′Tei ′(6)

3.3 Equation Expressions

In this section, we describe the proposed WF-GCN algorithm based on the equations used in the LightGCN algorithm [19].

The user-item interaction matrix R can be represented by Eq. (7). where M and N denote the number of users and items, respectively.

R∈RM×N(7)

The adjacency matrix A of the user-item graph can be represented as in Eq. (8). A diagonal matrix refers to a matrix in which all elements outside the diagonal have values of 0.

A=(0RRT0)(8)

The embedding matrix of the 0th layer is represented by Eq. (9), where T denotes the embedding size. The embedding value of the k+1th layer, calculated according to the propagation rule, is expressed by Eq. (10). In this context, D refers to a diagonal matrix with the dimensions M+(M+N)×(M+N). Eq. (11) is the process of calculating the predicted value from the final embedding of the existing models.

E(0)∈R(M×N)×T(9)

E(k+1)=(D−12AD12)E(k)(10)

E=∑k=0nαkE(k)→y^ui(11)

Eq. (12) represents the mathematical expression of the proposed WF-GCN algorithm: The WF-GCN algorithm determines the k+1th embedding value by multiplying the weight wk by E(k), which emerges after passing through the learning process of the kth layer. Through wk, different weights can be assigned to each layer, allowing for adjustment of the influence on the embedding.

E ′(k+1)=wk(D−12AD12)E ′(k)(12)

Eq. (13) represents the embedding obtained after completing the proposed learning process. Here, E ′ denotes the vector containing the last embedding value for both users and items. Using this last embedding vector, we can obtain the predicted value y^ui to assess the recommendation performance.

E ′=∑k=0nαkE ′(k)→y^ui ′(13)

4  Experiments

In this study, we proposed a WF-GCN algorithm to prevent the embedding value vanishing problem, which hinders the recommendation performance in RIS. LightGCN, SGL, and SimGCL are used to verify the proposed learning process. All of these models are based on LightGCN and share the same architecture for layer combination (weighted sum), making it possible to apply the suggested method uniformly across the three models. The experiment employed RecBole [23], an open-source library designed for GCN-based RIS models. This library, built using PyTorch, incorporates various recommendation algorithms to facilitate RIS research and development. In the experiment [24], we applied the suggested method to the models implemented using RecBole. Here is the link to that library: https://github.com/RUCAIBox/RecBole-GNN. The data, environment, and parameters used in the experiment are detailed in Sections 4.1 and 4.2, while the evaluation functions for the model recommendation performance evaluation are presented in Section 4.3. An analysis of the experimental results is presented in Section 4.4.

4.1 Dataset

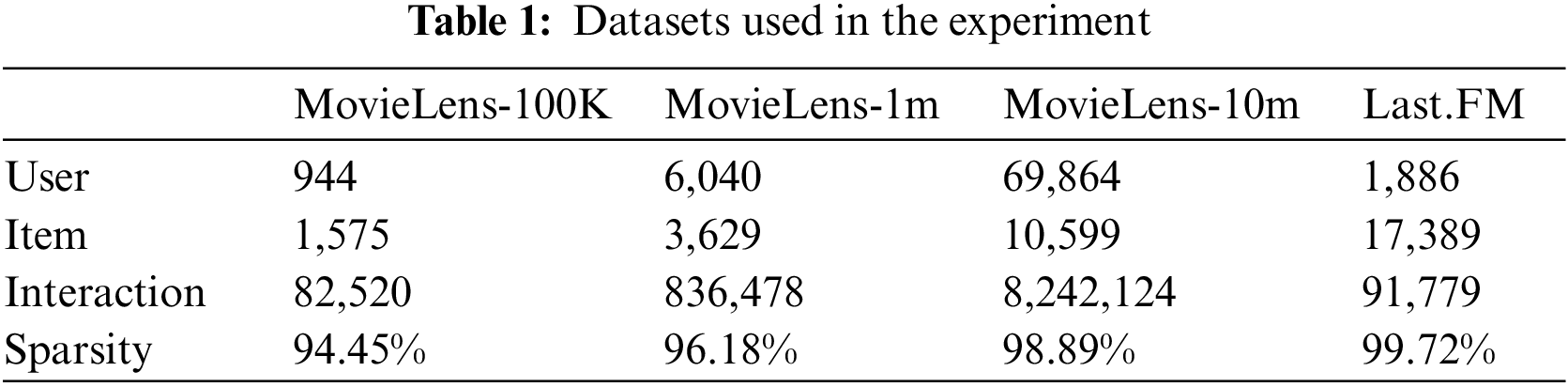
In the experiment, we utilized two types of datasets, listed in Table 1. The first is the MovieLens dataset [25], which is frequently used for movie RIS and contains users’ ratings and interaction information regarding movies. By leveraging the user context, the interactive relationship between users and movies can be represented as a graph. By learning these interactions, movie recommendations are made, allowing for the assessment of which model performs better on movie recommendation tasks using this dataset. The size of this dataset was divided based on the number of viewing records of the users.

In addition, experiments were conducted to evaluate the performance of the proposed method. The LAST.FM dataset [26] is a large-scale music dataset commonly used in research on music RIS. This includes users’ music listening records and artists’ information. The interaction information between users and music was utilized for the RIS and music-related analysis.

4.2 Experimental Environments

The experiments were conducted under the conditions listed in Table 2. Table 3 presents the variables related to the experimental environment, and Table 4 lists the parameters used in the model. Fig. 3 shows an example of random ordering and ratio-based splitting. If User A was associated with 20 items, they were randomly extracted based on the set ratio used for the experiment. The data split ratio was set as follows: training: 80%, validation: 10%, and test: 10%. Therefore, of the 20 items, 16 were used for learning, 2 for validation, and 2 for performance evaluation. The validation and test data were not used in the experiment.

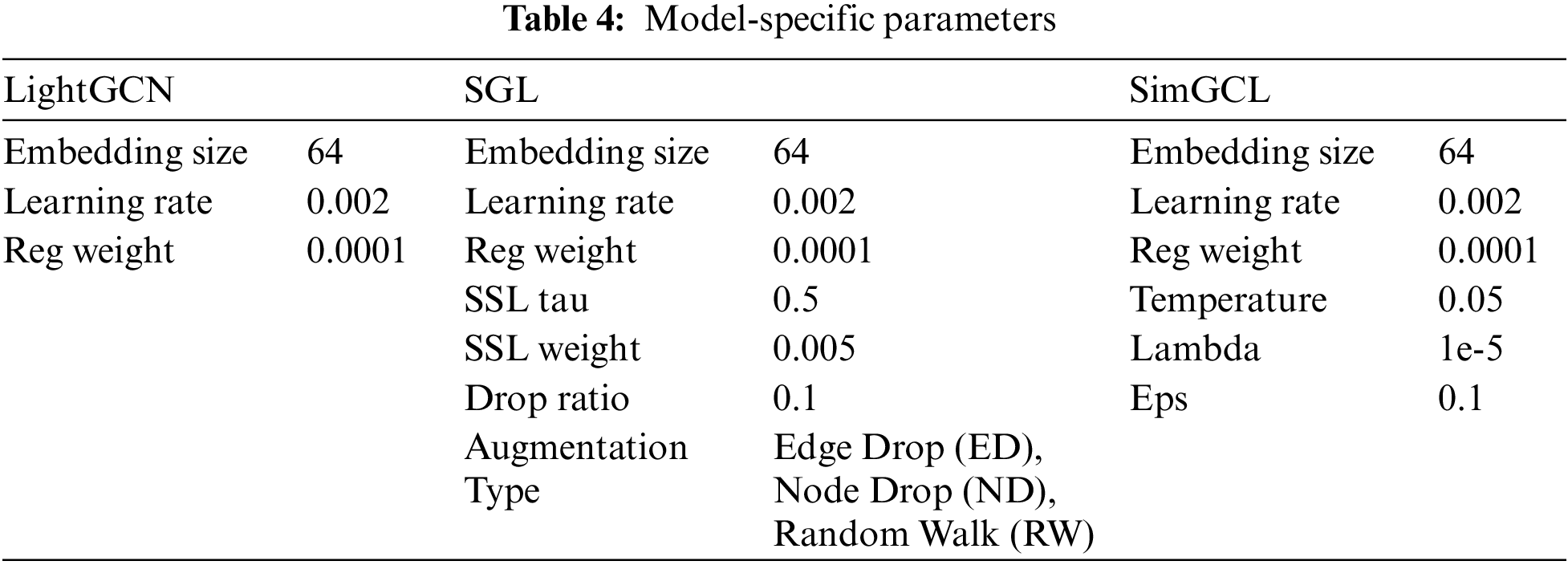
Figure 3: Random ordering, ratio-based splitting’s example

Additionally, we investigated the impact of varying the original parameters of the LightGCN model on different datasets (Last.FM, MovieLens-100K, MovieLens-1M, and MovieLens-10M). We found that with a learning rate of 0.001, the performance on the Last.FM dataset decreased for all performance metrics (precision, recall, NDCG, MRR, and hit ratio) compared with a learning rate of 0.002. For the MovieLens-100K dataset, the precision, recall, NDCG, and MRR increased slightly, but the hit values decreased. For the MovieLens-1M dataset, we observed mixed results with decreases in precision, recall, and hits but increases in NDCG and MRR. Finally, the MovieLens-10M dataset exhibited a significant decrease in all performance metrics. The study concluded that changing the learning rate in the LightGCN model did not significantly affect the results or hinder the performance, suggesting that numerical comparisons between parameters may not be important in this context. These results were used to evaluate the performance changes when applying the WF-GCN algorithm, which shares its basic structure with LightGCN, using the same parameters (learning rate = 0.002) in all the experiments.

4.3 Experimental Evaluation

For the evaluation of the model’s performance, precision, recall, Normalized Discounted Cumulative Gain (NDCG), Mean Reciprocal Rank (MRR), and hit indicators were used to assess the quality of the model from various perspectives. Precision and recall are used to evaluate the accuracy and diversity of the recommendations. NDCG and MRR assess how accurately the items of interest to the user are recommended in the top ranks. A hit evaluates the success of the RIS by suggesting at least one relevant item for the user.

Precision@K indicates the proportion of items recommended by the RIS that the user is interested in. Similarly, it measures the accuracy with which a user recommends their preferred. High precision suggests that RIS accurately recommends items that are highly relevant to the user. Recall@K represents the proportion of items in which the user is interested, as recommended by RIS. This metric assesses the number of relevant items the RIS has recommended, with a high recall indicating that the RIS suggests many pertinent items without missing any items. NDCG@K evaluates the relevance and ranking of the recommended items, with higher values when the user’s preferred items are ranked higher. Thus, a high NDCG value suggests that the RIS accurately recommends items of interest to users with higher rankings. MRR@K is the average rank of the first appearance of an item of interest among the recommended items. A high MRR indicates that the RIS quickly identifies the items preferred by the user. Hit ratio@K represents the proportion of items that the user prefers to be successfully included in the recommendation list. This metric measures whether the RIS recommends at least one item of interest to the user, with a high Hit Rate indicating that the RIS effectively includes items that the user prefers.

In Section 4.4, we summarize the recall and NDCG results, which are the main performance indicators used in previous studies. The results of the experiment are available at this link: https://wandb.ai/d9249/WFGR.

4.4 Experimental Result

A summary of the experimental results is presented in Tables 5–8. The [1,1,1] (base, non-weight) entry represents the results of a reproduction experiment to understand the basic performance of each model. The link provides results that compare model performance as the number of layers increases. According to the link, the layers exhibiting the best performance vary according to the data and model. Therefore, in this study, we conducted experiments based on three layers, which is consistent with the results of previous studies. The link displays the comprehensive experimental results not summarized in the tables, and it is evident that the proposed WF-GCN algorithm enhances performance across all indicators.

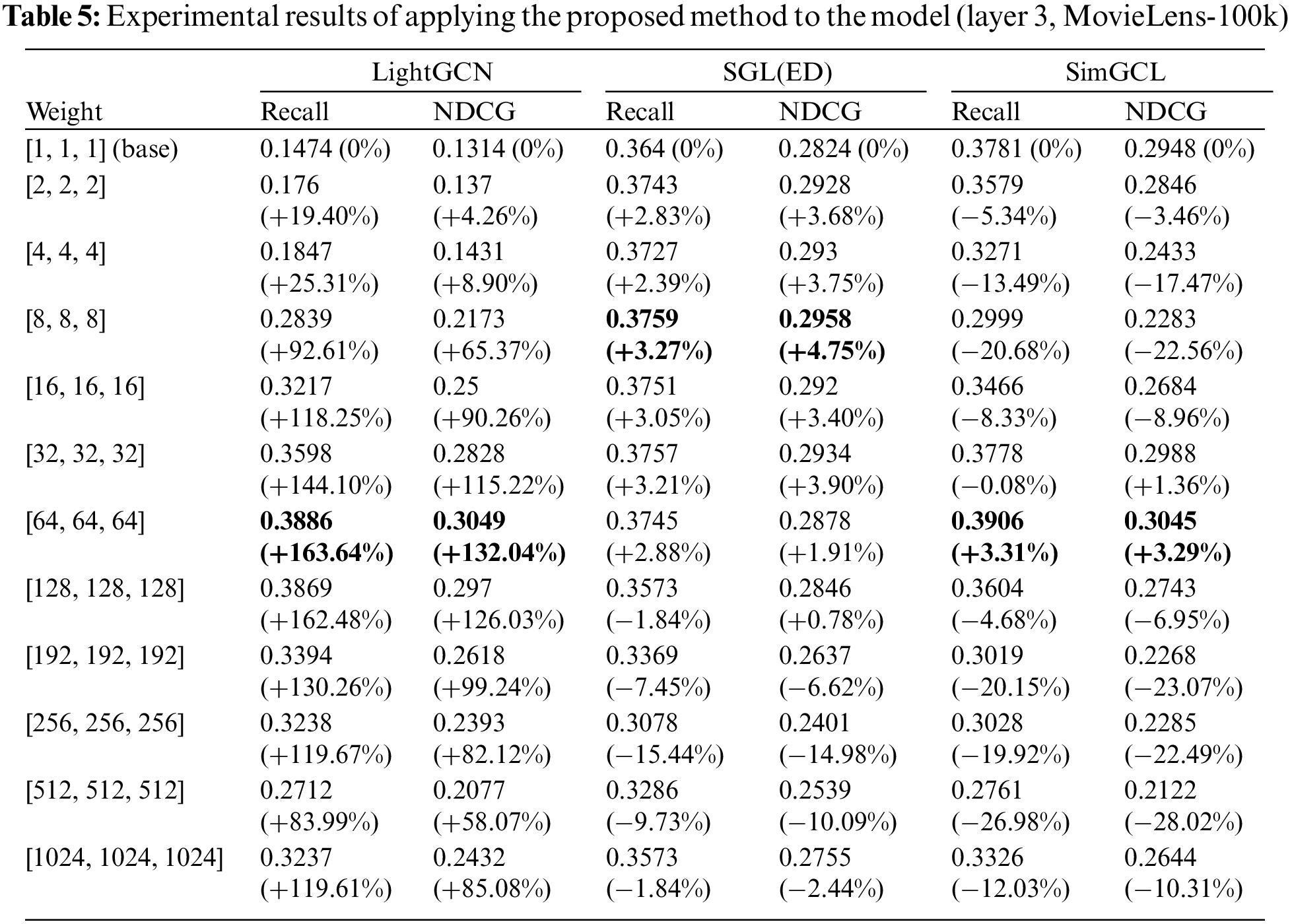
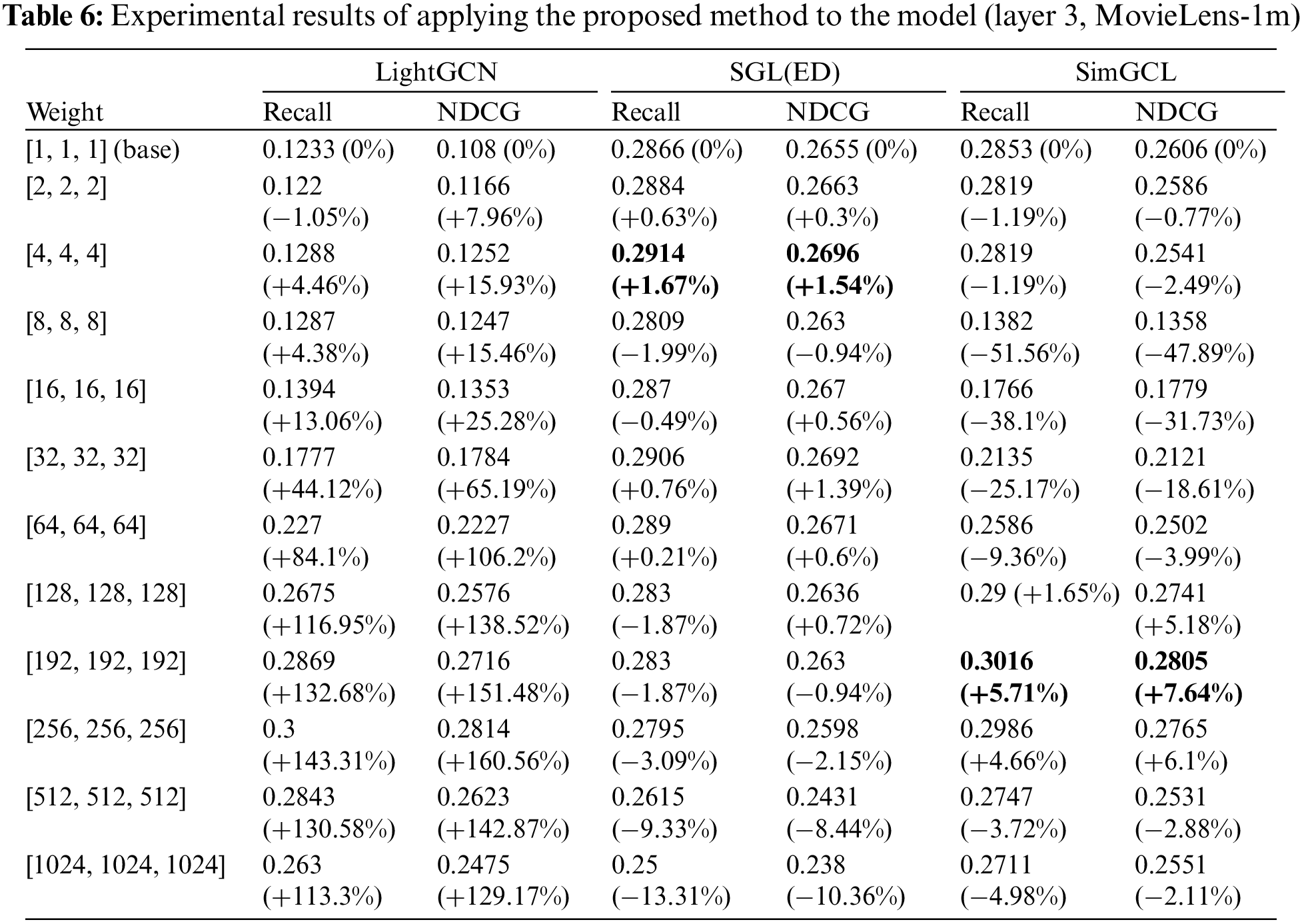
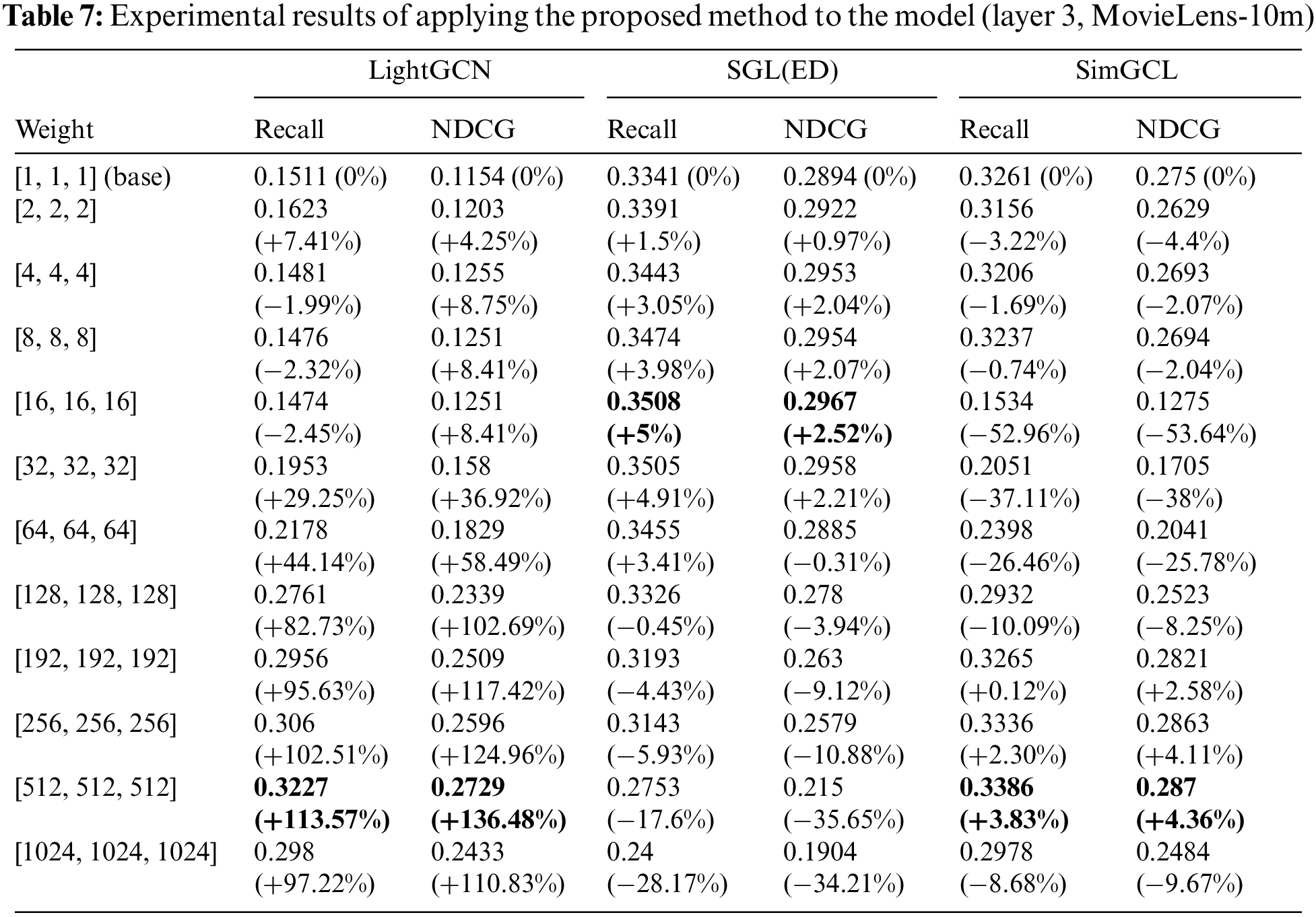
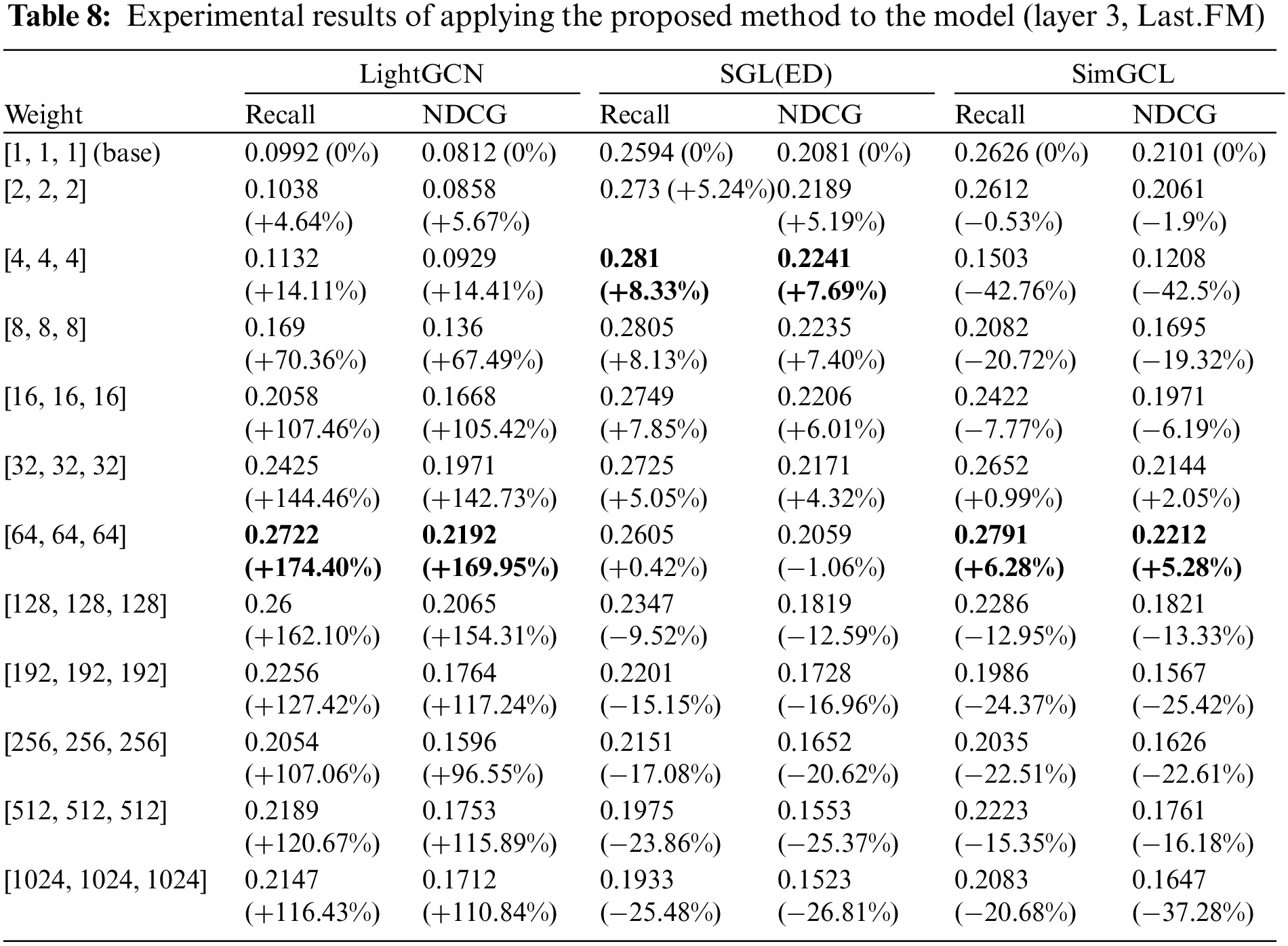
Table 5 presents the results for the MovieLens-100k dataset, Table 6 for the MovieLens-1m dataset, Table 7 for the MovieLens-10m dataset, and Table 8 for the Last.FM dataset. These tables summarize the experimental results for the three model datasets obtained when the proposed WF-GCN algorithm was applied. We observed a clear performance improvement in the RIS. However, even if the type of data remains the same, there are differences in the recommendation performance depending on the size of the data, and each model has its optimal weight. Specifically, LightGCN showed a performance improvement of approximately 200% compared with its original performance, whereas SGL and SimGCL showed performance improvements of 3%–8%. These results suggest that the removal of non-linear activation from the NGCF increases the accuracy of LightGCN and overcomes these problems. Moreover, not only can the commonly researched approach of aggregating node information further enhance the recommendation performance, but it can also properly analyze and utilize the model’s layer.

To understand the changes in the embedding value of the proposed WF-GCN algorithm, the statistical numerical analysis results of the layer-by-layer embedding of the model without weights are presented in Tables 9and 10.

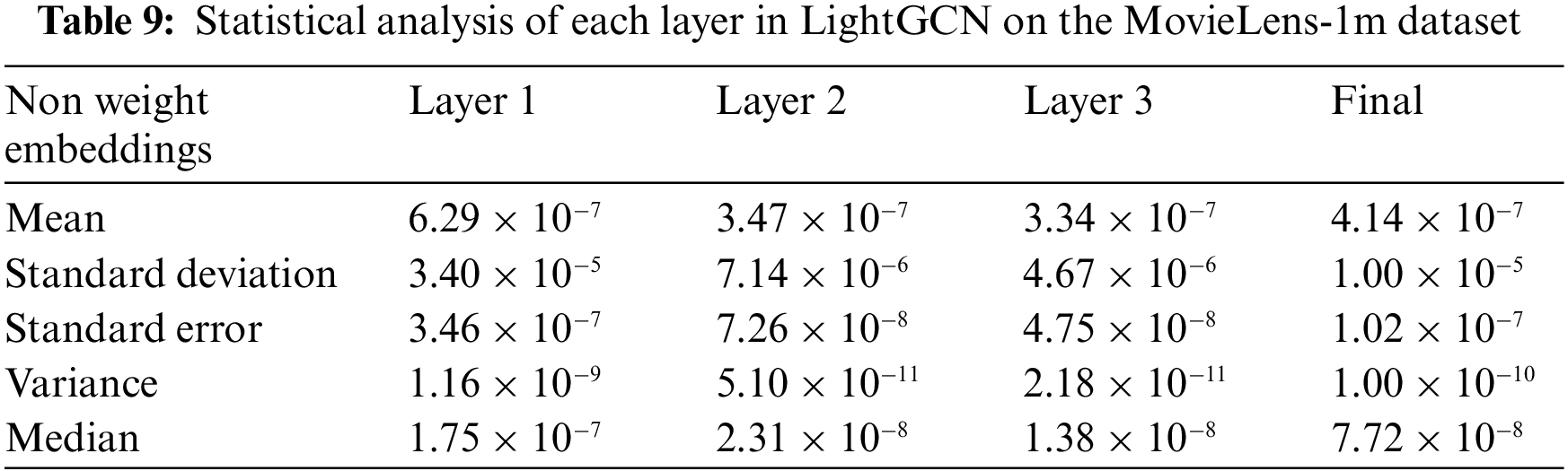
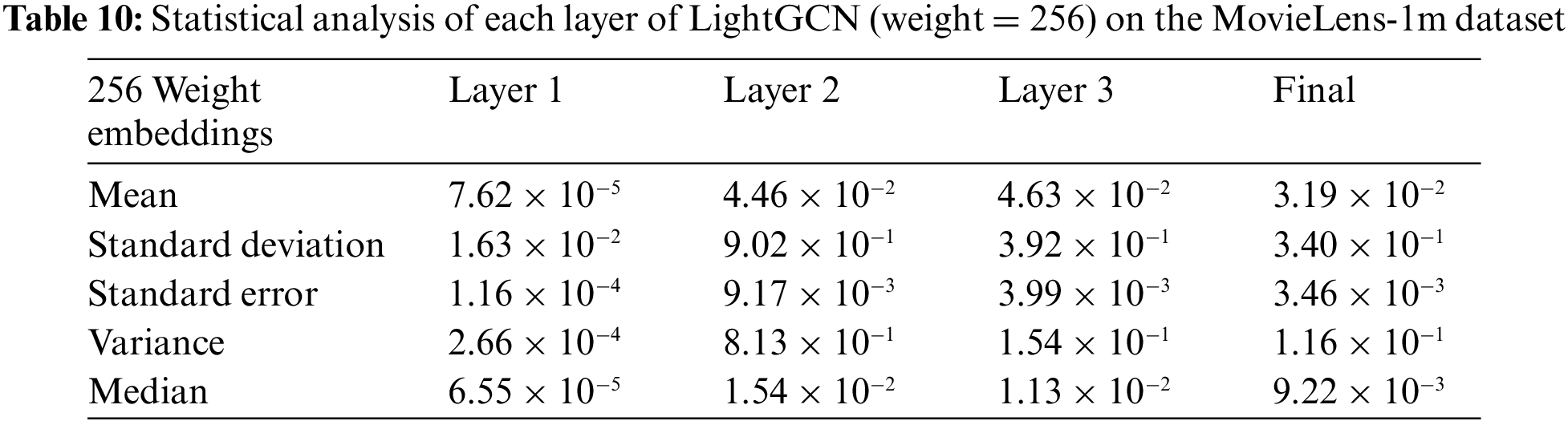
In the analysis, the models without assigned weights exhibited a distribution of average values within a narrow range. By contrast, the embedding values of the models with assigned weights generally had a higher average value. The average final embedding with the assigned weights was significantly higher than that without weights, suggesting that the center position of this embedding was higher than that of the other embeddings, as shown in Fig. 4. Moreover, significant increases in the average value and standard deviation indicate that using higher–weight embeddings can lead to a broader distribution of values. The distribution of embedding values in the model with assigned weights is generally spread, suggesting the possibility that the embedding of the model with weights contains diverse information. However, the embeddings of the base model were densely clustered around the average, focusing on specific properties or information. In addition, as the layer deepens, the distribution and properties of the embedded values tend to change. Based on this evidence, each layer learns different types of information and properties.

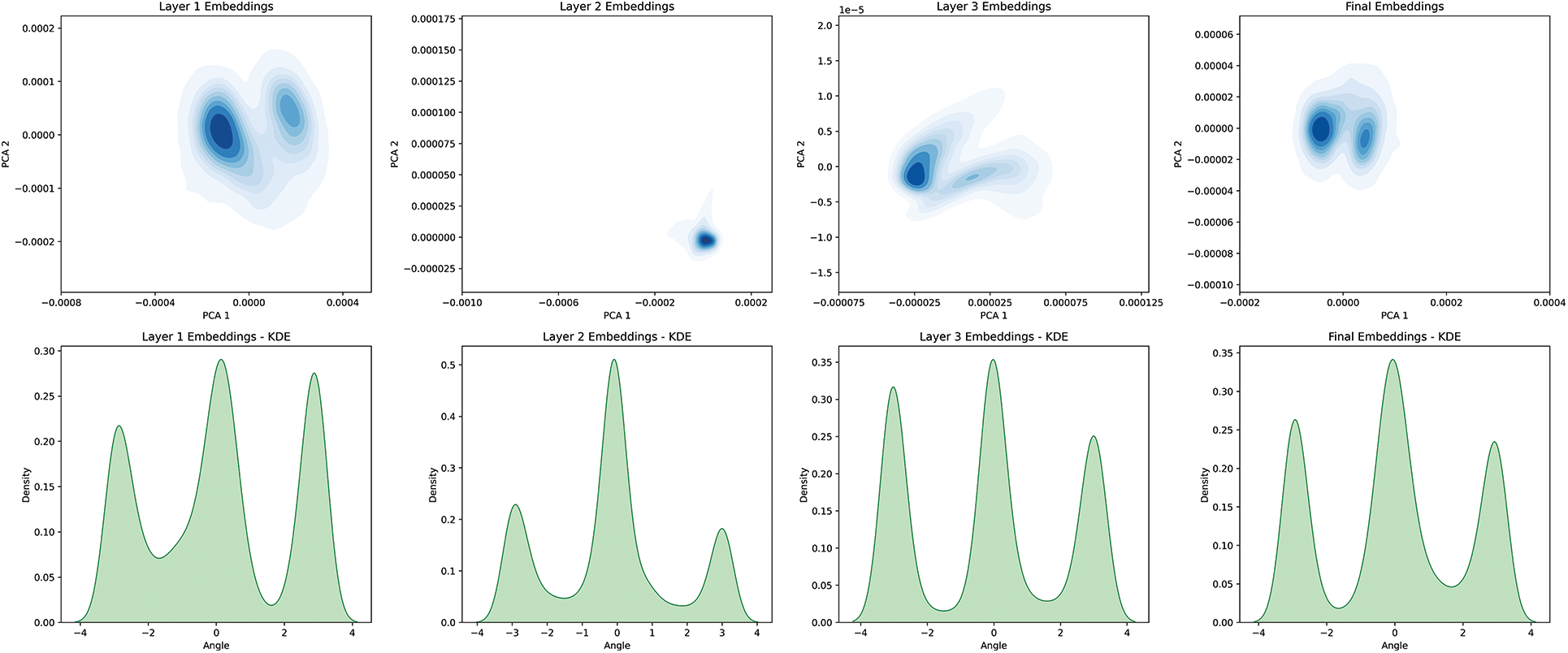
Figure 4: Visualize LightGCN (non weight), PCA, and KDE on the MovieLens-1m dataset

The embedding of the two models exhibited distinct properties and distributions. The model with the assigned weights had data spread widely around the average, encompassing a variety of information. By contrast, the embedding of the base model’s embedding has data densely clustered around the average, focusing on specific properties or information. This distinction led to an increase in recommendation accuracy.

Figs. 4 and 5 present the analysis results of the embedding values based on Dimensionality Reduction Techniques (DRT) according to weight. For this, we employed two methods: Principal Component Analysis (PCA) and Kernel Density Estimation (KDE) to investigate the distribution and density of the embeddings. For the base case, the PCA results showed data points appearing in multiple clusters, but the boundaries between each cluster were relatively indistinct. The KDE analysis exhibited a similar pattern, with a primary distribution peak present, but distinguishing multiple centroids or clusters was challenging. The embedding with a weight of 256 demonstrated the most outstanding results in all analyses. In PCA, the clustering was the most defined, and almost no outliers were observed. The KDE analysis also displayed the most pronounced peaks and density areas.

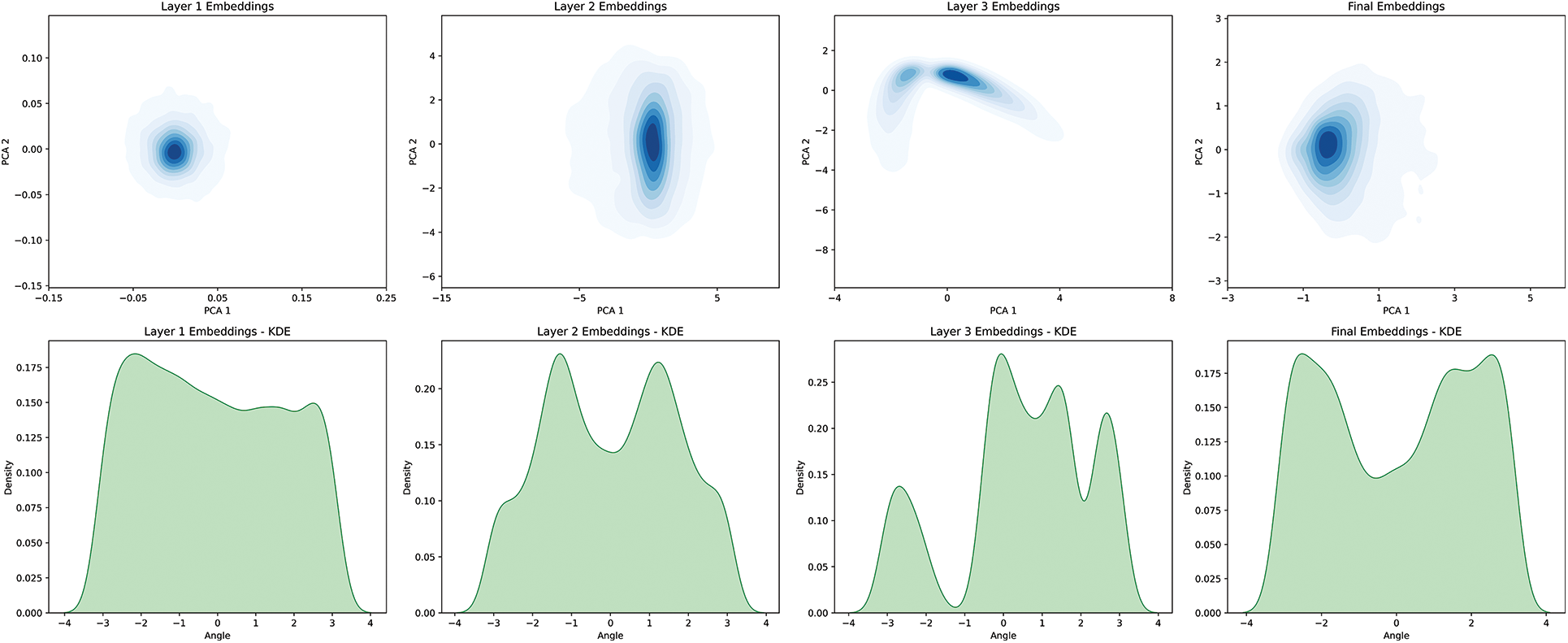
Figure 5: Visualize LightGCN (weight = 256), PCA, and KDE on the MovieLens-1m dataset

In conclusion, embedding the model using a weight of 256 through the proposed WF-GCN algorithm suggests that it captures properties better than the existing model. The performance increase achieved through the suggested method was confirmed using the DRT.

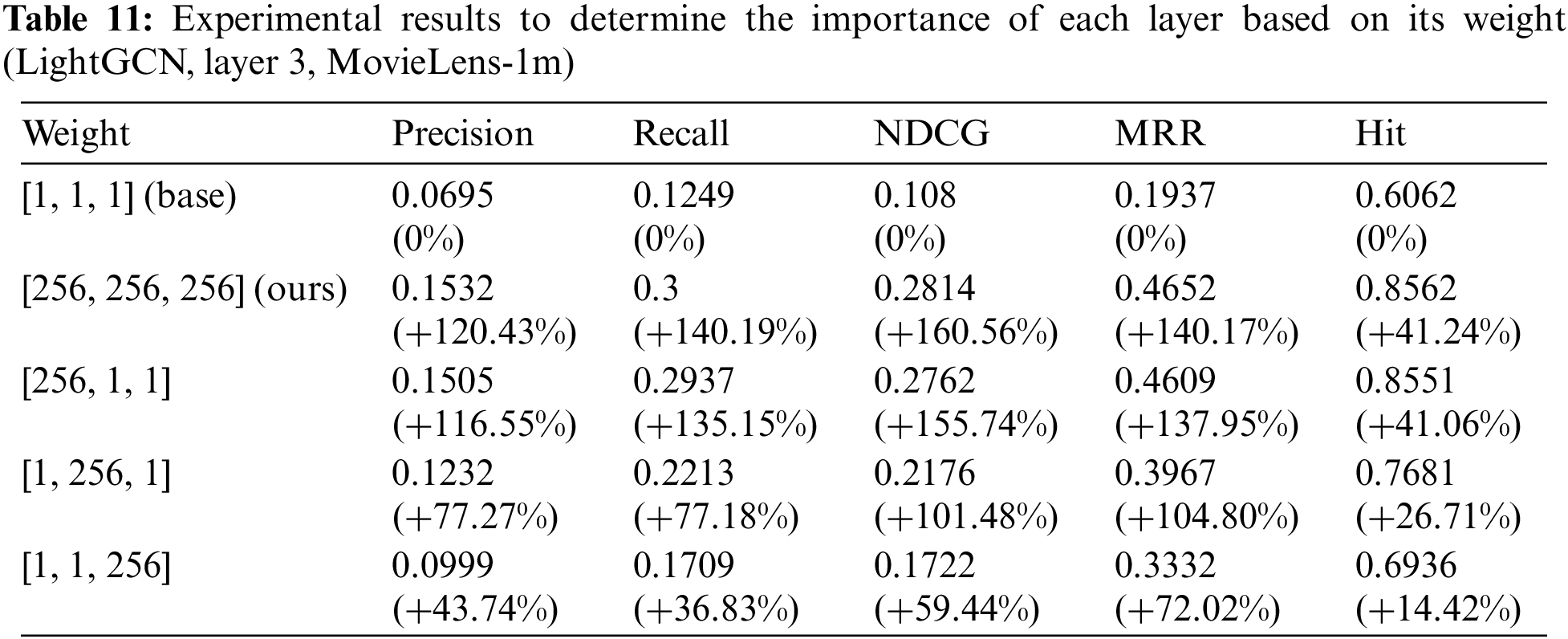
Additionally, we conducted an experiment in which different numbers, rather than common numbers, were inserted into a weight array. The experimental results are listed in Table 11. These results indicate that the performance of RIS varies significantly depending on the value provided by the propagation rule of the initial layer. Moreover, by merely applying an appropriate weight to the initial embedding, the recommendation performance can be drastically improved compared with the previous performance.

5  Conclusions

In this study, we propose the WF-GCN algorithm, which is an enhancement of the GCN algorithm used in the RIS model. The WF-GCN algorithm multiplies the embedding value of the previous embedding layer by weight and forwards it to the next layer when calculating the embedding value of each layer in the GCN algorithm. Consequently, by paying more attention to nodes with many neighbors, the WF-GCN algorithm, which learns fewer hop layers, can achieve the effect of learning deeper hop layers. Thus, the WF-GCN algorithm can infer a deeper relationship between users and items without requiring computations to calculate the depth of the layer. Therefore, the WF-GCN algorithm can mitigate the embedding value-vanishing problem of conventional GCN-based algorithms.

To verify the performance of the proposed WF-GCN algorithm, we applied the WF-GCN algorithm to representative GCN algorithms, namely LightGCN, SGL, and SimGCL. The performance was evaluated using the MovieLens and Last.FM datasets. In the MovieLens dataset, LightGCN exhibited performance improvements of up to +163.64% in recall and +132.04% in NDCG. The SGL demonstrated an enhancement of up to +5% in recall and +2.52% in the NDCG, whereas the SimGCL exhibited an enhancement of +5.71% in recall and +7.64% in the NDCG. In addition, on the LAST.FM dataset, LightGCN displayed a performance surge of up to +174.40% in recall and +169.95% in NDCG. SGL showed an increase of up to +8.33% in recall and +7.69% in NDCG, whereas SimGCL showed an enhancement of +6.28% in recall and +5.28% in NDCG.

The proposed method employs a layer combination using the weighted sum of the learning process and the resulting final embedding layer for recommendations in GCN algorithms. Our experimental results show that not all layer embeddings are necessary. This can be intuitively seen in the case of [256,1,1], where each embedding is weighted differently. If we treat the weight applied to each embedding as a learning parameter and apply a learned end-to-end approach to the weights, we can find the optimal combination of embeddings for higher recommendation performance. Higher recommendation performance can be achieved by improving the layer combination architecture of the GCN algorithms. Therefore, we plan to conduct future research to apply a layer-combination process and end-to-end learning.

Acknowledgement: None.

Funding Statement: This work was supported by the Kyonggi University Research Grant 2022.

Author Contributions: Sangmin Lee conducted the experiments and wrote the paper, and Namgi Kim is a corresphonding author and guided and supervised the research.

Availability of Data and Materials: A record of the entire experiment can be found at https://wandb.ai/d9249/WFGR and the full code for the experiment can be found at https://github.com/d9249/WFGR.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. D. Goldberg, D. Nichols, B. M. Oki and D. Terry, “Using collaborative filtering to weave an information tapestry,” Communications of the ACM, vol. 35, no. 12, pp. 61–70, 1992. [Google Scholar]

2. B. Sarwar, G. Karypis, J. Konstan and J. Riedl, “Item-based collaborative filtering recommendation algorithms,” in Proc. of WWW, Hong Kong, China, pp. 285–295, 2001. [Google Scholar]

3. K. C. Park and S. Lee, “Investigating consumer innovativeness for new media Infusion: Role of literacy in the context of OTT services in Korea,” KSII Transactions on Internet and Information Systems, vol. 16, no. 6, pp. 1935–1952, 2022. [Google Scholar]

4. M. Goyani and N. Chaurasiya, “A review of movie recommendation system: Limitations, survey and challenges,” ELCVIA: Electronic Letters on Computer Vision and Image Analysis, vol. 19, no. 3, pp. 18–37, 2020. [Google Scholar]

5. H. Wang, Z. Le and X. Gong, “Recommendation system based on heterogeneous feature: A survey,” IEEE Access, vol. 8, pp. 170779–170793, 2020. [Google Scholar]

6. T. L. Ho, A. C. Le and H. D. Vu, “Enhancing recommender systems by fusing diverse information sources through data transformation and feature selection,” KSII Transactions on Internet and Information Systems, vol. 17, no. 5, pp. 1413–1432, 2023. [Google Scholar]

7. R. Ying, R. He, K. Chen, P. Eksombatchai, W. L. Hamilton et al., “Graph convolutional neural networks for web-scale recommender systems,” in Proc. of KDD, London, UK, pp. 974–983, 2018. [Google Scholar]

8. S. Zhang, H. Tong, J. Xu and R. Maciejewski, “Graph convolutional networks: A comprehensive review,” Computational Social Networks, vol. 6, no. 1, pp. 1–23, 2019. [Google Scholar]

9. P. Chen, J. Zhao and X. Yu, “LighterKGCN: A recommender system model based on bi-layer graph convolutional networks,” Journal of Internet Technology, vol. 23, no. 3, pp. 621–629, 2022. [Google Scholar]

10. G. Rajchakit, P. Agarwal and S. Ramalingam, Stability Analysis of Neural Networks. Singapore: Springer, 2021. [Google Scholar]

11. N. Boonsatit, G. Rajchakit, R. Sriraman, C. P. Lim, P. Agarwal,“Finite-/fixed-time synchronization of delayed Clifford-valued recurrent neural networks,” in Advances in Difference Equations. Singapore: Springer, pp. 276, 2021. [Google Scholar]

12. N. Friedman, D. Geiger and M. Goldszmidt, “Bayesian network classifiers,” Machine Learning, vol. 29, pp. 131–163, 1997. [Google Scholar]

13. P. Resnick, N. Iacovou, M. Suchak, P. Bergstrom and J. Riedl, “GroupLens: An open architecture for collaborative filtering of netnews,” in Proc. of CSCW, Chapel Hill, NC, USA, pp. 175–186, 1994. [Google Scholar]

14. J. L. Herlocker, J. A. Konstan, A. Borchers and J. Riedl, “An algorithmic framework for performing collaborative filtering,” in Proc. of SIGIR, Berkley, CA, USA, pp. 230–237, 1999. [Google Scholar]

15. F. Scarselli, M. Gori, A. C. Tsoi, M. Hagenbuchner and G. Monfardini, “The graph neural network model,” IEEE Transactions on Neural Networks, vol. 20, no. 1, pp. 61–80, 2009. [Google Scholar] [PubMed]

16. Z. Wu, S. Pan, F. Chen, G. Long, C. Zhang et al., “A comprehensive survey on graph neural networks,” IEEE Transactions on Neural Networks and Learning Systems, vol. 32, no. 1, pp. 4–24, 2021. [Google Scholar] [PubMed]

17. K. Xu, W. Hu, J. Leskovec and S. Jegelka, “How powerful are graph neural networks?” in Proc. of ICLR, New Orleans, Louisiana, USA, 2019. [Google Scholar]

18. J. You, J. Leskovec, K. He and S. Xie, “Graph structure of neural networks,” in Proc. of ICML, Vienna, Austria, pp. 10881–10891, 2020. [Google Scholar]

19. X. He, K. Deng, X. Wang, Y. Li, Y. Zhang et al., “LightGCN: Simplifying and powering graph convolution network for recommendation,” in Proc. of SIGIR, China, pp. 639–648, 2020. [Google Scholar]

20. J. Wu, X. Wang, F. Feng, X. He, L. Chen et al., “Self-supervised graph learning for recommendation,” in Proc. of SIGIR, Canada, pp. 726–735, 2021. [Google Scholar]

21. J. Yu, H. Yin, X. Xia, T. Chen, L. Cui et al., “Are graph augmentations necessary?: Simple graph contrastive learning for recommendation,” in Proc. of SIGIR, Madrid, Spain, pp. 1294–1303, 2022. [Google Scholar]

22. X. Wang, X. He, M. Wang, F. Feng and T. S. Chua, “Neural graph collaborative filtering,” in Proc. of SIGIR, Paris, France, pp. 165–174, 2019. [Google Scholar]

23. W. X. Zhao, Y. Hou, X. Pan, C. Yang, Z. Zhang et al., “RecBole 2.0: Towards a more Up-to-date recommendation library,” in Proc. of CIKM, Woodstock, NY, USA, pp. 4722–4726, 2022. [Google Scholar]

24. W. X. Zhao, J. Chen, P. Wang, Q. Gu, J. Wen et al., “Wen revisiting alternative experimental settings for evaluating top-N item recommendation algorithms,” in Proc. of CIKM, Ireland, pp. 2329–2332, 2020. [Google Scholar]

25. F. M. Harper and J. A. Konstan, “The movielens datasets: History and context,” ACM Transactions on Interactive Intelligent Systems, vol. 5, no. 19, pp. 1–19, 2015. [Google Scholar]

26. T. B. Mahieux, D. P. W. Ellis, B. Whitman and P. Lamere, “The million song dataset,” in Proc. of ISMIR, Miami, Florida, USA, pp. 591–596, 2011. [Google Scholar]