MCWOA Scheduler: Modified Chimp-Whale Optimization Algorithm for Task Scheduling in Cloud Computing

1  Introduction

Cloud computing has revolutionized the way businesses and individuals’ access and utilize computational resources. It offers a diverse and adaptable resource pool accessible over the internet, providing users with the flexibility to tap into a wide array of resources as per their requirements. This paradigm shift in computing has been perceived as a robust solution to tackle an array of challenges in a world that demands scalability, efficiency, and accessibility [1–4]. In the context of cloud computing, Service Level Agreements (SLAs) play a pivotal role in ensuring customer satisfaction and maintaining a competitive edge. SLAs are contractual agreements that delineate the quality of service expected from the service providers, establishing a binding commitment between the provider and the customer. Within this framework, two critical parameters that SLAs predominantly focus on are makespan, which is the time taken to complete a particular service requested by a user, and energy consumption associated with executing the process, along with latency, which signifies the waiting time associated with each task. It is paramount for these service providers to offer superior service quality to maintain customer loyalty and uphold their reputation in the highly competitive cloud computing environment [5–9].

Cloud computing, although a promising technology, faces several inherent challenges, and one of the most prominent among them is the scheduling of tasks. Task scheduling in cloud computing is a complex and computationally intensive problem that falls under the category of NP-hard problems [10–13]. The objective is to optimally allocate computing resources to execute multiple tasks while meeting the stringent SLAs and minimizing operational costs. This is where the realm of meta-heuristic algorithms comes into play. These algorithms are employed to address the intricate task scheduling challenges in the cloud environment. Meta-heuristic algorithms are optimization techniques that guide the search for an optimal solution by iteratively exploring and exploiting the search space. They have been widely adopted due to their adaptability and effectiveness in handling complex and dynamic environments.

Each of these algorithms has its advantages and disadvantages, and they may encounter unique challenges depending on the problem characteristics and the optimization objectives. Some of the challenges faced by these algorithms in the context of task scheduling in cloud computing include:

1.    Balancing the trade-off between exploration and exploitation which involves avoiding being trapped in local optima while also exploiting promising regions of the search space.

2.    Adapting to the dynamic and uncertain nature of cloud environments: This requires the algorithms to adjust to changes in resource availability, task arrival rate, network latency, and other factors that influence the scheduling process.

3.    Handling the multi-objective and multi-constrained nature of task scheduling problems: This entails optimizing multiple conflicting objectives (such as makespan, cost, energy consumption, reliability, etc.) while satisfying various constraints (such as deadlines, budget, security levels, etc.).

In light of these challenges, this research paper proposes a novel solution to enhance task scheduling in cloud computing. Moreover, the motivation behind developing the Modified Chimp-Whale Optimization Algorithm (MCWOA) arises from the common goal of task-scheduling algorithms to enhance cloud computing performance. Existing algorithms, particularly those categorized as deadline-sensitive task-schedulers, face limitations in selecting parameters like makespan, energy consumption, and latency due to their time-sensitive nature. To overcome the challenges of complex search spaces and time consumption associated with current algorithms, MCWOA is introduced. The proposed algorithm, known as the Modified Chimp-Whale Optimization Algorithm (MCWOA), combines elements of the Chimp Optimization Algorithm (COA) and the Whale Optimization Algorithm (WOA) to address the intricate task scheduling problems. MCWOA aims to strike an optimal balance by minimizing the triad of key metrics: makespan, energy consumption, and latency. Unlike rudimentary heuristics, MCWOA leverages a fusion of nature-inspired tactics and computational intelligence, making it a tailor-made solution for the intricate demands of contemporary cloud ecosystems. In the subsequent sections, this paper provides a detailed exposition of MCWOA, explaining its intricate design and its potent ability to recalibrate the paradigms of task scheduling in cloud computing. Furthermore, to ensure the efficient initialization of the population, MCWOA employs the Sobol sequence, which ensures an even distribution of the population across the solution space. The use of this sequence contributes to the algorithm’s ability to explore the search space effectively from the outset. In the following sections of this research, we will present the detailed mechanics of MCWOA and the results of comprehensive experimental evaluations. The comparative analysis against benchmark algorithms will provide insights into the efficiency and effectiveness of MCWOA. This paper aims to establish MCWOA not as just another alternative, but as an efficient algorithm that can yield optimal solutions in the context of task scheduling for cloud computing environments. Through rigorous testing and thorough evaluations, the contributions of this article become apparent, as it endeavors to advance the state of the art in cloud computing task scheduling. Therefore, the following are some of the contributions that this article aims to provide:

1.    The introduction of the Modified Chimp-Whale Optimization Algorithm (MCWOA) is the main contribution of this research. This novel algorithm offers a strong answer to the challenging task scheduling problems in cloud computing by fusing components of the Whale Optimization Algorithm (WOA) and the Chimp Optimization Algorithm (COA). The goal of MCWOA is to provide a unique method that surpasses conventional heuristics by finding the ideal compromise between makespan, energy consumption, and latency.

2.    Moreover, the Modified Chimp-Whale Optimization Algorithm (MCWOA) is meticulously designed to function as a deadline-sensitive task scheduler, emphasizing the efficiency of task processing and the generation of an optimal solution set within minimal time constraints. In its role as a deadline-sensitive scheduler, MCWOA prioritizes the timely execution of tasks, aiming to fulfill predefined deadlines while simultaneously optimizing critical performance parameters such as makespan, energy consumption, and latency.

3.    By using the features from WOA and COA, the proposed algorithm is able to navigate and exploit diverse regions of the solution space and produce a better optimized solution-set. In addition to this, MCWOA aims to overcome the local minimal trap, a common concern in optimization problems where algorithms may get stuck in suboptimal solutions.

4.    By offering a thorough analysis of MCWOA and contrasting it with benchmark algorithms such as the Whale Optimization Algorithm (WOA), Chimp Algorithm (CA), Ant Lion Optimizer (ALO), Genetic Algorithm (GA), and Grey Wolf Optimizer (GWO), the research paper advances the field. The comparative analysis demonstrates MCWOA’s superiority and verifies its efficacy and efficiency in resolving cloud computing task scheduling issues. Thus, the study provides insightful information about the algorithm’s functionality and potential applications in real-world settings.

The subsequent portions of this document are structured as follows: Section 2delves into a review of prior studies and literature. Section 3 is dedicated to the presentation and discussion of the newly proposed algorithm. In Section 4, a recap of the experimental results is provided, and Section 5 rounds off the document with conclusions and directions for future research.

2  Related Works

Several research endeavors have been conducted to enhance the efficiency of resource consumption and task scheduling in cloud computing environments. All of these efforts have focused on optimization, aiming to find the ideal resource configuration that minimizes Quality of Services (QoS) parameters and enhances task scheduling performance while considering various workload constraints like budget and deadlines. While progress has been made in resource scheduling research, the anticipated results have not been fully achieved. This section provides an overview of the most commonly used multi-objective scheduling strategies and reviews the relevant literature in our research domain.

To address issues of load balancing, energy consumption, latency, and computational costs in the cloud environment, the Dueling Deep Q-Learning Based Chaotic Levy Flight (DDQ-CLF) algorithm proposed in [14] is used in a secure healthcare system with IoT, fog, and cloud tiers for effective data processing and secure transmission, evaluated for factors like energy consumption, latency, and network usage. A new hybrid algorithm merges a Chaotic Grasshopper Optimization Algorithm (CGOA) with a genetic algorithm (GA) for Fog-tier scheduling and is used in [15] to overcome challenges using chaos theory and opposition-based learning principles. Tested on the Google trace dataset for efficiency. The Hybrid Fuzzy Archimedes (HFA) algorithm introduced in [16] optimizes Mobile Edge Computing (MEC) node selection for cost and security. It combines with LGBM and XGBoost to reduce energy usage and latency in task scheduling. HFA refines Archimedes by introducing fuzzy factors and a normalized objective function, prioritizing security and cost efficiency. Light Gradient Boosting Machine LGBM-XGBoost minimizes energy and latency, considering makespan and energy metrics. The approach’s effectiveness is evaluated using resource usage, completion time, rate, and Computation Workload Completion Rate.

A layer fit algorithm is presented for task distribution between fog and cloud based on priorities in [17]. It combines with Modified Harris-Hawks Optimization (MHHO) to minimize makespan, task cost, and power usage while enhancing resource efficiency in both layers. Simulations using iFogSim reveal that MHHO surpasses traditional algorithms such as Ant Colony Optimization (ACO), Harris-Hawks Optimization (HHO), Firefly Algorithm (FA), and Particle Swarm Optimization (PSO) in energy, cost, and makespan. The Enhancing Container-Based Task Scheduling algorithm (ECBTSA-IRA) algorithm in [18] balances performance, cost, and energy efficiency. It assesses workloads for scheduling and shows task interdependencies using a Directed acyclic graph (DAG). Workloads are prioritized by an efficiency factor, which divides them up among processing nodes (FN or cloud) according to schedule duration, cost, and energy. Furthermore, Markov Decision Process (MDP)-based reinforcement learning finds the best resources.

The study proposed in [19] focuses on a resource-constrained fog system managing diverse real-time tasks. It introduces two modules: Task Classification and Buffering (TCB) for task categorization and buffering, and Task Offloading and Optimal Resource Allocation (TOORA) for efficient task delegation and resource allocation. It also presents a new algorithm, Whale Optimized Resource Allocation (WORA), compared to established models for performance evaluation. EPRAM, designed in [20] is for healthcare applications in Fog environments, which addresses resource management challenges. EPRAM integrates real-time resource allocation and a prediction algorithm. It comprises three modules: Resource Allocation Module (RAM), Effective Prediction Module (EPM), and Data Preprocessing Module (DPM). EPM employs PNN for forecasting, like predicting heart attacks based on IoT user data to minimize latency and enhance QoS metrics. The HHOLS algorithm proposed in [21] is an energy-focused metaheuristic that aims to enhance Task Scheduling in Fog Computing (TSFC) for improved Industrial Internet of Things (IIoT) Quality of Service (QoS). It addresses complex challenges through techniques like normalization and scaling. HHOLS is compared to other metaheuristics for performance evaluation.

A heuristic load balancing strategy is presented in [22] to improve the efficiency of cloud services by reducing makespan and task completion time. This dynamic task allocation approach takes energy efficiency, latency, and bandwidth into account for networks. Experiments with synthetic data are conducted to compare it with a queue-based approach, and the results show significant improvements in terms of energy, cost, and time savings in task scheduling when compared to current approaches. The study presents a task offloading strategy for wearable computing in [23], taking into account task requirements, mobility, cloud and network resources, and user payment patterns. Experimental results demonstrate significant improvements in many metrics when compared to baseline methods.

A smart edge-cloud model for efficient data processing is introduced in [24]. To process data between the cloud and IoT devices, it makes use of an edge node close to IoT nodes. A Deep Q-Network (DQN) minimizes makespan and energy by optimizing workflow scheduling in the device-edge-cloud continuum. ELECT is verified by a SHM service simulation in remote areas. The outcomes demonstrate how well ELECT reduced communication, energy, and makespan costs. The study done in [25], introduces a Multi-Objectives Particle Swarm Optimization (MOPSO) algorithm, incorporating a non-dominance sort, aimed at addressing the scheduling issues of time-sensitive business processes with several conflicting objectives. The algorithm endeavors to optimize three conflicting factors: makespan (total execution time), financial costs, and energy usage, all while respecting the budgetary and temporal restrictions of the business process. The work carried out in [26] proposed a framework called Subspace Clustering using Evolutionary algorithm, Off-Spring generation and Multi-Objective Optimization (SCEOMOO) to find the optimal subspace clusters.

Based on the conducted study, it can be deduced that all task-scheduling algorithms share a common goal, which is to improve the performance of cloud computing environments. To achieve this objective, these algorithms consider various parameters. However, when it comes to selecting specific parameters such as makespan, energy consumption, and latency, the options are limited. This limitation arises from the time-sensitive nature of these parameters, categorizing such algorithms as deadline-sensitive task-schedulers. In simpler terms, these algorithms aim to execute requested tasks within an expected time frame, indicating that latency should be minimized for each task, and energy consumption should be kept to a minimum. While there are several algorithms designed for deadline-sensitive task scheduling, they often involve complex search space mechanisms that consume a significant amount of time to identify the optimal results. To address this challenge, a novel algorithm is introduced to achieve the same optimal results but with reduced time consumption. This enhanced task-scheduling algorithm takes into account the minimization of makespan, energy consumption, and latency from various perspectives, including ecological and economic considerations. The algorithm, known as the Modified Chimp-Whale Optimization Algorithm (MCWOA), focuses on optimizing task scheduling and resource allocation among virtual machines in the cloud environment. MCWOA builds upon the Chimp Optimization Algorithm (COA) and the Whale Optimization Algorithm (WOA) to streamline the time and energy constraints, effectively fulfilling the intended objectives. Therefore, the algorithm is aptly named the Modified Chimp-Whale Optimization Algorithm.

The subsequent sections of this research paper are structured as follows: Section 3 delves into the theoretical formulation of the introduced MCWOA algorithm for enhancing task scheduling methods. Section 4 outlines the results obtained and their subsequent analysis. Finally, Section 5 provides a summary of the conclusions drawn from this work.

3  Proposed System

Cloud service providers have devised a cloud environment featuring both Physical Machines (PMs) and Virtual Machines (VMs), complete with a public-access interface for task submission. Once tasks are submitted, a resource manager collects, supervises, and maintains updates of all cloud resources, spanning CPU, storage, and memory. Efficiency hinges on optimal resource utilization, necessitating constant monitoring and updates. After resource management, the scheduler assumes control, aiming to schedule tasks in a way that minimizes the resultant fitness function. The scheduling process only begins when the scheduler has received all necessary data from the virtual machine manager and resource manager, aiding in optimal scheduling decisions. After data collation, the decision-making process determines which tasks should be assigned to which virtual machines. This assignment process can be significantly enhanced by knowing the exact position of the VMs and having a complete list of the tasks. Incorporating such data streamlines the process, leading to reductions in migration costs, total task execution time, load utilization, and overall cost. Effective task management and scheduling, combined with a comprehensive understanding of available resources and task specifics, can enhance efficiency and result in substantial cost savings. This leads to an optimized, user-friendly, and cost-effective cloud environment, maximizing resource utilization.

3.1 Architecture

In summary, within the sphere of cloud computing, when users delegate a specific task to the cloud with the expectation of a result, a series of dedicated processes and methodologies are enacted. These ensure that the task carried out by the cloud is executed both effectively and efficiently. Work distribution is evident within the cloud environment to manage distinct tasks, optimizing performance and throughput. When end-users send their specific tasks to the cloud framework, the task manager takes charge. This entity is entrusted with monitoring and archiving all tasks incoming from different users. Following this, a task scheduler algorithm is implemented to arrange the tasks. In this context, a newly introduced algorithm, named the MCWO algorithm, is applied. Key parameters such as makespan, latency, and energy consumption are taken into consideration when assessing the performance of the algorithm. Subsequently, control is transferred to the cloud service provider, which hosts a multitude of processes like resource management, and resource monitoring, among others. Following this, each task is directed to a data center equipped with a set of Virtual Machines (VMs). Here, each task is executed by the appropriate virtual machine as determined by the task scheduler. Consequently, the cloud is equipped to handle various tasks from users and assign the correct VMs to each task using the introduced task scheduler. This systematic approach ensures an efficient allocation and execution of tasks within the cloud environment. The below diagram Fig. 1 shows the architecture diagram of the cloud with MCWOA implemented in the task scheduler section.

Figure 1: Architecture diagram

3.2 Objective Function

Consider a set of  ′a ′ tasks denoted as T={T1,T2,…,Ta} that are required to be carried out. There is also a set of  ′b ′ Virtual Machines (VMs), represented as VM={vm1,vm2,…,vmb}, where every VM possesses the capability to process and execute the task allocated to it. Therefore, the scheduling of the task process can be symbolized by the function f: T → V. The fundamental goal is to construct a novel deadline task scheduling algorithm that not only results in a minimal makespan but also incurs a lower energy consumption and at the same time has low latency.

Objectivefunction=Norm(∑k=1aTk(MS+EC+LA))(1)

Based on the provided equation, the term Tk signifies a task chosen from the set T, and the value of k spans between [1, a], where ‘a’ denotes the count of tasks at hand. The variable MS denotes the makespan value which is calculated using Eq. (2), the variable EC represents the energy consumption which is calculated using Eq. (7), and the variable LA represents the latency value which is calculated using Eq. (8). The final value is normalized by Norm() to a range between 0 and 1 with seven decimal places, using the norm variable. This is done to evaluate the proposed algorithm with the mentioned parameters. Normalization (Norm()) is needed because EC has a much higher range than MS and LA, which have very small values. Norm() balances the weight of each variable.

3.2.1 Makespan Calculation Formula

MS=Min[∑q=1b(STq+Wtq)](2)

In this context, STq signifies the duration required to submit one particular task to the ‘qth’ virtual machine. Similarly, Wtq stands for the waiting time experienced by that task to be carried out by the ‘qth’ virtual machine. And finally, the Min() is used to select the minimum value from the given set.

3.2.2 Energy Consumption Formula

Typically, multiple components contribute to energy consumption in a cloud environment. These include host machines, electrical and network components, cooling systems, and storage devices. Among these, Host Machines (HMs), which are characterized by components like Central Processing Unit (CPU), Random Access Memory (RAM), and disk storage, are the primary contributors to energy consumption. The energy usage of HMs can be divided into two distinct categories: static energy (Estatic) and dynamic power (Edynamic). Static energy refers to the energy consumed by a machine even when idle, while dynamic power represents the energy consumption associated with active processes. Interestingly, an idle host machine can consume roughly 67.89% of the energy expended by a host operating at full CPU speed.

The total energy consumed within a cloud environment is the cumulative sum of both static and dynamic energies. This combined energy consumption encapsulates the entire power usage, accounting for both idle and active operational states of the host machines. Therefore, both these energy categories play a pivotal role in understanding and managing the overall energy consumption in a cloud environment.

Etotal=Estatic+Edynamic(3)

This study primarily concentrates on the dynamic energy (Edynamic), a type of energy that is directly influenced by the square of the supply voltage (vk)2, and its corresponding frequency (fk). The proportionality constant in this context is (αk), which is computed using Eq. (5). In this equation, the variable ‘k’ signifies the kth Host Machine. Thus, the formula employed to calculate Edynamic is illustrated below:

Edynamic=αk.(vk)2.(fk)(4)

Let, µk be the power ratio for the kth Host machine when idle Hkidle, fkmax is Hk’s maximal frequency and Ekmax is the maximum energy consumed by Hk. The proportionality constant αk of Hk can be computed as

αk=(1−µk).Ekmax(fkmax)2(5)

Now for the static energy, the energy is directly proportional to the energy it consumes in its idle state. Moreover, a set St⊆ (1,0) is used which indicates the status of the Host machine Hk at a given time t, where 1 represents Hk is active and 0 represents Hk is idle.

Estatic=µk.Ekmax.(St)(6)

Therefore, the final energy consumption formula combining Eqs. (4) and (6) can be expressed as:

Etotal=∫tstfαk.Ekmax.(St)+(1−µk).Ekmax(fkmax)2(vk)2.(fk)dt(7)

3.2.3 Latency Calculation Formula

LA=Min[∑q=1b(α.Etq)](8)

In the above-mentioned equation, the variable Etq signifies the duration required for a specific task to be executed by the ‘qth’ virtual machine. Meanwhile, the variable α is employed to normalize the timestamp values for each task. The normalization is necessary to obtain consistent values as these timestamps could fluctuate based on several factors, such as the number of iterations, and the availability of resources, among others. b represents the total virtual machine and finally, the Min() is used to select the minimum value from the given set.

3.3 Task Scheduling Process Using MCWO Algorithm

The algorithm being proposed in this research is a confluence of principles and strategies derived from two well-established optimization algorithms, namely, the Chimp Optimization Algorithm (COA) and the Whale Optimization Algorithm (WOA). Each of these algorithms is known for its unique merits, with the COA recognized for its superior search capabilities, global optimization ability, and other beneficial features. A distinguishing feature of the COA is its capability to adeptly balance between exploration (wide-ranging search) and exploitation (focused search). This equilibrium is integral to preserving the diversity of solutions while facilitating a steady convergence speed. Such a dynamic interplay allows the COA to generate accurate results consistently while delivering an impressive level of throughput. Despite its myriad of advantages, the COA is not without limitations. It encounters issues relating to local search constraints, as well as difficulties with updating the position of its four core category variables. Conversely, the WOA, another widely used algorithm in optimization problems, boasts of its high performance and swift convergence speed. However, its proficiency tends to decrease as the number of tasks increases, indicating a predilection for optimal performance with smaller tasks. Aiming to address the identified drawbacks of both the COA and WOA, this research introduces an innovative algorithm known as the Modified Chimp-Whale Optimization (MCWO) algorithm. This novel algorithm is not merely a patchwork of the two preceding algorithms; instead, it ingeniously builds upon the strengths of both COA and WOA. The MCWO algorithm aspires to consistently generate high-performance results and sustain throughput, regardless of the size of the task at hand. Its inherent design principles and mechanisms have been honed to respond efficiently to any situation, ensuring it remains versatile and adaptable.

Furthermore, this algorithm leverages exploration and exploitation procedures at the onset of every iteration, aimed at reducing the overall time to reach the desired solution. The primary novelty in the proposed algorithm lies in its superior performance and throughput concerning energy consumption, makespan, and latency (Quality of Service parameters), as compared to the two foundational algorithms. Additionally, due to its hybrid approach, the algorithm adeptly manages complexities such as heterogeneous resources, fluctuating workloads, inter-task dependencies, and real-time constraints. Most notably, it serves as a deadline-sensitive algorithm, ensuring tasks are completed within their specified timeframes. The following sections are the breakdown and explanation of the proposed MCWO algorithms.

3.3.1 Chimp Optimization Algorithm (COA)

The Chimp Optimization Algorithm (COA) is an ingenious bio-inspired optimization method used for task scheduling in cloud computing, drawing inspiration from the food-foraging behavior of chimpanzees [27]. In the wild, chimpanzees use a balance of exploration, exploiting known food sources, and exploration, searching for new ones. Similarly, COA employs this principle of balancing exploration (global search) and exploitation (local search), ensuring a dynamic approach towards finding optimal solutions for complex computational problems. In the realm of task scheduling within cloud computing, the COA operates by assigning tasks (indicated as food sources) to virtual machines (similar to chimpanzees). In this ecosystem, each task represents a job to be executed, and each virtual machine serves as a computational resource with the capacity to perform these tasks. The algorithm begins with random initialization, where each virtual machine is assigned a task randomly. This scenario mirrors the way a group of chimpanzees would disperse in different directions to find food.

The key to COA’s efficacy is its dynamic adaptation ability. Just as a chimpanzee may switch from exploiting a known food source to exploring new sources based on various factors, the COA also strategically shifts between exploration and exploitation based on the problem’s characteristics and the stage of optimization. During the exploration phase, the algorithm allows for a wide-ranging search of the solution space. This phase is crucial to avoid being trapped in local optima and to ensure diverse solutions are considered. In the exploitation phase, the algorithm fine-tunes the solutions, converging towards the optimal solution. Moreover, the COA incorporates a social hierarchy behavior observed in chimpanzee groups, further enhancing its optimization capabilities. It classifies solutions into four categories, namely, driver, barrier, chaser, and attackers, representing the lowest to the highest quality solutions, respectively. These categories influence the search strategy, with higher-ranked solutions contributing more to the global search phase and lower-ranked ones contributing more to the local search phase.

3.4 Mathematical Model Related to COA

In the following section, the equations and formulas used in the Chimp optimization algorithm are discussed. As mentioned earlier, there are 4 different independent groups of chimps involved, each of which is driving, blocking, chasing, and attacking groups. The objective of these groups is to obtain the required solution (here the correct mapping of a user-defined task to the available virtual machine). The complete COA is divided into 2 stages which are the exploration and exploitation stage.

3.4.1 Exploration Stage

The exploration stage suggests the process of global search within the solution space. It is the phase where the algorithm conducts a widespread search to discover new potential solutions. The exploration stage is inspired by the behavior of chimpanzees when they are searching for food in the wild. In this phase, each ``chimp" (a potential solution in the algorithm) embarks on a search for ``food" (the optimal solution). This is achieved by creating new potential solutions through random perturbations of the current solutions, akin to a chimpanzee moving in different directions in search of food. The objective during this stage is to ensure diversity in the search process and to avoid premature convergence to a suboptimal solution. By exploring a broad scope of the solution space, the algorithm is more likely to discover global optima. To perform this process and discover the potential solution, the following equations are utilized:

dis=|c.yprey(t)−mt.ychimp(t)|(9)

yprey(t+1)=yprey(t)−a.dis(10)

In the above Eq. (9), dis refers to the distance between prey (potential solution) and chimp. Here the variable yprey indicates the location vector of the potential solution/prey, variable ychimp indicated the location vector of the chimp and variable t indicates the iteration number. Eq. (10) is used to update the position of the prey based on the distance calculated in the previous iteration. Apart from this, variables such as mt,c, and a represent the coefficient vectors which are calculated using Eqs. (11)–(13).

a=2.f.r1−f(11)

c=2.r2(12)

mt+1=ƛmt(1−mt)(13)

In the equations mentioned above, the variable f undergoes a nonlinear reduction from 2.5 to 0 throughout the iterative process, which includes both the exploration and exploitation phases. Here, r1, r2 and r3 are random vectors that exist within the range [0, 1]. Lastly, mt denotes a chaotic vector computed based on different chaotic values from the preceding iteration. This calculation employs logistic mapping to enhance the hunting process of the chimp, thereby making the algorithm more effective. And ƛ represent the chaotic vector-based learning rate with value between 0 and 1.

3.4.2 Exploitation Stage

The exploitation stage in the Chimp Optimization Algorithm (COA) is the phase where the algorithm focuses on refining the current best solutions to find local optima. This phase draws inspiration from the behavior of chimpanzees when they are exploiting a known food source, concentrating on gathering as much as possible from it. During the exploitation phase, the algorithm takes the current best solutions (often represented by the driving, blocking, chasing, and attacking group solutions in the COA) and generates new potential solutions in their vicinity. This is done by applying small perturbations to the current best solutions, effectively probing the solution space around these points to find even better solutions. The goal here is to locate a near-optimal or optimal solution once a promising region of the solution space has been identified. To perform this process, equations similar to the ones seen in the exploration stage are utilized.

disattack=|c1.yatttack(t)−mt1.y(t)|,dischase=|c2.ychase(t)−mt2.y(t)|disblock=|c3.yblock(t)−mt3.y(t)|,disdrive=|c4.ydrive(t)−mt4.y(t)|(14)

y1(t)=yattack(t)−a1.disattack,y2(t)=ychase(t)−a2.dischase(15)

y3(t)=yblock(t)−a3.disblock,y4(t)=ydrive(t)−a4.disdrivey(t)=y1(t)+y2(t)+y3(t)+y4(t)4(16)

As previously mentioned, in the last phase, the chimps launch their attack and end the hunt when the prey ceases movement. The mathematical modeling of this attacking process involves reducing the value of f. It is worth emphasizing that the variation values of the variable a are also constricted by f. Essentially, a stands for a random variable within the span of [−2 f, 2 f], and the magnitude of f diminishes from 2.5 to 0 as iterations progress. Moreover, similar to Eq. (9), mti,ci, and ai(valueifrom1to4) represent the coefficient vectors which are calculated using Eqs. (11)–(13). When the stochastic values of a fall within the interval of [−1,1], the subsequent placement of a chimp can range anywhere between its current location and the location of the prey. Based on the operators mentioned earlier, the Chimp Optimization Algorithm (ChOA) facilitates the chimps in modifying their positions, correlating with the stances of the attacking, barrier, chasing, and driving chimps, ultimately initiating a pursuit on the prey.

The above two mentioned stages are the most important stages that display the mathematical working of the Chimp Optimization algorithm. An important fact of the COA in task scheduling is its effectiveness in handling various complexities inherent in cloud computing environments. These include the heterogeneity of resources, where different virtual machines may have varying capabilities, and the dynamic nature of workloads, where the number and characteristics of tasks can change over time. The COA’s flexible and adaptive nature allows it to effectively navigate these complexities, dynamically adjusting its search strategy based on the current state of the system and the tasks at hand.

3.5 Whale Optimization Algorithm (WOA)

The Whale Optimization Algorithm (WOA) is an optimization technique rooted in nature, specifically designed for task scheduling in cloud computing [28]. It takes cues from the hunting patterns of humpback whales. Notably, the algorithm emulates the bubble-net hunting strategy, where whales ascend in a spiral motion and exhale bubbles to create a ‘net’, effectively entrapping their target. In the realm of task scheduling in cloud computing, the WOA is adept at efficiently allocating tasks to virtual machines (VMs) to optimize specific objectives, such as minimizing total execution time, reducing cost, or balancing load. In the WOA, each whale represents a potential solution or a specific task-to-VM assignment in the context of task scheduling. The WOA begins with a population of whales dispersed randomly in the search space. It then performs a series of mathematical operations to model the hunting behavior of the whales. These operations involve shrinking encircling and spiral updating positions that correspond to the formation of the bubble-net and the spiraling behavior of the whales, respectively.

3.5.1 Mathematical Model Related to WOA

In the subsequent segment, we delve into the mathematical underpinnings and formulas inherent to the Whale Optimization Algorithm. The WOA, tailored for task scheduling within cloud computing, incorporates various mathematical principles, drawing inspiration from the predatory patterns of humpback whales. The algorithm’s initiation comprises a collection of prospective solutions, each epitomized as a point within a multi-faceted space. Every such point denotes a distinct task assignment to a Virtual Machine (VM).

3.5.2 Encircling Prey

During the exploitation phase, the whales (potential solutions) encircle their prey (the current best solution). This behavior is mathematically modeled by gradually updating the position of each whale towards the location of the optimal result found so far. This is done using equations that shrink the distance between each prey and whale over time, driving the whales to converge towards the best solution. the equation used in this stage is similar to Eqs. (9) and (10).

3.5.3 Bubble-Net Attacking Method

In the exploration phase, the WOA uses a mathematical model of the spiral-shaped bubble-net hunting behavior of whales. This is modeled using a logarithmic spiral equation that generates a spiral path moving toward the best solution. This allows the algorithm to conduct a local search around the current best solution while also maintaining some degree of exploration. In the Logarithmic Spiral position updating System approach, Initially, humpback whales embark on an exploration of their prey, assessing the distance that separates them. Following this, they engage in a distinctive logarithmic spiral motion akin to a cone’s shape to pursue their prey. Each whale adjusts its position in sync with this spiral movement path. The mathematical representation of this strategy is provided as follows:

dis=|c.Y(t)−y(t)|(17)

Y(t+1)=dis.ebl.cos⁡(2πl)+c.Y(t)(18)

In this context, Eq. (17) delineates the distance between the tth whale and its prey. The term Y(t) stands for the position vector of the chosen whale during the tth iteration, whereas y(t) indicates the position vector of the prospective solution, often referred to as the prey. Moving to Eq. (18), l is a random value falling within the interval [−1,1], and b serves as a constant that sketches out the logarithmic spiral patterns. Beyond their circular maneuvering around the prey, humpback whales also adopt a conical logarithmic spiral movement to corner their prey simultaneously. The revamped positions of the humpback whales are outlined by Eq. (18). Both methods of movement hold an equivalent probability of 50%, expressed as follows:

Y(t+1)={Y(t)−a.dis                            ifp<0.5dis.ebl.cos⁡(2πl)+Y(t) ifp>0.5(19)

In the aforementioned description, p denotes a random variable situated between 0 and 1. Beyond their bubble-net attack approach, humpback whales also engage in a random search tactic to identify their prey. The subsequent section offers a detailed mathematical portrayal of this randomized search method employed by the whales.

3.5.4 Search for Prey

If the whales cannot improve their solutions through encircling prey or bubble-net attacks, they will search for prey randomly. This is modeled by randomly updating the position of the whales within the search space. Eqs. (20) and (21) represent the search for prey.

dis=|c.yrand(t)−y(t)|(20)

y(t+1)=yrand(t)−a. dis(21)

In this context, a represents the humpback whales’ action of searching for prey. The value for the vector a should either exceed 1 or be less than −1. This stage differs from the exploitation stage as the location of the search agent is adjusted concerning a randomly chosen search agent, rather than the best agent identified up to that point. The condition a > 1 is incorporated into the WOA algorithm to facilitate the search for the global optimum and to sidestep the local optimum. The variable yrand(t) in Eq. (21) is derived from the current generation and represents a random position vector, indicating a random whale.

3.6 Modified Chimp-Whale Optimization Algorithm

As mentioned before, the proposed algorithm MCWO is based on two optimization algorithms the COA and WOA. Both these optimization algorithms are nature-inspired algorithms that can solve the required problem which is to improve the performance of the task scheduler. While the Chimp Optimization Algorithm (COA) offers several advantages in task scheduling for cloud computing, like all optimization algorithms, it also has certain limitations or drawbacks. While COA is designed to maintain a balance between exploitation and exploration to avoid local optima, it may still get trapped in local optima for certain complex or high-dimensional problems. As with any heuristic algorithm, COA does not guarantee to find the optimal solution. While it may find high-quality solutions in a reasonable time frame, there is no guarantee that these solutions are globally optimal. Moreover, the initial population calculation is assumed and there is no actual calculation involved due to which there is no guarantee of getting optimal solution all the time. Therefore, to enhance the performance of the COA, this study tries to propose a new algorithm called the modified Chimp-Whale Optimization algorithm, which tries to jump out of the local extreme value or optima using the technique called Bubble-net attacking method inspired by WOA. But by doing so the proposed algorithm will be able to provide a better solution with improved performances and throughput. Moreover, Both COA and WOA algorithms use random values to initial the population at the beginning, due to which the quality of the discovered solution reduces and the algorithm becomes less optimal. Thus, to understand the proposed better the algorithm is divided into 4 stages.

3.6.1 Stage 1–Population Initialization and Sequencing

As previously highlighted, population initialization is an integral component of an optimization algorithm. This stage involves two distinct yet interrelated processes: the initialization of pertinent parameters and their subsequent sequencing. The latter is employed to reduce computational time and strive towards enhanced algorithm performance. Initially, upon defining all the necessary parameters, such as tasks, available virtual machines, host machines, and so forth, it is essential to assign specific values to them. In this study, the primary emphasis is on the initialization and sequencing of the available set of tasks and the identification of the prey, this is done by taking their characteristics into account. The proposed algorithm utilizes the following equations during this crucial stage:

w={(2.rc)1s+1                         ifrc<0.51−[(2.(1−rc))1s+1]   ifrc>0.5(22)

In Eq. (22), the term w signifies the weight initializer, while rc stands for the character-variable, which is determined based on the selected task’s characteristics. The value of rc ranges between 0 and 1. Meanwhile, the variable s denotes the total count of tasks present at the initialization stage. This variable bears resemblance to the one utilized in Eq. (1).

δ=min[(Xu−X)(X−Xl)Xu−Xl](23)

X=Tk.(rc)s(24)

In the above Eq. (23), the two variables Xu and Xl refers to the upper limit and lower limit in the prey set Sprey and min() represents the minimal selection function. At the beginning of the algorithm, Xu and Xl are assigned values 0 and 1, and later on for each Tk (kth task), it is placed inside the set Sprey using Eq. (25) which is expressed as:

Sprey=Tk+w.δ(25)

From the equations discussed above, the algorithm can derive a set of tasks or prey, determined by the characteristics of each task. Once this is achieved, the elements of the set Sprey are arranged in ascending order, a process termed the sequencing process. The advantage of implementing this process lies in its ability to minimize the time the algorithm spends in determining the next task to be mapped. This is achieved by reducing the number of processes utilized in the Whale Optimization Algorithm (WOA) and the Chimp Optimization Algorithm (COA) to identify the subsequent prey. Additionally, this mechanism allows the algorithm to function effectively in a dynamic environment. It is worth noting that due to its reduced time consumption and superior performance and throughput, the algorithm is better equipped to operate in a deadline-sensitive manner. This means it can execute tasks within a specified timeframe, which is of paramount importance in many cloud computing contexts. Now once the prey’s location is calculated, the next step is to represent that particular prey/task on an arbitrary space using its position vector.

3.6.2 Stage 2–Group Division

In stage 2, the available set of chimps or virtual machines is divided into 4 different independent groups namely, attacking, blocking, chasing, and driving groups. Therefore, the objective of this stage is to create 4 different groups and assign the available virtual machines to each of these groups depending on certain properties (like the execution time of a task by the individual virtual machine, energy consumption, and many more). To create clusters, first, all the available set of virtual machines is represented in the same arbitrary space as that of the prey. After which 4 points are selected randomly in the space. These selected points are termed the centroid. Let Cen={cen1,cen2,cen3,cen4} represent a set of centroids for each group. Since the centroid represents the midpoint of a cluster, and initially these points are selected based on a random process, therefore to get the correct midpoint the following equations are used:

Scp={ychimp|ifychimpisneartocenp}(26)

cena=1|Sca|∑1p(yp)(27)

ap=min||yp−cena||2(28)

Eq. (26) is executed only once at the beginning after the centroids are selected. The updation of the centroid value of a cluster is done using Eq. (27), where |Sca| represents the total number of elements in the set Sca. In Eq. (28), each point is again assigned to a cluster set based on the minimum distance between the selected point and the centroid value. The updation Eqs. (27) and (28) are executed until the value obtained from Eq. (28) is similar to the value obtained from the same equation in the previous iteration. Once the clusters and their centroids are calculated, the next process is to find the coefficient vectors associated with these groups, that is

ap=2.fp.r1−fp(29)

cp=2.r2(30)

fp=(℧±2.(qt2)14)+η(31)

where variable ap is the distance coefficient for the cluster p, variable cp represents the outer perimeter of the cluster p, variable fp represents the cluster search range which is calculated using Eq. (31) and finally r1 and r2 are random vectors that exist within the range of [0,1]. In Eq. (31), the variables ℧ and η are quadratic and Gauss variables with values varying from [0,1], q represents the total number of points represented in cluster p and t represents the tth iteration. The main objective of Eq. (31) is to produce a nonlinear reduction from 3 to 0 throughout the iterative process after the prey comes in the vicinity of either of the cluster ranges, until the value of fp remains constant.

3.6.3 Stage 3-Bubble-Net Attacking Method

In this stage, the chimps from the different clusters or groups move towards the prey or the task in a move-defined manner compared to the COA exploration and exploitation stage, as the location of the prey is not known. However, due to the equation from stages 1 and 2, the locations of the prey as well as the centroids of the clusters are known. Based on this knowledge the chimps approach the prey or the target in a Logarithmic Spiral manner so that at any given point in time, the algorithm does not get trapped in local extreme values. In this methodology, the chimps, or centroids, initially gauge their distance from the prey. Subsequently, they navigate using a conical logarithmic spiral trajectory to capture the prey. Every chimp within the groups refines their position anchored to this spiral trajectory. This technique is articulated mathematically as follows:

dp=|cp.cenp(t)−sprey(o)|(32)

cenp(t+1)={cenp(t)−ap.dp.eal                    if dp>cpdp.e−al.cos⁡(2πl)+cenp(t)if dp≤cp(33)

In Eq. (32), the distance from the centroid of each cluster or group to the prey is calculated, and based on this value the centroid moves in a spiral manner toward the prey, the cluster which is far moves faster compared to the cluster which is close to the prey, this will ensure that all the cluster completer surround the prey after tth iteration. After tth iteration, using Eq. (33) if the value of the dp≤cp (that is the prey is in the range of the cluster p), then the value of the cluster search range (fp) starts to reduce and the clusters move in a spiral manner toward the prey, and this is done until dp becomes 0, which indicates that the chimp has successfully captured the prey, or the mapping of the virtual machine to the task is done. Moreover, as mentioned earlier, Eq. (33) will ensure that the algorithm moves uniformly in the direction of the prey and does not get trapped in local extreme values with the proper convergence rate and high performance and throughput.

3.6.4 Stage 4–Evaluation Using Objective Function

In stage 4, once the mapping of the chimp to the prey is done, the solution is stored in the set Sol. Since the problem is an optimization problem with lower values, each element in this set Sol is checked individually to assess whether the obtained result is the best result or not. This is done using the following Eq. (34):

result={1                                                     ifObjectivefunction<thresholdselect the next best cluster    ifObjectivefunction≥threshold(34)

In Eq. (34), the value of the threshold varies from task to task. Therefore, all the formulas and explanations mentioned above suggest that the proposed algorithm is enhanced compared to the COA and WOA algorithms. The algorithm for MCWOA is shown below:

4  Experimental Evaluation

In this section, an intricate exploration of the experimental assessment of the Modified Chimp-Whale Optimization Algorithm is presented. The intention behind this in-depth evaluation is to gain a clearer understanding of how the algorithm fares under scrutiny, especially when compared with other renowned meta-heuristic strategies. The techniques chosen for comparison are among the most widely recognized and esteemed in the research community. These include the Whale Optimization Algorithm (WOA), the chimp algorithm (CA), the Genetic Algorithm (GA), the Ant Lion Optimizer (ALO), and, not the Grey Wolf Optimizer (GWO). CloudSim toolkit is identified as the platform for conducting the simulations. This choice is attributed to its robust capabilities and its recognition in the research domain for similar projects [29]. This toolkit was vital in verifying that the simulation results were both valid and reliable. A proper experimental setup is paramount for reproducibility and comprehension of the conditions under which results were obtained. In this context, the testing was performed on a formidable desktop computer. This device is driven by an Intel i7 processor, housing 4 CPUs, each operating at a speed of 2 GHz. Furthermore, to cater to the intensive computational demands of the simulations, the computer is outfitted with 8 GB of RAM. It runs on a Windows 64-bit platform, ensuring a stable and compatible environment for the tests. A central aspect of the experimental design was the software development environment. Java was the chosen language, with the Java Development Kit (JDK) employed for constructing the simulator. Java’s selection was influenced by its flexibility, its ubiquity, and the convenience it provides in formulating complex algorithms and simulation frameworks.

4.1 Initialization of Variables

The input incorporated several variables, as shown in the table below. Specifically, Table 1 lists these variables and the initial values assigned to them during the setup phase.

In Table 1, parameters such as the number of iterations and the number of tasks considered for evaluation under each section are limited to a small value. The reason for this is, by focusing on a few select quantities of tasks, it becomes easier to benchmark the proposed Modified Chimp-Whale Optimization Algorithm against existing algorithms which are the Whale Optimization Algorithm (WOA), the chimp algorithm (CA), the Genetic Algorithm (GA), the Ant Lion Optimizer (ALO) and Grey Wolf Optimizer (GWO). This allows for a more controlled and direct comparison, enabling a clear assessment of how the proposed algorithm performs in different scenarios. Moreover, based on this result, the proposed algorithm can easily be projected to a higher number of iterations and tasks.

4.2 Makespan Evaluation

This section evaluates the performance of the presented algorithm, focusing on its execution time for a task set. For a comprehensive evaluation, between 100 to 400 tasks are taken into account. The execution is based on different arrival rates, specifically analyzing makespan at rates of 10 and 40. The arrival rate indicates the time gap (in microseconds) between tasks reaching the scheduler. Without regulating this rate, there is potential for the scheduler to be overwhelmed by a sudden flood of tasks. Using varied arrival rate values ensures efficient functioning and maintains low communication bus bandwidth. The algorithm’s results are compared to others such as WOA, CA, GWO, ALO, and GA. The outcomes from the experimental simulations are depicted in Figs. 2 and 3.

Figure 2: Makespan for the tasks with an arrival rate of 10

Figure 3: Makespan for the tasks with an arrival rate of 40

The performance, measured by task execution time, was evaluated. Simulations used 100 to 400 tasks, all with an arrival rate of 10. The results of the proposed algorithm were benchmarked against WOA, CA, GWO, ALO, and GA, in terms of the seconds each algorithm takes to complete a particular set of tasks and displayed in Fig. 2. For 100 tasks, the makespan values for MCWOA, WOA, CA, GWO, ALO, and GA are 13.78, 15.01, 16.21, 18.9, 15.73 and 32.32 s, respectively. For 200 tasks, the makespan values for MCWOA, WOA, CA, GWO, ALO, and GA are 25.9, 27.23, 31.09, 34.61, 29.05 and 67 s, respectively. For 300 tasks, the makespan values for MCWOA, WOA, CA, GWO, ALO, and GA are 36.56, 38.31, 46.31, 50.31, 40.02 and 75.5 s, respectively. Finally, for 400 tasks, the makespan values for MCWOA, WOA, CA, GWO, ALO, and GA are 50.4, 52.3, 58.42, 66, 53.1 and 124 s, respectively. From the data provided, it is evident that the MCWOA technique showcases superior performance in makespan values when compared with other methods like WOA, CA, GWO, ALO, and GA. Specifically, MCWOA yields improvements in makespan of 4.67%, 16.70%, 25.42%, 8.16%, and 57.61% when contrasted with the performance of WOA, CA, GWO, ALO, and GA algorithms, respectively.

The performance, measured by task execution time, was evaluated. Simulations used 100 to 400 tasks, all with an arrival rate of 40. The results of the proposed algorithm were benchmarked against WOA, CA, GWO, ALO, and GA, in terms of the seconds each algorithm takes to complete a particular set of tasks and displayed in Fig. 3. For 100 tasks, the makespan values for MCWOA, WOA, CA, GWO, ALO, and GA are 16.98, 17.01, 19.67, 22.68, 18.786 and 38.784 s, respectively. For 200 tasks, the makespan values for MCWOA, WOA, CA, GWO, ALO, and GA are 30.76, 32.36, 38.12, 41.53, 34.86 and 80.4 s, respectively. For 300 tasks, the makespan values for MCWOA, WOA, CA, GWO, ALO, and GA are 45.13, 46.12, 55.41, 60.37, 48.02 and 90.6 s, respectively. Finally, for 400 tasks, the makespan values for MCWOA, WOA, CA, GWO, ALO, and GA are 60.8, 62.3, 71.01, 79.2, 63.98 and 148.8 s, respectively. From the data provided, it is evident that the MCWOA technique showcases superior performance in makespan values when compared with other methods like WOA, CA, GWO, ALO, and GA. Specifically, MCWOA yields improvements in makespan of 2.61%, 16.57%, 24.59%, 7.22%, and 57.14% when contrasted with the performance of WOA, CA, GWO, ALO, and GA algorithms, respectively.

4.3 Energy Consumption

In this segment, the efficiency of the proposed algorithm is gauged based on the energy consumed by the virtual machine to process a series of tasks. For an in-depth analysis, batches of 200 and 400 tasks are examined. These tasks are carried out according to different iteration values, starting from the 5th iteration to the 25th iteration. The energy consumption results from this innovative method are compared with those of alternative algorithms such as WOA, CA, GWO, ALO, and GA. Moreover, each of the values recorded in this section is expressed in terms of Kilowatt-hour (KWh). The findings from the experimental simulation are illustrated in Figs. 4 and 5.

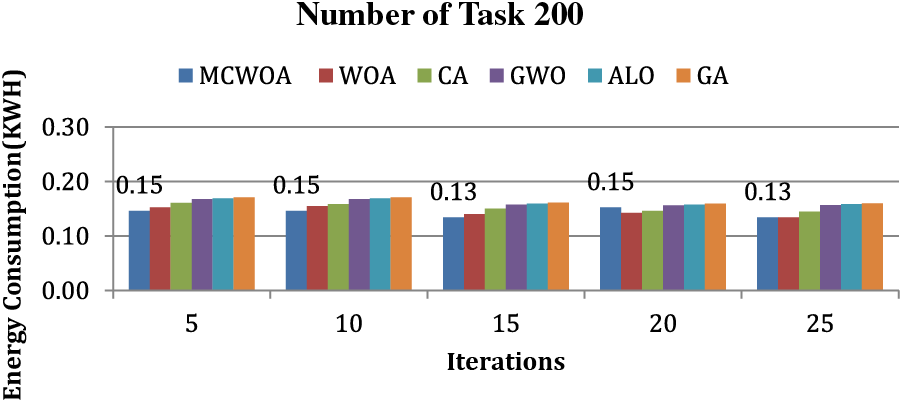
Figure 4: Energy consumption for 200 tasks

Figure 5: Energy consumption for 400 tasks

4.3.1 Energy Consumption for 200 Tasks

In this context, an energy consumption analysis is undertaken. For this simulation, 200 tasks were evaluated across diverse iterations. The outcomes of this analysis are showcased in Fig. 4. From the simulation data, it is clear that the newly introduced MCWOA algorithm effectively reduces energy consumption. From the graph, it is clear that during the 5th iteration, the consumption of energy for MCWOA, WOA, CA, GWO, ALO, and GA are 0.15, 0.15, 0.16, 0.17, 0.17 and 0.17 KWH. The consumption of energy during the 10th iteration for MCWOA, WOA, CA, GWO, ALO, and GA are 0.15, 0.16, 0.16, 0.17, 0.17 and 0.17 KWH. The consumption of energy during the 15th iteration for MCWOA, WOA, CA, GWO, ALO, and GA are 0.13, 0.14, 0.15, 0.16, 0.16 and 0.16 KWH. The consumption of energy during the 20th iteration for MCWOA, WOA, CA, GWO, ALO, and GA are 0.15, 0.14, 0.15, 0.16, 0.16 and 0.16 KWH and finally, the consumption of energy during the 25th iteration for MCWOA, WOA, CA, GWO, ALO, and GA are 0.13, 0.13, 0.14, 0.16, 0.16 and 0.16 KWH. From the data presented, it becomes evident that the MCWOA method is more energy-efficient than its counterparts, namely WOA, CA, GWO, ALO, and GA. When benchmarked against these methods, MCWOA demonstrated energy consumption of 1.47%, 6.17%, 11.49%, 12.37%, and 13.24% in comparison to WOA, CA, GWO, ALO, and GA, respectively.

4.3.2 Energy Evaluation for 400 Tasks

In this context, an energy consumption analysis is undertaken. For this simulation, 400 tasks were evaluated across diverse iterations. The outcomes of this analysis are showcased in Fig. 5. From the simulation data, it is clear that the newly introduced MCWOA algorithm effectively reduces energy consumption. From the graph, it is clear that during the 5th iteration, the consumption of energy for MCWOA, WOA, CA, GWO, ALO, and GA are 0.24, 0.25, 0.26, 0.28, 0.28 and 0.28 KWH. The consumption of energy during the 10th iteration for MCWOA, WOA, CA, GWO, ALO, and GA are 0.24, 0.25, 0.26, 0.28, 0.28 and 0.28 KWH. The consumption of energy during the 15th iteration for MCWOA, WOA, CA, GWO, ALO, and GA are 0.22, 0.23, 0.25, 0.26, 0.26 and 0.26 KWH. The consumption of energy during the 20th iteration for MCWOA, WOA, CA, GWO, ALO, and GA are 0.25, 0.23, 0.24, 0.26, 0.26 and 0.26 KWH. And finally, the consumption of energy during the 25th iteration for MCWOA, WOA, CA, GWO, ALO, and GA are 0.22, 0.22, 0.24, 0.26, 0.26 KWH and 0.26 KWH. From the data presented, it becomes evident that the MCWOA method is more energy-efficient than its counterparts, namely WOA, CA, GWO, ALO, and GA. When benchmarked against these methods, MCWOA demonstrated energy consumption of 1.47%, 6.17%, 11.49%, 12.37%, and 13.24% in comparison to WOA, CA, GWO, ALO, and GA, respectively.

4.4 Latency Evaluation

In this segment, the efficacy of the suggested algorithm is analyzed through its latency, meaning an examination of its response time performance. The evaluation involves measuring the interval from when a request is made to when a response is received, or the duration from task submission to its execution in a cloud setting. This algorithm’s latency values are then compared against those from benchmark algorithms, namely WOA, CA, GWO, ALO, and GA. To assess the latency across different algorithms, tasks ranging from 100 to 400 are provided and their average waiting time is expressed in milliseconds (ms) which is graphically represented in Fig. 6. For 100 tasks, the latency values for MCWOA, WOA, CA, GWO, ALO, and GA are 7.60, 7.68, 8.14, 8.06, 8.05 and 7.88 ms, respectively. For 200 tasks, the latency values for MCWOA, WOA, CA, GWO, ALO, and GA are 8.17, 8.26, 8.73, 8.64, 8.62 and 8.45 ms, respectively. For 300 tasks, the latency values for MCWOA, WOA, CA, GWO, ALO, and GA are 8.53, 8.62, 9.22, 9.13, 9.11 and 8.93 ms, respectively. And finally, for 400 tasks, the latency values for MCWOA, WOA, CA, GWO, ALO, and GA are 8.91, 9.01, 9.59, 9.50, 9.48 and 9.29 ms, respectively. From the data provided, it is evident that the MCWOA technique showcases superior performance in latency values when compared with other methods like WOA, CA, GWO, ALO, and GA. Specifically, MCWOA yields improvements in latency of 1.1%, 6.96%, 6.02%, 5.83%, and 3.91% when contrasted with the performance of WOA, CA, GWO, ALO, and GA algorithms, respectively.

Figure 6: Latency Evaluation

5  Conclusion

One novel approach to the complex problems of effective task scheduling in cloud computing environments is the proposed MCWOA (Modified Chimp-Whale Optimization Algorithm). This novel algorithm functions in the cloud computing environment, where Quality-of-Service (QoS) characteristics—latency, energy consumption, and makespan—are critical to task scheduling. Motivated by its multi-objective optimization methodology, MCWOA aims to balance these factors, guaranteeing that cloud-based systems perform at maximum effectiveness while meeting strict QoS requirements. When MCWOA is compared with a range of popular algorithms, such as the Whale Optimization Algorithm (WOA), Cuckoo Algorithm (CA), Grey Wolf Optimization (GWO), Ant Lion Optimizer (ALO), and Genetic Algorithm (GA), its uniqueness becomes evident. Through a series of rigorous experiments, MCWOA consistently shows the best results; it excels in makespan metrics and energy efficiency in particular. There were several different scenarios included in these experiments, with task quantities ranging from 100 to 500 and virtual machine (VM) quantities varying between 20 40, and 60. Every time, the results of these tests confirm the substantial and ongoing advancements that MCWOA brings to the field of cloud-based task scheduling. Focusing on the observable advantages that MCWOA provides to the sector makes it clear that the algorithm has a significant influence that goes well beyond research and development. Through a significant reduction in task turnaround times and an improvement in resource utilization, MCWOA embodies efficiency in task execution. Furthermore, the algorithm’s built-in capacity to reduce waste and conserve energy results in significant cost savings, which is crucial at a time when operating costs are constantly rising. The operational efficiency of MCWOA has a cascading effect on various industries and organizations. Companies that frequently struggle with the constant problem of cost optimization find in MCWOA a dependable ally that not only speeds up task completion but also significantly lowers operating costs.

Acknowledgement: The authors wish to express their thanks to Vellore Institute of Technology (VIT) Chennai for their extensive support during this work.

Funding Statement: The authors received no specific funding for this work.

Author Contributions: Conceptualization: C. Chandrashekar and P. Krishnadoss, methodology: V. K. Poornachary, software: B. Ananthakrishnan, validation: B. Ananthakrishnan and P. Krishnadoss, formal analysisb: P. Krishnadoss, investigation: P. Krishnadoss, resources: V. K. Poornachary, data curation: V. K. Poornachary, writing-original draft preparation: P. Krishnadoss, V. K. Poornachary, B. Ananthakrishnan, writing-review and editing: P. Krishnadoss, visualization: P. Krishnadoss, supervision: V. K. Poornachary, project administration: V. K. Poornachary, funding acquisition: V. K. Poornachary. All authors have read and agreed to the published version of the manuscript. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data can be shared on valid request made to corresponding author.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. Zuo, L. Shu, S. Dong, C. Zhu, and T. Hara, “A multi-objective optimization scheduling method based on the ant colony algorithm in cloud computing,” IEEE Access, vol. 3, no. 1, pp. 2687–2699, 2015. doi: 10.1109/ACCESS.2015.2508940. [Google Scholar] [CrossRef]

2. B. G. Batista et al., “Performance evaluation of resource management in cloud computing environments,” PLoS One, vol. 10, no. 11, pp. e0141914, 2015. doi: 10.1371/journal.pone.0141914. [Google Scholar] [PubMed] [CrossRef]

3. X. Zuo, G. Zhang, and W. Tan, “Self-adaptive learning PSO-based deadline constrained task scheduling for hybrid IaaS cloud,” IEEE Trans. Autom. Sci. Eng., vol. 11, no. 2, pp. 564–573, 2013. doi: 10.1109/TASE.2013.2272758. [Google Scholar] [CrossRef]

4. M. Abdullahi and M. A. Ngadi, “Symbiotic organism search optimization based task scheduling in cloud computing environment,” Future Gener. Comput. Syst., vol. 56, pp. 640–650, 2016. doi: 10.1016/j.future.2015.08.006. [Google Scholar] [CrossRef]

5. G. Natesan, N. Manikandan, K. Pradeep, and L. Sherly Puspha Annabel, “Task scheduling based on minimization of makespan and energy consumption using binary GWO algorithm in cloud environment,” Peer Peer Netw. Appl., vol. 2023, no. 5, pp. 1–14, 2023. [Google Scholar]

6. M. Nanjappan, G. Natesan, and P. Krishnadoss, “HFTO: Hybrid firebug tunicate optimizer for fault tolerance and dynamic task scheduling in cloud computing,” Wirel. Pers. Commun., vol. 129, no. 1, pp. 323–344, 2023. doi: 10.1007/s11277-022-10099-0. [Google Scholar] [CrossRef]

7. G. Natesan, J. Ali, P. Krishnadoss, R. Chidambaram, and M. Nanjappan, “Optimization techniques for task scheduling criteria in IaaS cloud computing atmosphere using nature inspired hybrid spotted hyena optimization algorithm,” Concurr. Comput. Pract. Exp., vol. 34, no. 24, pp. e7228, 2022. doi: 10.1002/cpe.7228. [Google Scholar] [CrossRef]

8. F. S. Prity, M. H. Gazi, and K. A. Uddin, “A review of task scheduling in cloud computing based on nature-inspired optimization algorithm,” Clust. Comput., vol. 26, no. 5, pp. 3037–3067, 2023. doi: 10.1007/s10586-023-04090-y. [Google Scholar] [CrossRef]

9. P. Krishnadoss, V. K. Poornachary, P. Krishnamoorthy, and L. Shanmugam, “Improvised seagull optimization algorithm for scheduling tasks in heterogeneous cloud environment,” Comput. Mater. Contin., vol. 74, no. 2, pp. 2461–2478, 2023. doi: 10.32604/cmc.2023.031614. [Google Scholar] [CrossRef]

10. S. Chakraborty, A. K. Saha, and A. Chhabra, “Improving whale optimization algorithm with elite strategy and its application to engineering-design and cloud task scheduling problems,” Cogn. Comput., vol. 15, pp. 1–29, 2023. doi: 10.1007/s12559-022-10099-z. [Google Scholar] [CrossRef]

11. S. Mangalampalli, G. R. Karri, and U. Kose, “Multi objective trust aware task scheduling algorithm in cloud computing using Whale Optimization,” J. King Saud Univ.-Comput. Inf. Sci., vol. 35, no. 2, pp. 791–809, 2023. doi: 10.1016/j.jksuci.2023.01.016. [Google Scholar] [CrossRef]

12. A. Y. Hamed, M. K. Elnahary, F. S. Alsubaei, and H. H. El-Sayed, “Optimization task scheduling using cooperation search algorithm for heterogeneous cloud computing systems,” Comput. Mater. Contin., vol. 74, no. 1, pp. 2133–2148, 2023. doi: 10.32604/cmc.2023.032215. [Google Scholar] [CrossRef]

13. P. Pirozmand, H. Jalalinejad, A. A. R. Hosseinabadi, S. Mirkamali, and Y. Li, “An improved particle swarm optimization algorithm for task scheduling in cloud computing,” J. Ambient Intell. Humaniz. Comput., vol. 14, no. 4, pp. 4313–4327, 2023. doi: 10.1007/s12652-023-04541-9. [Google Scholar] [CrossRef]

14. V. Gowri and B. Baranidharan, “An energy efficient and secure model using chaotic levy flight deep q-learning in healthcare system,” Sustain. Comput.: Inform. Syst., vol. 39, pp. 100894, 2023. doi: 10.1016/j.suscom.2023.100894. [Google Scholar] [CrossRef]

15. S. Singh and D. P. Vidyarthi, “An integrated approach of ML-metaheuristics for secure service placement in fog-cloud ecosystem,” Internet of Things, vol. 22, no. 9, pp. 100817, 2023. doi: 10.1016/j.iot.2023.100817. [Google Scholar] [CrossRef]

16. G. Kumaresan, K. Devi, S. Shanthi, B. Muthusenthil, and A. Samydurai, “Hybrid fuzzy archimedes-based Light GBM-XGBoost model for distributed task scheduling in mobile edge computing,” Trans. Emerg. Telecommun. Technol., vol. 34, no. 4, pp. e4733, 2023. doi: 10.1002/ett.4733. [Google Scholar] [CrossRef]

17. I. Z. Yakubu and M. Murali, “An efficient meta-heuristic resource allocation with load balancing in IoT-Fog-cloud computing environment,” J. Ambient Intell. Humaniz. Comput., vol. 14, no. 3, pp. 2981–2992, 2023. doi: 10.1007/s12652-023-04544-6. [Google Scholar] [CrossRef]

18. V. Sindhu and M. Prakash, “Energy-efficient task scheduling and resource allocation for improving the performance of a cloud-fog environment,” Symmetry, vol. 14, no. 11, pp. 2340, 2022. doi: 10.3390/sym14112340. [Google Scholar] [CrossRef]

19. R. Sing, S. K. Bhoi, N. Panigrahi, K. S. Sahoo, N. Jhanjhi and M. A. AlZain, “A whale optimization algorithm based resource allocation scheme for cloud-fog based IoT applications,” Electronics, vol. 11, no. 19, pp. 3207, 2022. doi: 10.3390/electronics11193207. [Google Scholar] [CrossRef]

20. F. M. Talaat, “Effective prediction and resource allocation method (EPRAM) in fog computing environment for smart healthcare system,” Multimed. Tools Appl., vol. 81, no. 6, pp. 8235–8258, 2022. doi: 10.1007/s11042-022-12223-5. [Google Scholar] [CrossRef]

21. M. Abdel-Basset, D. El-Shahat, M. Elhoseny, and H. Song, “Energy-aware metaheuristic algorithm for industrial-Internet-of-Things task scheduling problems in fog computing applications,” IEEE Internet Things J., vol. 8, no. 16, pp. 12638–12649, 2020. doi: 10.1109/JIOT.2020.3012617. [Google Scholar] [CrossRef]

22. D. Mukherjee, S. Nandy, S. Mohan, Y. D. Al-Otaibi, and W. S. Alnumay, “Sustainable task scheduling strategy in cloudlets,” Sustain. Comput.: Inform. Syst., vol. 30, pp. 100513, 2021. doi: 10.1016/j.suscom.2021.100513. [Google Scholar] [CrossRef]

23. M. Chowdhury, “A prediction and budget-aware offloading scheme for wearable computing,” Int. J. Sens. Netw., vol. 36, no. 4, pp. 204–215, 2021. doi: 10.1504/ijsnet.2021.117481. [Google Scholar] [CrossRef]

24. J. Yuan, H. Xiao, Z. Shen, T. Zhang, and J. Jin, “ELECT: Energy-efficient intelligent edge-cloud collaboration for remote IoT services,” Future Gener. Comput. Syst., vol. 147, pp. 179–194, 2023. doi: 10.1016/j.future.2023.04.030. [Google Scholar] [CrossRef]

25. F. Fakhfakh, S. Cheikhrouhou, B. Dammak, M. Hamdi, and M. Rekik, “Multi-objective approach for scheduling time-aware business processes in cloud-fog environment,” J. Supercomput., vol. 79, no. 8, pp. 8153–8177, 2023. doi: 10.1007/s11227-022-04690-2. [Google Scholar] [CrossRef]

26. R. Khamkar, P. Das, and S. Namasudra, “SCEOMOO: A novel subspace clustering approach using evolutionary algorithm, off-spring generation and multi-objective optimization,” Appl. Soft Comput., vol. 139, no. 1, pp. 1–11, 2023. doi: 10.1016/j.asoc.2023.110185. [Google Scholar] [CrossRef]

27. M. Khishe and M. R. Mosavi, “Chimp optimization algorithm,” Expert Syst. Appl., vol. 149, pp. 113338, 2020. doi: 10.1016/j.eswa.2020.113338. [Google Scholar] [CrossRef]

28. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Adv. Eng. Softw., vol. 95, no. 12, pp. 51–67, 2016. doi: 10.1016/j.advengsoft.2016.01.008. [Google Scholar] [CrossRef]

29. R. N. Calheiros, R. Ranjan, A. Beloglazov, C. A. de Rose, and R. Buyya, “CloudSim: A toolkit for modeling and simulation of cloud computing environments and evaluation of resource provisioning algorithms,” Softw.-Pract. Exp., vol. 41, no. 1, pp. 23–50, 2011. doi: 10.1002/spe.995. [Google Scholar] [CrossRef]