A Hybrid Model for Improving Software Cost Estimation in Global Software Development

1  Introduction

GSD has revolutionized the approach of software companies in implementing software development projects. As companies shift their business globally, GSD has developed as a critical paradigm, allowing companies to work worldwide to improve their development costs. A significant percentage of software projects is estimated to shift to GSD, driven by the comparative labor costs in countries like India and China and the strategic advantages of diverse, distributed teams [1,2]. The benefits of GSD are manifold, but they come with unique challenges, particularly in cost estimation.

This research is motivated by the urgent need for a cost estimation that acknowledges and integrates the factors of GSD. Software cost estimation is a crucial step during the initial phases of software development [3]. Different models for estimating software costs have been developed, Boehm’s Constructive Cost Model COCOMO I and II used for software cost estimation [4]. The COCOMO II effectively estimates the costs of highly complex projects, providing a comprehensive understanding of the scope [5]. The conventional cost estimation models that served traditional software development well are now being tested against the complexities of GSD. Models like COCOMO II, while robust for traditional projects and effective in co-located contexts, struggle in the GSD environment due to their reliance on historical data, which may not accurately reflect GSD’s dynamic nature and do not fully capture the additional cost drivers of GSD, such as cross-cultural communication, varying time zones, and distributed nature [6–8]. This reliance often leads to inaccuracies, as GSD projects frequently encounter unanticipated challenges and changes [9]. Moreover, traditional models necessitate expert judgment in setting parameters, introducing variability and subjectivity into the estimation process [10].

Numerous researchers have dedicated their efforts to developing cost estimation techniques and models customized explicitly for GSD. These estimation techniques include automated, model-driven, or regression-based approaches, providing a high-level overview of project estimation [11]. The study’s authors [12] emphasized that a critical factor contributing to this shortfall is the lack of consideration for cost drivers that significantly impact GSD’s overall cost. Unfortunately, the attention to cost estimation in the GSD context remains limited. The authors in [13] highlighted that companies incorporated GSD to reduce costs; however, their expectations were unmet due to the oversight of additional cost drivers related to GSD. The authors in [14–16] identified several complications in GSD, such as geographic dispersion, time zone differences, competence levels, and hidden costs, which significantly impact the project. In existing approaches [17–20], only a few cost drivers have been considered by the GSD-based cost estimation models, which leads to the development of an inefficient cost estimation process in terms of accuracy and reliability. One of the challenges GSD faces is developing software by teams in different geographic locations. So, the problems associated with geographic dispersion can be averted if the project does not have enough global resources; however, having fewer global resources may make coordination harder [21–22]. Despite the increasing trends and significance of utilizing GSD, few research studies have focused on improving cost estimation in GSD [18,20,23,24].

Existing models also exhibit limited flexibility to adapt to the unique requirements of GSD, making them less reliable for projects with diverse and distributed teams [25]. Furthermore, these models often do not integrate modern technological advances like machine learning, which can enhance the accuracy and adaptability of cost predictions in GSD environments [26]. Machine learning techniques have become increasingly important in software engineering. Many research studies use machine learning methods in various fields [27]. The authors in [5,28] discussed that few models were employed for effective software cost estimation in traditional software development. Their approach utilized four data mining techniques: ANN, K-Nearest Neighbours (KNN), Linear Regression, and Support Vector Machine (SVM). These techniques were implemented to enhance the accuracy and efficiency of software cost estimation. ANNs are suitable for addressing the challenges of GSD due to their ability to learn complex patterns and relationships from data [29,30]. GSD projects involve numerous variables and interactions, making the estimation process complex. ANN can handle non-linear relationships between variables, allowing them to capture intricate patterns in the data than traditional models. Thus, our motivation is to accurately estimate the software cost in the GSD environment by integrating the strengths of the COCOMO II and ANN.

Novelty: The novel aspect of this study is to recognize the research gap and introduce a novel hybrid model that integrates the established COCOMO II model with the advanced learning capabilities of Artificial Neural Networks (ANNs). The proposed hybrid model, tailored to the GSD context, is an evolution in cost estimation designed to recognize and adapt to the dynamic variables inherent in global software projects [5,27]. The innovative nature of the proposed hybrid model lies in its unique approach to integrating GSD-specific cost drivers with the foundational COCOMO II model, enhanced by the adaptive learning potential of ANNs. This integration goes beyond simple incorporation; it represents a significant increase in the estimation methodology by introducing a level of adaptability and precision previously unattainable with conventional models [31,32].

In this article, research contributions are as follows:

•   Innovation in Integration: This research introduces a novel hybrid model that integrates the structured COCOMO II model with the pattern recognition capabilities of ANNs, tailored with GSD-based cost drivers.

•   Benchmarking Excellence: The proposed hybrid model accuracy is benchmarked against the state-of-the-art machine learning-based models for software cost estimation, demonstrating superior accuracy as empirical results validate.

•   Empirical Validation: Utilizing the NASA 93 dataset, enhanced with 26 GSD-based cost drivers, the proposed hybrid model performance is precisely evaluated using MRE (Magnitude of Relative Error), MMRE (Mean Magnitude of Relative Error) and Mean Squared Error (MSE) as criteria, revealing its enhanced estimation capabilities over state-of-the-art models.

Organization: The rest of the article is organized: Section 2 discusses the related works; Section 3 describes the proposed methodology. Section 4 focuses on the experimental setup, evaluation, and result analysis, and Section 5 concludes with a conclusion.

2  Related Work

GSD is well known for the significant shift in traditional software development, leveraging the benefits of globalization. It addresses complex challenges formed by different factors, including customer requirements, methodologies, tools, and the non-physical nature of software. These factors directly effect project timelines, quality, and costs, making accurate cost estimation crucial for project success [25]. However, GSD cost estimation often fails to consider many critical cost drivers, as demonstrated in previous studies [13,19,20,21,28]. The lack of more significant and impactful cost drivers leads to less reliable estimates, highlighting a critical research gap affecting the ability to enhance estimation accuracy within GSD [22]. While key to successful software project completion, risk assessment remains underemphasized in the planning phase despite its potential to fail projects [33–37].

Numerous studies have been dedicated to exploring various methodologies for cost estimation in software projects [38,39]. One of the earliest models is the Software Life Cycle Model (SLIM), formulated by Lawrence H. Putnam. This work was introduced to the academic community in 1978 [5,40]. SLIM leverages the Source Lines of Code (SLOC) metric to forecast the software costs, grounded in Putnam’s life cycle cost analysis [5,11]. This model fundamentally relies on code size to determine software cost estimates, with the resulting calculation being the necessary effort [18]. In a more recent development from 2002, Ricardo Valerdi introduced the COSYSMO cost model, which is designed for systems engineering projects and represents the latest extension of the COCOMO suite of software cost estimation models [15,34]. Traditional cost estimation models like COCOMO, developed by Boehm, remain widely used for their effectiveness in this domain [38–41]. The groundwork for COCOMO II was laid in 1994 by Barry Boehm and his team at the University of Southern California [40]. Traditional models, including the SLIM and COCOMO, focus on parameters like Source Lines of Code (SLOC) but often fall short in the GSD context due to their inability to accommodate GSD-specific challenges such as cross-cultural communication and distributed team coordination.

Recent advancements in machine learning offer promising approaches to addressing these challenges in GSD cost estimation. Studies have explored techniques like Artificial Neural Networks (ANN) and deep learning to outperform traditional models [42]. However, they face limitations in data availability and interpretability, highlighting the need for models that are both accurate and understandable [43–47]. Advancements in machine learning are now adapting cost estimation in GSD. Recent studies have explored machine learning techniques, from ANN-based models [42,48–50] to deep learning approaches [51,52] demonstrating promising results. These innovative models often outperform the traditional cost estimation model, like the COCOMO, but face data limitations and generalizability challenges. Moreover, these models’ interpretability is a concern yet to be adequately addressed [38,39].

Integrating GSD-based cost drivers has led to refining models like COCOMO-II, offering more accurate and reliable cost estimates. Nevertheless, their applicability may be limited when project constraints are unknown [53]. Researchers have extensively reviewed traditional and machine learning-based methods for software cost estimation, comparing various models to identify effective models [54].

A detailed study of GSD-based drivers and existing cost estimation models for traditional and GSD contexts is performed. GSD software development faces challenges in accurately estimating costs. Although traditional models like COCOMO are established, there’s a shift towards using advanced machine learning techniques. Despite these advancements, refining GSD-based cost estimation remains an ongoing endeavor.

3  Proposed Methodology

This section discusses the proposed methodology used in his study. This section is divided into the following sub-sections: dataset, proposed hybrid model, data preprocessing and training.

3.1 Dataset

This study uses the NASA 93 dataset from the PROMISE software engineering repository [53]. The NASA 93 dataset is a comprehensive collection of 93 distinct software projects undertaken at various NASA centers. It is characterized by 17 effort multipliers and 5 scaling factors, offering different values across software projects. This dataset has been extensively utilized in software engineering research, particularly in cost estimation and project management [55]. Its diverse and detailed project metrics make it an ideal choice for testing and validating models in software engineering research. This research incorporated 26 GSD-based cost drivers identified in the previous study [56] to estimate software project costs with a hybrid model. The dataset described in Table 1 contains 93 projects and categorizes them into Low, Medium, and High. The identified GSD-based drivers are categorized according to the studies [13,16,19]. The modified dataset can be accessed publicly at: http://www.uoh.edu.pk/research-data#gsc.tab=0.

3.2 The Proposed Hybrid Model

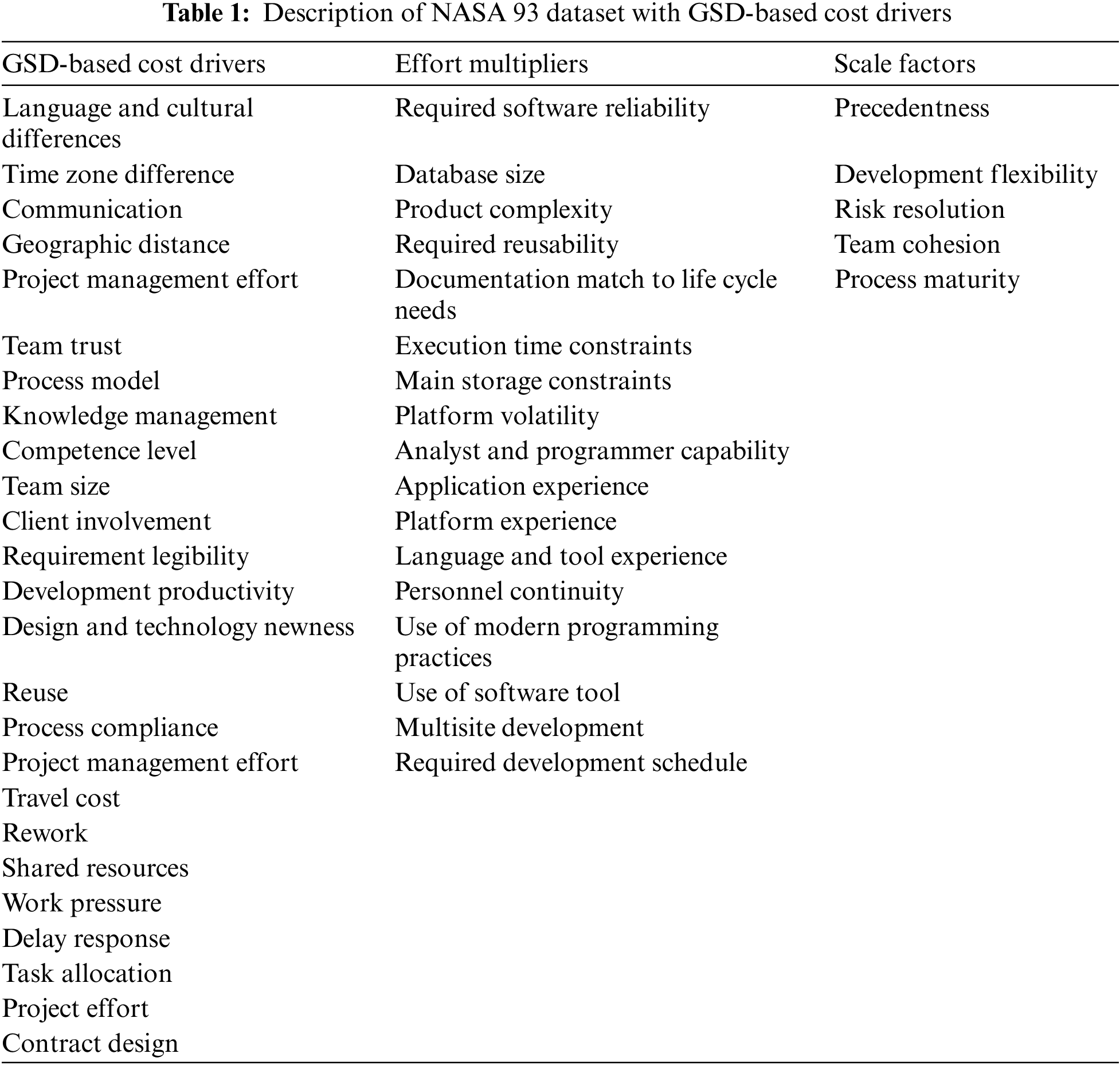
In this section, the study has proposed a novel hybrid model that consists of five main steps, as shown in Fig. 1. In the first step, GSD-based cost drivers and the base model COCOMO II are identified. The base model is a mathematical model used to estimate a project’s cost. The GSD-based cost drivers are factors that affect the cost of a project, such as the size of the project, the complexity of the project, and the experience of a team. The second step categorizes cost drivers and assigns values to the GSD-based cost drivers. The GSD-based cost drivers determine the values of the variables. The third step estimates cost using COCOMO II and GSD-based cost drivers. The fourth step is to amplify the cost estimation base model COCOM II with ANN and GSD-based cost drivers, resulting in a hybrid model COCOMO II-NN-GSD. The amplification accounts for factors not included in the base model. The fifth step is to produce the outcome. The outcome is the predicted cost of the project in the form of effort.

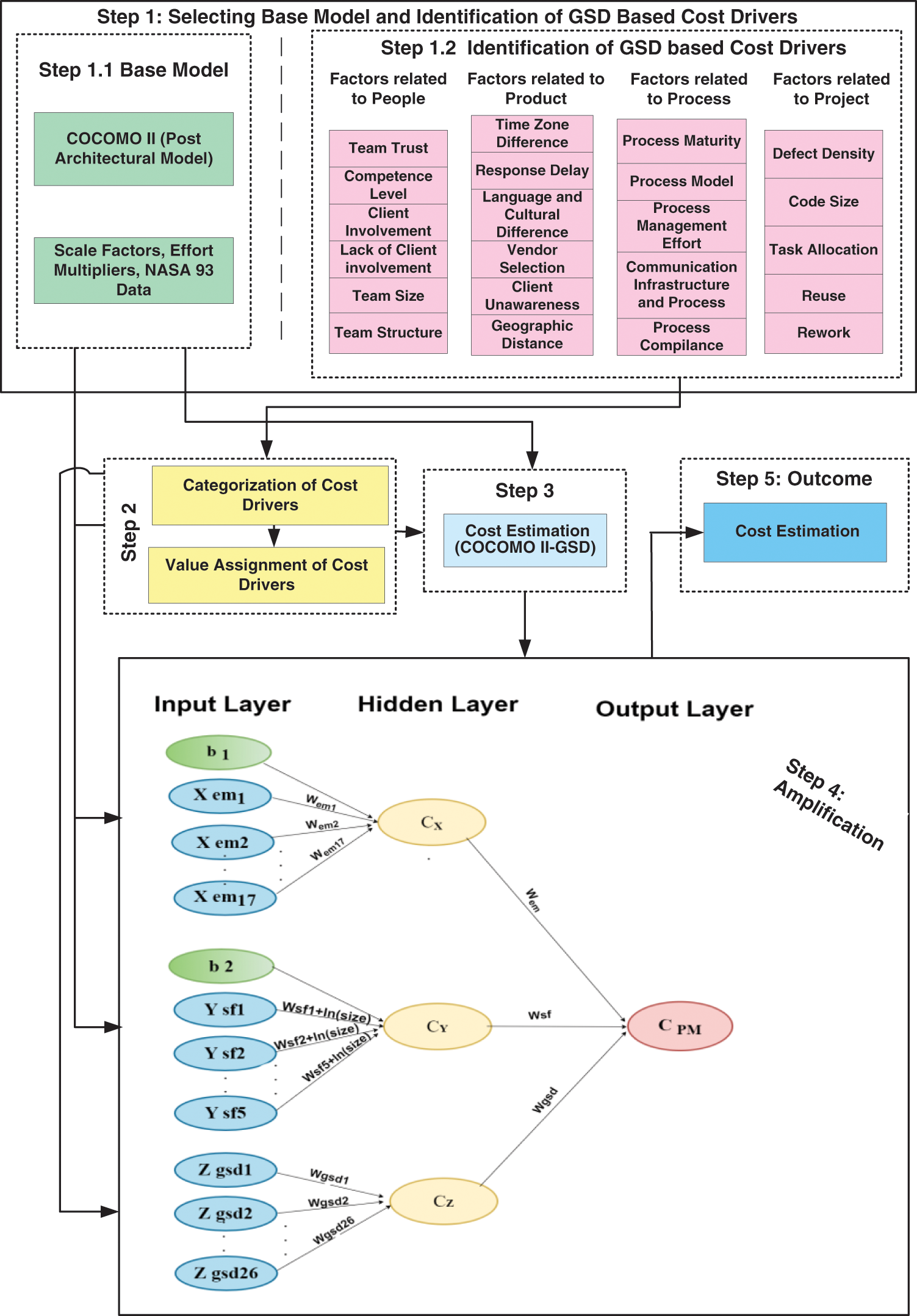
Figure 1: Architecture of the proposed hybrid model COCOMO II-NN-GSD

This study maps the software cost estimation problem in the GSD context as a regression problem. The objective is to build an estimation model using COCOMO II and ANN that can take input features such as project size, team composition, development time, and other relevant parameters and produce an output that represents the estimated cost of the software project.

3.2.1 Identification of Base Model and GSD-Based Cost Drivers

In this step, the research has identified the cost drivers that drive the costs associated with GSD, classified these cost drivers, and selected a base model for cost estimation. In previous research [56], the study systematically reviewed the literature to identify cost drivers in GSD and categorized them based on their significance. The previous study through SLR [56] identified all GSD context-relevant models reported in the literature to examine cost-estimating models. Among the techniques, COCOMO-II is the most widely known model for amplification in the GSD context, as it has built-in characteristics of distributed software development. This research surveyed about a hundred companies and found that most enterprises use expert judgment and other non-algorithmic techniques, highlighting the lack of a formal model in the GSD context. This study also classified the cost drivers into significant and low-significant categories, as Tables 2–5 outlined. The research presents the cost drivers identified through a systematic literature review and empirical studies, classifying them as significant or less significant. It incorporates them into the proposed hybrid model to address this industry gap.

Validation of GSD-Based Cost Drivers through Industrial Experts

This section elaborates on the survey process executed to validate the GSD-based cost drivers determined through SLR [56], involving a group of industrial experts. A detailed questionnaire was developed to evaluate the significance and relevance of these drivers in GSD context, including various aspects such as business approaches, organization sizes, system types, and geographical contexts. This approach gathered valuable feedback from over 100 companies engaged in GSD, supporting the realism and relevance of the identified cost drivers. The survey’s design included 30 questions both closed and open-ended. It used nominal scales for general questions and ordinal scales for more specific queries. The survey’s design, expert validation, and broad distribution intended to ensure a complete and reliable assessment of these cost drivers in the GSD context. Insights from 100 GSD-based companies were analyzed, findings show statistically consistent and do not exhibit a substantial variance. This suggests that the SLR’s results align with the industry survey results, providing validation and reliability to the SLR’s findings and significantly supported the robustness and practical applicability of the identified cost drivers, thereby establishing their relevance in the context of GSD. The results from this empirical study are publicly available at: http://www.uoh.edu.pk/research-data#gsc.tab=0.

3.2.2 Categorization and Value Assignment to the Cost Drivers

In this step, categorization and value assignment is performed. The categorization and value assignment of GSD-based cost drivers are performed with careful consideration, ensuring each driver’s complexity and cost effects are accurately reflected. This process involves grouping the cost drivers based on their level of complexity and potential cost impact in the GSD context. The categorization and subsequent value assignment is made with the help of the research [13,17] and according to standards set by the COCOMO II model. This approach ensures a refinement and contextually relevant integration of the cost drivers into the model, enhancing its accuracy and applicability in GSD settings.

Table 2 illustrates the categorization and values assignment of cost driver competency level. For competency level, experience is used as a criterion. The competency level is increased according to the number of experiences in the relevant field. The experience includes work on similar projects. Individuals with many projects have a higher level of competence.

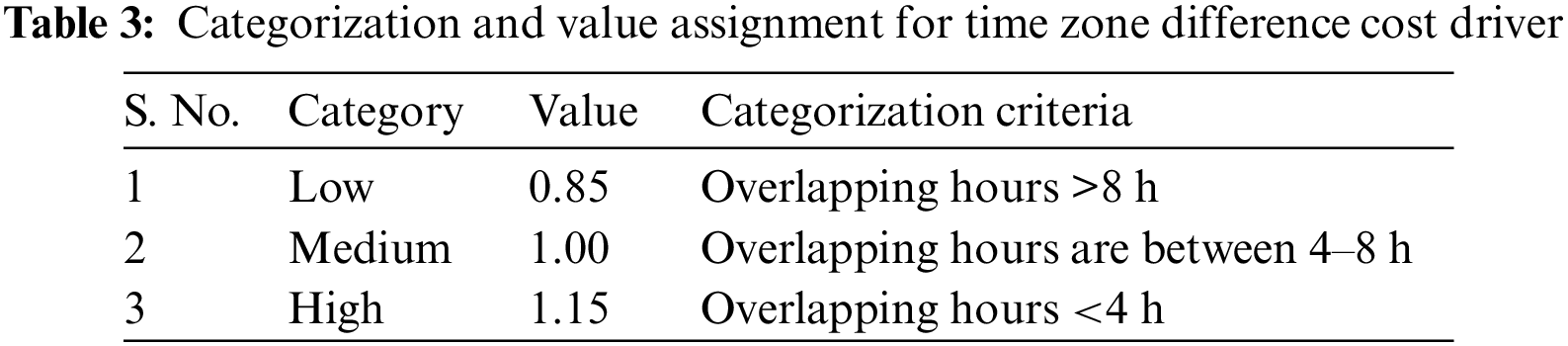
Table 3 shows the cost driver “time zone difference”, categories, criteria, and value assignments. A low time zone difference is assumed if remote team office hours’ overlap by more than 8 h. Medium overlap is considered if office hours overlap 4 to 8 h—medium time zone difference. A high category indicates a significant time zone difference. If the category overlap for less than 4 h, a greater value of 1.15 is assigned.

Table 4 illustrates the categorization and assigning value for the “language barrier” cost driver. A low category for language barrier is assumed if remote sites have the same mother tongue. A medium category is taken if remote sites use different mother tongues, but one of them is the project language. Whereas “High” indicates that remote sites use other mother tongues, none of which is the project language.

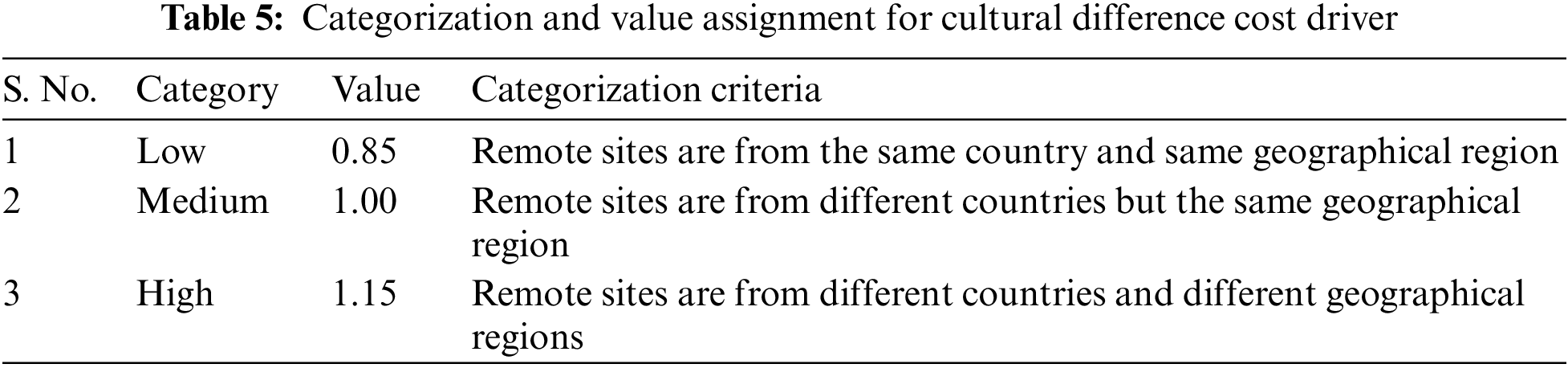
Table 5 illustrates the categorization and assigning value for the cost driver “cultural difference”. A low category for cultural difference is assumed if remote sites are from the same country and the exact geographic location. A medium category is assumed where remote sites are from different countries but in the same geographical region, whereas a “High” category is assumed where remote sites are from other countries and different geographical regions.

3.2.3 Cost Estimation Based on GSD and COCOMO II

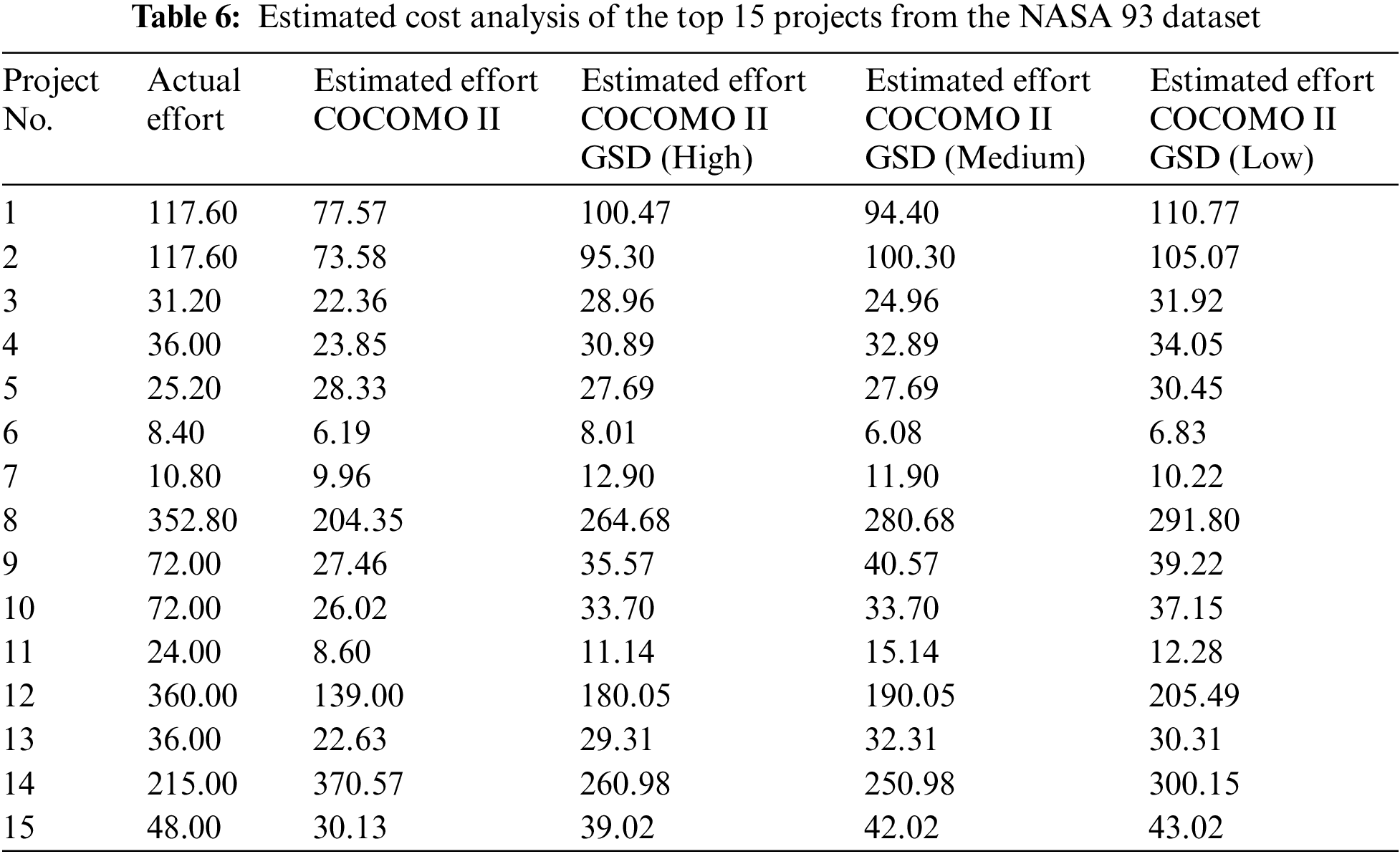
In this step, the cost estimation for each project in the NASA 93 dataset is calculated. This process uses the COCOMO II model amplified with 26 GSD-based cost drivers. The integration of these drivers is accomplished using the Eq. (1) which incorporates 17 effort multipliers, five scale factors, and the 26 GSD-based cost drivers. Table 6 presents a comparison for the top 15 projects from the NASA 93 dataset, comparing their actual effort, the effort estimated by the COCOMO II model, and the effort estimated using the COCOMO II amplified with 26 GSD-based cost drivers. This comparison highlights the improved cost estimation when integrated with GSD-based cost drivers.

3.2.4 Amplification

The fourth step of the proposed methodology involves amplification, wherein an ANN approach is utilized, which enhance the predictive capability of the COCOMO II model. Integrating ANN with COCOMO II involves training the neural network with historical project data i.e., NASA 93 dataset with GSD-based drivers, which also includes COCOMO II’s scale factors and effort multipliers. The ANN architecture is designed to process inputs from the COCOMO II model, including scale factors and effort multipliers, alongwith GSD-based cost drivers. The ANN learns to recognize complex patterns within the data, improving the accuracy of cost estimations. This hybrid model enhances the robustness of traditional cost estimation by introducing machine learning’s adaptive capabilities.

Artificial Neural Networks (ANNs) can significantly enhance the COCOMO II model’s accuracy and effectiveness in software cost estimation. COCOMO II, being an algorithmic model, often relies on predefined parameters and equations to estimate software development costs, which can sometimes lack adaptability to varying project characteristics. By integrating ANNs, the model can learn from historical data and improve its predictive power. Through its layers of interconnected neurons, the ANN learns to recognize patterns and relationships between project characteristics (like size, complexity) and the actual effort and time taken. The weights in the ANN can adjust dynamically, offering a more nuanced understanding of how different factors impact the overall cost and effort. Our proposed model combines the COCOMO II model with ANNs as shown in Fig. 1. The architecture of proposed model in Amplification step consists of input layer, hidden layer, output layer.

3.2.5 Input Layer

An input consists of 17 effort multipliers denoted by Xem, 5 scale factors denoted by Ysf, and 26 GSD-based cost drivers denoted by Zgsd. The proposed hybrid model extends the COCOMO II equation by multiplying GSD cost drivers, as mentioned in (1).

PM=(A)∗SizeE∗∏Xem=117Xem∗∏Zgsd=126Zgsd(1)

where A is the pre-multiplier that reflects the productivity of the development team, Size is the size of the software project and E is the exponent derived from scale factors, E can be determined

E=(B)+(0.01)∑y=15Ysf(2)

B is the base effort, and its value = 0.91, Xem shows COCOMO II effort multipliers, Ysf represents COCOMO II scale factors, and Zgsd are GSD cost drivers.

Eq. (1) can be expressed as

PM=(A) *(Size)0.91+0.01*∑Ysf=15Ysf * ∏Xem=117Xem* ∏Zgsd=126Zgsd(3)

3.2.6 Hidden Layer and Output Layer

The hidden layer in a neural network plays a crucial role in its ability to process and learn from complex data. A hidden layer can consist of one layer, each containing a number of neurons (or nodes). Our model consists of three neurons in one hidden layer. Each neuron in the hidden layer receives inputs from all of the neurons in the previous layer (input layer). These inputs are weighted, and biases are added. The sum of these weighted inputs and biases forms the input to an activation function. The activation function is crucial as it introduces non-linear properties to the network, allowing it to learn and model complex data patterns. We have used ReLU (Rectified Linear Unit) function, Algorithm 1 presents the training details. During training, the weights and biases in the hidden layers are adjusted through a process called backpropagation, which uses algorithms like gradient descent. The network learns by adjusting these weights to minimize the difference between its output and the actual output.

Eq. (3) of COCOMO II-NN-GSD is transformed into the linear function and is defined in (4).

ln(PM)=ln⁡[(A)∗(Size)0.91+0.01∗∑Ysf=15Ysf∗∏Xem=117Xem∗∏zgsd=126Zgsd](4)

we can write (4) as

ln(PM)=ln⁡(A)+ln⁡(S)0.91+0.01∗∑ysf=15Ysf+ln⁡(∏Xem=117Xem)+ln⁡(∏zgsd=126Zgsd)(5)

ln(PM)=ln⁡(A)+ln⁡(∏Xem=117Xem)+ln⁡(∏Zgsd=126Zgsd)+[0.91+0.01∑Ysf=15Ysf]∗ln⁡ (Size)(6)

ln⁡(PM)=ln(A)+ln(Xem1)+ln(Xem2)+ln(Xem3)+…ln(Xem17)+ln(Zgsd1)+ln(Zgsd2)+ln(Zgsd3)+…ln(Zgsd26)+[0.91+0.01(Ysf1)+0.01(Ysf2)…0.01(Ysf5)]ln(Size)(7)

If we ignore the constants, i.e., ln (A) and value of B, which is 0.91, from the above equation and use them as biases in the neural network, the result is

ln⁡(PM)=ln(Xem1)+ln(Xem2)+…ln(Xem17)+ln(Zgsd1)+ln(Zgsd2)+ln(Zgsd3)+…ln(Zgsd26)+[0.01(Ysf1)+…0.01(Ysf5)]ln(Size)(8)

The parameters in Eq. (7) can be given as inputs to the neural network. Thus, the resulting Eq. (8) can be defined

CPM=[b1+Wem1∗Xem1+Wem2∗Xem2+…+Wem17∗Xem17]+[b2+(Wsf1+ln⁡(size))∗Ysf1+(Wsf2+ln⁡(size))∗Ysf2+…(Wsf5+ln⁡(size))∗Ysf5+[b3+Wgsd1∗Zgsd1+Wgsd2∗Zgsd2+…Wgsd26∗Zgsd26](9)

where

CPM==ln⁡(PM);Xem1=ln⁡(Xem1);Xem2=ln⁡(Xem2);……………Xem17=ln⁡(Xem17);

Ysf1=ln⁡(Ysf1);Ysf2=ln⁡(Ysf2);……………Ysf5=ln⁡(Ysf5);

Zgsd1=ln⁡(Zgsd1);Zgsd2=ln⁡(Zgsd2);……………Zgsd26=ln⁡(Zgsd26);

b1=ln⁡(A);b2=0.91;b3=0.01

Wem1 to Wem17 are weight for Xem1 to Xem17, Wsf1 + ln(size) to Wsf5 + ln(size) for Ysf1 to Ysf5 and Wgsd1 to Wgsd26 are weight for Zgsd1 to Zgsd26.

CX=b1+∑Xem=117(Xem)(WXem)(10)

CY=b2+∑Ysf=15(Ysf)(WYsf+ln⁡(Size))(11)

CZ=b3+∑Zgsd=126(Zgsd)(WZgsd)(12)

The output layer of proposed model is computed using Eq. (13).

CPM=(CX∗Wem+(CY∗Wsf)+(CZ∗Wgsd)(13)

3.2.7 Outcome: The Amplification Module Outcome Is Predicted Effort Calculated Using Eq. (1)

4  Experimental Setup and Results Analysis

This section provides the experimental setup and the results derived from the proposed model. The results are discussed and compared with state-of-the-art models to assess the effectiveness and accuracy of the proposed model.

4.1 Data Preprocessing

Data preprocessing is critical for the ANN efficiency in proposed COCOMO II-NN-GSD model, involves filtering the NASA 93 dataset to improve ANN training. Incorrect data analysis and processing produce wrong outcomes, whereas preprocessing improves neural network performance. Inadequate and unclear data make training difficult. This step includes cleansing and normalizing data to address issues of missing values, crucial for model accuracy [57–59]. The preprocessing converts the COCOMO II-NN-GSD Eq. (3) into a linear function using a natural logarithm transformation. This transformation simplifies the data, facilitating more effective learning by the ANN and ensuring the model predictions are reliable.

Several preprocessing steps were taken on the data. These steps are as follows:

4.1.1 Removing Outliers

Initially, the dataset underwent a thorough cleaning process, which involved purifying the features and eliminating outliers. If an attribute does not contain any value, then we mark that attribute with value ‘0’. These anomalous records were excluded, resulting in a refined dataset comprising 93 records (projects) for the experimental analysis.

4.1.2 Normalization

During this stage, the cost drivers (attributes) used in the proposed model are assigned normalized numerical values using the min-max technique. Min-max normalization [59] is a technique used in data preprocessing to scale or transform numerical values in a dataset to a common scale, typically ranging from 0 to 1. This method involves adjusting the scale of the data without distorting differences in the ranges of values. The new numerical representations for these attributes are then input into the proposed model for further processing. In the experiments involving soft computing approaches like Artificial Neural Networks (ANN), the range of values for variables like actual effort was compressed through normalization, setting the range between 0 and 1.

4.1.3 Reducing Range of Variables

Since the proposed framework is a regression-based model, we used the logarithmic operator “ln” that is utilized to reduce the range of the variables in Eqs. (5)–(9).

4.2 Parameter Settings

This research has conducted several experiments with different parameter settings based on the learning rate and number of hidden neurons. The research tuned the model according to each category’s learning rate and number of hidden neurons. This research choose these parameter settings based on the convergence of the COCOMO II-NN-GSD hybrid approach. The experiments are performed with 100 iterations. In the proposed model, this research added the bias term to the weighted sum of the inputs before passing through the activation function. The study assigned values to the bias parameters used in Algorithm 1 at steps 18, 19 and 20, according to [60,61]. To minimize the loss function and update the model’s parameters, the research used Adam optimizer so that the model converges to the optimal solution. Due to Adam’s simplicity and stochastic regularization approaches, this optimizer prevents model overfitting. The research also used β1, β2, β3. The Adam optimizer’s hyperparameters that control the exponential decay rate for the first-moment, second-moment, and third-moment estimates of the gradients, respectively, that control momentum and scaling of the gradients. For the proposed model COCOMO-II-NN-GSD we set optimal parameter settings such as learning rate = 0.002, β1=0.01, β2=0.04, β3=0.06, number of hidden neurons = 10. These parameters control the momentum and scaling of gradients, contributing to a more stable and consistent learning process. The study analysis demonstrated that these specific settings were optimal for the proposed COCOMO II-NN-GSD hybrid model, improving accuracy.

4.3 Evaluation Metrics

The research objective is to refine the accuracy of the COCOMO II-NN-GSD model, which integrates COCOMO II with GSD-based cost drivers. Accuracy is measured by comparing estimated effort against actual effort. The model is evaluated against the original COCOMO II using MRE (Magnitude of Relative Error), MMRE (Mean Magnitude of Relative Error), and Mean Squared Error (MSE) as criteria. This research follows evaluation methods from prior research in the field [12,53,62]. MRE is a measure of the absolute error between an estimated and actual value, expressed as a percentage of the actual value and calculated using Eq. (14). The evaluation measures the model’s accuracy by comparing the estimated effort Eest with the actual effort Eact. MMRE is the average of the MREs over a set of estimates and defined by Eq. (15). Both metrics are used to assess the accuracy of prediction models in fields like software cost estimation. MSE emphasises minimizing large errors in the regression model when significant prediction errors are more heavily than smaller ones due to the squared term. MSE is used when predictions have relative deviations from the true values [62]. COCOMO II-NN-GSD model is evaluated based on MSE. It can be defined as Eq. (16), where yi is the predicted effort for target project i, y^i is the actual effort for target project i and n is the number of projects under evaluation.

MRE=|Eact−Eest|Eact∗100(14)

MMRE=1n∑i=1nMREi(15)

MSE=∑(yi−y^i)/n(16)

4.4 Result Analysis

This section discusses the results of the study experiments. The subsection highlights performance evaluation of COCOMO II GSD, the impact of hidden neurons, convergence analysis in COCOMO II-NN-GSD and evaluation using state-of-the-art models.

4.4.1 Performance Evaluation of COCOMO II GSD

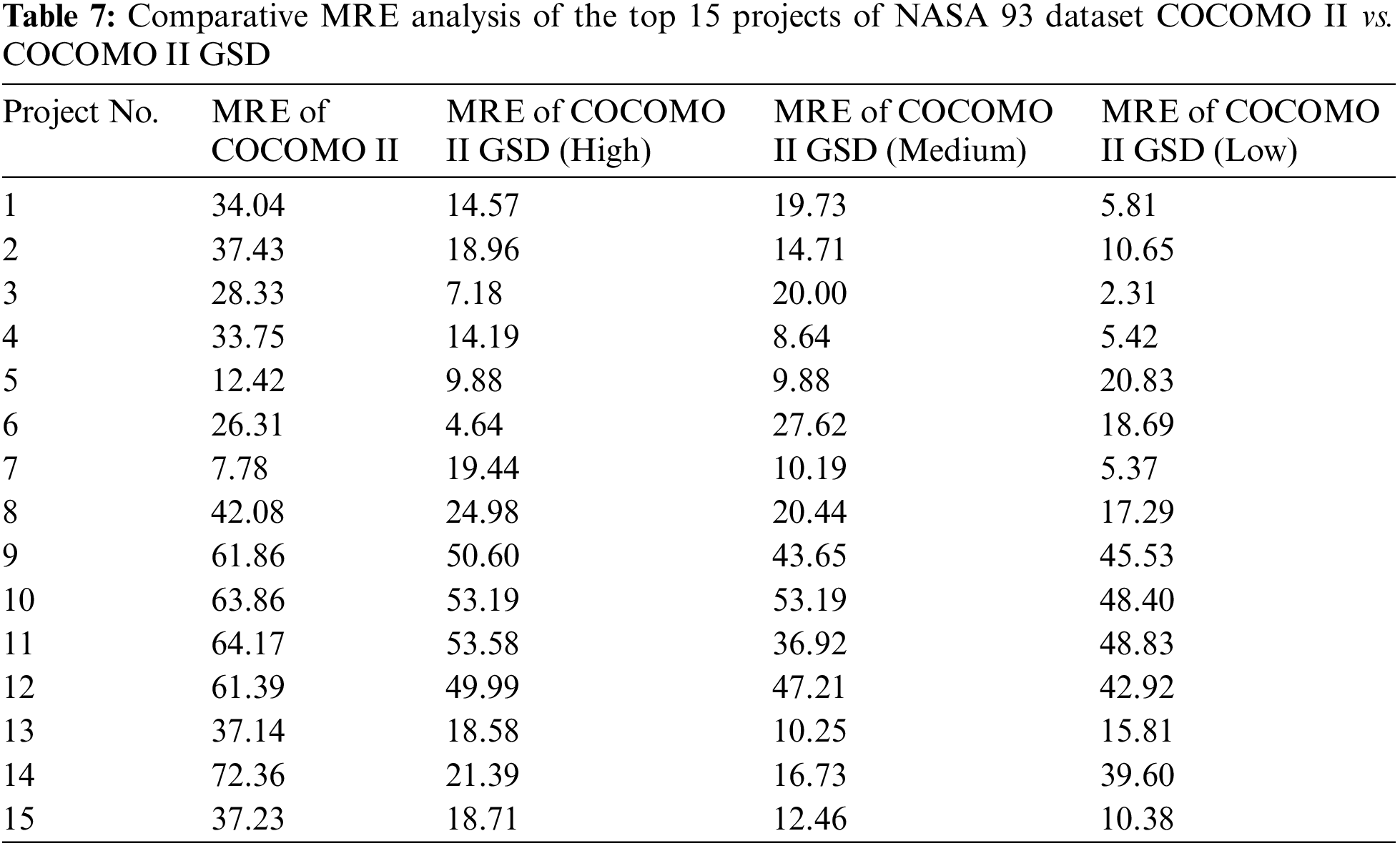
The performance evaluation showed that the COCOMO II GSD model is more effective than the standard COCOMO II for estimating software development costs in GSD settings. The improvement was quantified using the MRE and MMRE metrics. The research study in Tables 7 and 8 illustrated the MRE and MMRE for the top 15 projects from the NASA 93 dataset; the result shows that COCOMO II GSD provided more accurate cost predictions, demonstrating its practical applicability in the industry.

4.4.2 Impact of Hidden Neurons on Proposed Model

The research presents the results regarding the optimization of the neural network’s architecture for cost estimation. Experimentation with different numbers of hidden neurons within the proposed model reveals that a configuration with 10 hidden neurons provides optimal performance for the high GSD-based NASA 93 data category, as evidenced by the lowest MSE values shown in Fig. 2a. This specific architecture balances pattern recognition and the avoidance of overfitting, enhancing the model’s ability to generalize to new, unseen data. The model reaches convergence after 100 iterations, indicating stability in the learning process.

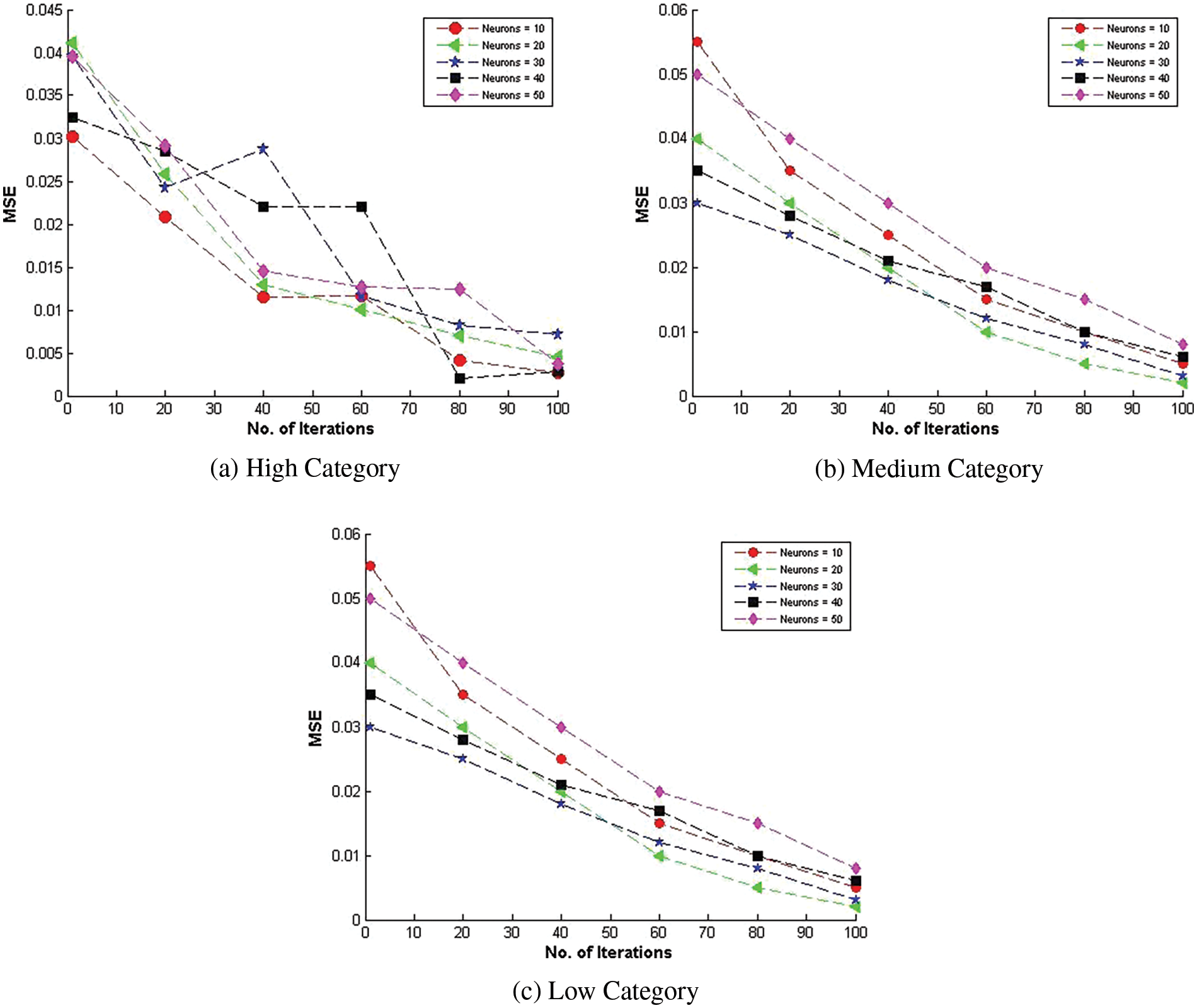
Figure 2: Optimal neural network configurations for COCOMO II-NN-GSD on NASA 93 dataset

The results show that the neural network’s efficacy depends on the correct configuration of hidden neurons customized to different complexity levels within the GSD-based NASA 93 dataset. The optimal number of hidden neurons for the medium category is 20, leading to improved model performance and convergence after 80 iterations, as shown in Fig. 2b. The same neuron count also applies to the low category, achieving improved performance with convergence at 80 iterations, as depicted in Fig. 2c. The research demonstrates that more hidden neurons can cause the model to overfit. It may perform exceptionally well on training data due to its capacity to learn detailed patterns, but it performs poorly on new, unseen data due to a lack of generalizability.

4.4.3 Convergence Analysis

The research provides clear evidence of the optimization of learning rates for a neural network model applied to the GSD-based NASA 93 dataset. The empirical results presented in Fig. 3a indicate that setting the learning rate to 0.002 yields the most favorable performance for high-complexity projects within the GSD context, with the model attaining convergence at 80 iterations. Further insights from Fig. 3b reveal that a learning rate of 0.004 is optimal for medium-complexity GSD projects, leading to improved model performance after 90 iterations. A learning rate of 0.005 is deemed most effective for high-complexity projects, as shown in Fig. 3c, with the model converging on the lowest MSE after 95 iterations.

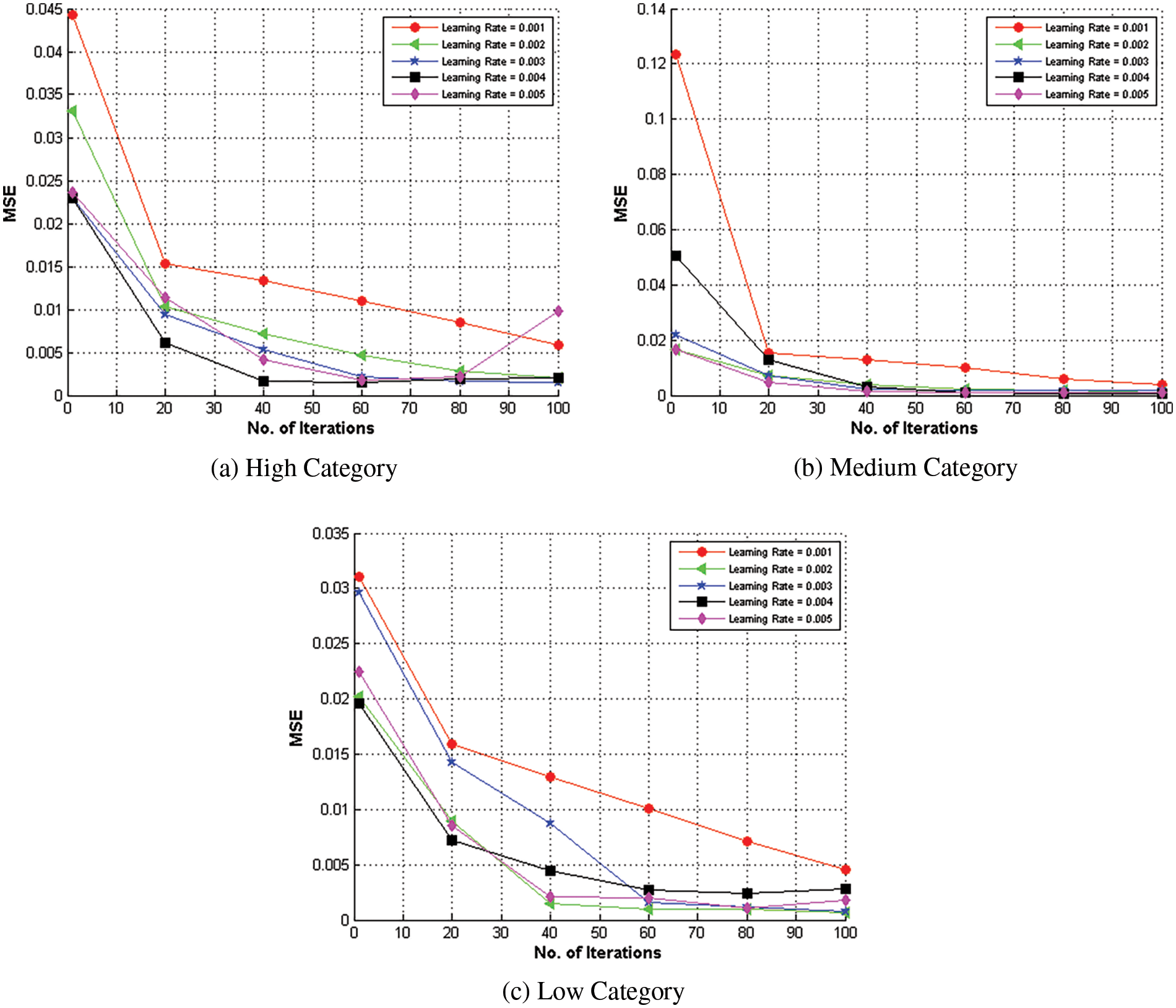
Figure 3: Convergence analysis of COCOMO II-NN-GSD on NASA 93 dataset

The research determines that careful tuning of the learning rate is essential for enhancing the model’s accuracy, with different rates yielding the best results for projects of varying complexity levels. Additionally, using the cross-entropy loss function for optimization has been validated through these experiments, demonstrating its efficacy in refining the proposed objective function for cost estimation in GSD. The findings are reported with a focus on precision, ensuring a clear understanding of the model’s performance under different learning rate configurations.

4.4.4 Evaluating the Impact of Learning Rate on the Proposed Model

The research performed experiments based on three categories of data related to the GSD-based NASA 93 dataset. This research selects a neural network model with one fully connected hidden layer containing three hidden units each and ReLU activation, with a batch size of 88. The research compared results with state-of-the-art [62–64].

Fig. 4a shows that validating MSE is less than the training MSE and is optimized at 96 iterations with a learning rate of 0.002 in high-category GSD-based NASA 93 data. From Fig. 4b, it is evident that MSE in training data is decreased at 100 iterations. The testing MSE is optimized at 57 iterations when the learning rate is set to 0.004 in the medium category GSD-based NASA 93 dataset.

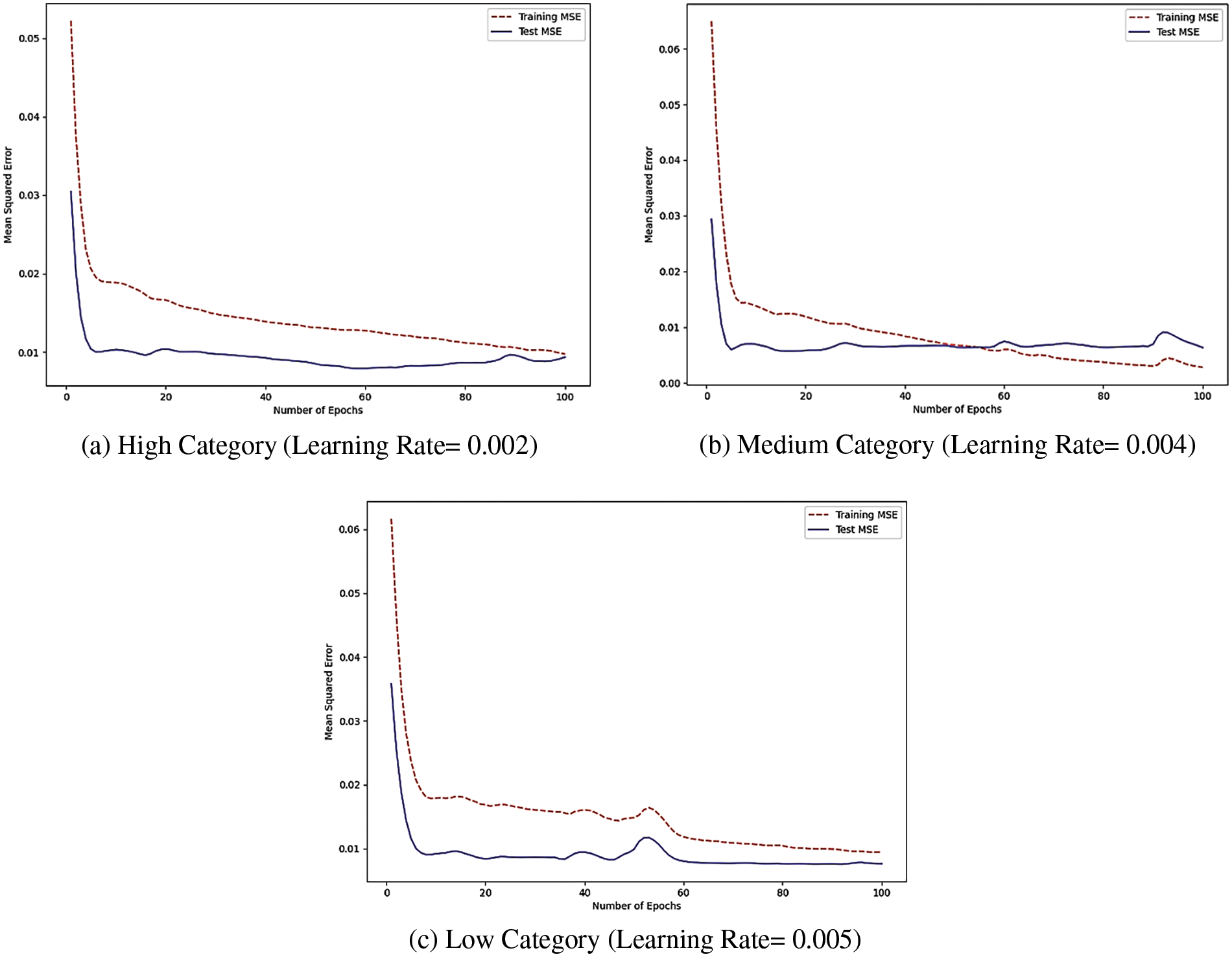
Figure 4: Comparative MSE trends across various learning rates for the GSD-based NASA 93 dataset

From Fig. 4c, it is evident that MSE in training data is optimized at 94 iterations, and testing data is optimized at 58 iterations when this research set the learning rate to 0.005 in low category GSD-based NASA 93 dataset.

4.4.5 Evaluation Using State-of-the-Art

The research compared the proposed COCOMO II-NN-GSD hybrid approach with state-of-art approaches such as Linear Regression [64], K-Nearest Neighborhood Regression [63] and Support Vector Regression [62]. All of these are recognized benchmarks in software cost estimation. Their selection was based on their representativeness of different estimation methodologies, from linear to non-linear techniques. These models contrast with our proposed COCOMO II-NN-GSD hybrid model, which integrates traditional COCOMO II aspects with the advanced capabilities of Artificial Neural Networks. Our approach specifically addresses the unique challenges of GSD, which these traditional models might not fully capture. The comparison aimed to demonstrate our hybrid model’s enhanced predictive accuracy and adaptability in the context of GSD cost estimation.

Proposed Model vs. State-of-the-Art Models: MSE Comparison on High GSD NASA 93 Dataset

Table 9 compares results obtained using various state-of-the-art and proposed models. This research observed that COCOMO II-NN-GSD hybrid approach performed well compared to state-of-the-art MSE for training and testing data for high category of GSD-based NASA 93 dataset.

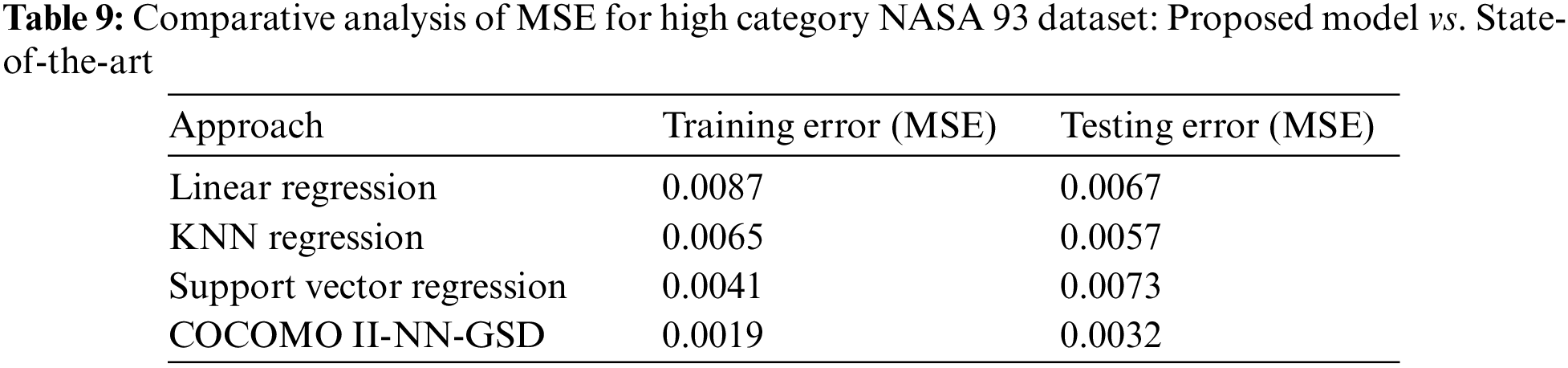
The research study determined the predicted project costs in terms of person-months and assessed these predictions using the MSE metric, comparing them with actual costs. It was observed that the COCOMO II-NN-GSD hybrid model yielded superior results in comparison to other state-of-the-art models.

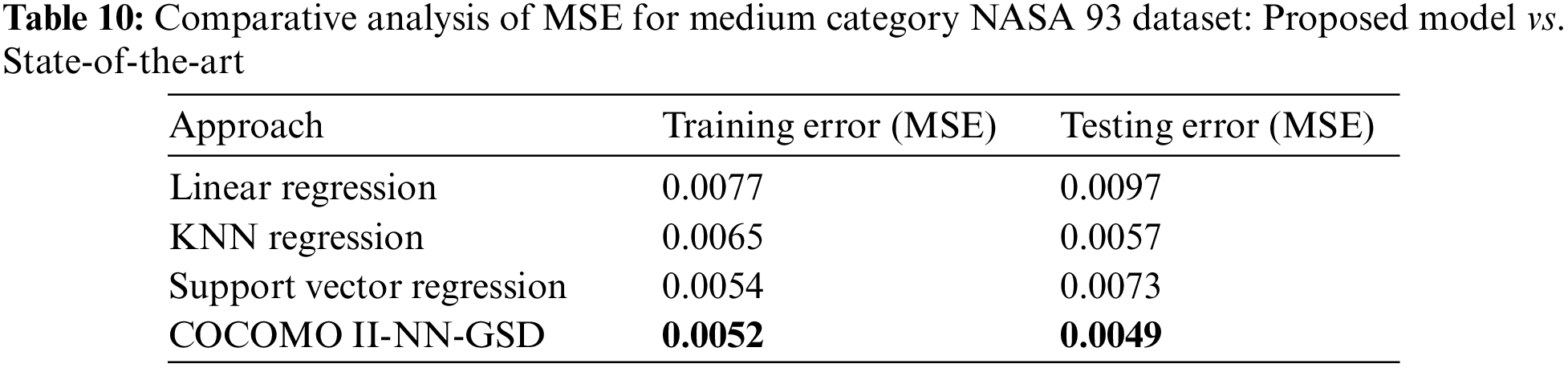
Proposed Model vs. State-of-the-Art Models: MSE Comparison on Medium GSD NASA 93 Dataset

Table 10 presents a comparative analysis demonstrating the superior performance of the COCOMO II-NN-GSD hybrid approach over the state-of-the-art in estimating software project costs. The model’s effectiveness is quantified using MSE metrics for training and testing datasets within the medium category of the GSD-based NASA 93 dataset. The predicted costs, expressed in person-months, were closely aligned with actual costs, confirming the hybrid model’s enhanced accuracy in cost estimation compared to the evaluated state-of-the-art.

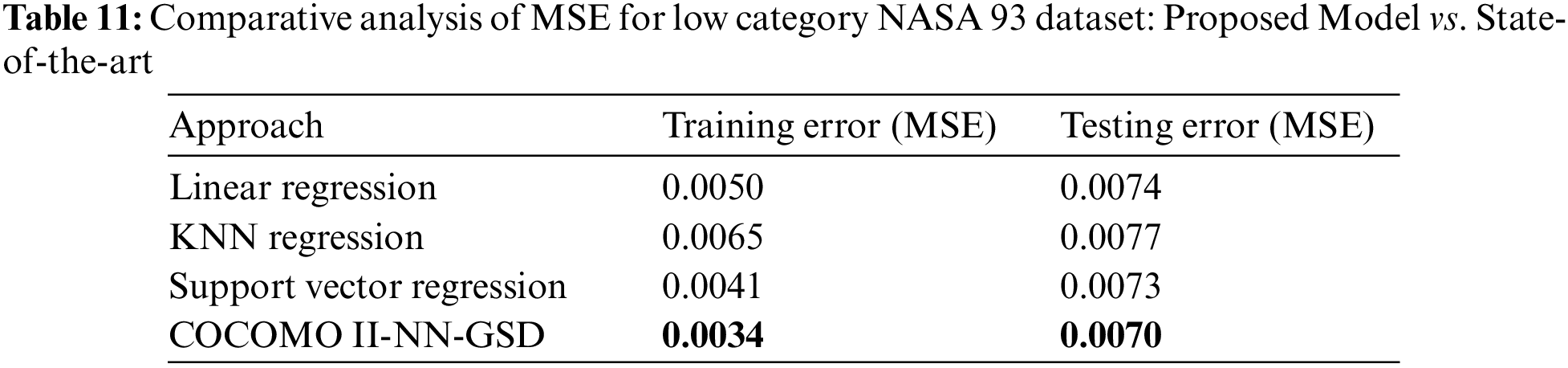
Proposed Model vs. State-of-the-Art Models: MSE Comparison on Low GSD NASA 93 Dataset

The results displayed in Table 11 indicate that the COCOMO II-NN-GSD hybrid model exhibits greater accuracy in cost estimation for projects in the low GSD category of the NASA 93 dataset, surpassing state-of-the-art. The model’s proficiency was assessed by measuring the MSE for training and testing data, where lower MSE values suggest a closer estimation to actual costs. The COCOMO II-NN-GSD model provided estimated costs, denominated in person-months, with higher precision and a stronger correlation to the actual project costs, emphasizing the model’s capability for precise cost forecasting in software development.

5  Conclusion

GSD has become a widely applied operational model for developing software systems; it can increase profits and decrease time-to-market. However, many challenges are associated with software development in a globally distributed fashion. One of the key challenges is software cost estimation in the GSD context. This study proposed a hybrid model that estimated the software cost based on ANN. The proposed COCOMO II-NN-GSD model provided a more accurate estimation than other state-of-the-art such as linear regression, KNN, and SVR.

Moreover, it is noted that the comparison between actual and estimated effort has been made to the NASA 93 dataset along with 26 GSD-based cost drivers. Thus, the MSE comparison is performed in a dataset only to evaluate this hybrid approach. The findings of this study show that the proposed model offers more accurate cost estimates than other state-of-the-art models, thus affirming its potential application in enhancing the cost estimation process in the GSD context.

One of the key challenges in software cost estimation is generalizing the results to other datasets. This means ensuring the trained hybrid models can accurately predict new, unseen data not encountered during training. Generalization is crucial because it allows the model to be applied to real-world scenarios beyond the training dataset. Future research will apply the proposed model to other datasets from different software industry domains. Similarly, the study will use other deep-learning techniques for software cost estimation.

Acknowledgement: We would like to take this opportunity to express our gratitude to all those who made a contribution to the completion of this article.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design: Mehmood Ahmed, Noraini Ibrahim, Wasif Nisar, Adeel Ahmad; Analysis and interoperation of results: Mehmood Ahmed, Noraini Ibrahim, Wasif Nisar, Adeel Ahmad, Muhammad Junaid; Draft manuscript preparation: Mehmood Ahmed, Noraini Ibrahim, Wasif Nisar, Adeel Ahmad, Emmanuel Soriano Flores, Divya Anand. All authors reviewed and approved the final version of the manuscript.

Availability of Data and Materials: The data and materials used to support the finding of this study are available from the corresponding authors upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. McCarthy, P. O’Raghallaigh, C. Fitzgerald and F. Adam, “Towards a framework for shared understanding and shared commitment in agile distributed ISD project teams,” in Proc. of the 27th European Conf. on Information Systems (ECIS), Stockholm & Uppsala, Sweden, pp. 1–15, 2019. [Google Scholar]

2. E.Ó. Conchúir, P. J. Ågerfalk, H. H. Olsson and B. Fitzgerald, “Global software development: Where are the benefits?” Communications of the ACM, vol. 52, no. 8, pp. 127–131, 2009. [Google Scholar]

3. S. Kumari and S. Pushkar, “Cuckoo search based hybrid models for improving the accuracy of software effort estimation,” Microsystem Technologies, vol. 24, no. 12, pp. 4767–4774, 2018. [Google Scholar]

4. S. Brad and E. Brad, “Enhancing SWOT analysis with TRIZ-based tools to integrate systematic innovation in early task design,” Procedia Engineering, vol. 131, pp. 616–625, 2015. [Google Scholar]

5. I. Keshta, “Software cost estimation approaches: A survey,” Journal of Software Engineering and Applications, vol. 10, pp. 824–842, 2017. [Google Scholar]

6. J. D. Herbsleb, “Global software engineering: The future of socio-technical coordination,” in Proc. of the Future of Software Engineering, Minneapolis, MN, USA, pp. 188–198, 2007. [Google Scholar]

7. A. A. Khan, J. Keung, M. Niazi, S. Hussain and M. Shameem, “GSEPIM: A roadmap for software process assessment and improvement in the domain of global software development,” Journal of Software: Evolution and Process, vol. 31, no. 1, pp. e1988, 2019. [Google Scholar]

8. M. El Bajta, A. Idri, J. N. Ros, J. L. Fernández-Alemán, J. M. Carrillo de Gea et al., “Software project management approaches for global software development: A systematic mapping study,” Tsinghua Science and Technology, vol. 23, no. 6, pp. 690–714, 2018. [Google Scholar]

9. K. Müller, C. Koch, D. Riehle and M. Stops, “Challenges of working from home in software development during COVID-19 lockdowns,” ACM Transactions on Software Engineering and Methodology, vol. 32, no. 1, pp. 1–41, 2023. [Google Scholar]

10. S. H. Ji, J. Ahn, H. S. Lee and K. Han, “Cost estimation model using modified parameters for construction projects,” Advances in Civil Engineering, vol. 2019, pp. 10, 2019. [Google Scholar]

11. M. Azzeh, “Software cost estimation based on use case points for global software development,” in Proc. of 5th Int. Conf. on Computer Science and Information Technology, Amman, Jordan, pp. 214–218, 2013. [Google Scholar]

12. J. A. Khan, S. U. R. Khan, J. Iqbal and I. U. Rehman, “Empirical investigation about the factors affecting the cost estimation in global software development context,” IEEE Access, vol. 9, pp. 22274–22294, 2021. [Google Scholar]

13. S. M. A. Suliman and G. Kadoda, “Factors that influence software project cost and schedule estimation,” in 2017 Sudan Conf. on Computer Science and Information Technology (SCCSIT), Ennhound, Sudan, pp. 1–9, 2017. [Google Scholar]

14. A. M. Majanoja, L. Linko and V. Leppänen, “Developing offshore outsourcing practices in a global selective outsourcing environment–the IT supplier’s viewpoint,” International Journal of Information Systems and Project Management, vol. 5, no. 1, pp. 27–43, 2017. [Google Scholar]

15. M. El Bajta, “Analogy-based software development effort estimation in global software development,” in Proc. 2015 IEEE 10th Int. Conf. on Global Software Engineering Workshops, Ciudad Real, Spain, pp. 51–54, 2015. [Google Scholar]

16. S. Betz and J. Mäkiö, “Amplification of the COCOMO II regarding offshore software projects,” in Offshoring of Software Development: Methods and Tools for Risk Management, Outshore, ICGSE Workshop 2007, Universitätsverlag Karlsruhe, pp. 33–46, 2007. [Google Scholar]

17. M. R. Chirra and H. Reza, “A survey on software cost estimation techniques,” Journal of Software Engineering and Applications, vol. 12, no. 6, pp. 226, 2019. [Google Scholar]

18. S. Ramacharan and K. V. Gopala Rao, “Scheduling based cost estimation model: An effective empirical approach for GSD project,” in 2016 Thirteenth Int. Conf. on Wireless and Optical Communications Networks (WOCN), Hyderabad, India, pp. 1–5, 2016. [Google Scholar]

19. R. Madachy, “Distributed global development parametric cost modeling,” in Proc. of Int. Conf. on Software Process (ICSP 2007), Minneapolis, MN, USA, 2007. [Google Scholar]

20. P. Keil, D. J. Paulish and R. S. Sangwan, “Cost estimation for global software development,” in Proc. of the 2006 Int. Workshop on Economics Driven Software Engineering Research, New York NY, USA, pp. 7–10, 2006. [Google Scholar]

21. M. Humayun and C. Gang, “Estimating effort in global software development projects using machine learning techniques,” International Journal of Information and Education Technology, vol. 2, no. 3, pp. 208, 2012. [Google Scholar]

22. R. S. Pressman, “Software engineering: A practitioner’s approach. Palgrave Macmillan,” 2005. [Online]. Available: https://books.google.com.my/books?id=i8NmnAEACAAJ (accessed on 15/08/2023). [Google Scholar]

23. E. E. Odzaly, D. Greer and P. Sage, “Software risk management barriers: An empirical study,” in Proc. of 3rd Int. Symp. on Empirical Software Engineering and Measurement, Florida, Lake Buena Vista, pp. 418–421, 2009. [Google Scholar]

24. C. Ebert and P. de Neve, “Surviving global software development,” IEEE Software, vol. 18, no. 2, pp. 62–69, 2001. [Google Scholar]

25. H. Zhang, B. Kitchenham and D. Pfahl, “Reflections on 10 years of software process simulation modeling: A systematic review,” in Proc. of the Int. Conf. on Software Process, ICSP 2008, Leipzig, Germany, pp. 345–356, 2008. [Google Scholar]

26. V. Vig and A. Kaur, “Test effort estimation and prediction of traditional and rapid release models using machine learning algorithms,” Journal of Intelligent & Fuzzy Systems, vol. 35, no. 2, pp. 1657–1669, 2018. [Google Scholar]

27. M. Ahmed, A. A. Siddiqui, S. Khan and M. Junaid, “Software cost estimation in global software development business: A review of models and cost drivers for economical business,” International Journal of Business and Economic Affair, vol. 6, no. 3, pp. 118–129, 2021. [Google Scholar]

28. P. Kumar and H. S. Behera, “Estimating software effort using neural network: An experimental investigation,” in Proc. of 2020 Computational Intelligence in Pattern Recognition: CIPR 2020, Singapore, Springer, pp. 165–180, 2020. [Google Scholar]

29. M. Azzeh, “Software cost estimation based on use case points for global software development,” in Proc. of 2013 5th Int. Conf. on Computer Science and Information Technology, Amman, Jordan, pp. 214–218, 2013. [Google Scholar]

30. V. Orujlu, “Implementation of ANN in software effort estimation: Boundary value effort forecast: A novel artificial neural networks model to improve the accuracy of effort estimation in software development projects,” Ph.D. dissertation, NOVA Information Management School Instituto Superior de Estatística e Gestão de Informação Universidade Nova de Lisboa, University in Lisbon, Portugal, 2022. [Google Scholar]

31. S. M. A. Suliman and G. Kadoda, “Factors that influence software project cost and schedule estimation,” in Proc. of 2017 Sudan Conf. on Computer Science and Information Technology (SCCSIT), Elnuhood, Sudan, pp. 1–9, 2017. [Google Scholar]

32. J. Koskenkylä, “Cost estimation in global software development–review of estimation techniques,” M.S. dissertation, Aalto University School of Economics, Espoo, Finland, 2012. [Google Scholar]

33. K. Suresh and R. Dillibabu, “A novel fuzzy mechanism for risk assessment in software projects,” Soft Computing, vol. 24, pp. 1683–1705, 2020. [Google Scholar]

34. E. M. Hall, Managing risk: Methods for software systems development. Pearson Education, 1998. [Online]. Available: https://www.amazon.com/Managing-Risk-Methods-SoftwareDevelopment/dp/0201255928 (accessed on 15/09/2023). [Google Scholar]

35. R. J. Madachy, “Heuristic risk assessment using cost factors,” IEEE Software, vol. 14, no. 3, pp. 51–59, 1997. [Google Scholar]

36. A. Iftikhar, S. M. Ali, M. Alam, S. Musa and M. M. Su’ud, “Analysis of risk factors in global software development: A cross-continental study using modified firefly algorithm,” Computational Intelligence and Neuroscience, vol. 2022, pp. 1–13, 2022. [Google Scholar]

37. S. Goyal and A. Parashar, “Machine learning application to improve COCOMO model using neural networks,” International Journal of Information Technology and Computer Science (IJITCS), vol. 3, pp. 35–51, 2018. [Google Scholar]

38. Y. Mahmood, N. Kama, A. Azmi, A. S. Khan and M. Ali, “Software effort estimation accuracy prediction of machine learning techniques: A systematic performance evaluation,” Software: Practice and Experience, vol. 52, no. 1, pp. 39–65, 2022. [Google Scholar]

39. I. Kaur, G. S. Narula, R. Wason, V. Jain and A. Baliyan, “Neuro fuzzy-COCOMO II model for software cost estimation,” International Journal of Information Technology, vol. 10, pp. 181–187, 2018. [Google Scholar]

40. T. Sharma, “A comparative study of COCOMO II and Putnam models of software cost estimation,” International Journal of Scientific & Engineering Research, vol. 2, no. 11, pp. 1–3, 2011. [Google Scholar]

41. P. S. Kumar, H. S. Behera, A. Kumari, J. Nayak and B. Naik, “Advancement from neural networks to deep learning in software effort estimation: Perspective of two decades,” Computer Science Review, vol. 38, pp. 100288, 2020. [Google Scholar]

42. Y. Deng, Z. Zeng, K. Jha and D. Huang, “Problem-based cybersecurity lab with knowledge graph as guidance,” Journal of Artificial Intelligence and Technology, vol. 2, no. 2, pp. 55–61, 2021. [Google Scholar]

43. A. Singh, A. Kumar and S. Namasudra, “DNACDS: Cloud IoE big data security and accessing scheme based on DNA cryptography,” Frontiers of Computer Science, vol. 18, no. 1, pp. 181801, 2024. [Google Scholar]

44. M. Sahu, N. Padhy, S. S. Gantayat and A. K. Sahu, “Local binary pattern-based reversible data hiding,” CAAI Transactions on Intelligence Technology, vol. 7, no. 4, pp. 695–709, 2022. [Google Scholar]

45. I. H. Hsiao and C. Y. Chung, “AI-infused semantic model to enrich and expand programming question generation,” Journal of Artificial Intelligence and Technology, vol. 2, no. 2, pp. 47–54, 2022. [Google Scholar]

46. R. Khamkar, P. Das and S. Namasudra, “SCEOMOO: A novel subspace clustering approach using evolutionary algorithm, off-spring generation and multi-objective optimization,” Applied Soft Computing, vol. 139, pp. 110185, 2023. [Google Scholar]

47. A. Ali and C. Gravino, “Improving software effort estimation using bio-inspired algorithms to select relevant features: An empirical study,” Science of Computer Programming, vol. 205, pp. 102621, 2021. [Google Scholar]

48. I. Javid, A. K. Zager Alsaedi, R. Ghazali, Y. M. Mohmad Hassim and M. Zulqarnain, “Optimally organized GRU-Deep learning model with chi2 feature selection for heart disease prediction,” Journal of Intelligent & Fuzzy Systems, vol. 42, no. 4, pp. 4083–4094, 2022. [Google Scholar]

49. R. R. Sinha and R. K. Gora, “Software effort estimation using machine learning techniques,” in Advances in Information Communication Technology and Computing: Proc. of AICTC 2019, Government Engineering College, Bikaner, Rajasthan, India, pp. 65–79, 2021. [Google Scholar]

50. L. Zhang, J. Wang, W. Wang, Z. Jin, Y. Su et al., “Smart contract vulnerability detection combined with multi-objective detection,” Computer Networks, vol. 217, pp. 1–12, 2022. [Google Scholar]

51. M. K. Hooshmand and D. Hosahalli, “Network anomaly detection using deep learning techniques,” CAAI Transactions on Intelligence Technology, vol. 7, no. 2, pp. 228–243, 2022. [Google Scholar]

52. J. A. Khan, S. Ur Rehman Khan, T. A. Khan and I. Ur Rehman Khan, “An amplified COCOMO-II based cost estimation model in global software development context,” IEEE Access, vol. 9, pp. 88602–88620, 2021. [Google Scholar]

53. P. Rijwani and S. Jain, “Enhanced software effort estimation using multi layered feed forward artificial neural network technique,” Procedia Computer Science, vol. 89, pp. 307–312, 2016. [Google Scholar]

54. M. S. Khan, R. Irfan, J. Iqbal, S. Hussain, S. S. Ullah et al., “Optimizing deep learning model for software cost estimation using hybrid meta-heuristic algorithmic approach,” Computational Intelligence and Neuroscience, vol. 2022, pp. 1–20, 2022. [Google Scholar]

55. M. Ahmed, N. Ibrahim, W. Nisar and A. Ahmad, “Systematic literature review on global software development based software cost estimation models and cost drivers,” The Indonesian Journal of Electrical Engineering and Computer Science, vol. 32, no. 3, pp. 1485–1494, 2023. [Google Scholar]

56. M. R. Asif, T. S. Bording, A. S. Barfod, D. J. Grombacher, P. K. Maurya et al., “Effect of data pre-processing on the performance of neural networks for 1-D transient electromagnetic forward modeling,” IEEE Access, vol. 9, pp. 34635–34646, 2021. [Google Scholar]

57. C. Fan, M. Chen, X. Wang, J. Wang and B. Huang, “A review on data preprocessing techniques toward efficient and reliable knowledge discovery from building operational data,” Frontiers in Energy Research, vol. 9, pp. 652801, 2021. [Google Scholar]

58. K. Maharana, S. Mondal and B. Nemade, “A review: Data pre-processing and data augmentation techniques,” Global Transitions Proceedings, vol. 3, no. 1, pp. 91–99, 2022. [Google Scholar]

59. I. Nino-Adan, E. Portillo, I. Landa-Torres and D. Manjarres, “Normalization influence on ANN-based models performance: A new proposal for Features’ contribution analysis,” IEEE Access, vol. 9, pp. 125462–125477, 2021. [Google Scholar]

60. A. Kaushik and N. Singal, “A hybrid model of wavelet neural network and metaheuristic algorithm for software development effort estimation,” International Journal of Information Technology, vol. 14, no. 3, pp. 1689–1698, 2022. [Google Scholar]

61. S. Namasudra, S. Nath and A. Majumder, “Profile based access control model in cloud computing environment,” in Proc. of 2014 Int. Conf. on Green Computing Communication and Electrical Engineering (ICGCCEE), Coimbatore, India, pp. 1–5, 2014. [Google Scholar]

62. K. Lee and K. T. Kwon, “Software cost estimation using svr based on immune algorithm,” in Proc. of 2009 10th ACIS Int. Conf. on Software Engineering, Artificial Intelligences, Networking and Parallel/Distributed Computing, Daegu, Korea, pp. 462–466, 2009. [Google Scholar]

63. M. Mailagaha Kumbure and P. Luukka, “A generalized fuzzy k-nearest neighbor regression model based on minkowski distance,” Granular Computing, vol. 7, no. 3, pp. 657–671, 2022. [Google Scholar]

64. A. Sharma and N. Chaudhary, “Linear regression model for agile software development effort estimation,” in Proc. of 2020 5th IEEE Int. Conf. on Recent Advances and Innovations in Engineering (ICRAIE), Jaipur, India, pp. 1–4, 2020. [Google Scholar]