Method for Detecting Industrial Defects in Intelligent Manufacturing Using Deep Learning

1  Introduction

With the rise of information technology and the Internet of Things (IoT), the era of Industry 4.0, led by intelligent manufacturing, is rapidly approaching. Global manufacturers are upgrading their production factories to embrace digitalization and intelligence [1]. Smart manufacturing also escalates the requirements for both the reliability and safety of production equipment. Rotating machinery is central to manufacturing operations, enduring continuous high loads for extended periods. This strain makes components like bearings and gearboxes susceptible to various failures, potentially causing performance instability and significant accidents.

Consequently, defect-detecting technology is gaining significance in Industry 4.0. It can identify whether manufacturing equipment deviates from its normal operating state, facilitating efficient risk management and preventing the economic loss caused by prolonged plant downtime. Smart factories can capture a considerable quantity of data through numerous sensors [2], such as vibration, temperature, pressure, and acoustics, representing the actual response of the manufacturing equipment to its working state. Utilizing these datasets enables the early identification of potential defects. Due to their demonstrated efficiency, vibration signal-based defect detection techniques have become the primary research focus in this area [3].

Researchers employed several signal processing techniques to sort out the valid fault information in the vibration signal. Dibaj et al. [4] used a parameter-optimized variational mode decomposition (VMD) to decompose signals. Han et al. [5] disintegrated the non-smooth gear signals into several intrinsic mode functions (IMF) by empirical mode decomposition (EMD). Saha et al. [6] used the Fast Fourier Transform (FFT) to convert the vibration data’s time waveform into a spectrum. Ding et al. [7] utilized the whale optimization technique to optimize the wavelet filter to identify the best frequency demodulation band for various defects. Nevertheless, these traditional methods are restricted to a few specific scenarios and excessively rely on the specialists’ technical expertise, which is inefficient in handling the copious amounts of data produced by the smart factory’s sensors.

We have devised a deep learning-based intelligent detection method to meet the Industry 4.0 era’s demand for diagnostic procedures with robust data processing capabilities. The method is designed for direct application to vibration signals within the operating environment of an intelligent factory, where it demonstrates excellent detecting performance and adaptability.

This study’s primary contributions are as follows: (1) We introduce the high-level feature learning block (HLFLB), which leverages residual learning and efficient channel attention (ECA), alongside the multi-scale feature learning block (MSFLB) that employs parallel dilated convolutions to comprehensively extract complex features from vibration signals, thereby enhancing feature extraction capabilities. (2) We implement a dynamic adaptive fusion block (DAFB) that dynamically adjusts the receptive field to integrate multi-level and multi-scale features within convolutional neural networks effectively. (3) Our proposed method undergoes rigorous validation across various datasets and is benchmarked against multiple methods for an extensive comparison. The experimental results demonstrate that our approach achieves superior diagnostic accuracy and stability.

We organize the paper as follows: Section 2 provides a literature review of detection methods based on deep learning. In Section 3, we present the composition blocks of the proposed method. Section 4 contains experimental cases and corresponding results. Furthermore, the last section ends with a conclusion.

2  Literature Review

The related works discussed in this section contain some application examples based on deep learning. Han et al. [8] explored the fusion of simulated annealing into a deep neural network (DNN) to detect chiller defects. Bhuiyan et al. [9] combined the deep belief network with the fundamental discrete wavelet transform for microgrid status monitoring. Mansouri et al. [10] presented an improved recurrent neural network (RNN) for detecting faults in wind energy conversion systems. Plakias et al. [11] created a soft-voting ensemble method of auto-encoders and its successful application to bearing and chemical process data.

More recently, convolutional neural network (CNNs) has seen increased usage in defect diagnosis. With a deep architecture, CNNs can capture representative features from high-dimensional vibration signals. Wang et al. [12] applied one-dimensional CNNs to vibration and acoustic signals from bearings for fault classification. Xie et al. [13] combined one-dimensional CNNs and a gated recurrent unit to detect anomalies in industrial control systems. Zhang et al. [14] added residual learning in the CNNs to lessen the gradient disappearance or explosion problem in deep convolutional networks and prevent degradation.

Given the intricate dynamic properties of industrial equipment and the multifaceted nature of defects, the data collected often encapsulates information across a range of time scales. Huang et al. [15] enhanced their network capability by incorporating a layer of convolutional kernels of varying sizes, enabling the amalgamation of information from disparate input scales. Shao et al. [16] fused three short-time gap feature learning structures based on multi-scale convolutions to learn the intricate features from the temporal signals of manufacturing plants.

The methodologies above significantly augment the learning capabilities of convolutional neural networks (CNNs); however, they introduce the challenge of discerning and leveraging the salient features conducive to classification while mitigating irrelevant or disruptive inputs. Shen et al. [17] incorporated a channel attention mechanism to selectively emphasize vectors extracted across diverse scales and channels, directing the network’s focus towards more pivotal features. Xu et al. [18] employed overlapping window operations to extract information at various granularity levels from the original signal, aiding the network in learning more valuable characteristics. Incorporating an adaptive scoring system, integrated through an attention mechanism, has further augmented the model’s generalization ability, ensuring robust performance across disparate datasets.

Motivated by the studies above, our research endeavors to explore a deep learning method for defect detection tasks, which aims to autonomously learn salient features indicative of potential defects, capable of demonstrating consistently high performance across diverse datasets.

3  Method

This section elucidates the architecture of the proposed defect detection method. Initially, a wide convolutional kernel with a size of 128 and a stride of 2 is applied in the first layer to diminish the noise within the signal. Next, we detail the high-level feature learning block (HLFLB), multi-scale feature learning block (MSFLB), and dynamic adaptive fusion block (DAFB).

3.1 High-Level Feature Learning Block

3.1.1 Residual Learning

Convolutional neural networks with complex layers have been developed to adequately extract feature information from the enormous amount of data that smart factories have collected. However, deeper convolutional models cause tricky problems in training. The gradient will progressively converge to 0 or show exponential inflation as the number of network layers rises, which is the problem of vanishing and exploding gradients. In addition, too much information loss causes the degradation of the network. He et al. [19] pioneered residual learning to alleviate these deficiencies.

3.1.2 Batch Normalization

The deep residual convolutional neural network contains a superposition of multiple layers. During model training, the input distribution of each layer alters based on the parameters of the preceding layer; consequently, the subsequent layers must adjust to the changed input distribution, a phenomenon known as internal covariate shift, making model training challenging and time-consuming. We employ Batch Normalization (BN) [20] to stabilize the distribution of input values in each layer, alleviate the influence of internal covariate shifts in deep residual network training, and accelerate model convergence.

3.1.3 Efficient Channel Attention

An attention mechanism is an instrumental tool that enables a neural network to allocate weights differentially across various segments of the input, thereby extracting more pertinent information. Its primary objective is to refine the network’s representational capacity by accentuating salient features while suppressing less relevant ones, facilitating more precise inferences without an excessive expenditure of computational resources. This section adds efficient channel attention (ECA) [21] to the residual network. We first compress the input feature map using the global average pooling (GAP) in the spatial dimension.

y=GAP(x)=1L∑i=1Lxi(1)

where L is the length of the feature. Then the channel weights ω are generated in Eq. (2) by one-dimensional convolution of size k, the kernel size k can be determined adaptively according to Eq. (3).

ω=σ(Convk1d(y))(2)

k=|log2⁡Cγ+bγ|odd(3)

where σ is the sigmoid function, |x|odd is the closest odd number, C represents channel dimensions, γ is 2 and b is 1.

Finally, the new feature map is created by element-wise multiplication with the original feature map.

3.1.4 The Construction of High-Level Feature Learning Block

Combining with residual learning, we propose the high-level feature learning block (HLFLB) in Fig. 1 to learn more features from the raw signal. Then, the attention module assigns various weights to the features obtained by the residual depth block to eliminate meaningless noise and enhance the discriminative defect characteristics. The process of HLFLB is as follows:

zl−1=δ(BN(zl−2wl−1+bl−1))(4)

zl=ECA(BN(zl−1wl+bl))(5)

zl=δ(zl+h(x))(6)

where w is weight, b is bias, δ is the relu activation function, h(x) refers to shortcut connection.

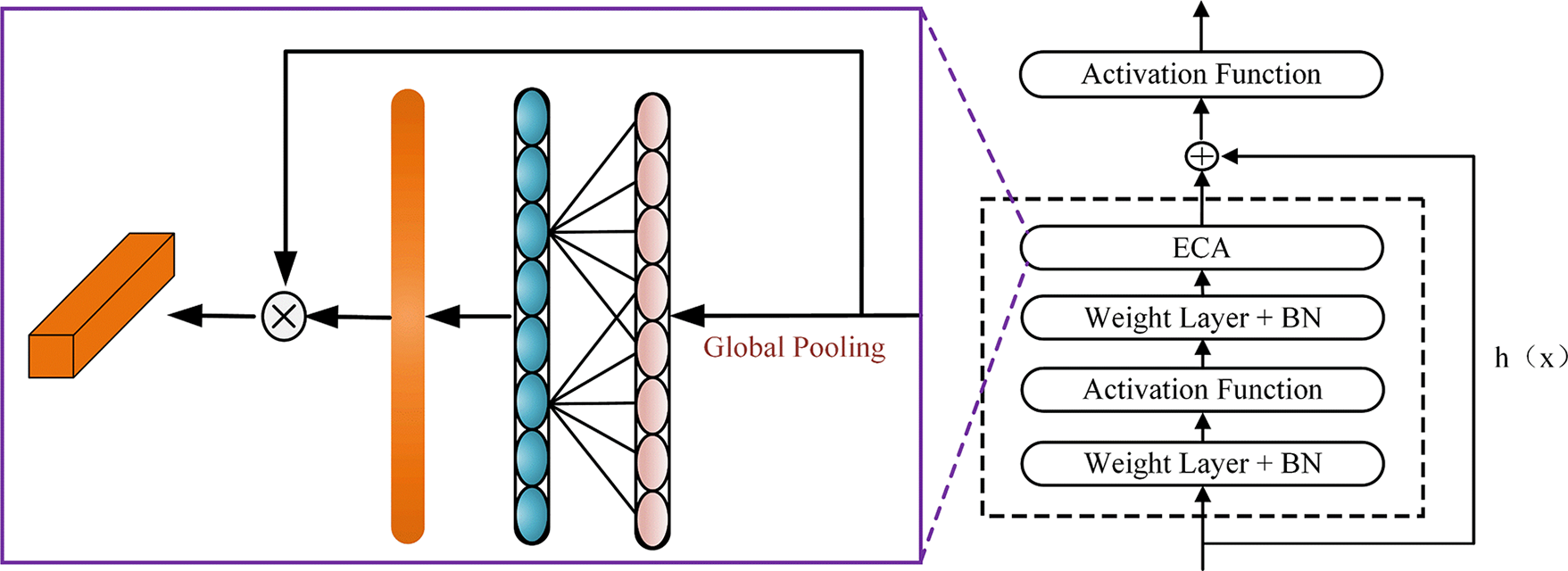
Figure 1: High-level feature learning block

3.2 Multi-Scale Feature Learning Block

3.2.1 Dilated Convolution

Dilated convolution [22] introduces a hyperparametric dilation rate that expands the neural network’s receptive field by inserting zero padding. Assuming the dilation rate is d, the equivalent convolution kernel k′ is:

k′=k+(k−1)(d−1)(7)

3.2.2 The Construction of Multi-Scale Feature Learning Block

Different types of defects typically yield unique spectral components within vibration signals. Moreover, fault severity disparities can significantly impact the amplitude. Equipment in the factory may undergo diverse operational states and encounter fluctuating load conditions throughout its operation. These factors collectively contribute to the emergence of distinct fault characteristic distributions across various scales. Gathering features across diverse scales can effectively unveil latent information within the signal, thereby improving the sensitivity and precision of defect diagnosis.

Hence, we incorporate the multi-scale feature learning block (MSFLB) [23] to capture the intricate different scale characteristics of the vibration signal. Within each MSFLB, as illustrated in Fig. 2, two parallel dilated convolutions with a kernel size of 3 are executed concurrently. Each set captures information at distinct scales, acquiring different levels of detail within the vibration signal. Subsequently, the feature maps obtained are concatenated and fed into the next sets. The block takes local residual learning to promote gradient flow throughout the training process. The first convolutional layer of the MSFLB employs 32 filters, while the second layer utilizes 64 filters.

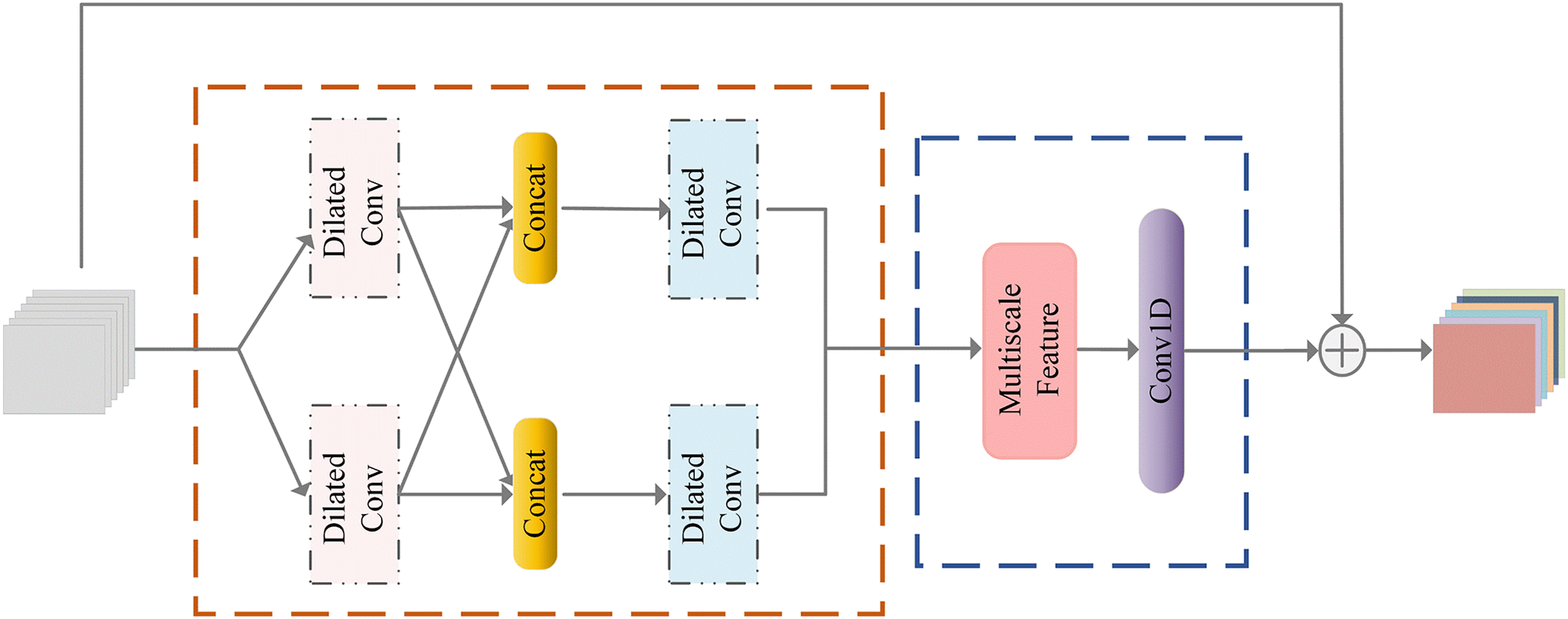
Figure 2: Multi-scale feature learning block

3.3 Dynamic Adaptive Fusion Block

Features at various levels encompass information with varying degrees of abstraction. Shallow parts primarily concentrate on signal details and capture local structural information, yet their capacity to gather global information is comparatively limited. In contrast, deep-level features comprise a plethora of abstract and complex data that excel in pinpointing defects, but they may sacrifice some spatial intricacies in the process. Strategically aggregating these hierarchical features empowers the network to capture broader and more intricate representations, enhancing its overall capabilities. This work uses a dynamic adaptive fusion block (DAFB) [24,25] to amalgamate features across various levels and scales while retaining their complementary characteristics, as shown in Fig. 3.

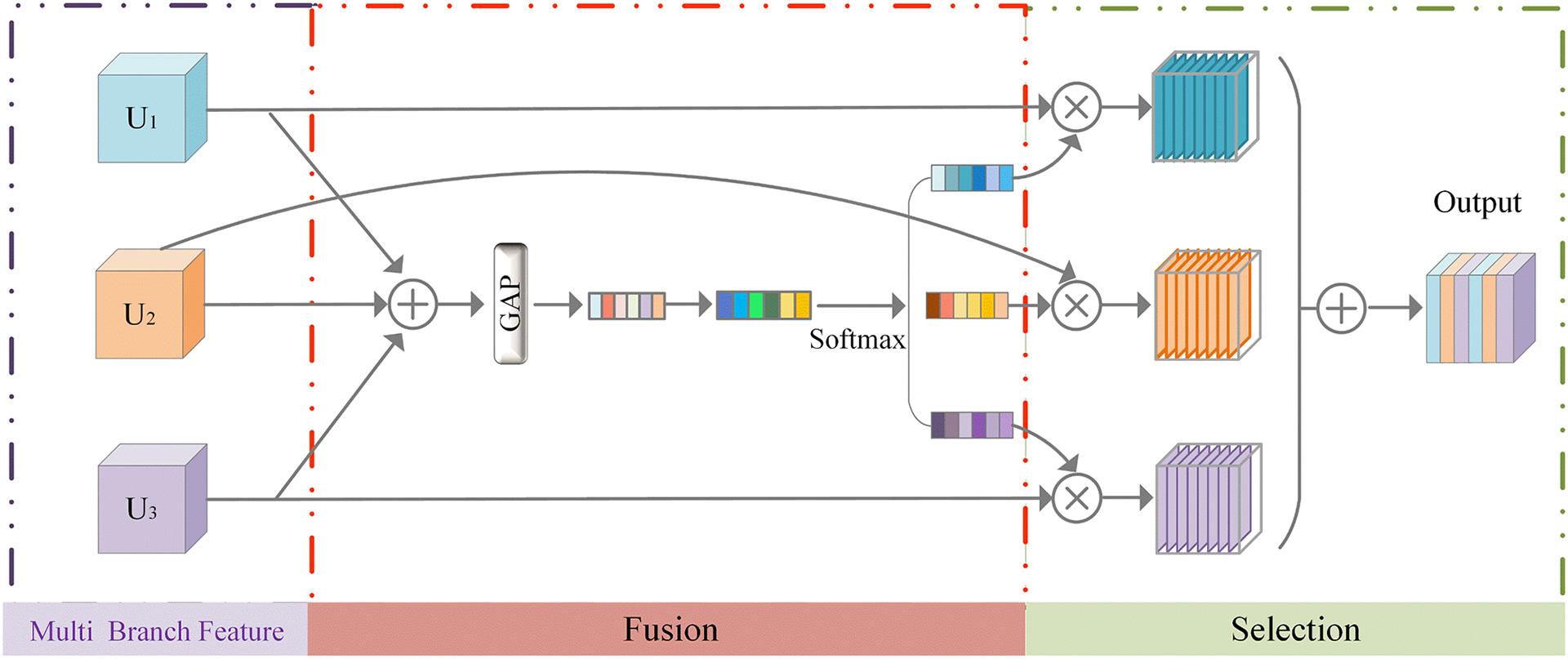
Figure 3: Dynamic adaptive fusion block

(1) Fusion

Following the extraction of rich and diverse features from signals utilizing various learning blocks, we fuse the copious features gathered from different branches via elementwise addition to produce a new feature map in Eq. (8).

U=U1+U2+U3(8)

Then extract aggregation feature descriptor from the new feature maps. For the channel descriptor, we compress the fused feature map Ualong the spatial dimension using global average pooling in Eq. (9) to obtain the global spatial information. After that, the compact feature Z is generated by a convolutional layer.

Sc=FGap(U)=11×L∑i=1LU(i,j)(9)

Z=Fconv(sc)=Relu(BN(Ws))(10)

where L is the length of the feature map.

(2) Selection

The primary objective of the selection process is to dynamically recalibrate feature maps at distinct levels by leveraging feature descriptors. Directing varying degrees of attention weights to these feature maps results in neurons with receptive fields of different sizes.

The weights of the three branches can be obtained adaptively by the cross-channel softmax.

a=eAczeAcz+eBcz+eCcz, b=eBczeAcz+eBcz+eCcz, c=eCczeAcz+eBcz+eCcz(11)

At last, dynamically recalibrated weights, and the original feature map are multiplied element-wise and summed to generate a calibrated output Y.

Yc=a⋅U1+b⋅U2+c⋅U3(12)

3.4 Classification

We smoothly extract rich and diverse features from signals using several different learning blocks. Then, the DAFB aggregates features at different levels. The fused feature maps enter the global average pooling (GAP) to be compressed into a one-dimensional vector. Since the manifestations of manufacturing equipment defects are diverse, softmax is suitable for the classification function in this defect multi-classification task, which maps the predicted probabilities of each category to [0,1].

p(zj)=softmax(zj)=ezj∑kezk(13)

where the j is the element of the vector z.

The proximity between the predicted and actual values can be measured using cross-entropy, pointing the network’s subsequent training in the proper direction.

H(p,q)=−∑xp(x)log⁡q(x)(14)

where p(x) is the probability distribution of the target, q(x) is the predicted distribution, and the base of the logarithm q(x)is e.

3.5 General Flow of the Method

The flow chart of the proposed method is depicted in Fig. 4, comprising three phases: data split, feature fusion, and diagnosis. The detailed steps are as follows:

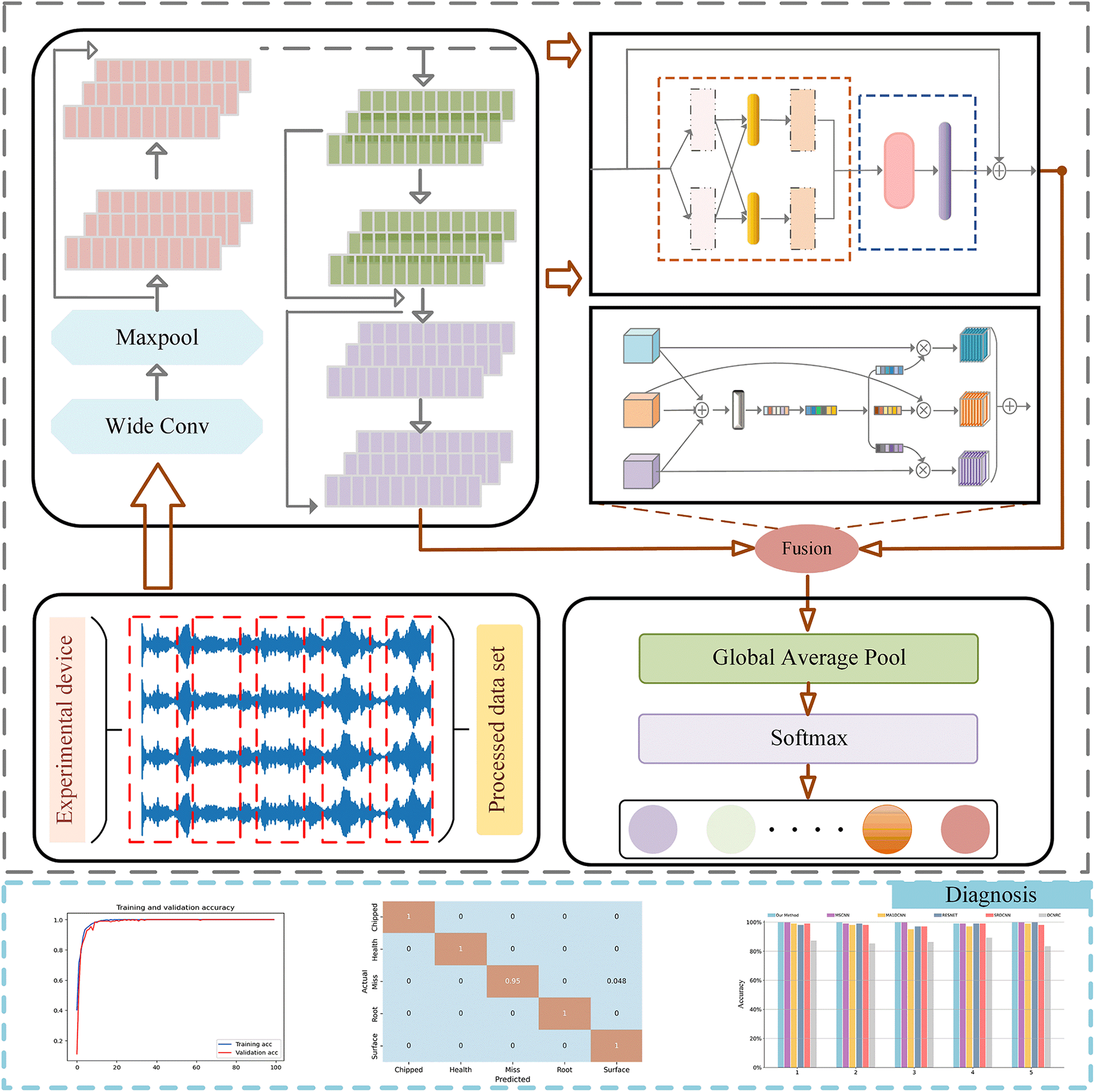
Figure 4: General flow of the proposed method

Data split: The gathered vibration signals are divided into equal lengths and labeled by one-hot codes. We split the data into the training, validation, and test sets in the ratio of 8/1/1, after which the z-score normalizes them in Eq. (15) to unify the feature attributes.

xnor=(x−μ)/s(15)

where μ indicates the mean value of x, s is the standard deviation of x.

Feature fusion: The depth feature map, designated as F1, is constructed sequentially by stacking three high-level feature learning blocks (HLFLBs) equipped with 64, 128, and 128 filters, respectively. The feature maps F2 and F3 are derived from a combination of the HLFLB and the multi-scale feature learning block (MSFLB). Subsequently, features extracted from multiple levels and scales are skillfully integrated using the dynamic adaptive fusion block (DAFB).

Diagnosis: Employ the softmax function to generate the predicted probabilities for each defect type, following applying global average pooling (GAP).

4  Experimental Verifications

In this section, we choose failure-prone manufacturing equipment components: gearboxes, and bearings to validate the method proposed in this paper.

4.1 Experimental Settings

The model performs on a PC with Windows 10 (64-bit), Intel Core i5-11400 CPU, and RTX3060 GPU. The framework used for the experiments is TensorFlow based on Python version 3.7. We employ Adam [26] as the optimizer with parameters β1 0.9 and β2 0.999. The learning rate is adjusted by Eq. (16), making it easier to approach the optimal solution and get better generalization performance.

lr′=lr∗βt/T(16)

where lr refers to the initial learning rate, β and denotes the decay factor.

4.2 Case Study 1

4.2.1 Data Description

In case study 1, we are working with pertains to gearbox data. The first dataset was collected under 20HZ-0V and 30HZ-2V. The test rig entails a motor, parallel gearbox, planetary gearbox, and brake [27]. It contains data for distinct defect categories: chipped, surface, miss, root, and healthy, with details in Table 1.

The second dataset comprises time-domain vibration signals from two-stage gearboxes with replaceable gears [28], and descriptions can be found in Table 2.

4.2.2 Results and Analysis

In this section, we examine the detection capability of the proposed network under gearbox data. We select a range of methods for comparative validation, including MSCNN [29], MA1DCNN [30], RESNET [31], SRDCNN [32], and DCNRC [33]. Fig. 5 presents the experimental results of these methods conducted over five trials on dataset A.

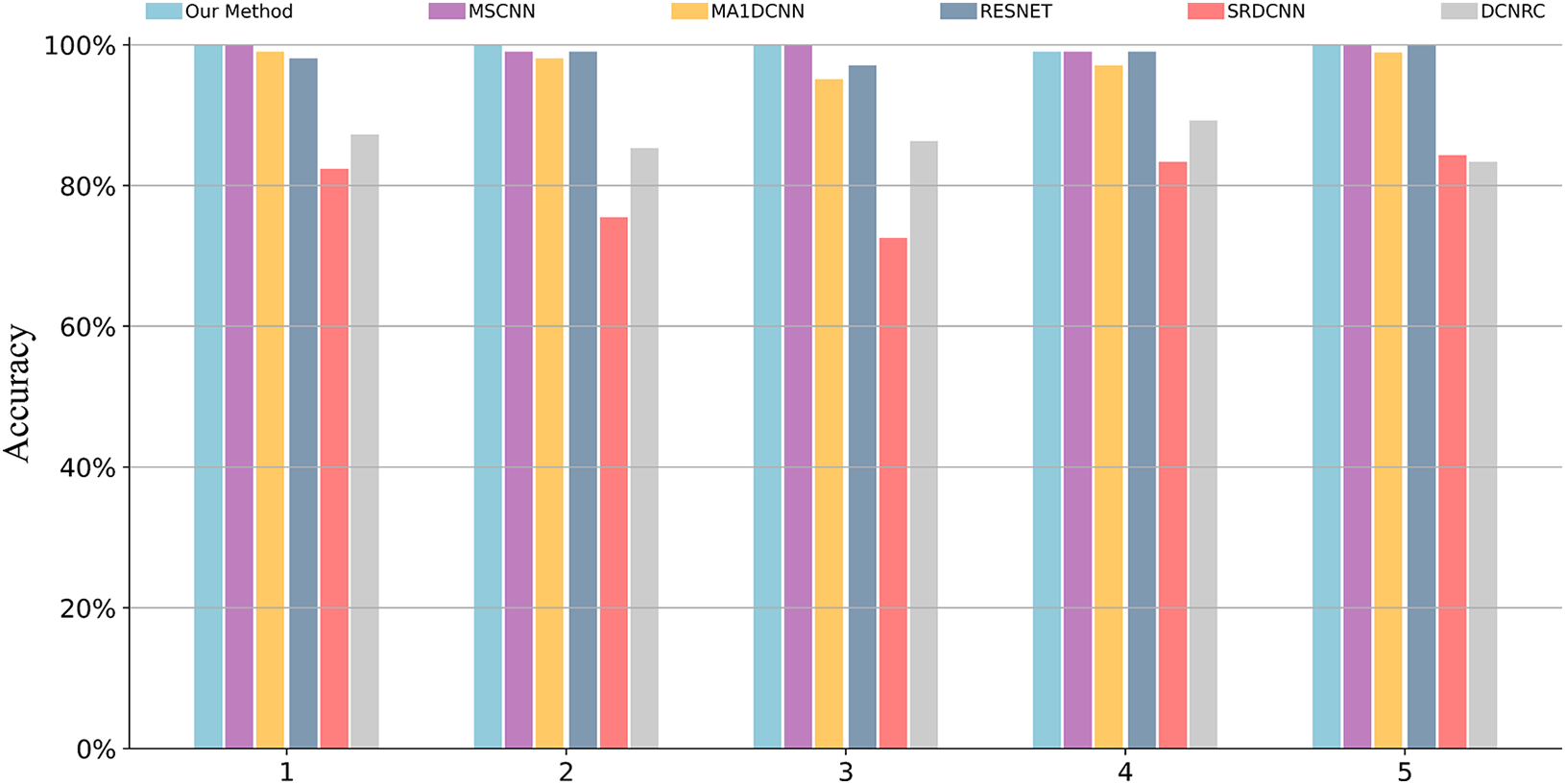
Figure 5: Results of five experimental trials on gearbox dataset 1

MSCNN utilizes multi-scale convolutions to capture information at various scales and attains a classification accuracy of nearly 100% on the gearbox dataset. In a comprehensive evaluation, MSCNN and the method presented in this study emerge as frontrunners in performance. MA1DCNN, which merges the channel attention, excitation attention, and joint attention module has achieved detection performance comparable to that of RESNET, positioning it solidly in the second tier of similar models. The recognition accuracy of DCNRC, with its diverse residual weights and dilation rates, consistently falls behind the performance of the above methods listed by a notable margin of more than 10%. SRDCNN, constructed by merging dilated convolutional layers and residual connections and incorporating the input gate structure of LSTM for information extraction, exhibits relatively insufficient detection capabilities.

We examine each tool’s impact on the proposed method’s detection capability. Fig. 6 presents the experimental outcomes after the exclusion of specific tools from dataset B. Subfigure (a) illustrates the curves derived from the training set, while subfigure (b) shows the corresponding results on the validation set. Experiments conducted on dataset B reveal that the network configured with all tools achieves the best accuracy, which indicates that incorporating rich, complementary features enhances the model’s generalization capabilities. Eliminating specific elements, like global average pooling (GAP), precipitates underfitting within the validation set, notwithstanding the accelerated convergence observed during the training phase. Additionally, the absence of a wide convolutional kernel results in a performance dip greater than 10%, underscoring the importance of wide kernels in capturing useful features and suppressing interference.

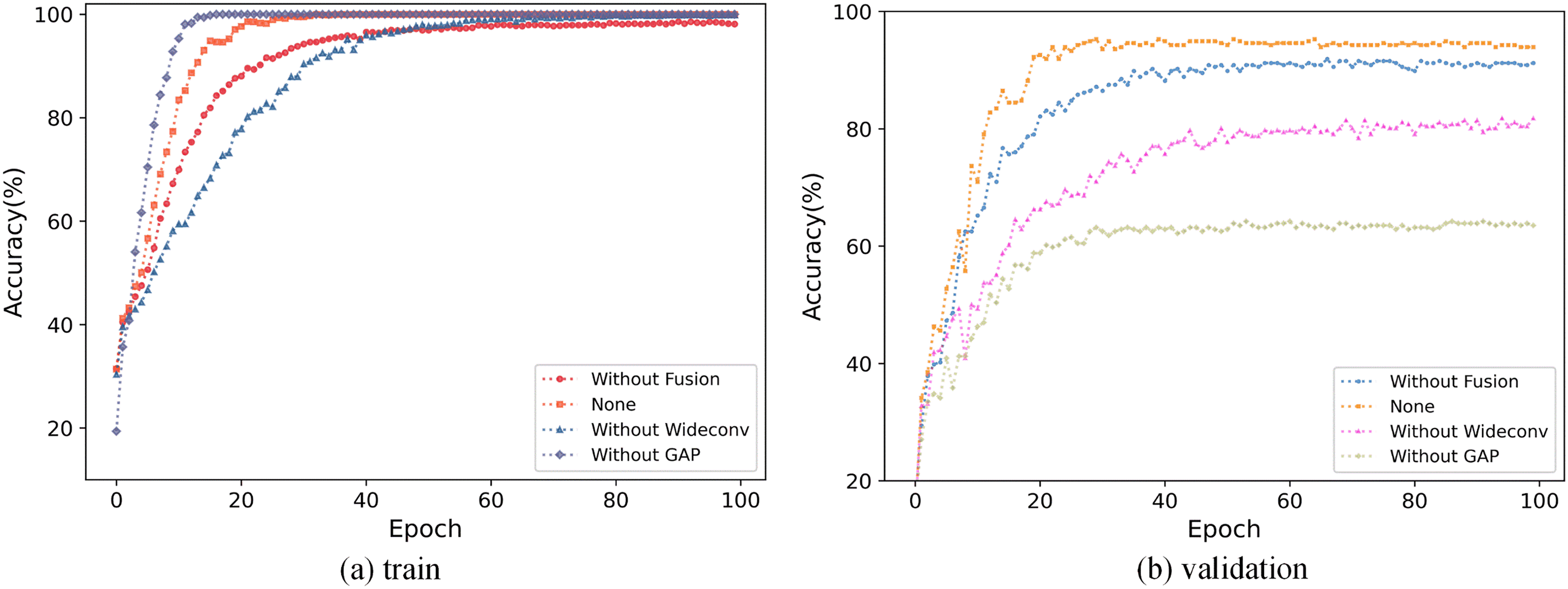
Figure 6: Results of our method and one without a particular tool

4.3 Case Study 2

4.3.1 Data Description

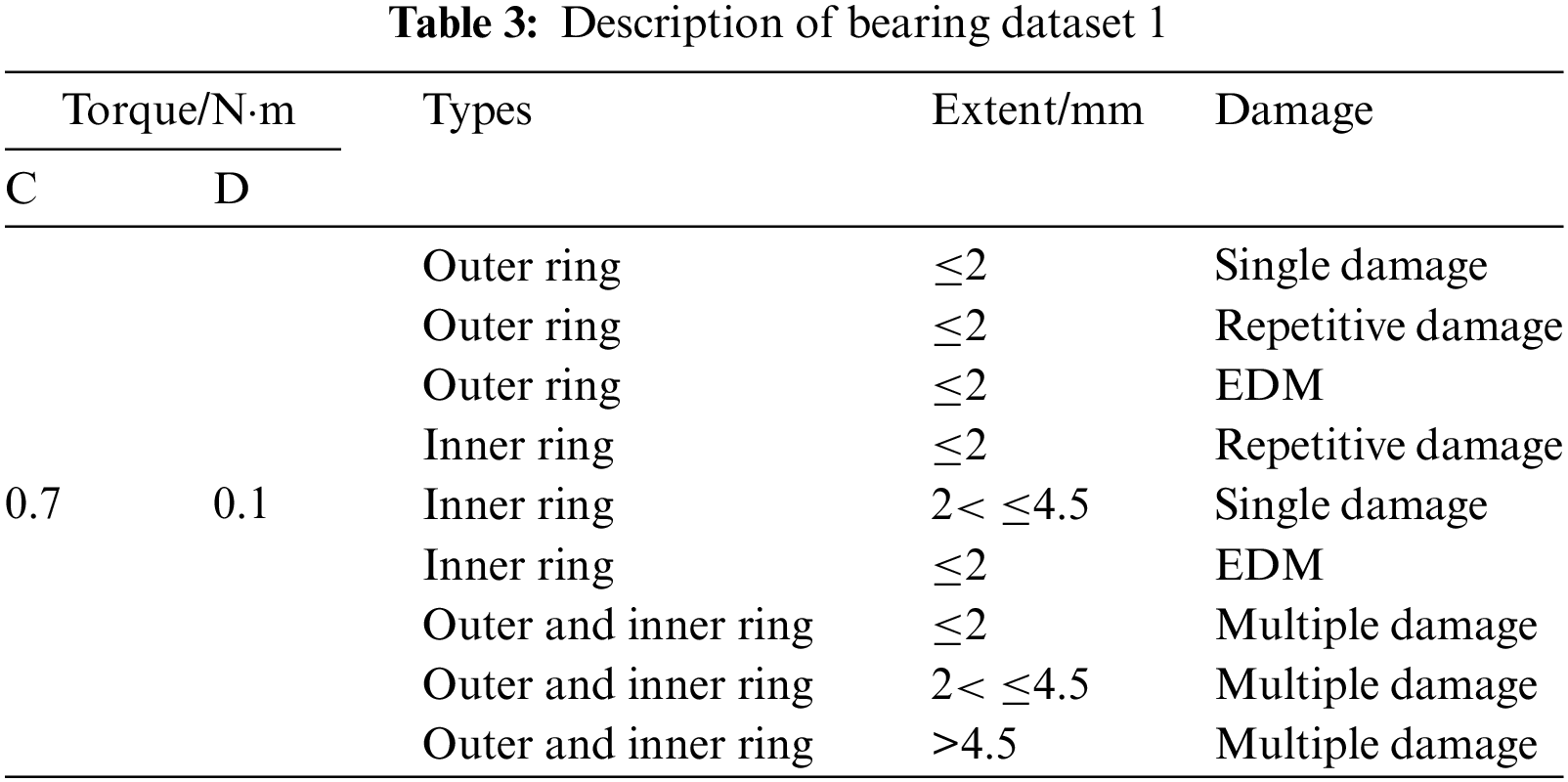
We further validate the proposed method using a dataset about ball bearings of type 6203, including multiple damage kinds and levels [34]. All of the data in this study have been collected at a frequency of 64 kHz and a temperature between 45 and 50 degrees Celsius. We use data from loads of 0.7 and 0.1 N·m at 1500 rpm. The damage manifestations encompass several distinct categories, classified based on the nature and extent of the damage, as detailed in Table 3.

4.3.2 Results and Analysis

Furthermore, in the context of intelligent factory operations characterized by continuous equipment usage over prolonged periods, the operational status of production devices frequently experiences dynamic fluctuations. This inherent variability means that the signals collected by the sensors contain information about the device in different operating scenarios. Consequently, our validation process encompasses evaluating each method within congruent and disparate domains, and the ensuing results are illustrated in Fig. 7.

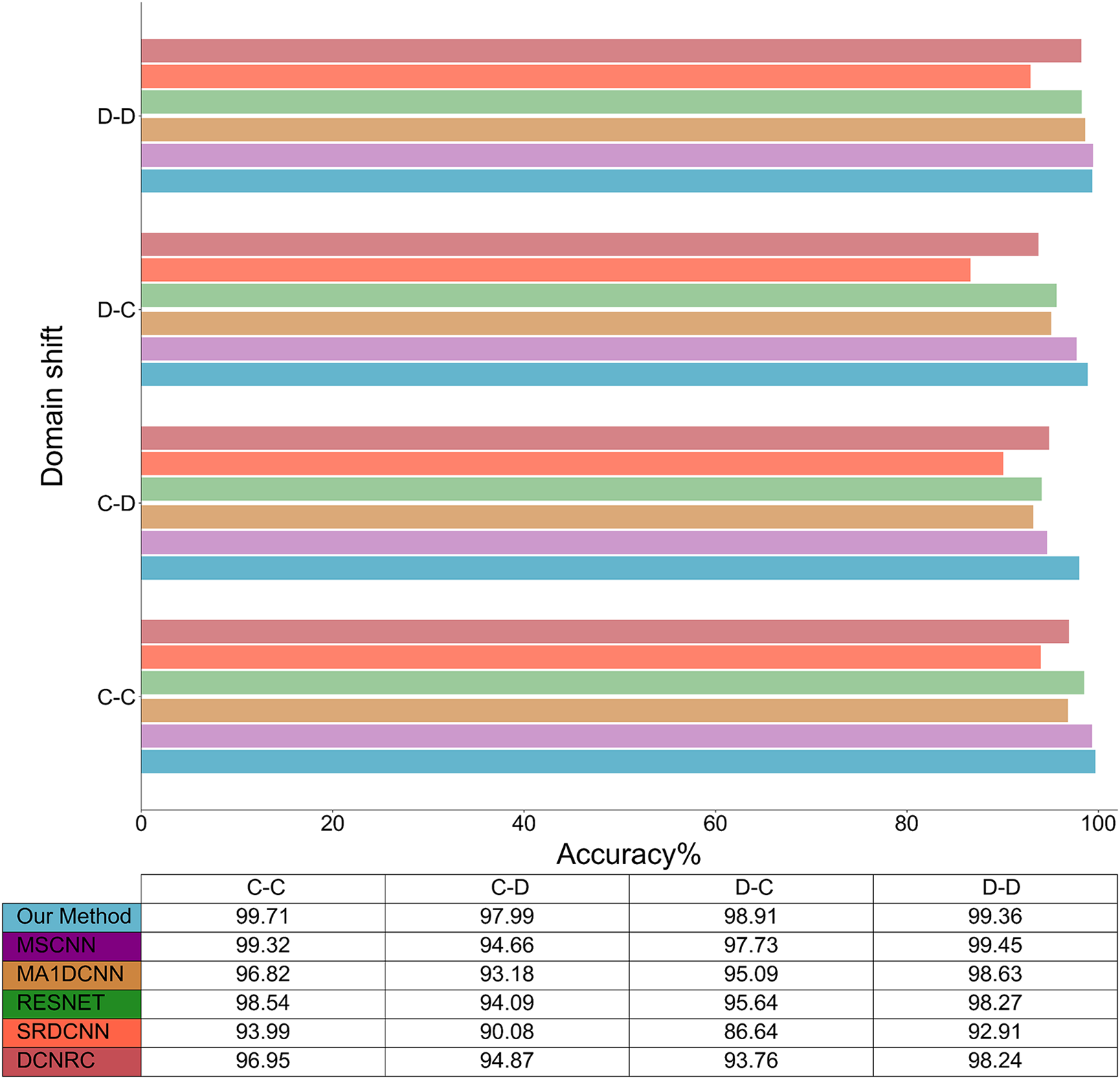
Figure 7: Performance of our method and others under varying domains

The proposed method exhibits robust detection ability across all scenarios. MSCNN closely follows in performance, demonstrating that multiscale extraction comprehensively captures fault-related features from the signal. In the C-D domain, RESNET and MA1DCNN attained accuracies of 94.09% and 93.18%, respectively, reflecting a decline of nearly 4% when compared to the accuracy attained by our proposed method. The accuracy of DCNRC in the D-C scene lags by approximately 5%. SRDCNN’s diagnostic performance is lackluster across all scenarios, with accuracy ranging from 86.64% to 93.99% for different domains, exhibiting a notable gap compared to the other well-performing methods.

5  Conclusion

This study has developed a comprehensive deep learning-based method for the automatic detection of manufacturing equipment defects using vibration data, aligning with the advanced requirements of intelligent manufacturing. Central to our approach is the integration of several feature learning blocks: the high-level feature learning block (HLFLB), the multi-scale feature learning block (MSFLB), and the dynamic adaptive fusion block (DAFB). These components are engineered to extract and process defect-related information efficiently, improving the network’s ability to express and interpret complex features as well as conducting a comprehensive analysis of vibration data.

Comprehensive validations across various industrial datasets have substantiated the efficacy of our proposed method. It has demonstrated a notable capacity to categorize distinct types of defects precisely, evidencing robust feature learning and a high level of generalizability. This approach is in harmony with the objectives of intelligence in the Industry 4.0 era, enabling end-to-end defect detection that eschews the need for traditional, complex manual feature selection, making it a powerful tool for defect detection in smart manufacturing.

In this paper, we have studied vibration signals in smart factories without considering other state information collected by sensors, such as current, temperature, pressure, etc. Furthermore, the research acknowledges the intrinsic challenge posed by the unbalanced nature of real-world data, where some defect types are more prevalent than others, leading to disproportionate class sample sizes that can skew the analysis and the effectiveness of the detection models.

The future scope of this research is to expand the horizons of defect detection by incorporating more holistic sensor data. The intention is to integrate multiple types of sensor data to create a more robust and comprehensive diagnostic framework that can effectively handle the challenges of unbalanced datasets. Such advancements will further improve defect detection performance, supporting the transition towards more intelligent and self-optimizing factories.

Acknowledgement: The authors would like to thank the open data from Southeast University, University of Connecticut, and Paderborn University.

Funding Statement: This research has been supported by the Natural Science Foundation of Heilongjiang Province (Grant Number: LH2021F002).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Bowen Yu; data collection: Bowen Yu, Chunli Xie; analysis and interpretation of results: Bowen Yu; draft manuscript preparation: Bowen Yu, Chunli Xie. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data presented in this study are available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. Y. Zhong, X. Xu, E. Klotz and S. T. Newman, “Intelligent manufacturing in the context of industry 4.0: A review,” Engineering, vol. 3, no. 5, pp. 616–630, 2017. [Google Scholar]

2. Z. M. Çınar, A. A. Nuhu, Q. Zeeshan, O. Korhan, M. Asmeal et al., “Machine learning in predictive maintenance towards sustainable smart manufacturing in Industry 4.0,” Sustainability, vol. 12, no. 19, pp. 8211, 2020. https://doi.org/10.3390/su12198211 [Google Scholar] [CrossRef]

3. M. H. M. Ghazali and W. Rahiman, “Vibration analysis for machine monitoring and diagnosis: A systematic review,” Shock and Vibration, vol. 2021, pp. 1–25, 2021. https://doi.org/10.1155/2021/9469318 [Google Scholar] [CrossRef]

4. A. Dibaj, R. Hassannejad, M. M. Ettefagh and M. B. Ehghaghi, “Incipient fault diagnosis of bearings based on parameter-optimized VMD and envelope spectrum weighted kurtosis index with a new sensitivity assessment threshold,” ISA Transactions, vol. 114, pp. 413–433, 2021. [Google Scholar] [PubMed]

5. D. Y. Han, N. Zhao and P. M. Shi, “Gear fault feature extraction and diagnosis method under different load excitation based on EMD, PSO-SVM and fractal box dimension,” Journal of Mechanical Science and Technology, vol. 33, no. 2, pp. 487–494, 2019. [Google Scholar]

6. D. K. Saha, M. E. Hoque and H. Badihi, “Development of intelligent fault diagnosis technique of rotary machine element bearing: A machine learning approach,” Sensors, vol. 22, no. 3, pp. 1073, 2022. https://doi.org/10.3390/s22031073 [Google Scholar] [PubMed] [CrossRef]

7. C. C. Ding, M. Zhao, J. Lin and J. Y. Jiao, “Multi-objective iterative optimization algorithm based optimal wavelet filter selection for multi-fault diagnosis of rolling element bearings,” ISA Transactions, vol. 88, pp. 199–215, 2019. [Google Scholar] [PubMed]

8. H. Han, L. Xu, X. Y. Cui and Y. Q. Fan, “Novel chiller fault diagnosis using deep neural network (DNN) with simulated annealing (SA),” International Journal of Refrigeration, vol. 121, pp. 269–278, 2021. [Google Scholar]

9. E. A. Bhuiyan, M. A. Akhand, S. R. Fahim, S. K. Sarker and S. K. Das, “A deep learning through DBN enabled transmission line fault transient classification framework for multimachine microgrid systems,” International Transactions on Electrical Energy Systems, vol. 2022, 2022. https://doi.org/10.1155/2022/6820319 [Google Scholar] [CrossRef]

10. M. Mansouri, K. Dhibi, M. Hajji, K. Bouzara, H. Nounou et al., “Interval-valued reduced RNN for fault detection and diagnosis for wind energy conversion systems,” IEEE Sensors Journal, vol. 22, no. 13, pp. 13581–13588, 2022. [Google Scholar]

11. S. Plakiasa and Y. S. Boutalis, “A novel information processing method based on an ensemble of auto-encoders for unsupervised fault detection,” Computers in Industry, vol. 142, pp. 103743, 2022. https://doi.org/10.1016/j.compind.2022.103743 [Google Scholar] [CrossRef]

12. X. Wang, D. X. Mao and X. D. Li, “Bearing fault diagnosis based on vibro-acoustic data fusion and 1D-CNN network,” Measurement, vol. 173, pp. 108518, 2021. https://doi.org/10.1016/j.measurement.2020.108518 [Google Scholar] [CrossRef]

13. X. Xie, B. Wang, T. C. Wan and W. L. Tang, “Multivariate abnormal detection for industrial control systems using 1D CNN and GRU,” IEEE Access, vol. 8, pp. 88348–88359, 2020. [Google Scholar]

14. W. Zhang, X. Li and Q. Din, “Deep residual learning-based fault diagnosis method for rotating machinery,” ISA Transactions, vol. 95, pp. 295–305, 2019. [Google Scholar] [PubMed]

15. W. Y. Huang, J. S. Cheng, Y. Yang and G. Y. Guo, “An improved deep convolutional neural network with multi-scale information for bearing fault diagnosis,” Neurocomputing, vol. 359, pp. 77–92, 2019. [Google Scholar]

16. X. R. Shao, C. S. Kim and D. G. Kim, “Accurate multi-scale feature fusion cnn for time series classification in smart factory,” Computers, Materials & Continua, vol. 65, no. 1, pp. 543–561, 2020. [Google Scholar]

17. Q. Shen, H. J. Qin, K. M. Wei and G. Z. Liu, “Multiscale deep neural network for obstructive sleep apnea detection using RR interval from single-lead ECG signal,” IEEE Transactions on Instrumentation and Measurement, vol. 70, pp. 1–13, 2021. [Google Scholar]

18. Z. F. Xu, C. Li and Y. Yang, “Fault diagnosis of rolling bearings using an improved multi-scale convolutional neural network with feature attention mechanism,” ISA Transactions, vol. 110, pp. 379–393, 2021. [Google Scholar] [PubMed]

19. K. M. He, X. Y. Zhang, S. Q. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]

20. S. Ioffe and C. Szegedy, “Batch normalization: Accelerating deep network training by reducing internal covariate shift,” in Proc. of the 32nd Int. Conf. on Machine Learning, Lille, France, pp. 448–456, 2015. [Google Scholar]

21. Q. L. Wang, B. G. Wu, P. F. Zhu, P. H. Li, W. M. Zuo et al., “ECA-Net: Efficient channel attention for deep convolutional neural networks,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, pp. 11531–11539, 2020. [Google Scholar]

22. F. Yu and V. Koltun, “Multi-scale context aggregation by dilated convolutions,” arXiv preprint arXiv:1511. 07122, 2015. [Google Scholar]

23. J. C. Li, F. M. Fang, K. F. Mei and G. X. Zhang, “Multi-scale residual network for image super-resolution,” in Proc. of the European Conf. on Computer Vision (ECCV), Munich, Germany, pp. 517–532, 2018. [Google Scholar]

24. X. Li, W. H. Wang, X. L. Hu and J. Yang, “Selective kernel networks,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, pp. 510–519, 2019. [Google Scholar]

25. S. W. Zamir, A. Arora, S. Khan, M. Hayat, F. S. Khan et al., “Learning enriched features for real image restoration and enhancement,” in Proc. of the European Conf. on Computer Vision (ECCV), Glasgow, UK, pp. 492–511, 2020. [Google Scholar]

26. D. P. Kingma and J. L. Ba, “Adam: A method for stochastic optimization,” arXiv preprint arXiv:1412. 6980, 2014. [Google Scholar]

27. S. Y. Shao, S. McAleer, R. Q. Yan and P. Baldi, “Highly accurate machine fault diagnosis using deep transfer learning,” IEEE Transactions on Industrial Informatics, vol. 15, no. 4, pp. 2446–2455, 2018. [Google Scholar]

28. P. Cao, S. L. Zhang and J. Tang, “Preprocessing-free gear fault diagnosis using small datasets with deep convolutional neural network-based transfer learning,” IEEE Access, vol. 6, pp. 26241–26253, 2018. [Google Scholar]

29. W. Chen and K. Shi, “Multi-scale attention convolutional neural network for time series classification,” Neural Networks, vol. 136, pp. 126–140, 2021. [Google Scholar] [PubMed]

30. H. Wang, Z. L. Liu, D. D. Peng and Y. Qin, “Understanding and learning discriminant features based on multi-attention 1DCNN for wheelset bearing fault diagnosis,” IEEE Transactions on Industrial Informatics, vol. 16, no. 9, pp. 5735–5745, 2019. [Google Scholar]

31. Z. G. Wang, W. Z. Yan and T. Oates, “Time series classification from scratch with deep neural networks: A strong baseline,” in Proc. of the Int. Joint Conf. on Neural Networks (IJCNN), Anchorage, AK, USA, pp. 1578–1585, 2017. [Google Scholar]

32. Z. L. Zhuang, H. C. Lv, J. Xu, Z. Z. Huang and W. Qin, “A deep learning method for bearing fault diagnosis through stacked residual dilated convolutions,” Applied Sciences, vol. 9, no. 9, pp. 1823, 2019. https://doi.org/10.3390/app9091823 [Google Scholar] [CrossRef]

33. H. P. Liang and X. Q. Zhao, “Rolling bearing fault diagnosis based on one-dimensional dilated convolution network with residual connection,” IEEE Access, vol. 9, pp. 31078–31091, 2021. [Google Scholar]

34. C. Lessmeier, J. K. Kimotho, D. Zimmer and W. Sextro, “Condition monitoring of bearing damage in electromechanical drive systems by using motor current signals of electric motors: A benchmark data set for data-driven classification,” in Proc. of the PHM Society European Conf., Bilbao, Spain, 2016. [Google Scholar]