Credit Card Fraud Detection Using Improved Deep Learning Models

1  Introduction

With the increasing incidences of fraudulent activity, detecting credit card fraud is important to guarantee financial security. As a result, there is a need to design a fraud detection model that can efficiently recognize and capture detailed patterns while correctly and reliably identifying abnormalities in credit transactions [1,2].

Credit card fraud detection encounters several challenges. Firstly, the imbalance between fraudulent and legitimate transactions in credit card datasets poses a significant issue (i.e., Imbalanced Dataset). Secondly, fraudsters constantly devise new and sophisticated methods to avoid detection (i.e., Concept Drift). Thirdly, precise feature selection and engineering are critical to the efficacy of fraud detection models. Finally, the ability of fraud detection systems to detect and prevent fraudulent transactions in real-time is critical (i.e., verification latency) [1,3–5]. To address these issues, continued research, new modeling approaches, and collaboration between financial institutions and data scientists are required.

Deep learning (DL) models play a crucial role in addressing the problem of detecting credit card fraud for several reasons. DL can automatically learn relevant features from raw transaction data, reducing the need for manual feature engineering. This is particularly valuable when dealing with a wide range of transaction features. As well DL models can be trained to handle imbalanced data through techniques like sampling, improving their ability to detect rare fraudulent cases. Also, DL models can be deployed to operate in real-time, providing immediate responses to transaction requests. This is crucial for stopping fraudulent transactions before they are approved. Additionally, DL models can scale effectively with the growth in transaction volume, making them suitable for large financial institutions and payment processors that handle millions of transactions daily. As well, DL models can be designed for continuous learning, allowing them to adapt to changing fraud patterns over time. This is essential as fraudsters continuously develop new tactics [6–10].

However, to attain optimal performance with these models their hyperparameters should be initialized with appropriate values using suitable evaluation metrics. In addition, one should avoid setting the parameters to biased or default settings to achieve accurate results. Hence, they are not suitable for complex recognition and prediction tasks in DL. Therefore, automated hyperparameter tuning techniques are required which play a crucial role in fine-tuning the models to improve their accuracy, robustness, generalization, and detection [11,12]. Automated hyperparameter tuning can be done through different methods such as grid search, random search, and Bayesian optimization. However, grid search has some limitations since it requires defining all possible hyperparameter values and evaluating each combination repeatedly. While it can give the best parameter combination, it can suffer from the curse of dimensionality and take longer to compute as the number of parameters increases. Therefore, it is important to use other methods such as random search and Bayesian optimization to address this issue in a faster and more efficient manner [13,14].

This paper aims to explore the significance of hyperparameter tuning in enhancing credit card fraud detection using three DL techniques, namely AutoEncoder (AE), Convolution Neural Network (CNN), and Long Short-Term Memory (LSTM). Additionally, the study examines the impact of resampling methods such as Synthetic Minority Oversampling Technique (SMOTE), Adaptive Synthetic Sampling (ADASYN), and Random Undersampling (RUS) in mitigating the effects of class imbalances in the dataset. The presence of imbalanced classes poses a challenge during hyperparameter tuning and results in biased accuracy assessment due to an over-reliance on the majority class. The paper addresses the following questions that can lead to advancements and contribute to more accurate and effective fraud detection models:

1.    How can hyperparameter adjustment improve the performance of DL models for credit card fraud detection?

2.    What effect do different hyperparameters have on the effectiveness of DL models in detecting credit card fraud?

3.    How can hyperparameter tuning approaches be used to improve credit card fraud detection models’ effectiveness?

4.    How can hyperparameter tuning strategies handle the issue of unbalanced data in credit card fraud detection and enhance fraud detection?

The organization of the paper: Section 2 presents several works in the area of concern. Section 3 provides a brief explanation of DL models used, and hyperparameter tuning concepts and shows the sampling techniques used in this paper. Section 4 describes the proposed DL models with Hyperparameter tuning while Section 5 analyses the results, and finally Section 6 concludes the paper.

2  Related Work

This section presents some previous works on credit card fraud detection, with an emphasis on the use of Machine Learning (ML) and DL models and the significance of hyperparameter optimization for achieving optimal performance.

Taha et al. [15] developed an intelligent method for detecting fraud in credit card transactions using an optimized light gradient boosting machine (OLightGBM). To intelligently adjust the parameters of a LightGBM, a Bayesian-based hyperparameter optimization technique is used. Experiments were conducted utilizing two real-world public credit card transaction datasets: European and UCSD-FICO, to illustrate the usefulness of the proposed OLightGBM for detecting fraud in credit card transactions. Based on a comparison of other techniques employing the two datasets, OLightGBM result outperforms the others, achieving the greatest accuracy of 98.40%, Area Under the Curve (AUC) of 92.88%, Precision of 97.34%, an F1-score of 56.95%. However, it is difficult to obtain insights into the underlying patterns that differentiate legitimate transactions from fraudulent ones due to the model’s lack of interpretability.

To accelerate the search process and enhance performance, an approach was presented [16] that integrates a feature engineering method for feature selection and Bayesian optimization for hyperparameter tunning with a LightGBM-based method for fraud detection. Experiments on IEEE-CIS fraud detection dataset revealed that the LightGBM-based method outperformed Support Vector Machine (SVM), extreme gradient boost (XGBoost), and Random Forest (RF). The accuracy and AUC of the model surpass 97%, indicating its superior performance in fraud detection. Still dealing with imbalanced data led to possible model overfitting, which could result in poor generalization capabilities and restricted use of the model in practical situations.

A credit card fraud detection hybrid model that combines supervised and unsupervised anomaly detection to improve prediction efficiency was proposed in [17]. The hybrid model uses the Support Vector Machine-Recursive Feature Elimination (SVM-RFE) for selecting the distinguished features and the grid search as a hyperparameter optimization method for tuning the RF hyperparameter. Moreover, to overcome the problem of the imbalanced dataset SMOTE sampling technique was used. The model was validated based on three datasets and the results showed high accuracy performance with 99%, sensitivity of 95%, and Area Under the Precision-Recall curve (AUC-PR) of 0.81.

The efficiency and robustness of the model for fraud detection in the European cardholder dataset are enhanced by utilizing a random search to find optimum hyperparameters for the LR and XGBoost models [18]. Furthermore, the SMOTE sampling method addresses the issue of an imbalanced dataset. To assess the models, accuracy, sensitivity, specificity, precision, recall, F1-score, and AUC-ROC were used which showed that the model achieved all scores greater than 90%. The process of constructing the model, however, required a longer amount of time.

A new system based on the attention mechanism and LSTM sequential modeling of data is developed [19]. The model combines the strength of three sub-methods; the uniform manifold approximation and projection (UMAP) to extract the most useful predictive features, LSTM for integrating transaction sequences, and the attention mechanism to enhance LSTM performances. The classifier identifies the most important transactions in the input sequence that led to a higher fraudulent prediction accuracy of 96% and 97% with European and synthetic Bank-Sim datasets, respectively.

Isangediok et al. [20] employed ML techniques such as LR, DT, RF, and XGBoost to increase precision while decreasing false positives in fraud detection. The classifiers are initially trained on two imbalanced benchmark fraud detection datasets: phishing website URLs and European cardholder credit card transactions. RUS, SMOTE, and edited nearest neighbor (SMOTEENN) sampling techniques are then used to generate three synthetically balanced datasets for each original dataset. The optimal hyperparameters for the experiments are determined using the RandomizedSearchCV method. AUC-ROC and AUC-PR measures were used to evaluate the models. The results reveal that XGBoost trained on the original data performs well in the unbalanced dataset, with AUC-ROC (99%) and AUC-PR (85%). However, there are no complete assessment standards available for the dataset.

A deep AE model was developed that can evolve into pattern changes [21]. The model consisted of four hidden layers, including a pair of encoders and a pair of decoders. In both the encoder and decoder, the activation functions “tanh” and “Relu” were used in the adjacent layers. To assess the model performance, three datasets: European, Australian, and Taiwan were used in the comparison and the results showed a higher accuracy of 99% with the Taiwan dataset, whereas the European dataset showed a lower accuracy of 70%.

The hyperparameter tuning of AE was implemented by the Bayesian search function [2]. The optimized hyperparameters were the number of nodes in the hidden layers, the activation function, the Epochs, and the batch size. The AE was used to encode data and then used to train three other models: K-nearest neighbors (KNN), LR, and SVM. Next, these models were applied to a European cardholder’s imbalanced credit card dataset. The results showed that AE gave a good accuracy of 99% and recall above 80%. The model struggles to identify complex and evolving fraud patterns that are not well represented in the training data

CatBoost and XGBoost were used to improve the performance of the LightGBM presented in [22] by using a voting mechanism. In addition, the hyperparameters with Bayesian optimization for tuning hyperparameters and DL weight-tuning preprocessing to deal with unbalanced European cardholders dataset issues. A five-fold cross-validation technique was used for evaluating CatBoost, LightGBM, and XGBoost. The results show that LightGBM and XGBoost achieved the highest performance including an ROC-AUC of 95%, precision of 79%, and recall of 80%.

A hybrid CNN-SVM model was developed by [23] by changing the output layer of the CNN model with an SVM classifier. The CNN classifier is fully connected with a softmax layer that is trained using an end-to-end approach, while the second is an SVM classifier that is stacked on top by deleting the final fully connected and softmax layer. The efficiency of the proposed hybrid model was tested using a public real credit card transaction dataset and the result shows classification performance with accuracy, precision, recall, F1-score, and AUC of more than 90%. However, there are certain drawbacks associated with the usage of SVM, particularly when it comes to dealing with datasets that are imbalanced or consist of high-dimensional noisy data.

Taha [24] proposed a system for detecting credit card fraud called HASC-DLCCFD, which utilizes a hybrid approach of Harris Hawks optimization and the sine cosine algorithm for feature selection. The system uses a convolutional neural network combined with long short-term memory to identify frauds, and the adaptive moment estimation algorithm is employed as a hyperparameter optimizer. The HASC-DLCCFD was tested on a simulated Sparkov credit card dataset, achieving an accuracy of 99.5%, recall of 99.4%, and AUC of 98.5%. The problem of imbalanced data is not dealt with in the study, and there is a lack of comprehensive information on how its parameters were optimized.

Previous studies on DL models have only explored a limited range of hyperparameters that affect the model’s performance. Additionally, credit card fraud is rare compared to genuine transactions, which leads to an imbalanced dataset. Current methods use accuracy as the performance indicator, which can be misleading when dealing with such a dataset.

To overcome these limitations, this paper investigates a broader range of hyperparameters to potentially achieve better credit card fraud detection. The hyperparameters include learning rate, batch size, number of neurons per layer, regularization techniques, and activation functions. To efficiently search for hyperparameters, random search, and Bayesian optimization techniques are used to narrow down the search space. The assessment metric used is the F1-score, which takes into account class imbalance and aims to improve hyperparameters accordingly. The cross-validation technique is utilized to mitigate overfitting and ensure the model’s generalizability.

3  Preliminary Concepts

This section provides a brief explanation of the theoretical background of the concept used in this paper.

3.1 Deep Learning Models

DL refers to multilayer neural networks that can learn by each input of the transaction it receives, group the transactions concerning patterns by taking into account several parameters, and classify the transaction as fraudulent or legitimate correctly. In this paper, three DL models are adopted including AE, CNN, and LSTM.

Firstly, the AE network is an unsupervised learning algorithm that utilizes backpropagation by setting the inputs and outputs identically [21,25]. The main goal of the AE is to approximate the distribution of the input value as accurately as possible [2]. AE can detect fraud effectively for the following reasons: its ability to extract meaningful features by decoding and encoding the input data automatically during the training process. As well as its ability to detect anomalies in data by learning to reconstruct the input data, if a transaction deviates significantly from what the model has learned as “normal,” it will have a higher reconstruction error. Moreover, AE can generalize well to detect unseen or novel fraud patterns. They learn to capture the underlying distribution of legitimate transactions and can identify anomalies that deviate significantly from that distribution [26–28].

Secondly, a specialized case of artificial neural networks (ANN) with a distinctive architecture designed to extract progressively complex features of the data at each layer to determine the output. CNN is a feedforward neural network that is built of local connections, shared weights, pooling, and the use of several layers (convolutional and fully connected layers) [23,29,30]. CNN learns the derivative features that are beneficial to the classification results and reduce the interference of human experience with the model [31,32]. CNN can utilize convolutional layers to extract important local features within transactions that may be indicative of fraudulent behavior. Also, it reduces the number of parameters to be learned by sharing parameters, making CNN more computationally efficient and capable of handling large-scale credit card transaction datasets. In addition to effectively suppressing noise and focusing on the most discriminative features by leveraging convolutional and pooling operations. So, CNN can improve the model’s ability to distinguish between fraudulent and legitimate transactions [23,32,33].

Finally, in the field of DL, a specific kind of artificial Recurrent Neural Network (RNN) architecture is utilized for modeling time series information. Compared to feedforward neural networks, The LSTM network, in contrast to feedforward neural networks, includes feedback connections between hidden units that correspond to specific time series. This architecture allows the LSTM to recognize long-term sequential patterns, allowing it to predict transaction labels based on the sequence of previous transactions [19,34,35]

3.2 Hyperparameter Tuning

The process of identifying the optimum set of hyperparameters that optimize the model’s performance is known as hyperparameter tuning. There are numerous techniques for tuning hyperparameters. This paper adopts two techniques: random search and Bayesian optimization.

Random search performs a randomized search over hyperparameters from certain distributions over possible hyperparameter values. The search process continues until the desired metric is reached or until the predetermined computational budget is exhausted [36,37].

Bayesian optimization is an iterative process that uses two key components: a probabilistic surrogate model and an acquisition function to select the next point for evaluation. The surrogate model is fitted to all previously observed data points of the objective function throughout each iteration. The acquisition function then uses the probabilistic model’s prediction distribution to evaluate the utility of different candidate points. When compared to other tuning functions, the acquisition function is computationally inexpensive, allowing for extensive optimization [38].

3.3 Data Sampling Techniques

Class imbalance techniques involve dealing with the unequal distribution of classes in a dataset. One technique is the use of RUS to undersample the majority class. Another technique is to use techniques such as SMOTE and ADASYN to oversample the minority class [1,39–42]. These techniques are intended to balance the class distribution and enhance the model’s performance while dealing with unbalanced data. Fig. 1 depicts sampling techniques including RUS, SMOTE, and ADASYN.

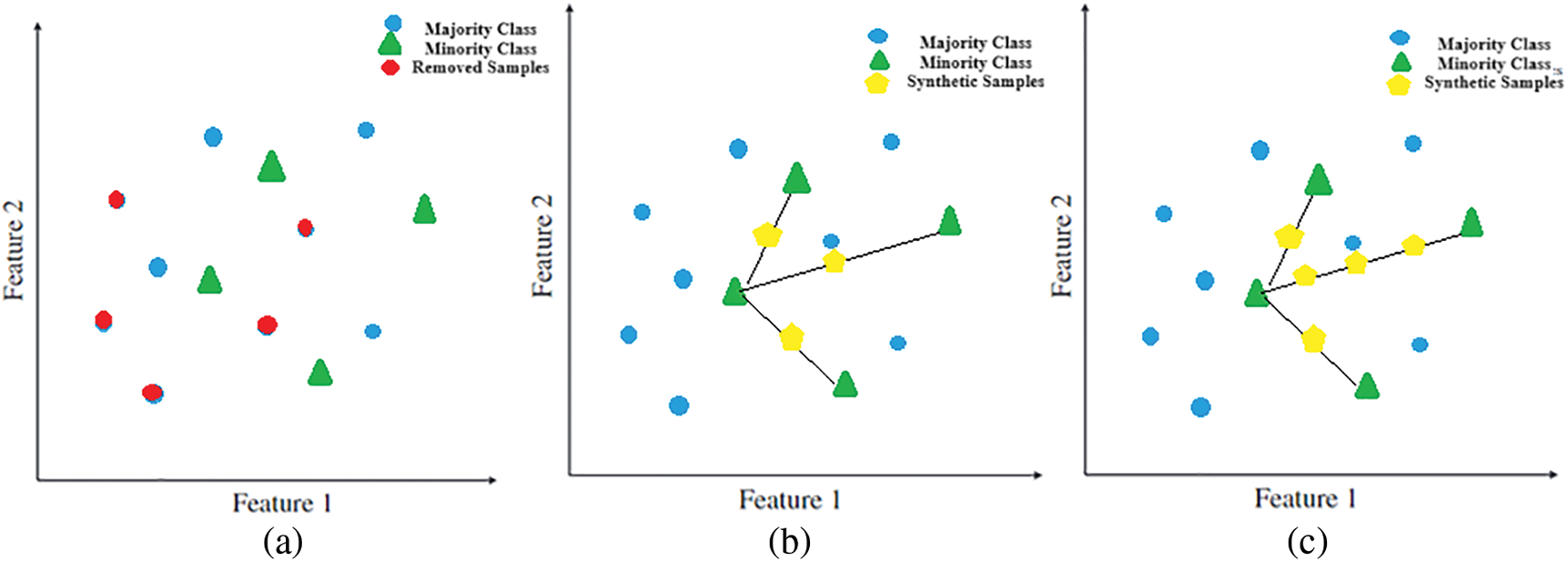
Figure 1: Sampling Techniques: (a) RUS, (b) SMOTE, and (c) ADASYN

•   RUS is a technique used to address class imbalance by reducing the number of samples in the majority class (legitimate transactions) to equal those of the minority class by removing majority class instances at random. The main issue of RUS is that the random removal of data can result in the loss of important data that may have been obtained in the removed samples.

•   SMOTE technique generates synthetic samples for the minority class (fraudulent transactions) to balance the class distribution, thus enhancing the model’s ability to detect fraud. SMOTE begins by locating the K closest minority samples based on the K-nearest neighbors (KNN) for a minority sample xi. Then, it chooses a sample xj from the k closest minority samples and produces a new minority sample x′ using Eq. (1).

x′=xi+ω(xi−xj)(1)

where ω random number is in the range [0,1].

•   ADASYN is an extension of SMOTE that addresses some of the limitations of traditional SMOTE. ADASYN focuses on generating synthetic samples for the minority class (fraudulent transactions) more adaptively, emphasizing more on difficult-to-learn examples by considering their density distributions (imbalance degree). ADASYN takes into account the distribution of the feature space and increases the focus on the samples that are harder to classify by adding more synthetic samples in those regions. For each minority class instance xi, ADASYN computes the imbalance degree (∆i) as the number of majority class instances among its k nearest neighbors. The density ratio for each minority instance, xi, is then computed. ADASYN adaptively determines the number of synthetic samples to be created for each minority instance based on the density ratio.

4  The Proposed DL Models with Hyperparameter Tuning

Detecting credit card fraud is a challenging task due to imbalanced data. The DL model should be designed with an appropriate hyperparameter. Different architectures and hyperparameters impact the credit card fraud detection model performance. The proposed models aim to develop a credit card fraud detection model with optimized hyperparameters that can achieve high accuracy and robustness in real-world scenarios. The model should effectively distinguish between genuine and fraudulent transactions, minimizing both false positives (legitimate transactions incorrectly classified as fraudulent) and false negatives (fraudulent transactions incorrectly classified as legitimate) while maintaining a seamless user experience and ensuring timely intervention against fraud by analyzing a large volume of credit card transaction data and accurately classifying transactions as legitimate or fraudulent. This can be achieved through many stages: At the initial stage, the input data is preprocessed to ensure its compatibility for further processing. The preprocessed data is then fed to three DL models namely, AE, CNN, and LSTM to classify credit card transactions as legitimate or fraudulent. These models are tuned by two approaches namely, random search and Bayesian optimization that systematically investigate and analyze various hyperparameter configurations to determine the most effective ones for each model. The block diagram of the proposed DL models with hyperparameter tuning is depicted in Fig. 2.

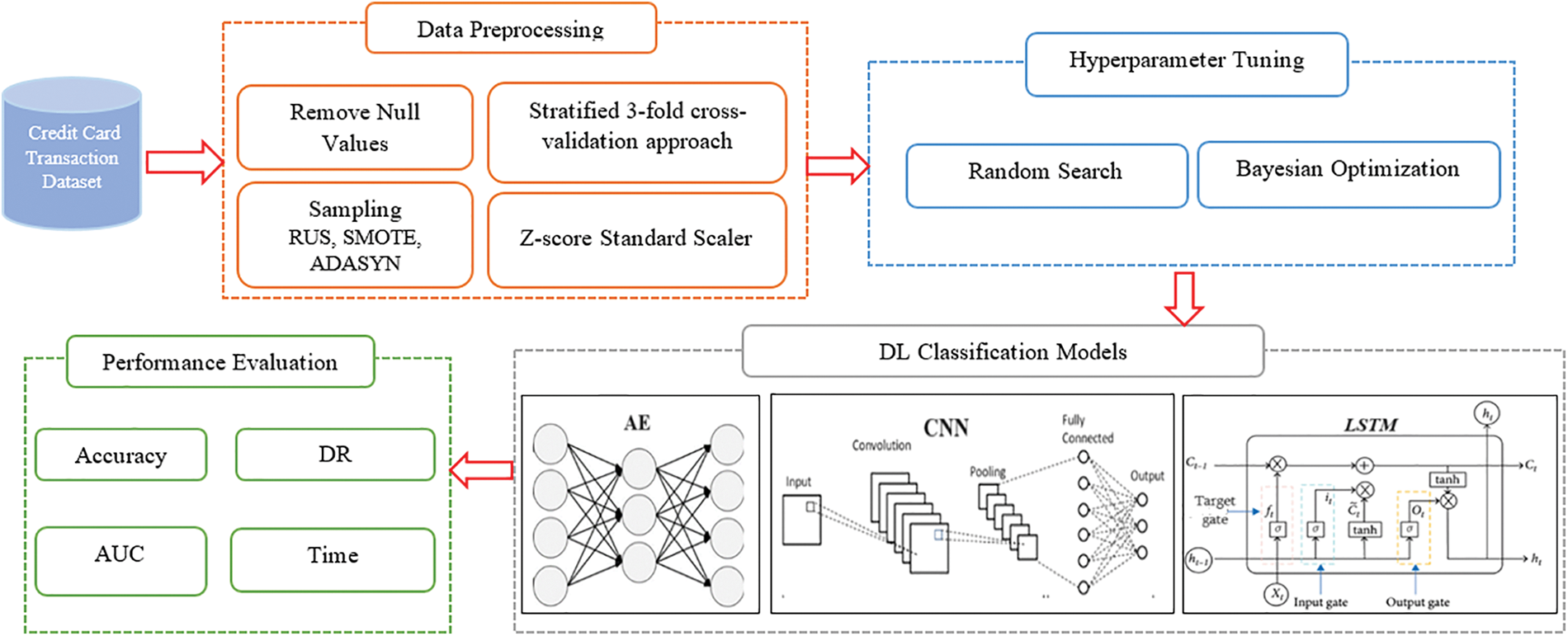
Figure 2: Block diagram of the proposed DL models with hyperparameter tuning

4.1 Data Preprocessing

Preprocessing the dataset is a crucial step to ensure that the data is in a suitable format for training and evaluating DL models. Four key preprocessing methodologies are performed to make the data easier to be processed by DL models.

Firstly, it is crucial to handle any missing values in the dataset properly to ensure that the model’s performance is not negatively impacted. In such cases, the missing values are either removed or imputed. If the percentage of missing values is less than an experimentally determined threshold, imputation will be done using the mean value of the missing feature. However, when such values exceed the threshold, transactions with missing feature values are removed from the dataset.

Secondly, a stratified k-fold was applied to ensure a fair distribution of normal and fraud classes in each fold, a stratified k-fold approach was employed to divide the credit card dataset into train and test sets. In this approach, each fold contains precisely one-third of the data from each class. The dataset is divided into three folds, each with an equal proportion of credit card transactions corresponding to a certain class label. One fold is employed as the testing set during each iteration, while the remaining two folds serve as the training set. This procedure is continued until all three folds have been used as the testing set to guarantee a thorough evaluation of the model’s performance across various data subsets. The DL models are then trained and evaluated k times, where each iteration uses a different fold as the testing set and the remaining folds as the training set.

Thirdly, sampling techniques such as RUS, SMOTE, and ADASYS are utilized to tackle the issue of class imbalance that often affects credit card fraud datasets. Credit card fraud datasets often suffer from class imbalance, where the number of legitimate transactions significantly outweighs the number of fraudulent transactions. This can cause the model to be biased towards the majority class and result in poor fraud detection.

Finally, feature scaling is performed to scale the numerical features to a similar range, preventing certain features from dominating the learning process. This technique further ensures that the optimization algorithm converges faster and prevents numerical instability in the model. The standardization method of z-score scaling, as shown in Eq. (2), is used to transform numerical features with a mean of 0 and a standard deviation of 1.

z=(x−μ)/σ(2)

where x is a single raw data value, μ is the feature mean, and σ is the feature standard deviation.

4.2 DL Models for Credit Card Fraud Detection

Given a dataset C, described as C={C1, C2…,Cn}, where n denotes the number of credit card transaction records, each credit card transaction data Ci∈C is characterized by m features. In addition, each credit card transaction is associated with class label L={0,1}, where 0 represents the normal class and 1 represents the fraud class. The proposed model that combines DL and hyperparameter tuning for credit card fraud detection involves using AE, CNN, and LSTM and optimizing their performance by searching for the best hyperparameters to categorize each credit card transaction data Ci, as normal or fraud.

Formally speaking, let A be a DL model with N hyperparameters. The set δ is indexed by h configuration variables representing the domain of the hth hyperparameter, while the complete hyperparameter space is denoted as δ=δ1×δ2×…×δN. Vector λ∈δ is used to represent a specific combination of hyperparameters, and when the hyperparameter of A is set to λ, it is denoted as Aλ. The hyperparameter values can be real, integer, binary, or categorical. The objective, given a dataset C, and model A is to find a solution λ′ that results in the best possible model performance using the tuning technique T as in Eq. (3). Table 1 describes symbol notation in this paper.

λ′=argmaxλ∈δT(Aλ,Ctr,Ctv)(3)

where T(Aλ,Ctr,Ctv) measures the objective function of a model generated by algorithm A with hyperparameters λ on training data Ctr and evaluated on validation data Ctv.

In this paper, the tuning process was carried out using F1-score as the objective function, as shown in Eq. (4), the reason for choosing this metric is to provide a trade-off between precision and detection rate.

F1score=2∗(DR+P)/(DR+P)(4)

where DR represents the detection rate which is also referred to as the true positive rate, that indicates the percentage of fraudulent activities that a model accurately identifies as fraudulent as defined in Eq. (5).

P, represents the precision that measures how often a model correctly detects fraud as defined in Eq. (6).

DR=TP/(TP+FN)(5)

P=TP/(TP+FP)(6)

where

True Positive (TP): denotes the number of credit card transactions identified as fraud,

False Positive (FP): denotes the number of credit card transactions identified as normal, and

False Negative (FN): denotes the number of legitimate credit card transactions identified as fraud.

Several deep learning hyperparameters that have a major impact on model training are investigated. These are the number of neurons in each layer, dropout rate, activation functions, batch size, optimization techniques, learning rate, and loss function. While the binary cross-entropy loss function is widely utilized in the literature, this paper adopts the focal loss function for credit card fraud detection. To our knowledge, this is the first time the focal loss function is employed in this field.

Algorithm 1 describes the steps of the proposed DL model combined with hyperparameter tuning. Three DL models are proposed.

First, the proposed AE model is defined by a pair of encoding E and decoding D layers. E encodes the input C into a hidden vector C’ to extract significant characteristics, which is subsequently mapped back to reconstruct C’’ by D. The distance between C and C’’ is calculated to yield MSE, which is then compared to the threshold, α. If MSE is more than α, then the credit card data transaction will be predicted as fraudulent; else, L’ is normal. The threshold chosen affects the performance of the AE model, and there are numerous works in the literature to determine α. In this paper, however, the threshold value is obtained by computing the percentile as shown in Eq. (7).

Percentile=(Vx/n)×10(7)

where

Vx: The number of data values less than x.

n = total number of credit card data transactions in the dataset.

Second, the proposed CNN model architecture is constructed with two convoluted layers, two pooling layers, one flatten layer, one dropout layer, and two dense layers to process the one-dimensional data. The sequential data C is converted to a three-dimensional image-like vector by adding the number of time steps as a third dimension. Then in the convolution layers, a set of weights referred to as kernels of size 3 are multiplied by inputs to produce a new feature map. While the pooling layer reduces the number of trainable parameters. Next, a flattened layer is applied to map the three-dimensional vector to one-dimensional input to the dense layers.

Finally, the proposed LSTM model consists of a single long-short-term memory layer to capture long-range dependencies in sequences with a single dense layer. A sequential credit card dataset C is transformed into a form suitable to be processed by LSTM layer. This transformation implies mapping two-dimensional data into a three-dimensional form of sequences, where each sequence can represent a time series or a sequence of events.

5  Results Discussion

European credit card dataset [43] is used for the model performance evaluation. It is made up of 284,807 transactions generated by European Cardholders over two days in September 2013. Each data transaction contains thirty-one features and a class label that indicates whether the transaction is fraudulent (1) or not. The dataset is highly biased since there only are 492 fraudulent transactions (i.e., 0.172% of total data).

The assessment of credit card fraud detection models involves the use of Accuracy (Acc), DR, and AUC measures. The evaluation of the DL models’ performance under various configurations and sampling techniques is considered to perform a comprehensive assessment. Each DL model was subjected to eight runs, four runs of random search, and four runs of Bayesian optimization. Within each tuning process, four dataset scenarios were tested, including cases without sampling, with SMOTE and ADASYN oversampling, and RUS techniques.

The experiments were carried out on a Windows 11 (64-bit Operating system) with 16 GB RAM and one Tera GB SSD. Python 3.9.7 was used on an Anaconda 3 Navigator for implementing the proposed credit card fraud detection model.

5.1 Hyperparameter Optimization Results

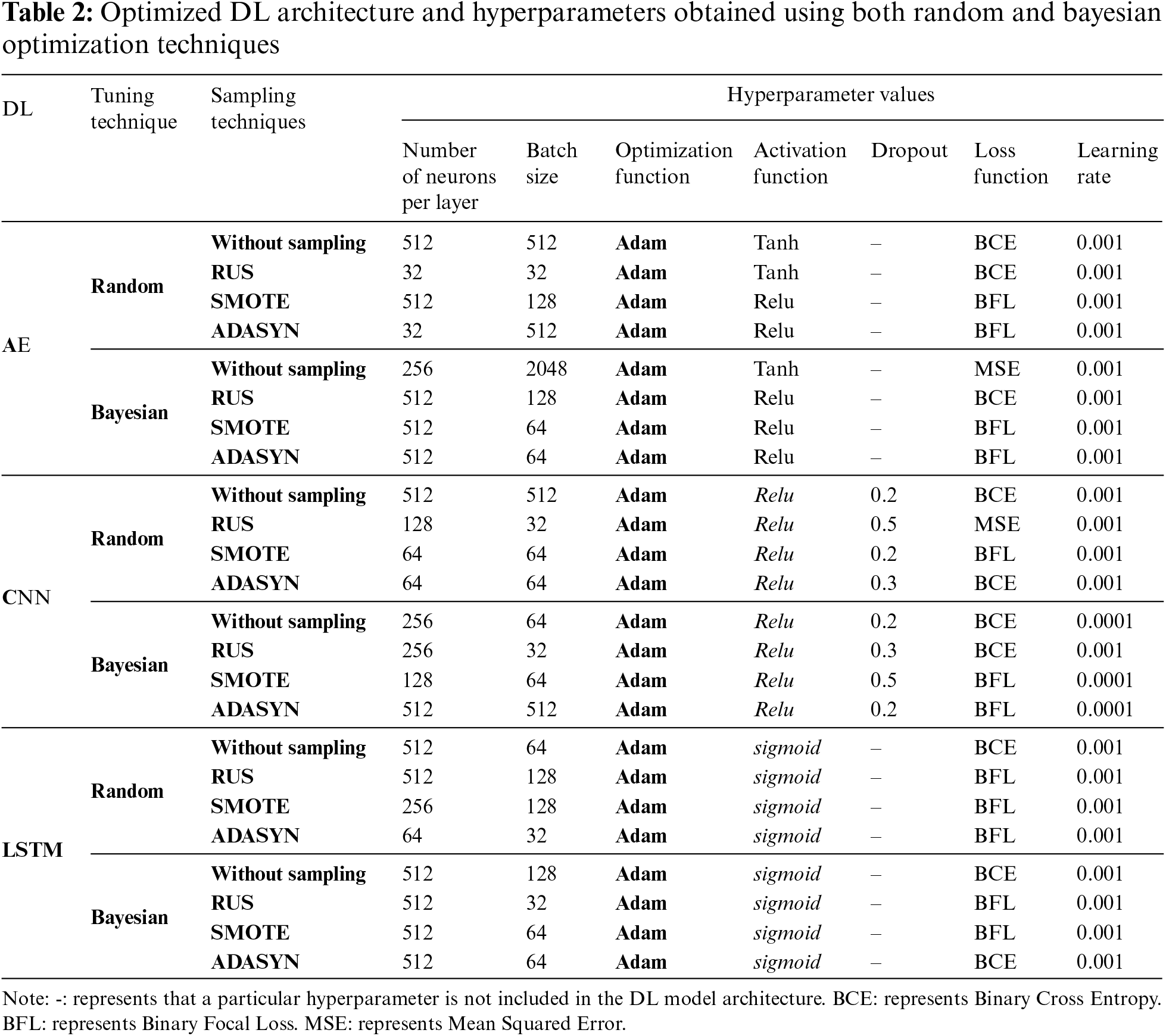
Table 2 provides the best value found for each hyperparameter of three DL models using both random and Bayesian optimization techniques.

The range or set of potential values for each hyperparameter throughout the hyperparameter tuning process is referred to as the hyperparameter search space. It describes the exploration area for determining the best hyperparameter combinations for DL models used in credit card fraud detection. It is critical to properly specify the hyperparameter search space in order to cover a wide range of potential values while keeping computing resources and time restrictions in consideration. The adopted hyperparameters and their corresponding search space that are used in this paper for credit card fraud detection are as follows:

1.    The number of neurons in each layer controls the model’s capacity to learn complex patterns and representations from the data. It has an impact on the network’s behavior and performance. Increasing the number of neurons in a layer raises the computational cost of training and makes the model more subject to overfitting. The choices for this parameter include 32, 64, 128, 256, and 512.

2.    Dropout hyperparameter: a regularization technique to prevent overfitting. It can help model convergence by preventing the network from being trapped in local minima during training. The potential values for this hyperparameter are 0.2, 0.3, and 0.5.

3.    Activation functions make it possible for neural networks to learn complicated patterns and correlations in data. Different activation functions have different effects on deep learning model training and performance. The activation functions parameter is set to Relu, sigmoid, and tanh.

4.    Batch size refers to the number of training examples utilized in one iteration. Batch size chosen can have several consequences on neural network training, including computing efficiency and generalization. Different batch sizes are considered including 32, 64, 128, 256, 512, and 2048.

5.    Optimization algorithms setting includes stochastic gradient descent (SGD), adaptive gradient (Adagrad), and adaptive moment estimation (Adam).

6.    Learning rate determines the step size during model parameter updates. A higher learning rate leads to faster convergence during training, since the model makes larger adjustments to its weights at each iteration. Three values for learning rate are considered including 0.01, 0.001, 0.0001.

7.    Loss function defines the objective that the model aims to minimize during training. It assesses the model’s performance by quantifying the difference between projected and actual goal values. The loss function can influence neural network training and behavior, including convergence speed and training stability. The choices for this parameter include binary focal loss (with gamma = 2), binary cross-entropy, and mean squared error (MSE).

It is clear from Table 2 that the Adam optimizer with different learning rates is by far the most preferred optimizer for all three DL models. This comes from Adam’s ability to combine the first-order moment of the gradients and the second-order moment of the gradients to allow adaptive learning rates and momentum-like updates at the same time. In addition, it performs a bias correction by scaling the first and second moments which ensures a more accurate estimation of the moments in the early stages of training.

Furthermore, the learning rate for the AE model remained similar throughout all eight experiments. This may be given to the architecture of the AE model or to the same range of learning rate values investigated during random search and Bayesian optimization, leading to the determination of a comparable optimal value.

Considering the CNN model, random search and Bayesian optimization provide consistent optimum activation function results throughout all eight runs, showing that it has arrived at its choice during the hyperparameter tuning phase. The dominance of this particular activation function is likely due to the specific design of the CNN architecture and the characteristics of the dataset, making it the best option independent of the optimization technique used. Regarding LSTM, both random and Bayesian techniques produce a sigmoid as the best activation function since LSTM architecture uses gate mechanisms to control the flow of information through the cell, allowing them to remember or forget information over time. The sigmoid activation function, with its range of [0,1], is ideal for gating operations as it can regulate the amount of information to be retained or discarded. Also, the credit card transactions’ sequential nature, forms time series data and the sigmoid activation function’s ability to maintain long-term dependencies makes it effective for modeling fraud patterns that may span multiple time steps.

5.2 Performance Evaluation

In this section, the performance of the DL models with hyperparameter tuning using random and Bayesian are analyzed and compared in terms of accuracy, DR, and AUC as shown in Table 3. From the results, it is clear when comparing the performance of DL models with hyperparameter tuning using random search and Bayesian optimization, Bayesian optimization surpasses random search in most cases. Also, one can see that the DL model with sampling techniques outperforms the DL model without sampling in all the experiments. This illustrates the beneficial effect of collaborating sampling techniques with DL models. Further, both SMOTE and ADASYN provide superior performance compared to RUS. This is due to their ability to effectively augment the training data that help the DL models learn more diverse and representative patterns and promote better generalization to unseen data. In contrast, RUS simply removes instances from the majority class, leading to a loss of potentially valuable information and increasing the risk of overfitting.

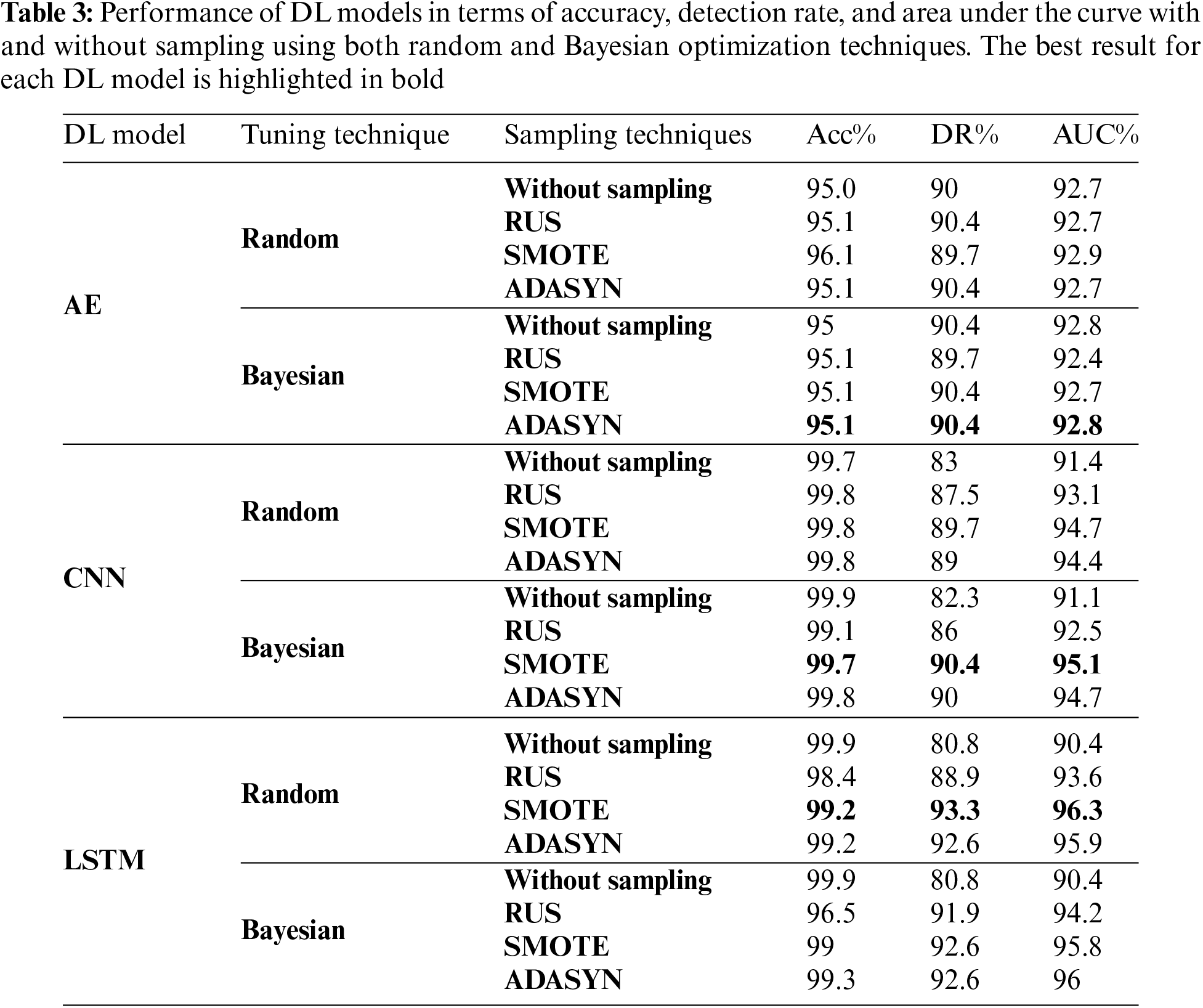
Furthermore, the selection between ADASYN and SMOTE is affected by the characteristics of the data and the type of DL being employed. ADASYN performs better when combined with AE, but SMOTE performs better when combined with CNN and LSTM. This is because ADASYN emphasizes producing samples for the minority class based on the dataset’s density distribution which is suitable with AE. While SMOTE generates synthetic samples depending on the interpolating between current minority-class samples which is suitable with CNN and LSTM.

On the other hand, LSTM and CNN models with SOMTE sampling demonstrated a better performance than AE due to their ability to handle sequential data, making them more suitable for capturing the temporal patterns and dependencies present in credit card transaction sequences. AE may not be as effective in modeling sequential information, as they treat the data as unordered and independent samples. Also, CNN and LSTM can automatically learn relevant features from the data during training. For CNN, this is achieved through convolutional and pooling operations, while LSTMs can effectively handle the vanishing gradient problem and learn meaningful features in long sequences.

5.3 Comparison Performance between the Proposed Models and Previous Works

The proposed model’s performance has been evaluated by comparing its results with previous works using the hyperparameter values reported in Table 4. The proposed DL model results are compared with [19,21,23,25] in terms of accuracy, DR, and AUC as shown in Table 5.

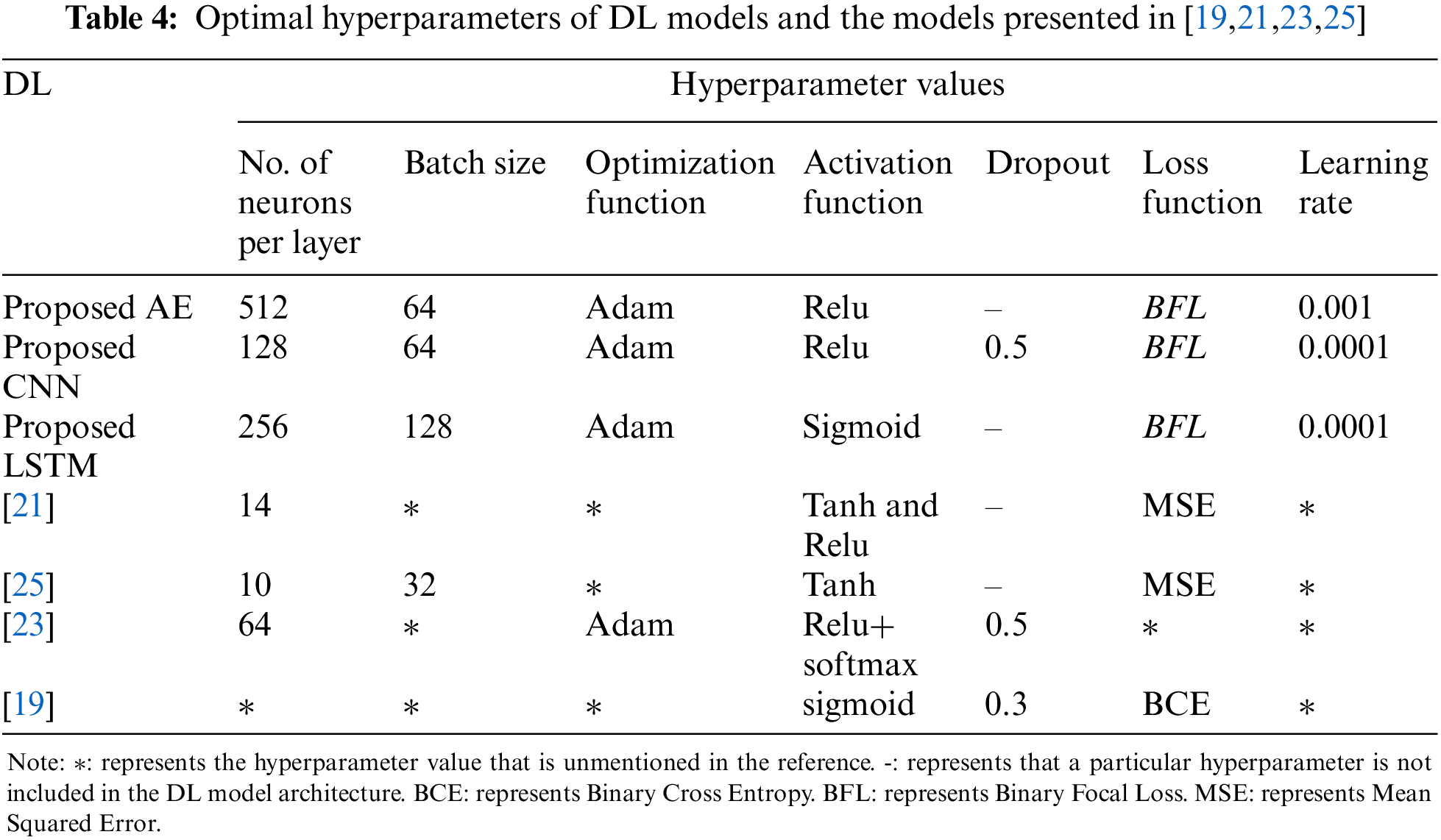
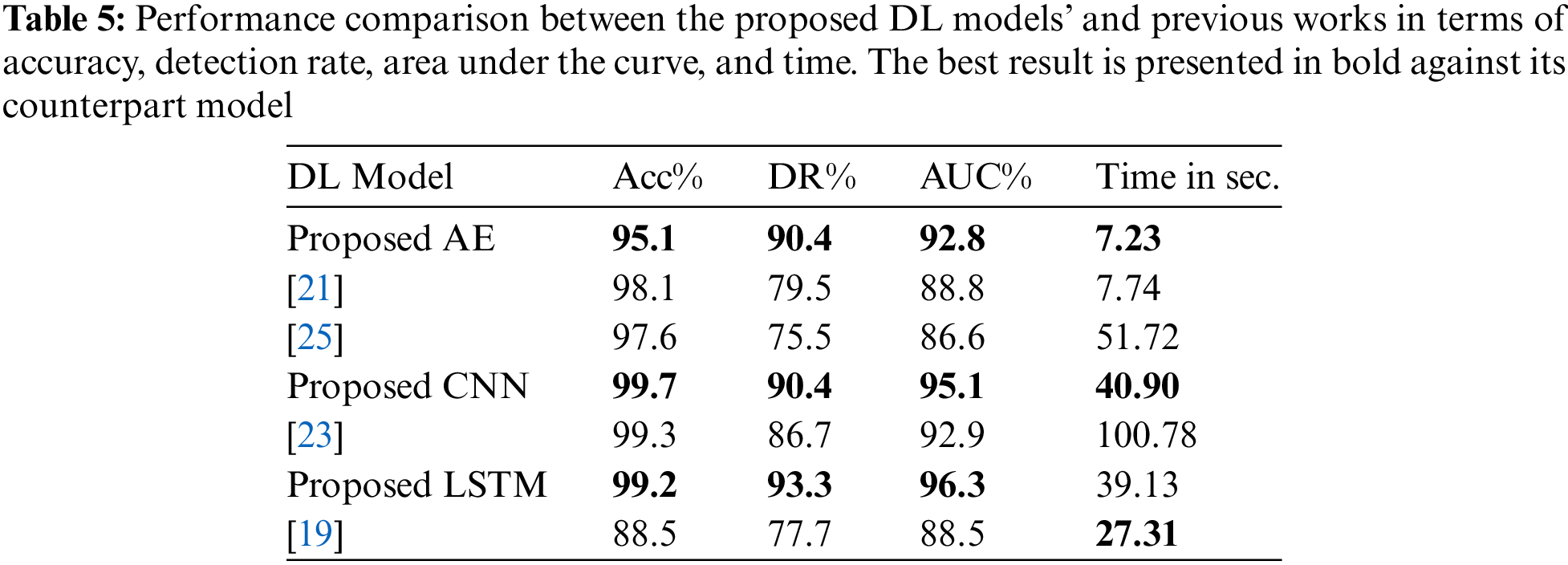
From Table 5, it is obvious that the proposed models surpass the previous works. This is due to the inclusion of an extra set of hyperparameters in the tuning technique that was not considered in the previous work which effectively helps DL to capture the interdependence between high-dimensional features. In addition, one can see that the fraud detection performance of the proposed model is significantly better than that of [19,21,23,25] because determining the best successful combination of hyperparameter values for detecting fraud in financial transactions and the usage of binary focal loss (BFL) function improved DR results by helping the models converge faster and better and avoid noisy samples during training, it also effectively down-weighting the easy to classify normal transactions and gave more emphasis to hard- classify fraudulent transactions.

Table 5 demonstrates that the proposed model reaches its optimal solution faster with AE and CNN models compared to those mentioned in [19,21,25]. On the other hand, when utilizing LSTM architecture, the time taken by the proposed model is longer due to the intricacies of its architectural design, although it outperforms the model described in [18]. The variations in timing result from the incorporation of early stopping techniques, and the use of a reduced batch size.

The proposed model can be evaluated by plotting the ROC curve. The ROC curve illustrates the relationship between the true positive rate (TPR) and the false positive rate (FPR) for different threshold values that allow for visualizing the trade-off between correctly and incorrectly classifying.

Figs. 3–5 depict the comparison of the proposed AE with related counterparts in [21,25], the proposed CNN against its counterpart in [23], and the proposed LSTM against its counterpart in [19], respectively. The figures clearly show that the proposed model exhibits a higher level of discrimination between normal and fraudulent transactions and its superior performance in credit card fraud detection compared to [19,21,23,25] and since the ROC curves of the proposed models are closest to the top-left corner of the graph that indicating have a high TPR (DR) and low FPR.

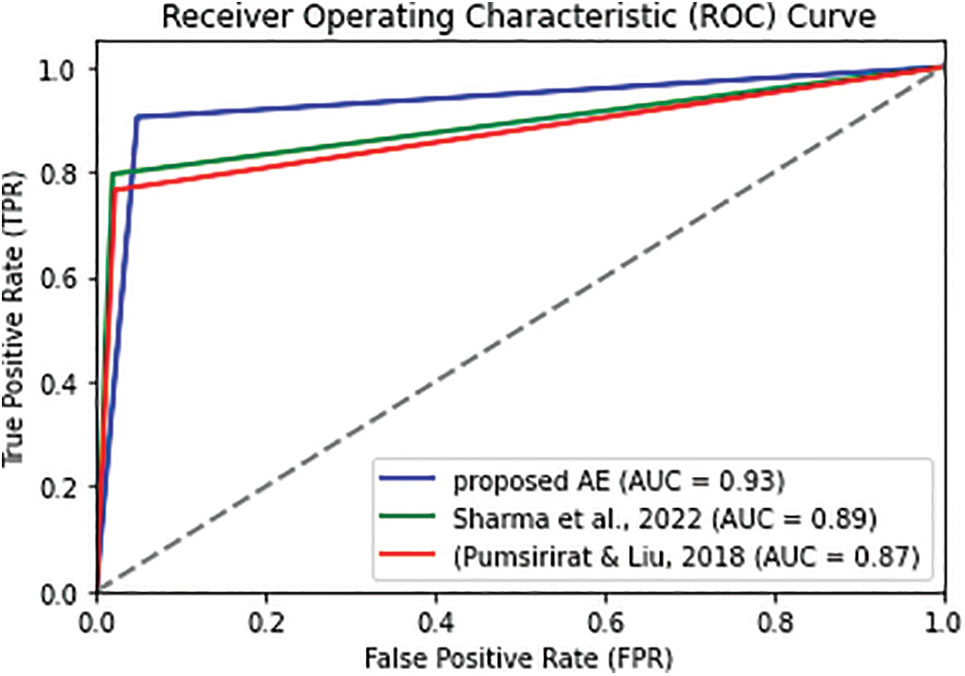
Figure 3: ROC curve visualization of the proposed AE model against Sharma et al. of [21] and Pumsirirat model of [25]

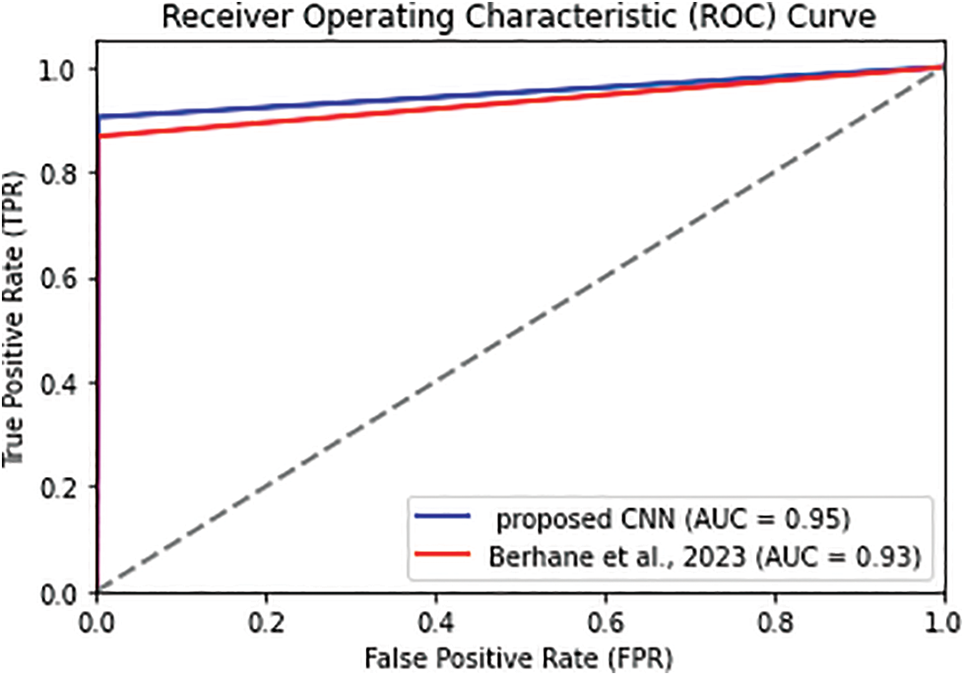
Figure 4: ROC curve visualization of the proposed CNN model against Berhane et al. model of [23]

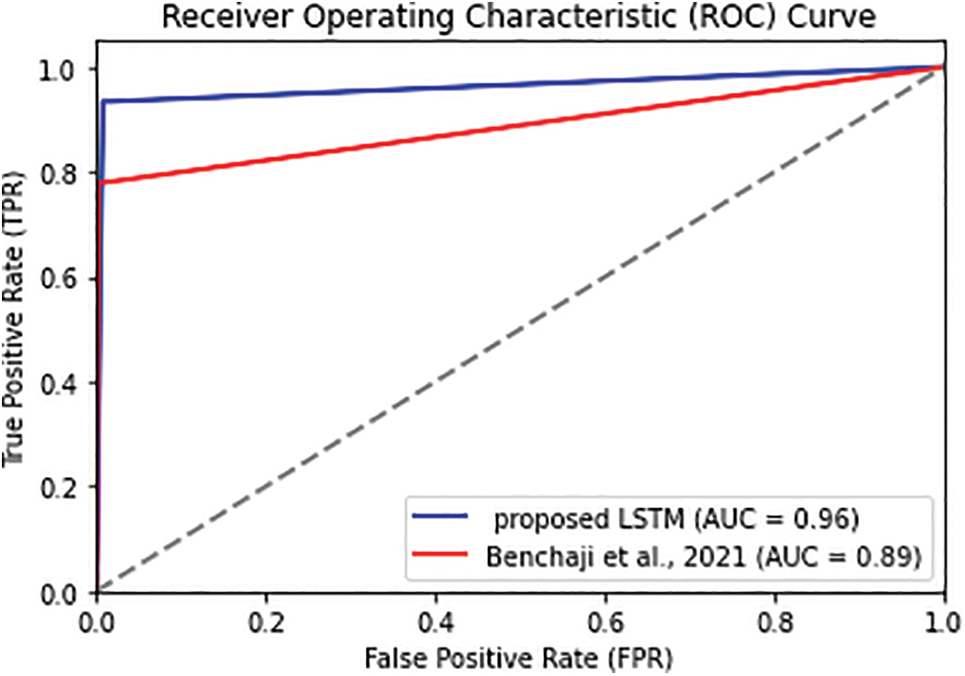
Figure 5: ROC curve visualization of the proposed LSTM model against Benghazi et al. model of [19]

6  Conclusions

The issue of global credit card fraud detection is a matter of great concern. The accurate identification of fraudulent transactions is crucial for financial institutions and researchers. The paper suggests a model that combines DL techniques with hyperparameter optimization to detect patterns in credit card transactions and determine the most effective hyperparameter settings. The models proposed for fraud detection rely on three DL techniques, namely AE, CNN, and LSTM. In addition, two optimizing techniques, random search, and Bayesian, are used for hyperparameter tuning. The proposed models differ from recent works in the number of hyperparameters, search space, and objective function (F1-score) used for optimization. The experiments were conducted using a dataset of European credit card transactions, employing the three DL models. The results illustrate that the proposed models can substantially improve the accuracy of identifying fraudulent transactions through data preprocessing, making it more suitable for DL models, and the optimization of hyperparameters. Furthermore, the proposed models exhibit superior performance compared to existing state-of-the-art models in terms of accuracy, DR, area AUC, and processing times. As a result, the proposed models can be a promising solution for detecting fraud in financial transactions.

One area of concern in the proposed models is the need to enhance the detection rate. Therefore, future research should focus on devising an oversampling method that can effectively boost the detection rate of credit card fraud.

Acknowledgement: None.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design: Sarab M. Hameed, Sumaya S. Sulaiman, Ibraheem Nadher; data collection: Sarab M. Hameed, Sumaya S. Sulaiman; analysis and interpretation of results: Sarab M. Hameed, Sumaya S. Sulaiman, Ibraheem Nadher; draft manuscript preparation: Sarab M. Hameed, Sumaya S. Sulaiman, Ibraheem Nadher. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All datasets and materials are publicly available.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Cherif, A. Badhib, H. Ammar, S. Alshehri, M. Kalkatawi et al., “Credit card fraud detection in the era of disruptive technologies: A systematic review,” Journal of King Saud University—Computer and Information. Science, vol. 35, no. 1, pp. 145–174, 2023. [Google Scholar]

2. N. Rosley, G. K. Tong, K. H. Ng, S. N. Kalid and K. C. Khor, “Autoencoders with reconstruction error and dimensionality reduction for credit card fraud detection,” in Proc. of the Int. Conf. on Computer, Information Technology and Intelligent Computing (CITIC), Cyberjaya, Malaysia, Atlantis Press, pp. 503–512, 2022. [Google Scholar]

3. N. Boutaher, A. Elomri, N. Abghour, K. Moussaid and M. Rida, “A review of credit card fraud detection using machine learning techniques,” in 5th Int. Conf. on Cloud Computing and Artificial Intelligence: Technologies and Applications (CloudTech), Marrakesh, Morocco, IEEE, pp. 1–5, 2020. [Google Scholar]

4. A. Dal Pozzolo, G. Boracchi, O. Caelen, C. Alippi and G. Bontempi, “Credit card fraud detection: A realistic modeling and a novel learning strategy,” IEEE Transactions on Neural Networks and Learning Systems, vol. 29, no. 8, pp. 3784–3797, 2017. [Google Scholar]

5. S. Makki, Z. Assaghir, Y. Taher, R. Haque, M. S. Hacid et al., “An experimental study with imbalanced classification approaches for credit card fraud detection,” IEEE Access, vol. 7, pp. 93010–93022, 2019. [Google Scholar]

6. E. Strelcenia and S. Prakoonwit, “Improving classification performance in credit card fraud detection by using new data augmentation,” AI, vol. 4, no. 1, pp. 172–198, 2023. [Google Scholar]

7. A. Wahid, M. Msahli, A. Bifet and G. Memmi, “NFA: A neural factorization autoencoder based online telephony fraud detection,” Digital Communications and Networks, 2023. https://doi.org/10.1016/j.dcan.2023.03.002 [Google Scholar] [CrossRef]

8. Y. Xie, A. Li, B. Hu, L. Gao and H. Tu, “A credit card fraud detection model based on multi-feature fusion and generative adversarial network,” Computers, Materials & Continua, vol. 76, no. 3, pp. 2707–2726, 2023. [Google Scholar]

9. N. H. Ali, M. E. Abdulmunem and A. E. Ali, “Learning evolution: A survey,” Iraqi Journal of Science, vol. 62, no. 12, pp. 4978–4987, 2021. [Google Scholar]

10. S. J. Muhamed, “Detection and prevention WEB-service for fraudulent E-transaction using APRIORI and SVM,” Al-Mustansiriyah Journal of Science, vol. 33, no. 4, pp. 72–79, 2022. [Google Scholar]

11. M. Feurer and F. Hutter, “Hyperparameter optimization,” in Automated Machine Learning: Methods, Systems, Challenges, in the Springer Series on Challenges in Machine Learning Book Series (SSCML), 1st ed., vol. 2, Switzerland, Cham: Springer, pp. 3–33, 2019. https://doi.org/10.1007/978-3-030-05318-5_1 [Google Scholar] [CrossRef]

12. P. Kumar, S. Batra and B. Raman, “Deep neural network hyper-parameter tuning through twofold genetic approach,” Soft Computing, vol. 25, no. 13, pp. 8747–8771, 2021. [Google Scholar]

13. J. Bergstra, R. Bardenet, Y. Bengio and B. Kégl, “Algorithms for hyper-parameter optimization,” in Advances in Neural Information Processing Systems, Curran Associates Inc., Spain, pp. 2546–2554, 2011. [Google Scholar]

14. M. Tayebi and S. El Kafhali, “Hyperparameter optimization using genetic algorithms to detect frauds transactions,” in Proc. of the Int. Conf. on Artificial Intelligence and Computer Vision (AICV2021), Cham, Settat, Morocco, Springer International Publishing, pp. 288–297, 2021. [Google Scholar]

15. A. A. Taha and S. J. Malebary, “An intelligent approach to credit card fraud detection using an optimized light gradient boosting machine,” IEEE Access, vol. 8, pp. 25579–25587, 2020. [Google Scholar]

16. K. Huang, “An optimized LightGBM model for fraud detection,” Journal of Physics: Conference Series, vol. 1651, no. 1, pp. 012111, 2020. [Google Scholar]

17. N. Rtayli and N. Enneya, “Enhanced credit card fraud detection based on SVM-recursive feature elimination and hyper-parameters optimization,” Journal of Information Security and Applications, vol. 55, pp. 102596, 2020. [Google Scholar]

18. M. Tiwari, V. Sharma and D. Bala, “Credit card fraud detection,” Journal of Algebraic Statistics, vol. 13, no. 2, pp. 1778–1789, 2022. [Google Scholar]

19. I. Benchaji, S. Douzi, B. El Ouahidi and J. Jaafari, “Enhanced credit card fraud detection based on attention mechanism and LSTM deep model,” Journal of Big Data, vol. 8, no. 1, pp. 151, 2021. [Google Scholar]

20. M. Isangediok and K. Gajamannage, “Fraud detection using optimized machine learning tools under imbalance classes,” in IEEE Int. Conf. on Big Data (Big Data), Osaka, Japan, pp. 4275–4284, 2022. [Google Scholar]

21. M. A. Sharma, B. G. Raj, B. Ramamurthy and R. H. Bhaskar, “Credit card fraud detection using deep learning based on auto-encoder,” in Fourth Int. Conf. on Advances in Electrical and Computer Technologies (ICAECT) ITM Web of Conf., Tamil Nadu, India, 2022. [Google Scholar]

22. S. K. Hashemi, S. L. Mirtaheri and S. Greco, “Fraud detection in banking data by machine learning techniques,” IEEE Access, vol. 11, pp. 3034–3043, 2023. [Google Scholar]

23. T. Berhane, T. Melese, A. Walelign and A. Mohammed, “A hybrid convolutional neural network and support vector machine-based credit card fraud detection model,” Mathematical Problems in Engineering, vol. 2023, pp. 8134627, 2023. [Google Scholar]

24. A. Taha, “A novel deep learning-based hybrid Harris hawks with sine cosine approach for credit card fraud detection,” American Institute of Mathematical Sciences (AIMS) Mathematics, vol. 8, no. 10, pp. 23200–23217, 2023. [Google Scholar]

25. A. Pumsirirat and Y. Liu, “Credit card fraud detection using deep learning based on auto-encoder and restricted Boltzmann machine,” International Journal of Advanced Computer Science and Applications, vol. 9, no. 1, pp. 18–25, 2018. [Google Scholar]

26. R. Ball, H. Kruger and L. Drevin, “Anomaly detection using autoencoders with network analysis features,” ORiON Journal of the Operations Research Society of South Africa, vol. 39, no. 1, pp. 1–44, 2023. [Google Scholar]

27. W. Hilal, S. A. Gadsden and J. Yawney, “Financial fraud: A review of anomaly detection techniques and recent advances,” Expert Systems with Applications, vol. 193, pp. 116429, 2022. [Google Scholar]

28. M. S. Kwon, Y. G. Moon, B. Lee and J. H. Noh, “Autoencoders with exponential deviation loss for weakly supervised anomaly detection,” Pattern Recognition Letters, vol. 171, pp. 131–137, 2023. [Google Scholar]

29. G. Habib and S. Qureshi, “Optimization and acceleration of convolutional neural networks: A survey,” Journal of King Saud University—Computer and Information. Science, vol. 34, no. 7, pp. 4244–4268, 2022. [Google Scholar]

30. T. A. Wotaifi and B. N. Dhannoon, “An effective hybrid deep neural network for arabic fake news detection,” Baghdad Science Journal, vol. 20, no. 4, pp. 1392, 2023. https://doi.org/10.21123/bsj.2023.7427 [Google Scholar] [CrossRef]

31. M. Haqi Al-Tai, B. M. Nema and A. Al-Sherbaz, “Deep learning for fake news detection: Literature Review,” Al-Mustansiriyah Journal of Science, vol. 34, no. 2, pp. 70–81, 2023. [Google Scholar]

32. Z. Zhang, X. Zhou, X. Zhang, L. Wang and P. Wang, “A model based on convolutional neural network for online transaction fraud detection,” Security and Communication Networks, vol. 2018, pp. 5680264, 2018. [Google Scholar]

33. H. H. Ali, J. R. Naif and W. R. Humood, “A new smart home intruder detection system based on deep learning,” Al-Mustansiriyah Journal of Science, vol. 34, no. 2, pp. 60–69, 2023. [Google Scholar]

34. W. M. S. Abedi, A. T. Sadiq and I. Nadher, “Modified CNN-LSTM for pain facial expressions recognition,” International Journal of Advanced Science and Technology, vol. 29, no. 3s, pp. 304–312, 2020. [Google Scholar]

35. S. Wang, C. Ma, Y. Xu, J. Wang and W. Wu, “A hyperparameter optimization algorithm for the LSTM temperature prediction model in data center,” Sensitive Compartmented Information, vol. 2022, pp. 6519909, 2022. [Google Scholar]

36. J. Bergstra and Y. Bengio, “Random search for hyper-parameter optimization,” Journal of Machine Learning Research, vol. 13, no. 2, pp. 281–305, 2012. [Google Scholar]

37. D. Vidyabharathi and V. Mohanraj, “Hyperparameter tuning for deep neural networks based optimization algorithm,” Intelligent Automation & Soft Computing, vol. 36, no. 3, pp. 2559–2573, 2022. [Google Scholar]

38. E. Bartz, T. Bartz Beielstein, M. Zaefferer and O. Mersmann, Hyperparameter Tuning for Machine and Deep Learning with R: A Practical Guide. Gateway East, Singapore: Springer Nature Singapore Pte Ltd., 2023. [Google Scholar]

39. T. K. Dang, T. C. Tran, L. M. Tuan and M. V. Tiep, “Machine learning based on resampling approaches and deep reinforcement learning for credit card fraud detection systems,” Applied Sciences, vol. 11, no. 21, pp. 10004, 2021. [Google Scholar]

40. T. H. Lin and J. R. Jiang, “Credit card fraud detection with autoencoder and probabilistic random forest,” Mathematics, vol. 9, no. 21, pp. 2683, 2021. [Google Scholar]

41. A. Muaz, M. Jayabalan and V. Thiruchelvam, “A comparison of data sampling techniques for credit card fraud detection,” International Journal of Advanced Computer Science and Applications, vol. 11, no. 6, pp. 477–485, 2020. [Google Scholar]

42. W. Falah and I. J. Mohammed, “Hybrid CNN-SMOTE-BGMM deep learning framework for network intrusion detection using unbalanced dataset,” Iraqi Journal of Science, vol. 64, no. 9, pp. 4846–4864, 2023. [Google Scholar]

43. “European card holders dataset,” [Online]. Available: https://www.kaggle.com/datasets/mlg-ulb/creditcardfraud (accessed on 08/06/2023). [Google Scholar]