IndRT-GCNets: Knowledge Reasoning with Independent Recurrent Temporal Graph Convolutional Representations

1  Introduction

Knowledge reasoning, as one of the fundamental tasks in natural language processing, has been extensively applied in various real-world scenarios such as disaster relief [1] and financial analysis [2]. However, due to the incompleteness of knowledge representation, its representational performance and application scope are limited. Traditional knowledge graph reasoning is regarded as a static representation of multiple relationships. Nevertheless, with the emergence of interactive data from relevant events, static representations struggle to capture the temporal dynamics within these interactive data. To address this issue, many researchers have proposed methods for representing and reasoning with temporal knowledge graphs [3]. Specifically, a temporal knowledge graph can be represented as a sequence of knowledge graphs with timestamps, where each knowledge graph contains events that occurred simultaneously at a given time. However, when performing inference on such data, establishing effective associations and dependencies between entities and relationships poses significant challenges. Moreover, reasoning efficiency also needs to be improved. Fig. 1 is an example of a temporal knowledge graph (TKG).

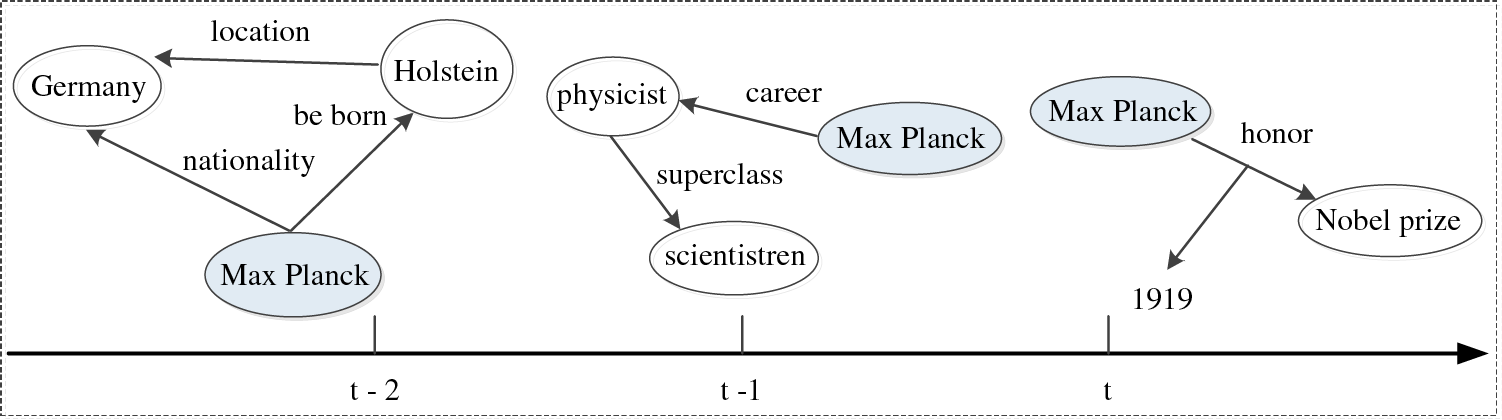
Figure 1: An instance of TKG

Previous knowledge reasoning methods mainly modeled the occurrence of all events as a single time point process to learn evolving entity representations, such as dynamic graph representation methods [4]. Although these methods can effectively improve reasoning efficiency and accuracy, they cannot effectively model concurrent events within the same period. To address these issues, recently, approaches based on temporal knowledge graph reasoning have been widely applied [3,5], such as temporal event graph-based recurrent event networks and sequence generation networks [6,7]. The recurrent event network processes concurrent events by capturing events related to a given entity, sequentially modeling and encoding them. Sequence generation networks model events with the same entities or relationships related to entities. They predict the overall event by focusing on reusing entities or relationships.

Although the above methods have shown some improvements in predictive performance, efficiency, and the ability to handle concurrent events, they focus solely on established entities and relationships, neglecting the structural dependencies among entities and relationships within the same period. Moreover, they tend to lose certain static details of entities during the modeling process. Furthermore, these methods involve extensive modeling of historical events during the encoding process, with a strong focus on predicting entities within events. This emphasis on entities in events often overlooks the significance of relationships to entities. In essence, entity and relationship prediction cannot be effectively integrated within the same network, leading to error accumulation and a decrease in the model’s reasoning efficiency.

To address the above issues, this paper unifies the modeling of the entire knowledge graph sequence to learn evolutionary representations of entities and relationships within each period. This approach effectively captures dependencies among entities and relationships within the knowledge graph, enables interactions between events, and efficiently models temporally adjacent events through independent recurrent neural network components. Furthermore, the model’s static graph constraint module accurately describes the static details of entities throughout the entire event. The main contributions of this research are as follows.

(1) This paper proposes a temporal graph convolution framework called Independent Recurrent Temporal Graph Convolution Networks (IndRT-GCNets) aimed at capturing the dependencies among concurrent events in the knowledge graph and the static details of entities in temporally adjacent events. By unified modeling, we encode all events into representations of entities and relationships to improve the model’s predictive accuracy.

(2) We design the evolutionary representation unit, namely, the Independent Recurrent Temporal Graph Convolution module (IndRT-GCM), using the aggregation and propagation capabilities of nodes in temporal graph convolution, to perceive structural dependency relationships and provide a further description of the static details of entities. This helps in modeling and evolving the interaction information between events and effectively perceives the correlation between entities and relationships.

(3) We embed the independent recurrent neural network into the evolutionary representation unit, utilizing the gated recurrent components for autoregressive modeling to effectively capture sequential patterns of all temporally adjacent events. It is worth mentioning the static attributes of entities in all events are merged using a static graph as a constraint. To optimize and adjust the proposed framework for obtaining optimal representations, we design a set of weighted losses. Finally, experimental validation is conducted on multiple baseline datasets, resulting in the best performance, along with good robustness and inference efficiency.

The remaining structure of this paper is as follows: Section 2 provides a detailed overview of related work in knowledge inference. Section 3 focuses on the proposed IndRT-GCNets framework and provides detailed descriptions of each module. Section 4 presents the experimental results and analysis, along with discussions on the provided examples. The conclusion and future research directions are provided in Section 5.

2  Related Work

Early knowledge inference mainly focused on using static knowledge graphs to infer missing events within the graph. Dettmers et al. [8] considered that the existing link prediction models learned fewer features than those learned by deep multi-layer models, so they introduced ConvE, proposing a multi-layer convolutional network model for link prediction, which achieved better performance on multiple datasets. Shang et al. [9] recognized there is no structural constraint in the embedding space of ConvE. They proposed a novel end-to-end structure-aware convolutional network (SACN), which combines the advantages of graph convolution and ConvE. SACN uses a weighted graph convolution network that incorporates knowledge graph node structure, node attributes, and edge relationship types to effectively locally aggregate detailed information from neighbors, thus embedding graph node semantics more accurately. Lin et al. [10] proposed a rule-enhanced iterative complementarity model to infer missing valid triples and improve the semantic representation of the knowledge graph. This method consists of three crucial components: rule learning, embedding learners, and triple discriminators. It enriches the semantics of the knowledge graph and further improves the completeness of rule learning for generating hidden triples. Zhao et al. [11] considered that graph attention tends to allocate attention to certain high-frequency relations, overlooking the correlations between target relations, so they proposed a hierarchical attention mechanism to aggregate information from multi-hop neighbors, aiming to obtain better node embedding representations. Zhang et al. [12] introduced a Multi-scale Dynamic Convolutional Network (M-DCN) model for knowledge graph embedding to generate richer features. Schlichtkrull et al. [13] proposed Relational Graph Convolutional Networks (R-GCNs) and applied them to two knowledge graph completion tasks: link prediction and entity classification. Vashishth et al. [14] presented a new graph convolution framework CompGCN, which jointly embeds nodes and relations into the graph, scaling based on the number of relations. Ye et al. [15] proposed a vectorized relational graph convolutional network that can simultaneously learn embeddings for graph entities and relations in a multi-relational network. This network incorporates role discrimination and translation properties from knowledge graphs into the convolution process. While these methods can improve inference performance, the quality of static knowledge graphs can impact reasoning results, and such methods may not effectively predict dynamic events.

Recently, temporal knowledge graph reasoning methods have received significant attention. Goel et al. [5] built novel models for temporal KG completion by equipping static models with a diachronic entity embedding function that provides the characteristics of entities at any point in time. The embedding function of the method is model-agnostic and can be potentially combined with any static model. Han et al. [16] proposed a non-Euclidean embedding approach that learns evolving entity representations in a product of Riemannian manifolds, where the composed spaces are estimated from the sectional curvatures of underlying data. Wu et al. [17] proposed the TeMP framework to address the temporal sparsity and variability of entity distributions in temporal knowledge graphs by combining graph neural networks, temporal dynamics models, data imputation, and frequency-based gating techniques. Xu et al. [18] proposed ATiSE, which incorporates time information into entity/relation representations by using Additive Time Series decomposition. Moreover, considering the temporal uncertainty during the evolution of entity/relation representations over time, they mapped the representations of temporal KGs into the space of multi-dimensional Gaussian distributions. Li et al. [19] observed that temporally similar facts exhibit sequential patterns and proposed a Recurrent Evolutionary Network that learns evolving representations of entities and relationships at each time point by recurrent modeling of the knowledge graph sequence. Similarly, Li et al. [20] introduced a Complex Evolutionary Network (CEN) and used Length-Aware Convolutional Neural Networks (CNNs) to handle evolving patterns of different lengths, representing entities and relationships through an easy-to-hard curriculum learning strategy. Park et al. [21] proposed EvoKG that jointly models both tasks in an effective framework and captures the evolving structure and temporal dynamics of the temporal knowledge graph through recurrent event modeling. They used a time neighborhood aggregation framework to model interactions between entities. Jiao et al. [22] presented an enhanced Complex Temporal Reasoning Network that improves complex temporal reasoning for temporal reasoning problems and captures implicit temporal features and relation representations. Nie et al. [23] introduced TAL-TKGC to capture the influence of time information on quaternion and node structure information. The time-aware module aims to capture deep connections between timestamp entities and semantic-level relations, while the importance-weighted graph convolution considers the structural importance and attention of time information on entities for weighted aggregation. Wang et al. [24] proposed TASTER, a time-aware knowledge graph embedding method using a sparse transfer matrix, aiming to use both global and local information. Specifically, the model treats the Temporal Knowledge Graph (TKG) as a static knowledge graph by ignoring the time dimension. TASTER first learns global embeddings based on this static knowledge graph to acquire global information. To capture local information at specific timestamps, TASTER evolves from global embeddings to local embeddings based on the corresponding subgraphs.

Although these methods effectively model entities and relationships in the knowledge graph, they overlook the correlation and dependency relationships between entities and relationships in the temporal knowledge graph. Moreover, they lose a significant amount of static details of entities during the modeling process.

3  Proposed IndRT-GCNets Model

In this section, we provide a detailed explanation of the basic workflow of the proposed IndRT-GCNets knowledge reasoning framework. Furthermore, each important component of the framework is described in detail, such as the Independent Recurrent Evolution Unit, which includes the Independent Recurrent Module and the Temporal Graph Convolution Module. We explain the decoding operations for entities and relationships using Conv-TransD and Conv-TransR and provide an overview of the process for entity-relationship representation.

3.1 Overview

Fig. 2 illustrates the overall structure of the proposed IndRT-GCNets knowledge reasoning framework. The main components of this framework include the Independent Recurrent Temporal Graph Convolution Module (IndRT-GCM), entity-relation decoding, and embedding learning prediction module. The IndRT-GCM consists of the Static Graph Constraint Module (SGCM), Independent Recurrent Module (IndRM), and Temporal Graph Convolution Module (T-GCM) [25]. The SGCM aims to model the detailed attributes of entities and relationships, enhancing the representation of entities and relationships in events. The T-GCM captures the internal structural dependencies of events in the knowledge graph and models the correlation among entities and relationships within the same period, thereby strengthening their interaction and improving the discriminative power of deep semantics. The IndRM sequentially represents the temporal or adjacent time steps through gating mechanisms, capturing useful sequential information. It also incorporates the static attributes of entities and relationships obtained from the static graph into the temporal knowledge graph, significantly improving the evolutionary representation performance. The entity decoder Conv-TransD [26] and the relationship decoder Conv-TransR [27] transform entities and relationships and establish associations between them while preserving the translational features of convolutions to the maximum extent. They work collaboratively to enhance the prediction performance of entities and relationships in events. It is worth noting that the embedding learning prediction module is combined with the entity-relation decoders to achieve the evaluation of the corresponding tasks.

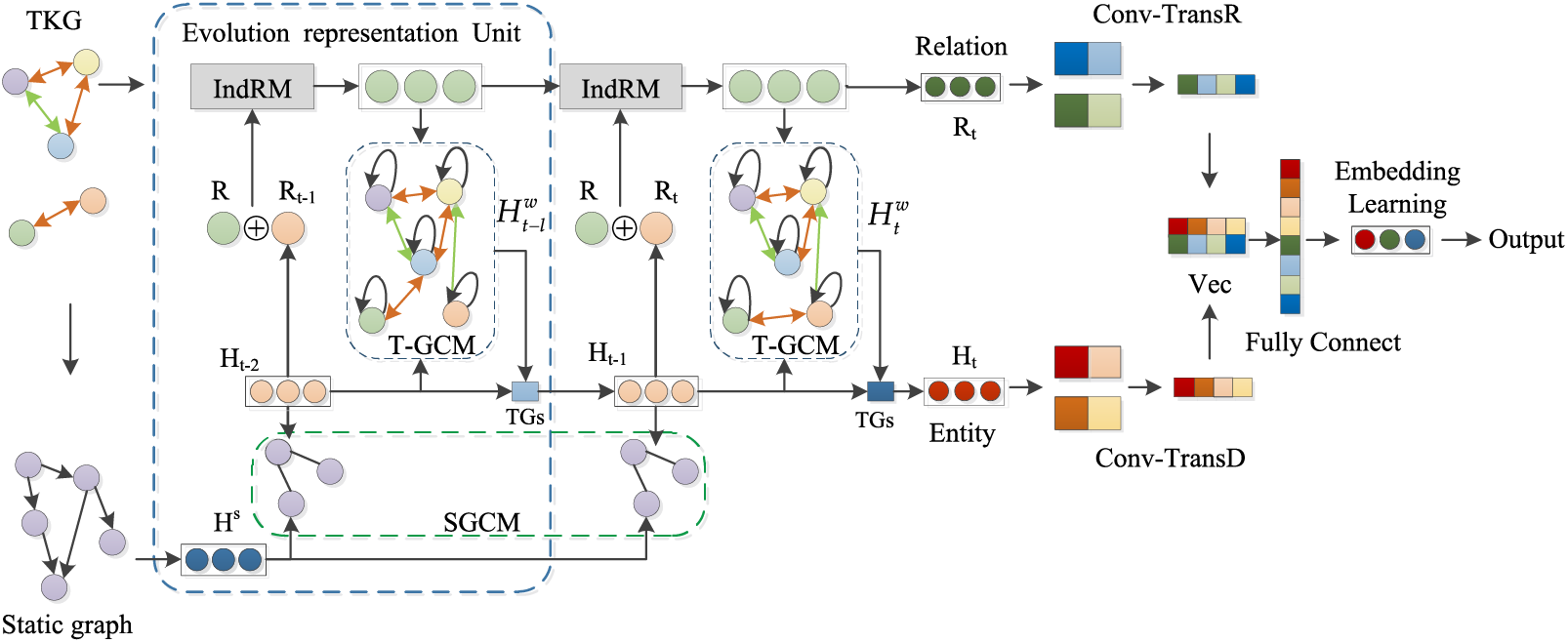
Figure 2: The overall network structure of IndRT-GCNets. The “IndRM” represents the Independent Recurrent Module, and the “T-GCM” represents the Temporal Graph Convolution Module. “TGs” indicates the time gates module. “SGCM” indicates static constrained graph convolution module. “Entity” and “Relation” respectively indicate entities and relationships. “Conv-TransD” and “Conv-TransR” represent the decoding components for entities and relationships. “Vec” denotes the vectorization operation. “Fully Connect” refers to the fully connected layer responsible for mapping entity-relation vectors. “Embedding Learning” primarily handles subsequent prediction tasks. R, Rt−1 and Rt−2 represent the relationship matrices within different periods of events. Ht, Ht−1 and Ht−2 denote the entity matrices for different periods of events

The prediction of entities and relations mainly focuses on predicting the missing entities and relations in the query event. Assuming the temporal knowledge graph is a knowledge graph sequence with time intervals, denoted as ς={ς1,…,ςt} where each knowledge graph can be represented as ςi=(ν,R,ϵi)∈ς, where v represents the set of graph nodes, i.e., entities in time. R represents the set of relations in the event. ϵi represents all the events within the period t and can be represented as a quadruple (s,r,o,t) that contains entities, relations, and time. The static graph aims to capture the detailed attributes of entities in the event and can be represented as ςs={(vs,Rs,εs)}, where vs represents the set of entities, Rs and εs represent the set of relations and edges, respectively. By constructing the aforementioned temporal and static graphs, we can model entities and relations to accurately infer entities and relations in the event.

3.2 Independent Recurrent Temporal Graph Convolution Module (IndRT-GCM)

IndRT-GCM is the evolutionary unit of entities and relationships in the knowledge reasoning framework. IndRT-GCM consists of a temporal graph convolutional module, two independent recurrent modules [28,29], and a static graph constraint component. The temporal graph convolutional module aims to capture the structural dependencies within the knowledge graph in each time interval and represent entities and relations. It establishes effective correlations between entities and relations by utilizing node propagation and aggregation functions to obtain deep semantic information while building associations between entities and relations. The static constraint component primarily models the static details of entities and embeds these attribute details into the temporal graph convolution to enhance entity representation. The operational steps of entities and relations within the independent recurrent temporal graph convolutional module are as follows.

Step 1. Assuming that the temporal knowledge graph during time intervals j to t can be represented as a sequence {ςt−j+1,ςt}, where the entity embedding matrix is denoted as {Ht−j+1,Ht}, and the relation embedding matrix is denoted as {Rt−j+1,Rt}. Considering the existence of correlations between entities within this time interval or the fact that a particular relation corresponds to multiple entities, it is also possible to obtain the relationships between entities through shared entities. This means that each knowledge graph can be a multi-relational graph, indicating the presence of concurrent events in the knowledge graph with strong structural dependencies. Therefore, there may be concurrent events within each time interval, and their structures are dependent on each other.

Step 2. For multi-relational graphs with concurrent events, we rely on the characteristic of graph convolution to effectively represent unstructured data and construct a deep temporal graph convolution module with L layers to model the structural dependencies in the relational graph. The embedding representation of entities and relations in the knowledge graph at the ith time step and lth layer is given by Eq. (1).

{ho,i(l)=σ(1λo∑i=1,z∈Zt,ZW1(l−1)⋅(hs,i(l−1)+ri)+W2(l−1)⋅ho,i(l−1))z=(s,r,o,t),Z=(s,r,o)∈ϵi,t∋i<t(1)

where ‘‘z’’ represents a quadruple that includes the entities, relation, and time, ‘‘s’’ and ‘‘o’’ denote the head entity and tail entity, respectively. ‘‘r’’ donates the relation between ‘‘s’’ and ‘‘o’’. ‘‘z’’ represents a triplet set of head entities, relationships, and tail entities. ϵi represents all the events within the period t. σ(⋅) denotes the activation function of the randomized rectified linear unit PReLU [30]. ho,i(l−1), hs,i(l−1) and ri represent the embedding representations of s, o and r, respectively, in the (l−1)th layer at time ith∈t and W1(l−1), W2(l−1) represent the weight matrices of the (l−1)th layer. λ0 represents the normalization constant of entity o. All graph nodes are self-loop nodes.

Step 3. Considering the correlation between adjacent events and the sequential patterns that provide effective contextual semantics over time, it is beneficial for improving the representation performance of entities and relations. Furthermore, to capture the contextual semantic details provided by correlation and sequential patterns, we model these events by stacking deep layers of temporal graph convolution. However, when the length of the knowledge graph sequence is large and multiple layers are stacked, it may lead to the issues of gradient vanishing or explosion, which can affect convergence and representation capacity. Therefore, we employ two temporal gating components (TGs) to alleviate these issues and determine the entity embedding matrix by the joint output of the temporal graph convolution module at the time tth and the time (t−1)th. The specific operation is shown in Eq. (2).

{ Ht=φt⊗Ht(L)−φt⊗Ht−1+Ht−1φt=σ1(W3Ht−1+θ)(2)

where σ1(⋅) represents the activation function ReLu [31]. W3 represents the weight matrix of the temporal gating component. ⊗ denotes the dot product operation. Ht(L) represents the entity embedding matrix of the last layer ((l)th layer) at time tth.

Step 4. In the embedding of relations, sequential patterns can also provide effective contextual semantics, and there is a correlation between entities and relations. Therefore, obtaining contextual semantic details is beneficial for the embedding representation of entities and relations. Due to the independence and cross-layer information propagation capabilities of the independent recurrent neural network, it is helpful to extract useful details from events across time. Therefore, we adopt the independent recurrent module to model it. The specific operation is shown in Eq. (3).

{ Rt=χδ(Rt−1,Rt')Rt'=GAPooling(Ht−1)⊕R(3)

where GAPooling(⋅) represents the global average pooling operation, which is beneficial for encoding global information and increasing the representation of global semantics in entities and relations. ⊕ represents the concatenation of feature matrices. χδ(⋅) represents the independent recurrent module (IndRM) for modeling relations, and IndRM is mainly composed of two layers of independent Recurrent neural networks. The specific operation of IndRM at the time tth is shown in Eq. (4).

{ χΔt=σΔ(ω⋅xt+μ⊙χΔt−1+θΔ)χΔn,t=σΔ(ωn⋅xn,t+μnχΔn,t−1+θΔn)(4)

where σΔ(⋅) represents the activation function RReLu [32]. ω represents the input weights. μ represents the recurrent weights. ⊙ represents the Hadamard product. θΔ represents the bias weights. χΔn,t represents the hidden layer output information of the tth neuron in IndRM.

Step 5. It is worth noting that the Static Graph Constraint Module (SGCM) can effectively capture the detailed attributes of entities in events to enhance the embedding representation of entities. The specific operations of the Static Graph Constraint Module are shown in Eq. (5).

{ hks=σs(1λk∑zkZkWrk⋅hk′k(ξ))zk=(rs,ξ)∈ϵs,Zk=(k,rs,ξ)∈ϵs(5)

where σs represents the LeakyReLu [33] activation function. Wrk represents the weight matrix for relations. λk represents the normalization constant, which is the number of connections between entities.

3.3 Entity and Relation Decoding and Prediction Module

This module mainly consists of the Conv-TransD and Conv-TransR decoders, which have a convolutional structure. They are used to decode and model the entities and relations in the events, respectively. These embedding vectors are mapped to a unified space to obtain better feature representations. While the embedding prediction component aims to integrate these decoding features and perform entity and relation prediction in the same space. The specific decoding and prediction process is shown in step 6.

Step 6. We take the entity matrix Ht and the relation matrix Rt, which are the outputs of the Independent Recurrent Temporal Graph Convolutional Module (IndRT-GCM) at the time tth, as inputs to the decoders. We use Conv-TransD to obtain the entity vector fHt and Conv-TransR to obtain the relation vector fRt. It is worth noting that Conv-TransR applies one-dimensional convolution with activation to map the relations, capturing decoding information while preserving translational properties to the maximum extent. The specific decoding embedding process is shown in Eq. (6).

{ fHt=ψctx(Ht)fRt=ψctr(Rt)(6)

where ψctx, ψctr represent the entity decoder Conv-TransD and the relation decoder Conv-TransR, respectively. The one-dimensional convolution operation Φctr in the Conv-TransR decoder is shown in Eq. (7).

ϕctr(s,o,n)=∑α=0G−1ω¯c(α,0)s^(n+α)+ω¯c(α,1)o^(n+α)(7)

Among them, G represents the size of the convolution kernel. ϖc represents the parameterization of the cth convolution kernel. n represents the index of the output vector.

Step 7. We perform another one-dimensional convolution operation on the decoded and dimension-aligned entity vectors and relationship vectors to map them to the same low-dimensional space, obtaining the embedding vector fvec. Next, we establish associations through the head entity and transmit this vector to a linear fully connected layer for embedding learning, to achieve accurate predictions of entities and relationships. The specific operations are shown in Eq. (8).

{ fvec=ϕ1×1([ fHt,fRt ])ffc(s,r,o)=FC(BN(fvec))(8)

where FC(⋅), BN(⋅) represent the fully connected layer and batch normalization operation, respectively. ϕ1×1(⋅) denotes the one-dimensional convolution operation with a kernel size of 1×1. The predictions are performed according to the Eq. (9).

ρ(s,r,o,t)=σρ(ffc(s,r,o))(9)

where σρ(⋅) represents the logistic sigmoid activation function.

In summary, our proposed IndRT-GCNets use the connectivity of temporal knowledge graph nodes to model entities and relationships, capturing static attribute representations of entities while enhancing the interaction between entities and relationships. In addition, Conv-TransD and Conv-TransR are employed to encode and integrate entities and relationships, achieving the final prediction. These operations effectively handle entities and relationships in concurrent events.

3.4 Reconstructed Loss Function

To facilitate the achievement of optimal performance in the proposed IndRT-GCNets knowledge reasoning framework, we develop a weighted loss function that allows for individual optimization and adjustment of each module handling entities and relationships. Specifically, for the loss function of the static graph constraint module τSGCM, it is defined as shown in Eq. (10).

{ τSGCM=∑k=0(| v |−1)Max(cosθa−cos(hks,ht−m+a,k)​,0)θa=Min(γa,90°)(10)

where γ represents the ascent rate. As for the embedding representation of entities and relationships in the independent recurrent temporal graph convolution module, it is defined as shown in Eq. (11).

{ τH=∑t=0T−1∑Z(t+1)2⋅| Yt+1H∩ρ(o|s,r,Ht,Rt) || Yt+1H|+|ρ(o|s,r,Ht,Rt) |τR=∑t=0T−1∑Z(t+1)2⋅| Yt+1R∩ρ(r|s,o,Ht,Rt) || Yt+1R|+|ρ(r|s,o,Ht,Rt) |(11)

where T represents time, and T>t∈T. The loss function τ for the decoding module is defined as shown in Eq. (12).

τ=∑i=0(|ν|−1)⁡Yt−1,ilogρi(s,r,o,t)(12)

To obtain an optimal representation, we have reconstructed these loss functions by weighting them, forming a new loss function τtotal as shown in Eq. (13).

τtotal=β1⋅τSGCM+β2⋅τH+β3⋅τR+β4⋅τ(13)

where {β1,β2,β3,β4} represent adjustable factors that control the loss functions.

In conclusion, the reconstructed loss provided by controlling each module separately enables the proposed IndRT-GCNets framework to achieve optimal performance, thereby improving the representation of entities and relationships. Algorithm 1 outlines the overall workflow of the proposed knowledge inference framework.

4  Experiments and Analysis

In this section, we validate the effectiveness of the proposed IndRT-GCNets framework through various evaluations, including internal module ablation and comparisons with other knowledge reasoning methods. Firstly, we provide data interpretation, experimental settings, and evaluation metrics. Secondly, we compare the framework with different knowledge graph reasoning methods and present the corresponding experimental results and analysis. Finally, we conducted internal module ablation experiments and provided analysis and discussions accordingly.

4.1 Dataset

The FB13 dataset consists of 13 relationship types and 75,043 entities. The FB15K dataset contains 1,345 relationship types and 14,951 entities. The FB15K-237 dataset contains 237 relationship types and 14,951 entities, with more complex relationship types. The WN11 dataset contains 11 relationship types and 38,696 entities. The WN18 dataset contains 18 relationship types and 40,943 entities. The WN18RR dataset contains 11 relationship types and 40,943 entities. The YAGO3-10 dataset is similar to the FB15K-237 dataset and contains many relationships with high degrees, meaning that for a given relationship, a head/tail entity may correspond to a large number of tail/head entities. The Nell-995 dataset contains 75,492 entities and 200 relationship types.

4.2 Environment and Parameter Settings

In experiments, we set the training iterations to 100. The learning rate is set to 1e-4, and the batch size is set to 1,024. In data processing, we define a time length of 1,024 as a time interval to divide the entire data. To ensure that the framework obtains optimal feature representation, we use AdamW as the optimizer with a decay rate of 1e-3. We also adopt a multi-step strategy to dynamically adjust the learning rate. Specifically, the dynamic step schedule is set as [45, 60, 70, 80, 90, 96], and the multiplicative factor for learning rate decay is set to 0.5. All experiments in this study are conducted in a unified environment. Python 3.7.6 is used as the programming language, and training and testing are performed on a machine with dual GPU RTX A5000. Other required environments include cu110, torch 1.7.0+cu110, numpy, and other deep-learning libraries.

4.3 Evaluation Metrics

To ensure experimental consistency, we adopted MRR (Mean Reciprocal Rank) and Hits@ [1,3,10] as the comprehensive evaluation metrics for this experiment. The specific equations are shown in Eq. (14).

{ MRR=1m∑i=1m1ϱiHits@n=1m∑i=1mΠ(ϱi≤n)(14)

where Π(⋅) represents an indicator function that returns 1 if the condition is true and 0 if the condition is false. ϱi represents the ranking of the ith entity or relation.

4.4 Comparative Experiments

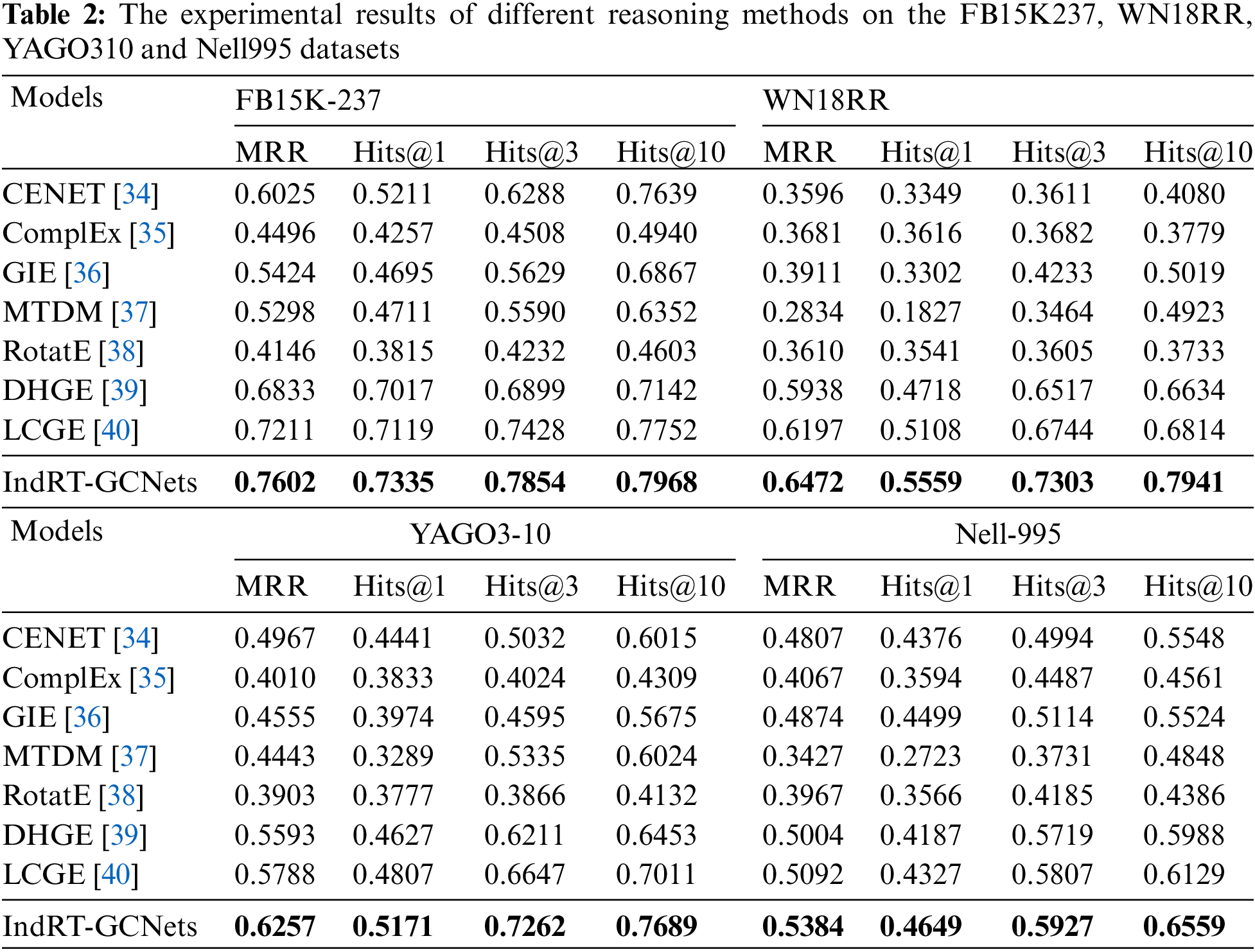
To demonstrate the effectiveness and superiority of the proposed IndRT-GCNets knowledge reasoning framework, we conducted experimental evaluations on various open-source baseline datasets and provided corresponding experimental results and analyses. The experimental results are shown in Tables 1 and 2.

Based on Tables 1 and 2, we can draw the following conclusions.

(1) Our proposed IndRT-GCNets model achieves optimal results on multiple benchmark datasets. The MRR for FB13, FB15, and FB15k237 datasets are 0.7632, 0.6043, and 0.7602, respectively. One reason is that the static graph constraint module models the detailed attributes of entities, capturing the contextual semantic information in events and improving the entity embedding representation. What’s more, embedding the IndRM and TGs in the temporal graph convolution avoids overfitting and the vanishing gradient problem caused by excessively long events, enhancing the interaction between entities and relations while capturing the structural dependencies of concurrent events. Finally, IndRT-GCNets uses different decoders for entities and relations, further fine-tuning the acquired semantic information, and establishing effective correlations between entities and relations, thereby enhancing the performance of the proposed model.

(2) However, our proposed IndRT-GCNets model does not achieve optimal performance on the FB15K dataset. While it improves the MRR metric by 0.0047 compared to the GIE [36] method, it decreases by 0.1226 compared to the CENET [34] method. It could be attributed to the fact that the CENET method can predict potential new events by jointly investigating historical and non-historical information to distinguish the most potential entities that best match a given query. Additionally, the FB15K dataset contains a significant imbalance in the amount of information included in the triples. Only a small portion of high-frequency entities played a crucial role in training, while other entities have a minor impact on training, resulting in significant data sparsity, which limits the performance of the proposed model.

(3) Compared to other reasoning methods, GIE has shown strong competitiveness in these datasets. For example, on FB13, WN11, and YAGO310 datasets, GIE achieves an improvement of 0.0682, 0.113, and 0.0545 in MRR compared to ComplEx [35], respectively. On WN18RR and Nell995 datasets, Hits@1 outperforms the MTDM [37] method by 0.1475 and 0.1776, respectively. One reason is that GIE can capture geometric interactions and learn reliable spatial structures, enhancing its capability to transfer reasoning rules in knowledge graphs with complex structures. What’s more, utilizing rich and expressive semantic matching between entities improves the performance of relation representation. The CENET also performs well on the YAGO310 and Nell995 datasets, with an MRR improvement of 0.0957 and 0.074 compared to the ComplEx method, respectively. Possible reasons are twofold: the YAGO310 and Nell995 datasets have a larger number of relation types and more complex data structures, leading to data imbalance and other challenges; CENET learns historical and non-historical dependency relations to distinguish the most potential entities that match a given query, while also investigating whether the current moment relies more on historical or non-historical events through contrastive learning, indicating relevant entities in the search space.

(4) RotatE [38] reasoning method exhibits the poorest performance on the FB15K237 and YAGO310 datasets. For example, Hits@10 decreases by 0.0337 and 0.0167 compared to ComplEx, respectively. One possible reason is that RotatE neglects to model complex relations, which diminishes the model’s performance. On the other hand, the ComplEx method harmonizes expressiveness and complexity by using complex-valued embeddings, while also exploring the connection between complex-valued embeddings and diagonalization, effectively modeling all possible relations. The CENET reasoning method achieves a lower MRR on the WN11 dataset compared to the ComplEx and RotatE reasoning methods, with decreases of 0.0152 and 0.0099, respectively. There are two possible reasons for this: On one hand, the WN11 dataset has simpler relation types, with fewer concurrent events in the same period; On the other hand, RotatE is an adversarial negative sampling technique that can model and infer various relationship patterns, including symmetry/asymmetry, inversion, and composition, especially in scenarios with a limited number of relations.

(5) On benchmark datasets, both DHGE [39] and LCGE [40] methods have achieved competitive results. For instance, on YAGO310, MRR is improved by 0.169 and 0.1885, respectively, compared with the RotatE method. On FB15K237, MRR is improved respectively compared with CENET. The DHGE method establishes hierarchical relationships between entities through the dual-view super-relationship structure, strengthening the affiliation between entities and concepts and improving reasoning performance. The LCGE method establishes constraints between logic and common sense, reducing their differences.

4.5 Ablation Studies

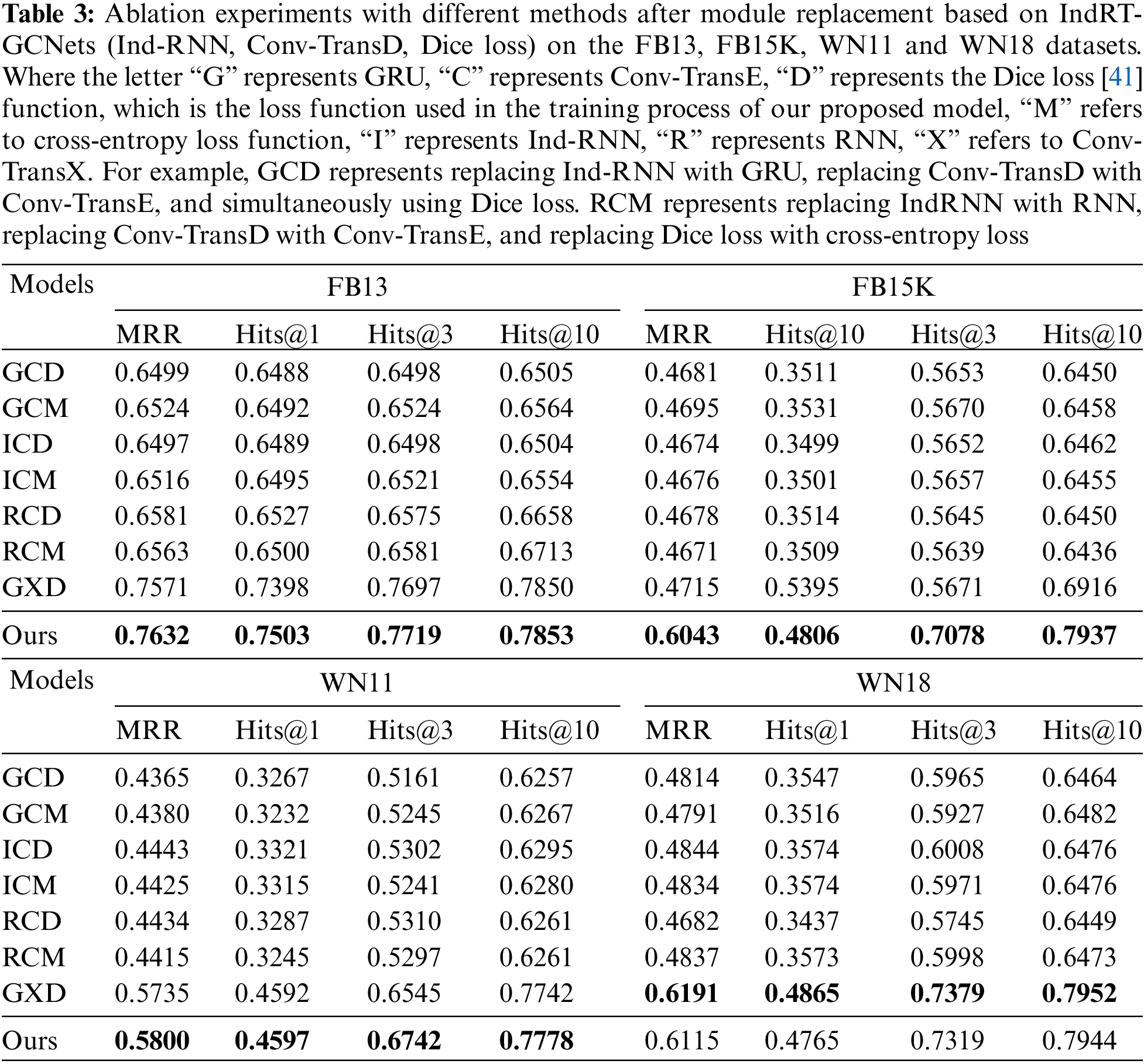
To demonstrate the positive contributions of each component in the proposed IndRT-GCNets knowledge reasoning framework to the overall model performance, we conducted experiments on multiple open-source datasets and provided corresponding experimental results and analysis. The specific experimental results are shown in Tables 3 and 4.

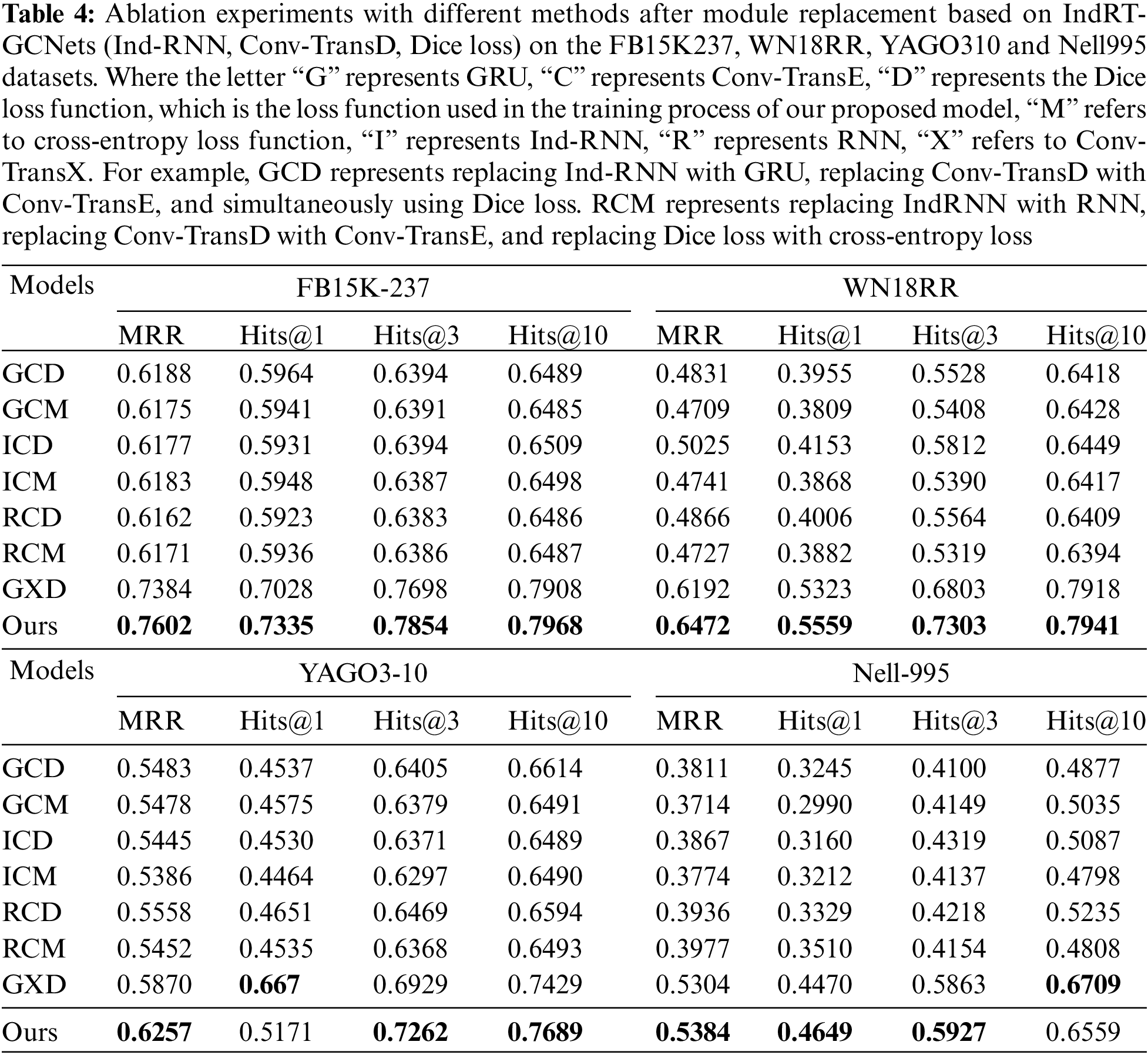
From Tables 3 and 4, several conclusions can be drawn.

(1) The collaboration between different modules in the proposed IndRT-GCNets knowledge reasoning framework is essential for achieving optimal performance. For example, in the Nell995 dataset, IndRT-GCNets outperforms GCD in terms of MRR and Hits@ [1,3] by 0.008, 0.0179, and 0.0064, respectively. Similarly, in the WN18RR dataset, IndRT-GCNets shows improvements over ICD in terms of MRR, Hits@1, Hits@3, and Hits@10 by 0.1447, 0.1406, 0.1491, and 0.1492, respectively. The possible reason for these improvements is that IndRM not only establishes effective long-term dependency relationships and alleviates the gradient vanishing problem but also relies on cross-layer information transfer and independent neurons within each layer to obtain more effective dependency relationships. Additionally, it captures the contextual semantics of entities and relations in temporal events, thereby enhancing the representation performance of entities and relations.

(2) Compared to optimizing entities and relations using cross-entropy, the Dice loss used in our proposed framework demonstrates better competitiveness. For instance, on the FB13 and FB15K datasets, the MRR of RCD is higher than that of RCM by 0.0018 and 0.0007, respectively. On the FB15K237 and YAGO310 benchmark datasets, the MRR of GCD is higher than that of GCM by 0.0013 and 0.0005, respectively. It demonstrates the effectiveness of Dice in optimizing entities and relations. On the WN11 and WN18 datasets, the MRR of GXD is higher than that of GCD by 0.137 and 0.1377, respectively. This indicates that Conv-TransD, as used in our framework, is more suitable for decoding entities compared to Conv-TransE, as it maximizes the preservation of translation invariance in entity vectors.

(3) In the FB15K237 dataset, the ICD method shows a decrease of 0.0007 in MRR and 0.0017 in Hits@1 compared to the ICM method. However, Hits@3 and Hits@10 improved by 0.0007 and 0.0011, respectively. The reason is that, compared to the cross-entropy loss function, the Dice loss function better addresses the class imbalance in this dataset, resulting in higher Hits@3 and Hits@10 scores. On the other hand, the cross-entropy loss function has a relatively faster convergence rate in the early stages of training, leading to better performance in MRR and Hits@1.

5  Conclusion and Future Work

This paper introduces a knowledge graph reasoning framework, IndRT-GCNets, which models the detailed attributes of entities using a static constraint graph and enhances entity representations by embedding a Temporal Graph Convolution Module (T-GCM). Furthermore, the Independent Recurrent Module (IndRM) models temporally adjacent events, effectively capturing contextual semantics of entities and relations within events, thereby strengthening the embedding representations of entities and relations. In addition, Conv-TransD and Conv-TransR are separately employed to decode entity and relation vectors, facilitating effective interactions between them. Meanwhile, a weighted loss function is designed, involving the optimization of various components using different loss functions, thereby enhancing the model’s performance. Finally, validation and evaluation were conducted on multiple benchmark datasets, demonstrating the effectiveness of the proposed model.

Although the proposed knowledge graph reasoning framework demonstrates good robustness and representation performance, two limitations were identified during the training process: (1) the framework has a high model complexity; (2) using decoders with different convolutions to decode entities and relations separately may overlook the correlation between entities and relations. Therefore, in future research, we will focus on addressing these two aspects and design a more efficient and concise temporal knowledge graph semantic representation network to further enhance the representation performance of entities and relations.

Acknowledgement: The authors thank all anonymous commenters for their constructive comments.

Funding Statement: The fund to support this work comes from the National Natural Science Foundation of China (62062062) hosted by Gulila Altenbek.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Y. Ma; data collection: Y. Ma, G. Altenbek, Y. Yu; analysis and interpretation of results: G. Altenbek, Y. Yu; draft manuscript preparation: Y. Ma. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are openly available in a public repository: https://github.com/thunlp/OpenKE/tree/OpenKE-PyTorch/benchmarks.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Zhang and J. Wang, “Trend analysis of global disaster education research based on scientific knowledge graphs,” Sustainability, vol. 14, no. 1, pp. 1492, 2022. [Google Scholar]

2. H. Wu, Y. Chang, J. Li and X. Zhu, “Financial fraud risk analysis based on audit information knowledge graph,” Procedia Computer Science, vol. 199, pp. 780–787, 2022. [Google Scholar]

3. A. García-Durán, S. Dumančić and M. Niepert, “Learning sequence encoders for temporal knowledge graph completion,” arXiv preprint arXiv:1809.03202, 2018. [Google Scholar]

4. Y. Fang, H. Wang, L. Zhao, F. Yu and C. Wang, “Dynamic knowledge graph based fake-review detection,” Applied Intelligence, vol. 50, pp. 4281–4295, 2020. [Google Scholar]

5. R. Goel, S. M. Kazemi, M. Brubaker and P. Poupart, “Diachronic embedding for temporal knowledge graph completion,” in Proc. of AAAI, New York, USA, pp. 3988–3995, 2020. [Google Scholar]

6. R. Trivedi, H. Dai, Y. Wang and L. Song, “Know-Evolve: Deep temporal reasoning for dynamic knowledge graphs,” in Proc. of PMLR, Amsterdam, Netherlands, pp. 3462–3471, 2017. [Google Scholar]

7. R. Trivedi, M. Farajtabar, P. Biswal and H. Zha, “DyRep: Learning representations over dynamic graphs,” in Proc. of ICLR, New Orleans, Louisiana, USA, 2019. [Google Scholar]

8. T. Dettmers, P. Minervini, P. Stenetorp and S. Riedel, “Convolutional 2D knowledge graph embeddings,” in Proc. of AAAI, Louisiana, USA, 2018. [Google Scholar]

9. C. Shang, Y. Tang, J. Huang, J. Bi, X. He et al., “End-to-end structure-aware convolutional networks for knowledge base completion,” in Proc. of AAAI, Honolulu, Hawaii, USA, pp. 3060–3067, 2019. [Google Scholar]

10. Q. Lin, J. Liu, Y. Pan, X. Hu and J. Ma, “Rule-enhanced iterative complementation for knowledge graph reasoning,” Information Sciences, vol. 575, pp. 66–79, 2021. [Google Scholar]

11. X. Zhao, Y. Jia, A. Li, R. Jiang, K. Chen et al., “Target relational attention-oriented knowledge graph reasoning,” Neurocomputing, vol. 461, pp. 577–586, 2021. [Google Scholar]

12. Z. Zhang, Z. Li, H. Liu and N. N. Xiong, “Multi-scale dynamic convolutional network for knowledge graph embedding,” IEEE Transactions on Knowledge and Data Engineering, vol. 34, no. 5, pp. 2335–2347, 2020. [Google Scholar]

13. M. Schlichtkrull, T. N. Kipf, P. Bloem, R. van den Berg, I. Titov et al., “Modeling relational data with graph convolutional networks,” in The Semantic Web: 15th Int. Conf., ESWC, Heraklion, Crete, Greece, pp. 593–607, 2018. [Google Scholar]

14. S. Vashishth, S. Sanyal, V. Nitin and P. Talukdar, “Composition-based multi-relational graph convolutional networks,” arXiv preprint arXiv:1911.03082, 2019. [Google Scholar]

15. R. Ye, X. Li, Y. Fang, H. Zang and M. Wang, “A vectorized relational graph convolutional network for multi-relational network alignment,” in Proc. of IJCAI, Macao, China, pp. 4135–4141, 2019. [Google Scholar]

16. Z. Han, Y. Ma, P. Chen and V. Tresp, “DyERNIE: Dynamic evolution of riemannian manifold embeddings for temporal knowledge graph completion,” arXiv preprint arXiv.2011.03984, 2020. [Google Scholar]

17. J. Wu, M. Cao, J. C. K. Cheung and W. L. Hamilton, “Temp: Temporal message passing for temporal knowledge graph completion,” arXiv preprint arXiv:2010.03526, 2020. [Google Scholar]

18. C. Xu, M. Nayyeri, F. Alkhoury, H. Yazdi and J. Lehmanm, “Temporal knowledge graph completion based on time series gaussian embedding,” in: ISWC 2020: The Semantic Web–ISWC 2020, Athens, Greece, pp. 654–671, 2020. [Google Scholar]

19. Z. Li, X. Jin, W. Li, S. Guan, J. Guo et al., “Temporal knowledge graph reasoning based on evolutional representation learning,” in Proc. of the 44th Int. ACM SIGIR Conf. on Research and Development in Information Retrieval, NY, USA, pp. 408–417, 2021. [Google Scholar]

20. Z. Li, S. Guan, X. Jin, W. Peng, Y. Lyu et al., “Complex evolutional pattern learning for temporal knowledge graph reasoning,” arXiv preprint arXiv:2203.07782, 2022. [Google Scholar]

21. N. Park, F. Liu, P. Mehta, D. Cristofor, C. Faloutsos et al., “Evokg: Jointly modeling event time and network structure for reasoning over temporal knowledge graphs,” in Proc. of the Fifteenth ACM Int. Conf. on Web Search and Data Mining, NY, USA, pp. 794–803, 2022. [Google Scholar]

22. S. Jiao, Z. Zhu, W. Wu, Z. Zuo, J. Qi et al., “An improving reasoning network for complex question answering over temporal knowledge graphs,” Applied Intelligence, vol. 53, no. 7, pp. 8195–8208, 2023. [Google Scholar]

23. H. Nie, X. Zhao, X. Yao, Q. Jiang, X. Bi et al., “Temporal-structural importance weighted graph convolutional network for temporal knowledge graph completion,” Future Generation Computer Systems, vol. 143, pp. 30–39, 2023. [Google Scholar]

24. X. Wang, S. Lyu, X. Wang, X. Wu and H. Chen, “Temporal knowledge graph embedding via sparse transfer matrix,” Information Sciences, vol. 623, pp. 56–69, 2023. [Google Scholar]

25. J. Zhu, X. Han, H. Deng, C. Tao, L. Zhao et al., “KST-GCN: A knowledge-driven spatial-temporal graph convolutional network for traffic forecasting,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 9, pp. 15055–15065, 2022. [Google Scholar]

26. S. Arora, “A survey on graph neural networks for knowledge graph completion,” arXiv preprint arXiv:2007.12374, 2020. [Google Scholar]

27. Y. Song, A. Li, H. Tu, K. Chen and C. Li, “A novel encoder-decoder knowledge graph completion model for robot brain,” Frontiers in Neurorobotics, vol. 15, pp. 674428, 2021. [Google Scholar] [PubMed]

28. B. Wu, L. Wang, S. X. Lv and Y. R. Zeng, “Forecasting oil consumption with attention-based IndRNN optimized by adaptive differential evolution,” Applied Intelligence, vol. 53, no. 5, pp. 5473–5496, 2023. [Google Scholar] [PubMed]

29. S. Li, W. Li, C. Cook, C. Zhu and Y. Gao, “Independently recurrent neural network (IndRNNBuilding a longer and deeper RNN,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, UT, USA, pp. 5457–5466, 2018. [Google Scholar]

30. K. He, X. Zhang, S. Ren and J. Sun, “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification,” in Proc. of ICCV, Santiago, Chile, pp. 1026–1034, 2015. [Google Scholar]

31. A. Krizhevsky, I. Sutskever and G. E. Hinton, “ImageNet classification with deep convolutional neural networks,” Communications of the ACM, vol. 60, no. 6, pp. 84–90, 2017. [Google Scholar]

32. B. Xu, N. Wang, T. Chen and M. Li, “Empirical evaluation of rectified activations in convolutional network,” arXiv preprint arXiv:1505.00853, 2015. [Google Scholar]

33. A. L. Maas, A. Y. Hannun and A. Y. Ng, “Rectifier nonlinearities improve neural network acoustic models,” in Proc. of ICML, Atlanta, USA, pp. 3, 2013. [Google Scholar]

34. Y. Xu, J. Ou, H. Xu and L. Fu, “Temporal knowledge graph reasoning with historical contrastive learning,” arXiv preprint arXiv:2211.10904, 2022. [Google Scholar]

35. T. Trouillon, J. Welbl, S. Riedel, E. Gaussier and G. Bouchard, “Complex embeddings for simple link prediction,” in Proc. of PMLR, New York, USA, pp. 2071–2080, 2016. [Google Scholar]

36. Z. Cao, Q. Xu, Z. Yang, X. Cao and Q. Huang, “Geometry interaction knowledge graph embeddings,” in Proc. of AAAI, Vancouver, Canada, pp. 5521–5529, 2022. [Google Scholar]

37. M. Zhao, L. Zhang, Y. Kong and B. Yin, “Temporal knowledge graph reasoning triggered by memories,” arXiv preprint arXiv:2110.08765, 2021. [Google Scholar]

38. Z. Sun, Z. H. Deng, J. Y. Nie and J. Tang, “Rotate: Knowledge graph embedding by relational rotation in complex space,” arXiv preprint arXiv:1902.10197, 2019. [Google Scholar]

39. H. Luo, E. Haihong, L. Tan, G. Zhou, T. Yao et al., “DHGE: Dual-view hyper-relational knowledge graph embedding for link prediction and entity typing,” in Proc. of AAAI, Washington DC, USA, pp. 6467–6474, 2023. [Google Scholar]

40. G. Niu and B. Li, “Logic and commonsense-guided temporal knowledge graph completion,” in Proc. of AAAI, Washington DC, USA, pp. 4569–4577, 2023. [Google Scholar]

41. F. Milletari, N. Navab and S. A. Ahmadi, “V-Net: Fully convolutional neural networks for volumetric medical image segmentation,” in Proc. of 3DV, California, USA, pp. 565–571, 2016. [Google Scholar]