Rao Algorithms-Based Structure Optimization for Heterogeneous Wireless Sensor Networks

1  Introduction

Wireless sensor networks (WSNs) are made up of multiple sensor nodes that interconnect wirelessly in an adaptive way and are deployed randomly or strategically in the physical environment to monitor natural events. WSNs have the following essential characteristics: flexibility, maintainability, scalability, self-monitoring, and fault tolerance. Furthermore, it delivers high-quality services and can complete tasks in harsh environments. WSNs have a wide variety of applications [1–3]. Othman et al. [1] have discovered, via their research on environmental modeling systems, that using WSNs in place of humans may significantly increase system performance. The authors of [4] showed that there is a growing interest in data buffering parallelization for Internet of Things (IoT) applications that use WSNs. Additionally, WSNs have the ability to measure architectural efficacy and create a secure image processing and transmission schema [5–8]. Consequently, it is evident that WSNs are essential to the operation of contemporary technology, and as such, their structural component needs to be optimized.

Accurate node localization to maximize the covered area of the targeted region is one of the fundamental challenges in WSN. This problem is referred to by various names in the literature, such as placement, coverage, or the deployment problem in WSNs [9]. Sensor deployment can either be random, such as dropping sensors in hostile terrains or disaster areas, or deterministic, such as strategically placing sensors along a pipeline for pressure and/or temperature monitoring and boundary surveillance [10]. The choice of deployment is primarily influenced by the application type, environment, and characteristics of the sensors themselves. The deployment strategy has a direct impact on the transmission rate of sensors, as well as the overall coverage and longevity of the network system, making it a critical concern in WSNs [11]. During deployment planning, multiple objectives need to be considered, including energy consumption, sensing coverage, network longevity, network connectivity, and more. These objectives often conflict with each other, requiring trade-offs to be made during network design [12].

An optimization problem is a computational problem in which the goal is to identify the optimal choice out of all possible solutions. In other words, the purpose of an optimization problem is to find a viable solution with the smallest (or greatest) value of the objective function. The mathematical relationships between the objective, constraint, and choice variables in an optimization problem impact how difficult it is to solve, as well as the optimization techniques or algorithms that can be employed to discover the optimal solution. Numerous optimization algorithms are available, including the genetic algorithm, particle swarm optimization (PSO) algorithm [13], Firefly algorithm [14], Ant Colony Optimization method [15], Jaya algorithm [16], and, most recently, the Rao algorithm [17].

Rao [17] introduced three optimization algorithms, namely Rao-1, Rao-2, and Rao-3, which are distinguished by their lack of parameters. These algorithms facilitate population movement within the search area through interactions created by the population with the best, the worst, and arbitrarily chosen solutions. The effectiveness of the Rao algorithms in tackling engineering design challenges and benchmark problems has been demonstrated in [18–20]. According to these publications, these algorithms have various properties in terms of exploration and exploitation. They aim to strike a balance between exploring the search space for better solutions and exploiting the current best solution. This characteristic can be beneficial for network systems as it allows for adaptability and resilience, potentially leading to better node survival and network lifetime.

Many studies have been conducted for the optimization of homogeneous networks [9,11], but few have been performed for heterogeneous WSNs [21]. One of the challenges in the WSNs is to find the network with the best node locations to reduce energy consumption and hence preserve the lifetime of the network nodes. In this paper, we rely on the Rao algorithms a class of optimization algorithms known for their effectiveness in addressing complex optimization problems, to optimize the network structure in heterogeneous WSNs, particularly benefiting cluster-based and chain-based routing protocols. The primary parameters for the optimization criterion are the energy level in each node and the distance of each node from the base station (BS).

Our proposed approach aims to place the nodes to enable efficient data transmission to the sink, while simultaneously minimizing the nodes’ energy consumption, this will enhance the performance and the efficiency of the heterogeneous WSNs. The simulation results demonstrate that our proposed methodology for optimizing the heterogeneous WSN increased the whole number of packets to cluster head and packets to BS, prolonged the lifetime of the network, and reduced the energy consumption of the network nodes.

The following are the main benefactions of this paper:

1.    The WSN structure population is created randomly and optimized using the three Rao algorithms.

2.    The fitness function employed for the study encompasses two different aspects of evaluation: the node’s energies as well as the nodes-to-sink distances.

3.    The WSN optimized using the proposed algorithms are tested for cluster-based (LEACH), chain-based routing (PEAGSIS), partition-based energy-efficient LEACH (PE-LEACH) [22], and the PEGASIS-NN protocols.

4.    The effectiveness of the proposed methodology is evaluated using two network sizes: a small-scale network (100 × 100) and a large-scale network (1000 × 1000).

The rest of the paper is organized as follows.

Section 2 discusses the related work. Section 3 provides a comprehensive overview of our proposed methodology and the optimization techniques employed. The outcomes of the simulation are presented and analyzed in Section 4. Section 5 concludes the paper and suggests future research directions.

2  Related Work

Choosing the locations of sensor nodes (sensor node deployment) with attention is an essential part of building most WSNs in order to maximize the coverage area of the intended region. Ineffective sensor node deployment might result in inefficient network connectivity or needless redundancy in coverage. WSN deployment is a major difficulty because a well-planned deployment strategy not only lowers costs but also increases the network's lifespan.

Reference [21] proposed an altered Jaya algorithm version that takes into account the remaining energy and the distance between nodes and sink nodes to optimize the structure of a heterogeneous WSN. Initially, a stochastic WSN population is created, consisting of m WSNs, each with n number of nodes. Each WSN node is assigned a random residual energy value below 100. Each WSN comprises one source node and four sink nodes. The fitness function, which includes two components – the energy and the node-sink distance, is defined to be optimized. The Minimized Jaya Algorithm and the Genetic Algorithm (GA) are utilized to optimize the fitness function.

The authors of [23] proposed a CH selection method that combines Particle Swarm Optimization (PSO) and the harmony search (HSA) approach. This approach takes advantage of PSO’s dynamic nature and the strong search capabilities of harmony search to effectively address the CH election dilemma. The harmony array is used for the search process, while PSO creates the CH selection fitness function. By updating the location and velocity in the search space, PSO aims to find the global optimal solution. The selection process considers distance and energy as metrics for CH election, with the goal of appointing the most suitable CH to enhance network performance.

Reference [24] presented a particle swarm optimization-based energy efficient clustering protocol (PSO-EEC) with the aim of improving the lifespan and performance of WSNs. The PSO algorithm is utilized to determine both the cluster head and relay nodes for the network. The cluster head selection process involves a fitness function based on PSO that takes into account various factors such as the node energy ratio (initial energy and remaining energy), node distance to the cluster head, and node connectivity. These factors are considered to identify the most suitable node to serve as the cluster head. For data transfer to the BS, the proposed technique employs a fitness value based on the residual energy of the cluster head and characteristics related to the distance to the BS. This fitness score is used to identify relay nodes for multi-hop data transport to the BS. The PSO-EEC protocol intends to improve energy efficiency and network longevity by exploiting these tactics.

Rao proposed three algorithms Rao1, Rao2, and Rao3 [17]. These algorithms utilize different strategies based on the best and worst solutions obtained during the optimization process, as well as randomly selected candidate solutions. These algorithms are designed to operate with only common control parameters such as the size of the population and the iteration number, eliminating the need for algorithm-specific control parameters. These algorithms explore and exploit the search space throughout the iterative stages by leveraging the iteration’s best solution, worst solution, and random interactions among the population. While the general flow of these three algorithms is similar, each uses a different movement equation. The Rao algorithms flowchart is shown in Fig. 1.

Figure 1: Rao algorithms flowchart

Let f(x) represent the desired function that needs to be minimized (or maximized). Suppose there are ‘m’ design variables and ‘n’ possible solutions (i.e., population size, k = 1,2,...,n). The optimal solution is determined by the optimal value of f(x) among all potential solutions, and the worst candidate is determined by the worst value of f(x) among all potential solutions. If xv,p,i is the value of the vth variable for the pth candidate during the ith iteration, then this value is modified per the following equations [17]:

xv,p,i′=xv,p,i+r1,v,i(xv,b,i−xv,w,i)(1)

xv,p,i′=xv,p,i+r1,v,i(xv,b,i−xv,w,i)+r2,v,i(|xv,p,iorxv,q,i|−|xv,q,iorxv,p,i|)(2)

xv,p,i′=xv,p,i+r1,v,i(xv,b,i−|xv,w,i|)+(|xv,p,iorxv,q,i|−(xv,q,iorxv,p,i))(3)

where xv,b,i is the value of the candidate for the superior f(x) for the vth variable and the ith iteration, xv,w,i is the candidate for the worst f(x) for iteration I and variable v. xv,q,i is a randomly selected candidate.

Rao algorithms are used in the literature for solving benchmark problems and engineering design problems. Rao algorithms with multiple objectives were proposed by [18]. Using dominance principles and crowding distance assessment, the suggested algorithms manage numerous objectives simultaneously. The suggested optimization algorithms are tested on a case study of a solar-assisted Brayton heat engine system and another case study of a Stirling heat engine system, and their performances have been enhanced. The optimization algorithms given are simple, strong, and straightforward to implement to handle various engineering optimization challenges [18]. The authors contend that employing a multi-population search technique significantly enhances the performance of specific aspects of advanced population-based optimization algorithms. This is achieved by dividing the entire population to locate the optimal solution.

In [20], the authors utilized Rao algorithms in the design optimization of mechanical system components. The designs acquired using Rao algorithms were compared to those obtained using different optimization strategies. The results demonstrate the capability and effectiveness of Rao algorithms in tackling complicated design optimization issues of mechanical components. The Rao-1 algorithm is utilized in [25] to evaluate the best size and location of capacitors in radial distribution systems to decrease active power loss and enhance voltage profile. Rao-1 is widely used in Radial Distribution Systems for capacitor placement and has proven to be extremely useful.

Reference [26] proposed EHRJAYA, a self-adaptive categorization learning hybrid JAYA and Rao-1 algorithm, to address large-scale computational problems and complex real-world engineering optimization challenges. In EHRJAYA, the evolution strategies of the JAYA and Rao-1 algorithms are chosen at random. Then, a novel self-adaptive categorization learning technique that fully incorporates input from multiple people is proposed. According to this logic, two distinct adaptive factors are introduced to push the population towards the best candidate and far from the worst. Lastly, merging the dynamic lens opposition-based learning approach with the linear decrease in population method greatly enhances the algorithm’s speed of convergence and capacity to surpass the local optimum.

Authors of [27] proposed an energy-aware, optimal, and efficient wireless sensor network scheme to improve network lifetime, coverage, and resource utilization. In their schema, they use PSO [13] for cluster head selection. The node with the superior fitness value is chosen as the CH. The goal of cluster formation is to maximize coverage while minimizing the number of active CHs. The nodes achieve this by finding and joining the closest CH. Data from cluster nodes is sent to respective CHs, which combine it and pass it on to the base station. The proposed method is different from ours as we used Rao’s algorithms for structure optimization of WSN but this uses PSO for cluster head selection, we applied our methodology for the large-scale network (1000 × 1000) and small network (100 × 100) and their method is evaluated for 100 × 100 WSN.

In this paper, we utilize Rao algorithms to identify the optimal structure of WSNs relying on their success in solving various optimization problems. We apply a new approach to locate sensor nodes in heterogenic WSNs and compare it to the methodology used in [22–24]. The results simulation demonstrate the effectiveness of our solution in minimizing energy consumption and extending network lifetime.

3  Proposed Methodology

The detail of our proposed methodology is presented in Fig. 2, a set of WSNs is randomly created, with m total WSNs, each containing n unique nodes. We have conducted two experiments with m = 20 and n = 100. In the first, each node’s maximum coordinate is set to be less than 1000 units, resulting in a WSN area of 106 square units. In the second experiment, the maximum coordinate of each node is assigned a value less than 100 units, resulting in a WSN area of 104 square units. Each WSN node is assigned an arbitrary residual energy value below 100. A single sink node and a single source node exist within each WSN.

Figure 2: The flowchart of the proposed methodology for optimizing WSN construction

Second, using Eqs. (4) and (5), the energy and node-sink distance parts of the fitness function are estimated [21]. After that, the fitness function is calculated using Eq. (6) [21]. Finally, the fitness function is optimized using Rao-1, Rao-2, and Rao-3 algorithms.

x1=∑j=1nEjEmax+nEThET(4)

Eq. (4) presents the normalized energy sum, which is the proportion of the remaining energy of every node Ej, to the highest remaining energy Emax, plus a term equivalent to n times the proportion of the threshold’s energy value, ETh, to the WSN’s overall energy, ET.

x2=∑j=1ndj,sdfar,s+ndavg(5)

In Eq. (5), the summation of normalized distance values, i.e., the proportion of each node’s distance from the sink, dj,s to the value of the furthest node’s distance from the sink, dfar,s plus the inverse of the mean distance davg, weighted by a coefficient n. The inverse of the mean distance is a measure of the network density.

FP=1αx1+βx2(6)

where α and β are the fitness function coefficients weight [21]. The residual remaining factor is denoted by α and the node-sink distance factor is denoted by β, α + β = 1. The weight coefficients α and β in Eq. (6) influence the fitness function by controlling how much importance is given to the energy and distance factors, respectively. If α is large, then the fitness function will be more sensitive to the energy factor. Conversely, if β is large, then the fitness function will be more sensitive to the distance factor. The values of α and β have a direct effect on the speed of convergence. We conducted several experiments for different values of α and β, the values of α = 0.6 and β = 0.4 produced the fastest fitness convergence.

3.1 Optimization Algorithms of the Fitness Function

3.1.1 Optimization with Jaya Algorithm

The fundamental principle of the Jaya algorithm [16] is to move farther from the worst occurrence in the population and toward the most ideal member of the population. In this scenario, the best solution should be as far away as possible from the WSN with the greatest fitness function (FP) and as near as possible to the WSN with the lowest FP. Their system determines the best and worst operating WSNs in each generation. Consider the parameter Xi for a WSN in a certain WSN population, where the highest-performing WSN has a parameter Xb and the lowest-performing WSN has a parameter Xw. To estimate the value of the parameter for the upcoming generation’s population, Xi′, Eq. (7) is applied. r1 and r2 are arbitrary weights that are changed in all generations and have a range from 0.0 to 1.0. The method is kept from overfitting by using these weights [16].

Xi′=Xi+r1(Xb−Xi)−r2(Xw−Xi)(7)

3.1.2 Optimization with Rao-1 Algorithm

Rao algorithms are population algorithms for optimization problems that are basic and straightforward to implement. These algorithms have no specified algorithm parameters or symbolic interpretations. The size of a population is the only variable that has to be adjusted. Therefore, it is significantly easier to apply these algorithms for engineering applications.

Rao-1 algorithm is the first algorithm of Rao’s algorithms. During the repeating process, this algorithm explores and exploits the search region by using both the optimal and least effective iteration solutions. First x1, x2, and FP are estimated for each WSN in the population under consideration using Eqs. (4)–(6), respectively. Eq. (1) is used to calculate x1new and x2new for the population in the following generation, where xv,p,i′ represents the xnew and Eq. (6) is used to compute FP. If the new solution corresponds to xnew is superior to to the prior solution then the prior solution is replaced with the new solution, if not discard the new solution. This process is repeated for g generations until FP converges. The details steps for FP optimization using Rao-1 are demonstrated in algorthim1.

3.1.3 Optimization with Rao-2 and Rao-3 Algorithms

The Rao-2 algorithm is predicated on randomly chosen potential solutions, as well as the most favorable and least favorable answers. First, for each WSN in a population x1, x2, and FP are estimated using Eqs. (3)–(5), respectively. Then a random candidate xv,q,i is selected. Eq. (2) is used to compute x1new and x2new for the population in the following generation. The interaction between the present solution (pth) and an arbitrary solution (qth) chosen from the present population is represented by the third term on the right-hand side in Eq. (2). These two terms rely on the FP values of the chosen solutions at random (qth) and the current (pth). The third term in Eq. (2) becomes r2,v,i(|xv,p,i|−|xv,q,i|) if the current solution value is greater than the randomly chosen solution value. Similarly, the third term in Eq. (2) becomes r2,v,i(|xv,q,i|−|xv,p,i|) if the randomly chosen solution value is better than the current solution value. This process is repeated for g generations until FP converges. Algorithm 2 presents the detailed steps for fitness function optimization using the Rao-2 algorithm.

The Rao-3 algorithm differs from the Rao-2 in the method used to update the values of x1new and x2new. While the Rao-2 utilizes Eq. (2) for this purpose, the Rao-3 employs Eq. (3).

4  Simulation Results and Discussion

4.1 Simulation Environment

The whole simulation of this study and experimentation is carried out in MATLAB. We built a Java simulator for PEAGIS, and we ran them on Windows 10 Enterprise, with Intel(R) Core(TM) i7-9750H CPU @ 2.60 GHz 2.59 GHz processor, 16.0 GB memory. Table 1 presents the simulation parameters for the network and the fitness function parameters that we have used in our experiments.

4.2 Fitness Function Convergence

Table 2 compares the fitness functions on initialization and convergence for the Jaya, Rao1, Rao2, and Rao3 optimization algorithms after 15 generations. It is clear that all of Rao’s algorithms converge better than Jaya’s algorithm, Rao2, and Rao3 fitness after 15 generations are 10−5 but for Jaya, it is 0.0077. Fig. 3 presents the fitness function convergence for Jaya, Rao1, Rao2, and Rao3 algorithms. It is worth noting that using Rao2 and Rao3 the fitness function is converged at 10 generations but for Jaya, it converged at 22 generations.

Figure 3: Comparison of absolute convergence of fitness function for Rao-1, Rao-2, Rao-3, and Jaya for different generations

4.3 LEACH Results for the Proposed Optimized WSNs

LEACH (low energy adaptive clustering hierarchy) [28] is the first WSN-specific hierarchical cluster-based routing system. LEACH groups sensor nodes into clusters based on the intensity of the received signal. Each cluster consists of a number of cluster nodes (CNs) and a single cluster head (CH). CH gathers data from their cluster’s CNs, combines it, and sends it to the sink node (see Fig. 4).

Figure 4: Data transmutation in LEACH protocol

This protocol is split into rounds, with each round consisting of two phases: setup and steady. During the setup phase, each node decides whether or not to become a CH irrespective of the other nodes. This decision considers when the node previously operated as a CH (nodes that have not been a CH for a long period are more likely to elect themselves than nodes that are currently a CH).

4.3.1 1000 × 1000 Optimized WSN Results

The simulation results are conducted based on network lifetime, node residual energy, packets to BS, and packets to CH. In the literature [29], there are numerous definitions of WSN lifetime, such as time until the first sensor node fails, time until a particular number of sensor nodes fails, time until the delivery of packets rate gets below a certain limit, time until all sensor nodes fail, and so on, and using a wrong definition may result in incorrect lifetime estimation. This may result in resource waste. The perception of a WSN’s operational status varies among different models in the literature. Some models rely on the connectivity of deployed nodes, while others consider the proportion of active nodes with sufficient energy to perform their designated tasks. The concept of sensor lifespan is subdivided into three ways for determining lifetime based on the type of service supplied by the network, which is First Node Dies (FND), Half of the Nodes Alive (HNA), and Last Node Dies (LND). The nature of functionality supplied by the network can influence the sensor lifetime metrics chosen. For example, a network that is used to monitor a critical infrastructure, such as a power grid, would likely use the FND metric. A network that is used to collect environmental data, such as temperature or humidity, would likely use the HNA metric. This is because the network can tolerate some node failure, as long as at least half of the nodes are still operational. A network that is used to track the movement of objects, such as animals or vehicles, would likely use the LND metric. This is because the network must be able to continue to track the objects even if some nodes fail.

Fig. 5 presents the percentage of the dead node in relation to the number of rounds for Jaya, Rao1, Rao2, and Rao3 algorithms. The number of nodes that die in the Rao algorithms is less than the Jaya over the same number of rounds. The Rao-1 algorithm clearly outperforms all other algorithms, it prolongs the network lifetime by more than ten percent.

Figure 5: Percentage of LEACH dead nodes for Jaya optimized WSN, and proposed Rao1, Rao2, and Rao3 optimized WSN in relation to the number of rounds

Table 3 demonstrates the total number of rounds for the LEACH protocol until 1%, 20%, 50%, and 90% of nodes died. It is worth noting that 20 percent, of nodes had depleted their energy reserves by the 119th round when using the Jaya algorithm. However, this happened respectively at the 194th, 146th, and 126th rounds in the network using Rao1, Rao2, and Rao3 algorithms. Over half of the nodes exhausted their energy reserves by the 333rd round for the Jaya algorithm, and this depletion occurred at the 394th round for the Rao-1 algorithm. Nodes lost 90% of their energies at the 2482th round in the Jaya algorithm, but nodes lost 90% of their energies respectively at the 5048th, 1929th, and 3701th, rounds for the proposed Rao-1, Rao-2, and Rao-3 algorithms. Our proposed method has prolonged the lifespan of WSN (both the initial node death, half node, and 90 percent node death). More precisely, the lifetime of WSN is prolonged by 51% for the death of 90 percent of its nodes and by 15% for the death of half the network nodes when using the Rao1 algorithm.

The proposed optimized WSNs using Rao1, Rao2, and Rao3 algorithms have a lower percentage of dead nodes than the Jaya algorithm. This is because the proposed optimized WSNs use more sophisticated node placement algorithms than the Jaya algorithm. This results in a more evenly distributed node placement, which reduces the number of dead nodes and improves network connectivity.

The energy needed for both sending and receiving information in a WSN can be calculated via Eqs. (8) and (9):

ETx(k,d)=Eelec×k+Emp×k×(d)2(8)

ERx(k)=Eelec×k(9)

where k is the length of the data being sent and received, ETx is the quantity of energy essential for sending k packets of data, ERx(k) is the total energy needed for receiving k data packets of data, Eelec = 50 nJ/bit, and Emp = 100 pJ/bit/m2 for the transmitter amplifier.

Fig. 6 presents the residual energy for the WSN concerning the number of rounds for Jaya, Rao1, Rao2, and Rao3 algorithms employing the LEACH routing protocol. As the figure demonstrates the residual energy for Rao’s algorithms is larger than for the Jaya algorithm. The residual energy for the Rao1 algorithm is the best one and it is greater than the Jaya algorithm by 500 Joul.

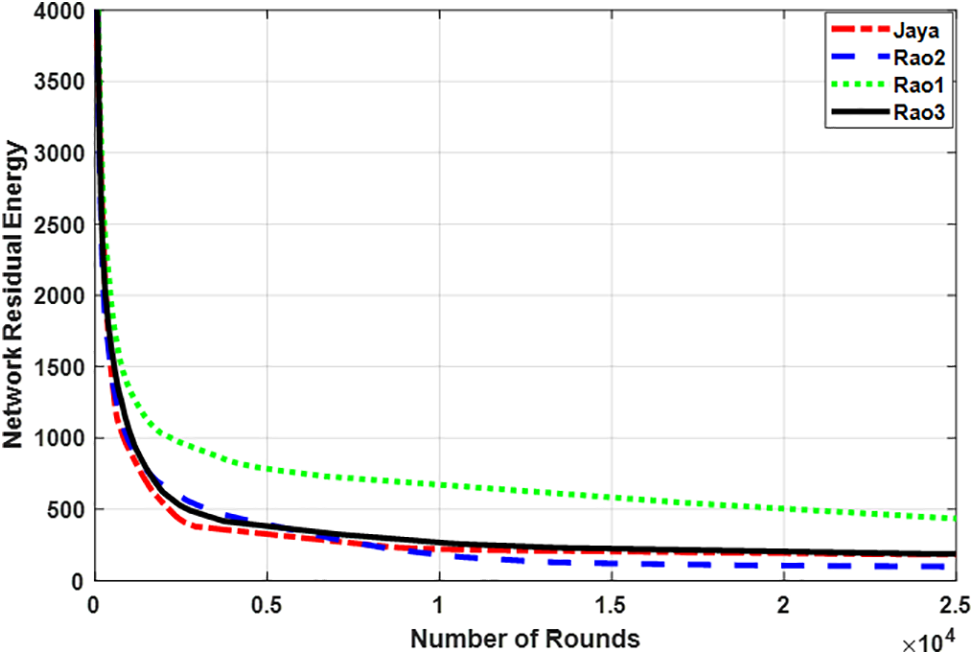
Figure 6: The residual energy of the constructed WSNs using the Jaya algorithm and proposed optimized WSNs using the Rao1, Rao2, and Rao3 algorithms for LEACH protocol with the number of rounds

Fig. 7 demonstrates the throughput of optimized WSNs using the Jaya algorithm as well as suggested optimized WSNs using the Rao1, Rao2, and Rao3 algorithms when LEACH is used as the routing protocol. The network’s throughput is defined as the overall amount of packets transmitted to BS in a round [22].

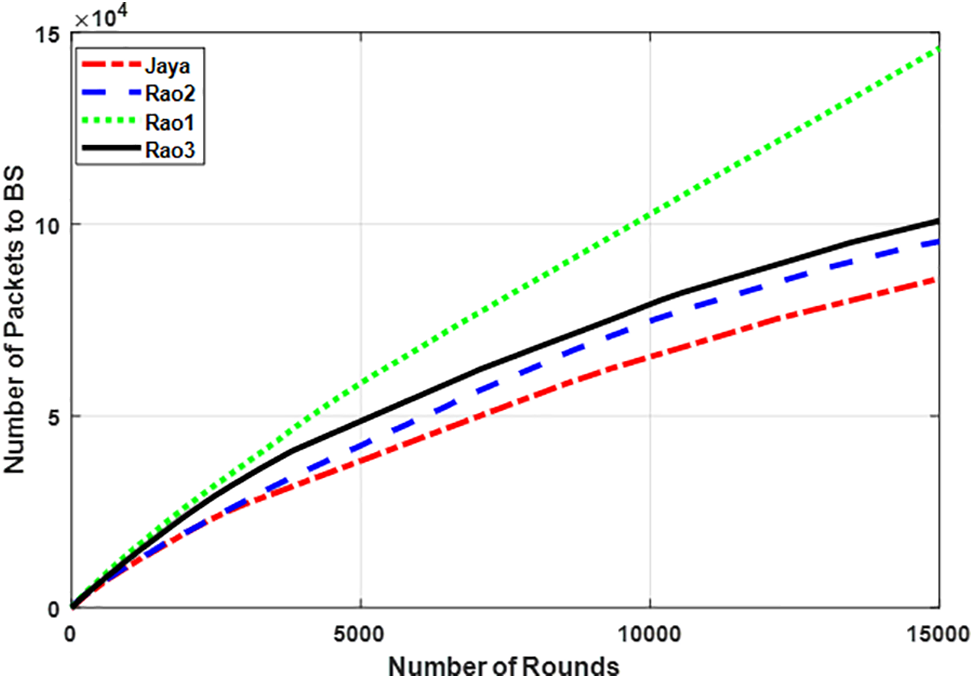
Figure 7: The throughput of optimized WSNs using the Jaya algorithm and proposed optimized WSNs using the Rao1, Rao2, and Rao3 algorithms

The throughputs of various algorithms are calculated for 15,000 rounds to evaluate their efficacy. The packets sent to BS by the Jaya algorithm are 78,215 and packets forwarded to BS when using Rao1, Rao2, and Rao3 algorithms as optimizing algorithms for WSN are 131,253, 86,027, and 100,937 packets which are higher than the existing Jaya algorithm. The highest sending rate is achieved when using the Rao-1 algorithm. The suggested WSN structure optimization approach based on Rao’s algorithms significantly increased network throughput.

Fig. 8 depicts the number of packets transmitted to the cluster head as a function of the number of rounds. Again, our suggested approach outperforms the Jaya algorithm, and Rao-1 outperforms the other two Rao algorithms.

Figure 8: The relation between the number of packets sent to the cluster heads and the number of rounds

Based on the preceding results, we can infer that optimizing the WSN structure with Rao’s algorithms for LEACH protocol extends the network lifetime, consumes less energy, and produces a high transmitting data rate to the CHs and BS. The Rao algorithms improve their performance over other algorithms like Jaya by using different update equations Eqs. (1)–(3) for energy and distance. This results in different optimized WSNs, with different node locations that directly affect the transmutation energy.

Specifically, Rao1’s update equation Eq. (1) for the energy component depends only on the energy of the greatest and least effective WSNs. This means that the new candidate solution will be closer to the best solution and further from the worst solution. Similarly, the Rao1’s distance component update depends only on the distance of the best and worst WSNs.

However, the Rao2 and Rao3 update equations (Eqs. (2) and (3)) for the energy and distance components are based on the most effective, least effective, and arbitrarily chosen candidate solutions. This means that the new candidate solution will be a compromise between the best, worst, and randomly selected candidate solutions. On the other hand, the Jaya algorithm [16] uses a weighted difference between the best, current, and worst solutions. This means that the new candidate solution will be closer to the most effective solution, but it may also be closer to the least effective solution, depending on the values of the weights.

4.3.2 100 × 100 Optimized WSN Results

Fig. 9 presents the percentage of LEACH dead nodes for Jaya-optimized WSN, PSO-EEC, and the proposed Rao1, Rao2, and Rao3-optimized WSN to the Number of Rounds for 100 × 100 WSN. As the figure illustrates the usage of Rao algorithms for the WSNs structure optimization has enhanced the lifespan of the network and its performance.

Figure 9: Percentage of LEACH dead nodes for Jaya optimized WSN, PSO-EEC, and the proposed Rao1, Rao2, and Rao3 optimized WSN to the number of rounds for 100 × 100 WSN

Table 4 compares the proposed approach to the existent Jaya, HSA-PSO, and PSO-EEC protocols based on different performance parameters. The proposed WSN Rao1 optimization method gives the best network lifetime and half-node dead rounds and Rao3 optimized methods give the best throughput of 108445 packets.

The detailed analysis of our results shows the proposed optimized WSN using the Rao1 algorithm outperforms the other algorithms in terms of HND and network lifetime. In the HND situation, Rao1-optimized WSN is better than HSA-PSO, PSO-EEC m = 0.2, PSO-EEC m = 0.3, and Jaya by 48%, 20%, 13%, and 2%, respectively. Moreover, Rao1 optimized WSN prolongs network lifetime by 40%, 15.7%, 11.5%, and 4.5% compared to HSA-PSO, PSO-EEC m = 0.2, PSO-EEC m = 0.3, and Jaya, respectively.

Rao2-optimized WSN also outperforms the other algorithms in terms of network lifetime, but not as significantly as Rao1-optimized WSN.

Rao2-optimized WSN prolongs network lifetime by 37%, 12%, 8%, and 1% compared to HSA-PSO, PSO-EEC m = 0.2, PSO-EEC m = 0.3, and Jaya, respectively. Rao3-optimized WSN is a tough competitor to Jaya for network lifetime and HND. Rao3 optimized WSN prolongs network lifetime by 33%, 8%, and 4% compared to HSA-PSO, PSO-EEC m = 0.2, and PSO-EEC m = 0.3, respectively. However, Rao3-optimized WSN has a slightly lower HND than Jaya.

Overall, the proposed optimized WSN using Rao1 algorithms outperforms the other algorithms in terms of HND and network lifetime. Rao2-optimized WSN also outperforms the other algorithms in terms of network lifetime, but not as significantly as Rao1-optimized WSN. Moreover, Rao3-optimized WSN is a tough competitor to Jaya for both network lifetime and HND. We notice that the PSO-EEC m = 0.3 has the best result for FND, but our Rao2 has a closer result.

4.4 PEAGSIS Results for the Proposed Optimized WSNs

PEGASIS [30] is an almost ideal chain-based routing protocol. This protocol’s main objective is to increase the lifespan of WSNs. Each WSN node connects only with its nearest neighbor in the PEGASIS protocol, and the nodes keep communicating with each other in turn until the collected information arrives at the Base Station. This kind of transmission consumes less energy per data transmission round. As a result, the PEGASIS protocol consumes half the energy of the LEACH protocol [30–32]. The PEGASIS protocol’s construction is composed of three stages: it begins by establishing a chain using a Greedy algorithm, then randomly choosing a leader for the established chain after information transmutation.

As it is well known the sensor node’s remaining energy is an important factor for all WSNs. Having a higher residual energy can have a number of positive implications for WSNs, including prolonged lifespan, improved performance, increased reliability, and enhanced scalability. In this work, we have applied the PEAGSIS protocol on the constructed WSNs by Rao-1, Rao-2, Rao-3, and Jaya algorithms and we have calculated the network residual energy.

Fig. 10 proposes the relation between the percentage of dead nodes and the number of rounds for Jaya, Rao1, Rao2, and Rao3 algorithms using PEAGSIS as the routing protocol. It is clear that the number of dead nodes in all Rao algorithms is less than the Jaya algorithm for the same number of rounds. In the first 4000 rounds, the Rao-1 algorithm gives the best results and the Rao-3 algorithm produces the best results for the remaining rounds.

Figure 10: Percentage of dead nodes using Rao1, Rao2, Rao3, and Jaya to the number of rounds for PEAGSIS protocol

Table 5 demonstrates the number of rounds for the PEAGSIS protocol until 1%, 20%, 50%, and 90% of nodes died. It is worth noting that when using the Jaya algorithm, 20% of nodes exhibited energy depletion in the 1441th round, and this circumstance appeared, at the 2751th, 2135th, and 1987th round in the network using Rao1, Rao2, and Rao3 algorithms. Also, more than 50% of nodes lost their energies at the 2151th round, and this circumstance appeared at the 3385th round when using the Rao1 algorithm. Nodes lost 90% of their energies at the 4561th round in Jaya, but nodes lost 90% of their energies at the 16536th round for the proposed Rao3. Thus, our proposed methodology has prolonged the lifespan of WSN (both the initial node death, half node death, and 90 percent node death). The lifespan of WSN is prolonged by 71% for the death of 90 percent of nodes and by 36% for the death of the half network nodes when using the Rao1 algorithm.

Rao’s algorithms contribute to enhancing performance by incorporating the principles of exploration and exploitation. They aim to strike a balance between exploring the search space for better solutions and exploiting the current best solution. This particular attribute can bring advantages to network systems, enabling adaptability and resilience that may result in enhanced node survival and network longevity.

Fig. 11 presents the relation between the residual energy for the WSN and the number of rounds using Jaya, Rao1, Rao2, and Rao3 algorithms employing the PEAGSIS routing protocol. As the figure demonstrates, the residual energy for Rao’s algorithms is higher than for the Jaya algorithm. The energy for the Rao1 algorithm is the best one and is greater than the Jaya algorithm by 400 Joule.

Figure 11: The residual energy of the constructed WSN for PEAGSIS protocol with the number of rounds for Rao1, Rao2, Rao3, and Jaya algorithms

4.5 PEGASIS-NN Protocol Results for the Proposed Optimized WSNs

PEGASIS-NN [33] Power-Efficient Gathering in Sensor Information Systems Neural Network routing protocol, begins with chain construction using the Greedy algorithm, similar to the PEGASIS protocol. Next, it employs a Neural Network (NN) to determine the chain leader by supplying the energies of all nodes as input to the NN and selecting the node with an output value of “1” as the chain leader. Data transmission then occurs from the chain ends towards the designated leader node.

•   PEGASIS-NN Chain Formation:

The PEGASIS-NN protocol employs a chain formation approach where the nodes are arranged in a sequence using a Greedy algorithm. This process starts from the node furthest away from the BS and proceeds towards it. The goal is to minimize power consumption by ensuring that each sensor node communicates with its two nearest neighbors.

•   Chain’s Leader Estimation in PEGASIS-NN:

A neural network is used in PEGASIS-NN to estimate the chain’s leader. An input layer, two hidden layers, and an output layer comprise the neural network’s four interconnected layers. The input layer receives data that can be of any type, such as images, text, or numbers. The input layer receives data of any type, including images, text, and numbers. PEGASIS-NN's input layer has a couple of nodes, one for energy and one for bias. Each hidden layer has five nodes, and the sigmoid function serves as the layer’s transfer function. The output layer is made up of a single node with a value of “1” to represent the leader node and a value of “0” to represent a non-leader node. The energies of all nodes in the WSN are fed into the neural network to estimate the leader of the chain. At its output, the neural network handles this input and allocates a value of “1” to the node determined to be the chain leader. The PEGASIS-NN protocol can use the neural network to determine the best node to act as the chain's leader based on the energy levels of the nodes in the network.

Fig. 12 depicts the relationship between the proportion of dead nodes and the number of rounds for the Jaya, Rao1, Rao2, and Rao3 algorithms using PEAGSIS-NN as the routing protocol. Rao’s methods have fewer dead nodes than Jaya’s for the same amount of rounds. The Rao1 algorithm generates the best outcomes in the first 10,000 rounds, while the Rao-3 method produces the best results in the remaining rounds. At round 4000th, the dead node percentage for adjusted WSN using the Jaya algorithm is 20%, 10%, and 10% higher than our proposed optimized WSN using Rao1, Rao2, and Rao3 algorithms, respectively. At round 14000th, the Jaya optimized WSN reached 100% nodes death, while the Rao1, Rao2, and Rao3 optimized WSNs had 88%, 90%, and 85% dead nodes, respectively.

Figure 12: Percentage of dead nodes for Jaya optimized WSN and the proposed Rao1, Rao2, and Rao3 optimized WSNs to the number of rounds for PEAGSIS-NN protocol

Table 6 shows the number of rounds until 1%, 20%, 50%, and 90% of nodes perished using the PEAGSIS-NN protocol. It is worth noticing that 20% of nodes lost their energies in the 1456th round of the network while using the Jaya algorithm, and the same circumstance occurred in the 2811th, 1335th, and 2056th rounds of the network when using the Rao1, Rao2, and Rao3 algorithms as optimized algorithms for the structure of WSN. Furthermore, more than 50% of nodes lost their energies in the 2198th round, and the same condition arose in the 3466th round while employing the Rao1 method. Nodes lost 90% of their energies in the 4982th round of Jaya, whereas nodes lost 90% of their energies in the proposed WSN structure optimization using Rao-3.

The details analysis of the results according to Table 6, the Rao1 algorithm is the most effective in prolonging the lifespan of a WSN using the PEAGSIS-NN protocol. It delays the node death rounds by 71.6% for the death of 90% of network nodes and by 36.5% for the death of half of the network nodes. The Rao2 algorithm is also effective in prolonging the lifespan of a WSN, but not as much as the Rao1 algorithm. The Rao3 algorithm is the best in prolonging the network lifetime, it improves the lifetime of the network by 73%. The Jaya algorithm is the least effective in prolonging the lifespan of a WSN. The results in Table 6 suggest that the Rao algorithm is a promising approach for prolonging the lifespan of WSNs.

Fig. 13 depicts the relationship between the residual energy for the WSN and the rounds number for utilizing the Jaya-optimized method and the suggested optimized methodology employing the PEAGSIS-NN routing protocol. The residual energy for Rao’s methods is larger than for the Jaya algorithm, as seen in the figure. The Rao1 WSN has the best energy for the first 5000 rounds, while the Rao3 optimized WSN has the greatest energy for the remaining rounds, outperforming the Jaya algorithm WSN by 600 Joule. Having a higher residual energy can have a number of positive implications for WSNs, including prolonged lifespan, improved performance, increased reliability, and enhanced scalability.

Figure 13: The residual energy for PEAGSIS-NN protocol with the number of rounds for Jaya algorithm optimized WSN and the proposed Rao1, Rao2, and Rao3 algorithms optimized WSN

4.6 PE-LEACH Protocol Results for the Proposed Optimized WSNs

PE-LEACH [22] is an energy-based clustering protocol with high performance. It aims to increase the energy efficiency of LEACH by introducing a network partitioning mechanism and making the sink node mobile in nature. It consists of two stages: setup and steady-state. The setup phase is in charge of creating clusters using the traditional LEACH protocol and choosing CH based on the remaining energy. The second step in the setup phase is to split the sensing area into sub-sensing area Qi numbers. The final task is to start TDMA scheduling to generate time instances for BS traversal.

The steady-state phase starts with the BS/sink node’s movement being initialized. The BS begins to move in order to gather data from the quadrant-segmented area’s sensor nodes. The BS waits for the specified amount of time in each quadrant, which is handled by time division multiple access (TDMA) scheduling. When the waiting period ends, TDMA starts a time-out session, causing the BS to move to the next quadrant. After gathering data from all quadrants, the BS goes back to its original location, the network’s center.

4.6.1 1000 × 1000 Optimized WSN Results

The proposed optimized larger scale WSN (1000 × 1000 nodes) is tested for PE-LEACH routing protocol. Table 7 demonstrates the statistics for the number of dead nodes in relation to the number of rounds. We reported on the calculation of the number of rounds when a node is first node dead (FND), half node dead (HND), or last node dead (LND).

The first node, half node, and all nodes died after 97, 827, and 9907 rounds, respectively, in the case of Jaya-optimized WSN. For instance, Rao1 optimized WSN’s FND, HND, and LND positions are 79, 952, and 10473 rounds, respectively. The FND, HND, and LND positions for Rao2 WSN are 52, 1023, and 9937, respectively, whereas for Rao3 WSN, the FND is at 41 rounds, HND is at 839 rounds, and LND is at 9793 rounds, demonstrating the superior performance of the proposed optimized WSN over Jaya optimized WSN.

The comprehensive analysis of results shows that the proposed Rao1, Rao2, and Rao3 outperform Jaya Optimized WSN for the HND position by 7%, 11%, and 1%, respectively, and for the LND position by 3, 1, and −0.5%. Except for the FND position, our proposed optimized networks outperform Jaya-optimized networks, and for the FND position, our proposed optimized WSNs are a tough competitor to Jaya-optimized WSNs. This result concludes that when using PE-LEACH as a routing protocol, the performance of a WSN optimized using Rao’s algorithms outperforms that of a Jaya-optimized network.

4.6.2 100 × 100 Optimized WSN Results

The proposed optimized small-scale network (100 × 100 nodes) is evaluated for the PE-LEACH routing protocol. As shown in Fig. 14, the proposed optimized small-scale network performs better than the Jaya algorithm in terms of the number of dead nodes at different rounds. This is because the proposed optimized WSNs use more sophisticated node placement algorithms, which results in a more evenly distributed node placement and reduces the amount of energy that nodes need to transmit data.

Figure 14: Performance comparison of Jaya optimized WSN and the proposed Rao1, Rao2, and Rao3 optimized WSN while using PE-LEACH as routing protocols for 100 × 100 network

Specifically, the Rao1-optimized WSN prolongs the network lifetime by 10%, the Rao2-optimized WSN extends the network lifetime by 4%, and the Rao3-optimized WSN extends the network lifetime by 7%. This means that the proposed optimized WSNs can help reduce the cost and complexity of maintaining the network and ensure that the network is always available.

5  Conclusions and Future Works

In this paper, we proposed a new methodology to optimize the structure of heterogenic WSNs based on Rao algorithms. In our approach, we have used the remaining energy and distance to BS to generate and optimize the fitness function. Our technique evaluated well-known routing protocols in the literature, LEACH, PEAGSIS, PEAGSIS-NN, and PE-LEACH.

We tested our proposed methodology for Rao-1, Rao-2, and Rao-3 algorithms. For the LEACH protocol, the proposed method prolongs the network lifetime by 51% for the Rao-1 algorithm, the network residual energy is greater than Jaya by 500 Joule. For the PEAGSIS protocol the network lifetime is enlarged by 71% and the residual energy by 400 Joule.

For PEGASIS-NN, the proposed methodology extends the network lifespan by 73% and conserves energy by 600 Joule. In the case of using PE-LEACH as a routing protocol for the proposed optimized WSNs, the network lifetime is extended by 10%. According to the presented results in the previous sections, our proposed scheme is proven to be efficient in terms of prolonging the network lifetime, preserving energy consumption, and increasing the packet's number reaching cluster heads and base stations. Rao algorithms are a promising approach for prolonging the lifespan of WSNs. It is relatively simple to implement and can be used with a variety of WSN network sizes. Additionally, the algorithm is robust to node failure, which makes it a good choice for WSNs that are deployed in harsh environments. In a future study, we will add more terms to fitness functions and apply Rao algorithms with multiple objectives to enhance the performance of WSNs.

Acknowledgement: I would like to express my deep gratitude to Professor S. Ali, Professor M. El-Melegy, and Assistant Professor H. El-Sayed my research supervisors, for their patient guidance, enthusiastic encouragement, and useful critiques of this research work. Our gratitude also goes to the editor and anonymous reviewers who reviewed this paper.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: The authors confirm their contribution to the paper as follows: H. El-Sayed and S. Refaay conceived the presented idea. S. Refaay developed the theory and performed the computations. S. Ali, M. El-Melegy, and H. El-Sayed supervised the findings of this work. All authors discussed the results and contributed to the final manuscript.

Availability of Data and Materials: All data generated or analyzed during this study are included in this published article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. F. Othman and K. Shazali, “Wireless sensor network applications: A study in environment monitoring system,” Procedia Engineering, vol. 41, pp. 1204–1210, 2012. [Google Scholar]

2. L. M. Borges, F. J. Velez and A. S. Lebres, “Survey on the characterization and classification of wireless sensor network applications,” IEEE Communications Surveys & Tutorials, vol. 16, no. 4, pp. 1860–1890, 2014. [Google Scholar]

3. P. Rai, M. K. Ghose and H. K. Sarma, “A game theory-based framework for reliable and energy-efficient data delivery in cognitive radio wireless sensor network,” in Trends in Communication, Cloud, and Big Data: Proc. of 3rd National Conf. on CCB, Singapore, pp. 31–39, 2020. [Google Scholar]

4. M. Jain, R. Saxena, S. Jaidka and M. K. Jhamb, “Parallelization of data buffering and processing mechanism in mesh wireless sensor network for iot applications,” in Proc. of ICACN, Singapore, vol. 2, pp. 3–12, 2020. [Google Scholar]

5. M. Elhoseny, A. Farouk, J. Batle, A. Shehab and A. E. Hassanien, Sensor Technology: Concepts, Methodologies, Tools, and Applications. Hershey, USA: IGI Global, 2020. [Google Scholar]

6. M. Frei, C. Deb, R. Stadler, Z. Nagy and A. Schlueter, “Wireless sensor network for estimating building performance,” Automation in Construction, vol. 111, pp. 1–17, 2020. [Google Scholar]

7. S. Sobhanayak, K. Jaiswal, A. K. Turuk, B. Sahoo and B. K. Mohanta, “Container-based task scheduling for edge computing in IoT-cloud environment using improved HBF optimisation algorithm,” International Journal of Embedded Systems, vol. 13, pp. 85–100, 2020. [Google Scholar]

8. K. Jaiswal and V. Anand, “EOMR: An energy-efficient optimal multi-path routing protocol to improve QoS in wireless sensor network for IoT applications,” in Wireless Personal Communications, pp. 2493–2515, 2020. [Google Scholar]

9. A. Konstantinidis, K. Yang, Q. Zhang and D. Zeinalipour-Yazti, “A multi-objective evolutionary algorithm for the deployment and power assignment problem in wireless sensor networks,” Computer Networks, vol. 54, no. 6, pp. 960–976, 2010. [Google Scholar]

10. N. J. Navimipour and A. M. Rahmani, “The new genetic based method with optimum number of super node in heterogeneous wireless sensor network for fault tolerant system,” in Int. Conf. on Intelligent Networking and Collaborative Systems, Barcelona, Spain, IEEE, pp. 187–193, 2009. [Google Scholar]

11. C. W. Tsai, “An effective WSN deployment algorithm via search economics,” Computer Networks, vol. 101, pp. 178–191, 2016. [Google Scholar]

12. J. Alonso, F. J. García, P. Matencio, J. J. Alcaraz and FJ. Castaño, “On the optimal random deployment of wireless sensor networks in non-homogeneous scenarios,” Ad Hoc Network, vol. 11, no. 3, pp. 846–860, 2013. [Google Scholar]

13. I. C. Trelea, “The particle swarm optimization algorithm: Convergence analysis and parameter selection,” Information Processing Letters, vol. 85, no. 6, pp. 317–325, 2003. [Google Scholar]

14. X. S. Yang, Nature-inspired metaheuristic algorithms, 2nd ed., Bristol, UK: Luniver Press, 2010. [Google Scholar]

15. V. T′kindt, N. Monmarché, F. Tercinet and D. Laügt, “An ant colony optimization algorithm to solve a 2-machine bicriteria flowshop scheduling problem,” European Journal of Operational Research, vol. 142, no. 2, pp. 250–257, 2002. [Google Scholar]

16. R. Rao, “Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems,” International Journal of Industrial Engineering Computations, vol. 7, no. 1, pp. 19–34, 2016. [Google Scholar]

17. R. Rao, “Rao algorithms: Three metaphor-less simple algorithms for solving optimization problems,” International Journal of Industrial Engineering Computations, vol. 11, no. 1, pp. 107–130, 2020. [Google Scholar]

18. R. Rao and H. S. Keesar, “Rao algorithms for multi-objective optimization of selected thermodynamic cycles,” Engineering with Computers, vol. 37, no. 4, pp. 3409–3437, 2021. [Google Scholar]

19. R. V. Rao and R. B. Pawar, “Self-adaptive multi-population Rao algorithms for engineering design optimization,” Applied Artificial Intelligence, vol. 34, no. 3, pp. 187–250, 2020. [Google Scholar]

20. R. V. Rao and R. B. Pawar, “Constrained design optimization of selected mechanical system components using Rao algorithms,” Applied Soft Computing, vol. 89, pp. 106–141, 2020. [Google Scholar]

21. P. Mishra, D. Sahoo, H. Khandelwal, N. Amman and S. Sobhanayak, “Minimised jaya algorithm-based structure optimisation for heterogeneous wireless sensor networks,” in Proc. of ICCCS, Patna, India, IEEE, pp. 1–8, 2020. [Google Scholar]

22. H. Mohapatra and A. Rath, “Fault tolerance in WSN through PE-LEACH protocol,” IET Wireless Sensor Systems, vol. 9, no. 6, pp. 358–365, 2019. [Google Scholar]

23. T. Shankar, S. Shanmugavel and A. Rajesh, “Hybrid HSA and PSO algorithm for energy efficient cluster head selection in wireless sensor networks,” Swarm and Evolutionary Computation, vol. 30, pp. 1–10, 2016. [Google Scholar]

24. P. Rawat and S. Chauhan, “Particle swarm optimization-based energy efficient clustering protocol in wireless sensor network,” Neural Computing and Applications, vol. 33, no. 21, pp. 47–65, 2021. [Google Scholar]

25. S. S. Halve, R. Arya and A. Koshti, “Metaphor-less RAO-1 optimization based algorithm to determine shunt capacitor capacity in distribution system,” in Proc. of ICSNT, Indore, India, IEEE, pp. 107–112, 2022. [Google Scholar]

26. Y. J. Zhang, Y. F. Wang, L. W. Tao, Y. X. Yan, J. Zhao et al., “Self-adaptive classification learning hybrid JAYA and Rao-1 algorithm for large-scale numerical and engineering problems,” Engineering Applications of Artificial Intelligence, vol. 114, pp. 105069, 2022. [Google Scholar]

27. K. N. Goyal, “An optimal scheme for minimizing energy consumption in WSN,” Global Research and Development Journal for Engineering, vol. 1, pp. 1–7, 2016. [Google Scholar]

28. R. Patel, S. Pariyani and V. Ukani, “Energy and throughput analysis of hierarchical routing protocol (LEACH) for wireless sensor network,” International Journal of Computer Applications, vol. 20, no. 4, pp. 32–36, 2011. [Google Scholar]

29. N. Mak and W. Seah, “How long is the lifetime of a wireless sensor network?,” in Proc. of Int. Conf. on Advanced Information Networking and Applications, Bradford, UK, IEEE, pp. 763–770, 2009. [Google Scholar]

30. S. Lindsey and C. S. Raghavendra, “PEGASIS: Power-efficient gathering in sensor information systems,” in Proc. of IEEE Aerospace Conf., Big Sky, MT, USA, 2002. [Google Scholar]

31. A. A. Abbasi and M. Younis, “A survey on clustering algorithms for wireless sensor networks,” Computer Communications, vol. 30, pp. 2826–2841, 2007. [Google Scholar]

32. J. Chang and L. Tassiulas, “Maximum lifetime routing in wireless sensor networks,” IEEE/ACM Transactions on Networking, vol. 12, no. 4, pp. 609–619, 2004. [Google Scholar]

33. H. El-Saye, S. Refaay, S. Ali and M. El-Melegy, “Chain based leader selection using neural network in wireless sensor networks protocols,” in Proc. of JAC-ECC, Alexandria, Egypt, IEEE, pp. 105–110, 2021. [Google Scholar]