Deployment Strategy for Multiple Controllers Based on the Aviation On-Board Software-Defined Data Link Network

1  Introduction

With the development of aviation technology, the avionics system has gone through many stages of development. However, due to the increasing complexity and diversity of combat tasks, the single-platform avionics system cannot meet the increasing demands of combat. To achieve tactical coordination and complementary capability among different platforms, a multi-data link network becomes an important means of flexible networking among aviation combat platforms. However, the complexity of multi-data link networks is increasing, and the challenge of airborne networks to integrate multi-data link and node resources is becoming more and more severe. In this case, the rational management and configuration of the airborne network, the effective integration of various data links and network node resources, will become the basic guarantee of future aviation multi-platform flexible network joint operations. Fig. 1 elucidates the comprehensive use of diverse communication links in modern warfare, spanning across the terrains of air, land, and sea. These communication links—among which include Link 11, Link 16, and U/V link—each showcase unique network topologies, architectures, and protocols. To assure coordinated operations, there is an implicit necessity for these diverse links to be interconnected and their resources collectively utilized. Complex combat scenarios necessitate a communication network capable of providing high-speed, high-precision, and high-reliability data transmission and management. However, traditional communication networks fall short of satisfying these requisites, prompting a shift towards more intelligent, flexible, and efficient communication technology. Software-Defined Networking (SDN) emerges as a significant trend in the trajectory of future networks, offering enhancements in network management flexibility, deployment speed, and scalability. Such attributes make it an apt solution for addressing the efficiency and optimization demands of communication networks [1,2].

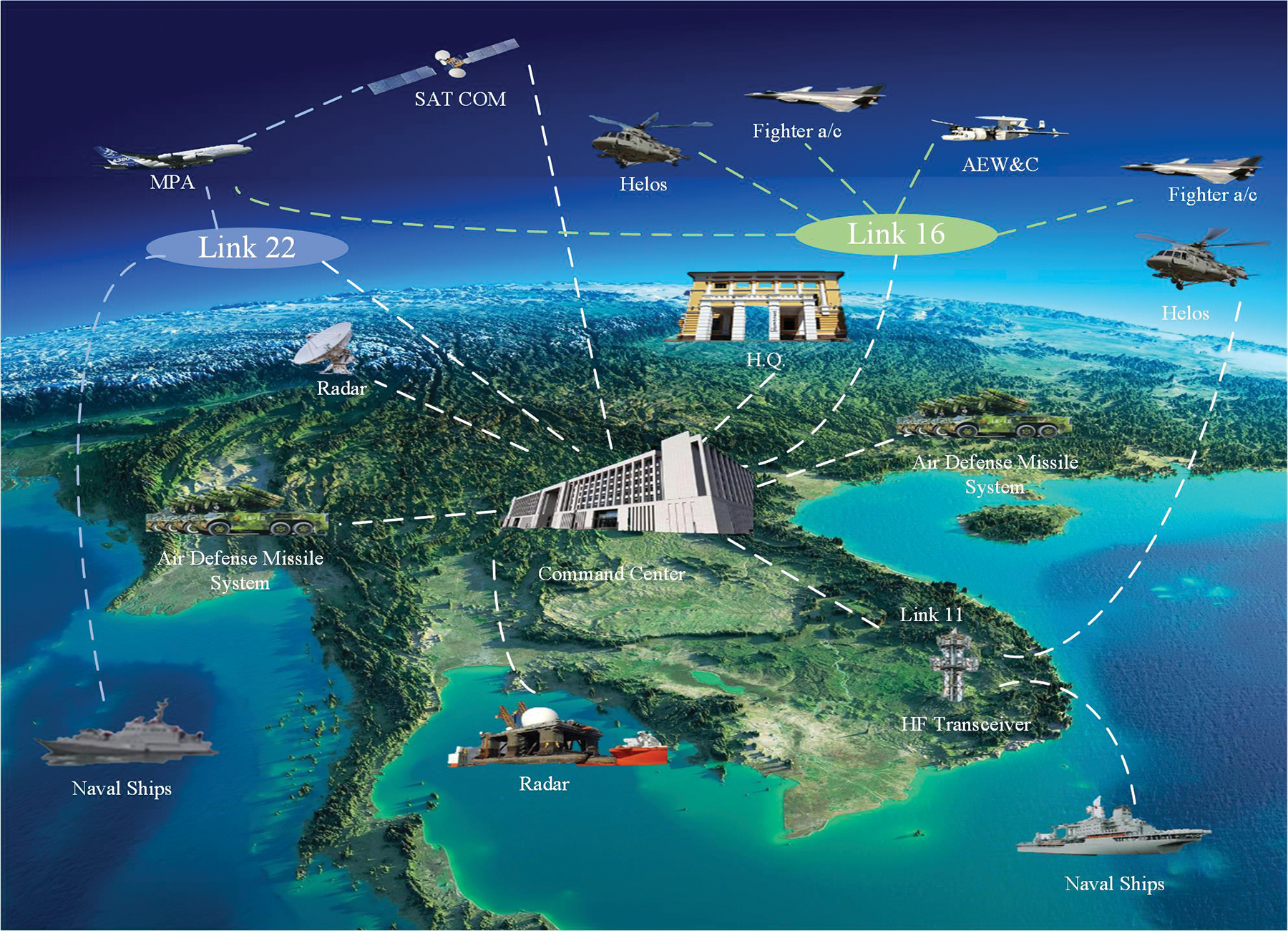
Figure 1: Schematic diagram of multi-domain data link services covering sea, land, and air

The main challenge that arises with airborne combat networks, housing multiple coexisting data links, is the diminution of the independent management mode for each data link. The transformation allows for enhanced collaboration and operation among different data links, bolstering compatibility and fostering inter-link communication and cooperation. This not only fortifies the security of the data links but also guarantees the safety and seamless execution of airborne operations.

In light of this situation, a proposition has been made for an airborne multi-data link control cluster grounded on SDN. This proposition primarily attends to the escalating control and management needs, which traditional communication networks find challenging to meet in an exponentially growing multi-data link network environment. Moreover, it augments the real-time performance, efficiency, and reliability of tactical communication networks within multi-controller environments [3]. As the complexity of multi-data link networks elevates, the relationships between network nodes become increasingly intricate, inducing network bloating and subsequently diminishing inter-node communication efficiency. Hence, research into the amalgamation of multiple data links and software-defined network technology has been instigated, to fortify the performance and efficiency of communication technology for intricate operational requirements, bolster the intelligence and adaptability of communication networks, and enhance the flexibility of network deployment and management [4–6].

In a multi-data link cluster environment, controllers grapple with challenges in effectuating efficient interaction with network nodes, primarily due to the inherent mobility and unreliability characteristics of data link nodes. Contrary to ground networks, controllers are unable to access the precise location and status information of nodes readily. Consequently, they cannot sense and react to network changes as swiftly as ground networks, impacting the robustness and scalability of the multi-data link communication platform.

To bolster the scalability of software-defined networks in expansive and dynamic environments, it becomes imperative to construct a flexible control plane, which can adapt to network needs. A controller must embody the following attributes:

(1) The capability to dynamically generate control messages and policies by varying network conditions and node states, rendering it suitable for multi-data link networks.

(2) The capacity for real-time management and control in response to changes in node position or connection interruptions.

(3) High adaptability and scalability, enabling the controller to manage large-scale nodes and complex network topologies.

The realization of these characteristics allows for the effective resolution of the lower scalability of software-defined networks in large-scale and dynamic environments, enabling the creation of a flexible control plane tailored to network requirements.

The development of a control plane adaptable to network needs within a multi-data link cluster environment is a crucial challenge faced by SDN. It is paramount to consider node mobility and unreliable characteristics and to design controller architecture and algorithms that are suitable for multi-data link networks to realize practical use and promote applications. The resolution of these key issues carries significant importance for the implementation of multi-data link networks. The processing capability of a solitary SDN controller is inherently constrained within data link networks. The voluminous traffic and multitude of requests may exceed its handling capacity, engendering sluggish speeds, management challenges, and an overall degradation in network performance. Such conditions foster delayed information processing and uneven load distribution.

In recent years, the study of Controller Placement Problem (CPP) is rising, and researchers have found that the number and location of controllers have a direct impact on the performance of the control level. In the airborne network, the deployment location of the controller may cause delays in new stream establishment, problems of network configuration and management efficiency, and affect the reliability of the network. Early CPP studies focused on fixed topologies of WIRED SDN, with a focus on performance metrics and search algorithms. Later, researchers proposed CPP considering reliability optimization and explored greedy algorithm and simulated annealing algorithm. In addition to latency and reliability, load balancing, network resilience, and fault tolerance are also important performance indicators for CPP problems. At present, the research of CPP focuses on the flat controller architecture without considering the need for hierarchical deployment. Because of the significant difference between airborne networks and terrestrial networks, the previous research on CPP cannot meet the needs of aviation cluster scenarios in the aspects of controller architecture design, performance measurement, and search algorithm. Therefore, in the research of CPP of aviation clusters, we should design the appropriate controller architecture, and select the appropriate performance index and algorithm. Due to the lack of these considerations in the current research, its guiding role in practical application is limited. Therefore, under the background of a tactical multi-data link network, it is the key to improve the network performance to establish the corresponding optimization model and algorithm for the CPP problem. This research can effectively solve the problem of limited controller performance and improve the reliability and stability of multi-data link networks.

Current research focuses on three sub-questions:

(1) with the development of aviation technology, the complexity and diversity of combat missions are increasing day by day, and the processing capacity of single-platform avionics systems is limited, which cannot meet the real-time service requirements of various operations.

(2) to meet the actual needs of a multi-platform data link cluster network, and with the increasing complexity of multi-data link network, this may result in reduced or paralyzed performance of the airborne network for multi-datalink cluster and node resource management.

(3) how to improve the reliability of airborne data link clusters and reduce the average propagation delay and average disconnection rate of clusters based on the load balance of multi-controllers.

The principal contributions of this study can be encapsulated as follows:

Foremost, in response to the conventional network performance inadequately accommodating the rapidly escalating service demands of various data links within an airborne cluster, this paper devises a system architecture for an airborne data link network and introduces a controller node deployment scheme. The deployment of controller nodes transpires across two phases: subdivision of domains and selection of central interactive nodes, thereby addressing current needs.

Secondly, in terms of the subdivision of domains in the SDN multi-controller milieu, this study propounds an algorithm for subdomain division predicated on a synthesis of node value and reliability. By assessing node value and reliability, this algorithm generates subdomain divisions congruent with contemporary requirements, thereby augmenting network reliability and performance.

Lastly, concerning the central interactive node selection conundrum, this study postulates a scheme that refines the Artificial Fish Swarm Algorithm (AFSA). Chaos algorithm is an optimization algorithm based on chaos theory. By introducing a chaos map, initial seed, and iteration number to search solution space, it has global search ability and convergence. To improve the search efficiency of the algorithm, chaos algorithm, and adaptive mechanism are introduced to improve the diversity and flexibility of fish initialization and avoid falling into local optimal solution. Simultaneously, the incorporation of crossover and mutation procedures from genetic algorithms amplifies the optimization capacity and search precision of the algorithm. This scheme, by evaluating the average propagation delay and average disconnection rate of the control path, facilitates optimal controller node placement.

The subsequent sections of this paper will unravel as follows: Initially, Section 2 will introduce the extant related works. Following this, in Section 3, we will dissect and model the pertinent problems. Subsequently, and elucidate in detail the specific implementation methodologies of the enhanced algorithm. Section 4 will introduce the simulation experiments we have undertaken, accompanied by an analysis of comparative results. Lastly, in Section 5, we will encapsulate our research conclusions and contemplate prospective research trajectories.

2  Related Work

2.1 SDN Technology

SDN technology enhances network centralization, programmability, and automation by SDN technology bolsters network centralization, programmability, and automation by disassociating network control and data forwarding. However, in large-scale networks, the capabilities of a single controller fall short of the requisite needs, thus prompting the suggestion of SDN multi-controller solutions to ameliorate network reliability and scalability.

The prevailing SDN multi-controller architectures predominantly bifurcate into vertical and horizontal structures. The vertical configuration imposes an upper control layer on multiple controllers to coordinate intercommunication among them, but it grapples with predicaments such as substantial top-node loads and potential paralysis in case of failure [6,7]. Conversely, the horizontal configuration aligns controllers at a similar level with uniform qualifications and roles, enhancing the scalability of the controllers and diminishing the performance prerequisites of individual controllers [8]. Nonetheless, the quandary of load balancing in SDN multi-controller architecture remains unresolved. To address this issue, the following countermeasures may be considered.

(1) The Port-Sharing scheme can divide physical ports into different logical ports. The primary controller occupies all physical ports, and the auxiliary controller balances the load only when the primary controller fails. This scheme enhances the disaster recovery capability of the primary controller but may affect the performance and load-balancing efficiency of the auxiliary controllers [9–12].

(2) The Partition-based scheme can divide the SDN topology into different regions, each managed by a controller, and prevents multiple controllers from controlling the same switch. This scheme can improve load balancing efficiency but needs to consider load balance in partitions and changes in topology [13–15].

(3) The Dynamic Load Balancing scheme uses dynamic load balancing technology to allocate controllers based on the real-time load of the SDN network. It can enhance the load balancing efficiency and fault tolerance of the controller, but it also needs to consider the real-time scheduling of controllers and the impact on network performance during actual deployment [16–18].

(4) The Controller Pooling scheme allows multiple controllers to simultaneously access the same group of switches using a controller pool and enhances network reliability and scalability by automatically balancing the load. This scheme can improve load balancing efficiency while reducing the number of controllers, but it needs to consider the management and maintenance of the controller pool [19–21].

2.2 Controller Deployment Techniques

The CPP technology of the SDN multi-controller deployment algorithm is used to address the issue of multi-controller deployment in the SDN controller architecture [22]. Its key solutions include static division algorithm, dynamic division algorithm, controller cooperation algorithm, and controller dynamic scheduling algorithm.

(1) The static division algorithm primarily divides the network topology graph into multiple subdomains according to certain rules, with each subdomain managed by one controller [23].

(2) The dynamic division algorithm adjusts the division of controller domains dynamically based on the real-time load of the SDN network, ensuring a more balanced load distribution [24].

(3) The controller cooperation algorithm achieves load balance and stability among various controllers through data synchronization and cooperation [25].

(4) The controller dynamic scheduling algorithm adaptively adjusts the load among different controllers, attaining optimal load balance and network performance [26].

Depending on the specific features and practical needs of different SDN networks, an appropriate algorithm must be selected to solve the multi-controller deployment issue. In recent years, various major manufacturers have also offered corresponding solutions, further promoting the development and application of the CPP technology for the SDN multi-controller deployment algorithm.

2.3 Optimization Approaches for Deployment Challenges

The exhaustive algorithm can find the optimal solution of CPP, but it takes too much computing time for large-scale networks, so it is necessary to use a heuristic algorithm to find the approximate optimal solution in a short time. To address the problem that the exponential growth of Internet applications requires expensive computing costs, Malik et al. [27] proposed a new software-defined network Deep learning model that can accurately identify various traffic applications in a short period, called deep-SDN. The optimal solution is obtained in terms of accuracy, precision, and recall rate. Li et al. [28] proposed SDN networks based on deep learning to solve the problem that networks cannot adapt to the rapidly changing traffic behavior and limit their play. Adaptive deep Q-learning (ADQN) is used to make a deep reinforcement learning routing plan, which improves load stability and network performance. Ibrahim et al. [29] proposed the Controller Placement Problem (CPP) framework for dynamic mapping between controllers and switch migration in SDN distributed network architecture to improve the reliability and scalability of SDN systems. The GA is then integrated with the distribution component to improve the controller position. Luong et al. [30] proposed the AHP-SA algorithm, which combined the analytic Hierarchy Process (AHP) with the simulated annealing (SA) method. In this algorithm, AHP is applied to determine the weight of network attributes, and then the SA algorithm is applied to determine the allocation of requests to the network to obtain the best link. Tahmasebi et al. [31] described the controller placement problem as a multi-objective optimization problem. In this regard, several constraints are considered, including reliability, fault tolerance, performance in terms of latency, synchronization overhead, and deployment costs. In addition, we utilize the Cuckoo optimization algorithm, a nature-inspired crowd-based meta-heuristic algorithm, to solve the optimization problem. Although many new mechanisms have been proposed, such as Ma et al.'s Fuzzy logic algorithm [32] and Zhu et al.'s Stochastic systems [33] to solve optimization problems in different scenarios, genetic algorithms (GA) and PSO are evolutionary algorithms that can theoretically solve any general purpose single or multi-objective CPP. Sanner et al. [34] used a Genetic Algorithm (GA) to search for the optimal controller position, but only optimized the delay between the controller and the switch, and Lin et al. proposed an optimization algorithm for SDN controller placement based on multi-objective genetic algorithm [35]. Xie et al. [36] proposed an improved PSO algorithm to solve the SDN controller placement, which regulates particle acceleration and velocity and considers optimization factor changes. Zhang et al. [37] also used particle swarm optimization to solve CPP and proposed an SDN-based method (PSOCB). A meta-heuristic method is used to allocate and optimize the existing cluster switches in the network between the source end and the destination end, which improves throughput and reduces latency. In the reference [38], Sharma et al. proposed a Bayesian framework to build an intelligent optimization framework for SDN resource management by using deep meta-reinforcement learning. Adaptive adjustment of controller parameter weights helps to deal with congestion caused by heavy loads. The algorithm determines the best action based on the prediction of reinforcement learning. In reference [39], Zheng et al. proposed an SDN load balancing algorithm based on Improved ant Colony Optimization load Balancing (ICO-LB). To prevent the algorithm from falling into local optimality, based on the improvement of the basic ant colony algorithm, the Kent chaos model is used to disrupt the migration probability of ant colonies. After experiments, it is found that the algorithm can dynamically adjust the routing scheme according to the changes of network link traffic and servers, to improve the utilization rate.

3  Modeling the Problem Domain

Within the context of multi-platform aviation warfare scenarios, an array of aircraft and equipment, encompassing drones, early-warning aircraft, attack aircraft, helicopters, ground control stations, and more, communicate through designated data links to execute coordinated operations. These platforms establish communication links between airborne or ground-based data link devices, facilitating the exchange of data and instructions, consequently achieving a wide spectrum of combat tasks throughout the operations, including but not limited to, information acquisition and analysis, target positioning and engagement, and data transmission and sharing.

As illustrated in Fig. 2, the current study employs a cooperative, multi-controller architecture predicated on data links and accommodates the unique application scenarios of airborne clusters. We partition the control plane into a layered structure of controller cooperative architecture. The superior layer comprises the Top Controllers (TCs), accountable for cross-regional network communication and resource management. TCs are typically stationed on platforms such as early warning and command aircraft, integrating data across diverse platforms to gain a comprehensive understanding of the network and task status within the aviation cluster. This overarching perspective enables a swift response and effective management of the entire network, thus bolstering the combat capability and operational efficacy of the aviation cluster while ensuring information transmission efficiency and reliability.

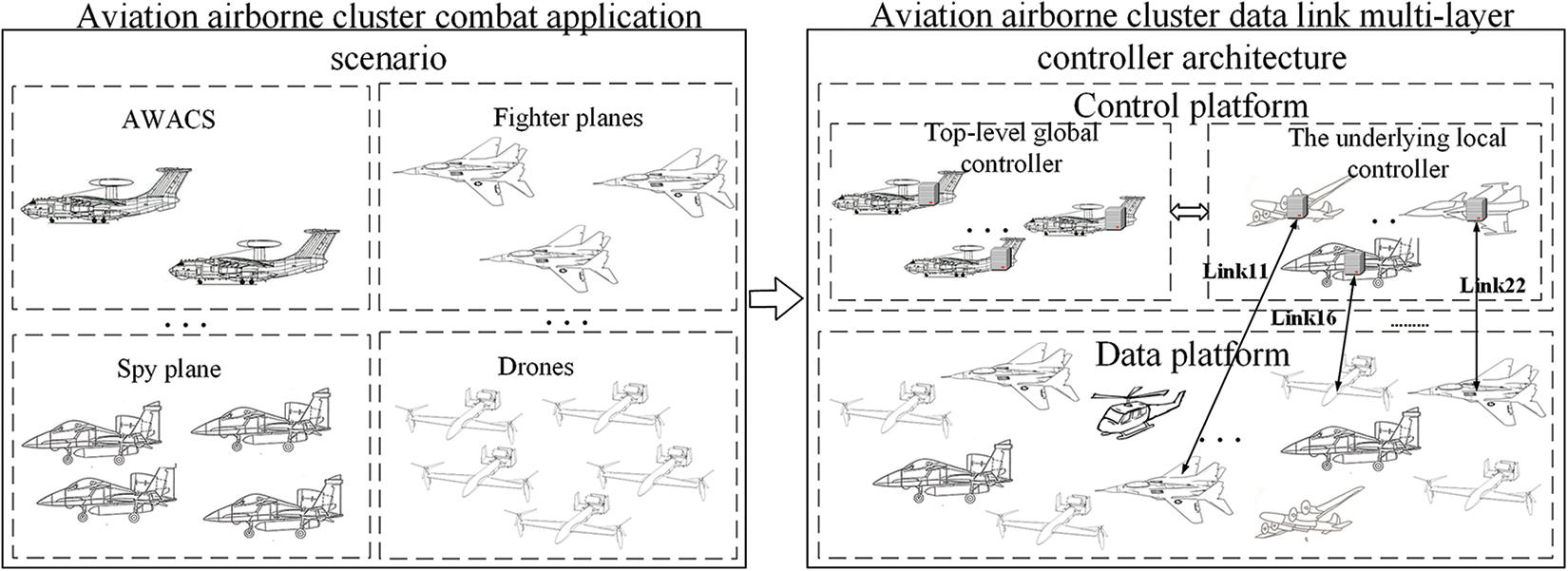
Figure 2: Schematic diagram of multi-controller cooperative architecture for airborne data link based on SDN

The underlying multi-controller architecture is populated by Local Controllers (LCs), each maintaining the network view solely within its domain of control and collaborating with the Top-level Controller (TC) to sustain a global network perspective. Each LC is charged with managing local devices and traffic and conducting downstream management. To accommodate node scale, network traffic, and other factors, LCs are deployed as needed, with the capability to be elastically activated or deactivated. This process creates a pool of local controller resources, forging a control plane with the top-level controller. This paper primarily delves into the deployment issues of LCs under this architecture.

In deploying a multi-controller cluster, distinct controller nodes can be stationed across various subnets, each corresponding to a collection of switches and terminal devices. The cluster can use the shortest path algorithm to ascertain the controller node within the corresponding subnet, calculating the controller node in closest proximity to each switch within the subnet and transmitting this controller node’s location information to each device. Devices can pinpoint the controller nodes along the path through communication with neighboring switches and relay their event and status information to their respective controller nodes. To boost the overall efficiency of the cluster, multiple controller nodes can be stationed and coordinated across different subnets. Should a controller node within a subnet fail, an automatic transition can be performed through other nodes in the cluster, thereby circumventing the repercussions of single-point failures.

This study embarks on an investigation of the determination process of a Local Controller (LC) deployment scheme that accommodates the exigencies of network management performance within a multi-layered controller architecture grounded in data link principles. This is undertaken under the predetermined conditions of the quantity and geographic distribution of network nodes as well as top-tier controllers. The ultimate objective of this exploration is to introduce an efficacious method to attain superior network management performance via the strategic deployment of LC controllers.

By delving into the locational data of network nodes and global controllers, this study endeavors to identify the collection of network nodes apt for LC controllers. Subsequently, contingent on the size and dispersal of this node conglomerate, a pertinent algorithm will be employed to derive the LC controller deployment scheme that satisfies performance prerequisites. The endgame of this process is to facilitate meticulous regulation of network devices and traffic, thereby constructing an efficient network control plane and boosting the holistic performance and managerial efficacy of the network.

Every platform within the operational network serves as a transmission node. The transmission linkage connecting the controller with the central interaction node is referred to as an out-of-band link. The network center converts the network, laden with multiple concurrent data links, into an undirected graph, denoted as G=(V,E,Tc,Lc). In this graph, V stands for the compilation of network nodes; E signifies the collection of inter-nodal links; Tc represents the array of local controllers; and Lc designates the assortment of local controllers, incorporating both elements Tc⊆V and Lc⊆V. Detailed network parameters along with their descriptions are comprehensively illustrated in Table 1.

3.1 Algorithm Description

Amid the execution process of airborne data link cluster tasks, changes in combat tasks may induce alterations in the network topology. Leveraging all network topology information, the Top-level Controller (TC) can generate the deployment scheme by the LC deployment algorithm. Broadcasting this LC deployment scheme across the entire network, this method fosters efficiency and convenience in the LC deployment procedure. Simultaneously, it can adeptly manage changes in the data link network structure, thereby facilitating intelligent management of network devices.

This study is predicated on the design of a multi-layer controller architecture based on data links, with the capability to effectively govern the network plane while fully leveraging data link resources. We introduce a sub-domain partitioning algorithm predicated on node importance ranking (NDVR), alongside an improved Artificial Fish Swarm Algorithm (IAFSA). Utilizing the positional information of network nodes and top-level controllers, the proposed algorithms can swiftly resolve an LC controller deployment scheme that meets network management performance requirements. The algorithms outlined in this paper possess practical implications and value in enhancing overall network performance and management efficiency.

3.2 Subdomain Division Algorithm Based on Node Importance Ranking

K-shell decomposition is a coarse-grained node importance classification method, which divides the network layer by layer from edge to core according to node location information. The K-shell value reflects the global position of the node in the network, and the larger the K-shell value, the more central the node’s position, and the more important the node. The steps of the K-shell decomposition method are as follows:

(1) Calculate the degree of all nodes in the network, and take the smallest degree value as K;

(2) Delete all nodes whose degree is K in the network, update the network, and recalculate the degree value. Recursively delete nodes whose degree is less than or equal to K until the degree of nodes in the network is greater than K, and mark the deleted nodes as k-shell;

(3) Repeat steps (1) (2) until all nodes in the network have been stripped and marked with K-shell values. The ranking algorithm based on node importance in this paper uses the K-shell algorithm to calculate the importance of each node.

In alignment with the design of the subdomain division algorithm based on node importance ranking, this section initially establishes the definition of node degree value, node reliability, and node importance as follows:

Definition 1. The degree value of a node is defined as

Vi=−∑j∈Γ(i)Ij⋅ln⁡Ij⋅ksj(1)

Ij=∑i≠j1N(N−1)dij(2)

In Eqs. (1) and (2), Ij represents the network efficiency of node j,N is the total number of nodes, dij is the shortest distance from node i to node j, and ksj is the ks value of node j.

Definition 2. Node reliability is defined as

Rj=∑i=1,i≠jNxijN(N−1)dij(3)

In Eq. (3), the average value of the sum of the reciprocals of the distances from node i to other nodes. Here, N is the total number of nodes, and xij represents the connectivity from node i to node j, with 1 for connected, and 0 for unconnected.

Definition 3. Node importance

Wi=Vi⋅Ri(4)

In Eq. (4), Vi is the value degree, and Ri is the reliability.

The algorithm for subdomain partitioning, anchored on the principle of node value ranking, bifurcates into two integral components: NDVRI: This component harnesses an advanced K-shell algorithm, with a focal point on node value, to ascertain the value degree of individual nodes. NDVRII: Drawing upon the value degrees procured, this segment computes the importance degrees, hierarchically orchestrates them, and consequently delineates the subdomains predicated on the derived outcomes. In the incipient phase, the NDVRI algorithm discerns nodes characterized by the most diminutive degree within the contemporaneous network, subsequently attributing to them an iteration factor termed IT. Predicated on a stipulated definition, the value degree of these nodes is represented as Vi, is calculated (Lines 1–2). Thereafter, nodes bearing the least degree are excised from the network. Upon the scenario where the total nodes in the network diminish to nil, a juxtaposition ensues to ascertain whether IT(max) aligns with the antecedent iteration factor, IT. In instances of congruence, the node exuding the zenith value degree within the set congruent to the present iteration factor, IT, is methodically amalgamated into the paramount value degree node ranking assembly (Lines 3–10). In the absence of such congruence, the metric of IT is augmented by a unit (Lines 11–14). Conclusively, the algorithm unveils a node ranking ensemble, fundamentally rooted in their respective value degrees (Line 15).

After this, the results obtained from NDVRI function as the input for NDVRII. Initially, it configures the preliminary network node matrix using the distance matrix and the greedy algorithm, calculates the value degree Vi and reliability Ri for each node under the formula, leading to the derivation of the importance Wi (Lines 1–3). Next, it orders the node set V in ascending order based on the Wi values, which produces the node set VCon, and selects the first k nodes to form the regional vertex S−con. If there is a presence of nodes sharing the same Wi value, one is chosen at random from these (Lines 4–8). It then embarks on traversing the entire topology, measuring the distance from each node to the regional vertex. Following the principle of minimal distance to the regional vertex, the network is divided into k subdomains N={N1,N2,…,Nk}. The algorithm finally concludes the loop and delivers the partitioned subdomain set N (Lines 9–13).

3.3 Optimization of Central Interaction Node Selection

3.3.1 Optimization of Performance Indices

This study elegantly reframes the problem of determining the optimal deployment sites for LCs within each subdomain. This is accomplished by reducing a multi-objective optimization problem to a single-objective one, with the express goal of curtailing the average propagation delay and the average disconnection rate in the control path.

Definition 4. Average Propagation Delay of the Control Path

Within the context of a sprawling airborne data link cluster, the average propagation delay of the control path is the aggregate of the average transmission lags from the transmission nodes to the LCs and from the LCs to the TCs. This metric is pivotal in ensuring effective control and swift response in the control plane.

Tavg=1N∑vi∈Vmind(vi,sj)⋅xij+1k∑si∈Smind(si,mj)⋅yij(5)

In Eq. (5), d(vi,sj) stands for the assemblage of the shortest path delays between the transmission node v and the LC node s;d(si,mj) signifies the collection of the shortest path delays between the LC node s and the TC node m.

Definition 5. Average Disconnection Rate of the Control Path

Given the prevalence of unstable link quality and high node disconnection rates within airborne data link clusters, the control path is often susceptible to interruptions. As such, the average disconnection rate of the control path serves as a crucial gauge of its reliability. This index offers an insightful view of the likelihood of control path interruptions within the network.

σavg=1N∑l∈(V,S)d1p1⋅xij+1k∑l∈(S,M)d1p1⋅yij(6)

In Eq. (6), l∈(V,S) symbolizes the ensemble of control paths extending from the transmission nodes to the LC nodes; l∈(S,M) refers to the collection of control paths from the LC nodes to the TC nodes; d1 embodies the interruption rate of the control link; and p1 pertains to the failure rate of the transmission nodes.

Definition 6. Optimization Objective Function

W=ασavg +βTavg ,α=0.5,β=0.5(7)

In Eq. (7), Tavg corresponds to the summation of average transmission delays, σavg  signifies the average disconnection rate of the control path, and both α and β hold a value of 0.5.

3.3.2 Algorithm for Selecting Central Interactive

Nodes as compared to the traditional CPP calculation methods, the optimization scheme proposed in this paper requires a comprehensive analysis of the controller link’s global attributes. This necessitates a system-wide viewpoint for deciding the placement of controllers in each subnetwork, escalating the complexity of the algorithm. To achieve the highest accuracy within a constrained time-frame, the research adopts the Improved Artificial Fish Swarm Algorithm (IAFSA). This heuristic search algorithm is optimally designed for resolving optimization challenges in a distributed environment, with key strengths including global search capabilities, simplicity of implementation, distributed optimization, ease of parameter tuning, and superior flexibility.

Chaotic Operator-Based Improved Fish Swarm Initialization Strategy

To amplify the global convergence capacity of the algorithm, the traditional Artificial Fish Swarm Algorithm is advanced by incorporating chaos mapping as an initialization approach for the fish swarm. The chaotic sequence, characterized by randomness, ergodicity, and regularity, assures the randomness and diversity of individual fish swarms, thereby ensuring an equitable distribution of the initial fish swarm across the solution space [40].

Empirical findings indicate that the application of Logistic chaos mapping for fish swarm initialization surpasses the standard difference algorithm’s random distribution approach. The chaos mapping technique optimally disperses the population across the solution domain, thereby enhancing diversity and effectively curbing the algorithm’s premature convergence issue. The fundamental Logistic chaos mapping equation is as stated below:

Xi+1=μ∗Xi(1−Xi),i∈{1,2,…},μ∈(0,4],Xi∈(0,1)(8)

Xi+1 is the chaos variable generated from i to j.

In Eq. (8), logistic chaos mapping, a frequently employed chaotic sequence, utilizes 0≤Xi≤1 and μ as control parameters encompassed within the range of 0<μ≤4. A salient characteristic of the Logistic chaos mapping sequence manifests when the scope of control parameter μ resides between 0 and 1. Irrespective of the system’s initial point or the selected value for μ, the chaotic sequence invariably gravitates towards zero as the iteration count escalates.

In Eqs. (9) and (10), the operative range for Logistic chaos mapping is bracketed between (0,1). Upon setting the control parameter μ to 4, it becomes feasible to engender chaotic variables. Conventionally, region [0,1] is partitioned into several subdivisions, facilitating the distribution of chaotic variables therein. For instance, region (0,1) is segmented into ten intervals, represented by (0,0.1], (0.1,0.2], …, (0.9,1].

Nonetheless, owing to the disproportionate allocation of chaotic variables within intervals [0,0.1) and [0.9,1), the algorithm’s efficacy potentially suffers. In light of this, an enhancement has been implemented in the Logistic chaos mapping, with the revised equation as follows:

Xi+1old=μ∗Xiold(1−Xiold),i∈{1,2,…},μ∈(0,4],Xiold∈(0,1)(9)

Xi+1new{0.1+0.8∗rand(0,1),Xi+1old≤0.1orXi+1old≥0.9andXi+1old,else(10)

In Eq. (11), the refined Logistic chaos mapping harmoniously reassigns the chaotic variables from regions 1 and 10 across other areas, exhibiting enhanced traversability. Consequently, utilizing the refined Logistic chaos mapping, the initialization of the population is executed according to the ensuing formula:

Xi,j0=Xj−min−Xi+1new∗(Xj−max−Xj−min)(11)

Within this context, Xj−min stands for the minimum boundary value of the j-th dimensional gene, whereas Xj−max signifies the maximum boundary value of the same dimensional gene.

Adaptive Visual Field and Step Length Algorithm

In a bid to amplify the algorithm’s global search capacity, this research introduces a piecewise adaptive function to modulate the visual field and the step size coefficient of the artificial fish. During the preliminary stages of the algorithm, the artificial fish possess an expanded visual field and step size, enabling a rapid evasion from local optima towards global search optimization. As the algorithm progresses, there is a gradual reduction in the visual field and step size, which refines the solution’s precision. This design enables the visual field and step size of artificial fish to be adaptively fine-tuned to match the unique traits of the problem space. In the early stages, an enlarged visual field and step size facilitate the global search for artificial fish, aiding in the discovery of the global optimal solution. Conversely, in the later stages, the visual field and step size are progressively reduced, narrowing the search range and improving the precision of the solution. By employing this piecewise adaptive function, an appropriate equilibrium between global search and solution precision is established. This dynamic adjustment method bolsters the algorithm’s global search potential, satisfying the optimization demands of varied problems.

To accomplish this objective, we opted for an exponential function-based piecewise adaptive function to modulate the artificial fish’s visual field and step size coefficient. The exponential decay coefficient in the function type undergoes rapid decay at the algorithm’s outset, thereby ensuring robust global search capacity. Meanwhile, the decay rate slightly slows down in the algorithm’s later stages, reinforcing the search for local solutions. Broadly, this adaptive function behaves as a decreasing function, with the decay rate modulated by parameters in the function, detailed as follows:

Va=V⋅fV(i)(12)

Sa=S⋅fS(i)(13)

In Eqs. (12) and (13), fV(i) and fS(i) respectively represent the adaptive functions for the field of view and step length, where i denotes the number of iterations.

fV(i)=KV⋅bVi(14)

fS(i)=KS⋅bSi(15)

In Eqs. (14)–(17), regarding the function coefficient KV=KS, its value domain is [ymin,ymax], starting from the maximum value ymax and ultimately reaching the minimum value ymin in the final iteration. The maximum number of iterations is denoted by genmax. Its exponential form is as follows:

KV=KS=ymax(yminymax)1gmax−1(16)

bV=bS=(yminymax)1genmax−1(17)

Bulletin Board Update Strategy Predicated on Genetic Algorithms

The Artificial Fish Swarm Algorithm (AFSA), a pioneering evolutionary algorithm proffered by Li [41], is distinguished by its capacity to tackle function optimization predicaments. The core of function optimization involves the mathematical modeling of actual scenarios, transmuted into an optimization problem in the function domain. The AFSA furnishes a comprehensive architecture for the resolution of such optimization conundrums.

The basic idea of the artificial fish swarm algorithm is to simulate the behavior of a fish swarm and find the optimal solution of the function through the interaction within the fish swarm. Artificial fish is built according to this characteristic, imitating the behavior of fish, including foraging, clustering, rear-end pursuit, etc. Each artificial fish corresponds to an optimization solution, which is optimized by the artificial fish swimming in the virtual waters, and the objective function value is expressed by the food concentration. The four behavior patterns of artificial fish are the core of the artificial fish swarm algorithm.

a) Foraging behavior

If the artificial fish is given two states, and the current state is Xn, Xm, which is a randomly selected state within its field of view:

Xn=Xm⋅V⋅Rand()(18)

In Eq. (18), Rand() produces a random number from 0 to 1, and V is the field of view.

If the food concentration is Yn > Ym, go one step in that direction.

Xmk+1=Xmk+Xn−Xmk‖Xn−Xmk‖⋅S⋅Rand()(19)

In Eq. (19), S is the step size and k is the number of iterations. If Ym > Yn, then X is chosen randomly again, and repeated attempts are made. If the maximum foraging times are reached, but the forward condition is not reached, the random behavior is performed.

Xmk+1=Xmk+S⋅ Rand()(20)

b) Clustering behavior

In the Eq. (20), the average state Xc of the artificial fish in the neighborhood can be obtained when the state Xm is known and the number of the artificial fish in the neighborhood is nf.

Xc=∑m=1nfXmnf(21)

In Eq. (22), if nf/N<δ is true (N is the number of artificial fish, δ is the degree of crowding, 0 < δ < 1), and Yc > Ym, it shows that the food concentration at Xc is high and not crowded, the artificial fish can go to Xc, or continue foraging.

Xmk+1=Xmk+Xc−Xmk‖Xc−Xmk‖⋅S⋅Rand()(22)

c) Rear-end behavior

In Eq. (22), the current state of the artificial fish is Xm, and its neighborhood Xbest is the optimal state. If nf/N<δ, it indicates that the food concentration at Xbest is not only high but not crowded, and the artificial fish moves to Xbest, otherwise it will continue foraging.

Xmk+1=Xmk+Xbest−Xmk‖Xbest−Xmk‖⋅S⋅Rand()(23)

d) Random behavior

After reaching the maximum number of foraging behaviors, the artificial fish performs random behaviors when the fitness is still not improved, that is, the artificial fish randomly swims to a certain state within its field of vision and takes this state as its next state, as shown in Eq. (20). Random behavior can make artificial fish jump out of the local optimal state and turn to the global optimal solution. In the behavior selection, artificial fish will evaluate the current environment, and then choose the appropriate behavior to carry out, and the default behavior is foraging. The bulletin board is used to record the optimal state of artificial fish in the optimization process.

However, the AFSA might encounter certain quandaries in problem-solving, such as the erratic motion of artificial fish or their congregation around local optima, consequently impairing convergence velocity and search precision. Incorporation of the crossover and mutation operations from genetic algorithms can counteract these issues, thereby refining the algorithm’s performance.

Genetic algorithms can be integrated into the AFSA operation via a bulletin board, utilized to catalog historical optimal individual states. If an individual retains its state or manifests minimal alterations after a series of successive iterations, this suggests that the individual has been consistently demonstrating superior states. At this juncture, crossover and mutation operations can be deployed to preserve the historically optimal state of the individual and to carry out crossover and mutation on other individuals with a certain probability. The inclusion of these operations amplifies the algorithm’s diversity, enhances its global search capacity, and precludes individuals from descending into local optima.

This enhanced technique can bolster the performance of the AFSA, thereby rendering it more fitting for the resolution of intricate problems. By amalgamating genetic algorithm operations, the algorithm’s convergence rate is quickened, search accuracy is bolstered, and the issue of succumbing to local optima is circumvented. Consequently, the AFSA will exhibit augmented robustness and optimization competency in problem-solving. The workflow of this improved AFSA (IAFSA) algorithm is illustrated in Fig. 3.

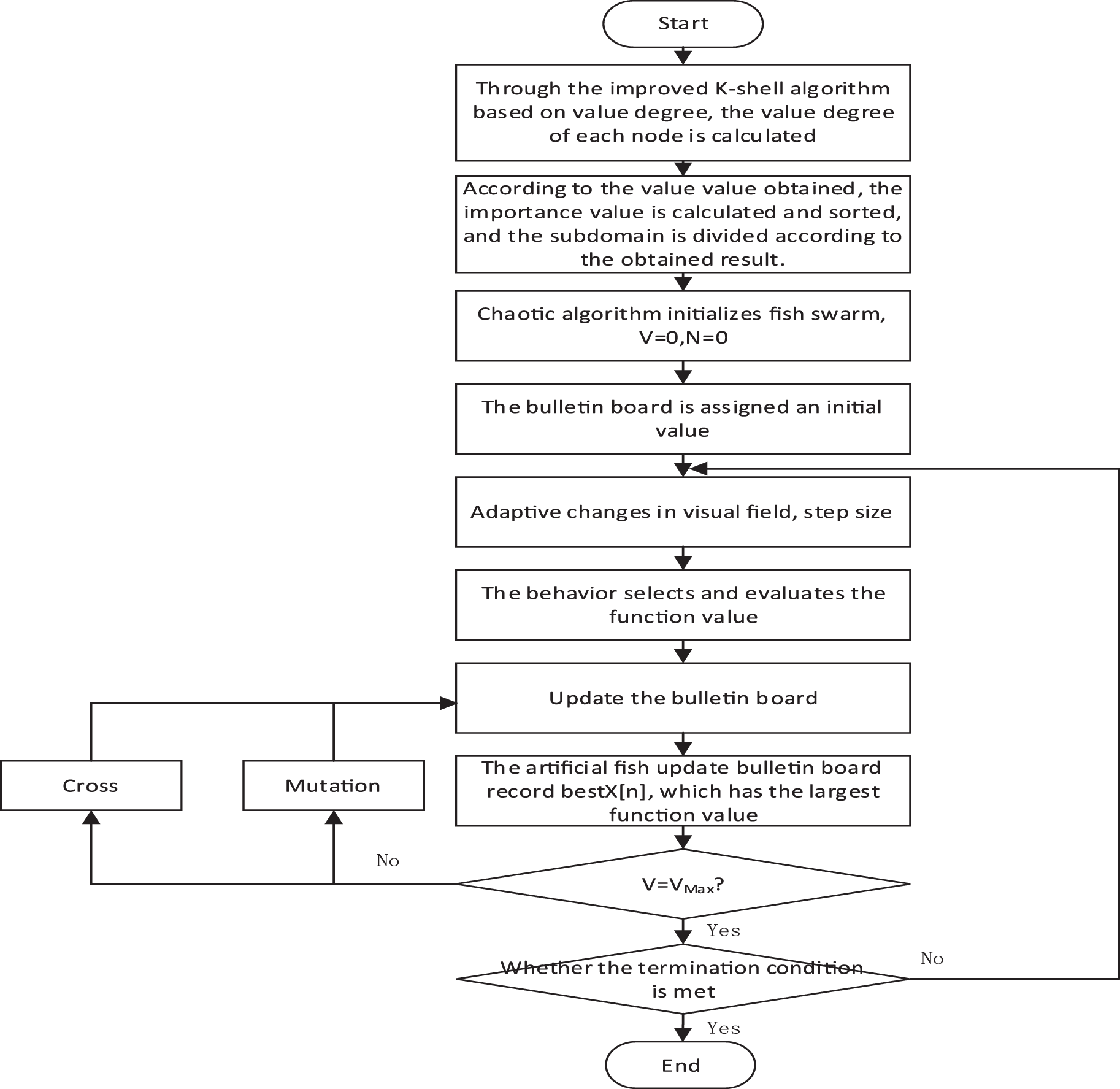
Figure 3: Flowchart of the IAFSA algorithm

The IAFSA commences by instigating an artificial fish swarm within the viable domain of control variables, leveraging a chaotic algorithm. The initial count of iterations, wherein the optimal artificial fish state on the notice board either remains static or undergoes minuscule alterations, is designated as Beststep = 0, while the initial iteration count is denoted as Num = 0 (Line 1). The algorithm then computes the current objective function value Y for each individual within the nascent swarm, recording the maximum value on the notice board. Each artificial fish adaptively modulates its field of view and step size predicated on the iteration cycle, emulating behaviors like trailing and swarming. The behavior engendering a larger objective function value is subsequently implemented (Lines 2–8).

Upon each artificial fish executing an action, its function value is juxtaposed against the one on the notice board. If superior, it supplants the board value, resetting Beststep to zero (Lines 9–15). The algorithm checks if Beststep has attained the maximum threshold value Beststepmax for minuscule or zero alterations. In the event of reaching the threshold, all artificial fish in the swarm (excluding the optimal individual on the notice board) undergo the following operations: Two individuals are selected at random with a crossover probability of C1 to effectuate a crossover operation. After this, the objective function values of the two novel individuals are calculated, and if larger than the optimum value on the notice board, it will be replaced. With a mutation probability M2, an individual is selected at random and initialized randomly. The algorithm then calculates the objective function value for each individual in the swarm, and if it surpasses the board value, it supplants the optimal value. In the absence of such an occurrence, the algorithm verifies if the termination condition has been met. If so, it exports the optimal solution, else, it advances to the subsequent iteration (Lines 16–34).

4  Experimental Simulation and Analytical Evaluation

4.1 Simulation Environment and Parameter Description

The experimental simulation was conducted on a Personal Computer equipped with a hexa-core processor operating at a clock speed of 2.59 GHz, complemented by a memory of 16 GiB. The platform of choice for the implementation and execution of the proposed algorithm was Matlab.

The principal objective was to illustrate the dynamic orchestration of various aerial combat units within the cluster, as well as the unpredictable alterations in the characteristics of the network topology. To carry out the experiments, we incorporated the following parameter configurations:

Generation of Network Topology: We randomly dispersed multiple nodes within a predefined geographical extent of 800 * 800 km. The generation of nodes within this spatial domain adhered to the specific density requirements outlined in the experimental design.

Calculation of the Shortest Path: We employed the Dijkstra algorithm to compute the shortest path between any two given points. This facilitated the emulation of communication and pathway selection between nodes, thereby ensuring effective relay communication among the combat units.

Definition of Node Communication Radius: The communication radius (R) of the nodes was configured at 120 km. Consequently, only those nodes that resided within this radius could establish a communication connection.

Configuration of Failure Rate: The failure rate associated with an individual node or link was defined by a random number within the range of [0, 0.05]. The generation of a random failure probability for each node and link allowed the simulation of potential malfunctioning of nodes and links under real-world conditions.

By adjusting these parameters, we were able to replicate more accurately the dynamic orchestration of various combat units within the aerial cluster and the unpredictable alterations in network topology. This enhanced level of realism allows the experiment to provide more relevant insights into real-world scenarios, thereby aiding in the research and optimization of communication and organizational mechanisms within aerial clusters.

4.2 NDVR Sub-Domain Partition Algorithm Simulation

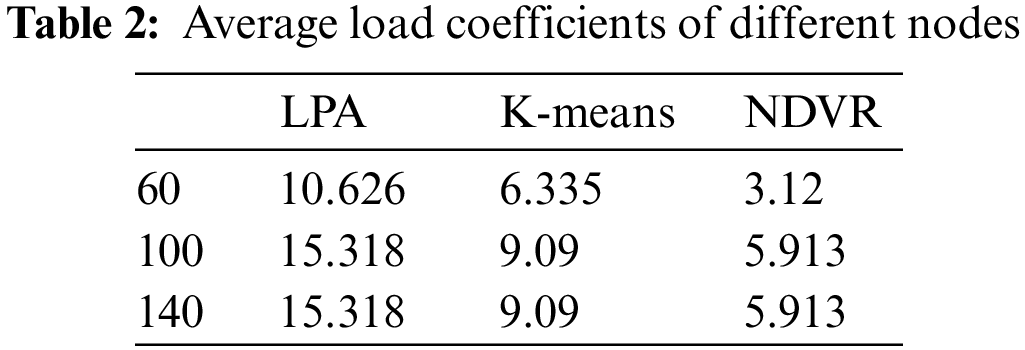
Addressing the issue of network nodes’ sub-domain partitioning, we executed a series of simulation experiments to ascertain the effectiveness of the Node Degree-based Virtual Router (NDVR) algorithm. These empirical explorations were predicated on the network environment inherent to airborne clusters, spanning across varying scales of node quantities (including 60, 100, 140, and 180). In an attempt to evaluate the NDVR algorithm’s performance, we compared load balance indices across different node scales. We implemented an averaging strategy entailing multiple simulations to yield a more accurate performance measure. To extend our understanding of the relationship between the number of controllers and the load balance index across different node scales, we juxtaposed our algorithm with the Partitioning Over Clustering (POCO) algorithm, Label Propagation Algorithm (LPA), and the K-means algorithm via comparative experiments.

The experimental simulation results are shown in Fig. 4 and Table 2. It can be seen from the figure that the load balancing index is used to compare the three algorithms. As the number of nodes increases, the load index also increases, basically meeting the expectation. Comparing the load index of the three algorithms under different nodes, the NDVR algorithm decreases by 66.8% and 45.36% on average compared with the LPA and K-means algorithms, respectively. In this paper, the three subdomain partitioning algorithms do not consider the limitation of controller capacity. After comparison, it is found that the LPA and K-means algorithms use the node random network to propagate to convergence and partition according to the minimum delay, resulting in poor algorithm effect. NDVR algorithm uses node importance information to divide network nodes into subdomains, which can effectively divide molecular domains according to node information, effectively reduce the load index, and improve the load balance of the controller. However, with the continuous increase of the partition area, the load balance index of the LPA and K-means algorithm fluctuates greatly and is significantly higher than that of the NDVR algorithm. Compared with LPA, K-means, and NDVR algorithm, the standard variance results are as follows: 1.671, 1.903, 0.411. The comparison shows that the average load index of NDVR is not only lower than the other two algorithms but also more balanced, which can provide reliable network service quality for the whole cluster.

Figure 4: Diagram of the relationship between load balance index and number of subdomains under different network scales

4.3 Performance Analysis of the IAFSA Algorithm

To rigorously assess the efficacy of the IAFSA algorithm in terms of performance optimization, we meticulously established a variety of scenarios and configured the algorithm parameters accordingly, as delineated in the accompanying Table 3. We employed a sub-domain division strategy, wherein the aggregate outcome of the average propagation delay and the average fault rate, duly weighted, serve as the objective function value. This value then guided the optimization of the LC deployment. Our experimental framework harnessed the potential of both the IAFSA and AFSA algorithms to tackle the problem at hand.

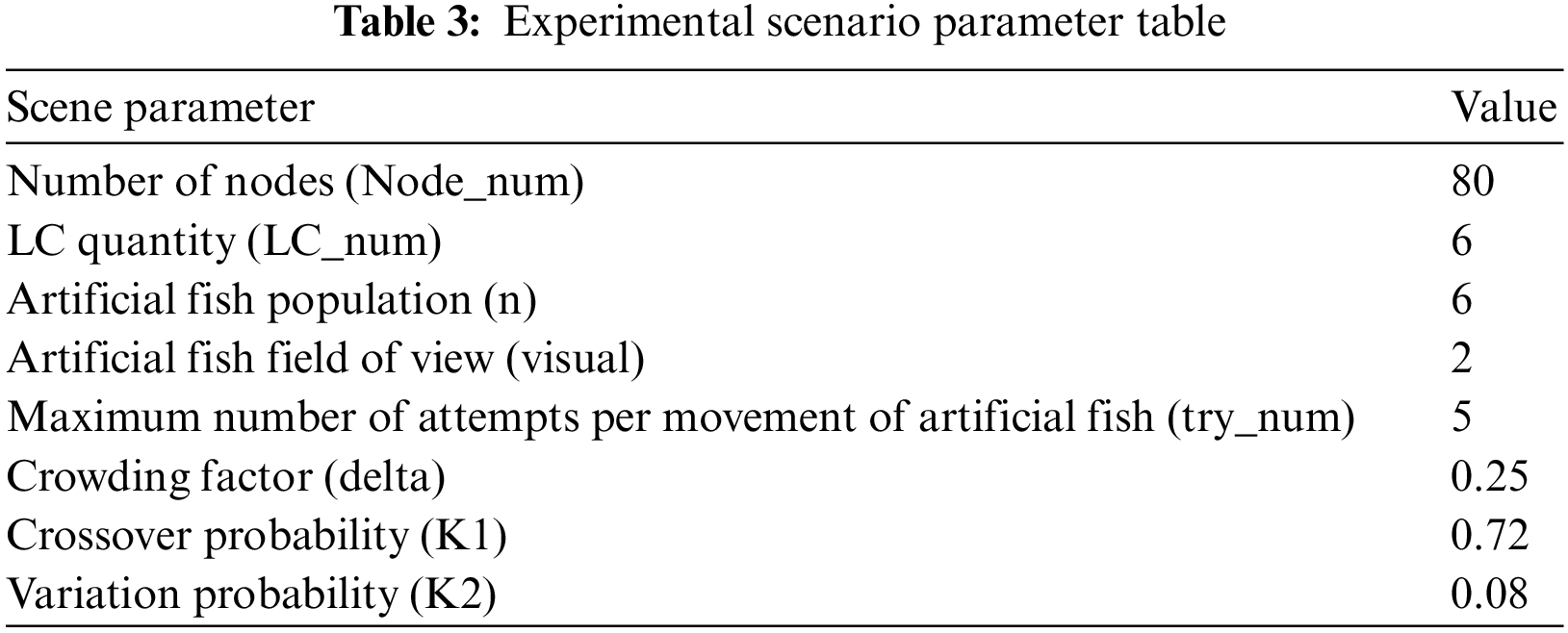
As illustrated in the Fig. 5 and Table 4, we subjected the IAFSA algorithm to a comprehensive reliability analysis, running a series of 100 experiments and diligently recording the corresponding values obtained for the optimized objective function W. The empirical data decisively underscored the superiority of the IAFSA algorithm over its AFSA counterpart, with the former consistently yielding superior outcomes. On the whole, we observed an average enhancement of 41.3% in the optimization value of the objective function W, thereby signifying a substantial optimization of the network performance objective.

Figure 5: Fluctuation schematic of the IAFSA algorithm experimental results over 100 trials

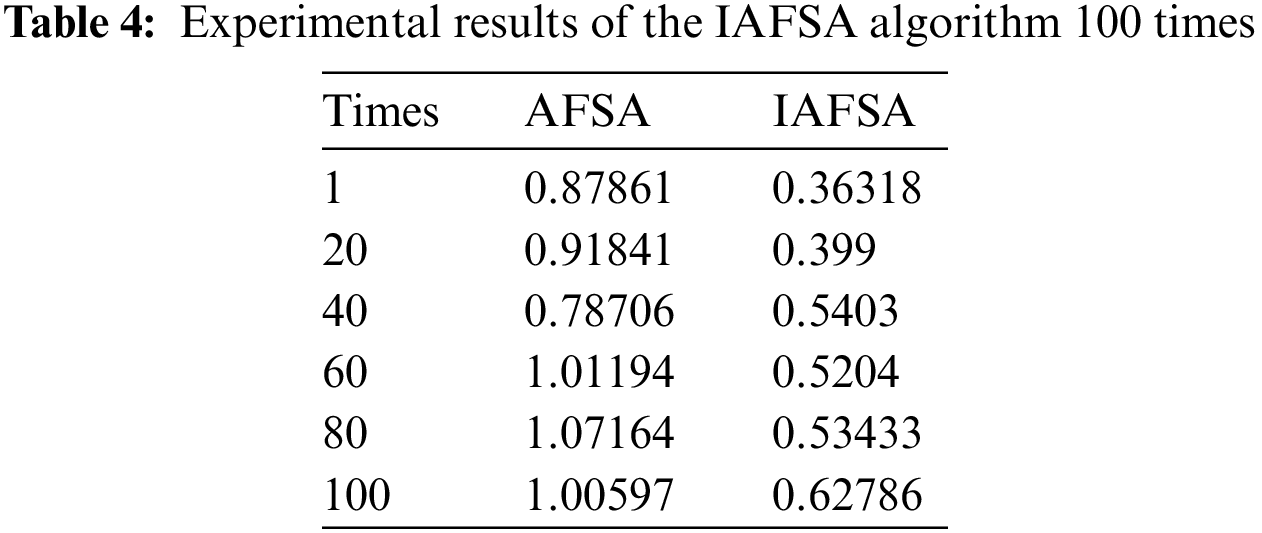
4.4 Performance Simulation of the NDVR-IAFSA Algorithm

This section presents an empirical validation of controller deployment optimization performance, employing algorithms such as LPA [42], K-means [43], POCO [44], and NDVR-IAFSA. Our simulation experiments, conducted on a network consisting of 100 airborne nodes, facilitate a comprehensive evaluation of the average propagation delay Tavg and average disconnection rate σavg under varying controller numbers. Figs. 6, 7 and Tables 5, 6 depict the average results derived from multiple computational iterations for each algorithm.

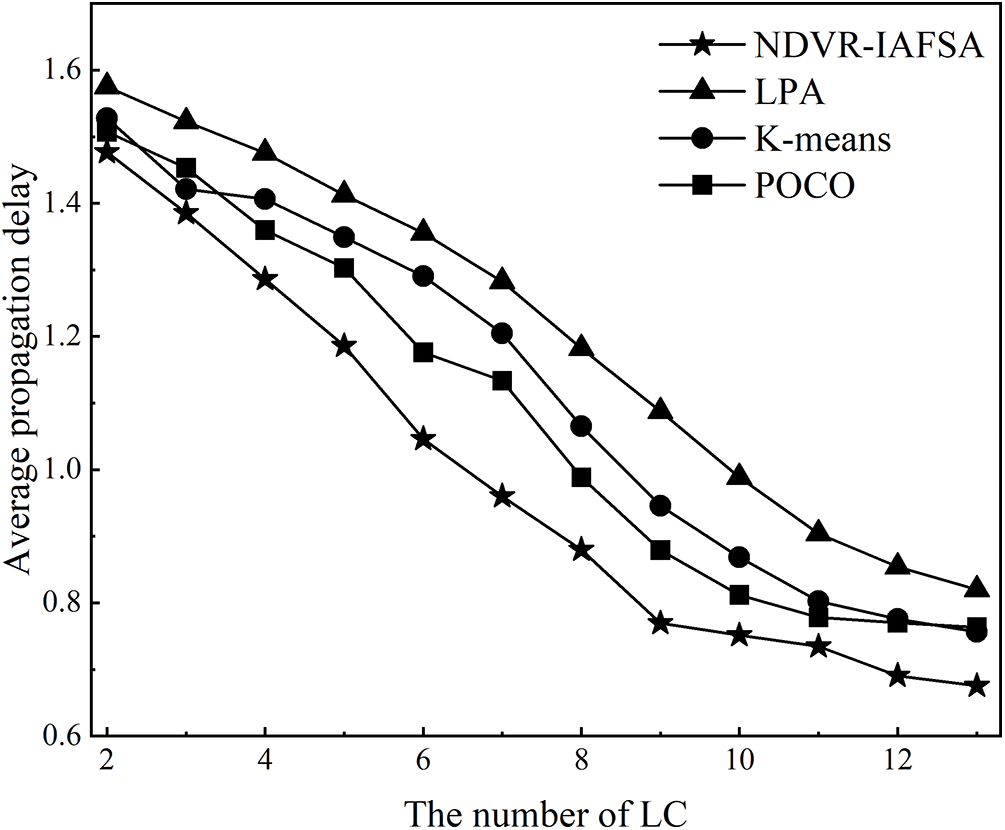
Figure 6: Diagram of the relationship between average propagation delay and LC number

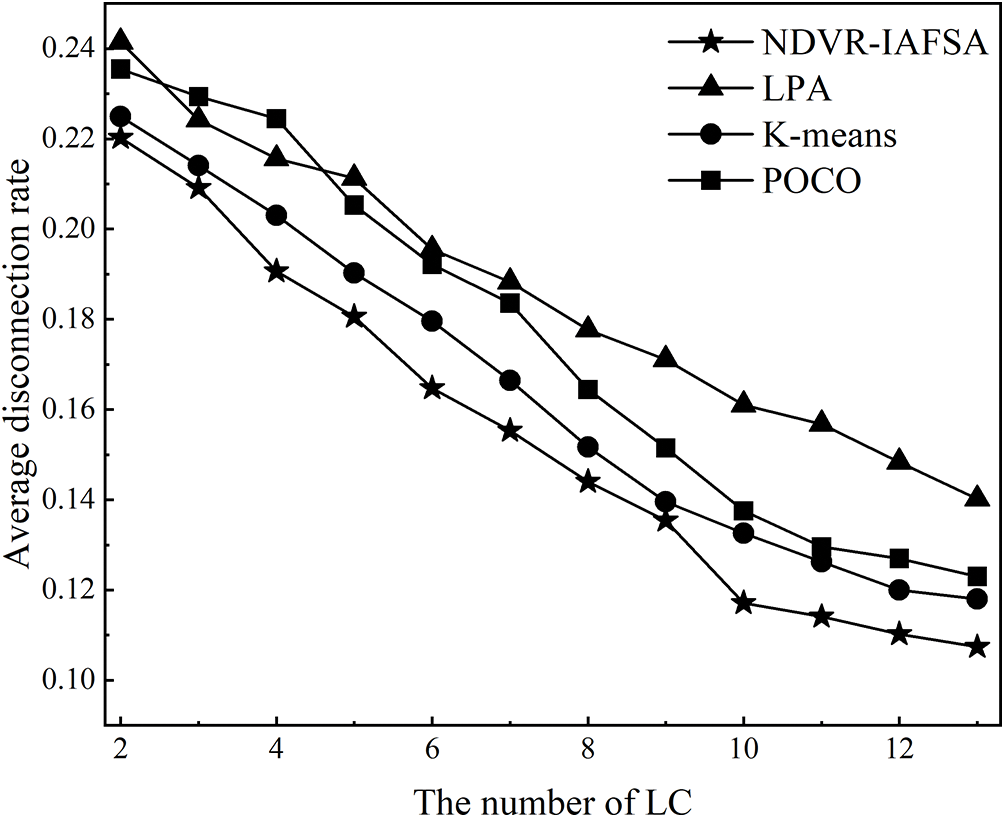
Figure 7: Diagram of the relationship between average disconnection rate and LC number

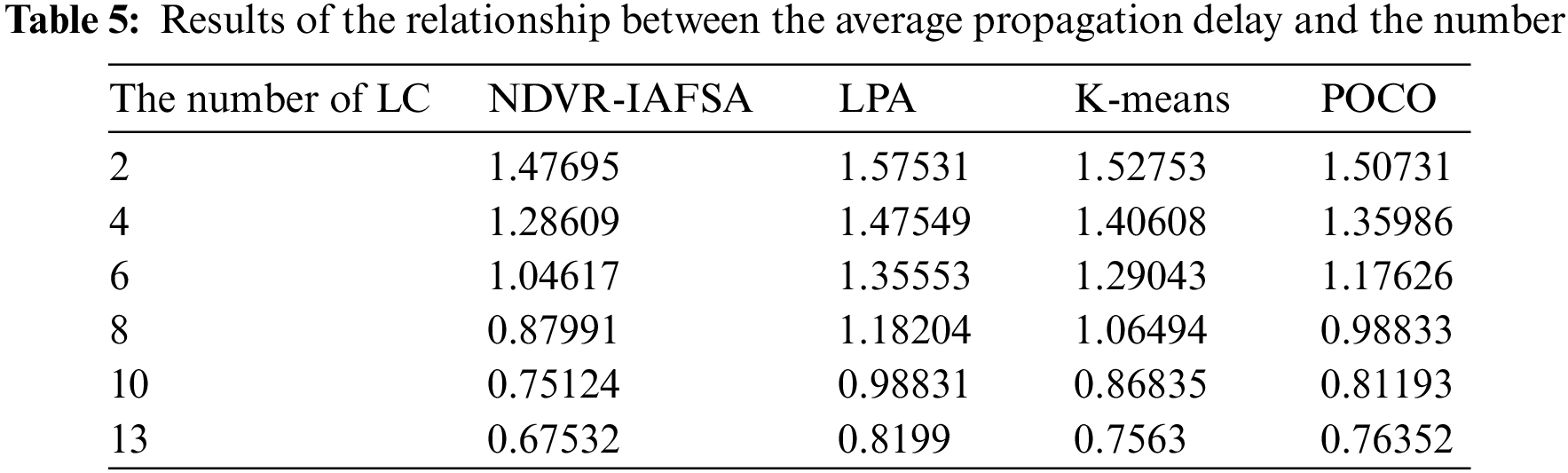
As revealed in Figs. 6 and 7, an increase in the number of LC nodes within the network area generally incurs an inversely proportional effect on the average propagation delay Tavg and average disconnection rate σang. It is thus inferred that the aviation data link network control link’s parameters Tavg and σang can be effectively diminished by augmenting the LC nodes. Comparatively, the NDVR-IAFSA optimization performance supersedes the three other algorithms, resulting in reductions of 18%, 11.8%, 8.7%, and 17.2\% , 6\% ,12\% , respectively. This superior performance can be attributed to our proposed algorithm, which judiciously incorporates sub-domain division based on node significance and leverages the IAFSA algorithm to select more suitable interaction center nodes. This approach imbues the algorithm with greater flexibility and improved effectiveness, particularly under circumstances with a high count of LC nodes.

To assess the efficiency of the NDVR-IAFSA algorithm, we devised an airborne cluster environment with varying LC and network nodes. We explored the correlation between distinct algorithms and time consumption, as demonstrated in the appended figure.

As depicted in Fig. 8 and Table 7, there exists a direct proportional relationship between the computation time of the four assessed algorithms and the escalating number of LCs. In particular, the POCO algorithm manifests a greater rate of change, whereas the remaining three algorithms generally exhibit steady growth with a more gradual increase rate. Of paramount importance is the fact that the algorithm proposed in this paper holds the shortest computation time. This favorable outcome is attributable to the efficient performance of the data chain network node deployment planning as the number of LCs rises when our proposed algorithm is applied. Fig. 9 and Table 8 elucidate that while maintaining a constant number of LCs and contrasting the algorithm’s efficiency under various node quantities, a direct proportional association between the number of nodes and the computation time is discernable across all four algorithms. Remarkably, the computational time of the POCO algorithm is, on average, approximately quadruple that of the NDVR-IAFSA algorithm. This deviation stems from the method of subdividing sub-domains for controller deployment within the domain, which, in comparison to the heuristic POCO algorithm, substantially mitigates the time complexity of extensive SDN controller deployment.

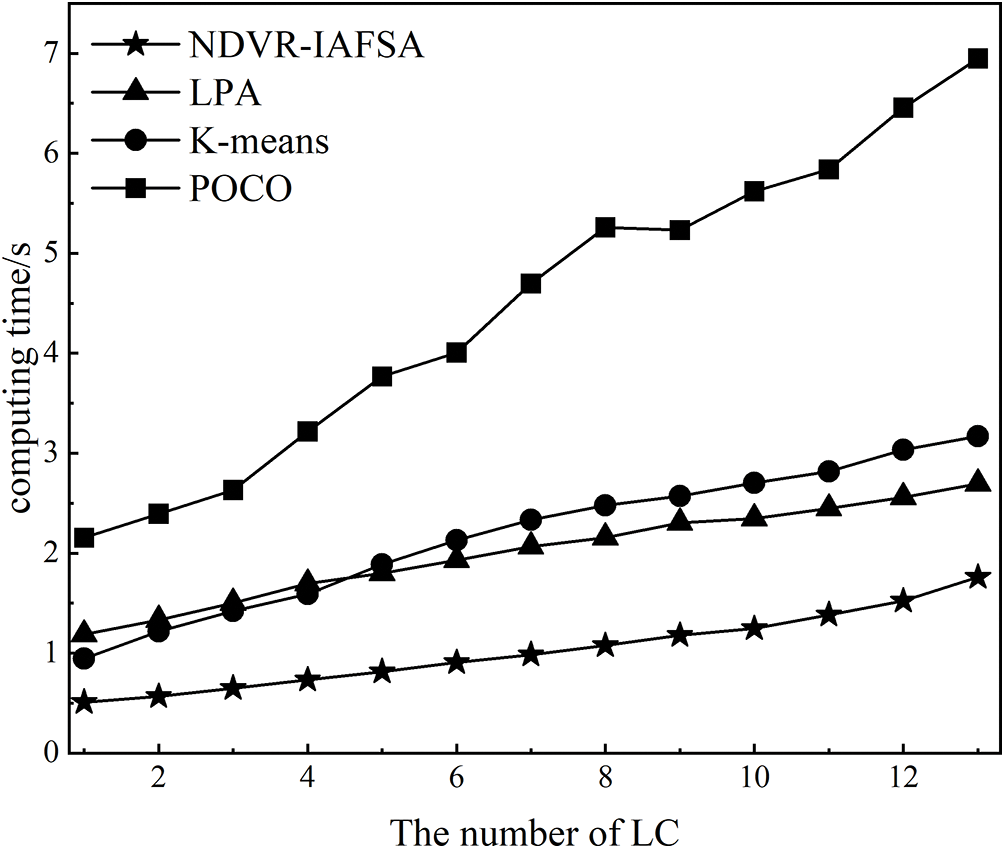
Figure 8: Diagram of the relationship between calculation time and LC number

Figure 9: Diagram of the relationship between calculation time and number of nodes

5  Structure Conclusions

In this paper, we introduce a pioneering resolution for the Airborne Data Link Cluster (ADLC) controller deployment issue (ADLC-Cpp) in the multi-controller setting of Software-Defined Networking (SDN). This innovative combination of the airborne data link cluster network and SDN technology involves a multi-controller collaborative architecture founded on the airborne data link cluster, converting the ADLC-Cpp into a sub-domain partitioning challenge and a central interaction node selection conundrum. Within this schema, we advance a sub-domain partitioning strategy built on node importance ranking and a central interaction node selection strategy premised on an augmented Artificial Fish Swarm Algorithm (AFSA). This enhanced stratagem assists in circumventing individual aggregation at local optima, consequently magnifying global search capabilities. The effectiveness and feasibility of the proposed enhancement strategy were assessed by juxtaposing it with other algorithms. Experimental evidence validated the successful amalgamation of the airborne data link cluster network scenario and SDN technology. Through the application of the proposed multi-controller collaborative deployment scheme, alongside the sub-domain partitioning strategy built on node importance ranking and the central interaction node selection strategy premised on the refined AFSA, the dependability, and availability of the airborne data link cluster network are amplified. This advancement furnishes technical support for bolstering the defensive capacity of the airborne data link cluster network platform. Existing research primarily concentrates on circumstances where resources are abundant for the SDN controller cluster, neglecting the fault analysis and resource deficiency necessary to meet cluster requirements. Therefore, future inquiries will be directed towards situation awareness and security assessment technologies within the airborne data link cluster networks’ context. This endeavor will facilitate a comprehensive understanding of network fault analysis and security risks and enhance the self-healing capability and safety of the airborne data link cluster network. This section is not mandatory but can be added to the manuscript if the discussion is unusually long or complex.

Acknowledgement: We would like to thank Professor Fu Yanfang and all the members involved in the collaborative project for their valuable advice and continued support. The author is very grateful to the reviewers for their valuable comments, which improved the presentation of the paper.

Funding Statement: This article was supported by the following funds: Defense Industrial Technology Development Program Grant: G20210513; Shaanxi Provincal Department of Science and Technology Grant: 2021KW-07; Shaanxi Provincal Department of Science and Technology Grant: 2022QFY01-14.

Author Contributions: Conceptualization, Y.Z. and Y.F.; project administration, Y.Z., C.Y. and Y.F.; investigation, Y.Z. and Y.F.; methodology, Y.Z.; resources, Y.F., C.Y. and D.P; software, Y.Z.; validation, Y.Z., H.S. and Y.F.; writing—original draft, Y.Z., J.Z.; writing—review and editing, D.P., Y.F. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: No applicable.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. H. Hantouti, N. Benamar, M. Bagaa and T. Taleb, “Symmetry-aware SFC framework for 5G networks,” IEEE Network, vol. 35, no. 5, pp. 234–241, 2021. [Google Scholar]

2. D. Kreutz, F. M. V. Ramos, P. E. Veríssimo, C. E. Rothenberg, S. Azodolmolky et al., “Software-defined networking: A comprehensive survey,” Proceedings of the IEEE, vol. 103, no. 1, pp. 14–76, 2015. [Google Scholar]

3. C. K. Zhang, Y. Cui, H. Y. Tang and J. P. Wu, “State-of-the-art survey on software-defined networking (SDN),” Journal of Software, vol. 26, no. 1, pp. 62–81, 2015. [Google Scholar]

4. J. Patil, S. Tokekar, A. Rajan and A. Rawat, “Port scanning based model to detect Malicious TCP traffic and mitigate its impact in SDN,” in Proc. of the 2nd Int. Conf. on Secure Cyber Computing and Communications, Jalandhar, India, pp. 365–370, 2021. [Google Scholar]

5. M. Sadiq, S. Ahmad, M. Tariq and A. Anpalagan, “Advances in software-defined networking: A survey,” Computer Networks, vol. 97, pp. 18312, 2022. [Google Scholar]

6. N. T. Nguyen, M. T. Diem and A. V. Tran, “Network slicing in software-defined networking: A comprehensive survey,” IEEE Communications Surveys & Tutorials, vol. 23, no. 1, pp. 528–574, 2021. [Google Scholar]

7. M. Casado, M. J. Freedman, J. Pettit, J. Luo, N. McKeown et al., “Ethane: Taking control of the enterprise,” Sigcomm Computer Communication Review, vol. 37, no. 4, pp. 1–12, 2007. [Google Scholar]

8. S. H. Yeganeh and Y. Ganjali, “Kandoo: A framework for efficient and scalable offloading of control applications,” in Proc. of the First Workshop on Hot Topics in Software Defined Networks, Helsinki, Finland, pp. 19–24, 2012. [Google Scholar]

9. J. Zhang and L. Li, “Research on port sharing technology in software-defined network,” Journal of Physics: Conference Series, vol. 783, no. 1, pp. 012147, 2021. [Google Scholar]

10. X. Liu, T. Huang, S. Liu and C. Han, “Design and implementation of an intelligent test system based on SDN port-sharing technology,” Journal of Physics: Conference Series, vol. 1643, no. 1, pp. 012074, 2020. [Google Scholar]

11. A. M. Mahmoud, O. M. Hassan, N. R. Abu-Elnour and A. Almasri, “A port-sharing approach to network function virtualization for Internet of Things,” Future Generation Computer Systems, vol. 92, pp. 218–230, 2019. [Google Scholar]

12. Y. Peng, E. Li, Y. Liu and J. Li, “Dynamic service function chaining with port sharing in SDN,” Journal of Communications, vol. 16, pp. 301–308, 2021. [Google Scholar]

13. H. Yang, H. Zhang, B. Liu and Y. Du, “Partition-based control plane separation scheme in large-scale SDN networks,” Journal of Computer Science and Technology, vol. 36, pp. 211–224, 2021. [Google Scholar]

14. K. Li, J. Qian, M. Chen and B. Li, “Design and implementation of zone-based partitioning technology in SDN,” Journal of Physics: Conference Series, vol. 1794, no. 1, pp. 012068, 2021. [Google Scholar]

15. X. Chen, X. Zhang, W. Huang and X. Gong, “Multi-task routing and resource allocation in partitioned SDN networks,” IEEE Transactions on Network and Service Management, vol. 18, no. 2, pp. 1273–1287, 2021. [Google Scholar]

16. C. Qin, L. Zhang, X. Wang and T. Hong, “Distributed dynamic load balancing in SDN for traffic engineering,” IEEE Transactions on Network and Service Management, vol. 18, no. 1, pp. 403–415, 2021. [Google Scholar]

17. Y. A. M. Saied and A. M. Wahdan, “An enhanced dynamic load balancing algorithm for an SDN network using fuzzy-based decision-making approach,” Journal of Intelligent & Fuzzy Systems, vol. 40, pp. 191–201, 2021. [Google Scholar]

18. Y. F. Fu, Y. T. Zhu, Z. J. Cao, Z. Q. Du, G. C. Yan et al., “Multi-controller load balancing algorithm for test network based on IACO,” Symmetry-Basel, vol. 13, no. 10, pp. 1901, 2021. [Google Scholar]

19. L. Fang, Y. Chen, Y. Wu and M. Wu, “A load balancing strategy based on control plane sharing in SDN controller pool,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, pp. 4681–4692, 2021. [Google Scholar]

20. M. Casoni, C. A. Grazia and M. Klapez, “SDN-based resource pooling to provide transparent multi-path communications,” IEEE Communications Magazine, vol. 55, no. 12, pp. 172–178, 2017. [Google Scholar]

21. Y. Liu, C. Sun, J. Liu and X. Zhang, “A controller synchronization architecture based on controller pool for software-defined networks,” Journal of Parallel and Distributed Computing, vol. 146, pp. 1–10, 2021. [Google Scholar]

22. X. Gao, B. Wang, W. Deng and J. Tao, “A survey of controller placement in SDN networks,” Tong Xin Xue Bao, vol. 38, no. 7, pp. 155–164, 2017 (In Chinese). [Google Scholar]

23. B. Heller, R. Sherwood and N. Mckeown, “The controller placement problem,” ACM SIGCOMM Computer Communication Review, vol. 42, no. 4, pp. 473–478, 2012. [Google Scholar]

24. Y. Zhang, C. Sun, B. Cui and Y. Li, “A dynamic controller partitioning method with minimal control overhead for large-scale SDN networks,” Frontiers of Information Technology & Electronic Engineering, vol. 22, no. 3, pp. 354–366, 2021. [Google Scholar]

25. Y. Li, Y. Li, X. Shi and B. Wang, “Improved cooperative game algorithm for distributed controller coordination in SDN,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, pp. 7379–7391, 2021. [Google Scholar]

26. J. Zhou, B. Li, W. Liu, M. He and Y. Zou, “Learning controller selection for end-to-end routing in software-defined networks,” Computer Networks, vol. 183, pp. 107429, 2020. [Google Scholar]

27. A. Malik, R. de Fréin, M. Al-Zeyadi and J. Andreu-Perez, “Intelligent SDN traffic classification using deep learning: Deep-SDN,” in 2020 2nd Int. Conf. on Computer Communication and the Internet, Nagoya, Japan, pp. 184–189, 2020. [Google Scholar]

28. J. Li, S. Wang, Y. Huang, K. Liao, F. Bi et al., “An adaptive deep Q-learning strategy for routing schemes in SDN-based data centre networks,” in 2022 Int. Symp. on Advances in Informatics, Electronics and Education, Frankfurt, Germany, pp. 178–186, 2022. [Google Scholar]

29. A. A. Z. Ibrahim, F. Hashim, A. Sali, N. K. Noordin and S. M. E. Fadul, “A modified genetic algorithm for controller placement problem in SDN distributed network,” in 2021 26th IEEE Asia-Pacific Conf. on Communications, Kuala Lumpur, Malaysia, pp. 83–88, 2021. [Google Scholar]

30. D. K. Luong, M. Ali, Y. F. Hu, J. P. Li, R. Asif et al., “Simulated annealing-based multilink selection algorithm in SDN-enabled avionic networks,” IEEE Access, vol. 9, pp. 145301–145316, 2021. [Google Scholar]

31. S. Tahmasebi, N. Rasouli, A. H. Kashefi, E. Rezabeyk and H. R. Faragardi, “SYNCOP: An evolutionary multi-objective placement of SDN controllers for optimizing cost and network performance in WSNs,” Computer Networks, vol. 185, pp. 107727, 2021. [Google Scholar]

32. Y. Ma, W. Wang, J. Gu and Q. Liu, “A fuzzy controller placement algorithm for SDN centralized controller clusters,” Journal of Ambient Intelligence and Humanized Computing, vol. 11, pp. 1755–1766, 2020. [Google Scholar]

33. Z. Zhu, Y. Pan, Q. Zhou and C. Lu, “Event-triggered adaptive fuzzy control for stochastic nonlinear systems with unmeasured states and unknown backlash-like hysteresis,” IEEE Transactions on Fuzzy Systems, vol. 29, pp. 1273–1283, 2021. [Google Scholar]

34. J. M. Sanner, M. Ouzzif, Y. Hadjadj-Aoul and J. E. Dartois, “Evolutionary algorithms for optimized SDN controllers & NVFs’ placement in SDN networks,” in SDN Day. Hal-Inria: Paris, France, 2016. [Google Scholar]

35. Y. Lin, H. Gao, R. Liang and C. Liu, “Multiobjective genetic algorithm-based controller placement optimization in software-defined networks,” Journal of Internet Technology, vol. 21, pp. 1891–1900, 2020. [Google Scholar]

36. X. Xie, S. Xu, B. Wang and Y. Peng, “An improved particle swarm optimization algorithm for SDN controller placement,” Journal of Computational Science, vol. 43, pp. 101156, 2020. [Google Scholar]

37. Y. Zhang, Z. Xu and Y. Xiang, “Controller placement for software-defined networking via a parameter-controlled particle swarm optimization,” Wireless Personal Communications, pp. 1–18, 2021. [Google Scholar]

38. A. Sharma, S. Tokekar and S. Varma, “Meta-reinforcement learning based resource management in software defined networks using bayesian network,” Management for Societal Impact Using Marketing, Entrepreneurship and Talent, pp. 1–6, 2023. [Google Scholar]

39. H. Zheng, J. Guo, Q. Zhou, Y. Peng and Y. Chen, “Application of improved ant colony algorithm in load balancing of software-defined networks,” The Journal of Supercomputing, vol. 79, no. 7, pp. 7438–7460, 2023. [Google Scholar]

40. F. Sun, M. Fan, B. Cao, B. Ye and L. Liu, “The terahertz image enhancement model based on adaptive teaching-learning based optimization algorithm with chaotic mapping and differential evolution,” Chinese Journal of Scientific Instrument, vol. 42, no. 4, pp. 92–101, 2021. [Google Scholar]

41. X. Li, “A new intelligent optimization method-artificial fish swarm algorithm,” Ph.D. dissertation, Zhejiang University, China, 2003. [Google Scholar]

42. B. Liu, B. Wang and X. Xi, “Heuristics for SDN controller deployment using community detection algorithm,” in 2016 7th IEEE Int. Conf. on Software Engineering and Service Science, Beijing, China, pp. 253–258, 2016. [Google Scholar]

43. G. Wang, Y. Zhao, J. Huang, Q. Duan and J. Li, “A K-means-based network partition algorithm for controller placement in software defined network,” in IEEE Int. Conf. on Communications, Kuala Lumpur, Malaysia, pp. 1–6, 2016. [Google Scholar]

44. S. Lange, S. Gebert, T. Zinner, P. Tran-Gia, D. Hock et al., “Heuristic approaches to the controller placement problem in large scale SDN networks,” IEEE Transactions on Network and Service Management, vol. 12, no. 1, pp. 4–17, 2015. [Google Scholar]