CFSA-Net: Efficient Large-Scale Point Cloud Semantic Segmentation Based on Cross-Fusion Self-Attention

1  Introduction

Large-scale semantic segmentation of point clouds holds significant practical applications in real-time intelligent systems, such as autonomous driving and remote sensing. However, due to the voluminous nature of large-scale point cloud datasets, often exceeding millions of points, efficiently conducting semantic segmentation on such a scale poses a formidable challenge. Furthermore, compared to two-dimensional image data, three-dimensional point cloud data exhibits characteristics of disorder and unstructured. Leveraging the underlying data structure of point clouds, designing a deep neural network tailored for the semantic segmentation of three-dimensional point clouds becomes an arduous and demanding research endeavor.

In addressing the challenges of point cloud semantic segmentation, researchers have devoted substantial efforts to exploring deep learning-based approaches for 3D point cloud semantic segmentation. Over the past years, a growing number of deep learning frameworks have been proposed to tackle this task. Notably, Qi et al. introduced the groundbreaking PointNet [1] network, which was the first model capable of directly processing point cloud data using neural networks without additional operations. However, the PointNet network did not account for local feature extraction, prompting subsequent studies to propose various methods to address this limitation. These methods [2–4] not only rely on individual points for feature extraction but also incorporate the aggregation of local geometric information to capture the point cloud's structural features. Additionally, graph-based [5–7] and kernel-based [8–10] convolution techniques, which have demonstrated significant advancements in the field of image processing, have been introduced to capture relationships between different local structural features through convolutional neural networks. While these algorithms have achieved noteworthy results in point cloud processing, they often partition the point cloud into small, independent blocks, such as 1 × 1 × 1-meter blocks, each containing 1024 points, for efficiency purposes. However, this partitioning approach proves impractical for large-scale point clouds as it disrupts the inherent three-dimensional object structure and incurs high computational costs. There are two primary reasons for the low efficiency of semantic segmentation in large-scale point clouds. 1) These methods often employ complex point sampling strategies to ensure the uniform distribution of points. However, these strategies are either computationally intensive or have low memory efficiency. 2) Previous research has typically treated feature information and coordinate information separately during the process of local feature aggregation. They simply concatenate the three-dimensional raw coordinates with the feature information, overlooking the comprehensive modeling of geometric information.

Currently, there are also existing approaches that can directly handle tasks involving large-scale point clouds. For instance, SPG [11] preprocesses point cloud data into superpoint graphs and then employs neural networks for semantic segmentation. RangeNet++ [12] and PCT [13] utilize projection-based and voxel-based methods to handle large-scale point clouds. However, these methods either entail computationally intensive and time-consuming preprocessing steps or require the partitioning of point clouds into smaller blocks for learning, resulting in suboptimal overall performance.

To tackle the aforementioned issues, this paper designs a new large-scale point cloud semantic segmentation framework. The framework uses a random reduced sampling strategy to process large amounts of point cloud data with fewer computing resources. Furthermore, this paper introduces a robust module for extracting local features, enhancing the network’s capacity to describe fine-grained features at a local level and model geometric information in a more comprehensive manner. To this end, this paper first establishes the efficacy of random sampling and subsequently emphasizes the necessity of designing a feature extraction module to comprehensively capture geometric information.

The downsampling of point clouds is a vital component in point cloud semantic segmentation networks. This step involves the selection of representative subset points from the point clouds, for which Farthest Point Sampling (FPS) [2] and Inverse Density Importance Sub-Sampling (IDIS) [14] are commonly used methods. The computational complexity of farthest point sampling is O(N), where N denotes the number of points in the point cloud. Inverse density sampling, on the other hand, exhibits a computational complexity of O(N2), assuming N points in the point cloud. It is worth noting that there exist other learning-based sampling methods [15–18], although they are not specifically mentioned in the paper. In contrast, Random Sampling (RS) exhibits a computational complexity of only O(1), making it an efficient option to consider when dealing with large-scale point clouds. However, while random sampling offers efficiency advantages, it comes with associated costs. This sampling method may result in a lack of representativeness within the sampled point set and the loss of crucial structural information within the point cloud, as depicted in Fig. 1. To overcome the potential drawbacks of random sampling, this paper proposes a local feature extraction module based on Cross-Fusion Self-Attention (CFSA), which effectively captures intricate local structures.

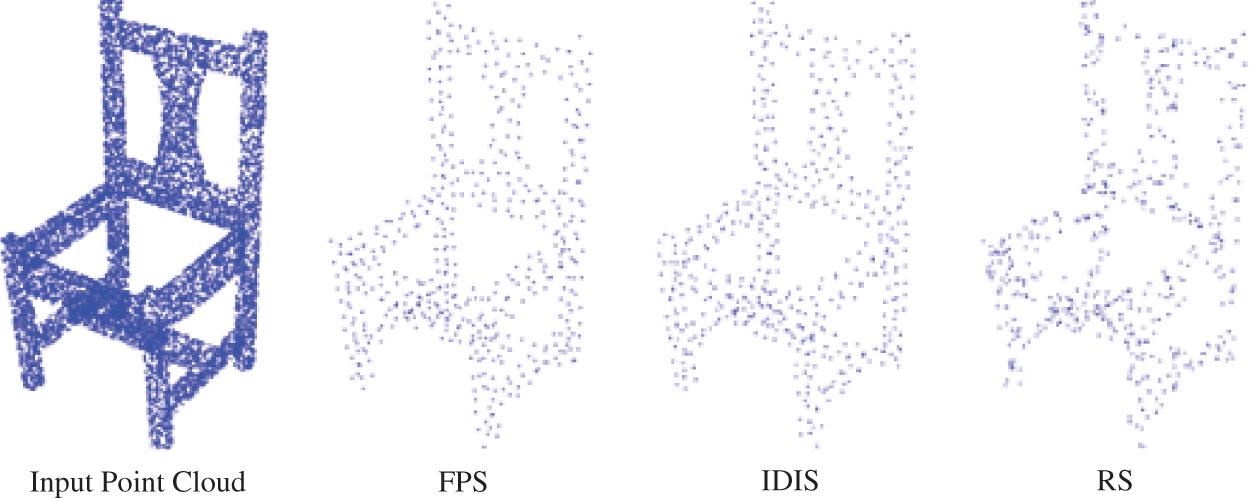
Figure 1: Sampling effect of different sampling methods under the same sampling ratio

The local feature extraction module, based on cross-fusion self-attention, consists of three pivotal components. Firstly, this paper proposes a hierarchical location coding module that conducts hierarchical sampling and relative location coding for each query point. This module effectively addresses the long-distance dependencies between points. Secondly, this study presents a cross-fusion self-attention pooling module, which facilitates the interactive fusion of features and coordinates information within the point clouds. The CFSA pooling module dynamically enhances the expressive capacity between features and coordinates, thereby preserving intricate local geometric structure information. Lastly, this paper introduces a residual optimization module, which enhances the performance of feature extraction by stacking the hierarchical position coding module and the cross-fusion self-attention pooling module. This integration increases the depth of the network and expands the receptive field of each point, thereby further improving the efficacy of feature extraction.

This paper makes significant contributions in the following aspects:

1. This paper, through meticulous analysis and comparison of existing sampling methods, has chosen random sampling as the down-sampling strategy in this paper to efficiently process large-scale point cloud data.

2. This paper proposes a local feature extraction module based on cross-fusion self-attention, which can better integrate the remote context dependence of the points, interactively enhance the coordinates and feature information of the points, and expand the receptive field of each point to model more complete geometric information.

3. Building upon the aforementioned contributions, this paper proposes CFSA-Net, a powerful network designed to effectively tackle the segmentation task of large-scale point clouds. Notably, CFSA-Net achieves competitive results on three mainstream datasets: S3DIS [19], Semantic3D [20], and SemanticKITTI [21].

The subsequent organization of this paper is outlined as follows: Section 2 provides a detailed overview of the classical approaches utilized in point cloud semantic segmentation tasks. In Section 3, we present an elaborate description of our proposed methodology. Comprehensive performance evaluations of the proposed method are conducted in Section 4 through comparative experiments and ablation studies. Finally, an objective summary is presented in Section 5 to conclude this paper.

2  Related Work

Projection-based and voxel-based methods: The methodologies based on projection and voxelization entail specific preprocessing steps for the raw point cloud. The projection-based [22–25] approach involves projecting the 3D point cloud onto a 2D plane, enabling the direct application of conventional 2D Convolutional Neural Networks (CNN). By leveraging the powerful capabilities of 2D CNN [26], semantic segmentation can be performed using the projected image information. On the other hand, the voxel-based [27–29] approach transforms the 3D point cloud into a regular 3D grid or voxel representation, facilitating processing through 3D CNN. This allows for capturing the spatial relationships between the voxels through 3D convolutions. However, the projection-based methods may suffer from information loss during the projection process and may encounter limitations in capturing fine-grained geometric details. On the other hand, voxel-based methods often face challenges in handling high-resolution data due to memory constraints and exhibit inefficiency when representing sparse point clouds. They also exhibit significant drawbacks when dealing with large-scale point clouds.

Point-based methods: The point-based methodologies involve direct manipulation of point cloud data to implement algorithms for semantic segmentation by assigning each point in the point cloud to its corresponding semantic class. Drawing inspiration from the groundbreaking work of PointNet [1], researchers have proposed a series of neural network models to directly process raw point cloud data. For instance, Qi et al. introduced the PointNet++ [2] network, which integrates a sophisticated multi-level local feature aggregation module, thereby facilitating enhanced aggregation of local features. Thomas et al. proposed KPConv [30], which introduces the novel concept of kernel points and adaptively selects certain points in the point cloud as templates for convolutional kernels. Li et al. introduced the PSNet [31] network, which provides a rapid data structuring approach for simultaneous point sampling and grouping. Ibrahim et al. proposed SAT3D [32], which introduces the first-ever technique based on the Slot Attention Transformer to effectively model object-centric features in point cloud data. Point-based methods exhibit remarkable performance in handling irregular and sparse point clouds as they directly capture the local geometric attributes of each point. These networks demonstrate promising results on small-scale point clouds. However, due to their high computational and memory costs, most networks face limitations in direct scalability to larger scenes, thus hindering their modeling capabilities for large-scale point clouds.

Large-scale point cloud semantic segmentation: Recently, various models have been introduced in academia to address the challenge of large-scale point cloud semantic segmentation. Among them, Landrieu et al. introduced SPG [11], which leverages the concept of a superpoint graph to transform point cloud data into a graph structure and utilizes graph neural networks for semantic segmentation. Additionally, to improve computational efficiency, some models convert 3D point clouds into 2D representations, enabling the utilization of efficient 2D convolutions for semantic segmentation. For example, Tatarchenko et al. [33] projected the local surface geometry of the point cloud onto the tangent plane of each point and process it using 2D convolutions. Wu et al. [24] employed point cloud spherical projection methods to transform point cloud data into a data format compatible with various mature 2D image processing techniques. Moreover, some methods directly operate on points to handle large-scale point clouds. Zhang et al. proposed PointCCR [34], which enhances efficiency through random sampling while leveraging the local structure of the point cloud and expanding the receptive field of individual points. Although the aforementioned methods have achieved significant results, the preprocessing steps involve substantial computational complexity, and the projections disrupt the 3D geometric structure of the point cloud. Motivated by these approaches, to balance efficiency and preserve the original 3D geometric relationships, we propose CFSA-Net, an end-to-end efficient network specifically designed for large-scale point cloud semantic segmentation.

Self-attention mechanism: The self-attention mechanism was initially introduced in the fields of natural language processing and 2D image processing [35], and it has garnered considerable attention in current research due to its remarkable ability to model contextual information. In recent years, researchers have focused on applying this mechanism to point cloud processing tasks to further enhance the processing capabilities of point cloud data. Several self-attention-based point cloud processing methods have been proposed. For instance, Fu et al. introduced FFANet [36], which effectively captures the contextual information of each point using the self-attention mechanism. Chen et al. introduced GAPNet [37], which integrates graph attention mechanisms into a series of stacked Multi-Layer Perceptron (MLP) layers to effectively learn the local features of input point clouds. Guo et al. proposed PCT [13], which adopts the self-attention mechanism from Transformers to effectively capture the relationships between points in point cloud data, enabling better capturing of fine-grained details. Ren et al. proposed PA-Net [38], which designs two parallel self-attention mechanisms that simultaneously focus on coordinate and feature information. Previous works have primarily handled coordinate and feature information separately. In contrast, our network employs a cross-fusion self-attention mechanism, which interactively captures and integrates coordinate and feature information, considering the relative positional relations of the point cloud, thereby modeling more comprehensive geometric information.

3  Methodology

3.1 Overview

The model, as illustrated in Fig. 2, utilizes an encoder-decoder architecture with skip connections to process a point cloud collection comprising N points. Each point encompasses xyz coordinate position information and feature attributes (e.g., color, normal vectors) as inputs. To capture the intricate characteristics of each point, the input point cloud undergoes a series of five encoding and decoding layers. During the encoding phase, the point cloud scale is reduced through the application of random sampling. By incorporating the Local Feature Extraction (LFE) module, the model enriches the coordinate information, enhances the interaction between coordinate and feature attributes, and expands the receptive field of each point. In the decoding phase, each point employs the K-Nearest Neighbor (KNN) approach to identify its nearest neighboring point. Subsequently, Up-Sampling (US) is performed using linear interpolation to restore the point cloud to its original scale. The features from the encoding phase and the skip connections are combined through summation and then input into a shared Multi-Layer Perceptron (MLP) to reduce the dimensionality of the features. Finally, the entire process is iteratively repeated to obtain the final segmentation result.

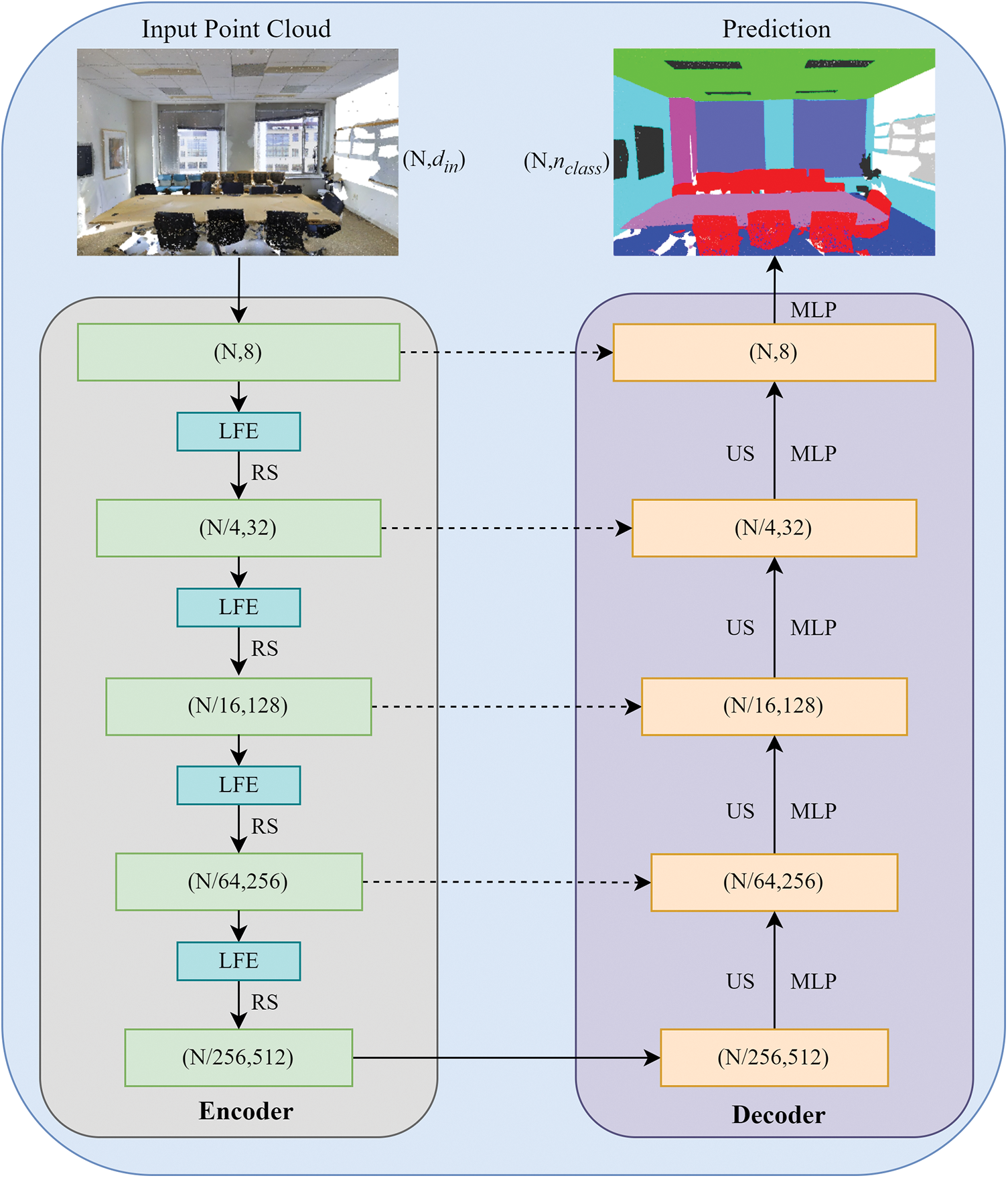
Figure 2: Network structural diagram

3.2 Local Feature Extraction Based on Cross-Fusion Self-Attention Mechanism

Local Feature Extraction (LFE) constitutes the core of the encoding layer and is composed of three primary components: Hierarchical Position Coding (HPC), Cross-Fusion Self-Attention (CFSA) pooling module, and Residual Optimization (RO) structure.

3.2.1 Hierarchical Position Coding (HPC)

The module encompasses hierarchical sampling and relative position encoding. The first is sampling. Common sampling methods usually only perform KNN-based sampling on neighboring points. However, this approach limits the receptive field of each query point, hindering the establishment of long-range contextual dependencies. To address this issue, a straightforward solution is to increase the sampling radius, but this results in increased computational memory requirements. To effectively aggregate distant contextual dependencies with lower memory costs, a hierarchical sampling strategy is introduced, as illustrated in Fig. 3. The specific strategy is defined as follows:

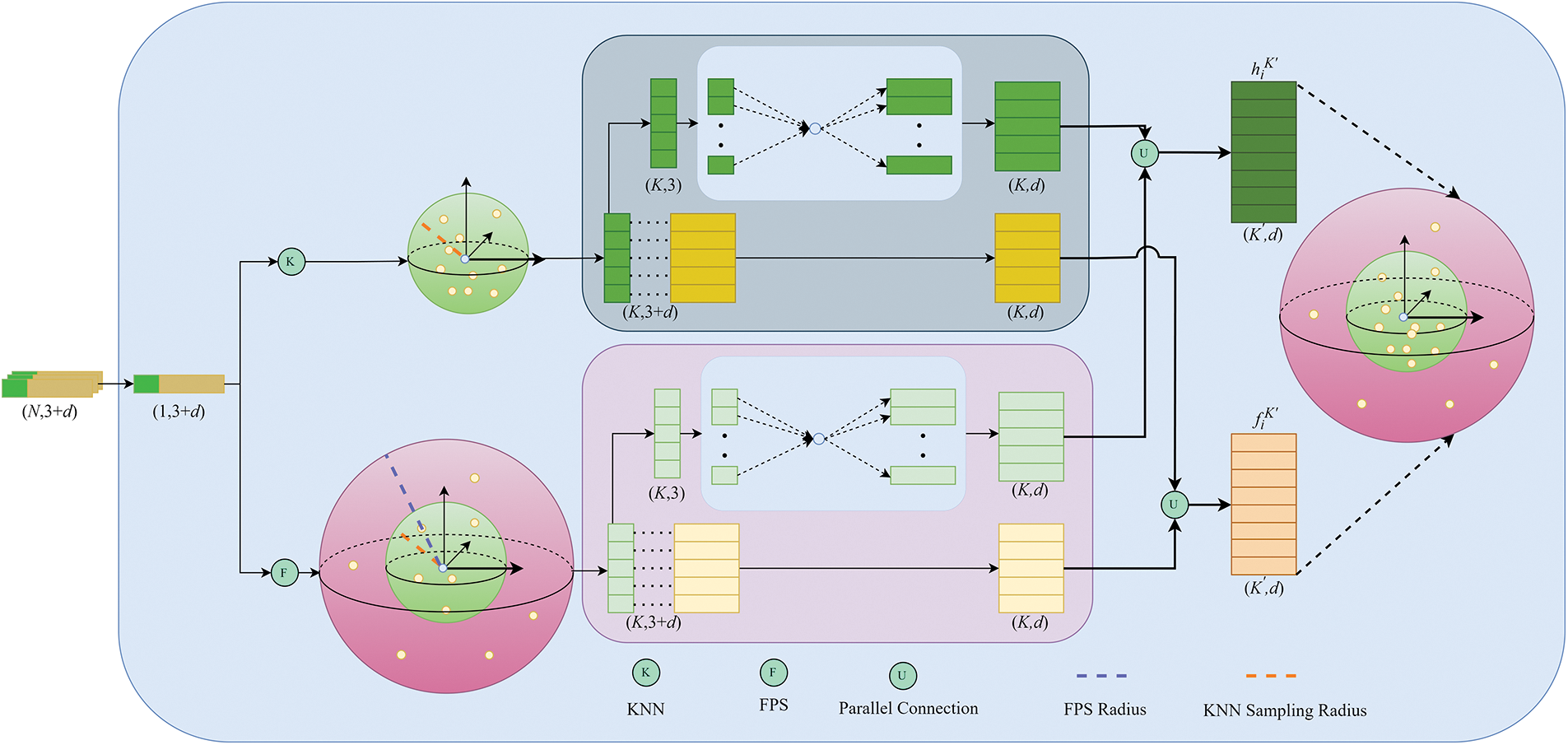
Figure 3: Hierarchical positional coding module

{K1=KNN(pi,fi)K2=FPS(pi,fi)K3=K1∪K2(1)

Given an input point set, denoted as P={pi,fi|i=1,2,3,…,n}, where n signifies the total number of points within the point cloud, pi represents the positional information (x, y, z), and fi represents the feature information (e.g., color, normal vectors, etc.), the following approach is employed for each query point: Initially, a dense selection of K neighboring points is performed using the KNN method, resulting in the set K1. Subsequently, a sparser selection of K neighboring points is achieved by employing the FPS method within a larger radius, forming the set K2. Finally, the two sets, K1 and K2, are merged and duplicate points are removed, resulting in the final set of neighboring points, denoted as K3.

Then the relative position coding is performed, and the neighbor point set K3 is encoded. The coding process is defined as follows:

hiK′=MLP(g(pi,piK′,pi−piK′,‖pi−piK′‖))(2)

where K′ is the number of points of the set K3; hiK′ is the result of spatial position encoding of points; pi is the coordinates of the query point; piK′ is the coordinates of K′ adjacent points; pi−piK′ is the relative coordinate between the query point and the adjacent point.; ‖pi−piK′‖ is the Euclidean distance between the query point and the adjacent points; g represents the connection operation, which connects the above relative position information; MLP extends the relative position information of the connection to the same dimension as fi.

As depicted in Fig. 3, the variable fiK′ denotes a feature information matrix of dimensions (K′×d). This matrix is derived from a set K3 comprising K′ neighboring points. It is worth noting that the matrix does not include coordinate information.

Ultimately, the HPC module produces the original feature information of K′ nearest neighbor points along with corresponding relative spatial positional information, which has the same dimension as the original features. Compared to conventional sampling methods, this approach involves additional computations for sparse neighboring points and effectively addresses long-range dependency issues. However, due to the sparsity of distant neighbor points, it does not excessively consume computational memory resources.

3.2.2 Cross-Fusion Self-Attention (CFSA) Pooling

The CFSA pooling module uses a powerful self-attention mechanism to interactively enhance local coordinate and feature information. It takes as input the output of the HPC module, which consists of the coordinates and feature information after being processed by HPC. The specific structure of this module is illustrated in Fig. 4.

Figure 4: Cross-fusing self-attention pooling module

The input of the upper part is hiK′, and after the linear transformation of hiK′, the three feature descriptions of hq,hk,hv are obtained. Similarly, fq,fk,fv are obtained after the linear transformation of the input fiK′ in the lower half. The process of linear transformation can be described as follows:

{hq,hk,hv=L(hiK′)fq,fk,fv=L(fiK′)(3)

where hiK′, fiK′ represent the input, L represents the function of a linear transformation, the q, k, and v correspond to the query, key, and value, respectively.

Some of the above elements are cross-fused to obtain the output ho and fo after self-attention calculation. The specific process is defined as follows:

{ho=hv⊗fa+hiK′fo=fv⊗ha+fiK′(4)

where ⊗ represents matrix multiplication, it can be seen from Eq. (4) that coordinates and feature information are effectively enhanced. ha and fa in the above equation are obtained by query and key weighting. The specific process is defined as follows:

{ha=softmax(sum(hqT⊗hk))fa=softmax(sum(fqT⊗fk))(5)

where ⊗ also represents matrix multiplication, the sum represents adding the first row of the result of ⊗ to each subsequent row, and finally assigning weights through softmax.

Compared with some traditional self-attention mechanisms, the cross-fusion self-attention mechanism enables the coordinates and feature information after HPC to be mutually enhanced. Finally, the new feature description Fout of the query point is obtained after sum pooling and MLP. The specific definition process is as follows:

Fout=MLP(∑K=1K′g(ho,fo))(6)

3.2.3 Residual Optimization (RO)

In this study, the residual optimization module is used to stack the HPC module and the CFSA pooling module to enhance the receptive field of individual points and mitigate the potential loss of key point information resulting from random sampling. According to the aforementioned theory, a higher number of stacked HPC modules and CFSA pooling modules leads to a more effective extension of the receptive field. However, computational efficiency and module transferability are taken into consideration. The residual optimization structure in this paper consists of two stacked HPC modules and CFSA pooling modules, complemented by residual connections. Additionally, a multilayer perceptron is incorporated before the input and after the output to achieve the necessary feature dimensions. Finally, the output features after stacking are added to the features of the input point cloud after shared MLP processing to obtain the final aggregation features. The specific structure is illustrated in Fig. 5.

Figure 5: Residual optimization module

After the first stacking operation, the receptive field of the query point is K′ points. After the second stacking operation, the receptive field will be raised to K′2 points. The receptive field expansion diagram is shown in Fig. 6.

Figure 6: Receptive field expansion diagram

4  Performance Analysis

In this section, the proposed network is evaluated on three mainstream semantic segmentation datasets (S3DIS, Semantic3D, SemanticKITTI). In addition, some related ablation experiments, including network structure analysis and self-attention mechanism selection, have been carried out to verify the proposed modules.

4.1 Data Set Introduction

This study primarily conducts evaluations on three datasets, namely S3DIS, Semantic3D, and SemantiKITTI. S3DIS represents a dataset of indoor scenes, Semantic3D represents a dataset of outdoor scenes, and SemantiKITTI represents a dataset of autonomous driving scenarios. Each dataset has distinct point counts and features. A detailed introduction to each dataset is provided below.

S3DIS represents a comprehensive dataset of indoor scenes, comprising six educational and office regions with a total of 271 rooms. This dataset encompasses 13 distinct categories. Each point cloud data within S3DIS is defined by nine features, encompassing coordinate information and color information, along with three corresponding normal vectors.

The Semantic3D dataset provides a vast collection of natural scene point clouds, exceeding a total of 4 billion points. It encompasses a diverse range of urban scenes, including churches, streets, railways, squares, villages, football fields, and castles. Each point cloud data is characterized by seven features, encompassing coordinate information (x, y, z), reflectance intensity, as well as color information (R, G, B).

SemanticKITTI stands as an authoritative dataset in the field of autonomous driving. This dataset incorporates various categories such as pedestrians, vehicles, and other traffic participants, along with ground facilities like parking lots and sidewalks. Each point cloud data within the SemanticKITTI dataset consists of four features, namely coordinate information (x, y, z), and reflectance intensity.

4.2 Experimental Environment

The experimental parameters are set as follows: The computations are performed on the Ubuntu 20.04 system utilizing the TensorFlow 2.6.0 framework, with acceleration provided by the NVIDIA Quadro P6000 GPU. The Adam optimizer is employed, and the batch sizes for the three datasets are respectively set to 6, 3, and 3. The initial learning rates are uniformly set to 0.01, and the maximum number of iterations for all datasets is established as 100.

4.3 Comparative Experiments and Results Analysis

4.3.1 Experimental Results Evaluation of S3DIS Dataset

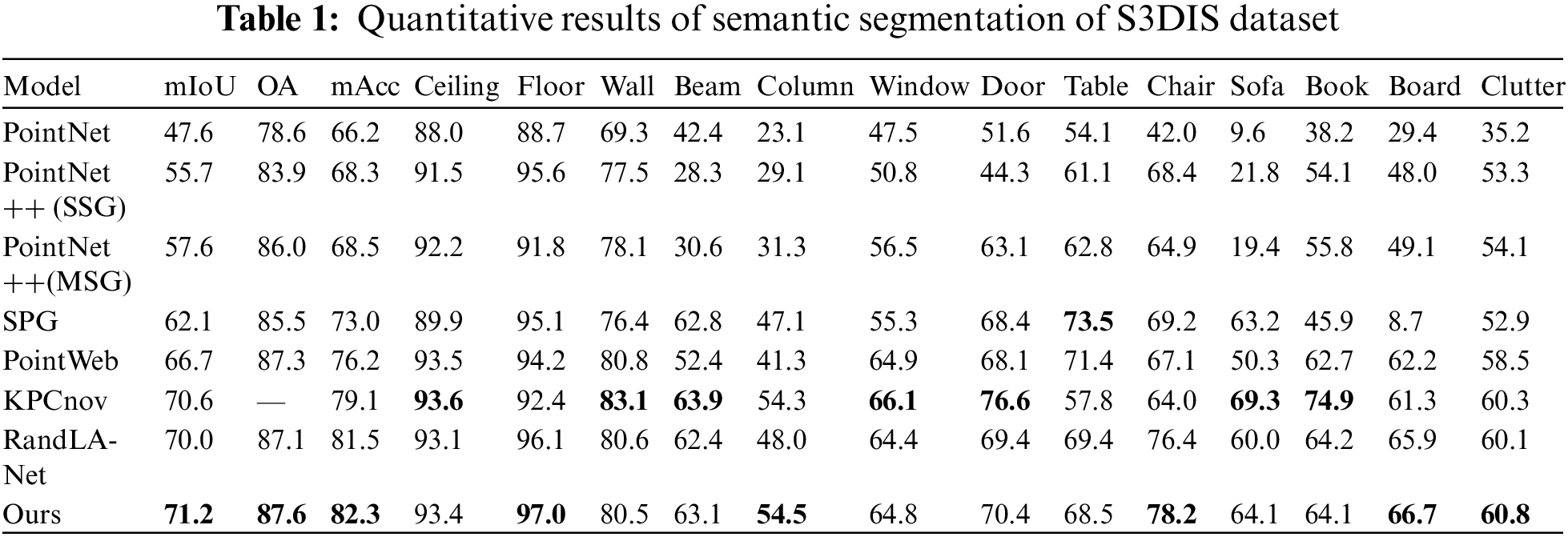
This study utilizes the S3DIS dataset, which partitions 271 rooms into 6 regions, to evaluate the performance of the proposed algorithm through 6-fold cross-validation on these regions. The quantitative results of comparing the proposed algorithm with other algorithms across the 6 regions are presented in Table 1, with the best results highlighted in bold. Our algorithm outperforms others in terms of three metrics: Overall Accuracy (OA), Mean Accuracy (mAcc), and Mean Intersection over Union (mIoU), achieving values of 87.6%, 82.3%, and 71.2%, respectively. The categories of floor, pillar, chair, whiteboard, and clutter exhibit the best performance in mIoU, with improvements of 0.9%, 0.7%, 1.8%, 0.8%, and 0.5%, respectively, compared to the best results of other algorithms in the table. Additionally, the segmentation accuracy is equally impressive for categories such as windows and doors.

Next, we compare the proposed algorithm with PointNet++ and RandLA-Net, and provide visual comparisons to demonstrate the advantages of our algorithm. As shown in Fig. 7, the first column represents a hallway scene, the second column depicts a conference room scene, and the third column illustrates an office scene. Each scene includes the ground truth labels, predictions from PointNet++, predictions from RandLA-Net, and predictions from our algorithm. The algorithm presented in this study demonstrates the capability to accurately predict the contours of visually similar objects, the edges of small-scale objects, and the contours of embedded objects. For instance, it effectively captures the intricate geometric shapes of objects such as pillars, beams, and corners of walls, which share similarities in their geometry. Moreover, it successfully identifies the boundaries of small objects like bookshelves housing books and miscellaneous items, as well as accurately outlines embedded objects like blackboards on walls. This is attributed to the local coordinate encoding module and the cross-attention interaction module. The local coordinate encoding module preserves rich local geometric information, while the cross-attention interaction module enhances the learning capability of coordinate and feature interactions.

Figure 7: S3DIS dataset semantic segmentation visualization

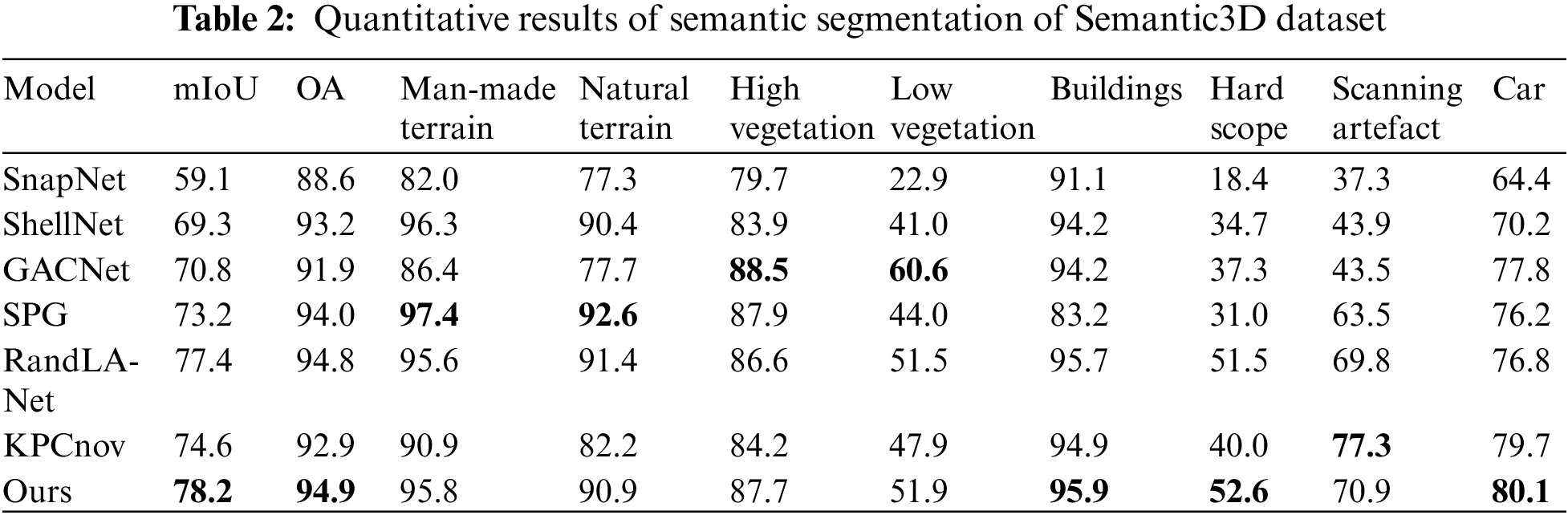
4.3.2 Experimental Results Evaluation of Semantic3D Dataset

The experimental evaluation was performed using the reduce-8 subset of the Semantic3D dataset, which comprises training point cloud data from 15 distinct regions and testing point cloud data from 4 regions. The quantitative results of the experiments are presented in Table 2. Our proposed algorithm surpasses the comparative algorithms in terms of both the mIoU and the OA on the Semantic3D dataset, achieving a mIoU of 78.2% and an OA of 94.9%. Particularly noteworthy is its outstanding performance in the domains of architecture (including structures such as churches, town halls, and stations), hard landscapes (a diverse category encompassing elements like garden walls, fountains, and banks), and automobiles. In comparison to the best results obtained by the comparative algorithms in this paper, our algorithm demonstrates improvements of 0.2%, 1.1%, and 0.4% in these respective categories. Furthermore, it achieves commendable results in classes such as artificial terrain and natural terrain.

The visualized test results are depicted in Fig. 8. Due to the unavailability of the ground truth labels for the test set of this dataset, the images from left to right represent the input point cloud data and the predicted labels, respectively. On the whole, our proposed algorithm exhibits remarkable segmentation performance, effectively discerning the boundaries of buildings, roads, and other target objects. It is worth noting that the distribution of the hard landscape category is uneven, and characterized by substantial variations in shape and structure. The internal geometric shapes, colors, and texture features also change with different environmental contexts. Nonetheless, our proposed algorithm achieves optimal segmentation performance even in such complex scenarios. Through data analysis and result visualization, it becomes evident that the algorithm can identify intricate details and complex components within the point cloud structure, accurately distinguishing features and nuances associated with different targets. These findings validate the network’s exceptional capabilities in feature extraction, spatial information aggregation, and precise segmentation, thereby providing comprehensive verification of the effectiveness of the feature extraction module.

Figure 8: Visualization results of semantic segmentation of Semantic3D dataset

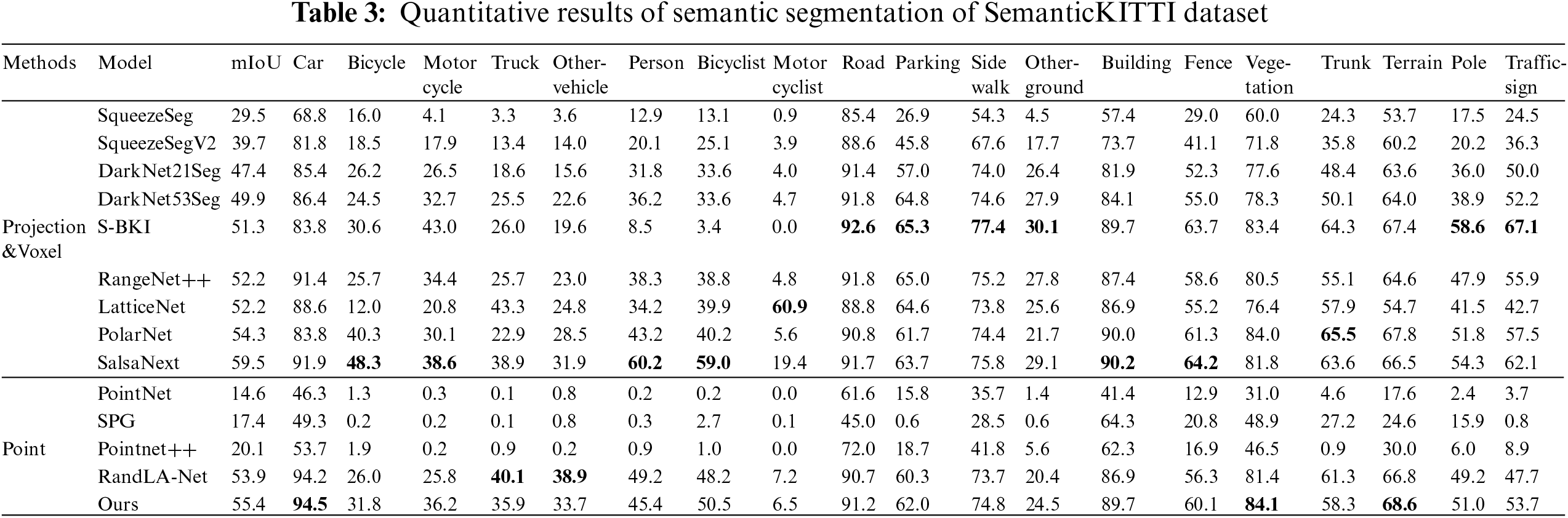
4.3.3 Experimental Results Evaluation of SemanticKITTI Dataset

The SemanticKITTI dataset serves as an extension of the KITTI dataset, and Table 3 provides a quantitative comparison of our algorithm with several classical algorithms on the SemanticKITTI dataset. The results from the table indicate the superiority of our algorithm over the majority of existing approaches, achieving a mIoU of 55.4%. Notably, our algorithm demonstrates outstanding segmentation performance in the categories of vehicles, vegetation, and terrain, surpassing other methods. Our algorithm exhibits remarkable advantages in point-based approaches and also demonstrates certain strengths in projection-based and voxel-based methods, ranking second only to the SalsaNext algorithm.

The segmentation results of our algorithm on the SemanticKITTI dataset are visually depicted in Fig. 9. From left to right, the images correspond to the ground truth labels, predictions from SqueezeSegV2, predictions from RandLA-Net, and predictions from our algorithm. It is evident from the figure that our algorithm achieves the closest approximation to the ground truth labels in vehicle predictions, while also demonstrating excellent segmentation performance in vegetation areas and along terrain edges. The visual analysis reveals that even on large-scale outdoor scene datasets characterized by sparse point cloud densities, our algorithm consistently achieves favorable segmentation results, effectively showcasing the efficacy of our network's feature extraction capabilities.

Figure 9: Visualization results of semantic segmentation of SemanticKITTI dataset

4.3.4 Discuss

S3DIS, Semantic3D, and SemantiKITTI are all point cloud datasets collected from the real world. S3DIS focuses on indoor scenes, Semantic3D covers large-scale outdoor scenes in various settings such as urban, rural, and natural environments, while SemantiKITTI specifically focuses on autonomous driving scenarios. These three datasets differ significantly in terms of scale and scenes. However, the proposed model in this paper has achieved competitive results on all three datasets, demonstrating its strong generalization ability. In future work, we plan to enhance the model's robustness to input data by introducing data augmentation techniques such as rotation, translation, and others during the training process.

4.4 Ablation Experiments

4.4.1 Efficiency Analysis of Sampling Method

This study aims to address the challenge of semantic segmentation in large-scale point clouds. We analyze existing semantic segmentation network models under the conditions of large-scale point clouds. Our findings reveal that the choice of sampling method significantly impacts both training time and memory consumption, thereby necessitating the establishment of an effective downsampling strategy. Such a strategy should enable the rational processing of large-scale point clouds and enhance the overall efficiency of the network. In this regard, we analyze five distinct sampling methods, namely Random Sampling (RS), Farthest Point Sampling (FPS), Generator-Based Sampling (GS), Policy Gradient-Based Sampling (PGS), and Inverse Density Importance Sampling (IDIS).

Fig. 10 presents the experimental comparison of sampling methods in terms of efficiency when dealing with point clouds of different scales. The number of point cloud data is plotted on the x-axis, while memory consumption and processing time are represented on the y-axis. The experimental results for the time and memory consumption of each sampling method are illustrated in Fig. 10. For smaller-scale point cloud quantities, all the aforementioned sampling methods exhibit similar time and memory consumption, suggesting minimal computational burden. However, as the number of point clouds gradually increases, FPS, GS, PGS, and IDIS either become highly time-consuming or significantly consume memory. In contrast, random sampling demonstrates relatively favorable performance in terms of time and memory consumption. This outcome indicates that most existing semantic segmentation network models perform well only when handling small-scale point clouds, primarily due to the limitations imposed by the employed sampling methods. In summary, considering the analysis of the six sampling methods discussed above, random sampling exhibits distinct advantages in terms of time and memory consumption. Consequently, this study opts to employ the random sampling algorithm for processing large-scale point cloud data.

Figure 10: Comparison of sampling effect

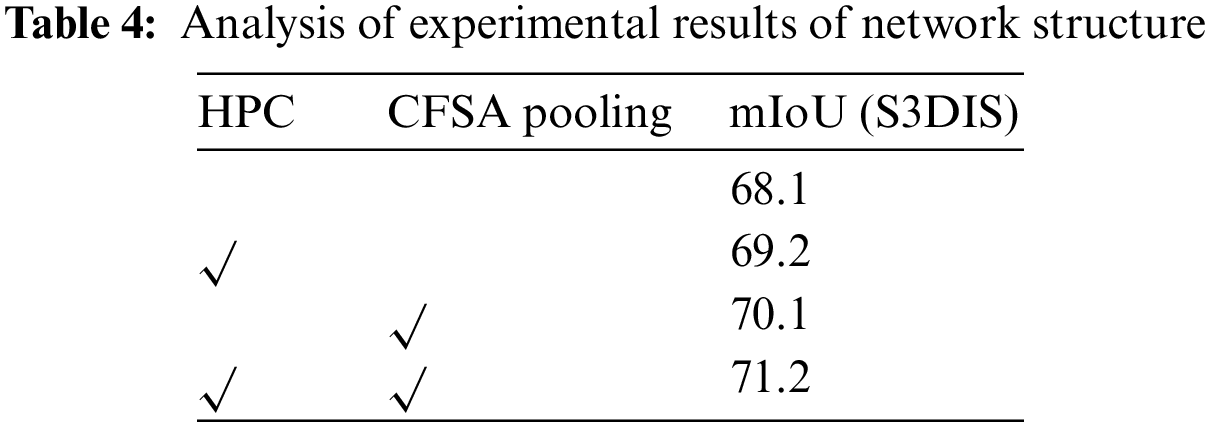
4.4.2 Network Structure Analysis

To validate the effectiveness of the proposed HPC and CFSA pooling modules, as shown in Table 4, we conducted meticulous tests by systematically adjusting each module within the same network architecture and evaluated their performance on the S3DIS dataset. In the absence of any added modules, the mIoU was merely 68.1%. When employing the HPC and CFSA pooling modules individually, the mIoU improved by 1.1% and 2.1%, respectively, resulting in values of 70.1% and 69.2%. Furthermore, when both modules were introduced and jointly utilized, the mIoU experienced a significant boost of 3.1%, reaching an impressive 71.2%. These results from the conducted ablation experiments unequivocally demonstrate the pivotal role of the proposed modules in feature extraction.

4.4.3 Selection of Self-Attention Mechanism

Table 5 presents the results of ablation experiments on the S3DIS dataset, examining the impact of different self-attention mechanisms within the constructed local feature extraction module. The evaluated mechanisms include channel self-attention (CSA), spatial self-attention (SSA), dual-channel self-attention (DCSA) with parallel spatial and channel interactions, and our proposed CFSA mechanism. These experiments aim to assess the influence of these various self-attention mechanisms on the performance of point cloud semantic segmentation. The results in the table demonstrate that the CFSA mechanism achieves the most favorable outcomes, thus substantiating the effectiveness of this approach.

5  Conclusions

This paper presents a novel CFSA-Net designed for large-scale semantic segmentation of point clouds. This paper's framework adopts a memory-efficient and computationally economical random sampling strategy. Furthermore, to mitigate the potential drawbacks associated with random sampling, this paper introduces a local feature extraction module based on cross-fusion self-attention, enabling a more comprehensive modeling of geometric information. This paper's network has exhibited exceptional performance in large-scale point cloud semantic segmentation tasks, as evidenced by comprehensive experiments conducted on public datasets, namely S3DIS, Semantic3D, and SemanticKITTI. The visualized results of our predictions clearly illustrate the network's ability to effectively adapt to variations in the shape, structure, and appearance of the target, thereby demonstrating its robust adaptability and generalization capabilities.

The primary limitation of this study emanates from the imperative of point-wise class annotations within the framework of the fully supervised learning paradigm, which presents a highly challenging task when dealing with large-scale point clouds. In future research, our research will be concentrated on exploring weakly/semi-supervised segmentation methods specifically tailored for large-scale point clouds, to alleviate the burden of manual annotation and reduce associated costs. The algorithm proposed in this paper can combine the multi-innovation theory and hierarchical identification principle [39–42] to enhance computational efficiency and accuracy.

Acknowledgement: The authors would like to express their gratitude for the valuable feedback and suggestions provided by all the anonymous reviewers and the editorial team.

Funding Statement: This study was funded by the National Natural Science Foundation of China Youth Project (61603127).

Author Contributions: Conceptualization, Jun Shu and Jie Zhang; Data curation, Jie Zhang; Formal analysis, Shiqi Yu and Jie Zhang; Investigation, Shiqi Yu; Methodology, Jun Shu, Shuai Wang and Jie Zhang; Software, Jun Shu and Shiqi Yu; Validation, Jun Shu and Shuai Wang; Visualization, Shuai Wang; Writing–original draft, Shuai Wang and Jie Zhang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The training data used in this paper were obtained from S3DIS, Semantic3D and SemantiKITTI, respectively. Available online via the following link: http://buildingparser.stanford.edu/dataset.html, http://semantic3d.net/, and http://semantic-kitti.org/.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. R. Qi, H. Su, K. Mo and L. J. Guibas, “PointNet: Deep learning on point sets for 3D classification and segmentation,” in 30th IEEE Conf. on Computer Vision and Pattern Recognition, Honolulu, HI, USA, pp. 77–85, 2017. [Google Scholar]

2. C. R. Qi, L. Yi, H. Su and L. J. Guibas, “PointNet++: Deep hierarchical feature learning on point sets in a metric space,” in 31st Annu. Conf. on Neural Information Processing Systems, Long Beach, CA, USA, pp. 5100–5109, 2017. [Google Scholar]

3. M. Jiang, Y. Wu, T. Zhao, Z. Zhao and C. Lu, “PointSIFT: A SIFT-like network module for 3D point cloud semantic segmentation,” 2018. https://doi.org/10.48550/arXiv.1807.00652 [Google Scholar] [CrossRef]

4. H. Zhao, L. Jiang, C. W. Fu and J. Jia, “Pointweb: Enhancing local neighborhood features for point cloud processing,” in 32nd IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 5560–5568, 2019. [Google Scholar]

5. H. Lei, N. Akhtar and A. Mian, “Spherical convolutional neural network for 3D point clouds,” 2018. https://doi.org/10.48550/arXiv.1805.07872 [Google Scholar] [CrossRef]

6. L. Wang, Y. Huang, Y. Hou, S. Zhang and J. Shan, “Graph attention convolution for point cloud semantic segmentation,” in 32nd IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 10288–10297, 2019. [Google Scholar]

7. Y. Wang, Y. Sun, Z. Liu, S. E. Sarma, M. M. Bronstein et al., “Dynamic graph CNN for learning on point clouds,” ACM Transactions on Graphics, vol. 38, no. 5, pp. 1–12, 2019. [Google Scholar]

8. Y. Li, R. Bu, M. Sun, W. Wu, X. Di et al., “PointCNN: Convolution on X-transformed points,” in 32nd Conf. on Neural Information Processing Systems, Montreal, QC, Canada, pp. 820–830, 2018. [Google Scholar]

9. A. Komarichev, Z. Zhong and J. Hua, “A-CNN: Annularly convolutional neural networks on point clouds,” in 32nd IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 7413–7422, 2019. [Google Scholar]

10. W. Wu, Z. Qi and L. Fuxin, “PointCONV: Deep convolutional networks on 3D point clouds,” in 32nd IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, United states, pp. 9613–9622, 2019. [Google Scholar]

11. L. Landrieu and M. Simonovsky, “Large-scale point cloud semantic segmentation with superpoint graphs,” in 31st Meeting of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 4558–4567, 2018. [Google Scholar]

12. A. Milioto, I. Vizzo, J. Behley and C. Stachniss, “RangeNet ++: Fast and accurate LiDAR semantic segmentation,” in 2019 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, Macau, China, pp. 4213–4220, 2019. [Google Scholar]

13. M. H. Guo, J. X. Cai, Z. N. Liu, T. J. Mu, R. R. Martin et al., “PCT: Point cloud transformer,” Computational Visual Media, vol. 7, no. 2, pp. 187–199, 2021. [Google Scholar]

14. F. Groh, P. Wieschollek and H. P. A. Lensch, “Flex-convolution: Million-scale point-cloud learning beyond grid-worlds,” in 14th Asian Conf. on Computer Vision, Perth, WA, Australia, pp. 105–122, 2019. [Google Scholar]

15. A. Abid, M. F. Balin and J. Zou, “Concrete autoencoders: Differentiable feature selection and reconstruction,” in 36th Int. Conf. on Machine Learning, Long Beach, CA, USA, pp. 694–711, 2019. [Google Scholar]

16. O. Dovrat, I. Lang and S. Avidan, “Learning to sample,” in 32nd IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 2755–2764, 2019. [Google Scholar]

17. X. Yan, C. Zheng, Z. Li, S. Wang and S. Cui, “PointASNL: Robust point clouds processing using nonlocal neural networks with adaptive sampling,” in 2020 IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 5588–5597, 2020. [Google Scholar]

18. M. Wang, H. Yi, F. Jiang, L. Lin and M. Gao, “Review on offloading of vehicle edge computing,” Journal of Artificial Intelligence and Technology, vol. 2, no. 4, pp. 132–143, 2022. [Google Scholar]

19. I. Armeni, O. Sener, A. R. Zamir, H. Jiang, I. Brilakis et al., “3D semantic parsing of large-scale indoor spaces,” in 29th IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 1534–1543, 2016. [Google Scholar]

20. T. Hackel, N. Savinov, L. Ladicky, J. D. Wegner, K. Schindler et al., “SEMANTIC3D.NET: A new large-scale point cloud classification benchmark,” in ISPRS Hannover Workshop 2017 on High-Resolution Earth Imaging for Geospatial Information, Hannover, Germany, pp. 91–98, 2017. [Google Scholar]

21. J. Behley, M. Garbade, A. Milioto, J. Quenzel, S. Behnke et al., “SemanticKITTI: A dataset for semantic scene understanding of LiDAR sequences,” in 17th IEEE/CVF Int. Conf. on Computer Vision, Seoul, Korea, pp. 9296–9306, 2019. [Google Scholar]

22. B. Wu, A. Wan, X. Yue and K. Keutzer, “SqueezeSeg: Convolutional neural nets with recurrent CRF for real-time road-object segmentation from 3D LiDAR point cloud,” in IEEE Int. Conf. on Robotics and Automation, Brisbane, QLD, Australia, pp. 1887–1893, 2018. [Google Scholar]

23. A. H. Lang, S. Vora, H. Caesar, L. Zhou, J. Yang et al., “Pointpillars: Fast encoders for object detection from point clouds,” in 32nd IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 12689–12697, 2019. [Google Scholar]

24. B. Wu, X. Zhou, S. Zhao, X. Yue and K. Keutzer, “SqueezeSegV2: Improved model structure and unsupervised domain adaptation for road-object segmentation from a LiDAR point cloud,” in 2019 Int. Conf. on Robotics and Automation, Montreal, QC, Canada, pp. 4376–4382, 2019. [Google Scholar]

25. P. Zhang, G. Li, C. Liu and J. Ma, “End-to-end BEV perception via homography matrix,” in 6th IEEE Information Technology, Networking, Electronic and Automation Control Conf., Chongqing, China, pp. 1352–1356, 2023. [Google Scholar]

26. S. D. Khan, L. Alarabi and S. Basalamah, “Deep hybrid network for land cover semantic segmentation in high-spatial resolution satellite images,” Information, vol. 12, no. 6, pp. 230, 2021. [Google Scholar]

27. L. P. Tchapmi, C. B. Choy, I. Armeni, J. Gwak and S. Savarese, “SEGCloud: Semantic segmentation of 3D point clouds,” 2017. https://doi.org/10.48550/arXiv.1710.07563 [Google Scholar] [CrossRef]

28. H. Y. Meng, L. Gao, Y. K. Lai and D. Manocha, “VV-net: Voxel VAE net with group convolutions for point cloud segmentation,” in 17th IEEE/CVF Int. Conf. on Computer Vision, Seoul, Korea, pp. 8499–8507, 2019. [Google Scholar]

29. W. Zhou, X. Zhang, X. Hao, D. Wang and Y. He, “Multi point-voxel convolution (MPVConv) for deep learning on point clouds,” Computers & Graphics, vol. 112, pp. 72–80, 2023. [Google Scholar]

30. H. Thomas, C. R. Qi, J. E. Deschaud, B. Marcotegui, F. Goulette et al., “KPConv: Flexible and deformable convolution for point clouds,” in 17th IEEE/CVF Int. Conf. on Computer Vision, Seoul, Korea, pp. 6410–6419, 2019. [Google Scholar]

31. L. Li, L. He, J. Gao and X. Han, “PSNet: Fast data structuring for hierarchical deep learning on point cloud,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 10, pp. 6835–6849, 2022. [Google Scholar]

32. M. Ibrahim, N. Akhtar, S. Anwar and A. Mian, “SAT3D: Slot attention transformer for 3D point cloud semantic segmentation,” IEEE Transactions on Intelligent Transportation Systems, vol. 24, no. 5, pp. 5456–5466, 2023. [Google Scholar]

33. M. Tatarchenko, J. Park, V. Koltun and Q. Y. Zhou, “Tangent convolutions for dense prediction in 3D,” in 31st Meeting of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 3887–3896, 2018. [Google Scholar]

34. F. Zhang and X. Xia, “Cascaded contextual reasoning for large-scale point cloud semantic segmentation,” IEEE Access, vol. 11, pp. 20755–20768, 2023. [Google Scholar]

35. R. Chen, D. Pu, Y. Tong and M. Wu, “Image-denoising algorithm based on improved K-singular value decomposition and atom optimization,” CAAI Transactions on Intelligence Technology, vol. 7, no. 1, pp. 117–127, 2022. [Google Scholar]

36. J. Fu, J. Liu, J. Jiang, Y. Li, Y. Bao et al., “Scene segmentation with dual relation-aware attention network,” IEEE Transactions on Neural Networks and Learning Systems, vol. 32, no. 6, pp. 2547–2560, 2021. [Google Scholar] [PubMed]

37. C. Chen, L. Z. Fragonara and A. Tsourdos, “GAPointNet: Graph attention based point neural network for exploiting local feature of point cloud,” Neurocomputing, vol. 438, pp. 122–132, 2021. [Google Scholar]

38. D. Ren, Z. Wu, J. Li, P. Yu, J. Guo et al., “Point attention network for point cloud semantic segmentation,” Science China Information Sciences, vol. 65, pp. 192104, 2022. [Google Scholar]

39. F. Ding, L. Xu, D. Meng, X. B. Jin, A. Alsaedi et al., “Gradient estimation algorithms for the parameter identification of bilinear systems using the auxiliary model,” Journal of Computational and Applied Mathematics, vol. 369, pp. 112575, 2020. [Google Scholar]

40. F. Ding, L. Xu, X. Zhang and Y. Zhou, “Filtered auxiliary model recursive generalized extended parameter estimation methods for Box–Jenkins systems by means of the filtering identification idea,” International Journal of Robust and Nonlinear Control, vol. 33, no. 10, pp. 5510–5535, 2023. [Google Scholar]

41. L. Xu and F. Ding, “Separable synthesis gradient estimation methods and convergence analysis for multivariable systems,” Journal of Computational and Applied Mathematics, vol. 427, pp. 115104, 2023. [Google Scholar]

42. F. Ding, “Least squares parameter estimation and multi-innovation least squares methods for linear fitting problems from noisy data,” Journal of Computational and Applied Mathematics, vol. 426, pp. 115107, 2023. [Google Scholar]