An Improved Multi-Objective Hybrid Genetic-Simulated Annealing Algorithm for AGV Scheduling under Composite Operation Mode

1  Introduction

The scheduling of AGVs is to dispatch a set of AGVs to complete a batch of pickup/drop-off jobs to achieve certain goals (e.g., shortest completion time, minimum AGV idle time, etc.) under given constraints [1]. The AGV scheduling problem has been proven to be an NP-hard problem, with its complexity growing exponentially with the size of the problem [2]. The AGV scheduling problem has been extensively studied. On the one hand, different optimization objectives were proposed for different scenarios including flexible manufacturing systems [3–5], intelligent job shops [6], automated warehouses [7] and container terminals [8–10]. On the other hand, a variety of new and improved algorithms have been proposed to optimize the solution process. The main optimization objectives are minimizing the total handling completion time [11], the shortest path cost [12], the maximum completion time [13–14], the number of AGVs [6], the total time for inbound and outbound order operations [15], the energy consumption of machines [5], carbon emission [16–18], etc.

In real manufacturing and logistics systems, there are many combinatorial optimization problems (COP) imposing on more complex issues, such as complex structure, nonlinear constraints, and multiple objectives to be handled simultaneously [19]. Karimi et al. [20] established a multi-objective scheduling optimization model with the objectives of reliability and minimizing the maximum completion time of AGVs, and calculated the optimal solution of the trolley dynamic scheduling scheme based on the non-dominated sorting cuckoo algorithm and the meta-heuristic algorithm of multi-objective teaching optimization through optimal sorting of several complexity results. A multi-objective adaptive clustering genetic algorithm based on time windows and Dijkstra was proposed with the three optimization objectives of minimizing maximum completion time, AGV travel time, and total machine load, and a cross-reorganization strategy including adaptive individual cross probabilities was used to enhance the superiority of the algorithm [21]. In addition to minimizing the maximum completion time and AGV travel time, Umar et al. [4] also considered the penalty cost caused by delays or conflicts, and the multi-objective fitness function was calculated using the adaptive weight method, and the genetic operator was controlled by the fuzzy expert method to adaptively control the crossover rate and mutation rate, which greatly improved the performance of the algorithm, but could only be applied with small data volumes. Yang et al. [22] also took the AGV task time penalty cost and total distance traveled as the optimization objectives and proposed the concept of a variable domain search based on the addition of an elite individual protection mechanism, which increased the volume of data in the late iteration of the algorithm and reduced the probability of prematureness of the algorithm, but the search method still had certain limitations. Devapriya et al. [23] constructed a scheduling model for product production and distribution with time constraints, with both fixed cost of vehicles and minimizing distribution time as the objectives, and considered the case of reciprocal vehicle distribution, which is solved using a heuristic algorithm combined with an evolutionary algorithm.

The genetic algorithm is one of the most popular evolutionary algorithms for finding a satisfactory solution in an acceptable time for NP-hard scheduling problems [24]. An improved genetic algorithm was proposed to promote productivity efficiency in collaborative manufacturing systems [25]. Morandin et al. [26] optimized the scheduling of machines and AGVs in flexible manufacturing systems. The proposed algorithm was tested in two scenarios of FMS (Flexible Manufacturing System) and validated by comparing its results with two other algorithms. A non-dominated sorting genetic algorithm (NSGA-II) was adopted to solve multi-objective scheduling problems [27]. Due to the higher probability of the genetic algorithm falling into a local optimum as the population iterates, lots of hybrid algorithms have emerged for solving AGV scheduling problems. Zhong et al. [28] proposed the hybrid genetic algorithm-particle swarm optimization (HGA-PSO) with the fuzzy logic controller to realize the integrated scheduling of multi-AGV with conflict-free path planning. The multi-objective and multi-dimensional optimal scheduling process was defined while considering energy consumption and multi-function of machines and the hybrid sectional encoding genetic algorithm and the discrete particle swarm optimization (HSE-GA-DPSO) was proposed to solve it [5]. Zade et al. [29] proposed a multi-objective hybrid meta-heuristic algorithm called hybrid fuzzy hitch cock bird (MOHFHB) to solve task scheduling problems. A fuzzy hybrid genetic algorithm-particle swarm optimization (GA-PSO) algorithm was proposed to optimize the AGV scheduling model [30]. Rao et al. introduced a developed hybrid whale and the grey wolf optimization algorithm (WGWOA) with a random forest classifier to determine the optimal subset of gait features [31].

This paper studies the AGVs scheduling problem under the composite operation mode which is more efficient than the single operation mode but lacks relevant research. Due to different operation modes, different mathematical models need to be built and effective algorithms should be applied to solve the problem efficiently. In this paper, the improved hybrid algorithm is the simulated annealing algorithm intervening in the genetic algorithm effectively, which was proposed to realize the multi-objective optimization of minimizing the maximum completion time, the total distance traveled by the AGV, and the empty-loaded travel distance. Similar hybrid algorithms have been studied and applied, but mostly in the fields of route planning and the structure of the algorithm fusion is relatively simple and usually treats the two algorithms as an inherited population, neglecting the combination of features between the two algorithms [32–33]. In addition, a grey entropy parallel analysis method combining the grey system theory and the information entropy method is applied to calculate the multi-objective fitness function [34].

The main contributions of this paper are as follows:

•   Firstly, a multi-objective scheduling model under composite operation mode was constructed, and a task vector was added to the model to represent the task mode.

•   Secondly, an improved hybrid genetic algorithm-simulated annealing algorithm based on task advance evaluation strategy (AEGA-SA) was proposed to realize the multi-objective model.

•   Thirdly, a combined coding, parallel decoding mode aiming at composite operation scheduling mode was designed and a grey entropy parallel analysis method was applied to calculate the multi-objective fitness function.

•   Finally, a task advance evaluation strategy was proposed for the crossover and mutation operators of the algorithm, which can effectively improve the convergence speed of the algorithm in the early stage.

The remainder of this paper is organized as follows. Section 2 describes the problem to be solved in this paper and establishes the mathematical model. Section 3 concretely illustrates each step of the improved hybrid algorithm. In Section 4, experiments are performed to investigate the effectiveness of the proposed algorithm. Finally, Section 5 summarizes the main conclusions of this study and puts forward the potential direction of further research in the future.

2  Problem Formulation

2.1 Application Scenarios

The AGVs studied in this paper are directly oriented to shelf operations and are mainly used for loading and unloading palletized goods, aiming too low and medium-level shelves for storage of goods or oriented to loading and unloading operations in storage entrances/exits. Such a scenario can be specifically applied in the low and medium-shelf storage area of automated storage systems and storage logistics centers, product storage area of flexible manufacturing systems, etc.

AGV operation mode can be divided into the single operation mode, which refers to a single task of outbound or inbound storage, and the composite operation mode, which combines outbound and inbound storage as a single task. Due to the lack of reasonable scheduling technology, when the inbound and outbound tasks arrive at the same time, the single operation mode is generally used to partially complete the inbound task and partially complete the outbound task or to complete the two tasks one after another, which is inefficient and causes waste of resources. The composite operation mode can effectively avoid shortcomings of the single operation mode in the coordination of inbound and outbound tasks. There are two kinds of processes of composite operation: First in, last out and first out, last in. The former process is illustrated in Fig. 1a: AGVs go to the inbound area to load the inbound task, run to the shelf, and put the goods into the shelf, then run to the shelf location of the outbound task and pick up the goods, and finally run to the outbound area to complete the outbound task. The latter process is illustrated in Fig. 1b: AGVs first go to the shelf location of the outbound task, pick up the goods, move to the outbound area to unload goods, and then move to the inbound area to load goods to the corresponding shelf.

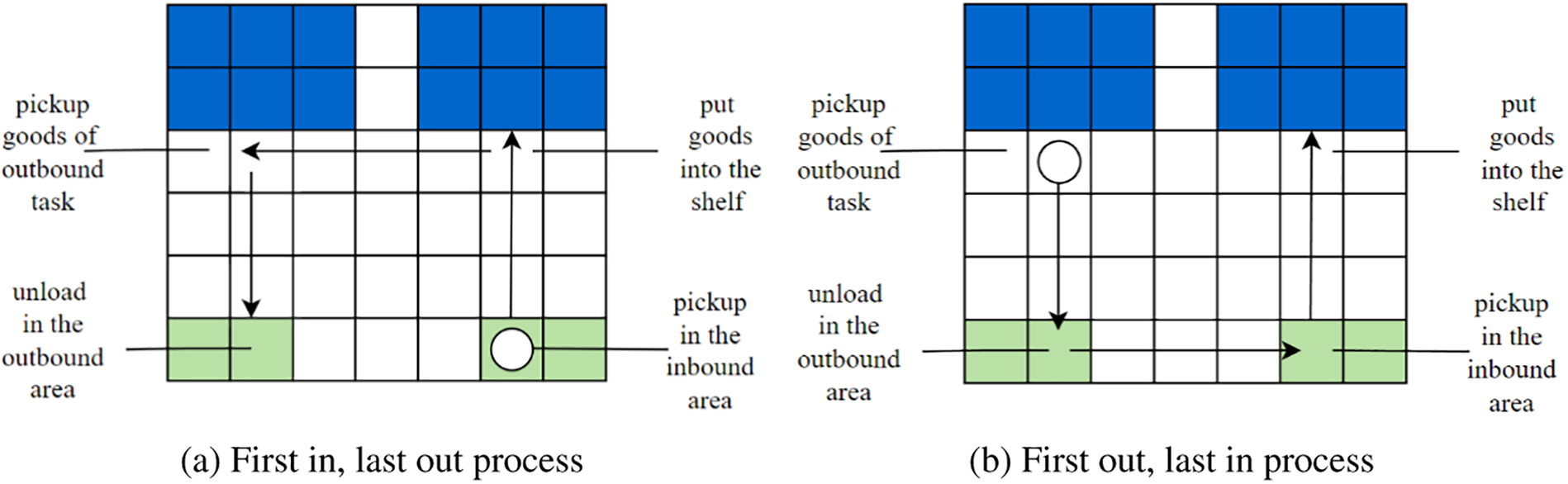
Figure 1: Two processes for composite operations

Raster is used to construct the map model, the specific information of each location of the raster map can be represented by a specific number and matrix, but the map information matrix can only indicate whether each raster is passable or not, so replace the original number with a particle that can store and modify information, as shown in Eq. (1): Each P in the matrix represents a particle and Pxy represents a particle located at the horizontal x and vertical in the map, which can record information such as the coordinates of the current location, whether it is passable or not, whether it is a shelf or an entrance/exit area.

(P11…P1y⋮⋱⋮Px1⋯Pxy)(1)

In this paper, the storage map space area is divided into four major parts: the shelf area, the out/inbound area, the aisle area and the AGV parking area, which has a certain universality, as shown in Fig. 2. The blue area indicates the shelf area, where the goods are stored. The green area indicates the in/outbound area, where the operation of the goods out/in is realized. The orange area is the AGV parking area, where the idle AGV stays after completing its task. The grey area indicates the aisles where the AGVs can run, with a single lane between the rows of shelves, allowing the storage/pickup of goods from both ends of the shelves, and a double lane between the columns, allowing two AGVs to run at the same time.

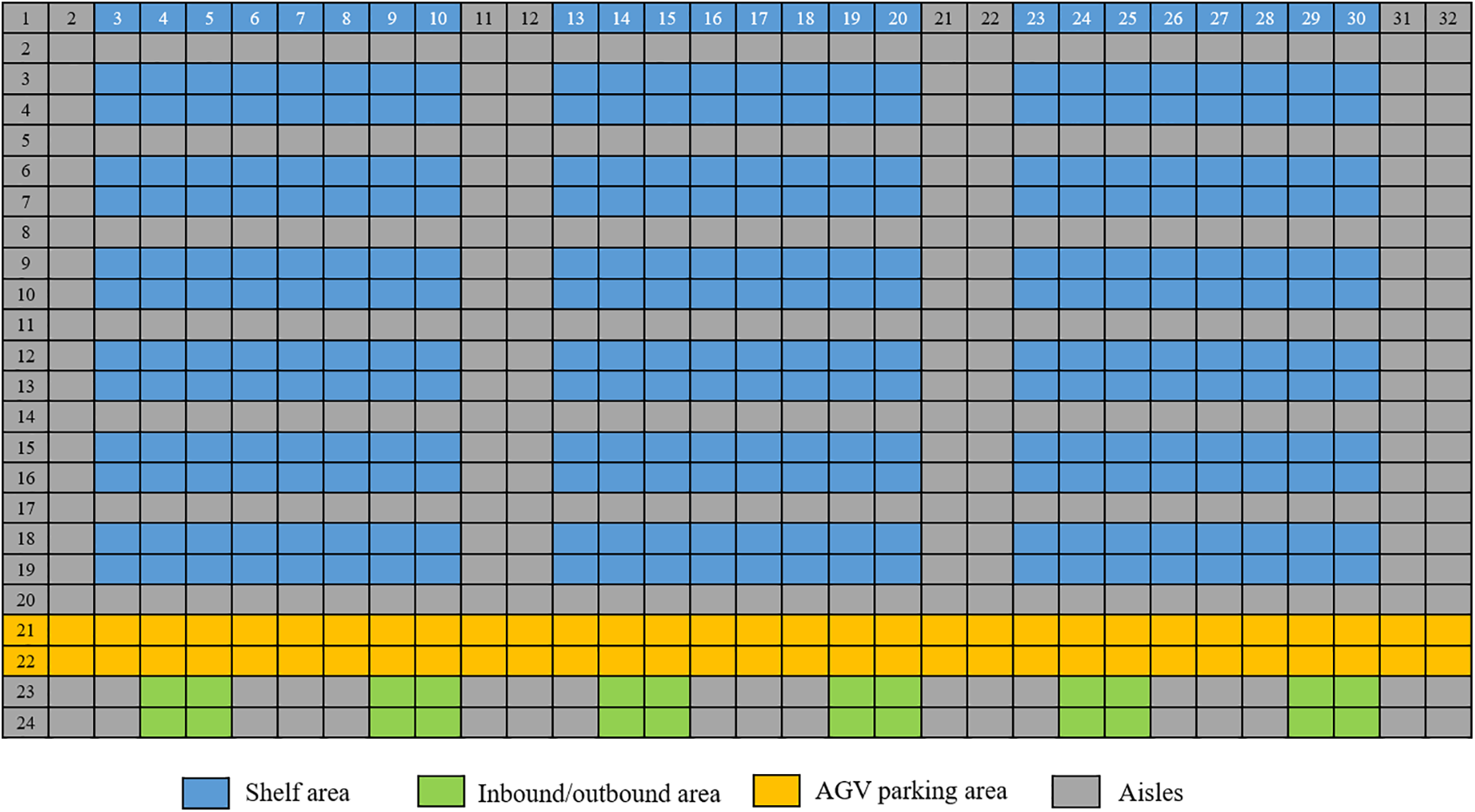
Figure 2: Raster map

2.2 Problem Description

The composite operation refers to an operation mode in which the sequences of AGV inbound and outbound tasks are matched according to certain rules and are completed as a task group. In the case of inbound and outbound orders arriving at the same time, the scheduling study of the composite operation mode can improve system operation efficiency and save system resources. It is important for companies to shorten the delivery time of their products or to respond quickly to customer needs. The distance traveled by the AGVs in the warehouse operation process is closely related to the power consumption of the system. The unloaded travel distance of the composite operation mode often reflects the actual efficiency of the AGVs. The three objectives of the scheduling model optimization in this paper are: 1) the time to complete all tasks should be as short as possible; 2) the distance traveled by all AGVs operations should be as short as possible; 3) the empty travel distance of the AGVs should be as short as possible.

2.3 Mathematical Formulation

2.3.1 Assumptions

The speed of the AGV during travel is directly related to the load status of the vehicle, the working time for pickup/drop-off is related to the lifting speed of the forks, the level and the height of the shelf on which the target goods are located, and the turning time loss is directly related to its turning radius. In addition to these factors, which are related to the performance parameters of the vehicle itself, the operational efficiency of the whole system is related to the solution of the AGV scheduling system. The following assumptions are therefore made for the calculation of the AGV scheduling process:

1) Only one pallet of goods can be handled by one vehicle at the same moment, and the AGV has sufficient power to ensure sufficient completion of the assigned tasks. 2) The input capacity and output capacity of the in/outbound area are large enough. 3) AGV travels at a uniform speed during its work. 4) The acceleration process of the AGV is fast to neglect the loss time of the AGV from motion to rest and from rest to motion. 5) AGV's loading and unloading time in the in/outbound area is fixed. 6) The lifting and lowering speed of the AGV forks is constant. 7) Conflicts such as traffic collisions and deadlocks are not considered in the calculation process. 8) There are five levels of shelf and the AGV can complete operations at this height. 9) Each pallet task has been planned through the system with a starting and ending location.

2.3.2 Notations

Based on the above problem description in Section 2.2 and analytical assumptions in Section 2.3.1, some of the parameters and the variables involved in the scheduling problem under composite AGV operations studied in this paper are defined as shown in Tables 1 and 2.

2.3.3 Mathematical Model

Three optimization objectives are proposed above in Section 2.2, and corresponding mathematical models are constructed regarding the paper [3] and [14] as follows:

(1) Minimizing the maximum completion time

Minimizef1=max{T1,T2,T3,…,Ti}(2)

Ti=∑j=1Citij(3)

tij=(tcij,trij,tkij)⋅η→(4)

η→={(1,1,1)T(0,1,1)T(1,0,1)T(5)

tcij=scijvc+tcija+zcij×ε(6)

trij=srijvr+trija+zrij×ε(7)

tkij=skijvk+zkij×ε(8)

tcija=trija=(d×hij+1)va(9)

In the composite operation mode, the completion of a task by AGV can be regarded as a cycle of three steps: inbound, empty-loaded and outbound task. A task vector is constructed to represent task mode in Eq. (5), and (1,1,1)T indicates a complete task, including all three steps, while (0,1,1)T and (1,0,1)T respectively means no outbound task and no inbound task.

(2) Minimizing the total distance traveled for AGV operations

Minmizef2=∑i=1mSi(10)

Si=∑j=1Cisij(11)

sij=(scij,srij,skij)⋅η→(12)

(3) Minimizing empty-loaded travel distance

Minimizef3=∑i=1m∑j=1Ciskij(13)

skij=|xij0−xij|+|yij0−yij|+g(x)(14)

In this mode the start and end positions of the AGV’s empty-loaded travel are generated in two main areas, one in the out/inbound area and the other in the shelf area. If the start and end positions are in the shelf area, the empty-loaded travel distance needs to be compensated numerically with the Manhattan distance. The compensation formula g(x) is related to the current position of the AGV and the shelf position where the dispatched task is located, as shown in Fig. 3.

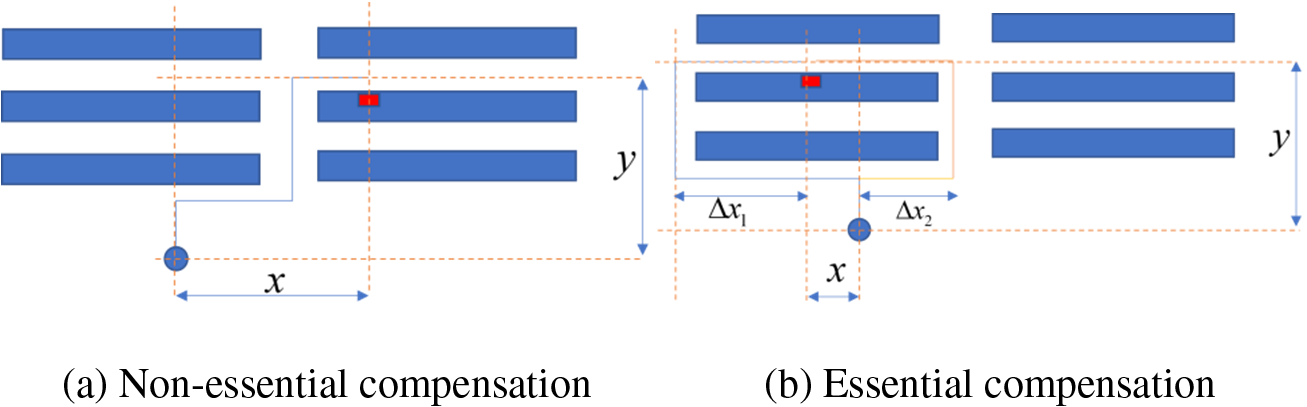
Figure 3: Distance compensation

As shown in Fig. 3a, if the nearest shelf to the location of the AGV is not in the same row of shelves as the shelf location of the task, no distance compensation is required and the AGV travel distance is Manhattan distance. Otherwise, as shown in Fig. 3b, the Manhattan distance is not the exact distance that AGV has traveled, thus a compensation distance is calculated to amend the distance and the distance compensation formula is Eq. (15).

g(x)=μ×min{|xij0−xijleft|,|xij0−xijright|}−1(15)

where μ is the compensation factor, which is 0 in the case of non-essential compensation and 2 in the case of essential compensation. xijleft and xijright are the leftmost horizontal coordinates of the shelf where task j of AGV i is located and the rightmost horizontal coordinate of the shelf, respectively.

(4) Constraints

Subject to

{(xi10,yi10)∈M(xiCi′,yiCi′)∈M(16)

∑j=1CiNij≤1(17)

∑i=1m∑j=1CiNij≤m(18)

tij0≥{t0+∑j=1j−1tijj>1t0j=1(19)

Pxy≤1,x=1,2,…,X,y=1,2,…,Y(20)

Rxyh≤1(21)

Constraint (16) indicates the start and the end point of the AGVs. Constraints (17) and (18) indicate that the task assignment is under the AGV capability, and Constraint (17) indicates that each AGV is performing at most one task while Constraint (18) indicates that the number of AGVs performing a task is no more than the total number of AGVs. Constraint (19) indicates the earliest time when an AGV completes the next task tij0 should be later than the time when the previous task is completed. Constraint (20) indicates that only one AGV is allowed to move and stop at each raster node, and the node can only be released after the AGV leaves, if there is a shelf on the node, it will always be occupied. Constraint (21) indicates that each cargo compartment of the shelf can only be placed in one kind of goods and no other goods can be placed until the goods have been picked up by the AGV.

3  Multi-Objective AEGA-SA for Composite Operation Scheduling

3.1 Improved Hybrid Algorithm Framework

The probability of the genetic algorithm falling into a local optimum would increase as the population iterates, while the simulated annealing algorithm keeps the solution in a wide interval during the computation, but lacks a mature evolutionary mechanism. This paper combines the genetic algorithm and the simulated annealing algorithm to effectively improve the solution quality of the algorithm. The framework of the hybrid algorithm is as follows: after receiving external data, the genetic algorithm is used to seek the global solution of the problem, which plays a role in exploration. In the evolutionary process, the population richness is judged by the variance of the population fitness, and when it remains low for a long time, the simulated annealing algorithm is intervened to improve the population richness, which plays a role in exploitation. The hybrid algorithm therefore makes full use of the advantages of both algorithms, so that the genetic algorithm can continue to have a rich population during the iterative process and can re-optimize the populations locally through the simulated annealing algorithm, maintaining an adequate balance between the local and global search abilities. The overall framework of the hybrid algorithm is illustrated in Fig. 4.

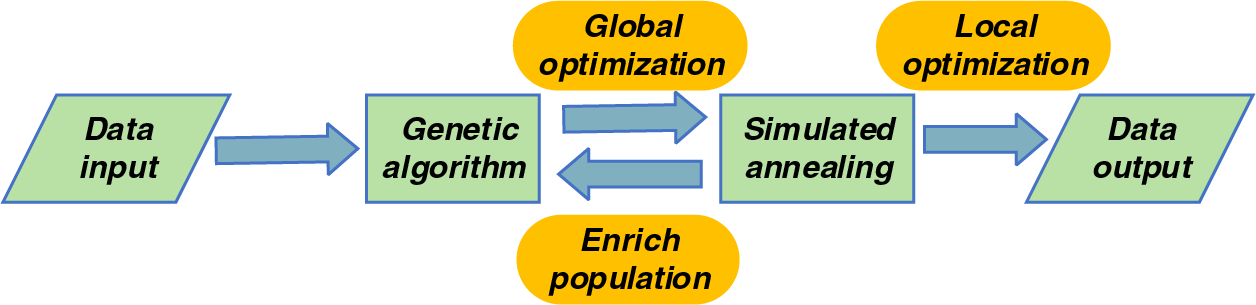
Figure 4: Framework of hybrid algorithm

In the design of both algorithms, the framework of the genetic algorithm is dominant and the simulated annealing algorithm is supplementary. In this paper, the hybrid algorithm is improved for the case of composite operation scheduling. Firstly, this paper adapts the coding and decoding rules of the composite operation model; secondly, the paper converts the original algorithm into a multi-objective solution algorithm through the method of the grey entropy parallel analysis; thirdly, the paper adds a task advance evaluation strategy in the crossover and mutation process to speed up global exploration and local exploitation, improving the efficiency of the algorithm and the accuracy of the calculation results. The specific framework of the designed algorithm is illustrated in Fig. 5.

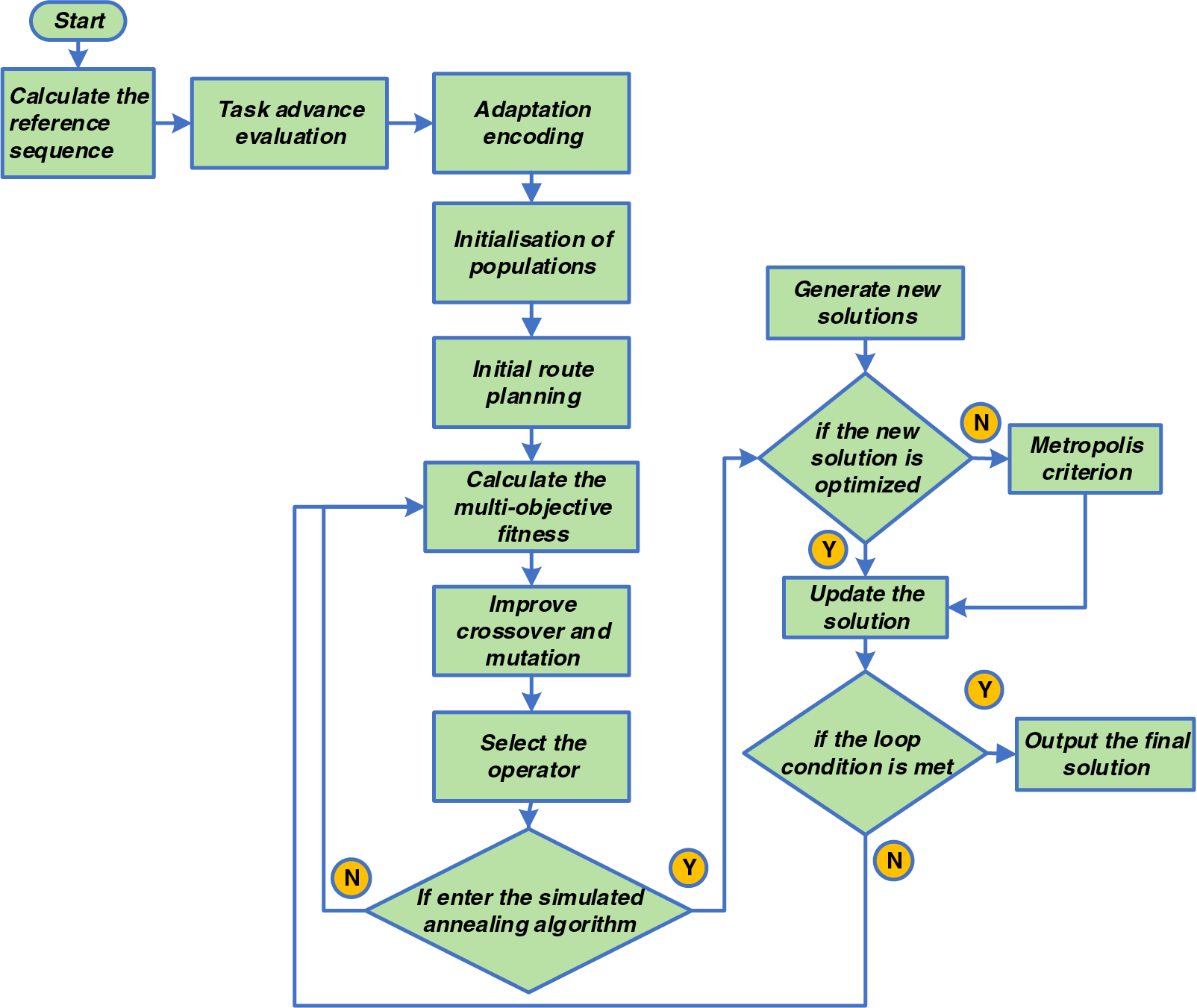
Figure 5: Improved hybrid algorithm flow in composite operation mode

Step1: Calculate the reference sequence. Run the algorithm to obtain the optimal solution for each objective as the reference sequence for the multi-objective solution.

Step2: Task advance evaluation. The task sequence of each AGV is evaluated and ranked to facilitate the improvement of the operator crossover and mutation.

Step3: Adaptation encoding. The AGV sequences, outbound task sequences and inbound task sequences are encoded.

Step4: Initialization of populations. A certain number of initial populations are generated in the global space as initial solutions.

Step5: Initial route planning. The A* algorithm is used to carry out initial route planning for the initial population in advance, targeting the load travel of the task and improving the accuracy of the algorithm's calculation results.

Step6: Calculate the multi-objective fitness. The grey entropy parallel analysis method is applied to calculate the multi-objective fitness function.

Step7: Improve crossover and mutation. Based on the task advance evaluation ranking results of Step2, this step combines with roulette ideas to adopt a point-to-point crossover and mutation approach.

Step8: Select the operator. Use a ranked selection strategy and the optimal preservation strategy.

Step9: Calculate the variance of the population fitness for the current generation. If the variance of 15 consecutive generations of the population is less than one-half of the mean of the variance of the previous 40 generations, enter the simulated annealing algorithm, otherwise go back to Step6.

Step10: Generate new solutions. New solutions are generated for one-fifth of the population's chromosomes by perturbing them in three ways.

Step11: Determine if the new solution is optimized. If yes, update the chromosome directly, otherwise use the Metropolis criterion to determine whether to accept the solution.

Step12: Determine if the loop condition is met, i.e., If the maximum number of iterations is reached, output the final solution. If not, go back to Step6.

3.2 Encoding and Decoding Design under Composite Operation

3.2.1 Combined Coding Design

To adapt to the composite operation model, the AGV sequence, the outbound task sequence and the inbound task sequence are each created with a corresponding chromosome, forming a three-chromosome combination encoding model.

The number of outbound tasks may not be equal to the number of inbound tasks in the composite operation mode, so further processing of the chromosomes is required. The steps are: 1) determine whether the lengths of the two task sequences are equal, and if so, encode them directly; 2) calculate the absolute value of the sequence length difference; 3) create empty particles that do not contain any information, and fill the chromosomes with the number of particle genes with the absolute value for the shorter sequence length. The final encoding is shown in Fig. 6.

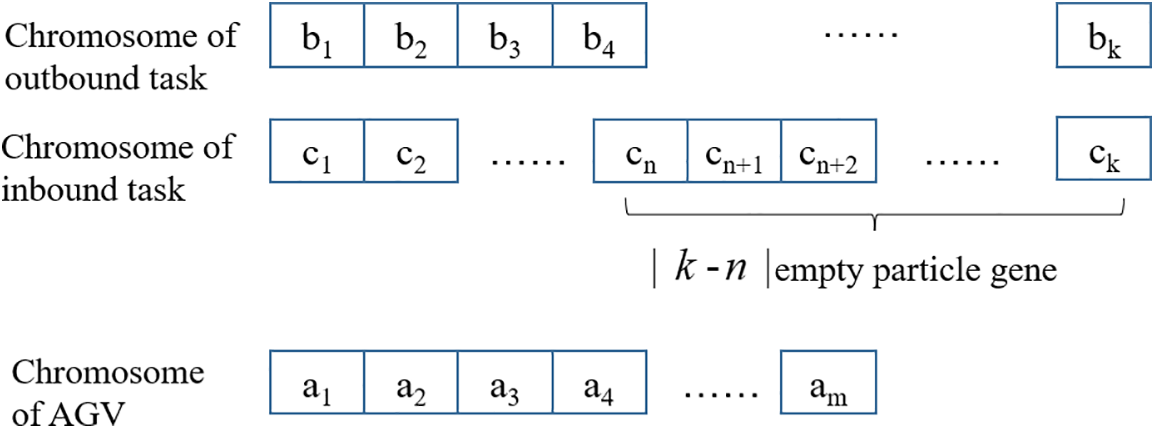
Figure 6: Chromosome coding for the composite mode of operation

3.2.2 Parallel Decoding Design

Treating the two task chromosomes as independent individuals. The number of tasks is k and the number of AGVs is m , Eq. (22) indicates the task sequence Ui for the i AGV.

Ui=∑j=0[k/m]Ni+j×[k/m]+Nγ(22)

where Nγ={Nk−k%n+ii≤k%n0i>k%n represents the allocation strategy for the remaining tasks if the total number of tasks k is not divisible by the number of AGVs m.

After chromosomes are decoded, the outbound task sequence AOi and the inbound task sequence AIi for each AGV respectively are obtained. AOi(x),AIi(x),x=1,2,…,n indicates specific tasks in the outbound and inbound task sequences and n indicates the number of tasks contained in the task sequence.

The sequences AOi and AIi are regarded as row vectors to form a matrix of 2 rows and n columns respectively, which are transformed into column vectors to obtain the final task sequence as shown in Eq. (23). Each Ui represents one cycle of an AGV job, and the AGV completes each operation cycle in the order of the final task sequence.

(Ui(1),Ui(2),…,Ui(n))=[AOi(1)AOi(2)…AOi(n)AIi(1)AIi(2)…AIi(n)](23)

3.3 Multi-Objective Problem Approach

The grey entropy parallel analysis method combines the characteristics of the grey correlation analysis and the information entropy [34], calculates the grey correlation coefficient for the data sequence, and calculates the information entropy and the entropy weight for the data sequence in the meantime. The grey-entropy parallel correlation is obtained by combining the grey correlation coefficient and the entropy weight. The hybrid application of two methods makes up for the deficiencies of grey correlation analysis in terms of data information loss and coefficient skewing, and also provides a computational basis for the information entropy theory, which has been applied to the field of shop floor scheduling by some scholars with good results [34,35]. Three parts of the grey-entropy parallel analysis method are specifically illustrated as follows: the grey correlation theory, the entropy weight theory, and the hybrid of two methods. This method is particularly suitable for discrete data problems because of its low requirements for data sequence distribution. In this section, it is applied to the calculation of multi-objective solution fitness functions for AGV scheduling. The specific steps are shown below.

3.3.1 Reference Sequence Calculation

The best solution is selected for each objective 20 times separately using the hybrid algorithm and the reference sequence X0′={x0′(1),x0′(2),x0′(3)} is formed by those best solutions, which forms the indicator data matrix (X0′,X1′,…,Xq′) with the population fitness sequence.

3.3.2 Grey Correlation Coefficients Calculation

The fitness sequences for each population are dimensioned to eliminate the effects of order of magnitude and dimensionality between the indicators in Eq. (24). The absolute difference between the comparison sequence and the corresponding element of the reference sequence is calculated by taking the maximum and minimum difference between the two data as in Eqs. (25) and (26). The grey correlation coefficient is calculated as in Eq. (27) where ρ takes the value of 0.5.

xi(k)=xi′(k)[∑i=1pxi′(k)]/p(24)

h=mini=1qmink=1p|x0(k)−xi(k)|(25)

H=maxi=1qmaxk=1p|x0(k)−xi(k)|(26)

ξi(k)=h+ρ×H|x0(k)−xi(k)|+ρ×H(27)

3.3.3 Entropy Weights Calculation

The dimensioned data is normalized in Eq. (28) and the data weight matrix of the Y is obtained. Entropy values between chromosomes are calculated in Eq. (29). Entropy weights are calculated in Eq. (30). Eq. (31) indicates that K is the Boltzmann constant and Eq. (32) indicates that the sum of the weights is 1.

fi(k)=xi(k)∑i=1qxi(k)(28)

Q(k)=K∑i=1qfi(k)×ln⁡fi(k)(29)

W(k)=1−Q(k)∑k=13[1−Q(k)](30)

K=−1ln⁡p(31)

∑k=13W(k)=1(32)

3.3.4 Multi-Objective Fitness Value Calculation

The grey correlation indicates the degree of similarity between the comparison sequence of a chromosome and the reference sequence, the entropy weights indicate the influence of each objective between chromosomes, and the two are multiplied and summed to calculate the fitness value of each chromosome in Eq. (33).

fitness(i)=Ri=∑k=13[Wi(k)×ξi(k)i](33)

where k=1,2,…,p, i=1,2,3…,popsize, and pop size indicates population size.

3.4 Crossover and Mutation Based on Task Advance Evaluation

The task scheduling problem under the composite operation mode is essentially a task allocation and sequencing problem, with an additional step of inbound and outbound task matching compared to the single operation mode. The results of matching inbound and outbound tasks have different degrees of influence on the three optimization objectives and the key influence is the distance of empty-loaded travel for AGVs. For example, if an inbound task and an outbound task at the same coordinates but different levels were matched into a set of composite tasks, the distance of empty-loaded traveling can be significantly reduced compared to a single task at a time. Therefore, a strategy for the advanced evaluation of composite tasks is proposed to improve the crossover and mutation process of the algorithm.

The strategy is divided into three main steps. Firstly, the advanced evaluation of tasks. Secondly, the roulette of the evaluation results. Thirdly, the specific process of crossover and mutation.

3.4.1 Advance Evaluation of Tasks

The evaluation steps devised in this paper are shown in Fig. 7.

Figure 7: Flow of evaluation process

The sequences of inbound and outbound tasks for each AGV are denoted as AOi={b1,b2,…,bk} and AIi={c1,c2,…,cn}, respectively, and the distances and the numbers of turns between all tasks of bk and AIi are calculated in advance based on the A* route planning algorithm to form the cost matrix Qk × n of k×n in Eq. (34).

Qk×n=[q11q12⋯q1nq21q22q2n⋮⋱⋮qk1qk2⋯qkn](34)

qkn=lkn+zkn×ε(35)

Eq. (35) indicates the calculation of the cost, where lkn and zkn indicate the distance of the route and the number of turns, respectively, and ε indicates the turning penalty cost factor, which is 3 in this case.

Sorting each column of Qk × n in descending order gives the evaluation ranking of task bi for all tasks in the inbound task sequence AIi.

3.4.2 Roulette of Evaluation Results

The advance evaluation of tasks provides direction for the algorithm to evolve in the process of producing new chromosomes. After the evaluation of tasks, each task is given a sequence of all task ordering levels on another chromosome, which is assumed to be bci={c1(i),c2(i),…,cn(i)}. An example of the results is illustrated in Fig. 8.

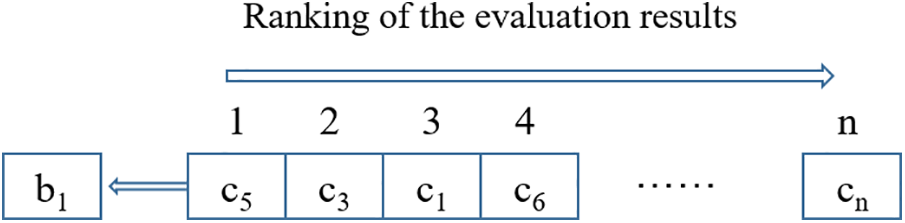
Figure 8: Example of task evaluation results

The idea of roulette is applied to select particles and particles with a higher rating are more likely to be selected. The calculated cost of each element in the bci sequence is assumed as qbi = {y1′,y2′,…,yn′}. Eq. (36) indicates that each element is negatively indexed. Eq. (37) indicates that yj is normalized to obtain the probability of each element Yj′. Eq. (38) indicates that the cumulative probability of each element Yj′ is calculated:

yj=max(yj′)−yj′+1max(yj′)−min(yj′)(36)

Yj′=yj∑j=1nyj,∑j=1nYj′=1(37)

Yj=∑j=1jYj′(38)

where j = 1, 2, …, n.

3.4.3 The Specific Process of Crossover and Mutation

Since particles with null information may be present in the chromosome, a mixture of point-to-point and task-advanced evaluation crossover strategies is applied. A select factor φ is set in Eq. (39), which is used to select the crossover strategy. In this equation, num denotes the current evolutionary generations and Ge denotes the maximum number of iterations.

φ=e−num×10Ge(39)

The crossover strategy based on evaluation results in Section 3.4.2 is mainly adopted in the early stage of algorithm convergence, while the point-to-point crossover strategy is mainly adopted in the middle and late stages of the algorithm to avoid forced perturbation leading to the destruction of the algorithm evolutionary law and premature convergence into local optimum. The random number R is generated using the Rand class, and the point-to-point crossover strategy will be adopted if R>φ while task advance evaluation crossover strategy will be adopted if R<φ.

Mutation operation based on the evaluation results is implemented in such a process. Firstly, two random numbers r1 and r2 are generated for the chromosome group without null information particle gene chromosome, and the two genes at that position are exchanged for the position. Secondly, random numbers r3 and r4 are generated, where r3∈(0,1), r4∈(0,1), and the roulette idea is used to select the tasks in the evaluation sequence and find their respective positions r5 and r6, which are exchanged point to point again, which is illustrated in Fig. 9.

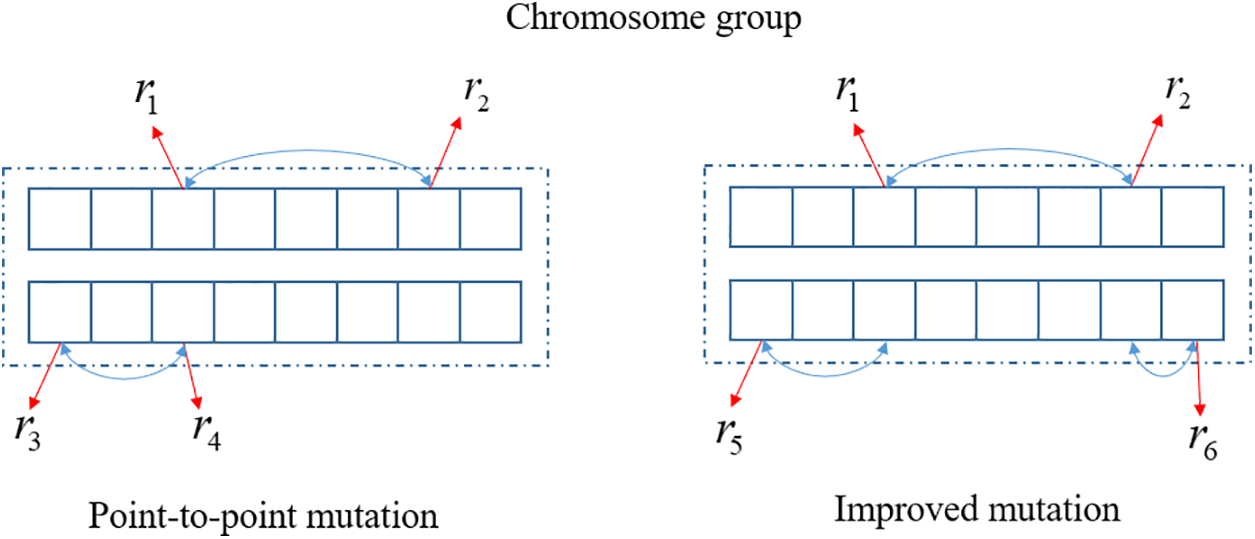
Figure 9: Improved mutation under composite operation

4  Computational Experiments

The optimization effect of the improved algorithm and the validity of the multi-objective solution approach are verified and analyzed respectively in Sections 4.1 and 4.2. The multi-objective advance evaluation strategy genetic algorithm-simulated annealing (AEGA-SA) solution for composite operation scheduling algorithms described in Section 3 is implemented in the visual studio 2022 software platform in C# programming language.

4.1 Algorithm Improvement Validation

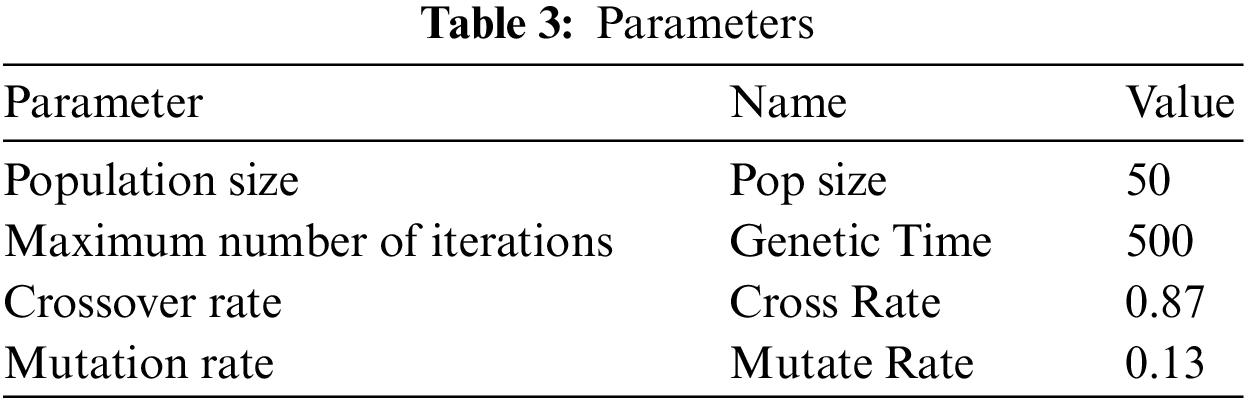
This section selects three kinds of algorithms to compare the convergence speed and solution results. They are the genetic algorithm (GA), the AEGA (advance evaluation strategy genetic algorithm) and the AEGA-SA (advance evaluation strategy genetic algorithm-simulated annealing). Computational simulation experiments are conducted to verify the effectiveness of the improved hybrid algorithm. The number of AGV is 10, and the settings of all parameter values are shown in Table 3.

The comparisons of the convergence curves of GA, AEGA and AEGA-SA are shown below. The maximum completion time is shown in Fig. 10, the total distance traveled for AGV operations is shown in Fig. 11 and the empty-loaded travel distance is shown in Fig. 12.

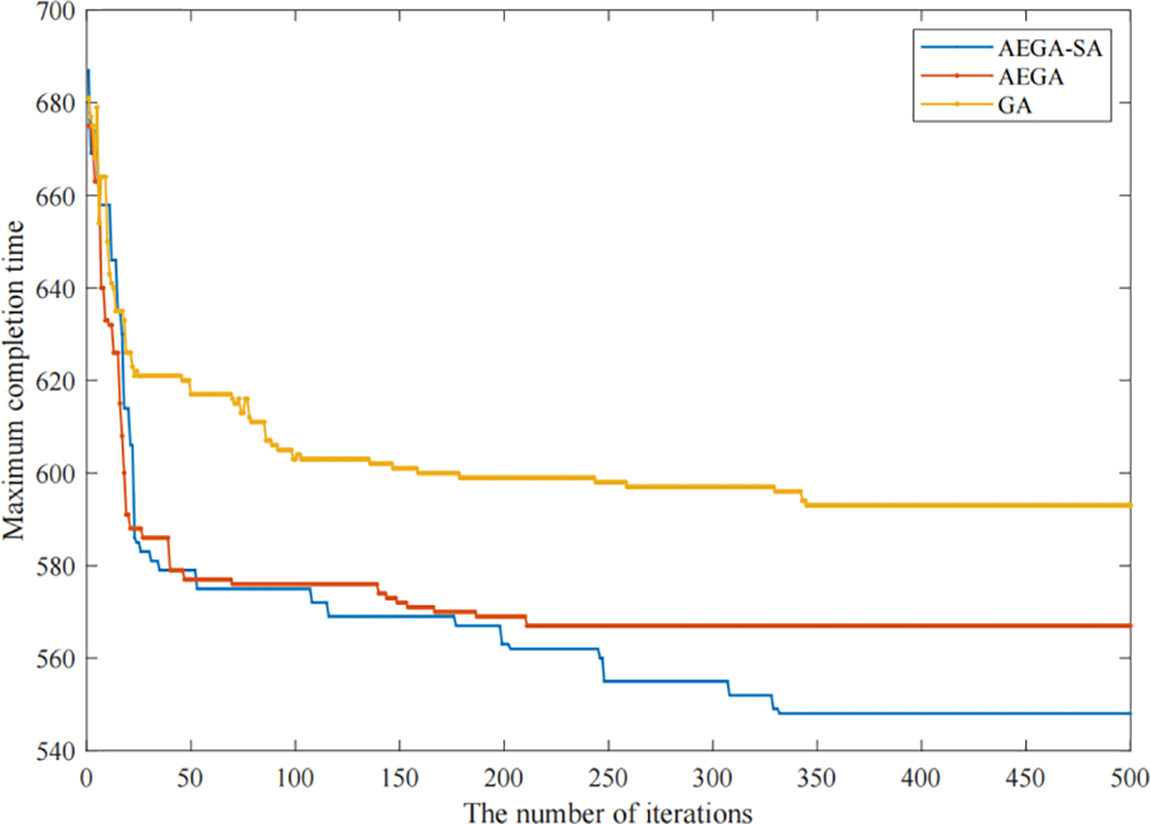
Figure 10: Comparison of maximum completion time

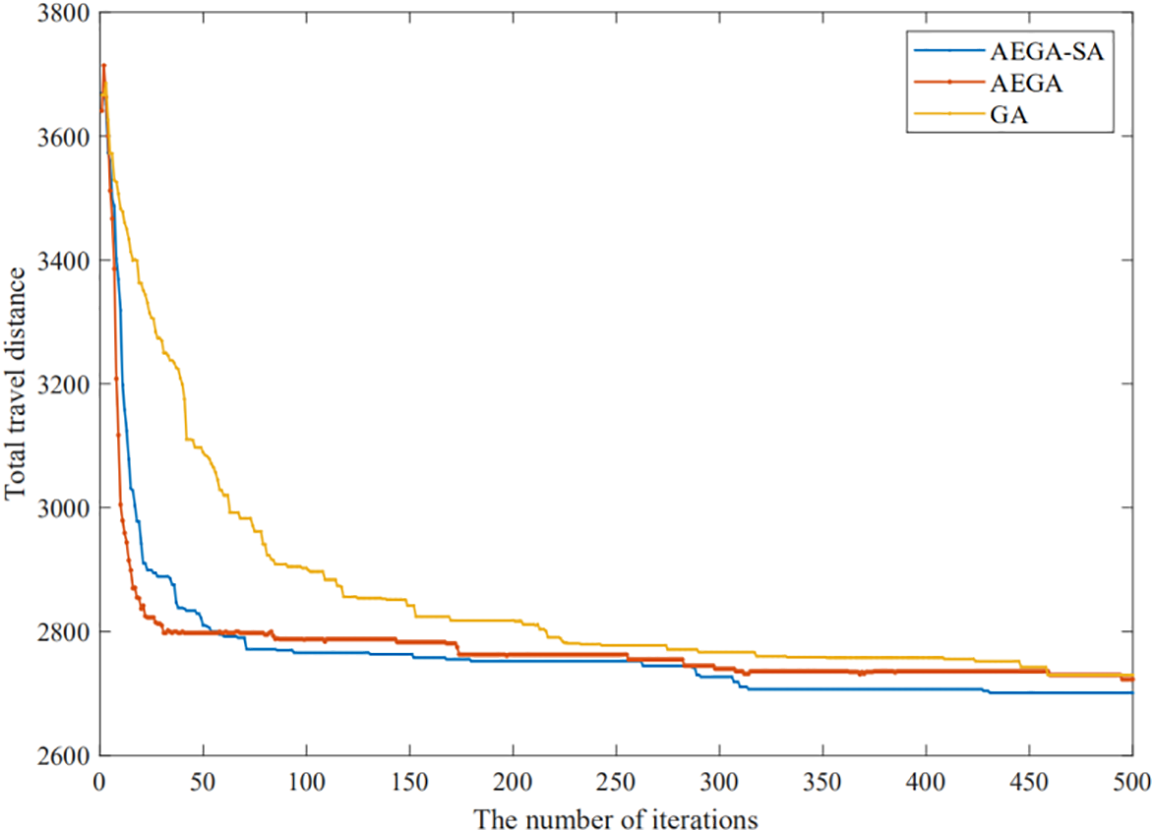
Figure 11: Comparison of total distance traveled for AGV operations

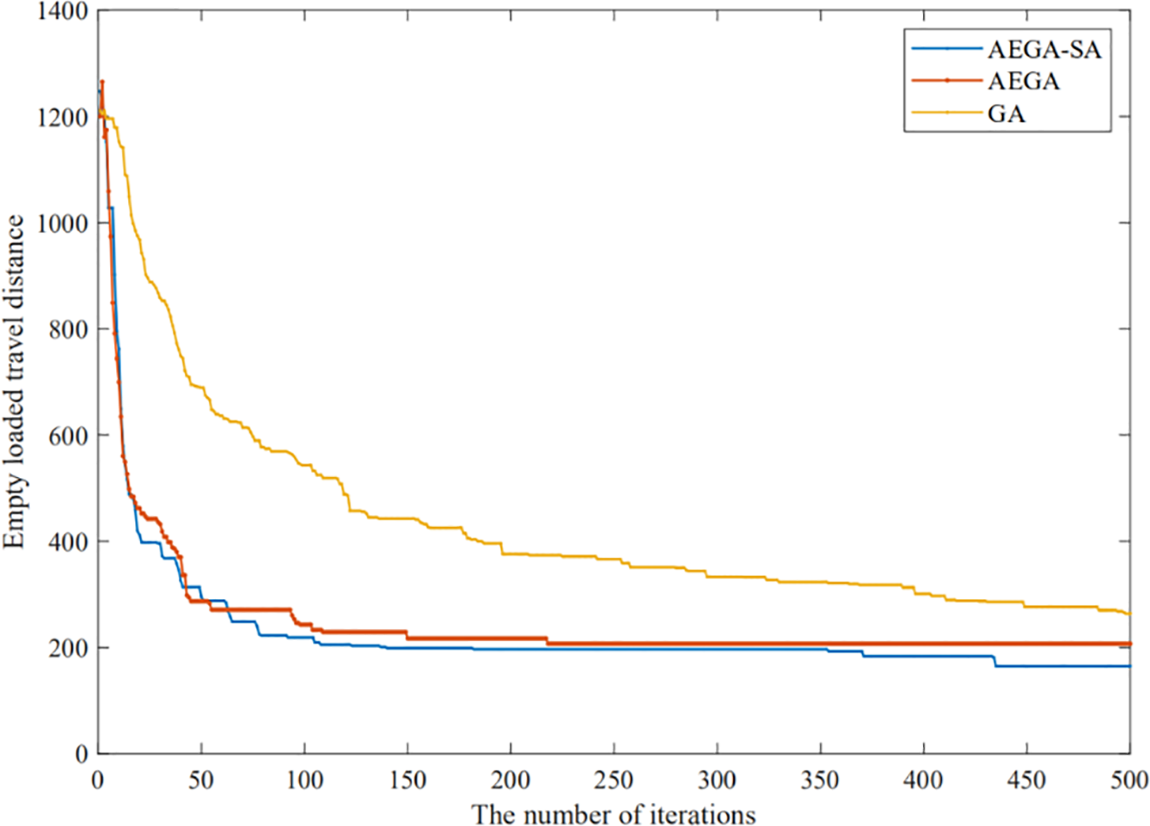
Figure 12: Comparison of empty-loaded travel distance

The comparisons of the above three computational experimental results can draw the following conclusions:

Comparing GA and AEGA, GA converges incompletely and more slowly, while AEGA converges faster in the early stage. Therefore, the task advance evaluation strategy can help the genetic algorithm to calculate the optimal solution faster in the composite operation mode and ensure that the algorithm reaches the convergence state within a specified number of iterations. However, AEGA still suffers from a tendency to fall into a local optimum.

Comparing AEGA and AEGA-SA, the convergence speed gap between them is very small in the early stage, and AEGA is even better than AEGA-SA in the total travel distance. However, AEGA-SA outperforms SA and AEGA in solving the optimal solution for all three objectives, and can optimize the original solution again in the middle and late stage of evolution, especially for the solution with the maximum completion time as the objective. Thus, the improved hybrid algorithm remains the advantage of fast convergence in the early stage of the AEGA with the addition of the task advance evaluation strategy and remains the ability of the hybrid algorithm (GA-SA) to locally optimize the solution again in the late stage of evolution.

As the improved hybrid algorithm is not designed to simply fuse the two algorithms in the form of inherited solutions, it uses the richness of the populations as the criterion for judgment, and the simulated annealing algorithm is organically intervened in the evolutionary process of the genetic algorithm. This step not only preserves the global solving capability of the genetic algorithm, but also gives full play to the local solving capability of the simulated annealing algorithm. The task advance evaluation strategy is proposed for the crossover and mutation operators of the algorithm, which can effectively improve the convergence speed of the algorithm in the early stage, and then cooperate with the local optimization-seeking ability of the hybrid algorithm to complete the local solution of the algorithm in the late stage, improving convergence speed more obviously. The experimental results show that both the speed and the capability of solving all three objectives of the AEGA-SA have been improved.

4.2 Multi-Objective Algorithm Validation

The grey entropy parallel correlation is regarded as the fitness, the three algorithms are compared and analyzed, where the data volume type is expressed in the form of number of outbound tasks, number of inbound tasks × number of AGVs shown in Table 4, and the reference sequences are constituted by solving each objective 20 times to obtain its optimal solution, respectively, and the optimal solution is obtained from the multi-objective algorithm solving 10 times.

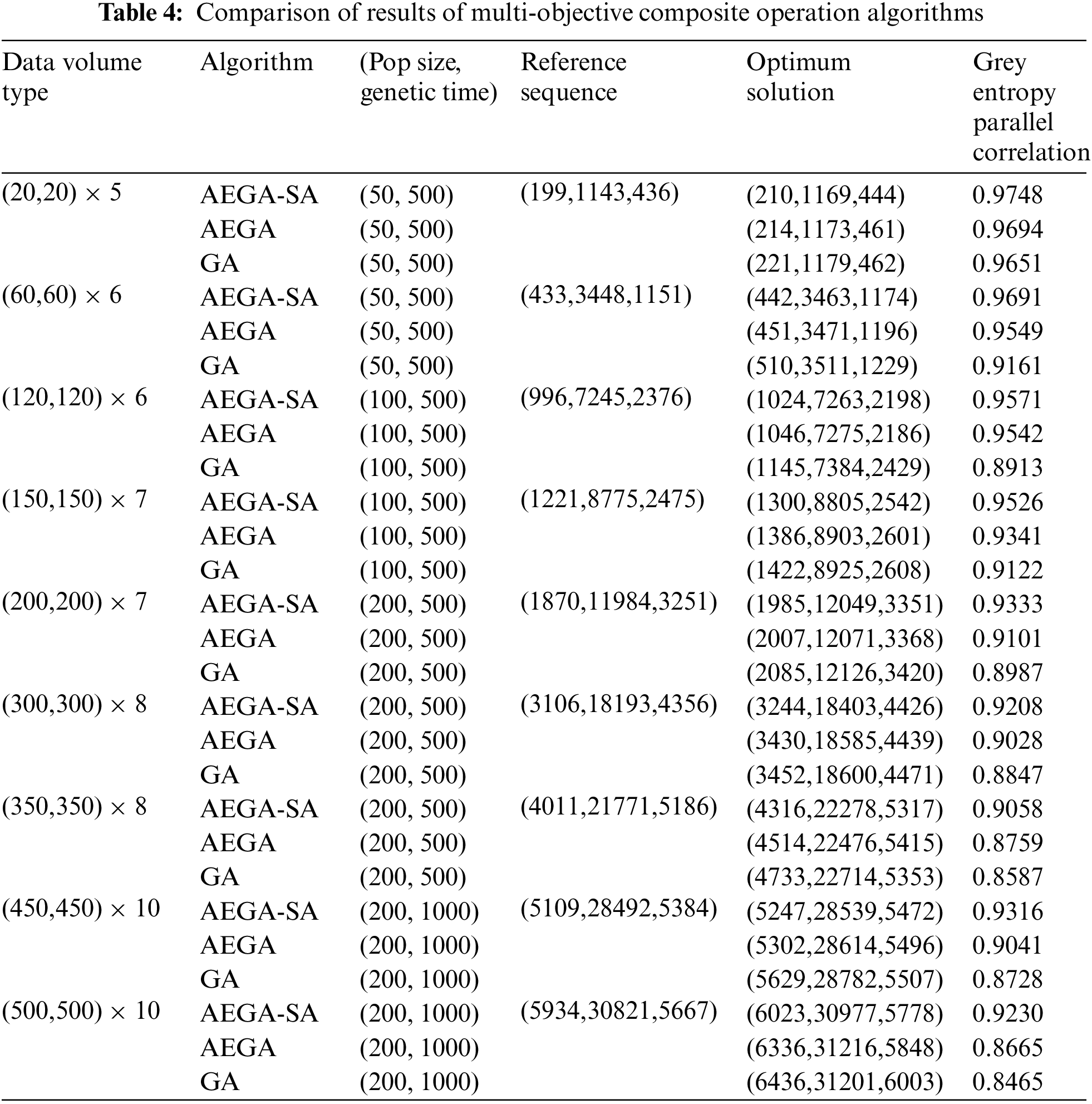
There are two indicators to evaluate the effectiveness of the multi-objective algorithm under the grey entropy parallel analysis method, which are the generation distance (GD) and the progress measure (PM) [34]. The former evaluates the distance between the non-inferior sequences and the reference sequences and can be used as an indicator of the convergence efficiency of multi-objective algorithms, as shown in Eq. (40). The latter evaluates the relative convergence of algorithms, in general, the smaller the PM, the better the convergence of the algorithm, as shown in Eq. (41).

GD=(∑i=1Wmaxdi2)12Wmax(40)

where Wmax is the number of non-inferior sequences in the set, taken as 50, and di is the Euclidean measure of the non-inferior sequences i against the reference sequences.

PM=ln⁡(Ψ1Ψgen)(41)

where ψ1,ψgen represent the value of the maximum grey entropy parallel correlation achieved in the first and the last iteration of algorithms.

As shown in Table 4, for the multi-objective composite operation scheduling problem, the grey parallel correlations obtained by the three algorithms remain above 0.8, and all of them can achieve good results. On the one hand, this is because the three objectives have a linear pattern, and on the other hand, it also shows that the grey entropy parallel analysis method has an exchange promotion effect on the whole population. When the task size is small, the grey entropy parallel correlations of the three algorithms can reach above 0.9, which is very close to the solution of the reference sequences. When the maximum number of iterations is 500, the grey entropy parallel correlations decrease as the task size increases.

Taking AEGA-SA as an example, when the data volume increases from (20,20) × 5 to (350,350) × 8, the grey entropy parallel correlations decrease from 0.9748 to 0.9058. This is because the algorithm takes a longer time to evolve as the amounts of computation increase, and the number of iterations is insufficient, resulting in low results. After adjusting the maximum number of iterations to 1000 and increasing the data type volume to (450,450) × 10, the grey entropy parallel correlation increased again to 0.9316 and the algorithm regained good results.

As shown in Table 5, comparing the results of the three algorithms with data volume, the results of the AEGA are better than the GA. According to the GD, the sets of non-inferior sequences obtained by the AEGA are smaller than those of the GA, which means that the AEGA can obtain better sets of non-inferior sequence solutions. According to the PM, the results of the AEGA are smaller than the GA, which indicates that the convergence effect of the AEGA is better, indicating that the intervention of the task advance evaluation strategy enables the algorithm to iterate faster and ensures the algorithm enough time for local optimization at the late stage. AEGA-SA, on the other hand, is further improved compared to the AEGA because it inherits the advantages of AEGA's fast convergence and integrates the local optimization capability of the SA. According to the GD, AEGA-SA has a higher probability of being the smallest among the three algorithms, which is because the algorithm not only has sufficient local optimization time but also better local optimization capability, providing high-quality non-inferior solutions for the non-inferior solution sets. Moreover, the PM is further improved based on the AEGA, which is due to the advantages of local optimization in the middle and late iteration of the hybrid algorithm.

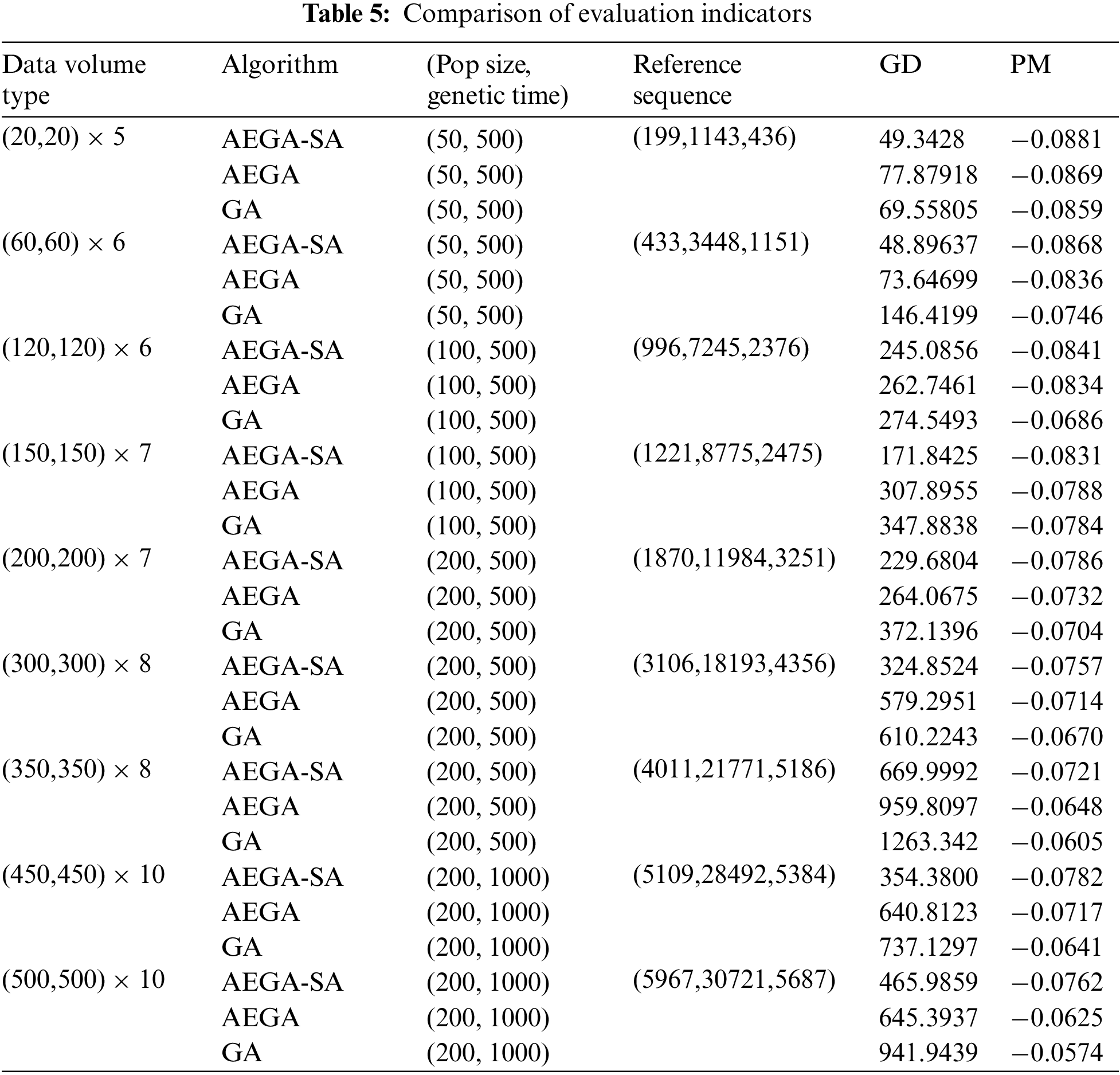
Zhu et al. [35] have demonstrated the ability of the genetic algorithm to solve multiple objectives under the grey entropy parallel analysis method and this paper provides a further enhancement to the algorithm's solving ability after an improvement of the genetic algorithm and the fusion with simulated annealing.

5  Conclusion

This paper deals with the multi-objective scheduling problem of AGVs under the composite operation mode. The AEGA-SA has been proposed to realize the multi-objective model. Specifically, a grey entropy parallel analysis method was applied to calculate the multi-objective fitness function. Additionally, this paper proposed a task-advance evaluation strategy to guide the crossover and mutation of operators, aiming to improve the convergence rates and solution accuracy of the algorithm. The computational experiments have shown that the convergence rate of the AEGA-SA was faster than the other two algorithms in most cases and the convergence results of the AEGA-SA for all three objectives were better than the other two algorithms. Particularly, AEGA-SA achieved a 7.6% improvement over GA and a 3.4% improvement over AEGA in terms of the objective of the maximum completion time. Moreover, the analyses of GD and PM also demonstrate that the ability of multi-objective solution algorithms has been comprehensively enhanced.

However, the proposed algorithm has some shortcomings. The convergence speed did not show significant improvement when compared to AEGA. Meanwhile, since the emphasis of this paper is on the elaboration of the multi-objective improved algorithm and the comparisons of three algorithms, the time complexity has not been analyzed in detail. The integration of other algorithms and the analysis of time complexity can be considered in future research.

Acknowledgement: The authors would like to thank the editor and the anonymous reviewers whose comments helped considerably in improving this paper.

Funding Statement: This work is funded by the Shandong Province Key Research and Development Program under Grant No. 2021SFGC0601.

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: J. M. Xiang, X. H. Cao; computational experiments: J. M. Xiang; analysis and interpretation of results: Y. Zhang, Z. G. Zhou; draft manuscript preparation: Y. Zhang, J. M. Xiang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The source code for this article is currently not available on the website. This work is funded by the Shandong Province Key Research and Development Program and we need to ask for permission to release it online.

Conflicts of Interest: The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

References

1. L. Qiu, W. Hsu, S. Huang and H. Wang, “Scheduling and routing algorithms for AGVs: A survey,” International Journal of Production Research, vol. 40, no. 3, pp. 745–760, 2002. [Google Scholar]

2. Z. Shen, C. Liang and M. Gen, “Scheduling of AGV with group operation area in automated terminal by hybrid genetic algorithm,” in Proc. of Int. Conf. on Management Science and Engineering Management, Toledo, Spain, vol. 78, pp. 427–442, 2021. [Google Scholar]

3. M. Mousavi, H. Yap, S. Musa and S. Dawal, “Multi-objective AGV scheduling in an FMS using a hybrid of genetic algorithm and particle swarm optimization,” PLoS One, vol. 12, no. 3, pp. e0169817, 2017. [Google Scholar] [PubMed]

4. U. Umar, M. Ariffin, N. Ismail and S. Tang, “Hybrid multi-objective genetic algorithms for integrated dynamic scheduling and routing of jobs and automated-guided vehicle in flexible manufacturing systems environment,” International Journal of Advanced Manufacturing Technology, vol. 81, no. 9, pp. 2123–2141, 2015. [Google Scholar]

5. W. Xu and S. Guo, “A multi-objective and multi-dimensional optimization scheduling method using a hybrid evolutionary algorithms with a sectional encoding mode,” Sustainability, vol. 11, no. 5, pp. 1329, 2019. [Google Scholar]

6. Z. Yang, C. Su, X. Hu and D. Chen, “Multi-objective scheduling optimization for multi-AGV systems of intelligent job shop,” Journal of Southeast University, vol. 49, no. 6, pp. 1033–1040, 2019. [Google Scholar]

7. X. Wu, M. Zhang and Y. Zheng, “An intelligent algorithm for AGV scheduling in intelligent warehouses,” in Int. Conf. on Swarm Intelligence, Qingdao, China, pp. 163–173, 2021. [Google Scholar]

8. M. Su, K. Kim and H. Kopfer, “Routing automated guided vehicles in container terminals through the Q-learning technique,” Logistics Research, vol. 3, no. 1, pp. 19–27, 2011. [Google Scholar]

9. Y. Yang, M. Zhong, Y. Dessouky and O. Postolache, “An integrated scheduling method for AGV routing in automated container terminals,” Computers & Industrial Engineering, vol. 126, pp. 482–493, 2018. [Google Scholar]

10. Z. Zhuang, Z. Zhang, H. Teng, W. Qin and H. Fang, “Optimization for integrated scheduling of intelligent handling equipment with bidirectional flows and limited buffers at automated container terminals,” Computers & Operations Research, vol. 145, pp. 105863, 2022. [Google Scholar]

11. N. Yu, T. Li, B. Wang and S. Yuan, “Multi-AGVs scheduling and path planning algorithm sorting warehouse,” Computer Integrated Manufacturing Systems, vol. 26, no. 1, pp. 171–180, 2020. [Google Scholar]

12. C. Liu, C. Zhang and Y. Sun, “Research on application of improved adaptive genetic algorithm in multi-load AGV scheduling,” Journal of Chinese Computer Systems, vol. 42, no. 11, pp. 2241–2245, 2021. [Google Scholar]

13. E. Manafi, R. Tavakkoli-Moghaddam and M. Mahmoodjanloo, “A centroid opposition-based coral reefs algorithm for solving an automated guided vehicle routing problem with a recharging constraint,” Applied Soft Computing, vol. 128, pp. 109504, 2022. [Google Scholar]

14. Y. Zou, Y. Song, Y. Wang and X. Wang, “AGV and machine integrated scheduling method based on discrete whale optimization algorithm,” Journal of Chongqing University, vol. 45, no. 6, pp. 55–74, 2022 (In Chinese). [Google Scholar]

15. X. Jiang, M. Wang, W. Liu, G. Yang, Y. Lu et al., “Integrated scheduling optimization of pharmaceutical warehouse stacker and AGV,” Computer Integrated Manufacturing Systems, vol. 28, no. 1, pp. 230–241, 2022. [Google Scholar]

16. W. Tan, X. Yuan, G. Huang and Z. Liu, “Low-carbon joint scheduling in flexible open-shop environment with constrained automatic guided vehicle by multi-objective particle swarm optimization,” Applied Soft Computing, vol. 111, pp. 107695–107710, 2021. [Google Scholar]

17. Y. Xiao and A. Konak, “A simulating annealing algorithm to solve the green vehicle routing & scheduling problem with hierarchical objectives and weighted tardiness,” Applied Soft Computing, vol. 34, pp. 372–388, 2015. [Google Scholar]

18. W. Xu, Y. Hu, W. Luo, L. Wang and R. Wu, “A multi-objective scheduling method for distributed and flexible job shop based on hybrid genetic algorithm and tabu search considering operation outsourcing and carbon emission,” Computers & Industrial Engineering, vol. 157, pp. 107318, 2021. [Google Scholar]

19. M. Gen, W. Zhang, L. Lin and Y. Yun, “Recent advances in hybrid evolutionary algorithms for multi-objective manufacturing scheduling,” Computers & Industrial Engineering, vol. 112, pp. 616–633, 2017. [Google Scholar]

20. B. Karimi, S. Niaki, H. Haleh and B. Naderi, “Bi-objective optimization of a job shop with two types of failures for the operating machines that use automated guided vehicles,” Reliability Engineering & System Safety, vol. 175, pp. 92–104, 2018. [Google Scholar]

21. Y. Zou, Y. Song, X. Wang and Y. Wang, “Clustering genetic algorithm for multi-objective integrated scheduling of AGVs and machines,” China Mechanical Engineering, vol. 33, no. 1, pp. 97–108, 2022. [Google Scholar]

22. H. Yang and S. Wang, “Application of variable neighborhood genetic algorithm in workshop logistics scheduling,” Computer systems applications, vol. 30, no. 12, pp. 288–298, 2021. [Google Scholar]

23. P. Devapriya, W. Ferrell and N. Geismar, “Integrated production and distribution scheduling with a perishable product,” European Journal of Operational Research, vol. 259, no. 3, pp. 906–916, 2017. [Google Scholar]

24. M. Gen and L. Lin, “Multi-objective genetic algorithm for scheduling problems in manufacturing systems,” Industrial Engineering & Management Systems, vol. 11, no. 11, pp. 310–330, 2012. [Google Scholar]

25. N. Ren, D. Liu, Y. Zhao and X. Ge, “AGV scheduling optimizing research of collaborative manufacturing system based on improved genetic algorithm,” Applied Mechanics & Materials, vol. 300–301, pp. 55–61, 2013. [Google Scholar]

26. O. Morandin, E. Kato and C. Tuma, “A strategy of production scheduling with the fitness function of genetic algorithm using Timed Petri net and considering AGV and the input buffer,” in 36th Annual Conf. on IEEE Industrial Electronics Society, Glendale, AZ, USA, pp. 1311–1316, 2010. [Google Scholar]

27. M. Gonzalom and P. Jordi, “Multi-objective scheduling algorithm for flexible manufacturing systems with Petri nets,” Journal of Manufacturing Systems, vol. 54, pp. 272–284, 2020. [Google Scholar]

28. M. Zhong, Y. Yang, Y. Dessouky and O. Postolache, “Multi-AGV scheduling for conflict-free path planning in automated container terminals,” Computers & Industrial Engineering, vol. 142, pp. 106371, 2020. [Google Scholar]

29. B. Zade, N. Mansouri and M. Javidi, “Multi-objective scheduling technique based on hybrid hitch cock bird algorithm and fuzzy signature in cloud computing,” Engineering Applications of Artificial Intelligence, vol. 104, pp. 104372, 2021. [Google Scholar]

30. M. Mousavi, H. J. Yap, S. Musa and S. Dawal, “A fuzzy hybrid GA-PSO algorithm for multi-objective AGV scheduling in FMS,” International Journal Simulation Modelling, vol. 16, no. 1, pp. 58–71, 2017. [Google Scholar]

31. P. S. Rao, P. Parida, G. Sahu and S. Dash, “A multi-view human gait recognition using hybrid whale and gray wolf optimization algorithm with a random forest classifier,” Image and Vision Computing, vol. 136, pp. 104721, 2023. [Google Scholar]

32. C. Li and J. Pei, “Application of new simulated annealing genetic algorithm in path optimization,” Modular Machine Tool & Automatic Manufacturing Technique, vol. 3, no. 3, pp. 52–55, 2022. [Google Scholar]

33. H. Fan, Z. Xu, Y. Li and X. Yang, “Chaos genetic simulated annealing algorithm for the open multi-depot split delivery vehicle routing problem,” Operations Research and Management Science, vol. 31, no. 1, pp. 92–98, 2022. [Google Scholar]

34. G. Zhu, Z. Feng and Z. Yang, “Solving multi-objective optimization problem with particle swarm algorithm guided by grey entropy parallel analysis method,” Systems Engineering and Electronics, vol. 36, no. 11, pp. 2233–2238, 2014. [Google Scholar]

35. G. Zhu and L. He, “Multi-objective flow shop schedule based on grey entropy parallel analysis optimization algorithm,” Computer Engineering, vol. 41, no. 10, pp. 165–170, 2015. [Google Scholar]