SCChOA: Hybrid Sine-Cosine Chimp Optimization Algorithm for Feature Selection

1  Introduction

In various domains, such as machine learning and data mining, datasets frequently consist of a multitude of features. However, it is important to note that not all of these features are relevant or beneficial for the specific learning task at hand. Irrelevant features can negatively impact the model’s performance. Additionally, as datasets grow, the dimensionality of the data also increases, resulting in higher demands on the efficiency of model training and prediction [1]. Consequently, Feature Selection (FS) plays a crucial role in identifying the most pertinent and valuable features from the original dataset [2]. This process reduces data dimensionality, improves model accuracy and generalization, and reduces computational costs. Due to its numerous benefits, FS finds wide-ranging applications in various fields [3]. As a result, it has gained significant attention as a vital research area in recent years.

In general, FS methods can be categorized into three categories based on their relationship with the learning algorithm: filter approaches, wrapper approaches, and embedded approaches. Filter approaches are considered to be the fastest FS methods as they do not require training models and have lower computational costs [4]. However, in many cases, filter approaches may not identify the optimal feature subset [5]. On the other hand, wrapper approaches consider FS and the learning algorithm as a whole. They iteratively train the learning algorithm with different feature subsets to choose the best subset for training the model. However, the quality of FS by wrapper methods is dependent on the classifier, which results in wrapper methods getting better classification accuracy but being slower [6]. Additionally, embedded approaches integrate FS with the training process of the learning algorithm [7]. They adapt the features during the training process to select the features that contribute the most to the performance of the learning algorithm. Embedded approaches have relatively weaker modeling performance compared to wrapper methods, but they offer better computational efficiency [8].

In order to improve FS, search methods for FS are continually evolving. Traditional search methods like Sequential Forward/Backward Selection (SFS/SBS) were formerly popular [9]. Yet, these methods possess several limitations, such as issues with hierarchy and high computational costs. Consequently, Floating FS methods such as Sequential Forward/Backward Floating Selection (SFFS/SBFS) were proposed as alternatives [10]. However, with the generation of large-scale high-dimensional datasets, floating search techniques may not necessarily yield the optimal solution.

In recent years, Metaheuristic Algorithms (MAs) have gained significant popularity for solving a wide range of optimization and FS problems. These algorithms have demonstrated success in quickly finding the closest solutions, without the need for computing gradients or relying on specific problem characteristics [11]. This inherent flexibility has contributed to their widespread adoption. MAs can be categorized into four main types: Evolutionary Algorithms (EAs), Swarm Intelligence Algorithms (SIs), Physics-Based Algorithms (PAs), and Human-Inspired Algorithms (HAs). EAs are inspired by biological processes and simulate the process of natural evolution. One of the most commonly used EAs is the Genetic Algorithm (GA) [12], which is based on Darwin’s theory of evolution. SIs are inspired by collective intelligence behavior. Examples of SIs include Particle Swarm Optimization (PSO) [13], Ant Colony Optimization (ACO) [14], and Whale Optimization Algorithm (WOA) [15]. Recently, some interesting SIs have been proposed, such as Beluga Whale Optimization (BWO) [16] and Artificial Rabbits Optimization (ARO) [17]. PAs are based on physical principles and motion laws. Examples include Simulated Annealing (SA) [18], Equilibrium Optimizer (EO) [19]. HAs mimic human behavior and interaction. Examples include Teaching-Learning-Based Optimization (TLBO) [20] and Imperialist Competitive Algorithm (ICA) [21], which are frequently cited techniques.

The Chimp Optimization Algorithm (ChOA) is a performance efficient SI algorithm proposed in 2020 by Khishe et al. [22]. This algorithm is inspired by the individual intelligence, sexual motivation, and predatory behavior of chimps. It effectively replicates chimps’ driving, chasing, and attacking patterns to develop an efficient optimization scheme. In recent years, the ChOA algorithm and its variations have been successfully applied to various engineering problems, including gear transmission design [23], multi-layer perceptron training [24], and the order reduction problem of Said-Ball curves [25].

The Sine Cosine Algorithm (SCA) is a PA method developed in 2016 [26]. By imitating the sine and cosine functions’ oscillation, which mimics the motion of waves in nature, the SCA looks for the best solution. As a result, it offers the advantages of fast convergence and easy implementation, and it finds extensive application across diverse domains for addressing optimization challenges.

While the ChOA algorithm exhibits good performance in solving specific problems, it faces challenges such as slow convergence speed and a tendency to get trapped in local optima when dealing with complex optimization problems [24]. Further research indicates that these limitations stem from ChOA's insufficient exploration capability. To tackle this issue, the present paper introduces a novel approach that combines the ChOA with SCA. This proposed method synergistically combines the exploration and exploitation capabilities of both algorithms by utilizing SCA to guide the ChOA for enhanced exploration in the search space. On one hand, the exploration capability mainly comes from SCA, and on the other hand, the exploitation part is handled by ChOA. The decision to combine the ChOA and SCA is primarily motivated by the simplicity and effectiveness of the ChOA, as well as the unique sine-cosine search capability of the SCA. The objective of combining these two heuristics is to develop a hybrid algorithm that is simpler and more efficient for feature selection. The main contributions of this paper are as follows:

•   Proposing a novel hybrid sine-cosine chimp optimization algorithm for feature selection. By combining the chimp optimization algorithm with the sine-cosine algorithm, the unique characteristics of both algorithms are effectively utilized.

•   Evaluating, classifying, and validating the efficiency of the selected feature subsets obtained from the hybrid algorithm using the KNN classifier.

•   Comparing the proposed hybrid feature selection method with seven advanced feature selection methods on 16 datasets using well-known evaluation metrics such as average fitness value, average classification accuracy, average number of selected features, and average runtime.

•   In addition, the Wilcoxon rank-sum test is conducted to examine the significant differences between the results obtained from the proposed hybrid feature selection technique and the compared methods.

The paper is structured as follows: Section 2 presents a comprehensive review of previous related work. Section 3 provides a detailed description of the proposed feature selection (FS) method. Section 4 explains the experimental setup and presents the analysis and results of the conducted experiments. Finally, Section 5 discusses the conclusions drawn from the study.

2  Literature Review

In recent years, there has been a growing trend among researchers to utilize MAs in order to tackle a diverse array of FS problems. Among these algorithms, GA has gained popularity due to its effectiveness in optimization problems. Yang et al. were pioneers in using GA to solve FS problems [27]. Additionally, Kennedy et al. suggested the BPSO [28], a variant of the PSO, which is particularly well-suited for binary optimization problems. Afterward, several variants of PSO emerged, such as a three-phase hybrid FS algorithm based on correlation-guided clustering and PSO [29], bare-bones PSO with mutual information [30], and multiobjective PSO with fuzzy cost [31]. These variants have achieved remarkable results in the field of feature selection. More recently, Mafarja et al. introduced a binary version of WOA specifically for FS and classification tasks [32]. Moreover, a novel FS method based on the Marine Predators Algorithm was developed for three coronavirus disease (COVID-19) datasets [33]. This demonstrates the increasing demand for innovative optimization methods and their subsequent impact on the development of new FS techniques tailored to specific challenges.

By combining the strengths of various MAs, it is possible to strike a balance between exploration and exploitation, effectively mitigating the limitations associated with individual algorithms. As a result, hybrid algorithms have received increasing attention in FS problems. For example, Al-Tashi et al. presented a discrete version of hybrid PSO and GWO, named BGWOPSO [34]. The experimental results demonstrated that BGWOPSO outperformed other methods in terms of both accuracy and cost time. Similarly, Ling et al. proposed the NL-BGWOA [35] for FS, which combined WOA and GOA to optimize the diversity in search. The results showed that this method had a high accuracy of up to 0.9895 and superiority in solving FS problems on medical datasets. Recently, a hybrid FS method that combined the Dipper Throated and Grey Wolf Optimization (DTO-GW) was proposed [36]. This method utilized binary DTO-GW to identify the best subset of the aim dataset. A comparative analysis, conducted on 8 life benchmark datasets, demonstrated the superior performance of this method in solving the FS problem. In order to enhance the classification model’s overall performance, researchers proposed two Stages of Local Search models for FS [37]. The two models were based on the WOA and the Great Deluge (GD). The effectiveness of the proposed models in searching the feature space and improving classification performance was evaluated using 15 standard datasets. Moreover, a novel wrapper feature selection method called BWPLFS was introduced, which combines the WOA, PSO, and Lévy Flight [38]. Experimental results demonstrated that BWPLFS selects the most effective features, showing promise for integration with decision support systems to enhance accuracy and efficiency. In order to improve the accuracy of cancer classification and the efficiency of gene selection, researchers proposed a novel gene selection strategy called BCOOT-CSA [39], which combined the binary COOT optimization algorithm with simulated annealing. Experimental results demonstrated that BCOOT-CSA outperformed other techniques in terms of prediction accuracy and the number of selected genes, making it a promising approach for cancer classification. Therefore, it is crucial to carefully select appropriate hybrid algorithms based on specific problem characteristics and conduct thorough experimental evaluations to validate their performance. Furthermore, ongoing research and development efforts should focus on advancing the techniques and methodologies of hybrid algorithms to further enhance their capabilities in FS and optimization tasks.

According to the No Free Lunch theorem [40], no optimization algorithm can solve all optimization problems, whether past, present, or future. While algorithms may perform well on specific datasets, their performance may decline when applied to similar or different types of datasets. Although the methods mentioned in the literature each have their own characteristics, none of them can address all FS issues. Therefore, it is essential to improve existing methods or propose novel approaches to enhance the resolution of FS problems. Following is a discussion of a hybrid wrapper-based method for selection features.

3  Methodology

The proposed method is a hybrid algorithm that combines the Chimp Optimization Algorithm and the Sine Cosine Algorithm. In this section, the fundamental knowledge of the proposed method will be explained, as well as a demonstration and discussion of the proposed method.

3.1 Chimp Optimization Algorithm (ChOA)

ChOA is a novel intelligent algorithm, proposed by Khishe et al. in 2020, which is based on chimp hunting behavior. Based on the behavior of group division of labor and cooperation, ChOA classifies the leaders of chimp groups into four types: attacker, barrier, chaser, and driver. In this scenario, the attacker is the role of the leader, and the others assist, with their level decreasing in order. The mathematical models of chimp driving, obstructing, and chasing prey are described as below:

d(t)=|c⋅Xprey(t)−m⋅Xchimp(t)|(1)

Xchimp(t+1)=Xprey(t)−a⋅d(t)(2)

here, d(t) represents the distance between the prey and the chimp at the current iteration t. The chaotic vector m is generated by chaotic maps. Xprey(t) is the position vector of the prey, and Xchimp(t+1) is the position vector of the chimp. The coefficient vectors a and c are represented by Eqs. (3) and (4), respectively.

a=2⋅f⋅r1−f(3)

c=2⋅r2(4)

where r1 and r2 are random numbers between 0 and 1. The parameter f is a decreasing factor that nonlinearly decreases from 2.5 to 0 with increasing iteration number. Therefore, the parameter a takes values between −f and f. When a is within the range of −1 to 1, the chimp launches an attack on the prey, thus ending the hunting process. Otherwise, the next position of the chimp can be arbitrarily selected from all chimp positions. Thus, the mathematical model of chimp attacking the prey is described by Eqs. (5)–(7).

da(t)=|c1⋅Xa(t)−m⋅X(t)|,db(t)=|c2⋅Xb(t)−m⋅X(t)|dc(t)=|c3⋅Xc(t)−m⋅X(t)|,dd(t)=|c4⋅Xd(t)−m⋅X(t)|(5)

X1=Xa(t)−a1⋅da(t),X2=Xb(t)−a2⋅db(t)X3=Xc(t)−a3⋅dc(t),X4=Xd(t)−a4⋅dd(t)(6)

X(t+1)=(X1+X2+X3+X4)/4(7)

where X(t) represents the current position of the chimp agent, Xa(t), Xb(t), Xc(t) and Xd(t) represent the positions of the current attacker, barrier, chaser, and driver, respectively, and da(t), db(t), dc(t) and dd(t) represent the distance vectors between the corresponding chimp and the current chimp agent. The next position of the chimp individual is randomly distributed within a circle determined by the positions of these top four individuals. In other words, the positions of the other chimps are guided by the positions of them.

In the final stage of hunting, when the chimps are satisfied with the prey, they are driven by social motivation to release their nature. At this point, the chimps will try to obtain food in a forced and chaotic way. Six deterministic chaotic maps [22] are used to describe this social behavior, with a 50% probability of choosing either the conventional position update way or the chaotic model. The mathematical representation of social motivation behavior is shown in Eq. (8).

X(t+1)=Chaotic_value(8)

where Chaotic_value is a chaotic map.

3.2 Sine Cosine Algorithm (SCA)

SCA is an efficient MA based on sine and cosine laws. The optimization process of SCA involves two phases: exploration and exploitation, which are balanced by the sine and cosine functions. During the exploration phase, the algorithm searches for promising areas with high randomness in a large search space, while during the exploitation phase, it performs local search near previously explored points. For both phases, the position of the candidate solution in SCA is updated using the following Eq. (9):

Xit+1={Xit+r1×sin⁡(r2)×|r3Xbt−Xit|,r4<0.5Xit+r1×cos⁡(r2)×|r3Xbt−Xit|,r4≥0.5(9)

here, Xit represents the current position of the solution, while Xit+1 represents the position for the next iteration. The i denotes the dimension, and t denotes the iteration number. The value of r1 linearly decreases from a to 0 as the iteration number increases, and its expression can be seen in Eq. (10); r2 is a random number between 0 and 2π, r3 is a random number between 0 and 2, and r4 is a random number between 0 and 1. Xbt represents the position of the best individual found so far after t generations.

r1=a−taT(10)

where a represents a constant, which is taken as 2.

3.3 The Proposed Hybrid SCChOA Algorithm

In this section, we introduce the proposed hybrid SCChOA algorithm. The proposed hybrid method combines the ChOA with the SCA. While the ChOA algorithm is effective for simple optimization problems, it tends to struggle with complex problems, such as high-dimensional feature selection, because it often gets trapped in local optimal solutions rather than finding the global. This is primarily attributed to the limited exploration capability of ChOA in handling complex tasks. On the other hand, the SCA utilizes unique sine and cosine waves for spatial exploration and offers advantages in terms of high convergence accuracy and strong exploration capability. Therefore, this improvement aims to enhance the exploration capability of ChOA by incorporating SCA as the local search component. Specifically, we propose integrating the SCA operator into the attack process of chimps to address the limitations of the standard ChOA version.

In the SCA, the value of r2 in the sine and cosine formulas is randomly chosen from the range 0 to 2π [26], resulting in sine and cosine values ranging from −1 to 1. However, the pseudo-random nature of r2 leads to non-uniform and unpredictable values. This can result in extreme situations, such as very small values for sine or cosine in the early iterations, and very large values later on. In this case, the SCA exhibits a weak search capability in early phases and poor exploitation capability later. Therefore, in order to better combine the SCA operator with ChOA, we propose a multi-cycle iteration strategy to address the shortcomings caused by this pseudo-randomness. This strategy is achieved by designing multi-cycle iteration factor λ, and its mathematical model is as follows:

λ=2kπ⋅(tT)(11)

where k represents the number of cycles, and different values can be chosen based on the characteristics of the feature space. In this paper, k is determined to be 16. Therefore, the mathematical model for the position update of ChOA combined with the SCA operator is as follows:

X1={Xa(t)+sin⁡(λ)×a1⋅da(t),rand1<0.5Xa(t)+cos⁡(λ)×a1⋅da(t),rand1≥0.5(12)

X2={Xb(t)+sin⁡(λ)×a2⋅db(t),rand2<0.5Xb(t)+cos⁡(λ)×a2⋅db(t),rand2≥0.5(13)

X3={Xc(t)+sin⁡(λ)×a3⋅dc(t),rand3<0.5Xc(t)+cos⁡(λ)×a3⋅dc(t),rand3≥0.5(14)

X4={Xd(t)+sin⁡(λ)×a4⋅dd(t),rand4<0.5Xd(t)+cos⁡(λ)×a4⋅dd(t),rand4≥0.5(15)

X(t+1)=(X1+X2+X3+X4)/4(16)

By embedding the SCA operator during the chimp attack phase, the individual chimps in the proposed algorithm exhibit stronger search capabilities compared to the original ChOA algorithm. This is mainly attributed to the SCA operator providing a wider search space for the chimps through cosine and sine oscillations, enabling them to overlook local optima and quickly capture global optima. Specifically, when a chimp individual is satisfied with its current food source (local optima), the SCA operator drives it to explore the vicinity of the current solution with cosine and sine oscillations. This is effective for all four leaders among the chimps, and other chimps update their positions based on the locations of these four leaders. Additionally, the introduction of the multi-cycle factor ensures that during the iteration process, the search range becomes more specific, allowing individuals to continue exploring nearby small spaces while maintaining their cosine and sine oscillation states. As a result, the proposed algorithm can not only perform global search through chimp attacks but also conduct more precise local search with the probing abilities of SCA, thereby better discovering global optimal solutions. Algorithm 1 presents the pseudocode for SCChOA.

3.4 The Proposed Feature Selection Method

In this section, we introduce the proposed feature selection method. A binary process is involved in feature selection, which relies on whether a particular feature is chosen to solve a problem or not. In order for the hybrid SCChOA algorithm to be applicable for feature selection, it needs to be converted into binary format. Subsequently, the classifier KNN is combined with the binary SCChOA algorithm to form a binary hybrid wrapper feature selection algorithm. The resulting optimal solution is converted to binary 0 or 1 to select the best subset. Typically, a sigmoid function is employed for this conversion, as depicted in the following equation, where Xbest represents the optimal position at iteration number t.

X(t+1)={0,if sigmoid (Xbest) < 0.51,otherwise(17)

sigmoid(x)=11+e−10(x−0.5)(18)

The quality of the candidate solutions obtained by the proposed algorithm is evaluated using a fitness function. The fitness function is designed to minimize the size of the selected feature subset and maximize the classification accuracy of the selected learning algorithm [32]. Its calculation method is as follows:

fFS=α×(err)+β×|R||Num|(19)

The α and β are parameters that control the contribution weights of selecting the feature subset size and the classification accuracy of the selected learning algorithm. The sum of their weights is 1. err represents the classification error of the classifier used, and R represents the number of selected features out of the total number of features (Num) in the dataset.

Hence, the flowchart of the proposed feature selection method is shown as Fig. 1.

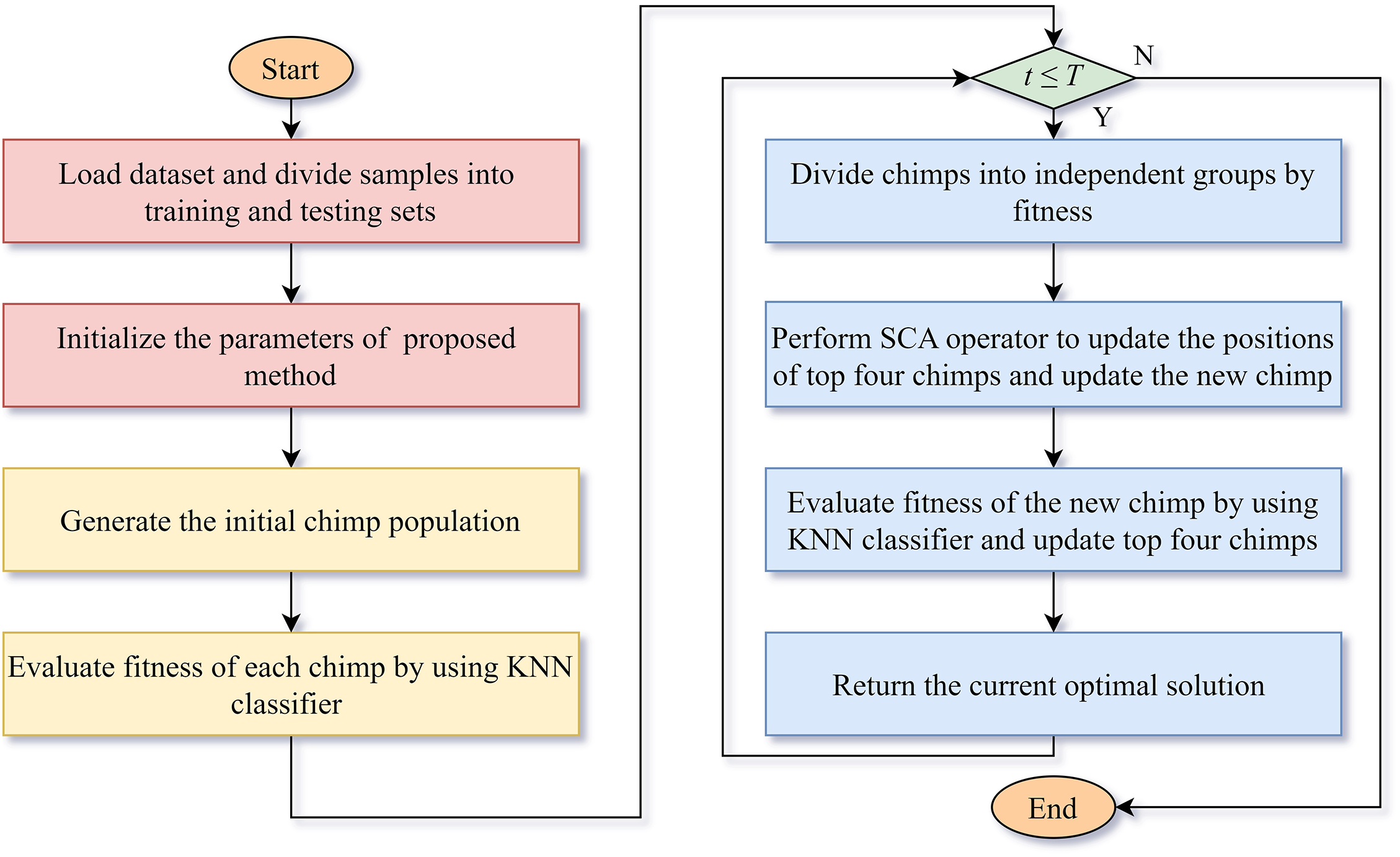
Figure 1: The flowchart of proposed feature selection method

4  Experimental Results

In this section, we discussed the experimental setup and presented and discussed the experimental results.

4.1 Description of the Datasets

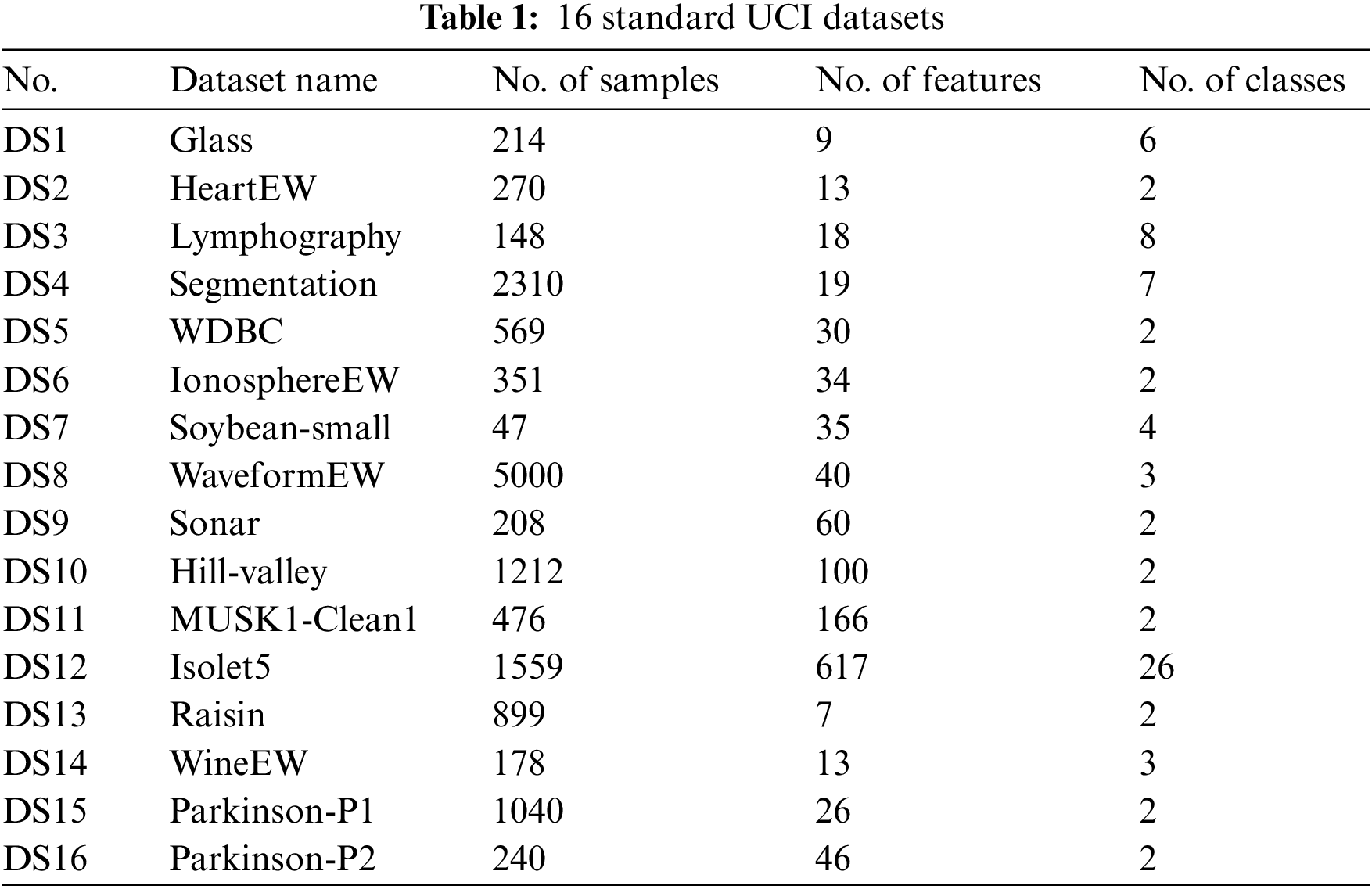
To analyze the performance of SCChOA, we conducted experiments using 16 standard UCI datasets [41]. These datasets are sourced from various domains, which demonstrates the versatility of the proposed method. Table 1 presents fundamental details about the datasets. The inclusion of datasets with varying numbers of features and instances enables us to assess the effectiveness of the proposed approach.

4.2 Experimental Configurations

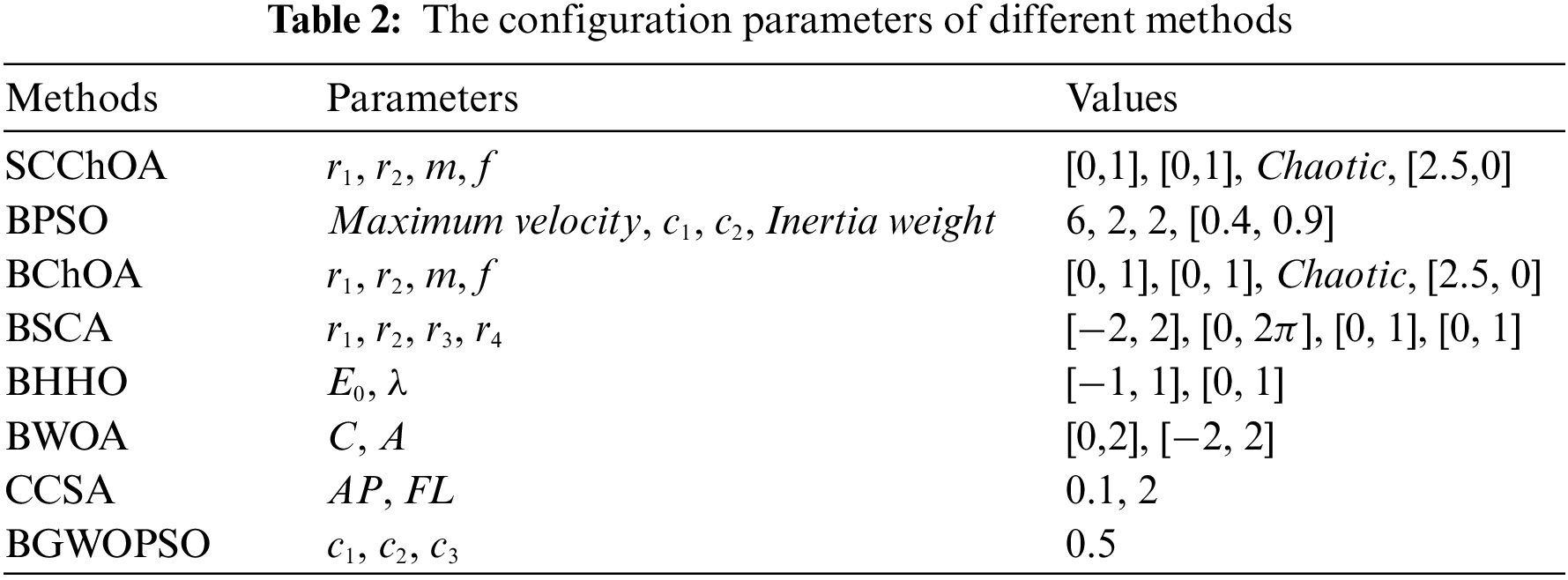
The proposed SCChOA method is compared with seven advanced metaheuristic methods mentioned in the literature. These methods include BPSO [28], BChOA [22], BSCA [26], BHHO [42], BWOA [32], CCSA [43], and BGWOPSO [34]. The parameters of the comparison algorithms can be found in Table 2. To ensure a fair evaluation, the population size and number of iterations are consistently set to 20 and 100, respectively. To assess the quality of the generated solutions, the KNN classifier is used as the wrapper framework, configured with K = 5. To further enhance the reliability of the results, k-fold cross-validation with k = 10 is employed to train and test the classifier. For each optimizer, twenty independent runs are conducted to account for variability. The simulation experiments are performed on a computer equipped with an Intel(R) Core(TM) i5-7200U CPU operating at a frequency of 2.50 GHz and 12 GB of memory. Meanwhile, MATLAB 2019b is utilized as the software platform for conducting the experiments.

4.3 Evaluation Criteria

In this paper, four well-known metrics are used to evaluate the proposed method. These four metrics are as follows:

(1) Average fitness value: The average fitness value represents the average of the fitness values over all the runs.

Average fitness=1tmax∑i=1tmaxFiti(20)

here tmax denotes the maximum number of runs and Fiti denotes the value of the best fitness of the i-th individual. The calculation of Fiti can be referred to as Eq. (19).

(2) Average classification accuracy: The average classification accuracy represents the average of the classification accuracies over all the runs.

Average accuracy=1tmax∑i=1tmaxAcci(21)

where Acci represents the classification accuracy of the classifier in the i-th iteration.

(3) Average feature selection number: The average number of selected features represents the average of the number of selected features over all the runs.

Average feature number(FN)=1tmax∑i=1tmaxlen(BSi)(22)

where len(BSi) represents the number of selected features in the best solution of the i-th feature selection. The smaller the value of FN, the more capable the algorithm is in reducing the number of features in the dataset.

(4) Average running time (seconds): The average running time is calculated by taking the average of the running times of all the runs.

Average running time=1tmax∑i=1tmaxtimei(23)

here, timei represents the running time of the i-th feature selection run.

4.4 Evaluation Results

In this section, we compare and analyze the proposed method and other methods based on the four metrics mentioned above. Moreover, we conduct a detailed analysis of the results and perform statistical analysis using the Wilcoxon’s rank-sum test.

Table 3 displays the average fitness values of SCChOA and other competing methods for each selected dataset. It is evident that SCChOA achieves the best average fitness values for 14 datasets. While CCSA and BGWOPSO obtain the best fitness values for DS5 and DS10, respectively, their performance on other datasets is generally poor. In summary, SCChOA exhibits the lowest overall average fitness value of 0.1313 across all methods and datasets. Furthermore, Fig. 2 illustrates that SCChOA has the best Friedman average fitness ranking at 1.47, indicating its competitiveness in minimizing the fitness value. In other words, the SCChOA can effectively streamline the number of features to be selected while minimizing the classification error.

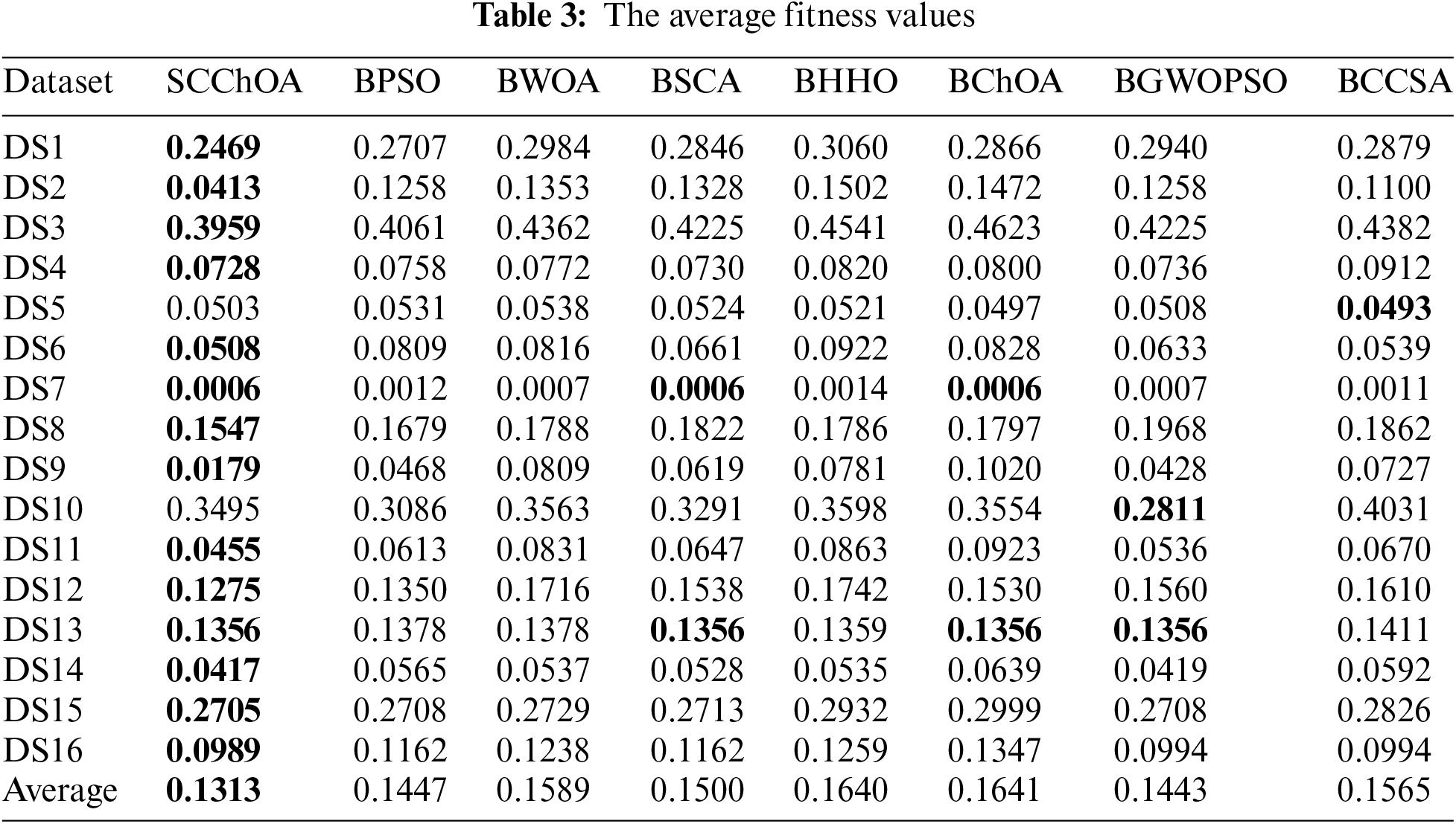
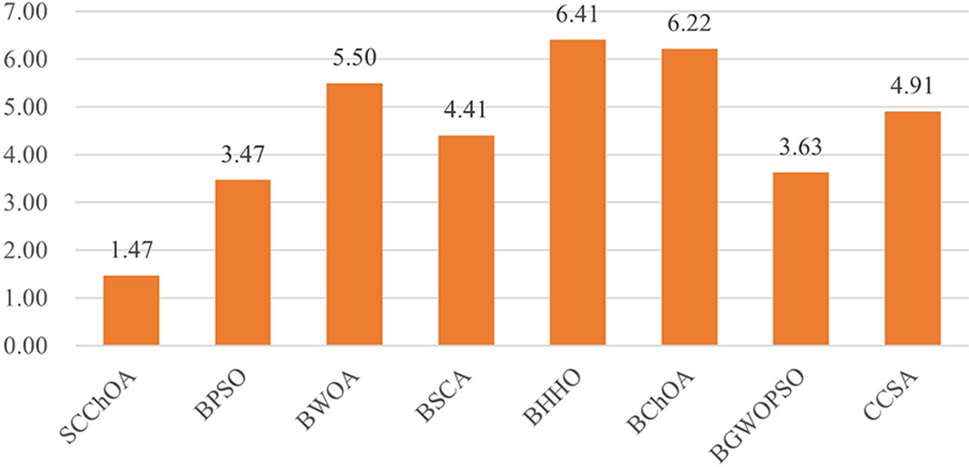
Figure 2: The friedman average fitness value ranking

Table 4 presents a comparison of the SCChOA method with other methods in terms of classification accuracy. Among the 16 datasets analyzed, SCChOA achieves the highest classification accuracy in 14 of them. In contrast, the BGWOPSO and CCSA methods only obtain the highest classification accuracy in 2 datasets, while others obtain worse classification accuracy. Notably, all methods achieve 100% classification accuracy on dataset DS7, which can be attributed to the smaller number of individuals in that dataset, making the classification task less challenging. However, as the number of features and instances increases, the performance of most algorithms tends to decline. When considering more complex high-dimensional datasets, it is evident that SCChOA consistently maintains a high level of classification accuracy, surpassing other algorithms and securing the top ranking in classification accuracy for multiple high-dimensional datasets. This underscores the strong competitiveness of SCChOA in addressing complex high-dimensional feature selection classification problems. Upon evaluating the classification accuracy results from the 16 datasets, the average classification accuracy for all algorithms is computed. SCChOA achieves the highest average classification accuracy of 0.8767. The following three algorithms, namely BPSO, BPSOGWO, and BSCA, closely follow with average classification accuracies of 0.8598, 0.8574, and 0.8519, respectively. Furthermore, the Friedman average ranking of classification accuracy as Fig. 3 reveals that SCChOA has an average ranking of 1.47, placing it in the first position. This further emphasizes the effectiveness of SCChOA in feature selection for classification tasks.

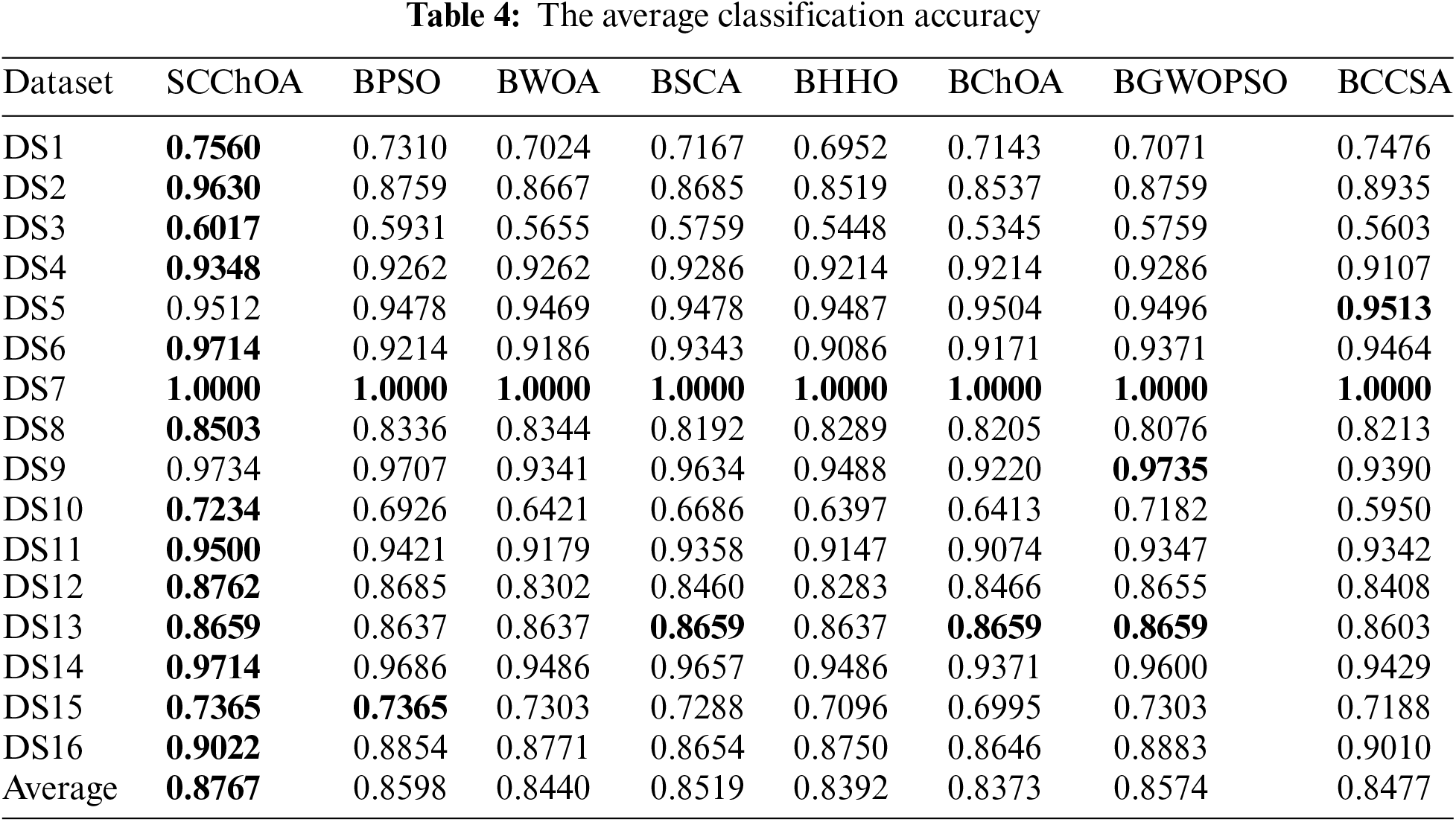
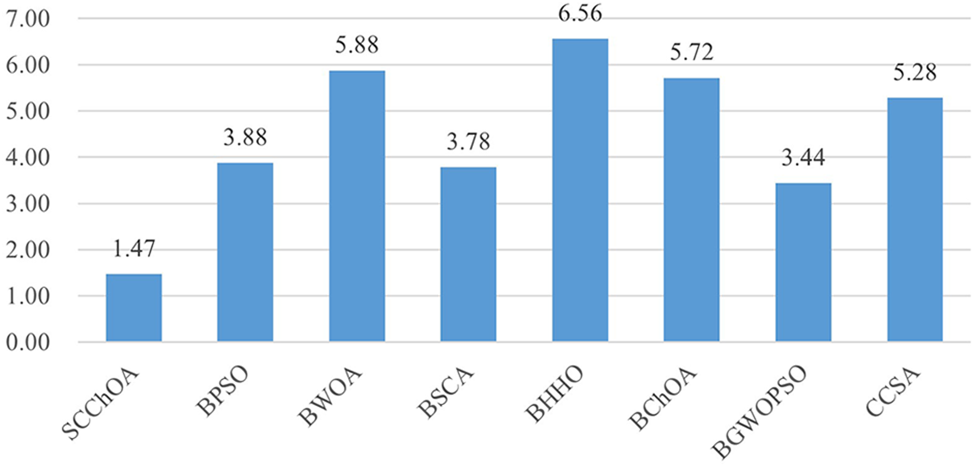
Figure 3: The Friedman average classification accuracy ranking

In terms of the number of selected features, Table 5 presents a comparison of different methods on 16 selected UCI datasets. From the results in Table 5, it can be observed that the proposed algorithm has an average number of selected features of 19.6 and ranks second among the evaluated algorithms. Additionally, SCChOA achieved the minimum number of selected features in 5 datasets, which is not the best among the methods. BChOA and BSCA achieved the minimum number of selected features in 7 and 8 datasets, respectively. However, both of these methods did not perform well in terms of classification accuracy and fitness value ranking. This indicates that the primary objective of feature selection is to ensure higher classification accuracy, followed by reducing the number of features. Based on this observation, SCChOA demonstrates strong competitiveness in solving feature selection problems as it is able to maintain high classification accuracy while effectively reducing the number of features.

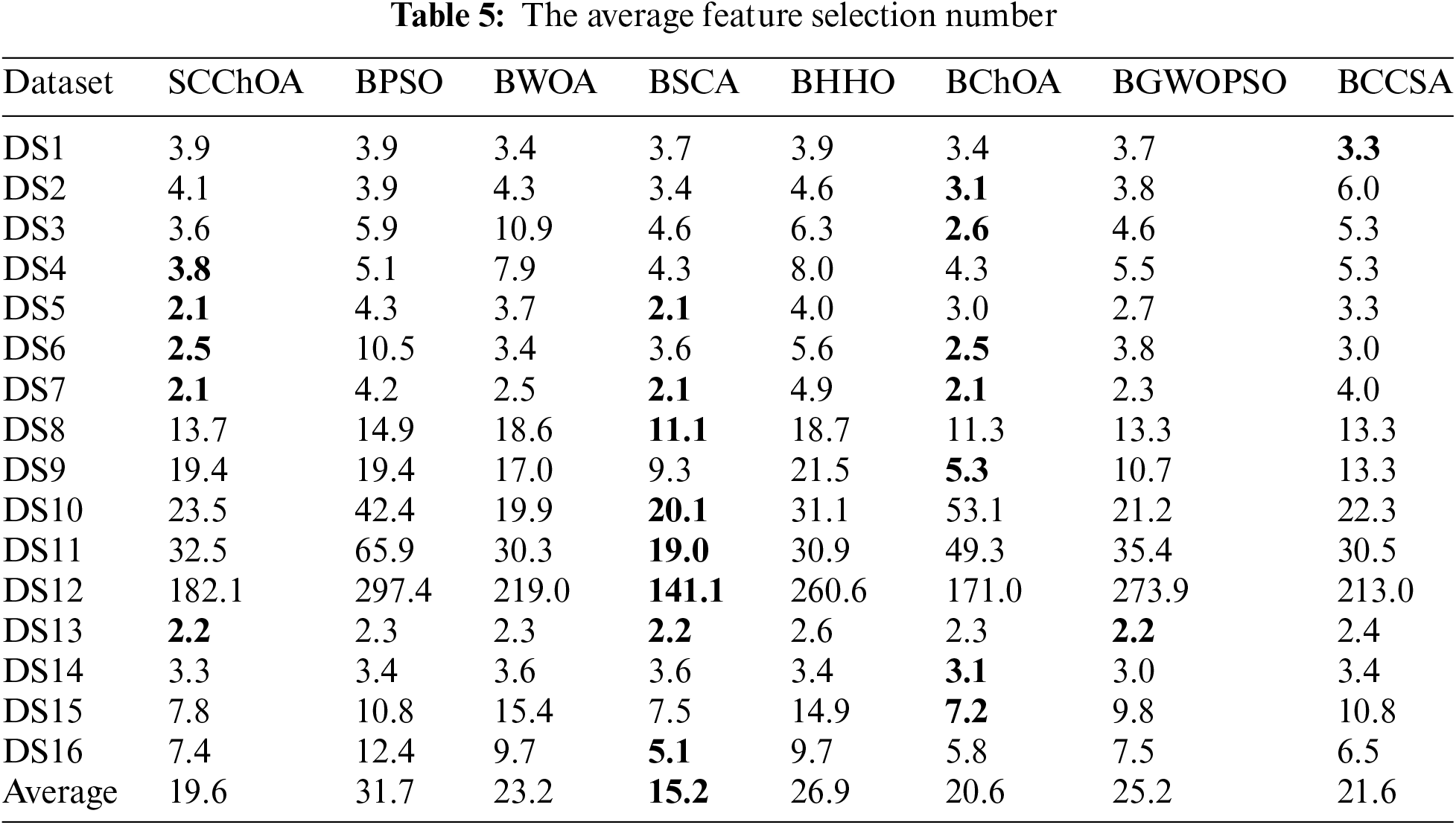
On the other hand, Table 6 presents a comparison of the actual running times of different methods on all datasets. It can be observed that SCChOA shows comparable average time costs to BSCA and BChOA, without exhibiting higher time expenses. Overall, in comparison to other methods, SCChOA also demonstrates a relatively faster running speed compared to the majority of the compared algorithms. This suggests that SCChOA can achieve satisfactory performance in feature selection while also offering certain advantages in terms of time costs.

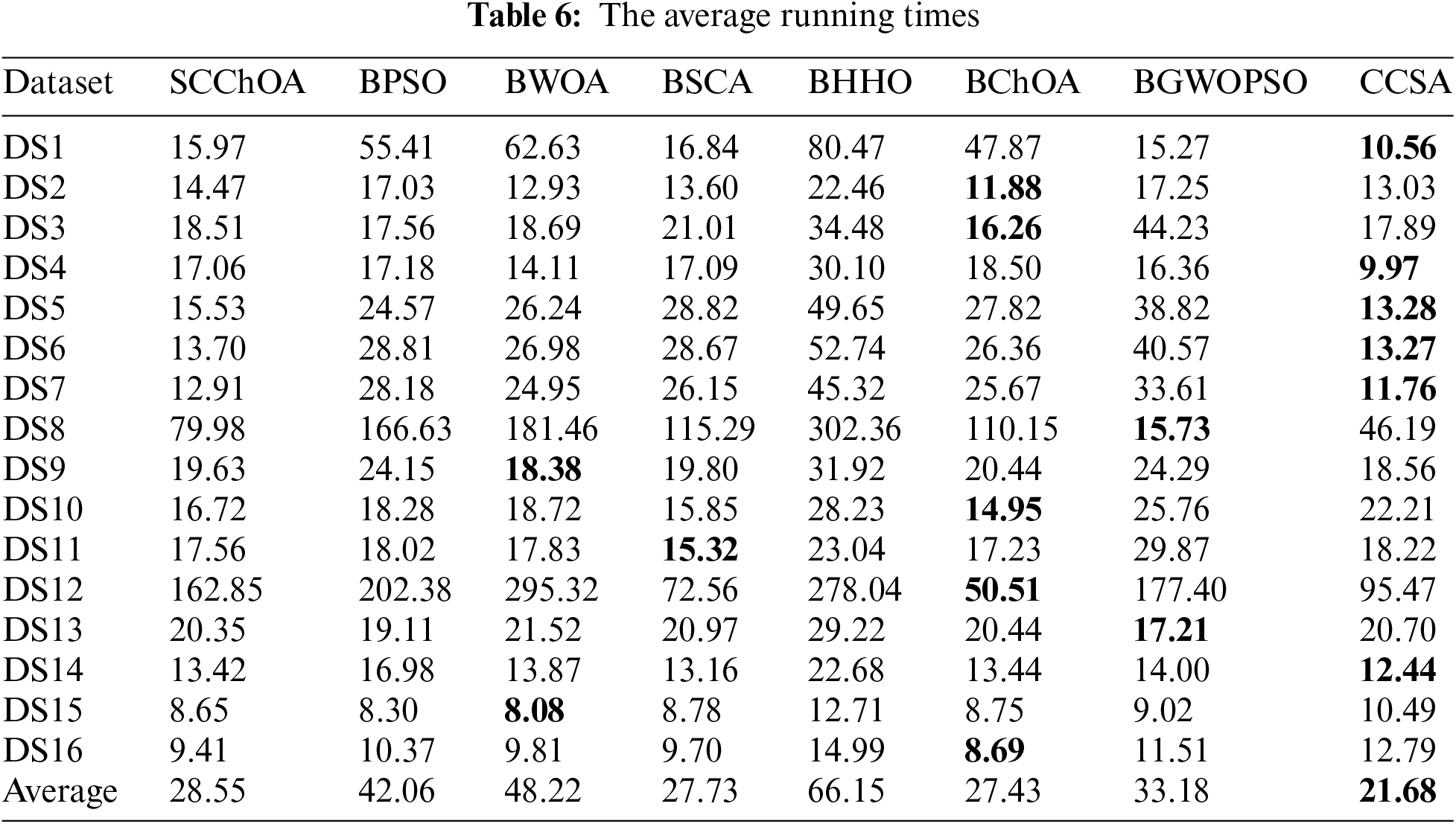
Based on the aforementioned four indicators, the proposed method outperforms all other compared methods in terms of average fitness value and average classification accuracy, which are the two most important indicators. Moreover, the proposed method also exhibits certain advantages in terms of average number of the selected features and the average runtime. These results can be attributed to the embedded SCA operator, which provides additional search possibilities for individual gorillas during the search process. In situations where a chimp individual becomes trapped in a local optimum, the SCA operator assists in escaping from this local value, enabling the chimp to further explore superior solutions by avoiding complacency with the current food source. Furthermore, the proposed hybrid algorithm showcases a similar average runtime compared to the original ChOA and SCA without incurring any additional time overhead. This is due to the fact that the embedded SCA operator does not introduce any additional time complexity, thereby ensuring simplicity and efficiency in the algorithm.

To provide a more intuitive demonstration of SCChOA’s effectiveness in tackling the feature selection problem, Fig. 4 shows a visualized comparison showcasing the objective function fitness values obtained by various methods across a set of representative datasets. Notably, SCChOA consistently achieves the best results when compared to other methods, thereby emphasizing its superiority and effectiveness in addressing the feature selection problem.

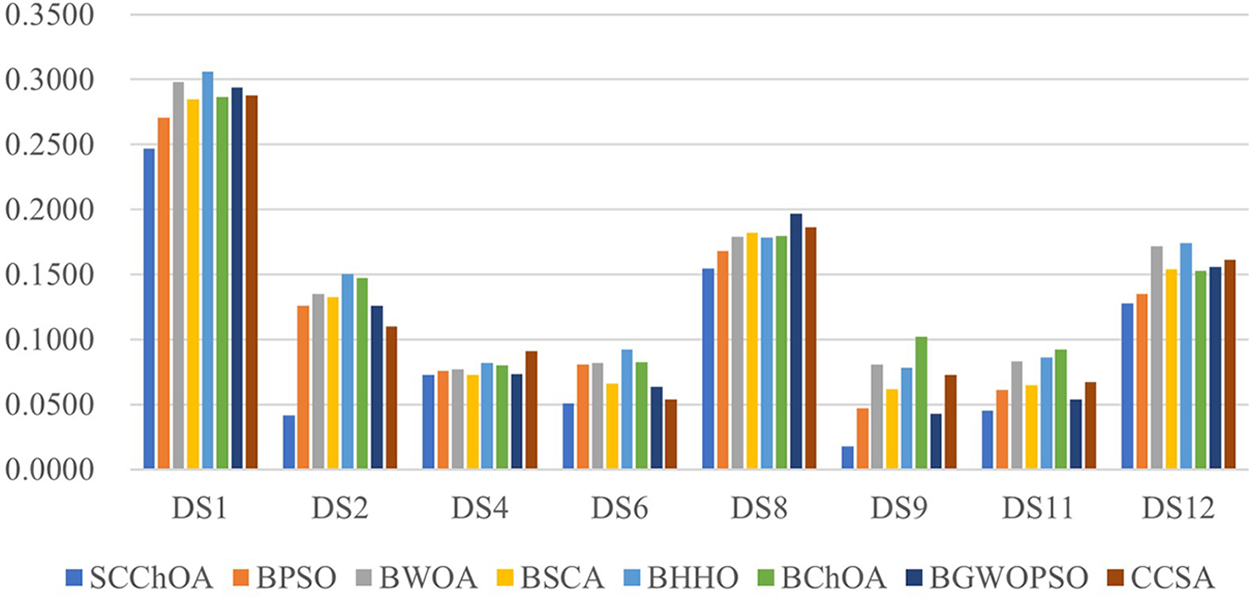
Figure 4: The visualized comparison of fitness values

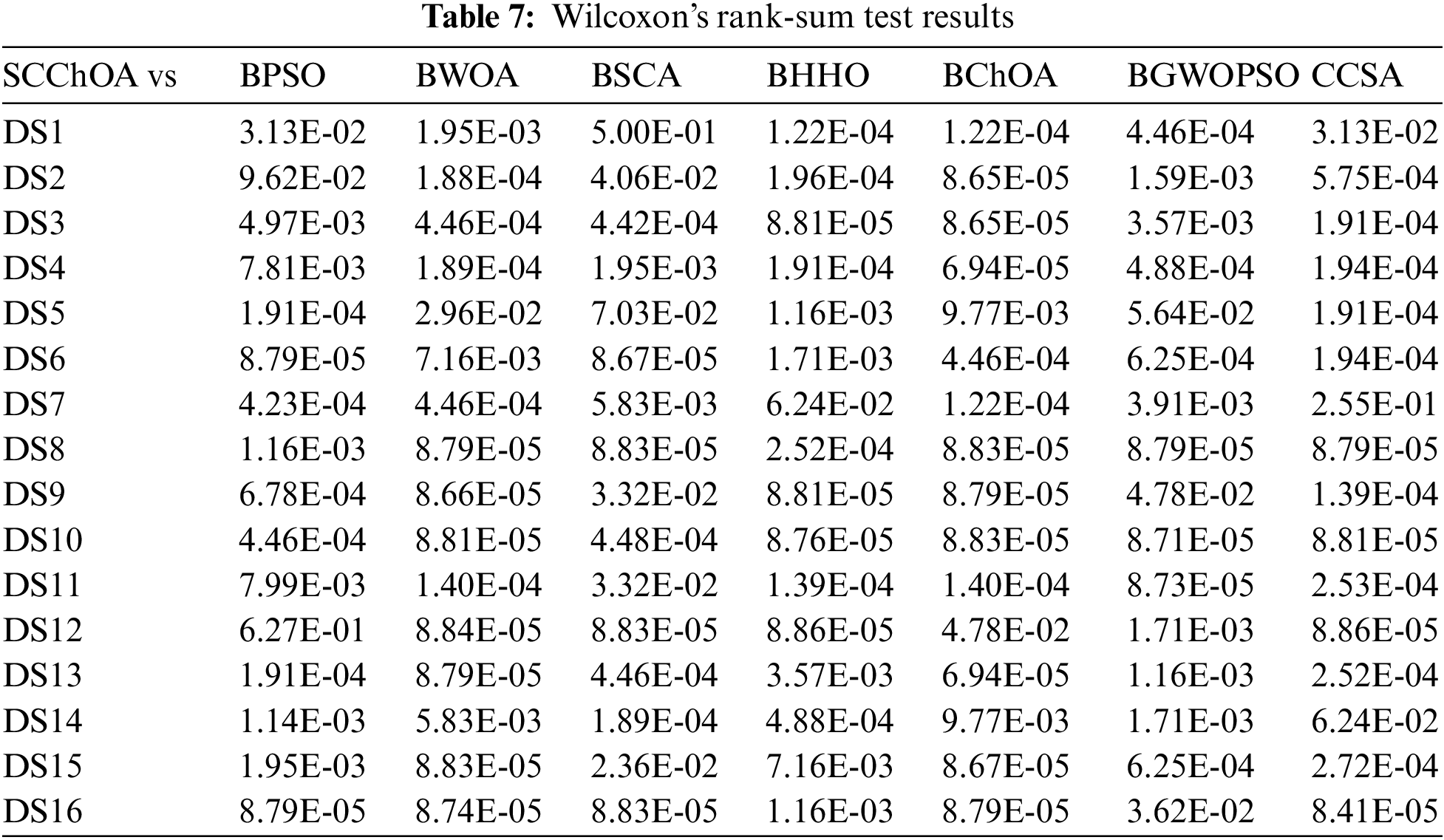
To determine the statistical significance of the previously obtained results, a Wilcoxon’s rank-sum test is conducted on the experimental data. The significance level chosen for the test is 5%. The results of the test are displayed in Table 7. This particular test evaluates the hypothesis for two independent samples and produces a p-value as the outcome. The null hypothesis states that there is no significant difference between the two samples, and if the p-value is greater than 0.05, it raises doubts about the validity of the null hypothesis. The statistical test results reveal that for almost all datasets, the p-values are below 5%. Overall, the performance of SCChOA demonstrates significant distinctions when compared to the other seven algorithms, suggesting that SCChOA is more effective than the other comparison methods.

5  Conclusions

This paper presents the SCChOA, a novel hybrid algorithm for feature selection problems. This method combines the characteristics of the SCA and ChOA to effectively address feature selection challenges. In order to assess the performance of the proposed method, it is evaluated on 16 UCI datasets using four evaluation metrics: average fitness value, average classification accuracy, average feature selection number, and average running time. The SCChOA is compared with seven state-of-the-art metaheuristic-based feature selection methods, including BPSO, BWOA, BSCA, BHHO, BChOA, BGWOPSO, and CCSA. The results indicate that SCChOA achieves the best results in terms of average fitness value and average classification accuracy. The average fitness value and average classification accuracy are 0.1313 and 0.8767, respectively. Furthermore, this method exhibits satisfactory performance with regards to average feature selection count and average running time. These results demonstrate the high competitiveness of SCChOA in addressing feature selection problems. Additionally, statistical tests confirmed the algorithm’s significant effectiveness.

In our future research, we aim to explore the potential of SCChOA in feature selection problems across diverse domains, such as surface defect classification in industrial steel belts and feature selection in real medical datasets like breast cancer datasets. This exploration holds the promise of improving quality control processes in industrial environments and contributing to disease diagnosis and treatment in the medical field. Additionally, investigating the potential of SCChOA in workshop scheduling and wind power prediction is also a promising direction. These research endeavors are expected to uncover practical applications of SCChOA in various domains or problems.

Acknowledgement: The authors wish to acknowledge the editor and anonymous reviewers for their insightful comments, which have improved the quality of this publication.

Funding Statement: This work was in part supported by the Key Research and Development Project of Hubei Province (No. 2023BAB094), the Key Project of Science and Technology Research Program of Hubei Educational Committee (No. D20211402), and the Teaching Research Project of Hubei University of Technology (No. 2020099).

Author Contributions: Study conception and design: Shanshan Wang, Quan Yuan; Data collection: Weiwei Tan, Tengfei Yang and Liang Zeng; Analysis and interpretation of results: all authors; Draft manuscript preparation: Quan Yuan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data and materials are available in UCI machine learning repository.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. W. Qian, J. Huang, F. Xu, W. Shu and W. Ding, “A survey on multi-label feature selection from perspectives of label fusion,” Information Fusion, vol. 100, pp. 101948, 2023. [Google Scholar]

2. E. Alhenawi, R. Al-Sayyed, A. Hudaib and S. Mirjalili, “Feature selection methods on gene expression microarray data for cancer classification: A systematic review,” Computers in Biology and Medicine, vol. 140, pp. 105051, 2022. [Google Scholar] [PubMed]

3. T. Dokeroglu, A. Deniz and H. E. Kiziloz, “A comprehensive survey on recent metaheuristics for feature selection,” Neurocomputing, vol. 494, pp. 269–296, 2022. [Google Scholar]

4. F. Karimi, M. B. Dowlatshahi and A. Hashemi, “SemiACO: A semi-supervised feature selection based on ant colony optimization,” Expert Systems with Applications, vol. 214, pp. 119130, 2023. [Google Scholar]

5. F. Masood, J. Masood, H. Zahir, K. Driss, N. Mehmood et al., “Novel approach to evaluate classification algorithms and feature selection filter algorithms using medical data,” Journal of Computational and Cognitive Engineering, vol. 2, no. 1, pp. 57–67, 2023. [Google Scholar]

6. N. Karlupia and P. Abrol, “Wrapper-based optimized feature selection using nature-inspired algorithms,” Neural Computing and Applications, vol. 35, no. 17, pp. 12675–12689, 2023. [Google Scholar]

7. H. Liu, M. Zhou and Q. Liu, “An embedded feature selection method for imbalanced data classification,” IEEE/CAA Journal of Automatica Sinica, vol. 6, no. 3, pp. 703–715, 2019. [Google Scholar]

8. C. W. Chen, Y. H. Tsai, F. R. Chang and W. C. Lin, “Ensemble feature selection in medical datasets: Combining filter, wrapper, and embedded feature selection results,” Expert Systems, vol. 37, no. 5, pp. e12553, 2020. [Google Scholar]

9. M. Dash and H. Liu, “Feature selection for classification,” Intelligent Data Analysis, vol. 1, no. 1–4, pp. 131–156, 1997. [Google Scholar]

10. B. Xue, M. Zhang, W. N. Browne and X. Yao, “A survey on evolutionary computation approaches to feature selection,” IEEE Transactions on Evolutionary Computation, vol. 20, no. 4, pp. 606–626, 2015. [Google Scholar]

11. T. Dokeroglu, E. Sevinc, T. Kucukyilmaz and A. Cosar, “A survey on new generation metaheuristic algorithms,” Computers & Industrial Engineering, vol. 137, pp. 106040, 2019. [Google Scholar]

12. A. Lambora, K. Gupta and K. Chopra, “Genetic algorithm-A literature review,” in 2019 Int. Conf. on Machine Learning, Big Data, Cloud and Parallel Computing (COMITCon), Faridabad, India, pp. 380–384, 2019. [Google Scholar]

13. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. of ICNN’95-Int. Conf. on Neural Networks, Perth, WA, Australia, IEEE, pp. 1942–1948, 1995. [Google Scholar]

14. M. Dorigo and G. di Caro, “Ant colony optimization: A new meta-heuristic,” in Proc. of the 1999 Cong. on Evolutionary Computation-CEC99, Washington DC, USA, pp. 1470–1477, 1999. [Google Scholar]

15. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67, 2016. [Google Scholar]

16. C. Zhong, G. Li and Z. Meng, “Beluga whale optimization: A novel nature-inspired metaheuristic algorithm,” Knowledge-Based Systems, vol. 251, pp. 109215, 2022. [Google Scholar]

17. L. Wang, Q. Cao, Z. Zhang, S. Mirjalili and W. Zhao, “Artificial rabbits optimization: A new bio-inspired meta-heuristic algorithm for solving engineering optimization problems,” Engineering Applications of Artificial Intelligence, vol. 114, pp. 105082, 2022. [Google Scholar]

18. S. Kirkpatrick, C. D. Gelatt Jr and M. P. Vecchi, “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, 1983. [Google Scholar] [PubMed]

19. A. Faramarzi, M. Heidarinejad, B. Stephens and S. Mirjalili, “Equilibrium optimizer: A novel optimization algorithm,” Knowledge-Based Systems, vol. 191, pp. 105190, 2020. [Google Scholar]

20. R. V. Rao, V. J. Savsani and D. Vakharia, “Teaching-learning-based optimization: A novel method for constrained mechanical design optimization problems,” Computer-Aided Design, vol. 43, no. 3, pp. 303–315, 2011. [Google Scholar]

21. E. Atashpaz-Gargari and C. Lucas, “Imperialist competitive algorithm: An algorithm for optimization inspired by imperialistic competition,” in 2007 IEEE Cong. on Evolutionary Computation, Singapore, pp. 4661–4667, 2007. [Google Scholar]

22. M. Khishe and M. R. Mosavi, “Chimp optimization algorithm,” Expert Systems with Applications, vol. 149, pp. 113338, 2020. [Google Scholar]

23. G. Dhiman, “SSC: A hybrid nature-inspired meta-heuristic optimization algorithm for engineering applications,” Knowledge-Based Systems, vol. 222, pp. 106926, 2021. [Google Scholar]

24. H. Jia, K. Sun, W. Zhang and X. Leng, “An enhanced chimp optimization algorithm for continuous optimization domains,” Complex & Intelligent Systems, vol. 8, no. 1, pp. 65–82, 2022. [Google Scholar]

25. G. Hu, W. Dou, X. Wang and M. Abbas, “An enhanced chimp optimization algorithm for optimal degree reduction of Said-Ball curves,” Mathematics and Computers in Simulation, vol. 197, pp. 207–252, 2022. [Google Scholar]

26. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, pp. 120–133, 2016. [Google Scholar]

27. J. Yang and V. Honavar, “Feature subset selection using a genetic algorithm,” IEEE Intelligent Systems and their Applications, vol. 13, no. 2, pp. 44–49, 1998. [Google Scholar]

28. J. Kennedy and R. C. Eberhart, “A discrete binary version of the particle swarm algorithm,” in 1997 IEEE Int. Conf. on Systems, Man, and Cybernetics. Computational Cybernetics and Simulation, Orlando, FL, USA, pp. 4104–4108, 1997. [Google Scholar]

29. X. F. Song, Y. Zhang, D. W. Gong and X. Z. Gao, “A fast hybrid feature selection based on correlation-guided clustering and particle swarm optimization for high-dimensional data,” IEEE Transactions on Cybernetics, vol. 52, no. 9, pp. 9573–9586, 2022. [Google Scholar] [PubMed]

30. X. Song, Y. Zhang, D. Gong and X. Sun, “Feature selection using bare-bones particle swarm optimization with mutual information,” Pattern Recognition, vol. 112, pp. 107804, 2021. [Google Scholar]

31. Y. Hu, Y. Zhang and D. Gong, “Multiobjective particle swarm optimization for feature selection with fuzzy cost,” IEEE Transactions on Cybernetics, vol. 51, no. 2, pp. 874–888, 2021. [Google Scholar] [PubMed]

32. M. Mafarja and S. Mirjalili, “Whale optimization approaches for wrapper feature selection,” Applied Soft Computing, vol. 62, pp. 441–453, 2018. [Google Scholar]

33. Z. Beheshti, “BMPA-TVSinV: A binary marine predators algorithm using time-varying sine and V-shaped transfer functions for wrapper-based feature selection,” Knowledge-Based Systems, vol. 252, pp. 109446, 2022. [Google Scholar]

34. Q. Al-Tashi, S. J. Abdul Kadir, H. M. Rais, S. Mirjalili and H. Alhussian, “Binary optimization using hybrid grey wolf optimization for feature selection,” IEEE Access, vol. 7, pp. 39496–39508, 2019. [Google Scholar]

35. L. Fang and X. Liang, “A novel method based on nonlinear binary grasshopper whale optimization algorithm for feature selection,” Journal of Bionic Engineering, vol. 20, no. 1, pp. 237–252, 2023. [Google Scholar] [PubMed]

36. D. Khafaga, E. S. El-kenawy, F. Karim, M. Abotaleb, A. Ibrahim et al., “Hybrid dipper throated and grey wolf optimization for feature selection applied to life benchmark datasets,” Computers Materials & Continua, vol. 74, no. 2, pp. 4531–4545, 2022. [Google Scholar]

37. M. Alzaqebah, M. Alsmadi, S. Jawarneh, J. Alqurni, M. Tayfour et al., “Improved whale optimization with local-search method for feature selection,” Computers, Materials & Continua, vol. 75, no. 1, pp. 1371–1389, 2023. [Google Scholar]

38. M. S. Uzer and O. Inan, “A novel feature selection using binary hybrid improved whale optimization algorithm,” The Journal of Supercomputing, vol. 79, no. 9, pp. 10020–10045, 2023. [Google Scholar]

39. E. Pashaei and E. Pashaei, “Hybrid binary COOT algorithm with simulated annealing for feature selection in high-dimensional microarray data,” Neural Computing and Applications, vol. 35, no. 1, pp. 353–374, 2023. [Google Scholar]

40. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 67–82, 1997. [Google Scholar]

41. A. Frank, “UCI machine learning repository,” 2010. [Online]. Available: http://archive. ics. uci. edu/ml (accessed on 01/10/2022) [Google Scholar]

42. T. Thaher, A. A. Heidari, M. Mafarja, J. S. Dong and S. Mirjalili, “Binary harris hawks optimizer for high-dimensional, low sample size feature selection,” in Evolutionary Machine Learning Techniques: Algorithms and Applications, Singapore: Springer, pp. 251–272, 2020. [Google Scholar]

43. G. I. Sayed, A. E. Hassanien and A. T. Azar, “Feature selection via a novel chaotic crow search algorithm,” Neural Computing and Applications, vol. 31, no. 1, pp. 171–188, 2019. [Google Scholar]