MF2-DMTD: A Formalism and Game-Based Reasoning Framework for Optimized Drone-Type Moving Target Defense

1  Introduction

In recent years, as the scope of modernization coverage expands in embedded platforms, heterogeneous wireless systems such as unmanned aircraft and sensors are being rapidly applicated across mission-critical system domains like the battlefield, where both the safety and cybersecurity of the organization should be continuously guaranteed. However, as the existing closed communication regulations remain, although the composition of a dedicated countermeasure is not standardized, the issue of cyber uncertainty, which is attacker-dominant owing to the inherently vulnerable surfaces of applied embedded systems, is also on the rise [1–4]. Thus, to satisfy these security requirements, the cybersecurity research community affiliated with national defense and critical systems has fully adopted MTD [5,6]. MTD is a proactive cybersecurity technology that asymmetrically maximizes defense superiority and attack complexity according to a cyber mobility-based mutation to minimize the effects of illegal compromises.

However, most existing MTD studies for the replacement of conventional security have concentrated on the unique specifications of wired networks and related sub-protocols with low volatility and relatively easy employment of security resources, such as smart grids, smart factories, and industrial control systems (ICS). That is, only a few official studies have independently reduced the potential vulnerabilities [7,8] of wireless drones with attributes [9] that are extremely unfavorable for rapid operation (i.e., passivity and heterogeneity, decision-making dependency, and environmental hostility). In addition, related wireless cases also only maximized cyber agility [10] based on the micro-air vehicle link (MAVLink) protocol standard. And resilient definitions and verifications to ensure the availability of unmanned wireless drone platforms as mission-critical systems in reported research have not been also formalized with MTD.

Accordingly, when the configuration of the MTD specialized to ensure high levels of both cyber agility and resiliency [11,12] of wireless drones is not preemptively accompanied, it will not only be impossible to protect the cybersecurity vulnerabilities of the unmanned drone, but it will also be impossible to continuously guarantee the operational stability of the target drone. To alleviate these limitations, it is necessary to achieve proactive defense based on active avoidance and to specify the dedicated MTD [13], which can secure cyber resilience based on both the internal and external structures of the rugged drone, detailed attack surface [14], and recognized vulnerabilities. And, to calculate the quantitative defense performance of the MTD for each proposition based on the formal specifications of an unmanned drone, formal verification with added mathematical proofs should be also performed in parallel. Thus, this study aims to minimize the compromise success rate of attackers by mutating unique fingerprint information groups with drone-type MTD related to the internal functions of unmanned drones and external communication. This study also proposes MF2-DMTD, a formal framework with model-checking-based formalism and an iterative zero-sum equilibrium logic-based competitive game, to simulate and validate an optimized drone-type MTD that adaptively determines the calculated mutation periods through decision trees with automata and the Markov decision process (MDP) [15]. Finally, as a formal verification according to the specifications in MF2-DMTD, the trade-off optimization of the drone-type MTD is achieved by further plotting the normalized Pareto frontier with MIQCP [16], detailed constraints, and multi-objective genetic optimization (MOGO) [17].

The main contributions of this study are as follows:

■   First, the deceptive defense efficiency (cyber agility), functional continuity (cyber resilience), and interoperability of drone-type MTD, which have not been considered in previous MTD studies from the research domain perspective, can be specified and evaluated in terms of threat modeling.

■   Second, through this study, the zero-sum game-based combat model can more realistically assume a competitive relationship in cyberspace related to the structural/functional correlation of drones. To embed cyber deception into this model, the decision-making flow for each actor can be standardized so that it is not highly dependent on prior knowledge such as the attacker’s ability, motivation, and kill chain for drone vulnerability. This model can be also additionally configured to force an inferior judgment that was not optimized based on subjective beliefs, differences of information and view, and misperception established according to information uncertainty.

■   Third, formal specifications for wireless unmanned drone threat modeling can be achieved by structuring conceptualized two decision trees based on the priced-timed Markov decision process (PTMDP) [18] according to automata states such as vulnerabilities, threats, and countermeasures.

■   Fourth, through zero-sum game logic based on perfect Bayesian Nash equilibrium (PBNE) [19] and Bayesian Stochastic Stackelberg (BSS) [20], and formalism embedded with Uppaal Stratego [21], the performance of drone-type MTD can be verified while achieving Pareto optimization.

■   Fifth, based on the analyzed optimal results of drone-type MTD’s performance, along with the formal specification and verification, the adaptive configuration of the operational strategy considering both the cyber agility and resiliency of the unmanned drone placed in the mission-critical system domain can be advanced in the form of an actual tactical prototype.

The remainder of this paper is organized as follows. Chapter 2 examines and analyzes previous research cases related to the existing MTD. Chapter 3 presents MF2-DMTD, which is a formal framework that additionally specifies internal and external drone threat modeling that reflects both transitivity and causality as a decision tree structure. In addition, the competition logic related to the zero-sum game is determined using regularized equations. Chapter 4 derives the drone-type MTD performance inference results owing to MIQCP and multi-objective genetic optimization in the form of Pareto frontier, and performs sensitivity analysis. Chapter 5 discusses the results. Finally, Chapter 6 concludes the study.

2  Related Works

Here, this section classifies studies that served as major inspirations when proposing the MF2-DMTD.

2.1 Background of MTD and Conceptual Limitations

Since 2011, “Trustworthy Cyberspace: Strategic Plan for The Federal Cybersecurity Research and Development Program” [22], MTD has emerged as a key deceptive security technology that can effectively replace existing conventional security based on the great interest of various cybersecurity research communities in critical systems and national defense. However, most of the reported previous studies on MTD were limited to performing performance evaluations only for heterogeneous platforms placed in stable wired networks, or limited the design of software-defined network (SDN)-based testbeds virtualized as controllers and testing them with detailed communication protocol standards [23]. Related cases of wireless communication have also been reported as limited simulations focusing only on the variation in the radio frequency (RF)-based received signal strength indicator (RSSI) [24]. In addition, studies that determined and verified lightweight MTD sequences for embedded domains mainly studied only the Internet of Things (IoT), which is characterized by the uniqueness of an arbitrary domain [25], such as industrial IoT (IIoT) and Internet-of-Vehicles (IoV). That is, the specification and evaluation of maneuvering platforms that maximize mobility and heterogeneity owing to six degrees of freedom (6DOF), such as drones, and the optimization of trade-offs to maintain seamless availability are insufficient [26].

Accordingly, to solve all limitations of previous studies, formal specifications based on formalism that considers all the internal/external configurations of drones, authorized vulnerabilities, and countermeasure strategies are required. In addition, formal verification of security and availability according to the MTD application should be additionally preempted as optimization owing to iterative game simulation. Thus, to research the trade-off between the drone-type MTD optimized based on formalism and repetitive games, and to receive differentiated inspiration, this study analyzes studies preceded by game theory or formalism.

2.2 Analysis of the Existing MTD with Game Theory

The key to previous studies that evaluated MTD performance using game theory was to optimize reward, utility, and effort to achieve imperfect goals based on prior knowledge possessed by each competing cyber actor, such as attack surfaces, vulnerable points, and kill chain steps. That is, the optimization of MTD is calculated in the direction of minimizing the attacker’s advantage by providing responsiveness and adaptability to the mutation mechanism, regularizing the overall parameters for the mutation period, mutation target, and mutation sampling to maximize the expected gain of the defending actor, or quantitatively introducing thresholds that detect the loss of initiative according to system faults and failures due to an attacker’s compromise. Representative examples include the general game-theoretic literature based on Nash theory, Stackelberg game-theoretic literature based on Bayes’ theorem and Stackelberg’s solution, and stochastic game-theoretic literature based on probabilistic transitions.

2.2.1 General Game Theoretic Literature

Here, this subsection describes previous MTD studies by adopting general game theory based on the Nash equilibrium. Zhu et al. [27] first demonstrated a trade-off between enhanced security and reduced functional availability of MTD-applied proactive defense actors by determining mathematical game metrics and parameters related to the MTD principle and quantitatively simulating them in the form of a two-player game. Ge et al. [28] simulated an incentive-compatible MTD game framework based on migration-type communication mapping to continuously provide the stability of organization services to legitimate users, even within a wired topology with MTD applied, and formalize proactive agility elements that ensure functional availability with an upper threshold. Neti et al. [29] constructed an MTD guide framework based on an anti-coordination game for quantifying deceptive metrics by mobility attributes and dynamically inferring the mutual feedback relationship between actors by episode. To minimize the side effect caused by actors of sophisticated distributed denial-of-service (DDoS) attacks, Wright et al. [30] designed a heuristic two-player game framework that optimizes all pre-conditions, mutation factors, and stability and security criteria for each design principle required for the construction of an adaptive MTD strategy. Carter et al. [31] further specified the MTD game architecture to optimize migration tactics that ensure a seamless connection of services available to legitimate internal users while maintaining the cognitive bias of illegal attackers induced in the defender-dominant container environment as much as possible. Colbaugh et al. [32] amplified the mathematical counterevidence of MTD sampling in a follow-up counter-example study.

2.2.2 Stackelberg Game Theoretic Literature

Here, this subsection describes previous MTD studies that simulated a causal relationship in which the follower’s scope of judgment and decision-making flow was limited according to the actions of the leader by adopting the Stackelberg game theory. Through the proposed co-resident attack mitigation and prevention architecture, Hasan et al. [33] detected co-resident attacks based on anomaly detection thresholds within a virtualized operating network that shares limited resources and formalized an MTD strategy that minimizes the invasion impact of lateral movement. Feng et al. [34] presented an MTD sequence that causes the disturbance, misleading, and confusion of attacker’s decision-making according to artificial disinformation by establishing an information disclosure framework that mathematically applies both the signal game and the Stackelberg game, which performs reactive mutual feedback. In a follow-up study, Zhu et al. [35] designed an advanced adaptive MTD model to maximize the induction efficiency of an attacker who bypasses the defense scheme and initially penetrates it by further expanding the scope of the attacker’s cognitive bias in units of routing protocols and packets. Sengupta et al. [36] developed a zero-sum game framework that optimizes the MTD to maximize proactive avoidance according to the mutation target and detailed sampling schemes, and simulated this for each decision tactic while minimizing the negative availability issue of the defender owing to side effects when these MTD are available in a wired-type simple topology that operates web applications, operating systems, and cloud services. In addition, a study on the optimization of MTD considering general sum game-based competition [37] was conducted to achieve robust mutation-based avoidance against advanced persistent threat attacks in the cloud network. In a related follow-up study, Li et al. [16] further amplified the hydraulic properties of the spatial-temporal attack surface that changed with MTD mutation by formalizing the Markov Stackelberg model optimized based on the average-cost semi-Markov decision process and discrete-time Markov decision process. Finally, Seo et al. [38] added an adaptive cognitive disturbance scheme to the existing MTD and constructed a deceptive game considering the continuous operability of the organization by combining this with a layered social engineering decoy. Also, in this work, a general sum game-based testbed was proposed to improve the proactive defense of the IoT-based sub-farm network cluster further.

2.2.3 Stochastic Game Theoretic Literature

Here, this subsection describes previous MTD studies that adopted stochastic game theory, considering probabilistic correlation. Manadhata [39] formalized a game model that adaptively reflects the three principles of MTD, which change in real-time, based on probabilistic transitions according to the decision-making flow, to determine each optimized MTD strategy according to the potential attack surface characterized by each domain. Zhang et al. [40] quantified the trade-off relationship resulting from the calculation of the MTD-based mutation factor in the form of sensitivity analysis and designed a nash-Q game framework based on the attacker’s strategy selection frequency and distribution to analyze the performance of each decision tactic concerning the rule of sharing incomplete information.

2.3 Analysis of the Existing MTD Literature with Formalism

Here, based on attack-defense trees and directed acyclic graph (DAG), structural diagrams, and propositional semantics derived from priced timed automata (PTA) interpretation, the key to previous studies that perform MTD performance inference by introducing formalism is to optimize the activation frequency of the three conceptualized MTD principles.

Hong et al. [41] first designed an MTD mechanism by integrating it into a hierarchical attack representation model (HARM) as an attack graph-based study to quantitatively evaluate and compare the deceptive defense effectiveness of the MTD applied to proactively protect various communication domains, such as virtualized and wireless sensor networks. In a follow-up study [42], they utilized a temporal graph-based graphical security model (T-HARM) to present dynamic security metrics to evaluate the overall performance of the MTD related to cyber mobility attributes, such as granularity, flexibility, and elasticity, and to capture dynamic attack surface changes according to the MTD application. To optimize the MTD trade-offs that significantly mitigate the damaging impact of DDoS cost-effectively, Zhou et al. [43] proposed a multi-objective Markov decision process (MOMDP) that incorporates detailed interactions among attackers, defenders, and users based on trilateral game logic. They also demonstrated practical differentiation by designing and simulating the MOMDP within the SDN. Rahim et al. [44] proposed a formal methodology that can be formally verified based on Uppaal, an open model checker, for a formally specified MTD mechanism. Additionally, they performed a comparative evaluation of the mutation quality, mutation stability, and cost of the random host mutation technique based on repeated experiments. Finally, Ballot et al. [18], in state-of-the-art research on the formalism of MTD, formalized PTMDP based on the DAG and PTA. They first proposed the PTMDP by structuring it as a decision tree based on threat modeling with attack vectors, subgoals, and MTD-based mitigation. Using Uppaal Stratego for formal verification, they mathematically performed a proof-of-concept by normalizing the optimal activation frequency set of each modeled MTD tactic in the form of a Pareto frontier.

3  MF2-DMTD, Reasoning Formal Framework of Drone-Type MTD

Here, this study formalizes the main modules in the proposed MF2-DMTD and defines formal specifications based on probabilistic PTMDP and decision trees, and all methods, metrics, attributes, and equations for formal verification based on model checking and feedback-type iterative zero-sum games.

3.1 Design Principle

As shown in Fig. 1, the MF2-DMTD, which is proposed to cause deceptive defense and resilient availability of the drone-type MTD by adopting formalism, a zero-sum-based competition game, and meta-heuristic optimization, is designed by focusing on three main modules.

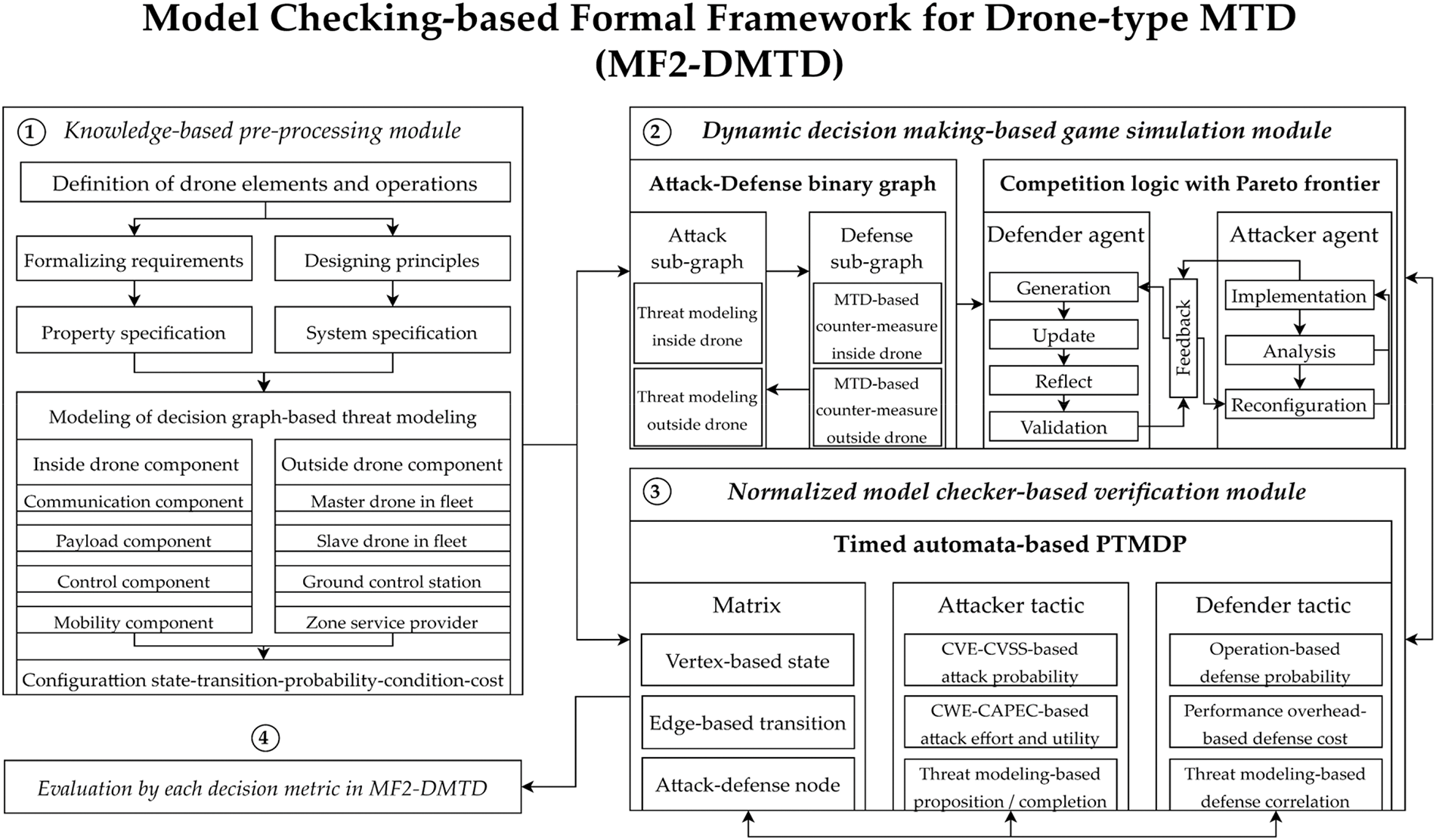
Figure 1: A main overview of MF2-DMTD for formalism and game-based reasoning with MTD

In MF2-DMTD, first, the knowledge-based preprocessing module (1) adopts all the elements of functional components (communication, payload, control, and mobility units) within a single rugged drone and external communication entities that collaborate with target drones (swarming drone cluster, GCS, and ZSP), related state and goals, transition considering the prior-post probability according to Bayes’ theorem, and interoperable sequences to define threat modeling containing the attack-defense tree concept and then specify it mathematically. In addition, formal metrics to apply the drone-type MTD’s feedback behavior for each identified drone internal and external vulnerability element are determined, and main parameters related to three MTD principles (‘what-to-move’, ‘when-to-move’, ‘how-to-move’) are also configured in detail, and used in the dynamic decision-based game competition simulation module (2) and the normalized model checker-based verification module (3).

Next, the threat modeling specified according to the Common Vulnerabilities and Exposures (CVE) vulnerability in (1) is detailed as a PTMDP-based decision tree in the dynamic decision-based game competition simulation module, which is calculated to contribute to the decision of the optimum for each mutation period of the drone-type MTD by structuring mutually competitive relationships between actors based on continuous ratchet-type causality and normalizing zero-sum game with PBNE, BSS, and MIQCP.

Finally, the normalized model checker-based verification module in MF2-DMTD is evaluated using Uppaal Stratego, a state-of-art model checker, and a feedback-type repetitive engagement model to evaluate drone-type MTD performance based on PTMDP-based drone internal and external decision trees specified in (1) and (2). Additionally, along with (4), the comparison results of analyzing the performance of the drone-type MTD are finally derived in the form of Pareto frontier with multi-objective optimization such as non-dominated sorting genetic Algorithm II (NSGAII) and pareto archived evolution strategy (PAES).

3.2 Formalization of Decision Tree

Next, drone threat modeling [45] configured to specify all major assets, attack surfaces, threat vectors, and MTD-based countermeasures within this MF2-DMTD is computed as a PTMDP-based decision tree structure that includes all concepts of action, goal, relationship, and continuous causality based on the attack-defense tree, as shown in Figs. 2 and 3. These specified decision trees are used as conceptual templates within the model checking and zero-sum game accompanying the formal verification process, supporting the calculation of the payoff between actors related to the cyber-kill-chain (CKC).

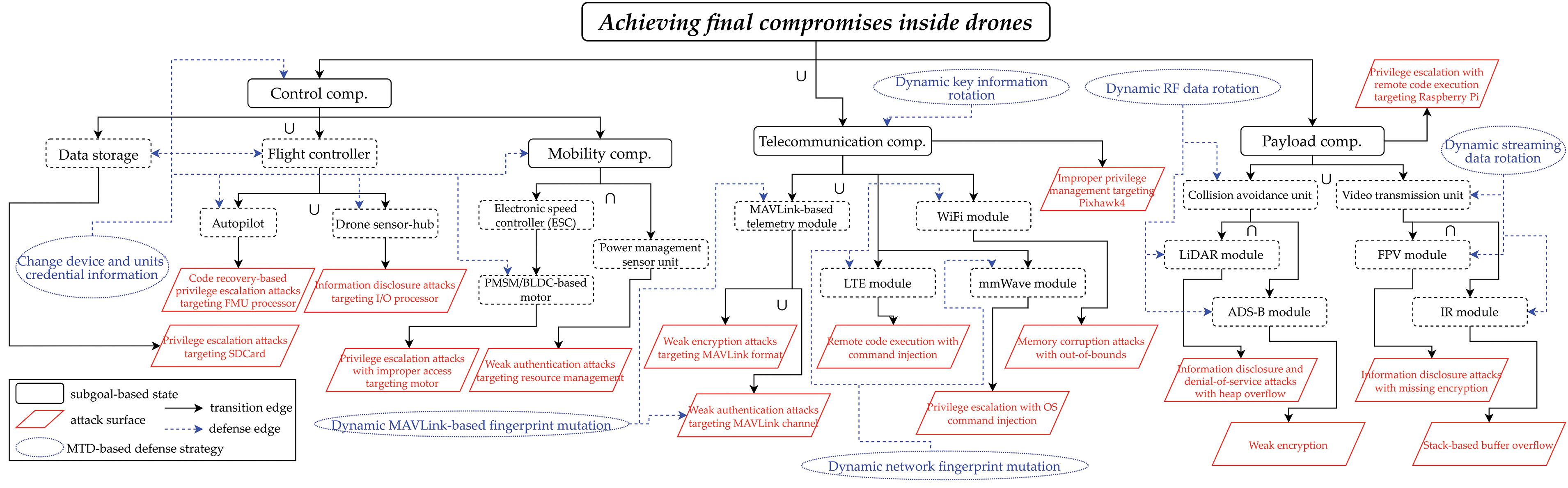
Figure 2: Threat modeling-based detailed decision tree by drone internal functional components

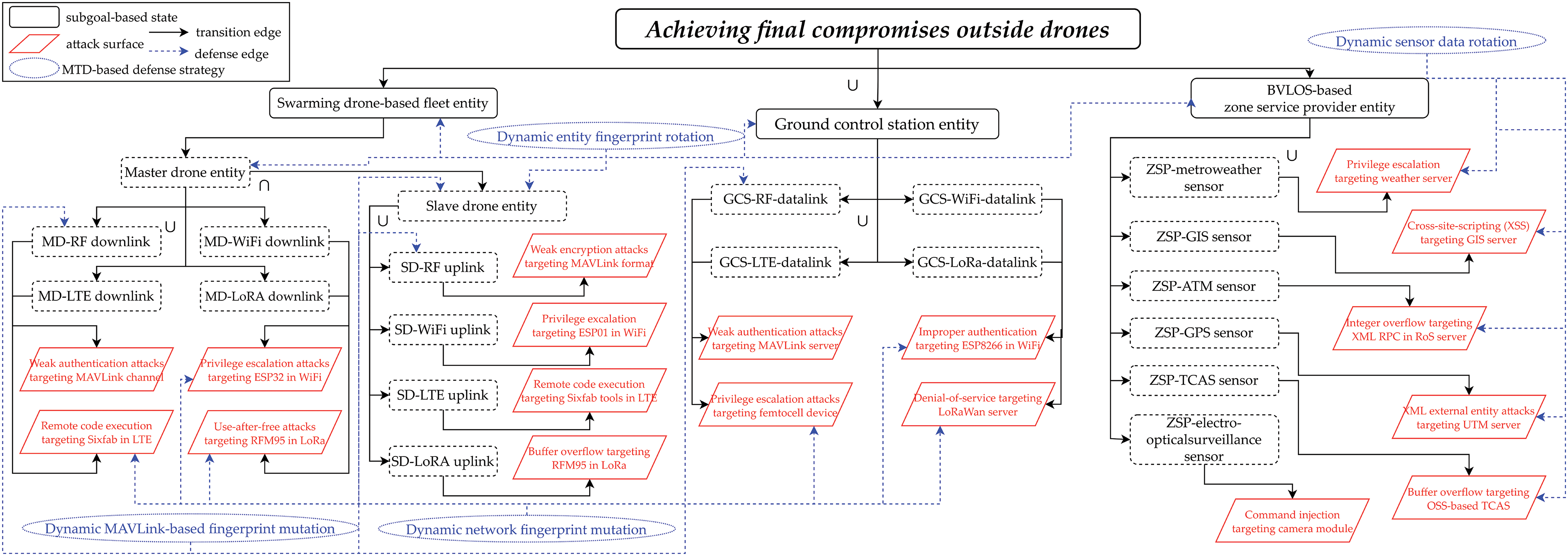
Figure 3: Threat modeling-based detailed decision tree by drone external communication entities

The decision tree in Fig. 2 is formalized for each of the four internal components to conceptualize continuous operational behaviors such as communication with MAVLink [46] of a single rugged drone armed with multiple antennas, payload-based sensing, control via bus traffic, and three-dimensional maneuvering to ensure line-of-sight (LoS) and non-LoS (NLoS) propagations. The control-maneuvering unit was structured with a focus on the correlation between Pixhawk4, a flight controller, and Zubax equipment, an electronic speed controller, whereas the communication unit was also configured according to the dependency of the MAVLink telemetry independently configured in the Pixhawk4 controller and the sub-wireless communication sensors (RF, WiFi, LTE, mmWave) mounted on the wireless mobile antenna modules. As the payload unit is also conceptualized based on a lightweight mission companion computer to operate additional sub-party functions of a single drone, such as Raspberry Pi, both the spatial-temporal recognition function through RF and the real-time video transmission function through mobile communication were additionally determined.

To simulate the interoperable behaviors of any external communication entities cooperating with rugged drones deployed on a battlefield for intelligence, surveillance, and reconnaissance (ISR) after belonging to the space-air-ground integrated network [47], the decision tree in Fig. 3 is also composed of three types of drone external communication entities: swarming tactical drone cluster, GCS, and ZSP [48]. Based on NLoS-based wireless communication relay and adaptive situational awareness, the swarming tactical drone network was clustered according to the dependency between the master drone that controls the clustered fleet in the form of star topology and the slave drone subordinated based on C2 (command & control). Inspired by the uplink-based remote control of a random swarming drone network deployed on the battlefield, the GCS entity operated under the presence of a senior commander was detailed as an RF uplink communication sensor performing flight control and a wireless mobile communication sensor performing packet transportation. As the ZSP entity is also conceptualized to contain a beacon-type wireless communication sensor hub that transmits useful regional status information to rugged drones on the mission, it was decided to improve the operational efficiency of drones by providing real-time states such as weather, geographic information system (GIS), and air traffic management (ATM) data regularly.

In the detailed decision trees based on PTMDP in Figs. 2 and 3, the subgoal state and attack surface element are formalized in the form of graph nodes in complex systems, and drone-type MTD-based countermeasure tactics are formalized in detail according to Tables 1–3. Accordingly, to conceptualize the subgoals related to rugged drones in competitive engagements by actors, Table 1 shows the functional internal components and external communication entities that are subdivided and correlated.

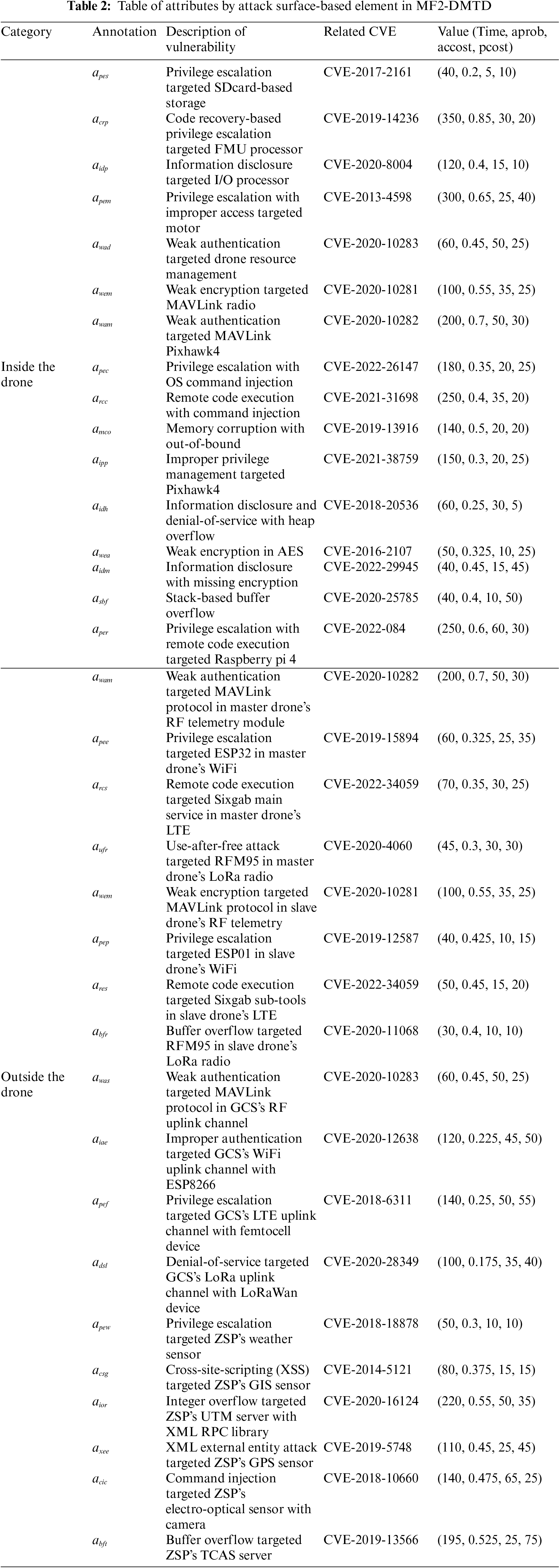
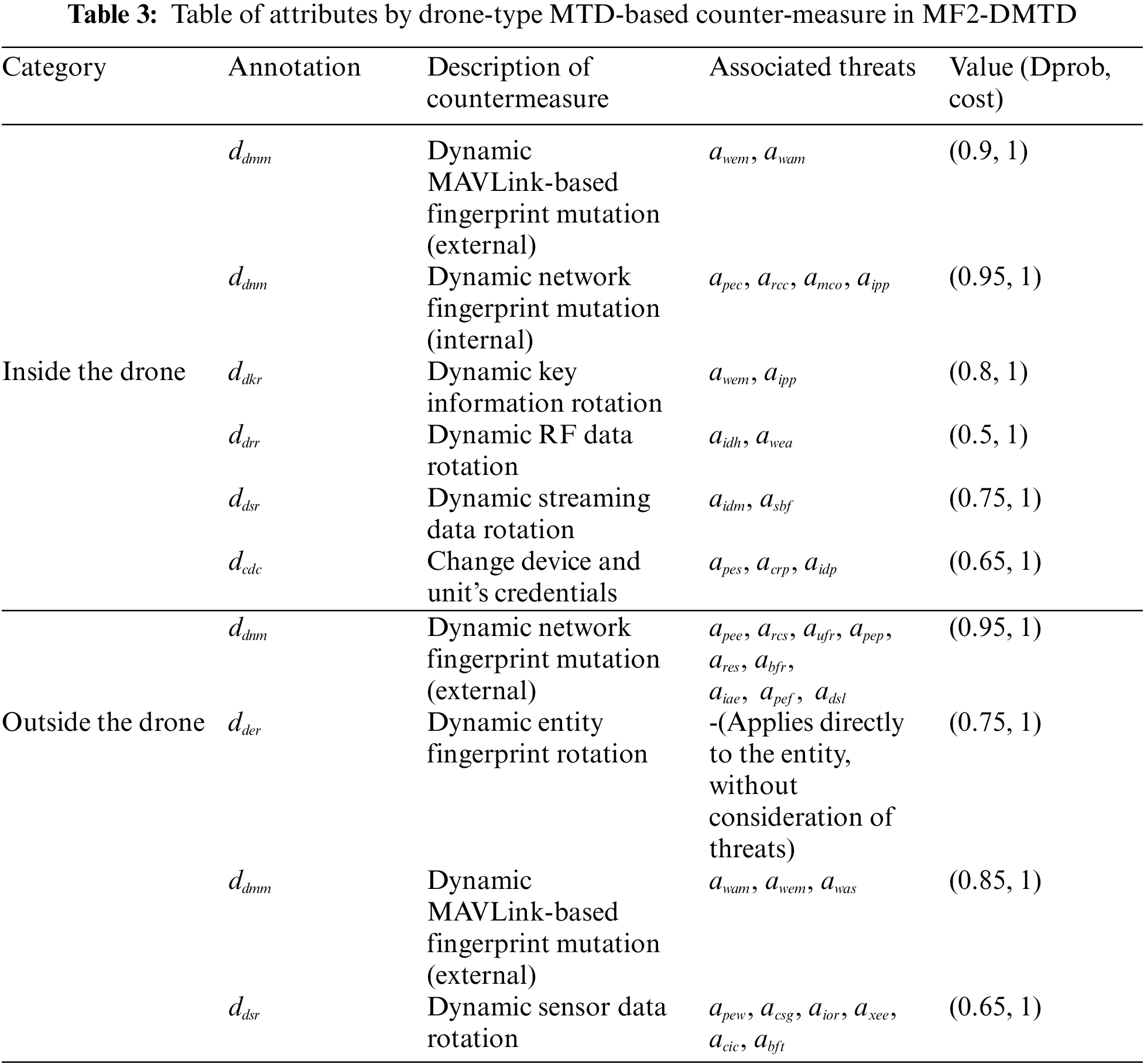
Next, the attack surface elements defined to simulate the main vulnerabilities and penetration vectors inside and outside the drone are quantified based on both the recognized CVEs that were potentially related to the communication vulnerability of the rugged drone and the related Common Vulnerability Scoring System (CVSS), as shown in Table 2. To perform incursion using specific vulnerabilities, the proposition that should be achieved preemptively formally determines the penetration difficulty and damage impact for each type of cyber threat specialized for the target drone by quantifying atomic attack metrics such as attack time (time), attack success probability (aprob), pre-cost for launching an attack (accost), and post-cost for continuing an attack (pcost).

Finally, the propositions of MTD tactics dedicated to each drone’s internal and external configuration were also further quantified as atomic defense metrics such as defense success probability (dprob) and defense cost (cost) owing to the multi-layered multitenancy structure dedicated to each associated attack surface element, as shown in Table 3. To realize proactive defense in terms of communication and operation within the drone targeting all physical, host, data link, and network layers, normalization is performed for the optimal trade-off required at the minimum.

3.3 Configuration of Dynamic Zero-Sum Game Model

Modeling a game competition simulation module based on dynamic decision-making that performs a zero-sum-based competitive engagement simulation along with a model checker within the proposed MF2-DMTD contributes to the probabilistic formal verification of the drone-type MTD. Thus, the zero-sum attack-defense competition between actors configured within the module is schematized based on a multistage evolutionary repetitive game tree, as shown in Fig. 4.

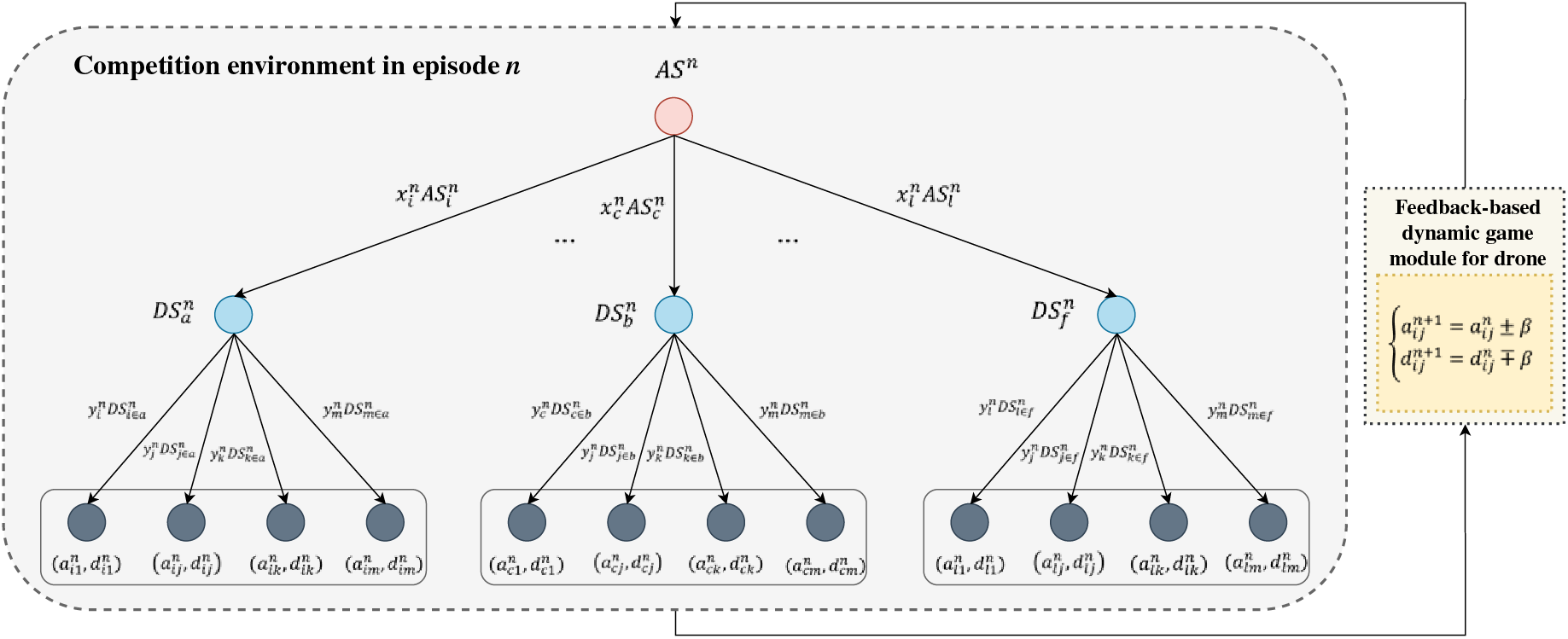
Figure 4: Conceptual overview of the zero-sum-based multistage game in MF2-DMTD

To determine the randomized spatial-temporal entropy within this game tree, the PBNE, which has a privatized asymmetric judgment relation and a rule of sharing incomplete information according to the Dirac delta function and the Boltzmann probability distribution is adopted to maximize the defender’s payoff per episode. In addition, the additional application of BSS within the game tree optimizes the quantitative sequential relationship for micro-macro rewards for each actor by structurally forming a dependent ratchet-type causality between an active leader and a passive follower. It is also conceptualized to maintain the mutation initiative by forcing the attacker’s priori belief and confusion to a high level with the defender’s dominance.

It is also shown that the game tree is adaptively configured according to the development of n, an engagement step in an arbitrary episode k. First, attacker A selects ASn, which is the most optimized set of invasion strategies within a certain n, to attempt an initial incursion or maintain the previous occupation, performing preliminary actions related to the reconnaissance, weaponization, and lateral movement phases within the CKC. Thereafter, {xin,xcn,xln}, dynamically determined stochastic components, as shown in Eq. (1), are used mathematically according to the quantitative state information (reward, revenue, and cut-off solution of equilibrium) conserved by attacker A through the previous engagement, attack surface-based approximate intelligence to predict and select {ASin,AScn,ASln}, and the elements that define attack tactics and techniques in ASn. In this case, ω, the exploration factor of actors, determines the scope of the subjective judgment regarding the intelligence that competitors radiate to the outside.

xhn=exp(ω⋅QA(Sh,ax,ay))/∑h=0nexp(ω⋅QA(Sh,ax,ay))∗(1)

After that, to proactively respond to the invasion of attacker A according to the selected ASin, defender D selects {DSi∈an,DSj∈an,DSk∈an,DSm∈an}, which are elements that specify drone-type MTD tactics and techniques within DSan, an optimized defense strategy according to {yin,yjn,ykn,ymn}, the dynamic stochastic components in Eq. (2) to get into the engagement. After adopting DSi∈an, β, a factor representing incentive and punishment for each actor, is calculated by simulating zero-sum competition within the engagement stage. Additionally, through β and the feedback-based game module for drone, (ai1n+1,di1n+1) representing the payoff of attacker A and defender D at n+1, the next engagement stage is calculated.

ytn=exp(ω⋅QD(St,ax,ay))/∑t=0nexp(ω⋅QD(St,ax,ay))∗(2)

And, through these (1), (2), binary values γ for the representation of competition results, the game tree-based workflow of multistage competition in Fig. 4 is embodied as Algorithm 1. Algorithm 1 determines the payoff of A and D by changing the reward of n according to β, γ, and the inherent x and y, and also defines the initial reward of n+1. If D succeeds in deceptive defense against A ‘s AS through DS, positive revenue is added to DS and negative revenue is applied to AS. If D fails to enter the defensive state by the expiration of CKC, negative revenue is applied to the DS and positive revenue is added to the AS.

At this point, within the game tree and Algorithm 1 containing this repeated feedback sequence, the endpoint of an engagement episode between actors is determined by whether a cutoff solution of the equilibrium can be calculated through the zero-sum game calculated according to the normalized PBNE and BSS. Therefore, the payoff optimization of defender D using the drone-type MTD is defined in detail as a Bellman value iteration [49] based Q-value scheme that performs adaptation according to behavioral changes, as in Eq. (3) related to (1) and (2). Sk in (3) is a finite state calculated based on GSk and SSk, TSk configured within episode k and contains multiple levels to stochastically define the structural state-transition in PTMDP. In addition, ax and ay denote the finite actions based on the half-duplex transition of attacker A for Sk and the full-duplex transition of defender D, respectively. In this case, GSk=(GSASk, GSDSk) is a set of strategies dynamically determined according to DSk of defender D  and ASk of attacker A, whereas SSk=(SSASk, SSDSk) is a set of BSS-based decision tactics that are asymmetrically activated according to the coercive feedback signaling initiative. In addition, TSk=(TSASk, TSDSk) is a set of intelligence elements unique to each actor. For attacker A, it is a private information element group based on the attack surface effective threshold ρ, and for defender D, it is configured as a threat modeling-based element group identified to apply the MTD inside and outside the drone.

Q(Sk,ax,ay)=R(Sk,ax,ay)+U∑Sk+1θ(Sk,ax,ay,Sk+1)⋅TSk⋅OPT(Sk+1)+CU(3)

Additionally, R is a function that calculates the payoff that can be obtained within episode k when attacker A and defender D perform actions ax and ay, respectively, in Sk, and it is used to maximize as the key constraint until defender D, taking this into account, calculates a solution of equilibrium. If the actions of ax and ay are performed in θ or Sk, the probability of reaching the next state, Sk+1, is defined as a probability distribution function calculated based on the Dirac delta function and the Boltzmann probability distribution in the PBNE. U, zero-sum-based discount factor function, is used to calculate an approximated solution of the equilibrium considering meta-heuristic optimization, as it cuts off the scope of factor judgment for each actor within [0, 1]. CU is also defined as a utility function that imposes effort and cost on each actor within the zero-sum model. OPT, which is fine-tuned from defender D’s point of view, also calculates an optimized reward by reflecting all available SSk+1 in Sk+1, as in Eq. (4) related to (3).

OPT(Sk+1)=maxSSk+1minax∑ayQ(Sk,ax,ay)⋅(ssDSk+1|i=0,1,2,…)(4)

Finally, payoff optimization normalized according to the drone’s internal functional components and external communication entities was determined according to Eqs. (5)–(6) based on (3) and (4), respectively. Thereafter, (5) adjusts the optimized payoff by adding SMF, which is a [0, 1] threshold considering the security state inside the drone. To reflect the unique wireless communication characteristics outside the drone, (6) also amplifies all of Prx=−10×nlog10⁡D+Ptx, an indicator of the received signal strength related to trilateration (Ptx is the transmission strength, n is the Friis propagation loss model-based constant of path loss), D=|Drx−Dtx|, which is the relative distance value, and PL(D)=(10×log⁡(Ptx/1mW))−(10×log⁡(Prx/1mW)), which is a power density function.

OPTinternal(Sk+1)=OPT(Sk+1)⋅SMF(5)

OPTexternal(Sk+1)=OPT(Sk+1)⋅Prx⋅PL(D)(6)

4  Experiments and Results

Next, the node-based state and edge-based transition concepts specified in Figs. 2 and 3 and Tables 1–3 were used to compare and simulate the performance inference of the drone-type MTD.

4.1 Construction of Experimental Testbed

The main simulation parameters required to optimize the Pareto solutions related to the security and functionality of the drone-type MTD were determined as listed in Table 4.

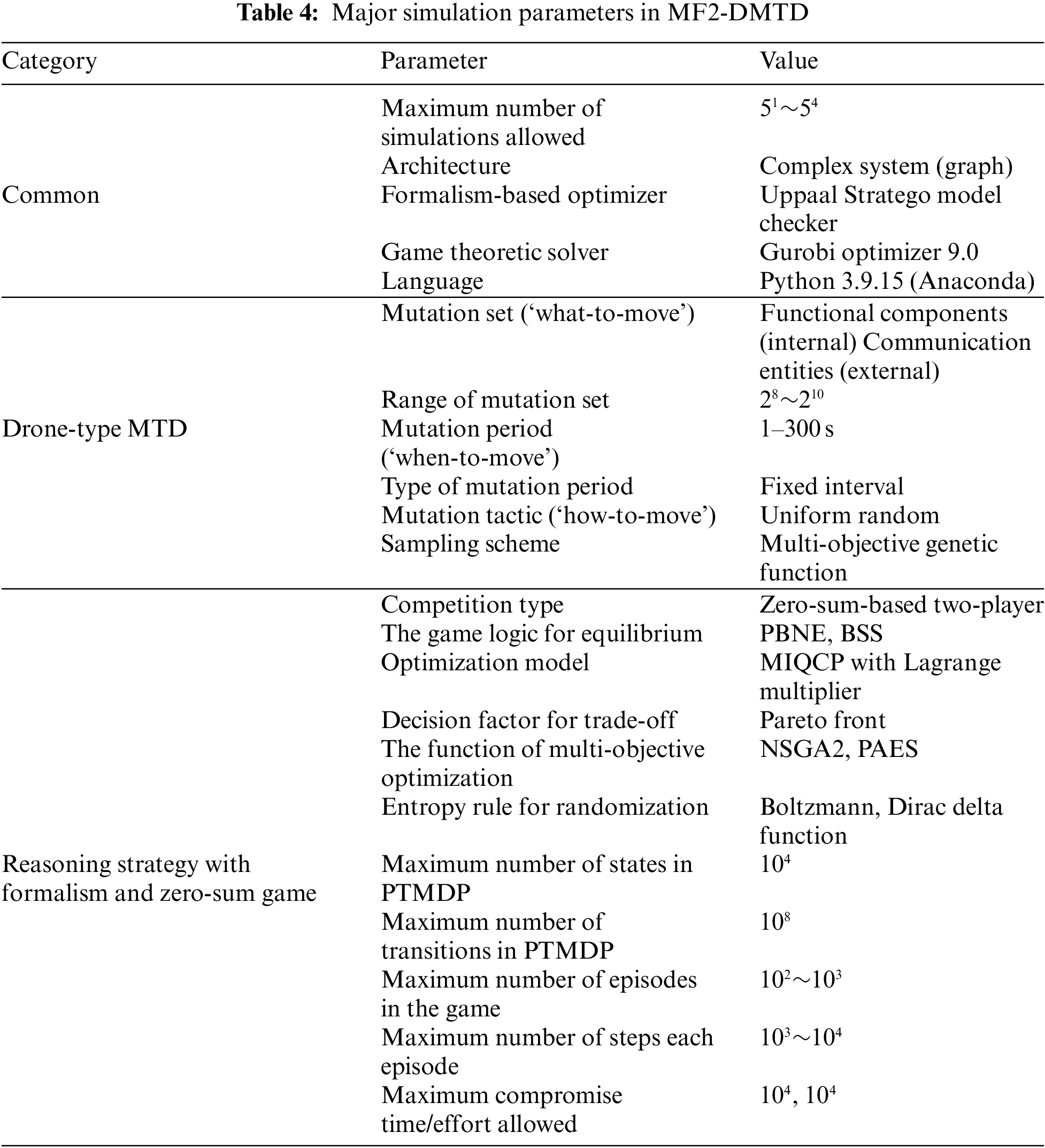
First, in the case of the drone-type MTD, the three main concepts (‘what-to-move’, ‘when-to-move’, and ‘how-to-move’) based on mutation sets, mutation periods, and mutation tactics are determined for each argument. In addition, unique internal and external drone specifications and correlations are considered to ensure that the mutation target range, genetic sampling scheme, and periodic selection methodology are amplified in the detailed optimal parameter standard. Next, for a zero-sum-based two-player game logic that determines competitive engagement modeling for each attack-defense actor, the MIQCP model adopting a Lagrange multiplier associated with entering the equilibrium state through PBNE and BSS is mainly used to contribute to the Pareto frontier computation via NSGA2 and PAES. In addition, the dynamic entropy rule for the continuity simulation of the acts of engagement in an episode is randomized by applying the Boltzmann probability distribution and Dirac delta function. In addition, the metrics (state, transition, episode, step, effort, and time) for each PTMDP and the repetitive game logic introduced to achieve formal specification and formal verification were also calculated to formulate them for statistical comparative analysis based on the Monte Carlo method in the MF2-DMTD.

At this time, MIQCP and MOGO schemes adopted to perform mutation cycle-based Pareto optimization for drone-type MTD are defined as a value iteration mechanism considering bilevel optimization problems like Algorithm 2. In Algorithm 2, MC is the mutation configuration set, |MC| is the number of mutation configuration set, and ϵ is initialized to 0.1 as the convergence threshold. α is the mutation time slot length of the drone-type MTD, where α^ denotes the supremum and α˘ denotes the infimum. And θ denotes the time loss required until the drone-type MTD responds, and π denotes the probability distribution based on the Boltzmann and Dirac delta functions. Additionally, PV is defined as the near-optimal policy value associated with Algorithm 2, and V is defined as the decision vector of MTD.

4.2 Results 1-Sensitivity Analysis for MTD Performance for Drone Interior

Next, the calculated decision-tree-based threat-modeling structure, feedback-type competition relationship, constraints per actor, state-transition proposition, and fine-tuned related parameters were all formally specified to simulate performance inference for the drone-type MTD. In addition, a formal verification to optimize the security-functional Pareto frontier was performed in parallel using normalized model checking. Considering the volume in this study, these results limit the scope of the analysis by performing a final comparative analysis by cutting off the space of the solution within a fixed mutation period of 140 s or less after classifying the Pareto optimization results of dedicated MTD-based mitigations independently applied for each internal and external element, which is a mutation set.

Thus, the performance inference results of the MTD normalized to the functional components inside the drone were formalized as shown in Figs. 5–10. In this case, ‘Expected compromise time’ on the X-axis is determined to mean the expected attack time (s) required as a minimum for an attacker to successfully achieve penetration into the drone, whereas ‘Expected compromise effort’ on the Y-axis is determined to mean the expected attack cost required as a minimum. The legend axis is also configured to represent the fixed mutation period (s) of the drone-type MTD corresponding to each internal component.

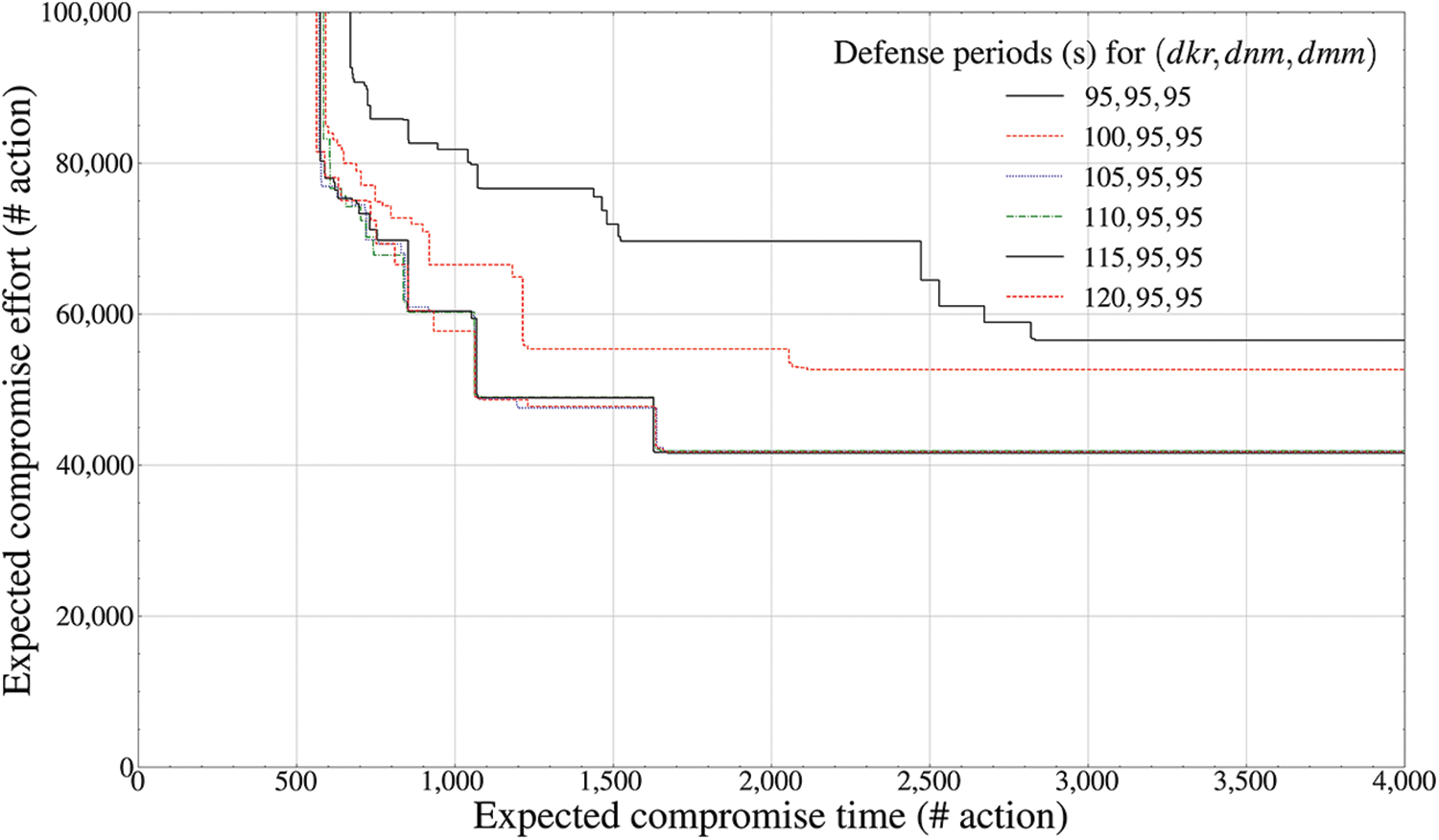
Figure 5: Pareto frontier-based comparison results of defense performance by mutation periods (telecommunication component inside the drone, ddkr, 95–120 s)

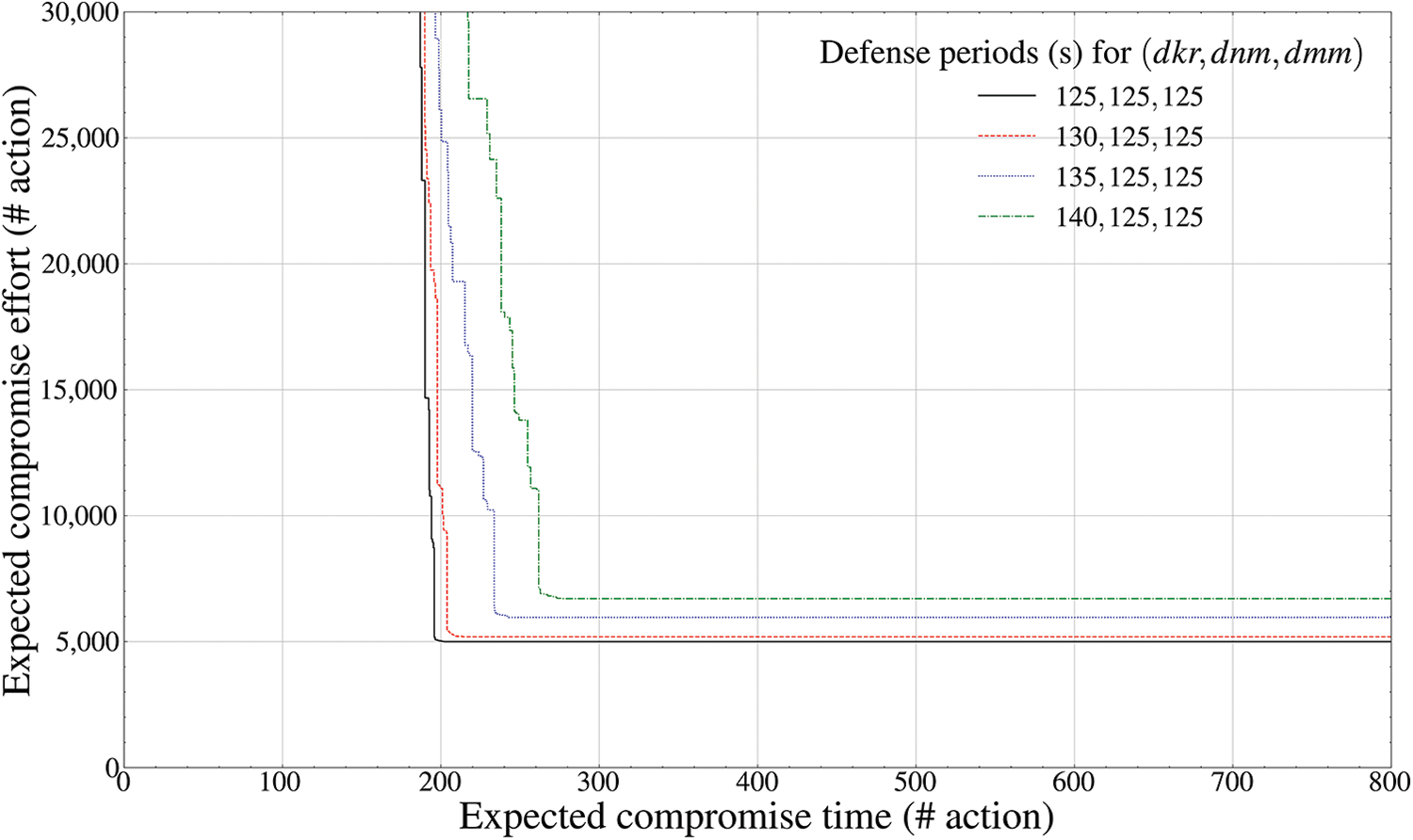
Figure 6: Pareto frontier-based comparison results of defense performance by mutation periods (telecommunication component inside the drone, ddkr, 125–140 s)

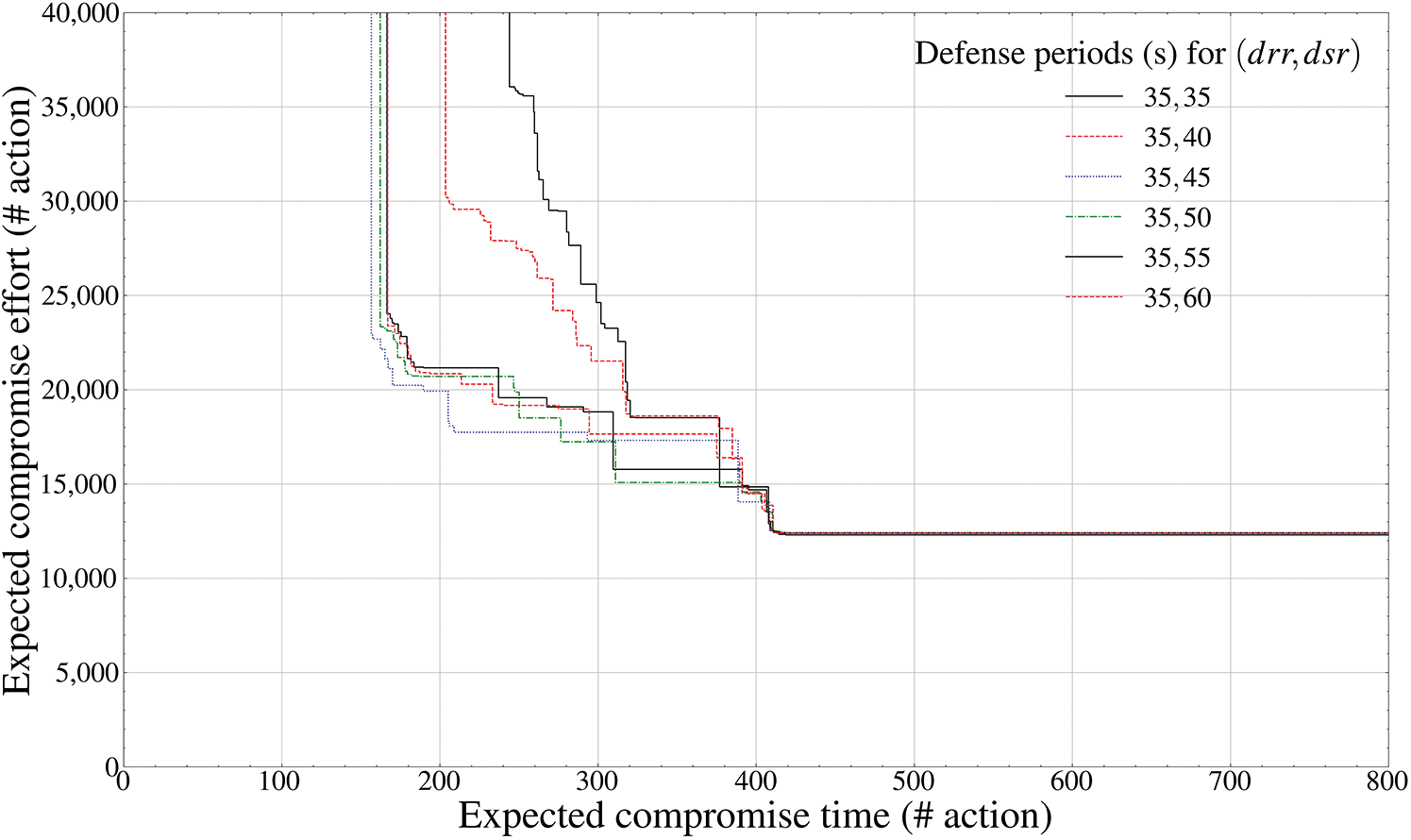
Figure 7: Pareto frontier-based comparison results of defense performance by mutation periods (payload component inside the drone, ddsr, 35–60 s)

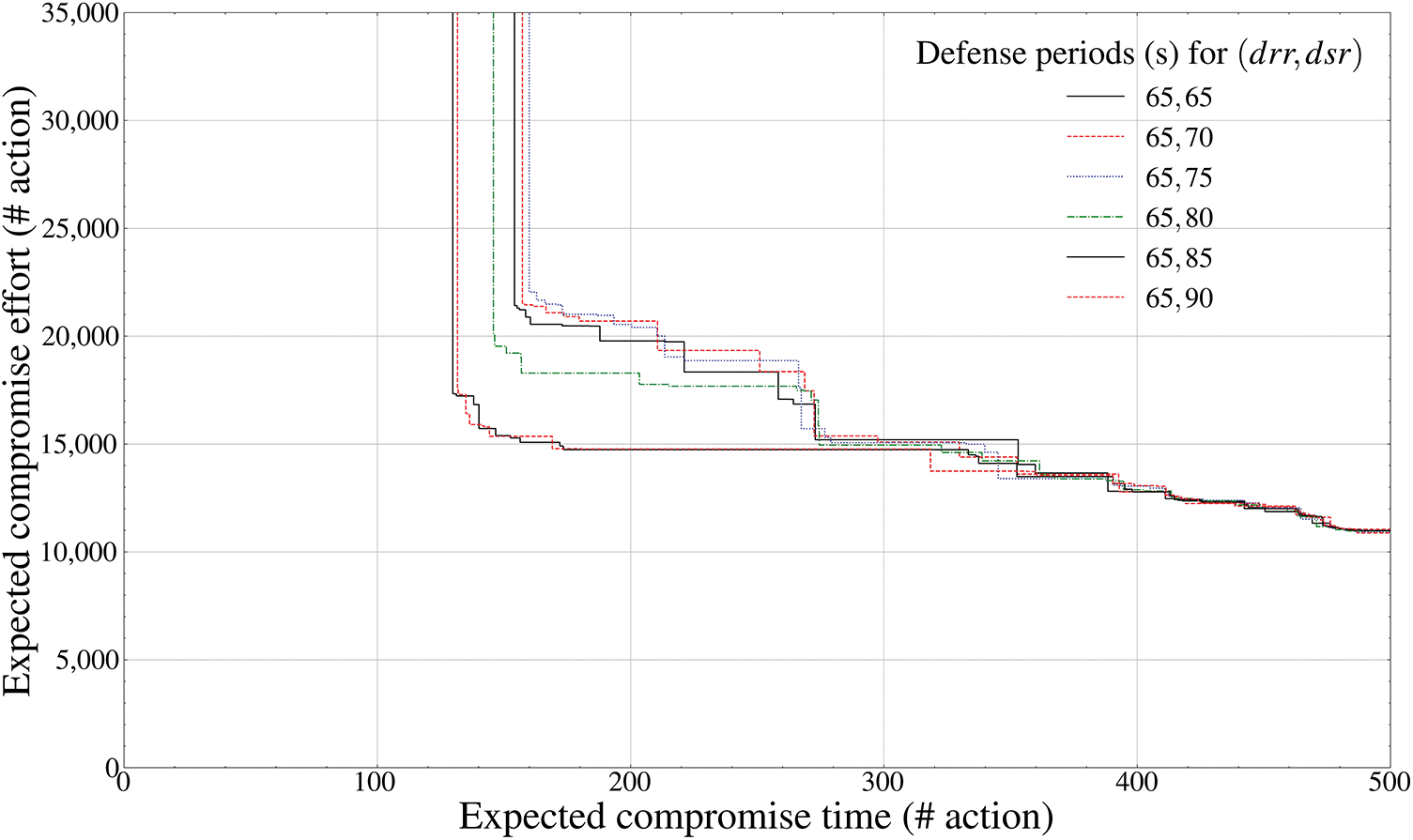
Figure 8: Pareto frontier-based comparison results of defense performance by mutation periods (payload component inside the drone, ddsr, 65–90 s)

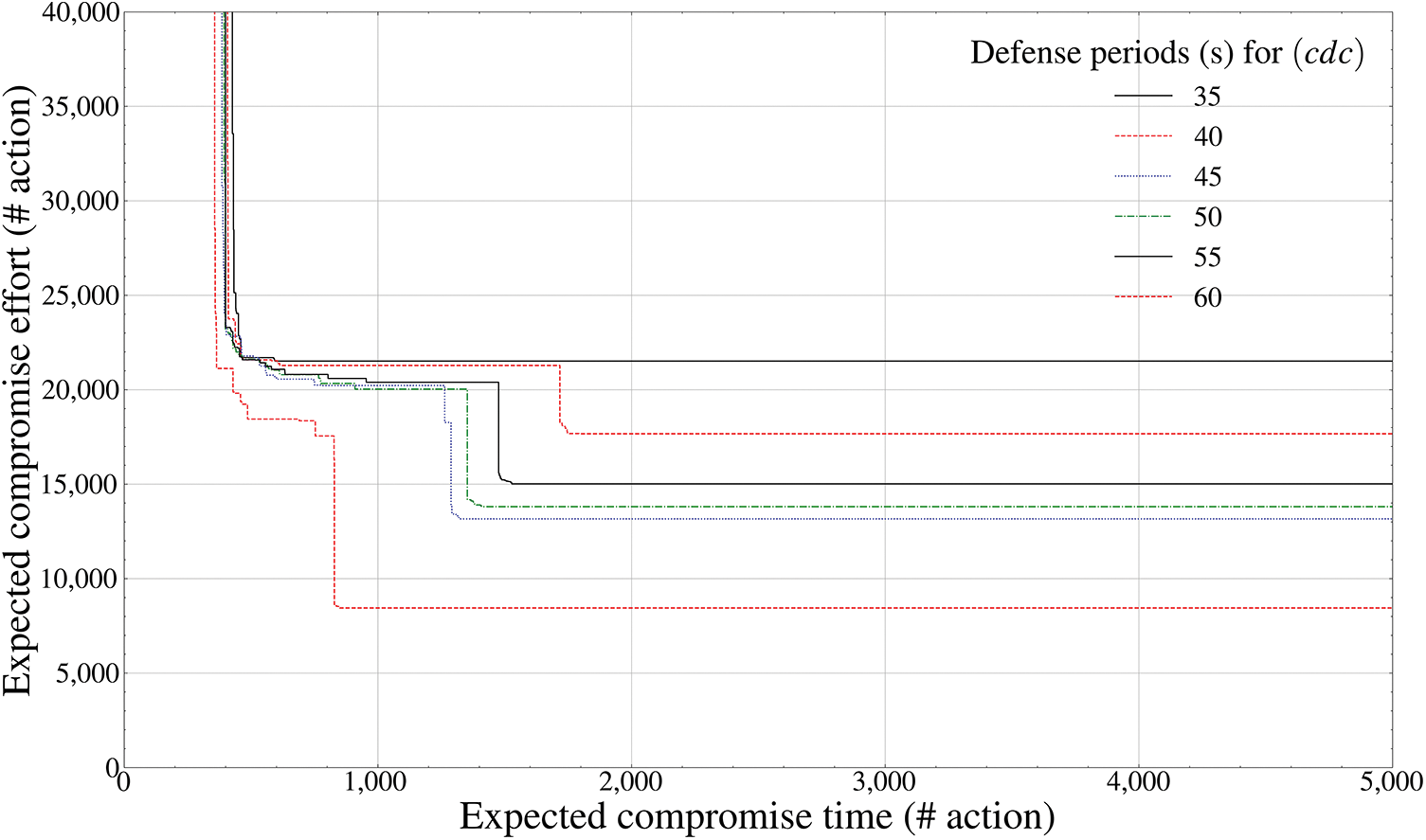
Figure 9: Pareto frontier-based comparison results of defense performance by mutation periods (control-mobility component inside the drone, dcdc, 35–60 s)

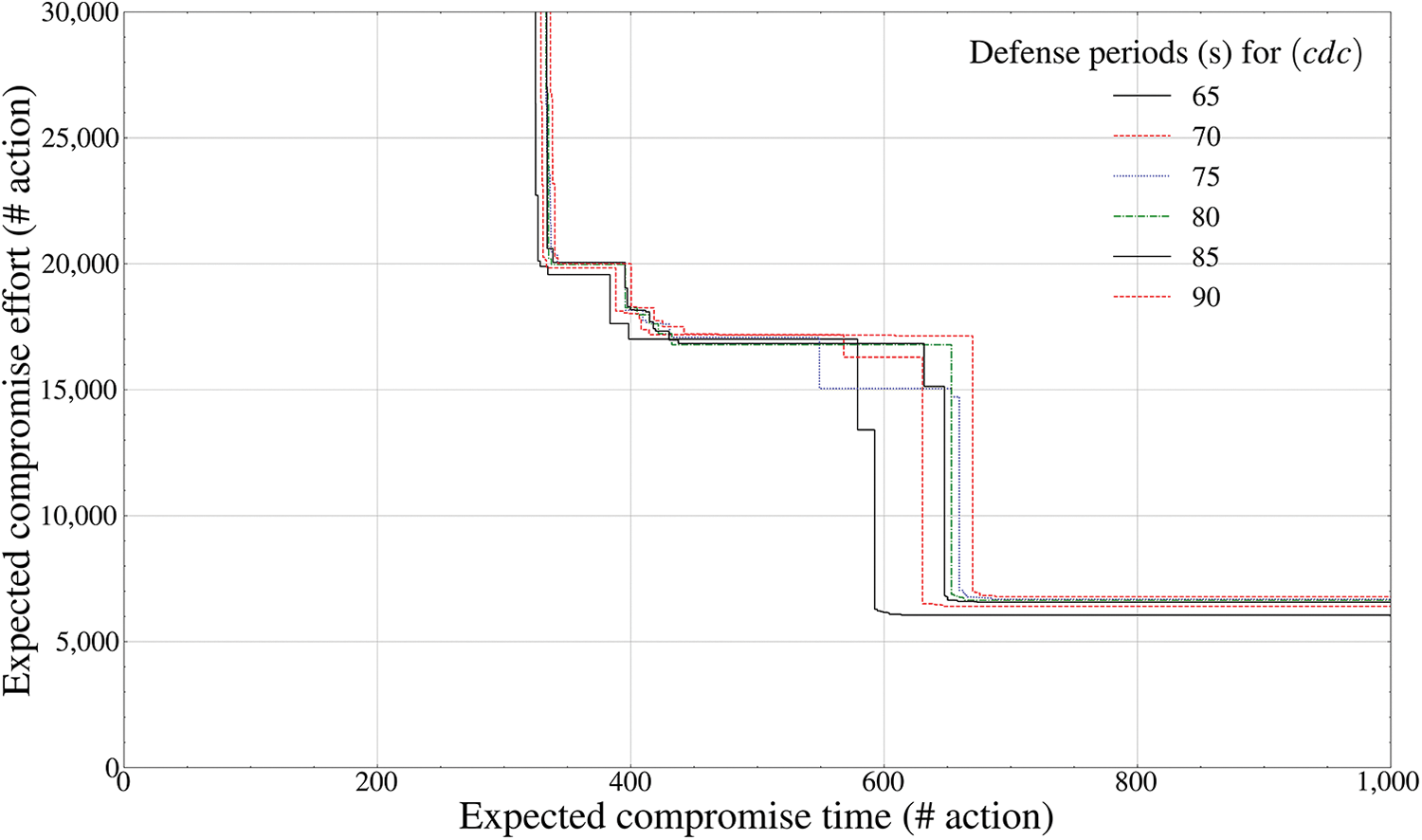
Figure 10: Pareto frontier-based comparison results of defense performance by mutation periods (control-mobility component inside the drone, dcdc, 65–90 s)

Fig. 5 shows the final convergence of the best Pareto optimum solution of the ddkr tactic, which mutates public key cryptography information within the communication channel to (200, 5000), targeting the internal communication components that perform MAVLink-based RF telemetry and wireless mobile communication (WiFi, LTE, mmWave). It can be further confirmed that the deceptive defense efficiency of ddkr also continuously decreases in the form of behaviors of the log graph with a positive gradient and base whenever the fixed mutation period increases every 5 s within the range of [95, 120], and an attacker-dominant Pareto frontier is formed so that it gradually approaches even based on the ideal point of the drone attacker. This can be proven to be a quantitative reflection of the spatial-temporal asymmetry characteristics in which the weaponization success rate of an attacker within a certain time inevitably increases linearly as the frequency of the MTD mutation cycle gradually decreases.

However, Fig. 6 shows that when the deceptive defense effectiveness of the ddnm tactics that mutate network/datalink layer information related to wireless mobile communication and the ddmm tactics that mutate MAVLink information inherent in the physical layer is secured naively above a certain level, increasing the frequency of ddkr’s mutation cycle conversely contributes to attenuating the attack success rate contrary to the defender’s prediction. This aspect, unlike other MTD tactics, shows a relatively high amount of resources for the defender required for the ddkr tactic that periodically mutates the public key encryption information itself. Therefore, these overhead-based factors of side effects can be analyzed as deeply spread into the total defense efficiency measurement. Thus, it can be finally derived that the optimal mutation period of the ddkr tactic for the drone’s internal communication component is 120 s or less.

Figs. 7 and 8, like LiDAR-based collision avoidance and FPV-based image processing, calculate the Pareto frontier of the ddsr tactic that mutates real-time video payloads, targeting an internal payload component that additionally provides various sub-party functions within a single drone. Fig. 7 shows a pattern that whenever the mutation period increases by 5 s within the range of [35, 60], ddsr’s deceptive defense efficiency decreases in the form of a linear function containing a positive gradient for 45 s compared to the previous period, and then becomes stagnant after 45 s. Similarly, Fig. 8 shows that ddsr’s deceptive defense efficiency decreases significantly based on the behaviors of the exponential graph until the fixed mutation period of 85 s within the range of [65, 90], but solutions are fixed within specific Pareto frontier after 85 s. Thus, it can be finally confirmed that the Pareto optimum solution of ddsr for Fig. 7 converges to (315, 15000), whereas the Pareto optimum solution of ddsr for Fig. 8 converges to (135, 17250).

The aspects of Figs. 7 and 8 can be analyzed as a theoretical reflection of an asymmetric dominance relationship that the effectiveness of the defender intelligence available to the attacker within a certain time inevitably increases exponentially as the frequency of the MTD mutation period gradually decreases. In addition, unlike the MTD tactics available in Figs. 5 and 6, the operating ranges of the ddsr and ddrr tactics of the internal payload target are completely divided hierarchically and conceptualized, proving that the overhead impact owing to the overlapping application of other tactics to the target component is configured relatively low. Thus, it can be finally derived that the optimal mutation period of the ddsr tactic for the drone’s internal payload component results in 45 and 85 s, respectively.

Finally, Figs. 9 and 10 calculate the Pareto frontier of the dcdc tactic that mutates the UAVCAN payload for each target device fingerprint targeting Pixhawk4-based internal control-maneuvering components responsible for both six DOF flight function and central control function. Fig. 9 shows a pattern that whenever the fixed mutation period changes within the range of [35, 60], the deceptive defense efficiency slightly decreases in the form of a log graph with a positive base for 55 s compared to the previous one, and then changes to a linear function form after 55 s and decreases.

Fig. 10 shows a pattern that a momentum issue occurs in a form that does not stably converge to a practical random Pareto optimal value; however, it spreads to a random local minimum extremal value based on a specific saddle point from a fixed transition period of 65 s or more. Unlike other internal components, the fact itself that it adaptively engages an attacker who has penetrated even into the most hidden control maneuvering component inside the drone is because the part of the dcdc tactic’s avoidance concept is already incapacitated. Therefore, it can be analyzed that the global gradient problem of multi-objective genetic function related to MIQCP-based Pareto optimization cannot be mitigated, unless the frequency of the mutation period of dcdc is increased to overcome these negative issues.

Thus, it can be finally derived that the optimal mutation period of the dcdc tactic gradually applied to the drone internal control-maneuvering component is 65 s or less, and the Pareto optimum solutions all converge to (390, 17500).

4.3 Results 2-Sensitivity Analysis for MTD Performance for Drone Outerior

Figs. 11–16 show the performance inference results of the drone-type MTD normalized for the full-duplex communication environment established outside the drone so that sub-drones belonging to a random swarming cluster network are remotely controlled based on a command and control (C2) entity, such as a commander and GCS, and are additionally provided with real-time tactical information related to weather, geographic information, and air traffic control from auxiliary objects deployed in battlefield such as ZSP.

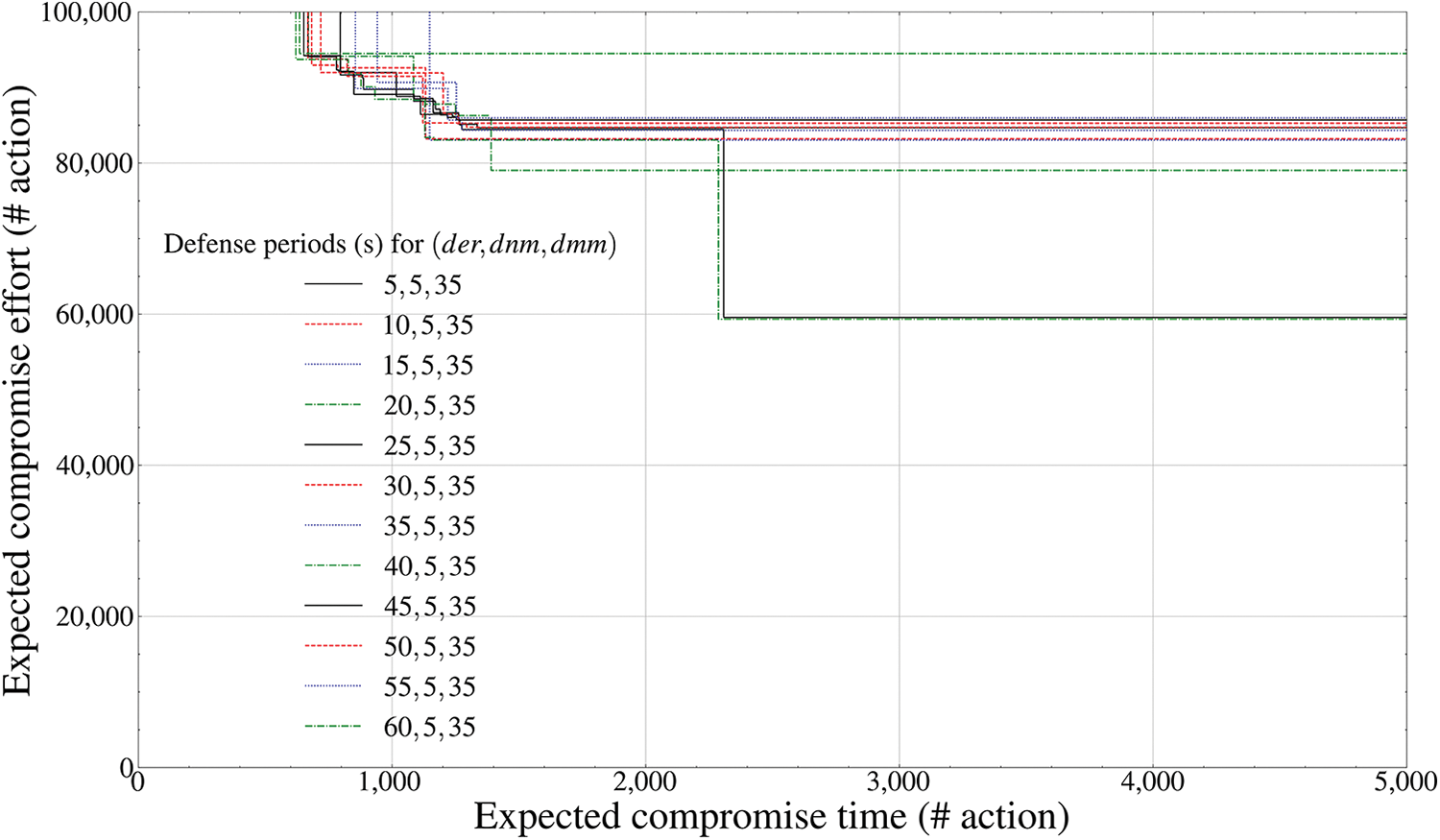
Figure 11: Pareto frontier-based comparison results of defense performance by mutation periods (swarming cluster entity outside the drone, dder, 5–60 s)

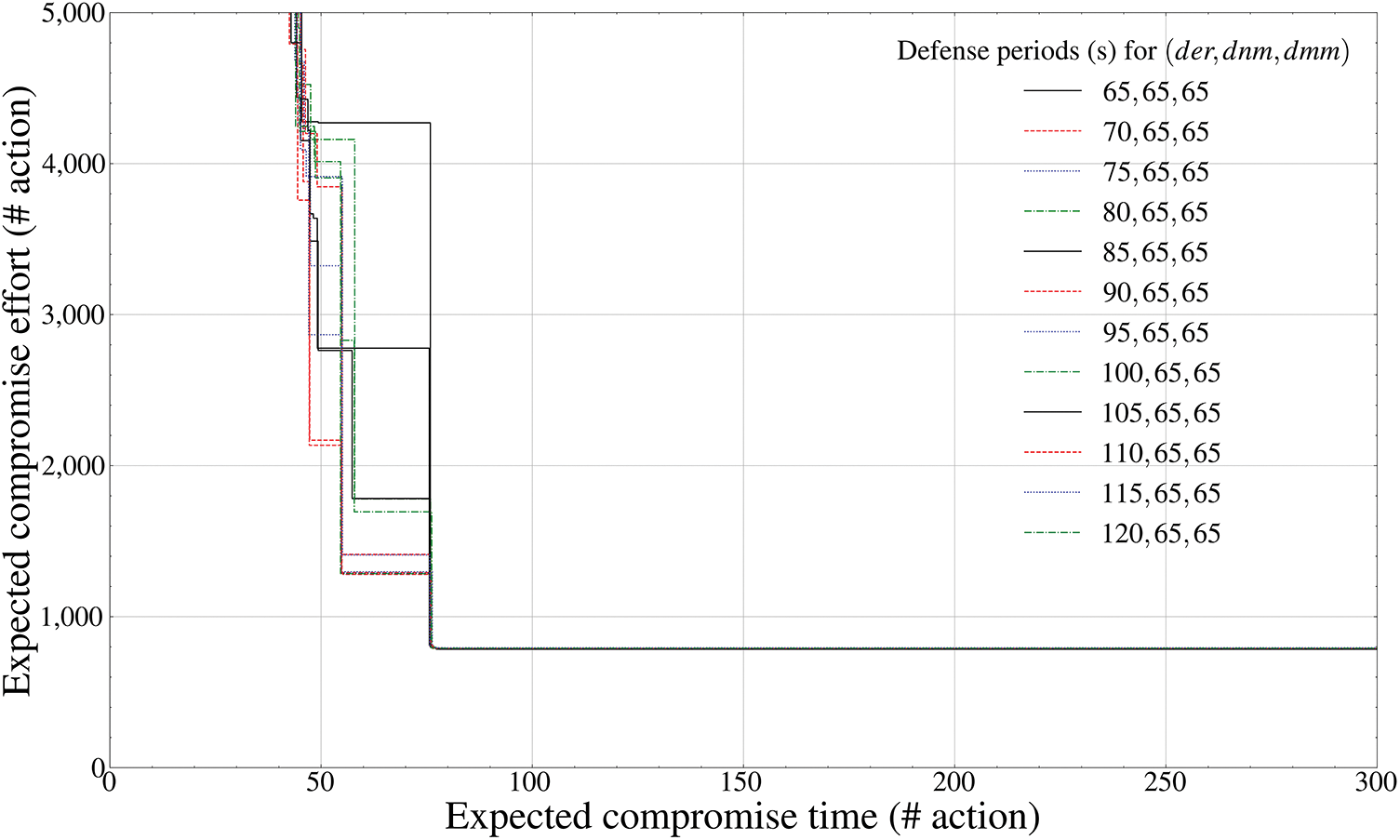
Figure 12: Pareto frontier-based comparison results of defense performance by mutation periods (swarming cluster entity outside the drone, dder, 65–120 s)

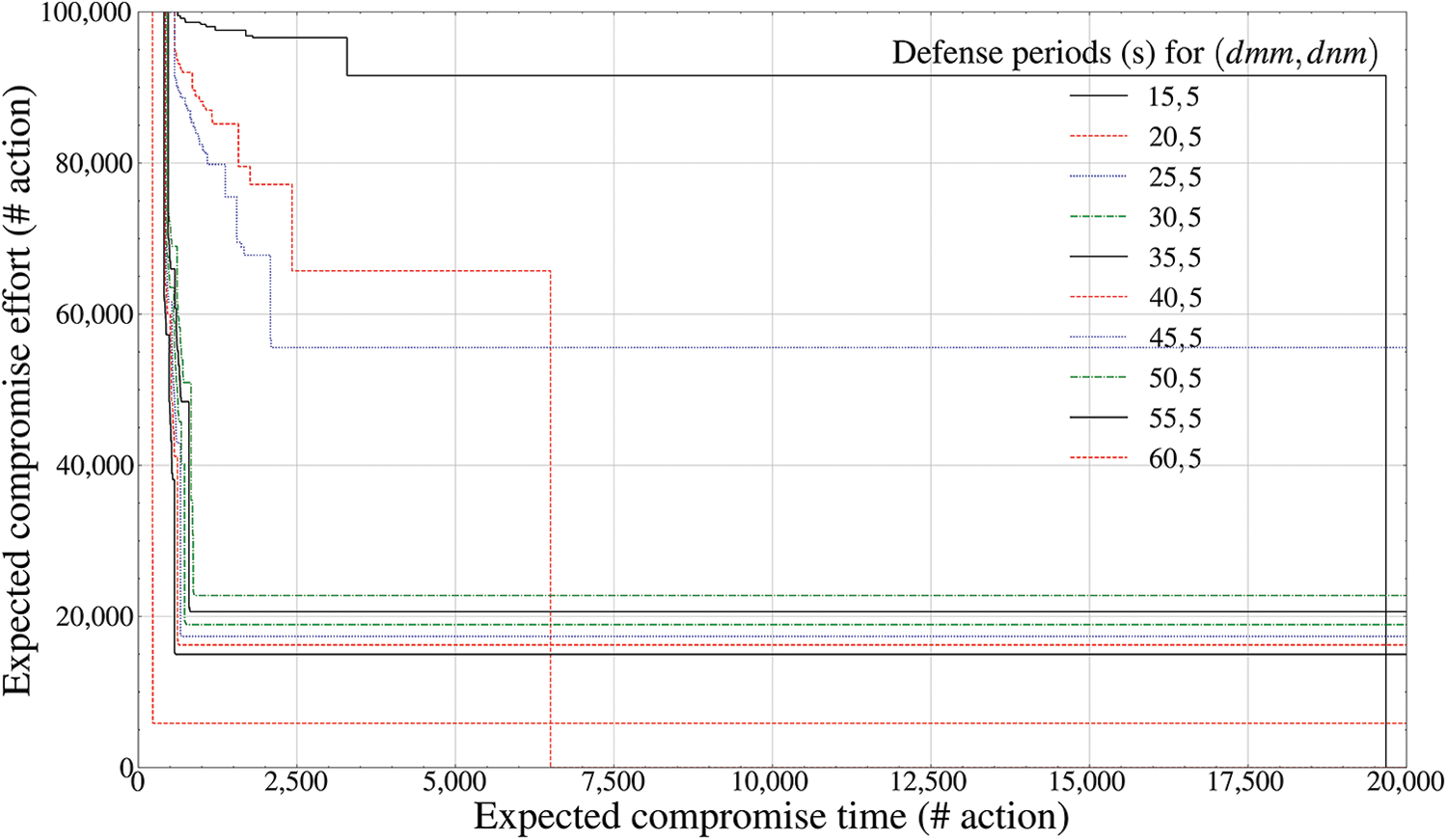
Figure 13: Pareto frontier-based comparison results of defense performance by mutation periods (GCS entity outside the drone, ddmm, 5–60 s)

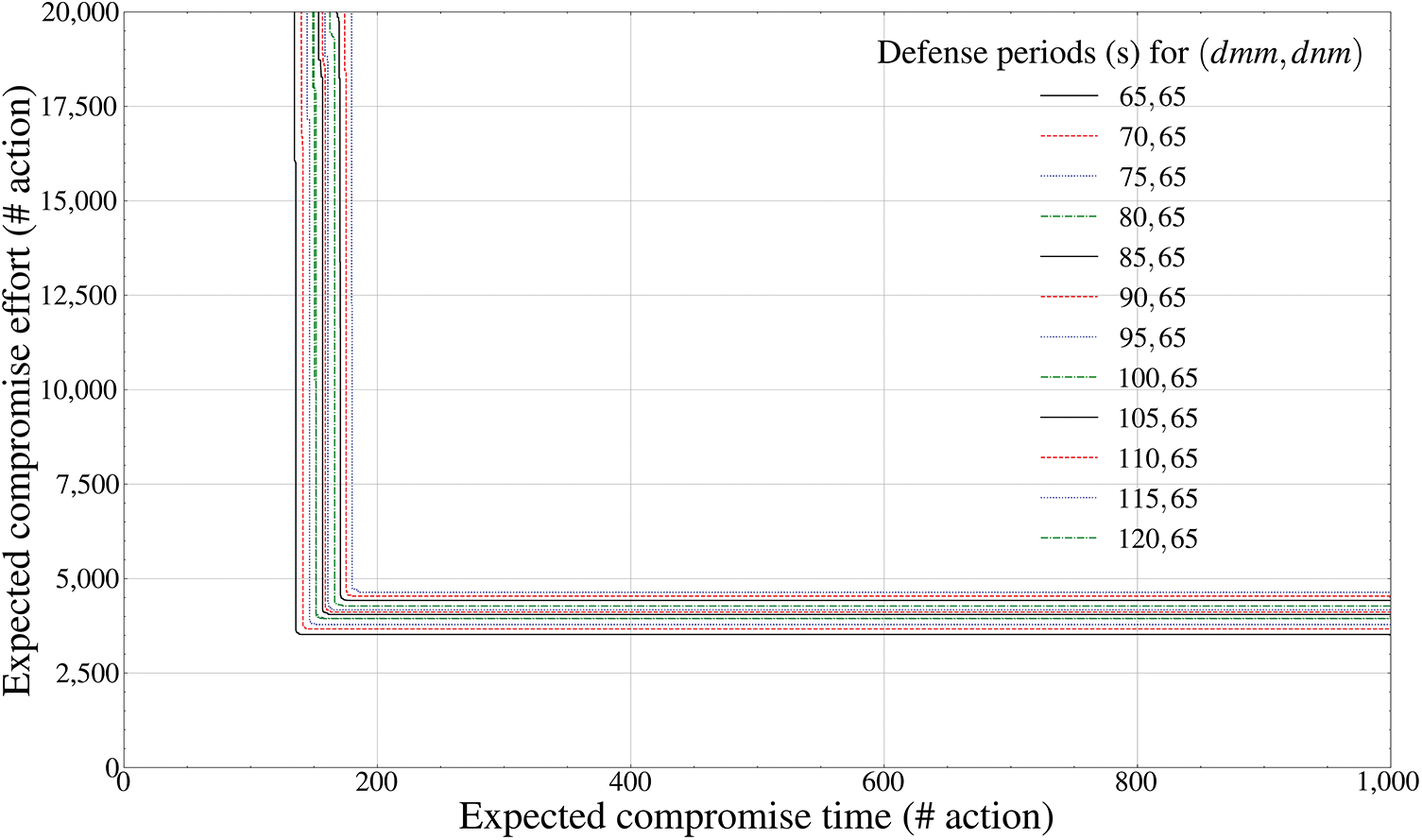
Figure 14: Pareto frontier-based comparison results of defense performance by mutation periods (GCS entity outside the drone, ddmm, 65–120 s)

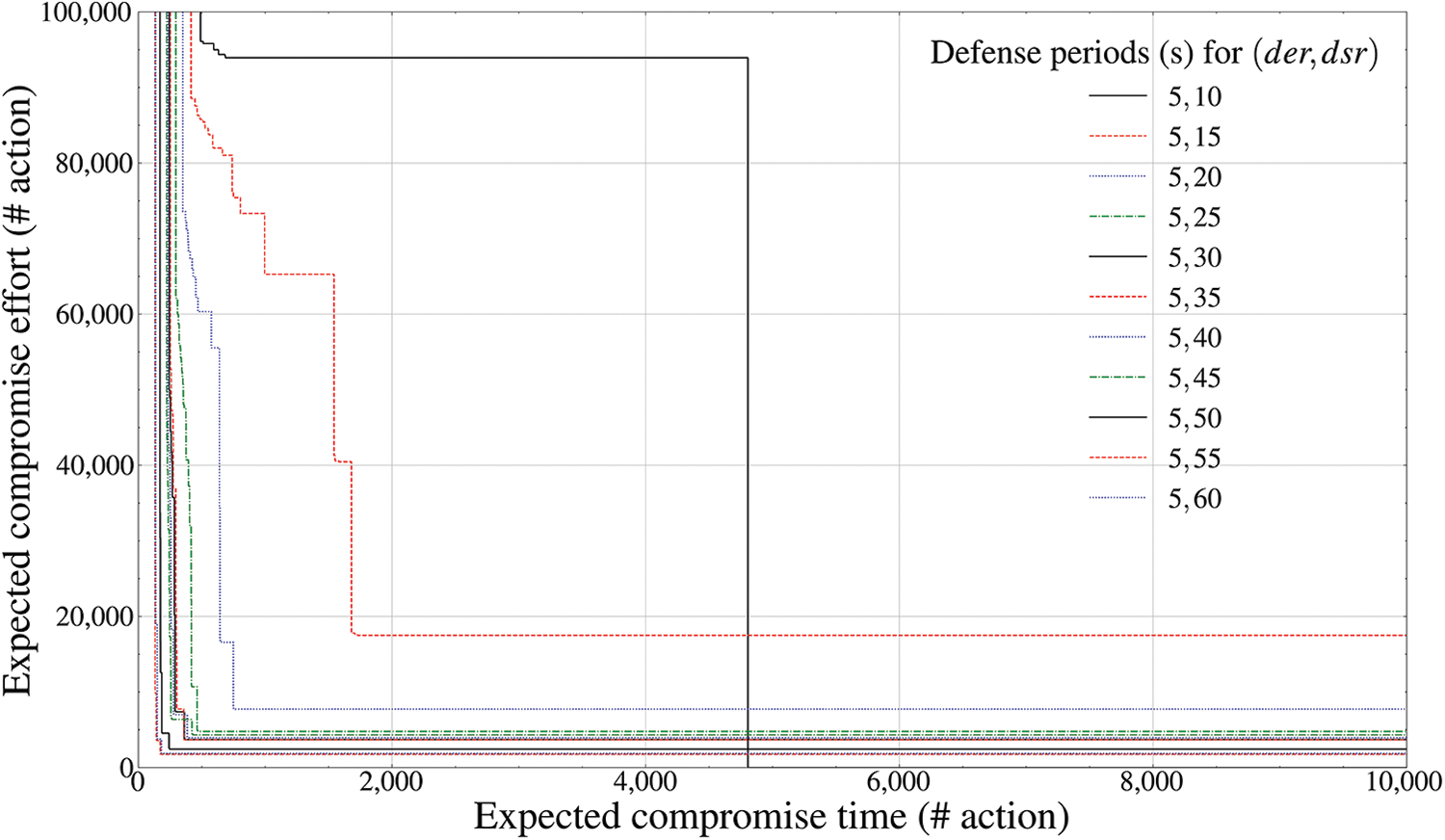
Figure 15: Pareto frontier-based comparison results of defense performance by mutation periods (ZSP entity outside the drone, ddsr, 5–60 s)

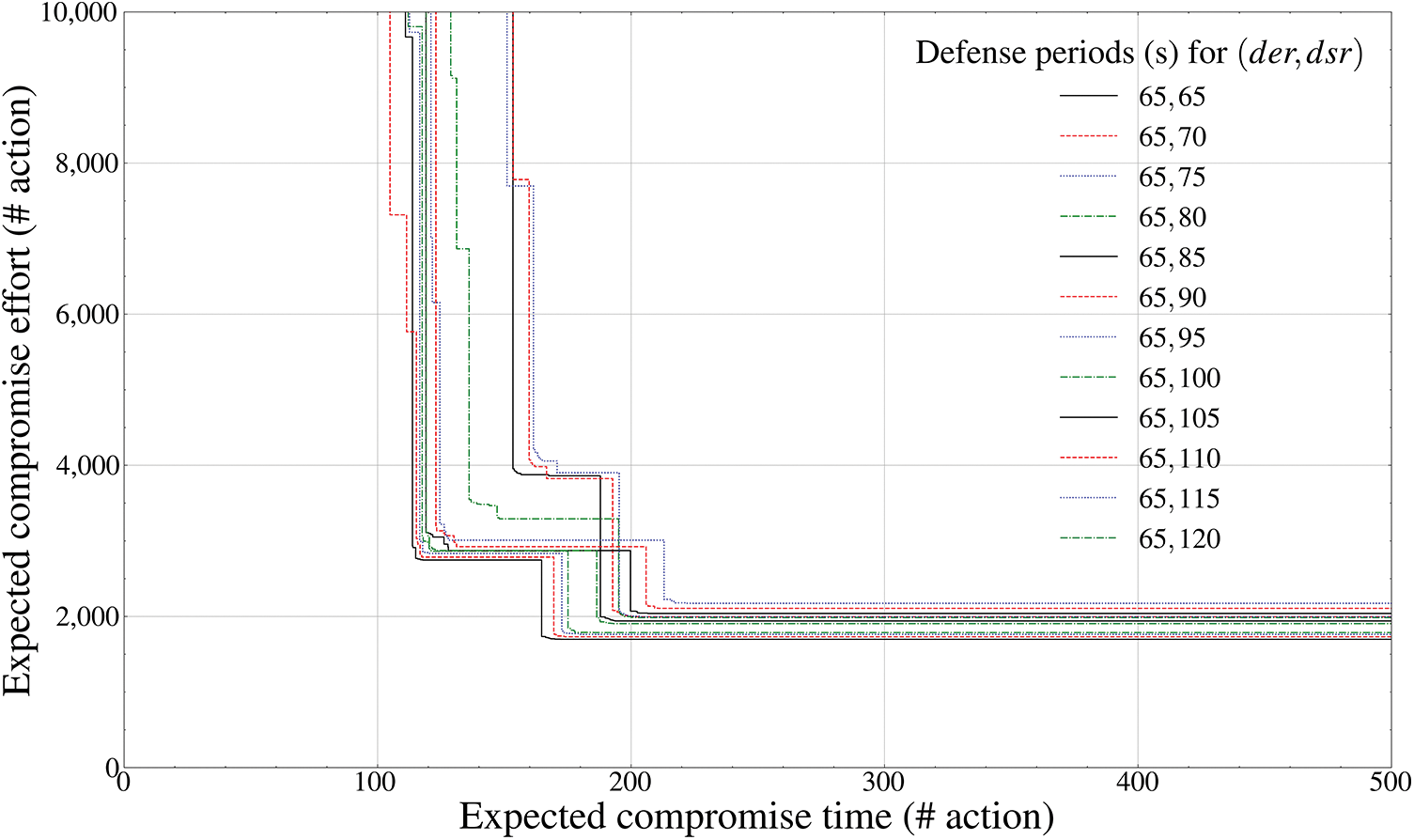
Figure 16: Pareto frontier-based comparison results of defense performance by mutation periods (ZSP entity outside the drone, ddsr, 65–120 s)

‘Expected compromise time’ on the X-axis in Figs. 11–16 denotes the expected attack time (seconds) required as a minimum for an attacker to successfully achieve invasion for each communication entity independently deployed outside the drone, whereas ‘Expected compromise effort’ on the Y-axis denotes the expected attack cost required as a minimum. In addition, the legend axis calculates the fixed mutation period (seconds) of the drone-type MTD corresponding to each external communication entity.

To transmit and receive both battlefield information based on the MAVLink format and spatial-temporal location information based on the GPS format, Figs. 11 and 12 first calculate the Pareto frontier of the dder tactic that mutates the host fingerprint information uniquely exposed by the attached drone entities by targeting the swarming tactical drone network, which has an inherent interdependency between the upper master drone entity and the lower slave drone entity performing a non-line-of-sight communication relay. Fig. 11 shows a pattern in which whenever the mutation period increases by 5 s within the range of [5, 60], dder’s deceptive defense efficiency continues to decrease in the form of behaviors of a log graph with a positive base up to 25 s, compared to the previous one. After 25 s, the deceptive defense efficiency was significantly reduced as an exponential function with a positive gradient, and this change was derived. When the MTD mutation period frequency is high (25 s or less), unlike dder, the ripple effect of the proactive defense of the ddmm tactic, which performs MAVLink information mutation by being applied together to the data link-network-based upper communication layer, and the ddnm tactic, which performs wireless mobile communication payload mutation, is higher than that of dder. Therefore, the side effect of the decrease in the frequency of dder’s mutation period is also a quantitative reflection of the hierarchical characteristics, which are inevitably lower than those of other tactics. When the mutation period frequencies of the commonly applied MTD tactics were all lowered (after 25 s), the defense efficiencies of ddmm and ddmm tactics, which were preemptively avoided in the network and data link-based upper layers, exponentially decreased. Therefore, it is further confirmed that the importance of the dder tactic, which is operated to suboptimally avoid invasion by an attacker who succeeds in bypassing the wireless communication domain, has become relatively high.

Fig. 12 configured to determine the mutation period of dder within the range of [65, 120] additionally calculated that similar to Fig. 11. The deceptive defense efficiency decreases in the form of an exponential function for 70 s; however, a momentum issue that causes it to not stably converge to the practical Pareto frontier after 70 s occurs. Similar to Fig. 10, this is also an unfavorable situation in which the attacker engaging with the defender at that point has already bypassed and neutralized ddmm and ddnm considerably and maliciously occupied the drone communication area. Therefore, the attacker’s dominance cannot be lowered unless the frequency of the dder mutation period increases significantly within the current game state. Therefore, it can be finally derived that the Pareto optimum solution of the dder tactic in Fig. 11 converges to (2350, 59500), and the Pareto optimum solution in Fig. 12 converges to (55, 1300). In addition, it can be calculated that the optimal mutation periods of the dder tactic used for the drone external swarming tactical drone network also result in 25 and 70 s, respectively.

Figs. 13 and 14 calculate the Pareto frontier of the ddmm tactic that mutates the MAVLink payload within an uplink session by targeting the upper GCS in charge of real-time remote control processing of multiple drones used with multiplexed uplink communication channels. Fig. 13 shows that whenever the fixed mutation period changes every 5 s within the range of [5, 60], the deceptive defense efficiency of ddmm compared to the previous one continuously decreases in the form of a log function. Conversely, as shown in Fig. 14, it can be further confirmed that ddmm’s deceptive defense efficiency within the range of [65, 120] is extremely reduced in the form of behaviors of a linear graph with a low amount of gradient.

The aspect of Figs. 13 and 14 is analyzed to be closely related to the bypass possibility of an attacker who tries to preemptively infiltrate early using static data link layer information in GCS. That is, as the effectiveness of the defender intelligence adaptively available to the attacker increases exponentially before 60 s, the degree of success of weaponization-based exploit also increases. From 65 s or above, however, effective weaponization is already completed before mutation, proving that the deceptive defense efficiency determined by each mutation cycle cannot change significantly. Therefore, it can be derived that the optimal mutation period of the ddmm tactic applied to the GCS target outside the drone is 60 s or less, and it can be finally confirmed that the Pareto optimal solution is also determined as (175, 3650).

Finally, Figs. 15 and 16 calculate the Pareto front of the ddsr tactic that mutates the payload in the mobile communication packet transmitted by the wireless sensor targeting ZSP that resiliently supports the sustainability of tactical missions of drones by transmitting changing environmental information such as weather and geographic sensing data and air traffic control information in real-time to tactical drones in the battlefield under the presence of an arbitrary centralized command center. Fig. 15, similar to Fig. 13, shows the continuous decrease in deceptive defense efficiency in the form of behaviors of a logarithmic graph with a positive base whenever the fixed mutation period changes within the range of [5, 60]. This can be analyzed as reflecting the fact that independent avoidance performance for the target object is guaranteed for each tactic applied because the ddsr tactic is conceptualized to be operated hierarchically completely divided from the accompanying dder tactic for the mutation of specification information of the equipment. That is, the scope of spatial-temporal application between dder and ddsr tactics does not overlap; therefore, an asymmetric zero-sum relationship in which the attacker’s weaponization efficiency increases exponentially when the mutation cycle frequency linearly decreases is always reflected in a naive way.

Fig. 16, which is the result for [65, 120], derives the pattern in which the deceptive defense efficiency decreases slightly in the form of a linear graph with a positive gradient until the fixed mutation period of 85 s, and solutions are fixed within a specific Pareto front after 85 s. Thus, it can be derived that the optimal mutation periods of the ddsr tactic progressively available to ZSP outside the drone are 85 s or less, respectively, and it can be finally derived that the Pareto optimal solution also converges to (115, 2800).

4.4 Summary of Experimental Results and Comparison

Finally, the optimal periodic mutation cycle of drone-type MTD and the related solution value of MIQCP-MOGO-based Pareto frontier, which was proof-of-concept (PoC) with MF2-DMTD in Sections 4.1 and 4.2, are all summarized in Table 5. Both of these optimal mutation cycles and Pareto solution set support wireless drones performing drone-type MTD in formalism-based experimental testbed to achieve maximum proactive defense performance with minimum defense cost.

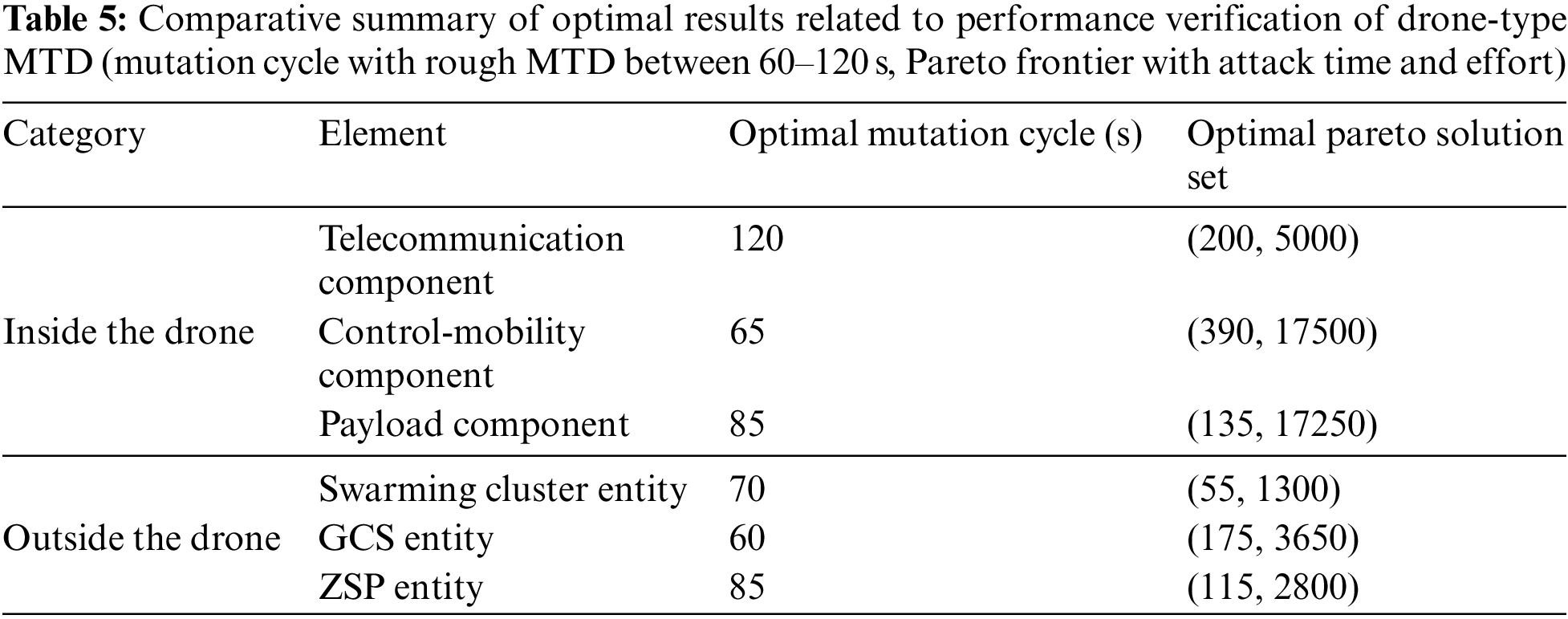
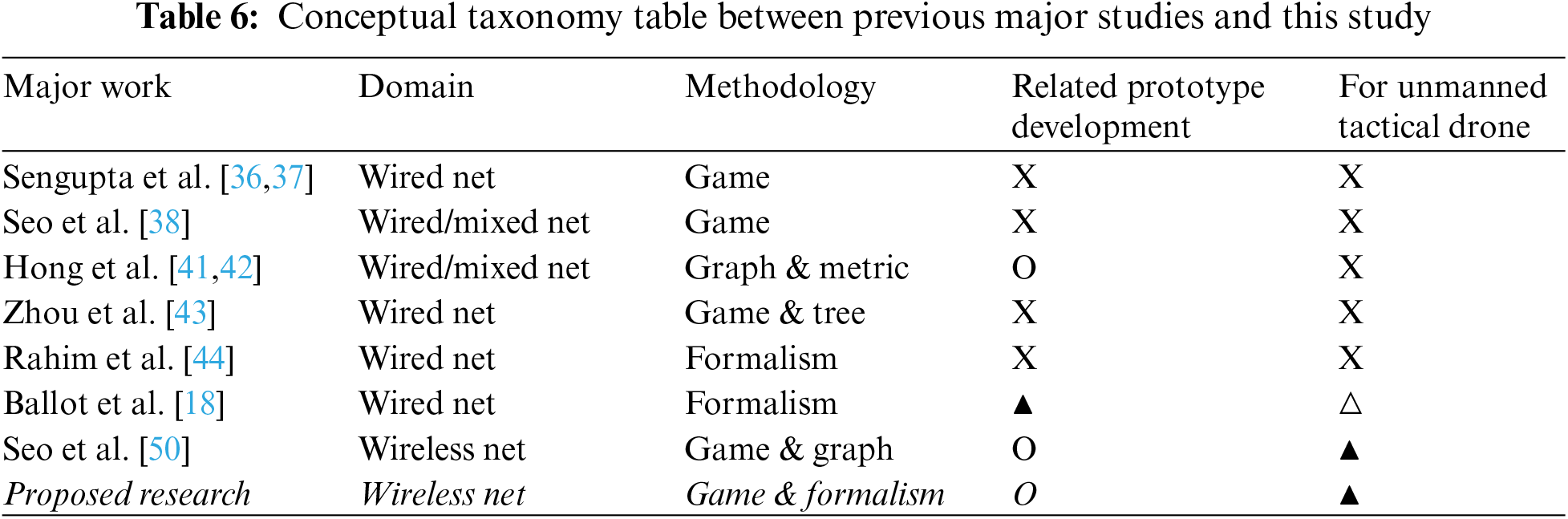
In addition, based on the optimized quantitative measures specified in Table 5, the differences in this study are also presented separately for each major conceptual attribute in Table 6. This study, which is different from previous studies, specified real-time system architecture that combines game theory and formalism for the internal and external communication structure of tactical rugged drones, and also verified the optimal variation period of drone-type MTD by introducing the model checker. In addition, the formal feedback flow of the mutation scheme was also normalized to suit the drone-type MTD designed to meet the continuity and compatibility of tactical drones operated on the battlefield.

5  Discussion and Threat-to-Validity

This study extended the scope of adaptation of mutation principles as ‘what-to-move,’ ‘when-to-move,’ ‘how-to-move’ and the scope of a configuration of the MTD mechanisms selected to provide high attenuation of the spatial-temporal asymmetry of attacker dominance over the potential attack surface of mission-critical systems that must be highly secure and safe to unmanned wireless embedded maneuvering platforms such as tactical drones. Based on a Pareto solver that considers both cyber-agility and resilience, to reason and prove the adaptive deception performance of the proposed drone-type MTD based on a formal method, this study integrated and performed a structural specification based on diversified decision trees according to PTMDP-based formalism, and verification based on zero-sum games and model checking.

This allowed us to calculate the optimized tradeoff between the drone-type MTD mutation period and mutation cost in the form of a Pareto frontier, according to each correlation between the internal functional components and external communication entities of the rugged drone determined based on the de facto standard. This study can also compare and analyze changes in the Pareto critical point with a multivariate real-valued function based on metaheuristic optimization according to the fine-tuning of key indicators, such as the mutation period, by classifying them into each component and entity.

However, all the calculated drone-type MTD-based sensitivity analysis results simulated only the mutation period and mutation target among the MTD principles, and the mutation tactic that determines the priority of the mutation target at the next time point, considered only a limited uniform random scheme. Therefore, a conceptualization of more reinforced random-sampling-based mutation tactics is required. Moreover, despite the regulation of the decision boundary of actors to subjectively recognize the asymmetric information currently available to avoid relying on prior knowledge, the issue remains that the decision-making flow is limited to the range of dedicated drone invasion scenarios according to the decision trees inside and outside the drone configured statically. Thus, the definition of a new probability index in the PTMDP is required to materialize the precalculated engagement process, similar to the concept of an attack graph. In addition, as the internal and external vulnerabilities of drones abstracted within the decision-tree-type threat modeling are attributed only to single CVE vulnerability-based CVSS quantitative scores, they are different from the standards, unique policies, and interoperable rules considered by organizations that operate drones based on critical systems. Therefore, the actualization of the proposed formal framework will be conducted by applying all technical requirements and security controls in the Cybersecurity Framework (CSF) and Risk Management Framework (RMF) standards of the National Institute of Standards and Technology (NIST).

6  Conclusion and Future Work

To protect the unmanned wireless tactical drone, which was not reflected in previous studies that calculated MTD principles by focusing only on operational strategies for wired communication fingerprints and manned-type non-embedded systems, this study proposes a drone-type MTD that performs adaptive mutation on the unique fingerprint of critical system-based rugged drones. This article also presents MF2-DMTD, a formal framework that can simultaneously reason, evaluate, and optimize cyber agility and resilience, which fluctuate according to the application of this MTD.

To this end, this study realized formalism by normalizing the drone’s internal and external threat modeling based on a PTMDP-based decision tree that contains unique vulnerability vectors, attack types, countermeasures, and sub-goals. Additionally, this paper specified conflict modeling for decisions to simulate intentionally non-optimized mutual competition based on information uncertainty according to PBNE and BSS-based zero-sum game logic. In addition, Pareto optimization for the drone-type MTD was achieved by performing both game simulation and model checking based on the MIQCP for formal verification according to preemptive formal specifications.

Consequently, this study can mathematically prove the proactive avoidance efficiency, post-response function continuity, and independent operation of wireless drones, which are unmanned critical systems. Additionally, this research can calculate the causal relationship associated with privatized asymmetric cognitive judgments for each actor based on incompleteness, subjectivity, perturbation, and a priori belief.

To simultaneously realize the optimization performance improvement and domain expansion of the proposed drone-type MTD in the future, these authors plan to advance the drone-type MTD and MF2-DMTD by applying a decoy that performs induction and isolation and hyper game theory, an unbalanced meta-game. To apply and operate these ideas practically in the mission-critical system domain, these authors also plan to upgrade the testbed in the form of a prototype [50] that can be placed on a trial basis within the space-air-ground integrated network based on combat net radio with aerial telemetry sensor [51].

Acknowledgement: The authors thankfully acknowledge support by the Challengeable Future Defense Technology Research and Development Program through the Agency For Defense Development (ADD) funded by the Defense Acquisition Program Administration (DAPA) in 2023. And, the authors also gratefully acknowledge the helpful comments and valuable suggestions of the reviewers, which have improved the academic contributions.

Funding Statement: This research was received external funding by the Challengeable Future Defense Technology Research and Development Program through the Agency For Defense Development (ADD) funded by the Defense Acquisition Program Administration (DAPA) in 2023 (No. 915024201).

Author Contributions: Conceptualization, S.S.; methodology, S.S.; software, S.S.; validation, S.S. and D.K.; formal analysis, S.S. and D.K.; investigation, S.S. B.K. and W.L; resources, S.S. J.L. B.K. W.L. and D.K.; data curation, S.S. and D.K.; writing—original draft preparation, S.S. and D.K.; writing—review and editing, S.S. and D.K.; visualization, S.S.; supervision, J.L. and D.K.; project administration, S.S. J.L. and D.K; funding acquisition, J.L. and D.K. All authors have read and agreed to the published version of the manuscript.

Availability of Data and Materials: Please contact the corresponding author at karmy01@kyonggi.ac.kr.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. Bryan, D. Patt and H. Schramm, Mosaic Warfare: Exploiting Artificial Intelligence and Autonomous Systems to Implement Decision-Centric Operations, Center for Strategic and Budgetary Assessments (CSBA2020. [Online]. Available: https://csbaonline.org/uploads/documents/Mosaic_Warfare_Web.pdf [Google Scholar]

2. A. Martyanov, The (Real) Revolution in Military Affairs, Atlanta: Clarity Press, Inc., 2019. [Online]. Available: http://resistir.info/livros/revolution_military_affairs.pdf [Google Scholar]

3. U. S. army, FM 3-12: Cyberspace Operations and Electromagnetic Warfare, Headquarters, Department of the Army, 2021. [Online]. Available: https://irp.fas.org/doddir/army/fm3-12.pdf [Google Scholar]

4. H. C. Kemp,“ Left of launch: Countering theater ballistic missiles,” Issue Briefs and Reports, Washington DC, USA: Atlantic Council, pp. 1–12, 2017. [Google Scholar]

5. R. E. Navas, F. Cuppens, N. Boulahia Cuppens, L. Toutain and G. Z. Papadopoulos, “MTD, where Art Thou? A systematic review of moving target defense techniques for IoT,” IEEE Internet of Things Journal, vol. 8, no. 10, pp. 7818–7832, 2021. [Google Scholar]

6. K. Kang, J. T. Seo, S. H. Baek, C. W. Kim and K. Park, “SD-MTD: Software-defined moving-target defense for cloud-system obfuscation,” KSII Transactions on Internet and Information Systems, vol. 16, no. 3, pp. 1063–1075, 2022. [Google Scholar]

7. N. Saputro, S. Tonyali, A. Aydeger, K. Akkaya, M. A. Rahman et al., “A review of moving target defense mechanisms for Internet of Things applications,” in Modeling and Design of Secure Internet of Things, 1st ed., vol. 1, Hoboken, NJ, USA: Wiley-IEEE Press, pp. 563–614, 2020. [Google Scholar]

8. J. H. Cheon, K. Han, S. M. Hong, H. J. Kim, J. Kim et al., “Toward a secure drone system: Flying with real-time homomorphic authenticated encryption,” IEEE Access, vol. 6, pp. 24325–24339, 2018. [Google Scholar]

9. T. D. Paul and V. Rathinasabapathy, “Evaluation of LoRaWAN in a highly dense environment with design of common automated metering platform (CAMP) based on LoRaWAN protocol,” KSII Transactions on Internet and Information Systems, vol. 16, no. 5, pp. 1540–1560, 2022. [Google Scholar]

10. J. D. Mireles, E. Ficke, J. H. Cho, P. Hurley and S. Xu, “Metrics towards measuring cyber agility,” IEEE Transactions on Information Forensics and Security, vol. 14, no. 12, pp. 3217–3232, 2019. [Google Scholar]

11. D. J. Bodeau, R. D. Graubart, R. M. McQuaid and J. Woodill, Cyber Resiliency Metrics, Measures of Effectiveness, and Scoring: Enabling Systems Engineers and Program Managers to Select the Most Useful Assessment Methods, MITRE, 2018. [Online]. Available: https://www.mitre.org/sites/default/files/2021-11/prs-18-2579-cyber-resiliency-metrics-measures-of-effectiveness-and-scoring.pdf [Google Scholar]

12. I. Linkov and K. Alexander, “Fundamental concepts of cyber resilience: Introduction and overview,” in Cyber Resilience of Systems and Networks, 1st ed., vol. 1, Cham: Springer, pp. 1–25, 2018. [Google Scholar]

13. J. H. Cho, D. P. Sharma, H. Alavizadeh, S. Yoon, N. Ben-Asher et al., “Toward pro-active, adaptive defense: A survey on moving target defense,” IEEE Communications Surveys & Tutorials, vol. 22, no. 1, pp. 709–745, 2020. [Google Scholar]

14. P. K. Manadhata and J. M. Wing, “An attack surface metric,” IEEE Transactions on Software Engineering, vol. 37, no. 3, pp. 371–386, 2010. [Google Scholar]

15. S. Wang, H. Shi, Q. Hu, B. Lin and X. Cheng, “Moving target defense for Internet of Things based on the zero-determinant theory,” IEEE Internet of Things Journal, vol. 7, no. 1, pp. 661–668, 2020. [Google Scholar]

16. H. Li, W. Shen and Z. Zheng, “Spatial-temporal moving target defense: A Markov stackelberg game model,” in Proc. of AAMAS, Richland, SC, USA, pp. 717–725, 2020. [Google Scholar]

17. A. Konak, D. W. Coit and A. E. Smith, “Multi-objective optimization using genetic algorithms: A tutorial,” Reliability Engineering & System Safety, vol. 91, no. 9, pp. 992–1007, 2006. [Google Scholar]

18. G. Ballot, V. Malvone, J. Leneutre and E. Borde, “Reasoning about moving target defense in attack modeling formalisms,” in Proc. of ACM Workshop on Moving Target Defense, Los Angeles, CA, USA, pp. 55–65, 2022. [Google Scholar]

19. C. Lei, H. Q. Zhang, L. M. Wan, L. Liu and D. H. Ma, “Incomplete information Markov game theoretic approach to strategy generation for moving target defense,” Computer Communications, vol. 116, no. 14, pp. 184–199, 2018. [Google Scholar]

20. S. Sengupta and S. Kambhampati, “Multi-agent reinforcement learning in bayesian stackelberg Markov games for adaptive moving target defense,” arXiv:2007.10457, 2020. [Google Scholar]

21. Uppaal Stratego, 4.1.20-7, 2019. [Online]. Available: https://uppaal.org/casestudies/stratego/ [Google Scholar]

22. Executive Office of the President, Trustworthy Cyberspace: Strategic Plan for the Federal Cybersecurity Research and Development Program, National Science and Technology Council, White House, 2011. [Online]. Available: https://www.nitrd.gov/pubs/Fed_Cybersecurity_RD_Strategic_Plan_2011.pdf [Google Scholar]

23. Z. Wan, J. H. Cho, M. Zhu, A. H. Anwar, C. A. Kamhoua et al., “Foureye: Defensive deception against advanced persistent threats via Hypergame theory,” IEEE Transactions on Network and Service Management, vol. 19, no. 1, pp. 112–129, 2021. [Google Scholar]

24. P. Madani, N. Vlajic and I. Maljevic, “Randomized moving target approach for MAC-layer spoofing detection and prevention in IoT systems,” Digital Threats: Research and Practice, vol. 3, no. 4, pp. 1–24, 2022. [Google Scholar]

25. X. Liang, Y. Wu, Y. Huang, D. W. K. Ng, P. Li et al., “Performance optimization and analysis on P2P mobile communication systems accelerated by MEC servers,” KSII Transactions on Internet and Information Systems, vol. 16, no. 1, pp. 188–210, 2022. [Google Scholar]

26. J. Giraldo and A. A. Cardenas, “Moving target defense for attack mitigation in multi-vehicle systems,” in Proactive and Dynamic Network Defense. Advances in Information Security, 1st ed., vol. 74. Cham: Springer, pp. 163–190, 2019. [Google Scholar]

27. Q. Zhu and T. Basa̧r, “Game-theoretic approach to feedback-driven multi-stage moving target defense,” in Int. Conf. on Decision and Game Theory for Security, FortWorth, TX, USA, pp. 246–263, 2013. [Google Scholar]

28. L. Ge, W. Yu, D. Shen, G. Chen, K. Pham et al., “Toward effectiveness and agility of network security situational awareness using moving target defense (MTD),” in Proc. of SPIE, Baltimore, MD, USA, vol. 9085, pp. 1–9, 2014. [Google Scholar]

29. S. Neti, A. Somayaji and M. E. Locasto, “Software diversity: Security, entropy and game theory,” in Proc. of HotSec-USENIX Workshop on Hot Topics in Security, Bellevue, WA, USA, pp. 1–6, 2012. [Google Scholar]

30. M. Wright, S. Venkatesan, M. Albanese and M. P. Wellman, “Moving target defense against DDoS attacks: An empirical game-theoretic analysis,” in Proc. of ACM Workshop on Moving Target Defense, Vienna, Austria, pp. 93–104, 2016. [Google Scholar]

31. K. M. Carter, J. F. Riordan and H. Okhravi, “A game theoretic approach to strategy determination for dynamic platform defenses,” in Proc. of the First ACM Workshop on Moving Target Defense, AZ, USA, pp. 21–30, 2014. [Google Scholar]

32. R. Colbaugh and K. Glass, “Predictability-oriented defense against adaptive adversaries,” in 2012 IEEE Int. Conf. on Systems, Man, and Cybernetics (SMC), Seoul, Korea, pp. 2721–2727, 2012. [Google Scholar]

33. M. M. Hasan and M. A. Rahman, “Protection by detection: A signaling game approach to mitigate co-resident attacks in cloud,” in Proc. of IEEE Int. Conf. Cloud Computing, Honolulu, HI, USA, pp. 552–559, 2017. [Google Scholar]

34. X. Feng, Z. Zheng, D. Cansever, A. Swami and P. Mohapatra, “A signaling game model for moving target defense,” in Proc. of IEEE INFOCOM, Atlanta, GA, USA, pp. 1–9, 2017. [Google Scholar]

35. Q. Zhu, A. Clark, R. Poovendran and T. Basar, “Deceptive routing games,” in Proc. of IEEE Conf. on Decision Control, Maui, HI, USA, pp. 2704–2711, 2012. [Google Scholar]

36. S. Sengupta, S. G. Vadlamudi, S. Kambhampati, A. Doupé, Z. Zhao et al., “A game theoretic approach to strategy generation for moving target defense in web applications,” in Proc. of AAMAS, São Paulo, Brazil, vol. 1, pp. 178–186, 2017. [Google Scholar]

37. S. Sengupta, A. Chowdhary, D. Huang and S. Kambhampati, “General sum Markov games for strategic detection of advanced persistent threats using moving target defense in cloud networks,” in Proc. of Int. Conf. on Decision Game Theory Security, Stockholm, Sweden, pp. 492–512, 2019. [Google Scholar]

38. S. Seo and D. H. Kim, “IoDM: A study on a IoT-based organizational deception modeling with adaptive general-sum game competition,” Electronics, vol. 11, no. 10, pp. 1–38, 2022. [Google Scholar]

39. P. K. Manadhata, “Game theoretic approaches to attack surface shifting,” in Moving Target Defense II, 1st ed., vol. 100, New York, NY, USA: Springer, pp. 1–13, 2013. [Google Scholar]

40. H. Zhang, K. Zheng, X. Wang, S. Luo and B. Wu, “Strategy selection for moving target defense in incomplete information game,” Computers, Materials & Continua, vol. 62, no. 2, pp. 763–786, 2020. [Google Scholar]

41. J. B. Hong and D. S. Kim, “Assessing the effectiveness of moving target defenses using security models,” IEEE Transactions on Dependable and Secure Computing, vol. 13, no. 2, pp. 163–177, 2016. [Google Scholar]

42. J. B. Hong, S. Y. Enoch, D. S. Kim, A. Nhlabatsi, N. Fetais et al., “Dynamic security metrics for measuring the effectiveness of moving target defense techniques,” Computers & Security, vol. 79, no. 3, pp. 33–52, 2018. [Google Scholar]

43. Y. Zhou, G. Cheng, S. Jiang, Y. Zhao and Z. Chen, “Cost-effective moving target defense against DDoS attacks using trilateral game and multi-objective Markov decision processes,” Computers & Security, vol. 97, pp. 101976, 2020. [Google Scholar]

44. M. A. B. U. Rahim, Q. Duan and E. Al-Shaer, “A formal analysis of moving target defense,” in Proc. of IEEE COMPSAC, Madrid, Spain, pp. 1802–1807, 2020. [Google Scholar]

45. S. Seo, S. W. Han and D. H. Kim, “D-CEWS: DEVS-based cyber-electronic warfare M&S framework for enhanced communication effectiveness analysis in battlefield,” Sensors, vol. 22, no. 9, pp. 1–26, 2022. [Google Scholar]

46. A. Koubâa, A. Allouch, M. Alajlan, Y. Javed, A. Belghith et al., “Micro air vehicle link (MAVlink) in a nutshell: A survey,” IEEE Access, vol. 7, pp. 87658–87680, 2019. [Google Scholar]

47. J. Liu, Y. Shi, Z. M. Fadlullah and N. Kato, “Space-air-ground integrated network: A survey,” IEEE Communications Surveys & Tutorials, vol. 20, no. 4, pp. 2714–2741, 2018. [Google Scholar]

48. M. Gharibi, R. Boutaba and S. L. Waslander, “Internet of drones,” IEEE Access, vol. 4, pp. 1148–1162, 2016. [Google Scholar]

49. R. Bellman, “The theory of dynamic programming,” Bulletin of the American Mathematical Society, vol. 60, no. 6, pp. 503–515, 1954. [Google Scholar]

50. S. Seo, H. E. Moon, S. H. Lee, D. H. Kim, J. Y. Lee et al., “D3GF: A study on optimal defense performance evaluation of drone-type moving target defense through game theory,” IEEE Access, vol. 11, pp. 59575–59598, 2023. [Google Scholar]

51. N. M. Balamurugan, S. Mohan, M. Adimoolam, A. John, G. Thippa et al., “DOA tracking for seamless connectivity in beamformed IoT-based drones,” Computer Standards & Interfaces, vol. 79, no. 103564, pp. 1–12, 2022. [Google Scholar]