Assessing the Efficacy of Improved Learning in Hourly Global Irradiance Prediction

1  Introduction

Increasing concern about the effects of climate change and the need to diversify energy sources has led to a significant increase in the development of renewable energy sources. Among these, solar energy has emerged as a viable option due to its abundance and potential to reduce carbon emissions. Moreover, as oil and gas resources become less available, developing renewable energy sources is becoming increasingly important for the country’s long-term energy security. According to the recent the intergovermental panel on climate change (IPCC) report, solar energy has the potential to meet a significant portion of the world’s energy needs, and Algeria is no exception [1].

Accurately estimating the amount of solar radiation hitting the Earth’s surface is critical for various applications such as photovoltaic systems, heating, medical research, agriculture, and architecture. This is usually done with solar measurement devices such as solarimeters or pyranometers. However, it is difficult to measure solar radiation in many places in Algeria because the meters are too expensive, and the systems are very complex. Even if there are several meteorological stations in different locations in Algeria, measurements may not always be available due to power outages or limitations on the number of variables that can be recorded [2].

To address these challenges, researchers have developed models that use readily available meteorological data to predict global solar radiation (GSR) more accurately. These predictive models are becoming more advanced daily, but results vary by location. Therefore, it is important to use sophisticated GSR prediction techniques to improve solar energy potential prediction accuracy in Algeria [3].

Many research efforts have been made to predict solar radiation (SR) in different areas of the world using various techniques such as artificial intelligence and empirical methods. One popular method is Multilayer Perceptron (ANN-MLP) artificial neural network technology. However, other methods, such as decision tree models, support vector machines (SVMs), and feed-forward radial basis functions (FF-RBFs), have also been used to estimate solar radiation. Researchers such as [4–10] have used SVMs, and others have also used FF-RBF. Loutfi et al. [11] presented three different Feed-Forward Neural Network (FFNN) model topologies for generating global, direct and diffuse hourly solar radiation in Fez, Morocco. In order to perform a comparative study, different models were implemented, including the decision tree model, random forest model, generalized linear models, artificial neural network, linear regression model, and adaptive fuzzy neural interference system model [12]. Bamisile et al. [13] developed and compared eight artificial intelligence models for solar radiation prediction at different time intervals (hourly, every minute, and daily average) using datasets from 6 African countries. They found that different AI models suited different solar radiation estimation tasks. Extreme gradient boost algorithm (XG-Boost) boost was the best model for 10 of the 13 case studies considered in this work. They concluded that hourly solar irradiance prediction is more accurate for the models than the daily average and minute time step.

Solar energy is a focus of Algeria’s ambitious energy policy, which allocates significant resources to solar thermal and photovoltaic resources. Projections indicate that solar energy will account for more than 37% of the country’s electricity generation by 2030 [14]. The annual sunshine duration in Algeria is more than 3,900 h in the Sahara and 3,000 h on the plateaus. The daily energy gain on a horizontal surface of 1 m2 averages 5 KWh [10], in most regions of the country [15]. Thus, solar energy is a good basis to help the country meet its energy needs. However, accurate solar radiation estimates are needed to exploit this potential fully. In this study, we use state-of-the-art machine learning techniques to improve the predictability of solar energy potential in Algeria.

The main objective of this research is to develop a method to optimize the hyperparameters of traditional machine learning using the multilayer perceptron (MLP) and support vector machines, thus increasing the reliability of hourly predictions of global irradiance. We used the FNN-MLP and SVM models to produce a reliable forecast of global solar irradiance at one-hour intervals at stations with different climates in Algeria. The following overview provides the framework for this research work: the materials and processes are discussed in Section 2, while the construction of the model is covered in Section 3, and the results and discussion are presented in Section 4. The paper concluded with a conclusion.

2  Materials and Methods

2.1 Studied Region and Database Collection

In this investigation, two radiometric stations were used to compile the database. The first station, “Shems”, located in Bouzareah in Algeria, recorded experimental data using Kipp and Zonen pyranometers to measure the global horizontal irradiation (GHI). The second station, located in Tamanrasset in the Sahara Desert in southern Algeria, is equipped with an Eppley PSP pyranometer and has the highest solar energy resources in an arid desert environment. Table 1 presents comprehensive information on the two stations used for training and testing purposes, including station ID, station name, latitude, longitude, elevation, climate zone, and data periods. The table indicates that the training station, Bouzareah (BOU), is located in the Mediterranean climate zone and covers the period between January 01, 2014, and December 31, 2014. In contrast, the testing station, Tamanrasset (TAM), is in the hot desert climate zone and covers the period from July 01, 2019, to December 17, 2020. The information in the table is crucial for understanding the data used in the investigation and interpreting the results obtained.

Table 2 provides statistical analysis results for the input and output variables of solar radiation prediction at the BOU and TAM stations for temperature (TMP), humidity (HUM), wind speed (WSP), and global horizontal irradiance at the BOU and TAM stations. The BOU station has a maximum temperature of 44.11°C, a minimum humidity of 8.28%, a mean wind speed of 4.62 m/s, and a mean GHI of 517.88 Wh/m2. The TAM station has a maximum temperature of 38.5°C, a minimum humidity of 2%, a mean wind speed of 5.19 m/s, and a mean GHI of 678.76 Wh/m2. The correlation between these variables and solar radiation is further explored in Table 3. The results show that temperature positively correlates with solar radiation at both stations, with humidity having a negative correlation at BOU and a weak negative correlation at TAM. Wind speed has a weak negative correlation at BOU and a positive correlation at TAM. These correlations can be useful for developing accurate solar irradiance prediction models and designing effective solar energy systems.

Fig. 1 displays the frequency counts of GHI between the two stations, BOU and TAM, at different bin center intervals. The plot reveals that TAM has higher frequency counts of GHI than BOU at all bin center intervals. The highest frequency counts for TAM are at the bin centers of 250, 350, and 450 Wh/m2, with 508, 254, and 192 counts, respectively. In contrast, BOU has its highest frequency counts at the bin centers of 250, 450, and 550 Wh/m2, with 508, 490, and 458 counts, respectively. These results indicate that TAM receives more GHI than BOU due to their different geographic locations and climatic conditions. Such analysis is valuable for understanding the variability of GHI and designing solar energy systems.

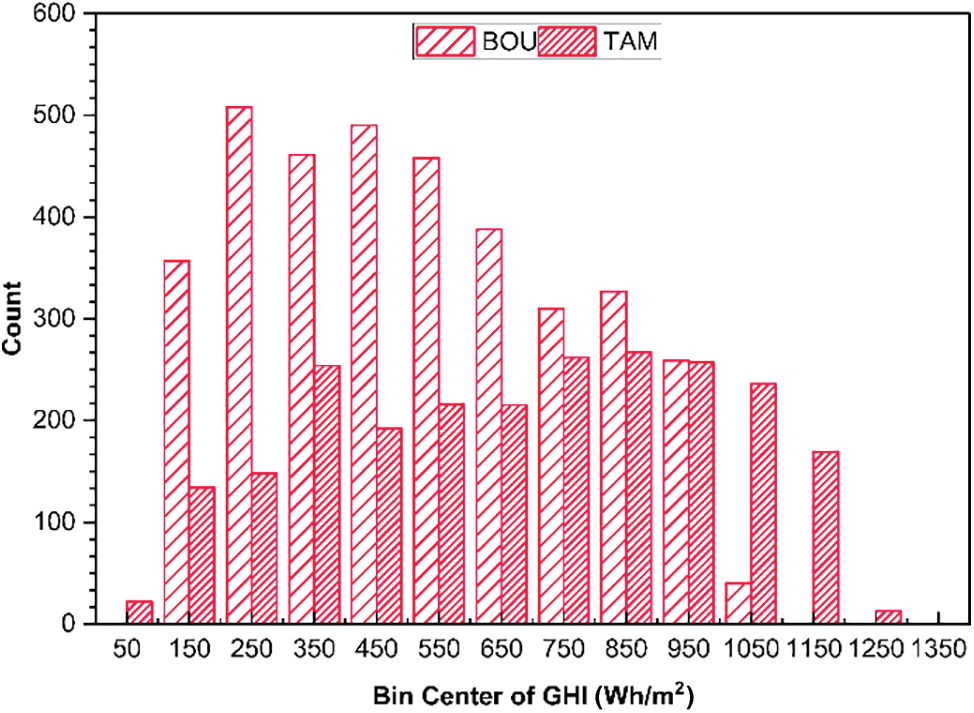
Figure 1: Graphical depiction of the GHI as a function of the relative frequency of each station

2.2 Feedforward Neural Networks Multi-Layer Perceptron (FNN-MLP)

Feedforward Neural Networks’ multilayer perceptron, also known as FNN-MLP, is modeled on the human brain’s information processing. Their known ability to learn from their environment makes them ideal for nonlinear modeling systems that are difficult to characterize analytically. Even though the architecture allows for arbitrarily small approximation errors with related weight values, there is still an obstacle to their efficiency in some form of training. The multilayer perceptron, whose architecture defines multiple layers of neurons, is today’s most widely used supervised neural network for approximation problems.

The “FNN-MLP” consists of three layers: an input layer, a hidden layer, and an output layer. Each of these layers hides information from the other two layers. Synaptic weights, Wij. connect the neurons in a layer to the neurons below it. These weights determine the relative importance of each input to the output of each neuron. An activation function ensures that each neuron picks up all the information transmitted by the neurons that preceded it in the layered structure. After this step, an output signal is generated, ready for transmission to the neurons in the subsequent layer [11,16]. An “FNN-MLP” with three layers is shown in Fig. 2 and is used to predict GHI.

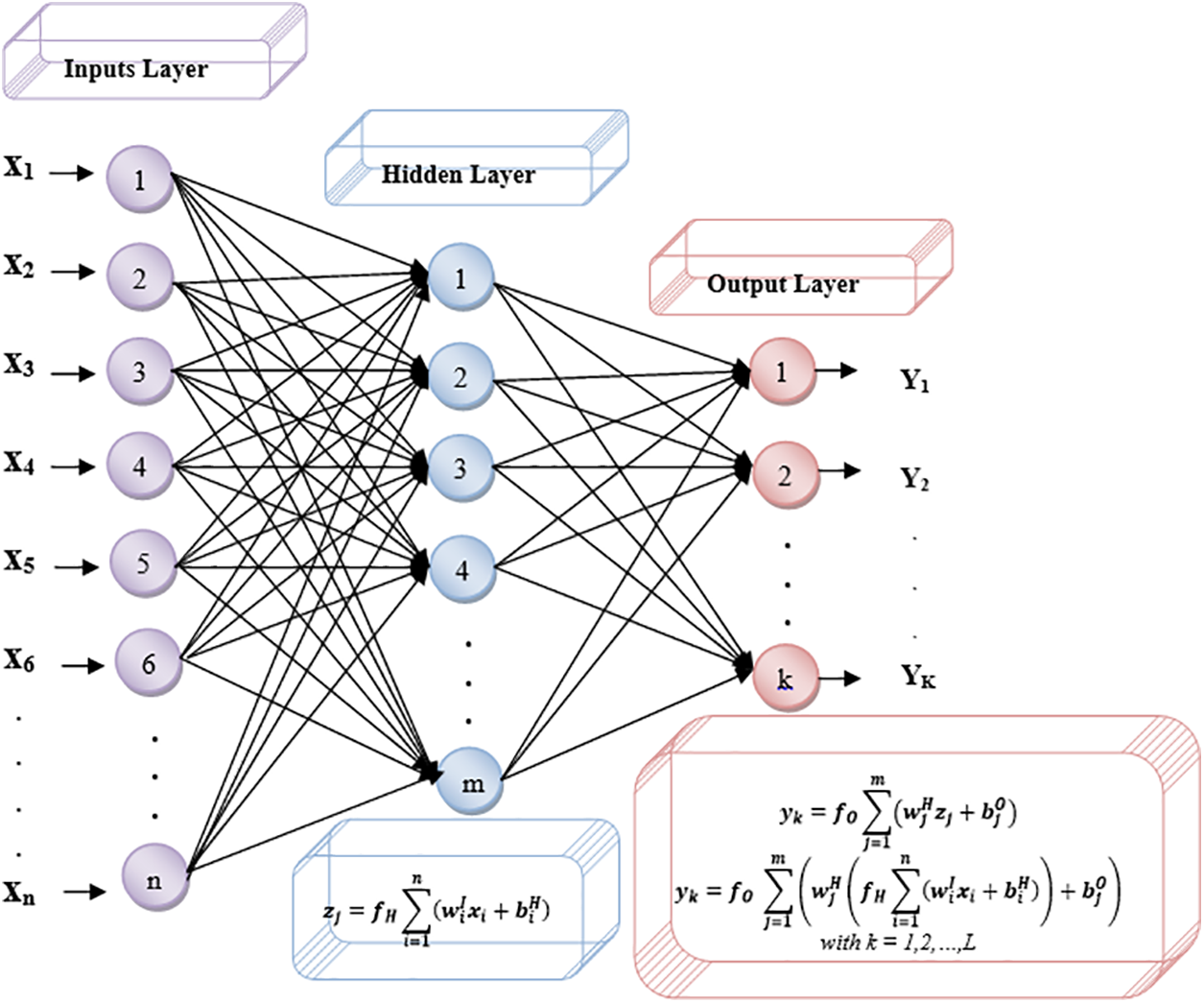
Figure 2: Three-layer feed-forward neural network multilayer perceptron

wI, and wh: connection weights (input-hidden, hidden-output)

bh, and bo: columns vector of neuron bias hidden and output, respectively.

The following Eqs. (4) and (5) represent the assimilation of the GHI in an accurate model that includes all inputs xi.

The instance outputs Zj of the hidden layer:

Zj=fH[∑i=108wjiIxi+bjH]=exp⁡(∑i=108wjiIxi+bjH)−exp⁡(−∑i=108wjiIxi+bjH)exp⁡(∑i=108wjiIxi+bjH)+exp⁡(−∑i=108wjiIxi+bjH)(1)

j = 1, 2… 23

The output “GHI”

GHI=f0[∑j=123w1jHZj+b1o]=∑j=123w1jHZj+b1o(2)

The following mathematical formula, which accounts for all inputs and represents the global solar radiation, is produced when Eqs. (1) and (2) are combined.

GSR =∑j=123w1jHexp⁡(∑i=108wjiIxi+bjH)−exp⁡(−∑i=108wjiIxi+bjH)exp⁡(∑i=108wjiIxi+bjH)+exp⁡(−∑i=108wjiIxi+bjH)+b1o(3)

The “FNN-MLP” framework was optimized for GHI prediction using MATLAB 2020b. The methods, database distribution, layer depth, neuron count, and activation functions are all included. Table 4 displays the optimized FNN-MLP model’s structure.

2.3 Support Vector Machines (SVM)

The Support Vector Machine, commonly known as SVM, is a supervised learning method that has gained significant popularity recently for its ability to predict meteorological data such as temperature [17] and wind speed [18]. The ease of use and adaptability of the SVM method makes it suitable for a wide range of classification and regression problems across various sectors, including mechanical engineering, energy, finance [19], and more. Despite its potential use in studies with small sample sets, the SVM method has been shown to provide balanced predicted performance due to its unique characteristics [20]. In an SVM model, the regression function can model nonlinear relationships between input and output. The output of an SVM model can be determined by solving a specific equation [21]:

f(xi)=ωT∅(xi)+b,i=1,2,…,n(4)

f(xi) : The predicted data.

∅(xi): The implicitly constructed nonlinear function.

ω: The SVM model’s weight vector.

b: The SVM model’s bias.

The dataset has a D-dimensional input vector xi∈RD and a scalar output yi∈R.

The following equations provide the SVM optimization model (for the training set):

{minR(w,ξ,ξ∗,ε)=12‖w‖2+C[vε+1N∑i=1N(ξi+ξi∗)]subjective to :yi−wTφ(xi)−b≤ε+ξiwTφ(xi)+b−yi≤ε+ξiξ∗,ε≥0(5)

C: The factor that balances model complexity with empirical risk ‖w‖2

ξi∗: The slack variable to represent the sample’s distance from the -tube

The problem above can be solved in the same manner as a standard nonlinear restricted optimization problem by utilizing the concepts of Lagrange multipliers to generate a dual optimization problem:

{maxR(ai,ai∗)=∑i=1Nyi(ai,ai*)−12∑i=1N∑j=1N(ai,ai∗)(aj,aj*)K(xi,xj)subjective to :∑i=1Nyi(ai,ai*)=00≤ai,ai∗≤C/N∑i=1N(ai+ai∗)≤C.v(6)

K(xi,xj): Mercer’s condition-satisfying kernel function.

ai and ai∗: The non negative Lagrange multipliers.

y^=f(xi)=∑i=1N(ai−ai∗)K(x−xi)+b,i=1,2,…,n(7)

2.4 Model Development

Two models were used to develop an accurate prediction of hourly global solar irradiance: The FNN-MLP and the SVM. The process used to evaluate and improve the structure of the FNN-MLP and SVM models is shown in detail in Fig. 3. The datasets were divided into different subsets for each model. The FNN-MLP model’s datasets were divided into three subsets: The training, validation, and testing phases. For the SVM model, on the other hand, the datasets were divided into two subsets, the training phase, and the testing phase. Both subsets were created from the entire data set.

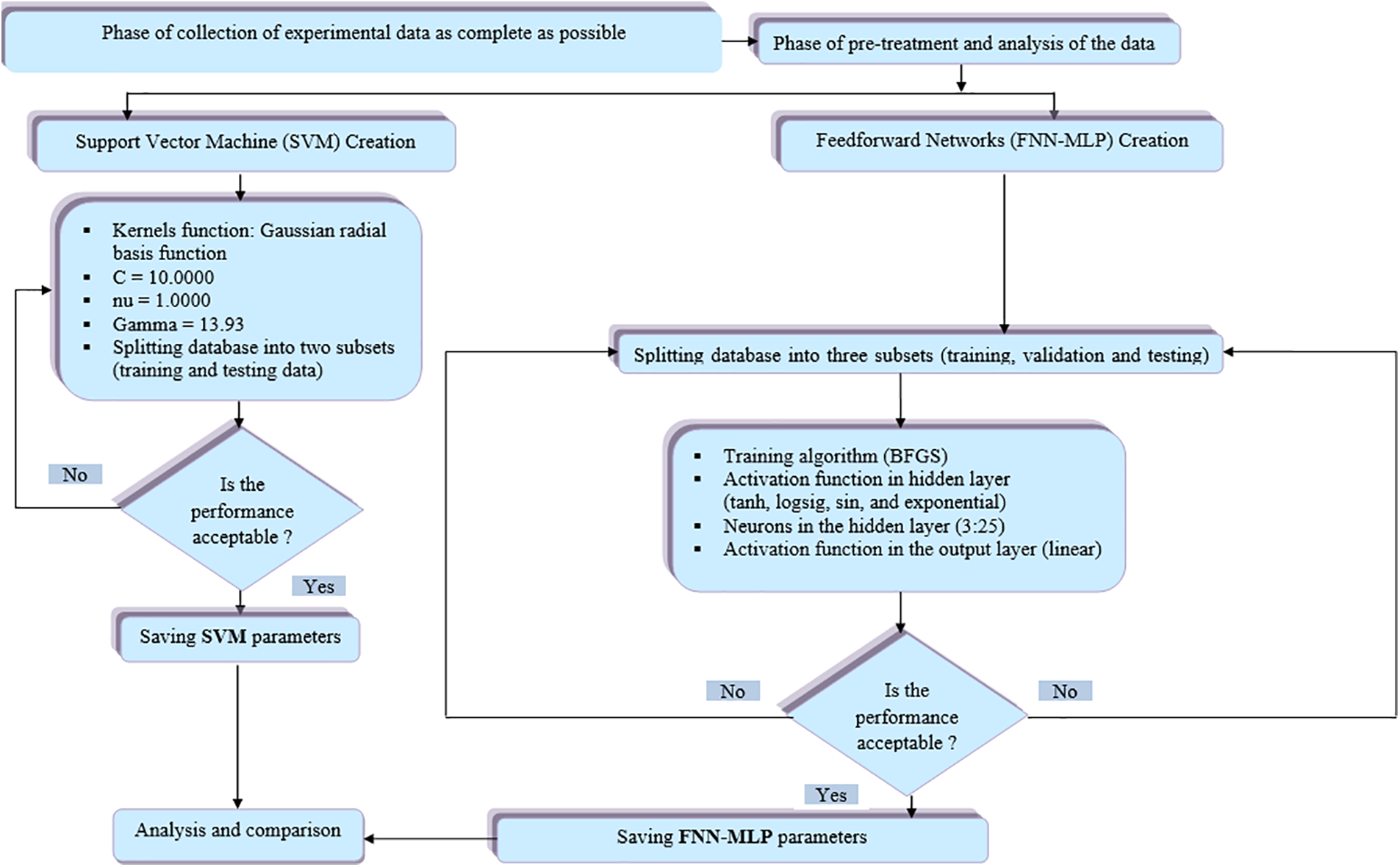
Figure 3: Flow diagram for the two models (FNN-MLP) and (SVM) development

Several techniques were used to determine the most effective FNN-MLP model. The BFGS quasi-Newton training algorithm (trainbfg) was used, four activation functions (log sigmoid, tangent sigmoid, exponential, and sin) were used in the hidden layer, and a single transfer function (identity) was used. Experiments were performed with different sizes for the hidden layers (from 3 to 25 neurons) to obtain the most accurate model possible. An iterative testing process was performed to determine the FNN-MLP model with the best performance. An optimal SVM model was developed using the support vector machine learning strategy for the SVM technique. The selection of appropriate kernel features is critical to the success of the SVM model. The STATISTICA software provides a wide range of kernel functions for SVM models. The penalty term for the Gaussian radial basis function parameters was set to nu = 1.0000, C = 10.0000, and Gamma = 13.93. This process determined the optimal values for the target parameters of the SVM model.

2.5 Evaluation Criteria

In this study, various error measures were employed to determine the level of accuracy of the prediction models. These error measures include the Correlation Coefficient (R), mean percentage error (MPE), and Root Mean Squared Error (RMSE). These measures are mathematically represented by Eqs. (8)–(10) as described in [22–32]. These error measures allow for a comprehensive evaluation of the performance of the prediction models, providing a clear understanding of their strengths and weaknesses.

R=∑i=1n(Yi,exp−Yi,exp¯)(Yi,cal−Yi,cal¯)∑i=1n(Yi,exp−Yi,exp¯)2∑i=1n(Yi,cal−Yi,cal¯)2(8)

MPE=100n∑i=1n|Yi,cal−Yi,exp|Yi,exp(9)

RMSE=∑i=1n(Yi,cal−Yi,exp)2n(10)

n is the number of data points; Yi,exp and Yi,cal are the experimental and calculated data points of global solar radiation, respectively; and Yi,exp¯ is the mean experimental data.

3  Results and Discussion

This subsection presents the results of the models developed in the study to predict hourly global irradiation. Initially, data collected from the Bouzareah station generated two models: The FNN-MLP and SVM. The performance of these models was evaluated using three different data divisions for training, validation, and testing. The results were visualized in Fig. 4, which depicts the correlation coefficient (R) error values obtained for each division. It can be observed that division 3 outperforms the other two divisions in terms of R-values for the testing phase, yielding R = 0.9567 for the FNN-MLP model and R = 0.9715 for the SVM model. For the FNN-MLP model, division 3 consisted of 60% of the data for training, 20% for validation, and 20% for testing. For the SVM model, division 3 had 60% of the data for training and 40% for testing. The results suggest that division 3 provides the most accurate predictions, making it the optimal choice for testing the FNN-MLP and SVM models.

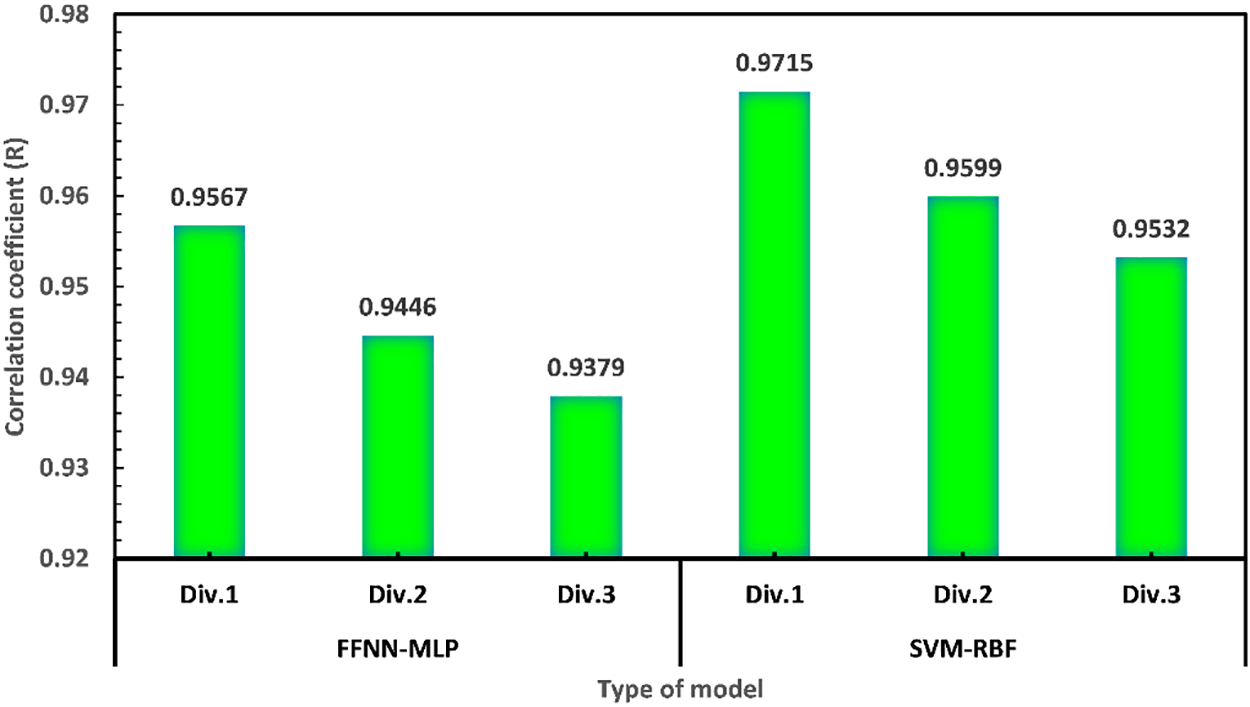
Figure 4: Effect of the division of the database in term coefficient correlation (R) for the testing phase

The performance statistics of the optimal FNN-MLP model for the training, validation, testing, and overall phases in terms of R, MPE, and RMSE are presented in Table 5. The coefficient R-values of 0.9543 or higher during the training phase indicate a strong agreement between the predicted and experimental values. The testing phase’s correlation coefficient “R” measures the model’s ability to interpolate the experimental data accurately. The correlation value of 0.9567 for the testing phase demonstrates a high level of consistency between the experimental and predicted global solar radiation values (see Fig. 5), indicating the effectiveness of the FNN-MLP model.

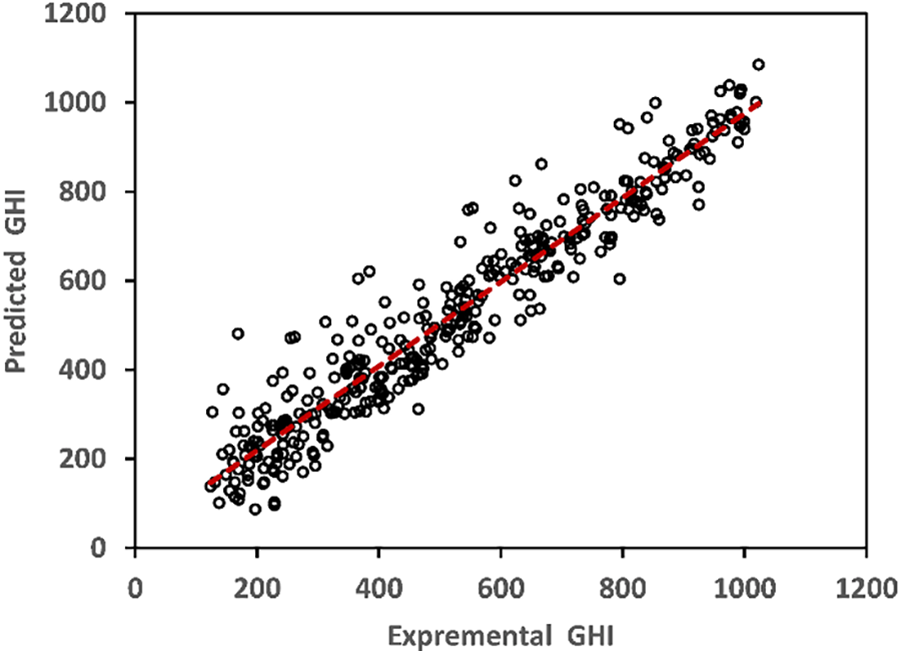
Figure 5: Comparison of predicted and experimental data in the testing phase

Table 6 evaluates several support vector machine (SVM) models utilizing various kernels, including linear, polynomial, radial basis function (RBF), and sigmoid kernels. The performance of each model is evaluated using the root mean square error (RMSE) and the correlation coefficient (R) in different phases, including the training phase, testing phase, and total phase.

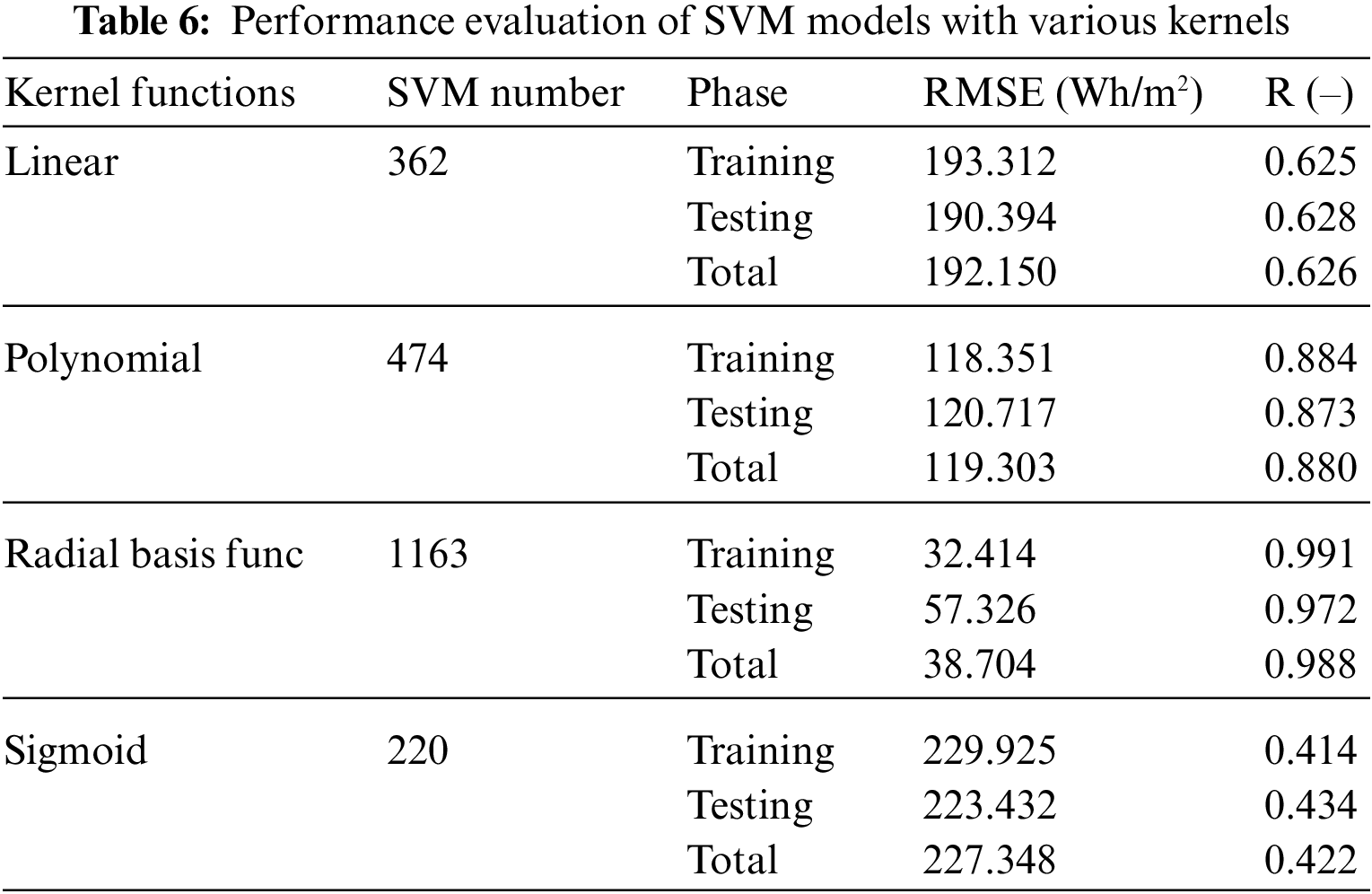
The linear SVM model with C = 10 and E = 0.1 achieved an RMSE of 193.312 Wh/m2 and R of 0.625 in the training phase, an RMSE of 190.394 Wh/m2 and R of 0.628 in the testing phase, and an overall RMSE of 192.150 Wh/m2 and R of 0.626. The polynomial SVM model with C = 10, nu = 1, Degree = 3, and Gamma = 0.125 achieved the lowest RMSE of 118.351 Wh/m2 and highest R of 0.884 in the training phase, an RMSE of 120.717 Wh/m2 and R of 0.873 in the testing phase, and an overall RMSE of 119.304 Wh/m2 and R of 0.880.

The RBF-SVM model with C = 10, nu = 1, and Gamma = 13.93 achieved the lowest RMSE of 32.414 Wh/m2 and highest R of 0.991 in the training phase but had a higher RMSE of 57.326 Wh/m2 and lower R of 0.972 in the testing phase, resulting in an overall RMSE of 38.706 Wh/m2 and R of 0.988. The sigmoid SVM model with C = 10, nu = 0.1, and Gamma = 0.125 had the highest RMSE of 229.925 Wh/m2 and lowest R of 0.414 in the training phase, an RMSE of 223.432 Wh/m2 and R of 0.434 in the testing phase, and an overall RMSE of 227.348 Wh/m2 and R of 0.422.

Overall, the RBF-SVM model with C = 10, nu = 1, and Gamma = 13.93 outperformed the other evaluated models, achieving the lowest RMSE and the highest R-value in the training phase, as well as the second-lowest RMSE and the second-highest R-value in the testing phase. This resulted in the lowest overall RMSE and the highest overall R-value. In comparison to the linear and sigmoid SVM models, the RBF-SVM model demonstrated a substantial improvement in both RMSE and R-values during the training and testing phases, indicating its efficacy in predicting hourly global horizontal irradiation. Furthermore, Fig. 6 reveals a robust alignment between the predicted and actual values gathered from the solar irradiation measurement station, further substantiating the models’ dependability and precision in predicting global irradiation using the chosen input features.

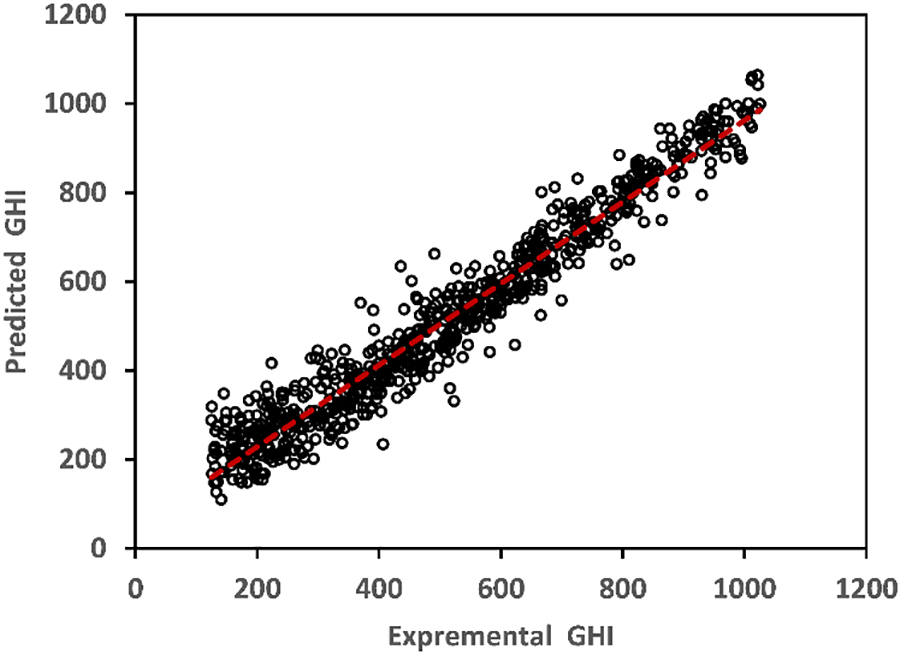
Figure 6: Comparison of predicted and actual hourly global solar irradiation

Following a comprehensive verification process, we present the performance evaluation of the FNN-MLP and RBF-SVM models for solar radiation prediction at BOU and TAM stations in Table 7. The evaluation criteria include the R, MPE, and RMSE across the training, testing, and total phases.

Both models demonstrated reasonable accuracy in predicting solar radiation. However, the SVM-RBF model exhibited superior performance compared to the FNN-MLP model in terms of R and RMSE values for both stations, particularly during the testing phase. During the training phase, the FNN-MLP model achieved R values of 0.9544 and 0.9322 for the BOU and TAM stations, respectively. In contrast, the SVM-RBF model achieved notably higher R-values of 0.9914 and 0.9204 for the same stations.

Moreover, incorporating additional inputs such as MON, PRE, and WID did not yield improvements in the model’s performance. These findings indicate that the SVM-RBF model provides a more accurate GHI prediction than the FNN-MLP model.

The performance of the present work model in predicting hourly global solar radiation was compared with different techniques used in previous studies. Table 8 compares different machine learning models used in literature studies, providing insights into the effectiveness of the present work model compared to other techniques. The RBF-SVM model used in the present work achieved the highest prediction accuracy (R = 0.9876), outperforming other models such as random forest, artificial multi-neural, and adaptive approach, which also achieved high prediction accuracies ranging from R = 0.95 to R = 0.96. The K-means clustering-NAR model had the lowest prediction accuracy (R = 0.93).

4  Conclusion

This study aims to improve the accuracy of hourly global horizental irradiation prediction by using advanced machine-learning techniques. The main objective is to develop a method that optimizes the hyperparameters of conventional machine learning models, specifically multilayer Perceptron Feedforward Neural Networks (FNN-MLP) and Support Vector Machines (SVM). To achieve this, two models were used: the FNN-MLP and the SVM.

To create the most effective model FNN-MLP, the BFGS quasi-Newton method was used as the training algorithm, four activation functions were tested in the hidden layer, and a single transfer function was used. The dimensions of the hidden layers were also varied to obtain the most accurate model possible. Regarding power and performance, the SVM model with the radial basis function (RBF) kernel function gives significantly better results than the SVM models with other functions. The RBF kernel function also shows a superior capacity in characterizing the SVM model’s hourly global solar irradiance forecast.

The statistical error difference values between the RBF-SVM model and the FNN-MLP model are significant, indicating the higher accuracy of the proposed RBF-SVM model in predicting global solar irradiance compared to the FNN-MLP model. Moreover, all the machine learning methods discussed in this study provide highly accurate predictions of global solar irradiance at different temporal resolutions. However, our results show that the RBF-SVM model performs better than the FNN-MLP-BFGS model in predicting hourly global solar irradiance, with an R-value of 0.99 and an RMSE of 38.70 Wh/m2 over all phases. Moreover, this study also investigates the performance of the proposed models in different climatic regions of Algeria, which is crucial for accurately predicting solar radiation at a specific location. In this way, it could help in the design and installation of solar energy systems as well as in the evaluation of thermal conditions in building studies.

In summary, this study provides a promising alternative to the traditional methods currently used in Algeria to predict solar radiation. With its superior accuracy and performance, the RBF-SVM model can be a valuable tool for predicting global solar irradiance at any location, thus supporting the development and implementation of renewable energy sources in the country. In addition, the study opens the possibility of using these techniques in other countries with similar climate and energy needs.

Acknowledgement: The authors would like to thank the University of Relizane and the University of Dr. Yahia Fares-Laboratory Medea’s of Biomaterials and Transport Phenomena for their assistance with this work.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design, Y. Ammi, N. Bailek, S. Hanini, L. Abualigah, E. El-kenawy; analysis and interpretation of results, A. Dahmani, Y. Ammi, S. Hanini, I. Colak, L. Abualigah; draft manuscript preparation, A. Dahmani, Y. Ammi, E. El-kenawy; writing—review and editing: N. Bailek, A. Kuriqi, N. Al-Ansari, I. Colak, L. Abualigah. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the reported findings are all available within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Takilalte, S. Harrouni, M. R. Yaiche and L. Mora-López, “New approach to estimate 5-min global solar irradiation data on tilted planes from horizontal measurement,” Renewable Energy, vol. 145, pp. 2477–2488, 2020. [Google Scholar]

2. M. Laidi, S. Hanini, A. Rezrazi, M. R. Yaiche, A. A. El Hadj et al., “Supervised artificial neural network-based method for conversion of solar radiation data (case study: Algeria),” Theoretical and Applied Climatology, vol. 128, no. 1–2, pp. 439–451, 2017. [Google Scholar]

3. A. Rezrazi, S. Hanini and M. Laidi, “An optimisation methodology of artificial neural network models for predicting solar radiation: A case study,” Theoretical and Applied Climatology, vol. 123, no. 3–4, pp. 769–783, 2015. [Google Scholar]

4. K. Mohammadi, S. Shamshirband, M. H. Anisi, K. A. Alam and D. Petković, “Support vector regression based prediction of global solar radiation on a horizontal surface,” Energy Conversion and Management, vol. 91, pp. 433–441, 2015. [Google Scholar]

5. J. L. Chen and G. S. Li, “Evaluation of support vector machine for estimation of solar radiation from measured meteorological variables,” Theoretical and Applied Climatology, vol. 115, no. 3, pp. 627–638, 2014. [Google Scholar]

6. J. Piri, S. Shamshirband, D. Petković, C. W. Tong and M. H. ur Rehman, “Prediction of the solar radiation on the Earth using support vector regression technique,” Infrared Physics & Technology, vol. 68, pp. 179–185, 2015. [Google Scholar]

7. L. Olatomiwa, S. Mekhilef, S. Shamshirband, K. Mohammadi, D. Petkovic et al., “A support vector machine-firefly algorithm-based model for global solar radiation prediction,” Solar Energy, vol. 115, pp. 632–644, 2015; [Google Scholar]

8. Z. Ramedani, M. Omid, A. Keyhani, B. Khoshnevisan and H. Saboohi, “A comparative study between fuzzy linear regression and support vector regression for global solar radiation prediction in Iran,” Solar Energy, vol. 109, pp. 135–143, 2014. [Google Scholar]

9. M. Guermoui, R. Abdelaziz, K. Gairaa, L. Djemoui and S. Benkaciali, “New temperature-based predicting model for global solar radiation using support vector regression,” International Journal of Ambient Energy, vol. 43, no. 1, pp. 1397–1407, 2020. [Google Scholar]

10. S. Chen, C. He, Z. Huang, X. Xu, T. Jiang et al., “Using support vector machine to deal with the missing of solar radiation data in daily reference evapotranspiration estimation in China,” Agricultural and Forest Meteorology, vol. 316, pp. 108864, 2022; [Google Scholar]

11. H. Loutfi, A. Bernatchou, Y. Raoui and R. Tadili, “Learning processes to predict the hourly global, direct, and diffuse solar irradiance from daily global radiation with artificial neural networks,” International Journal of Photoenergy, vol. 2017, pp. 1–13, 2017. [Google Scholar]

12. A. Jain and T. Roy, “Evaporation modelling using neural networks for assessing the self-sustainability of a water body,” Lakes & Reservoirs: Research & Management, vol. 22, no. 2, pp. 123–133, 2017. [Google Scholar]

13. O. Bamisile, D. Cai, A. Oluwasanmi, C. Ejiyi, C. C. Ukwuoma et al., “Comprehensive assessment, review, and comparison of AI models for solar irradiance prediction based on different time/estimation intervals,” Scientific Reports, vol. 12, no. 1, pp. 9644, 2022 [Google Scholar] [PubMed]

14. M. Zaid, S. Khouildat and A. R. Siagh, “Strategy of the renewable energy in Algeria, as an inevitable drift to diversification of the economy,” Transport, vol. 13, no. 13, 889, pp. 3–9, 2017. [Google Scholar]

15. A. B. Stambouli, Z. Khiat, S. Flazi and Y. Kitamura, “A review on the renewable energy development in Algeria: Current perspective, energy scenario and sustainability issues,” Renewable and Sustainable Energy Reviews, vol. 16, no. 7, pp. 4445–4460, 2012; [Google Scholar]

16. B. Amiri, R. Dizène and K. Dahmani, “Most relevant input parameters selection for 10-min global solar irradiation estimation on arbitrary inclined plane using neural networks,” International Journal of Sustainable Energy, vol. 39, no. 8, pp. 779–803, 2020. [Google Scholar]

17. Y. Radhika and M. Shashi, “Atmospheric temperature prediction using support vector machines,” International Journal of Computer Theory and Engineering, vol. 1, no. 1, pp. 55–58, 2009. [Google Scholar]

18. M. A. Mohandes, T. O. Halawani, S. Rehman and A. A. Hussain, “Support vector machines for wind speed prediction,” Renewable Energy, vol. 29, no. 6, pp. 939–947, 2004. [Google Scholar]

19. S. G. Meshram, V. P. Singh, O. Kisi, V. Karimi and C. Meshram, “Application of artificial neural networks, support vector machine and multiple model-ANN to sediment yield prediction,” Water Resources Management, vol. 34, no. 15, pp. 4561–4575, 2020. [Google Scholar]

20. M. A. Hassan, N. Bailek, K. Bouchouicha, A. Ibrahim, B. Jamil et al., “Evaluation of energy extraction of PV systems affected by environmental factors under real outdoor conditions,” Theoretical and Applied Climatology, vol. 150, no. 1, pp. 715–729, 2022. [Google Scholar]

21. J. García-Alba, J. F. Bárcena, C. Ugarteburu and A. García, “Artificial neural networks as emulators of process-based models to analyse bathing water quality in estuaries,” Water Research, vol. 150, pp. 283–295, 2019. [Google Scholar]

22. Y. Ammi, L. Khaouane and S. Hanini, “A comparison of neural networks and multiple linear regressions’ models to describe the rejection of micropollutants by membranes,” Kemija U Industriji, vol. 69, no. 3–4, pp. 111–127, 2020. [Google Scholar]

23. N. Aoun, K. Bouchouicha and N. Bailek, “Seasonal performance comparison of four electrical models of monocrystalline PV module operating in a harsh environment,” IEEE Journal of Photovoltaics, vol. 9, no. 4, pp. 1057–1063, 2019. [Google Scholar]

24. M. Jamei, N. Bailek, K. Bouchouicha, M. A. Hassan, A. Elbeltagi et al., “Data-driven models for predicting solar radiation in semi-arid regions,” Computers, Materials & Continua, vol. 74, no. 1, pp. 1625–1640, 2023. [Google Scholar]

25. I. J. Mohammed, B. T. Al-Nuaimi and T. I. Baker, “Weather forecasting over Iraq using machine learning,” Journal of Artificial Intelligence and Metaheuristics, vol. 2, no. 2, pp. 39, 2023. [Google Scholar]

26. M. H. Yehia, M. A. Hassan, N. Abed, A. Khalil and N. Bailek, “Combined thermal performance enhancement of parabolic trough collectors using alumina nanoparticles and internal fins,” International Journal of Engineering Research in Africa, vol. 62, pp. 107–132, 2022. [Google Scholar]

27. S. Xu, W. Li, Y. Zhu and A. Xu, “A novel hybrid model for six main pollutant concentrations forecasting based on improved LSTM neural networks,” Scientific Reports, vol. 12, no. 1, pp. 14434, 2022 [Google Scholar] [PubMed]

28. T. Song, R. Han, F. Meng, J. Wang, W. Wei et al., “A significant wave height prediction method based on deep learning combining the correlation between wind and wind waves,” Frontiers in Marine Science, vol. 9, 2022. [Google Scholar]

29. H. S. Kim, K. M. Han, J. Yu, J. Kim, K. Kim et al., “Development of a CNN+LSTM hybrid neural network for daily PM2.5 prediction,” Atmosphere, vol. 13, no. 12, 2022. [Google Scholar]

30. G. Wang, X. Wang, X. Wu, K. Liu, Y. Qi et al., “A hybrid multivariate deep learning network for multistep ahead sea level anomaly forecasting,” Journal of Atmospheric and Oceanic Technology, vol. 39, no. 3, pp. 285–301, 2022. [Google Scholar]

31. A. A. M. Ahmed, S. J. J. Jui, M. S. AL-Musaylh, N. Raj, R. Saha et al., “Hybrid deep learning model for wave height prediction in Australia's wave energy region,” Applied Soft Computing, pp. 111003, 2023. [Google Scholar]

32. D. Adytia, D. Saepudin, D. Tarwidi, S. R. Pudjaprasetya, S. Husrin et al., “Modelling of deep learning-based downscaling for wave forecasting in coastal area,” Water, vol. 15, no. 1, 2023. [Google Scholar]

33. N. Al-rousan, H. Al-najjar and O. Alomari, “Assessment of predicting hourly global solar radiation in Jordan based on rules, trees, meta, lazy and function prediction methods,” Sustainable Energy Technologies and Assessments, vol. 44, pp. 100923, 2021. [Google Scholar]

34. K. Benmouiza and A. Cheknane, “Forecasting hourly global solar radiation using hybrid k-means and nonlinear autoregressive neural network models,” Energy Conversion and Management, vol. 75, pp. 561–569, 2013. [Google Scholar]

35. M. A. Jallal, S. Chabaa and A. Zeroual, “A new artificial multi-neural approach to estimate the hourly global solar radiation in a semi-arid climate site,” Theoretical and Applied Climatology, vol. 139, no. 3, pp. 1261–1276, 2020. [Google Scholar]

36. O. García-hinde, G. Terrén-serrano, M. Á. Hombrados-herrera and V. Gómez-verdejo, “Engineering applications of artificial intelligence evaluation of dimensionality reduction methods applied to numerical weather models for solar radiation forecasting,” Engineering Applications of Artificial Intelligence, vol. 69, pp. 157–167, 2018. [Google Scholar]

37. E. Akarslan and F. Onur, “A novel adaptive approach for hourly solar radiation forecasting,” Renewable Energy, vol. 87, pp. 628–633, 2016. [Google Scholar]

38. M. Guermoui, S. Benkaciali, K. Gairaa, K. Bouchouicha, T. Boulmaiz et al., “A novel ensemble learning approach for hourly global solar radiation forecasting,” Neural Computing and Applications, vol. 34, no. 4, pp. 2983–3005, 2021. [Google Scholar]

39. L. Benali, G. Notton, A. Fouilloy, C. Voyant and R. Dizene, “Solar radiation forecasting using artificial neural network and random forest methods: Application to normal beam, horizontal diffuse and global components,” Renewablse Energy, vol. 132, pp. 871–884, 2019. [Google Scholar]