 Open Access
Open Access
ARTICLE
A Mathematical Approach for Generating a Highly Non-Linear Substitution Box Using Quadratic Fractional Transformation
1 Department of Mathematics, Division of Science and Technology, University of Education, Lahore, Pakistan
2 Department of Mathematics, University of Management and Technology, Sialkot Campus, 51310, Pakistan
3 School of Mathematical Sciences, Zhejiang Normal University, Jinhua, 321004, China
4 Department of Mathematics, University of Management and Technology, Lahore, 54770, Pakistan
5 Section of Mathematics, International Telematic University Uninettuno, Corso Vittorio Emanuele II, Roma, 39-00186, Italy
6 Department of Statistics and Operations Research, College of Science, King Saud University, P.O. Box 2455, Riyadh, 11451, Saudi Arabia
* Corresponding Author: Rana Muhammad Zulqarnain. Email:
(This article belongs to the Special Issue: Multimedia Encryption and Information Security)
Computers, Materials & Continua 2023, 77(2), 2565-2578. https://doi.org/10.32604/cmc.2023.040371
Received 15 March 2023; Accepted 07 June 2023; Issue published 29 November 2023
Abstract
Nowadays, one of the most important difficulties is the protection and privacy of confidential data. To address these problems, numerous organizations rely on the use of cryptographic techniques to secure data from illegal activities and assaults. Modern cryptographic ciphers use the non-linear component of block cipher to ensure the robust encryption process and lawful decoding of plain data during the decryption phase. For the designing of a secure substitution box (S-box), non-linearity (NL) which is an algebraic property of the S-box has great importance. Consequently, the main focus of cryptographers is to achieve the S-box with a high value of non-linearity. In this suggested study, an algebraic approach for the construction of 16 × 16 S-boxes is provided which is based on the fractional transformation and finite field. This technique is only applicable for the even number exponent in the range (2-254) that are not multiples of 4. Firstly, we choose a quadratic fractional transformation, swap each missing element with repeating elements, and acquire the initial S-box. In the second stage, a special permutation of the symmetric group is utilized to construct the final S-box, which has a higher NL score of 112.75 than the Advanced Encryption Standard (AES) S-box and a lower linear probability score of 0.1328. In addition, a tabular and graphical comparison of various algebraic features of the created S-box with many other S-boxes from the literature is provided which verifies that the created S-box has the ability and is good enough to withstand linear and differential attacks. From different analyses, it is ensured that the proposed S-boxes are better than as compared to the existing S-boxes. Further these S-boxes can be utilized in the security of the image data and the text data.Keywords
The amount of data being exchanged has risen substantially as a result of recent technology advancements and its successful use in daily life. The confidential nature of data necessitates the development of tools and safeguards against misuse. Data from a user must be altered before transmission so that an attacker cannot understand it. Symmetric block ciphers have become among the most extensively utilized approaches for such purposes given their ease of implementation and able to give much-required encryption security [1,2]. By utilizing a symmetric key and a varied number of several rounds, one common sort of block cipher converts an input block of data into a nonsensical output block via substitution and permutation techniques. On the input block of data, substitution, and permutation operations are typically performed in each cycle. A replacement process uses a substitution box (S-box) to swap out an input block with another output block [3]. The most widely used symmetric block cipher is AES, as an illustration.
S-box is a Vectorial Boolean function that is defined mathematically as, φ:Zu2→Zv2 which maps the u input bit into the v output bit. As a crucial part of modern block ciphers, an S-box creates a randomized cipher text from the input plaintext. The single nonlinear component of contemporary block ciphers is the S-box, which provides a complicated link between the plaintext and the cipher text. The algebraic and statistical features of the S-box, such as non-linearity, Bit Independent Criterion (BIC), Strict Avalanche Criterion (SAC), Differential Uniformity (DU), and Linear Approximation Probability (LAP) are used to assess its validity. Numerous methods and technologies are used throughout literature to create securely powerful Substitution-boxes. A method to create robust and resistant S-boxes that can help in the modification of block cryptosystems was proposed by Dragomir et al. [4]. The authors of [5] proposed a novel S-box constructed system using group theory ideas. Reference [6] Describes a unique genetic approach for evolving S-boxes with high non-linearity scores. Artuğer et al. [7] present a new technique for improving the performance of Chaos-Based S-boxes. They have implemented their system on a large number of S-boxes. In [8], an efficient algebraic approach for evolving S-boxes with reasonable strength is presented. Particle Swarm Optimization was used by Musheer et al. [9] to generate a robust S-box. In [10], an efficient S-box with essentially optimum characteristics was created. For this, the authors used a methodical group theoretical method. Javeed et al. [11] created an S-box with outstanding cryptographic features using a freshly created chaotic map and the suitable S256 component. In [12], Khan et al. created an S-box utilizing (Difference Distribution Table) DDT and a chaotic logistic map. In contrast to previously established S-boxes based on chaos, it was a significant effort to generate an S-box that had an extremely low value of differential approximation probability. To construct an S-box that has excellent cryptographic features, Ahmad et al. [13] suggested a unique approach that utilizes artificial bee colony optimization and chaotic maps. A unique method to build safe S-boxes using the fractional-order chaotic Chen scheme was put out by Özkaynak et al. [14]. To ensure the accuracy of Chen scheme’s numerical findings, they used the predictor-corrector approach. It is a straightforward approach for creating an S-box using Chen’s fractional-order chaotic Chen scheme. By utilizing Lorenz equations, Khan et al. [15] established a novel S-box method of construction. To develop a robust S-box, Ahmad et al. looked at the traveling salesman problem and piecewise linear chaotic map [16]. Five strong S-boxes were created by Ullah et al. [17] using a chaotic map and a linear fractional transformation (LFT). Different techniques are utilized for the construction of S-boxes and other techniques to solve different model issues [18–29].
This article is a continuation of the work done by Mahboob et al. [30] to create an S-box using a Quantic Fractional Transformation and finite field. They used the mapping Q(x)=1a(x)m+b to construct a reliable S-box in their research, although it was only effective for odd values of m in the range of (0–255), and the authors also demonstrated that this mapping is bijective for odd values of m but there is no construction of S-boxes is available in literature which uses the fractional transformation 1a(z)m+b when m∈{2+4n|0≤n≤63} since the proposed mapping is not bijective in this fashion. We provide a unique approach for the creation of S-boxes utilizing this fractional transformation and use m=2 for an example to create a specimen S-box in this paper. By changing the value of m, we may create several S-boxes. The following is the main contribution of our study in this paper:
1. An innovative and simple fractional transformation is defined for the construction of S-boxes. By altering their parameters, a large number of S-boxes can be constructed using this technique.
2. We use the Quadratic Fractional Transformation (QFT) as an illustration to create a specimen S-box by maintaining the value of m=2.
3. To boost the unpredictability of the first S-box, suitable permutations of the symmetric group were utilized, and the suggested S-box was constructed whose average nonlinearity is 112.75 which is greater than AES S-box.
4. Additionally, visual and tabular comparisons of various algebraic analyses, including NL, BIC, DU, SAC, and LAP of the proposed S-box, were used, and a comparison of these results with the other S-boxes established in literature is presented to demonstrate that the suggested S-box is capable of withstanding linear and differential attacks.
The remainder of the paper is arranged as follows: Section 2 delves into the algebraic structure of the S-box’s construction. In Section 3, the constructed S-box is examined through its security analysis, and its results are compared with those of other S-boxes. In Section 4, we illustrate the discussion of our results and discuss our findings. Finally, Section 5 concludes the study.
Step 1: To begin, let us define a fractional transformation, Q:Z257→Z257 as [30]:
Q(z)=1α(z)m+β(mod257),α(z)m+β≠0,(1)
whereα∈Z257−{0},β∈Z257, & m∈{2+4n|0≤n≤63}.
This Eq. (1) is taken from [30].
Given that a bijective 16×16 S-box is essentially any rearrangement of the numbers (0–255). The Prime Field Z257 is frequently used to ensure that all outputs remain within this range. Due to this, we restrict the parameters α and β. These parameters allow for the creation of a vast number of S-boxes because each adjustment to one of the parameters results in the creation of a new S-box that differs from the previous ones.
Here we choose m=2, α=57 & β=24 to generate a specimen substitution box, then the quadratic fractional transformation (QFT) becomes:
Q(z)=157(z)2+24(mod257),z∈Z257(2)
After that, put all the elements from Z257 into Eq. (2) and then write the outputs in a set W obtained from the quadratic fractional transformation after solving under mod257.
W={Q(z)|z∈Z257}
Since it is to be noted that the set W may include the number 256 but never have 0 we deducted 1 from each element of the set W to maintain the range (0–255).
Finally, to keep the S-box bijective, we put all missing numbers from (0–255) in ascending order in set {u1,u2,…,un} and duplicated numbers from (0–255) in descending order in set {v1,v2,…,vn} and replace every uj by vj for j=1,2,…,n.
Table 1 explains the above method for eradicating the sequence {0,1,2,3,…,255}. After destroying the initial sequence of numbers {0,1,2,…,255}, we retrieved our initial S-box 16×16 matrix present in Table 2, whose average nonlinearity is 103.25.
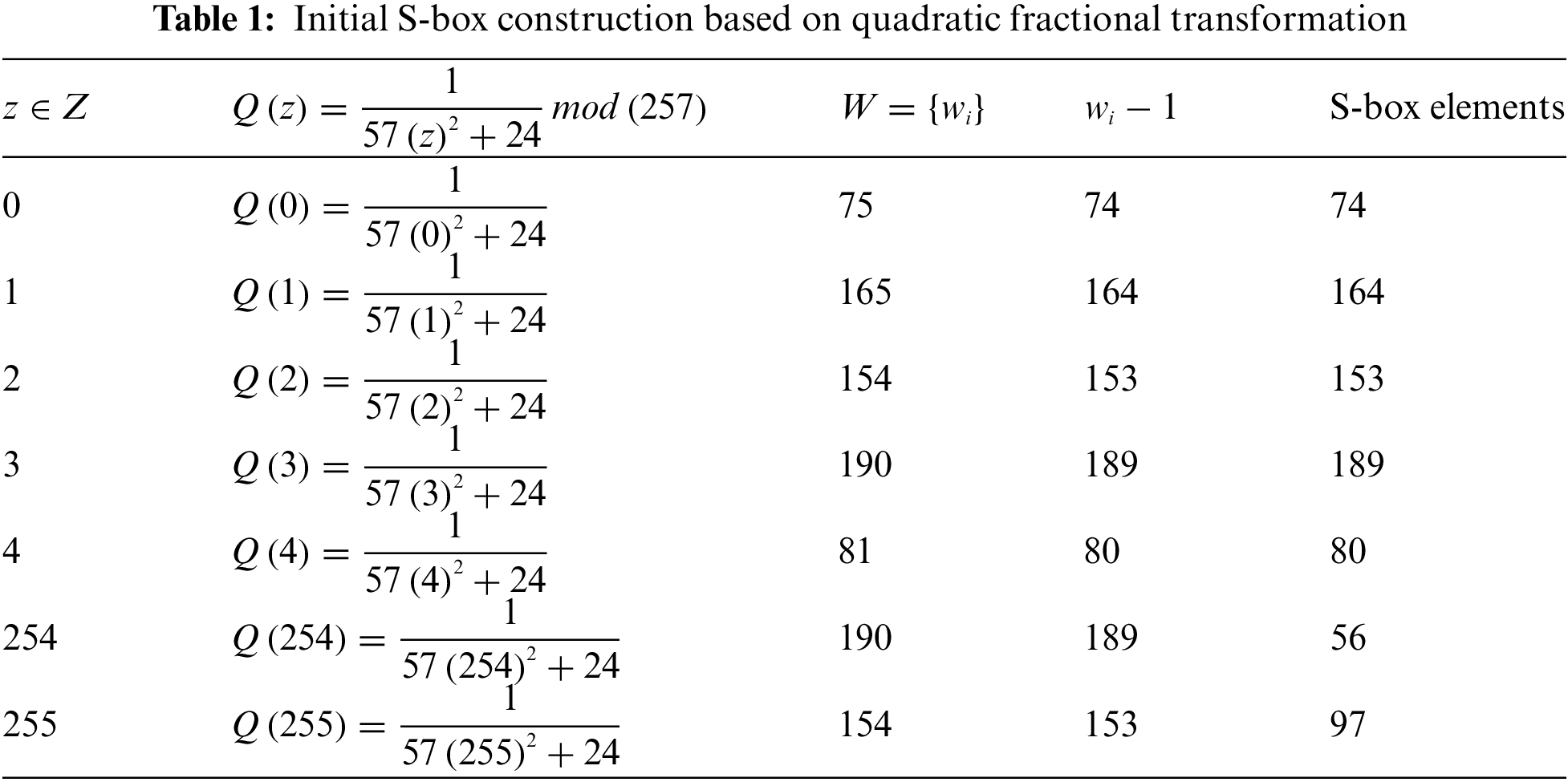

Step 2: To improve the random nature of our constructed S-box, we utilized a permutation of symmetric group S256 (shown in Table 3) to modify the location of the S-box’s elements and generated a proposed S-box (shown in Table 4) with a mean non-linearity value of 112.75.


In this part, we assess the cryptographic performance of recommended S-box (provided in Table 4) to generally recognized traditional S-box performance criteria. Five essential evaluations are utilized to assess the resilience of the S-box: nonlinearity, linear approximation probability, bit independence criterion, differential approximation probability, and strict avalanche criterion. We achieve fantastic results, which shows the high quality of the planned design.
This is a critical factor for determining the efficacy of S-box in contrast to linear and differential cryptanalysis. Pieprzyk and Finkelstein introduced this test in 1988 [31]. The nonlinearity of ψ:Zn2→Z2, where ψ is a Boolean function of n variables is defined as the minimum distance among ψ and the set of affine transformations An.
NL(ψ)=d(ψ,An)=minγϵAnd(ψ,γ)(3)
Accordingly, the NL score is 0 when all affine transformations are linear. For n×n S-box, the highest value of NL is, 2n−1−2n2−1. Thus, the ideal value of NL over GF(28) is 120 in AES. The high NL value of the S-box is a crucial component for creating a good cryptosystem. The recommended S-box has a minimum value of nonlinearity is 112, the maximum value of nonlinearity is 114, and the mean value of nonlinearity is 112.75. Table 5 displayed the NL scores for 8 Boolean functions, and Fig. 1 contrasts the mean NL number of the final S-box with those of numerous other S-boxes.

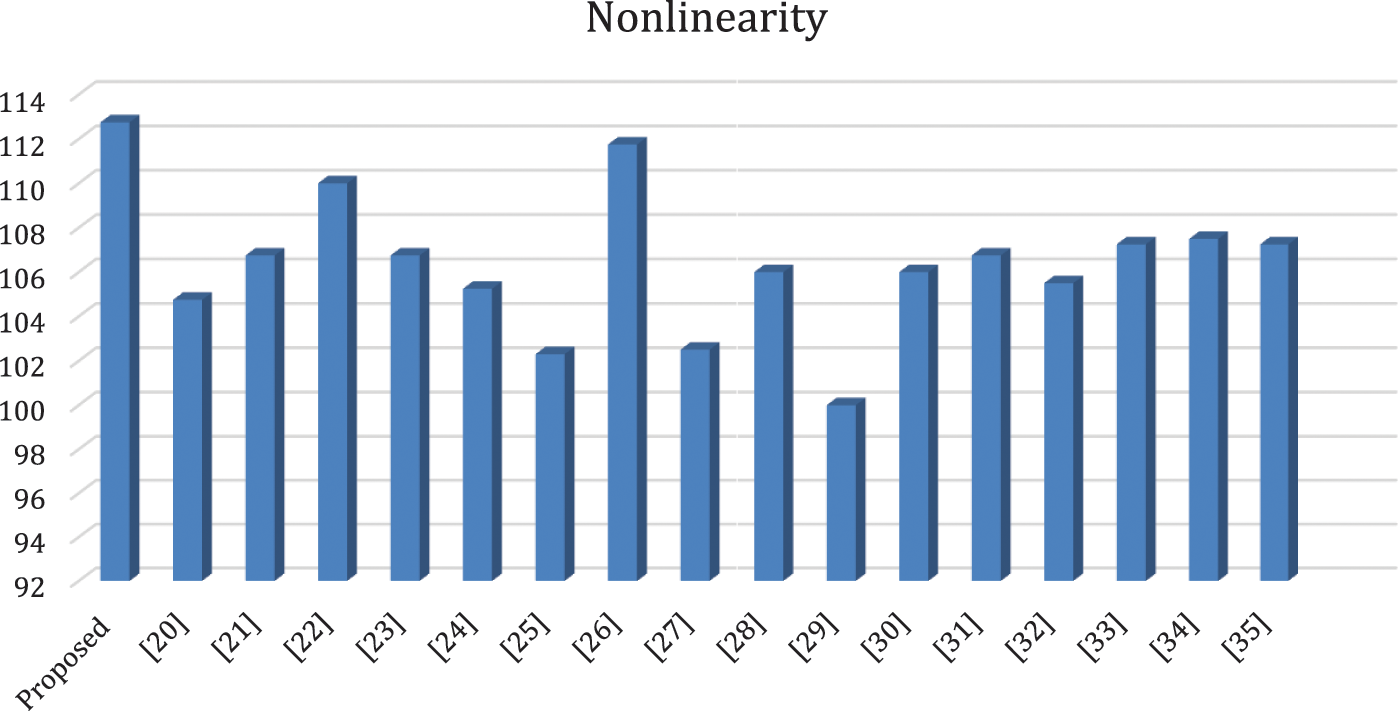
Figure 1: Analysis of mean NL score of suggested S-box with various S-boxes
Fig. 1 shows the comparison of non-linearity of our purposed S-box and existing S-boxes. The non-linearity is the very important and main component to check the strength of S-box. So, from Fig. 1, it is ensured that our S-box have average non-linearity 112.75 which is higher than other existing S-boxes.
3.2 Strict Avalanche Criterion (SAC)
In [32], Webster et al. suggested this essential algebraic criterion of S-box. SAC shows that output bits changed by 12 of probability or 50% if a single bit changes in the input result. S-box is considered strong against cryptanalyst attacks whose SAC value is 0.5. The SAC criterion is conducted by using a dependency matrix. The SAC value of the suggested S-box is present in Table 6, which is close to the ideal value of SAC.

3.3 Bit Independence Criterion (BIC)
This is another relevant criterion for measuring the strength of the S-box, which is defined as the two output bits changing independently when any single input is modified. Webster et al. [32] presented BIC as an effective criterion in symmetric cryptosystems. Table 7 shows the BIC Non-linearity values of the proposed S-box.

Table 8 provide the BIC-SAC values for the final S-box.

Table 9 and Fig. 2 provide a comparison of the BIC NL and BIC SAC values of the proposed S-box with existing S-boxes.
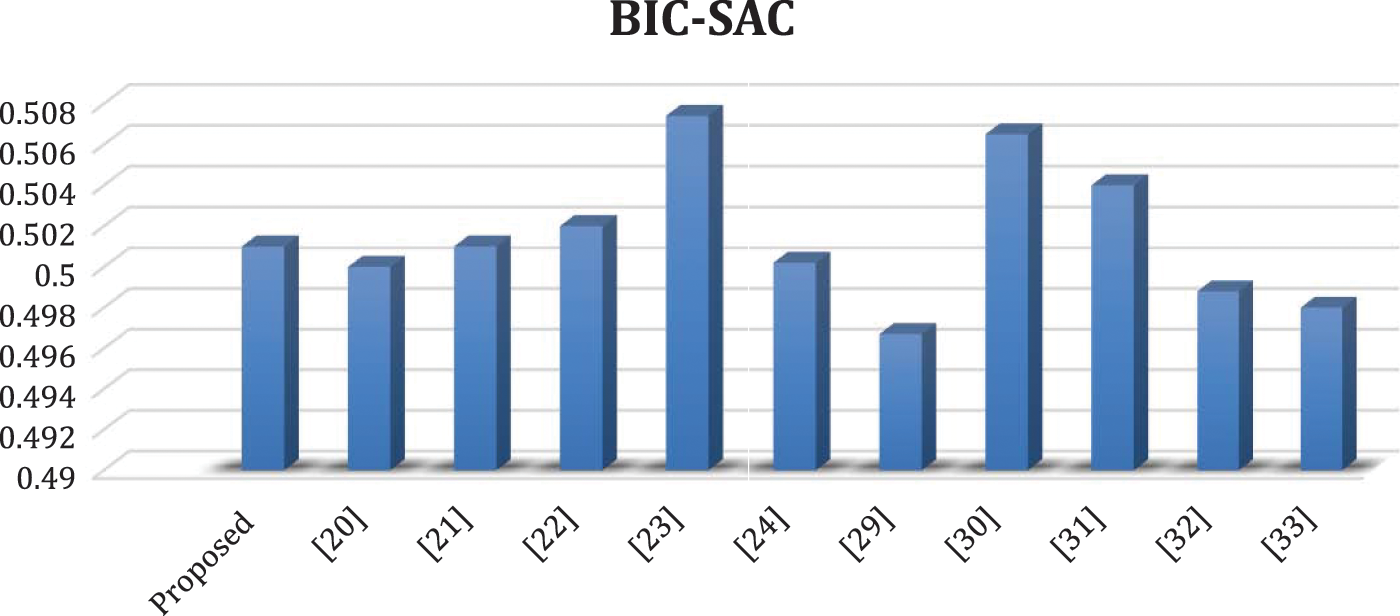
Figure 2: Analysis among BIC-SAC values of proposed S-box with other S-boxes
3.4 Differential Uniformity (DU)
Biham et al. [48] devised this test. To overcome differential assaults, a low value of differential uniformity (DU) is proposed, and S-box is deemed more secure. Eq. (4) provides a mathematical formula for calculating the DU.
DUψ=maxΔr≠0,Δs[#{r∈M|ψ(r)⊕ψ(r⊕Δr)=Δd}](4)
where M={0,1,2,…,255}, Δs and Δr denote output and input differentials respectively, ψ is a Boolean function and the symbol ⊕ represents the XOR operation. Table 10 depicts the suggested S-box’s differential distribution table. The maximum DU score of the suggested S-box is 12 and the differential probability (DP) value is 0.0468. This low DP score demonstrated that the S-box is highly resistant to differential assaults. Table 11 compares DU with several S-boxes, and Fig. 3 depicts a graphical comparison of the suggested S-box’s DP values with those of previously developed S-boxes in the literature.
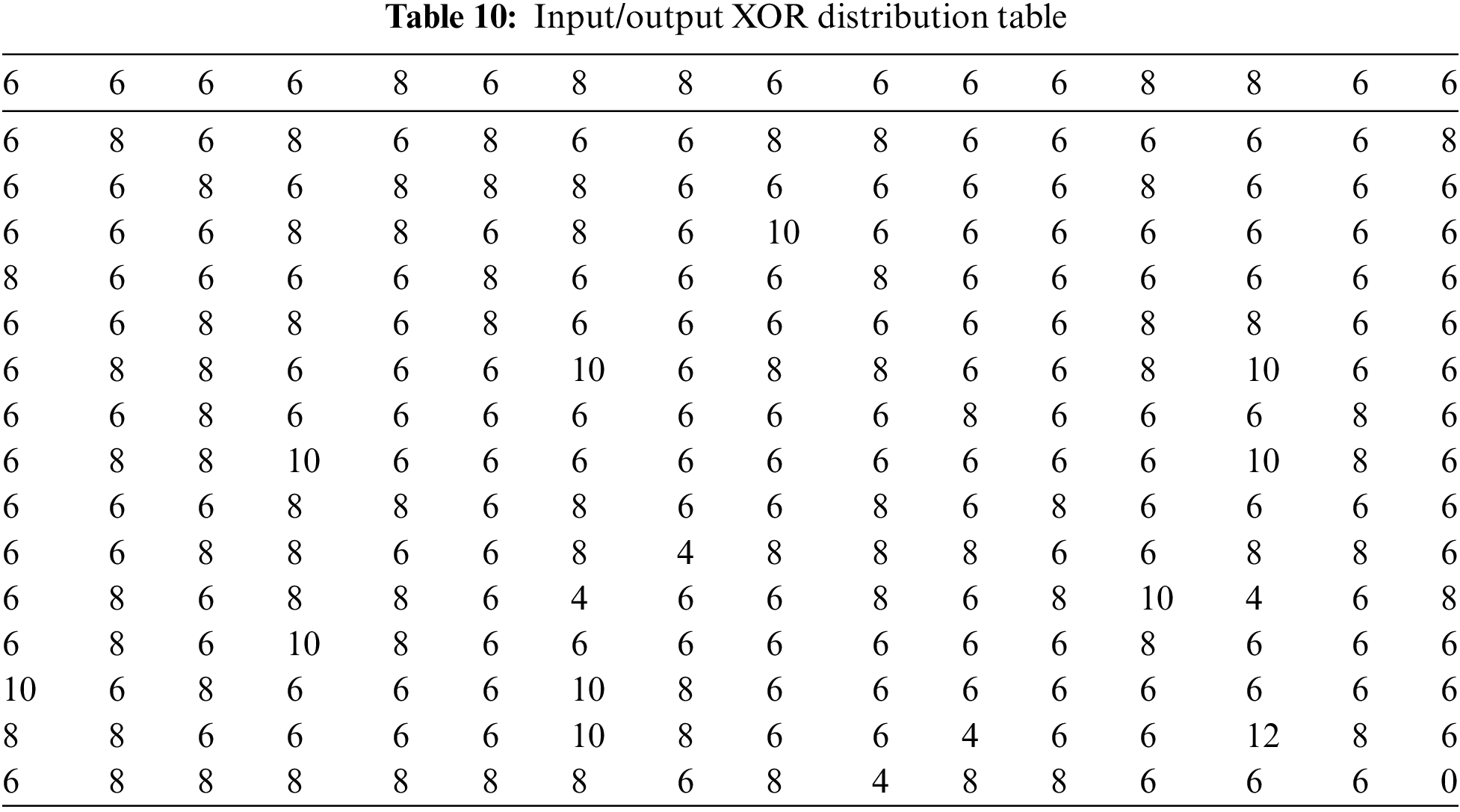

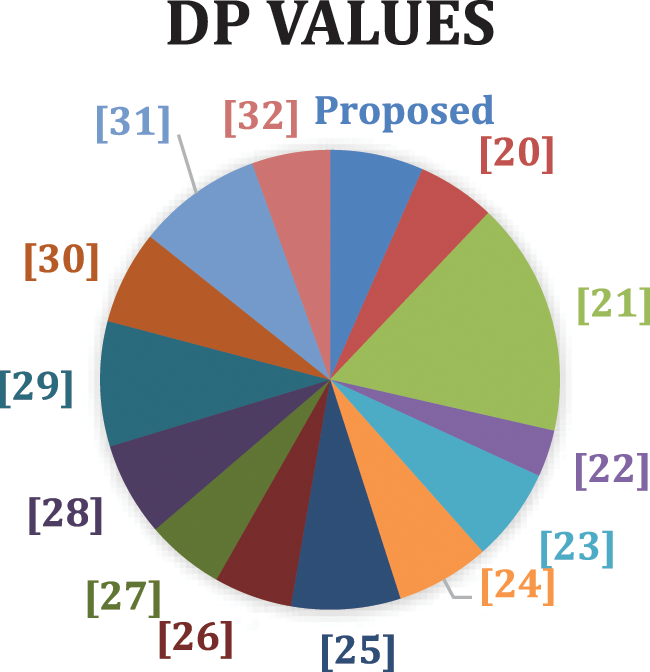
Figure 3: Pie chart of DP values of recommended S-box with some other S-boxes
3.5 Linear Approximation Probability (LAP)
LAP criterion is used to check the strength and resistance of the S-box to linear assaults. In [49], Matsui provided this algebraic feature of S-box. The S-box is considered more secure whenever the value of LAP is smaller. A mathematical formula to calculate LAP is:
LAP=maxλp,λq≠0|#{p|p.λp=ψ(p).λq}2n−12|(5)
where λp and λq denote the input and output mask, respectively, 2n is the total number of elements of the S-box and ψ represents the Boolean functions. The LAP value of the created S-box is 0.13281. Table 11 indicates the comparison among the LAP scores of the suggested S-box and various other S-boxes.
Researchers’ major emphasis for the creation of powerful substitution boxes is a significant nonlinearity score. Our S-box has a mean nonlinearity of 112.75, which is higher than the AES S-box as well as the other S-boxes from the literature shown in Table 6.
1. The S-box creators’ ultimate goal is to obtain the ideal SAC value of 0.5. Our S-box has a SAC score of 0.4973, which is close to 0.5 when contrasted to other S-boxes in Table 10. We can claim that our S-box is impervious to cryptanalysis.
2. The proposed S-box BIC NL and BIC SAC scores are 103.64 and 0.501, respectively. Table 9 and Fig. 2 provide a comparison of the values of BIC NL and BIC SAC.
3. Low DP S-boxes are resilient to different types of attacks. The DP score of the created S-box in Fig. 3 is 0.0468, which is lower than the DP numbers of many other S-boxes.
4. The recommended S-box’s LAP value is 0.13281. This low value implies that the proposed S-box is resistant to linear assaults. Table 11 compares the LAP value of created S-box to that of other S-boxes.
In this study an algebraic strategy for generating the substitution boxes was introduced. This methodology depends on fractional transformation and finite field. We designed a general form of transformation and choose quadratic fraction transformation as an example to generate an S-box. The nonlinearity of the proposed S-box after applying the permutations of S256 is 112.75 which is higher than AES S-box. The other algebraic properties of the S-box are good enough to stand against linear and differential approaches. The comparison between the algebraic and statistical properties of our S-box with many other S-boxes from the literature indicates that the recommended S-box withstands cryptanalysis attacks and can be used further to improve a security. Although a static prototype S-box is created in this study, it will be feasible to create dynamic S-boxes in the future by utilizing the suggested mathematical methodology, which will enable the creation of a robust and effective cryptosystem that will safeguard sensitive and private data.
This study develops a fractional transformation for creating substitution boxes that are applied to even values of m when m={2,6,10,…,254} and we simply swap each missing element with a repeating element to keep the S-box bijective. If m is a multiple of 4, it is impossible to construct an S-box and it is impossible to maintain the bijectivity of the S-box because elements repeat more than once.
Acknowledgement: The authors present their appreciation to King Saud University for funding the publication of this research.
Funding Statement: The authors received the funding for this study from King Saud University, Riyadh, Saudi Arabia under the research supporting project Number RSP 2024R167. Sameh Askar received this grant from King Saud University.
Author Contributions: The authors confirm their contribution to the paper as follows: Study conception and design: A. Mehboob, M.Asif, R. M. Zulqarnain; data collection: M. Asif, I. Saddique; analysis and interpretation of results: A. Mehboob, I. Siddique, H. Ahmad, S. Askar; draft manuscript preparation: A. Mehmood, R. M. Zulqarnain, H. Ahmad, S. Askar, All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: All data generated or analyzed during this study are included in this article and are available from the corresponding author upon reasonable request.
Conflicts of Interest: The authors declares that they have no conflicts of interest to report regarding the present study.
References
1. C. Paar, J. Pelzl and B. Preneel, Understanding Cryptography, 1st ed., Berlin, Germany: Springer, 2010. [Google Scholar]
2. A. Shamir, “Stream ciphers: Dead or alive?” in ASIACRYPT, pp. 78, 2004. [Google Scholar]
3. D. Lambić and M. Živković, “Comparison of random S-Box generation methods,” De L’institut Mathématique, vol. 93, no. 107, pp. 109–115, 2013. [Google Scholar]
4. I. R. Dragomir and M. Lazăr, “Generating and testing the components of a block cipher,” in 2016 8th Int. Conf. on Electronics, Computers and Artificial Intelligence (ECAI), Ploiesti, Romania, IEEE, pp. 1–4, 2016. [Google Scholar]
5. I. Hussain, T. Shah, H. Mahmood and M. A. Gondal, “A projective general linear group based algorithm for the construction of substitution box for block ciphers,” Neural Computing and Applications, vol. 22, no. 6, pp. 1085–1093, 2013. [Google Scholar]
6. Y. Wang, Z. Zhang, L. Y. Zhang, J. Feng, J. Gao et al., “A genetic algorithm for constructing bijective substitution boxes with high nonlinearity,” Information Sciences, vol. 523, no. 1, pp. 152–166, 2020. [Google Scholar]
7. F. Artuğer and F. Özkaynak, “A novel method for performance improvement of chaos-based substitution boxes,” Symmetry, vol. 12, no. 4, pp. 571, 2020. [Google Scholar]
8. S. Hussain, S. S. Jamal, T. Shah and I. Hussain, “A power associative loop structure for the construction of non-linear components of block cipher,” IEEE Access, vol. 8, pp. 123492–123506, 2020. [Google Scholar]
9. M. Ahmad, I. A. Khaja, A. Baz, H. Alhakami and W. Alhakami, “Particle swarm optimization based highly nonlinear substitution-boxes generation for security applications,” IEEE Access, vol. 8, pp. 116132–116147, 2020. [Google Scholar]
10. M. A. Yousaf, H. Alolaiyan, M. Ahmad, M. Dilbar and A. Razaq, “Comparison of pre and post-action of a finite abelian group over certain nonlinear schemes,” IEEE Access, vol. 8, pp. 39781–39792, 2020. [Google Scholar]
11. A. Javeed, T. Shah and A. Ullah, “Construction of non-linear component of block cipher by means of chaotic dynamical system and symmetric group,” Wireless Personal Communications, vol. 112, no. 1, pp. 467–480, 2020. [Google Scholar]
12. M. A. Khan, A. Ali, V. Jeoti and S. Manzoor, “A chaos-based substitution box (S-Box) design with improved differential approximation probability (DP),” Iranian Journal of Science and Technology, Transactions of Electrical Engineering, vol. 42, no. 2, pp. 219–238, 2018. [Google Scholar]
13. M. Ahmad, M. N. Doja and M. S. Beg, “ABC optimization based construction of strong substitution-boxes,” Wireless Personal Communications, vol. 101, no. 3, pp. 1715–1729, 2018. [Google Scholar]
14. F. Özkaynak, V. Çelik and A. B. Özer, “A new S-box construction method based on the fractional-order chaotic Chen system,” Signal Image and Video Processing, vol. 11, no. 4, pp. 659–664, 2017. [Google Scholar]
15. F. A. Khan, J. Ahmed, J. S. Khan, J. Ahmad and M. A. Khan, “A novel substitution box for encryption based on Lorenz equations,” in 2017 Int. Conf. on Circuits, System and Simulation (ICCSS), London, UK, IEEE, pp. 32–36, 2017. [Google Scholar]
16. M. Ahmad, N. Mittal, P. Garg and M. M. Khan, “Efficient cryptographic substitution box design using travelling salesman problem and chaos,” Perspectives in Science, vol. 8, no. 3, pp. 465–468, 2016. [Google Scholar]
17. A. Ullah, S. S. Jamal and T. Shah, “A novel construction of substitution box using a combination of chaotic maps with improved chaotic range,” Nonlinear Dynamics, vol. 88, no. 4, pp. 2757–2769, 2017. [Google Scholar]
18. I. Khalid, T. Shah, S. M. Eldin, D. Shah, M. Asif et al., “An integrated image encryption scheme based on elliptic curve,” IEEE Access, vol. 11, pp. 5483–5501, 2022. [Google Scholar]
19. I. Khalid, T. Shah, K. A. Almarhabi, D. Shah, M. Asif et al., “The spn network for digital audio data based on elliptic curve over a finite field,” IEEE Access, vol. 10, pp. 127939–127955, 2022. [Google Scholar]
20. A. Mahboob, M. Asif, I. Siddique, A. Saleem, M. Nadeem et al., “A novel construction of substitution box based on polynomial mapped and finite field with image encryption application,” IEEE Access, vol. 10, pp. 119244–119258, 2022. [Google Scholar]
21. M. Asif, J. K. K. Asamoah, M. M. Hazzazi, A. R. Alharbi, M. U. Ashraf et al., “A novel image encryption technique based on cyclic codes over galois field,” Computational Intelligence and Neuroscience, vol. 2022, no. 1, pp. 1–9, 2022. [Google Scholar]
22. S. Hussain, M. Asif, T. Shah, A. Mahboob and S. M. Eldin, “Redesigning the serpent algorithm by PA-Loop and its image encryption application,” IEEE Access, vol. 11, pp. 29698–29710, 2023. [Google Scholar]
23. A. S. Alanazi, N. Munir, M. Khan, M. Asif and I. Hussain, “Cryptanalysis of novel image encryption scheme based on multiple chaotic substitution boxes,” IEEE Access, vol. 9, pp. 93795–93802, 2021. [Google Scholar]
24. M. Khan, S. S. Jamal, M. M. Hazzazi, K. M. Ali, I. Hussain et al., “An efficient image encryption scheme based on double affine substitution box and chaotic system,” Integration, vol. 81, no. 3, pp. 108–122, 2021. [Google Scholar]
25. M. Asif, S. Mairaj, Z. Saeed, M. U. Ashraf, K. Jambi et al., “A novel image encryption technique based on mobius transformation,” Computational Intelligence and Neuroscience, vol. 2021, no. 2, pp. 1–14, 2021. [Google Scholar]
26. M. Asif and T. Shah, “BCH Codes with computational approach and its applications in image encryption,” Journal of Intelligent & Fuzzy Systems, vol. 37, no. 3, pp. 3925–3939, 2019. [Google Scholar]
27. A. Mahboob, M. Asif, R. M. Zulqarnain, I. Siddique, H. Ahmad et al., “An innovative technique for constructing highly non-linear components of block cipher for data security against cyber attacks,” Computer Systems Science & Engineering, vol. 47, no. 2, pp. 2547–2562, 2023. [Google Scholar]
28. A. Mahboob, I. Siddique, M. Asif, M. Nadeem and A. Saleem, “Construction of highly non linear component of block cipher based on mclaurin series and mellin transformation with application in image encryption,” Multimedia Tools and Applications, pp. 1–19, 2023. [Google Scholar]
29. D. Shah, T. Shah and S. S. Jamal, “A novel efficient image encryption algorithm based on affine transformation combine with linear fractional transformation,” Multidimensional Systems and Signal Processing, vol. 31, pp. 885–905, 2020. [Google Scholar]
30. A. Mahboob, M. Asif, M. Nadeem, A. Saleem, I. Siddique et al., “A cryptographic scheme for construction of substitution boxes using quantic fractional transformation,” IEEE Access, vol. 10, pp. 132908–132916, 2022. [Google Scholar]
31. J. Pieprzyk and G. Finkelstein, “Towards effective nonlinear cryptosystem design,” IEE Proceedings E-Computers and Digital Techniques, vol. 135, no. 6, pp. 325–335, 1988. [Google Scholar]
32. A. F. Webster and S. E. Tavares, “On the design of S-boxes,” in Conf. on the Theory and Application of Cryptographic Techniques, Berlin, Heidelberg, Germany, Springer, pp. 523–534, 1985. [Google Scholar]
33. I. Hussain, T. Shah, M. A. Gondal, W. A. Khan and H. Mahmood, “A group theoretic approach to construct cryptographically strong substitution boxes,” Neural Computing and Applications, vol. 23, no. 1, pp. 97–104, 2013. [Google Scholar]
34. S. S. Jamal, T. Shah and A. Attaullah, “A group action method for construction of strong substitution box,” 3D Research, vol. 8, no. 2, pp. 1–10, 2017. [Google Scholar]
35. L. Shuai, L. Wang, L. Miao and X. Zhou, “S-boxes construction based on the Cayley graph of the symmetric group for UASNs,” IEEE Access, vol. 7, pp. 38826–38832, 2019. [Google Scholar]
36. A. Razaq, A. Yousaf, U. Shuaib, N. Siddiqui, A. Ullah et al., “A novel construction of substitution box involving coset diagram and a bijective map,” Security and Communication Networks, vol. 2017, no. 48, pp. 1–16, 2017. [Google Scholar]
37. I. Hussain, T. Shah, M. A. Gondal and W. A. Khan, “Construction of cryptographically strong 8 × 8 S-boxes,” World Applied Sciences Journal, vol. 13, no. 11, pp. 2389–2395, 2011. [Google Scholar]
38. S. S. Jamal, M. U. Khan and T. Shah, “A watermarking technique with chaotic fractional S-box transformation,” Wireless Personal Communications, vol. 90, no. 4, pp. 2033–2049, 2016. [Google Scholar]
39. A. H. Zahid, A. M. Iliyasu, M. Ahmad, M. M. U. Shaban, M. J. Arshad et al., “A novel construction of dynamic S-box with high nonlinearity using heuristic evolution,” IEEE Access, vol. 9, pp. 67797–67812, 2021. [Google Scholar]
40. A. A. Abd EL-Latif, B. Abd-El-Atty and S. E. Venegas-Andraca, “A novel image steganography technique based on quantum substitution boxes,” Optics & Laser Technology, vol. 116, no. 3, pp. 92–102, 2019. [Google Scholar]
41. A. K. Farhan, R. S. Ali, H. Natiq and N. M. Al-Saidi, “A new S-box generation algorithm based on multistability behavior of a plasma perturbation model,” IEEE Access, vol. 7, pp. 124914–124924, 2019. [Google Scholar]
42. M. Khan, T. Shah and S. I. Batool, “Construction of S-box based on chaotic Boolean functions and its application in image encryption,” Neural Computing and Applications, vol. 27, no. 3, pp. 677–685, 2016. [Google Scholar]
43. V. M. Silva-García, R. Flores-Carapia, C. Rentería-Márquez, B. Luna-Benoso and M. Aldape-Pérez, “Substitution box generation using Chaos: An image encryption application,” Applied Mathematics and Computation, vol. 332, no. 1, pp. 123–135, 2018. [Google Scholar]
44. M. Khan, T. Shah, H. Mahmood and M. A. Gondal, “An efficient method for the construction of block cipher with multi-chaotic systems,” Nonlinear Dynamics, vol. 71, no. 3, pp. 489–492, 2013. [Google Scholar]
45. S. S. Jamal and T. Shah, “A novel algebraic technique for the construction of strong substitution box,” Wireless Personal Communications, vol. 99, no. 1, pp. 213–226, 2018. [Google Scholar]
46. A. H. Zahid, E. Al-Solami and M. Ahmad, “A novel modular approach based substitution-box design for image encryption,” IEEE Access, vol. 8, pp. 150326–150340, 2020. [Google Scholar]
47. B. Arshad, N. Siddiqui and Z. Hussain, “A novel method for designing substitution boxes based on mobius group,” 2021. https://doi.org/10.21203/rs.3.rs-173305/v1 [Google Scholar] [CrossRef]
48. E. Biham and A. Shamir, “Differential cryptanalysis of DES-like cryptosystems,” Journal of CRYPTOLOGY, vol. 4, no. 1, pp. 3–72, 1991. [Google Scholar]
49. M. Matsui, “Linear cryptanalysis method for DES cipher,” in Workshop on the Theory and Application of of Cryptographic Techniques, Berlin, Heidelberg, Germany: Springer, pp. 386–397, 1993. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF
 Downloads
Downloads
 Citation Tools
Citation Tools
