A Nonstandard Computational Investigation of SEIR Model with Fuzzy Transmission, Recovery and Death Rates

1  Introduction

Mathematical modeling has played a key role in better understanding the behavior of infectious diseases. Infectious disease modeling is a powerful technique that has been used to research the dynamic transmission of infections, forecast the trajectory of an outbreak, and assess the most effective epidemic disease control measures. The transmission of infectious diseases and their prevention are frequently better understood through the use of mathematical models. To find solutions to manage diseases in the population, numerous studies have been carried out using the mathematical model method. To learn more about the dynamics of infectious disease transmission and control, numerous models on the disease's dynamics have been created and studied. Over the past few years, there has been a collective worldwide initiative to expedite advancements in creating a global surveillance network aimed at addressing the challenges posed by emerging and re-emerging infectious diseases during pandemics. To quickly assess potentially urgent situations, scientists from medicine and molecular biology to computer science and applied mathematics have collaborated. Consequently, the utilization of mathematical modeling plays a vital role in predicting, evaluating, and managing potential outbreaks. In order to gain a deeper comprehension of contagious dynamics, it is necessary to extensively investigate the influence of various variables. These variables encompass aspects ranging from the microscopic level of host-pathogen interactions to the dynamics of transmission between hosts, alongside the broader ecological, social, economic, and demographic factors prevalent worldwide. Thorough studies focusing on these factors are essential [1,2].

Mathematical models have been critical in understanding the spread of directly transmissible infectious diseases. Since the mid-twentieth century, mathematical epidemiology appears to have grown at an exponential rate. Many different models for infectious diseases have been developed, mathematically analyzed, and applied. The concept underlying compartmental models involve classifying the entire population according to their epidemiological condition. The type of epidemic model is determined by the number of compartments considered. A mathematical model is a condensed representation of existing clinical and biological knowledge that incorporates elements that seem pertinent to the question being researched regarding disease dynamics and progression. As a result, a model is a simplified representation of a complex reality, and its structure is determined by the processes under consideration and extrapolated [3].

Mathematical and statistical models, as well as computational engineering, are helping to shed light on the problem and aid in decision making. In 1766, the first publication on mathematical modeling of epidemics was published. To study smallpox mortality in England, which was one in 14 of total mortality at the time, a mathematical model developed by Daniel Bernoulli. Bernoulli's model demonstrated that immunization anti-virus treatment would add about three years to life expectancy at birth. This work's English translation can be found in [4]. The deterministic compartmental epidemic modeling was developed by Kermack et al. [5–7]. Enko created a probabilistic model to describe the measles epidemic in discrete time and calculated the number of contacts between infected and susceptible people in the population [8]. After that, a huge number of models were created, examined, and used both qualitatively and quantitatively to study a variety of infectious diseases. In addition to being used to compare, plan, implement, evaluate, and optimize various detection, preventive, therapeutic, and control programs, mathematical models have become useful tools for studying the transmission and management of infectious diseases.

The susceptible, exposed, infectious, and recovered (SEIR) model is used to imitate the spread of an infectious illness within a population. It is frequently used to investigate the dynamics of infectious diseases and to assess the possible impact of various interventions such as vaccination campaigns, social distancing measures, and quarantine regimes. The compartment structure may differ depending on the nature of the disease [9]. Ngwa et al. [10] developed a malaria model in an endemic scenario with a changeable human and mosquito population. Sheikh investigated an SEIR model that took into account limited treatment resources [11]. Zhang et al. investigated an SEIR model that included continuous inflows of new susceptible, exposed, infective, and recovered. This model includes a disease-related death rate [12]. Zhou et al. conducted a study on an SEIR epidemic model that incorporated a saturated recovery process [13]. Yi et al. conducted studied the dynamic behaviors of an SEIR model that incorporated seasonal transmission rate forcing. In order to assess the dynamics of the system, the study considered scenarios with one, two, and three variable parameters [14]. Sun et al. examined an SEIR model with varying population sizes and vaccination strategies. They identified three threshold parameters crucial for disease eradication, including the total number of infectives and their proportion in the population [15]. Kolawole et al. investigated an SEIR model to determine the significance of saturation. The Runge-Kutta (RK) method was used to solve the model numerically. The susceptible and infected compartments of the model are significantly impacted by the saturation term, according to the results of the numerical simulation. The saturation phrase, on the other hand, affects susceptible individuals more so than infected individuals [16]. Hukmah et al. developed a COVID-19 disease model by modifying the SEIR model to include quarantine and vaccination compartments [17]. Chen et al. created an SEIR model for information propagation in complex networks with the effect of a hot search. Mathematical and numerical simulations were also carried out [18]. Yang et al. [19] studied an SEIR epidemic model that included both sexual and non-sexual transmission routes. Mohajan investigated a COVID-19 SEIR model [20].

Many infectious diseases can be stopped from spreading by susceptible people's immunity, and certain infections provide recovered patients temporary or permanent protection from re-infection. The dynamic spread of the susceptible, infectious and recovered (SIR), SEIR, susceptible, vaccinated, exposed, infectious and recovered (SVEIR), and many other epidemic models had been investigated thoroughly by a number of researchers. For a better comprehension of the disease's transmission, Olopade et al. investigated an SEIR mathematical model including natural immunity and treatment rates [21]. Immunity can be obtained through targeted immunization; it can also be obtained naturally after a person has fully recovered from infection; and, in some cases, the mother's antibodies may be transferred to the newborn to confer a certain level of immunity. Immunity duration varies depending on the disease, with some diseases providing almost lifelong immunity and others only providing a brief period of insensitivity. Vaccine-induced immunity frequently requires a boost after a period of time, such as when the vaccine's effectiveness decreases due to a lack of disease exposure. In the case of measles, for example, vaccinated individuals have less immunity than those who have natural immunity [22,23]. Some mass vaccination models were presented by Scherer and McLean, and they can be used to provide crucial insights into the anticipated effects of immunization campaigns. They demonstrate how to determine the vaccination coverage rate necessary to eradicate an infection, examine the effects of vaccine-induced immunity that deteriorates with time, and examine the interactions between strains of infectious agents that are both vaccine vulnerable and vaccine resistant [24]. A mathematical model for cholera epidemics was given by Sanches et al. [25] and takes seasonality, host immunity decline, and cholera control measures into account. Innate immunity was the subject of research by Jain et al. in disease modeling [26].

Zadeh first proposed the fuzzy theory in 1965 [27]. Fuzzy theory plays an important role in mathematical modeling by providing a way to handle uncertain or ambiguous information in a mathematical framework. Traditional mathematical models assume that all variables are precise and can be accurately measured or calculated. In many real-world circumstances, however, variables may be inaccurate or impossible to assess, leading to model uncertainty. Fuzzy theory provides a mathematical framework for dealing with uncertainty by allowing variables to take on values that are not explicitly stated, but rather are characterized by degrees of membership in a set. This allows for more flexible and realistic variable representation, allowing mathematical models to reflect the complex and uncertain nature of real-world systems more accurately. In mathematical modeling, fuzzy parameters are used to indicate the degree of uncertainty or imprecision in parameter values. When the interactions between variables are complex and exact data is lacking, fuzzy parameters are extremely useful. They allow for the quantitative representation of uncertainty and imprecision, as well as the incorporation of subjective knowledge and expert opinion into mathematical models. Fuzzy theory has been applied in a wide range of mathematical modeling applications. Researchers can construct more accurate and robust models that can handle uncertainty and imprecision by combining fuzzy theory into mathematical models, resulting in better predictions and judgments. The fuzzy theory has been applied in various ways to develop and enhance epidemic models. Barros et al. [28] and Mondal et al. [29] investigated epidemic models with fuzzy transmission coefficients. Mishra et al. suggested a Susceptible Infectious-Recovered-Susceptible (SIRS) model for the fuzzy transmission of worms in a computer network [30].

Many traditional schemes, such as forward Euler, Runge-Kutta, and others, occasionally fail by generating oscillations, chaos, and false steady states. One option for avoiding all of these numerical instabilities is to build schemes using the nonstandard finite-difference method. This technique, pioneered by Mickens [31], has resulted in the development of new numerical schemes that preserve physical qualities such as stability, positivity, and boundedness, etc. Using the NSFD approach, Verma et al. investigated the generalized Burgers-Huxley (GBH) equation [32]. To assess influenza disease, Khalsaraei et al. presented an NSFD technique. Some intriguing aspects of the developed scheme are investigated, and numerical results are presented [33]. Razza et al. investigated a stochastic model of HIV/AIDS based on NSFD theory in a bisexual population, taking counseling and antiretroviral therapy into account, and concluded that the stochastic model of the HIV/AIDS epidemic is more pragmatic than the deterministic model. All of the important properties of the disease dynamical model were retained by the NSFD stochastic scheme [34]. Jawaz et al. investigated a delayed reaction-diffusion epidemic model and developed an NSFD-based scheme to study HIV/AIDS [35]. The NSFD theory proposed by Mickens is extensively used in disease mathematical and numerical modeling [36,37], just to mention a few. The susceptible-infected-treatment-recovered (SITR) model was developed by Aslefallah et al. to explore the dynamics of the new coronavirus (COVID-19). Error analysis is performed to assess the model's accuracy [38]. Singular boundary approach is used to solve a modified anomalous diffusion process in two dimensions with a nonlinear source term, initial and Dirichlet-type boundary conditions. In terms of Riemann-Liouville fractional derivatives, they modeled the process as a two-dimensional nonlinear time-fractional sub-diffusion equation [39]. The singular boundary method (SBM) is used to solve the telegraph equation in two dimensions, regardless of domain shape [40]. A study focuses on the spectral meshless radial point interpolation of two-dimensional pseudo parabolic equations. To approximate time derivatives, the finite difference time-stepping approach is used. This meshless approach's stability and convergence are thoroughly discussed and theoretically verified [41]. Allehiany et al. investigated a Covid-19 model with fuzziness and numerically solved it using the NSFD scheme [42]. Alhebshi et al. looked into a computer virus model that used fuzzy criteria [43].

The novelty of the current work is the development, accomplishment, and numerical analysis of the first order explicit numerical technique with NSFD in a fuzzy environment, particularly with fuzzy parameters. The use of fuzzy theory in mathematical modeling has the potential to improve our understanding of disease transmission and to inform the development of more effective control strategies. To our knowledge, the model under study has never been studied in the literature in the NSFD and fuzzy senses, and this is the first study of this model in this sense. The primary goal of this study is to investigate an effective implicit numerical integration method for the solution of the SEIR model natural immunity and treatment rates. The convergence, positivity and consistency of the developed scheme are investigated in this work. We claim that the tool for the suggested numerical integration scheme is trustworthy, effective, and adopts all the dynamical characteristics for long-term disease behavior.

2  SEIR Mathematical Model with Fuzzy Parameters

In this research, the model proposed by Olopade et al. [21] is took into account.

{dSdt=−βIS−μS+π+θR+kE,dEdt=−(μ+σ+k)E+(1−ϵ)βSI,dIdt=−(μ+δ+ω)I+ϵβSI+σE,dRdt=ωI−(μ+θ)R.(1)

The fuzzy model that corresponds to the model mentioned above can be expressed as

{dSdt=−β(ϑ)IS−μS+π+θ(ϑ)R+kE,dEdt=−(μ+σ+k)E+(1−ϵ)β(ϑ)SI,dIdt=−(μ+δ(ϑ)+ω)I+ϵβ(ϑ)SI+σE,dRdt=ωI−(μ+θ(ϑ))R.(2)

The disease transmission, recovery from the disease, and death due to disease rates of the infected individuals are considered fuzzy numbers due to their uncertain natures. These parameters are denoted by β(ϑ), θ(ϑ) and δ(ϑ), respectively, and are defined below:

β(ϑ)={0,ϑ≤ϑminϑ−ϑminϑM−ϑmin,ϑmin<ϑ≤ϑM1,ϑM<ϑ,(3)

θ(ϑ)=θ0−1ϑMϑ+1,  0≤ϑ≤ϑmin,(4)

and

δ(ϑ)={(1−ξ)−ϵ0ϑminϑ+ϵ0,0≤ϑ≤ϑmin1−ξ,ϑmin<ϑ.(5)

The death rate δ(ϑ) will be higher at the higher virus level, i.e., ϑ0<ϑ and 1−ξ, (ξ≥0) is the maximum death while θ0>0 is the minimum recovery rate.

2.1 Equilibrium Analysis

Case 1: If If ϑ<ϑmin, we obtain

C0(S0,E0,I0,R0)=(πμ,0,0,0).

Case 2: If ϑmin<ϑ≤ϑM, then we have β(ϑ)=ϑ−ϑminϑM−ϑmin and C∗(S∗,E∗,I∗,R∗) is obtained, where

S∗=π+θ(ϑ)R∗+kE∗β(ϑ)I∗+μ,

E∗=(1−ϵ)β(ϑ)S∗I∗μ+σ+k,

I∗=σEμ+δ(ϑ)+ω−ϵβ(ϑ)S∗,

R∗=ωI∗μ+θ(ϑ).

Case 3: If ϑM<ϑ<ϑmax, then we have β(ϑ)=1 and C∗∗(S∗∗,E∗∗,I∗∗,R∗∗) is obtained, where

S∗∗=π+θ(ϑ)R∗∗+kE∗∗I∗∗+μ,

E∗∗=(1−ϵ)S∗∗I∗∗μ+σ+k,

I∗∗=σEμ+δ(ϑ)+ω−ϵS∗∗,

R** = ωI**μ+θ(ϑ)x′.

2.2 The Fuzzy Basic Reproductive Number (BRN) R0f

The BRN R0 is given by

R0=β(ϑ)π(σ+ϵ(μ+σ+k)−σϵ)μ(μ+σ+k)(μ+δ(ϑ)+ω).(6)

Since R0 is a direct function of the virus ϑ, it can be analyzed as follows:

Case 1: If ϑ<ϑmin, then we have β(ϑ)=0 and we obtain

R0(ϑ)=0.

Case 2: If ϑmin<ϑ≤ϑM, then we have β(ϑ)=ϑ−ϑminϑM−ϑmin and we obtain

R0(ϑ)=β(ϑ)π(σ+ϵ(μ+σ+k)−σϵ)μ(μ+σ+k)(μ+δ(ϑ)+ω).

Case 3: If ϑM<ϑ<ϑmax, then we have β(ϑ)=1 and we obtain

R0(ϑ)=π(σ+ϵ(μ+σ+k)−σϵ)μ(μ+σ+k)(μ+δ(ϑ)+ω).

R0(ϑ) can be written as

R0(ϑ)=(0,β(ϑ)π(σ+ϵ(μ+σ+k)−σϵ)μ(μ+σ+k)(μ+δ(ϑ)+ω),π(σ+ϵ(μ+σ+k)−σϵ)μ(μ+σ+k)(μ+δ(ϑ)+ω)).

The fuzzy reproduction number can be found as follows [33]:

R0f=E[R0(ϑ)],

 =π(σ+ϵ(μ+σ+k)−σϵ)(2β(ϑ)+1)4μ(μ+σ+k)(μ+δ(ϑ)+ω).

2.3 Stability Analysis

At disease free equilibrium (DFE), the Jacobean matrix of the system (2) is given by

J(C0)=[−μk0θ0−A10000σ0−A20ω−A3],

where A1=μ+σ+k, A2=μ+δ+ω and A3=μ+θ.

Eigenvalues of the above matrix are λ1=−μ, λ2=−A1, λ3=−A2 and λ4=−A3. All eigenvalues of the Jacobean of the system (2) at DFE are less than one which shows that the system is locally asymptotically stable at C0.

3  Numerical Modeling

3.1 NSFD Scheme

The NSFD scheme consists of a general set of numerical analysis methods that provide numerical solutions for differential equations by building a discrete model. R. E. Mickens was the one who first proposed it as a method to increase the accuracy and stability of numerical solutions. He used nonstandard analysis concepts, a type of mathematical logic, to create difference equations that more precisely mimic the continuous differential equations. The creation of the NSFD schemes for ordinary differential equations (ODEs) was one of Mickens' early contributions. He demonstrated that by employing nonstandard difference formulas that integrate higher-order derivatives, it is possible to improve accuracy and properly capture the oscillatory nature of solutions. Mickens extended his work to NSFD methods for partial differential equations (PDEs) in the late 1990s and early 2000s. The advantages of NSFD approaches over typical finite difference systems in terms of accuracy, stability,and efficiency are established. NSFD scheme for the system (2) is

{Sn+1=Sn+h(π+θ(ϑ)Rn+kEn)1+h(β(ϑ)In+μ),En+1=En+h(1−ϵ)β(ϑ)Sn+1In1+h(μ+σ+k),In+1=In+h(ϵβ(ϑ)Sn+1In+σEn)1+h(μ+δ+ω),Rn+1=Rn+hωIn1+h(μ+θ).(7)

3.2 Positivity of the NSFD Scheme

Given that all the state variables within the model represent segments of a population, it is necessary for at least one of them to be positive, while the other subpopulations must remain nonnegative at every instance in time. Ensuring the positivity of state variables is a crucial aspect in compartmental epidemic models. This fundamental property is thoroughly examined and upheld through the application of the principle of mathematical induction within an implicit numerical integration scheme. The following theorem is particularly advantageous in effectively addressing this concern.

Theorem: Let S,E,I and R involved in the NSFD scheme are positive at t=0; moreover, if θ, π, μ, ϵ, β, σ, k, ω and δ are also positive, then Sn+1≥0,En+1≥0,In+1≥0 and Rn+1≥0.

Proof: Consider the system (7), we have

Sn+1=Sn+h(π+θ(ϑ)Rn+kEn)1+h(β(ϑ)In+μ),

En+1=En+h(1−ϵ)β(ϑ)SnIn1+h(μ+σ+k),

In+1=In+h(ϵβ(ϑ)SnIn+σEn)1+h(μ+δ(ϑ)+ω),

Rn+1=Rn+hωIn1+h(μ+θ(ϑ)).

Putting n=0, in the above scheme, we have

S1=S0+h(π+θ(ϑ)R0+kE0)1+h(β(ϑ)I0+μ)≥0,

E1=E0+h(1−ϵ)β(ϑ)S0I01+h(μ+σ+k)≥0,

I1=I0+h(ϵβ(ϑ)S0I0+σE0)1+h(μ+δ(ϑ)+ω)≥0,

R1=R0+hωI01+h(μ+θ(ϑ))≥0.

Putting n=1, in the above scheme, we have

S2=S1+h(π+θ(ϑ)R1+kE0)1+h(β(ϑ)I1+μ)≥0,

E2=E1+h(1−ϵ)β(ϑ)S1I11+h(μ+σ+k)≥0,

I2=I1+h(ϵβ(ϑ)S1I1+σE1)1+h(μ+δ(ϑ)+ω)≥0,

R2=R1+hωI11+h(μ+θ(ϑ))≥0.

Next, assume that the above system of equations ensures that the value of has the attribute of positivity for n=2,3,4,…,n−1, i.e., Sn≥0;En≥0;In≥0; and Rn≥0; for n=2,3,4,…,n−1.

The positivity will now be examined for a random positivity integer n∈Z, we observe that

Sn+1=Sn+h(π+θ(ϑ)Rn+kEn)1+h(β(ϑ)In+μ)≥0,

En+1=En+h(1−ϵ)βSnIn1+h(μ+σ+k)≥0,

In+1=In+h(ϵβSnIn+σEn)1+h(μ+δ(ϑ)+ω)≥0,

Rn+1=Rn+hωIn1+h(μ+θ(ϑ))≥0.

Therefore, for any positive integer values of n, the proposed NSFD scheme guarantees positivity for the state variables, S,E,I and R.

3.3 Convergence Analysis

If the Eigenvalues of the system (7) lie within the unit circle the suggested implicit numerical integration scheme demonstrates convergence. To prove this, assume that

C1=S+h(π+θ(ϑ)R+kE)1+h(β(ϑ)I+μ),

C2=E+h(1−ϵ)β(ϑ)SI1+h(μ+σ+k),

C3=I+h(ϵβ(ϑ)SI+σE)1+h(μ+δ(ϑ)+ω),

C4=R+hωI1+h(μ+θ(ϑ)).

The Jacobean matrix corresponding to the system (7) is

J=[∂C1∂S∂C1∂I∂C1∂E∂C1∂R∂C2∂S∂C2∂I∂C2∂E∂C2∂R∂C3∂S∂C4∂S∂C3∂I∂C4∂I∂C3∂E∂C3∂R∂C4∂E∂C4∂R],

J=[11+hβ(ϑ)I+hμhk1+hβ(ϑ)I+hμ−hβ(ϑ)[S+h(π+θ(ϑ)R+kE)](1+hβ(ϑ)I+hμ)20h(1−ϵ)β(ϑ)I1+h(μ+σ+k)11+h(μ+σ+k)h(1−ϵ)β(ϑ)S1+h(μ+σ+k)0hϵβI1+h(μ+δ(ϑ)+ω)I+hσ1+h(μ+δ(ϑ)+ω)1+hϵβ(ϑ)S1+h(μ+δ(ϑ)+ω)000hω1+h(μ+θ(ϑ))11+h(μ+θ(ϑ))],

J(C0)=[11+hμhk1+hμ00011+h(μ+σ+k)000I+hσ1+h(μ+δ(ϑ)+ω)11+h(μ+δ(ϑ)+ω)000hω1+h(μ+θ(ϑ))11+h(μ+θ(ϑ))],

Eigenvalues of the above Jacobean matrix are λ1=11+hμ<1, λ2=11+h(μ+σ+k)<1, λ3=11+h(μ+δ(ϑ)+ω)<1 and λ4=11+h(μ+θ(ϑ))<1. All of the eigenvalues of the Jacobean matrix will be contained within a unit circle, ensuring that the proposed NSFD scheme is convergent at DFE point C0.

3.4 Consistency Analysis

The Taylor's series is used to check the consistency of the proposed scheme. From first equation of the system (7),

Sn+1[1+h(β(ϑ)In+μ)]=Sn+h(π+θ(ϑ)Rn+kEn).

For the consistency, the Taylor’s series expansion is considered as follows:

Sn+1=Sn+hdSdt+h22!d2Sdt2+h33!d3Sdt3+…,

Substituting the value of Sn+1 in the above equation and after some simplifications, we get

dSdt=−β(ϑ)InSn−μSn+π+θ(ϑ)Rn+kEn,

 ⇒dSdt=−β(ϑ)IS−μS+π+θ(ϑ)R+kE.

From the second equation of the NSFD scheme, we have

En+1(1+h(μ+σ+k))=En+h(1−ϵ)β(ϑ)Sn+1In,

The Taylor’s series expansion for En+1 is

En+1=En+hdEdt+h22!d2Edt2+h33!d3Edt3+…,

Substituting the value of En+1 in the above equation and after some simplifications, we get

dEdt=−(μ+σ+k)En+(1−ϵ)β(ϑ)Sn+1In,

 ⇒dEdt=−(μ+σ+k)E+(1−ϵ)β(ϑ)SI.

Similarly, from the third equation of the NSFD scheme we have

In+1(1+h(μ+δ(ϑ)+ω))=In+h(ϵβ(ϑ)Sn+1In+σEn),

The Taylor’s series expansion for In+1 is

In+1=In+hdIdt+h22!d2Idt2+h33!d3Idt3+…,

Substituting the value of In+1 in the above equation and after some simplifications, we get

dIdt=−(μ+δ(ϑ)+ω)In+ϵβ(ϑ)Sn+1In+σEn,

 ⇒dIdt=−(μ+δ(ϑ)+ω)I+ϵβ(ϑ)SI+σE,

Similarly, we can get

dRdt=ωI−(μ+θ(ϑ))R

by applying Taylor’s series on the last equation of system (7). It is therefore concluded that our proposed scheme is consistent of order 1.

4  Numerical Simulations

Table 1 displays the values of parameters used for numerical simulations.

The graphical behavior of exposed populations at two different values of the step sizes are shown in Fig. 1 at DFE and endemic equilibrium (EE) points for all three cases. The graphs show smooth, stable and converging behavior at both the step sizes and the increase in the values of the step size does not affect it. Convergence and positivity are the two major characteristics of these types of models as these models consist of the population which cannot be negative. The developed scheme preserve these feature which can be seen in these graphs.

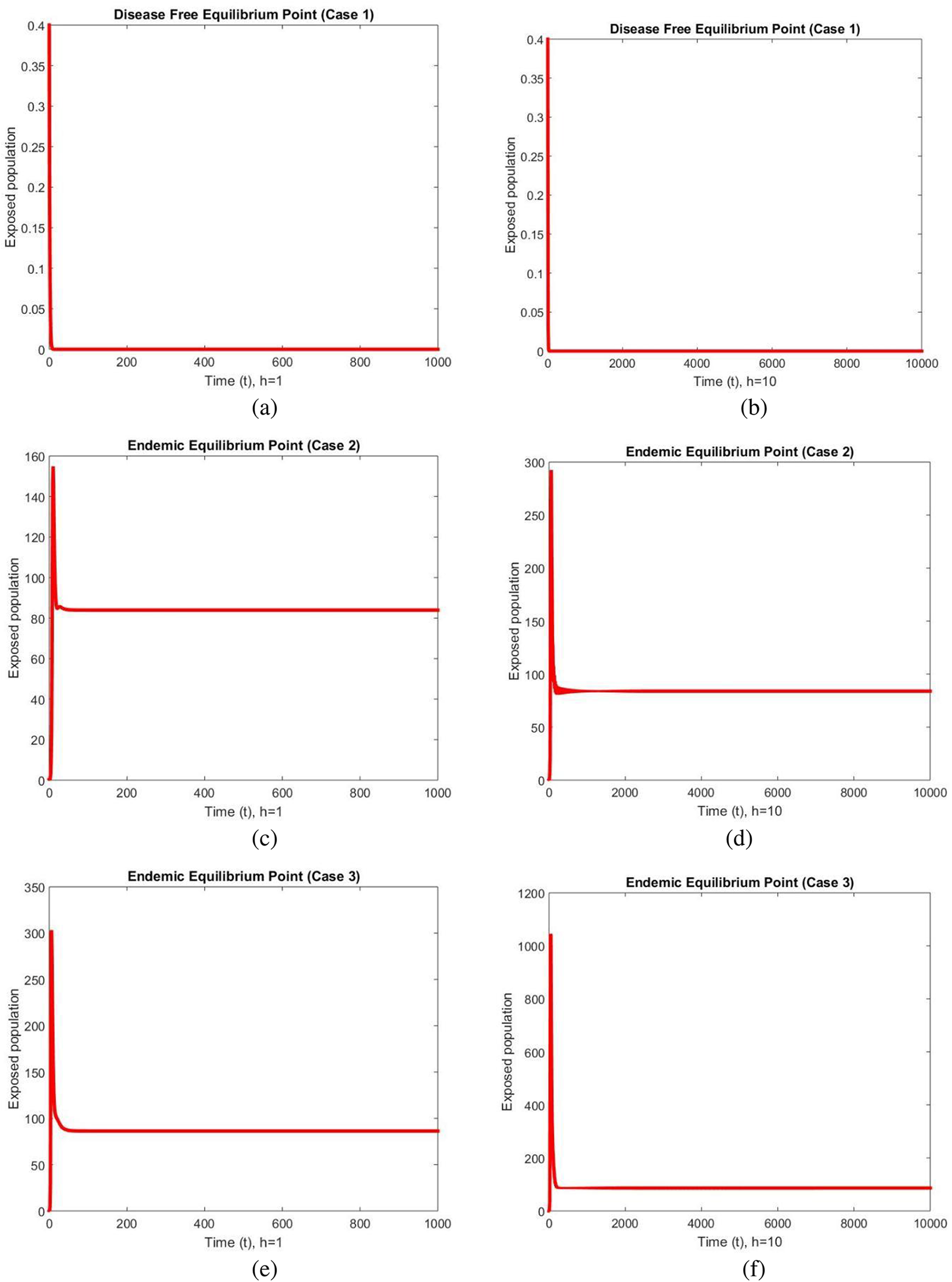
Figure 1: Exposed populations at different step sizes

Fig. 2 depicts the graphical behavior of infected populations at two different values of the step sizes at DFE and EE points for all three cases. The graphs exhibit convergent and stable behavior for both step sizes, and an increase in step size values has no impact on them. Since the behavior of the method is not affected with an increase in the values of the step size. It can be concluded that the NSFD theory can be used to study the long-term behavior of the model. This is an interesting feature of the developed method which many other classical methods such as Euler and many other do not keep at increasing step sizes. This behavior shows the superiority of the NSFD scheme over Euler’s method in fuzzy conditions.

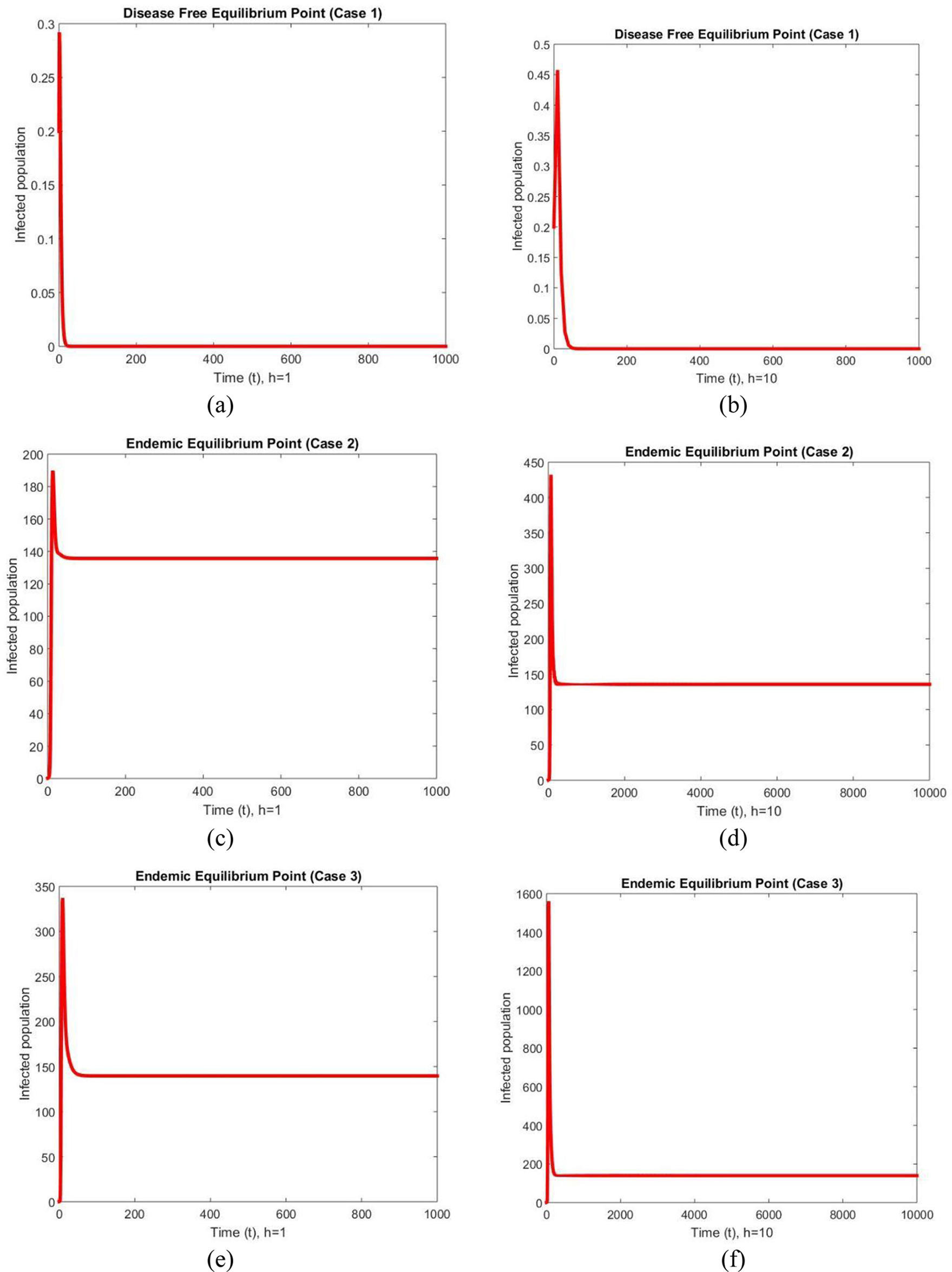
Figure 2: Infected populations at different step sizes

The graphs of the recovered population are shown in Fig. 3 at different values of the step size for case 1, case 2 and case 3. The graphs behave similarly at different values of the step size and converge smoothly. We can conclude from this behavior that the NSFD method is capable of reflecting the dynamics of the studied model in fuzzy conditions. The typical standard schemes that exist inthe literature can cause chaos and misleading variations for some passions of the discretization constraints [44].

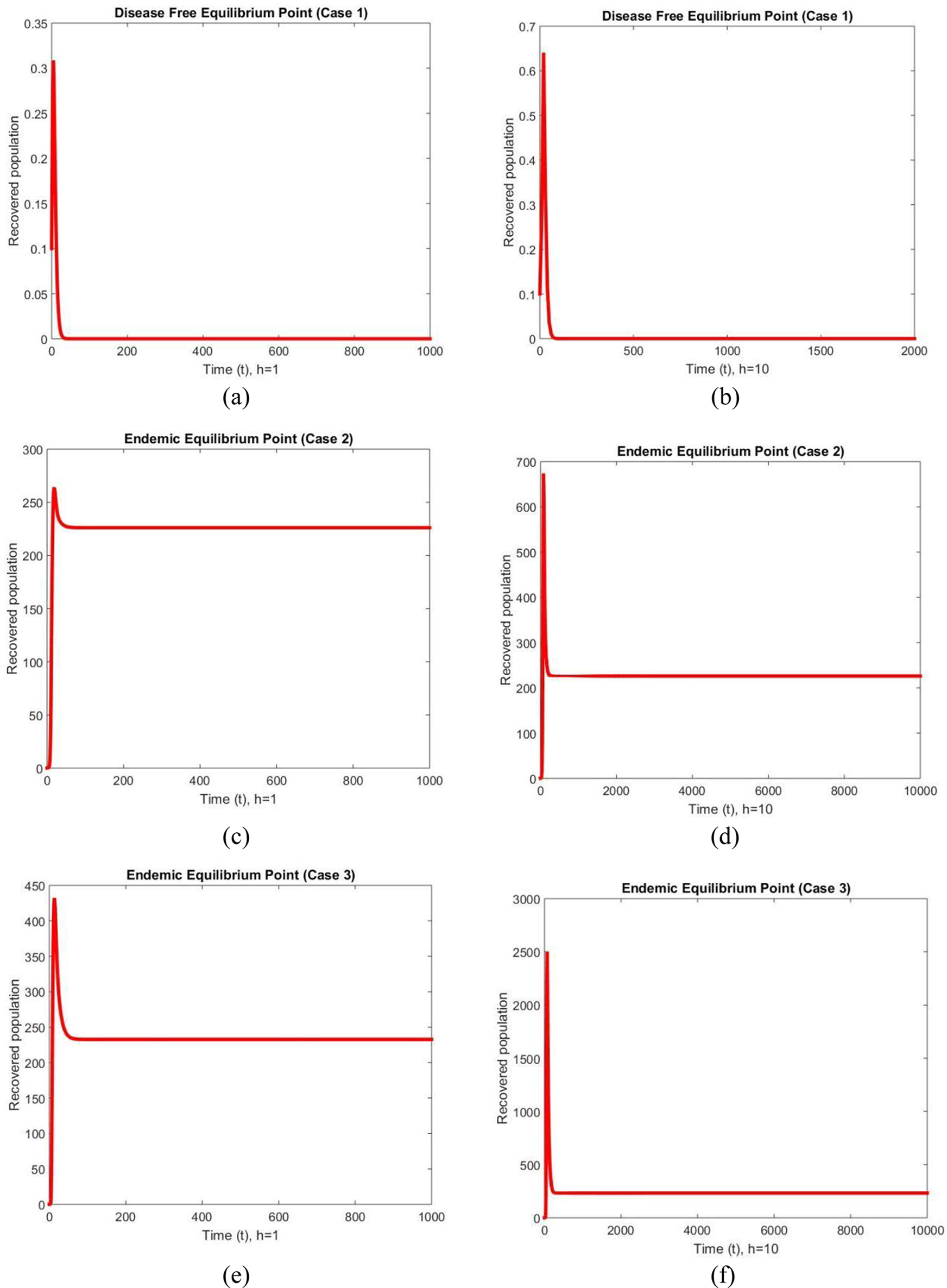
Figure 3: Infected populations at different step sizes

The effects of the natural immunity are presented in Fig. 4. Low immunity causes greater infection and the infection decreases with an increase in the natural immunity. Immunity boosting is crucial in epidemiology, particularly in the context of infectious diseases. When a pathogen enters the body, the immune system mobilizes to defend against the invader. This response can include a variety of mechanisms such as antibody production, immune cell activation, and inflammation. The severity and duration of the illness can be determined by the strength of the immune response. Immune enhancement can help prevent or lessen the severity of infections. Vaccines, for example, stimulate the immune system, causing it to produce a protective response against specific pathogens. This can help prevent infection or lessen the severity of an infection if it occurs. Aside from vaccines, other ways to boost immunity include eating a healthy diet, exercising regularly, getting enough sleep, and reducing stress. These measures can help improve the immune system's overall function, making it more capable of fighting infections.

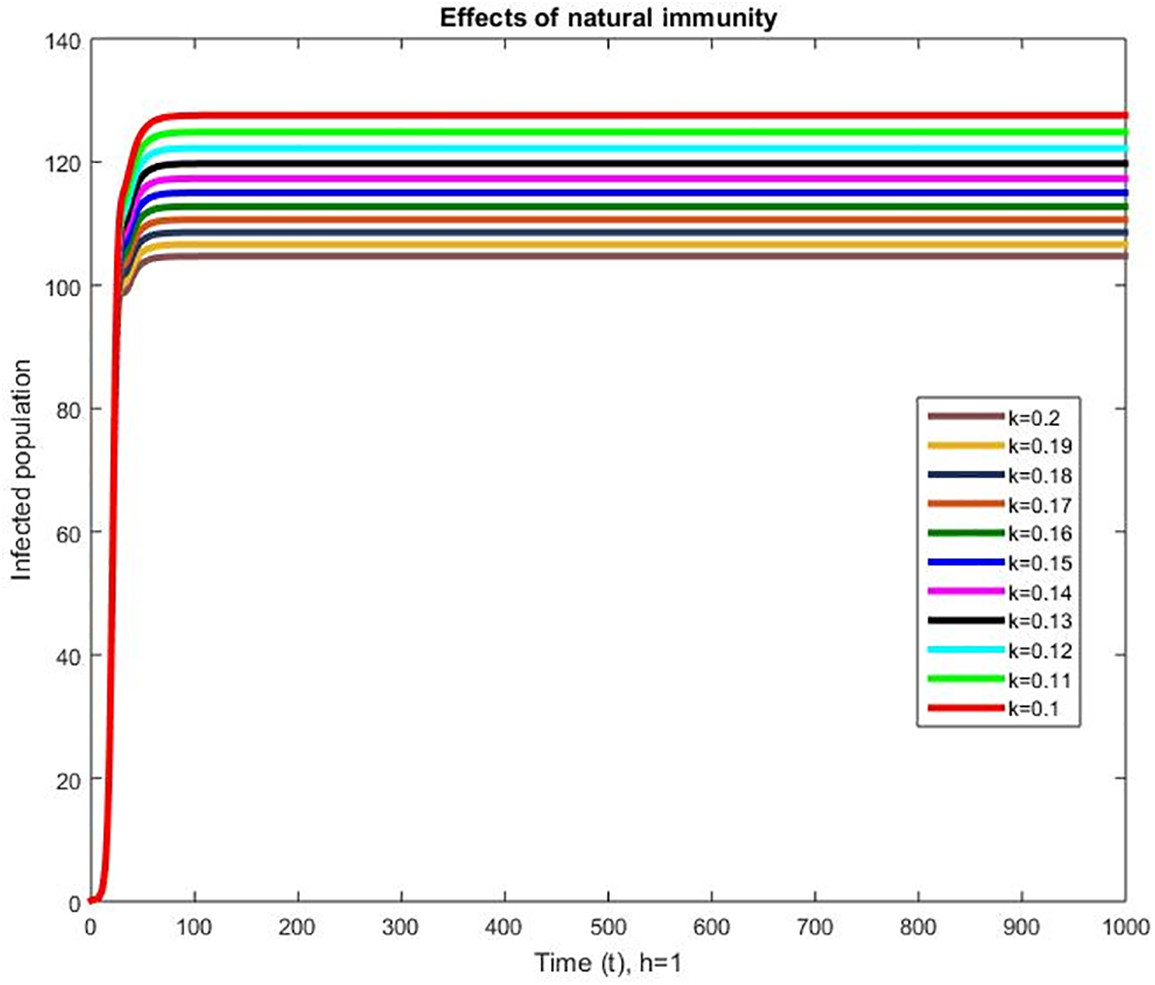
Figure 4: Effects of natural immunity on infected population

5  Conclusion

Epidemic modeling is a useful tool for understanding and controlling the spread of infectious diseases. In real life, however, the parameters used to model the disease may not be precisely known. Fuzzy theory can be used in such cases to incorporate uncertainty into models. In this article, an SEIR epidemic model is studied. The positivity and boundedness of the model are investigated. Equilibrium points and basic reproduction number are studied in fuzzy senses. For the numerical solution of the model, an NSFD method is developed. Positivity, convergence and consistency of the proposed method are investigated. Positivity is one of the major characteristic of these epidemic models since non positive values are meaningless due to the fact that these models deals with population which cannot be negative. Many classical standard finite difference techniques do not hold this property for some values of the discretization parameter. The proposed technique preserves positivity for all values of the discretization parameter. Convergence is the other important property in these type of models and the suggested method preserves this.

Natural immunity is an important aspect of disease dynamics, and failing to account for it can result in a variety of modeling disasters. We have shown mathematically and numerically that increasing natural immunity can lead to a decrease in infection. Immunity boosting plays a critical role in epidemiology by preventing and controlling infectious diseases, protecting vulnerable populations, achieving herd immunity, preventing future pandemics, improving the treatment of infections, and promoting individual responsibility for health. This study could help in the modeling of other similar diseases. Natural immunity can be applied to other compartmental models. Future work can consider saturated incidence, treatment, delayed, fractional, and stochastic directions.

Acknowledgement: The authors extend their appreciation to the Deputyship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through Project Number ISP22-6.

Funding Statement: This research was funded by the Ministry of Education in Saudi Arabia of funder Grant Number ISP22-6 and the APC was funded by the Ministry of Education in Saudi Arabia.

Author Contributions: Study conception and design: Fazal Dayan and Muhammad Rafiq; data collection: Fazal Dayan and Nauman Ahmed; analysis and interpretation of results: Abdullah Ali H. Ahmadini and Hassan A. Hamali; draft manuscript preparation: Fazal Dayan, Ahmed H. Msmali. All authors have reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data will be made available on request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Lessler and D. A. Cummings, “Mechanistic models of infectious disease and their impact on public health,” American Journal of Epidemiology, vol. 183, no. 5, pp. 415–422, 2016. [Google Scholar] [PubMed]

2. J. Huo, H. Zhao and L. Zhu, “The effect of vaccines on backwards bifurcation in a fractional order HIV model,” Nonlinear Analysis: Real World Applications, vol. 26, no. 3, pp. 289–305, 2015. [Google Scholar]

3. S. Mandal, R. R. Sarkar and S. Sinha, “Mathematical models of malaria–A review,” Malaria Journal,vol. 10, no. 1, pp. 1–19, 2011. [Google Scholar]

4. D. Bernoulli and S. Blower, “An attempt at a new analysis of the mortality caused by smallpox and of the advantages of inoculation to prevent it,” Reviews in Medical Virology, vol. 14, no. 5, pp. 275–288, 2004. [Google Scholar] [PubMed]

5. W. O. Kermack and A. G. McKendrick, “A contribution to the mathematical theory of epidemics,” Proceedings of the Royal Society A, vol. 115, no. 772, pp. 700–721, 1927. [Google Scholar]

6. W. O. Kermack and A. G. McKendrick, “Contributions to the mathematical theory of epidemics. II.—The problem of endemicity,” Proceedings of the Royal Society A, vol. 138, no. 834, pp. 55–83, 1932. [Google Scholar]

7. W. O. Kermack and A. G. McKendrick, “Contributions to the mathematical theory of epidemics,” Part III, Proceedings of the Royal Society B, vol. 141, pp. 94–112, 1933. [Google Scholar]

8. P. D. En’ko, “On the course of epidemics of some infectious diseases,” International Journal of Epidemiology, vol. 18, no. 4, pp. 749–755, 1989. [Google Scholar] [PubMed]

9. J. L. Aron, “Mathematical modelling of immunity to malaria,” Mathematical Biosciences, vol. 90, no. 1–2, pp. 385–396, 1988. [Google Scholar]

10. G. A. Ngwa and W. S. Shu, “A mathematical model for endemic malaria with variable human and mosquito populations,” Mathematical and Computer Modelling, vol. 32, no. 7–8, pp. 747–763, 2000. [Google Scholar]

11. S. A. Al-Sheikh, “Modeling and analysis of an SEIR epidemic model with a limited resource for treatment,” Global Journal of Science Frontier Research, vol. 12, no. 14, pp. 57– 66, 2012. [Google Scholar]

12. J. Zhang, J. Li and Z. Ma, “Global dynamics of an SEIR epidemic model with immigration of different compartments,” Acta Mathematica Scientia, vol. 26, no. 3, pp. 551–567, 2006. [Google Scholar]

13. X. Zhou and J. Cui, “Analysis of stability and bifurcation for an SEIR epidemic model with saturated recovery rate,” Communications in Nonlinear Science and Numerical Simulation, vol. 16, no. 11, pp. 4438–4450, 2011. [Google Scholar]

14. N. Yi, Q. Zhang, K. Mao, D. Yang and Q. Li, “Analysis and control of an SEIR epidemic system with nonlinear transmission rate,” Mathematical and Computer Modelling, vol. 50, no. 9–10, pp. 1498–1513, 2009. [Google Scholar] [PubMed]

15. C. Sun and Y. Hsieh, “Global analysis of an SEIR model with varying population size and vaccination,” Applied Mathematical Modelling, vol. 34, no. 10, pp. 2685–2697, 2010. [Google Scholar]

16. M. K. Kolawole, O. L. Moshood, K. A. Bashiru, A. I. Alaje, A. O. Popoola et al., “On the effects of saturation terms on a SEIR epidemic model with infected and susceptible compartments,” Jambura Journal of Mathematics, vol. 5, no. 1, pp. 1–24, 2023. [Google Scholar]

17. H. Hukmah, M. R. Nisardi, S. Sulma and M. Suriani, “Mathematical model of COVID-19 with quarantine and vaccination,” Jurnal Matematika, Statistika dan Komputasi, vol. 19, no. 2, pp. 266–285, 2023. [Google Scholar]

18. X. Chen and S. Zhang, “An SEIR model for information propagation with a hot search effect in complex networks,” Mathematical Biosciences and Engineering, vol. 20, no. 1, pp. 1251–1273, 2023. [Google Scholar] [PubMed]

19. Q. Yang, H. F. Huo and H. Xiang, “Analysis of an edge-based SEIR epidemic model with sexual and non-sexual transmission routes,” Physica A: Statistical Mechanics and its Applications, vol. 609, no. 2, pp. 128340, 2023. [Google Scholar]

20. D. Mohajan and H. K. Mohajan, “Mathematical analysis of SEIR model to prevent COVID-19 pandemic,” Journal of Economic Development, Environment and People, vol. 11, no. 4, pp. 5–30, 2022. [Google Scholar]

21. A. I. Olopade, A. O. Adesanya and T. O. Akinwumi, “Mathematical transmission of SEIR epidemic model with natural immunity,” Asian Journal of Pure and Applied Mathematics, vol. 3, no. 1, pp. 19–29, 2021. [Google Scholar]

22. J. Mossong and C. P. Muller, “Modelling measles re-emergence as a result of waning of immunity in vaccinated populations,” Vaccine, vol. 21, no. 31, pp. 4597–4603, 2003. [Google Scholar] [PubMed]

23. E. Leuridan and P. van Damme, “Passive transmission and persistence of naturally acquired or vaccine-induced maternal antibodies against measles in newborns,” Vaccine, vol. 25, no. 34, pp. 6296–6304, 2007. [Google Scholar] [PubMed]

24. A. Scherer and A. McLean, “Mathematical models of vaccination,” British Medical Bulletin, vol. 62, no. 1, pp. 187–199, 2002. [Google Scholar] [PubMed]

25. R. P. Sanches, C. P. Ferreira and R. A. Kraenkel, “The role of immunity and seasonality in cholera epidemics,” Bulletin of Mathematical Biology, vol. 73, no. 12, pp. 2916–2931, 2011. [Google Scholar] [PubMed]

26. S. Jain and S. Kumar, “Dynamic analysis of the role of innate immunity in SEIS epidemic model,” The European Physical Journal Plus, vol. 136, no. 4, pp. 1–28, 2021. [Google Scholar]

27. L. A. Zadeh, “Fuzzy sets,” Information Control, vol. 8, no. 3, pp. 338–353, 1965. [Google Scholar]

28. L. C. Barros, M. B. F. Leite and R. C. Bassanezi, “The SI epidemiological models with a fuzzy transmission parameter,” Computers & Mathematics with Applications, vol. 45, no. 11, pp. 1619–1628, 2003. [Google Scholar]

29. P. K. Mondal, S. Jana, P. Haldar and T. K. Kar, “Dynamical behavior of an epidemic model in a fuzzy transmission,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, vol. 23, no. 5, pp. 651–665, 2015. [Google Scholar]

30. B. K. Mishra and S. K. Pandey, “Fuzzy epidemic model for the transmission of worms in computer network,” Nonlinear Analysis: Real World Applications, vol. 11, no. 5, pp. 4335–4341, 2010. [Google Scholar]

31. R. E. Mickens, “A fundamental principle for constructing non-standard finite difference schemes for differential equations,” Journal of Difference Equations and Applications, vol. 11, no. 2, pp. 645–653, 2005. [Google Scholar]

32. A. K. Verma and S. Kayenat, “An efficient Mickens’ type NSFD scheme for the generalized Burgers Huxley equation,” Journal of Difference Equations and Applications, vol. 26, no. 9–10, pp. 1213–1246, 2020. [Google Scholar]

33. M. M. Khalsaraei, A. Shokri, H. Ramos and S. Heydari, “A positive and elementary stable nonstandard explicit scheme for a mathematical model of the influenza disease,” Mathematics and Computers in Simulation, vol. 182, no. 1, pp. 397–410, 2021. [Google Scholar]

34. A. Raza, M. Rafiq, D. Baleanu, M. S. Arif, M. Naveed et al., “Competitive numerical analysis for stochastic HIV/AIDS epidemic model in a two-sex population,” IET Systems Biology, vol. 13, no. 6, pp. 305–315, 2019. [Google Scholar] [PubMed]

35. M. Jawaz, N. Ahmed, D. Baleanu, M. Rafiq and M. A. Rehman, “Positivity preserving technique for the solution of HIV/AIDS reaction diffusion model with time delay,” Frontiers in Physics, vol. 7, no. 1, pp. 1–10, 2020. [Google Scholar]

36. J. Cresson and F. Pierret, “Nonstandard finite difference schemes preserving dynamical properties,” Journal of Computational and Applied Mathematics, vol. 303, no. 2, pp. 15–30, 2016. [Google Scholar]

37. D. Baleanu, S. Zibaei, M. Namjoo and A. Jajarmi, “A nonstandard finite difference scheme for the modeling and nonidentical synchronization of a novel fractional chaotic system,” Advances in Difference Equations, vol. 2021, no. 1, pp. 1–19, 2021. [Google Scholar]

38. M. Aslefallah, S. Yuzbasi and S. Abbasbandy, “A numerical investigation based on exponential collocation method for nonlinear SITR model of COVID-19,” Computer Modeling in Engineering & Sciences, vol. 136, no. 2, pp. 1687–1706, 2023. [Google Scholar]

39. M. Aslefallah, S. Abbasbandy and E. Shivanian, “Numerical solution of a modified anomalous diffusion equation with nonlinear source term through meshless singular boundary method,” Engineering Analysis with Boundary Elements, vol. 107, no. 12, pp. 198–207, 2019. [Google Scholar]

40. M. Aslefallah and D. Rostamy, “Application of the singular boundary method to the two-dimensional telegraph equation on arbitrary domains,” Journal of Engineering Mathematics, vol. 118, no. 1, pp. 1–14, 2019. [Google Scholar]

41. E. Shivanian and M. Aslefallah, “Stability and convergence of spectral radial point interpolation method locally applied on two dimensional pseudo-parabolic equation,” Numerical Methods for Partial Differential Equations, vol. 33, no. 3, pp. 724–741, 2017. [Google Scholar]

42. F. M. Allehiany, F. Dayan, F. F. Al-Harbi, N. Althobaiti, N. Ahmed et al., “Bio-inspired numerical analysis of COVID-19 with fuzzy parameters,” Computers, Materials & Continua, vol. 72, no. 2, pp. 3213–3229, 2022. [Google Scholar]

43. R. M. Alhebshi, N. Ahmed, D. Baleanu, U. Fatima, F. Dayan et al., “Modeling of computer virus propagation with fuzzy parameters,” Computers, Materials & Continua, vol. 74, no. 3, pp. 1–18, 2023. [Google Scholar]

44. N. Ahmed, A. Raza, A. Akgül, Z. Iqbal, M. Rafiq et al., “New applications related to hepatitis C model,” AIMS Mathematics, vol. 7, no. 6, pp. 11362–11381, 2022. [Google Scholar]