An Enhanced Equilibrium Optimizer for Solving Optimization Tasks

1  Introduction

As the advancement of the society rapidly, a number of optimization issues are required to be resolved. These problems are previously usually tackled with traditional numerical computational methods, but these are inefficient and difficult to deal with high-dimensional and non-linear optimization problems [1]. Consequently, researchers have pioneered the development of metaheuristic algorithms, drawing inspiration from the intricate social behaviors exhibited by biological colonies and the governing principles of natural phenomena. These algorithms, characterized by their stochastic nature and the absence of a need for priori knowledge, exhibit remarkable flexibility in their problem-solving capabilities [2].

Recently, some excellent metaheuristics have been developed and successfully employed to address optimization problems in different domains. In [3], the hunger games search algorithm (HGS) is introduced as an innovative approach. This algorithm takes its inspiration from the behaviors and behavioral selections of animals driven by the necessity to overcome hunger. The performance of HGS is verified on function cases and engineering design cases, and the results prove that HGS has excellent optimization performance. In [4], a novel metaheuristic technique based on the idea of weight means is developed, called INFO. Comparative experiments with basic and advanced algorithms prove that INFO has outstanding convergence performance. In [5], a novel algorithm, the rime optimization algorithm (RIME), is proposed. RIME simulates the growth and crossover behavior of the rime-particle population. Extensive comparative experiments justify that the RIME has promising convergence performance. In [6], the coati optimization algorithm (COA) that draws inspiration from the natural behaviors of coatis, is introduced as a solution for tackling global optimization problems. COA obtains superior performance on functional problems and some practical cases. In [7], a nature-inspired method called the nutcracker optimizer (NOA) is proposed. NOA is mimicking the search, hiding, and recovery behaviors of nutcrackers. Comprehensive experimental results verify the performance of NOA. Well-performing algorithms, including those mentioned above, provide researchers in different fields with tools to resolve optimization problems in their domains. Nature-inspired approaches are successfully applied in different fields and metaheuristic techniques are gaining popularity in fields such as engineering and science [8].

This article directs its focus towards a novel physics-based metaheuristic algorithm referred to as EO. Initially introduced by Faramarzi et al. in 2020 [9], EO presents a range of compelling advantages. These encompass a streamlined framework, straightforward operational principles, simplified implementation, a reduced parameter set, and expedited processing times. Furthermore, EO has showcased its prowess in optimization, surpassing the performance of certain other metaheuristics like PSO [10] and FA [11]. It is widely embraced as a solution for numerous intricate optimization challenges. For example, in [12], the adaptive EO (AEO) is introduced for multi-level threshold processing, which modifies the basic EO by making adaptive decisions on the dispersion of non-performance search agents. The performance of the AEO is assessed on benchmark function cases and compared with other methods. The comparison shows that AEO outperforms other competitors. Then the AEO is employed to optimize the multilevel thresholding problem and obtain the best value by minimizing the objective function. In [13], an improved EO algorithm (IEO) incorporating linear reduced discretization and local minimum elimination method is proposed. A number of comparative experiments indicate that IEO is much superior. This algorithm effectively predicts unknown parameters within the single diode model, double diode model, and triple diode model. In [14], an enhanced EO is presented to tackle the challenges of parameter identification across various photovoltaic (PV) cell models. The analysis illustrates that the improved EO has highly competitive advantages and can accurately extract PV parameters.

Despite EO’s exceptional performance in tackling functional problems and engineering design cases, it does exhibit certain drawbacks, such as the exploration-exploitation imbalance, population diversity loss, and susceptibility to local optima. To address these limitations, numerous scholars have proposed a range of enhanced EO algorithms. In [15], an adaptive EO (LWMEO) with three machanisms is developed. The effectiveness of LWMEO is rigorously assessed using CEC2014 functions and classical multimodal functions, revealing its competitive performance. In [16], a modified EO algorithm (m-EO) is put forth, featuring Gaussian mutation and an exploitative search mechanism grounded in population segmentation and reestablishment principles. Through extensive testing on 33 benchmark problems and comparisons to the EO and other advanced approaches, the m-EO demonstrates its superiority over competitors. In [17], an enhanced iteration of EO (IEO) is introduced, incorporating a declining equilibrium pool strategy. The evaluation of IEO encompasses 29 benchmark functions, along with three engineering task, highlighting its versatility and efficacy.

Although these EO variants strengthen the overall performance of the basic EO, the shortcomings of the exploration-exploitation imbalance, the proneness to become trapped in local optimization, and the loss of population diversity have not been adequately addressed. This is primarily because most of the existing EO variants are designed to improve one of the limitations, rather than all of them. Based on the above motivation, the present work introduces a novel EO variant, referred to as SCEO, to refine the performance of the canonical EO. The key points of this study are outlined below.

(1)   A new EO version is introduced, known as SCEO, which involves three strategies, namely adaptive inertial weight, Cauchy mutation, and adaptive sine cosine mechanism. The component study in Section 4.4 examines the validity of the three mechanisms of SCEO.

(2)   To assess the performance of the newly SCEO, it undergoes rigorous testing on 15 classical benchmark functions as well as the comprehensive CEC2017 test suite. This assessment involves a comparative analysis against state-of-the-art techniques, as well as the foundational EO and its various iterations. Additionally, the gathered experimental data undergoes meticulous statistical scrutiny through the utilization of both the Friedman test and the Wilcox signed rank test.

(3)   To substantiate the practical viability of the SCEO algorithm, its capabilities are demonstrated through its application to an MRPP task. The algorithm can plan satisfactory paths for mobile robots in different environments.

The subsequent sections are structured as follows: Section 2 outlines the canonical EO for contextual reference. Section 3 elaborates on the three pivotal enhancement strategies and introduces the refined SCEO approach. In Section 4, an exhaustive evaluation of SCEO’s effectiveness is conducted across the spectrum of 15 classical benchmark functions and the comprehensive CEC2017 test suite. Furthermore, Section 5 delves into the SCEO-driven path-planning technique. Finally, Section 6 encapsulates this study with a comprehensive summary and conclusion.

2  Basic EO Algorithm

2.1 Initialization

Similar to most metaheuristic methods, EO utilizes initialized candidate solutions to commence the optimization process. The initial concentration is described below.

Xi=Xmin+randi(Xmax−Xmin),i=1,2,⋯,N(1)

where Xi is the concentration of the i-th initial particle; Xmax and Xmin denote the upper and lower boundaries of the exploration space, respectively; N signifies the scale of the population under consideration.

2.2 Equilibrium Pool

The four particles with the optimal fitness and the mean of these four particles are selected to create the equilibrium pool. Xeq_pool and Xeq_ave are expressed below, respectively.

Xeq_pool={Xeq1,Xeq2,Xeq3,Xeq4,Xeq_ave}(2)

Xeq_ave=Xeq1+Xeq2+Xeq3+Xeq44(3)

2.3 Exponential Term (F)

The exponential factor F plays a crucial role in maintaining the delicate exploration-exploitation balance. This factor is determined by Eq. (4).

F=e−λ(t−t0)(4)

where λ represents a randomly generated variable within the range of [0,1]; t is a non-linear computation, formulated as follows.

t=(1−ItT)(a2ItT)(5)

where It corresponds to the current iteration count and T corresponds to the predefined maximum iteration count; a2 stands as a constant parameter. t0 is expressed below.

t0=1λln⁡(−a1sign(r−0.5)[1−e−λt])+t(6)

where a1 takes on a value of 2 and a2 takes on a value of 1; sign(r − 0.5) effectively determines the direction of development; r symbolizes a random variable confined within the range of [0,1]. Substituting Eq. (6) into Eq. (4), we get:

F=a1sign(r−0.5)[1−e−λt](7)

2.4 Generation Rate (G)

The parameter responsible for regulating the extent of exploitation is known as the generation rate G, and its definition is provided below.

G=G0e−λ(t−t0)=G0F(8)

where

G0=GCP(Xeq−λX)(9)

GCP={0.5r1,r2≥GP0,r2<GP(10)

where r1 and r2 represent random values of [0,1], GCP signifies the generation rate control parameter, calculated through the generation probability GP.

Thus, the update method of EO is below.

X=Xeq+(X−Xeq).F+GλV(1−F)(11)

3  Structure of SCEO

In this subsection, to modify the overall performance of the basic EO, we introduce an improved EO algorithm, called SCEO. SCEO increases the performance of the basic EO by proposing new strategies while keeping the original update mechanism intact.

3.1 Adaptive Inertia Weight Mechanism

Regarding metaheuristic techniques, the exploration-exploitation balance is essential. As can be observed from Eq. (11), which F is employed to influence concentration changes to reach equilibrium, while the equilibrium candidate is a randomly chosen candidate from the equalization pool. Once it gets stuck in a local optimum, the best solution will prematurely stagnate during the search. Thus, to avoid this problem, the adaptive search for the random candidate is carried out, and we design an adaptive update formula to instead of Eq. (11). The novel updating equation is below.

X=ω×Xeq+(X−Xeq).F+GλV(1−F)(12)

where ω is an inertia weight.

Inspired by the PSO, the inertia weight mechanism is broadly employed in metaheuristic approaches. For instance, Ding et al. [18] revise the update equation of the salp swarm algorithm (SSA) by introducing an adaptive inertia weight factor. Wang et al. [19] use an inertia weight to modify the leader position of the SSA.

In this study, a novel adaptive inertial weight coefficient is designed and mathematically expressed as follows.

ω=ωmin+(ωmax−ωmin)×11+ab(It−T2)(13)

where ωmax represents the upper limit of the weight; ωmin signifies the lower limit of the weight; a and b are constants.

3.2 The Cauchy Mutation

To deal with the problem that EO tends to become stuck in local optimum and thus loses population diversity, this work employ the Cauchy mutation to improve the population diversity. The Cauchy distribution exhibits a narrower peak at its origin and a wider spread towards both extremes. By using the Cauchy mutation, a larger perturbation can be generated near the particle of the current variation, thereby allowing the Cauchy distribution function to search all areas of the solution space. This approach effectively leverages the mutation effects at the distribution’s edges to optimize individuals, thereby achieving the global optimum while simultaneously preserving population diversity. The Cauchy distribution function is described below.

Ft(x)=12+1πarctan⁡(xt)(14)

where t > 0.

Based on the Cauchy distribution function, we can further update the position of the particles. The update equation is below.

X′=X+X×Cauchy(0,1)(15)

where Cauchy (0,1) represents a randomly generated value drawn from the Cauchy distribution, X denotes the position of the current iteration, X′ signifies the position of the mutated particle.

3.3 Adaptive Sine Cosine Mechanism

In the standard EO, the update mechanism can readily become ensnared in local optima, leading to a decline in its capacity for global exploration. To address the limitations, this work introduces the position update equation of the sine cosine algorithm (SCA) [20] with inertia weight factor to perform adaptive search of the particles. The novel position update equation is below.

X″={X+r3×sin⁡(r4)×|ω×r5×gbest−X|,r6<0.5X+r3×cos⁡(r4)×|ω×r5×gbest−X|,r6≥0.5(16)

r3=a(1−ItT)(17)

where a is set to 2; r3 linearly decreases from 2 to 0. r4 is derived from a uniform random distribution that encompasses the interval [0,2π]. r5 and r6 signfy random numbers in [0,1]. gbest is the global optimum solution. X signifies the position of the current iteration. X″ represents the updated position.

3.4 SCEO Algorithm

The developed SCEO algorithm updates the particle positions and does not affect the framework of the basic EO. Firstly, it injects an adaptive inertial weight to enhance the navigation of a stochastic equilibrium candidate. During iterations, the inertia weight continually adjusts the position of the equilibrium candidate and hopes to move it to a more prospective region. Next, the entire particle is updated again using the adaptive SCA to promote the search capability. The sine-cosine function decides the exploration horizon of the search individual’s next position by controlling the direction of the particle’s search. Once stuck in a local optimum, the search direction is changed, effectively avoiding search stagnation. Finally, population diversity is ensured by the addition of the Cauchy mutation mechanism in case of increased ability. By harnessing the distinctive characteristics of the Cauchy distribution, which exhibits a significant shift from a peak at the origin to an elongated distribution at its extremities, substantial perturbations are strategically induced near particles throughout the iterative process. This enables the algorithm to explore all areas and increase the particles diversity. Based on the above analysis, the flowchart of SCEO is given in Fig. 1.

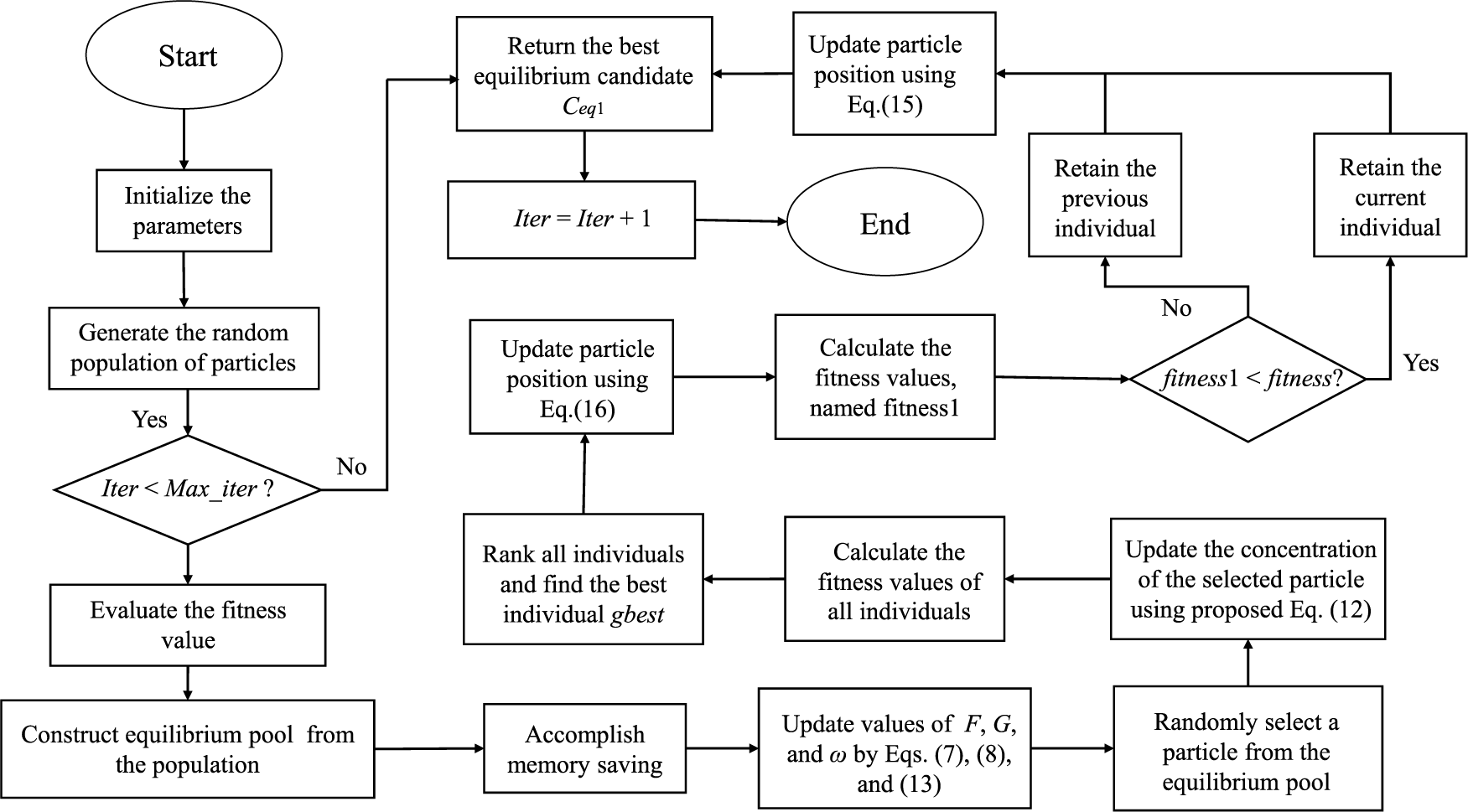
Figure 1: The flowchart of SCEO

3.5 Computational Complexity

The computational complexity of an optimization approach is an essential criterion for analyzing performance. In this paper, the Big-O notation is adopted to denote complexity. This complexity is contingent upon key factors such as the particle numbers (N), the dimensions (d) and the iterations (t), and (f) is the fitness evaluation.

O(SCEO) = O(initialization) + O(fitness evaluation) + O(memory saving) + O(concentration update) + O(SCA updating strategy) + O(Cauchy mutation).

Consequently, the computational complexity of SCEO can be elucidated below.

O(SCEO)=O(N×d+t×f×d+t×N+t×N×d+N(1+t+t×d)+t×N×d)≅O(t×f×d+t×N×d).

The computational complexity of EO is expressed as O(t × f × d + t × N × d). In essence, it can be summarized that the SCEO maintains the same computational complexity as the basic EO algorithm.

3.6 Convergence Analysis

In this subsection, we delve into a theoretical exploration of SCEO to substantiate its efficiency. The methodology employed for this proof is outlined in the subsequent steps.

We classify SCEO into three stages: adaptive inertial weight position update, adaptive sine cosine position update, and Cauchy mutation update.

Phase 1: From Eq. (12), during the iteration, ωXeq, F, λ, V, GCP are constants held constant, then 1−FλV is also a constant, let GCP=a1, 1−FλV=a2, (t + 1)th: Xeq = n1, (t + 2)th: Xeq = n2.

Thus, the problem is elaborated below:

X(t+2)−(F−λa1a2)2X(t)=n1(F−λa1a2)(1−F+a1a2)+n2(1−F+a1a2)(18)

Let F−λa1a2=A, we get

X(t+2)−A2X(t)=n1A(1−F+a1a2)+n2(1−F+a1a2)(19)

The characteristic equation of Eq. (19) is

λ2−A2=0(20)

Clearly, Δ=4A2≥0, the following two cases need to be considered.

(1) Δ=0. Only when A=0, Δ=0. At this point, the characteristic roots are λ1=λ2=0. The general solution is

X(t)=p0+p1λ1t+p2tλ2t=p0(21)

where p0 is the constant coefficient to be determined.

(2) Δ>0, where A≠0. The characteristic roots are λ1,2=±A2. The general solution is

X(t)=p0+p1λ1t+p2λ2t(22)

where p0, p1, p2 are constant coefficients to be determined.

When t→∞, X(t) has a limit and converges to a finite value, it implies that the iteration converges. If X(t) of the above two cases is made to converge, the conditions need to be satisfied ∥λ1∥<1, ∥λ2∥<1.

When Δ=0, λ1=λ2=0, the convergence condition is satisfied. In this case, X(t) converges.

When Δ>0, the convergence region should satisfy:

{4A2>0|±A2|<1(23)

From Eq. (23), the convergence region is −1<A<1. According to Eqs. (7) and (10), F−λa1a2∈(−1,1), so A∈(−1,1) in the convergence range. In this case, X(t) converges.

In summary, Phase 1 converges.

From Eq. (16), it can be seen that Phase 2 has the same search pattern as Phase 1, and it can be proved in the same way that Phase 2 also converges.

Phase 3: From Eq. (15), Cauchy(0,1) is constants held constant, let (t + 1)th: Cauchy(0,1)=V1, (t + 2)th: Cauchy(0,1)=V2.

A second-order linear differential equation is obtained, and the problem be expressed in the following form:

X(t+2)−(1+V1)(1+V2)X(t)=0(24)

The characteristic equation of Eq. (24) is

λ2−(1+V1)(1+V2)=0(25)

Clearly, Δ=4(1+V1)(1+V2). Because V1>0, V2>0, Δ>0.

When Δ>0, the characteristic roots are λ1,2=±(1+V1)(1+V2). The general solution is

X(t)=s1λ1t+s2λ2t(26)

where s1, s2 are constant coefficients.

When t→∞, X(t) has a limit and converges to a limited value, it implies that the iteration converges. If X(t) is made to converge, the conditions need to be satisfied ∥λ1∥<1, ∥λ2∥<1.

Because limt→∞V1=0, limt→∞V2=0, limt→∞(λ1,2)=limt→∞(±(1+V1)(1+V2))=±1.

It satisfies the convergence condition. In this case, X(t) converges. In summary, Phase 3 converges.

Overall, the SCEO algorithm converges.

4  Simulation and Comparisons

4.1 15 Test Functions

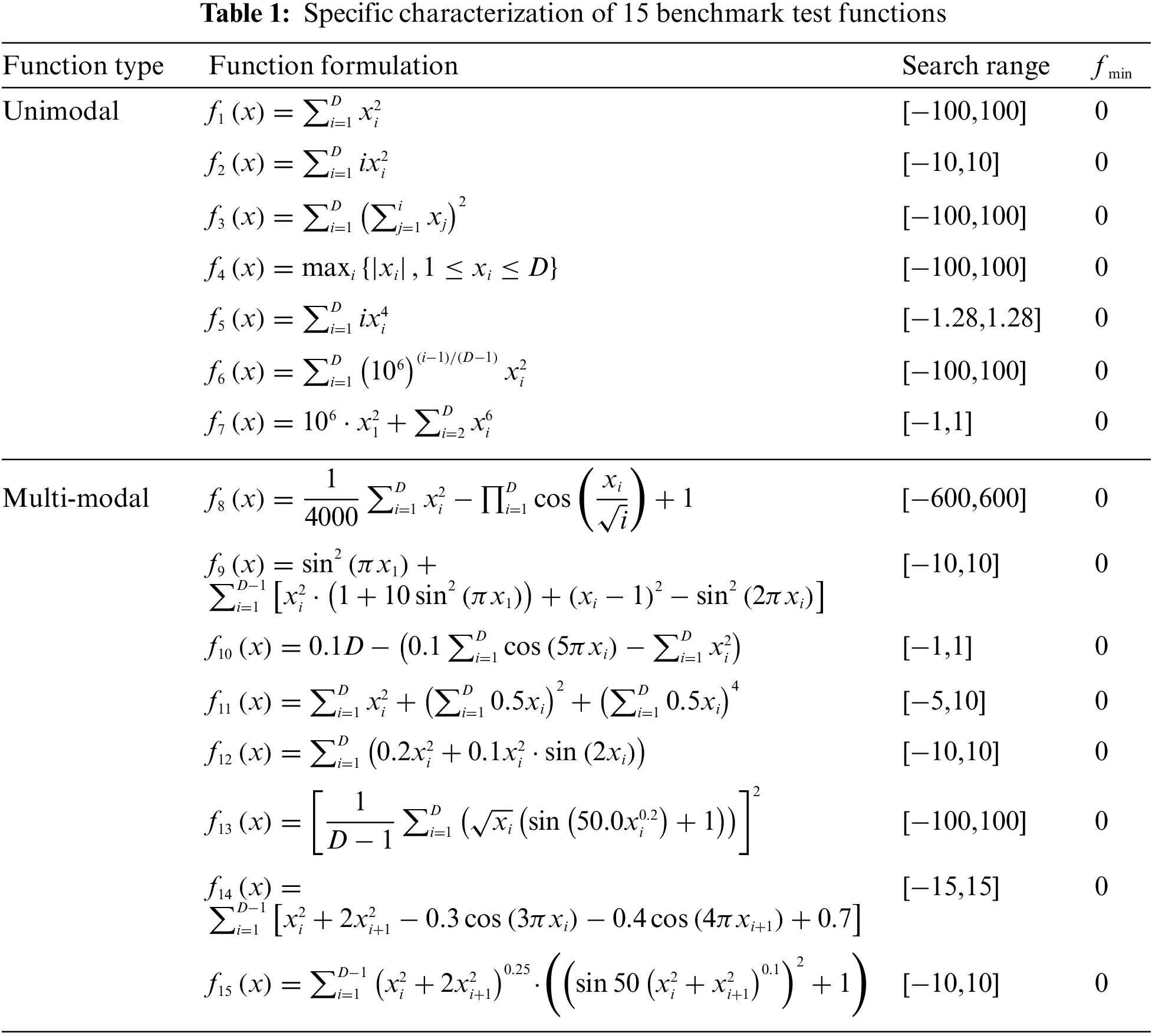
To ascertain the efficacy of the SCEO, 15 typical benchmark functions are applied. These functions are meticulously detailed in Table 1. According to Table 1, they have various features, which contain 7 unimodal functions and 8 multi-modal functions.

4.2 Compared with EO and EO Variants

To thoroughly assess the performance of SCEO, this paper compares the SCEO algorithm with five novel EO variants, including the basic EO [9], LWMEO [15], m-EO [16], IS-EO [21], and IEO [17]. To ensure equitable evaluation, a consistent population scale of 30 and a uniform maximum iteration count of 500 are maintained across all tests. Each optimizer is subjected to 30 independent runs, all conducted under identical conditions with a fixed function dimension of 100. Mean minimum (Mean) values and their corresponding standard deviations (Std) are employed as key indicators to gauge the performance of all methods. Furthermore, the Wilcoxon signed rank test is adopted to provide a comprehensive assessment. The findings, including Friedman’s rank and the Wilcoxon rank-sum test, are succinctly presented in Table 2. The symbols “+/−/=” in Table 2 signify that the SCEO algorithm demonstrates superior, inferior, or similar performance compared to other algorithms, respectively. The “N/A” notation indicates instances where no statistical significance is observed.

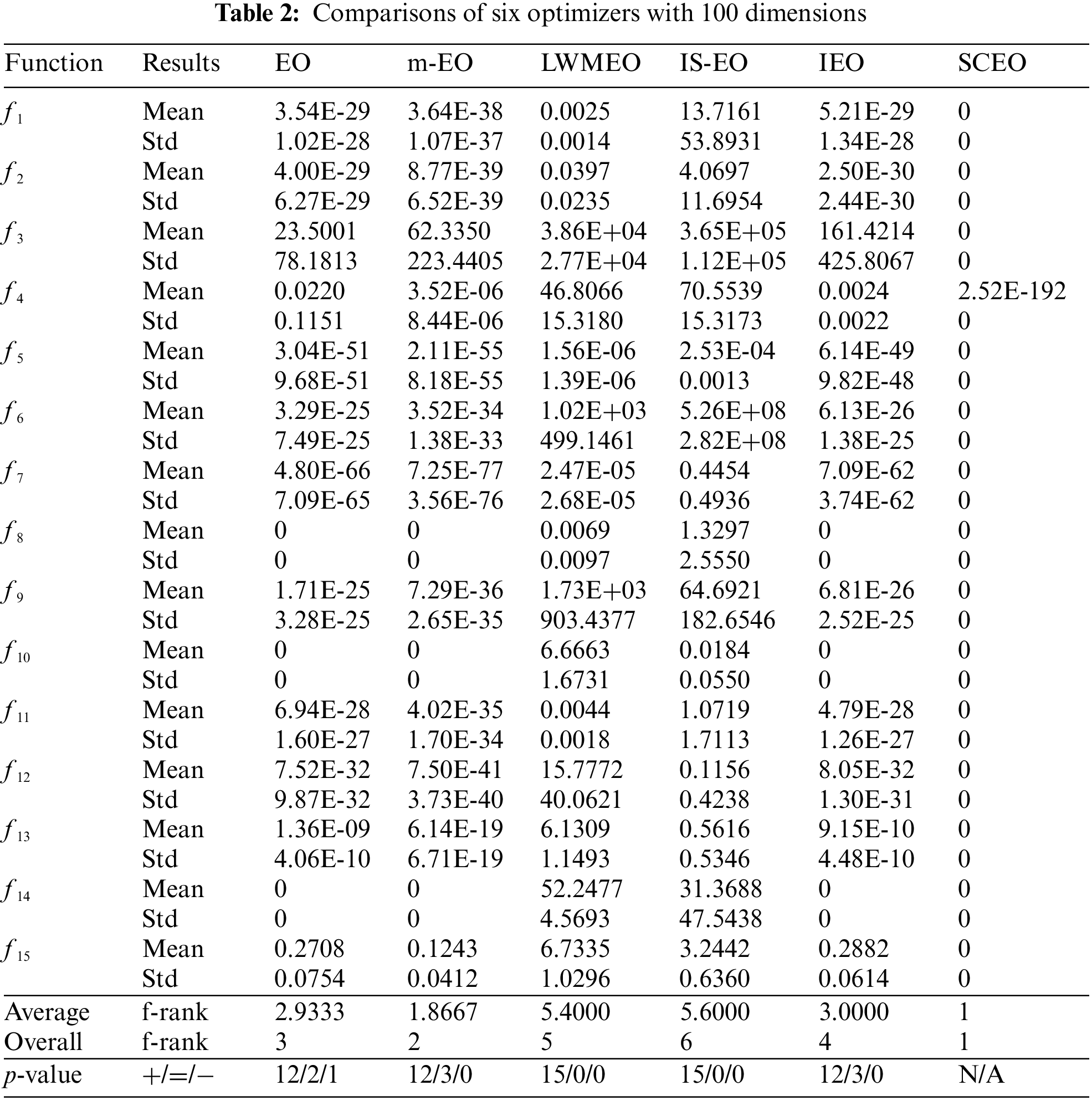
Based on Table 2, it reveals that the SCEO finds the theoretical best solution on all cases except f4. For this function, although the theoretical optimal values are not achieved, the SCEO is still better than the other competitors. Compared with the basic EO and IEO, SCEO performs better across 12 test functions. With respect to LWMEO and IS-EO, SCEO gets better results on all of the benchmark problems. For f2, SCEO and m-EO provide similar results. SCEO is superior to m-EO on 12 functions, and on the rest 3 functions the two algorithms get similar results. For f8, f10, and f 14, SCEO, m-EO and IEO obtains similar results. SCEO resembles basic EO on 2 functions and is inferior to basic EO on f8. Based on the Friedman’s rank test, it can be observed that SCEO ranks first followed by m-EO, EO, IEO, LWMEO, and IS-EO, which reveals that SCEO provides the best performance. The p-values consistently remain below the threshold of 0.05 within the 100-dimensional environments, which reveals that the distinctions between the SCEO and the other methods are statistically significant. In summary, SCEO presents more competitive performance than other comparative algorithms for 15 traditional benchmark functions.

4.3 Comparison with Other Metaheuristics

To prove the validity of the SCEO, it is compared with some advanced metaheuristics, including the enhanced SSA (RDSSA) [22], the improved grey wolf optimizer (OGWO) [23], the modified moth-flame optimization algorithm (DMMFO) [24], adaptive salp swarm optimization (ASSO) [25], and improved particle swarm optimization (BPSO) [26]. 15 test functions in Table 1 are adopted and the function’s dimension is configured to 100. The Mean and Std values for the six metaheuristics are meticulously documented in Table 3. Additionally, the outcomes of Friedman’s rank test and the Wilcoxon rank-sum test are presented at the base of the table. In Table 3, the symbols “+/−/=” are employed to signify instances where the SCEO algorithm demonstrates superior, inferior, or comparable performance to other algorithms, respectively. The notation “N/A” is employed when no statistically significant difference is observed.

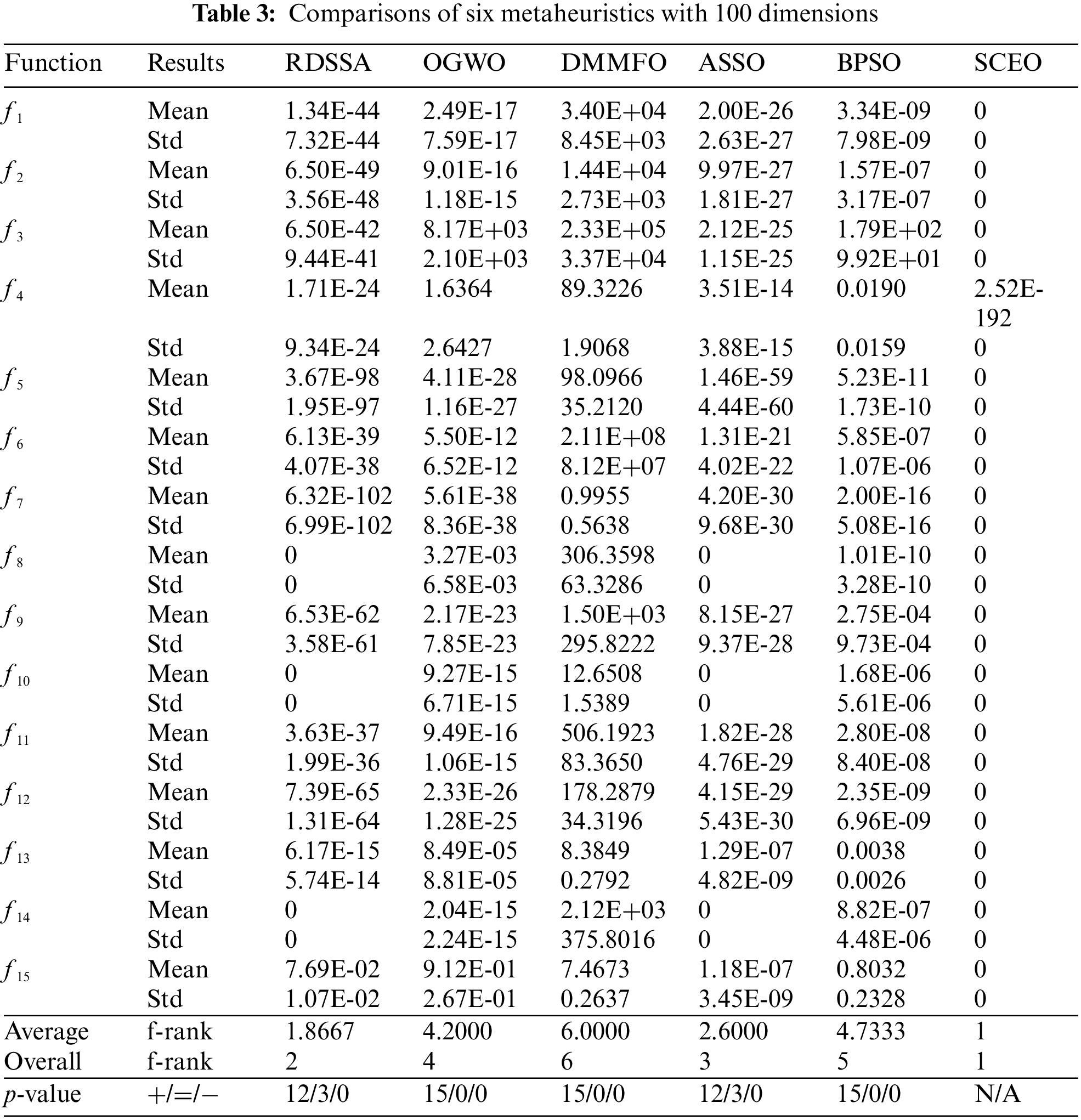
From the data in Table 3, for f8, f10, f14, RDSSA, ASSO, and SCEO obtain the theoretical optimal solution. Compared with DMMFO, OGWO, and BPSO SCEO reaches better performance on all of its cases. With respect to RDSSA, and ASSO, SCEO obtains better on 12 cases and has similar results on 3 cases. According to the Friedman mean ranks acquired by eight approaches on 15 test functions, it can be shown that SCEO is first, followed by RDSSA, ASSO, OGWO, BPSO, and DMMFO. The p-values consistently remain below the threshold of 0.05 within the 100-dimensional environments, which reveals that the differences observed between SCEO and the alternative methods hold substantial statistical significance.

Table 4 presents the average runtime duration (measured in seconds) of seven different techniques across the set of 15 benchmark functions. Notably, Table 4 highlights that EO boasts the shortest average runtime compared to the other techniques. Importantly, the average runtime of SCEO closely aligns with that of EO across all scenarios. This observation underscores the fact that the devised SCEO achieves performance enhancements without compromising runtime efficiency.

4.4 Convergence Analysis

In this subsection, we investigate the convergence behavior of each method by visually showing the convergence process of these methods. The 15 benchmark test problems are employed from Table 1, and the dimension is set to 100. Fig. 2 displays the convergence curves of eleven methods across selected cases.

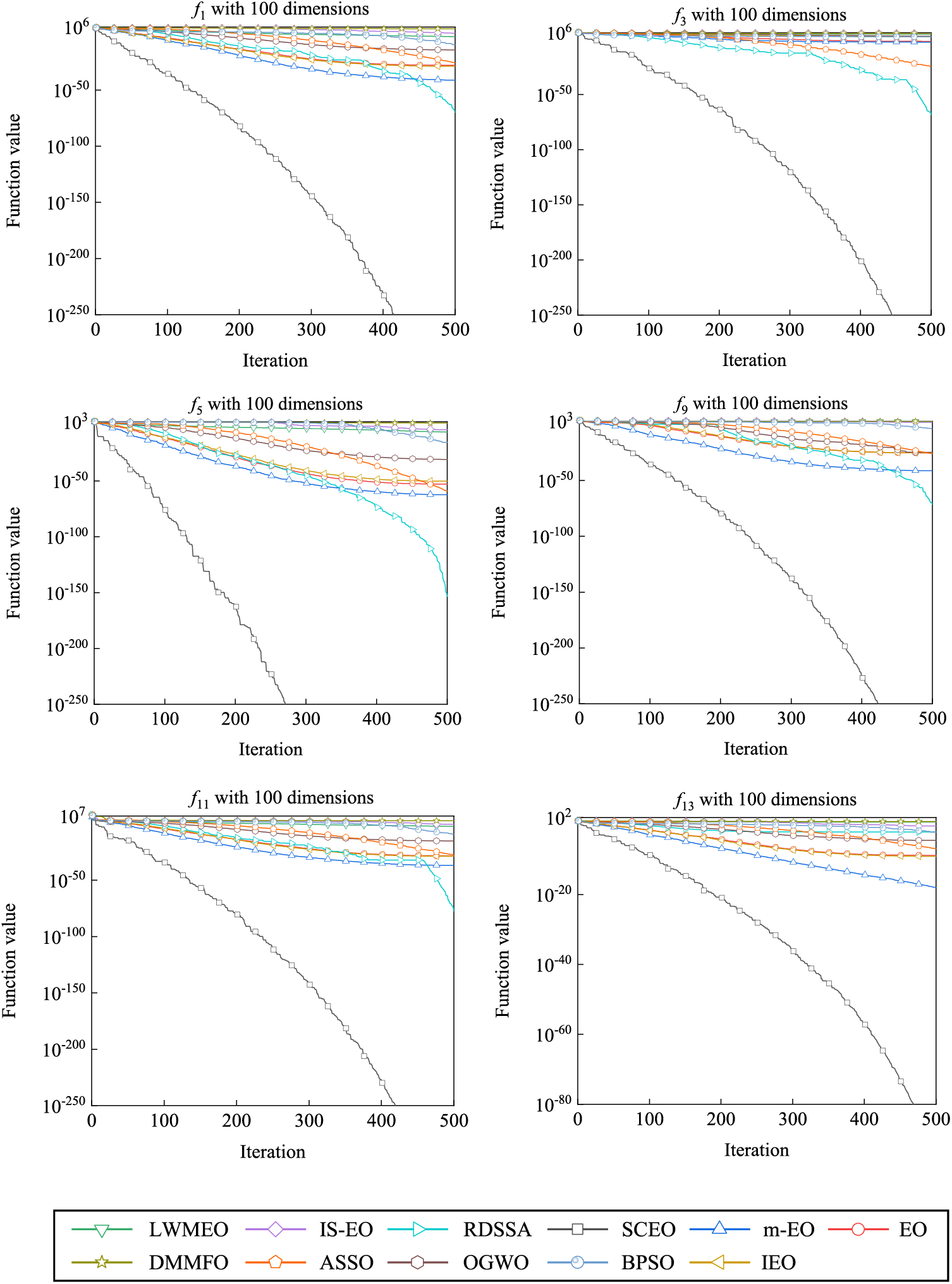
Figure 2: Convergence curves of eleven algorithms with 100 dimensions

Observing Fig. 2, it becomes evident that SCEO exhibits a gradual convergence rate in the initial phases of the search process. At the later stage, the convergence speed is accelerated and the convergence curve is smoother. This behavior is attributed to a strategic trade-off: during the early stages, the algorithm intentionally prioritizes preserving population diversity, thus modestly compromising early convergence. Subsequently, the algorithm transitions from broad global exploration to focused local search, boosting solution accuracy by exploiting previously explored areas. According to the experimental results, SCEO finds better solutions quicker than other all compared algorithms across more than half of the cases tested. Notably, SCEO not only accelerates convergence but also demonstrates heightened accuracy in solution outcomes when contrasted with alternative algorithms. Overall, these results underscore the pronounced convergence advantages of SCEO over other EO variants and the broader spectrum of compared algorithms.

4.5 Experiments on CEC 2017 Test Suite

This subsection comprehensively evaluates the performance of SCEO employing the CEC2017 test suite. The outcomes of SCEO are meticulously compared against the basic EO, various EO variants, and a spectrum of advanced metaheuristics including the EO, m-EO, LWMEO, IS-EO, IEO, RDSSA, OGWO, DMMFO, ASSO, BPSO, and VC-SSA [18]. For this experiment, the upper limit of evaluations is prudently established at D × 104. Consistency is maintained in terms of parameter settings for both the compared methods and SCEO, mirroring those employed in Section 4.2. All methods are subjected to 30 independent runs, and the functional dimension remains consistent at 100. The performance of the 13 methods on the CEC2017 benchmark function with 100 dimensions is summarized in Table 5.

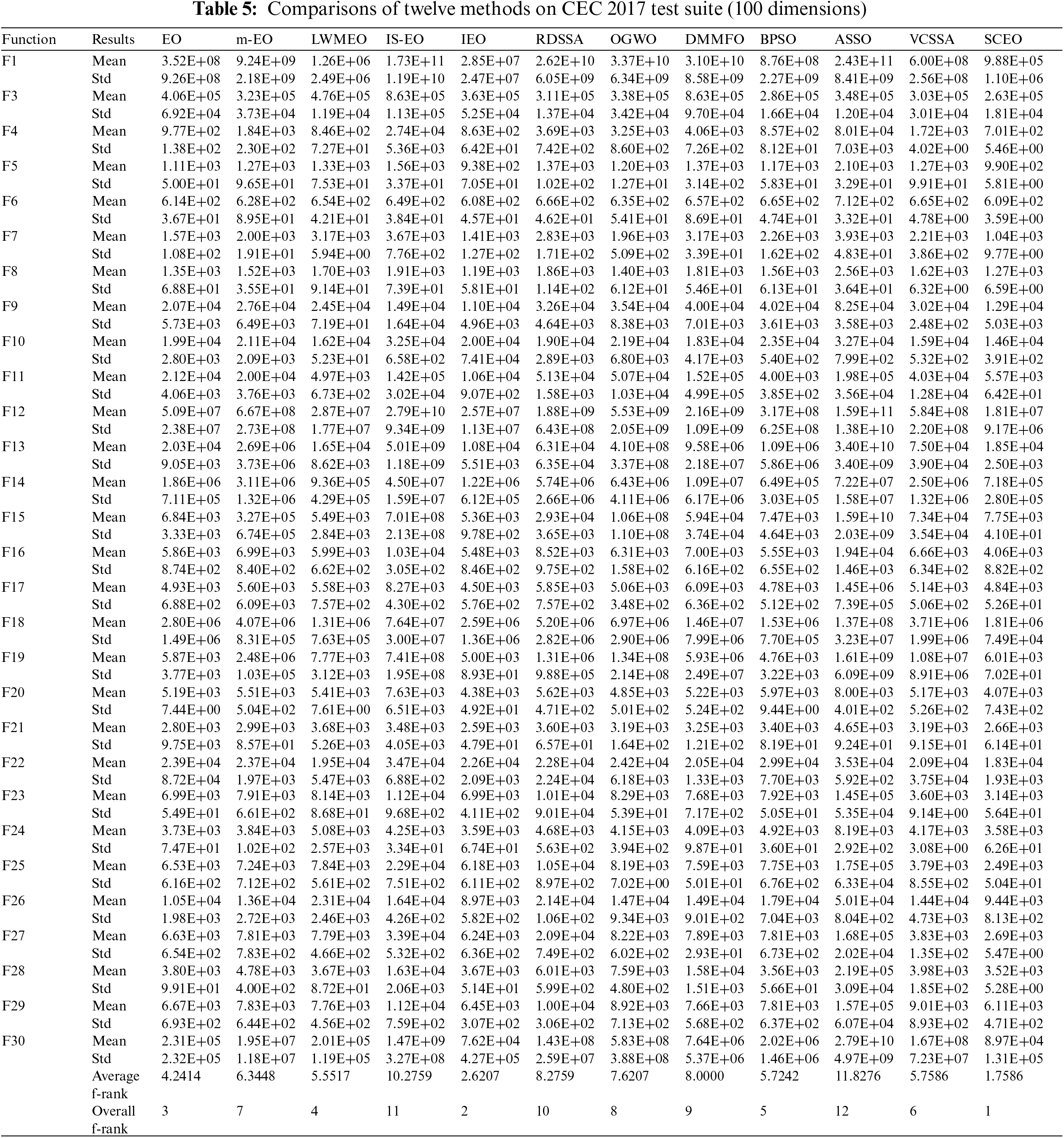
According to Table 5, SCEO performs better to other comparative algorithms across 15 functions and is inferior to the other algorithms on 14 functions. With respect to m-EO, IS-EO, RDSSA, OGWO, DMMFO, and ASSO, SCEO is superior on all functions. Compared with BPSO, SCEO gets better and worse results on 24 and 5 functions. For F15 and F19, SCEO is worse compared with the EO. SCEO beats IEO in 18 cases and is inferior in 11 cases. SCEO is better than LWMEO on 25 functions, but SCEO is inferior on F11, F13, F15, and F18. For F15, F17, and F19, IEO and BPSO have better results than SCEO. For F11, LWMEO and BPSO are superior to SCEO. According to the average ranking, SCEO obtains the first rank, followed by IEO, EO, LWMEO, BPSO, VC-SSA, m-EO, OGWO, DMMFO, RDSSA, IS-EO, ASSO. SCEO outperforms EO on 27 functions and underperforms on 2 functions. SCEO outperforms VC-SSA on all functions. Overall, these data reveal that SCEO is significantly superior to its competitors on the CEC2017 test suite.

5  Robot Path Planning

In robotics, MRPP is the critical intermediate part. MRPP is the process of finding the best path without collisions with obstacles from a specified starting point to a predetermined destination point, based on certain evaluation standards. Since mobile robots emerged, many scholars have conducted a series of studies to design efficient path-planning methods for mobile robots.

5.1 Robot Path Planning Problem Description

Recently, many metaheuristics-based MRPP techniques have been developed. Wang et al. [27] use a modified SSA variant to tackle the MRPP problem. Wu et al. [28] harness an modified ant colony optimization (ACO) for the MRPP task. Wang et al. [29] introduce an improved SSA and apply the novel SSA variant to the MRPP problem. Luan et al. [30] propose an MRPP method based on a hybrid genetic algorithm (HGA).

In this subsection, we adopt the SCEO to plan the best collision-avoidance path. Acknowledging the intricacies of the MRPP problem, an adaptation function with the route length and obstacle avoidance is established to assess the mass of the produced paths based on the SCEO algorithm in the MRPP problem. The fitness function is described below.

fit=kL+(1−k)E(27)

where k is the weight, L is the route length, E is the path collision penalty function.

5.2 Results and Analysis

In this subsection, we utilize the developed SCEO for the MRPP task. The SCEO is compared with some classical optimization techniques such as GWO [31], ABC [32], PSO [10], FA [11], and VC-SSA [18]. It is examined in the three maps provided in [33]. The general parameter settings are the same as those in the original work. The shortest path lengths generated by the six algorithms on the three maps are shown in Table 6. The trajectory routes for six algorithms are shown in Figs. 3–5.

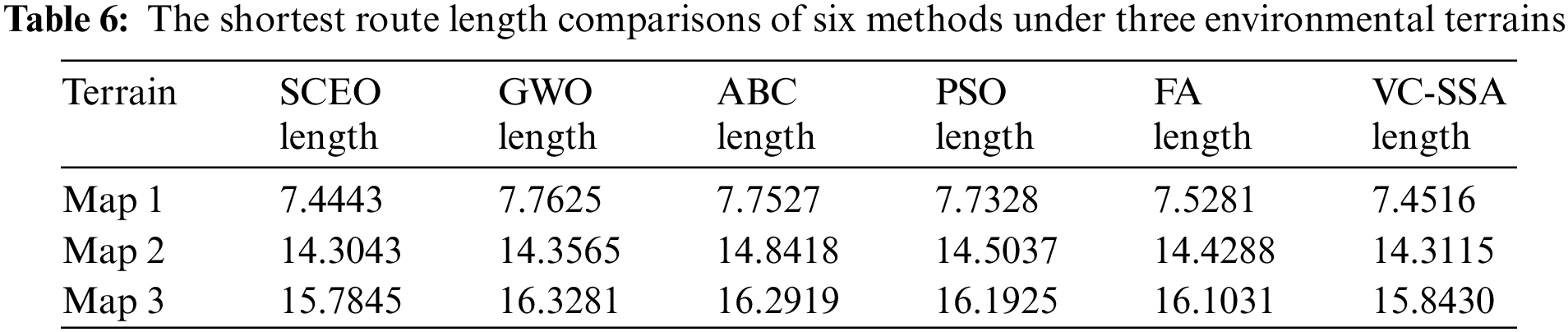
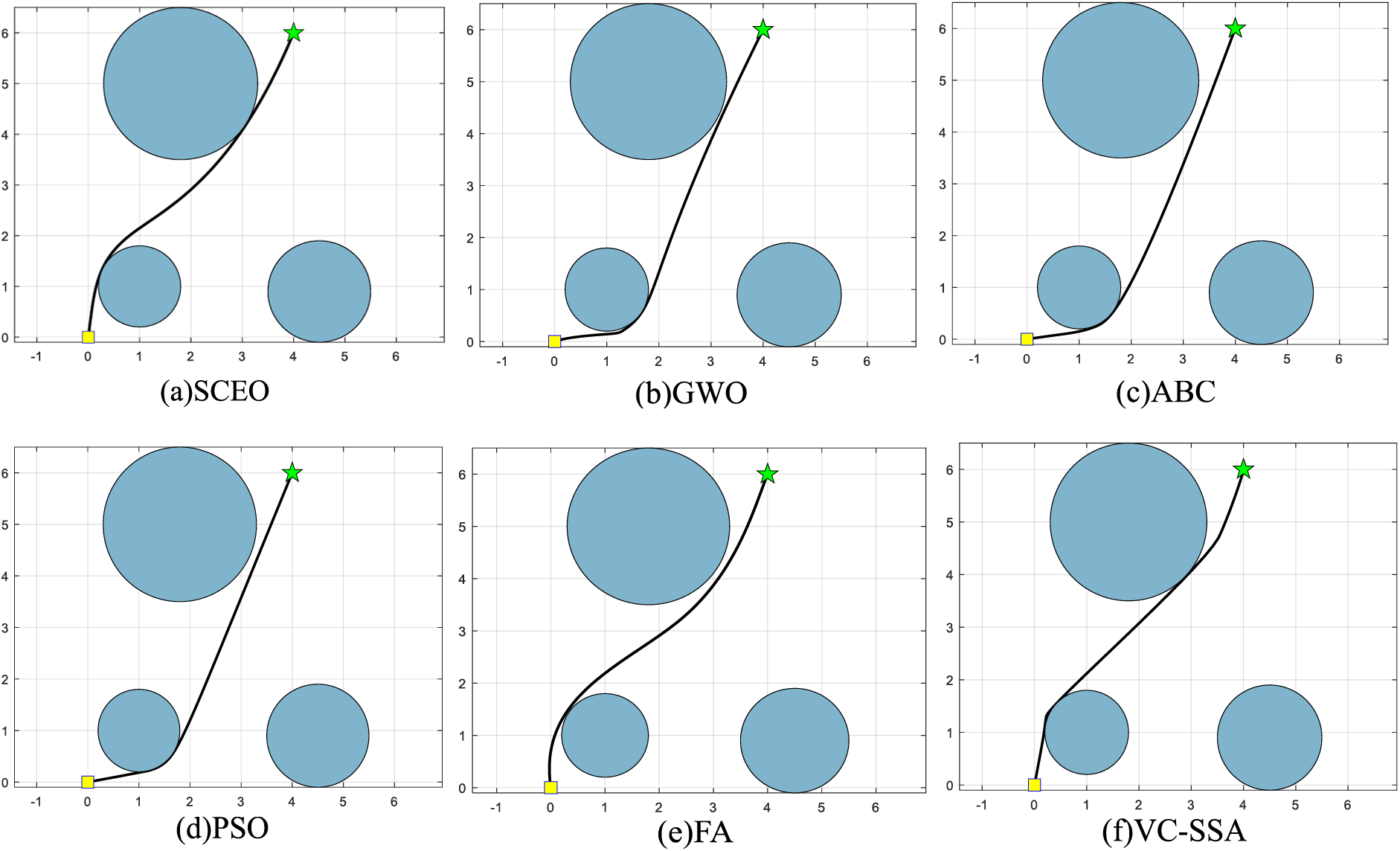
Figure 3: Trajectory routes of the six methods in Map 1

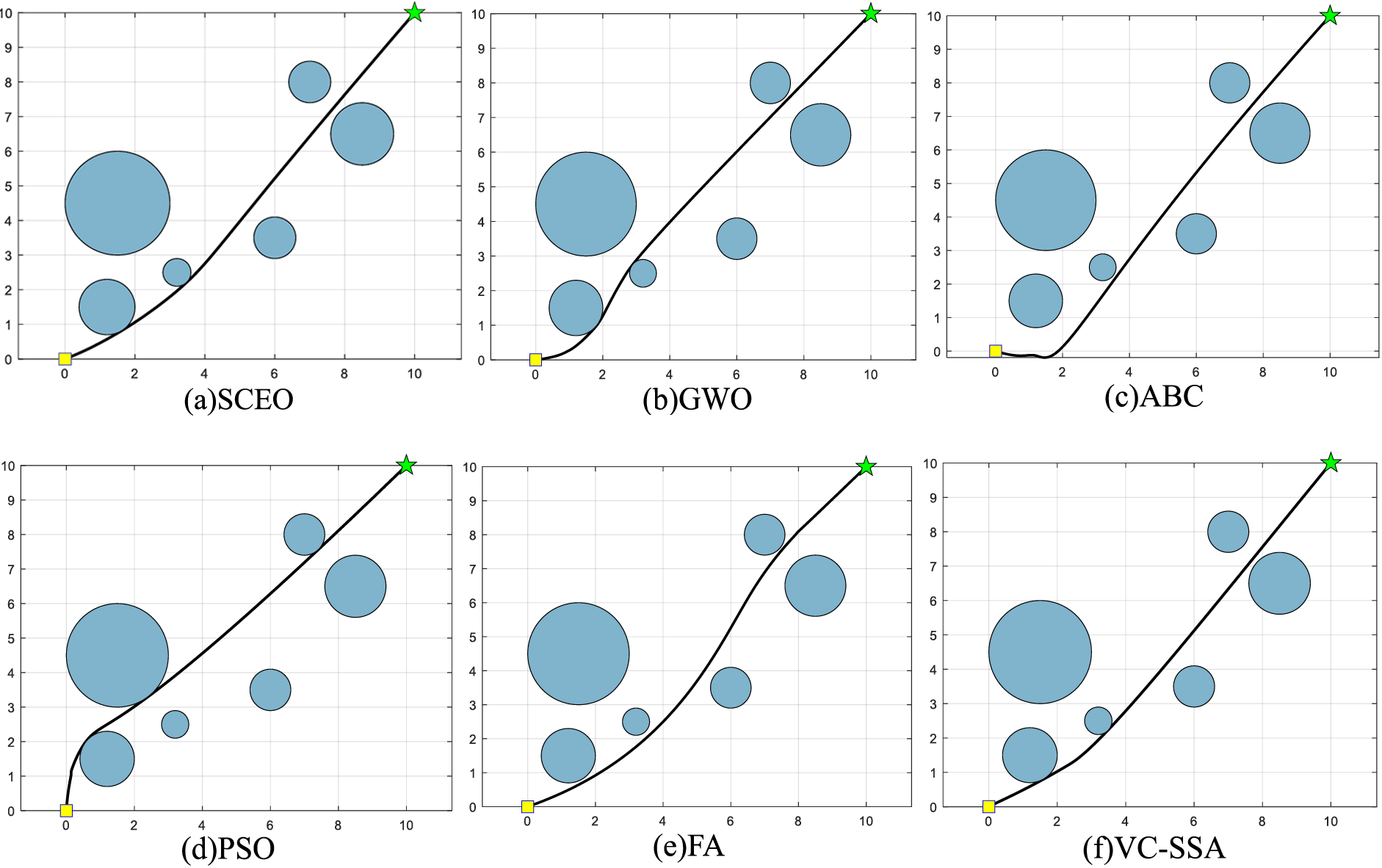
Figure 4: Trajectory routes of the six methods in Map 2

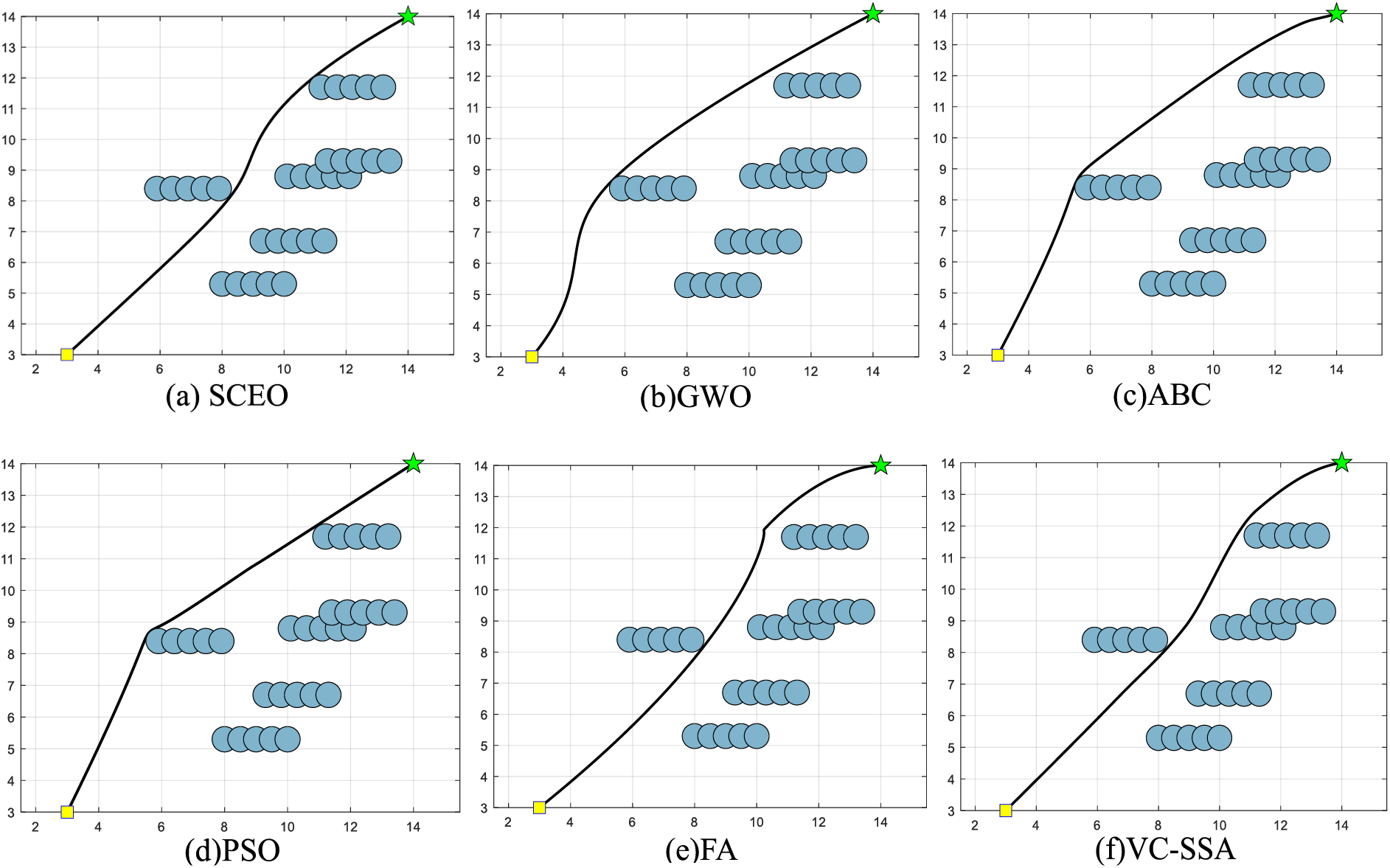
Figure 5: Trajectory routes of the six methods in Map 3

From the data in Table 6, it can be viewed that the path planning task SCEO-based plans the shortest path for collision avoidance on all three terrains compared with the other approaches, which illustrates that the SCEO can get satisfying paths for simple and complex environmental settings in the MRPP task. The trajectory routes produced by all algorithms are described in detail below.

Figs. 3a–3f displays the comparison of the trajectory routes of the six algorithms in the first map. As can be noticed from the figure, all methods can plan a safe route because this environment is a simple terrain. Compared with other algorithms, SCEO has the shortest path. PSO, ABC, and GWO map an identical path, which is smooth but not optimal. FA, VC-SSA, and SCEO design an alternative trajectory route. The route of VC-SSA has more inflection points. FA has a smooth path but not its optimal path. Figs. 4a–4f depict the trajectory routes of the second environment map. Upon examining the figures, it becomes evident that SCEO yields the shortest path among the showcased options. SCEO, VC-SSA, ABC, and FA produce similar trajectory routes, while GWO and PSO provide another trajectory routes. The route of ABC gets stuck in local optimum, which results in redundancy of the produced trajectories, and thus the path is the longest. The paths of VC-SSA, GWO, PSO, FA are smooth but not optimal. The best trajectories of environment map are shown in Figs. 5a–5f. GWO, ABC, and PSO provide a trajectory route through the outside of the danger area, which avoids collision with the obstacle area but increases the fuel burn of the robot. The route of FA has more inflection points and increases the path length. The route of VC-SSA is smoother but not optimal. In conclusion, SCEO is the most favorable algorithmic tool, and is the superior algorithm among all the techniques.

6  Conclusion

In this article, a novel EO variant, referred to as SCEO, is developed to concentrate on reaching an appropriate exploration-exploitation balance, preventing the reduction of population diversity and escaping from the local optimal. SCEO introduces three mechanisms to enhance stability. First, a new update equation based on an adaptive inertia weight mechanism is employed to efficiently balance between exploration-exploitation. Next, the adaptive SCA method is combined to enhance the exploration capability. Lastly, to enhance population diversity, the Cauchy mutation mechanism is introduced. The resultant SCEO is subjected to a comprehensive evaluation, spanning 15 classical benchmark problems, the CEC2017 test function suite, and the Mobile Robot Path Planning (MRPP) challenge. These evaluations involve a comparison with the foundational EO, various EO variants, and a diverse array of other metaheuristic techniques. The simulation results reveal that improved mechanisms are extremely effective and the comprehensive performance of SCEO emerges as remarkably competitive. SCEO presents great potential for solving various complex problems. Consequently, in our future work, we will concentrate on the applications of SCEO to practical and complex engineering optimization problems, such as vehicle scheduling problems.

Acknowledgement: The authors extend their gratitude to the Ministry of Education of Yunnan Province and Yunnan University for their invaluable support and assistance.

Funding Statement: This research endeavor receives support from the National Natural Science Foundation of China [Grant Nos. 61461053, 61461054, and 61072079], Yunnan Provincial Education Department Scientific Research Fund Project [2022Y008].

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Yuting Liu, Hongwei Ding, Gaurav Dhiman, Zhijun Yang; data collection: Yuting Liu, Zongshan Wang, Peng Hu; analysis and interpretation of results: Yuting Liu, Zongshan Wang; draft manuscript preparation: Yuting Liu, Zongshan Wang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The datasets used or analyzed during the current study are available from the corresponding author on reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. D. Rani, “Solving non-linear fixed-charge transportation problems using nature inspired non-linear particle swarm optimization algorithm,” Applied Soft Computing, vol. 146, pp. 110699, 2023. [Google Scholar]

2. Z. H. Jiang, J. Q. Peng, R. X. Yin, M. M. Hu, J. G. Cao et al., “Stochastic modelling of flexible load characteristics of split-type air conditioners using grey-box modelling and random forest method,” Energy and Buildings, vol. 273, pp. 112370, 2022. [Google Scholar]

3. Y. T. Yang, H. L. Chen, A. A. Heidari and A. H. Gandomi, “Hunger games search: Visions, conception, implementation, deep analysis, perspectives, and towards performance shifts,” Expert Systems with Applications, vol. 177, no. 8, pp. 114864, 2021. [Google Scholar]

4. I. Ahmadianfar, A. A. Heidari, S. Noshadian, H. L. Chen and A. H. Gandomi, “INFO: An efficient optimization algorithm based on weighted mean of vectors,” Expert Systems with Applications, vol. 195, no. 12, pp. 116516, 2022. [Google Scholar]

5. H. Su, D. Zhao, A. A. Heidari, L. Liu, X. Zhang et al., “RIME: A physics-based optimization,” Neurocomputing, vol. 532, no. 5, pp. 183–214, 2023. [Google Scholar]

6. M. Dehghani, Z. Montazeri, E. Trojovská and P. Trojovský, “Coati optimization algorithm: A new bio-inspired metaheuristic algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 259, no. 1, pp. 110011, 2023. [Google Scholar]

7. M. Abdel-Basset, R. Mohamed, M. Jameel and M. Abouhawwash, “Nutcracker optimizer: A novel nature-inspired metaheuristic algorithm for global optimization and engineering design problems,” Knowledge-Based Systems, vol. 262, no. 3, pp. 110248, 2023. [Google Scholar]

8. M. Nssibi, G. Manita and O. Korbaa, “Advances in nature-inspired metaheuristic optimization for feature selection problem: A comprehensive survey,” Computer Science Review, vol. 49, pp. 100559, 2023. [Google Scholar]

9. A. Faramarzi, M. Heidarinejad, B. Stephensa and M. Seyedali, “Equilibrium optimizer: A novel optimization algorithm,” Knowledge-Based Systems, vol. 191, pp. 105190, 2020. [Google Scholar]

10. R. Poli, J. Kennedy and T. Blackwell, “Particle swarm optimization: An overview,” Swarm Intelligence, vol. 1, no. 1, pp. 33–57, 2007. [Google Scholar]

11. I. Fister, I. Fister Jr, X. S. Yang and J. Brest, “A comprehensive review of firefly algorithms,” Swarm and Evolutionary Computation, vol. 13, no. 3, pp. 34–46, 2013. [Google Scholar]

12. A. Wunnava, M. K. Naik, R. Panda, B. Jena and A. Abraham, “A novel interdependence based multilevel thresholding technique using adaptive equilibrium optimizer,” Engineering Applications of Artificial Intelligence, vol. 94, pp. 103836, 2020. [Google Scholar]

13. M. Abdel-Basset, R. Mohamed, S. Mirjalili, R. K. Chakrabortty and M. J. Ryan, “Solar photovoltaic parameter estimation using an improved equilibrium optimizer,” Solar Energy, vol. 209, no. 3, pp. 694–708, 2020. [Google Scholar]

14. J. Wang, B. Yang, D. Li, C. Zeng, Y. Chen et al., “Photovoltaic cell parameter estimation based on improved equilibrium optimizer algorithm,” Energy Conversion and Management, vol. 236, no. 3, pp. 114051, 2021. [Google Scholar]

15. J. Liu, W. Li and Y. Li, “LWMEO: An efficient equilibrium optimizer for complex functions and engineering design problems,” Expert Systems with Applications, vol. 198, no. 9, pp. 116828, 2022. [Google Scholar]

16. S. Gupta, K. Deep and S. Mirjalili, “An efficient equilibrium optimizer with mutation strategy for numerical optimization,” Applied Soft Computing, vol. 96, no. 1, pp. 106542, 2020. [Google Scholar]

17. L. Yang, Z. Xu, Y. Liu and G. Tian, “An improved equilibrium optimizer with a decreasing equilibrium pool,” Symmetry, vol. 14, no. 6, pp. 1227, 2022. [Google Scholar]

18. H. W. Ding, X. G. Cao, Z. S. Wang, G. Dhiman, P. Hou et al., “Velocity clamping-assisted adaptive salp swarm algorithm: Balance analysis and case studies,” Mathematical Biosciences and Engineering, vol. 19, no. 8, pp. 7756–7804, 2022. [Google Scholar] [PubMed]

19. Z. S. Wang, H. W. Ding, J. Wang, P. Hou, A. S. Li et al., “Adaptive guided salp swarm algorithm with velocity clamping mechanism for solving optimization problems,” Journal of Computational Design and Engineering, vol. 9, no. 6, pp. 2196–2234, 2022. [Google Scholar]

20. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, no. 63, pp. 120–133, 2016. [Google Scholar]

21. X. Zhang and Q. Lin, “Information-utilization strengthened equilibrium optimizer,” Artificial Intelligence Review, vol. 55, no. 5, pp. 4241–4274, 2022. [Google Scholar]

22. H. Ren, J. Li, H. Chen and C. Li, “Stability of salp swarm algorithm with random replacement and double adaptive weighting,” Applied Mathematical Modelling, vol. 95, no. 5, pp. 503–523, 2021. [Google Scholar]

23. X. Yu, W. Y. Xu and C. L. Li, “Opposition-based learning grey wolf optimizer for global optimization,” Knowledge-Based Systems, vol. 226, pp. 107139, 2021. [Google Scholar]

24. L. Ma, C. Wang, G. N. Xie, M. Shi, Y. Ye et al., “Moth-flame optimization algorithm based on diversity and mutation strategy,” Applied Intelligence, vol. 51, no. 8, pp. 5836–5872, 2021. [Google Scholar]

25. F. A. Ozbay and B. Alatas, “Adaptive salp swarm optimization algorithms with inertia weights for novel fake news detection model in online social media,” Multimedia Tools and Applications, vol. 80, no. 26–27, pp. 34333–34357, 2021. [Google Scholar]

26. H. R. R. Zaman and F. S. Gharehchopogh, “An improved particle swarm optimization with backtracking search optimization algorithm for solving continuous optimization problems,” Engineering with Computers, vol. 38, no. 4, pp. 2797–2831, 2022. [Google Scholar]

27. Z. S. Wang, H. W. Ding, J. J. Yang, J. Wang, B. Li et al., “Advanced orthogonal opposition-based learning-driven dynamic salp swarm algorithm: Framework and case studies,” IET Control Theory & Applications, vol. 16, no. 10, pp. 945–971, 2022. [Google Scholar]

28. L. Wu, X. Huang, J. Cui, C. Liu and W. Xiao, “Modified adaptive ant colony optimization algorithm and its application for solving path planning of mobile robot,” Expert Systems with Applications, vol. 215, no. 23, pp. 119410, 2023. [Google Scholar]

29. Z. S. Wang, H. W. Ding, Z. J. Yang, B. Li, Z. Guan et al., “Rank-driven salp swarm algorithm with orthogonal opposition-based learning for global optimization,” Applied Intelligence, vol. 52, no. 7, pp. 7922–7964, 2022. [Google Scholar] [PubMed]

30. P. G. Luan and N. T. Thinh, “Hybrid genetic algorithm based smooth global-path planning for a mobile robot,” Mechanics Based Design of Structures and Machines, vol. 51, no. 3, pp. 1758–1774, 2023. [Google Scholar]

31. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]

32. D. Karaboga and B. Basturk, “A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm,” Journal of Global Optimization, vol. 39, no. 3, pp. 459–471, 2007. [Google Scholar]

33. D. Agarwal and P. S. Bharti, “Implementing modified swarm intelligence algorithm based on Slime moulds for path planning and obstacle avoidance problem in mobile robots,” Applied Soft Computing, vol. 107, no. 4, pp. 107372, 2021. [Google Scholar]