Consortium Chain Consensus Vulnerability and Chain Generation Mechanism

1  Introduction

With the great success of the permissionless blockchain application in electronic cryptocurrency, blockchain networks based on decentralized identity authentication and group consensus attract increasing attention. However, limited by the scale, performance, and deployment cost of distributed application systems, permissionless blockchain technology is challenging to use widely. Consortium Blockchain (CBC) inherits the security characteristics of public chain to some extent with the openness that private chain does not provide, so more research focuses on CBCs [1–3]. The CBC limits the proposer set to a few known nodes and relies on a trusted service or consortium organization to authenticate the nodes. Based on proof of interest of chain or Byzantine Fault Tolerance (BFT), CBC proposes new blocks in the way of fault-tolerant consensus and verifies new transactions without needing confirmations, thus reducing the influence of potential Byzantine nodes on the system. Moreover, liquidity is achieved by deploying and running smart contracts on CBCs [4], of which the efficiency is significantly higher than that of the permissionless public chain driven by the proof-of-work mechanism. With the continuous expansion of the application scenarios of CBC in recent years, the diversity and durability of the services it can provide have been improved unprecedentedly. Therefore, CBC provides a new way for identity authentication and trust transfer among parties in the network [5–7].

The consensus mechanism of CBC ensures the consistency of contents stored by each node in the distributed ledger and protects data from unauthorized access, which is important for realizing the scalability, transaction speed, transaction certainty, and security of CBC [8,9]. The consensus mechanism of CBC is constantly improved to maintain compatibility of high efficiency and scalable applications such as side chain and sharding mechanisms [10–12]. Users of the CBC can create parallel and separate CBCs through the Application Program Interface (API) and set the initial consensus mechanism, allowing different parallel and separate CBCs belonging to the same consortium organization to adopt different consensus mechanisms. Meanwhile, the consensus mechanism of each parallel and separate CBC can be upgraded through voting at any time. The system can reach a consensus safely among several side chains or sharding chains by deploying smart contracts in CBC.

However, under the environment of a Byzantine partition consortium network, the information service entities of heterogeneous CBCs interact frequently and lack collaborative management, making it difficult for the data owner to control the access of other trusted domain entities to the data, resulting in the risk of data being stolen, tampered with and replayed when the data is shared across domains [13]. Chen et al. [14] proposed a blockchain-based cross-domain data-sharing method for the Internet of Things (IoT), which uses the threshold proxy re-encryption method to process the ciphertext to avoid collusion between malicious agents and visitors. Yu et al. [15] proposed an industrial IoT data-sharing scheme based on blockchain and proxy re-encryption, where cloud servers verify whether user attributes meet the access policy and generate decryption parameters to send to users when data users request cross-domain data. Existing consensus mechanisms can satisfy the scalability or security of distributed systems, but it is impossible to do both as long as the consensus mechanism of the final determination of block conflict is different and the impact of system scalability on security is also different. Thus, the consensus mechanism based on asynchronous communication still faces challenges. Therefore, it is of great academic significance and extensive application value to further research the consensus mechanism of CBC to improve the security and scalability of the partitioning network consensus mechanism in heterogeneous CBCs based on privacy protection and increase the efficiency of trust transfer and data sharing between different trust domains [16–19].

This paper established a new consortium chain generation model to solve the above problems. The rules of chain generation are extracted. The behaviors of nodes are analyzed and verified, based on which the consensus vulnerability of CBCs is deeply analyzed. Based on this, the paper proposes a novel generation mechanism for CBC based on the Asynchronous Binary Byzantine Consensus Mechanism (ABBCM). The main contributions of this work are as follows:

(1) A new generation model of CBC is established. The influence of logical and physical topology structure on the CBC performance is analyzed from the perspective of the chain generation process. The single-chain generation rule is given to avoid chain forking.

(2) The node behavior is analyzed and verified. Based on the node behavior, the consensus vulnerability of CBCs is deeply analyzed. The normalized verification node aggregation index is obtained to represent the consensus ability of consortium institutions.

(3) A novel CBC generation mechanism, ABBCM, based on asynchronous binary Byzantine consensus, is proposed, which extends the general definition of Byzantine consensus and allows a definite set of consensus values to combine multiple proposals. The experimental results show that under the four classical Byzantine node attack behaviors, BA1 to BA4, the ABBCM obtains better time delay than the Coin, a classical random Byzantine consensus mechanism, and can meet the throughput of most IoT applications.

This paper is structured as follows. Section 2 describes the related work of CBCs and consensus algorithms. Section 3 analyzes the effect of logical and physical topology on the CBC performance from the perspective of chain generation and gives the single chain generation rule avoiding chain forking. Section 4 analyzes the consensus vulnerability of CBCs based on node behavior. Section 5 introduces a novel consortium chain generation mechanism based on asynchronous binary Byzantine consensus. In Section 6, the proposed mechanism is simulated, and the results are discussed. Section 7 concludes with lessons learned and a plan for future work.

2  Related Works

Decentralized applications based on CBC have been involved in data governance [20], cloud storage [21], IoT [22], supply chain [23], and other fields to establish a trusted environment for stakeholders, achieving trusted and durable services. However, its low scalability and throughput limit the performance of the hosted decentralized applications. The section enfolds works to improve the performance of CBCs in recent years: mainstream platforms and consensus mechanisms. Various works related to the cross-domain consensus of CBCs are also compared based on research description, techniques, and limitations.

2.1 CBC Platforms

The mainstream CBC platforms include HyperLedger, Corda, and Quorum. In 2015, led by the Linux Foundation, International Business Machines Corporation (IBM), Intel, Cisco, and others announced the establishment of the HyperLedger project, which provides open-source reference and implementation for transparent, public, and decentralized enterprise-level distributed ledger technology. It also introduces blockchain into the application of distributed consortium ledger for the first time, which is grounds for building an efficient business network based on blockchain in the future [24–27]. Like Hyperledger, Corda uses a distributed notary mechanism to meet growing business demands [28,29]. However, the distributed consensus mechanism’s performance between nodes significantly impacts ledger synchronization between nodes and system performance. This project provides consensus mechanism selection strategies for different businesses. For example, in applications with high trust between nodes, Raft, Paxos, and other Crash Fault Tolerance (CFT) algorithms are selected to achieve high system performance.

On the contrary, the BFT class algorithm is applied to obtain higher system security and reliability. Subsequently, JPMorgan launched a distributed ledger protocol, Quorum, based on the Raft consensus mechanism based on Ethereum. It greatly improved the system performance by introducing the Enclave module with transaction isolation and specific encryption functions to realize parallel operation [30,31]. Although the implementation schemes of the above CBC platforms are different, they pursue usability and scalability to ensure performance and adapt to different industries’ requirements.

2.2 Consensus Mechanism Based on CBCs

Based on the existing CBC platform, much research has been done to improve its performance [32]. Some performance-driven consensus protocols of CBCs ensure ledger consistency and partition fault tolerance through the delegation mechanism [33–37] but reduce the number of core nodes participating in the consensus and the security brought by system decentralization. Sun et al. [38] proposed a blockchain-based on-board social network data-sharing system. This scheme can realize one-to-many data sharing, but the identity of the shared entity needs to be determined in advance, making it difficult to realize large-scale and fine-grained data sharing. Su et al. [39] proposed an authorization Byzantine fault-tolerant algorithm based on node reputation, which can reach consensus among the various authorization partitions in CBCs. Yang et al. [40] built a new blockchain-based energy management architecture for IoT-assisted smart homes, enabling smart homes to interact with the grid and other users in an energy Internet system. Based on [40], Abishu et al. [41] proposed a new consensus mechanism, which takes advantage of practical Byzantine fault tolerance and proof of reputation to ensure the high reliability of energy transactions. Zhang et al. [42] proposed a consensus mechanism based on credit risk assessment to realize credit management of counterparties in distributed energy transactions. However, the above consensus research based on CBC still cannot meet high concurrency, low delay, and strong security in Byzantine cross-domain applications.

There are also researches such as Tezos [43], which proposed an on-chain governance model to generate blocks dynamically and realized the autonomous management of chain ecology by establishing a digital federation, thus simplifying the verification process of transactions and smart contracts, which has a broad application prospect in IoT where the computing power of node is limited. A time segmentation solution of CBC based on the Tezos blockchain was proposed by [44], which allows computing devices with low storage capacity to keep only the latest segmentation ledger instead of the whole consortium ledger. It supports the construction of mobile self-organizing CBC and inter-chain transactions under a 5G network of heterogeneous vehicle networking and conducts the built-in form verification of some transactions and smart contracts. Qasse et al. [45] tried to solve the cross-domain authentication and trust transfer between independent Inter-blockchain Communication (IBC) systems based on CBC to ensure the security of multi-domain consensus consistency of user identity. Practical Byzantine Fault Tolerance (PBFT) and other BFT consensus protocols do not require verification nodes to solve encryption problems or provide proof of stake to determine the ownership of accounting rights [46,47]. Generally, only a subset of participating nodes need to run the BFT protocol. The consensus can be reached by exchanging rounds of messages so that nodes can reach the consensus of the current round before the next round starts. Therefore, it has good anti-fork and potential application prospects in CBCs [48].

BFT protocol usually can be verified mathematically as long as 2/3 of the participants follow the protocol. Then, the BFT protocol can ensure no block conflicts regardless of whether there is an upper limit of network delay [46]. Some studies further explored solutions to improve the performance of the BFT consensus mechanism [49]. They proposed that cloud computing and programmable hardware can be used to improve the efficiency of the BFT consensus, allowing the consortium chain to deliver higher throughput, lower latency, and the ability to scale with better network bandwidth and hardware environments. However, BFT-like consensus protocols still face challenges, such as the communication systems’ high complexity and weak scalability.

Table 1 compares the existing research with the proposed work based on the research description, techniques, and limitations. However, these existing solutions usually require some nodes to be coordinators. If the coordinators are non-Byzantine nodes and messages are delivered timely in the asynchronous round, they broadcast their proposals to all nodes in the consortium network. If not, exploiting its power within the consensus round can significantly hinder the performance. This paper proposed a new consortium chain generation mechanism, which can realize cross-domain asynchronous message passing between multi-consortium chains without reducing the system’s security.

3  Chain Generation Model

CBC is usually endorsed by institutions to determine the set of verification nodes and the block generation mechanism. In CBC, child blocks are voted from existing blocks to build a growing tree of blocks, the root of which is called a “creation block”. Normally, blocks form a single chain under the block generation mechanism, meaning a parent block has only one child block. However, due to network delays or malicious attacks, one parent block inevitably generates more than one child block to be confirmed. The consensus of CBC is to select only one child block from several unconfirmed child blocks of each parent block when asynchronous nodes are executed asynchronously and sequentially, that is, to select the most authoritative chain from the block tree.

The following is an Asynchronous node-based CBC Generation Model (ACCGM), of which the practicability and effectiveness are illustrated by experiments. From the perspective of chain generation, the influence of the logical and physical topology structure of the CBC network on its performance is analyzed. Then, a single chain generation rule is given to prevent CBC from forking.

Definition 1: Asynchronous Node Set (ANS). ANS refers to a set of asynchronous sequential execution nodes and their public keys in CBC, denoted as Γ={n1,n1PK,n2,n2PK,⋯,nk,nkPK}. “Asynchronous” means that each node works at a specific speed that varies over time, and the node’s performance is transparent to others. “Sequence” means that each node performs one atomic step at a time as the work progresses.

ANS communicates by exchanging data through an asynchronous and reliable point-to-point consortium network. Any pair of nodes can be connected through a two-way communication channel. The transaction will not be lost, copied, or tampered with in the network transmission process, but there is a transaction transmission delay. ni∈Γ represents the CBC node, and B represents the block. It is assumed that each node has obtained part or all of the block ledger ℬ on the chain when t≥0, i.e., ℬnit={B,t≥0}. Genesis Block g is the only block known to all nodes at the initial time, i.e., ℬni0={g}. The public and private keys of each node are generated by an elliptic curve encryption algorithm. The node private key is used to verify the new block.

The ACCGM chain generation model satisfies the following properties:

Property 1: Recursion. Each new block B is linked to the current tail block P(B) by the mapping function P. The relationship between blocks can be expressed recursively as:

P0(B):=B(1)

P2(B):=P(P(B))(2)

Pi(g):=ϕ,i∈N(3)

∀B→Pi(B):≠B,i∈N(4)

Eqs. (1) and (2) are recursive representations of blockchains. In Eq. (3), g is a creation block without a parent block. Eq. (4) defines that there is no cycle between blocks. By property 1, we defined a chain C(B) that generates and contains a block B as the path from B to g, i.e.,

CB:=(B,P(B),⋯,Pi−1(B),g)(5)

Property 2: Locality. Due to network delay, eclipse attack, and other reasons, different CBC nodes are allowed to perceive different block sets in the chain generation model, namely:

ℬnit≠ℬnj,ni,nj∈Nt,t>0(6)

Property 3: Inheritance. In the process of CBC generation, blockchain consensus has inheritance, namely:

∀(s,t>0)and(s>t)→ℬnit⊆ℬnjs

h(B)=k⇔Pk(B)=g(7)

If B′≠B, and B′∈CB, then, B′ is called the ancestor block of B, while B is called the descendant block of B′; if B′=P(B), then B is called the direct descendant node of B′. Property 3 indicates that the state of the blockchain in which the block B resides is obtained by executing all transactions in CB from Genesis Block g.

It is assumed that a maximum of 𝒦 (3𝒦+1<k) Byzantine nodes are allowed to exist in CBC consisting of k nodes. They may crash, fail to send or receive messages, send any messages, start at any state, perform any state transitions, etc. For example, they can also use honest node “pollution” calculations by sending a message with the same content as a partial honest node error estimate, thus affecting the system consensus. Byzantine nodes cannot delay receiving messages indefinitely but can control the network by modifying the order in which messages are received. In particular, no consensus mechanism can ensure system security and scalability in a completely asynchronous messaging system [36]. This paper assumes an upper limit time δ for message transmission and node computation delay to ensure the system reaches the final consensus after a certain time.

Definition 2: Upper limit time δ. If any node v of CBC receives a message at time t, other nodes in the chain can guarantee the message receive within the time window [t,t+δ].

In Definition 2, the local time deviation of each node on CBC is incorporated into δ. It is assumed that the node na is currently processing a block with a timestamp of ta_Stamp when a block has a timestamp of tb_Stamp, and tb_Stamp>ta_Stamp, meaning that a block with a timestamp of tb_Stamp occurs in the future. Node na will reject the block. If tb_Stamp<ta_Stamp−δ indicates that the block with timestamp tb_Stamp has been confirmed, node na will also reject the block.

Definition 3: δ-Validation. Under the upper limit of delay time δ, the system considers a legitimate verification that at time ts_Stamp, which contains the block header s, the highest block height l(s), the block hash H(s), the hash h(s|u) of the new proposed block u, and the valid signature 𝒱 created by the private key of the verifier v, and satisfies Eq. (8) as a correct verification, indicated as ⟨s,l(s),H(s),H(s|u),ts_Stamp,𝒱⟩δ.

{s=Pi(u),i≥1𝒱PK∈Γ(8)

It can be seen that the correctness of node voting depends on the chain in which the node votes. Typically, the verifier v broadcasts a six-tuple voting message: block header s of the current tail node, the height l(s), the hash H(s) to the block header s, the hash h(s|u) to the new proposed block u, the timestamp, and the signature of the verifier v. The current tail node s must be the ancestor of the new proposed block u; otherwise, the vote is considered illegal. If the public key of the verifier v is not in the verifier set, then this vote is also illegal.

Definition 4: If block s on CBC has a descendant block u, and u obtains the correct votes exceeding the threshold value, then block s is considered to be determined. That is:

{justified(g)andfinalised(g)==1s=Pi(u),i≥1u=Pj(u′),j≥1IsValidated⟨s,l(s),H(s),H(s|u),ts_Stamp,𝒱⟩δ,sthreshold==1IsValidated⟨u,l(u),H(u),H(u|u′),tu_Stamp,𝒱⟩δ,uthreshold==1(9)

As a basis for the recursive definition, it is generally assumed that Genesis Block g has both received the correct votes over the threshold and is final. In Definition 4, block u′ is the descendant block of block u. If both block s and its descendant block u obtain correct votes exceeding the threshold value, then block s is considered to be determined. sthreshold and uthreshold are the consensus threshold values when the upper limit of delay is δ.

Definition 5: Absolute majority link. An absolute majority link means that for ordered block (s,u), denoted as s→u, at least one verifier exceeding the threshold has issued a confirmation vote for the current end-of-chain block s and a δ-verification for the newly packaged block u.

Definition 6: Block conflict. Block conflict is considered to occur between blocks s and u if and only if the two blocks s and u sharing the same Genesis Block g are located in different branches. That is:

{justified(g)andfinalised(g)==1s≠Pi(u),i≥1u≠Pj(s),j≥1IsValidated⟨s,l(s),H(s),H(s|u),ts_Stamp,𝒱⟩δ,sthreshold==0(10)

From Definitions 2 to 6, it can be seen that if neither block s nor block u on the chain is the ancestor or descendant of the other, the two finally determined blocks conflict. Therefore, the tail block s is final; either it is the genesis block or if and only if

(1) The tail block s has obtained a verification node vote exceeding the threshold;

(2) There is an absolute majority link s→u;

(3) Blocks s and u do not conflict;

(4) Block height h(u)=h(s)+1.

Thus, the single chain generation rule avoiding chain forking and ensuring at most one reasonable block height n(n>0) on a single alliance chain is obtained:

Rule 1: Unequal height rule. If ∃g makes Pi(s1)=Pj(s2)=g (i>0,j>0), and s1→u1 and s2→u2 are distinct absolute majority joins, then h(u1)≠h(u2).

Rule 2: Exclude rule. If ∃g makes Pi(s1)=Pj(s2)=g (i>0,j>0), and s1→u1 and s2→u2 are distinct absolute majority joins, then h(s1)<h(s2)<h(u2)<h(u1) is not true.

Rule 3: Nonoverlapping rule. For any height n(n>0), at most, one absolute majority joins s→u such that h(u)=n.

4  Vulnerability Analysis

The existing access mechanism of CBC helps improve the ability of the ACCGM-based CBC system to resist external attacks. Still, it cannot identify and prevent the threats of Byzantine nodes to the system. The impact of the behavior of Byzantine nodes in the ACCGM consensus on the system is analyzed as follows.

4.1 Behavior of Verification Node

In the ACCGM consensus process, Byzantine nodes can initiate abnormal voting without violating the rules to obtain a final result or retain the intermediate data in the calculation process to infer and snoop the data of other participants. On the one hand, when the verification node initiates non-voting behavior, the correct voting proportion of the verifier will be lower than the consensus threshold, and a consensus block will not be generated. On the other hand, if two or more conflicting validation blocks are generated in the same round due to malicious voting or incorrect behavior of the verifier, either the chain forks or the off-chain governance mechanism is used to support one branch at the expense of the other. Therefore, the analysis of verification node behavior matters in constructing the system incentive mechanism and ensuring the correct formation of CBC.

The voting behavior of the verification node will be written into the block as a transaction, which can be divided into correct voting, malicious voting, incorrect voting, and no voting.

A. Correct voting

If only a single block meets Definition 3 and has verification nodes exceeding the threshold and voting correctly in a certain round, the block will be written into CBC, and each node synchronizes the ledger.

B. Malicious voting

Malicious voting means that the verifier votes for two new blocks in the same round simultaneously, which meets Definition 6, thus causing a conflict.

C. Incorrect voting

Incorrect voting refers to the situation in which the verifier cannot vote correctly in the same consensus round due to some incorrect behavior. Typical cases of incorrect voting are as follows:

(1) The verifier sends the vote later, resulting in the vote not reaching CBC within the consensus round.

(2) Some nodes do not propagate the vote of a verification node, resulting in the vote not reaching CBC within the consensus round.

(3) The vote does not reach CBC within the consensus round due to network delay.

(4) The signature of the verifier’s vote is invalid.

(5) The voting block is not generated in the current highest block.

D. No voting

No voting includes no voting of the verification node and voting loss.

Non-byzantine nodes may produce votes A and C, and Byzantine nodes may produce votes B, C, and D. When dealing with voting transactions, CBC based on ABBCM only processes the correct voting A and malicious voting B defined above; the incorrect voting and no voting are invalid votes and will be ignored. If only correct votes exist, the system will select a single legal block within a specified time cycle and record it in CBC. Otherwise, the system may fail to obtain consensus due to the failure to obtain more than the threshold number of verification signatures in a specific time round, called active failure, or the system forks due to two conflicting blocks being finalized simultaneously, called a security failure.

The consortium institutions will use the punishment mechanism for cases B, C, and D. The mechanism is affected by the following aspects:

(1) The larger the proportion of malicious voting nodes, incorrect voting nodes, or non-voting nodes, the more serious the penalty will be.

(2) Failure to consensus or chain forks will increase punishment. The following is a formal analysis.

It is assumed that m blocks (m is constant) are written on a block s in CBC, and block s is confirmed by probability, then the Block Finalisation Factor (BFF) of block s in round i is:

BFFi,rs,i={0,rs,i=0rs,i,rs,i<mm,rs,i≥m,h(si)−h(s)≥mh(si)−h(s),rs,i≥m,h(si)−h(s)<m(11)

where rs,i∈N is the consensus round experienced from block s writing into CBC to the current round i. When rs,i≥m,h(si)−h(s)<m, it indicates that there are non-consensus rounds in rs,i rounds after block s. For example, the correct voting cannot reach the preset consensus threshold due to the large proportion of malicious voting nodes, incorrect voting nodes, or non-voting nodes. Thus, consensus cannot be obtained.

vj∈V,0<j≤Mi, where Mi is the total number of verification nodes in round i, and the vote of verification node vj in round i is denoted as Ψvj,i.

Ψvj,i={1,Verification node vj votes correctly in round i0,otherwise(12)

By analyzing the behavior of validation nodes, the polymerization index of validation nodes was obtained to represent the consensus ability of consortium institutions. The node polymerization index Ci for normalization verification of the mechanism in round i can be expressed as:

Ci={∑vj∈VΨvj,i⋅(1−a)Mi⋅|BFFi−N|,BFFi<N∑vj∈VΨvj,i⋅(1−a)/Mi,BFFi=N(13)

According to the Byzantine node proportion a∈(0,1/3), 2/3<(1−a)<1, and when BFFi<N, |BFFi−N|≥1, so Ci∈(0,1).

4.2 Vulnerability of CBC Consensus

In the chain generation model ACCGM, the CBC network is partially synchronous, and the transaction transfer between nodes has an upper bound finite delay. Although the verification node can independently choose the time for issuing the voting transaction within each consensus round, it cannot ensure that the voting transaction of each verification node in each round will be synchronized among the CBC nodes before the end of the round. If the voting transaction is issued too early, the verification node will fail to vote on other more competitive blocks within the consensus round. Late issuance of voting transactions may result in activity consensus failure. In addition, the authentication node update transaction is allowed to be sent after only consensus blocks are generated in each consensus round, and the authentication node set is dynamically managed. Therefore, in a single consensus round, it is necessary to consider the impact of network partition, network delay, Byzantine node proportion, verification node state, and other factors on the consensus. Network partition and delay have been explained in the previous section. The following focuses on analyzing the influence of Byzantine node proportion and verification node state on the consensus.

4.2.1 Consensus Vulnerability Based on Byzantine Node Proportion

Consortium nodes are divided into ordinary nodes, which sort transactions and package blocks in the underlying chain, and verification nodes, which vote for new blocks; however, they are somewhat interdependent. Ordinary nodes collect and classify transactions, determine the order of transactions in CBC, and write global computer state information (contract variables, etc.) and related data into the block as part of the transaction. The voting transaction sent by the verification node is the same as the ordinary transaction, which needs to be packaged and recorded by the ordinary node. Byzantine ordinary nodes can refuse to include the voting transactions of some verification nodes in their proposed blocks. It can also improve the probability of successful execution of the above attacks by increasing the proportion of Byzantine nodes in a working state, sending out voting transactions in advance in consensus rounds, or even forcing other nodes to perform the same operation by network attacks.

When enough non-Byzantine nodes are offline in a certain period, the proportion of Byzantine nodes will increase, greatly improving the possibility of chain forking in the system. It is assumed that the proportion of Byzantine nodes in ACCGM-based CBC is a, and the honest nodes working together on the single CBC account for the majority. In the actual working scenario, node offline, network delay, eclipse attack, sybil attack, etc., will impact a. In the ACCGM-based CBC network, Byzantine nodes in the current tail block s may create a longer chain than the current chain. The probability of the above event decreases exponentially to the block height difference m of the forked block s and the new tail block s′ (s≠s′). When the Byzantine node attacks, if there are m descendant blocks after the original chain block s, the probability of generating a longer forked chain s′ from the block s is (a/(1−a))m. When m is large enough, the above malicious attacks will become impractical. The relationship between Byzantine node proportion and system security is shown in Fig. 1.

Figure 1: The relationship between Byzantine node proportion and system security

It can be seen that when a is constant, the probability of generating Byzantine chain forking will be significantly lower as m increases. When a=1/3,m=9, the probability of generating Byzantine chain forking will be about 5×10−4, almost negligible. However, as a increases, especially approaches 0.5, the probability of producing a Byzantine chain forking approaches 1 for any value of m.

4.2.2 Consensus Vulnerability Based on Node Reputation

In the ACCGM-based CBC distributed network environment, the initial reputation of the node is provided by the endorsement of the institutions, which is a static trust management mechanism based on authentication and authorization. However, when each node participates in the calculation autonomously, using the initial reputation to evaluate the node often presents a lag to some extent. For example, nodes in the CBC network have the capability of routing and forwarding transactions or blocks. Nodes with high initial reputations hijacked by malicious forces can independently change the forwarding route or discard part of transactions or blocks. If nodes with high initial reputations provide fraudulent services or do not provide services, the system consensus will be seriously threatened. This paper established a node trust model of CBC based on consensus rotation information feedback and proposed a dynamic maintenance mechanism of node reputation relying on weighted trust feedback from nodes to improve the accuracy and dynamic adaptability of node reputation evaluation. The above model is quantitatively evaluated to further analyze the relationship between node reputation and CBC consensus.

Definition 7: Node reliability evaluation function. The reliability evaluation of node p to node q in consensus round i is defined as function f(p,q)i:

f(p,q)i={f(p,q)i−1+∂(1−f(p,q)i−1),i>01/2,i=0(14)

where ∂ is the standard deviation of the trust degree of the consortium institution to the consortium node set.

Definition 8: Node set trust evaluation function. It is assumed that the number of CBC nodes in each consensus round is k, and η∈(0,1] represents the proportion of verification nodes that normally work within a period. (1−η) represents the proportion of verification nodes that work abnormally, and the institutional credit value changes dynamically with η, then the trust degree of the node set of the consortium institutions in consensus round i can be expressed as Eq. (15).

DΓ,i={η⋅∑k=0i∑p,q∈𝒮f(p,q)ik2,i>0η,i=0(15)

In Eq. (15), i=0 indicates that there is no interaction history between nodes in the initial round, so the direct trust degree of the initial round is set as η.

Before the system reaches a consensus at the beginning of each round, when the value of the trust evaluation function DΓ,i of the verification node set is lower than the threshold, the set is dynamically adjusted by

(1) keeping the credit value of the verification node whose value of credibility evaluation function is higher than the preset value in each round unchanged;

(2) reducing the credibility value of verification nodes whose credibility evaluation function value is lower than the preset value or does not vote;

(3) removing the verification nodes whose reputation value is lower than the reputation threshold from the set of verification nodes, which will increase the influence of normally working verification nodes in the consortium institutions, significantly reducing the risk of system consensus.

5  Asynchronous Binary Byzantine Consensus-Based Chain Generation Mechanism

The above analysis of the influence of network partition, network delay, Byzantine node proportion, verification node state, and other factors on the consensus found that in CBC with 𝒦<k/3 Byzantine nodes, the consensus between k nodes can be probabilistically achieved by using the local random strategy of nodes or the shared common random strategy. However, these solutions typically require a unique coordinator process, sometimes called a leader, to be non-faulty. The advantage is that if the coordinator is non-faulty and the messages are delivered timely in an asynchronous round, then the coordinator broadcasts its proposal to all processes, and this value is decided after a constant number of message delays. The drawback is that a faulty coordinator can dramatically impact the algorithm’s performance by leveraging the power and imposing its value on all. Non-faulty processes thus have no choice but to decide nothing in this round. Thus, the above method cannot effectively achieve consensus in asynchronous messaging systems. For the above problems, the influence of Byzantine nodes on CBC consensus is further analyzed, and a novel mechanism of CBC generation based on asynchronous binary Byzantine consensus mechanism is presented, which is time optimal and resilience optimal without needing signatures. Unlike a classic (strong) coordinator, the weak coordinator in this mechanism does not impose its value. On the one hand, this allows non-faulty processes to decide a value quickly without the coordinator’s help. On the other hand, the coordinator helps the algorithm terminate if non-faulty processes know that they proposed distinct values that might all be decided.

The ABBCM-based CBC generation mechanism relies on many-to-many communication of binary values of nodes, extending the common definition of Byzantine consensus and allowing a definite set of consensus values to combine multiple proposals. On the one hand, it is assumed that values proposed only by Byzantine nodes cannot be agreed upon, and non-Byzantine nodes can quickly achieve consensus without the help of coordinating nodes. On the other hand, if the consensus values proposed by non-Byzantine nodes are not consistent, the round of consensus will be terminated early. Let ℜ be a set of consensus values proposed by the node. In the multivariate consensus, ℜ may contain any number of values. To simplify the problem, let ℜ = {0,1} in the binary consensus. Assuming that each non-Byzantine node proposes a value for consensus, the binary Byzantine consensus problem can be translated into having each node determine a value in a way that satisfies the following properties:

•   Certainty. Each non-Byzantine node will eventually propose a value for consensus.

•   Consistency. No two non-Byzantine nodes determine different values.

•   Validity. If all non-Byzantine nodes propose the same value for the consensus, the final consensus value will not be something else.

ABBCM relies on many-to-many communication (binary value broadcast) of node binary values, expressed as BiVa-B. In the BiVa-B instance, each non-Byzantine node ni broadcasts the current round of binary values for consensus and obtains a set of binary values for consensus proposed by other nodes over the network, stored in the local read-only variable set ξi, where ξi is initialized to ϕ, and the element in set ξi is added when a new value is received.

The following rules define BiVa-B:

Rule 1: Incremental rule. If at least (κ+1) non-Byzantine nodes ni broadcast the same value ℜ, then each node ni adds ℜ to its local read-only variable set ξi.

Rule 2: Reverse rule. If ni is a non-Byzantine node and ℜ ∈ ξi, ℜ has been broadcast by a non-Byzantine node.

Rule 3: Diffusion rule. If a non-Byzantine node ni adds ℜ to its local read-only variable set ξi, eventually, for every non-Byzantine node nj, there is ℜ ∈ ξi.

Rule 4: Balancing rule. Finally, the local read-only variable set ξi for each non-Byzantine node ni is not empty.

Based on the above rules, the set of local read-only variables ξi for each non-Byzantine node ni: (1) becomes non-empty, (2) becomes equal, (3) contains all values broadcast by non-Byzantine nodes, and (4) contains no values broadcast only by Byzantine nodes.

System model ABBCMδk,𝒦[𝒦<k/3] is established below, which can provide strong effectiveness and consistency in asynchronous message communication system, as well as certainty to meet the needs of CBC applications. The local variables involved in node ni are shown in Table 2, and the main process is shown in Algorithm 1. Node ni proposes the initial consensus value by calling bin-propose (ℜi) in the asynchronous round and assigns ℜi to the local current estimate estimatei of the binary proposal consensus value; After that, each non-Byzantine node enters a series of asynchronous rounds. In any rotation r, the non-Byzantine node ni proceeds in three stages.

Stage 1: Consensus value cleaning to filter out the consensus value proposed by the Byzantine node. Node ni enters the next round and broadcasts its current binary consensus value estimate. In BiVa-broadcast(), node ni receives the same consensus proposal value from 𝒦+1 nodes and rebroadcasts the value. When ℜ is received from 2𝒦+1 different processes, each node ni adds it to ξi [r] and forwards the value. Also, when BiVa-deliver forwards a consensus proposal value, it is added to ξi [r]. Finally, the set ξ of all non-Byzantine nodes becomes non-empty and equal and contains only all the consensus proposal values broadcast by non-Byzantine nodes.

Stage 2: Consensus value estimate exchange to reach a consensus. At this stage, node ni broadcasts the message Auxiliary[r](), whose content is c. Node ni then waits until it receives a set of αi that satisfy the following two properties:

•   The values of αi come from Auxiliary[r]() sets of at least (k-𝒦) different nodes.

•   αi ⊆ ξi[ri]. Because the BiVa-broadcast() return values of Byzantine nodes can be filtered out in the first stage, even if Byzantine nodes send their false message set Auxiliary[r](), which contains values proposed only by Byzantine nodes, αi will also only contain consensus estimates broadcast by non-Byzantine nodes.

Thus, in any round of r, αi⊆{0,1} contains only the values broadcast by non-Byzantine nodes with BiVa-broadcast() algorithm.

Stage 3: Consensus values converge, a local calculation stage, to determine the candidate of consensus value of node ni. The convergence process of consensus value depends on the content of αi.

•   If αi contains a single element ℜ, ℜ becomes the new consensus estimate for node ni and a candidate for consensus determination.

•   If αi={0,1}, nodes ni cannot determine the new estimate of consensus value. Since both values are presented by non-Byzantine nodes, to converge uniformly, ni can choose one of them as its new estimate of consensus value based on the sharing strategy, for example, b=rmod2, because the value is the same among all non-Byzantine nodes in the same round.

In the above ABBCM-based CBC generation mechanism, node ni obtains the consensus value ℜ of the current round by calling decide (ℜ). However, calling decide (ℜ) does not terminate its participation in the algorithm, which means node ni continues to execute circularly after the call returns because it may be necessary to help other nodes converge to the determined consensus value in the following two rounds in the node decision-making.

6  Experiments

To test the performance of the asynchronous binary Byzantine consensus-based chain generation mechanism proposed in this paper, we built the Ethereum simulation test environment consisting of 100 virtual verification nodes on five servers and compared its performance with “Coin,” the recent randomized algorithm from Mostéfaoui et al. [52] used in the HoneyBadger blockchain. Experiments show that under all our workloads, our mechanism outperforms “Coin,” which is known to terminate in O (1) round in expectation. This is due to the overhead of the Coin implementation that slows down every round and the risks of being unlucky at tossing the coin by increasing the number of rounds needed to decide. Even with Byzantine behaviors, our method is always superior to the latter.

The experimental platform was CPU Xeon-E5 with memory size 64 G and operating system Ubuntu-64bit. Consortium chain CA was constructed. The total number of verification nodes is n=100, the proportion of Byzantine nodes is denoted as a, the time interval for consortium chain to construct transactions is denoted as Δ, and the number of consensus transactions in a single round is denoted as τ.

Considering that the behavior of Byzantine node can greatly affect chain generation based on binary Byzantine consensus, the following four typical Byzantine attack behaviors are constructed for performance testing:

BA1: Byzantine nodes send bit flip value; when the protocol specification expects to send bit b~, the Byzantine node sends bit b.

BA2: Byzantine nodes send the combination of the random value and the flipped value of the bit.

BA3: Byzantine nodes do not respond to any transactions.

BA4: Byzantine nodes form consortiums to block the consensus of non-Byzantine nodes in each round by sending messages.

6.1 Delay Test

To eliminate the influence of the time interval of constructing transactions on the delay, referring to the previous work [53] and take Δ=1 ms, under the four classical attack behaviors BA1 to BA4 of the Byzantine node defined in this paper, the comparison of the delay under the classical Byzantine consensus mechanism Coin [52] proposed by Mostéfaoui et al. is shown in Fig. 2.

Figure 2: Delay comparison between ABBCM and Coin

As shown in Fig. 2, when the Byzantine node proportion a gradually increases, the time delay of both ABBCM and Coin increases. The larger a is, the more significant the delay increment of the two algorithms is, indicating that the transaction processing delay is positively correlated with the Byzantine node proportion. Under the specific value of a and the four classical Byzantine node attack behaviors BA1 to BA4 limited in this paper, the time delay of ABBCM is better than Coin’s. Under the four attacks, the total delay of ABBCM is reduced by 52% compared with Coin. When a→0+, the transaction delay between ABBCM and Coin tends to be stable. As a increases, the transaction delay presents a certain weak robustness under four classical Byzantine node attack behaviors BA1 to BA4. In Fig. 2c, under the attack behavior of BA3, ABBCM obtains a minimum average delay of 382 ms. In Fig. 2d, under the attack behavior of BA4, ABBCM obtains a maximum average delay of 331 ms.

6.2 Throughput Test

(1) The consensus round time r is not limited

Consensus round time r is not limited, which means that r is set to be large enough so that transactions of block can reach consensus within a time less than r. In this case, consensus round time will not impact consensus time and throughput. According to the delay test results, r is set as 1 s, the proportion of Byzantine nodes a=33%, the interval for the consortium chain to construct transactions Δ=1 ms, and the number of consensus transactions in a single round τ=10,20,30,40. The throughput test is conducted under the four classical Byzantine node attack behaviors BA1 to BA4 limited in this paper, of which the results are shown in Fig. 3.

Figure 3: Throughput test under unrestricted conditions

As can be seen from Fig. 3, when consensus round time r is not limited, throughput in four Byzantine attack scenarios increases with the increase of consensus transactions in a single round. In a specific Byzantine attack scenario, when the consensus transactions in a single round increase slowly from 1, the system throughput increases significantly, such as the phase from τ=10 to τ=20 in Fig. 3. When the consensus transactions in a single round increase to a certain extent, the system throughput increment slows down, such as the phase from τ=30 to τ=40 in Fig. 3. Under the four attack scenarios, Byzantine attack BA3 has the weakest impact on system throughput, with a maximum average throughput of 243TPS, which is because the attack mode of Byzantine nodes without any response increases the proportion of non-Byzantine nodes, reducing the consensus time to some extent. On the contrary, Byzantine attack BA4 has the strongest effect on system throughput, with a maximum average throughput of 232TPS.

(2) The consensus round time r is limited

Consensus round time r is limited, so setting r to a reasonable value affects consensus time and throughput. According to the delay test results, r is set to 500 ms, the proportion of Byzantine nodes a=33%, the interval for consortium chain to construct transactions Δ=1 ms, and the number of consensus transactions in a single round τ=10,20,30,40. The throughput test is conducted under the four classical Byzantine node attack behaviors BA1 to BA4 limited in this paper, of which the results are shown in Fig. 4.

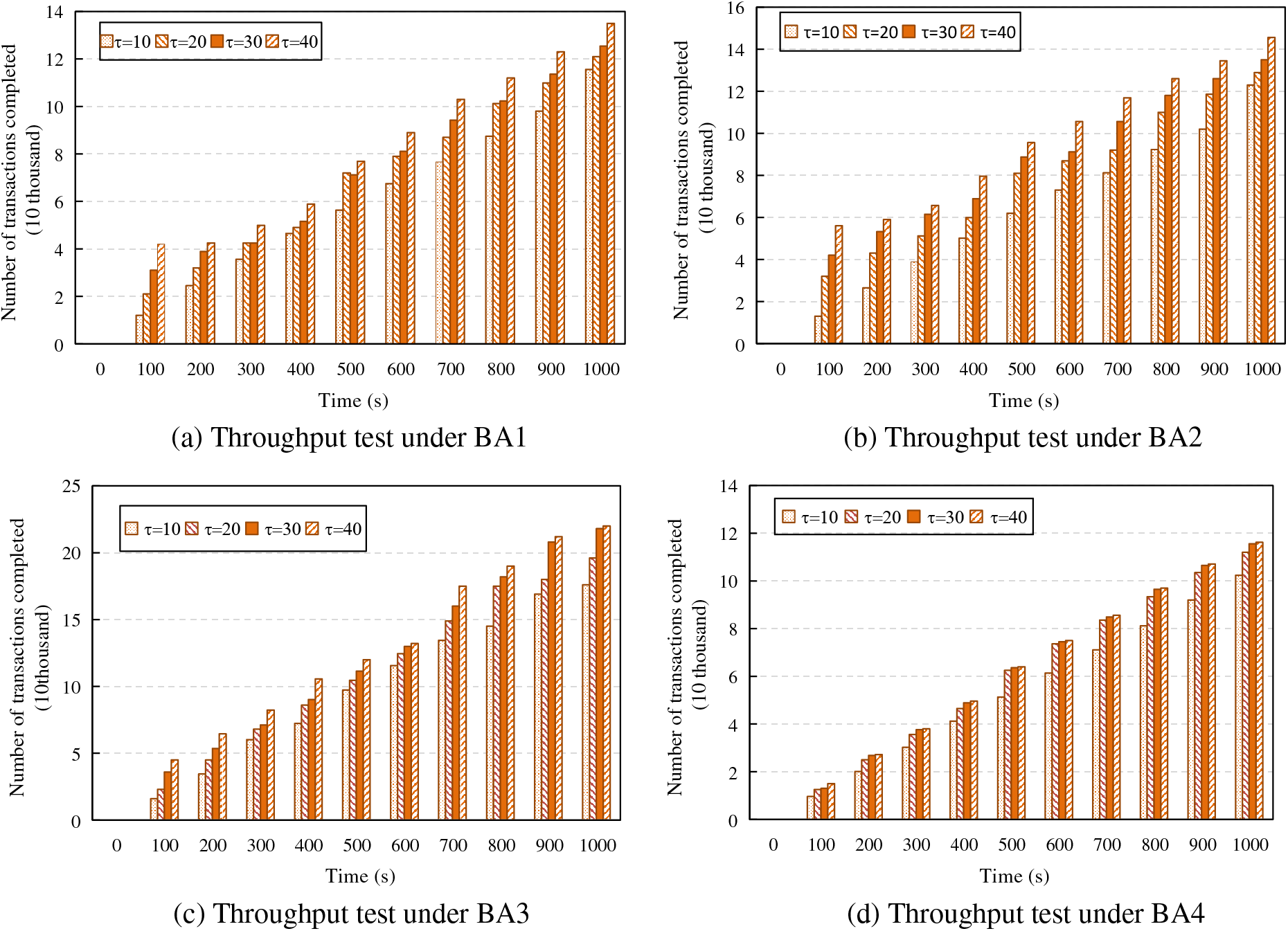
Figure 4: Throughput test under restricted conditions

Compared with the throughput test under unrestricted conditions, the system throughput decreases under the four attack modes when the consensus round time is set to 500 ms in Fig. 4. Under the same conditions, the average value of the highest throughput decreases by 9.2%, and the average value of the lowest throughput decreases by about 50%. In Fig. 4c, under attack BA3, system throughput declines slightly because Byzantine nodes do not respond to anything, which increases the influence of non-Byzantine nodes to some extent and thus weakens the influence of the reduction of consensus round time on consensus efficiency. In Figs. 4a and 4d, under attacks BA1 and BA4, the system throughput decreases greatly because the influence of Byzantine nodes reduces the consensus efficiency, failing part of the consensus to be completed within a consensus round time, especially when the number of consensus transactions in a single round is large. In addition, under attack BA4, after Byzantine nodes form a consortium, they cannot control the speed or order of messages from non-Byzantine nodes. However, they can observe and decide the time to send messages according to the time when non-Byzantine nodes receive or forward messages. Thus, they can significantly hinder the consensus progress within the round.

7  Conclusion

There is not yet an effective consensus algorithm ensuring safety and liveness in fully asynchronous message-passing systems, and even a single process may cause a consortium chain system to crash. However, the crash failure model is less severe than the Byzantine failure model because if the process commits Byzantine failure, the system cannot reach a consensus. To ensure consensus is reached, a consortium chain generation model based on ANS in the Byzantine environment is established to further analyze the influence of chain structure on its performance, obtaining single chain generation rules to avoid chain forking. On this basis, the influence of network partition, network delay, Byzantine node proportion, and verification node state on the consensus process is further analyzed, and a novel consortium chain generation mechanism based on asynchronous binary Byzantine consensus is proposed. The mechanism neither uses a classical (strong) coordinator nor relies on randomization or signatures, meaning it does not wait for a specific message. The above mechanism shows better consensus efficiency under the four classical Byzantine aggression behaviors and asynchronous environment. In the future, based on the study of the asynchronous binary Byzantine consensus mechanism, the relationship between the effectiveness of multiple Byzantine consensus mechanisms and the behavior of nodes in the chain generation process will be studied to meet the needs of more practical application scenarios.

Acknowledgement: The authors gratefully acknowledge the helpful comments and suggestions of the reviewers, which have improved the presentation.

Funding Statement: This work is supported by Henan University Science and Technology Innovation Talent Support Program (23HASTIT029), the National Natural Science Foundation of China (61902447), Tianjin Natural Science Foundation Key Project (22JCZDJC00600), Research Project of Humanities and Social Sciences in Universities of Henan Province (2024-ZDJH-061), Key Scientific Research Projects of Colleges and Universities in Henan Province (23A520054) and Henan Science and Technology Research Project (232102210124).

Author Contributions: Study conception and design: Rui Qiao; data collection: Shi Dong; analysis and interpretation of results: Rui Qiao, Shi Dong; draft manuscript preparation: Rui Qiao, Shi Dong. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the paper.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Dabbagh, K. Choo, A. Beheshti, M. Tahir and N. S. Safa, “A survey of empirical performance evaluation of permissioned blockchain platforms: Challenges and opportunities,” Computers & Security, vol. 100, no. 1, pp. 1–18, 2021. [Google Scholar]

2. W. Liang, Y. Yang, C. Yang, Y. Hu, S. Xie et al., “PDPChain: A consortium blockchain-based privacy protection scheme for personal data,” IEEE Transactions on Reliability, vol. 8, no. 5, pp. 586–598, 2022. [Google Scholar]

3. L. Vishwakarma and D. Das, “SmartCoin: A novel incentive mechanism for vehicles in intelligent transportation system based on consortium blockchain,” Vehicular Communications, vol. 33, no. 6, pp. 1–11, 2022. [Google Scholar]

4. M. Firdaus, S. Rahmadika and K. Rhee, “Decentralized trusted data sharing management on Internet of Vehicle Edge Computing (IoVEC) networks using consortium blockchain,” Sensors, vol. 21, no. 7, pp. 2410–2421, 2021. [Google Scholar] [PubMed]

5. K. Huang, X. Zhang, Y. Mu, X. Wang, G. Yang et al., “Building redactable consortium blockchain for industrial Internet-of-Things,” IEEE Transactions on Industrial Informatics, vol. 15, no. 6, pp. 3670–3679, 2019. [Google Scholar]

6. P. Li, G. Wang, X. Chen, F. Long and W. Xu, “Gosig: A scalable and high-performance byzantine consensus for consortium blockchains,” in SoCC’20: ACM Symp. on Cloud Computing, New York, NY, USA, pp. 223–237, 2020. [Google Scholar]

7. H. Huang, X. Chen and J. Wang, “Blockchain-based multiple groups data sharing with anonymity and traceability,” Science China Information Sciences, vol. 63, no. 3, pp. 1–13, 2020. [Google Scholar]

8. P. Zheng, Q. Xu, Z. Zheng, Z. Zhou, Y. Yan et al., “Meepo: Sharded consortium blockchain,” in 2021 IEEE 37th Int. Conf. on Data Engineering (ICDE), Chania, Greece, pp. 1847–1852, 2021. [Google Scholar]

9. C. Wang, C. Jiang, J. Wang, S. Shen, S. Guo et al., “Blockchain-aided network resource orchestration in intelligent Internet of Things,” IEEE Internet of Things Journal, vol. 10, no. 7, pp. 6151–6163, 2023. [Google Scholar]

10. S. Aggarwal and N. Kumar, “A consortium blockchain-based energy trading for demand response management in vehicle-to-grid,” IEEE Transactions on Vehicular Technology, vol. 70, no. 9, pp. 9480–9494, 2021. [Google Scholar]

11. T. Meng, Y. Zhao and K. Wolter, “On consortium blockchain consistency: A queueing network model approach,” IEEE Transactions on Parallel and Distributed Systems, vol. 32, no. 6, pp. 1369–1382, 2021. [Google Scholar]

12. F. Xiao, T. Lai, Y. Guan, J. Hong, H. Zhang et al., “Application of blockchain sharding technology in Chinese medicine traceability system,” Computers, Materials & Continua, vol. 76, no. 1, pp. 35–48, 2023. [Google Scholar]

13. J. Grover, “Security of vehicular ad hoc networks using blockchain: A comprehensive review,” Vehicular Communications, vol. 34, no. 1, pp. 100458–100477, 2022. [Google Scholar]

14. Y. Chen, B. Hu, H. Yu, Z. Duan and J. Huang, “A threshold proxy re-encryption scheme for secure IoT data sharing based on blockchain,” Electronics, vol. 10, no. 19, pp. 2359–2377, 2021. [Google Scholar]

15. K. Yu, L. Tan, M. Aloqaily, H. Yang and Y. Jararweh, “Blockchain-enhanced data sharing with traceable and direct revocation in IIoT,” IEEE Transactions on Industrial Informatics, vol. 17, no. 11, pp. 7669–7678, 2021. [Google Scholar]

16. P. Sun, S. Shen, Z. Wu, H. Zhou and X. Gao, “Stimulating trust cooperation in edge services: An evolutionary tripartite game,” Engineering Applications of Artificial Intelligence, vol. 116, no. 11, pp. 1–6, 2022. [Google Scholar]

17. S. Yu, Z. Jie, G. Wu, H. Zhang and S. Shen, “FedNRM: A federal personalized news recommendation model achieving user privacy protection,” Intelligent Automation & Soft Computing, vol. 37, no. 2, pp. 1729–1751, 2023. [Google Scholar]

18. G. Wu, L. Xie, H. Zhang, J. Wang, S. Shen et al., “STSIR: An individual-group game-based model for disclosing virus spread in social Internet of Things,” Journal of Network and Computer Applications, vol. 214, no. 1, pp. 1–7, 2023. [Google Scholar]

19. S. Shen, X. Wu, P. Sun, H. Zhou, Z. Wu et al., “Optimal privacy preservation strategies with signaling Q-learning for edge-computing-based IoT resource grant systems,” Expert Systems with Applications, vol. 225, no. 1, pp. 1–6, 2023. [Google Scholar]

20. R. Garcia, G. Ramachandran, R. Jurdak and J. Ueyama, “Blockchain-aided and privacy-preserving data governance in multi-stakeholder applications,” IEEE Transactions on Network and Service Management, vol. 19, no. 4, pp. 3781–3793, 2022. [Google Scholar]

21. Y. Ren, Y. Leng, J. Qi, P. Sharma, J. Wang et al., “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Generation Computer Systems, vol. 115, no. 1, pp. 304–313, 2021. [Google Scholar]

22. T. Cai, H. Lin, W. Chen, Z. Zheng and Y. Yu, “Efficient blockchain empowered data sharing incentive scheme for Internet of Things,” Journal of Software, vol. 32, no. 4, pp. 953–972, 2021. [Google Scholar]

23. Z. Liu and Z. Li, “A blockchain-based framework of cross-border e-commerce supply chain,” International Journal of Information Management, vol. 52, no. 6, pp. 1–9, 2020. [Google Scholar]

24. C. Cachin, “Architecture of the hyperledger blockchain fabric,” in Workshop on Distributed Cryptocurrencies and Consensus Ledgers, Chicago, USA, pp. 1–4, 2016. [Google Scholar]

25. H. Sukhwani, N. Wang, K. Trivedi and A. Rindos, “Performance modeling of hyperledger fabric (permissioned blockchain network),” in 2018 IEEE 17th Int. Symp. on Network Computing and Applications (NCA), Cambridge, MA, USA, pp. 1–8, 2018. [Google Scholar]

26. D. Agrawal, S. Minocha and S. Namasudra, “A robust drug recall supply chain management system using hyperledger blockchain ecosystem,” Computers in Biology and Medicine, vol. 140, no. 1, pp. 1–15, 2022. [Google Scholar]

27. N. Sammeta and L. Parthiban, “Hyperledger blockchain enabled secure medical record management with deep learning-based diagnosis model,” Complex & Intelligent Systems, vol. 8, no. 1, pp. 625–640, 2022. [Google Scholar]

28. J. Minango, M. Zambrano and W. Parada, “Proof of concepts of corda blockchain technology applied on the supply chain area,” in Trends in Artificial Intelligence and Computer Engineering, Riobamba, Ecuador, pp. 619–631, 2023. [Google Scholar]

29. S. Panda, S. Daliyet and S. Lokre, “Distributed ledger technology in the construction industry using corda,” The New Advanced Society: Artificial Intelligence and Industrial Internet of Things Paradigm, vol. 1, no. 1, pp. 15–41, 2022. [Google Scholar]

30. M. Mazzoni, A. Corradi and V. Di Nicola, “Performance evaluation of permissioned blockchains for financial applications: The consensys quorum case study,” Blockchain: Research and Applications, vol. 3, no. 1, pp. 1–12, 2022. [Google Scholar]

31. T. Kuo and A. Pham, “Quorum-based model learning on a blockchain hierarchical clinical research network using smart contracts,” International Journal of Medical Informatics, vol. 169, no. 1, pp. 1–9, 2023. [Google Scholar]

32. S. Saad and R. Radzi, “Comparative review of the blockchain consensus algorithm between Proof of Stake (PoS) and Delegated Proof of Stake (DPoS),” International Journal of Innovative Computing, vol. 10, no. 2, pp. 1–6, 2020. [Google Scholar]

33. C. Akcora, Y. Gel and M. Kantarcioglu, “Blockchain networks: Data structures of Bitcoin, Monero, Zcash, Ethereum, Ripple, and Iota,” Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, vol. 12, no. 1, pp. 1–35, 2022. [Google Scholar]

34. A. Kiayias, A. Russell, B. David and R. Oliynykov, “Ouroboros: A provably secure proof-of-stake blockchain protocol,” in Advances in Cryptology-CRYPTO 2017, Cham, Switzerland: Springer, pp. 357–388, 2017. [Google Scholar]

35. H. Sukhwani, J. M. Martínez, X. Chang, K. S. Trivedi and A. Rindos, “Performance modeling of PBFT consensus process for permissioned blockchain network (Hyperledger Fabric),” in 2017 IEEE 36th Symp. on Reliable Distributed Systems (SRDS), Hong Kong, China, pp. 253–255, 2017. [Google Scholar]

36. M. Conti, A. Gangwal and M. Todero, “Blockchain trilemma solver algorand has dilemma over undecidable messages,” in Proc. of the 14th Int. Conf. on Availability, Reliability and Security, Canterbury, UK, pp. 1–8, 2019. [Google Scholar]

37. M. Yin, D. Malkhi, M. K. Reiter, G. G. Gueta and I. Abraham, “Hotstuff: BFT consensus with linearity and responsiveness,” in Proc. of the 2019 ACM Symp. on Principles of Distributed Computing (PODC ‘19), New York, NY, USA, pp. 347–356, 2019. [Google Scholar]

38. J. Sun, H. Xiong, S. Zhang, X. Liu, J. Yuan et al., “A secure flexible and tampering-resistant data sharing system for vehicular social networks,” IEEE Transactions on Vehicular Technology, vol. 69, no. 11, pp. 12938–12950, 2020. [Google Scholar]

39. Z. Su, Y. Wang, Q. Xu, M. Fei, Y. Tian et al., “A secure charging scheme for electric vehicles with smart communities in energy blockchain,” IEEE Internet of Things Journal, vol. 6, no. 3, pp. 4601–4613, 2018. [Google Scholar]

40. Q. Yang and H. Wang, “Privacy-preserving transactive energy management for IoT-aided smart homes via blockchain,” IEEE Internet of Things Journal, vol. 8, no. 14, pp. 11463–11475, 2021. [Google Scholar]

41. H. Abishu, A. Seid, Y. Yacob, T. Ayall, G. Sun et al., “Consensus mechanism for blockchain-enabled vehicle-to-vehicle energy trading in the Internet of Electric Vehicles,” IEEE Transactions on Vehicular Technology, vol. 71, no. 1, pp. 946–960, 2021. [Google Scholar]

42. Y. Zhang, “Distributed energy intelligent transaction model and credit risk management based on energy blockchain,” Journal of Information Science & Engineering, vol. 37, no. 1, pp. 55–66, 2021. [Google Scholar]

43. V. Allombert, M. Bourgoin and J. Tesson, “Introduction to the tezos blockchain,” in 2019 Int. Conf. on High Performance Computing & Simulation (HPCS), Dublin, Ireland, pp. 1–10, 2019. [Google Scholar]

44. M. Allouche, T. Frikha and M. Mitrea, “Lightweight blockchain processing case study: Scanned document tracking on tezos blockchain,” Applied Sciences, vol. 11, no. 15, pp. 1–17, 2021. [Google Scholar]

45. I. Qasse, M. Talib and Q. Nasir, “Toward inter-blockchain communication between hyperledger fabric platforms,” Trust Models for Next-Generation Blockchain Ecosystems, vol. 4, no. 1, pp. 251–272, 2021. [Google Scholar]

46. S. Gupta, J. Hellings, S. Rahnama and M. Sadoghi, “An in-depth look of BFT consensus in blockchain: Challenges and opportunities,” in Proc. of the 20th Int. Middleware Conf. Tutorials, New York, NY, USA, pp. 6–10, 2019. [Google Scholar]

47. R. Saltini, “BigFooT: A robust optimal-latency BFT blockchain consensus protocol with dynamic validator membership,” Computer Networks, vol. 204, no. 1, pp. 1–33, 2022. [Google Scholar]

48. Y. Li, L. Qiao and Z. Lv, “An optimized Byzantine fault tolerance algorithm for consortium blockchain,” Peer-to-Peer Networking and Applications, vol. 14, no. 1, pp. 2826–2839, 2021. [Google Scholar]

49. K. Sit, M. Bravo and Z. István, “An experimental framework for improving the performance of BFT consensus for future permissioned blockchains,” in Proc. of the 15th ACM Int. Conf. on Distributed and Event-Based Systems, Virtual Event, Italy, pp. 55–65, 2021. [Google Scholar]

50. R. Anu and S. Prakash, “A privacy-preserving authentic healthcare monitoring system using blockchain,” International Journal of Software Science and Computational Intelligence, vol. 14, no. 1, pp. 1–23, 2022. [Google Scholar]

51. C. Esposito, M. Ficco and B. Gupta, “Blockchain-based authentication and authorization for smart city applications,” Information Processing & Management, vol. 58, no. 2, pp. 1–16, 2021. [Google Scholar]

52. A. Mostéfaoui, H. Moumen and M. Raynal, “Signature-free asynchronous Byzantine consensus with t < n/3 and O(n2) messages,” in Proc. of the 2014 ACM Symp. on Principles of Distributed Computing, Paris, France, pp. 2–9, 2014. [Google Scholar]

53. R. Qiao, X. Luo, S. Zhu, X. Yan and Q. Wang, “Dynamic autonomous cross consortium chain mechanism in e-healthcare,” IEEE Journal of Biomedical and Health Informatics, vol. 24, no. 8, pp. 2157–2168, 2020. [Google Scholar] [PubMed]