Digital Image Encryption Algorithm Based on Double Chaotic Map and LSTM

1  Introduction

While the arrival of the information age brings convenience to people, it also brings about the problem of information security. How to protect personal information security in a wide range of information exchanges has become the focus of research in digital society [1]. Because of their intuitiveness and convenience, digital images and video became the main element of data transmission in the network. The information of digital images is figurative and vivid and becomes an important means for people to describe information. Security protection is of representative significance. It contains many data, and their correlation is very high [2]. In most image encryption (IM) research, the ciphertext is used at the transmission end and the receiver end, and then decrypted by the secret key. The encryption system directly uses text encryption technology which results in poor encryption and decryption (ED) quality [3]. With the constant exploration of chaos theory, IM schemes based on chaos are gradually applied. Nonlinear dynamic learning pass is the essence of chaos which has the pseudo-random characteristics of motion trajectory. Chaotic encryption technology has the advantages of high encryption efficiency and strong security [4]. The kernel of chaotic IM is a chaotic signal, which is mainly generated by two chaotic systems. The first is a low-dimensional chaotic system. The system is clear in structure, fast in operation and easy to implement by hardware. But the system is easy to degenerate and the secret key space is small. The second is the high-dimensional chaotic system, which has more complex comfort and more parameters [5]. The authors introduce a new image encryption algorithm that utilizes n-dimensional conservative chaos and is based on the generalized Hamiltonian system. This algorithm demonstrates excellent chaotic characteristics, including wide ergodicity, no attractors, and resistance to reconstruction attacks. It incorporates dynamic scrambling and diffusion techniques, which are controlled by external and internal key streams, ensuring a strong relationship between the ciphertext and the plaintext. Experimental simulations and performance analysis confirm the algorithm’s improved security and suitability for real-time communication [6]. For this reason, the chaotic signal of PRS is obtained by using DCM. The LSTM network is optimized by the IPSO algorithm. Then the chaotic signal is reconstructed. Finally, the chaotic signal is encrypted. A DIE algorithm based on dual chaotic mapping and LSTM is constructed.

The main contribution of the paper is discussed as follows:

This paper proposes a digital image encryption (DIE) algorithm that uses deep learning neural networks and chaotic mapping to encrypt image data securely. The algorithm generates chaotic signals using dual logistic maps and predicts them using long and short-term memory networks. An improved particle swarm optimization (IPSO) algorithm is introduced to optimize the LSTM network. The chaotic signals are then used to get highly secure encrypted images. The combination of deep learning, chaotic mapping, and IPSO delivers a robust solution for image encryption, enhancing security and privacy.

The remainder of the paper is structured as follows: the related work of the proposed model is discussed in Section 2; then Section 3 discusses the design of the DIE algorithm based on DCM and LSTM, and the performance analysis of the DIE algorithm based on DCM and LSTM is represented in Section 4; finally, an overall summary of the proposed model is discussed in Section 5.

2  Related Works

Complex dynamic behaviour and initial value sensitivity of chaotic systems emerge with the development of chaos theory. It has important applications in encryption technology. Three components of the colour image are scrambled using the Arnold algorithm and determine the number of iterations. Then a double chaotic system was proposed to generate chaotic sequences [7]. Finally, the component image and chaotic sequence were converted into a Deoxyribonucleic Acid (DNA) sequence to realize IM. A double-parameter fractal sort vector (DPFSV) was used to control the iterative node relationship in the spatiotemporal chaotic system, and a new one was constructed to realize the permutation diffusion synchronization encryption [8]. Five control parameters are introduced into the function to solve the problem that a one-dimensional chaotic function would be damaged due to the collapse of orbit to a specific period in cryptography [9]. The function as a counting generator generated a new IM algorithm. A fractional hyperchaos system is used to promote the efficiency and security of the image compression encryption algorithm. Then DNA coding was used to encrypt the generated image [10–14]. In the generation of secure keys for IM, chaotic maps had the problem of over-tuning. To solve this problem, an IM technology based on a non-dominated sorting genetic algorithm and local chaotic search was proposed to adjust the super parameters of a chaotic map [15]. A pseudo-random and complex characteristics joint encryption technology is proposed based on hyperchaos behaviour and DNA coding. To use nonlinear analysis tools to better select keys, the global dynamics of the financial hyperchaos system were studied [16]. To protect multiple digital images in the network and maintain users’ personal privacy information, chaos theory and elliptic curve ElGamal cryptosystem is used to generate cryptographic images and shared keys and encrypt relevant information. An innovative encryption scheme specifically designed for encrypting multiple images. The scheme is based on a 3D cube structure and employs a hyper-chaotic system for efficient scrambling and sequence generation. The algorithm generates a hash value and key point and utilizes the robust ElGamal encryption technique. Through comprehensive analyses and tests, the algorithm demonstrates superior security and efficiency compared to existing systems for the secure transmission of multiple images [17].

LSTM artificial neural network is a time-recursive neural network that can capture long-term dependencies between sequences. LSTM models have advantages in digital image encryption analysis, such as the ability to capture sequential relationships and contextual understanding, handle variable-length inputs, retain important information, train on large datasets, and potentially aid in decryption. However, the effectiveness of these models is dependent on the encryption scheme and dataset implemented. A hybrid feature selection technique consisting of the Pearson correlation coefficient and random forest model. The data memory training was based on deep learning, multi-layer perceptron and LSTM [18]. Transformer’s pre-training language model to generate context embedding of text sequences to detect and eliminate hate speech in online social media. The model was compared with a one-dimensional convolutional neural network (1D-CNN) and LSTM model [19]. To estimate the battery using life (BUL) even in the case of capacity regeneration, A BUL prediction technology is proposed based on LSTM considering multiple measurable data of the battery management system [20]. A data-driven prediction model is proposed for weather prediction based on LSTM by using local information transduction in time series prediction [21]. Bi-LSTM is combined with data sequencing to predict the diameter of the jet grouting column in soft soil in real-time [22]. To achieve accurate short-term solar irradiance prediction, a convolution neural network (CNN) is applied to extract spatial features. Then, LSTM was applied to extract spatial features, combined spatiotemporal correlation, and proposed a new prediction model [23]. To predict the power generation of photovoltaic power plants, put forward two hybrid models, CNN-LSTM and ConvLSTM. This realized the prediction of power generation, provided accurate information for the staff, and facilitated the decision-making of the next work content of the power plant [24]. The Prophet model is used to predict the original load data using linear and nonlinear data, resulting in partial nonlinear residual data. LSTM was used to train it, and then it needs to further improve the prediction accuracy through Back-propagation (BP) neural network training [25]. A new image encryption algorithm is proposed that utilizes the Once Forward Long Short-Term Memory Structure (OF-LSTMS) and the Two-Dimensional Coupled Map Lattice (2DCML) fractional-order chaotic system. The algorithm divides the original image into blocks and employs input and output gates for initialization. It incorporates permutation and diffusion operations to ensure synchronization. By leveraging the 2DCML chaotic system’s enhanced chaotic ergodicity and larger sequence values, the algorithm proves effective for image encryption. Simulation results demonstrate superior security and efficiency compared to existing encryption approaches [26]. A novel approach for encrypting colour images is introduced by leveraging deep learning techniques. The proposed method utilizes a Long Short-Term Memory (LSTM) network to train and predict four-dimensional hyper-chaotic Lorenz signals. The resulting signals are employed to construct a chaotic colour image cryptosystem framework. The intricate nature of this method poses challenges for potential attackers, and extensive simulations demonstrate its superior security compared to conventional image encryption algorithms [27]. An image encryption algorithm that combines an improved Arnold transform with a chaotic pulse-coupled neural network. It introduces an oscillatory reset voltage to generate a chaotic sequence, which is used to pre-encrypt the image using the Exclusively-OR (XOR) operation. The algorithm then applies an enhanced Arnold transform to further scramble the encrypted image [28]. The algorithm demonstrates superior encryption effectiveness compared to partial encryption methods, shows high sensitivity to both keys and plaintexts, offers a large key space, and effectively defends against differential attacks and noise attacks. A new image encryption technique that combines the beta chaotic map, nonsubsampled contourlet transform, and genetic algorithm is proposed in [29]. It involves decomposing images into subbands, generating a pseudo-random key, and optimizing the genetic algorithm using a multiobjective fitness function. Experimental results demonstrate faster computation and stronger encryption, confirming the effectiveness of the proposed technique. A new colour image encryption algorithm that utilizes a 3D chaotic Hopfield neural network and random row-column permutation. The algorithm generates diffusion and permutation keys, rearranges the image, divides it into subgraphs, and encrypts each part using diffusion keys [30]. Simulations and security analysis show that the encryption scheme performs well and provides robust security. A novel image encryption algorithm that utilizes the Once Forward Long Short-Term Memory Structure (OF-LSTMS) and the Two-Dimensional Coupled Map Lattice (2DCML) fractional-order chaotic system. The algorithm divides the original image into blocks, applies input and output gates, and synchronizes permutation and diffusion operations. The 2DCML chaotic system is chosen for its superior chaotic properties and larger sequence values, making it well-suited for image encryption. Simulation results demonstrate that the proposed algorithm outperforms previous schemes in terms of both security and efficiency [31].

3  Design of DIE Algorithm Based on DCM and LSTM

3.1 Random Sequence Generation Based on DCM

Chaotic systems are highly sensitive to initial values because of their definition and characteristics. The encryption system based on that is constructed under its characteristics. According to the modern cryptosystem, the ED is achieved through the transformation operation of the key. For encryption systems, the security and reliability are mainly determined by the quality of key generation. If the PRS obtained from the key generation stream has very good randomness, the overall security of the system will be higher. The long-term behaviour of the chaotic system is completely random and has inherent randomness. Common one-dimensional chaotic systems include Logistic maps and Chebyshev maps. Logic mapping is defined as follows formula (1):

xk+1=μxk(1−xk),xk∈(0,1)(1)

In formula (1), when the parameter μ meets the condition 3<μ≤4, a chaotic sequence will be obtained. This paper studies the ED of digital images using the chaotic system, which makes the encryption process and image compression process independent of each other. The overall functional diagram of the dual chaotic IM system is shown in Fig. 1.

Figure 1: Overall functional structure of dual-chaos DIE system

For encryption systems, the quality of key generation determines the security and reliability. To improve that of the system, IM based on the PRS number obtained from the Logistic chaotic map is studied. The probability distribution function of the PRS generated by the Logistic map is shown in formula (2).

ρ(x)={1π1−x2,x∈(0,1)0,x∉(0,1)(2)

According to the probability distribution function obtained from formula (2), the mean value of chaotic PRS is obtained as shown in formula (3).

x¯=limN→∞⁡∑l=0N−1xlN=∫01xρ(x)dx=0(3)

After obtaining the mean value of the PRS, the correlation degree needs to be calculated, and the correlation function is shown in formula (4).

c(l)=limN→∞⁡∑l=0N−1(xl−x¯)(yl−y¯)N=∫01∫01ρ(x,y)(x−x¯)(τ(l)(y)−y¯)(4)

The joint probability distribution function is shown in formula (5).

ρ(x,y)=ρ(x)ρ(y)(5)

From the above formulas, the PRS and white noise produced by the chaotic system have relatively similar statistical characteristics. The settlement result of the sequence mean value and correlation function is 0, with high randomness. Two Logistic maps (L1 and L2) are set in the specific random sequence generation module to create PRS. Its function is shown in Fig. 2.

Figure 2: Diagram of random sequence generation module

First, a random sequence X1 is calculated by L1. Then the elements in the sequence are calculated as L2 parameters. A floating-point number in the interval (0,1) is randomly selected as the initial value of the L2 calculation. A random sequence X2 is obtained again. The random sequence obtained through integration is shown in formula (6).

X=(x1×x1′+min(logx1,logx′)2,…,xM×N+min(logxM×N,logxM×N′)2)(6)

In formula (6), M and N are the pixel width and pixel height of the digital image, respectively. xM×N is one of the elements in sequence X1. In the calculation process, the parameter μ1 value of L1 is set to 3.99 to ensure that it completely enters the chaotic state. The parameters of deep learning are sensitive. As the key of the encryption algorithm, it can increase the difficulty of exhaustive attacks. Through the above operations, four random sequences are generated based on the dual logistic chaotic map.

3.2 LSTM New Chaotic Signal Generation and DIE and Decryption

To improve security, a new chaotic signal is generated based on the random sequence of the chaotic system using the LSTM artificial neural network. LSTM is an event-recursive neural network (RNN). However, in practical applications, RNN is easily affected by gradient disappearance or gradient explosion. It is difficult to capture the long-term dependence between sequences, making training more difficult. LSTM can solve this problem well. The LSTM training model is shown in Fig. 3.

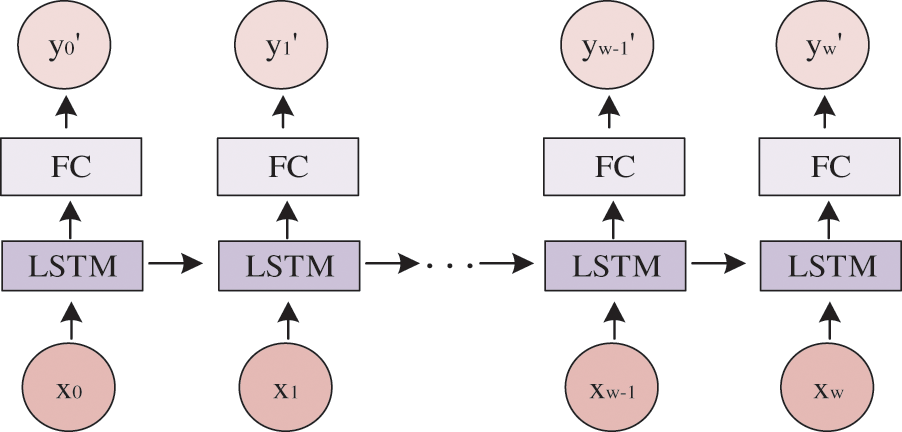
Figure 3: Schematic diagram of LSTM training model

The key generated by the chaotic system is shown in formula (7).

K={x0,y0,z0,w0,r1,r2}(7)

In formula (7), {x0,y0,z0,w0} is the initial state value. r1 and r2 are integer random values with a value range of [0,255]. Taking the value in K as the initial value of the chaotic system, four pseudorandom sequences are obtained. The PRS is intercepted from a part of the sequence with a fixed length, and the LSTM network is used for deep learning to obtain the predicted new sequence. It judges whether the obtained sequence is chaotic, and if so, continues to the next step. The sequence is generated into a matrix with formula (8).

{X(k,l)={floor[(|x(k−1)×N+l+y(k−1)×N+1′|mod1)×1013]modMN}+1Y(k,l)={floor[(|y(k−1)×N+l′|mod1)×1013]}+mod256Z(k,l)={floor[(|z(k−1)×N+l|mod1)×1013]modM}+1W(k,l)={floor[(|w(k−1)×N+l|mod1)×1013]modM}+1(8)

In formula (8), the range of k value is k=1,2,…, M. The range of the l value is l=1,2,…, N. Floor(t) returns the largest integer less than or equal to t. mod1 is used to take the fractional part of the sequence. A new random signal based on LSTM is obtained. The IM of the dual-chaos DIE system studied contains three stages: scrambling, diffusion and confusion. The principle of LCM is shown in Fig. 4.

Figure 4: Schematic diagram of LCM principle

After the pseudo-random matrix is obtained, the diffusion method is used to change the plaintext image into matrix A. The conversion function is shown in formula (9).

A(i,j)=[P(i,j)⊕Y(i,j)⊕r1]mod256(9)

In formula (9), P(i,j) is the clear text image. A(i,j) is the transformed chaotic matrix. j=j+1 converts P(i,j) to A(i,j), as shown in formula (10).

A(i,j)=[P(i,j)⊕∑i=1NA(i,j−1)⊕Y(i,j)]mod256(10)

If j<N, continue to use formula (9) for conversion. If it is greater than or equal to N, set j=1,i=i+1. After meeting the above requirements, if i≤M, formula (11) is used to obtain a new matrix.

A(i,j)=[P(i,j)⊕∑i=1NA(i−1,j)⊕Y(i,j)]mod256(11)

When i,j reaches the maximum value, the diffusion ends. After diffusion, a scrambling algorithm is used to scramble image A into image B. For a pixel coordinate given in image A, the new coordinate value is obtained according to formula (12).

{m=[∑l=1NA(Z(i,j),l)×1013modM]+1n=[∑k=1MA(k,W(i,j))×1013modN]+1(12)

In formula (12), if m=i or Z(i,j), or n=j or W(i,j), A(i,j) and A(m,n) positions are interchanged. When the coordinates traverse the pixels used in the image in the scanning order from left to right and from top to bottom, repeat the operation of (12) to convert image A into image A′. After obtaining the new image, it uses formula (13) for processing.

A′=reshape(A,1, MN)(13)

In formula (13), reshap() converts the image into an MN-dimensional row vector. Similarly, the pseudo-random matrix X is converted into an MN-dimensional row vector. After conversion, only one duplicate element in the X is retained. The elements in the set that do not appear in X are arranged behind the matrix in order from small to large. Then image A′ is scrambled, as shown in formula (14).

{A′(Xi)=A′(XMN−i+1)i=1,2,…,floor(MN2)(14)

It converts image A′ to image B, as shown in formula (15).

B=reshape(A′, M, N)(15)

Then the last pixel of the image is spread forward, and image B is changed into matrix C under the aid of pseudo-random matrix Y. The matrix C is the obtained ciphertext image. First, the ciphertext image C, 4 pseudorandom matrices and 2 pseudorandom numbers are input, and then the diffusion algorithm, scrambling algorithm and obfuscation algorithm is inversely operated to obtain the plaintext image P. Through the above operations, the sequence is input into LSTM for deep learning, and the predicted new sequence and the sequence generation matrix are obtained. Then it is to encrypt and decrypt the digital image.

3.3 Optimization Strategy of DIE Algorithm

Scrambling the pixel image is realized by adjusting the memory position of pixel points after sorting the scrambling random sequences. Sorting is required during scrambling. The main reason is that the probability density function (PDF) of the LCM is not uniform, and the sequence number cannot be mapped to the interval with equal probability. To improve the efficiency of the dual-chaos DIE scheme in image pixel scrambling, the number of scrambling sequences obtained by LCM is studied to be homogenized. The PDF corresponding to the random variable satisfies formula (16).

∫ixf(t)dt=∫kyg(t)dt(16)

In formula (16), f(x) and g(y) are PDFs corresponding to two random variables, which are integrable on the interval (i,j) and (k,l), respectively. According to the basic meaning of PDF, any random variable in the interval can be obtained. There is only one element in (k,l), which makes the probability of two random variables equal. To obtain a monotonic function with a value range of (c,d) and a defined range of (i,j), as shown in formula (17).

y=f(x)(17)

If the random variable y satisfies the condition of the uniform distribution on the interval (0,1), formula (18) is obtained.

y=∫ixf(t)dt(18)

After formula (18) is obtained, its corresponding random variable distribution is mapped, so that the random variable is converted into a uniformly distributed random variable in the (0,1) interval. According to the probability distribution function of the PRS generated by Logistic, formula (19) is obtained.

y=∫0x1π(1−t2)dt=2πarcsin(x2)(19)

Because random variables satisfy the condition of uniform distribution in the interval, the pseudo-random sequence number is converted into a sequence number vector with uniform distribution in the interval through monotone function calculation. Then, in the subsequent scrambling, the original scrambling pseudorandom number sequence is homogenized according to formula (19) to obtain the random sequence number. Then perform amplification processing is shown in formula (20).

Yi=int(N×M×yi)+1(20)

Then a vector is got, in which the elements satisfy the relevant conditions. It can be directly used for digital image pixel scrambling. In this way, it is no longer necessary to sort the original PRS, thus improving the efficiency of the encryption. When LSTM is used to process the PRS obtained from the chaotic system, a series of super parameters such as learning rate and batch size in the model need to be set first. However, it is impossible to explore the optimal parameter collocation of the model only through manual debugging. For this reason, the IPSO algorithm is selected to optimize it. Particle Swarm Optimization (PSO) is often preferred over Genetic Algorithm (GA) for digital image encryption algorithms due to its faster convergence, simpler structure, and suitability for continuous search spaces. To avoid local optima, techniques such as increasing the population size, random initialization, reducing inertia weight, modifying neighbourhood topology, and employing hybrid approaches can be employed. These techniques help enhance exploration and prevent PSOs from getting stuck in suboptimal solutions. Overall, PSO offers advantages for digital image encryption algorithms and can be optimized to avoid local optima. It also has several advantages in image encryption such as enabling key generation, designing optimal S-Boxes, aiding in cryptanalysis, optimizing encryption parameters, and improving efficiency and speed. However, thorough evaluation and analysis are necessary to ensure the effectiveness and robustness of using PSO in encryption algorithms. The principle of the traditional PSO algorithm is shown in Fig. 5.

Figure 5: PSO algorithm principle

The IPSO algorithm improves the inertia weight of the PSO algorithm. The parameter that controls the influence of the previous speed on the current speed is inertia weight. Its size indicates that it inherits the speed of its parent particle. The improvement is shown in formula (21).

w=w(wminmax∗tan(ttmaxπ4()))max(21)

In formula (21), w means the inertia weight parameter. t represents the number of iterations. The inertia coefficient determines the search step size, and can flexibly adjust search capabilities. The particles jump out of the previous search to ensure the PSO algorithm expands and reduces the population search in iterative, and then a broader search is conducted. This can keep the diverse population. The particle speed update method is shown in formula (22).

vi(t+1)=w(t)∗Vi(t)+c1∗rand∗(Pi(t)−Xi(t))+c2∗rand∗(Pg(t)−Xi(t))(22)

In formula (22), X is a particle; pg is the global best position; V is the velocity of particles; c1 and c2 are acceleration constants with positive values; a rand is a random number between 0 and 1. The particle update is as shown in formula (23).

Xi(t+1)=Xi(t)+Vi(t+1)(23)

Based on the above operations, the scrambling algorithm of the random sequence is improved and the parameters of the LSTM training process are optimized. Thus, the design of the DIE algorithm based on DCM and LSTM is completed. The whole structure of the algorithm is expressed in Fig. 6.

Figure 6: Overall framework of digital encryption algorithm

4  Performance Analysis of the DIE Algorithm Based on DCM and LSTM

In this research, the main objective is to reconstruct a chaotic signal using the obtained PRS (Preserved Residual Signal). To achieve this, an LSTM (Long Short-Term Memory) deep learning network is selected for the signal reconstruction. The IPSO (Improved Particle Swarm Optimization) algorithm is utilized to improve and optimize the LSTM model. The LSTM and the improved IPSO-LSTM models are trained in the same environment to test the effectiveness of the optimization. By integrating IPSO into the LSTM training process, the goal is to enhance the LSTM network’s performance in reconstructing the chaotic signal. The comparative analysis between the LSTM and IPSO-LSTM models helps evaluate the impact of incorporating the IPSO algorithm. The specific training situation is shown in Fig. 7.

Figure 7: Comparison of iterations before and after LSTM improvement

In Fig. 7, with the increase of the iterations, the RMSE and Loss values of the two models showed a downward trend. The improved IPSO-LSTM reached the target RMSE value after 69 iterations. LSTM had iterated 136 times, 67 times more than IPSO-LSTM. IPSO-LSTM reached the target value of Loss when it iterated 81 times. LSTM needed 202 iterations, 121 more than IPSO-LSTM. According to the analysis in Fig. 7, the improved IPSO-LSTM model has better convergence and can achieve training objectives with fewer iterations.

To improve DIE’s security, a new chaotic signal was built with LSTM imitating chaotic characteristics. The significance of improving the security of the Digital Identity Ecosystem (DIE) using Differential Chaos Modulation (DCM) and Long Short-Term Memory (LSTM) lies in multiple factors. Firstly, it protects against evolving cyber threats, ensuring the integrity of the ecosystem. Secondly, it safeguards individuals’ privacy by implementing robust security measures. Thirdly, it effectively combats identity fraud and unauthorized access attempts within the DIE. Additionally, enhancing security fosters trust among users and facilitates wider adoption of the system. Lastly, compliance with regulations is ensured, providing legal protection and demonstrating a commitment to privacy and security. Overall, integrating DCM and LSTM into DIE’s security framework strengthens its reliability and establishes a secure digital environment. To test the rationality of the chaotic signal constructed by the improved LSTM, the chaotic mapping of four images was studied, and the two types of chaotic signals were compared and analyzed, as shown in Fig. 8.

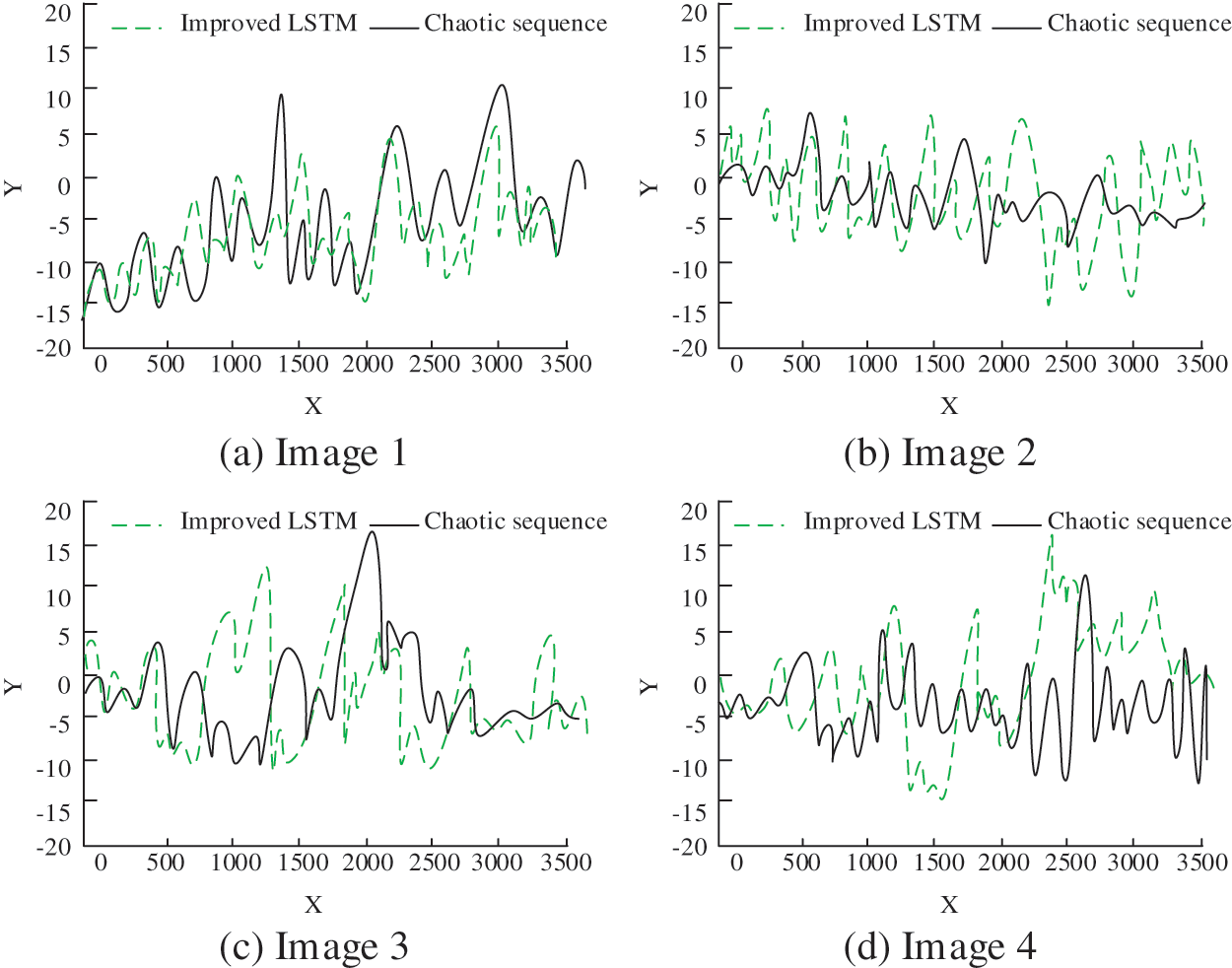
Figure 8: Comparison of chaotic signals of four images before and after using LSTM

In Fig. 8, the new chaotic signal obtained by deep learning did not coincide with the curve obtained by double mapping chaos, and the difference was large. The chaotic signals generated by the two were different, and the new signal curve obtained by improved LSTM prediction was more complex. According to the contents of Fig. 8, the improved LSTM can improve the security of DIE.

To test the encryption ability of the DIE designed by the research institute, the histogram method was used to measure and analyze it. The histogram method is important for testing the encryption ability of a DIE designed by a research institute. It allows for statistical analysis and detection of patterns in the encrypted data, helping to evaluate encryption strength and test robustness against different attacks. Additionally, the histogram method enables comparison and benchmarking of different encryption algorithms. However, it should be used in conjunction with other evaluation techniques for a comprehensive assessment of the encryption algorithm’s security and effectiveness. The histogram of digital image was used to describe the distribution of image colours, and could directly reflect the overall proportion of different colors in the image. Histogram can reflect the difference in colour space between two images. A plaintext image is encrypted by this algorithm. The histogram before and after encryption is shown in Fig. 9.

Figure 9: Distribution of image color histogram before and after encryption

In Fig. 9, the histogram of the image before encryption on the R, G and B components of the (Red Blur Green) RGB colour was also completely different from the histogram of the encrypted image. After encryption, the colour distribution in the image became chaotic, and the colour distribution of the original image could not be observed. Comprehensive analysis showed that the algorithm could significantly change the colour space in confusion processing, and effectively promote encryption security.

To deeply test the encryption effect, pixel correlation was introduced as an important factor to measure whether the encryption algorithm was good or not. By calculating the relationship between the R, G, and B colour components of each adjacent pixel of the digital image before and after encryption, the correlation between each pixel was obtained. The correlation distribution of colour components before and after encryption is shown in Fig. 10.

Figure 10: Comparison of image correlation before and after encryption

In Fig. 10, there was a relatively concentrated colour distribution between the adjacent pixels of the clear text image, with an obvious correlation. However, in a ciphertext image, all pixels were evenly distributed and had no centralized correlation characteristics. Its pixel correlation was eliminated after encryption, ensuring that there was no connection between the original and the encrypted image, and the security was high. Eliminating pixel correlation after encryption is important to enhance the security and confidentiality of the encrypted data. It prevents information leakage, protects against cryptanalysis, increases randomness, and improves resistance to image processing operations. By removing pixel correlation, the encrypted data becomes more secure, making it difficult for attackers to extract information or exploit patterns. Overall, eliminating pixel correlation strengthens the encryption scheme and ensures the privacy of the encrypted data.

The key sensitivity is the security analysis when the wrong key is used in the ED. To test the sensitivity to ciphertext and plaintext, it was studied to record the pixel change rate of the decryption and encryption results by changing the different number of pixel’s colour values, as shown in Table 1.

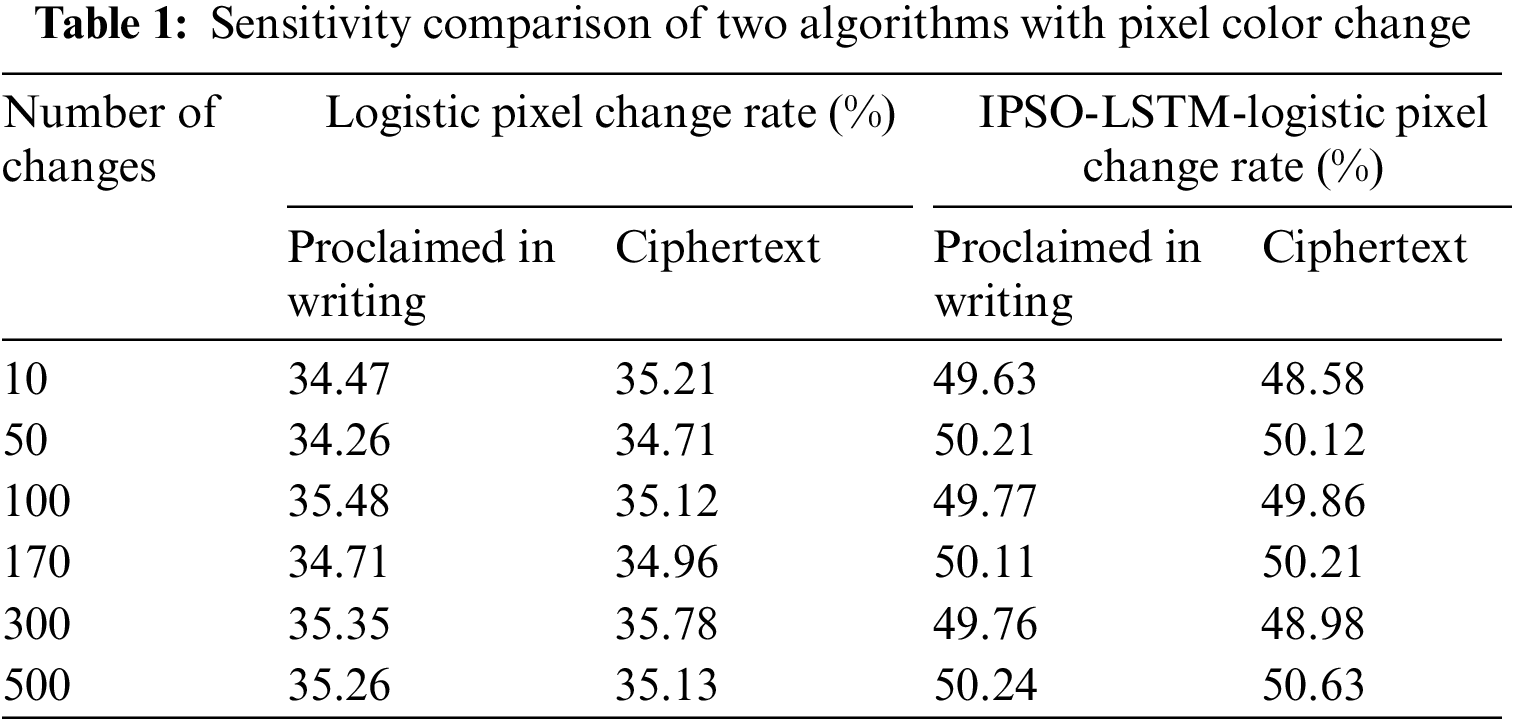
In Table 1 and Fig. 11, there was no relationship between the number of pixel changes and the pixel change rate. The pixel change rate of ED results of the research and design algorithm was about 50%. The avalanche effect would occur after changing the pixel colour values in ciphertext and plaintext. The change rate of the encryption algorithm based on traditional Lostic mapping was about 35%, 15% lower than the research algorithm. From the comprehensive table, the research and design algorithm had high sensitivity.

Figure 11: Sensitivity comparison of two algorithms with pixel color change

The differential attack is a kind of selective plaintext attack. After changing a pixel value and encrypting the image, it is to observe the distinction between the two encrypted ciphertext images and find the cracking algorithm. NPCR and UACI are two important indicators of differential attack. The research used algorithms to encrypt different images. To further verify the anti-attack ability of the algorithm, the experiment introduced the research algorithm (Proposed algorithm) into several encryption algorithms, including one based on a chaotic system and dynamic DNA coding (Chaotic system and dynamic DNA coding algorithm), one based on Latin square (Latin square algorithm), and one based on LCM (LCM algorithm) for comparison. The corresponding evaluation index values are shown in Table 2 and Fig. 12.

Figure 12: Comparative analysis of anti-attack indicators of encryption algorithms

From Table 2 that Proposed algorithm was more resistant to differential attack than the other three algorithms. It can realize DIE with high security and sensitivity, and ensure the security of personal information on the Internet. The NPCR (Normalized Pixel Change Rate) and UACI (Unified Average Changed Intensity) values are metrics used to assess the effectiveness of algorithms in image encryption. In this scenario, a higher NPCR value and a lower UACI value indicate better anti-attack performance. Results analysis of the performance of four different algorithms are discussed as follows:

Proposed algorithm demonstrates strong anti-attack performance with an average NPCR value of 99.56% and a UACI value of 33.46%. These values are very close to the theoretical ideals of 99.604% and 33.4635%, respectively. The algorithm achieves a high level of consistency in pixel changes and effectively disperses the modified intensities, making it difficult for attackers to detect and reverse-engineer the encryption.

Chaotic system and dynamic DNA coding algorithm shows slightly lower performance, with an average NPCR value of 92.50% and a UACI value of 31.385%. Although the NPCR value is lower than in Proposed algorithm, it still suggests a reasonable level of consistency. The UACI value indicates that the algorithm disperses changes, but not as effectively as Proposed algorithm.

In Latin square algorithm, the average NPCR value further decreases to 90.36%, indicating reduced consistency in pixel changes. The UACI value is slightly lower at 30.51%, suggesting a slight improvement in dispersing changes compared to Chaotic system and dynamic DNA coding algorithm, but still falling short of the performance achieved by Proposed algorithm.

LCM algorithm has a similar performance to Latin square algorithm, with an average NPCR value of 90.60% and a UACI value of 30.29%. The NPCR value remains consistent with Latin square algorithm, while the UACI value shows a slightly better dispersion of changes.

5  Conclusion

Digital images contain a lot of data, and the correlation between the data is very high. Therefore, to achieve image information security, DIE is a useful way. The chaotic signal of PRS was got by using DCM. Then the chaotic signal was reconstructed by IPSO-LSTM. Finally, the chaotic signal was encrypted. A DIE algorithm based on dual chaotic mapping and LSTM was constructed. Through experiments, the improved IPSO-LSTM achieved the target RMSE value in 69 iterations, while LSTM iterated 136 times; IPSO-LSTM reached the target value of Loss when it iterated 81 times, and LSTM needed to iterate 202 times. IPSO-LSTM algorithm had excellent convergence. After changing the pixel colour values in ciphertext and plaintext, the pixel change rate of the ED results of the algorithm was about 50%. The algorithm could significantly change the colour space in confusion processing, and encryption security was effectively promoted. The average NPCR value of Proposed algorithm was 99.56%, and the UACI value was 33.46%. Proposed algorithm was more resistant to differential attack than the other three algorithms. The algorithm produced a highly secure and reliable encryption scheme.

Limitations and Future Work:

Due to the inherent limitations of computer accuracy and technology, data obtained may contain information noise points. However, future research can focus on developing noise reduction techniques to address this issue. Additionally, incorporating digital image compression algorithms and image-hiding technology into the encryption algorithm can further enhance both the practicality and security of encrypted images.

Acknowledgement: The authors would like to express their heartfelt gratitude to the techniques that have made valuable contributions to this research.

Funding Statement: No funds or grants were received by any of the authors.

Author Contributions: Luoyin Feng contributed to the design and methodology of this study; Jize Du and Chong Fu contributed for the assessment of the outcomes and the writing of the manuscript.

Availability of Data and Materials: None to declare.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. Wang, X. Wu and T. Gao, “Double colour images compression–encryption via compressive sensing,” Neural Computing and Applications, vol. 33, no. 19, pp. 12755–12776, 2021. [Google Scholar]

2. M. Z. Talhaoui, X. Wang and M. A. Midoun, “A new one-dimensional cosine polynomial chaotic map and its use in image encryption,” The Visual Computer, vol. 37, pp. 541–551, 2021. [Google Scholar]

3. S. E. El-Khamy and A. G. Mohamed, “An efficient DNA-inspired image encryption algorithm based on hyper-chaotic maps and wavelet fusion,” Multimedia Tools and Applications, vol. 80, pp. 23319–23335, 2021. [Google Scholar]

4. A. H. Khaleel and I. Q. Abduljaleel, “A novel technique for speech encryption based on k-means clustering and quantum chaotic map,” Bulletin of Electrical Engineering and Informatics, vol. 10, no. 1, pp. 160–170, 2021. [Google Scholar]

5. J. S. Muthu and P. Murali, “Review of chaos detection techniques performed on chaotic maps and systems in image encryption,” SN Computer Science, vol. 2, pp. 1–24, 2021. [Google Scholar]

6. X. Liu, X. Tong, Z. Wang and M. Zhang, “A new n-dimensional conservative chaos based on generalized Hamiltonian system and its’ applications in image encryption,” Chaos, Solitons & Fractals, vol. 154, pp. 111693, 2022. [Google Scholar]

7. Q. Liu and L. Liu, “Color image encryption algorithm based on DNA coding and double chaos system,” IEEE Access, vol. 8, pp. 83596–83610, 2020. [Google Scholar]

8. Y. Xian, X. Wang, L. Teng, X. Yan, Q. Li et al., “Cryptographic system based on double parameters fractal sorting vector and new spatiotemporal chaotic system,” Information Sciences, vol. 596, pp. 304–320, 2022. [Google Scholar]

9. R. A. Elmanfaloty and E. Abou-Bakr, “An image encryption scheme using a 1D chaotic double section skew tent map,” Complexity, vol. 2020, pp. 1–18, 2020. [Google Scholar]

10. Y. G. Yang, B. W. Guan, Y. H. Zhou and W. M. Shi, “Double image compression-encryption algorithm based on fractional order hyperchaotic system and DNA approach,” Multimedia Tools and Applications, vol. 80, pp. 691–710, 2021. [Google Scholar]

11. S. Gao, R. Wu, X. Wang, J. Liu, Q. Li et al., “Asynchronous updating boolean network encryption algorithm,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 1, pp. 99, 2023. [Google Scholar]

12. S. Gao, R. Wu, X. Wang, J. Wang, Q. Li et al., “A 3D model encryption scheme based on a cascaded chaotic system,” Signal Processing, vol. 202, pp. 108745, 2023. [Google Scholar]

13. S. Gao, R. Wu, X. Wang, J. Liu, Q. Li et al., “EFR-CSTP: Encryption for face recognition based on the chaos and semi-tensor product theory,” Information Sciences, vol. 621, pp. 766–781, 2023. [Google Scholar]

14. R. Wu, S. Gao, X. Wang, S. Liu, Q. Li et al., “AEA-NCS: An audio encryption algorithm based on a nested chaotic system,” Chaos, Solitons & Fractals, vol. 165, pp. 112770, 2022. [Google Scholar]

15. M. Kaur, D. Singh, K. Sun and U. Rawat, “Color image encryption using non-dominated sorting genetic algorithm with local chaotic search based 5D chaotic map,” Future Generation Computer Systems, vol. 107, pp. 333–350, 2020. [Google Scholar]

16. V. F. Signing, R. T. Mogue, J. Kengne, M. Kountchou and Saïdou, “Dynamic phenomena of a financial hyperchaotic system and DNA sequences for image encryption,” Multimedia Tools and Applications, vol. 80, pp. 21–23, 2021. [Google Scholar]

17. A. Sahasrabuddhe and D. S. Laiphrakpam, “Multiple images encryption based on 3D scrambling and hyper-chaotic system,” Information Sciences, vol. 550, pp. 252–267, 2021. [Google Scholar]

18. I. Hidayat, M. Z. Ali and A. Arshad, “Machine learning based intrusion detection system: An experimental comparison,” Journal of Computational and Cognitive Engineering, vol. 1, pp. 22–27, 2022. [Google Scholar]

19. S. Mukherjee and S. Das, “Application of transformer-based language models to detect hate speech in social media,” Journal of Computational and Cognitive Engineering, vol. 1, pp. 10–12, 2022. [Google Scholar]

20. K. Park, Y. Choi, W. J. Choi, H. Y. Ryu and H. Kim, “The LSTM-based battery remains useful for life prediction with multi-channel charging profiles,” IEEE Access, vol. 8, pp. 20786–20798, 2020. [Google Scholar]

21. Z. Karevan and J. A. K. Suykens, “Transductive LSTM for time-series prediction: An application to weather forecasting,” Neural Networks, vol. 125, pp. 1–9, 2020. [Google Scholar] [PubMed]

22. S. L. Shen, P. G. Atangana Njock, A. Zhou and H. M. Lyu, “Dynamic prediction of jet grouted column diameter in the soft soil using Bi-LSTM deep learning,” Acta Geotechnica, vol. 16, no. 1, pp. 303–315, 2021. [Google Scholar]

23. H. Zang, L. Liu, L. Sun, L. Cheng, Z. Wei et al., “Short-term global horizontal irradiance forecasting based on a hybrid CNN-LSTM model with spatiotemporal correlations,” Renewable Energy, vol. 160, pp. 26–41, 2020. [Google Scholar]

24. A. Agga, A. Abbou, M. Labbadi and Y. E. Houm,“Short-term self-consumption PV plant power production forecasts based on hybrid CNN-LSTM, ConvLSTM models,” Renewable Energy, vol. 177, pp. 101–112, 2021. [Google Scholar]

25. B. Tasarruf, H. Y. Chen, F. T. Muhammad and L. Q. Zhu, “Short-term electricity load forecasting using hybrid prophet-LSTM model optimized by BPNN,” Energy Reports, vol. 8, pp. 1678–1686, 2022. [Google Scholar]

26. Y. He, Q. Zhang, X. He and Y. Wang, “A new image encryption algorithm based on the OF-LSTMS and chaotic sequences,” Scientific Reports, vol. 11, no. 1, pp. 6398, 2021. [Google Scholar] [PubMed]

27. S. Zhou, Z. Zhao and X. Wang, “Novel chaotic colour image cryptosystem with deep learning,” Chaos, Solitons & Fractals, vol. 161, pp. 112380, 2022. [Google Scholar]

28. J. Ye, X. Deng, A. Zhang and H. Yu, “A novel image encryption algorithm based on improved Arnold transform and chaotic pulse-coupled neural network,” Entropy, vol. 24, pp. 1103, 2022. [Google Scholar] [PubMed]

29. M. Kaur and V. Kumar, “Beta chaotic map-based image encryption using genetic algorithm,” International Journal of Bifurcation and Chaos, vol. 28, no. 11, pp. 1850132, 2018. [Google Scholar]

30. W. Yao, K. Gao, Z. Zhang, L. Cui and J. Zhang, “An image encryption algorithm based on a 3D chaotic Hopfield neural network and random row–column permutation,” Frontiers in Physics, vol. 11, pp. 1162887, 2023. [Google Scholar]

31. B. Cao, Y. Gu, Z. Lv, S. Yang, J. Zhao et al., “RFID reader anticollision based on distributed parallel particle swarm optimization,” IEEE Internet of Things Journal, vol. 8, pp. 3099–3107, 2021. [Google Scholar]