Linguistic Knowledge Representation in DPoS Consensus Scheme for Blockchain

1  Introduction

The concept of blockchain originated from Bitcoin, which was first proposed in 2008. Blockchain is the core part of electronic money—bitcoin. It works as a public ledger in various Bitcoin systems, which is in charge of recording all the transactions in chronological order [1,2]. From the perspective of the application, blockchain is a distributed database, which shows some features of decentralization, non-tampering, transparency, and traceability [3]. Owing to its capabilities, blockchain can provide a trusted, secure, and efficient environment for different application scenarios [4]. It has shown successful applications in the fields of transport systems [5], industrial IoT (Internet of Things) systems [6,7], medical information-sharing platforms [8–10], and smart cities [11,12].

Blockchain comprises four core technologies, which are the distributed ledger, asymmetric encryption, smart contract, and consensus mechanism, respectively [13]. All of them cooperate for completing the functions of data storage, data security, data application, and data processing. The distributed ledger adopts the design philosophy of decentralization to build a blockchain platform as a distributed network [14]. Persons can freely join the distributed blockchain network and then participate in the recording activities of transactions together. At the same time, people usually cannot achieve consensus when the number of involved persons keeps increasing. The consensus scheme can solve the problem that how to achieve consensus in blockchain under the distributed environment.

The Delegated Proof of Stake (DPoS) [15] was proposed by Daniel Larimer. It is an efficient and democratic alternative for solving the consensus problem. DPoS requires the blockchain nodes to vote and then elect delegates to govern the blockchain network and then propose core changes [16]. How to represent the collective voting information and select delegates is a new open problem. In the traditional DPoS consensus scheme, each blockchain node votes for the nodes in each round of selection [17]. The blockchain nodes having the first n largest number of votes are selected as delegates when n delegates are needed. In this study, the nodes voted for their trusting nodes or abstained, while the “opposition” opinion was not considered. To consider the “opposition” opinion, Xu et al. [18,19] used the vague set that can express “support”, “abstention”, and “opposition” opinions that were given by all the nodes for the voted nodes.

To the best of our knowledge, only the study of Xu et al. [18] focused on how to represent collective voting information on the voted blockchain nodes. However, the study of Xu et al. [18] still had a big challenge in that the intensities of the “support” and “opposition” opinions are not considered. This case may lead to information loss and then decrease the accuracy of knowledge representation. To overcome this challenge, we propose a novel fine-grained knowledge representation method to improve the existing DPoS consensus schemes. Our contributions are listed as follows:

(1) The symmetrical linguistic term set (LTS) is used to provide fine-grained voting options for voting nodes. The symmetrical LTS can explicitly contain different intensities of “support”, and “opposition” opinions. It can better express the subtle attitude of voting nodes.

(2) The concept of proportional hesitant fuzzy linguistic term set (PHFLTS) is used to represent the collective voting information of the voting nodes on the voted nodes. It provides an accurate way to model the collective opinions of the voting nodes.

(3) Based on the cumulative possibility degree and the lottery algorithm, a novel delegate selection algorithm is proposed to rank blockchain nodes and then elect delegates. Two numerical examples are provided to illustrate the implementation process of the proposed delegate selection algorithm.

(4) To validate the superiority of the novel delegate selection algorithm, the simulations are conducted to compare the novel delegate selection algorithm with the existing algorithms. The results show that the novel delegate selection algorithm is better than the existing algorithms.

The remainder of this study is organized as follows: Section 2 briefly reviews the existing studies of consensus schemes for blockchain. The basic knowledge of the linguistic term sets (LTSs) and proportional hesitant fuzzy linguistic term sets (PHFLTSs) are presented in Section 3. Section 4 improves the DPoS consensus scheme based on the LTS and PHFLTS, and then proposes a novel delegate selection algorithm. One numerical example and a series of simulations are conducted to show the performance superiority of the novel delegate selection algorithm in Section 5. In Section 6, some valuable conclusions are given. In the Section 7, limitations and future scope are discussed.

2  Studies about DPOS Consensus Scheme

The DPoS consensus scheme runs like a democratic system, where the blockchain nodes who stake a token have the chance to elect a fixed number of delegates for validating blocks [20–22]. The election of delegates is a continuous process [23]. It starts automatically at set intervals. The elected delegates are always at risk of being replaced by the blockchain nodes who will get more votes in the next round [24]. Due to its excellent features, the DPoS consensus scheme has become the research focus in the blockchain field [25]. The master node has the authority to sort and broadcast transactions, but it may be a selected malicious node. Therefore, the selection of the master node poses a threat to the distributed blockchain system [26].

To decrease the probability of selecting the malicious nodes as the delegates and also prevent the centralization of the blockchain, Liu et al. [27] used the k-means algorithm to select good nodes in the DPoS consensus scheme. Tao et al. [28] introduced the Borda count voting method [29] to elect delegates. To satisfy the performance requirements of blockchain systems, Luo et al. [30] improved the ring-based election algorithm to select delegates. In the traditional DPoS consensus scheme [31,32], the blockchain nodes vote for other blockchain nodes, and the blockchain nodes with more votes are selected as delegates. The traditional DPoS consensus scheme does not consider the influence of negative votes on the delegate selection results. To address this problem, Xu et al. [18] improved the traditional DPoS consensus scheme by using vague sets. The vague sets are employed to accurately express the collective voting information that contains positive votes, neutral votes, and negative votes. Liu et al. [20] further improved the study of Xu et al. [18] by introducing the concept of average fuzziness.

Through the above discussions, it can be seen that few of the existing research studies focus on the knowledge representation of the collective voting information in the DPoS consensus scheme. Although the existing studies [26] used vague sets to express the collective voting information of the blockchain nodes, they still cannot express the fine-grained voting attitudes of positive and negative votes. In this case, the fairness of the delegate election process in the DPoS consensus scheme will be lowered.

Hence, in this paper, the concept of PHFLTS is used to represent the collective voting information of the voting nodes on the voted nodes. A novel delegate selection algorithm is proposed to rank blockchain nodes and then elect delegates, which provides an accurate way to model the collective opinions of the voting nodes. To validate the superiority of the novel delegate selection algorithm, numerical examples are conducted to compare the novel delegate selection algorithm with the existing algorithms. The results show that the novel delegate selection algorithm is better than the existing algorithms.

3  Preliminaries

In this section, some basic information about the LTS and the PHFLTS is briefly reviewed.

3.1 Linguistic Term Sets

The LTS [33–37] is an essential tool, which is used to provide the available linguistic variables for linguistic computational models. It is a set that consists of an odd number of linguistic terms. There are two classes of LTSs, which are categorized into asymmetric LTSs and symmetric LTSs, respectively. The definition of a common LTS is given as follows.

Definition 1 [33]. Let S={sε|ε=−θ,…,−1,0,1,…,θ} denote a symmetric LTS, in which the linguistic terms are ordered according to the ascending order of their subscripts. θ is an even number and θ+1 is the cardinality of the LTS S. s−θ and sθ are the lower bound and upper bound of S.

3.2 Proportional Hesitant Fuzzy Linguistic Term Sets

The definition of PHFLTSs was proposed by Chen et al. [38] to express the collective voting information from a group of voting nodes. It is designed based on LTS and probability distribution information of linguistic terms [39–41]. Its mathematical definition can be described as follows:

Definition 2 [38]. Let S={sε|ε=−θ,…,−1,0,1,…,θ} denote an LTS and P={(sε,pε)|ε=−θ,…,−1,0,1,…,θ} be the probability distribution information of linguistic terms, then a PHFLTS PS={(sε,pε)|ε=−θ,…,−1,0,1,…,θ}, where 0≤pε≤1 and ∑ε=−θθ⁡pε=1.

For each voted node, its received voting information can be modeled as a PHFLTS. To rank nodes and select delegates, the PHFLTSs should be compared.

Chen et al. [38] developed the possibility degree to compare PHFLTSs. The definition of possibility degree is given as follows:

Definition 3 [38]. Let S={sε|ε=−θ,…,−1,0,1,…,θ} represent an LTS, and PS1={(sε1,pε1)|sε1∈S} and PS2={(sε2,pε2)|sε2∈S} be any two PHFLTSs, then the possibility degree between them is defined as:

ρ(PS1≥PS2)=∑ε1∈{−θ,…,−1,0,1,…,θ}⁡∑ε2∈{−θ,…,−1,0,1,…,θ}⁡R(sε1,sε2),(1)

where R(sε1,sε2) is the relation value between sε1 and sε2.

Definition 4 [38]. Let S={sε|ε=−θ,…,−1,0,1,…,θ} represent an LTS, and PS1={(sε1,pε1)|sε1∈S} and PS2={(sε2,pε2)|sε2∈S} be any two PHFLTSs, then the relation value between sε1 and sε2 is defined as:

R(sε1,sε2)={pε1pε2,sε1>sε212pε1pε2,sε1=sε20,sε1<sε2,(2)

where pε1 and pε2 are the probability distribution information of sε1 and sε2, respectively.

Property 1 [38]. Let PS1 and PS2 be any two PHFLTSs, then we have ρ(PS1≥PS2)+ρ(PS1≤PS2)=1. Especially, if PS1=PS2, then we have ρ(PS1≥PS2)=ρ(PS1≤PS2)=0.5.

4  Novel DPoS Consensus Mechanism

In this section, a novel full associative voting architecture of the novel DPoS consensus mechanism is described. After that, the knowledge representation of collective voting information is given, and a novel delegate selection algorithm is presented.

4.1 Knowledge Representation

To ensure the fairness of the delegate selection results in the DPoS consensus mechanism, we propose a novel full associate voting architecture for collecting the voting information of all the blockchain nodes.

In the full associate voting architecture, each blockchain node should choose a linguistic term from the LTS S to vote on each blockchain node in the blockchain network. Thus, each blockchain node will receive the voting information from all the blockchain nodes including itself as shown in Fig. 1.

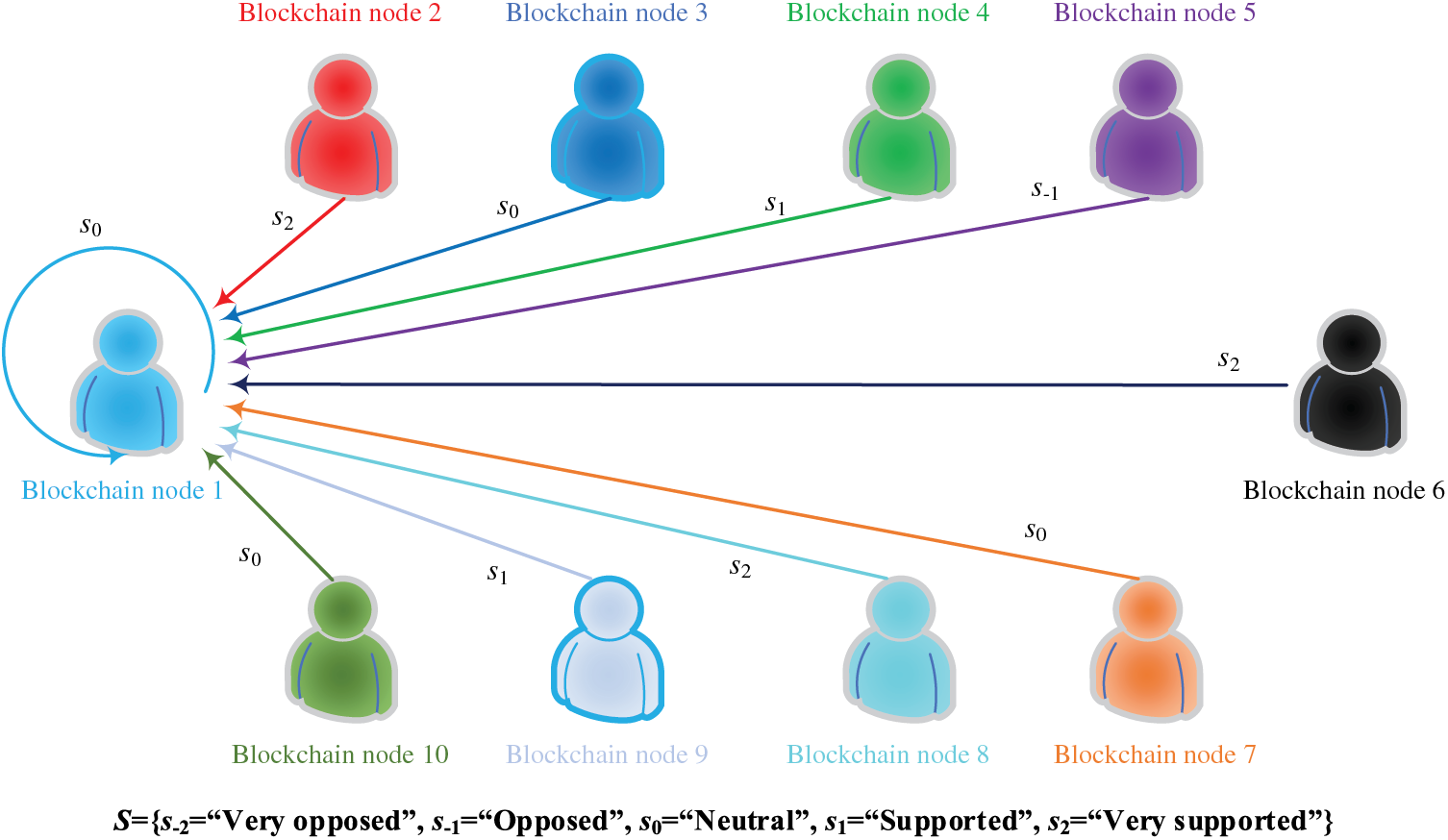
Figure 1: The full associate voting architecture

Here, a symmetric LTS S is used to provide the fine-grained voting options for blockchain nodes as follows : S={s−2=″Veryopposed″,s−1=″Opposed″,s0=″Neutral″,s1=″Supported″,s2=″Verysupported″}.

By using this symmetric LTS, each blockchain node can express its more fine-grained opinion by choosing one linguistic term from this LTS. The linguistic term s0 indicates the neutral attitude of the blockchain nodes. If the blockchain nodes abstain, then the linguistic term s0 is used to express their opinions.

Example 1. For the blockchain node 1 as depicted in Fig. 1, the collective voting information from all the blockchain nodes for the blockchain node 1 can be represented as a PHFLTS PS={(s−2,0),(s−1,0.1),(s0,0.4),(s1,0.2),(s2,0.3)}. We can find that the PHFLTS shows accurate information way without information loss.

4.2 Delegate Selection Algorithm

For a blockchain network, there are n blockchain nodes and all the blockchain nodes should vote for each other using the voting options from the symmetric LTS S. Based on the above discussion, the steps of the delegate selection algorithm are developed as follows:

(1) Each blockchain node selects one linguistic term from the symmetric LTS S to vote for blockchain nodes in the blockchain network every time t. If the blockchain node abstains, the linguistic term s0 in the symmetric LTS S is used to express his/her voting information.

(2) For each blockchain node in the blockchain network, the voting information from all the blockchain nodes is collected, and the probability distribution information of linguistic terms is calculated. Then, the PHFLTS is used to model the collective voting information of each blockchain node i as PSi={(sεi,pεi)|sεi∈S},i=1,2,…,n.

For more details, please refer to Example 1.

Thus, all the collective voting information of n blockchain nodes in the blockchain network can be expressed as a set of n PHFLTSs. Then, the delegate selection can be formulated to be a blockchain node rank problem by comparing their PHFLTSs.

(3) The pairwise comparisons of all the blockchain nodes are conducted, and then a possibility degree matrix can be obtained as follows:

p=[0.5ρ12⋯ρ1nρ210.5⋯ρ2n⋮⋮⋱⋮ρn1ρn2⋯0.5],

where ρij=ρ(PSi≥PSj), ρij+ρji=1, and ρii=0.5.

(4) The cumulative possibility degree ρi of each blockchain node i is calculated as

ρi=1n∑j=1nρij,i=1,2,…,n.(3)

(5) The cumulative possibility degrees of blockchain nodes are ranked in descending order as ρ(1)≥ρ(2)≥⋯≥ρ(m−(m1+1))≥ρ(m−m1)≥⋯≥ρ(m−1)≥ρ(m)≥ρ(m+1)≥⋯≥ρ(m+m2)≥⋯≥ρ(n), where {ρ(1),ρ(2),…,ρ(n)} is a permutation of {ρ1,ρ2,…,ρn} that satisfies ρ(i)≥ρ(j).

If ρ(m)≠ρ(m+1), then the blockchain nodes with the largest m cumulative possibility degrees are selected as delegates.

If all the cumulative possibility degrees of blockchain nodes satisfy the following condition:ρ(m−(m1+1))>ρ(m−m1)=⋯=ρ(m−1)=ρ(m)=ρ(m+1)=⋯>ρ(m+m2)>ρ(m+m2+1), then the blockchain nodes that possess the largest m−(m1+1) cumulative possibility degrees are selected as delegates. Then, the lottery algorithm is used to select the rest m1+1 delegates from the blockchain nodes that own the cumulative possibility degrees ρ(m−m1),…,ρ(m−1),ρ(m),ρ(m+1),…,ρ(m+m2).

Example 2. Let us assume that there exist two nodes A and B, the LTS S is used to provide fine-grained voting options for blockchain nodes. The voting information received by them is listed in Table 1. Based on the voting information in Table 1, the collective voting information for nodes A and B can be modeled as the following two PHFLTSs:

PSA={(s−2,110),(s−1,110),(s0,210),(s1,210),(s2,410)}={(s−2,0.1),(s−1,0.1),(s0,0.1),(s1,0.2),(s2,0.4)},

PSB={(s−2,110),(s−1,010),(s0,410),(s1,410),(s2,110)}={(s−2,0.1),(s−1,0.0),(s0,0.4),(s1,0.4),(s2,0.1)}.

Let us consider choosing one node from node A and node B as the delegate. If the voting result of one node is computed as the difference value of positive votes and negative votes, then the voting result of node A is computed as 4+2−1−1=4 and the voting result of node B is computed as 1+4−1−0=4. In this case, node A and node B are indistinguishable, and then the delegate cannot be chosen. That is because the neutral attitudes of blockchain nodes, and the intensity of support attitudes and opposition attitudes are not considered. If our delegate selection algorithm is used, then the possibility degree between nodes A and B is computed as ρ(PSA≥PSB)=0.595.

According to Property 1, ρ(PSB≥PSA)=0.405. Therefore, it is considered that the voting result of node B is superior to that of node A, and node B can be selected as the delegate.

In the following part, another example is given to compare the traditional DPoS consensus algorithm with our proposed DPoS consensus algorithm as follows:

Example 3. Let us assume that there exist two nodes C and D, and the LTS S is used to provide fine-grained voting options for blockchain nodes. The voting information received by them is listed in Table 2. Based on the voting information in Table 2, the collective voting information for nodes C and D can be modeled as the following two PHFLTSs: PSC={(s−2,0.2),(s−1,0.3),(s0,0.1),(s1,0.1),(s2,0.3)}, PSD={(s−2,0.0),(s−1,0.1),(s0,0.6),(s1,0.0),(s2,0.3)}.

Let us consider choosing one node from node C and node D as the delegate. If the traditional DPoS consensus algorithm is used, only the number of positive votes is considered to choose the delegate. In this case, the number of positive votes of node C is 4, while the number of positive votes of node D is 3. Then, node C is selected to be the delegate when the traditional DPoS consensus algorithm is used. However, from Table 2, it can be seen that the number of negative votes of node C is 5. It is more than that of node D. Moreover, the number of neutral votes of node C is also less than that of node D. Thus, it is unreasonable to choose node C to be the delegate. When our proposed DPoS consensus algorithm is used, the possibility degree is computed as ρ(PSD≥PSC)=0.62>0.5. Thus, node D is selected as the delegate. It demonstrates the rationality of our proposed DPoS consensus algorithm. The security of the blockchain network is improved.

5  Numerical Analysis

5.1 Experiment Analysis of the Novel DPoS Consensus Mechanism

Let us consider an example that there exist 21 nodes, each of which can give its voting information to all the nodes including itself by using the LTS S. The voting information received by these 21 nodes is listed in Table 3.

(1) Our DPoS consensus algorithm (DPoS-PHFLTS)

Based on Table 3, the collective voting information of these 21 nodes can be modeled as the following PHFLTSs:

PS1={(s−2,121),(s−1,121),(s0,0),(s1,621),(s2,1321)},

PS2={(s−2,621),(s−1,221),(s0,221),(s1,221),(s2,921)},

PS3={(s−2,421),(s−1,221),(s0,221),(s1,221),(s2,1121)},

PS4={(s−2,221),(s−1,421),(s0,421),(s1,621),(s2,521)},

PS5={(s−2,321),(s−1,621),(s0,421),(s1,221),(s2,621)},

PS6={(s−2,1021),(s−1,0),(s0,521),(s1,0),(s2,621)},

PS7={(s−2,621),(s−1,421),(s0,621),(s1,0),(s2,521)},

PS8={(s−2,221),(s−1,421),(s0,621),(s1,621),(s2,321)},

PS9={(s−2,221),(s−1,421),(s0,0),(s1,621),(s2,921)},

PS10={(s−2,221),(s−1,421),(s0,0),(s1,921),(s2,621)},

PS11={(s−2,821),(s−1,421),(s0,621),(s1,0),(s2,321)},

PS12={(s−2,321),(s−1,521),(s0,521),(s1,521),(s2,321)},

PS13={(s−2,221),(s−1,221),(s0,0),(s1,1221),(s2,521)},

PS14={(s−2,1421),(s−1,0),(s0,421),(s1,0),(s2,321)},

PS15={(s−2,121),(s−1,221),(s0,0),(s1,0),(s2,1821)},

PS16={(s−2,121),(s−1,221),(s0,0),(s1,1021),(s2,821)},

PS17={(s−2,721),(s−1,221),(s0,421),(s1,421),(s2,421)},

PS18={(s−2,421),(s−1,421),(s0,521),(s1,421),(s2,421)},

PS19={(s−2,921),(s−1,921),(s0,121),(s1,0),(s2,221)},

PS20={(s−2,1621),(s−1,0),(s0,0),(s1,521),(s2,0)},

PS21={(s−2,1121),(s−1,0),(s0,521),(s1,521),(s2,0)}.

According to Definitions 3 and 4, the cumulative possibility degree ρi of each node i is computed as:

ρ1=121∑j=121ρ1j=0.7333,ρ2=121∑j=121ρ2j=0.5407,

ρ3=121∑j=121ρ3j=0.6104,ρ4=121∑j=121ρ4j=0.5468,

ρ5=121∑j=121ρ5j=0.5059,ρ6=121∑j=121ρ6j=0.4178,

ρ7=121∑j=121ρ7j=0.4367,ρ8=121∑j=121ρ8j=0.5090,

ρ9=121∑j=121ρ9j=0.6223,ρ10=121∑j=121ρ10j=0.5888,

ρ11=121∑j=121ρ11j=0.3671,ρ12=121∑j=121ρ12j=0.4788

ρ13=121∑j=121ρ13j=0.6060,ρ14=121∑j=121ρ14j=0.2974,

ρ15=121∑j=121ρ15j=0.7750,ρ16=121∑j=121ρ16j=0.6632,

ρ17=121∑j=121ρ17j=0.4457,ρ18=121∑j=121ρ18j=0.4806,

ρ19=121∑j=121ρ19j=0.2999,ρ20=121∑j=121ρ20j=0.2475,

ρ21=121∑j=121ρ21j=0.3271.

According to the descending order of cumulative possibility degree, these 21 blockchain nodes can be ranked as: N15>N1>N16>N9>N3>N13>N10>N4>N2>N8>N5>N18>N12>N17>N7>N6>N11>N21>N19>N14>N20.

Therefore, node 15, node 1, node 16, node 9, and node 3 are selected as the delegates for validating the transactions.

(2) Difference value method (DV)

The voting result of one node is computed as the difference value of positive votes and negative votes in DV. In this part, we calculated the number of affirmative and negative votes in Table 3, and the statistical results are shown in Table 4. The difference value method is used to calculate the voting result of each blockchain node as follows:

ξ1=13+6−1−1=17,ξ2=9+2−2−6=3,

ξ3=11+2−2−4=7,ξ4=5+6−4−2=5,

ξ5=6+2−6−3=−1,ξ6=6+0−0−10=−4,

ξ7=5+0−4−6=−5,ξ8=3+6−4−2=3,

ξ9=6+9−4−2=9,ξ10=9+6−4−2=9,

ξ11=3+0−4−8=−9,ξ12=3+5−5−3=0,

ξ13=5+12−2−2=13,ξ14=3+0−0−14=−11,

ξ15=18+0−2−1=15,ξ16=8+10−2−1=15,

ξ17=4+4−2−7=−1,ξ18=4+4−4−4=0,

ξ19=2+0−9−9=−16,ξ20=0+5−0−16=−11,

ξ21=0+5−0−11=−6.

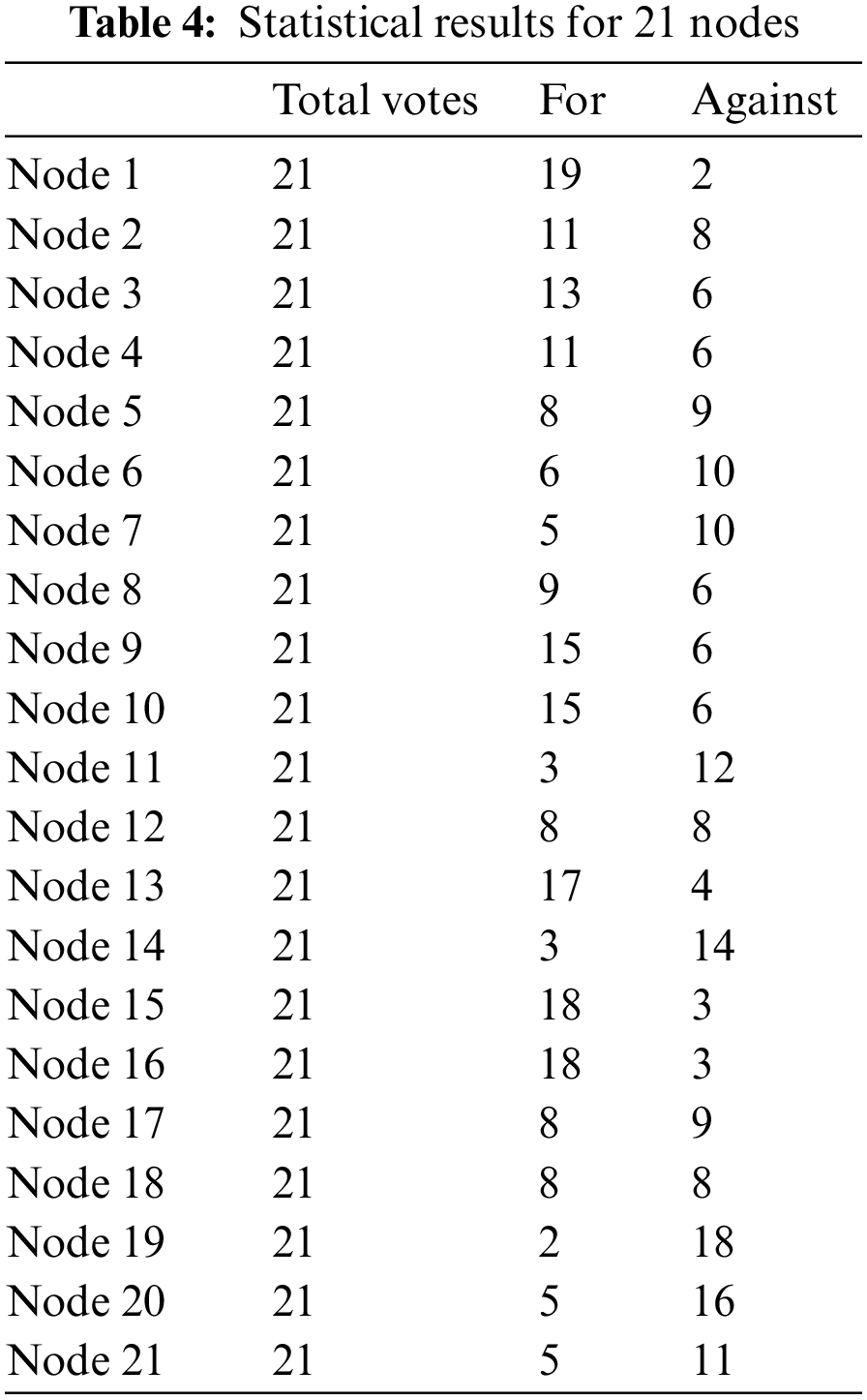
According to the voting result, these 21 blockchain nodes are ranked as: N1>N15=N16>N13>N9=N10>N3>N4>N2=N8>N17>N12=N18>N5>N6>N7>N21>N11>N14>N20>N19.

Thus, node 1, node 15, node 16, and node 13 are directly selected as the delegates. However, the voting results of node 9 and node 10 are equal. They cannot be indistinguishable and the remaining delegate cannot be obtained when the difference value method is used.

(3) Traditional DPoS consensus algorithm (T-DPoS)

The voting result of one node is computed as the value of positive votes in T-DPoS. In this part, according to the statistical results as shown in Table 4, the traditional DPoS consensus algorithm is used to compute the voting result of each blockchain node as:

δ1=13+6=19,δ2=9+2=11,

δ3=11+2=13,δ4=5+6=11,

δ5=6+2=8,δ6=6+0=6,

δ7=5+0=5,δ8=3+6=9,

δ9=9+6=15,δ10=9+6=15,

δ11=3+0=3,δ12=3+5=8,

δ13=5+12=17,δ14=3+0=3,

δ15=18+0=18,δ16=8+10=18,

δ17=4+4=8,δ18=4+4=8,

δ19=2+0=2,δ20=0+5=5,

δ21=0+5=5.

According to the voting result, these 21 blockchain nodes are ranked as: N1>N15=N16>N13>N10=N9>N3>N4=N2>N8>N18=N17=N12=N5>N6>N21=N20=N7>N14=N11>N19.

Thus, node 1, node 15, node 16, and node 13 are directly selected as the delegates. However, the voting results of node 9 and node 10 are equal. They cannot be distinguishable and the remaining delegate cannot be obtained when the difference value method is used.

(4) PBFT consensus algorithm based on vague sets (VS-PBFT)

In this part, the PBFT consensus algorithm based on vague sets (VS-PBFT) [42] is used. As listed in Table 5, the collective voting information for these 21 blockchain nodes is modeled using vague sets, and their corresponding fuzzy values are computed.

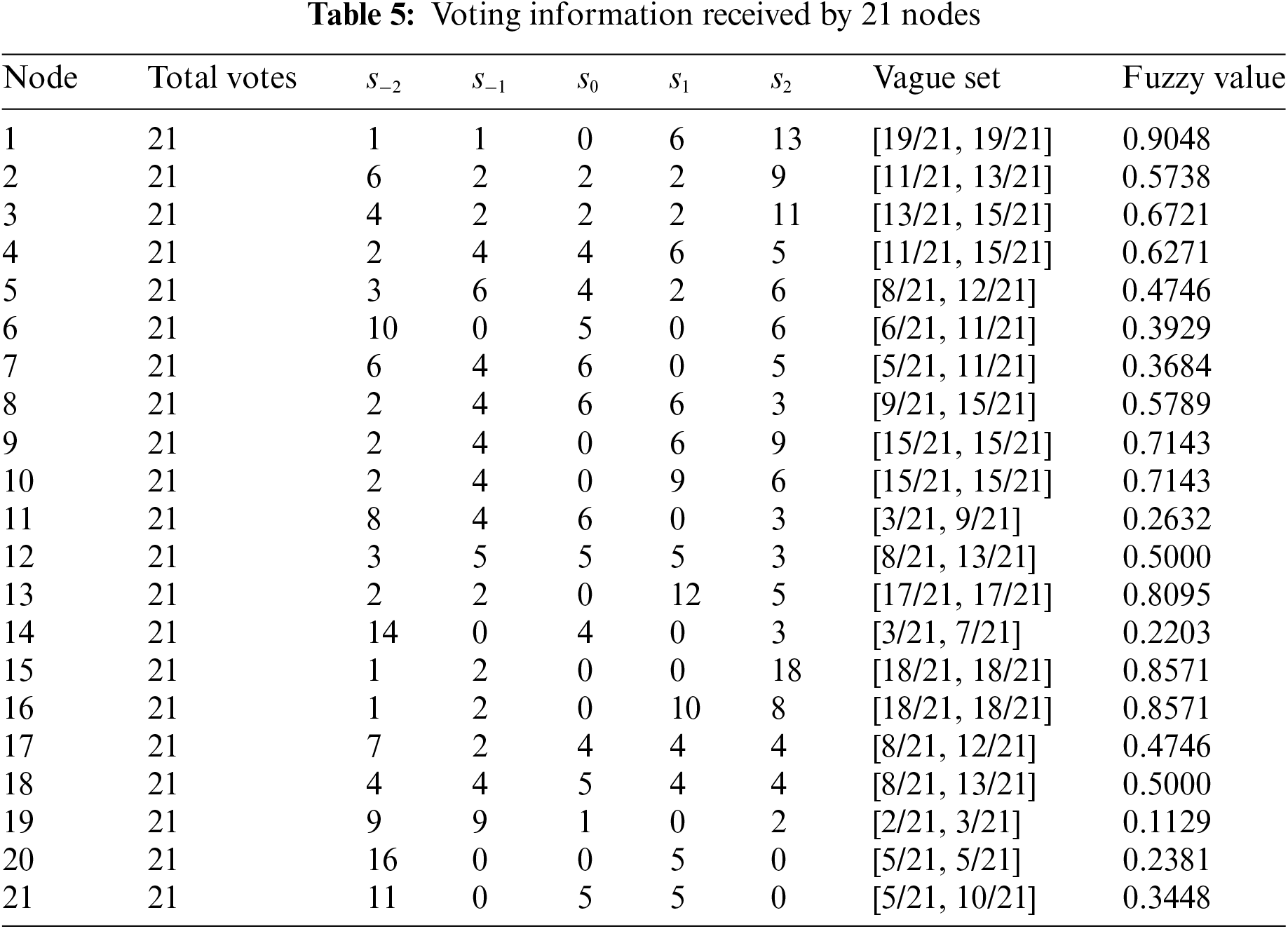
According to the fuzzy values, these 21 nodes are ranked as:

N1>N15=N16>N13>N9=N10>N3>N4>N8>N2>N12=N18>N5=N17>N6>N7>N21>N11>N20>N14>N19.

Thus, node 1, node 15, node 16, and node 13 are directly selected as the delegates. However, the fuzzy values of node 9 and node 10 are equal. They cannot be indistinguishable and the remaining delegate cannot be obtained.

To show the superiority of our DPoS-PHFLTS algorithm, the ranking results obtained by four algorithms are summarized in Table 6.

As shown in Table 6, it can be seen that our DPoS-PHFLTS algorithm can effectively obtain 5 delegates from all the nodes, while the rest algorithms only select 4 delegates and the rest one delegate cannot be directly obtained from node 9 and node 10. Nevertheless, we can perceive from the voting results of node 9 and node 10 that there is a stronger intention to support node 9. From the analysis result, it can be seen that our DPoS-PHFLTS algorithm has better performance than the existing algorithms in this example.

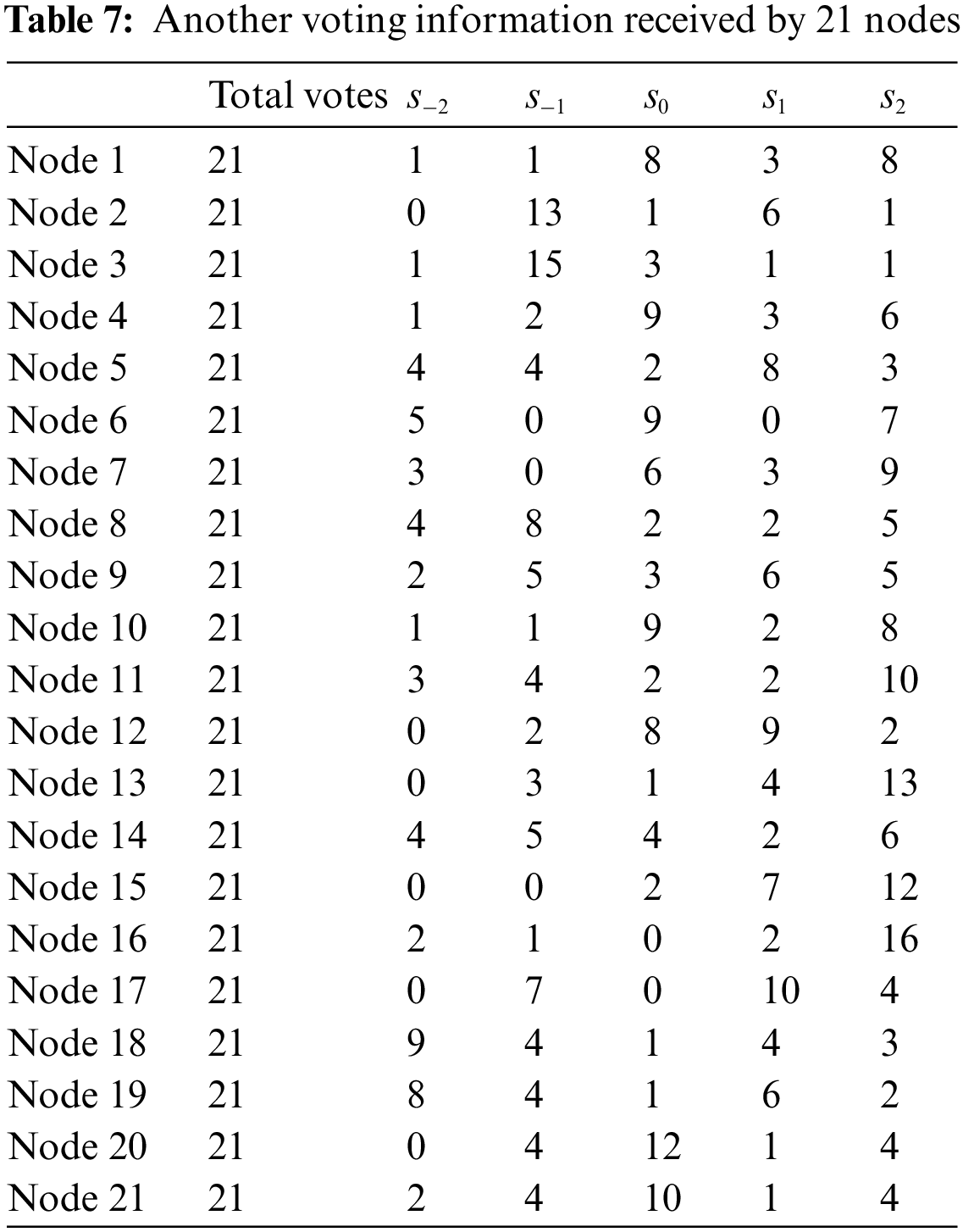
Another voting information received by these 21 nodes is listed in Table 7.

(1) Our DPoS consensus algorithm (DPoS-PHFLTS)

Based on Table 7, according to Definitions 3 and 4, the cumulative possibility degree ρi of each node i is computed as:

ρ1=121∑j=121ρ1j=0.5843,ρ2=121∑j=121ρ2j=0.3673,

ρ3=121∑j=121ρ3j=0.2835,ρ4=121∑j=121ρ4j=0.5329,

ρ5=121∑j=121ρ5j=0.4469,ρ6=121∑j=121ρ6j=0.4764,

ρ7=121∑j=121ρ7j=0.5807,ρ8=121∑j=121ρ8j=0.3930,

ρ9=121∑j=121ρ9j=0.4942,ρ10=121∑j=121ρ10j=0.5749,

ρ11=121∑j=121ρ11j=0.5532,ρ12=121∑j=121ρ12j=0.5234,

ρ13=121∑j=121ρ13j=0.6957,ρ14=121∑j=121ρ14j=0.4430,

ρ15=121∑j=121ρ15j=0.7323,ρ16=121∑j=121ρ16j=0.7245,

ρ17=121∑j=121ρ17j=0.5259,ρ18=121∑j=121ρ18j=0.3235,

ρ19=121∑j=121ρ19j=0.3387,ρ20=121∑j=121ρ20j=0.4700,

ρ21=121∑j=121ρ21j=0.4358.

According to the descending order of cumulative possibility degree, these 21 blockchain nodes can be ranked as:

N15>N16>N13>N1>N7>N10>N11>N4>N17>N12>N9>N6>N20>N5>N14>N21>N8>N2>N19>N18>N3.

(2) Difference value method (DV)

In this part, we calculated the number of affirmative and negative votes in Table 7, and the statistical results are shown in Table 8. The difference value method is used to calculate the voting result of each blockchain node as follows:

ξ1=3+8−1−1=9,ξ2=1+6−0−13=−6,

ξ3=1+1−1−15=−14,ξ4=3+6−1−2=6,

ξ5=8+3−4−4=3,ξ6=0+7−5−0=2,

ξ7=3+9−3−0=9,ξ8=2+5−4−8=−5,

ξ9=6+5−2−5=4,ξ10=2+8−1−1=8,

ξ11=2+10−3−4=5,ξ12=9+2−0−2=9,

ξ13=4+13−0−3=14,ξ14=2+6−4−5=−1,

ξ15=7+12−0−0=19,ξ16=2+16−2−1=15,

ξ17=10+4−0−7=7,ξ18=4+3−9−4=−6,

ξ19=6+2−8−4=−4,ξ20=4+1−0−4=1,

ξ21=4+1−2−4=−1.

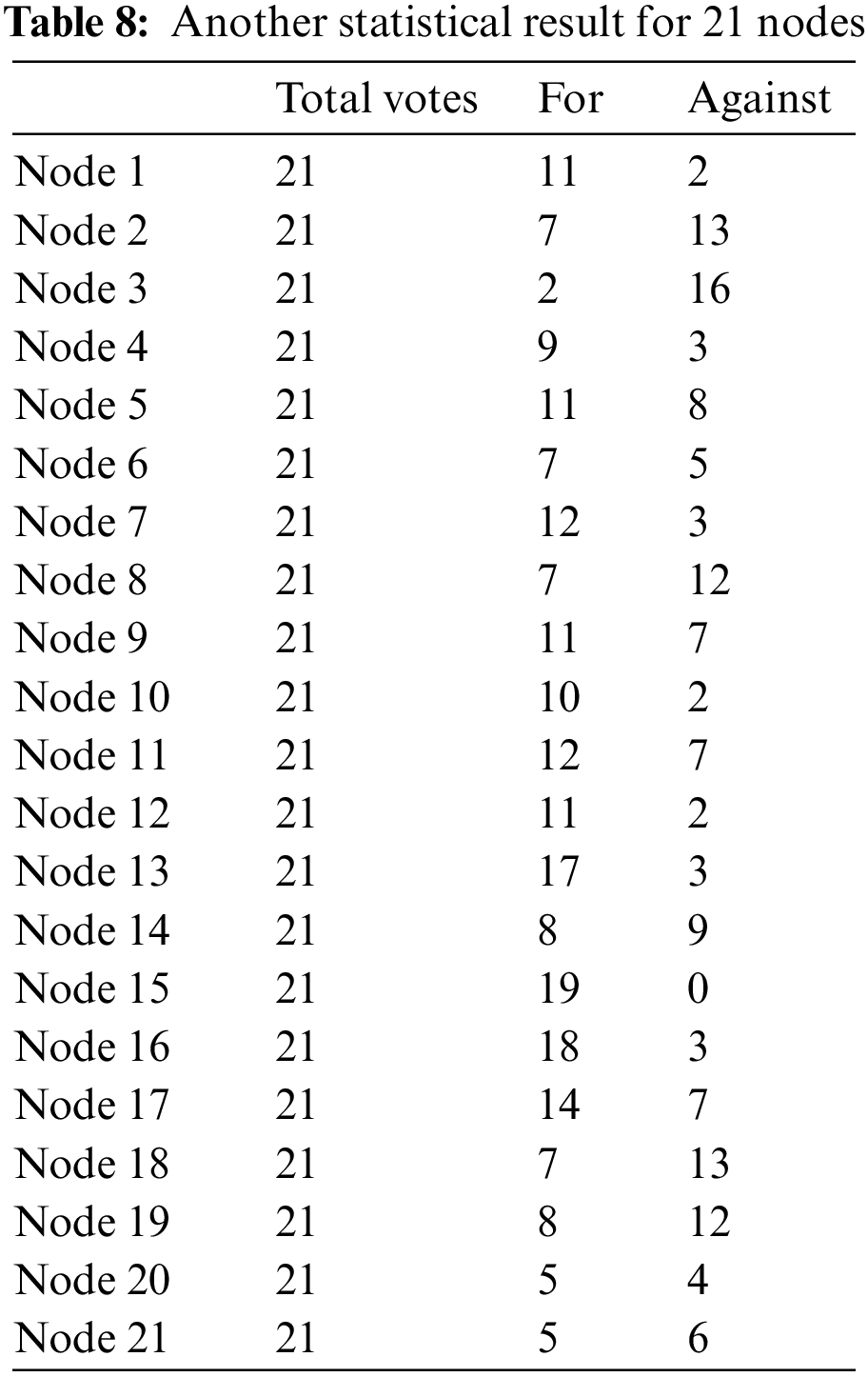
According to the voting result, these 21 blockchain nodes are ranked as: N15>N16>N13>N7=N12=N1>N10>N17>N4>N11>N9>N5>N6>N20>N14=N21>N19>N8>N2=N18>N3.

Thus, node 15, node 16, and node 13 are directly selected as the delegates. However, the voting results of node 7, node 12, and node 1 are equal. They cannot be indistinguishable and the remaining delegate cannot be obtained when the difference value method is used.

(3) Traditional DPoS consensus algorithm (T-DPoS)

In this part, according to the statistical results as shown in Table 8, the traditional DPoS consensus algorithm is used to compute the voting result of each blockchain node as:

δ1=3+8=11,δ2=6+1=7,

δ3=1+1=2,δ4=3+6=9,

δ5=8+3=11,δ6=0+7=7,

δ7=3+9=12,δ8=2+5=7,

δ9=6+5=11,δ10=2+8=10,

δ11=2+10=12,δ12=9+2=11,

δ13=4+13=17,δ14=2+6=8,

δ15=7+12=19,δ16=2+16=18,

δ17=10+4=14,δ18=4+3=7,

δ19=6+2=8,δ20=1+4=5,

δ21=1+4=5.

According to the voting result, these 21 blockchain nodes are ranked as N15>N16>N13>N17>N7=N11>N1=N5=N9=N12>N10>N4>N14=N19>N2=N6=N8=N18>N20=N21>N3.

Thus, node 15, node 16, node 13, and node 17 are directly selected as the delegates. However, the voting results of node 7 and node 11 are equal. They cannot be indistinguishable and the rest one delegate cannot be obtained when the difference value method is used.

(4) PBFT consensus algorithm based on vague sets (VS-PBFT)

In this part, the PBFT consensus algorithm based on vague sets (VS-PBFT) is used. As listed in Table 9, the collective voting information for these 21 blockchain nodes is modeled using vague sets, and their corresponding fuzzy values are computed.

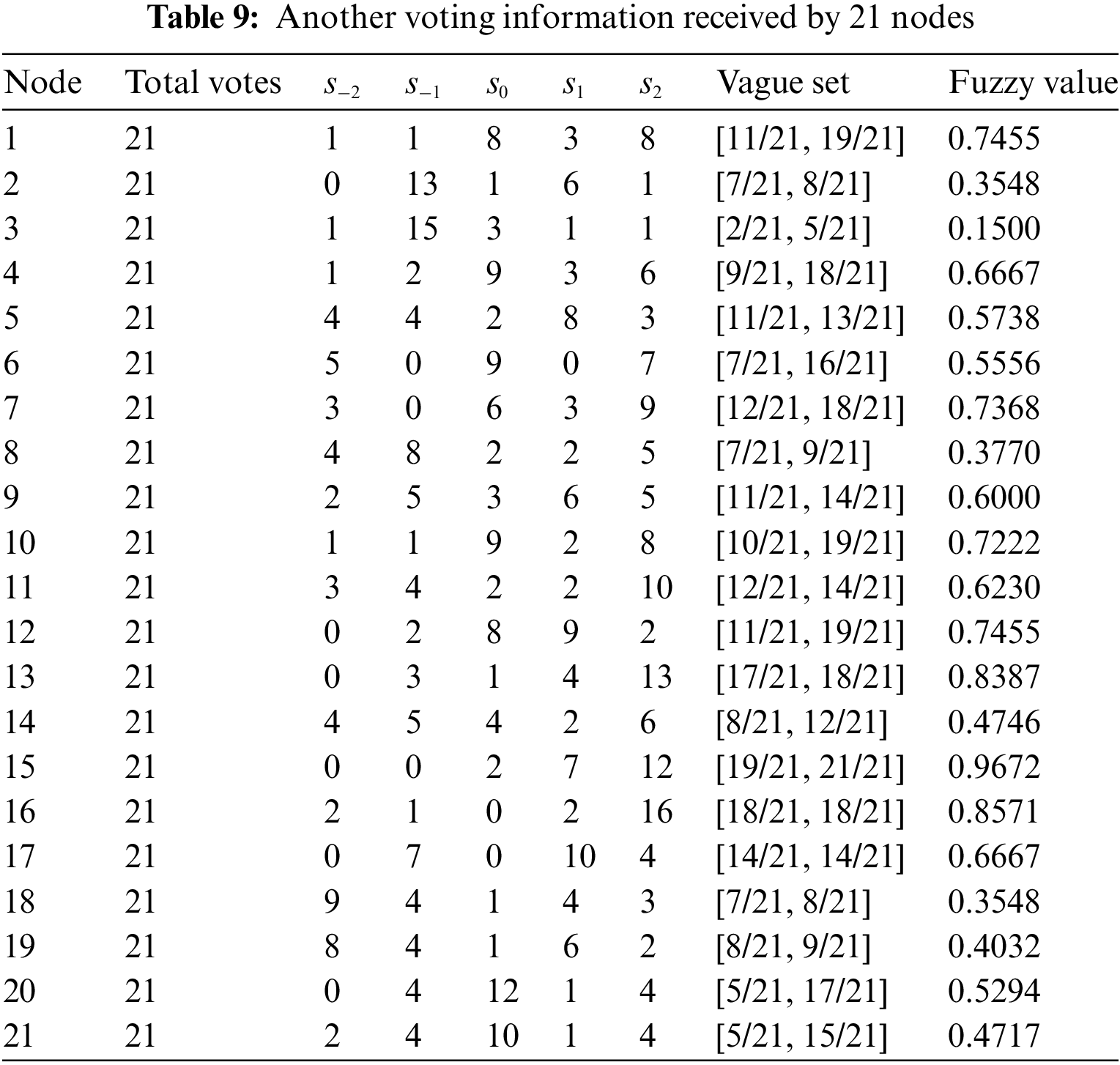
According to the fuzzy values, these 21 nodes are ranked as: N15>N16>N13>N1=N12>N7>N10>N4=N17>N11>N9>N5>N6>N20>N14>N21>N19>N8>N2=N18>N3.

Thus, node 16, node 17, node 13, and node 19 are directly selected as the delegates. However, the fuzzy values of node 2 and node 18 are equal. They cannot be indistinguishable and the remaining delegate cannot be obtained.

To show the superiority of our DPoS-PHFLTS algorithm, the ranking results obtained by four algorithms are summarized in Table 10.

As shown in Table 10, it can be seen that our DPoS-PHFLTS and VS-PBFT algorithms can effectively obtain 5 delegates from all the nodes, while the rest algorithms only select 4 delegates and the rest of one delegate cannot be directly obtained. Nevertheless, we can perceive from the voting results of node 1 and node 12 that there is a stronger intention to support node 1 in VS-PBFT. From the analysis result, it can be seen that our DPoS-PHFLTS algorithm has better performance than the existing algorithms in this example.

5.2 Fairness Verification of the Algorithm

If 5 delegates are elected from 21 nodes in different examples, then it will also happen that the cumulative possibility degree of the fifth node is equal to that of the sixth node. To further show the advantage of our DPoS-PHFLTS algorithm, the simulations are conducted. Let us continue the example that 5 delegates are selected from 21 nodes. The voting information of blockchain nodes is randomly selected from the LTS S and then 21 PHFLTSs should be randomly generated at each time. DPoS-PHFLTS, DV, T-DPoS, and VS-PBFT are used to rank these 21 PHFLTSs to rank the corresponding blockchain nodes. This process is performed 1000 times, 10000 times, and 100000 times. The probabilities of the fifth node and sixth node with equal ranking results are shown in Fig. 2.

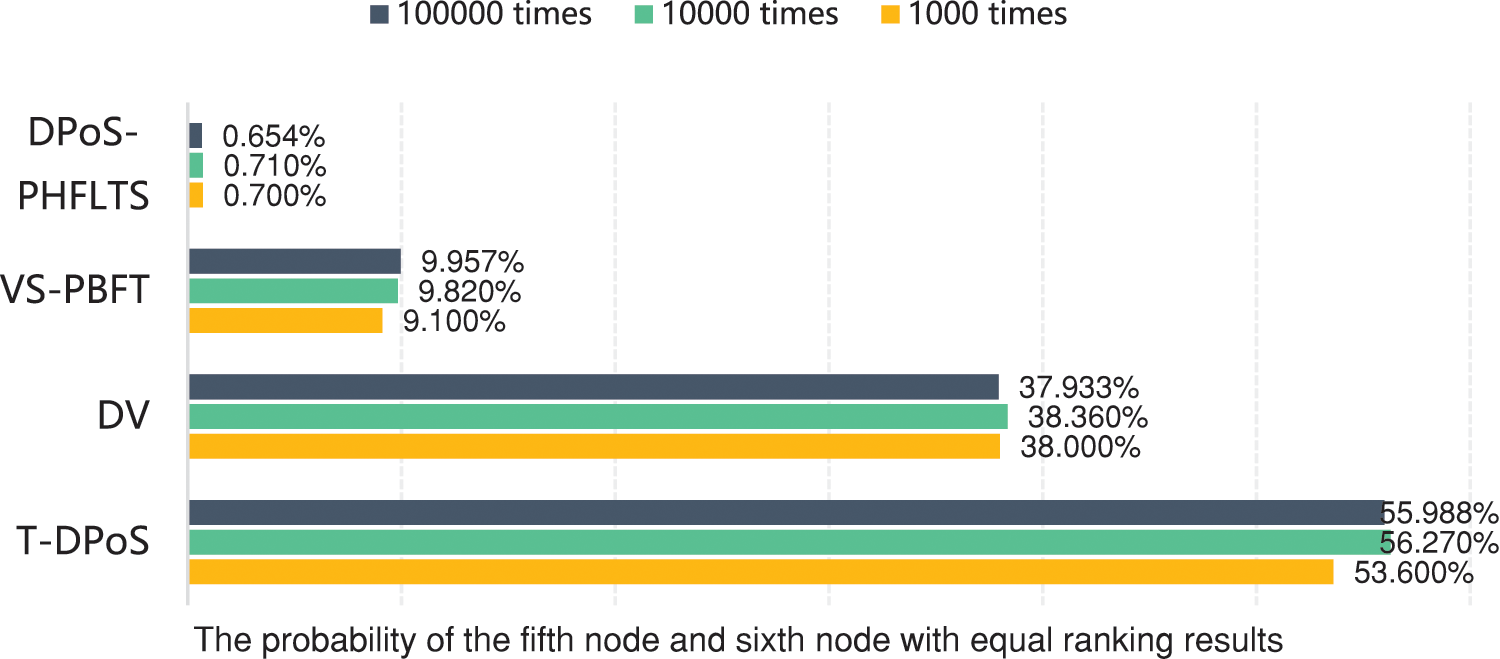
Figure 2: The probability of the fifth node and sixth node with equal ranking results when different algorithms are performed

As shown in Fig. 2, it is seen that the probabilities of the fifth node and the sixth node with equal ranking results are 0.700%, 0.710%, and 0.654% when our DPoS-PHFLTS algorithm is used. They are very low. However, the probabilities of the fifth node and sixth node with equal ranking results are much higher when these existing DV, T-DPoS, and VS-PBFT algorithms are used. The reasons can be analyzed as follows.

In the T-DPoS algorithm, it elects the top 5 blockchain nodes with the largest number of “Supported” and “Very Supported” votes as delegates. Thus, the T-DPoS algorithm only considers the positive votes but ignores the impact of the negative votes on the ranking results. The DV algorithm solves this drawback. It selects the top 5 blockchain nodes with the largest difference value of the positive votes and the negative votes as delegates. Therefore, the DV algorithm obtains a lower probability than the T-DPoS algorithm. However, both the DV algorithm and the T-DPoS algorithm do not consider the number of neutral votes. The VS-PBFT algorithm introduces the vague set to model the collective voting information, which can model the distribution information of positive votes, negative votes, and neutral votes. Thus, the probability of the fifth node and sixth node with equal ranking results is greatly lowered when the VS-PBFT algorithm is used. It is lower than 10%.

Furtherly, our DPoS-PHFLTS algorithm uses the PHFLTS to express the collective voting information of blockchain nodes. It can express not only the distribution information of positive votes, negative votes, and neutral votes but also the intensities of positive votes and negative votes. Thus, our DPoS-PHFLTS algorithm provides one more accurate and fine-grained means of modeling the collective voting information than the existing DV, T-DPoS, and VS-PBFT algorithms. It greatly decreases the probability of the fifth node and sixth node with equal ranking results. Its probability is lowered to be much less than 1%. The comparative analysis shows that our DPoS-PHFLTS shows the best performance among these algorithms.

6  Conclusions

In this study, a novel fine-grained knowledge representation method is put forward to improve the traditional DPoS consensus algorithm. According to the voting rule of the traditional DPoS consensus algorithm, a novel full associate voting architecture is proposed. Then, the LTS is used to capture the fine-grained voting options for voting blockchain nodes. Based on the LTS, the PHFLTS is utilized to express the collective voting information of voted blockchain nodes. Afterward, a novel delegate selection algorithm is designed to rank blockchain nodes and then select the delegates. The efficacy of the proposed approach is evaluated through comparative analysis, which demonstrates its superior performance compared to existing algorithms.

7  Limitations and Future Scope

In this study, only the overall performance of the blockchain nodes is voted. In future research, we plan to identify some attributes of the blockchain nodes, and the blockchain nodes are voted in terms of multiple attributes.

Acknowledgement: The authors thank the Editor, Associate Editor, and reviewers for providing the useful comments to improve the quality of this study.

Funding Statement: The authors received no specific funding for this study.

Author Contributions: Study conception and design: Yixia Chen, Mingwei Lin; data collection: Yixia Chen; analysis and interpretation of results: Yixia Chen; draft manuscript preparation: Yixia Chen, Mingwei Lin. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the article.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. Yang, “The blockchain: State-of-the-art and research challenges,” Journal of Industrial Information Integration, vol. 15, pp. 80–90, 2019. [Google Scholar]

2. X. Q. Li, P. Jiang, T. Chen, X. P. Luo and Q. Y. Wen, “A survey on the security of blockchain systems,” Future Generation Computer Systems, vol. 107, pp. 841–853, 2020. [Google Scholar]

3. Z. B. Zheng, S. A. Xie, H. N. Dai, X. P. Chen and H. M. Wang, “Blockchain challenges and opportunities: A survey,” International Journal of Web and Grid Services, vol. 14, no. 4, pp. 352–375, 2018. [Google Scholar]

4. S. Nanayakkara, M. N. N. Rodrigo, S. Perera, G. T. Weerasuriya and A. A. Hijazi, “A methodology for selection of a blockchain platform to develop an enterprise system,” Journal of Industrial Information Integration, vol. 23, pp. 100215, 2021. https://doi.org/10.1002/ett.4317 [Google Scholar] [CrossRef]

5. S. Kumar, S. Velliangiri, P. Karthikeyan, S. Kumari, S. Kumar et al., “A survey on the blockchain techniques for the internet of vehicles security,” Transactions on Emerging Telecommunications Technologies, pp. e4317, 2021. [Google Scholar]

6. L. D. Xu, Y. Lu and L. Li, “Embedding blockchain technology into IoT for security: A survey,” IEEE Internet of Things Journal, vol. 8, no. 13, pp. 10452–10473, 2021. [Google Scholar]

7. S. Misra, A. Mukherjee, A. Roy, N. Saurabh, Y. Rahulamathavan et al., “Blockchain at the edge: Performance of resource-constrained IoT networks,” IEEE Transactions on Parallel and Distributed Systems, vol. 32, no. 1, pp. 174–183, 2020. [Google Scholar]

8. A. I. Khan, A. Saad, F. J. Alsolami, Y. B. Abushark, A. Almalawi et al., “Integrating blockchain technology into healthcare through an intelligent computing technique,” Computers, Materials & Continua, vol. 70, no. 2, pp. 2835–2860, 2022. [Google Scholar]

9. Y. Chen, S. Ding, Z. Xu, H. D. Zheng and S. L. Yang, “Blockchain-based medical records secure storage and medical service framework,” Journal of Medical Systems, vol. 43, pp. 1–9, 2019. [Google Scholar]

10. C. Zhang, D. Li and J. Liang, “Multi-granularity three-way decisions with adjustable hesitant fuzzy linguistic multigranulation decision-theoretic rough sets over two universes,” Information Sciences, vol. 507, pp. 665–683, 2020. [Google Scholar]

11. U. Majeed, L. U. Khan, I. Yaqoob, S. M. A. Kazmi and K. Salah, “Blockchain for IoT-based smart cities: Recent advances, requirements, and future challenges,” Journal of Network and Computer Applications, vol. 181, pp. 103007, 2021. [Google Scholar]

12. C. Zhang, J. Ding, J. Zhan, A. K. Sangaiah and D. Li, “Fuzzy intelligence learning based on bounded rationality in IoMT systems: A case study in Parkinson's disease,” IEEE Transactions on Computational Social Systems, vol. 10, no. 4, pp. 1607–1621, 2023. [Google Scholar]

13. X. D. Qi, Z. Zhang, C. Q. Jin and A. Y. Zhou, “A reliable storage partition for permissioned blockchain,” IEEE Transactions on Knowledge and Data Engineering, vol. 33, no. 1, pp. 14–27, 2020. [Google Scholar]

14. T. T. A. Dinh, R. Liu, M. H. Zhang, G. Chen, B. C. Ooi et al., “Untangling blockchain: A data processing view of blockchain systems,” IEEE Transactions on Knowledge and Data Engineering, vol. 30, no. 7, pp. 1366–1385, 2018. [Google Scholar]

15. D. Wang and X. Zhang, “Secure ride-sharing services based on a consortium blockchain,” IEEE Internet of Things Journal, vol. 8, no. 4, pp. 2976–2991, 2021. [Google Scholar]

16. L. Jiang, S. Xie, S. Maharjan and Y. Zhang, “Blockchain empowered wireless power transfer for green and secure Internet of Things,” IEEE Network, vol. 33, no. 6, pp. 164–171, 2019. [Google Scholar]

17. X. Cong, L. L. Zi and D. Z. Du, “DTNB: A blockchain transaction framework with discrete token negotiation for the delay tolerant network,” IEEE Transactions on Network Science and Engineering, vol. 8, no. 2, pp. 1584–1599, 2021. [Google Scholar]

18. G. X. Xu, Y. Liu and P. W. Khan, “Improvement of the DPoS consensus mechanism in blockchain based on vague sets,” IEEE Transactions on Industrial Informatics, vol. 16, no. 6, pp. 4252–4259, 2020. [Google Scholar]

19. G. Xu, J. Dong, C. Ma, J. Liu and U. G. O. Cliff, “A certificateless signcryption mechanism based on blockchain for edge computing,” IEEE Internet of Things Journal, vol. 10, no. 14, pp. 11960–11974, 2023. [Google Scholar]

20. Y. Liu and G. X. Xu, “Fixed degree of decentralization DPoS consensus mechanism in blockchain based on adjacency vote and the average fuzziness of vague value,” Computer Networks, vol. 199, pp. 108432, 2021. [Google Scholar]

21. M. Yuan, Y. Xu, C. Zhang, Y. Tan, Y. Wang et al., “TRUCON: Blockchain-based trusted data sharing with congestion control in Internet of Vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 24, no. 3, pp. 3489–3500, 2023. [Google Scholar]

22. L. Abdullah, H. M. Pouzi and N. A. Awamg, “Intuitionistic fuzzy DEMATEL for developing causal relationship of water security,” International Journal of Intelligent Computing and Cybernetics, vol. 16, no. 3, pp. 520–544, 2023. [Google Scholar]

23. J. W. Leng, S. D. Ye, M. Zhou, J. L. Zhao, Q. Liu et al., “Blockchain-secured smart manufacturing in Industry 4.0: A survey,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 51, no. 1, pp. 237–252, 2021. [Google Scholar]

24. X. Fu, H. M. Wang and P. C. Shi, “A survey of blockchain consensus algorithms: Mechanism, design and applications,” Science China Information Sciences, vol. 64, pp. 1–15, 2021. [Google Scholar]

25. Y. M. Guo, Z. L. Huang, J. Guo, X. R. Guo, H. Li et al., “A bibliometric analysis and visualization of blockchain,” Future Generation Computer Systems, vol. 116, pp. 316–332, 2021. [Google Scholar]

26. L. You, Z. Wang, G. Hu, C. Cao and L. Li, “An improved model on the vague sets-based DPoS's voting phase in blockchain,” IEEE Transactions on Network Science and Engineering, pp. 1–10, 2023. https://doi.org/10.1109/TNSE.2023.3279571 [Google Scholar] [CrossRef]

27. W. Liu, Y. Li, X. J. Wang, Y. F. Peng, W. She et al., “A donation tracing blockchain model using improved DPoS consensus algorithm,” Peer-to-Peer Networking and Applications, vol. 14, no. 5, pp. 2789–2800, 2021. [Google Scholar]

28. C. Tao and L. Xiong, “DPoSB: Delegated proof of stake with node’s behavior and borda count,” in 2020 IEEE 5th Information Technology and Mechatronics Engineering Conf., Chongqing, China, pp. 1429–1434, 2020. [Google Scholar]

29. M. Orouskhani, D. Shi and X. Cheng, “A fuzzy adaptive dynamic NSGA-II with fuzzy-based borda ranking method and its application to multimedia data analysis,” IEEE Transactions on Fuzzy Systems, vol. 29, no. 1, pp. 118–128, 2021. [Google Scholar]

30. Y. H. Luo, Y. Q. Chen, Q. Chen and Q. L. Liang, “A new election algorithm for DPoS consensus mechanism in blockchain,” in 2018 7th Int. Conf. on Digital Home, Guilin, China, pp. 116–120, 2018. [Google Scholar]

31. J. Liu, M. Xie, S. Chen, C. Ma and Q. Gong, “An improved DPoS consensus mechanism in blockchain based on PLTS for the smart autonomous multi-robot system,” Information Sciences, vol. 575, pp. 528–541, 2021. [Google Scholar]

32. S. Jiang, J. Cao, H. Wu, K. Chen and X. Liu, “Privacy-preserving and efficient data sharing for blockchain-based intelligent transportation systems,” Information Sciences, vol. 635, pp. 72–85, 2023. https://doi.org/10.1016/j.ins.2023.03.121 [Google Scholar] [CrossRef]

33. M. W. Lin, Z. Y. Chen, Z. S. Xu, X. J. Gou and F. Herrera, “Score function based on concentration degree for probabilistic linguistic term sets: An application to TOPSIS and VIKOR,” Information Sciences, vol. 551, pp. 270–290, 2021. [Google Scholar]

34. M. W. Lin, Z. S. Xu, Y. L. Zhai and Z. Q. Yao, “Multi-attribute group decision-making under probabilistic uncertain linguistic environment,” Journal of the Operational Research Society, vol. 69, no. 2, pp. 157–170, 2018. [Google Scholar]

35. H. C. Liu, X. Luan, Z. W. Li and J. N. Wu, “Linguistic petri nets based on cloud model theory for knowledge representation and reasoning,” IEEE Transactions on Knowledge and Data Engineering, vol. 30, no. 4, pp. 717–728, 2018. [Google Scholar]

36. H. C. Liu, J. X. You, X. Y. You and Q. Su, “Linguistic reasoning petri nets for knowledge representation and reasoning,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 46, no. 4, pp. 499–511, 2016. [Google Scholar]

37. M. W. Lin, X. M. Li and L. F. Chen, “Linguistic q-rung orthopair fuzzy sets and their interactional partitioned heronian mean aggregation operators,” International Journal of Intelligent Systems, vol. 35, no. 2, pp. 217–249, 2020. [Google Scholar]

38. Z. S. Chen, K. S. Chin, Y. L. Li and Y. Yang, “Proportional hesitant fuzzy linguistic term set for multiple criteria group decision making,” Information Sciences, vol. 357, pp. 61–87, 2016. [Google Scholar]

39. M. W. Lin, C. Huang and Z. S. Xu, “TOPSIS method based on correlation coefficient and entropy measure for linguistic pythagorean fuzzy sets and its application to multiple attribute decision making,” Complexity, vol. 2019, pp. 1–16, 2019. [Google Scholar]

40. O. F. Gorcun, D. Pamucar and S. Biswas, “The blockchain technology selection in the logistics industry using a novel MCDM framework based on Fermatean fuzzy sets and Dombi aggregation,” Information Sciences, vol. 635, pp. 345–374, 2023. [Google Scholar]

41. M. W. Lin, J. H. Wei, Z. S. Xu and R. Q. Chen, “Multiattribute group decision-making based on linguistic pythagorean fuzzy interaction partitioned bonferroni mean aggregation operators,” Complexity, vol. 2018, pp. 24, 2018. [Google Scholar]

42. G. X. Xu and Y. S. Wang, “Improved PBFT algorithm based on vague sets,” Security and Communication Networks, vol. 2022, pp. 6144664, 2022. [Google Scholar]