A New S-Box Design System for Data Encryption Using Artificial Bee Colony Algorithm

1  Introduction

The rise of multimedia technology and information sharing via insecure channels necessitates robust security for sensitive data, including images of finances, personal information, and medical records [1]. As color images increasingly serve as digital communication mediums, securing them against unauthorized access is vital. Image encryption is key to maintaining the confidentiality and integrity of such data. While traditional text encryption may not suffice for images, a blend of security techniques can protect information at different network communication layers. Physical layer protection may involve modulation systems and spread spectrum techniques, while cryptographic methods, including encryption, decryption, and digital signatures, safeguard the application layer [1,2]. Techniques like watermarking, steganography, and fingerprinting embed information within other data for proof of ownership or authenticity and content usage tracking [3]. Encryption systems typically fall into two categories: symmetric and asymmetric. Symmetric encryption uses one key for encryption and decryption, while asymmetric uses a public encryption key and a private decryption key. Enhancing encryption involves employing substitution boxes (S-boxes) that use mathematical functions to substitute one-bit sequences. This increases the complexity of the key-cipher text relationship, which determines the encryption strength, with the nonlinearity of S-boxes significantly intensifying this complexity.

This research focuses on creating highly nonlinear S-boxes [4,5] that are suitable for chaotic encryption systems. Chaotic maps have proven to be effective in encryption algorithms, for instance, a novel image encryption algorithm leveraging new fractional beta chaotic maps is proposed in [6]. The presented approach employs chaotic maps to generate pseudo-random sequences that reshuffle image pixels. The proposed scheme, characterized by a large key space and high key sensitivity, resulted in impressive entropy and low correlation coefficients, enhancing overall image encryption security. Similarly, in [7], the authors introduced a novel S-box generator using a deterministic algorithm over elliptic curves, resulting in dynamic, key-sensitive, and secure S-boxes. It was successfully applied in an image encryption scheme, demonstrating resistance against several types of cryptographic attacks. Besides, the authors [8] presented the use of chaotic systems for big data encryption, particularly image encryption, proposing a one-dimensional piece-wise quadratic polynomial chaotic map (PWQPCM). Coupled with a robust S-box construction method and a secure image encryption algorithm, the proposed model shows advantages in data loss resistance, time efficiency, and adjustable security strength. Moreover, the authors in [9] presented a new two-dimensional discrete hyperchaotic map, which possesses wider continuous chaotic intervals and larger Lyapunov exponents. This map is employed to generate S-boxes and pair them, resulting in a sophisticated encryption algorithm. Additionally, a two-dimensional chaotic map-based encryption method for images was discussed by Amina et al. [10], utilizing confusion and diffusion at the bit level. The analysis of this method demonstrates satisfactory and efficient encryption performance. Additionally, a four-dimensional chaotic system-based algorithm for color image encryption is presented by Li et al. [11] which exhibits good security, robustness, and efficiency through simulations and analysis. However, it is found that some existing encryption methods may lack sufficient security. Encryption involves two phases of confusion and diffusion. Confusion makes the relationship between plaintext and ciphertext complex through operations like substitution and permutation. Diffusion scatters the impact of each plaintext symbol across multiple ciphertext symbols, achieved through block ciphers and transformations. Substitution boxes contribute to confusion while scrambling algorithms aid diffusion [12]. Previous work in the field of application layer security has already been done by Kaur et al. [13], and chaos has been widely used in cryptography due to its sensitivity to initial conditions. One of the most critical characteristics of an efficient encryption system is its sensitivity to the key, the keyspace analysis, and the time analysis [14]. In the case of images, the correlation between neighboring pixels is high, making it challenging to provide security to them using traditional systems. Deoxyribonucleic Acid (DNA) and hyperchaos-based encryption discussed by Liu et al. [15] were proposed and the system works very well for the security of images. Hyperchaos-based encryption schemes are a type of cryptographic algorithm that utilizes numerous chaotic systems with different initial conditions to achieve high encryption performance. These schemes offer several advantages, including strong security, efficient processing, and resistance to various attacks. Moreover, it employs multiple chaotic systems with distinct initial conditions which makes it challenging for attackers to reconstruct the encryption key. However, parallel processing techniques enable efficient handling of large amounts of data in real-time which is far better than Hyperchaos-based encryption schemes as it lacks flexibility due to their dependability on specific chaotic systems and initial conditions. It also limits their adaptability to different encryption scenarios. Basic requirements for efficient encryption systems are also discussed in related work [16]. Several similar works can be found in literature, such as the authors in [17] proposed a novel image encryption algorithm utilizing a two-dimensional spatiotemporal chaotic system that combines linear neighborhood coupling and nonlinear chaotic map coupling of lattices, offering enhanced cryptographic features compared to the traditional coupled map lattices system. Bit-level permutation further strengthens the cryptosystem security, with simulations illustrating a large key space, high key sensitivity, and resistance to attacks. Similarly, in [18] the authors introduced a unique image encryption scheme, exploiting DNA-based sequencing and chaotic sequencing. The image transforms DNA encoding, shuffling for diffusion, substitution for confusion, and repeated DNA fusion operations to disrupt pixel correlations. The ciphered image meets all standard benchmarks, proving the effectiveness of this innovative approach. Besides, the authors in [19] presented a hybrid image encryption method combining a logistic sine system, two-dimensional cellular automata, and Finite State Machines (FSM)-based DNA rule generator. Each of the three stages of encryption employs unique rules, delivering robust defense against various cryptographic attacks. The proposed method proves to be effective for secure encryption of classified grayscale images.

Encryption systems rely on key sensitivity, keyspace analysis, and time analysis. In images, pixel correlation can affect image quality; high correlation may lead to blurriness, while low correlation may result in noise. Effective encryption algorithms reduce this correlation, making histograms uniformly distributed, achieved by scrambling—shuffling pixel groups to diminish neighboring block correlation. This contributes to diffusion, vital for images with high neighborhood correlation. The S-box’s properties, including non-linearity and the avalanche effect, determine encryption strength. A secure S-box exhibits significant output changes with input modifications and satisfies the strict avalanche criterion. The S-box’s strength influences the confidentiality and integrity of encrypted data, with robust S-boxes enhancing security against unauthorized access. Therefore, this paper focuses on generating S-boxes exhibiting non-linearity, resilience, and compatibility with existing encryption algorithms. This work aims to develop highly nonlinear S-boxes for encryption, enhancing digital content security during transmission and storage. The focus is on incorporating these S-boxes in the encryption system’s confusion phase and using various scrambling algorithms in the diffusion phase. The proposed system’s effectiveness will be evaluated based on key sensitivity, keyspace analysis, time analysis, and the uniform distribution of encrypted image histograms.

The key contributions of this paper are:

1.    Generation of highly nonlinear substitution boxes (S-boxes) using Artificial Bee Colony (ABC) algorithm that adheres to the key statistical security parameters such as Strict Avalanche Criteria (SAC), bijectivity, and Bit Independent Criteria (BIC). These highly nonlinear S-boxes enhance the security of digital content during transmission and storage.

2.    Development of a novel encryption system for colored images, which innovatively incorporates the generated S-boxes into the confusion phase and employs different scrambling algorithms in the diffusion phase making it suitable for color image encryption.

3.    A comprehensive and diverse security analysis has been presented for the proposed encryption system. This analysis includes brute force attack resistance, National Institute of Standards and Technology (NIST) statistical test, histogram analysis, differential analysis, time analysis, and key sensitivity analysis.

The rest of the paper is organized as follows: Section 2 introduces essential concepts used in S-box generation, outlines the process of generating and analyzing the S-boxes, and presents the proposed encryption system. Section 3 presents the extensive security analysis of the proposed encryption system followed by a concise and clear conclusion in Section 4.

2  Basic Theory and the Proposed S-Boxes-Based Encryption System

In this section of the paper, the basics of the algorithm used in the proposed encryption system are discussed.

2.1 Artificial Bee Colony Algorithm (ABC)

The ABC algorithm, introduced by Karaboga in 2005, mimics the foraging behavior of honey bee colonies to solve optimization problems [20]. It involves finding a vector that minimizes an objective function. The algorithm starts with a random population of solution vectors and iteratively searches for the best solution. In this study, the random search behavior of bee colonies is utilized to create S-boxes. The ABC algorithm is composed of four distinct phases, explained in detail in the following section.

2.1.1 Initialization Phase

All the possible vectors of the populations are initialized by the scout bee and the control parameters are set. The initialization is performed according to Eq. (1) [20].

yna=ja+rand(0,1)∗(vi−ji)(1)

Here is the population vector which holds  (a=1,2,3,…,n), this needs to be optimized to get a minimized objective function. vi and  ji are the higher and lesser bounds of the  yna.

2.1.2 Employee Bee Phase

The task of the employee is to search for a new food source and determine its richness. Mathematically richness can be quantified through a fitness function. For finding the nearest food source the relation in Eq. (2) [20] can be used.

uma=yna+∅na(yna−yla)(2)

Here yna is a randomly selected food source and is a randomly chosen number from  (−a, a). The fitness function for the solution might be figured using the relation as in Eq. (3) [20].

fitn={11+fn(yn→)if fn(yn→)≥01+abs(fn(yn→))if fn(yn→)<0}(3)

where fn(yn→) is the objective function value of the solution of yna.

2.1.3 Onlooker Bee Phase

Apart from the employed bees there exist two other groups named onlooker bees and scout bees. Employer bees share the food source evidence with onlooker bees. The onlooker bees compute the fitness value of the food source and based on this evidence the food source is selected or rejected. If rejected, the same process goes iteratively. The probability with which a food source is chosen is given by Eq. (4) [20].

Pn=fn(yn→)∑n=1SNfn(yn→)(4)

2.1.4 Scout Bees

Scouts are a group of bees who chooses their food sources randomly. After some predefined number of trials, employed bees whose solution is not improved become scouts. Scouts start the search process by choosing from a random location.

2.2 Logistic Chaotic Map

Owing to sensitivity to preliminary conditions, chaos has been commonly used in cryptography. The logistic chaotic map is given by Eq. (5) [21].

yn+1=ryn(1−yn)(5)

Here yn is the initial condition of the chaotic map, and its value is between zero and one. r ∈ (0, 4). The map reveals chaotic behavior for 3.56< r <4. Here is the initial condition yn is calculated from the 32-length encryption key using the procedure in Eqs. (6) to (11) [21].

sum=[x(1,1)+x(1,2)+x(1,3)+x(1,4)+⋯+x(1,32)](6)

y1=[x(1,19)+x(1,17)+sum28+0.01](7)

y2=[x(1,14)+x(1,12)+sum28+0.01](8)

y3=y1−floor(y1+0.01)+0.01(9)

y4=y2−floor(y2+0.01)+0.01(10)

yn=[y3,y4](11)

2.3 Generation of Exclusive OR (XOR) Map

To decrease the association amongst the neighboring pixels first, we have to generate a chaos-based map of the same dimension of the image. The process of generating an XOR map is given below:

Step 1: The initial conditions for the logistic map are obtained using the technique discussed in the above section.

Step 2: The logistic chaotic map is iterated 10,000 times. The value for each iteration lies between 0 and 1. This value is multiplied by 1000000 and then the mode 256 operations are performed.

Step 3: The final values for each iteration are in the range 0 to 255.

Step 4: From these values, an N × N logistic map is calculated, which will be utilized in the proposed encryption system for the process of diffusion.

2.4 Shuffling Algorithm

The algorithm used for shuffling involves moving rows in a specific manner. In each channel, the first row remains unchanged, while the second row is shifted left circularly by one. The third row is shifted circularly to the right by two, and the nth row is shifted circularly to the right by N-1. During decryption, the opposite of this process takes place, with circular left shifting being performed instead of circular right shifting. This shuffling technique generates diffusion in the cryptosystem, making it difficult to establish a relationship between the plaintext and ciphertext.

2.5 Proposed S-Box Generation

Three S-boxes have been proposed in this paper and are displayed in Tables 1–3, respectively. The proposed S-boxes are generated from the position vectors of the bees of the ABC algorithm. The S-boxes are designed and calculated as depicted in Fig. 1. The procedure is described as:

Figure 1: The proposed system for the generation of highly non-linear S-boxes

Step 1: The number of bees in the ABC along with their starting positions is initiated.

Step 2: The fitness function is calculated and based on the fitness function outcome the position is updated or terminated.

Step 3: All the position vectors of the bees are calculated and stored. In a vector, in each iteration, this process is carried out.

Step 4: Saved position vectors are loaded and multiplied by a large number and then mode 256 is performed.

Step 5: The outcome from step 4 is stored in a 1 × 256 vector. This vector contains unique values as no values should not be repeated.

Step 6: The proposed S-box is checked for non-linearity. If the nonlinearity is less than 110. The S-box is discarded otherwise it is saved.

2.6 Non-Linearity

The nonlinearity of S-boxes is essential for ensuring the security of encryption systems. Randomness and unpredictability makes it challenging for intruders to decipher encrypted data. Linear S-boxes, on the other hand, are more vulnerable to intruding. Therefore, incorporating nonlinearity adds complexity and strengthens the security of the encryption system. It is crucial to assess and maintain sufficient degrees of nonlinearity in the S-boxes to ensure a high level of security. The nonlinearity of the S-boxes can be calculated using the relation in Eq. (12).

Non−linearity of Boolean function, fb=12(2x−Wmax(fb))(12)

Here x is the total of input bits, in our case  x=8. Wmax(fb) is the Walsh-Hadamard transform of  (f), and can be calculated in the relation in Eq. (13).

Wmax(fb)=H2N|(−1)fb|(13)

The nonlinearity of the S-boxes is calculated and tabularized in Table 4. The comparison of the proposed S-box with the newly proposed S-boxes nonlinearity is given in Table 5. From the non-linearity analysis, it is clear that the encryption system utilizing these S-boxes will possess a high degree of immunity to linear cryptographic attacks.

2.7 Strict Avalanche Criteria (SAC)

SAC is the 50% modification in output when the input is altered by only one bit. In our case, the SAC of the proposed S-boxes is calculated and tabulated in Table 5. The calculated values of SAC come out to be approximately 0.5 which is near to the theoretical value. The SAC of the proposed S-boxes is compared with the recently proposed S-boxes in Table 5. The comparison reveals that the proposed S-boxes will provide a high degree of immunity to differential cryptanalysis.

2.8 Bijectivity

The bijectivity of S-boxes is crucial for the security of cryptographic systems, ensuring the confidentiality and integrity of information. Bijectivity means that each input has a unique output and vice versa, preventing duplication or repetition. Non-bijective S-boxes pose risks, as different inputs could yield the same output, potentially leading to information loss and security breaches. Designers employ techniques like using known bijective functions or nonlinear functions with proven bijectivity, such as the Advanced Encryption System (AES) S-box. Our S-boxes fulfill the criteria of bijectivity within the range of [0, 255], making them unique and secure.

2.9 Bit Independent Criteria (BIC)

In BIC we are checking the correlation of the two resultant vectors that are created by altering one bit in the input. Let vector A is obtained by altering bit 0 of the input vector and vector B be obtained by altering bit 2 of the input vector. The BIC can be calculated using the relation in Eq. (14).

BIC(Ai,Bj)=max1<c≤n⁡|correlation (Ai,Bj)|(14)

The outcome of BIC lies in the [0, 1] range. The ideal value of BIC is 0.5. We have calculated the values of BIC and tabulated them in Table 5. The comparison reveals that the proposed S-boxes will provide a high degree of immunity to differential cryptanalysis.

2.10 Encryption Using the Proposed S-Boxes

To check the power of the Proposed S-boxes, here we present an encryption system. This encryption system utilizes the proposed S-boxes. The implemented encryption system, which is depicted in Fig. 2 comprises the following steps.

Figure 2: Encryption using the proposed S-boxes

Step 1: Considerations for the logistic chaotic map are initiated from the encryption key as discussed in Section 2.2 of the article.

Step 2: The XOR map is generated as discussed in Section 2.2 and in parallel, the original image is split into R, G, and B channels, respectively.

Step 3: The three maps are XORed with the R, G, and B channels, respectively, by doing so the high correlation is smashed amongst the pixels.

Step 4: The process of shuffling as discussed in Section 2.4 is performed. Here the process of diffusion is completed.

Step 5: The S-box is generated from the ABC algorithm as discussed in Section 3. Here in this step utilizing these S-boxes, the process of substitution is performed.

Step 6: All three channels are joined to obtain the final encrypted Red-Green-Blue (RGB) Image.

3  Security Analysis

Conducting a thorough security analysis is essential for robust encryption systems. It identifies vulnerabilities, strengthens security, and safeguards sensitive data. Our research includes comprehensive security analyses to assess the resilience of our proposed encryption system, incorporating S-boxes, against diverse cryptographic attacks.

3.1 Brute Force Attack

The brute force attack is a technique used by hackers to discover passwords or encryption keys by systematically trying all possible combinations. Skilled attackers find this attack valuable because it does not rely on prior knowledge of the target password or key. Longer and more complex passwords or keys are harder to crack using brute force attacks due to the increasing number of combinations. Our research focuses on generating initial conditions that offer high resistance to brute force attacks in encryption systems, as explained in Section 2.2 of the paper.

3.2 Histogram Analysis

The histogram is a representation of the number of pixels in an image. For high-contrast images, the histogram is non-uniform and spread out over the x-axis. This can give intruders information about the image’s contrast and brightness, which they can use to break the encryption. To prevent this, the encrypted image’s histogram must be uniform. In Fig. 3, the histogram of the plain image is shown, and it can be seen that they are non-uniform. However, in Fig. 3, the histogram of the encrypted R, G, and B channels is shown to be uniform and devoid of any useful information for intruders. Our S-boxes-based system is thus claimed to be secure against histogram-based attacks based on this histogram analysis.

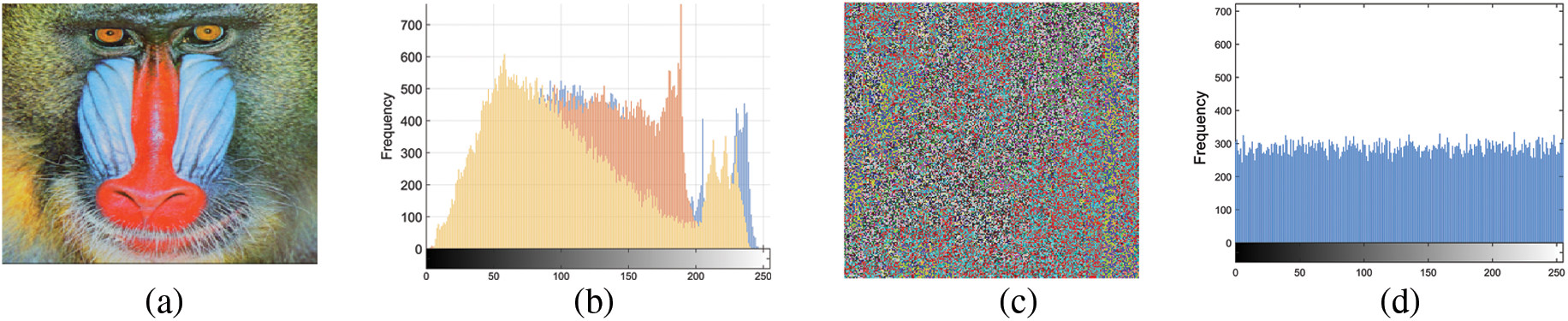
Figure 3: Histogram analysis; (a) plaintext image, (b) histogram of plaintext image, (c) encrypted image, and (d) histogram of encrypted image

3.3 Differential Analysis

In differential analysis, the intruder takes an image, encrypts it, and then changes one pixel in the plain image and again encrypts that image and they try to find the function of the encryption system from these pairs of plain images and encrypted images to resist differential analysis. Any encryption system must have a 99% score for Number of Pixel Change Rate (NPCR) and a 33% score for Unified Averaged Changed Intensity (UACI). The NPCR and UACI are calculated and discussed in the following section. The NPCR of an image having dimension X × Y × 3 is calculated using the relation in Eq. (15).

NPCR=1X×Y×3∑i=1X∑j=1Y∑k=13p(i,l,k)×100(15)

where,

p(i,j,k)={1I1(i,j,k)=I2(i,j,k)0elsewhere(16)

where I1 is the result of encryption of the unchanged image and I2 is the result of encryption of one pixel changed image. The NPCR of the two images is calculated and tabulated in Table 6. The UACI of an image having dimension X × Y × 3 is calculated using the relation in Eq. (17).

UACI=1X×Y×3∑i=1X∑j=1Y∑k=13|I1(i,j,k)−I2(i,j,k)|255×100(17)

where I1 is the result of encryption of the unchanged image and I2 is the result of encryption of one pixel changed image. The UACI of the two images is calculated and tabulated in Table 7.

3.4 Computational Complexity Analysis

The subjectivity of time analysis relies on the platform used for the encryption system. In the case of Field Programmable Gate arrays, a complex system can be encrypted in mere seconds. Our team implemented the encryption system in MATLAB, which was installed on a computer containing an Intel(R) Core(TM) i7-7700 processor @ 3.60 GHz processor and 8 GB of Random Access Memory (RAM). We compared the time analysis of our system with the AES by encrypting the same images using both systems and then we presented the results in Table 8.

3.5 National Institute of Standards and Technology (NIST) Statistical Test

To keep encrypted images safe from intruders, the randomness of the encryption key is of utmost importance. To test the efficacy of the proposed encryption system, tests based on NIST SP 800-22 criteria have also been conducted.

Each test produced a real number between 0 and 1, which was then compared with a pre-established significance degree α. If the value of p was greater than α, then it meant that the encryption system had passed the test successfully. In the proposed system, the value of α was set to 0.01. The results of the test were tabulated in Table 9, and it can be inferred that the proposed encryption system has excellent statistical properties and is a superior choice for image encryption.

3.6 Key Sensitivity Analysis

The employed technique demonstrates remarkable sensitivity to even a slight modification in the encryption key. The starting condition for the erratic and unpredictable logistic map is equivalent to the key for the encryption method. Upon encrypting an image, the same initial conditions are utilized at the decryption end for the formation of the S-box. After creating the S-box, inverse S-boxes are generated for decryption. By varying the key, i.e., initial conditions of the chaotic map, the produced S-box is entirely distinct, and the decrypted image does not reveal any essential information. Fig. 4 exhibits the decrypted image using the original key and the decrypted image with a marginally altered key. The chaotic map, which has been XORed in step 2, is responsible for this key sensitivity.

Figure 4: Key sensitivity analysis: (a) plain image; (b) encrypted image, (c) correctly decrypted image, (d) decrypted image through slightly changing the key

4  Conclusion

In conclusion, this research has proposed a unique and innovative method for generating substitution boxes (S-boxes) for encryption systems in the context of multimedia technology. As the strength of the entire encryption system depends on the cryptographic strength of the S-box, it is essential to ensure its reliability and robustness. By integrating the Proposed S-boxes into the encryption system’s design and analyzing their nonlinearity, as well as other security parameters such as NPCR and UACI, we have demonstrated that the Proposed S-boxes provide a high degree of security to digital content during transmission and storage. This research provides valuable insights into enhancing the security of information sharing through insecure communication channels. Future studies could consider integrating multiple chaotic maps to enhance the robustness of the encryption scheme, optimizing the algorithm for better performance with large-scale real-world applications, and developing a dynamic key generation mechanism to increase security.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2024R333), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: This work was funded by Deanship of Scientific Research at Najran University under the Research Groups Funding Program Grant Code (NU/RG/SERC/12/3) and also by Princess Nourah bint Abdulrahman University Researchers Supporting Project Number (PNURSP2024R333), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Author Contributions: The authors confirm their contribution to the paper as follows: study conception and design: Y. Y. Ghadi, M. S. Alshehri, S. Almakdi, O. Saidani, N. Alturki, F. Masood, M. S. Khan; data collection: Y. Y. Ghadi, M. S. Alshehri, S. Almakdi; analysis and interpretation of results: M. S. Alshehri, S. Almakdi, O. Saidani, N. Alturki, F. Masood; draft manuscript preparation: O. Saidani, N. Alturki, M. S. Khan. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data is available with the corresponding author upon appropriate request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Wang and Q. Wang, “A novel image encryption algorithm based on dynamic S-boxes constructed by chaos,” Nonlinear Dynamics, vol. 75, no. 3, pp. 567–576, 2014. [Google Scholar]

2. M. Khan, L. Khan, M. M. Hazzazi, S. S. Jamal and I. Hussain, “Image encryption scheme for multi-focus images for visual sensors network,” Multimedia Tools and Applications, vol. 81, no. 12, pp. 16353–16370, 2022. [Google Scholar]

3. A. Elmoasry, L. S. Khan, M. Khan and I. Hussain, “A dual layer security scheme for medical images using Hessenberg and singular value decompositions,” Multimedia Tools and Applications, vol. 81, no. 10, pp. 14001–14022, 2022. [Google Scholar]

4. E. Tanyildizi and F. Özkaynak, “A new chaotic S-box generation method using parameter optimization of one dimensional chaotic maps,” IEEE Access, vol. 7, pp. 117829–117838, 2019. [Google Scholar]

5. M. Khan and T. Shah, “A construction of novel chaos base nonlinear component of block cipher,” Nonlinear Dynamics, vol. 76, no. 1, pp. 377–382, 2014. [Google Scholar]

6. R. W. Ibrahim, H. Natiq, A. Alkhayyat, A. K. Farhan, N. M. G. Al-Saidi et al., “Image encryption algorithm based on new fractional beta chaotic maps,” Computer Modeling in Engineering & Sciences, vol. 132, no. 1, pp. 119–131, 2022. [Google Scholar]

7. M. A. M. Khan, N. A. Azam, U. Hayat and H. Kamarulhaili, “A novel deterministic substitution box generator over elliptic curves for real-time applications,” Journal of King Saud University-Computer and Information Sciences, vol. 35, no. 1, pp. 219–236, 2023. [Google Scholar]

8. S. Zhu, X. Deng, W. Zhang and C. Zhu, “Secure image encryption scheme based on a new robust chaotic map and strong S-box,” Mathematics and Computers in Simulation, vol. 207, pp. 322–346, 2023. [Google Scholar]

9. S. Zhou, Y. Qiu, X. Wang and Y. Zhang, “Novel image cryptosystem based on new 2D hyperchaotic map and dynamical chaotic S-box,” Nonlinear Dynamics, vol. 111, no. 10, pp. 9571–9589, 2023. [Google Scholar]

10. S. Amina and F. K. Mohamed, “An efficient and secure chaotic cipher algorithm for image content preservation,” Communications in Nonlinear Science and Numerical Simulation, vol. 60, pp. 12–32, 2018. [Google Scholar]

11. Z. Li, C. Peng, W. Tan and L. Li, “A novel chaos-based color image encryption scheme using bit-level permutation,” Symmetry, vol. 12, no. 9, pp. 1497, 2020. [Google Scholar]

12. X. Wang and R. Si, “A new chaotic image encryption scheme based on dynamic L-shaped scrambling and combined map diffusion,” Optik, vol. 245, pp. 167658, 2021. [Google Scholar]

13. M. Kaur and V. Kumar, “A comprehensive review on image encryption techniques,” Archives of Computational Methods in Engineering, vol. 27, no. 1, pp. 15–43, 2020. [Google Scholar]

14. M. Khan, A. S. Alanazi, L. S. Khan and I. Hussain, “An efficient image encryption scheme based on fractal Tromino and Chebyshev polynomial,” Complex & Intelligent Systems, vol. 7, no. 5, pp. 2751–2764, 2021. [Google Scholar]

15. Z. Liu, C. Wu, J. Wang and Y. Hu, “A color image encryption using dynamic DNA and 4-D memristive hyper-chaos,” IEEE Access, vol. 7, pp. 78367–78378, 2019. [Google Scholar]

16. G. Alvarez and S. Li, “Some basic cryptographic requirements for chaos-based cryptosystems,” International Journal of Bifurcation and Chaos, vol. 16, no. 8, pp. 2129–2151, 2006. [Google Scholar]

17. Y. He, Y. Q. Zhang and X. Y. Wang, “A new image encryption algorithm based on two-dimensional spatiotemporal chaotic system,” Neural Computing and Applications, vol. 32, no. 1, pp. 247–260, 2020. [Google Scholar]

18. A. Alghafis, F. Firdousi, M. Khan, S. I. Batool and M. Amin, “An efficient image encryption scheme based on chaotic and deoxyribonucleic acid sequencing,” Mathematics and Computers in Simulation, vol. 177, pp. 441–466, 2020. [Google Scholar]

19. S. Khan, L. Han, H. Lu, K. K. Butt, G. Bachira et al., “A new hybrid image encryption algorithm based on 2D-CA, FSM-DNA rule generator, and FSBI,” IEEE Access, vol. 7, pp. 81333–81350, 2019. [Google Scholar]

20. D. Karaboga, “An idea based on honey bee swarm for numerical optimization,” Technical Report, Erciyes University, Engineering Faculty, Computer Engineering Department, vol. 200, pp. 1–10, 2005. [Google Scholar]

21. R. M. May, “Simple mathematical models with very complicated dynamics,” Nature, vol. 261, no. 5560, pp. 459–467, 1976. [Google Scholar] [PubMed]

22. S. S. Jamal, M. U. Khan and T. Shah, “A watermarking technique with chaotic fractional S-box transformation,” Wireless Personal Communications, vol. 90, no. 4, pp. 2033–2049, 2016. [Google Scholar]

23. M. Khan and Z. Asghar, “A novel construction of substitution box for image encryption applications with gingerbreadman chaotic map and S8 permutation,” Neural Computing and Applications, vol. 29, no. 4, pp. 993–999, 2018. [Google Scholar]

24. D. Lambić, “S-box design method based on improved one-dimensional discrete chaotic map,” Journal of Information and Telecommunication, vol. 2, no. 2, pp. 181–191, 2018. [Google Scholar]

25. T. Ye and L. Zhimao, “Chaotic S-box: Six-dimensional fractional Lorenz–Duffing chaotic system and O-shaped path scrambling,” Nonlinear Dynamics, vol. 94, no. 3, pp. 2115–2126, 2018. [Google Scholar]

26. M. Ahmad, I. A. Khaja, A. Baz, H. Alhakami and W. Alhakami, “Particle swarm optimization based highly nonlinear substitution-boxes generation for security applications,” IEEE Access, vol. 8, pp. 116132–116147, 2020. [Google Scholar]

27. F. Özkaynak, “Chaos based substitution boxes as a cryptographic primitives: Challenges and opportunities,” Chaotic Modeling Simulation, vol. 1, pp. 49–57, 2019. [Google Scholar]

28. A. Belazi, M. Khan, A. A. A. El-Latif and S. Belghith, “Efficient cryptosystem approaches: S-boxes and permutation–substitution-based encryption,” Nonlinear Dynamics, vol. 87, no. 1, pp. 337–361, 2017. [Google Scholar]

29. H. A. Ahmed, M. F. Zolkipli and M. Ahmad, “A novel efficient substitution-box design based on firefly algorithm and discrete chaotic map,” Neural Computing and Applications, vol. 31, no. 11, pp. 7201–7210, 2019. [Google Scholar]