A Novel Approach for Image Encryption with Chaos-RNA

1  Introduction

With the continuous popularization of big data and artificial intelligence technology, the importance of image transmission and encryption technology is becoming increasingly prominent. Image encryption finds diverse applications across various domains, encompassing scientific research, finance, healthcare, military safeguarding of confidential information, and scenarios like network communication and video surveillance. In the context of image transmission, ensuring the protection of the information contained within is paramount to prevent unauthorized access. But traditional encryption algorithms like Data Encryption Standard (DES), Rivest Cipher 4 (RC4), Blowfish, and Advanced Encryption Standard (AES) [1–4] have proven ineffective in encrypting large amounts of data, often with images that exhibit strong correlation and redundancy, rendering them unsuitable for image encryption purposes. The image encryption method through chaotic systems has emerged as a viable solution to address these challenges.

Chaotic systems are dynamic systems whose behavior is characterized by unpredictability and disorder. These systems exhibit desirable properties such as pseudo-aperiodicity, initial conditions sensitivity, ergodicity, and randomness, which make them well-suited for high-strength encryption protection [5]. Matthews introduced a typical logistic map in 1989, which is based on the Logistic map, as a means of generating chaotic sequence lists for text encryption [6]. However, it was not until 1998 that Fridrich first introduced real image encryption using a chaotic map by scrambling images directly with sequence values [7]. Subsequently, a plethora of algorithms has emerged that combine image encryption with chaotic systems [8–13]. Liu et al. [8] proposed a 4-dimensional conservative chaotic system, which has been comprehensively analyzed to exhibit stronger ergodicity and more robust pseudo-random sequences compared to dissipative chaotic systems, thus providing resistance against reconstruction attacks. In general, effective image encryption entails dividing the process into distinct stages of scrambling and diffusion.

Scrambling is a conventional encryption technique that has been used in early image encryption methods. The technique involves rearranging the position of pixels in plaintext images to achieve encryption. Examples of scrambling methods include Zigzag, Arnold, and spiral transformations, among others [14–18]. These methods rearrange the pixel positions in different ways, thereby making it difficult for unauthorized parties to access the original image data. Although these methods are useful, they are not without limitations. For instance, Zigzag transformation is an encryption method based on position replacement, which can be easily cracked by analysis of data distribution rules. Additionally, since the Zigzag transformation rearranges the original data, the amount of encrypted data increases, increasing the cost of storage and transmission. In summary, any encryption algorithm has certain limitations and defects, and it is essential to choose an appropriate encryption method based on specific application scenarios and requirements.

Diffusion is commonly employed to modify the values of regular image pixels, enhancing the encryption process. Several techniques have been utilized for diffusions, such as block diffusion, Boolean network, and fractal sorting matrix [19–21]. These methods transform the pixel values in a manner that guarantees the security of the encrypted image data and makes it challenging to access without the appropriate decryption keys. Recently, researchers have proposed a diffusion algorithm that utilizes Deoxyribonucleic Acid (DNA) sequence encoding and decoding. This approach involves converting binary values into DNA bases and modifying image pixels using DNA sequence binary operations. By adopting this method, encryption strength can be significantly enhanced, leading to improved security. Consequently, when selecting an encryption algorithm, it is crucial to consider specific application scenarios and requirements. Appropriate encryption methods should be chosen to enhance security.

DNA possesses excellent characteristics, such as a large storage capacity, fast calculation speed, and low energy consumption. Consequently, several methods utilizing DNA base sequences have been proposed for image encryption [22–25]. For example, Mohammed et al. [22] proposed a novel encryption algorithm by combining DNA and Salsa20. However, this method is susceptible to brute-force attacks despite having a lower correlation coefficient than other approaches. Literature [23] employed a comprehensive set of techniques, including quantum chaos, DNA sequences, the hash algorithm, matrix permutation, bitwise Exclusive OR (XOR), discrete wavelet transform, and image block permutation, to encrypt and protect multimedia content. However, the article lacks sufficient experimental data to demonstrate the effectiveness and superiority of the proposed encryption algorithm, especially regarding encryption speed testing and resistance against cropping attacks.

In recent years, there are relatively few studies on RNA encryption algorithms, and most of the literature [26–29] utilized the codon algorithm for encryption. Additionally, some studies employ RNA operations to encrypt each pixel in the image, where the RNA sequence is obtained by encoding the pixel value. Mahmud et al. [26] supposed a method converts images into binary sequences and codon arrays using a customized codon truth table. Subsequently, the codon array is updated by employing the key and the RNA table to establish the initial population for the genetic algorithm. Eventually, the genetic algorithm is applied to optimize the population. Despite demonstrating good information entropy, this scheme is unsuitable for encrypting color images and lacks robustness against cropping and noise attacks. Literature’s [29] operation involves base pair-based encryption operations, which can enhance encryption security. However, it results in low encryption efficiency and is unsuitable for encrypting a large number of images.

Based on the above discussion, the importance of image encryption is self-evident. Chaotic systems have shown promise in providing robust encryption foundations due to their unpredictable nature. However, existing algorithms face challenges such as inadequate chaotic characteristics, insufficient key randomness, and vulnerabilities in RNA coding. To address these issues, this study presents a novel chaos-RNA encryption scheme. The article presents the following contributions:

(1) An improved 1DCM system with better randomness and chaotic characteristics is obtained by improving the one-dimensional chaotic system.

(2) Four new RNA operation rules are proposed, improving the complexity and security of RNA encryption.

(3) A method for image-filling pixel blocks of images is proposed. The pixel filling is performed first, then the plaintext image is split into multiple block matrices.

(4) A new RNA diffusion method is proposed, using 1DCM to generate chaotic sequences as the basis for randomly selecting encoding rules, decoding rules, and participating in RNA encoding operations.

The rest of the paper is structured as follows: Section 2 provides the theoretical background, Section 3 introduces the encryption scheme, Section 4 presents the simulation results, Section 5 conducts the performance analysis, and finally, the paper concludes in Section 6.

2  Theoretical Background

2.1 An Improve One-Dimensional Chaotic Map

According to the description in literature [30], optimizing trigonometric functions and correlation coefficients can enhance the performance of the reference chaotic map by constructing an improved one-dimensional chaotic map (1DCM).

In the 1DCM, this research uses the following iterative formula:

xn+1=f(xn)(1)

f(x)=πarcsin⁡(cos⁡(rx))(2)

Here r is a parameter, and r ∈ [0, 10], x is the variable, x ∈ [−5, 5].

The histogram of sequence statistics in literature [30], as shown in Fig. 1a, indicates that the distribution of the chaotic sequence of a one-dimensional chaos map is not uniform enough, and some data is concentrated on the left side. However, for a chaotic system to be effective, its chaotic sequence should have a uniform numerical distribution. Optimization measures can be taken to address this issue and improve the chaotic performance. For instance, the histogram of the improved 1DCM proposed in this paper is presented in Fig. 1b. The improved function mapping has a broader range and higher randomness, enabling it to enter the chaotic state more quickly and effectively. Fig. 1c displays the bifurcation diagram of the one-dimensional chaotic map when the parameter r is in the range of [0, 10] and the iteration range of the state variable x is within [−5, 5]. Fig. 1d displays the Lyapunov exponent (LE) diagram of the system, which demonstrates the excellent chaotic performance of the system. The behavior of the 1DCM system varies at different values of the parameter r, as follows:

Figure 1: 1DCM performance: (a) Histogram of literature [29] chaotic sequence. (b) Histogram of the 1DCM sequence. (c) Bifurcation diagram. (d) Lyapunov exponent diagram

r = 0: the system converges to a fixed point where x stabilizes around 4.93.

0 < r < 0.313: the system exhibits periodic dynamic behavior with all negative LE, indicating asymptotic stability. Moreover, as r increases, the number of cycles gradually grows.

r≈0.313: the system reaches its first bifurcation point, leading to a transition from periodic behavior to chaotic behavior.

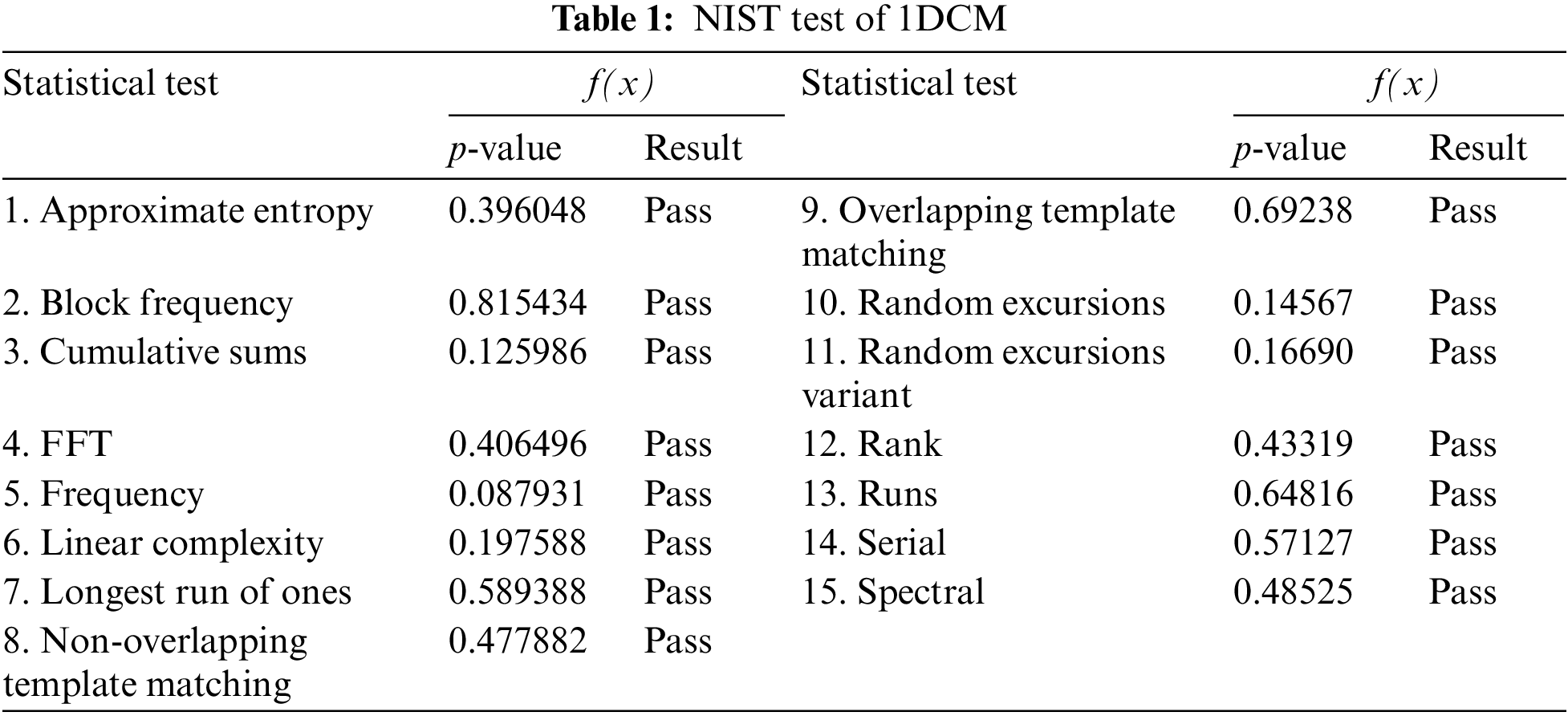
0.313 < r ≤ 10: the system displays chaotic dynamic behavior with positive LE. Additionally, we conducted the National Institute of Science and Technology (NIST) randomness test on the binary numbers generated by the pseudo-random sequence of the chaotic map. The test results, demonstrating the successful passing of all items, are presented in Table 1. Therefore, the chaos system utilized in the RNA diffusion stage of this paper demonstrates significant randomness. As a result, the 1DCM has a wider dynamic range, stronger pseudo-randomness, and better chaotic behavior than other systems. In addition, the mathematical formula is relatively simple, can generate random numbers faster, and can speed up the related work of RNA diffusion.

2.2 Lü Hyperchaotic System

The Lü chaotic system is a three-dimensional (3D) chaotic map proposed by Lü et al. in 2001 [31] that represents the transition process between the Lorenz and Chen systems. The system has a wide range of initial values, and its formula is given by:

x˙=a(y(t)−x(t))(3)

y˙=−x(t)z(t)+c(y(t))(4)

z˙=x(t)y(t)−b(z(t))(5)

when a = 36 and b = 3, different chaotic states can be prevented by changing the value of c, as follows:

12.7 < c < 17.0: showing the state of Lorenz attractor.

17.0 < c < 23.0: showing the state of Lorenz and Chen transitional attractor.

23.0 < c < 28.5: showing Chen’s chaotic attractor state.

In this study, the parameters a and b are given inputs, and the values of c are varied to observe the different chaotic states. When c = 15, c = 20, c = 28, and c = 28.8, the ordinary differential Equations 45 (ode45) equations were used to solve the problem, and the multi-scroll attractor was drawn. Figs. 2a–2d depict the three-dimensional attractor diagrams of the Lü chaos system for different values of c. This study selects the chaotic state of the Lü system at 23.0 < c < 28.5, which is similar to Chen’s chaotic state but has a larger initial value range, better chaotic characteristics, and a larger dynamic range than other value intervals.

Figure 2: 3D chaotic attractor diagram of Lü chaotic map when a = 36, b = 3. (a) c = 15. (b) c = 20. (c) c = 28. (d) c = 28.8

The Lü chaos system has three Lyapunov exponents. As illustrated in Fig. 3a. When three initial values of the Lü chaotic system are 0.2, the resulting LE are LE1 = 1.26881, LE2 = 0.00783, and LE3 = −20.14903. The chaotic system is characterized by two positive Lyapunov exponents, which are classified as a hyperchaotic system. At the same time, it can observe its randomness from the iterative trajectories of the attractor Fig. 3b. Hence, the Lü chaotic system is a relatively complex, disordered, parameter-sensitive, and controllable system that exhibits chaotic and hyperchaotic behavior, depending on the choice of parameter values.

Figure 3: Lü chaotic system: (a) Lyapunov exponent diagram. (b) Attractor iterative trajectory diagram

2.3 RNA Encoding and Operations

RNA consists of four bases: adenine (A), cytosine (C), guanine (G), and uracil (U). Unlike DNA, RNA uses uracil instead of thymine. RNA bases pair with each other through hydrogen bonds, with A-U and G-C pairings being the most stable. By using the properties of RNA coding, it is possible to convert numbers or characters into RNA sequences, allowing for encryption. According to Table 2, the binary form of the number 27 can be RNA-coded using rule 2 to obtain the RNA sequence ACGU. Decoding using rule 6 would then yield the binary number 1011 0001, which is equivalent to 177 in decimal. The complementary relationship between A and U and C and G can be utilized in designing encoding rules. There are eight possible coding rules, allowing for more complex encryption operations to be performed.

Based on the RNA complementary pairing rules, and operation rules, eight RNA operators have been designed: addition (+), subtraction (−), XOR (⊕), XNOR (⊙), addition and inversion (+~), subtraction and inversion (−~), reverse addition (~+) and reverse subtraction (~−). By incorporating four additional operation rules into the traditional set, the strength of RNA operation encryption has been enhanced. Table 3 presents the newly introduced four RNA operation rules. In computing, the proposed eight RNA coding rules and eight RNA binary operations can generate 64 different encryption schemes for the operation between two bases, greatly enhancing the complexity and safeguarding of RNA encryption.

It is important to note that four of these operators are user-defined: addition and inversion operation (bitwise inversion operation after addition), subtraction and inversion (bitwise inversion operation after subtraction), reverse addition (addition after bitwise inversion operation) and reverse subtraction (bitwise inversion operation followed by subtraction).

3  Encryption Algorithms

This section presents a novel image encryption method for RNA coding, utilizing a chaotic system consisting of four key components. Firstly, the SHA-384 hash function produces the initial value, parameter, and block size. Secondly, the original image is divided into blocks based on the block size determined by the Lü chaotic map and the hash value and then subjected to Fisher-Yates permutation and sort permutation. Thirdly, introduces an improved 1DCM, which generates a chaotic sequence for encoding, decoding, and operation rules in the RNA diffusion process. Finally, the RNA encoding, decoding, and computing operations are executed. This encryption technique is designed for plaintext image encryption with M rows and N columns.

3.1 Key and Initial Value Generation

To prevent potential compromise of the encryption algorithm through pixel manipulation, the SHA-384 hash function is employed to generate 384-bit hash values. Subsequently, each 32-bit binary number is partitioned into twelve groups, ordered from the front to the back. This expression can be formulated as: K = K1, K2,...,K12. Ki = {ki,0, ki,1,...,ki,31}, and i is 1...12.

The initial values I1(x1, x2, x3) of the 1DCM chaotic system and the system parameter r are calculated by Eqs. (6) and (7):

x(i)=mod(bi2de(Ki⊕Ki+2⊕Ki+4),232)/256i=1,2,3(6)

r=−5+10×(bi2de(K1⊕K5⊕K11)/232)(7)

where bi2de(a) converts binary number a to decimal, a⊕b performs XOR operation on a and b, and mod (a, b) takes the result modulo (a, b).

The calculation of initial value I2(x4, x5, x6) and system parameter c of Lü super system is through Eqs. (8) and (9):

x(i)=mod(bi2de(Ki⊕Ki+3⊕Ki+6),232)/256i=4,5,6(8)

c=23+5.5×(bi2de(K2⊕K6⊕K12)/232)(9)

The sub-block size of the image to be split is determined by calculating rows’ number (m) and columns (n) using Eqs. (10) and (11):

m=mod(bi2de(K1⊕K5⊕K11),5)+4(10)

n=mod(bi2de(K2⊕K5⊕K12),5)+4(11)

3.2 Scrambling and Diffusion Scheme

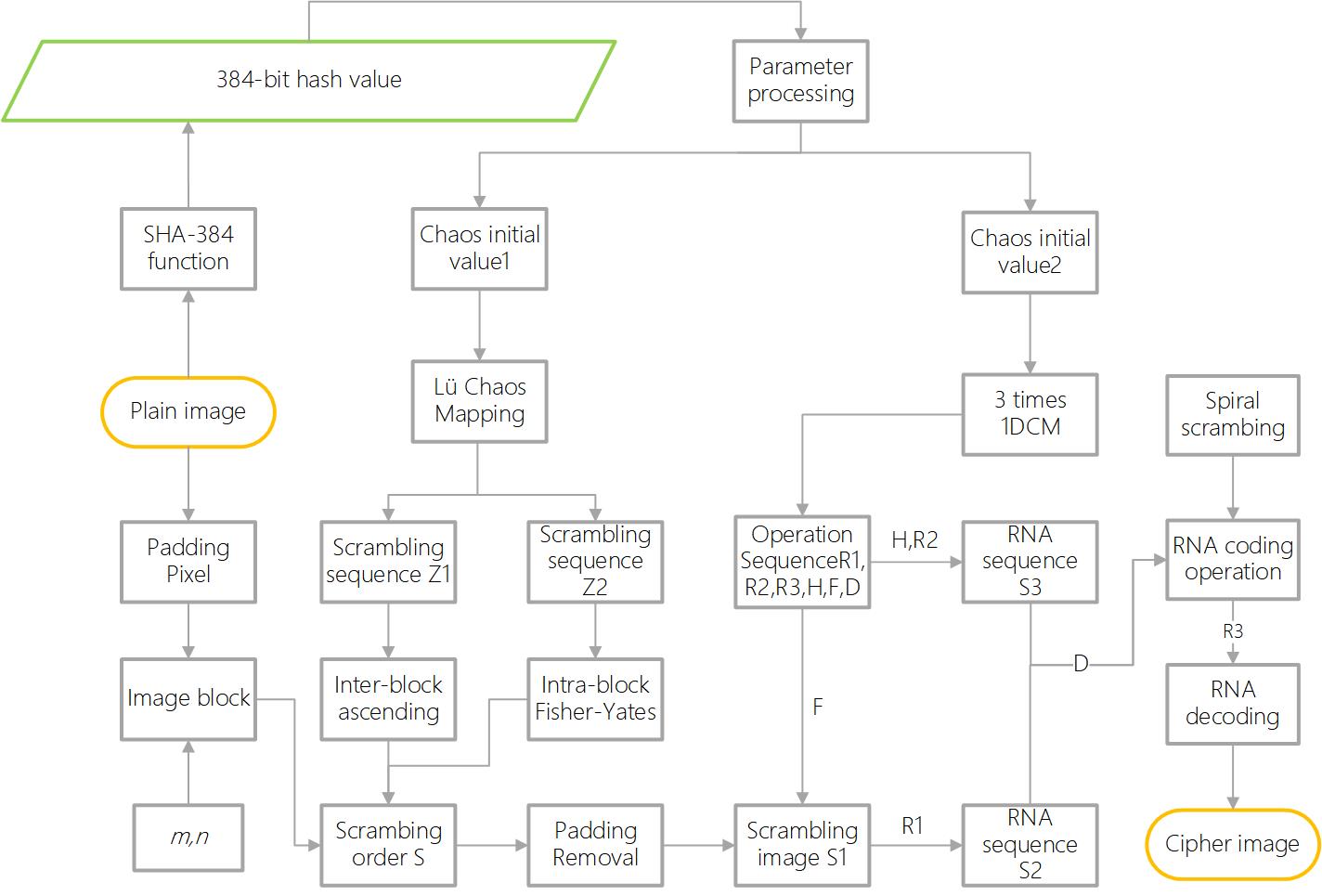
To increase the security of the encryption algorithm, the study explores a novel diffusion and permutation model. Fig. 4 depicts a comprehensive flowchart of this encryption algorithm.

Figure 4: Flowchart of encryption algorithm

The encryption scheme involves the following specific steps:

Step 1: The sub-block size of the image after block partitioning needs to be calculated from the above equation and results in an m × n size for each sub-block. However, pixel padding is required since an image can not be divided into complete sub-blocks. The padding is applied by adding mb rows and nb columns to the original image. Additionally, these pixels are assigned a value of 260 using Eq. (12). The img means the padded image. The ones (m, n) operation creates a matrix of size m rows and n columns filled with ones.

{mb=m−mod(M,n)nb=n−mod(N,n)img=img+260×ones(M,mb)img=img+260×ones(nb,N+nb)(12)

Step 2: Initialize the Lü hyperchaotic system with the initial values x4, x5, x6, and the value of the parameter c, and iterate it for 1024 + (M + mb) × (N + nb) times. To eliminate the transient effects, remove the first 1024 iterations and obtain three chaotic sequences, T1, T2, and T3, for scrambling operations.

Step 3: T1, T2, and T3 are further transformed by using Eqs. (13) and (14) to obtain two additional permutation sequences, Z1 and Z2, which greatly enhance the randomness of the original sequences.

Z1=mod(|T1(end−(M+mb)×(N+nb)m×n+1:end)|×215,1)(13)

Z2=mod(T2+T3(end−⌊(M+mb)×(N+nb)m×n⌋/2+1:end)×215,1)(14)

Step 4: To perform an effective intra-block and inter-block scrambling, rearrange each m × n-sized sub-block of img according to the sort index of the permutation sequence Z1. Then, apply the Fisher-Yates permutation method to each block pixel using the permutation sequence Z2 to combine intra-block and inter-block scrambling operations. The resulting matrix S represents the scrambled image.

In this case, the 3 × 3 sub-block is taken as an example, Fig. 5 depicts the specific schematic diagrams illustrating the process of scrambling the pixels in ascending order. Fig. 6 illustrates the sequential operation within the block, following the steps of the Fisher-Yates algorithm. In each step, the value at the current position is exchanged with the value at a randomly chosen position, with the constraint that it cannot be exchanged with itself.

Figure 5: Inter-block scrambling

Figure 6: Intra-block scrambling

Step 5: Perform a scrambling operation on img according to the obtained block scrambling matrix S. The filled pixel values are removed to finally obtain the scrambled image S1.

Step 6: For the 1DCM chaotic system, r is used as a parameter, and the system initial values x1, x2, and x3 are respectively substituted into the 1DCM system for 3MN iterative operations to get three chaotic sequences X1, X2, and X3.

Step 7: To diffuse the pixel value of S1, two addition modulo operations are performed, resulting in the diffused pseudo-random image S2 through Eq. (15).

S2=mod(S1+mod(floor(X3(1:MN))×216,256),256)(15)

Step 8: The RNA codec rules R1 and R2, decoding rule R3, chaotic sequences H, F, and diffusion operation rule D are generated based on Eqs. (16) and (17).

{R1=mod(floor(X1(1:MN)×216),8)R2=mod(floor(X1(MN+1:2MN)×216),8)R3=mod(floor(X2(1:MN)×216),8)(16)

{H=mod(floor(X2(MN+1:2MN)×216),256)F=mod(floor(X3(1:MN)×216),256)D=mod(floor(X3(MN+1:2MN)×216),256)(17)

Step 9: Applying the RNA encoding process to diffuse images S2 and chaotic sequences H, based on the RNA coding rules R1 and R2. The image is dynamically encoded pixel by pixel using the corresponding coding rules, resulting in an RNA matrix, RNA sequence Sd. Furthermore, the chaotic sequences H and F are encoded using the R2 codec rule, producing the sequences H1 and F1.

Step 10: The ciphertext matrix C is calculated by applying spiral diffusion operation to the M × N pixels based on the random values in the diffusion sequence Sd and further scrambling the image. The specific ciphertext matrix is generated using Eqs. (18) to (20). These operations greatly increase the complexity and security of encryption.

C(1:8)=img(1:8)⊕H1(1:8)(18)

C(8i−7:8i)=cmd(Sd(8s−7,8s),H1(8i−7,8i),D1(8i−7,8i),F(8s−7,8s),C(8i−15,8i−8))(19)

cmd(A,B,C,D,E){A⊕B+∼C∼−D+EF(i)=0A⊕B+∼C∼−D−EF(i)=1A⊙B+∼C∼−D+EF(i)=2A⊙B+∼C∼−D−EF(i)=3A⊕B−∼C∼+D+EF(i)=4A⊕B−∼C∼+D−EF(i)=5A⊙B−∼C∼+D+EF(i)=6A⊙B−∼C∼+D−EF(i)=7(20)

Here, cmd is a custom formula. s = spiral(i), define s as the position of i within the spiral matrix. i = {2, 3,..., MN}. Operator: ⊕, ⊙, +, −, +~, −~, ~+, and ~− represent the XOR operation, Exclusive NOR (XNOR) operation, addition, subtraction, addition with negation, subtraction with negation, addition after negation, and subtraction after negation, respectively of RNA.

Step 11: After the operations above, the encrypted image CP is obtained by decoding the ciphertext image C and converting it into an M × N-sized image, according to the RNA decoding rule R3.

The decryption process, which is the reverse of the previously described process, is not described here.

4  Simulation Results

The experimental simulations were performed using MATLAB R2022A on a laptop equipped with an Intel i5-12500H processor, 16 GB of memory, and running the Windows 11 system.

Fig. 7 displays the scrambled and encrypted decrypted images of four plaintext images of different sizes and colors. The figures indicate that the scrambled and encrypted images both contain noise. However, the encrypted images that underwent diffusion appear to have undergone more sophisticated encryption than the scrambled images. The proposed encryption algorithm effectively conceals valuable information, as extracting any information from scrambled and encrypted images is impossible. What's more, the football image was successfully encrypted using the algorithm, proving its adaptability to non-square images of different sizes and colors. Overall, the results indicate the validity of the encryption algorithm and its adaptability to diverse image sizes and colors.

Figure 7: Shows the simulation results for different images: (a) Plane (512 × 512). (b) Couple (256 × 256). (c) Football (320 × 256). (d) Airport (1024 × 1024) grayscale image

5  Performance Analysis

5.1 Differential Attack

A secure encryption algorithm should produce a significant difference between the plaintext image and ciphertext images when a pixel value in a normal image is changed [32]. To test the impact of a single-pixel change on the entire image encrypted by the proposed algorithm, two commonly used metrics were employed: Normalized Pixel Change Rate (NPCR) and Unified Average Changing Intensity (UACI) [33]. NPCR and UACI can be calculated for RGB images using Eqs. (21) to (23).

NPCRR,G,B=1W×H∑i,jDR,G,B(i,j)×100%(21)

DR,G,B(i,j)={1,C1(i,j)≠C2(i,j)0,C1(i,j)=C2(i,j)(22)

UACIR,G,B=1W×H(∑i,j|C1R,G,B(i,j)−C2R,G,B|255)×100%(23)

C1 and C2 represent the encrypted images before and after a pixel value in the plaintext image is modified. The parameters W and H refer to the width and height of the images.

Table 4 shows that the NPCR values were close to the ideal value, with a deviation of less than 0.02%, and the average NPCR values were all greater than 99.6094%. The expected value of UACI for two random images is approximately 33.4635%, and all UACI values in Table 4 were close to this value. These results demonstrate the high sensitivity of the proposed encryption algorithm to changes in normal images and its ability to withstand various attacks. Furthermore, compared with other algorithms in the literature [34–37], Table 5 shows that this method better closer to the theoretical values. Specifically, the proposed encryption algorithm outperforms other algorithms in NPCR and UACI, which indicates that the modified pixel values significantly affect the statistical characteristics of the encrypted image, thereby enhancing the algorithm’s security.

5.2 Histogram Analysis

An image’s pixel value distribution is often represented through histograms, a statistical feature. The consistency of the pixel values can be assessed by graphing the frequency of pixels for each color intensity level. Figs. 8a–8c display the histograms of color plaintext images “Lena”, “Lake”, and “Plane” and Figs. 8f–8h display the histograms of their ciphertext images. Figs. 8d and 8i, respectively, show the histograms of the grayscale image “Airport” and its ciphertext images, while Figs. 8e and 8j show the histograms of pure “Black-white” plaintext and cipher images for comparison. It is clear from Fig. 8 that the histogram of the encryption image is relatively informal, and no hidden plaintext information can be discerned.

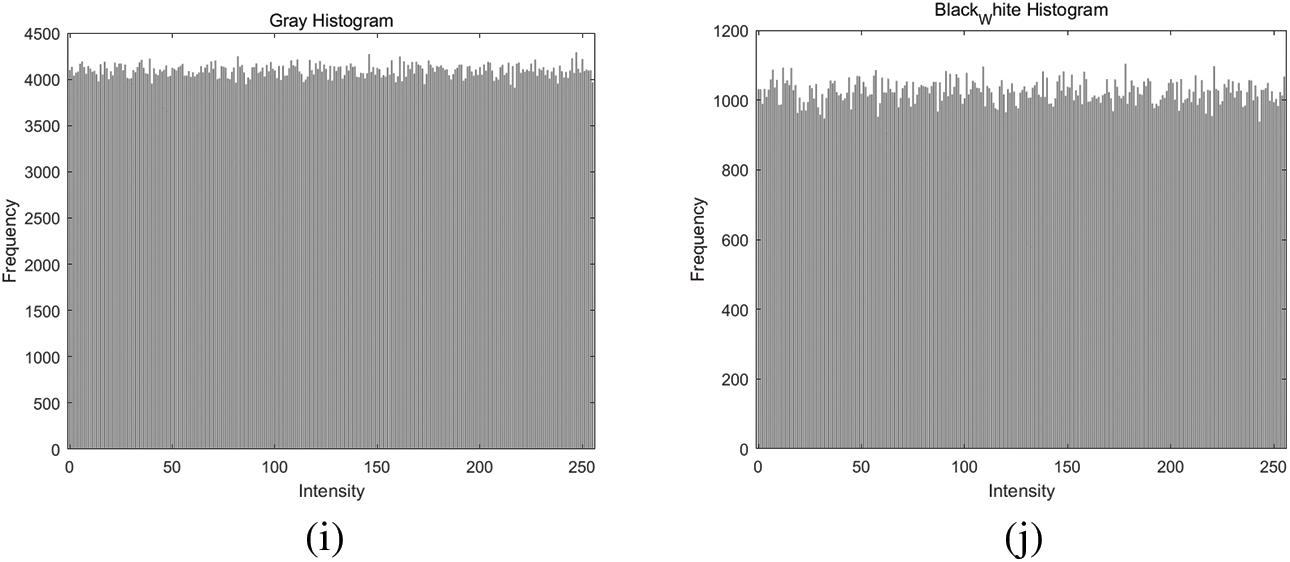
Figure 8: Histogram of the original image and encryption image

5.3 Key Analysis

An effective image encryption algorithm requires a sufficiently large key space to withstand brute force attacks. The key consists of 384 binary arrays generated via the SHA-384 algorithm. Therefore, the size of the encryption algorithm proposed in this paper is 2384. Clearly, the proposed encryption algorithm has a key space much larger than the encryption requirement of 2100. This is far beyond the processing capability of current computing technology, indicating that the key space is difficult to crack with traditional methods.

A high-quality encryption algorithm should be highly sensitive to changes in the keys, where a small alteration can result in a significant change in the output. In this paper, the algorithm's sensitivity to modifying one bit of the hash value of the key’s SHA-384 is analyzed. The specific changes are as follows:

K = 52ee65115c89ec88990d3cec71aad8bfc39e17ebd4156f0a5be002dc5fd797a59c52a0cc9332d465f92c108a73f5be84;

K1 = 42ee65115c89ec88990d3cec71aad8bfc39e17ebd4156f0a5be002dc5fd797a59c52a0cc9332d465f92c108a73f5be84.

Decrypting the ciphertext image encrypted with K using K1 does not yield the correct plaintext image (as Fig. 9c). Furthermore, the decrypted image using K1 demonstrates average values of NPCR (99.60%) and UACI (32.23%) that closely resemble the ideal values of the ciphertext. This observation highlights the high sensitivity of the encryption key.

Figure 9: Key sensitive: (a) Encrypted image. (b) Decrypted image using K. (c) Decrypted image using K1

5.4 Correlation Analysis of Adjacent Pixels

In addition to histogram analysis, pixel correlation analysis is also significant. Four thousand adjacent pixels were chosen from the plaintext and encrypted images in different directions. The results of correlations in different directions on the R channel, G channel, and B channel are presented in Fig. 10, which showcases the Lena test image. The figure clearly demonstrates that the RGB channels of plaintext images exhibit strong correlations in all three directions. In contrast, the corresponding cryptographic images have low correlations and a uniform distribution of adjacent pixels. The image correlation results are presented in Table 6. The algorithm successfully eliminates image correlation and effectively withstands statistical attacks.

Figure 10: Correlation analysis of different channel of Lena: (a) RGB channel of Lena image. (b) RGB channel of encrypted Lena image

5.5 Entropy Analysis

The randomness of a system and the uncertainty of image information are assessed using information entropy. A higher entropy value usually indicates more uncertainty and less visual information. The entropy formula is Eq. (24):

H(m)=−∑i=0Lp(mi)log⁡p(mi)(24)

where L refers to the gray level of the pixel, and p(mi) denotes the possibility of pixel mi.

Table 7 presents the computed entropy values of multiple plaintext and ciphertext images using the proposed algorithm, including the average entropy. From these data, it can be seen that entropy values for all encrypted images are nearly 8, indicating that the encrypted photos produced by the algorithm have a more uniform random distribution. In addition, the average entropy value of the encrypted images is 7.9991, which is bigger than the average value of the plaintext images. This indicates that the encrypted images using the encryption algorithm have an excellent random distribution function. The results demonstrate that the algorithm has better entropy characteristics than existing methods.

5.6 MLC Comparison

Majority logic criteria (MLC) is a metric used to assess the properties of Boolean functions and is a commonly employed texture feature in fingerprint image processing. In addition to correlation coefficients and information entropy, which have been previously analyzed, it also includes contrast, energy, and homogeneity. As shown in Table 8, different tests (contrast, homogeneity, correlation, energy, and entropy) are applied for comparison with other encryption algorithms to verify encryption quality. From Table 8, it can be observed that there is a significant change in the texture of the cipher image compared to the original Lena image when comparing MLC parameters before and after encryption. Additionally, the MLC parameters of the cipher image outperform the reference algorithm in terms of entropy, homogeneity, contrast, and energy, indicating a strong encryption effect of this algorithm.

5.7 Robustness Analysis

The transmission of images may result in data loss or information changes. Therefore, a robust encryption algorithm should be capable of recovering most of the valuable information even in these situations. This section tests the algorithms against clipping and noise attacks. A clipping attack refers to setting some pixel values of the ciphertext image to black, simulating an image being cropped. Fig. 11 shows the decrypted images of encrypted images (such as Fig. 7c) with different size blocks removed, respectively. It is evident from Fig. 11 that even when 56.25% (384 × 384 block) of data information is lost, the decrypted picture still contains a substantial amount of information and can recognize the general knowledge of the plaintext picture. This demonstrates that the algorithm is resistant to clipping.

Figure 11: Clipping attacks analysis. (a) 64 × 64 block removal. (b) 128 × 128 block removal. (c) 256 × 256 block removal. (d) 384 × 384 block removal. (e–h) Represent the decrypted images of (a–d)

Noise attack refers to the interference of ciphertext images with different degrees and types of noise. A reliable encryption system must have some degree of resistance to noise during transmission. In the following experiment, this study added dual noise to the encrypted image shown in Fig. 7c. The cipher images were corrupted with both salt & pepper noise and Gaussian noise, with the degree ranging from 0.00001 to 0.01. As the variance increases, the decrypted images in Fig. 12 show the decrypted image corrupted by varying degrees of salt & pepper and Gaussian noise. When the variance is 0.01, the plaintext image can still be seen clearly, indicating that the encryption algorithm can resist noise attacks well and is robust against them.

Figure 12: Decrypted images with different degrees of noise. (a) 0.00001. (b) 0.0001. (c) 0.001. (d) 0.01

5.8 Complexity and Speed Analysis

“Complexity and Speed Analysis” is regarded as one of the crucial criteria for assessing the efficiency of an algorithm. This analysis entails the evaluation of the algorithm’s time complexity and execution speed. The proposed image encryption algorithm consists of three methods: block scrambling, RNA dynamic encoding and decoding, and RNA diffusion. The block scrambling method has a time complexity of O(mb × nb × M × N), while RNA dynamic encoding and decoding have a time complexity of O(M × N). The RNA diffusion method has a time complexity of O(8 × M × N). Overall, the time complexity of this encryption algorithm is O(8 × M × N). The speed test of encryption can be used to evaluate the efficiency of encryption algorithms because a faster encryption speed usually means higher security for image transmission. Table 9 shows the encryption time of 512 × 512 × 3 Lena color images. It can be seen from the table that the encryption algorithm we proposed has higher efficiency, which means that the algorithm can encrypt and decrypt images faster, thereby improving the security of image transmission.

6  Conclusion

This paper presents a novel image encryption scheme that combines chaos and RNA techniques. This paper introduces a novel 1DCM, which demonstrates excellent diffusion characteristics assessed through bifurcation analysis, LE, NIST test, and chaos sequence analysis. The 1DCM algorithm is utilized to modify the pixel values of images, and it establishes RNA encoding, decoding, and operation rules. Additionally, 3D Lü chaos serves as a pseudo-random matrix, generating inter-block sorting scrambling and intra-block Fisher-Yates scrambling, thus enhancing the encryption intensity. Moreover, this study proposes four new RNA operation rules to enhance the security of the ciphertext.

The experimental results on grayscale and color images illustrate that the encryption scheme offers several advantages, including a significant key space, heightened sensitivity, high entropy, and adaptability for various image applications. Furthermore, it exhibits high resistance to noise, cropping, and known plaintext attacks. Therefore, the proposed encryption scheme is secure and reliable for image encryption and can be applied to secure communication. In future research, we aim to extend this method to multi-image encryption while enhancing the key space.

Acknowledgement: We would like to take this opportunity to express our heartfelt gratitude to all those who made a contribution to the completion of this article.

Funding Statement: This work was supported in part by the National Natural Science Foundation of China (NSFC) under Grant 62105004, and in part by the Open Fund of the State Key Laboratory of Mining Response and Disaster Prevention and Control in Deep Coal Mine under the Grant (SKLMRDPC19KF10).

Author Contributions: The authors confirm their contributions to the paper as follows: study conception and design: Y. Hong, J. Su; data collection: W. Xu, Y. Wei, J. Wu; draft manuscript preparation: S. Fang, Z. Yang. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data and materials used to support the findings of this study are available from the corresponding author upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. P. Raja, “Secured medical image compression using DES encryption technique in Bandelet multiscale transform,” International Journal of Wavelets, Multiresolution and Information Processing, vol. 16, no. 4, pp. 1850028, 2018. [Google Scholar]

2. K. Xu, L. He, Z. Dai and X. B. Fan, “The analysis of the number of fixed points in the key extending algorithm of RC4,” Science in China Series A: Mathematics, vol. 51, no. 3, pp. 407–415, 2008. [Google Scholar]

3. P. Karthigai Kumar and K. Baskaran, “An ASIC implementation of low power and high throughput blowfish crypto algorithm,” Microelectronics Journal, vol. 41, no. 6, pp. 347–355, 2010. [Google Scholar]

4. P. Muthukumar, P. Balasubramaniam and K. Ratnavelu, “Synchronization of a novel fractional order stretch-twist-fold (STF) flow chaotic system and its application to a new authenticated encryption scheme (AES),” Nonlinear Dynamics, vol. 77, no. 4, pp. 1547–1559, 2014. [Google Scholar]

5. Y. Zhou, Z. Hua, C. Pun and C. Chen, “Cascade chaotic system with applications,” IEEE Transactions on Cybernetics, vol. 45, no. 9, pp. 2001–2012, 2014. [Google Scholar] [PubMed]

6. R. Matthews, “On the derivation of a ‘chaotic’ encryption algorithm,” Cryptologia, vol. 13, no. 1, pp. 29–42, 1989. [Google Scholar]

7. J. Fridrich, “Symmetric ciphers based on two-dimensional chaotic maps,” International Journal of Bifurcation and Chaos, vol. 8, no. 6, pp. 1259–1284, 1998. [Google Scholar]

8. X. Liu, X. Tong, Z. Wang and M. Zhang, “A new n-dimensional conservative chaos based on generalized Hamiltonian System and its’ applications in image encryption,” Chaos, Solitons & Fractals, vol. 154, no. 4, pp. 111693, 2022. [Google Scholar]

9. X. Wang and S. Gao, “Application of matrix semi-tensor product in chaotic image encryption,” Journal of the Franklin Institute, vol. 356, no. 18, pp. 11638–11667, 2019. [Google Scholar]

10. X. Wang, S. Gao, L. Yu, Y. Sun and H. Sun, “Chaotic image encryption algorithm based on bit-combination scrambling in decimal system and dynamic diffusion,” IEEE Access, vol. 7, pp. 103662–103677, 2019. [Google Scholar]

11. Z. Hua, Y. Zhou and H. Huang, “Cosine-transform-based chaotic system for image encryption,” Information Sciences, vol. 480, no. 8, pp. 403–419, 2019. [Google Scholar]

12. Y. Xian, X. Wang, Y. Zhang, X. Yan and Z. Leng, “A novel chaotic image encryption with FSV based global bit-level chaotic permutation,” Multimedia Tools and Applications, vol. 82, no. 1, pp. 407–426, 2023. [Google Scholar]

13. A. Mahboob, I. Siddique, M. Asif, M. Nadeem and A. Saleem, “Construction of highly non linear component of block cipher based on Mclaurin series and Mellin transformation with application in image encryption,” Multimedia Tools and Applications, vol. 9, no. 20, pp. 1–19, 2023. [Google Scholar]

14. T. Pan and T. Li, “Image encryption algorithm based on 3D Arnold cat and Logistic map,” Advanced Materials Research, vol. 317–319, pp. 1537–1540, 2011. [Google Scholar]

15. X. Wang and S. Gao, “A chaotic image encryption algorithm based on a counting system and the semi-tensor product,” Multimedia Tools and Applications, vol. 80, no. 7, pp. 10301–10322, 2021. [Google Scholar]

16. W. Chen and X. D. Chen, “Optical image encryption using multilevel Arnold transform and non interferometric imaging,” Optical Engineering, vol. 50, no. 11, pp. 117001, 2011. [Google Scholar]

17. X. Wang and N. Guan, “A novel chaotic image encryption algorithm based on extended Zigzag confusion and RNA,” Optics & Laser Technology, vol. 131, no. 6, pp. 106366, 2020. [Google Scholar]

18. P. Ramasamy, V. Ranganathan, S. Kadry, R. Damaševičius and T. Blažauskas, “An image encryption scheme based on block scrambling, modified zigzag transformation and key generation using enhanced logistic—Tent map,” Entropy, vol. 21, no. 7, pp. 656, 2019. [Google Scholar] [PubMed]

19. Z. Tang, Y. Yang, S. Xu, C. Yu and X. Zhang, “Image encryption with double spiral scans and chaotic maps,” Security and Communication Networks, vol. 2019, no. 2, pp. 1–15, 2019. [Google Scholar]

20. X. Wang, S. Gao, X. Ye, S. Zhou and M. Wang, “A new image encryption algorithm with cantor diagonal scrambling based on the PUMCML system,” International Journal of Bifurcation and Chaos, vol. 31, no. 1, pp. 2150003, 2021. [Google Scholar]

21. Y. Xian, X. Wang and L. Teng, “Double parameters fractal sorting matrix and its application in image encryption,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 6, pp. 28–37, 2021. [Google Scholar]

22. R. A. Mohammed, M. A. A. Khodher and A. Alabaichi, “A novel lightweight image encryption scheme,” Computers, Materials & Continua, vol. 75, no. 1, pp. 2137–2153, 2023. [Google Scholar]

23. X. Wang and S. Gao, “Image encryption algorithm for synchronously updating Boolean networks based on matrix semi-tensor product theory,” Information Sciences, vol. 507, no. 2, pp. 16–36, 2020. [Google Scholar]

24. X. Wang, Q. Zhang and X. M. Bao, “A novel chaotic image encryption scheme using DNA sequence operations,” Optics and Lasers in Engineering, vol. 73, no. 10–11, pp. 53–61, 2015. [Google Scholar]

25. R. Guesmi, M. A. B. Farah, A. Kachouri and M. Samet, “A novel chaos-based image encryption using DNA sequence operation and secure hash algorithm SHA-2,” Nonlinear Dynamics, vol. 83, no. 3, pp. 1123–1136, 2016. [Google Scholar]

26. M. Mahmud, M. Lee and J. Y. Choi, “Evolutionary-based image encryption using RNA codons truth table,” Optics & Laser Technology, vol. 121, pp. 105818, 2020. [Google Scholar]

27. H. M. Mousa, “Partially deep-learning encryption technique,” Computers, Materials & Continua, vol. 74, no. 2, pp. 4277–4291, 2023. [Google Scholar]

28. A. A. Abbasi, M. Mazinani and R. Hosseini, “Chaotic evolutionary-based image encryption using RNA codons and amino acid truth table,” Optics & Laser Technology, vol. 132, no. 12, pp. 106465, 2020. [Google Scholar]

29. D. Zhang, L. Chen and T. Li, “Hyper-chaotic color image encryption based on transformed zigzag diffusion and RNA operation,” Entropy, vol. 23, no. 3, pp. 361, 2021. [Google Scholar] [PubMed]

30. A. C. Dascalescu, R. E. Boriga and A. V. Diaconu, “Study of a new chaotic dynamical system and its usage in a novel pseudorandom bit generator,” Mathematical Problems in Engineering, vol. 2013, no. 3, pp. 1–10, 2013. [Google Scholar]

31. J. Lü and G. Chen, “A new chaotic attractor coined,” International Journal of Bifurcation and Chaos, vol. 12, no. 3, pp. 659–661, 2002. [Google Scholar]

32. S. K. Rajput and N. K. Naveen, “Known-plaintext attack-based optical cryptosystem using phase-truncated Fresnel transform,” Applied Optics, vol. 52, no. 4, pp. 871–878, 2013. [Google Scholar] [PubMed]

33. G. Chen, Y. Mao and C. Chui, “A symmetric image encryption scheme based on 3D chaotic cat maps,” Chaos, Solitons & Fractals, vol. 21, no. 3, pp. 749–761, 2004. [Google Scholar]

34. X. Zhang, Z. Zhao and J. Wang, “Chaotic image encryption based on circular substitution box and key stream buffer,” Signal Processing: Image Communication, vol. 29, pp. 902–913, 2014. [Google Scholar]

35. H. Luo and B. Ge, “Image encryption based on Henon chaotic system with nonlinear term,” Multimedia Tools and Applications, vol. 78, no. 24, pp. 34323–34352, 2019. [Google Scholar]

36. H. Li, Y. Wang and Z. Zuo, “Chaos-based image encryption algorithm with orbit perturbation and dynamic state variable selection mechanisms,” Optics and Lasers in Engineering, vol. 115, pp. 197–207, 2019. [Google Scholar]

37. Y. Wen, J. Su, Y. Hong and P. Gong, “Hybrid mapping algorithm based on 1-DCM and Lorenz,” IET Image Processing, vol. 16, no. 9, pp. 2467–2482, 2022. [Google Scholar]

38. M. Asif, J. K. K. Asamoah, M. M. Hazzazi, A. R. Alharbi, M. U. Ashraf et al., “A novel image encryption technique based on cyclic codes over galois field,” Computational Intelligence and Neuroscience, vol. 2022, no. 1, pp. 1–9, 2022. [Google Scholar]

39. A. Mahboob, I. Siddique, M. Asif, M. Nadeem, A. Saleem et al., “A novel construction of substitution box based on polynomial mapped and finite field with image encryption application,” IEEE Access, vol. 10, pp. 119244–119258, 2022. [Google Scholar]

40. X. Gao, J. Mou, S. Banerjee, Y. Cao, X. Li et al., “An effective multiple-image encryption algorithm based on 3D cube and hyperchaotic map,” Journal of King Saud University-Computer and Information Sciences, vol. 34, no. 4, pp. 1535–1551, 2022. [Google Scholar]

41. X. Wang, Y. Su, C. Luo, F. Nian and L. Teng, “Color image encryption algorithm based on hyperchaotic system and improved quantum revolving gate,” Multimedia Tools and Applications, vol. 81, no. 10, pp. 45–65, 2022. [Google Scholar]

42. H. Zhu, Y. Zhao and Y. Song, “2D logistic-modulated-sine-coupling-logistic chaotic map for image encryption,” IEEE Access, vol. 7, pp. 14081–14098, 2019. [Google Scholar]