Solving Arithmetic Word Problems of Entailing Deep Implicit Relations by Qualia Syntax-Semantic Model

1  Introduction

Solving arithmetic word problems entailing deep implicit relations is a critical branch problem of solving arithmetic word problems. Arithmetic word problems entailing deep implicit relations are the AWPs that can be solved only after adding the deep implicit relations. Two example types of DIR-AWPs are the AWPs of entailing commonsense or specific domain knowledge. “Chicken and rabbit in the same cage” is an example of entailing commonsense. People use this problem as a touchstone to judge whether the solver is powerful. In other words, people think that DIR-AWPs are the most difficult AWPs. However, there are only so many satisfactory algorithms for solving DIR-AWPs. The paper has studied this problem. The reason is that the type of problem represents the highest degree of difficulty in solving AWPs. This paper proposes discovering deep implicit relations by qualia inference to solve DIR-AWPs, such as entailing commonsense or subject-domain knowledge.

In response to this issue, deep implicit knowledge has been proposed to tackle the challenge of multi-steps of implicit relations reasoning during the problem-solving of DIR-AWPs. The syntax-semantic relation graph (S2RG) is a middle-state that facilitates the qualia structure from the S2 model. The S2RG enhances the knowledge representation and reasoning capability of solving DIR-AWPs in real-world scenarios. This paper proposes the three steps used to conduct the inference process.

Yu et al. proposed a Vectorized Syntactic-Semantic (V-S2) method [1,2] for solving word problems. This method encapsulates mathematical knowledge into S2 models and leverages a neural network miner to discover implicit quantity relations. The authors extend this paper by proposing a novel approach called the Qualia Syntax-Semantic Model (QS2M). The QS2M method leverages qualia-based relation inference to discover deep implicit relations. Compared to traditional similarity matching and pattern recognition-based inference approaches, the graph-based inference method QS2M provides a more logically controllable and understandable solution to solving word problems. This modification offers a more sophisticated approach to discovering implicit relations in word problems. This understanding is achieved through QS2M methods, which extract relations from external qualia-based datasets and uncover relations from an expanded understanding of the problem. The proposed algorithm highlights the AWP text, scenario understanding and inference of deep implicit knowledge.

This paper uses a tutorial based on an algorithm approach that leverages the generalized problem-solving principle. They contend that learners can more effectively learn by focusing on relational operations instead of concentrating only on the system of equations. This approach divides the task of obtaining a system of equations into two simpler sub-tasks: identifying relations and their transformation into equations. The proposed algorithm, known as the “relation-centric solving algorithm”, addresses the growing demand for advanced intelligent tutoring systems [3]. The contributions of this paper can be summarized as follows:

1. The QS2M has been proposed for solving DIR-AWP characterized by complex problem scenarios. The QS2M approach utilizes graph-based inference, which provides a logically controlled and coherent framework compared to traditional methods.

2. Implicit knowledge addition by the QS2M model represents the relationships between mathematical entities and their attributes. The qualia role patterns in different problem scenarios are to extract the DIR-AWP quantity relations from fully connected S2RG.

2  Related Work

The development of methods for acquiring quantity relations from problem texts has involved using manually crafted rules [4,5] or templates in their early stages [6]. Rule-based [7] systems rely on predefined rules, such as predicate logic, for unambiguous deductions. Alternatively, semantic parsing-based methods [8] utilized the semantic structure of problems to retrieve historical knowledge more efficiently. However, this approach came at the expense of ambiguity and inference interpretation [9,10]. Yan et al. [11] proposed a seq2seq model that translated problem sentences into expressions.

Furthermore, Liang et al. [12,13] designed the teacher module to associate the encoding to match the correct solution and analogical pairs in a latent space. Above all, Yu et al. [1] proposed a state-action paradigm that utilized knowledge expressions and action transformations. Advanced methods can be categorized into knowledge-addition and state action-based methods that adopt a relation-centric approach based on this paradigm.

2.1 The Knowledge-Addition Method Solving DIR-AWP

The main objective of the research is to employ S2RG to bridge the gap of implicit knowledge for DIR-AWP. The paper reviewed related knowledge acquisition and reasoning work to achieve this goal. Walter et al. [14] proposed a two-frame framework for solving AWPs, utilizing knowledge and solution frames to store problem-understanding outcomes. In Natural Language Processing (NLP), knowledge-addition methods have shown the potential to enhance problem comprehension through the utilization of explicit expert knowledge. Several recent studies [15–17] have focused on using additional information to aid in understanding problems. For instance, Graph2Tree [18] was introduced to capture relationships and order information among quantities. In the field of observation, there is a particular emphasis on improving the expression reasoning process [19,20]. Researchers have proposed various methods, such as Goal-Driven Tree-Structured (GTS) Neural Model [21], which utilizes a goal-driven decomposition mechanism to reason an expression tree. Shen et al. [19] also created an ensemble of multiple encoders and decoders, combining semantic understanding and reasoning strengths. The deep learning framework approach to reasoning implicit relations is based on the semantic hint of the shallow implicit knowledge, which directly adding shallow implicit mathematical relationships cannot represent the content of the DIR-AWPs.

Overall, by building on these related studies, the research aims to apply S2RG to enhance the acquisition of implicit knowledge for solving DIR-AWP. A knowledge-addition solver is an automated system that utilizes a knowledge base to represent subject-domain knowledge. It surpasses the performance of traditional problem-solving methods by leveraging its superior computing capacity. This approach to problem-solving is characterized by its reliance on subject-specific knowledge and its ability to generate innovative solutions.

2.2 The State-Action Framework Reasoning DIR-AWP

This study aims to develop a syntax-semantic relation graph-based approach to enhance the efficiency of quantity relation extraction for resolving DIR-AWPs. The quantity relations and solution goals in such problems are founded on ontology, and hence, recognizing and extracting ontology relations can pave the way for generating the quantity relations. Therefore, the associations between words in the text can be leveraged to obtain ontology relations. Prior research proposes the concept of qualia role [22], a set of relations referred to as qualia that can signify the meaning of a word based on the concept of the words. Furthermore, a set of semantic roles called qualia structure, including formal, constitutive, agentive, and telic roles, is proposed to represent the meaning of nominal and implicit information described in [23].

Knowledge graph completion [24,25] is a relevant task in S2RG due to the explicit knowledge graph formed. This task involves learning unknown edges in the knowledge graph using existing edges. Various approaches have been proposed, such as Bordes et al. [26] interpreting knowledge semantics through translation operations and Pei [27] capturing structure information and long-range dependencies through a geometric perspective. Other types of knowledge, including background knowledge [28], logical knowledge [29], and implicit knowledge in pre-trained language models, have also been investigated. Special forms of knowledge, such as logic rules [30] and mathematical properties [31], have also been studied in various research works.

The study differs from previous knowledge acquisition research in that it utilizes implicit mathematical knowledge through its reasoning approach S2RG, a general framework based on a state-action paradigm, and a relation-centric approach. Moreover, the paper introduces a QS2M within S2RG, improving solution accuracy and reasoning interpretability. The work contributes to the field by presenting a comprehensive approach that combines explicit and implicit knowledge learning to enhance reasoning abilities.

3  The Qualia DIR-AWPs Solver

3.1 Overview

This section details the proposed qualia-based DIR-AWPs solver to discover implicit quantity relations for solving AWPs with complex problem scenarios. The proposed QS2M framework represents two main steps in Fig. 1. First, solving AWPs is based on relations from the S2 model, and the entity relation representation S2RG is an intermediate state for solving the problem in Fig. 2. Second, based on the S2 model, the implicit relations are extracted from expanded S2RG of implicit knowledge.

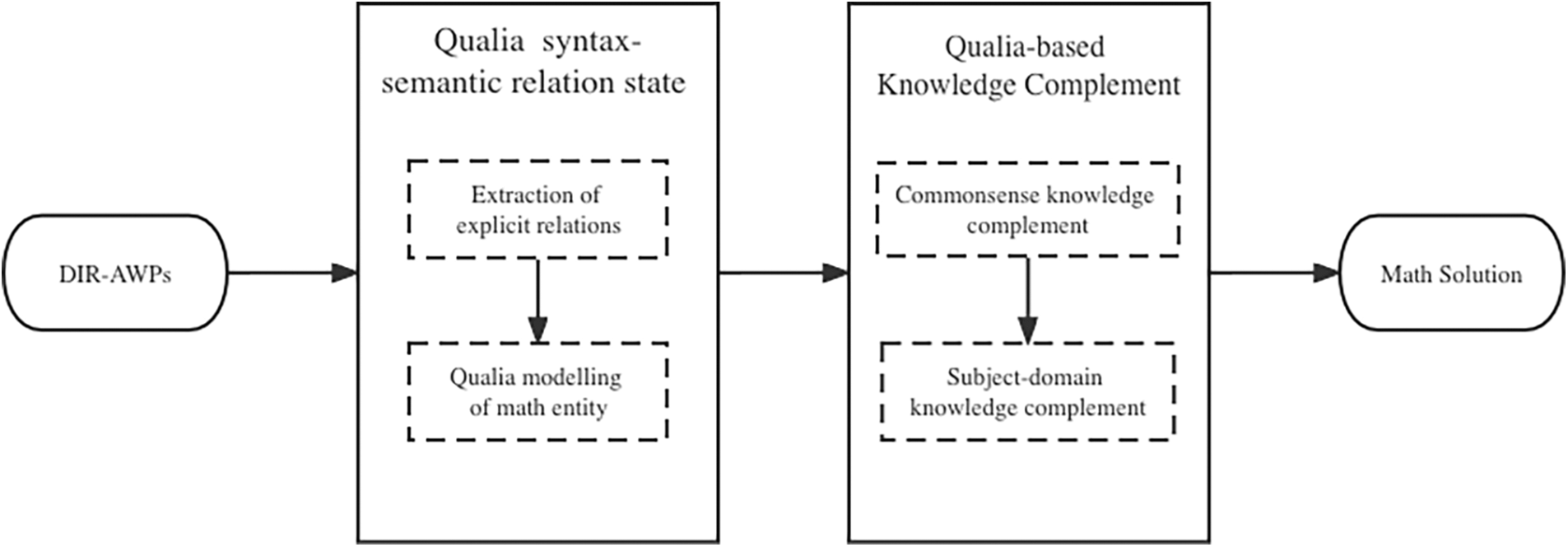
Figure 1: The framework for solving DIR-AWPs using the proposed QS2M method

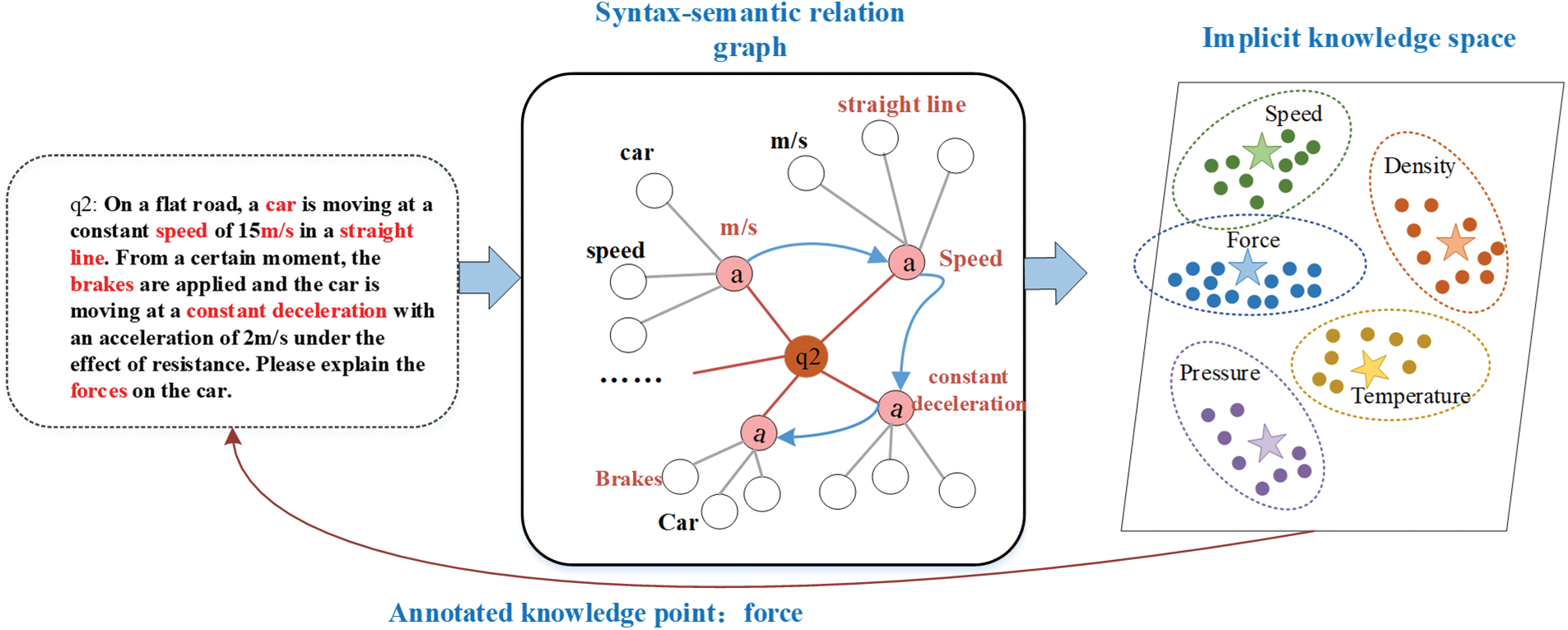
Figure 2: The example of solving DIR-AWPs by using the proposed QS2M method

Compared to traditional knowledge models, the advantage of QS2M is the cross-scenario multi-step inference for discovering implicit knowledge entities N and quantity relations R. A given arithmetic word problem P could be translated into a triple of <N, R, g> that contains a set of knowledge entities N = Ne ∪ Ni and quantity expressions R = Re ∪ Ri as well as the solution goal g to be solved, where Ne and Re are knowledge entities and quantity expressions that are directly stated in P. Ni and Ri are implicit knowledge entities and quantity expressions indicated by implicit knowledge of DIR-AWPs.

Definition 1 (Knowledge entity): A knowledge entity ea = {e1, e2, ..., ei} mentioned is a word in solving DIR-AWPs, e.g., “speed” and “uniform linear motion” are often used to explain relevant knowledge points in knowledge scenarios. For these terms with a clear knowledge orientation, em is a knowledge attribute, where m is the number of knowledge attribute words. These knowledge-attributing words are selected from many teaching resources, including textbooks and test questions.

Definition 2 (Syntax-semantic relation graph): Each DIR-AWP is constructed as a syntax-semantic relation graph, denoted as S2RG = <EE, IE, ER, IR>. which captures the relations between the DIR-AWP knowledge words and their neighbors to highlight the knowledge point. As shown in Fig. 2. The knowledge entity is directly connected to nodes, and neighboring entities are connected to their corresponding knowledge entities. The qualia relations of knowledge entities also form a scenario-aware knowledge representation.

Definition 3 (Implicit knowledge space): The implicit knowledge space S is based on the knowledge point to enrich the connotation and extension of knowledge points. Its knowledge entity combinations in different knowledge scenarios are S = {i1, i2, ..., ik}, and k is the number of knowledge points. In the hidden knowledge space, the closer the knowledge is to each other, the more similar the knowledge features are.

3.2 Qualia Syntax-Semantic Model

The solvable state of DIR-AWPs requires constructing a connected S2RG of relations, which provides a comprehensive understanding of the process involving using the S2RG to represent and reason knowledge in knowledge entities. On the S2RG, quantity relations are represented by a set of connected attribute nodes belonging to one or more entity nodes, which can be viewed as sub-graphs by applying a graph traversal. A quantity relation mining algorithm translates such sub-graphs into quantity relations.

The quantity relations indicated by the relations among knowledge entities and their attributes can be modeled as a set of knowledge models named the QS2M. The QS2M is structured as a quintuple,

QS2M=(Ne,Ni,Qr,Qp,Ri)(1)

where: Ne is the explicit knowledge entity stated in the AWPs to be calculated in the solving process.

Ni is the knowledge entity to link AWP entities in the solving process.

Qr is the semantic pattern AWPs that constructs the qualia relation to link Ni scenario entities.

Qp is the syntax-semantic structure pattern for converting math relations from the S2RG.

Ri is the quantity relations associated with the qualia role pair <Ne, Ni>.

The QS2M linked the AWP explicit relation and the implicit relation. The set of QS2M, Mi = (Ne, Ni, Qr, Qp, Ri), i = 1, 2,..., m denotes the pool of qualia-based knowledge models.

As a syntax relationship between entities, the qualia structure can be incorporated into the existing S2 model to construct S2RG. The knowledge description ability of S2RG lies in the concept network centered on nouns as entities. The QS2M allows the model to perform multi-step reasoning. The quantity expressions indicated by knowledge entities and attributes can be modelled as a set of S2RG. Inspired by the qualia structure system [19], the knowledge base uses the QES2 to represent the structure of AWP, and entities form its object eo, entity attribution ea, and values. The entity is independent and used to distinguish different knowledge entities, and attribution is attached to the entity and used to present numeric values. A hierarchical structure of Entity−Attribution−Value can represent the quantity relations. Object entities and their attributions form the basic form for representing quantitative relations. Identifying an application’s object entity is the key to extracting quantitative relations and understanding and solving problems.

The AWPs scenario has three main categories of factual facts: reflexive fact, connective fact, and con-vergence fact. The expressions are presented as facts that facts could further translate into mathematical operations to calculate the final answers. The knowledge entity relation can be described as a qualia structure denoted as Rc. Each element rc is <esrc, edst, Qp, Ri>, where esrc and edst are two knowledge entities, Qr denotes the semantic role of edst associated with esrc, Qp denotes the syntax-semantic pattern related to Qr. The six kinds of qualia roles Qr for solving AWPs: Formal role (FOR), Constitutive role (CON), Unit role (UNI), Material role (MAT), Telic role (TEL), Evaluation role (EVA), Handle role (HAN), Action role (ACT) and Orientation role (ORI).

As a result, quantity facts in AWPs could be divided into the following three categories accordingly:

Reflexive Fact: reflexive fact presents the expressions amount different attributes ea of a knowledge entity object eo. The relation between the target entity and its quantity, length, weight, speed, the relation between the speed-time distance of the target entity, etc., which associates with the qualia roles of FOR and UNI.

Connective Fact: connective fact presents the expressions amount different entity objects eoi, e.g., comparative relations: “there are five more apples than pears”, multiplicative/proportional relations: “the number of pears is twice the number of peaches”. Which associates with qualia roles of EVA, MAT, and ORI.

Convergence Fact: convergence fact describes the convergence relation between an object entity and two or more object entities, e.g., summation relation: “38 trees were planted in Year 3 and 22 trees were planted in Year 4. How many trees were planted in both years?”. which usually associates with qualia roles of CON, TEL, ACT, HAN, MAT, and ORI.

Based on the aforementioned definition, reflexive facts can be represented as constitutive roles linking a mathematical entity with its associated attributes. For instance, the constitutive role C (rabbit, leg) establishes a connection between the knowledge entity “rabbit” and its attribute “legs”. Similarly, the constitutive role C (circle, area, radius) links the attributes “area” and “radius” of a “circle” mathematical entity. Unlike reflexive facts, connective facts are context-dependent and may take on various forms, such as “is-a” relationships between knowledge entities, “used-for” relations, “created-by” relations, and so forth. For instance, the source formula “rabbit. Legs = 4” can be deduced from the constitutive role C (rabbit, leg), and the formula “area = PI * radius * radius” can be derived from the C (circle, area, radius).

This study uses the Language Technology Platform (LTP) [32] natural language processing tool for word segmentation and part-of-speech tagging of word problems. For a DIR-AWP text P entered in natural language, a lexical tagging(POS) algorithm uses transformers’ tokenizer to separate the AWP into lexical subdivisions of the text andtheir lexical roles. In Algorithm 2, the explicit entities are extracted from the S2 model, and then the entities are constructed as S2RG through the entity dependency relation and S2 relation.

3.3 Implicit Knowledge Addition by Qualia Syntax-Semantic Model

Implicit relation Ri recovery refers to an entity eo corresponding to attribute ea in qualia disciplines. However, its value does not explicit in the problem text; the paper defines this knowledge as implicit knowledge fact. AWPs implicit knowledge contains two types of implicit relation sources: missing entity and subject-domain relations. The generated prompt questions Qr are embedded in the S2RG and as clues to traverse the nodes in the S2RG. Implicit quantity relation mining is designed to discover implicit quantity relations from the updated S2RG.

The S2RG nodes as an indicator to match the pattern of POS: entities Ee and attributes Ae from the expressions Re, and solution goals g. The S2RG generated math relations from explicit entities connect the solution goal g, inference domain knowledge Rd in the knowledge model. The purpose of the S2RG generation algorithm is to implement the addition and inference of implicit expressions. On the S2RG, the entities and attribute values are represented as nodes and relations. In the qualia role description system, entity relations are modelled by the qualia roles of entities. Specifically, the qualia roles of entities are determined by the syntactic structures, and the paper uses six qualia roles [19] to describe the knowledge entity relations in Chinese AWPs.

The reasoning of the solution chains is achieved from the discrete S2RG to be holistic knowledge as a fully connected S2RG. By modeling the entity relations of the DIR-AWP, the object roles between entities are obtained and added to R. R holds the entity qualia roles obtained after modeling for the input DIR-AWP. The related information in R must be completed by classifying the AWP scenario and obtaining the entity relation combination of the current AWP scenario in Table 1.

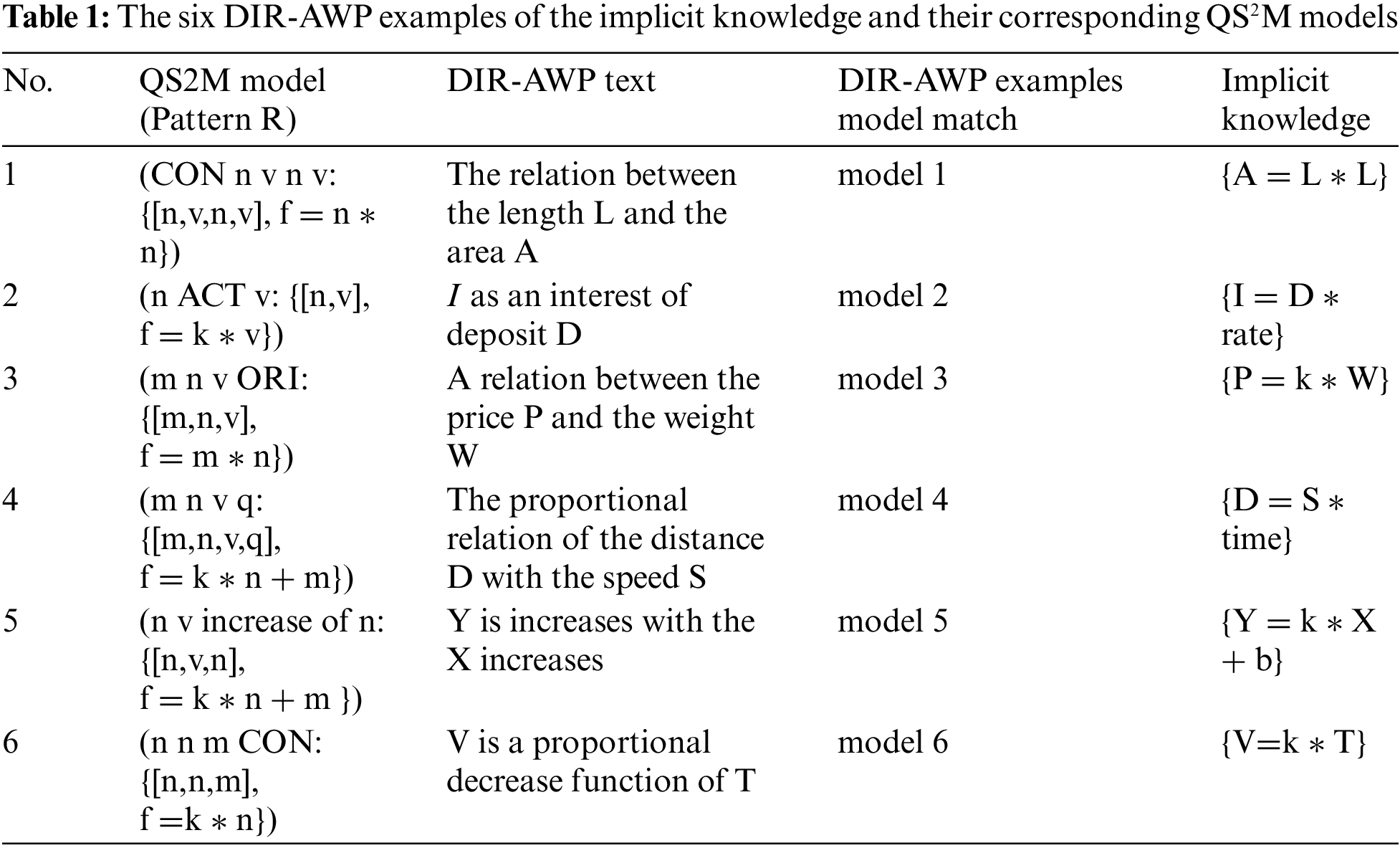
3.3.1 Commonsense Foreground Knowledge: S2RG Node Generation

The S2RG of DIR-AWPs is the solving process state of reasoning missing nodes. Based on the S2RG scenario feature, the model defines the input position sequence nodes Ne. The knowledge model combined the manual prompt pattern for inquiring about implicit AWP knowledge entity candidates for AWPs from the pre-train language model.

After setting up the template, the explicit entities Ne follow prompt Qr to complement a node Ni, the attributes are ea, and the links Qr. The model needs to fill the candidate entities into the structure of the incomplete triple u = <Ne, Qr, Ni>: the label words match the Chinese pre-trained language model L = chinese-roberta-wwm-ext for MLM (Masked Language Model) to get the Chinese grammatical words [MASK]. Ranking the candidate entities according to scores.

Where Ni represents the output of the prompts f (Ne):

Ni=fQr(Ne)(2)

The Ne is the indicator to match pattern Qr to traverse the nodes in the S2RG. The implicit nodes Ni and domain Rd through Qr. The prompt pattern Ni = fQr(Ne) defines the input position and explicit nodes Ne.

3.3.2 Subject-Domain Background Knowledge: S2RG Implicit Relation Generation

Subject-domain relations exist in the DIR-AWP scenario-solving process, represented as S2RG complements the DIR-AWP’s problem-solution chain. The construction of entities by obtaining the qualia roles of entities based on a syntactic format and then describing the entity relations through the qualia roles.

Ri=fDomainFormula(E1,E2,...,En)(3)

Compared with the S2 model defined in Yu et al. [1], this definition extends the QS2M method that provides a mechanism for acquiring the knowledge items from function problem text. The paper manually designs 150 logical cues for arithmetic reasoning based on the problem context of the topic by splitting the solution expression into multiple sub-expressions based on different topic contexts and giving logical explanations described in natural language based on each sub-operational unit according to the pattern of thought chain reasoning. which covered the five contextual categories summarised in Table 1, including 20 for the plane problem; 32 for the task problem; 38 for price problems; 36 for task problems; 24 for MovePath problems.

Solving DIR-AWPs involves combining explicit and implicit knowledge into a fully connected graph S2RG, which involves searching for a chain of nodes that connect the known information to the solution goal g. The S2RG is enhanced using a structural qualia syntax-semantic pattern, transforming it into a relation-centric representation. This pattern includes various elements such as lexical markers, keywords, dependency relations, and sequential relations within the sentence to construct a semantic scenario. Overall, the approach provides a more comprehensive and rigorous framework for problem-solving in Algorithm 3.

Ri=fs2(E1,E2,...,En)(4)

4  Experiment

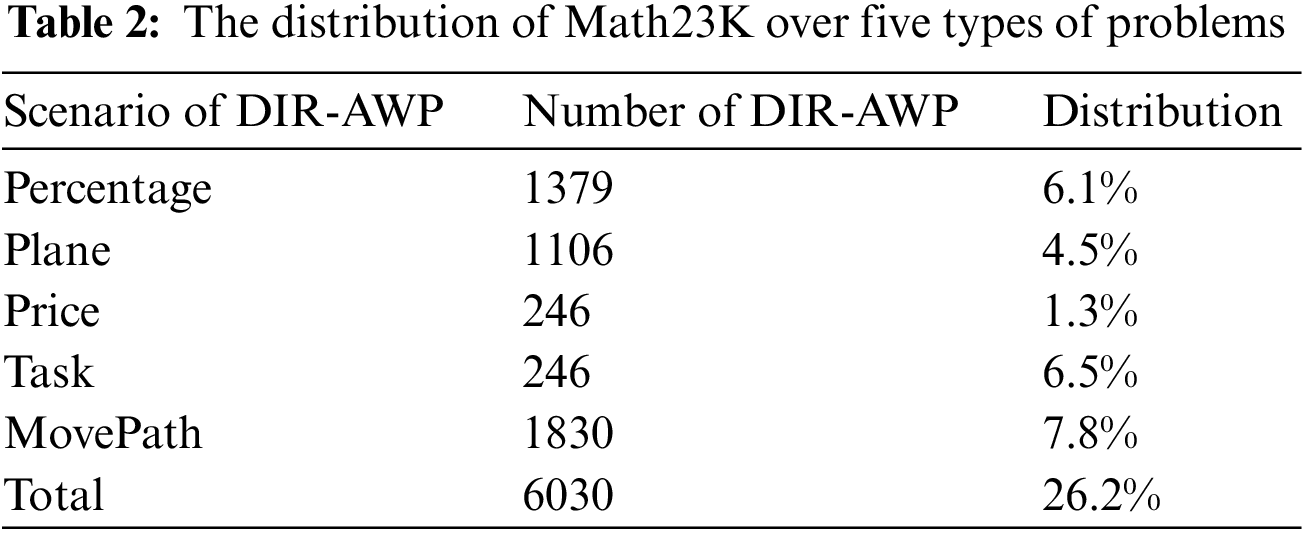
The paper presents the “scenario category” for the DIR-AWPs and constructs a comprehensive entity relation graph S2RG. Specifically, the study investigates five scenario categories of primary school DIR-AWPs and provides a detailed account of each category’s entity and qualia role combinations. These findings shed light on the underlying structures of the DIR-AWP types and offer insights into how to model entity relations effectively. This section presents the empirical findings compared to the Math23K, a publicly available dataset.

4.1 Dataset

In this study, the paper employed the Math23K [11] dataset, which is widely used to evaluate math problem solvers, and contains both story and non-story problems (e.g., equations, formulas, numbers). The approach, QS2M, was explicitly applied to story problems. Previous researches by Mayer [33], Cheng et al. [34], Hong et al. [35], and He et al. [36] have shown that AWPs can be classified into various scenarios based on their storylines, which impact the problem-solving process and the quantity relations involved. To assess the effectiveness of the algorithm on different problem categories, the paper classified 6030 problems from Math23K into five distinct groups to create a new dataset for evaluation. The goal was to evaluate the performance of QS2M across these different categories. The newly created dataset comprises only one-quarter of the original Math23K dataset and comprises five DIR-AWPs types. The dataset includes 6030 problems, sufficient to demonstrate the universality of AWP solvers, as it represents typical cases encountered in AWPs. Table 2 provides detailed information regarding the new dataset and is available for download.

Baselines. Three methods compared the model as below:

• S2 model [2]: a theoretical framework has been developed for addressing arithmetic word problems that involve explicit statements and require the use of a set of S2 models. This framework offers a systematic approach to solving such problems by incorporating various linguistic and mathematical concepts to represent and manipulate the problem’s elements effectively.

• GTS [21]: a math word problem solver, structured as a goal-oriented tree, is utilized for the purpose of producing solution expressions.

• Graph2Tree [18]: a deep learning architecture that integrates the strengths of graph-based encoders and tree-based decoders to generate expressive solutions. This model achieves enhanced performance in generating solution expressions by leveraging the inherent structural properties of both graph and tree representations.

• QS2M: the model proposed in this paper.

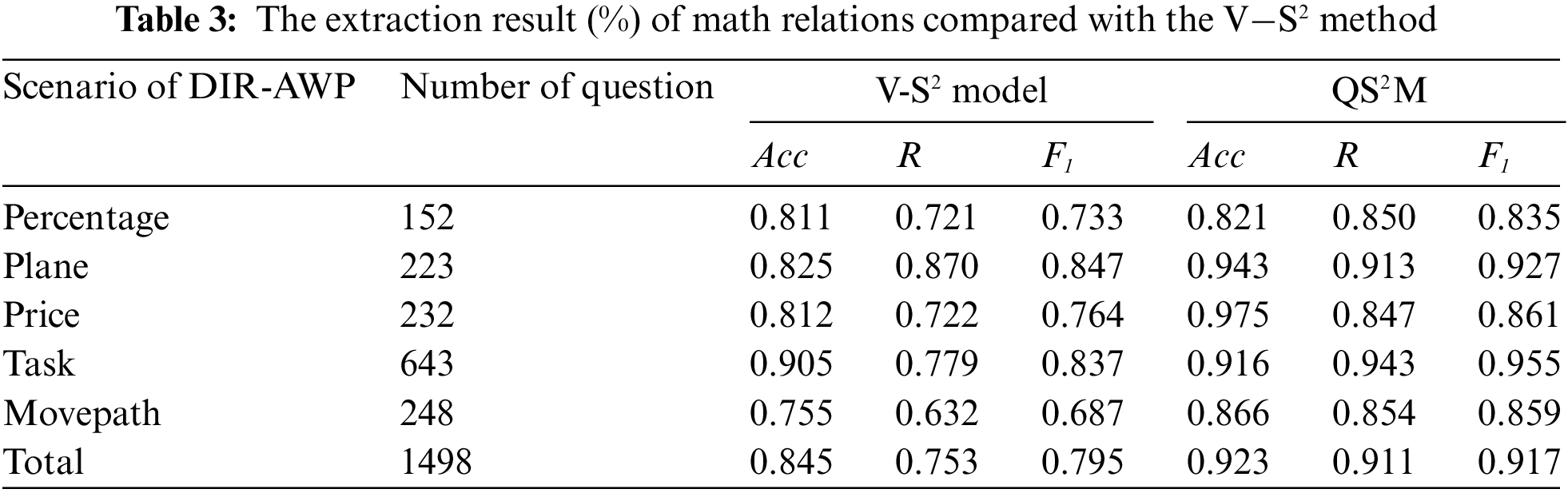
4.2 Performance on Quantity Relation Extraction

The evaluation of quantity relation extraction is not commonly performed by all neural solvers, and the lack of large-scale ground truth for quantity relation evaluation posed a significant challenge. To assess the performance of quantity relation extraction, accuracy (Acc), recall (R), and F1-score metrics were compared to the V−S2 model. The results of the test are summarized in Table 3 and show that the proposed QS2M model significantly outperforms the V–S2 model by 7.8% in overall accuracy. Specifically, the QS2M model outperforms neural models by 11.8% and 11.1% on the Plane and MovePath problems, respectively.

The authors of [37] employed a methodology where they encoded the problem statement and the output of Algorithm 2 using the AWP solvers, such as GTS and Graph2Tree. This approach was designed to evaluate problem-solving accuracy, and the results were reported in Table 4. According to the results presented in Table 4, it can be observed that the incorporation of the QS2M tasks has led to a significant improvement in the average accuracy of both the Graph2Tree and GTS models.

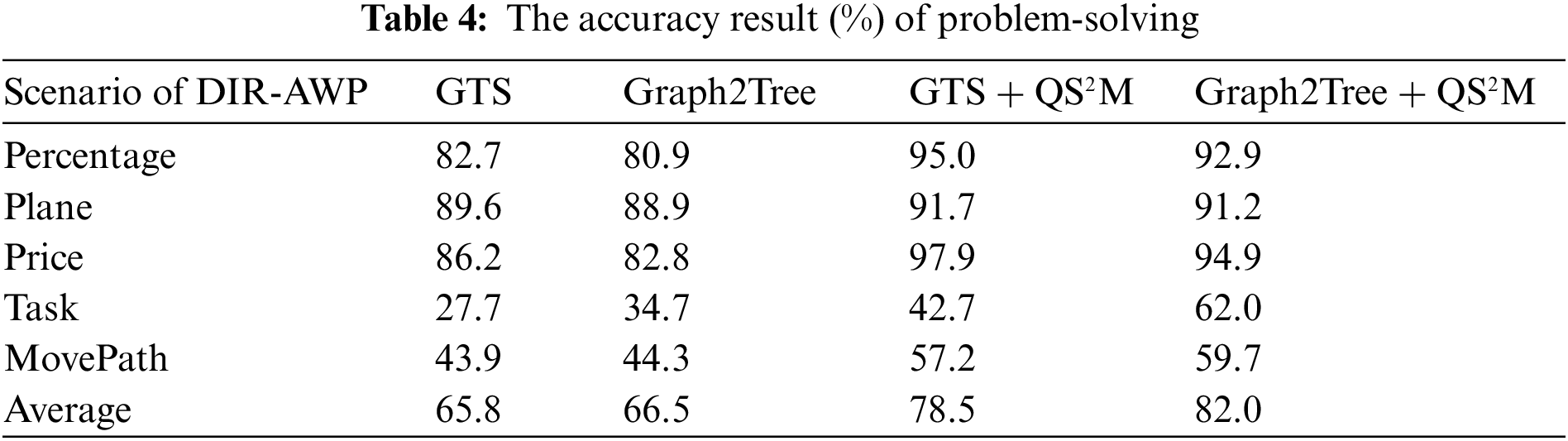
Specifically, the injection of the extracted quantity expressions has resulted in an average accuracy of 82.0% and 78.5% for the Graph2Tree and GTS models, respectively. These findings suggest that the proposed approach is highly effective in solving AWPs that require more implicit relations.

5  Conclusions and Future Work

This paper acknowledges the notable advancements achieved in solving AWPs. However, it also recognizes the absence of an effective method for uncovering deep implicit relations for addressing DIR-AWPs, including those related to common sense or subject-specific knowledge. The present paper suggests utilizing the three-step qualia-quantity approach for discovering deep implicit relations. In the initial stage, the S2 method extracts all the explicit relations and identifies scenarios using a pre-existing set of qualia-quantity models. Subsequently, the missing entities are incorporated under the identified scenarios, and qualia-quantity models are employed to establish deep implicit relations. Finally, an S2RG is proposed to represent all the obtained relations, which is then condensed by pruning superfluous branches to solve the given problem. The answers are obtained by solving the distilled relations.

The study proposed a novel method called QS2M that represents quantity expressions linked with uncorrelated entities to address the lack of hidden relations in complex scenarios. In future endeavors, the paper aims to enhance this solver for a broader range of issues and construct a more comprehensive knowledge repository, based on qualia role, to construct problem solvers. Furthermore, the paper has plans to design an intelligent tutoring system and to explore more efficient educational strategies utilizing the system to guide and teach students.

Acknowledgement: I would like to express my deep gratitude to Professor Xinguo Yu, my research supervisors, for his patient guidance, enthusiastic encouragement and useful critiques of this research work. I would also like to thank Dr. Bin He, for her advice and assistance in keeping my progress on schedule. My grateful thanks are also extended to Mr. Litian Huang for his help in doing the meteorological data analysis, to Mr. Liang Xue, who helped me calculate the wind pressure coefficient and to Mr. Zongyou Qiu for their support in the site measurement. I would also like to extend my thanks to the technicians of the laboratory of National Engineering Research Center for E-Learning (NERCEL) for their help in offering me the resources in running the program. Finally, I wish to thank my parents for their support and encouragement throughout my study.

Funding Statement: The National Natural Science Foundation of China (No. 61977029) supported the work. This work was supported partly by Nurturing Program for Doctoral Dissertations at Central China Normal University (No. 2022YBZZ028).

Author Contributions: H. Meng: review and editing, writing original draft, funding acquisition; X. Yu: conceptualization, methodology, funding acquisition; B. He: investigation, project administration, supervision; L. Huang: software, validation, visualization; L. Xue, Z. Qiu: data collection.

Availability of Data and Materials: Data will be made available on request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Yu, X. Lyu, R. Peng and J. Shen, “Solving arithmetic word problems by synergizing syntax-semantics extractor for explicit relations and neural network miner for implicit relations,” Complex & Intelligent Systems, vol. 9, no. 1, pp. 697–717, 2023. [Google Scholar]

2. X. Yu, M. Wang, W. Gan, B. He and N. Ye, “A framework for solving explicit arithmetic word problems and proving plane geometry theorems,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 33, no. 7, pp. 1940005, 2019. [Google Scholar]

3. S. Liu, “An effective learning evaluation method based on text data with real-time attribution-A case study for mathematical class with students of junior middle school in china,” ACM Transactions on Asian and Low-Resource Language Information Processing, vol. 22, no. 3, pp. 1–22, 2023. [Google Scholar]

4. B. Yefim, “Robust understanding of word problems with extraneous information,” arXiv preprint math/0701393, 2007. [Google Scholar]

5. F. Charles R, “Understanding and solving arithmetic word problems: A computer simulation. In: Behavior research methods,” Instruments & Computers, vol. 17, no. 5, pp. 565–571, 1985. [Google Scholar]

6. D. Zhang, L. Wang and L. Zhang, “The gap of semantic parsing: A survey on automatic math word problem solvers,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 42, no. 9, pp. 2287–2305, 2019. [Google Scholar] [PubMed]

7. P. A. Jaques, H. Seffrin, G. Rubi, F. de Morais, C. Ghilardi et al., “Rule-based expert systems to support step-by-step guidance in algebraic problem solving: The case of the tutor PAT2Math,” Expert Systems with Applications, vol. 40, no. 14, pp. 5456–5465, 2013. [Google Scholar]

8. R. Koncel-Kedziorski, H. Hajishirzi and Sabharwal, “Parsing algebraic word problems into equations,” Transactions of the Association for Computational Linguistics, vol. 3, pp. 585–597, 2015. [Google Scholar]

9. M. J. Hosseini, H. Hajishirzi and O. Etzioni, “Learning to solve arithmetic word problems with verb categorization,” in Empirical Methods in Natural Language Processing (EMNLP), Doha, Qatar, pp. 523–533, 2014. [Google Scholar]

10. A. Mitra and C. Baral, “Learning to use formulas to solve simple arithmetic problems,” in Proc. of the 54th Annual Meeting of the Association for Computational Linguistics, Berlin, Germany, vol. 1, pp. 2144–2153, 2016. [Google Scholar]

11. W. Yan, X. Liu and S. Shi, “Deep neural solver for math word problems,” in Proc. of the 2017 Conf. on Empirical Methods in Natural Language Processing, Copenhagen, Denmark, pp. 845–854, 2017. [Google Scholar]

12. Z. Liang and X. Zhang, “Solving math word problems with teacher supervision,” in Proc. of 30 Int. Joint Conf. on Artificial Intelligence, Virtual Only, pp. 3522–3528, 2021. [Google Scholar]

13. Z. Liang, J. Zhang and X. Zhang, “Analogical math word problems solving with enhanced problem-solution association,” arXiv preprint arXiv:2212.00837, 2022. [Google Scholar]

14. K. Walter and J. G. Greeno, “Understanding and solving word arithmetic problems,” Psychological Review, vol. 92, no. 1, pp. 109–29, 1985. [Google Scholar]

15. J. Qin, X. Liang, Y. Hong, J. Tang and L. Liang, “Neural-symbolic solver for math word problems with auxiliary tasks,” in Proc. of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th Int. Joint Conf. on Natural Language Processing, Association for Computational Linguistics, vol. 1, pp. 5870–5881, 2021. [Google Scholar]

16. Z. Huang, Q. Liu, W. Gao, J. Wu, Y. Yin et al., “Neural mathematical solver with enhanced formula structure,” in Proc. of the 43rd Int. ACM SIGIR Conf. on Research and Development in Information Retrieval (SIGIR 2020), pp. 1729–1732, 2020. [Google Scholar]

17. Q. Wu, Q. Zhang and Z. Wei, “An edge-enhanced hierarchical graph-to-tree network for math word problem solving,” in Findings of the Association for Computational Linguistics: EMNLP, Punta Cana, Dominican Republic, pp. 1473–1482, 2021. [Google Scholar]

18. J. Zhang, “Graph-to-tree learning for solving math word problems,” in Proc. of the 58th Annual Meeting of the Association for Computational Linguistics, pp. 3928–3937, 2020. [Google Scholar]

19. Y. Shen and C. Jin, “Solving math word problems with multi-encoders and multi- decoders,” in Proc. of the 28th Int. Conf. on Computational Linguistics, Barcelona, Spain, pp. 2924–2934, 2020. [Google Scholar]

20. Z. Jie, J. Li and W. Lu, “Learning to reason deductively: Math word problem solving as complex relation extraction,” in Proc. of the 60th Annual Meeting of the Association for Computational Linguistics (ACL 2022), Dublin, Ireland, Association for Computational Linguistics, pp. 5944–5955, 2022. https://aclanthology.org/2022.acl-long.410 [Google Scholar]

21. Z. Xie and S. Sun, “A goal-driven tree-structured neural model for math word problems,” in Proc. of the 28 Int. Joint Conf. on Artificial Intelligence (IJCAI-19), Macao, China, pp. 5299–5305, 2019. [Google Scholar]

22. Y. Yuan, “A study of Chinese semantic knowledge system based on the theory of generative lexicon and argument structure,” Jorunal of Chinese Information Processing, vol. 27, no. 6, pp. 23–30, 2013. [Google Scholar]

23. J. Pustejovsky, “The generative lexicon,”Massachusetts Institute of Technology (MIT) Press, 1995. [Google Scholar]

24. T. Bansa, D. Juan, S. Ravi and A. McCallum, “A2N: Attending to neighbors for knowledge graph inference,” in Proc. of the 57th Annual Meeting of the Association for Computational Linguistics, Florence, Italy, pp. 4387–4392, 2019. [Google Scholar]

25. K. Cheng, Z. Yang, M. Zhang and Y. Sun, “Uniker: A unified framework for combining embedding and definite horn rule reasoning for knowledge graph inference,” in Proc. of the 2021 Conf. on Empirical Methods in Natural Language Processing, Punta Cana, Dominican Republic, pp. 9753–9771, 2021. [Google Scholar]

26. A. Bordes, N. Usunie, A. Garcia-Durán, J. Weston and O. Yakhnenko, “Translating embed-dings for modelling multi-relational data,” in Proc. of the 26th Int. Conf. on Neural Information Processing Systems, Lake Tahoe Nevada, USA, vol. 2, pp. 2787–2795, 2013. [Google Scholar]

27. H. Pei, “Geom-GCN: Geometric graph convolutional networks,” in Int. Conf. on Learning Representations, Virtual Only, 2020. [Google Scholar]

28. M. Peyrard and R. West, “KLearn: Background knowledge inference from summarization data,” in Findings of the Association for Computational Linguistics (EMNLP 2020). Association for Computational Linguistics, pp. 2073–2085, 2020. [Google Scholar]

29. Z. Yang, J. Qin, J. Chen, L. Lin and X. Liang, “Logicsolver: Towards interpretable math word problem solving with logical prompt-enhanced learning,” arXiv preprint arXiv:2205.08232, 2022. [Google Scholar]

30. M. Qu and J. Tang, “Probabilistic logic neural networks for reasoning,” in Advances in Neural Information Processing Systems, (NeurIPS), pp. 7710–7720, 2019. [Google Scholar]

31. H. Pei, B. Wei, K. Chang, C. Zhang and B. Yang, “Curvature regularization to prevent distortion in graph embedding,” in Proc. of the 34th Int. Conf. on Neural Information Processing, Vancouver, BC, Canada, pp. 20779–20790, 2020. [Google Scholar]

32. W. Che, Y. Feng, L. Qin and T. Liu, “N-LTP: An open-source neural language technology plat-form for Chinese,” in Proc. of the 2021 Conf. on Empirical Methods in Natural Language Processing: System Demonstrations, Punta Cana, Dominican Republic: Association for Computational Linguistics, pp. 42–49, 2021. [Google Scholar]

33. R. E. Mayer, “Frequency norms and structural analysis of algebra story problems into families, categories, and templates,” Instructional Science, vol. 10, no. 2, pp. 135–175, 1981. [Google Scholar]

34. W. Cheng, X. Yu and J. Wang, “Discovering implicit quantity relations using convolutional network,” in 2019 14th Int. Conf. on Computer Science Education, Toronto, Ontario, Canada, pp. 231–236, 2019. [Google Scholar]

35. Y. Hong, Q. Li, R. Gong, D. Ciao, S. Huang et al., “Smart: A situation model for algebra story problems via attributed grammar,” in Proc. of the AAAI Conf. on Artificial Intelligence, Toronto, Ontario, Canada, vol. 35, pp. 13009–13017, 2021. [Google Scholar]

36. B. He, H. Meng, Z. Zhang, R. Liu and T. Zhang, “Qualia role-based quantity relation extraction for solving algebra story problems,” Computer Modeling in Engineering & Sciences, vol. 136, no. 1, pp. 403–419, 2023. [Google Scholar]

37. Z. Liang, J. Zhang and L. Wang, “MWP-BERT: Numeracy-augmented pre-training for math word problem solving,” in Findings of the Association for Computational Linguistics (NAACL), Seattle, United States, pp. 997–1009, 2022. [Google Scholar]