Modified MMS: Minimization Approach for Model Subset Selection

1  Introduction

Cybersecurity attacks have become increasingly complex and challenging to detect and prevent because of the rapid advancement of networks and related technologies [1]. Organizations rely on various security measures, including firewalls, Intrusion Detection Systems (IDS), Intrusion Prevention Systems (IPS), anti-virus, anti-malware, two-factor authentication, encryption, vulnerability scanning, employee training, and awareness creation. However, IDS is often considered the best solution for intrusion detection owing to its ability of real-time monitoring, both signature and anomaly-based detection; it minimizes performance impact and helps organizations maintain their regulations.

An IDS is an essential component of network security designed to detect and respond to unauthorized access and malicious activities. An IDS analyzes the network traffic or system log to identify patterns or behaviors that are consistent with known attacks or suspicious activities. Host-based IDS and Network-based IDS are the primary categories of IDS, where signature-based and anomaly-based are the detection methods of IDS [2]. Signature-based IDS depends on predefined patterns or signatures of known attacks and compares network traffic against these known signatures to detect potential threats [3]. Anomaly-based IDS uses statistical or Machine Learning (ML) approaches to establish the baseline behavior of normal and deviations of the threats [2].

Designing an effective IDS can be challenging owing to the diversity and complexity of modern threats and attacks. Employing a single classifier is not sufficient for constructing a powerful IDS [4]. The ensemble approach has emerged as a promising approach to address these challenges and improve the performance of IDS [5]. Ensemble learning for an IDS involves combining multiple models or classifiers to improve the overall accuracy and reduce false positives and false negatives [4]. Three techniques are used to increase the performance of an IDS: bagging, boosting, and stacking. Bagging involves the use of multiple models on different subsets of data and combining their output, in boosting involves training a model sequentially and giving more weight to misclassified instances over time. Stacking involves combining the output of various models using meta-classifiers [6].

Ensemble methods can be grouped into two major categories: homogenous and heterogeneous [4,7]. Homogenous ensembles have the same types of models and architectures with different subsets of training data. Predictions of every subset are combined to produce the outcome. Bagging [3–6,8–12], Boosting [3–6,8,10–19] are the type of homogeneous ensembles, which uses different methods to determine final prediction. Specifically, majority voting [3–6,9–11,17,18], weighted voting [4,6,7,9,10], average voting are prevalent methods used in existing studies. Several models and architectures have been integrated to produce a final product in heterogeneous ensembles. These models employed different subsets of data, algorithms, and parameters. In a heterogeneous ensemble, stacking [3–6,8,14,18,20] is an example in which the output of various models is used as the input for a metamodel to integrate the results. Another type of model is the cascade, which uses the output of one model as an input to another.

Various ensemble techniques have been implemented for intrusion detection in existing studies, although ensemble learning has limitations in certain aspects of detection. The main aim of the ensemble is to incorporate multiple models to improve performance in terms of accuracy, precision, recall, etc. Along with performance improvement, computational cost, maintenance, overfitting, transparency, and applicability are difficulties to be treated in ensemble learning. To address these issues, model selection for the ensemble is an important process because it determines the quality and diversity of individual models. The two main objectives of the model selection focused on the diversity and performance of the models. The diversity of the model is important for reducing overfitting and improving accuracy, robustness, and flexibility. Model diversity can be achieved by the measure’s correlation and entropy; this process is called ensemble pruning. Based on the correlation coefficients of the models, a subset of the models is generated for the ensemble.

Ensemble models gained widespread adoption due to substantial improvements in accuracy and robustness. However, they encounter challenges arising from model complexity, resource requirements, maintenance, and training models. Existing studies have extensively covered different ensemble models, with a particular emphasis on feature selection. However, the selection of an appropriate model for an ensemble still raises uncertainties and concerns. The primary motivation behind the research is to address the crucial aspect of model selection in the context of ensemble methods, driven by the existing knowledge gap. This work aims to bridge the gap and provide insights into effective model selection techniques.

The NSL-KDD dataset is commonly used in the field of network security and intrusion detection to evaluate model performance. It is essential to use datasets to assess the ability of models to generalize, compare their performances, and identify areas of improvement. The proposed model is evaluated using the NSL-KDD dataset and considered accuracy, precision, recall, and F1-score as evaluation metrics. In addition, ROC curves are used to summarize the performance of the model.

The major contributions of this study are as follows:

•   To develop an intrusion detection system with the classifiers LR, NBC, KNN, DT, SVM, and RF individually

•   Generate a Correlation-Based Diversity Matrix (CDM) between individual classification algorithms to ensure the diversity of each model.

•   To develop a Modified-Minimization approach for Model Subset Selection (Modified-MMS) to select the minimal model for the ensemble, that should achieve objective diversity and performance.

•   To develop an aggregated prediction of model subsets using majority voting and compare the performance with all classifier ensemble combinations.

2  Related Work

The rapid growth of technology has increased the threat to network users [21]. Providing privacy and mitigating security threats are important factors for multipurpose network applications [19]. A vulnerability in a network causes significant damage to an organization [2], and a large amount of network traffic and a growing number of attacks are recognized as issues to deal with [22]. Traditional detection methods lack the modality of data, and interdependence among features results in the model being unable to detect network attacks in real-time [14]. The process of extracting important and relevant features from large amounts of network traffic data is a critical step in developing highly effective intrusion detection systems [23]. The high False Positive Rate (FPR) and Detection Rate (DR) are the most common problems to be treated in IDS [10], which can be effectively improved by the ensemble methods compared to conventional single classification algorithms [12]. In the ensemble process, moderately accurate components of classifiers are combined to obtain highly accurate classifiers [12]. Several techniques have been proposed to produce efficient and diversified base classifiers for ensemble construction were discussed below.

The effectiveness of the model is affected by redundant and irrelevant features. To eliminate pointless features from the dataset, the authors [21] suggested using an ensemble method with Recursive Feature Elimination (RFE), in which DT, SVM, and RF were used as base classifiers. To identify the irrelevant features of the attack groups Denial-of-Service (DoS), Probe, Remote to User (R2L), and User to Root (U2R), each classifier uses RFE to create an ensemble for prediction, to classify all types of attacks. The author [2] suggested a hybrid classification based on Ranker’s algorithm utilizing the Weka tool to address the weaknesses of network vulnerabilities. Ranker’s attribute assessment approach was used to select the pertinent attributes. The Pertinent attribute in the proposed strategy reduces the time complexity and resource utilization of the model. The classification algorithm selected for the proposed hybrid classification is Instance-Based Learner (IBk), Random Tree (RT), Reduced Error Pruning (REP) Tree, J48 graft, and RF. To construct a collection of ensemble solutions for successful intrusion detection, the author [11] presented a hybrid strategy that combines the Multi-Objective Genetic Algorithm (MOGA) and Neural Network (NN) to resolve the issue of bias toward attack classes, either majority or minority. The proposed work is implemented in two stages. Instep 1, a set of Pareto optimum solutions is constructed, and each model response is combined using the majority vote. In step 2, the proposed strategy is compared against established bagging and boosting methods with performance metrics. To determine the best technique for intrusion detection, the authors [22] proposed a hybrid model using ML and Deep Learning (DL) techniques. The suggested hybrid strategy combines the pre-processing method with missing value management, data balancing with Synthetic Minority Oversampling Method (SMOTE), and Extreme Gradient Boosting (XGBoost) for the best feature selection to feed into algorithms to construct the model. ML models RF, DT, KNN, and DL models Multi-Layer Perceptron (MLP), Convolution Neural Network (CNN), and Artificial Neural Network (ANN) are used to develop a hybrid proposed approach and the suggested approach reduces overfitting, Type 1, and Type 2 error.

To better serve applications, the authors [19] suggested an Optimized Ensemble-Intrusion Detection system (OE-IDS) using AutoML. The techniques utilized for data balance in the pre-processing stage include SMOTE, SMOTE-TOMEK (pair of instances of opposite classes in proximity), Adaptive Synthetic Sampling Approach (ADASYN), and Random Oversampling Examples (ROSE). Kendall’s test, Pearson’s correlation, and Spearman’s correlation were used for feature analysis. Soft voting was used to obtain the ensemble prediction results, and the performance was assessed using classification evaluation metrics.

The most frequent issues in IDS that require treatment are high FPR and Detection Rate (DR). To address this issue, the authors [10] presented a two-stage model solution in which stage 1 offers a Pareto optimal solution for base models, and stage 2 makes the final prediction via a majority vote. Pareto-optimal solutions are produced using the Archived-based Micro Genetic Algorithm (AMGA) algorithm. The MLP classifier is the foundational model and the weights are initialized randomly. The best-performing models were chosen for an ensemble using overproduce and to choose the technique. The authors [4] suggested a dual ensemble, which combines two existing ensemble approaches, to decrease the False Alarm Rate (FAR) and boost DR. The fundamental learning algorithms are Gradient Boosting Decision Tree (GBDT) and bagging. The Classification and Regression Tree (CART) was regarded as a weak learner by the basic GBDT. The performance of the base learners was improved using a variety of dual ensembles, including the improved GBDT, Gradient Boosting Machine (GBM), LightGBM, Category Boosting (CatBoost), and XGBoost. The Friedman rank test was applied to rank ensemble performance. The disadvantages of traditional intrusion detection systems include their poor accuracy and detection rate, the authors [12] proposed Ensemble Learning algorithm-based Anomaly Detection in Communication Networks (EL-ADCNS) is a unique anomaly detection technique that is suggested as a solution to the problem. Correlation-based Feature Selection (CFS) and RF are used to lower the dimensionality. RF, SVM, AdaBoost, and Bagging classifiers are used in hybrid Ensemble Learning (EL) training, and the result is average-voted before being input to the Hybrid Ada Boosting Bagging Algorithm (HABBA) classifier [12].

To address the key difficulty for IDS and IPS in malware prediction in new locations with high accuracy and detection rate, the authors [15] proposed the ensemble’s implementation using accuracy and Kappa value in the Weka tool. The foundation classifiers for ensembles are NB, LR, and DT, whereas the aggregation techniques employed are Bagging and Boosting. To defend the computing infrastructure against the metamorphic and polymorphic behavior of malware, a powerful IDS is required. The XGBoost, Bagging Classifier, Extra Tree, and RF classification algorithms are the learners for the proposed [3] Stacked Ensemble-based IDS(SE-IDS). The output of the base learner is provided to the meta-learner as input for the final classification; MLP is used here. Various sets of features are sent to each base learner, and each model’s final value is determined by majority voting before being fed to the meta-learner. A varied set of features was chosen using Sequential Forward feature Selection (SFS). Ten separate runs were conducted to test the performance of the model.

For the development of new attacks, a single classification system and an outdated dataset are insufficient. For dimensionality reduction, the authors [5] presented a heuristic technique based on the CFS and Bat Algorithm (BA). The basis classifiers for the ensemble consist of C4.5, RF, and Forest by Penalizing Attribute (Forest PA). Soft voting, which uses the average probability, was used to make the final prediction. To address new threats to network-connected systems, the authors [18] presented an ensemble of discriminant classifiers. A discriminant classifier is a method for transforming a weak learner into a strong learner. The model selection for the ensemble was performed using a random subspace approach. Empirical analysis of the 5-cross-fold subgroup that was chosen at random. Here, four were utilized for training, one for testing, and the final prediction was made by majority vote.

In the ensemble process, moderately accurate components of classifiers are combined to obtain highly accurate classifiers. The author [7] proposed a bagging and arcing (adaptively resample and combine) ensemble with homogenous and heterogeneous models respectively, and the performance of the models was evaluated using accuracy measures. The Radial Basis Function (RBF) and SVM are the classifiers used as a base classifier, and a 10-fold cross-validation technique is applied to calculate accuracy. Bagging was performed with RBF and SVM and compared with the base classifiers in terms of accuracy. For heterogeneous ensembles using arcing classifier creates a hybrid RBF-SVM and the final output is decided by weighted voting.

Multiple M-AdaBoost with Particle Swarm Optimization (PSO) and Modified AdaBoost with an area under the curve (M-AdaBoost-A) were proposed by the authors [13] to create an effective intrusion detection system to deal with large-scale, unbalanced, and multiclass data. The base learner, sub-learner, and expert learner in the M-AdaBoost-A-SMV model are integrated using simple majority voting.

Conventional detection techniques fall short of the real-time network dataset requirements. The authors [14] introduced Multi-dimensional Feature Fusion and Stacking Ensemble Mechanism (MFFSEM), which effectively detects anomalous behavior from real-time network data. Map Reduce-based Ensemble for IDS (MR-EIDS) was proposed [20] to detect intruders and attackers from real-time datasets. The security model is a key component of the fog-computing network, which facilitates the quality of service. The authors [24] suggested a hybrid optimization-driven ensemble classifier using the Ride Sea Lion Optimization (RSLO) algorithm, which combines the Rider Optimization Algorithm (ROA) and Sea Lion Optimization Algorithm (SLnOA). For feature selection, a filter approach based on the Kolmogorov-Smirnov correlation was applied. The categorization models utilized in the ensembles are the RideNN, Deep Neuro-Fuzzy Network (DNFN), and Shepard Convolution Neural Network (ShCNN). Comprehensive features were chosen from the fundamental characteristics to be combined with other features and input into the classifiers. By adding the probabilities of each classifier, a meta-classifier is created, which generates the final prediction from the classifiers. employing DT and RF to stack the classifiers for the ensembles. The combination of classes was evaluated along with the precision, recall, accuracy, and F1-score. Big data plays a major role in organizations that extract useful information from data, for which the authors [25] suggested an intelligent intrusion detection system employing binary Grey Wolf Optimization (GWO) to safeguard the power grid from intrusion and ensure its dependable and efficient operation. GWO is used for feature selection in Binary Grey Wolf Optimization Ensemble Classification (BGWO-EC).

An excellent Internet-of-Things (IoT) infrastructure is required for the efficient operation of smart cities. The authors [8] suggested an ensemble method for intrusion detection to improve the security of IoT-based applications. The author employed classification models RF, KNN, ANN, and SVM as stacking ensemble techniques used for model aggregation. Providing security for an IoT-based global network. Local Search-Pigeon Inspired Optimization (LS-PIO) has been proposed [9] for the selection of features from datasets. The author used PIO, Tabu Search, and Hill Climbing as local search techniques, and weighted voting was used to determine the outcome. The ensemble combinations used were One-Class Support Vector Machine (OC-SVM), Isolation Forest (IF), and Local Outlier Factor (LOF) for effective classification. In addition, the author assessed the complexity of the phases of feature selection and intrusion detection. IoT combines sensors and devices to automate routine business processes in industries. By adopting a voting-based ensemble approach, the authors [16] proposed a framework for the Industrial IoT (IIoT) to identify cyberattacks. Histogram gradient Boosting (HGB), CatBoost, RF, and the final prediction made using the hard voting method made up the ensemble. The author suggests a two-step approach that entails traffic analysis and abnormal event detection to address the security issues with IoT systems. The ensemble containing Extra tree, RF, and Deep Neural Network (DNN) was utilized for the traffic analysis step and the event detection step, respectively. Accuracy, precision, recall, F1-score, and Balanced Accuracy (BAcc) are the performance metrics utilized for evaluation. BAcc measures the detection performance in an unbalanced dataset by averaging the recall for each class [26]. SVM integration with Chaos Game Optimization (CGO) was suggested by the authors [17] to handle heterogeneous data. The final prediction made by voting is included in the k times SVM (SVM1, SVM2, …, SVMk) used as an ensemble for training.

In the existing studies on intrusion detection, numerous classification models have been explored. But, many of these models have focused widely on features selection and performance improvement of the ensemble model. From the existing studies, it is observed that there is a lack of transparency in the process of model selection for an ensemble. This lack of clarity hinders the ability to justify the choices for constructing an ensemble. The table presented below showcases a compilation of diverse ensembles derived from existing studies, as depicted in Table 1.

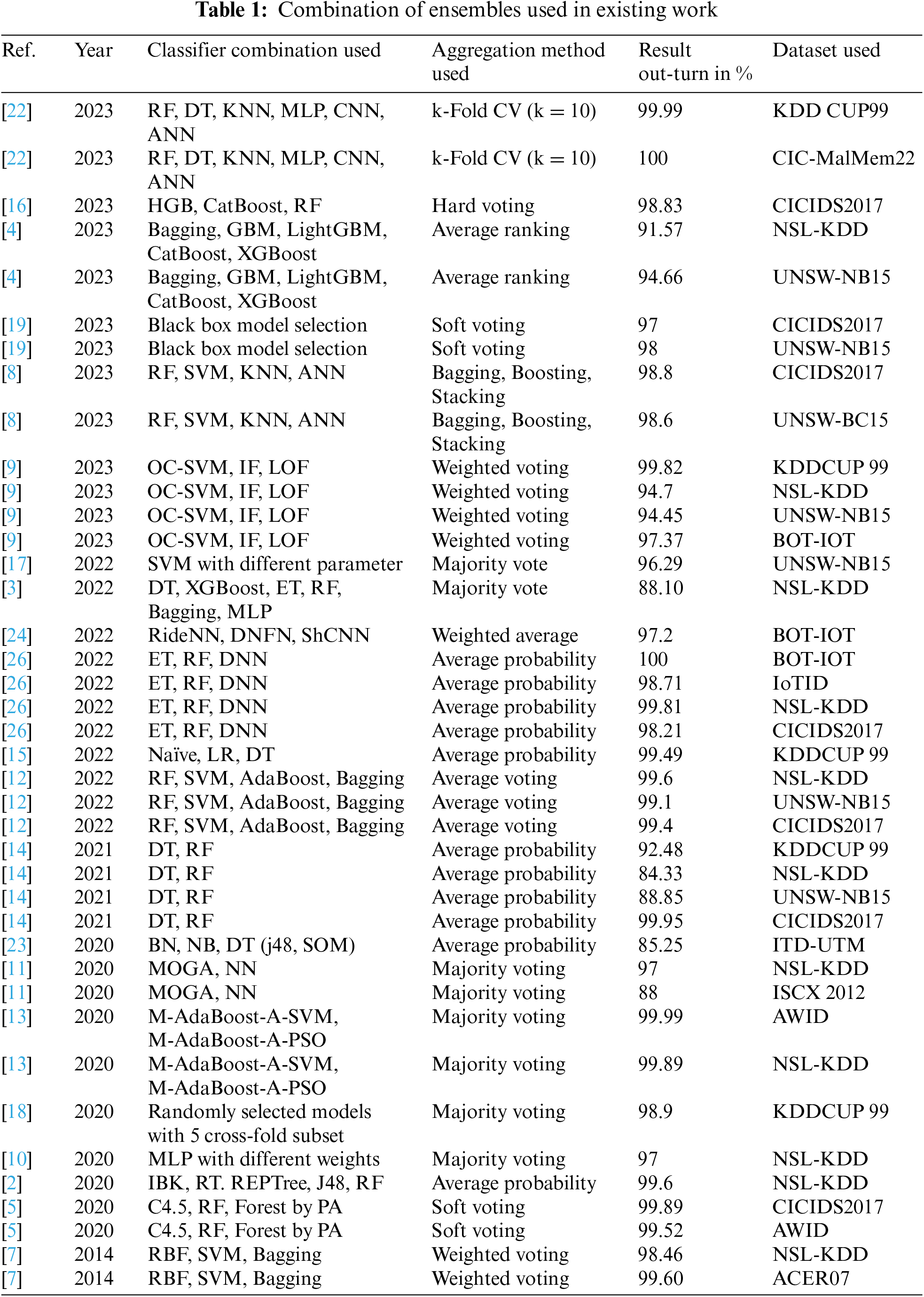
The selection of a dataset is an important component in building an efficient machine-learning model. According to the State of Data Science 2022 report [27], preparation and understanding of the data is an important and time-consuming task of ML model building. To serve a real-world application, model building should be evaluated using quality data. Depending on the need and problem statement the authors used various datasets for the intrusion detection system. The datasets listed in Table 2 have been widely used and proven to be valuable resources in the existing literature on intrusion detection.

3  Proposed Work

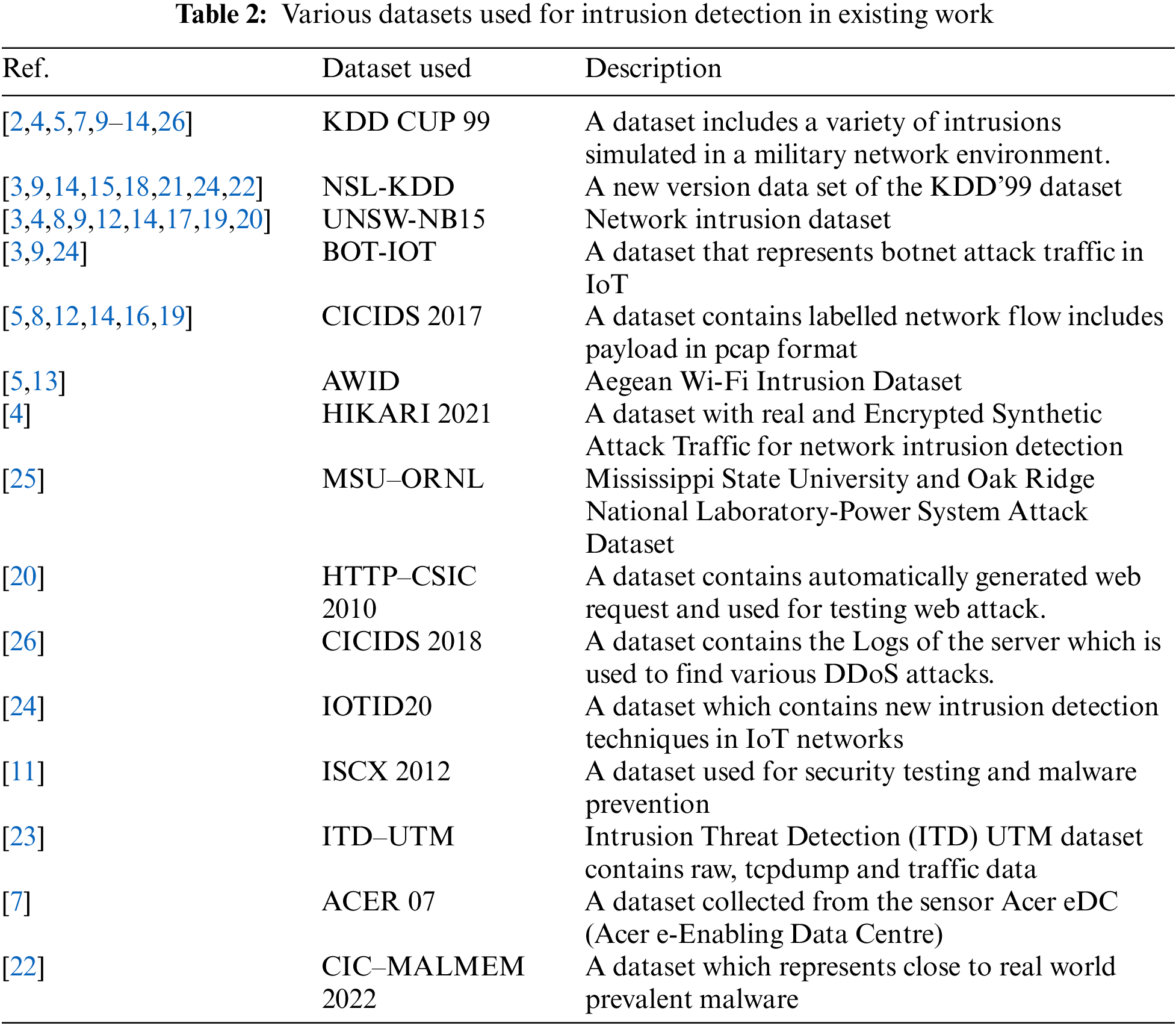
The proposed work objective is to address the model selection for an ensemble by selecting the most suitable models based on the application requirements. Through the implementation of the proposed Modified MMS approach, the aim is to offer a justification for model selection within an ensemble. Furthermore, research findings indicate that the identified models can be combined in an ensemble that can reduce the space complexity of the problem. In the following section, the steps involved in the proposed approach are described.

3.1 Model Selection for Ensemble

Ensemble learning combines the predictions of various models to produce a powerful and reliable model that can be generalized more effectively to new data. Because it specifies which model will be included in the ensemble and how it will be mixed, model selection is a crucial stage in ensemble learning. The caliber of the individual models and the ensemble diversity both affect the performance of the ensemble. Selecting models that are complementary to one another and that have various strengths and weaknesses is crucial. Fig. 1 depicts the overall architecture of the proposed system which comprises various modules, including preprocessing, individual model training, creating a correlation matrix for the individual models, selection of the models for the ensemble, and aggregation.

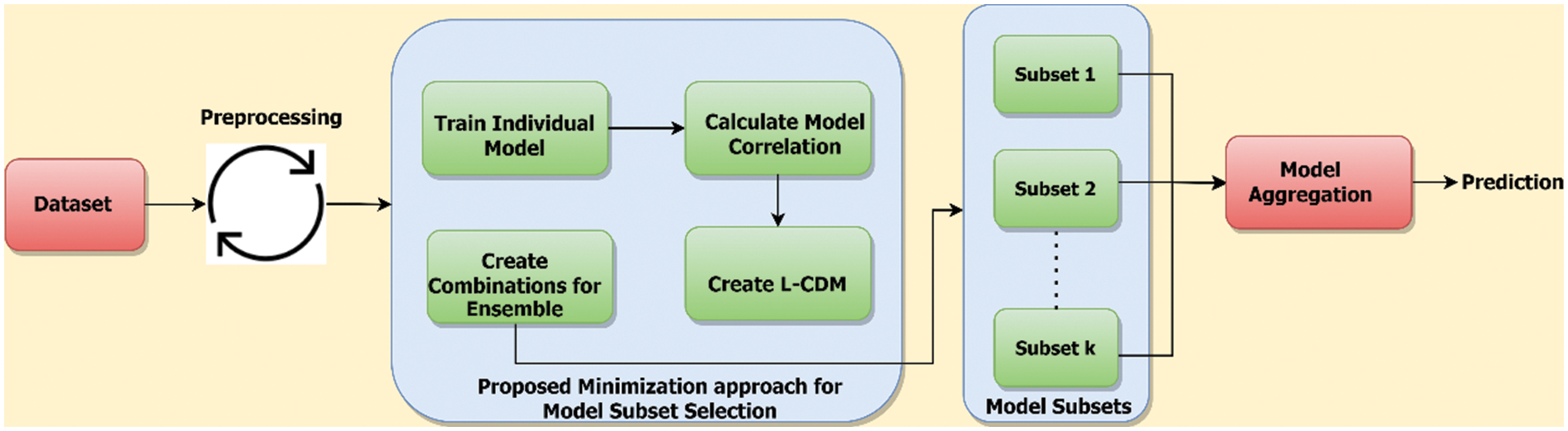
Figure 1: Proposed method architecture. A model which comprises dataset, pre-processing, and the proposed model selection Modified-MMS modules. The models selected from the proposed system are aggregated to produce the final class prediction

3.1.1 Correlation-Based Diversity Matrix (CDM)

Model selection for an ensemble relies on the objective of improving the performance and diversity of the model. The importance of diversity in ensemble learning lies in the fact that it helps reduce overfitting and improves model robustness. CDM is used to measure the diversity between individual models in an ensemble. It evaluates the similarity between different models in terms of their predictions using the same input data.

To create CDM constructed as follows:

Step 1–For each model, generate a set of predictions

Step 2–Calculate the correlation coefficients of all the individual models

Step 3–Create a Correlation-based Diversity Matrix.

The linear relationship between the variables is defined by the statistical measure correlation coefficient, which also describes the degree of the relationship between two variables. Here the variables represent the predictions generated by each model. The correlation coefficient ranges from −1 to 1, where a value of −1 indicates a negative correlation, 0 indicates no correlation and 1 indicates a positive correlation.

The CDM can be visualized in a square matrix, where each row and column represent a model in an ensemble. The diagonal of the matrix contains the correlation coefficient between the model and itself, which is always equal to one. The off-diagonal elements contain the correlation coefficients between the pairs of models. From the pairs of models select the models, with low correlation coefficients to maximize the performance and diversity of the ensemble. Highly correlated models mean that they are making a similar error and may not provide much new information to an ensemble.

If the ensemble has an n classifier, then the matrix will be n × n.

CDM =[1clf12clf13clf14…clf1nclf211clf23clf24…clf2nclf31clf321clf34…clf3nclf41clf42clf431…clf4n⋮⋮⋮⋮1⋮clfn1clfn2clfn3clfn4…1](1)

Here, clfij, indicates the classifier row, and column indexes represented by i and j, respectively.

3.1.2 Exploiting Symmetry of Matrix

A symmetric matrix is a matrix in which the transpose of the given matrix is equal to the original matrix. In a symmetric matrix, the entries above the diagonal are equal to those below the diagonal. This means that matrix is completely determined by its diagonal entries and either the upper or lower triangular parts. By taking advantage of symmetry, computational complexity, and memory usage can be reduced.

Let us consider the CDM from Eq. (1), if the transpose of CDM is equal to the original CDM, then this implies that the matrix is symmetrical about its diagonal. This can be expressed mathematically as follows:

CDMT=CDM(2)

In terms of the matrix elements, the symmetry property can be expressed as:

a_ij=a_ji ∀ i, j(3)

where a_ij is the element of the ith row and jth column of the matrix.

If the given matrix satisfies the property of symmetry, either the lower triangular part or the upper triangular part can be used further, which provides the advantage of computational efficiency and reduces storage requirements.

3.1.3 Modified Minimization Approach for Model Subset Selection (Modified-MMS)

Minimization is the process of finding the smallest possible value of a quantity, typically a function. From the CDM, the lower triangular part (L-CDM) is considered for subset selection. From the L-CDM the model subsets must be selected for input to the ensemble. Subset for the ensembles selected from the following steps.

Setting up the threshold significantly impacts the performance of the classification model. To improve the diversity of the model, a combination of low-correlated models works efficiently. Combining the models with a high correlation will not be able to predict new errors and improve the accuracy.

To select subsets for an ensemble, this research opted to use the concept of Deterministic Finite Automata (DFA) minimization. DFA minimization is the process of reducing the number of states in DFA while preserving its language recognition capability. The Myhill-Nerode Theorem or Table filling method [28] is used in the minimization of DFA, in which the minimal equivalent version of any DFA includes a minimum number of states possible.

Steps for minimization in DFA [29]:

1.    Create a pair of states involved in a given DFA.

2.    Mark all pairs (Qa, Qb) such that Qa is the final state and Qb is a non-final state.

3.    If there is any unmarked pair (Qa, Qb) such that δ(Qa, x) and δ(Qb, x) are marked, then mark (Qa, Qb). where x is an input symbol. Repeat this step until no more marking can be made.

4.    Combine all the unmarked pairs and make them a single state in minimized DFA.

The proposed Modified-MMS uses the concept of table filling method of DFA Minimization. In the Modified-MMS the base classifiers are considered nodes, and the Threshold T (Correlation Coefficient Value) should have a minimum correlation value. A node that has low performance in terms of evaluation metrics is considered a threshold node. Fig. 2 shows the workflow of the proposed Modified MMS.

Figure 2: Workflow representation of Modified-MMS

Step 1–Let M1, M2, …, Mn be a set of models

Create a pair with all states (models) from L-CDM.

Step 2–Let C1, C2, …, Cm be a set of conditions

Step 3–Combine the pairs Clfi and Clfj as a subset to input ensemble, here i, j indicates the models.

If value [(Clfi, Clfj)] <= T, then Clfi and Clfj ← Sk (Subset k)

Combine the pairs Clfi and Clfj as a subset to input ensemble

If (Clfi € threshold node) OR (Clfj € threshold node), then Clfi and Clfj ← Sk (Subset k)

Step 4–Make the pairs to input.

Let X be a set of n classifiers, and let r(i, j) be the correlation coefficient between i and j. Then the subset S of the models that have pairwise correlation coefficient less than or equal to threshold t can be defined as:

S={x_i€ X|x_i is included in subset}(4)

where x_i is the i-th model in X, and the condition for inclusion in the subset is:

∀ i, j€{1,2…n},i≠j,r(i, j)<=t(5)

The subset S includes all classifiers x_i in X such that the correlation coefficient between x_i and every other variable x_j in X is less than or equal to threshold t.

3.2 Aggregation Method

An aggregation method is a technical approach to integrating the predictions generated by multiple individual models. Each model is trained on a subset of the data and then makes its prediction. These individual predictions are aggregated using specific voting rules to produce the final predictions. The most used aggregation methods in the existing study include majority voting, weighted voting, and stacked voting. The voting aims to improve the accuracy and robustness of the models, especially when individual models are prone to overfitting or have a high bias.

Subsets k created in the phase Modified-MMS trained with the dataset individually and the result was obtained using majority voting by combining the prediction. The implementation of majority voting serves to enhance both the accuracy and robustness of the model by effectively minimizing the influence of errors and biases associated with individual models.

Let us consider N individual models in an ensemble, each of which produces a binary outcome of 0 or 1. Let x_i be the output of the ith model, where i = 1, 2, …, N.

The majority voting combines the outputs of all N models to produce the final prediction (0 or 1).

x=1 if sum(x_i)>N/2(6)

x=0 if sum(x_i)<=N/2(7)

For example, consider 5 classifiers in ensemble, and the prediction of each model is

x_1 = 0, x_2 = 1, x_3 = 0, x_4 = 1, x_5 = 1

Then, the final prediction is

x = 1 if sum(x_i) > 5/2 by Eq. (6)

x = 0 if sum(x_i) <=5/2 by Eq. (7)

sum(x_i) = 3, which is greater than 5/2, so the final prediction is x = 1.

4  Experimental Setup

This section outlines the key components of the experiment, including the dataset description and validation procedure employed.

4.1 Data Set Description

The NSL-KDD dataset is an effective benchmark dataset that is widely used to compare the performance of models in IDS, which is a refined version of KDD CUP’99. Furthermore, the effectiveness of the dataset can be improved by default partitioning to KDD_Train+, KDD_Test+, and KDD_Train+_20 percent. The advantage of partitioning is that it runs the model conveniently and efficiently. A subset of NSL-KDD 20 percent data evaluates the performance of intrusion detection and machine learning model more efficiently and requires minimal resources than using the entire NSL-KDD dataset.

The dataset used for an experiment contains 25192 instances, in which 13449 are normal and 11743 are abnormal connections. Traffic input for intrusion detection referring 41 features and the target column represent the label ‘normal’ or ‘abnormal’. The dataset is publicly available to download, along with the full NSL-KDD dataset and documentation. The initial pre-processing steps involve several tasks, including identifying and handling missing and duplicate values, performing encoding, scaling the features, and splitting the data into training and testing sets, all of which are necessary to prepare the data to load into the model.

4.2 Evaluation Parameters

The performance of the proposed models was evaluated using the following performance metrics: Accuracy, precision, recall, and F1-score [30]. Defining evaluation metrics for a model is an integral part of estimating the accuracy of future data. To derive performance measures, an understanding of the confusion matrix is required. The confusion matrix is a representation of the prediction results. Each prediction can be any one of the outcomes based on how equivalent it is to the actual value.

4.2.1 Accuracy

It is a measure of the performance of the classification model, which indicates the proportion of correct predictions made by the model with overall prediction.

Accuracy =TP+TNTP+TN+FP+FN(8)

Accuracy is a suitable measure for dealing with balanced datasets. The precision, recall and F1-score are more suitable when the data are imbalanced [31]. Accuracy is the measure of correctly classified instances; similarly, misclassification rate is the measure of incorrectly classified instances.

Misclassification Rate=FP+FNTP+TN+FP+FN(9)

4.2.2 Precision

The proportion of correctly predicted positive classes and total positive observation

Precision =TPTP+FP(10)

4.2.3 Recall

The proportion between correctly predicted positive class and actual positive observations

Recall =TPTP+FN(11)

4.2.4 F1-Score

The F1-score was the harmonic mean of the precision and recall system measurements. The overall correctness of the model was derived from the F1-score.

F1-Score =2 * Recall∗PrecisionRecall+Precision(12)

5  Results and Analysis

Following the experimental setup, this section presents the obtained results and a comprehensive analysis of the performance of the proposed Modified MMS.

5.1 Correlation-Based Diversity Matrix (CDM)

In conducted experiment, six base classifiers were utilized for training: LR, NBC, KNN, DT, SVM, and RF. Each classifier was assigned a label: clf1, clf2, clf3, clf4, clf5, and clf6, respectively. The correlation between the predictions of these individual classifiers was represented as a matrix denoted by CDM and presented in Eq. (1).

CDM =[10.750.940.940.960.940.7510.750.740.750.740.940.7510.970.960.980.930.740.9710.960.990.960.750.960.9610.970.940.740.980.990.971](13)

Eq. (13) is derived from Eq. (1), which represents the correlation between the prediction of the six base classifiers used in the experiment. In the matrix representation, each row and column in CDM corresponds to a specific base classifier, while the value in each cell of the matrix indicates the degree of correlation between the predictions of the pair of classifiers. By analyzing CDM insights model relationships and predictive performance can be derived.

The CDM can be effectively visualized as a grid, which is shown in Fig. 3. Each row and column in the grid correspond to an individual base classifier used in experiments. To make the matrix more interpretable the values are represented as a heat map, where darker colors indicate strong correlation and lighter colors indicate weak correlation.

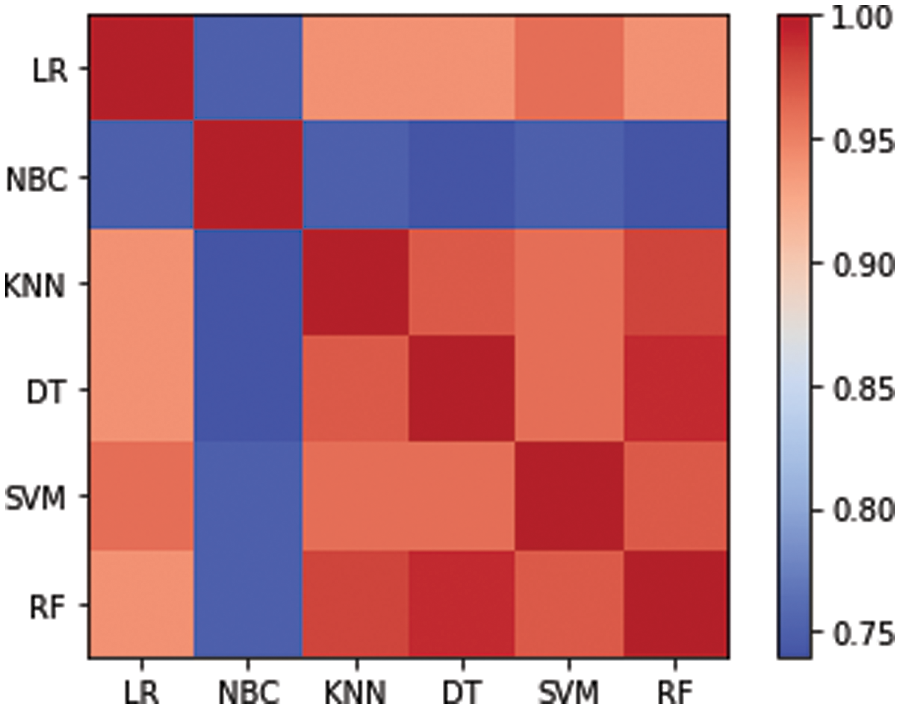
Figure 3: Heat map of base classifier correlation

From Eq. (2), the property of matrix symmetry is utilized to significantly reduce the computational cost and the memory requirement for certain operations. The correlation between two classifiers is the same regardless of the order in which they are considered and can utilize the advantage of symmetry property. The transposition of the CDM is shown in below Eq. (14):

CDMT=[10.750.940.940.960.940.7510.750.740.750.740.940.7510.970.960.980.930.740.9710.960.990.960.750.960.9610.970.940.740.980.990.971](14)

From Eq. (14), either the lower or upper half part of the matrix represents the correlation values, which eases further implementation. For a conducted experiment on model subset selection, the lower triangular part of the matrix is chosen, denoted as L-CDM. Considering the correlation values for the pairs of variables where the row index is greater than the column index. The L-CDM is represented in Eq. (15) below:

L-CDM =[1000000.75100000.940.7510000.930.740.971000.960.750.960.96100.940.740.980.990.971](15)

Model subsets from L-CDM (2,1), (3,1), (3,2), (4,1), (4,2), (4,3), (5,1), (5,2), (5,3), (5,4), (6,1), (6,2), (6,3), (6,4), (6,5) were chosen for the next phase of minimization.

5.2 Modified Minimization Approach for Model Subset Selection (Modified-MMS)

DFA minimization aims to minimize the states in an automaton, in which the minimized DFA is also accepted by the language as the original DFA. Acquiring the concept of minimization to select the minimal model which should produce the same performance of multiple model combinations. Selecting the minimal models for an ensemble reduces the complexity, enhanced diversity, and improved efficiency.

Here the classifiers clf1, clf2, clf3, clf4, clf5, and clf6 are considered as a state of automaton, the correlation coefficient between the models is considered as a transition value, and the low-performing model/classifier consider as an end node in an automaton. The subset derived from L-CDM is given to the proposed Modified-MMS method to minimize the ensemble models. The steps involved in the model selection are itemized below.

In the first step, create pairs of all the models derived from L-CDM. These pairs include (2,1), (3,1), (3,2), (4,1), (4,2), (4,3), (5,1), (5,2), (5,3), (5,4), (6,1), (6,2), (6,3), (6,4), (6,5). Then group these models according to their components. The LR model (denoted by clf1) has combinations (2,1), (3,1), (4,1), (5,1), and (6,1) as depicted in Fig. 4a. This work selects the subset of combinations that satisfy the Modified-MMS condition for the ensemble input. Similarly, repeat this process for all the base classifiers, which include NBC, KNN, DT, SVM, and RF (denoted as clf2, clf3, clf4, clf5, and clf6, respectively). The classifiers combination NBC, KNN, DT, SVM, and RF are depicted in Figs. 4b–4f.

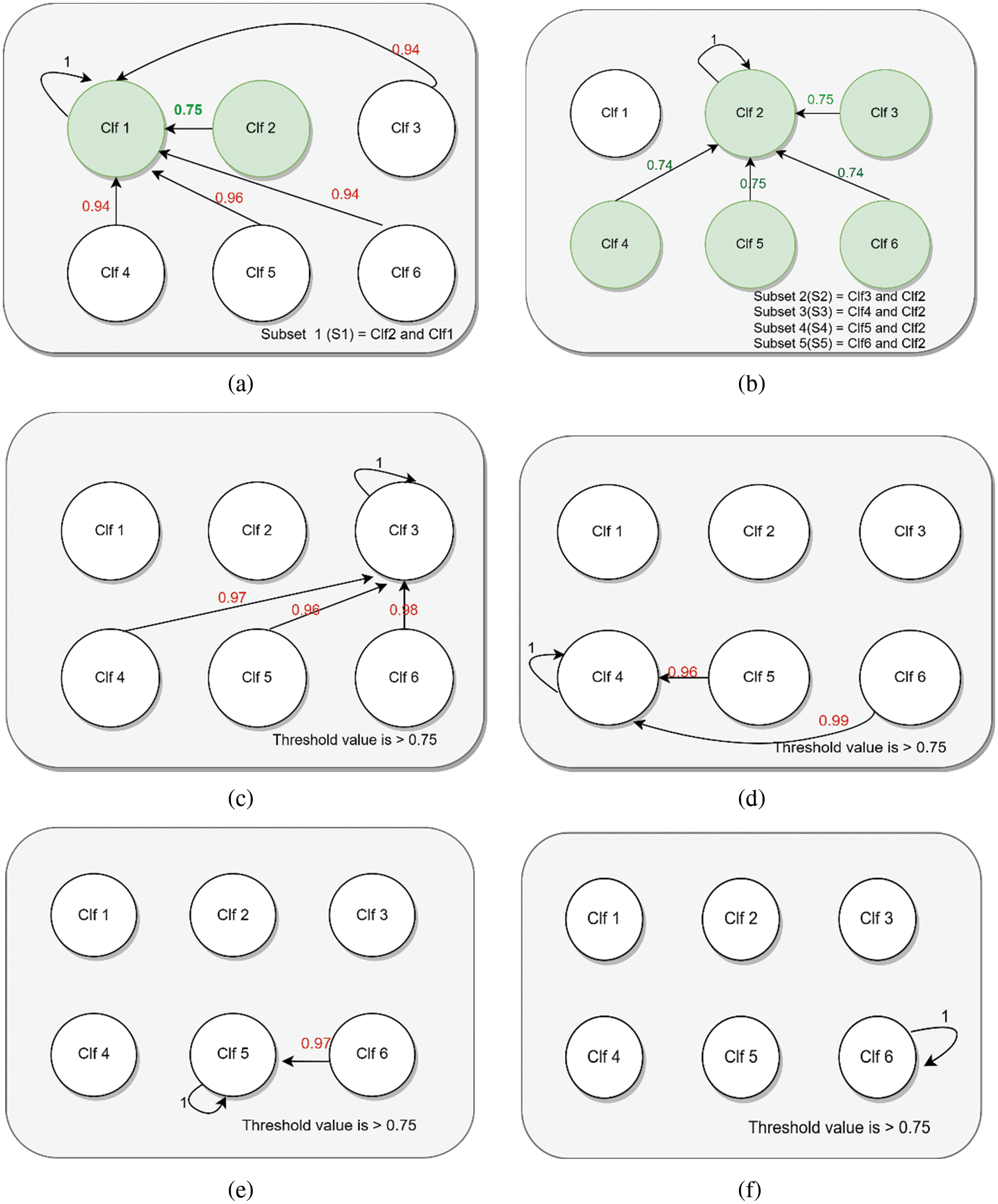
Figure 4: Creating subsets concerning State i (i = clf1, clf2, clf3, clf4, clf5, clf6), clfi represents classification models

Based on Fig. 4. the selected model combinations that satisfy the condition for the ensemble input are as follows:

•   From Fig. 4a. the subset selected is (2,1), which indicates that the recommended combination for an ensemble is NBC and LR.

•   From Fig. 4b. the selected subsets are (3,2), (4,2), (5,2), and (6,2) which include the combinations (KNN, NBC), (DT, NBC), (SVM, NBC), (RF, NBC) respectively. Other combinations failed to satisfy the rules of Modified-MMS.

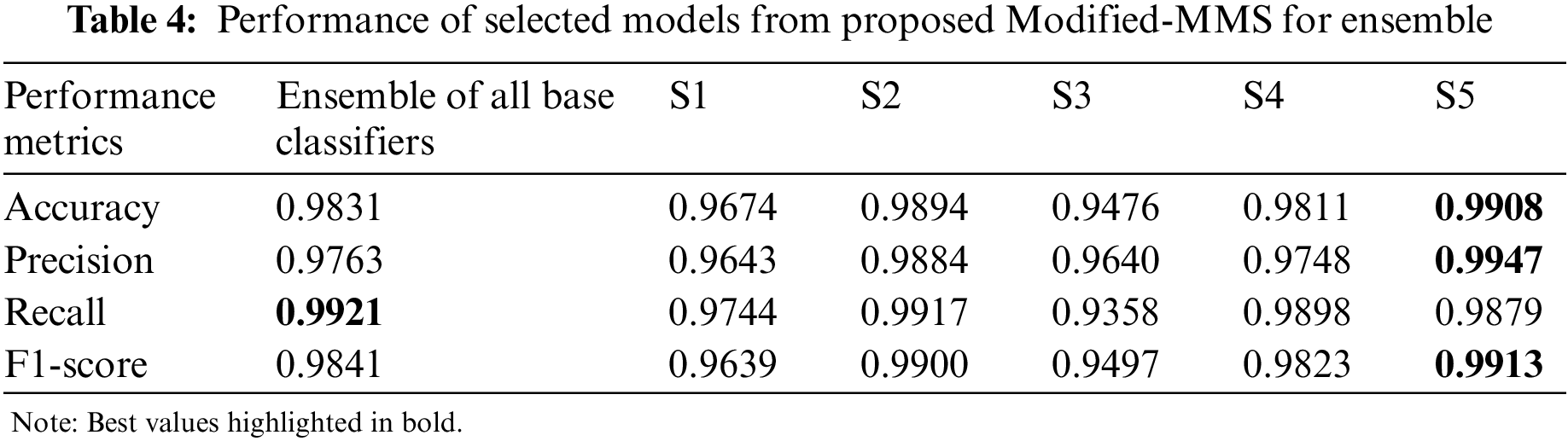
The above-mentioned model combinations, namely S1 (NBC and LR), S2 (KNN and NBC), S3 (DT and NBC), S4 (SVM and NBC), and S5 (RF and NBC) are the recommended ensemble from Modified-MMS.

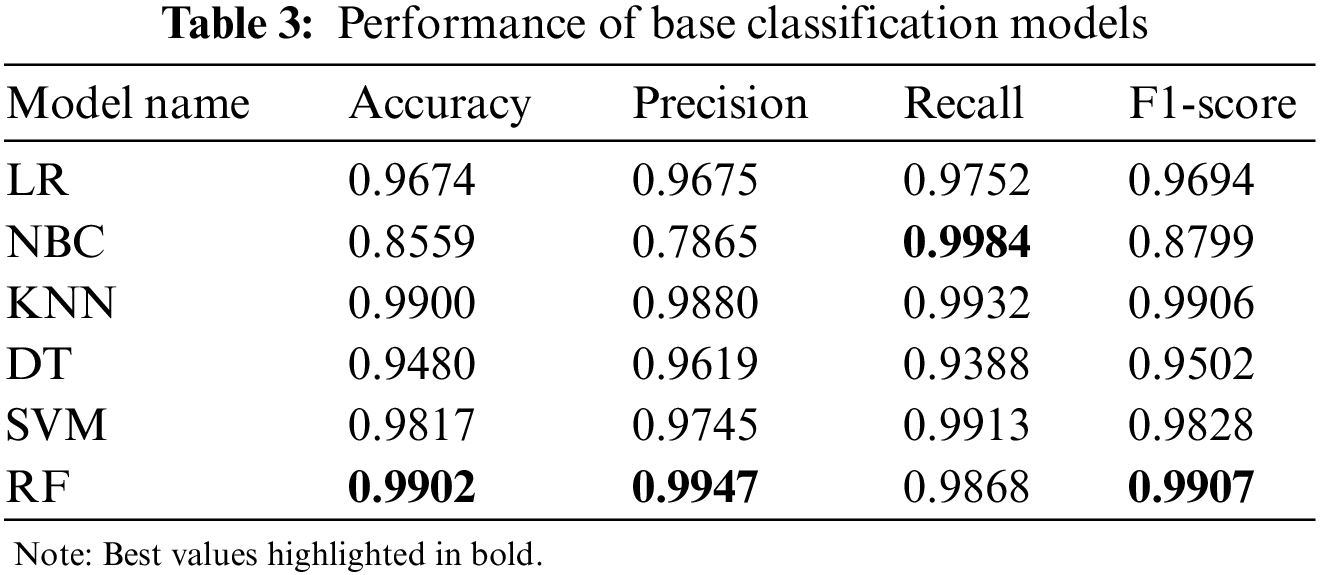
Table 3 displays the performance of the base classification models, while Table 4 shows the combination of a subset of these models selected using the proposed Modified-MMS technique and their corresponding performance. The hyperparameter for the selected classifiers was calculated using grid search cv = 5, and the evaluated performance was recorded in Table 5. The results from Tables 4 and 6 indicate the noticeable improvement in accuracy, precision, recall, and F1-score of the ensembles. Additionally, the performance of the model subsets compared with the ensemble made with all base classification models. The proposed research work achieved higher performance with only two base classifiers than the six-based classifier ensemble.

Hyperparameter tuning is the process of selecting an optimal set of hyperparameters for the model. Selecting the hyperparameter for the model is a crucial part to achieve high performance. In conducted experiment Grid Search CV (Cross-Validation) to find the best hyperparameter for the model is used. The selected hyperparameter for the experiment data is listed below in Table 5.

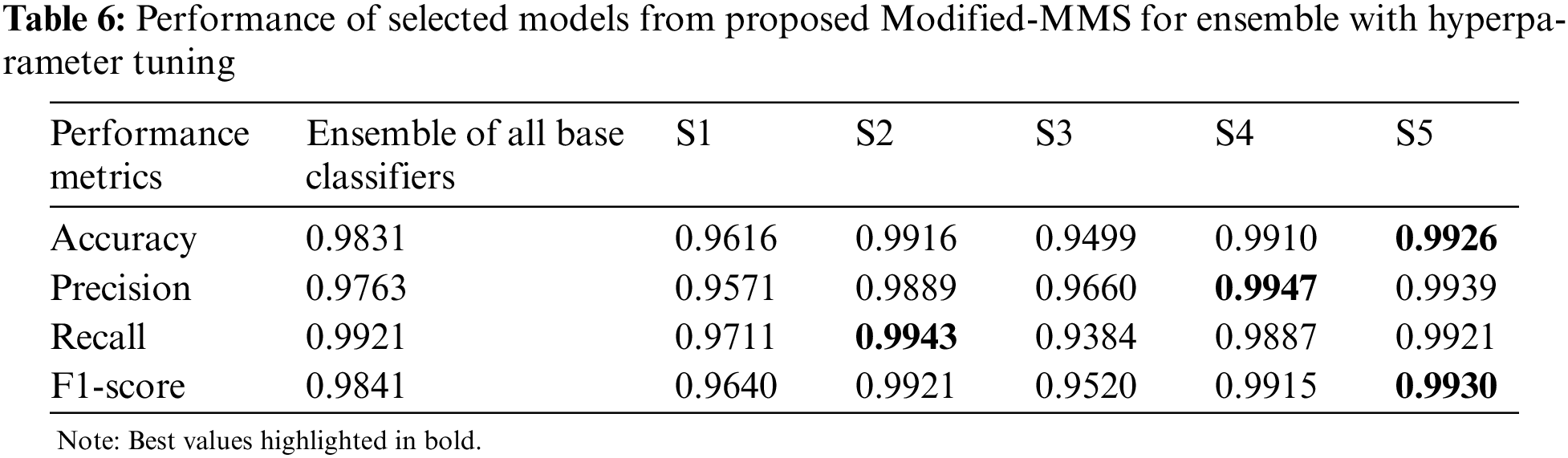
The term ROC stands for Receiver Operating Characteristic, and it is commonly used to evaluate the effectiveness of a binary classification system. The ROC curve is created by plotting True Positive Rate (TPR) against FPR for various classification thresholds. By analyzing the ROC curve, a performance summary of the classifier is obtained. From the results of the conducted experiment, Fig. 5 illustrates the performance of each classifier, while Fig. 6 demonstrates the performance of the base classifier and the ensemble of all base classifiers. From Fig. 7, the performance of each subset selected from the proposed Modified MMS is identified. Fig. 8 shows the comparison of different performance metrics of selected subsets.

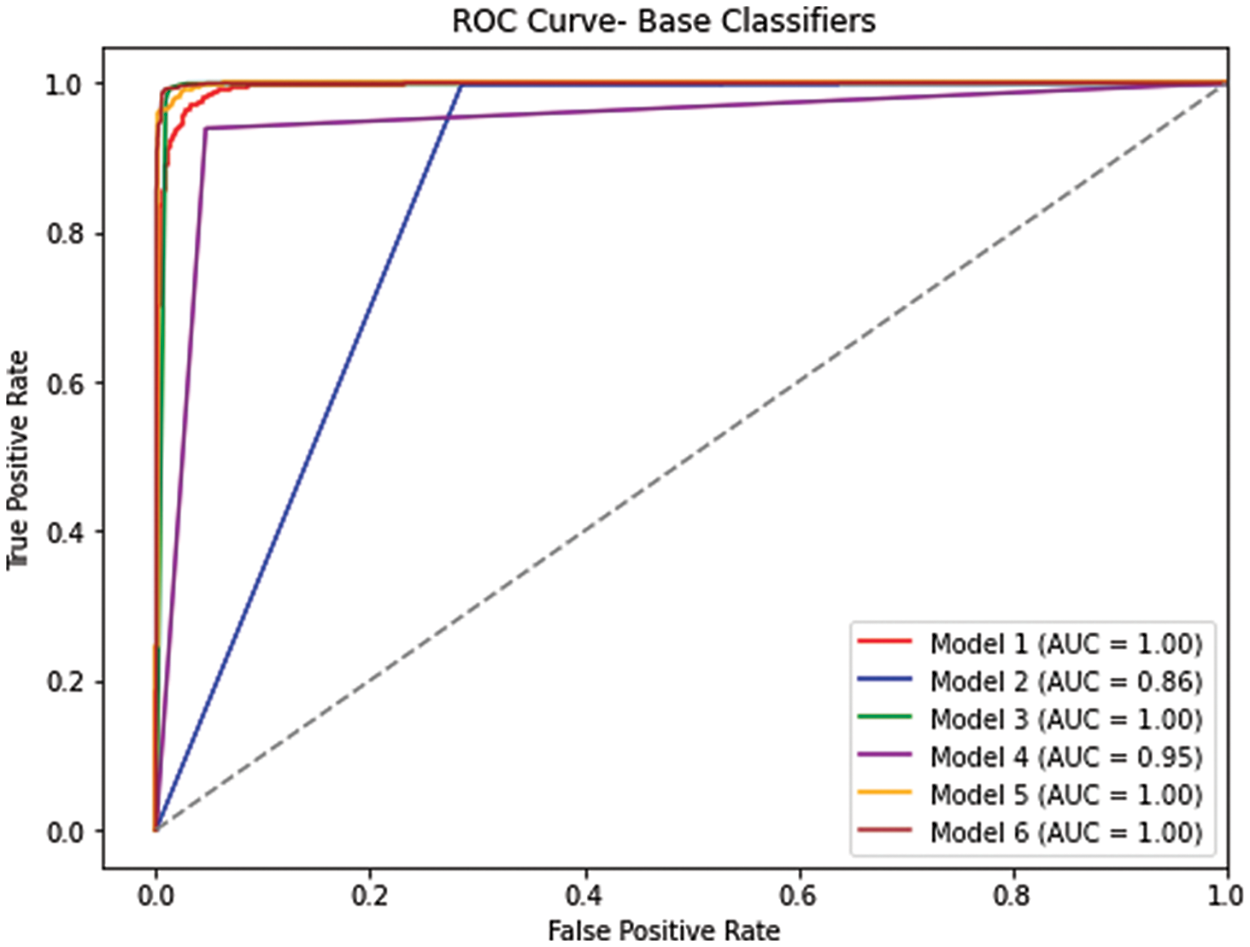
Figure 5: ROC between all base classifiers

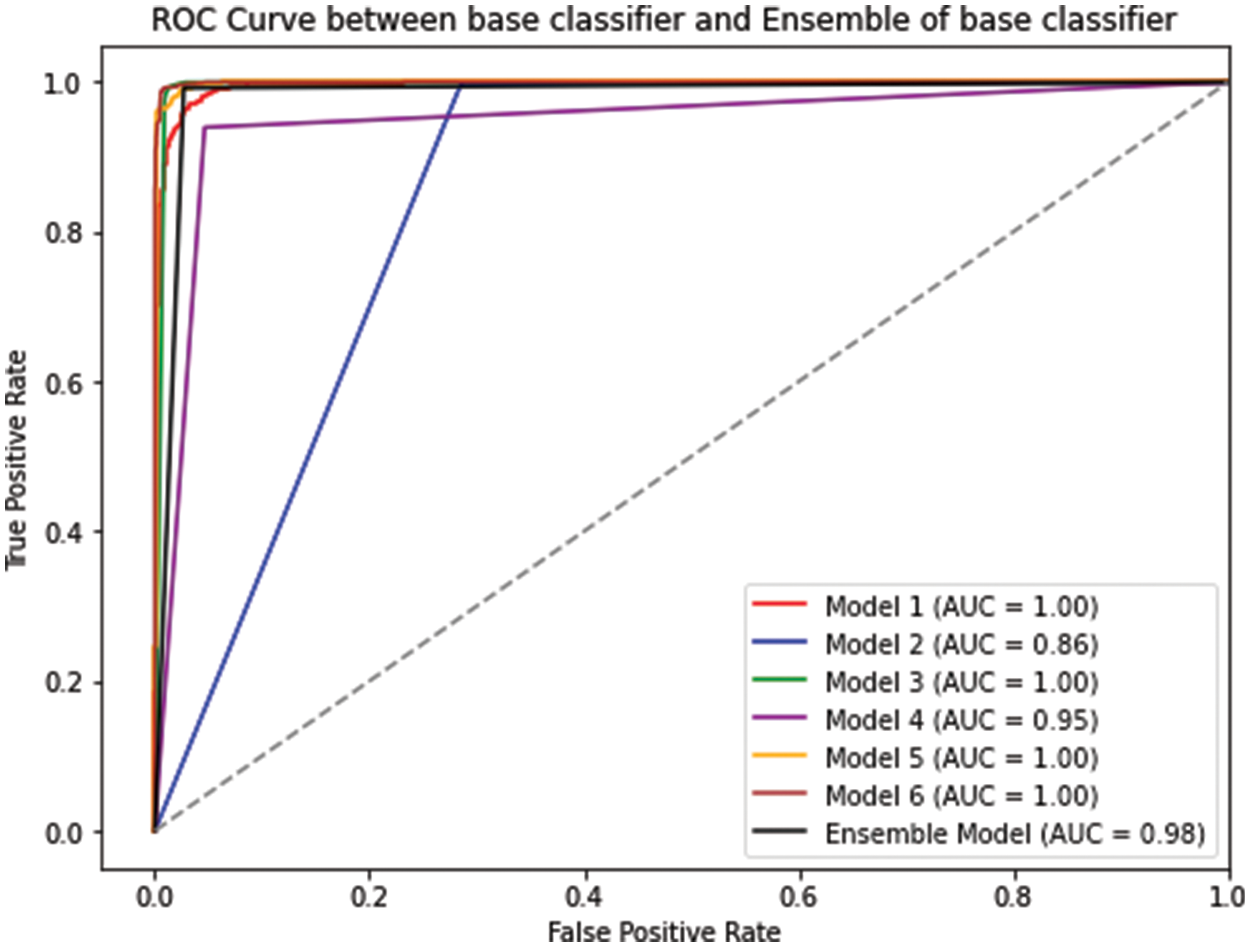
Figure 6: ROC between base classifier vs. ensemble of classifier

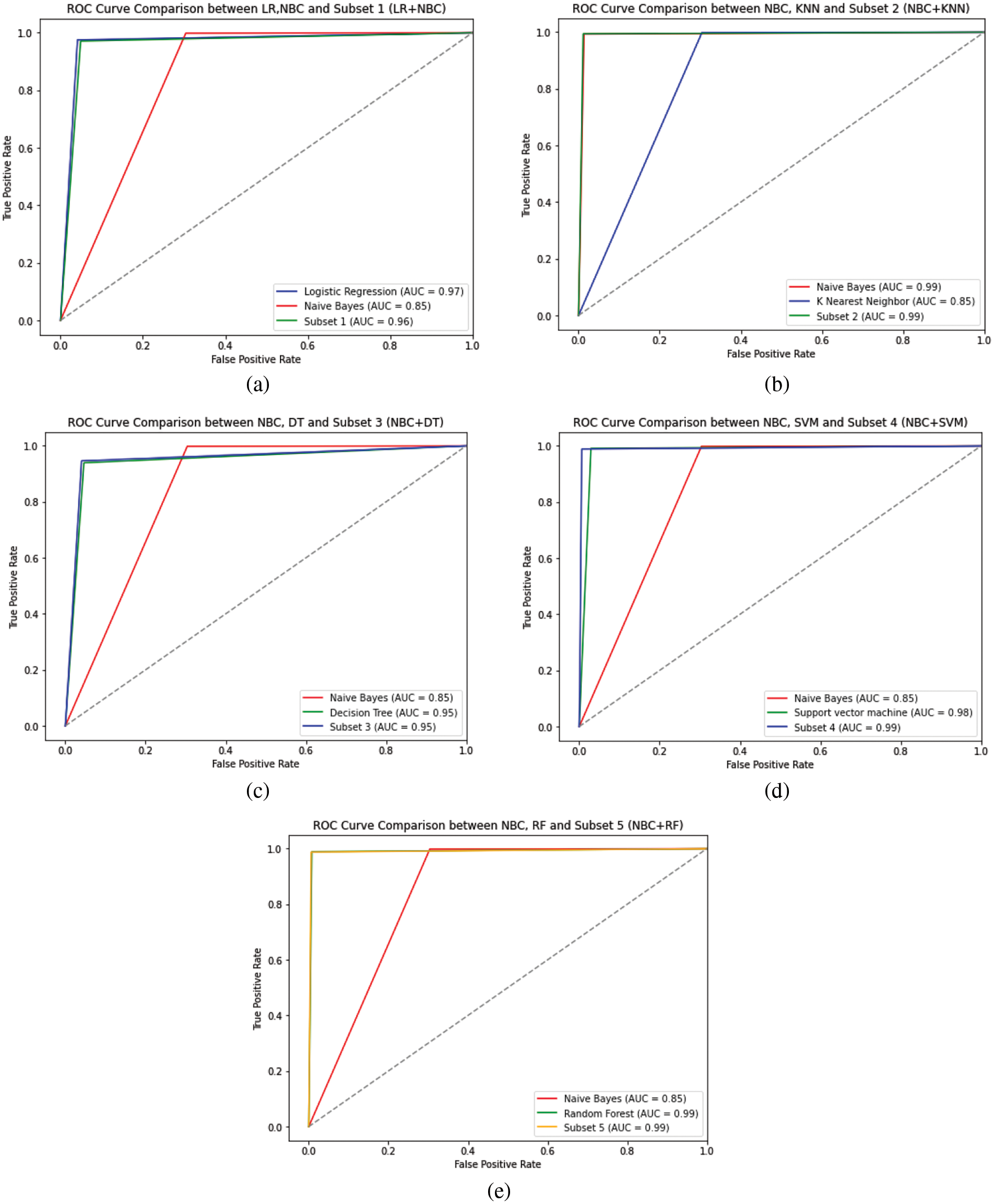
Figure 7: Comparison of ROC curves between selected subsets from proposed Modified-MMS

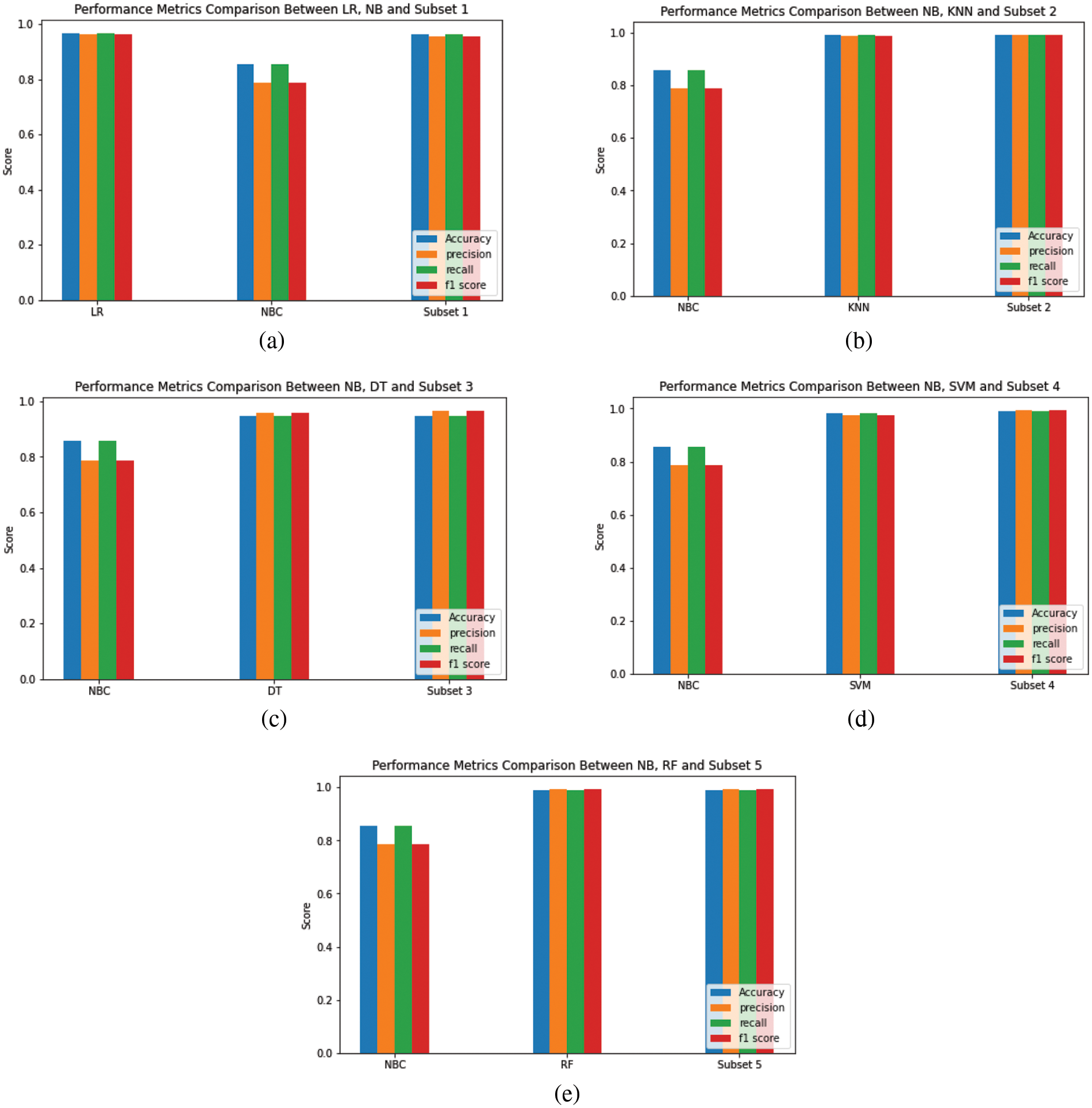
Figure 8: Comparative analysis of individual models and their ensemble subsets

6  Conclusion and Future Work

In this study, the random forest algorithm exhibited strong performance as a standalone classification model, achieving an accuracy of 99.02%. However, to further enhance the performance and diversity of the model, a Modified-MMS technique was proposed to select a subset of the ensemble models. The proposed system selected only two models for the subset, which resulted in substantial improvements in performance and diversity as evaluated by metrics. Interestingly, the subset ensembles outperformed the ensembles of all six base classifiers. The subset containing only Random Forest and Naive Bayes classifiers (Subset 5) from Table 5 achieved an accuracy of 99.26%, surpassing the ensemble of all six base classifiers which achieved an accuracy of only 98.31% refer to Table 4. Subset 4 consisting of a Support Vector Machine and Naive Bayes classifiers achieved a precision score of 99.47%, Subset 2 with K-Nearest Neighbors and Naive Bayes classifiers achieved a recall score of 99.43%, and Subset 5 with Random Forest and Naive Bayes classifiers provided an F1-score of 99.30%. All these scores were higher than the corresponding metrics obtained from the ensemble of all six base classifiers. This indicates that the combination of just two base classifiers can achieve both high performance and diversity, as compared to the ensemble of all six classifiers.

The task of selecting an appropriate model for an ensemble is critical as it can greatly influence the ensemble’s performance. Incorporating models that have varying characteristics can lead to a substantial improvement in performance, as opposed to combining similar models. To address this objective, a novel approach called Modified-MMS for selecting a subset for an ensemble is proposed. Apart from advantages, the proposed minimization approach suffers from the non-uniqueness problem, where a unique solution for the model selection cannot be fixed. The process of combining models for the ensemble relies on factors such as the choice of base classifiers, the selection of performance metrics, the diversity of models, and the specific problem at hand.

Acknowledgement: We would like to thank the support of School of Computer Science and Engineering (SCOPE), VIT, Chennai.

Funding Statement: The APC was funded by the Vellore Institute of Technology (VIT).

Author Contributions: Study conception and design: Rukmani P, Rajathi C; data collection: Rajathi C; analysis and interpretation of results: Rukmani P, Rajathi C; draft manuscript preparation: Rajathi C. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data presented in this study are openly available online: https://www.kaggle.com/datasets/hassan06/nslkdd?select=KDDTrain%2B_20Percent.txt. Accessed on 13 January 2023.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. B. A. Tama and S. Lim, “Ensemble learning for intrusion detection systems: A systematic mapping study and cross-benchmark evaluation,” Computer Science Review, vol. 39, pp. 100357, 2021. [Google Scholar]

2. M. Dua, “Attribute selection and ensemble classifier based novel approach to intrusion detection system,” Procedia Computer Science, vol. 167, pp. 2191–2199, 2020. [Google Scholar]

3. E. Mushtaq, A. Zameer and A. Khan, “A two-stage stacked ensemble intrusion detection system using five base classifiers and MLP with optimal feature selection,” Microprocessors and Microsystems, vol. 94, pp. 104660, 2022. [Google Scholar]

4. M. H. L. Louk and B. A. Tama, “Dual-IDS: A bagging-based gradient boosting decision tree model for network anomaly intrusion detection system,” Expert Systems with Applications, vol. 213, pp. 119030, 2023. [Google Scholar]

5. Y. Zhou, G. Cheng, S. Jiang and M. Dai, “Building an efficient intrusion detection system based on feature selection and ensemble classifier,” Computer Networks, vol. 174, pp. 107247, 2020. [Google Scholar]

6. A. A. Aburomman and M. B. I. Reaz, “A survey of intrusion detection systems based on ensemble and hybrid classifiers,” Computers & Security, vol. 65, pp. 135–152, 2017. [Google Scholar]

7. M. Govindarajan, “Hybrid intrusion detection using ensemble of classification methods,” International Journal of Computer Network and Information Security, vol. 6, no. 2, pp. 45–53, 2014. [Google Scholar]

8. O. Bukhari, P. Agarwal, D. Koundal and S. Zafar, “Anomaly detection using ensemble techniques for boosting the security of intrusion detection system,” Procedia Computer Science, vol. 218, pp. 1003–1013, 2023. [Google Scholar]

9. O. A. Alghanam, W. Almobaideen, M. Saadeh and O. Adwan, “An improved PIO feature selection algorithm for IoT network intrusion detection system based on ensemble learning,” Expert Systems with Applications, vol. 213, no. 22, pp. 118745, 2023. [Google Scholar]

10. H. Zhao, M. Li and H. Zhao, “Artificial intelligence-based ensemble approach for intrusion detection systems,” Journal of Visual Communication and Image Representation, vol. 71, no. 4, pp. 102736, 2020. [Google Scholar]

11. G. Kumar, “An improved ensemble approach for effective intrusion detection,” The Journal of Supercomputing, vol. 76, no. 1, pp. 275–291, 2020. [Google Scholar]

12. H. W. Oleiwi, D. N. Mhawi and H. Al-Raweshidy, “MLTs-ADCNs: Machine learning techniques for anomaly detection in communication networks,” IEEE Access, vol. 10, pp. 91006–91017, 2022. [Google Scholar]

13. Y. Zhou, T. A. Mazzuchi and S. Sarkani, “M-AdaBoost-A based ensemble system for network intrusion detection,” Expert Systems with Applications, vol. 162, pp. 113864, 2020. [Google Scholar]

14. H. Zhang, J. L. Li, X. M. Liu and C. Dong, “Multi-dimensional feature fusion and stacking ensemble mechanism for network intrusion detection,” Future Generation Computer Systems, vol. 122, pp. 130–143, 2021. [Google Scholar]

15. G. Jakka and I. M. Alsmadi, “Ensemble models for intrusion detection system classification,” International Journal of Smart Sensor and Adhoc Network, vol. 3, no. 2, pp. 8, 2022. [Google Scholar]

16. R. Golchha, A. Joshi and G. P. Gupta, “Voting-based ensemble learning approach for cyber-attacks detection in industrial internet of things,” Procedia Computer Science, vol. 218, pp. 1752–1759, 2023. [Google Scholar]

17. A. Ponmalar and V. Dhanakoti, “An intrusion detection approach using ensemble support vector machine-based chaos game optimization algorithm in big data platform,” Applied Soft Computing, vol. 116, no. 7, pp. 108295, 2022. [Google Scholar]

18. B. S. Bhati, C. S. Rai, B. Balamurugan and F. Al-Turjman, “An intrusion detection scheme based on the ensemble of discriminant classifiers,” Computers & Electrical Engineering, vol. 86, no. 3, pp. 106742, 2020. [Google Scholar]

19. M. A. Khan, N. Iqbal, H. Jamil and D. H. Kim, “An optimized ensemble prediction model using AutoML based on soft voting classifier for network intrusion detection,” Journal of Network and Computer Applications, vol. 212, no. 3, pp. 103560, 2023. [Google Scholar]

20. M. S. U. M. Rao and L. Lakshmanan, “Map-reduce based ensemble intrusion detection system with security in big data,” Procedia Computer Science, vol. 215, pp. 888–896, 2022. [Google Scholar]

21. N. V. Sharma and N. S. Yadav, “An optimal intrusion detection system using recursive feature elimination and ensemble of classifiers,” Microprocessors and Microsystems, vol. 85, no. 3, pp. 104293, 2021. [Google Scholar]

22. M. A. Talukder, K. F. Hasan, M. M. Islam, M. A. Uddin, A. Akhter et al., “A dependable hybrid machine learning model for network intrusion detection,” Journal of Information Security and Applications, vol. 72, no. 1, pp. 103405, 2023. [Google Scholar]

23. D. Stiawan, A. Heryanto, A. Bardadi, D. P. Rini, I. M. I. Subroto et al., “An approach for optimizing ensemble intrusion detection systems,” IEEE Access, vol. 9, pp. 6930–6947, 2020. [Google Scholar]

24. M. P. Ramkumar, T. Daniya, P. M. Paul and S. Rajakumar, “Intrusion detection using optimized ensemble classification in fog computing paradigm,” Knowledge-Based Systems, vol. 252, pp. 109364, 2022. [Google Scholar]

25. M. Panthi and T. K. Das, “Intelligent intrusion detection scheme for smart power-grid using optimized ensemble learning on selected features,” International Journal of Critical Infrastructure Protection, vol. 39, pp. 100567, 2022. [Google Scholar]

26. C. A. de Souza, C. B. Westphall and R. B. Machado, “Two-step ensemble approach for intrusion detection and identification in IoT and fog computing environments,” Computers & Electrical Engineering, vol. 98, pp. 107694, 2022. [Google Scholar]

27. The State of Data 2022. [Online]. Available: https://www.anaconda.com/state-of-data-science-report-2022 [Google Scholar]

28. Myhill-Nerode Theorem. [Online]. Available: https://en.wikipedia.org/wiki/Myhill%E2%80%93Nerode_theorem [Google Scholar]

29. Steps for Minimization of DFA by Geeks for Geeks. [Online]. Available: https://www.geeksforgeeks.org/minimization-of-dfa-using-myhill-nerode-theorem/ [Google Scholar]

30. Q. R. S. Fitni and K. Ramli, “Implementation of ensemble learning and feature selection for performance improvements in anomaly-based intrusion detection systems,” in Proc. of IAICT, Bali, Indonesia, pp. 118–124, 2020. [Google Scholar]

31. N. I. Mowla, J. Rosell and A. Vahidi, “Dynamic voting based explainable intrusion detection system for in-vehicle network,” in Proc. of ICACT, PyeongChang, Korea, pp. 406–411, 2022. [Google Scholar]