 Open Access
Open Access
ARTICLE
Information Security Evaluation of Industrial Control Systems Using Probabilistic Linguistic MCDM Method
College of Computer and Cyber Security, Fujian Normal University, Fuzhou, 350117, China
* Corresponding Author: Mingwei Lin. Email:
Computers, Materials & Continua 2023, 77(1), 199-222. https://doi.org/10.32604/cmc.2023.041475
Received 24 April 2023; Accepted 07 September 2023; Issue published 31 October 2023
Abstract
Industrial control systems (ICSs) are widely used in various fields, and the information security problems of ICSs are increasingly serious. The existing evaluation methods fail to describe the uncertain evaluation information and group evaluation information of experts. Thus, this paper introduces the probabilistic linguistic term sets (PLTSs) to model the evaluation information of experts. Meanwhile, we propose a probabilistic linguistic multi-criteria decision-making (PL-MCDM) method to solve the information security assessment problem of ICSs. Firstly, we propose a novel subscript equivalence distance measure of PLTSs to improve the existing methods. Secondly, we use the Best Worst Method (BWM) method and Criteria Importance Through Inter-criteria Correlation (CRITIC) method to obtain the subjective weights and objective weights, which are used to derive the combined weights. Thirdly, we use the subscript equivalence distance measure method and the combined weight method to improve the probabilistic linguistic Visekriterijumska Optimizacija I Kompromisno Resenje (PL-VIKOR) method. Finally, we apply the proposed method to solve the information security assessment problem of ICSs. When comparing with the existing methods such as the probabilistic linguistic Tomada deDecisão Iterativa Multicritério (PL-TODIM) method and probabilistic linguistic Technique for Order Preference by Similarity to Ideal Solution (PL-TOPSIS) method, the case example shows that the proposed method can provide more reasonable ranking results. By evaluating and ranking the information security level of different ICSs, managers can identify problems in time and guide their work better.Keywords
With the continuous promotion of the “Industrial Internet” and “Made in China 2025”, industrial control systems (ICSs) [1] have been widely employed in various industries and have become an indispensable part of national infrastructure. ICSs is a general term for several types of control systems, including supervisory control and data acquisition (SCADA) systems, distributed control systems (DCS), and some other control systems. ICSs are commonly used in industries such as power, automotive manufacturing and industrial production, oil and gas, chemical, and transportation, etc. ICSs provide a great convenience for industrial production, but they also come with many issues. As the ICSs run through the whole industrial production cycle, it is possible to lead to the crashes of the whole system and bring considerable losses to the enterprise once the problem occurs. Hence, the information security issues of ICSs must be taken seriously. According to Chinese industry information statistics, there were 2238 global industrial control security incidents involving 15 industries from 2012 to 2019 [2], which shows its large number and wide scope.
The deep integration of information technology (IT) and industrialization has made ICSs and products increasingly connect to public networks in various ways. At the same time, viruses, Trojan horses, and other threats are spreading to ICSs, and then the information security problem of ICSs is becoming increasingly serious [3,4]. Therefore, the information security assessment of ICSs becomes an essential part, which plays a vital role in the timely detection of information security problems and potential risks of ICSs [5,6]. At present, many researchers have carried out research in the information security assessment of ICSs [7–11]. A hierarchically structured model for information security risk assessment using fuzzy logic was proposed by Abdymanapov et al. [12], which considers only qualitative information without quantitative information. A security effectiveness evaluation method was put forward by Fu et al. [13] to analyze channel throughput variation and system robustness, which determines the security of the system only by analyzing the data. Nazmul et al. [14] analyzed the relevance of risk assessment in monitoring and Supervisory Control and Data Acquisition (SCADA) systems to determine the vulnerability of each component to attacks. Mi et al. [15] proposed an objective and quantitative integrated security and safety assessment scheme based on Fuzzy Analytic Hierarchy Process (FAHP). But Nazmul et al. [14] and Mi et al. [15] did not consider the subjective and objective weights of the criteria. An association analysis-based Dynamic Cyber Security Risk Assessment (CSRA) approach was proposed by Qin et al. [16] to reduce the complexity of the modeling process in the CSRA. Most of the existing studies focused on the ranking and correlation between criteria, lacking a comprehensive consideration of a single assessment criterion. Furthermore, the majority of the approaches only involved either qualitative or quantitative data, causing them inadequate for achieving comprehensive results. To address the above problems, this paper uses PL-MCDM method based on the PLTSs, which effectively captures qualitative information regarding expert preferences through linguistic terms and expresses quantitative information about the degree of preferences using probabilities. In the process of assessing the information security of ICSs, it is essential to obtain expert ratings on the security status of system. The rating results, serving as raw data, also have directly impact on the result. However, due to the inherent uncertainty of linguistic expressions, precise numerical values may occasionally fall short of accurately conveying the true opinions of the experts. Fortunately, the PL-MCDM method offers decision-makers the ability to express their viewpoints using uncertain information, facilitating a more precise representation of their opinions. As a result, this method presents significant advantages in the information security assessment of ICSs.
PLTSs were proposed by Pang et al. [17] and evolved from fuzzy sets [18]. Since PLTSs can express both qualitative and quantitative information [19–20], it has turned into a research hotspot in decision analysis. As the research advances, the issues of its underlying operations are gradually revealed [21,22]. Taking the distance measure of PLTSs as an example, the distance measure proposed by Pang et al. [17] is capable of calculating the distance between two PLTSs in most cases. However, some counter-examples exist where the distance between two distinct PLTSs may erroneously amount to zero. After that, many researchers have proposed their own distance measures. Zhang et al. [23] put forward a new distance measure for defining the probabilistic linguistic preference relationship. Wang et al. [24] proposed a new distance measure in the extended TOPSIS-VIKOR method based on PLTSs. Lin et al. [25] first found the problems of the above distance measures and put forward a more scientific method, but it still exist some counter-examples like before. In such cases, this paper proposes a novel distance measure to solve this problem.
Multi-criteria decision-making (MCDM) methods generally involve multiple different evaluation criteria. They are widely applied in various fields, such as marketing [26,27], finance [28,29], environmental management [30–32], and supplier selection [33–35], etc. Therefore, there are many studies conducted on MCDM methods [36,37]. Al-Hchaimi et al. [38] proposed a fuzzy decision opinion score method (Fermatean-FDOSM) framework for evaluating Denial-of-Service Attack countermeasure techniques (DoS A-CTs) in the context of MPSoCs-based IoT. They built the decision matrix for eighteen defense approaches based on thirteen criteria. The CRITIC method for criteria weighting was followed by the development of the Fermatean-FDOSM method for ranking. Dang et al. [39] provided an MCDM framework to select sustainable suppliers, which integrates a spherical fuzzy Analytical Hierarchical Process (SF-AHP) and grey Complex Proportional Assessment (G-COPRAS). A case study in the automotive industry in Vietnam is presented to demonstrate the effectiveness of the proposed approach. Mohapatra et al. [40] used the MCDM method to select an optimal route between the utility center and the consumer by considering multiple criteria. Garg [41] presented a decision-making (DM) framework using Fuzzy-euclidean-Taxicab distance-based approach (Fuzzy-ETDBA) to solve the cloud deployment model selection problem, then gave a case study involving the evaluation and selection of four cloud deployment models over three decision parameters consisting of seventeen sub-parameters. Liu et al. [42] integrated a grey DM trial and evaluation laboratory (DEMATEL) with uncertain linguistic multi-objective optimization by ratio analysis plus full multiplicative form (UL-MULTIMOORA) to propose a novel MCDM method. They used the proposed method to find the optimal location of electric vehicle charging stations (EVCSs). Gireesha et al. [43] presented an Improved Interval-Valued Intuitionistic Fuzzy Sets-Weighted Aggregate Sum and Product Assessment (IIVIFS-WASPAS) to solve the problem of cloud service provider selection. Khan et al. [44] proposed multiple distance measures based on the complex hesitant fuzzy set (CHFS) and integrated those measures with the TOPSIS method. A practical example related to the effectiveness of COVID-19 tests was presented for the practical application and validity of the proposed method. Ali et al. [45] used multiple different MCDM methods to examine the importance of three renewable energy sources. Based on experimental validation, the Complex Proportional Assessment (COPRAS) or VIKOR emerged as the most effective MCDM method for selecting renewables in the proposed framework. Besides, the MCDM method can be combined with intrusion detection [46] and privacy protection [47] for network security defense. Based on the above analysis, it can be seen that the MCDM method is very widely used. Inspired by [45], we integrate the PLTSs with the VIKOR method in this work. So we can combine the advantages of them to obtain more precise results.
In this paper, we introduce the probabilistic linguistic multi-criteria method to the information security assessment of ICSs. The main contributions of the article are as follows:
(1) After analyzing the existing distance measure methods of PLTSs, we propose a novel subscript equivalence distance measure and verify the validity of the formula.
(2) We optimize the standardization method for PLTSs based on the subscript equivalence distance measure.
(3) To obtain the weights of the criteria, we combine the BWM and CRITIC methods to obtain subjective and objective weights, then derive the combined weights of the criteria.
(4) A practical example of the information security assessment of SCADA system is given to show the decision process of the PL-VIKOR method. Finally, we present a comparative analysis to highlight the superiority of the PL-VIKOR method.
The rest of this paper is organized as follows: Section 2 reviews the concept of PLTSs and its distance measure, then proposes the subscript equivalence distance measure. Section 3 provides the combined weight method, which demonstrates the specific steps of the BWM method and CRITIC method. Section 4 gives the specific steps of the proposed method. Finally, a case study is provided in Section 5 to illustrate the usefulness of our methods, and the conclusions are included in Section 6.
This section introduces the basic knowledge of PLTSs. Afterward, we propose a novel subscript equivalence distance measure for PLTSs and analyze the differences with other methods.
2.1 Probabilistic Linguistic Term Sets
PLTSs are based on linguistic term sets (LTSs), most commonly additive linguistic term sets, so the linguistic term sets here refer to additive LTSs, and the definition of LTSs is given first.
Definition 1 [23]: The LTS is finite and ordered, and can be defined as follows:
where
(1) If
(2) The negation operator is defined as follows:
For example,
Definition 2 [17]: Let
where
In the evaluation process, experts first assess each criterion based on the LTS
Definition 3: Let
where
For comparing different PLTSs, Pang et al. [17] defined the score function and deviation function.
Definition 4 [17]: Let
The value of the score function is a linguistic term with the subscript
The deviation function is defined as
For any two PLTSs
(1) If
(2) If
·If
·If
2.2.1 Distance Measure of Pang et al. [17]
The distance measure of Pang et al. [17] needs three steps. Firstly, we need to normalize the probabilities. Secondly, the number of PLTEs in PLTSs should be normalized. Thirdly, the linguistic terms in PTLSs should be ordered. These three steps are defined as follows.
Definition 5 [17]: If the sum of probabilities less than 1, complementing the probabilities by
Definition 6 [17]: If
Definition 7 [17]: Let
The definition of the distance measure of Pang et al. [17] is given as follows:
Definition 8 [17]: There are two PLTSs
This formula given by Pang et al. [17] requires ordering the PLTSs in the third step. However, the ordering process loses some information. There is an example as follows:
Example 1: there are two PLTS,
2.2.2 Subscript Equivalence Distance Measure
After analyzing the distance measure of Pang et al. [17], we propose the subscript equivalence distance measure. Firstly, the PLTSs should be standardized as follows:
Definition 9: Our normalization process has two steps (1) and (2), as follows:
(1) Probability normalization. If the sum of probabilities less than 1, complementing the probabilities by
(2) Reference missing term supplementation. When the linguistic term part of
According to the reference missing term supplementation, for a known PLTS, the standardized result is different when compared with different PLTS. For example,
The following is the definition of the subscript equivalence distance measure.
Definition 10: Let
where
The subscript equivalence distance measure satisfies the following properties:
(1) Boundedness:
(2) Self-reflexivity:
(3) Symmetry:
Proof.
(1) Boundedness.
(2) Self-reflexivity.
(3) Symmetry.
To test the validity of the subscript equivalence distance measure, we calculate Example 1 using our distance measure.
Several researchers have proposed improvements to the distance measure for PLTSs. We make a comparison between the subscript equivalence distance measure and the distance measures of other researchers. The reference LTS for the below comparison is

There are only two cases that will lead to the result of the subscript equivalence distance measure equal to 0. The first scenario is that
which means that there is only one PLTE in both
There are two methods for obtaining weights: the subjective weights method and the objective weights method. The subjective weights method determines weights based on the inherent meaning of criteria, offering an advantage in terms of subjective interpretation. However, it may lack objectivity. On the other hand, the objective weights method determines weights independent of the actual meaning of criteria, but it fails to capture the importance that decision-makers assign to different criteria. Therefore, we combine the subjective weights method and objective weights method to obtain the combined weights method. In this section, we demonstrate the BWM method and CRITIC method and provide the combined weights calculation method.
The Analytic Hierarchy Process (AHP) method [48] is a subjective weights method, which compares the relative importance of evaluation criteria two-by-two. Thus the AHP method requires
Assuming that there are n evaluation criteria
Step 1: Compare n evaluation criteria, and choose the best criterion
Step 2: Determine the comparison vector BO (Best-to-Others) for the optimal criterion to the other criterion, and the comparison vector OW (Others-to-Worst) for the other criterion to the worst criterion. For simplified representation, BO is denoted as
A scale of 1–9 is used to represent the comparative relationship between the optimal criterion and other criteria, with 1 indicating that two criteria are of equal importance and 9 indicating that the former is extremely important relative to the latter.
Step 3: Calculate the optimal weights.
A nonlinear programming model is used to minimize the maximum absolute deviation value between the weight ratio value and its corresponding comparative preference value, to obtain the weight value that matches the expert opinion best. The model is defined as follows:
Model 1:
where
Model 2:
By solving the above model, the optimal weights
The consistency ratio is calculated with the formula below:
where,

The CRITIC method was proposed by Diakoulaki et al. [50] and it is an objective weights method. The method uses the contrast intensity of evaluation criteria and the conflicts between them to reflect the importance of each criterion. The greater the contrast intensity and conflict, the greater the amount of information contained, and the higher the weight of the criteria. The CRITIC method works well to calculate the criterion weights when there are correlations between the criteria, hence we use it to calculate the objective weights. The specific steps are listed below.
Step 1: Suppose that there is an initial matrix
Step 2: To preserve the intensity of the contrast between the criteria without being affected, the normalization process is replaced by forward processing and inverse processing. If the value of the evaluation criterion should be as large as possible, then the forward processing is shown in Eq. (9). If the value of the evaluation criterion should be as small as possible, then the inverse processing is shown in Eq. (10).
Step 3: Calculate the criterion variability
where,
Step 4: Calculate the criteria conflict
where
Step 5: Calculate the amount of information for each criterion
Step 6: Calculate the weights for each criterion
3.3 Solving for Combined Weights
Due to the different principles in weight determination between the BWM method and the CRITIC method, where the former obtains subjective weights and the latter obtains objective weights, we employ the multiplicative weighted assignment method to determine the combined weights. Let
4 Probabilistic Linguistic Multi-Criteria Decision-Making Method
The VIKOR method is an effective multi-criteria compromise ranking solution utilized for evaluating alternatives. The core concept revolves around establishing a positive ideal solution and a negative ideal solution by comparing alternative evaluation values with the ideal criterion value. The positive ideal solution represents the best value among the evaluation criteria, whereas the negative ideal solution represents the worst value. Through the optimization of group benefits and minimization of individual losses, a compromise solution of the alternatives can be obtained.
In this paper, we propose a novel MCDM method by integrating probabilistic linguistics with the VIKOR method. We accomplish this by aggregating evaluation information from multiple experts to derive a probabilistic linguistic initial decision matrix. Additionally, we utilize the comparison method and distance measure method of PLTSs during the calculation process to ultimately yield the decision results. The overall flowchart is shown in Fig. 1. The content in the dashed box is where this paper differs from the traditional VIKOR method.
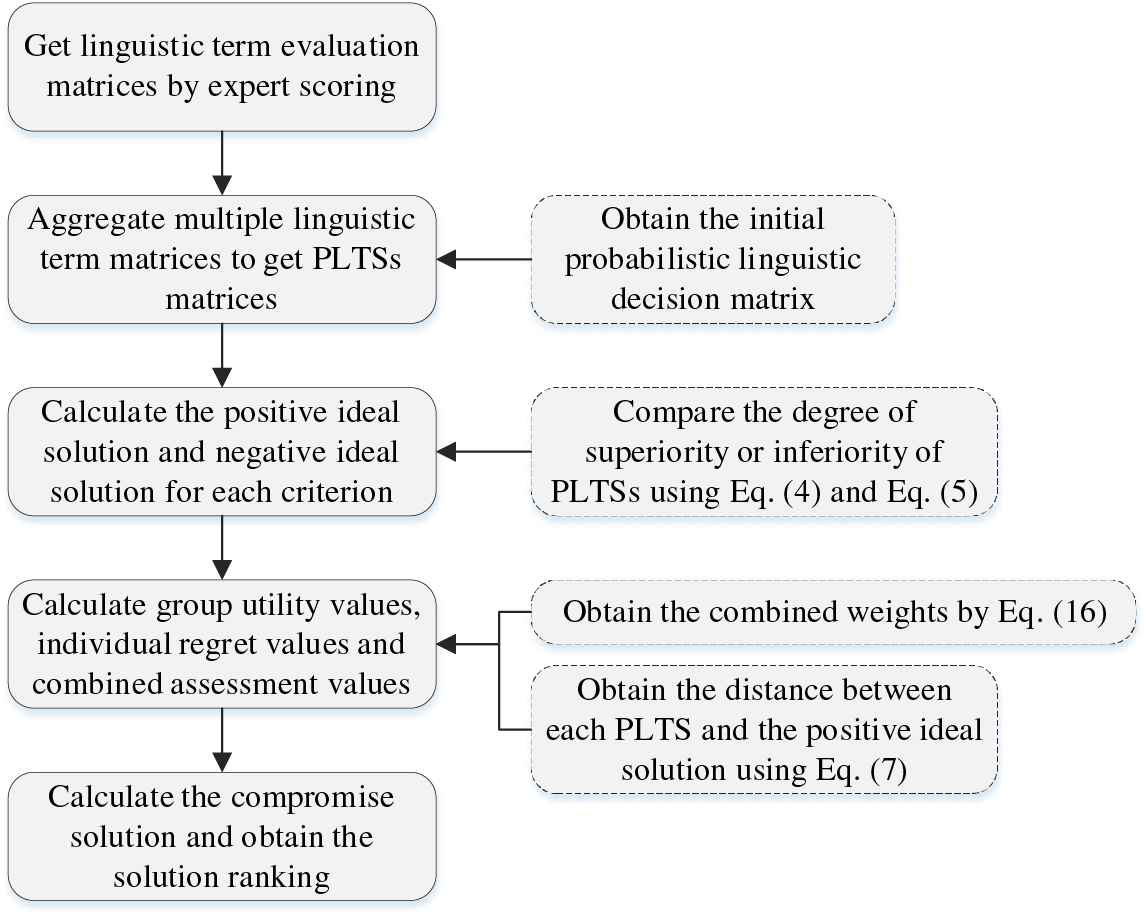
Figure 1: The overall flowchart of the probabilistic linguistic VIKOR method
For a certain multi-criteria decision problem with
Step 1:

Step 2: Aggregate
Step 3: Compare the degree of superiority and inferiority of the PLTSs corresponding to each criterion using Eq. (4) and Eq. (5), the positive and negative ideal solutions of the criterion are determined.
where
Step 4: Compute the combined weight of the criteria. Calculate the subjective weights of the criteria by following the steps in Section 3.1. Calculate the objective weights of the criteria by following the steps in Section 3.2. Then, combine the subjective weights and objective weights using Eq. (16) to obtain the combined weights of the criteria.
Step 5: Calculate the group utility value
where
Step 6: Rank the alternatives and obtain the decision solution. If we order the alternatives as
(1)
(2) The alternative
If the above two conditions cannot hold simultaneously, a compromise solution is obtained. There are two cases:
(1) If only (2) is not satisfied, then the solutions
(2) If (1) is not satisfied, the compromise solution is
In this section, we utilize a case study to confirm the validity of the proposed method.
5.1 Evaluation Criteria System of Information Security Assessment of ICSs
To enhance the information security of ICSs, China has implemented several countermeasures and introduced relevant regulations, including the group standards “Implementation Specification for Industrial Control System Security Protection Construction” and “Basic Requirements for Emergency Response Exercise of Industrial Control System Information Security Events”. These regulations guide enterprises on how to effectively safeguard the information security of ICSs. By analyzing the standard “Guideline for Security Control Application of Industrial Control Systems” (GB/T 32919-2016) [52], an evaluation criteria system is established. There are three key areas, which are subdivided into 12 second-level criteria, as illustrated in Fig. 2.
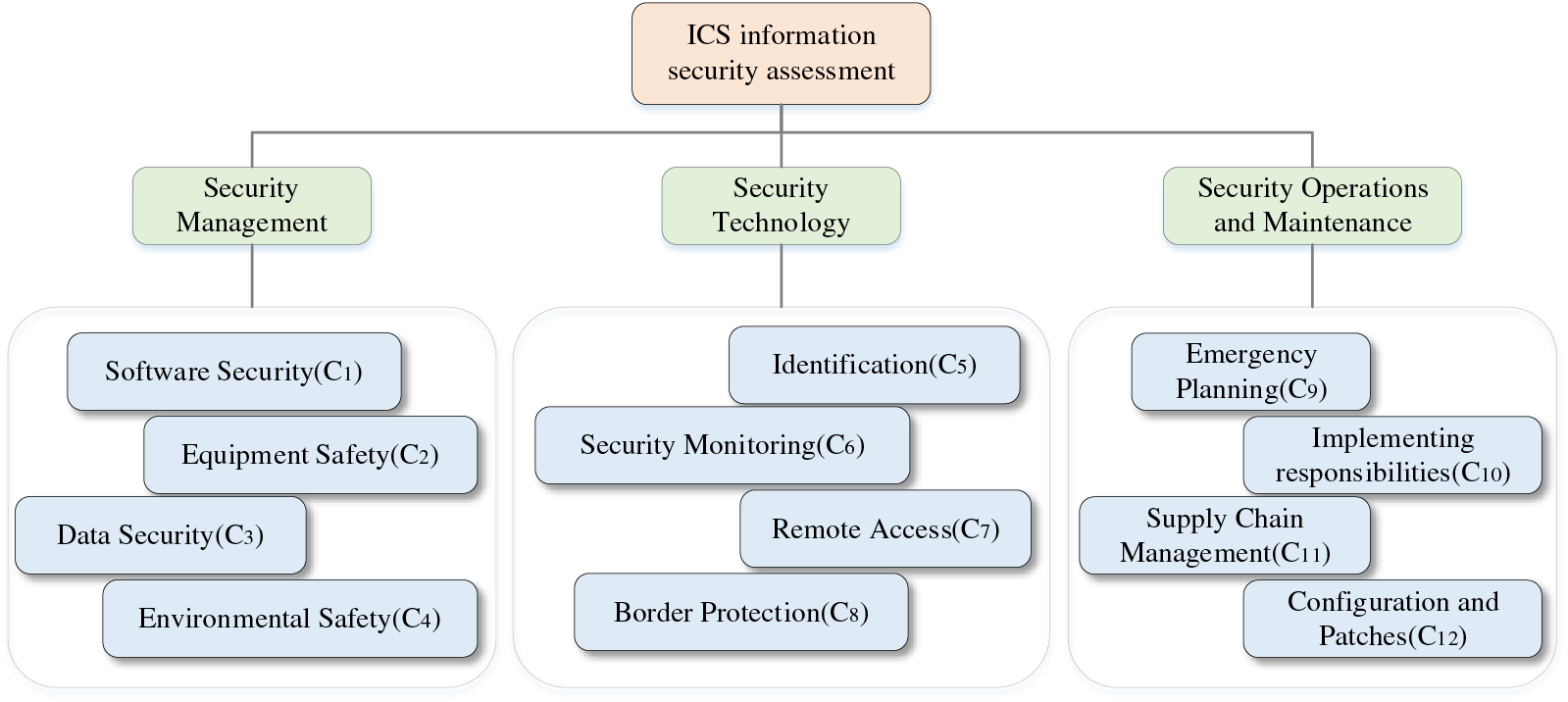
Figure 2: The information security assessment of the ICSs guidelines system
In the following part, 12 second-level criteria are described:
(1) Software Security: Design and implement secure and reliable software systems to protect them from cyber-attacks.
(2) Equipment Safety: Protect computers, phones, tablets, IoT devices, and other electronic devices from malicious attacks and unauthorized access.
(3) Data Security: Protect data from unauthorized access, use, disclosure, tampering, destruction, or loss.
(4) Environmental Safety: Protect information systems and networks from physical and environmental threats.
(5) Identification: Identify users to grant them access to information systems or network resources.
(6) Security Monitoring: Real-time monitoring and analysis of information systems and networks to detect and respond to potential security threats and attacks.
(7) Remote Access: Users can access information systems or network resources from a remote location via a network connection.
(8) Border Protection: Prevent unauthorized access and malicious traffic from entering the enterprise network by deploying security devices and measures at the network edge.
(9) Emergency Planning: A series of response measures developed by an organization or enterprise to protect information systems and network resources and reduce losses in the event of a security incident.
(10) Implementing Responsibilities: The organization or enterprise clarifies security management responsibilities and implements them for each employee and department.
(11) Supply Chain Management: Management and supervision of suppliers and partners of enterprise information systems and network resources.
(12) Configuration and Patches: Management and maintenance of software and configurations in information systems and networks.
To comply with higher authority regulations, a power generation company intends to assess the security of its SCADA systems across its four city branches. Six information security professionals scored the 12 second-level criteria. We denote the 4 branches as
Step 1: Firstly, The experts scored 12 criteria to assess the risk degree of the SCADA systems, and obtained 6 scoring matrices of linguistic terms with the following data:
Step 2: The initial probabilistic linguistic decision matrix
Step 3: Based on the BWM method, experts engaged in a discussion to identify the optimal criterion, which was determined to be software security
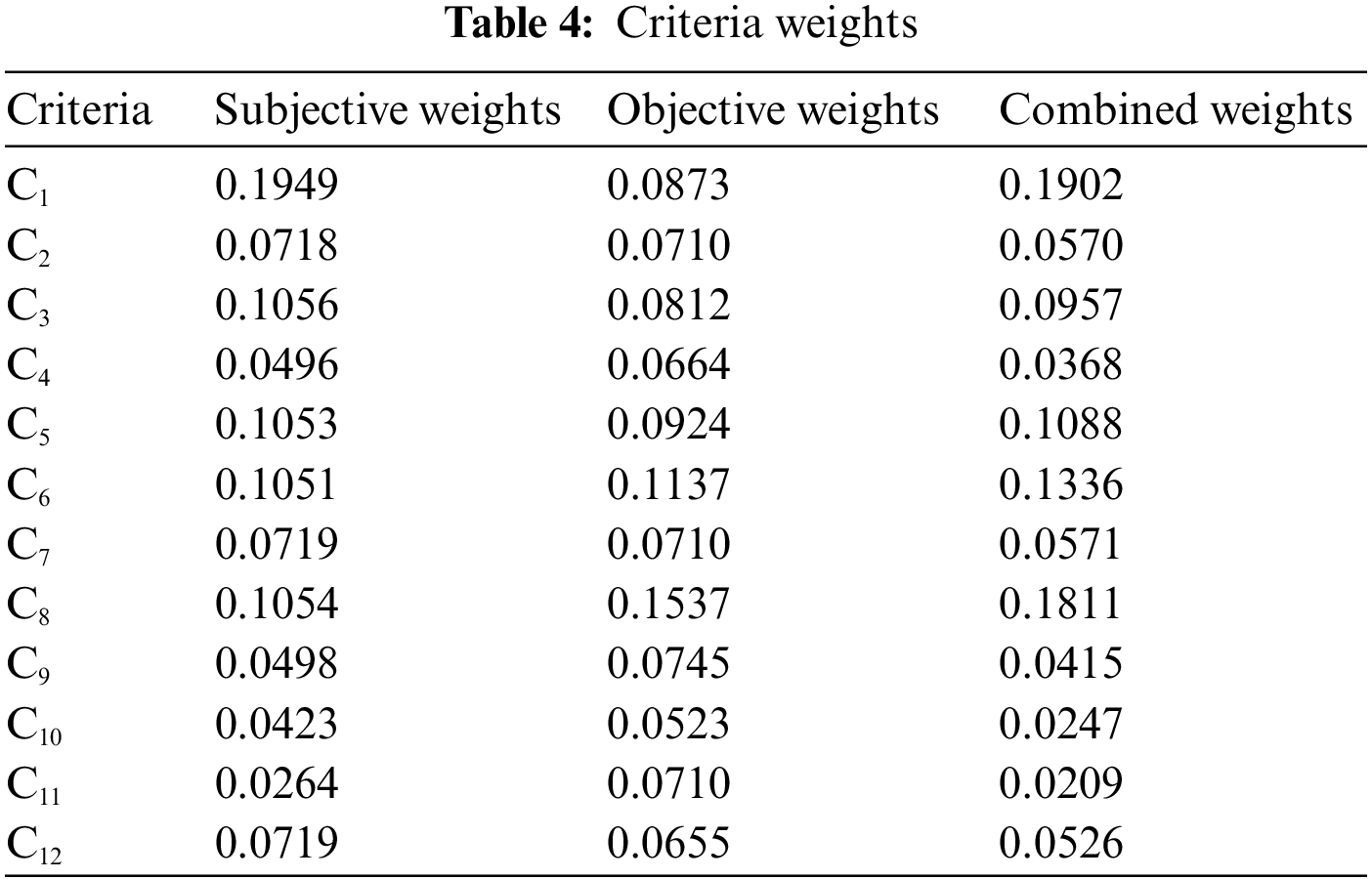
The combined weight data is used to generate a bar chart, as presented in Fig. 3, which demonstrates a clear visualization of the rankings. Software security is the most significant criterion. The software of ICSs is typically customized to meet specific industrial control and management requirements, making it highly specialized and challenging to substitute. Data generation is also dependent on software, so software security becomes a critical aspect. In most cases, ransomware viruses are responsible for the majority of network attacks on ICSs. These malicious programs infiltrate computers, gain unauthorized access to files, and subsequently encrypt them. Therefore, the information security of ICSs is highly dependent on good border protection. Based on the data presented in Fig. 3, it can be observed that the importance of border protection ranks second, closely following software security. The security of ICSs can be broadly classified into internal and external security. Internal security is closely tied to the regular work of members and emphasizes daily protection, while external security is prevention-oriented and aims to establish a protective network.
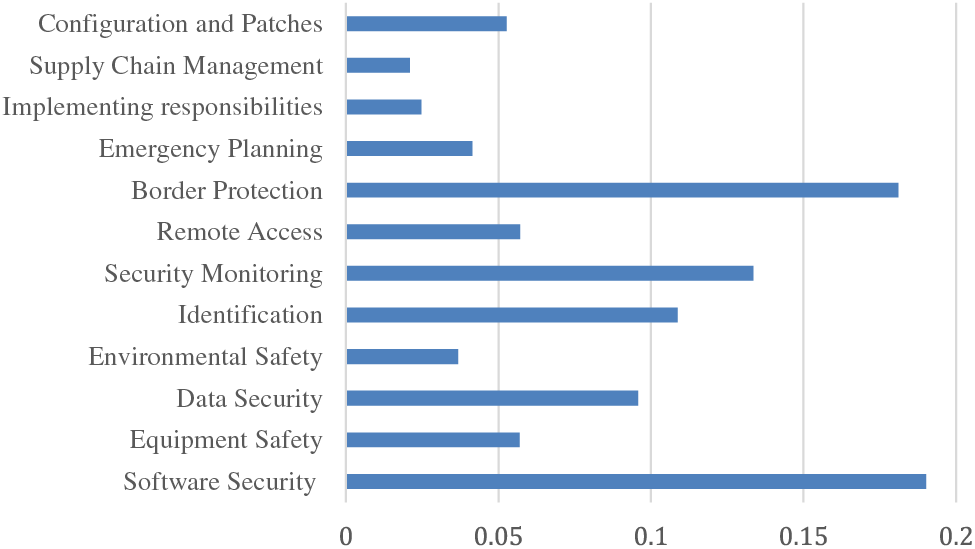
Figure 3: Combined weight bar chart
Step 4: Calculate the distance of each PLTS in
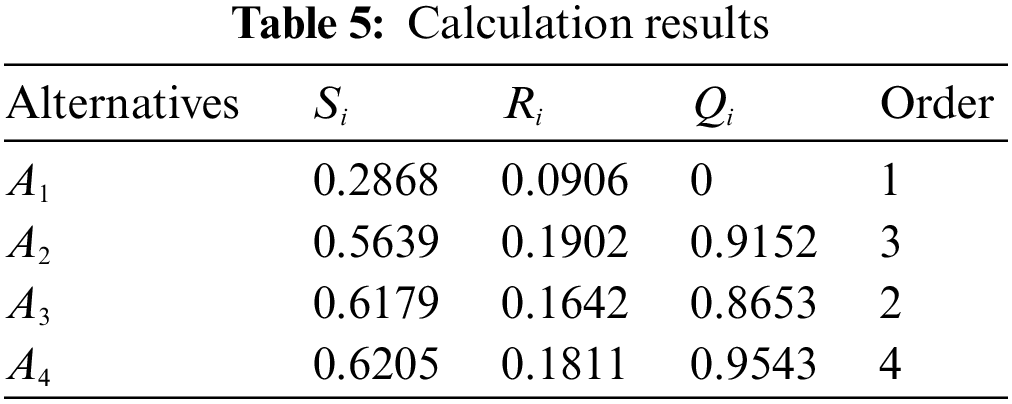
According to Step 6 in Section 4, we ordered
By assessing the system security situation of different branches, problems in lower-ranked branches can be identified and promptly adjusted to eliminate potential safety hazards. At the same time, ranking the branches can serve as a motivational tool, enhancing employee enthusiasm, boosting efficiency for both individuals and the organization, and fostering personal and corporate growth.
In Eq. (21), the value of
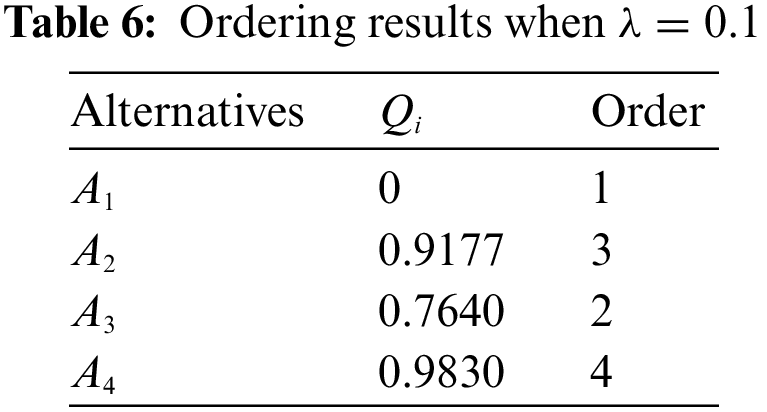
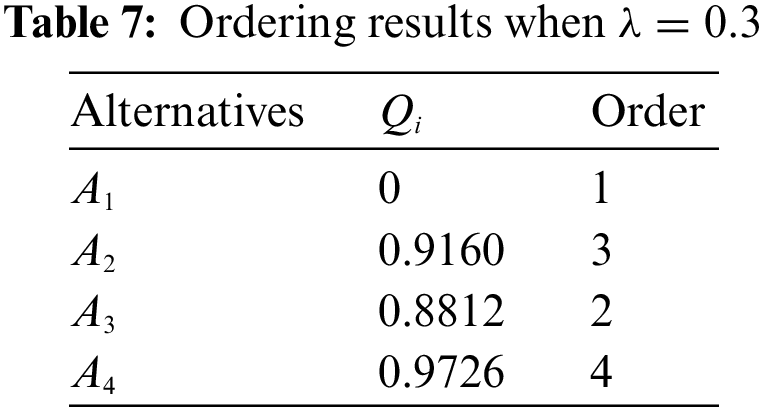
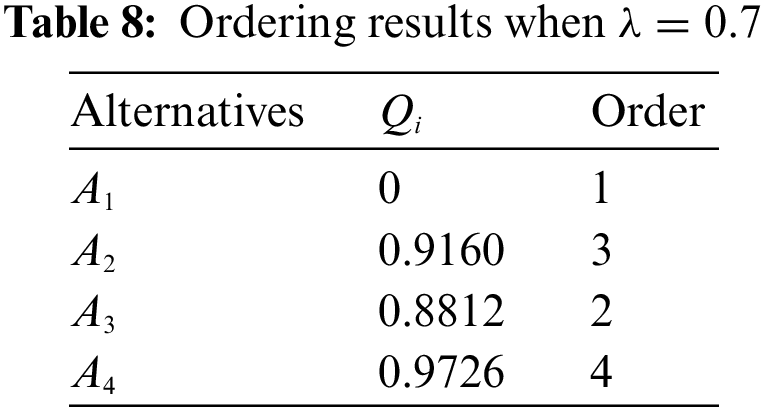
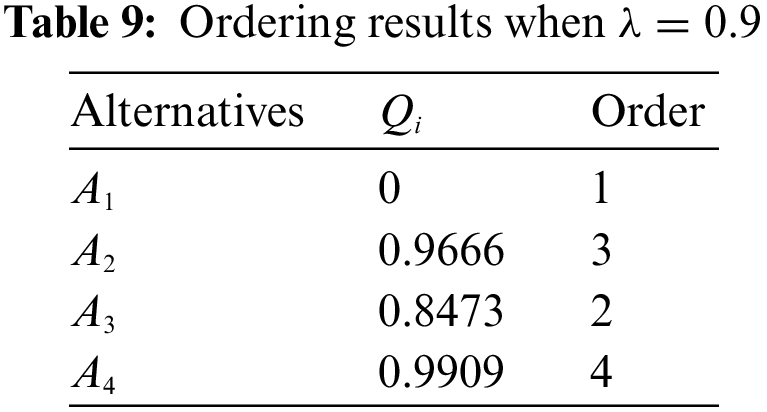
From the above results, it can be seen that the final ranking of the alternatives is always
5.3.2 Comparison of the Proposed Method and Other DM Methods
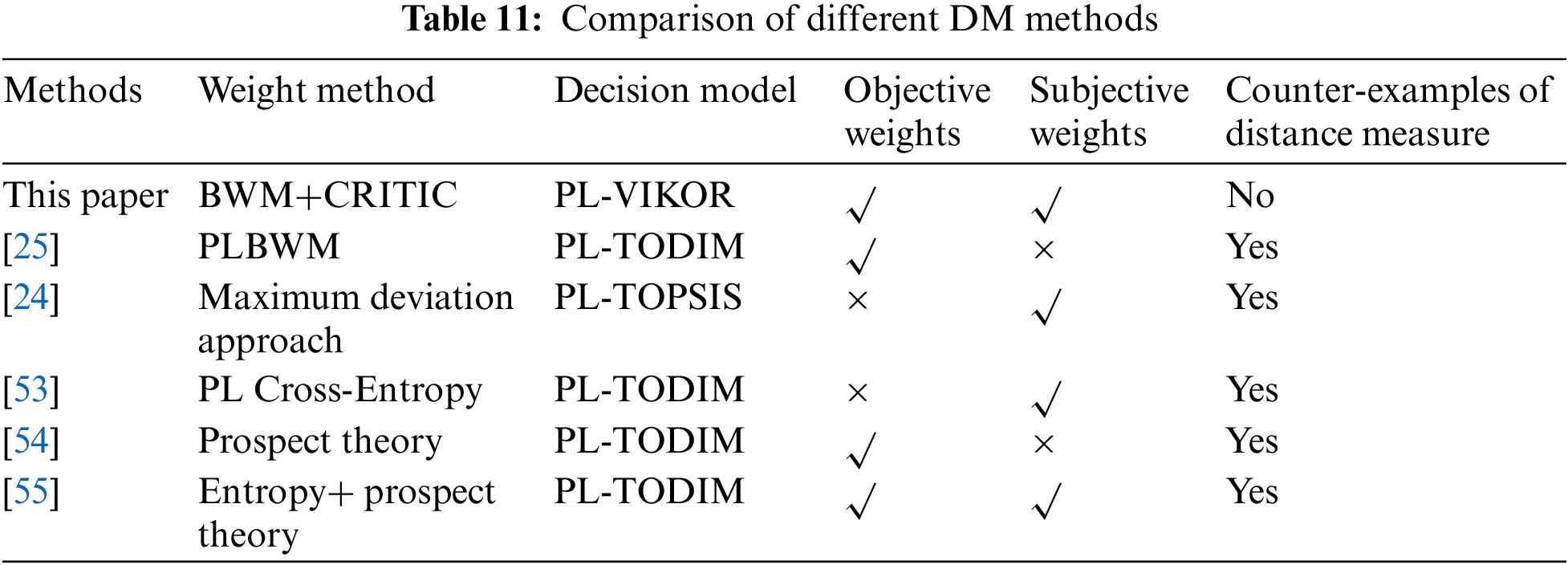
To verify the effectiveness of the proposed method, we compared it with existing DM methods, namely PL-TODIM [25], PL-TOPSIS [24], PL-TODIM [53], PL-TODIM [54], and PL-TODIM [55] method. The comparison and result of each method ranking are as follows. From the results in Table 10, it can be seen that the results of this paper are different from those obtained by other methods. In Table 11, the differences between the DM methods used in this paper and other DM methods are listed. The reasons for the differences in the two tables are as follows.
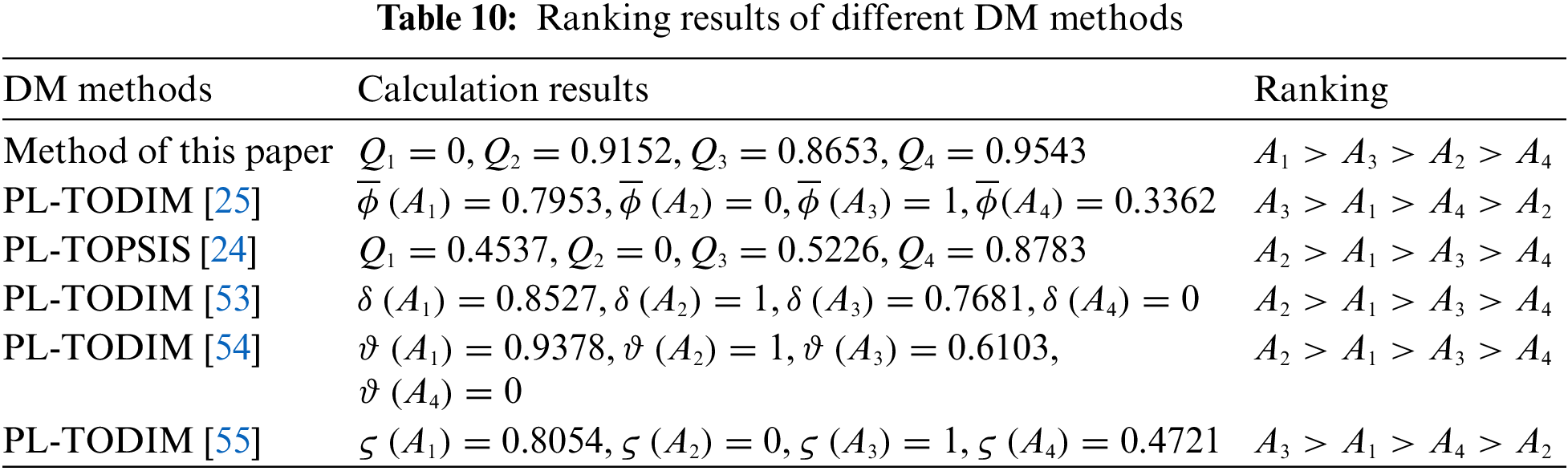
(1) All the DM methods outlined in Table 10 are based on the PLTSs, where the entire computational process relies on operations associated with these PLTSs. The standardization of the PLTSs used in other studies involves three steps, and the third step is ordering the PLTEs in descending order according to the multiplication of subscript of linguistic term and its probability. However, this process only focuses on the arrangement of PLTEs and overlooks the relative relationships with the PLTSs being compared, thereby resulting in a deficiency of crucial information. In contrast, the normalization method employed in this study takes a different approach. It begins by normalizing the probabilities and subsequently supplements the PLTS by incorporating the missing terms based on the subscripts of the PLTS being compared. This method completes the missing linguistic terms of the current PLTS and assigns a probability of 0, thus providing a more comprehensive comparison process. This step can align the subscripts of linguistic terms in two PLTSs. During the comparison, only the probabilistic linguistic terms with equivalence subscripts are taken into account, thereby eliminating the need to order the PLTSs. Thus the information loss caused by the previous methods is compensated through this process. The distance measure of the PL-TODIM [25], PL-TOPSIS [24], and PL-TODIM [53] are known to exist in some counter-examples, where the distance between those initially unequal PLTSs is calculated as 0. When it comes to such cases, it will lead to errors. The subscript equivalence distance measure represents a significant improvement over the existing methods.
(2) The PL-TOPSIS [24] method employs the maximum deviation method to determine criteria weights. This method only focuses on the variability of individual criteria but fails to effectively compare the differences between criteria. The PL-TODIM [25] method utilizes the probabilistic linguistic BWM method to compute weights, this method benefits from the limited number of comparisons in the BWM method. Nevertheless, the subjectivity of the method increases since all the comparison data is entirely provided by experts. The PL-TODIM [53] method employs the probabilistic linguistic entropy and probabilistic linguistic cross-entropy methods to determine weights, which can accurately capture the variability of criteria but fail to perform comparisons between criteria. Moreover, the method has a high dependency on data, making it susceptible to errors. In this paper, we propose the BWM+CRITIC method to determine the criterion weights, which combines the subjective opinions of experts with the objective data of the criteria. The BWM method can reflect the comparative relationship among criteria with a concise calculation process. By combining it with the CRITIC method, the subjectivity, objectivity, the relationship between the criteria themselves, and the relationship between criteria are considered as a whole, resulting in a more comprehensive perspective. Consequently, the weights generated through this approach exhibit a higher level of accuracy.
ICSs, functioning as the integral “brain” of industrial production, constitute a vital component of the industrial sector. Therefore, conducting an information security assessment of ICSs is essential to ensure that they work properly. This assessment is capable of assisting in identifying potential vulnerabilities and threats, enabling timely resolution, and ensuring the efficient and safe operation of industrial production. In this paper, we propose a novel subscript equivalence distance measure and verify the validity of the formula. We combine the BWM and CRITIC methods to obtain subjective weights and objective weights, then derive the combined weights of the criteria. Finally, we use the probabilistic linguistic VIKOR method to demonstrate the DM process for information security assessments of ICSs. Managers can guide the work of the company based on the assessment results. The proposed method also has some limitations. The application of the probabilistic linguistic VIKOR method depends on the operation rules of PLTSs, which shall lead to complex calculations when dealing with large volumes of data. Specifically, simultaneous consideration of subscripts of linguistic terms in PLTSs and their probabilities results in complicated calculations. Therefore, the proposed method is well-suited for decision problems with fewer alternative solutions and evaluation criteria.
In future work, further validation and empirical research are needed to assess the reliability and applicability of the proposed methods in practical applications. The proposed method can also be extended to other small forms of DM. For example, engineering quality assessment, supply chain risk assessment, etc. On the other hand, we can research the application of the proposed methods to those problems with larger datasets.
Acknowledgement: Not applicable.
Funding Statement: The authors received no specific funding for this study.
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Wenshu Xu, Mingwei Lin; data collection: Wenshu Xu; analysis and interpretation of results: Wenshu Xu; draft manuscript preparation: Wenshu Xu, Mingwei Lin. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: Not applicable.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. R. Zhang, “Improved control for industrial systems over model uncertainty: A receding horizon expanded state space control approach,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 50, no. 4, pp. 1343–1349, 2020. [Google Scholar]
2. A. Humayed, J. Lin, F. Li and B. Luo, “Cyber-physical systems security—A survey,” IEEE Internet of Things Journal, vol. 4, no. 6, pp. 1802–1831, 2017. [Google Scholar]
3. F. Ö. Sönmez and B. G. Kılıç, “A decision support system for optimal selection of enterprise information security preventative actions,” IEEE Transactions on Network and Service Management, vol. 18, no. 3, pp. 3260–3279, 2021. [Google Scholar]
4. W. Iqbal, H. Abbas, M. Daneshmand, B. Rau and Y. A. Bangash, “An in-depth analysis of IoT security requirements, challenges, and their countermeasures via software-defined security,” IEEE Internet of Things Journal, vol. 7, no. 10, pp. 10250–10276, 2020. [Google Scholar]
5. C. Ren, Y. Xu, B. Dai and R. Zhang, “An integrated transfer learning method for power system dynamic security assessment of unlearned faults with missing data,” IEEE Transactions on Power Systems, vol. 36, no. 5, pp. 4856–4859, 2021. [Google Scholar]
6. Y. Wang, V. Vittal, M. Abdi-Khorsand and C. Singh, “Probabilistic reliability evaluation including adequacy and dynamic security assessment,” IEEE Transactions on Power Systems, vol. 35, no. 1, pp. 551–559, 2020. [Google Scholar]
7. M. Lin, J. Wei, Z. Xu and R. Chen, “Multiattribute group decision-making based on linguistic pythagorean fuzzy interaction partitioned bonferroni mean aggregation operators,” Complexity, vol. 2018, pp. 1–25, 2018. [Google Scholar]
8. X. Luo, H. Wu, H. Yuan and M. Zhou, “Temporal pattern-aware QoS prediction via biased non-negative latent factorization of tensors,” IEEE Transactions on Cybernetics, vol. 50, no. 5, pp. 1798–1809, 2020. [Google Scholar] [PubMed]
9. X. Luo, Z. Liu, S. Li, M. Shang and Z. Wang, “A fast non-negative latent factor model based on generalized momentum method,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 51, no. 1, pp. 610–620, 2021. [Google Scholar]
10. C. Zhang, J. Ji, R. Li, D. Zhang and S. Dalia, “Determinants and spatial spillover of inter-provincial carbon leakage in China: The perspective of economic cycles,” Technological Forecasting & Social Change, vol. 194, pp. 1–14, 2023. [Google Scholar]
11. L. Hu, X. Yuan, X. Liu, S. Xiong and X. Luo, “Efficiently detecting protein complexes from protein interaction networks via alternating direction method of multipliers,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 16, no. 6, pp. 1922–1935, 2019. [Google Scholar] [PubMed]
12. S. A. Abdymanapov, M. Muratbekov, S. Altynbek and A. Barlybayev, “Fuzzy expert system of information security risk assessment on the example of analysis learning management systems,” IEEE Access, vol. 9, pp. 156556–156565, 2021. [Google Scholar]
13. R. Fu, X. Huang, Y. Xue, Y. Wu, Y. Tang et al., “Security assessment for cyber physical distribution power system under intrusion attacks,” IEEE Access, vol. 7, pp. 75615–75628, 2019. [Google Scholar]
14. H. Nazmul, D. Taposh, I. Tariqul and A. H. Md, “Cyber security risk assessment method for SCADA system,” Information Security Journal: A Global Perspective, vol. 31, no. 5, pp. 499–510, 2022. [Google Scholar]
15. J. Mi, W. Huang, M. Chen and W. Zhang, “A method of entropy weight quantitative risk assessment for the safety and security integration of a typical industrial control system,” IEEE Access, vol. 9, pp. 90919–90932, 2021. [Google Scholar]
16. Y. Qin, Y. Peng, K. Huang, C. Zhou and Y. C. Tian, “Association analysis-based cybersecurity risk assessment for industrial control systems,” IEEE Systems Journal, vol. 15, no. 1, pp. 1423–1432, 2021. [Google Scholar]
17. Q. Pang, H. Wang and Z. Xu, “Probabilistic linguistic term sets in multi-attribute group decision making,” Information Sciences, vol. 369, pp. 128–143, 2016. [Google Scholar]
18. H. Bustince, E. Barrenechea, M. Pagola, J. Fernandez, Z. Xu et al., “A historical account of types of fuzzy sets and their relationships,” IEEE Transactions on Fuzzy Systems, vol. 24, no. 1, pp. 179–194, 2016. [Google Scholar]
19. I. Couso and H. Bustince, “From fuzzy sets to interval-valued and Atanassov intuitionistic fuzzy sets: A unified view of different axiomatic measures,” IEEE Transactions on Fuzzy Systems, vol. 27, no. 2, pp. 362–371, 2019. [Google Scholar]
20. M. Lin, C. Huang, R. Chen, H. Fujita and X. Wang, “Directional correlation coefficient measures for Pythagorean fuzzy sets: Their applications to medical diagnosis and cluster analysis,” Complex & Intelligent Systems, vol. 7, no. 2, pp. 1025–1043, 2021. [Google Scholar]
21. J. Gao, Z. Xu, Z. Liang and Y. Mao, “Two integral models and applications of hesitant fuzzy information fusion,” IEEE Transactions on Fuzzy Systems, vol. 31, no. 1, pp. 25–39, 2023. [Google Scholar]
22. T. Yao, W. Wang, R. Miao, J. Dong and X. Yan, “Damage effectiveness assessment method for anti-ship missiles based on double hierarchy linguistic term sets and evidence theory,” Journal of Systems Engineering and Electronics, vol. 33, no. 2, pp. 393–405, 2022. [Google Scholar]
23. Y. Zhang, Z. Xu, H. Wang and H. Liao, “Consistency-based risk assessment with probabilistic linguistic preference relation,” Applied Soft Computing, vol. 49, pp. 817–833, 2016. [Google Scholar]
24. X. Wang, J. Wang and H. Zhang, “Distance-based multicriteria group decision making approach with probabilistic linguistic term sets,” Expert Systems, vol. 36, no. 2, pp. e12352, 2019. [Google Scholar]
25. M. Lin, C. Huang, Z. Xu and R. Chen, “Evaluating IoT platforms using integrated probabilistic linguistic MCDM method,” IEEE Internet of Things Journal, vol. 7, no. 11, pp. 11195–11208, 2020. [Google Scholar]
26. W. Su, S. Chen, C. Zhang and K. W. Li, “A subgroup dominance-based benefit of the doubt method for addressing rank reversals: A case study of the human development index in Europe,” European Journal of Operational Research, vol. 307, no. 3, pp. 1299–1317, 2023. [Google Scholar]
27. X. Zhou, M. Lin and W. Wang, “Statistical correlation coefficients for single-valued neutrosophic sets and their applications in medical diagnosis,” AIMS Mathematics, vol. 8, no. 7, pp. 16340–16359, 2023. [Google Scholar]
28. X. Luo, M. Zhou, S. Li, Y. Xia, Z. You et al., “Incorporation of efficient second-order solvers into latent factor models for accurate prediction of missing QoS data,” IEEE Transactions on Cybernetics, vol. 48, no. 4, pp. 1216–1228, 2018. [Google Scholar] [PubMed]
29. C. Zhang, D. Li and J. Liang, “Multi-granularity three-way decisions with adjustable hesitant fuzzy linguistic multigranulation decision-theoretic rough sets over two universes,” Information Sciences, vol. 507, pp. 665–683, 2020. [Google Scholar]
30. Y. Zheng, Z. Xu and W. Pedrycz, “A granular computing-driving hesitant fuzzy linguistic method for supporting large-scale group decision making,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 52, no. 10, pp. 6048–6060, 2022. [Google Scholar]
31. C. Zhang, J. Ding, J. Zhan, A. K. Sangaiah and D. Li, “Fuzzy intelligence learning based on bounded rationality in IoMT systems: A case study in Parkinson’s disease,” IEEE Transactions on Computational Social Systems, vol. 10, no. 4, pp. 1607–1621, 2023. [Google Scholar]
32. X. Wu, H. Liao and W. Pedrycz, “Probabilistic linguistic term set with interval uncertainty,” IEEE Transactions on Fuzzy Systems, vol. 29, no. 11, pp. 3532–3545, 2021. [Google Scholar]
33. J. L. Zhou and J. A. Chen, “A consensus model to manage minority opinions and noncooperative behaviors in large group decision making with probabilistic linguistic term sets,” IEEE Transactions on Fuzzy Systems, vol. 29, no. 6, pp. 1667–1681, 2021. [Google Scholar]
34. C. Huang, M. Lin and Z. Xu, “Pythagorean fuzzy MULTIMOORA method based on distance measure and score function: Its application in multicriteria decision making process,” Knowledge and Information Systems, vol. 62, no. 11, pp. 4373–4406, 2020. [Google Scholar]
35. L. Xin, Y. Yuan, M. Zhou, Z. Liu and M. Shang, “Non-negative latent factor model based on β-divergence for recommender systems,” IEEE Transactions on Systems, Man, and Cybernetics: Systems, vol. 51, no. 8, pp. 4612–4623, 2021. [Google Scholar]
36. C. Zhang, W. Su, S. Chen, S. Zeng and H. Liao, “A combined weighting based large scale group decision making framework for MOOC group recommendation,” Group Decision and Negotiation, vol. 32, no. 3, pp. 537–567, 2023. [Google Scholar] [PubMed]
37. X. Gou, Z. Xu and H. Liao, “Hesitant fuzzy linguistic entropy and cross-entropy measures and alternative queuing method for multiple criteria decision making,” Information Sciences, vol. 388–389, pp. 225–246, 2017. [Google Scholar]
38. A. A. J. Al-Hchaimi, N. B. Sulaiman, M. A. B. Mustafa, M. N. B. Mohtar, S. L. B. M. Hassan et al., “Evaluation approach for efficient countermeasure techniques against Denial-of-Service attack on MPSoC-Based IoT using multi-criteria decision-making,” IEEE Access, vol. 11, pp. 89–106, 2023. [Google Scholar]
39. T. T. Dang, N. A. T. Nguyen, V. T. T. Nguyen and L. T. H. Dang, “A two-stage multi-criteria supplier selection model for sustainable automotive supply chain under uncertainty,” Axioms, vol. 11, no. 5, pp. 228, 2022. [Google Scholar]
40. H. Mohapatra, B. K. Mohanta, M. R. Nikoo, M. Daneshmand and A. H. Gandomi, “MCDM-Based routing for IoT-enabled smart water distribution network,” IEEE Internet of Things Journal, vol. 10, no. 5, pp. 4271–4280, 2023. [Google Scholar]
41. R. Garg, “MCDM-based parametric selection of cloud deployment models for an academic organization,” IEEE Transactions on Cloud Computing, vol. 10, no. 2, pp. 863–871, 2022. [Google Scholar]
42. H. C. Liu, M. Yang, M. Zhou and G. Tian, “An integrated multi-criteria decision making approach to location planning of electric vehicle charging stations,” IEEE Transactions on Intelligent Transportation Systems, vol. 20, no. 1, pp. 362–373, 2019. [Google Scholar]
43. O. Gireesha, N. Somu, K. Krithivasan and V. S. Shankar Sriram, “IIVIFS-WASPAS: An integrated multi-criteria decision-making perspective for cloud service provider selection,” Future Generation Computer Systems, vol. 103, pp. 91–110, 2020. [Google Scholar]
44. M. S. A. Khan, F. Anjum, I. Ullah, T. Senapati and S. Moslem, “Priority degrees and distance measures of complex hesitant fuzzy sets with application to multi-criteria decision making,” IEEE Access, vol. 11, pp. 13647–13666, 2023. [Google Scholar]
45. G. Ali, H. N. Musbah, H. H. Aly and T. Little, “Hybrid renewable energy resources selection based on multi criteria decision methods for optimal performance,” IEEE Access, vol. 11, pp. 26773–26784, 2023. [Google Scholar]
46. C. Zhu, Y. Pu, K. Yang, Q. Yang and C. L. P. Chen, “Distributed optical fiber intrusion detection by image encoding and SwinT in multi-interference environment of long-distance pipeline,” IEEE Transactions on Instrumentation and Measurement, vol. 72, pp. 1–12, 2023. [Google Scholar]
47. Z. Wu, S. Shen, X. Lian, X. Su and E. Chen, “A dummy-based user privacy protection approach for text information retrieval,” Knowledge-Based Systems, vol. 195, pp. 1–14, 2020. [Google Scholar]
48. C. Yi, H. Wang, Q. Zhou, Q. Hu, P. Zhou et al., “An adaptive harmonic product spectrum for rotating machinery fault diagnosis,” IEEE Transactions on Instrumentation and Measurement, vol. 72, pp. 1–12, 2023. [Google Scholar]
49. J. Rezaei, “Best-worst multi-criteria decision making method,” Omega, vol. 53, pp. 49–57, 2015. [Google Scholar]
50. D. Diakoulaki, G. Mavrotas and L. Papayannakis, “Determining objective weights in multiple criteria problems: The critic method,” Computers & Operations Research, vol. 22, no. 7, pp. 763–770, 1995. [Google Scholar]
51. Y. Luo, X. Zhang, Y. Qin, Z. Yang and Y. Liang, “Tourism attraction selection with sentiment analysis of online reviews based on probabilistic linguistic term sets and the IDOCRIW-COCOSO model,” International Journal of Fuzzy Systems, vol. 23, pp. 295–308, 2021. [Google Scholar]
52. GB/T 32919-2016, Application guide for safety control of industrial control systems. Beijing: China Standards Press, 2016. [Google Scholar]
53. P. Liu and F. Teng, “Probabilistic linguistic TODIM method for selecting products through online product reviews,” Information Sciences, vol. 485, pp. 441–455, 2019. [Google Scholar]
54. Y. Yang, Z. Guo and Z. He, “Multi-attribute decision making method based on probabilistic linguistic term sets and its application in the evaluation of emergency logistics capacity,” Journal of Intelligent & Fuzzy Systems, vol. 42, no. 3, pp. 2157–2168, 2022. [Google Scholar]
55. Y. Su, M. Zhao, C. Wei and X. Chen, “PT-TODIM method for probabilistic linguistic MAGDM and application to industrial control system security supplier selection,” International Journal of Fuzzy Systems, vol. 24, pp. 202–215, 2022. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools