Solving Algebraic Problems with Geometry Diagrams Using Syntax-Semantics Diagram Understanding

1  Introduction

Solving Algebraic Problems with Geometry Diagrams (APGDs) is a challenging task in artificial intelligence due to the complexity and diversity of geometric relations that exist between geometric objects. APGDs are typically narrated by both textual descriptions and geometry diagrams, making it a multimodal reasoning task that requires a joint understanding of both modalities [1]. The additional information provided by the diagram, such as the relative location of lines and points, makes it essential for solvers to be able to parse the diagram. Furthermore, APGDs often require extra theorem knowledge in the problem-solving process. Although significant progress has been made in developing algorithms for solving math word problems [2,3], the research on solving APGDs is still limited. This presents a significant research challenge and opportunity to develop algorithms that can automatically solve APGDs, potentially providing valuable applications in education, such as intelligent tutoring systems.

In recent years, various methods have been developed to address APGD solving. These methods can be primarily categorized into two main types: Sequence-to-sequence (Seq2seq) methods and relation-centric methods. Seq2seq methods, such as Neural Geometric Solver (NGS) [4] and Geoformer [5], show the feasibility of using Seq2seq solution generation for solving APGDs. However, these methods currently suffer from limited readability and interpretability of the generated solution steps, which are often represented as sequential structures that do not resemble natural language. Additionally, the accuracy of these methods in solving APGDs remains a challenge, with existing methods often failing to achieve high accuracy rates. These limitations hinder the potential of using Seq2seq methods for effectively tutoring students in APGD solving.

Except for Seq2seq methods, the majority of current algorithms for solving APGDs, which belong to relation-centric methods, can be divided into two primary steps: problem understanding and symbolic solving. Similar to the algorithms used in solving arithmetic word problems [3], the symbolic solver in solving APGDs heavily relies on the relations of the output of problem understanding. The ability to obtain the necessary geometric knowledge for problem-solving from geometry diagrams is a critical issue. As a result, significant research focus on developing algorithms for understanding APGDs. As demonstrated by previous research [6], understanding APGDs involves two primary tasks: text understanding and diagram understanding. Both tasks are critical, with diagram understanding playing a key role in acquiring the knowledge from the diagram for solving the APGD. The challenge lies in effectively extracting and utilizing advanced knowledge embedded within the problem text and diagram. For text understanding, previous studies [1,7] showed that methods based on syntax semantic models can be successfully applied to extracting geometric knowledge in the problem text. In contrast, diagrams offer supplemental geometric information that complements the data not explicitly stated in the problem text. To achieve diagram understanding, the previous methods can be divided into two primary categories: rule-based method [8–10] and machine learning-based method [11]. Both rule-based and machine learning-based methods primarily focus on identifying basic elements and labels in geometry diagrams, which serves as a fundamental step toward generating simple geometric relations. However, a deep understanding of geometric relations is necessary for accurate problem-solving. Unfortunately, there are currently few studies that focus on achieving a deep understanding of geometric relations in geometry diagrams. Thus, there remains a need for a more comprehensive and effective approach to understanding diagrams in APGDs.

In this study, a three-phase scheme for solving APGDs is proposed, consisting of three phases: applying the state-transformer paradigm, employing the generalized APGD-solving approach, and developing a specific APGD-solving algorithm. This scheme underscores a progressive algorithm design process, transitioning from abstract concepts to concrete implementations, enabling a systematic and modular blueprint for constructing APGD-solving approaches. With the structured guidance of the three-phase scheme, a specialized APGD-solving algorithm is designed, encompassing the following key components: 1) the text understanding part employs the Syntax-Semantics (S2) model [1,7] for extracting geometric relations from problem text; 2) the diagram understanding part takes parsed diagrams as inputs and uses a vectorized S2 model to extract basic geometric relations; 3) derived geometric relations are generated based on the diagramet theory proposed by Xia et al. [6]. After integrating all extracted relations, the comprehensive set of relations is fed into existing solvers. Fig. 1 illustrates the process of solving a given APGD by the proposed algorithm, which is designed to ensure a more in-depth understanding of the problem and holds the potential to provide more accurate and comprehensive solutions to APGDs. The experiments are conducted on datasets of APGDs from both primary and secondary school levels, including geometry calculation problems and shaded area problems, demonstrating that the proposed APGD-solving method significantly improves problem-solving accuracy.

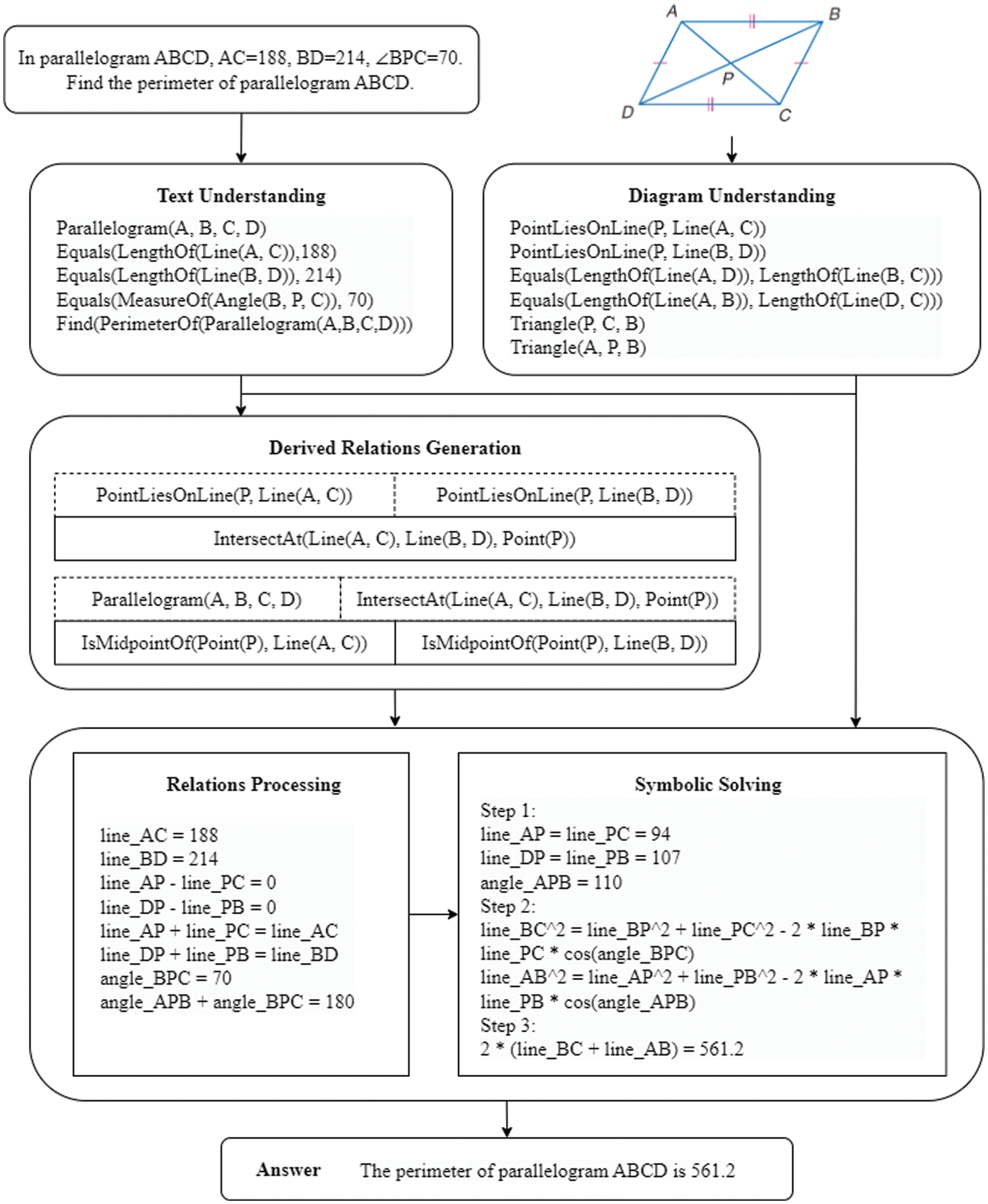
Figure 1: The process that the proposed algorithm solves the given APGD

In summary, this study contributes to solving APGDs by:

1.    Proposing a novel three-phase scheme, specifically designed to systematize and modularize APGD-solving approaches. This scheme bridges the gap between abstract problem-solving concepts and their practical implementation, allowing for more efficient and effective exploration of the APGD-solving process.

2.    Development of a unique algorithm, the first of its kind to lay special emphasis on diagram understanding in the context of APGDs. The algorithm employs the vectorized S2 model for extracting basic geometric relations and leverages diagramet theory-based method to generate derived geometric relations. This combination fosters a more comprehensive understanding of the geometric diagrams, thereby enhancing the algorithm’s overall problem-solving capability.

3.    Demonstrating the effectiveness of the proposed method through experiments on real-world datasets. The method led to significant enhancements in the accuracy of problem-solving, ranging from around 4% to 10% across different datasets and problem types. It exhibited a remarkable performance, particularly in complex problem goals like shaded area calculation, underscoring its potential for robust and effective problem-solving in the domain of APGDs.

The remainder of this paper is organized as follows: Section 2 provides an overview of related work; Section 3 illustrates the proposed three-phase scheme, with a focus on the paradigm phase and approach phase; Section 4 describes the proposed algorithm for solving APGDs; Section 5 presents the experimental results; and Section 6 concludes the paper and discusses future work.

2  Related Work

In this section, two main aspects of the literature related to the study are discussed. The first aspect provides an overview of existing methods for solving APGDs, including geometry calculation problems and shaded area problems. Research on both Seq2seq-based methods and relation-centric methods will be covered, highlighting their similarities and differences in addressing APGDs. The second aspect focuses on diagram understanding, which is particularly relevant to this study, as it aims to improve the overall performance of APGD-solving algorithms by comprehensively understanding the geometry diagram. In this part, various techniques and methods for parsing and understanding geometry diagrams are reviewed, which form the basis for generating geometric relations required in relation-centric methods. By examining the state-of-the-art methods in these areas, the foundation for the proposed method is laid, and its novelty in comparison to the existing research is demonstrated.

2.1 Methods of Solving APGDs

In recent years, two primary types of methods have emerged for solving APGDs: Seq2seq methods and relation-centric methods. Seq2seq methods have shown promise in solving APGDs. Chen et al. [4] introduced the GeoQA dataset and proposed NGS, which utilizes a co-attention mechanism to fuse text and diagram representations, predicting explainable programs based on the cross-modal representation. Chen et al. [5] advanced this research by constructing the UniGeo benchmark. They also proposed a unified geometric transformer framework called Geoformer, which is capable of handling geometry calculation and proof reasoning simultaneously. Despite these advancements, the main limitations of these Seq2seq methods include the limited interpretability and generalization capabilities and insufficient accuracy rates in their solutions.

Unlike Seq2seq methods, relation-centric methods aim to identify and utilize the underlying relationships and structures present in APGDs. The following studies showcase some notable advancements in relation-centric methods for APGD-solving tasks. G-ALIGNER by Seo et al. [8] and its subsequent improvement, GEOS [9], are pioneering attempts that align visual elements with their textual descriptions in APGDs. However, their approach essentially reduces the task to an optimization problem, aiming to find which choice satisfies all constraints. This approach lacks the reasoning process involved in actual problem-solving. Lu et al.’s Inter-GPS [10] utilized formal language and symbolic reasoning to address the complexities of APGD-solving tasks. However, their method focuses too heavily on the semantic aspects of the problems, leading to less accurate relation extraction from the given text. Yu et al. [12] proposed a two-phase algorithm for understanding and solving text-diagram function problems with impressive accuracy. Despite its strengths, the method falls short in terms of the interpretability of solutions, which is a crucial aspect of APGD-solving tasks. Alvin et al.’s approach called GeoShader [13] and Feng et al.’s approach [14] are both tailored to tackle shaded area problems, formalizing and solving such tasks efficiently. Despite their effectiveness for this specific problem type, these methods exhibit limitations in their applicability, as they are primarily designed to solve shaded area problems. While these studies each provide significant advancements in the field, a common limitation across all methods is their reliance on inputting simple geometric relations into the solver. This reliance hinders their ability to deeply understand geometry diagrams and extract more complex geometric relations, which in turn, affects the overall accuracy of problem-solving.

The proposed method is developed after an in-depth examination of existing methods and addressing identified strengths and weaknesses. Emphasizing the importance of diagram understanding, it extracts and interprets geometric relations from diagrams through dedicated procedures. By integrating relations from both text and diagrams, the method facilitates a profound understanding of APGDs. Symbolic reasoning is employed in the final problem-solving phase, utilizing the consolidated representation from previous phases for robust solution generation. The method thereby not only enhances APGD-solving efficiency but also ensures the interpretability of solutions, applicable across various problem types.

2.2 Methods of Understanding Geometry Diagrams

Understanding geometry diagrams is a crucial and necessary step in relation-centric methods for solving APGDs. The ability to accurately comprehend and interpret diagrams is essential for the subsequent identification of geometric elements and relations, which ultimately aids in problem-solving tasks. Seo’s foundational work [8,9] primarily relies on computer vision techniques, identifying simple relationships within diagrams but lacking comprehensive interpretability. Some studies [1,15,16] utilized numerical verification-based methods to extract relations from diagrams. While effective for specific scenarios, these methods lack a universal strategy for relation extraction, which can limit their applicability to more diverse problem sets. Xia et al. [6] introduced the diagramet theory for K−12 education, a promising concept still in its nascent stage and requiring further development. Zhang et al. [11] offered PGDPNet, an end-to-end deep learning model, but it lacks interpretability, limiting the transparency in relation identification. These studies collectively demonstrate the increasing importance and feasibility of automating the process of understanding geometry diagrams, which holds great potential for applications in education and intelligent tutoring systems. However, existing methods struggle to deeply comprehend advanced geometric relations within diagrams and rely on traditional methods that do not effectively handle the diversity of geometric styles and the complex relationships between primitives. These shortcomings restrict the accuracy and overall effectiveness of automatic APGD-solving methods.

As a precursor to the current research, Huang et al. [17] introduced a uniform vectorized S2 model for automatic APGD understanding. This foundational method provided a simultaneous approach to both text and diagram understanding, which distinguished it from traditional methods. Building upon this foundational work, the present research introduces significant advancements, notably in efficiency, accuracy, and scalability. It employs an innovative three-phase scheme for APGD-solving that fosters a more systematic problem-solving approach, better equipped to handle complex problems, and enhances the interpretability of the solution process. These improvements represent a clear progression from the prototype-like algorithm of the previous work. Furthermore, this study strives to advance relation-centric methods in APGD-solving tasks, addressing the limitations noted in previous studies. A more robust problem-understanding method based on the vectorized S2 model is proposed, which transforms problem text and diagrams into geometric relations automatically. Emphasizing interpretability, the proposed method utilizes symbolic reasoning and incorporates theorem knowledge as conditional rules, facilitating step-by-step reasoning, and enhancing the performance of APGD-solving algorithms. This advancement marks a significant improvement over previous research, making a considerable contribution to the field of automatic APGD-solving.

3  State-Transformer Paradigm and Generalized APGD-Solving Approach

In this study, a three-phase scheme (paradigm, approach, and algorithm) is adopted for solving APGDs. This scheme establishes a bridge between abstract concepts and specific implementations, offering a hierarchical and systematic framework for the research. Firstly, the state-transformer paradigm is established, serving as the foundation for the problem-solving approach design. Next, a generalized APGD-solving approach under the state-transformer paradigm is illustrated, outlining the solving process that encompasses multiple methods. Lastly, details of the algorithmic implementation are delved into, with the development and optimization of techniques to efficiently navigate through the states and transformers, ultimately generating a reliable and accurate solution to the given APGD. Through the adoption of this three-phase scheme, a comprehensive and coherent exploration of the research topic is facilitated. Each phase builds upon the previous one, ultimately resulting in a well-rounded and effective problem-solving method. This section presents the details of the state-transformer paradigm and APGD-solving approach.

3.1 State-Transformer Paradigm

The first phase, the state-transformer paradigm, is inspired by the state-action paradigm proposed by Yu et al. [3]. The state-transformer paradigm, as shown in Fig. 2, is a general framework for solving APGDs. It consists of various states representing different phases of the APGD-solving process and transformers representing different operations that enable transitions between these states. The core idea behind the state-transformer paradigm is to systematically explore the state space by applying different transformers, enabling the algorithm to effectively navigate from an initial problem state to a desired solution state.

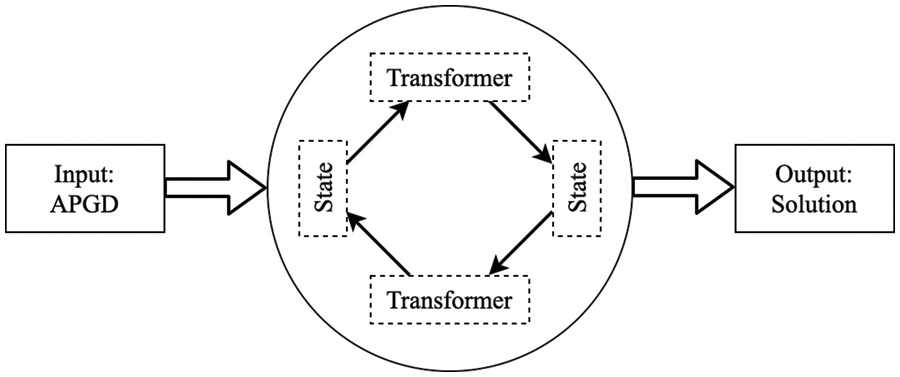
Figure 2: The state-transformer paradigm for solving APGDs

Definition 1 (State) A state signifies the diverse phases or conditions that the APGD problem-solving process traverses. Each state is characterized by its distinctive input and output formats, capturing a particular facet of the problem-solving process.

Definition 2 (Transformer) A transformer corresponds to the operations or procedures affecting transitions between different states. It encapsulates the distinct algorithms that convert the output from one state into the input of another, thus allowing for the modularity and reusability of the components of the APGD-solving approach.

The shift from the original state-action paradigm to the state-transformer paradigm has been made in this study to emphasize the crucial role of transformers in enabling transitions between different states during the APGD-solving process. For a comprehensive understanding of the original state-action paradigm and its definitions, refer to the study [3].

3.2 Generalized APGD-Solving Approach

In the second phase, the state-transformer paradigm is elaborated on by describing a generalized approach for solving APGDs. This approach encapsulates the common characteristics and processing steps found in various methods. Fig. 3 below illustrates the transitions between different states using the transformers in the proposed approach. An elliptical node represents a state, and an arrow represents a transformer.

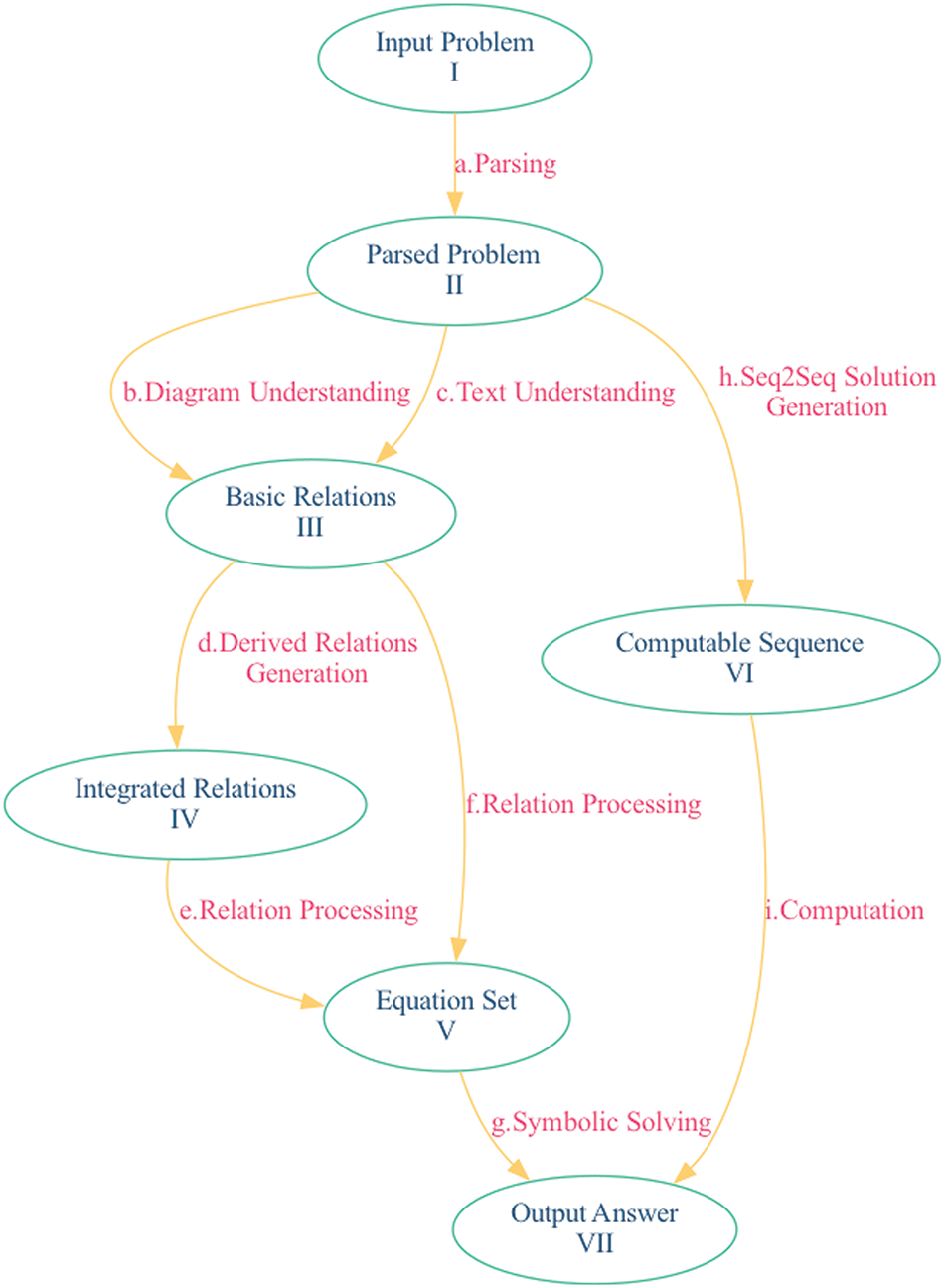
Figure 3: APGD-solving approach under state-transformer paradigm

The key components of the proposed approach include:

States:

•   Input Problem: The original APGD, including the text and diagrams.

•   Parsed Problem: The problem after parsing, which includes structured data of the APGD. These structured data encapsulate the essential information extracted from both the problem text and diagrams, organized in a systematic and structured manner conducive to further processing and problem-solving.

•   Basic Relations: A group of geometric relations that present fundamental connections between elements like points, lines, and shapes, including adjacency, collinearity, parallelism, etc.

•   Integrated Relations: A group of geometric relations that integrate basic and derived relations, offering a more comprehensive understanding of geometric problems.

•   Equation Set: A collection of mathematical equations generated from geometric relations.

•   Computable Sequence: A sequence that can be directly computed to obtain the final answer.

•   Output Answer: The final answer to the APGD.

Transformers:

•   Parsing: Parse the text and diagrams into structured data called parsed problem.

•   Diagram Understanding: Analyze a geometric diagram to identify and interpret geometric primitives and symbols, ultimately generating basic geometric relations that capture the visual information in the diagram.

•   Text Understanding: The process of extracting and interpreting geometric keywords and entities from the textual description of the APGD. The outcome is basic geometric relations extracted from the problem text.

•   Derived Relations Generation: The process of combining basic relations extracted from text and diagram understanding to generate derived relations that are more complex than basic relations.

•   Relation Processing: Convert geometric relations into equations.

•   Symbolic Solving: Solve equations and get the solution to the APGD.

•   Seq2seq Solution Generation: Use the Seq2seq method to directly generate the computable sequence.

•   Computation: Computes the final answer from the computable sequence.

Table 1 presents concrete examples illustrating how this generalized approach can be applied to various methods: Seq2seq methods directly embed the text and diagrams through transformer a, then decode the embeddings using transformer h to generate the computable sequence, and finally utilize transformer i to obtain the final answer. Traditional relation-centric methods parse geometry diagrams with transformer a, acquire basic relations through transformers b and c, convert basic relations into equations using transformer f, and input equations into a symbolic solver to obtain the final answer through transformer g.

In this study, a state called Integrated Relations is introduced. By considering both basic and derived relations, a comprehensive representation of the diagram is obtained. In contrast to traditional relation-centric methods, the proposed method employs transformer d to generate derived relations and fuses them with basic relations to obtain integrated relations. Then, these integrated relations are converted into equations using transformer e, enabling more accurate and efficient solutions when utilized.

Through this section, the state-transformer paradigm and its application in the approach for APGD solving are introduced. In the next section, a detailed description of the algorithm design that stems from the APGD-solving approach will be provided.

4  The Proposed Algorithm for APGD Solving

This section introduces the proposed algorithm for solving APGDs, which demonstrates a concrete implementation of the generalized APGD-solving approach.

4.1 Algorithm Outline

In this section, a three-step algorithm based on the APGD-solving approach to address APGDs is presented. The first step involves acquiring a set of basic geometric relations through text understanding and diagram understanding. The second step generates derived geometric relations based on basic geometric relations, while the third step transforms all geometric relations into equations that are then input into a symbolic solver to determine the unknown value, which serves as the solution to the APGD. These three steps form the proposed algorithm, as illustrated in Algorithm 1. To implement the tasks of the algorithm, three procedures are employed: Procedure 1 for text understanding, Procedure 2 for diagram understanding, and Procedure 3 for derived relations generation.

4.2 Geometric Relations Extraction

This subsection outlines the methods for extracting geometric relations in detail. It encompasses three components: (1) text understanding, (2) diagram understanding, and (3) derived relations generation. Before delving into text understanding and diagram understanding, it is crucial to preprocess the raw text and diagram separately to obtain structured representations suitable for further analysis. For the original text, parsing and annotation methods mentioned in [1] are employed to transform it into a sequence of tokens with associated Part-Of-Speech (POS) labels. This structured text representation serves as the input for text understanding. For the diagram, a combination of techniques, including the Hough transform [18] and object detector such as RetinaNet [19], is used to extract geometric primitives (points, lines, angles, arcs, circles), labels (textual description of geometric primitives) and symbols (vertical and parallel symbols, etc.). After obtaining the structured diagram representation, it becomes the input for diagram understanding, which helps build a comprehensive understanding of the problem and extract essential geometric relations for solution generation.

4.2.1 Text Understanding

In this part, an S2 model-based method [1,7] is introduced to implement text understanding for APGDs. The syntax elements of the S2 models consist of POS patterns, while the semantic elements are formed by keyword structures. The S2 models are employed in Procedure 1 for extracting geometric relations from the text. Procedure 1 operates effectively once a suitable pool of S2 models has been prepared.

Definition 1 (S2 Model) An S2 model, or syntax-semantics model, can be represented by a triplet m=(K, P, R), where K stands for semantic keyword structures, P denotes POS labels, and R denotes the output geometric relations. The collection of all prepared S2 models is symbolized by M={mi=(Ki, Pi,Ri)|i=1, 2, …, n}, and is referred to as the pool of S2 models for APGDs.

In Fig. 4, an example of an S2 model and its components are provided. The S2 model identifies the keyword structure K and the corresponding POS labels P within the parsed text T. It then replaces the elements in the matched sections of T with the geometric relation template R, generating the output.

Figure 4: Example of an S2 model and its components

As shown in Procedure 1, the text understanding process starts with initializing an empty group of basic geometric relations ΣT. Then, the pool of prepared S2 models M={mi|i=1,2,…,n} is loaded. For each model in the pool, the algorithm attempts to match the model with the portions of the parsed problem text. For every matched portion, the geometric entities in the text are used to instantiate the elements in the corresponding S2 model. Finally, an instance of the relation of the matched model is added to the set ΣT. This process iterates through all the models in the pool, ensuring that all geometric relations are extracted from the given input text. The output of this procedure is a set of geometric relations that are used for further analysis.

4.2.2 Diagram Understanding

This part introduces a method for understanding diagrams using a vectorized model called the Syntax-Semantics Diagram S2D model. The S2D model is particularly useful for analyzing the geometric diagram because it converts the diagram into a form that is suitable for efficient matching. Consequently, vectorization reduces the dimensionality of the data and speeds up the matching process, resulting in a more accurate and robust understanding of the diagram.

The S2D model extends the concepts of semantic keyword structures and syntactic POS labels from the S2 model to geometric diagrams. In the S2D model, the structure of geometric primitives defines the type of geometric primitives that are placed in each position of the vector, thus providing the underlying semantic structure of the diagram. The geometric primitives reveal information about the type of geometric primitive in each location, thus providing the syntactic structure of the diagram. In addition, some geometric relations require numerical validation of the geometric primitives within them (e.g., perpendicularity, bisection). Therefore, the matching functions are added to determine whether the numerical relationships between geometric primitives match the model.

Definition 2 (S2D Model) An S2D model is represented by a quadruplet m¯=(V,GP,F,R). V denotes the structure of geometric primitives, GP denotes the geometric primitives, F represents the matching functions, R represents the output geometric relations. The collection of all prepared S2D models is symbolized by M¯={m¯i=(Vi, GPi,Fi,Ri)|i=1, 2, …, n}, and is referred to as the pool of S2D models for APGDs.

In Fig. 5, a visual representation of an S2D model and its components, based on an example diagram D, is provided. The geometric primitives GP and its structure V are combined to form a single vector, which will be utilized for matching with the portions of the diagrams. The matching function set F contains primitives that require numerical verification and corresponding functions. The geometric relations set R which contains the relation templates are provided as the output.

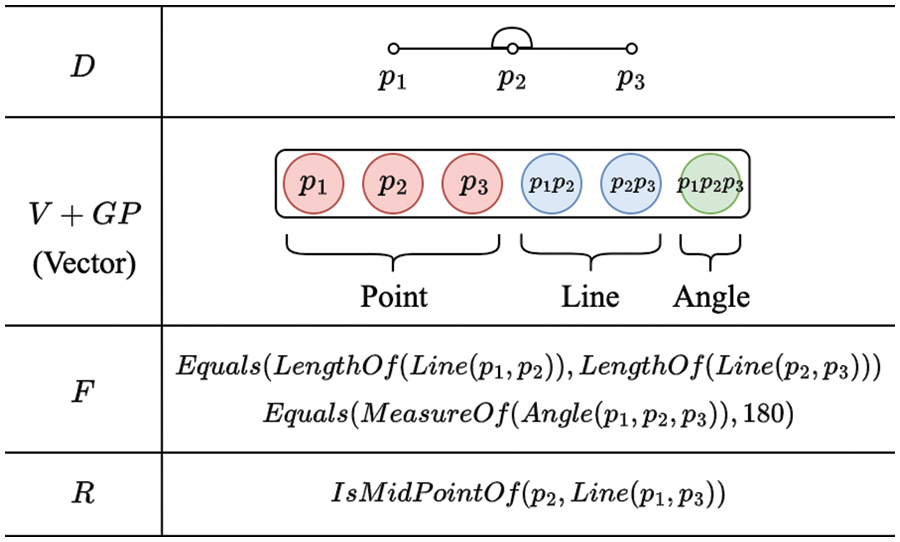
Figure 5: Example of an S2D model and its components

As shown in Procedure 2, the process begins by initializing an empty set ΣD. Next, the pool of prepared S2D models M¯ is loaded. The models are clustered to create a list of tensors ΓM¯. The geometry diagram is encoded into the vector form ED. Based on ΓM¯ and ED, a list ΓD which consists of candidate tensors to be matched is generated, and an empty list W is initialized. For each tensor in ΓD, the method attempts to match the candidates with the corresponding models in ΓM¯. When a candidate matches a model, the pair of candidate and model is added to the list W. After all candidates have been processed, the algorithm iterates through each matched candidate in W, decodes the candidate, and adds it to the set ΣD. This diagram understanding method efficiently extracts geometric relations from the given diagram input. The overview of the diagram understanding method is shown in Fig. 6.

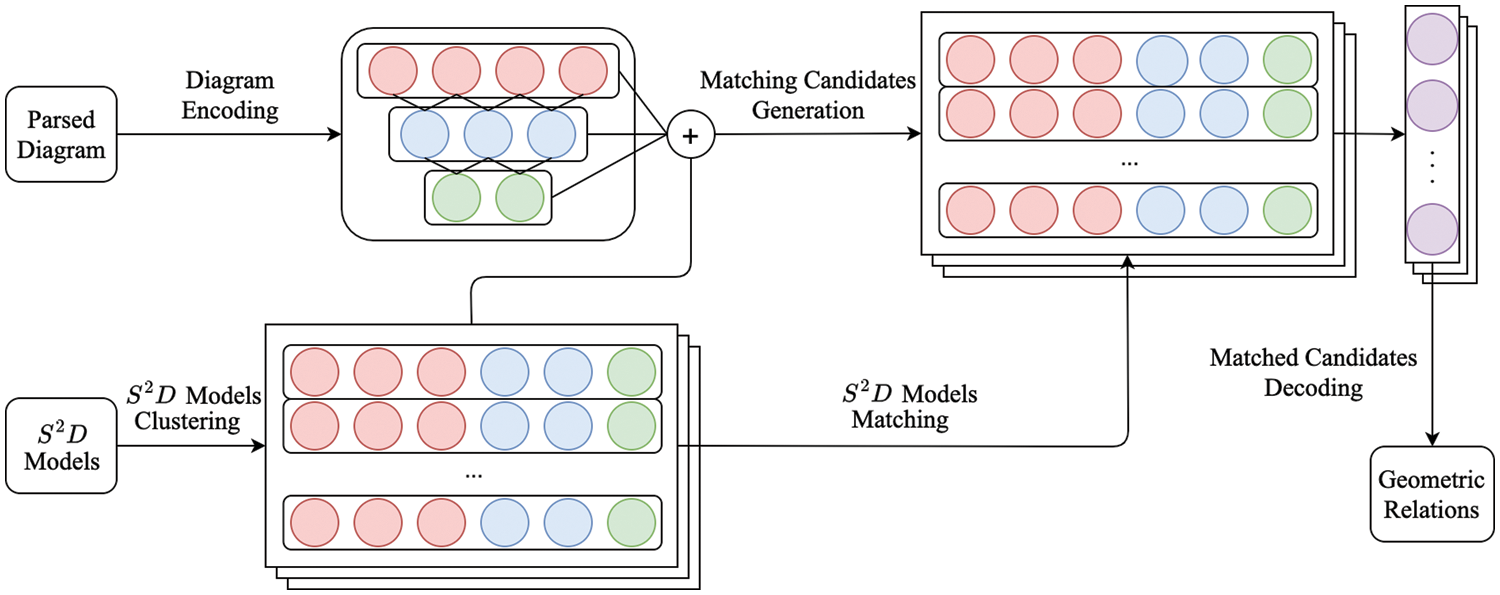
Figure 6: The method of diagram understanding based on S2D models

In the following discussion, the details of Steps 3 to 7 in Procedure 2 are further explored.

Step 3: S2D Model Clustering

Given a pool of prepared S2D models M¯, each model comprises the structure of geometric primitives, multiple primitives, matching functions, and the geometric relations provided as output. As there are five distinct primitives, the primitive-count vector of model m¯i can be defined as Nm¯i=[np,nl,na,ns,nc], with np,nl,na,ns,nc representing the count of points, lines, angles, arc segments, and circles included in miD, respectively. The models in M¯ are clustered based on their primitive-count vector, resulting in a cluster set C={cj|j=1,2,…,k}. The primitive-count vectors of C can be expressed as Φ={Ncj|j=1,2,…,k}, where Ncj represents the primitive-count vector of all S2D models in cj.

As a result, all vectorized S2D models in the cluster cj can be created as tensor γjM¯. Then, a list of tensors ΓM¯={γjM¯|j=1,2,…,k} can be generated, making it feasible for model matching.

This clustering process enables the prepared S2D models to be represented as tensors, which are essential for matching with the unique features of diagrams and for enhancing the matching speed and accuracy.

Step 4: Diagram Encoding

The geometric diagram complements the textual description by providing additional geometric information for problem-solving. To enable efficient matching with the S2D models, the geometric diagram should be represented in vector form as well. Inspired by the vector graph representations in [20], a bilayer undirected graph is designed to model the point-line-angle relationships. In the first layer, each segment represents a point in the diagram, and each element within a segment corresponds to a line that passes through that point. Since each line is associated with two points, it appears in two segments. Pointers to the other end of the line are kept in the elements of the segmented vector, which facilitates graph traversal. Additionally, a separate vector containing the lengths of each line is used to encode the line length information. In the second layer, each segment corresponds to a line in the diagram, and each element within a segment represents an angle formed by that line. Similarly, an additional vector that contains the degrees of the angles is used to include the angle information of the diagram. By using this bilayer undirected graph, the geometry diagram is encoded into the vector form ED consisting of vector tables.

Fig. 7 shows an example of encoding the geometry diagram into vector tables. The left side of Fig. 7 shows an undirected graph that represents the topological structure between geometric primitives, while the right side shows the corresponding vector table. The Fig. 7 demonstrates how points are connected to form lines within the diagram, while the lower table reveals how lines interact with each other to form angles in the same diagram. The “segment-descriptor” in the table header represents the number of edges connected to the corresponding vertex (e.g., the segment-descriptor of A is 2, which means that vertex A is connected to two edges, AC and AM). The “cross-pointer” represents the indices of the vertices connected to the corresponding vertex (e.g., the cross-pointer of A is 4, indicating that A is connected with vertex C, which has an index of 4, to form the edge AC).

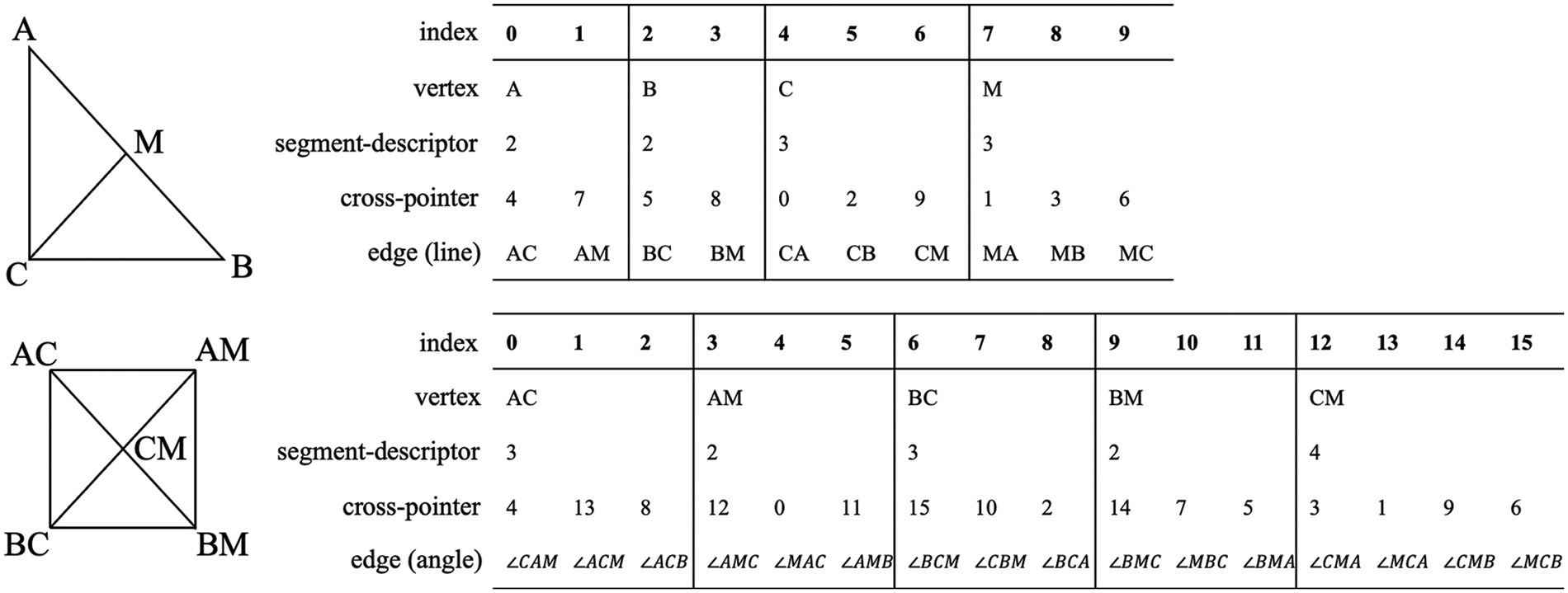
Figure 7: Example of encoding the geometry diagram into vector tables

The next step will use this vector table to generate candidate vectors. The advantage of this method is that it ensures that the primitives in the generated candidate vectors exist in the geometry diagram, which can avoid the occurrence of invalid candidate vectors and speed up the matching process.

Step 5: Candidate Vectors Generation

A combination function is introduced to generate a diverse range of candidate vectors for a specified geometric diagram. Given the encoded representation of a geometric diagram, ED, the combination module stochastically selects primitives from ED to construct candidate vectors by the set of primitive-count vectors Φ of ΓM¯. For each Ncj∈Φ, the combination module can identify numerous vector sequences sharing identical primitive counts:

γjD=Comb(ED,Ncj)(1)

where Comb represents a combination function that locates all candidate vectors with the same primitive counts and groups them into a tensor.

Ultimately, a collection of candidate tensors can be produced as ΓD={γjD|j=1,2,…,k}.

Step 6: S2D Model Matching

In the model-matching process, the objective is to identify matched models in γjM¯ corresponding to a given candidate in γjD. To ascertain whether the model matches the candidate, a two-step process is employed: anchoring and numerical verification.

Definition 3 (Anchoring) Anchoring is the initial step in the S2D model matching process, which aims to find matched models whose primitive structures are identical to the primitive structure of a given candidate vector. Successful anchoring between the two vectors implies that they share the same topology in the geometry diagram.

To implement the anchoring process, the simplest method would be to directly compare each primitive in the candidate vector with the corresponding primitive in the model vector. However, this method requires considering the order of primitives during matching, resulting in the generation of numerous candidate vectors with varying primitive orders, which in turn reduces matching efficiency. Therefore, this study adopts a method that transforms vector matching into graph matching. During the matching process, only the topological structure of the primitives within the vectors needs to be considered, without considering the order of the primitives. This significantly reduces the number of candidate vectors generated and improves matching efficiency.

To perform the anchoring process between candidate vectors and model vectors using graph matching, first, both the candidate vector and the model vector are converted into graph structures, with these graphs hierarchically divided based on points, lines, and angles. Next, matching between the two graphs is carried out by focusing on the outdegree of nodes. For each node in both the candidate graph and the model graph, a list is created, consisting of the node’s outdegree and the outdegrees of its child nodes. By comparing these lists of outdegrees for each node in the candidate vector graph with the corresponding lists in the model vector graph, it becomes possible to identify one-to-one correspondences between nodes. When two nodes from the candidate graph and the model graph have identical outdegree lists, it indicates that they share a one-to-one correspondence. Finally, if every node in the two graphs has a one-to-one correspondence, a mapping between the points in the candidate vector and the points in the model vector is obtained as below:

μ:GPh′→GPi(2)

where μ is a mapping between the primitives in the two vectors, GPh′ and GPi are the primitives in the h-th candidate vector to be matched and the vector of S2D model m¯i, respectively. Due to the symmetry characteristics of geometric diagrams, the obtained mapping may not be unique at times. In such cases, it is essential to eliminate unreasonable combinations and select the appropriate mapping for decoding matched candidates.

An illustrative example of the anchoring process is provided in Fig. 8, which visually demonstrates the aforementioned steps. The anchoring process is performed between the S2D model vector and the candidate vector composed of points (A, M, B), lines (MA, MB), and angle (∠BMA). After the successful anchoring process, a mapping between the points (A, M, B) in the diagram and those in the S2D model is obtained.

Figure 8: Example of the anchoring process based on graph matching

If the anchoring process fails, it indicates that the model vector and the candidate vector do not match. However, if the anchoring process is successful, the next step is to perform numerical verification for the primitives. This is necessary because some geometric relations cannot be confirmed solely based on topological relationships. Using the primitive mapping obtained from the anchoring process, the variables in the matching function of the S2D model are replaced with the corresponding primitives from the candidate vector. Let f(x1,x2,…,xn) be one of the matching functions of m¯i, where x1,x2,…,xn are the variables representing a portion of primitives in GPi. After substituting the corresponding primitives from the candidate vector using the mapping function μ, the verification is considered successful if the following condition is satisfied:

f(y1,y2,…,yn)=0(3)

where y1,y2,…,yn represents a portion of primitives in GPh′.

In the case of Fig. 8, by using the mapping, the lengths of lines and the measure of angle are substituted into the matching functions F in S2D model. Then, it is verified whether the lengths of segments AM and MB are equal and if ∠BMA measures 180 degrees.

To sum up, if both the anchoring process and numerical verification are completed, it indicates that the candidate vector matches the S2D model. Following the above process, all the successfully matched candidate vectors and their corresponding models are added to a list W for decoding.

Step 7: Matched Candidates Decoding

In the final decoding phase, for each candidate vector in the list W, the corresponding S2D model’s geometric relation template is instantiated using the previously obtained mapping from the anchoring process. By substituting the primitives from the candidate vector into the model’s geometric relation template, the template is effectively instantiated with the specific primitives, resulting in a concrete geometric relation that reflects the original input diagram. These instantiated geometric relations are then collected into a set ΣD. The set ΣD represents the basic geometric relations obtained after performing diagram understanding on the input diagram D.

4.2.3 Derived Relations Generation

In this part of the process, the set of basic geometric relations Σ0 is obtained by integrating geometric relations ΣT and ΣD, which are extracted from text understanding and diagram understanding:

Σ0=ΣT∪ΣD(4)

Most basic features of the geometry diagram, including the quantity and position of geometric primitives, can be described by the basic geometric relations in Σ0. However, these basic geometric relations alone are insufficient to solve the geometric problem. Therefore, it becomes necessary to consider derived relations, which are generated from the basic geometric relations, to describe more advanced geometric features.

Following the diagramet theory proposed in [6], a derived relations generation model is introduced that can define a type of diagramet and generate the corresponding derived geometric relations. To constrain the model’s scope, a diagram corpus U containing all diagrams from plane geometry theorems is defined, along with a pool of diagramets for U.

The generation process of derived relations is outlined in Procedure 3. First, a pool of diagramet models for the geometry problem is loaded. The model searches the pool based on the relations in Σ0 and identifies instances of diagramets. Next, a mapping between primitives in the basic relations and primitives in the relation representation of the diagramet is established, leading to the generation of the derived relation. Finally, all obtained derived relations are collected into Σ1. This comprehensive set of derived relations, combined with the basic geometric relations, provides a more complete and accurate representation of the geometric problem, allowing for a deeper understanding of the underlying geometric features and relations.

5  Experiments

5.1 Experimental Settings

5.1.1 Datasets and Evaluation Metrics

Experiments are conducted on four datasets: Geometry Calculation Problems for Primary School (GCP-PS), Geometry Calculation Problems for Secondary School (GCP-SS), Shaded Area Problems for Primary School (SAP-PS), and Shaded Area Problems for Secondary School (SAP-SS). In the GCP-PS dataset, 217 problems are collected from multiple versions of primary school math textbooks (including Beijing Normal University Press, People’s Education Press, and Jiangsu Education Press). For GCP-SS, the Geometry3K dataset [10] is used, containing 3,002 problems. Regarding the SAP-PS dataset, 120 problems are collected from various versions of primary school math textbooks, while for SAP-SS, Feng’s dataset [14] containing 192 problems is utilized. All problem texts have been translated into English.

To evaluate the performance of the proposed method, accuracy on different datasets is considered. To facilitate the evaluation of the solutions, all problems are transformed into a single-choice question format with four numerical choices. For the proposed method, if the obtained numerical result has the smallest absolute difference with a choice corresponding to the ground truth, the answer is considered correct. If the numerical result has the same absolute difference with multiple choices, a random selection is made from these choices. If the method fails to produce a result, a random choice is selected from the four choices.

5.1.2 Baselines

In the following section, the performance of the proposed method, referred to as PROPOSED, will be compared with several existing baseline methods on the four datasets. The aim of this comparison is to evaluate the effectiveness and robustness of PROPOSED against established approaches in the field.

GEOS [9] is the first automated system that solves SAT geometry problems by combining text understanding and diagram interpretation. The approach identifies a formal problem description compatible with both problem text and diagram and then feeds it into a geometric solver to determine the correct answer.

Inter-GPS [10] is a geometry problem-solving approach that leverages formal language and symbolic reasoning. It parses problem text and diagrams into formal language using rule-based text parsing and neural object detection. Inter-GPS incorporates theorem knowledge as conditional rules and performs symbolic reasoning step-by-step. As a key component of the approach, it features a theorem predictor, which is responsible for inferring the theorem application sequence, ultimately leading to a more efficient and reasonable search path.

FengAlg [14] is a method specifically designed for solving shaded area problems. It focuses on constructing equations to generate readable solutions, addressing the challenges associated with the diverse expressions of such problems and the complex relationships between shaded areas and other areas. By acquiring a system of equations and using a variety of techniques to construct them from inputs, FengAlg offers a concise and understandable solving process.

Due to GEOS and Inter-GPS being specialized in solving geometry calculation problems, and FengAlg being focused on shaded area problems, PROPOSED will be compared with GEOS and Inter-GPS on GCP-PS and GCP-SS, and with FengAlg on SAP-PS and SAP-SS.

5.1.3 Implementation Details

In the experimental process, both the proposed method and the baselines follow a similar process that starts by taking the problem, including the textual description and associated geometry diagram, as input. Each method employs a phase for understanding the problem text and the diagram separately, extracting relevant geometric relations. These relations are subsequently integrated into a unified representation that is used as input to the symbolic solver.

During the experiments, different symbolic solvers are employed for two types of problems.

For geometry calculation problems, the symbolic solver proposed in [10] is adopted, which takes the geometric relations extracted from PROPOSED as input. This solver has proven effective in handling various geometric calculations and provides a robust solution for problems in this category.

For shaded area problems, the symbolic solver from Feng’s method [14] is selected, which also takes the geometric relations obtained by PROPOSED as input. This solver is specifically designed to address the challenges associated with computing shaded areas in geometric diagrams. It considers the unique aspects of such problems and delivers accurate results accordingly.

5.2 Experimental Results

5.2.1 Comparisons with Baselines

In the evaluation, a comparison of PROPOSED with several baseline methods on four datasets is presented: GCP-PS and GCP-SS for Table 2, and SAP-PS and SAP-SS for Table 3. Considering that geometry calculation problems encompass multiple problem goals (length, angle, area, and ratio), the performance of several methods is measured in terms of solving accuracy across different problem goals on GCP-PS and GCP-SS datasets. On the other hand, shaded area problems focus solely on area calculation; hence, only the overall solving accuracy is considered on SAP-PS and SAP-SS datasets.

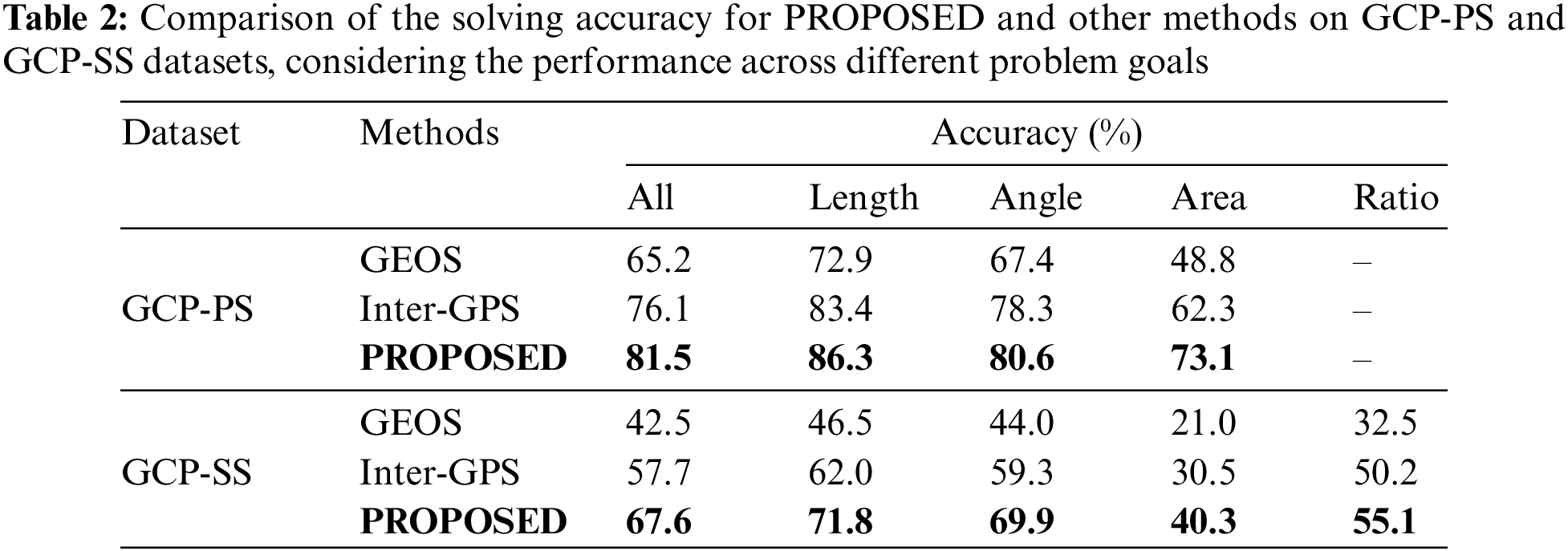
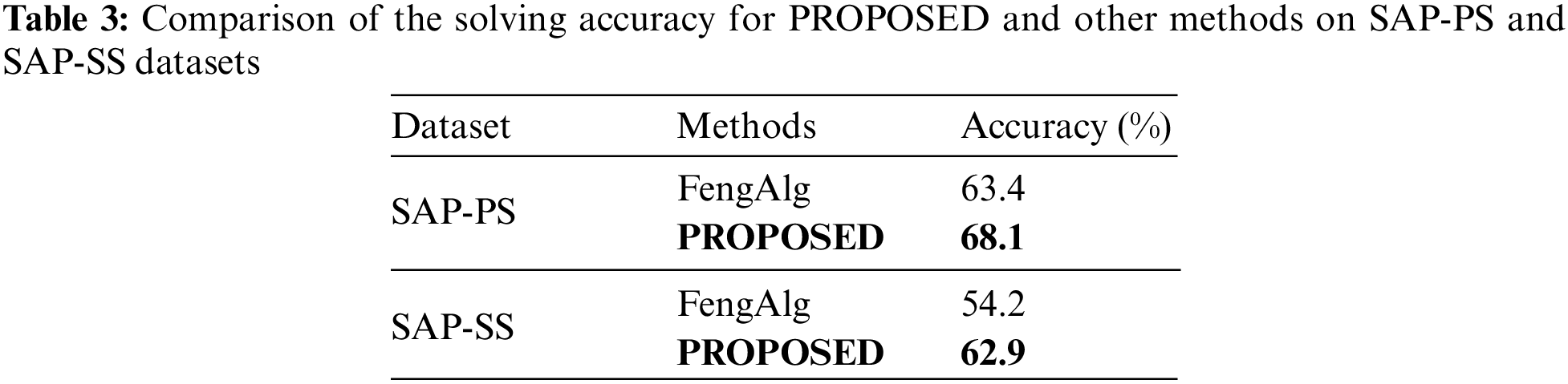
Table 2 showcases the solving accuracy of PROPOSED and the baselines on both GCP-PS and GCP-SS datasets. PROPOSED outperforms all other methods, achieving an accuracy of 81.5% and 67.6% on the GCP-PS and GCP-SS datasets, respectively. It can be observed that the improvement of PROPOSED over the other baselines on the GCP-PS dataset is not as significant as on the GCP-SS dataset. The reason for this difference is that the GCP-PS dataset contains problems related to primary school geometry, which involve relatively simple geometric relations. In contrast, the GCP-SS dataset includes problems of secondary school geometry, which require more complex geometric relations to solve. This demonstrates that PROPOSED exhibits a greater advantage when tackling problems involving complex geometric relations. Notably, PROPOSED shows a significant improvement in the problem goal Area compared to the baselines. The substantial improvement in the problem goal Area can be attributed to the fact that area calculation typically necessitates a more extensive set of geometric relations. PROPOSED is particularly effective in extracting these more geometric relations, which contributes to its enhanced performance in the problem goal Area.

Table 3 compares PROPOSED with FengAlg on the SAP-PS and SAP-SS datasets. PROPOSED again surpasses the baseline method, achieving an accuracy of 68.1% on the SAP-PS dataset and 62.9% on the SAP-SS dataset. FengAlg, as a baseline, shows a reasonable performance but is still outperformed by PROPOSED.

In summary, PROPOSED demonstrates superior performance across all datasets and problem goals, indicating its effectiveness in solving APGDs. The results also highlight the improvements achieved by PROPOSED, particularly in the more challenging problem goals such as Area.

5.2.2 Ablation Study

In the ablation study, the examination of the impact of various components of PROPOSED on the overall accuracy is divided into two cases: (1) comparing the performance of using basic relations and integrated relations, and (2) comparing the performance with and without text understanding and diagram understanding. The results are presented in Table 4.

In Case 1, the performance of the method when using only basic geometric relations (Basic) vs. the proposed approach of utilizing integrated geometric relations (Integrated) is compared. The method using integrated relations significantly improves the accuracy across all datasets, with a 6.9% increase in overall accuracy. Notably, the improvements in GCP-SS and SAP-SS datasets are more pronounced, indicating that integrated relations play a more substantial role in solving problems that require more complex relations.

In Case 2, the importance of text understanding and diagram understanding in PROPOSED is assessed. In the case of Text & Diagram w/o, the results show that relying solely on the text without the diagram is insufficient for solving APGDs accurately. On the other hand, when only diagram understanding is included (Text w/o & Diagram), the accuracy improves substantially, indicating that relying on the information from the diagrams alone can still solve a portion of APGDs. The highest accuracy is achieved when both text understanding and diagram understanding are combined (Text & Diagram), emphasizing the importance of utilizing both components.

5.2.3 Threats to Validity

Threats to validity are potential weaknesses in the design or execution of a study that could impact the credibility of the results. In the case of this research, certain limitations are present that could pose threats to both the internal and external validity of the findings.

In terms of internal validity, certain limitations are identified that directly affect the accuracy of the results. Two specific instances where PROPOSED encounters these limitations are illustrated in Fig. 9. The first example shows a situation where the problem requires the construction of auxiliary lines within the diagram for its solution. Currently, PROPOSED lacks the capability to draw auxiliary lines in the geometry diagrams, a vital step in solving specific types of problems. This constraint contributes to an incomplete solution in this case. The second example highlights a failure case where PROPOSED is unable to interpret the implicit information present within the text. As a result, it fails to establish a connection between calculating the geometric area and the actual problem-solving goal. This points out a limitation in the text understanding component, necessitating improvements to better handle implicit information and effectively link textual data with the geometric diagram.

Figure 9: Failure examples of PROPOSED

Regarding the external validity, the method is designed to handle a broad range of APGDs. Nevertheless, its effectiveness may vary based on the complexity and specificity of the problem. The current research primarily targets standard geometric problems typically encountered in primary school textbooks. The applicability of PROPOSED to other types of problems is yet to be thoroughly tested, posing a potential threat to the generalizability of the findings.

Future efforts will aim to mitigate these threats to validity, with a focus on improving the performance and broad applicability of PROPOSED.

6  Conclusion

In this paper, the problem of solving APGDs is addressed by employing an algorithm designed based on a systematic and modular three-phase scheme. The state-transformer paradigm is first applied to model the problem-solving process, which effectively represents the intermediate states and transformations that occur during the process. This paradigm paves the way for a structured approach to problem-solving and facilitates the integration of various algorithms and techniques. Next, the generalized APGD-solving approach is employed, which provides a high-level strategy for extracting and utilizing geometric knowledge from both textual descriptions and geometry diagrams. This approach ensures the effective extraction of relevant information and lays the foundation for developing specific APGD-solving algorithms. Lastly, a specific APGD-solving algorithm is developed that incorporates the S2 model for extracting geometric relations from the problem text and the S2D model for relation extraction from diagrams. In addition, a derived geometric relations generation method is proposed to extract derived relations from the basic geometric relations. The proposed method enables a more in-depth understanding of the problem and leads to a more accurate and comprehensive solution to APGDs. The experimental results on real-world datasets of primary and secondary school level problems demonstrate that the proposed method significantly improves APGD problem-solving accuracy across various problem types, including geometry calculation problems and shaded area problems.

However, there are limitations to the current approach, as demonstrated by the failure cases. These cases indicate areas for future improvement, such as developing the ability to construct auxiliary lines in diagrams and enhancing the understanding of implicit textual information. Future work will focus on addressing these limitations and further enhancing the proposed method’s capabilities to provide more accurate and comprehensive solutions to APGDs. This will not only contribute to the advancement of research in artificial intelligence but also pave the way for valuable applications in education, such as intelligent tutoring systems.

Acknowledgement: Sincere gratitude is extended to the fellow researchers for their invaluable expertise and insightful guidance throughout this study.

Funding Statement: This work is supported by the National Natural Science Foundation of China (No. 61977029) and the Fundamental Research Funds for the Central Universities, CCNU (No. 3110120001).

Author Contributions: Study conception and design: Litian Huang and Xinguo Yu; data collection: Litian Huang and Zihan Feng; analysis and interpretation of results: Litian Huang and Lei Niu; draft manuscript preparation: Litian Huang, Xinguo Yu and Lei Niu. All authors have reviewed the results and given their approval for the final version of the manuscript.

Availability of Data and Materials: The data used in this study is available from the corresponding author upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. W. Gan, X. Yu, C. Sun, B. He and M. Wang, “Understanding plane geometry problems by integrating relations extracted from text and diagram,” in Proc. of Image and Video Technology: 8th Pacific-Rim Symp., Wuhan, China, pp. 366–381, 2017. [Google Scholar]

2. X. Lyu and X. Yu, “Solving explicit arithmetic word problems via using vectorized syntax-semantics model,” in Proc. of the 1st IEEE Int. Conf. on Engineering, Technology & Education, Wuhan, China, pp. 1–7, 2021. [Google Scholar]

3. X. Yu, X. Lyu, R. Peng and J. Shen, “Solving arithmetic word problems by synergizing syntax-semantics extractor for explicit relations and neural network miner for implicit relations,” Complex & Intelligent Systems, vol. 9, no. 1, pp. 697–717, 2023. [Google Scholar]

4. J. Chen, J. Tang, J. Qin, X. Liang, L. Liu et al., “GeoQA: A geometric question answering benchmark towards multimodal numerical reasoning,” in Findings of the Association for Computational Linguistics: ACL-IJCNLP 2021, Bangkok, Thailand, pp. 513–523, 2021. [Google Scholar]

5. J. Chen, T. Li, J. Qin, P. Lu, L. Lin et al., “UniGeo: Unifying geometry logical reasoning via reformulating mathematical expression,” in Proc. of the 2022 Conf. on Empirical Methods in Natural Language Processing, Abu Dhabi, United Arab Emirates, pp. 3313–3323, 2022. [Google Scholar]

6. J. Xia and X. Yu, “A paradigm of diagram understanding in problem solving,” in Proc. of the 1st IEEE Int. Conf. on Engineering, Technology & Education, Wuhan, China, pp. 531–535, 2021. [Google Scholar]

7. W. Gan and X. Yu, “Automatic understanding and formalization of natural language geometry problems using syntax-semantics models,” International Journal of Innovative Computing, Information and Control, vol. 14, no. 1, pp. 83–98, 2018. [Google Scholar]

8. M. Seo, H. Hajishirzi, A. Farhadi and O. Etzioni, “Diagram understanding in geometry questions,” in Proc. of the 28th AAAI Conf. on Artificial Intelligence, Québec City, Canada, pp. 2831–2838, 2014. [Google Scholar]

9. M. Seo, H. Hajishirzi, A. Farhadi, O. Etzioni and C. Malcolm, “Solving geometry problems: Combining text and diagram interpretation,” in Proc. of the 2015 Conf. on Empirical Methods in Natural Language Processing, Lisbon, Portugal, pp. 1466–1476, 2015. [Google Scholar]

10. P. Lu, R. Gong, S. Jiang, L. Qiu, S. Huang et al., “Inter-GPS: Interpretable geometry problem solving with formal language and symbolic reasoning,” in Proc. of the 59th Annual Meeting of the Association for Computational Linguistics and the 11th Int. Joint Conf. on Natural Language Processing, Bangkok, Thailand, pp. 6774–6786, 2021. [Google Scholar]

11. M. Zhang, F. Yin, Y. Hao and C. Liu, “Plane geometry diagram parsing,” in Proc. of the 31st Int. Joint Conf. on Artificial Intelligence, Vienna, Austria, pp. 1636–1643, 2022. [Google Scholar]

12. X. Yu, H. Sun and C. Sun, “A relation-centric algorithm for solving text-diagram function problems,” Journal of King Saud University—Computer and Information Sciences, vol. 34, no. 10, pp. 8972–8984, 2022. [Google Scholar]

13. C. Alvin, S. Gulwani, R. Majumdar and S. Mukhopadhyay, “Synthesis of solutions for shaded area geometry problems,” in Proc. of the 30th Int. Florida Artificial Intelligence Research Society Conf., Marco Island, USA, pp. 14–19, 2017. [Google Scholar]

14. Z. Feng, X. Yu, Q. Li and H. Sun, “Solving shaded area problems by constructing equations,” in Proc. of the 2nd Int. Conf. on Artificial Intelligence in Education Technology, Wuhan, China, pp. 105–115, 2022. [Google Scholar]

15. X. Chen, D. Song and D. Wang, “Automated generation of geometric theorems from images of diagrams,” Annals of Mathematics and Artificial Intelligence, vol. 74, pp. 333–358, 2015. [Google Scholar]

16. D. Song, Q. Yao and J. Lu, “A novel geometric information retrieval tool for images of geometric diagrams,” in Proc. of the 2020 Int. Conf. on Information Science and Education (ICISE-IE), Sanya, China, pp. 403–411, 2020. [Google Scholar]

17. L. Huang, X. Yu and B. He, “A novel geometry problem understanding method based on uniform vectorized syntax-semantics model,” in Proc. of the 1st Int. Conf. on Intelligent Education and Intelligent Research, Wuhan, China, pp. 78–85, 2022. [Google Scholar]

18. G. Stockman and L. G. Shapiro, Computer Vision, 1st ed. USA: Prentice-Hall, 2001. [Google Scholar]

19. T. Lin, P. Goyal, R. Girshick, K. He and P. Dollár, “Focal loss for dense object detection,” in Proc. of the 2017 IEEE Int. Conf. on Computer Vision, Venice, Italy, pp. 2980–2988, 2017. [Google Scholar]

20. G. Blelloch, Vector Models for Data-Parallel Computing, vol. 2. Cambridge: MIT Press, 1990. [Google Scholar]