Exercise Recommendation with Preferences and Expectations Based on Ability Computation

1  Introduction

With the accelerating popularity of education informatization and mobile applications, online education has attracted many student users to learn on online platforms. However, the massive amount of educational resources available online dramatically increases the difficulty for learners to find learning resources at different learning stages [1]. Hence, a science-based approach must be used to analyze students and educational resources to provide personalized learning services for students. Personalized recommendation algorithms can effectively solve this problem and have become a popular research direction. As a vital educational resource, exercises are essential in testing studentsʼ learning abilities. An important issue is how to compute studentsʼ ability and learning progress from their exercises and then provide learners with personalized exercise recommendations based on their learning stage preferences and expectations of the exercisesʼ difficulty. Therefore, from the viewpoint of enhancing studentsʼ productivity and interest, it is important to study how to accurately compute students’ ability, compute students’ learning progress and compute the difficulty of exercises for students, and recommend exercise resources that meet students’ different learning stages, learning stage preferences and expectations of difficulty based on student’s ability and difficulty of exercises.

In the personalized exercises recommendation, it is crucial to compute the student’s ability to understand different knowledge concepts accurately. Because the student’s forgetting behavior [2] and thus the student’s ability to forget knowledge concepts decreases during the learning progress, the difficulty of the exercises involving forgotten knowledge concepts increases for the student. A student’s learning progress should also be considered in the personalized exercise recommendations. It is also essential to accurately compute the progress of students’ knowledge and adjust the recommendation process according to their changing learning stage preferences (review or exploration) to help them learn efficiently. We also consider students’ expectations of the difficulty of the exercises to maximize the learning needs of students, and how to evaluate whether students’ expectations are reasonable [3] is also an issue to be considered in the recommendation system. A student’s reasonable expectation means that the difference between their expected difficulty and their actual ability should not be too great. From the above analysis, we know that it is very challenging to compute students’ ability and the difficulty of the exercises in the exercise recommendation and recommend exercises that meet students’ desired difficulty according to their learning stage preferences.

In the current study, Wu et al. [4] proposed a recommendation system that recommends exercises that match students’ abilities according to their learning progress but does not consider students’ learning stage preferences, forgetting behavior during learning, and the reasonableness of students’ expectations about the difficulty of the exercises. Zhu et al. [5] proposed an exercise recommendation system based on cognitive diagnosis, which computes the student’s ability and combines collaborative filtering to recommend the student exercises. However, the student’s learning progress and the student’s learning stage preferences should be taken into account in this recommendation system. These studies suggest that present research needs to propose valid solutions to recommend suitable exercise for students according to their progress and abilities, especially considering their learning stage preferences and forgetting behavior.

In this paper, LFCKT-ER is presented to address the limits of the present study. The LFCKT-ER takes into account students’ abilities, learning stage preferences, expectations, and forgetting behavior. It can recommend exercises for students that better match their learning stage preferences, abilities, and learning progress to maximize personalized services for students to enhance their study productivity and interest. Among the contributions, this paper has the following:

1) A model is proposed to compute students’ ability LFCKT-ER, which considers students’ learning rate and forgetting behavior in learning to model each student individually and output students’ mastery of each knowledge in real-time, allowing students to understand their learning progress better. Additionally, LFCKT-ER can provide better feedback for educators to understand students’ learning situations better, thus providing better support.

2) By integrating students’ learning stage preferences into the learning progress computation and evaluating whether students’ expectations for the difficulty of the exercises are reasonable, LFCKT-ER can dynamically adjust the exercise recommendations according to student’s learning stage preferences and expectations and use optimization algorithms to maximize the diversity of the exercise recommendations when recommending them, maximizing students’ satisfaction and learning efficiency.

3) The recommendation model LFCKT-ER proposed in this paper was evaluated on three real open-source datasets and compared with other mainstream models. LFCKT-ER improved in the corresponding evaluation metrics. Specifically, LFCKT can recommend appropriate exercises to students, allowing them to master knowledge more effectively and improve learning outcomes.

This paper is organized as follows. Section 2 discusses the related recommendation algorithms. Section 3 describes the proposed exercise recommendation method LFCKT-ER. Section 4 provides the experimental results and analyzes the experimental results. Section 5 summarizes the paper.

2  Related Work

Recommendation systems are essential applications of cognitive computing [6], and due to the importance of education, many researchers have worked on recommendation technologies in education. In particular, Linden et al. [7] proposed a K-Nearest Neighbor (KNN) collaborative filtering method to find the students with the most similar answer profiles by calculating the Jaccard similarity between students through their existing exercise scores, then predicting the aim students’ scores according to the most similar students’ scores, and then recommending the exercises according to the predicted scores. Torre [8] selected exercises from the set of exercises to be recommended according to the level of student knowledge mastery diagnosed by Deterministic Inputs, Noisy “And” gate model (DINA) and recommended exercises related to the knowledge concepts where students’ knowledge mastery is weak and those where knowledge mastery is vital. Many studies introduce knowledge graphs into recommendation systems [9–11], Xing et al. [9] proposed a unification-based approach to address the interference of too-distant supplementary information in the knowledge graph with entity information by reconstructing the knowledge graph and also designed a neighborhood aggregation structure based on a distance strategy to achieve a shorter training overhead by reducing the order of aggregation. Chen et al. [10] applied knowledge graph and reader portrait techniques to book recommendation retrieval by constructing reader-book knowledge graphs and combining book topic models and reader portraits to model the semantic associations between books and reader preferences, respectively, to mine the semantic associations behind reader-reader, reader-book, and book-book. The semantic relationships between readers and readers, readers and books, and books and books are analyzed to enhance the recommendation retrieval effect. Zhang et al. [11] proposed a knowledge graph recommendation via the influence effect of a similar user model with fused influence effects, which expands the interaction between users and items. Many researchers apply knowledge-tracking techniques [12–14] to recommended exercises. Ma [12] proposed a personalized exercise recommendation method that combines a deep knowledge tracking model with a collaborative filtering method to address the fact that most of the existing exercise recommendation methods for knowledge modeling ignore the use of common features among similar students. Zhu et al. [13] combined collaborative filtering with knowledge tracing to recommend exercises to students and added the influence of forgetting factors in calculating students’ learning progress to fully explore students’ knowledge mastery level and typical characteristics of similar students and used them based on dynamic key-value memory networks for knowledge tracing model to accurately explore students’ knowledge concept mastery level to ensure the recommendation of appropriate difficulty exercises. He et al. [14] proposed an exercise recommendation method based on knowledge tracing and conceptual prerequisite relations, which considers the difficulty of the exercises and the prerequisite relations of the knowledge concepts in the recommendation and sets thresholds for the mastery of the knowledge concepts into very poorly mastered, essentially mastered, and very well mastered, recommending moderately complex exercises can guide students in the right direction of learning and also stimulate their interest in learning. However, these studies rarely consider student forgetting, student preferences, and student expectations during the learning progress. In this paper, we first predict students’ learning progress and add students’ weights on learning stage preferences in the final output layer to filter out the exercises that meet students’ learning progress and preferences, then calculate students’ ability on each concept and evaluate the reasonableness of students’ expectations for the exercises based on their ability and make corresponding adjustments, and finally filter out the exercises that meet students’ expectations on difficulty and maximize the diversity of the exercises using simulated annealing optimization algorithm to stimulate students’ learning interest.

3  The Model of LFCKT-ER

The framework of the exercise recommendation system proposed in this paper is shown in Fig. 1. First, the model computes for each knowledge concept the probability that at the next moment based on students’ interaction sequences through the Knowledge Concept Computation with Preference (KCCP) to select the knowledge concepts that match students’ learning stage preferences and students’ learning progress. Then, the ability computation layer computes the student’s ability for each knowledge concept. Finally, the exercise selection with expectation and diversity layer evaluates whether the student’s expectations are reasonable, filters the set of exercises that best meet the student’s expectations based on their mastery of each knowledge, and uses an improved simulated annealing algorithm is used to optimize the combination of the filtered exercise sets to minimize the similarity of the recommended list of exercises and to achieve the effect of diversifying the exercises to stimulate students’ interest in learning.

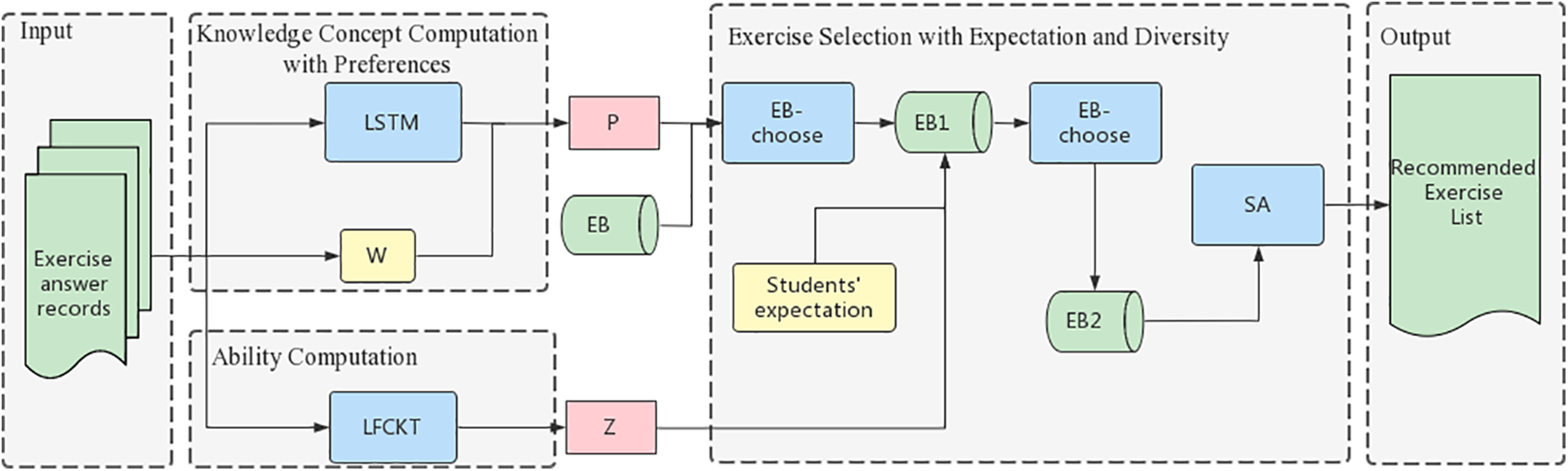
Figure 1: Framework of LFCKT-ER

3.1 Definition of the Problem

An exercise generalizes a knowledge concept and usually contains one or more knowledge concepts. In this paper, we only consider the exercise with a knowledge concept. The goal of LFCKT-ER is to recommend exercises that match the student’s learning progress, learning stage preferences (review or exploration), and learning expectations, and reduce the number of similar exercises after the student has completed the exercise. In general, we can formalize an exercise recommendation as follows: given a sequence of student interactions X={x1,x2,⋯,xn}, the xt is a tuple (et,at) that denotes an interaction. The et represents the exercise answered at time step t and a∈{0,1} means whether the answer to the et is correct (1 means right, 0 means incorrect).

3.2 Knowledge Concept Computation with Preferences

For the target students at a particular time, the students’ problem sequences are firstly filtered by KCCP to find out the exercise bank EB1 that matches the student’s learning progress and learning stage preferences. First, the students’ interaction sequences are input into the Long Short-Term Memory (LSTM) [15] to model the students’ learned knowledge concepts and predict the probability of students’ possible learning concepts in the next moment. Then, an exercise bank that matches both the student’s learning progress and their learning stage preferences is computed based on the student’s learning stage preferences.

3.2.1 Knowledge Concept Computation

Using the order of occurrence of knowledge concepts from 0 to t to compute the probability of occurrence of each knowledge concept at the moment t+1 is a sequence prediction problem. LSTM [15] can predict students’ learning progress. Fig. 2 shows the LSTM-based knowledge learning progress model, where the A indicates the model’s current state at the moment t. The Kt denotes the knowledge concept appearing at the moment t, which can be obtained from student interactions X. The Kt+1 indicates the probability of the knowledge concept appearing at the moment t+1 accepted by model prediction.

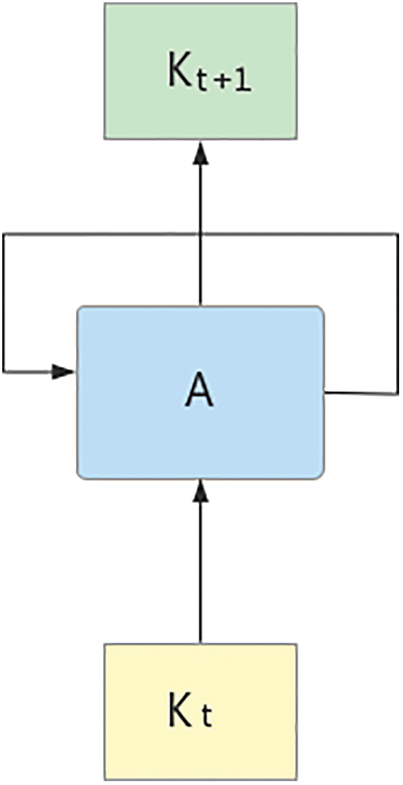
Figure 2: Framework of LSTM

The one-hot encoding [16] of Kt is required before the sequence of students’ doing exercises is input into the LSTM model, and the result is φ(Kt). The model’s input is a vector with a dimension equivalent to the amount of all knowledge concepts, and the model’s output has an extent equal to the input dimension. The model’s output represents the prediction of the knowledge concept at the next moment, and the input φ(Kt+1) at the moment t+1 represents the learning vector of actual knowledge concepts. LSTM models the knowledge concept learning range prediction problem at the end of a training period T. The loss function uses binary cross-entropy to train the model as in Eq. (1).

L=∑t=0Tℓ(Kt+1⋅φ(Kt+1),1)(1)

where T denotes an LSTM training period, Kt+1 denotes the vector of the actual t+1 moment knowledge concepts, and φ(Kt+1) denotes the vector of t+1 moment knowledge concept predictions output by the model.

The output of the final model is a vector of length as long as the amount of knowledge concepts, as in Eq. (2).

Y(K)=[y(k1),y(k2),⋯,y(km)](2)

where y(ki) denotes the probability that the i th knowledge concept occurs at the moment t+1 and m denotes the number of all knowledge concepts.

3.2.2 Exercises Selection with Preference

The fundamental purpose of exercise recommendation is to help students master knowledge, including not only new knowledge that they have not been exposed to but also old knowledge that they have not learned and need to review. Hence, it needs to be studied and explored dynamically according to students’ learning stage preferences. To satisfy students’ stage preferences for learning, a weight vector matching students’ learning stage preferences is added to the output layer of the LSTM model, as shown in Fig. 3. This ensures that exercises that students have already done but have a high error rate can have a relatively high weighting and can also satisfy different stage preferences of students. It has a length equal to the amount of knowledge concepts as in Eq. (3).

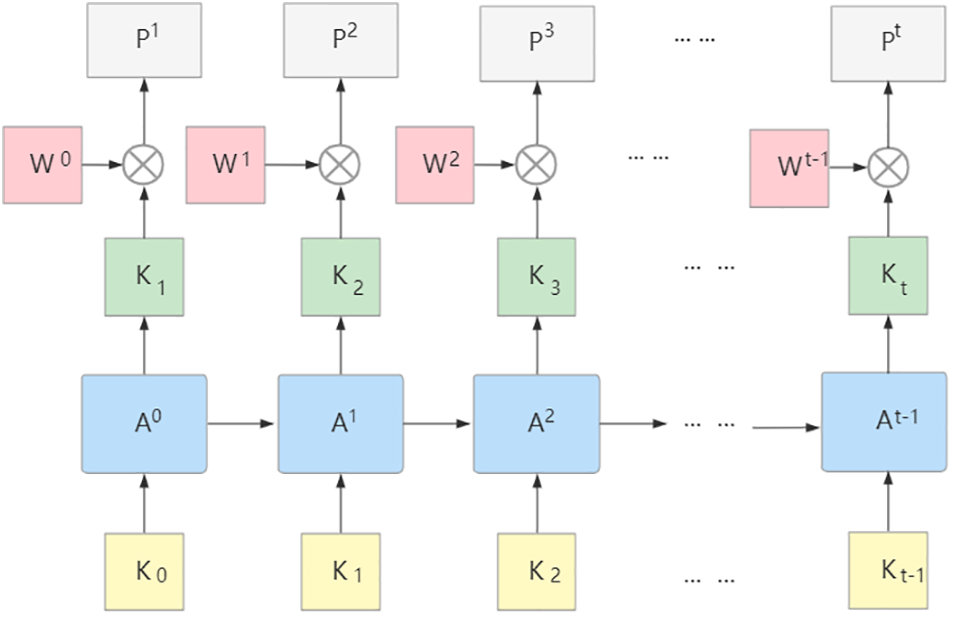
Figure 3: Process of KCCP

W(K)=[w(k1),w(k2),⋯,w(km)](3)

The w(ki) is expressed as Eq. (4).

w(ki)={1−rici,    ci≠0{0,1},     ci=0(4)

where ci denotes the number of times students learned a knowledge concept i in the period T, and ri denotes the number of times students correctly answered the knowledge concept i in the period T. When the ci is equal to 0, it means students have not done exercises on this knowledge concept. The value w(ki) depends on students’ learning stage preferences, for example, the w(ki)=0 indicates that students’ learning stage preferences is to review. The w(ki)=1 indicates students’ learning stage preferences is to explore.

The combination of the output of the LSTM model and the weight vector can be used to obtain the probability vector of the occurrence of the student’s preferred knowledge concept in the next exercise P(Kt+1), as in Eq. (5).

P(Kt+1)=Y(K)⋅W(K)(5)

where Kt+1 denotes the knowledge concept at the moment t+1, and P(Kt+1) means the probability of the student’s knowledge concept at the moment t+1 after adding the student’s learning stage preference; Y(K) denotes the LSTM model output vector with the length of the number of all knowledge concepts, which represents the probability vector of the student’s learning progress; W(K) denotes the student’s vector about learning stage preference with the length of the number of all knowledge concepts.

After obtaining the probability of the occurrence of students’ knowledge concepts about preferences, an initial selection of the exercises is performed to filter out the top N sets of knowledge concepts that most closely match what students are most likely to learn about their preferences EB1.

3.3 Ability Computation

The cognitive computing model used in this paper adopts the LFCKT [17] model. Fig. 4 shows the framework diagram of the model, which consists of an embedding module, knowledge state extraction module, forgetting module, and prediction module. The model first stitching the exercise embedding with the student’s answer results as interaction records through the embedding vector of the embedding layer learning exercises, and then obtains the students’ learning behavior information through the students’ historical interaction sequence. Then the data on students’ learning behavior is obtained through historical interaction sequences. Then, LFCKT has a hierarchical convolutional layer to extract students’ knowledge state features. Then the forgetting layer update the matrix of the student’s ability at the present moment. Lastly, the probability that the students answer the following exercise correctly is obtained from the predicting layer.

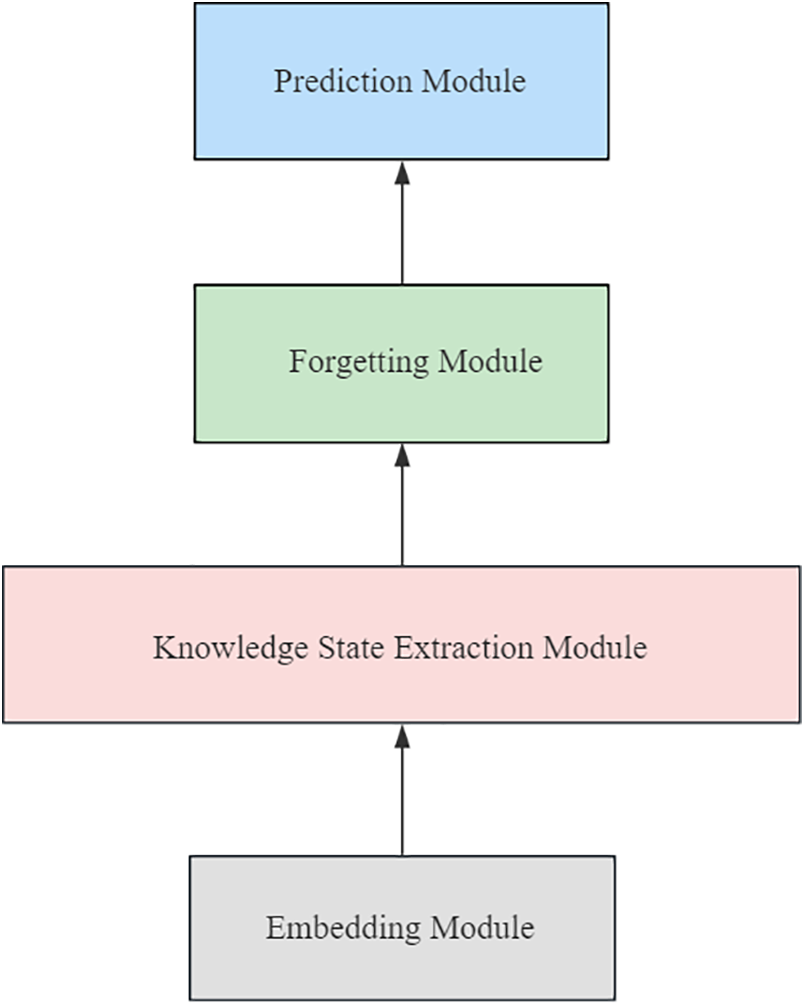
Figure 4: Framework of LFCKT

We design a module in the model for learning the degree of knowledge loss in ability computation matrix and the final output of the student’s knowledge state matrix Z∈RN×K at each time step, which N denotes the number of student interaction records and zt∈RK represents the student’s knowledge state at the moment. The probability p(t+1) that the student correctly answers the following exercise et+1 is obtained by the dot product operation of the student’s knowledge state zt with the exercise et+1 to be answered at the next step, as shown in Eq. (6).

p(t+1)=sigmoid(et+1⋅zt)(6)

where p(t+1) denotes the percentage of students answering the exercise et+1 correctly in the next moment and zt indicates the student’s knowledge mastery. sigmoid(⋅) is the mapping of the obtained probabilities to [0,1].

3.4 Exercise Selection with Expectations and Diversity

The previous section described how to select the knowledge concepts among them to match students’ learning stage preferences and progress. The LFCKT-ER has already obtained the students’ mastery of the knowledge concepts Z. This section will build on that to select the exercises that meet the students’ expected difficulty and maximize the diversity of the recommended exercises at a time. Fig. 5 shows the structure. First, the model obtains students’ knowledge mastery status according to their interaction sequences. Then, the model computes the distance between each knowledge concept mastery status and expectation in EB1, according to students’ expectation to take the top M knowledge concepts. Finally, the model combines the most diverse set of exercises recommended to students by a simulated annealing optimization algorithm [18–20].

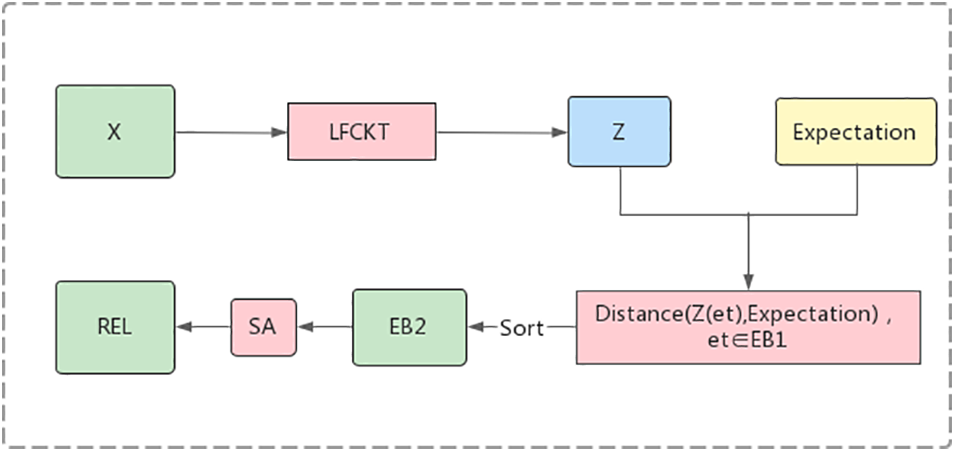
Figure 5: Process of exercise selection

3.4.1 Exercise Selection with Expectations

The primary purpose of this subsection is to select the exercise that best matches the student’s expectation of difficulty E after filtering the exercises that match the student’s learning progress and preference. After the students set their expectations (E∈[0,1]), it is critical to evaluate whether their expectations are reasonable, as shown in Eq. (7).

E={E,             if E−Ze≤β,e∈EB1E−α,      if E−Ze>β,e∈EB1E+α,      if Ze>E,e∈EB1(7)

where E denotes the student’s expectation, Ze means the student’s average mastery state of the knowledge concept e in EB1 and α, β denotes parameters, and the size of parameters verifies in the experiment section. The model will remind students to lower their expectations if their expectations are too different from their knowledge mastery. Conversely, if their expectations exceed their ability, the model will remind them to raise their expectations.

After evaluating that the student’s expectations are reasonable, the distance between the mastery state of each knowledge concept and the expectation is calculated based on the student’s expectation, and the top M exercises that are closest to the expectation are selected in order. Eq. (8) shows the formula for calculating the distance.

Dis=abs(E−pe),e∈EB1(8)

where Dis denotes the distance between the student’s expectation and the possibility of answering the exercise correctly, abs(⋅) means the absolute value, E denotes the student’s expectation, and pe denotes the student’s probability of answering the exercise e correctly at the next moment. The EB1 denotes a library of exercises filtered by learning stage preference and learning progress.

3.4.2 Exercise Selection with Diversity

After selecting the first M exercises EB2 closest to the student’s desired difficulty, the exercises which are in EB2 are combined and optimized using a simulated annealing algorithm to choose a set of exercises with the most diversity. It can be understood as a function optimization problem with multivariate conditional constraints in optimization problems. In LFCKT-ER, the model learns the representation vector of different knowledge concepts. Then the objective function of the optimization problem is to select a set of exercises with the slightest similarity to recommend to students to stimulate their learning interest as in Eq. (9).

f=∑ei,ej∈EB2,i≠jCossim(ei,ej)(9)

where f is the objective function of the simulated annealing optimization algorithm, ei, ej, denotes the exercise that is selected to be closest to the desired difficulty, and CosSim(⋅) suggests the similarity between different exercises.

The LFCKT-ER personalized exercise recommendation method selects exercises matching students’ learning progress and learning stage preferences by calculating and combining their learning progress with their learning stage preferences. It then recommends exercises to students based on their expectations of exercise difficulty. LFCKT-ER can evaluate whether a student’s expectation of exercise difficulty is reasonable and adjust their expectations accordingly. The recommended exercises can reflect students’ current learning progress and recommend various personalized exercises for students who desire a specific level of difficulty, thus enhancing students’ learning interests and abilities. The algorithm for LFCKT-ER is described in Algorithm 1.

Algorithm 1 shows the whole process of exercise recommendation by LFCKT-ER. After calculating the probability P(Kt+1) of occurrence of the students’ knowledge concepts about preferences, this probability can calculate the similarity with each exercise in the exercise bank. Then the similarity is sorted from largest to smallest. Finally, the top N exercises that best meet the conditions are selected. Then the students’ expectations are adjusted, the M exercises that best meet the expectations are computed according to the expectations, and finally, the most diverse REL is combined according to the simulated annealing optimization algorithm.

4  Experiments

We perform a multi-group experimental study to validate the validity and advantages of our model. The performance of the proposed model LFCKT-ER in computing students’ ability is compared with the performance of different methods on different datasets and the recommendation performance of the LFCKT-ER practice recommendation algorithm on various datasets.

4.1 Datasets

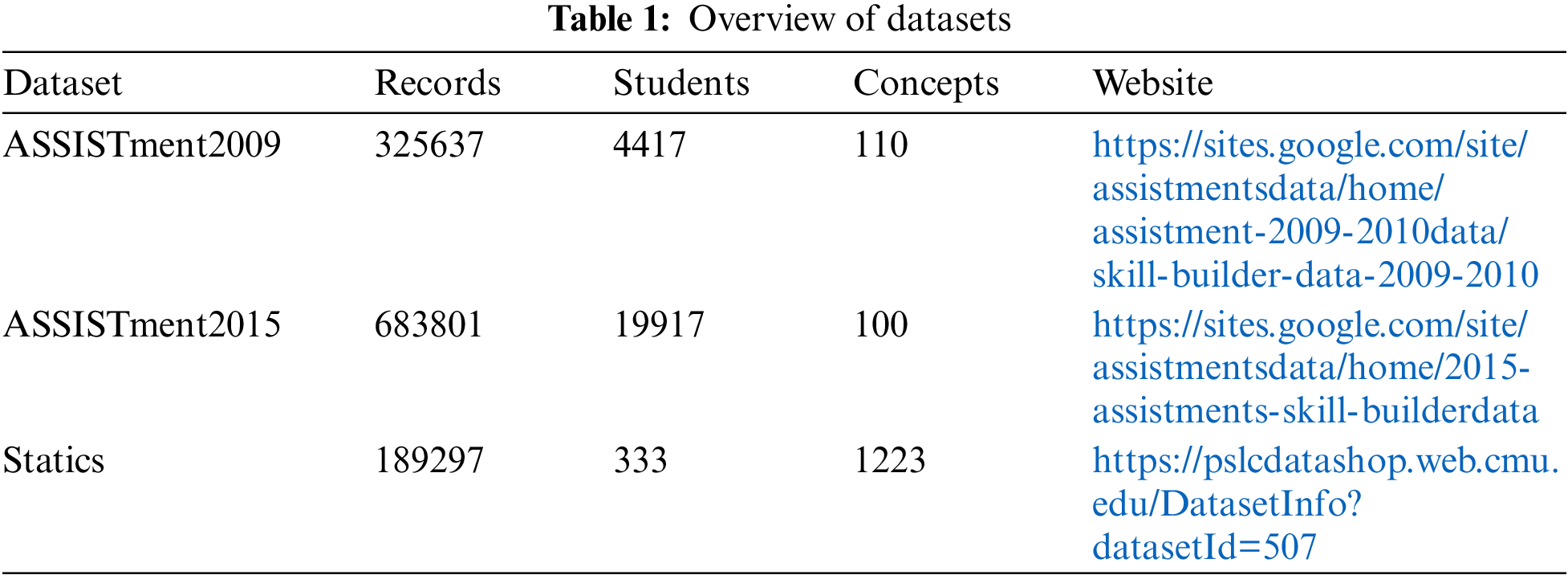
Three publicly available datasets are used to validate the validity of our experiments, ASSISTments2009 and ASSISTments2015 are elementary school math problem-solving datasets collected from the online education platform ASSISTments in 2009 and 2015, respectively. Statics2011 comes from the “Engineering Statics" course. They are widely used open-source educational datasets. Table 1 shows a brief description of all datasets.

4.2 Experimental Setup

4.2.1 LFCKT-ER Model Training

In the data preprocessing, we remove the answer records which are fewer than five, and students with more than 383 answer records were truncated to improve the performance of the model better. The parameters of the LFCKT-ER model in this paper are set as follows. The learning rate of model training is 0.003. An epoch is 50 times. Each iteration is ten rounds, the decay coefficient of the learning rate is 0.2; the dimension of exercise embedding is 100; each layer has six convolutional kernels. The initial value of the dropout rate for the set of residual modules was 0.05. LFCKT-ER has been validated for computing student ability in our previous work [17].

4.2.2 LSTM Model Training

The input dimension of the model is the amount of knowledge concepts in the datasets. When the i th bit of the vector is 1 indicates that the exercise belongs to the knowledge concept i. The datasets with less than five response records are removed in the data processing stage. Epoch set 100. To prevent overfitting, the dropout between layers sets 0.4 [21]. The dropout helps to randomly drop out some of the units in the LSTM network during training, which prevents the network from relying too heavily on any single unit or feature. This encourages the network to learn more generalizable features and reduces the risk of overfitting the training data. The optimization is performed using the Adam optimizer.

4.3 Baseline Approaches

4.3.1 Ability Computation Baseline Approach

Three typical knowledge tracking models are chosen for the comparison experiments, which are Deep Knowledge Tracing (DKT) [22], Dynamic Key-Value Memory Networks for Knowledge Tracing (DKVMN) [23], and Convolutional Knowledge Tracing (CKT) [24], and they are broadly described as follows:

DKT: For the first time, recurrent neural networks are used for knowledge tracking tasks, a classical model widely used in knowledge tracking.

DKVMN: Using dynamic key-value pair memory networks to store and update students’ knowledge states for each knowledge concept improves the interpretability of the model.

CKT: Student features are enriched by considering students’ prior knowledge and using convolutional neural networks to extract students’ learning rates when computing student states.

4.3.2 Exercise Recommendation Baseline Approach

The experiments compare the recommendation algorithm proposed in this paper with the following two baseline models, Student-Based Collaborative Filter (SB-CF) [25] and Exercise-Based Collaborative Filter (EB-CF) [26].

SB-CF: This model refers to collaborative filtering to find exciting content for specific users. In the exercise recommendation, the recommendation is based on the similarity of students. The similarity matrix among students is constructed based on their question records. Then the top 10 students with the most similar answers to the target students are identified. Then the questions of practical difficulty are extracted from the answer records of each similar student for the recommendation.

EB-CF: This model refers to the idea of recommendation by the similarity between items and uses the intrinsic quality or inherent properties of things to make recommendations. In the exercise recommendation, we set difficulty weights for each exercise based on the student’s answers to the exercises, then calculate the exercise similarity matrix and extract from it the exercises that are similar to the exercises already done, and then make recommendations based on the desired difficulty weights of the exercises.

4.4 Evaluation Metrics

4.4.1 Knowledge Tracing Evaluation Metrics

We compare our model with three other knowledge tracking models using evaluation metrics commonly used in the knowledge tracking domain, as follows:

•   Area Under the Curve (AUC) is a commonly used evaluation metric for knowledge tracking. This area is the area under the receiver operation characteristic curve that is often used to detect how accurate a method is. The larger the AUC is, the better the model performs.

•   Accuracy (ACC) is the number of correct predictions as a percentage of the overall results, and when the value of ACC is higher, it means that the model has better predictions.

•   The square of Pearson correlation (R2) can normalize relative to the variance in the data set, and is a measure of the proportion of variance.

4.4.2 Exercise Recommendation Evaluation Metrics

We use four standard evaluation metrics to compare our exercise recommendation model with others, which are as follows:

1) Accuracy

Accuracy [27,28] here refers to whether the difficulty of the recommended exercises to the students meets the students’ expectations. The higher the accuracy value, the more the recommended exercises encounter the ideal problem for the students. Here we compute the distance between the student’s expectation and the difficulty of the exercise for the student, that is, the student’s mastery of the knowledge concept, and the smaller the distance, the more consistent it is, as in Eq. (10):

Accuracy=1−∑i=0i=len(REL)abs(E−pei)len(REL)(10)

where i denotes the number of recommended exercises, REL represents the list of exercises recommended to the student, E denotes the student’s expectation, and pei denotes the probability that the student may answer correctly about the exercise ei, which is the difficulty of the exercise for the student.

2) Novelty

The second evaluation metric is the novelty [29] of the exercises; the more students’ unanswered knowledge or incorrectly answered knowledge concepts are included in the recommended exercises, the greater the wonder. We usually use the Jaccard similarity coefficient [30] to compare the similarity and difference between finite sample sets; the more significant the coefficient, the greater the sample similarity. Since we use only consider the case where the exercise contains one knowledge concept, the e(i) can then represent the knowledge concept of the i th exercise and e(i)r defines whether the knowledge concept e(i) is answered correctly, with a correct answer of 1 and a no in of 0. Thus the novelty of the recommended exercise can be expressed as Eq. (11):

Novelty=∑i=1i=len(REL)1−Jaccsim[e(i),e(i)r]len(REL)(11)

where e(i) denotes the knowledge concept of the i th exercise, e(i)r designates whether the knowledge concept of the i th exercise is answered correctly, and has been answered correctly is indicated by 1; otherwise is 0. REL denotes the list of recommended exercises at one time, and len(REL) denotes the number of recommended exercises at one time.

3) Diversity

The third evaluation index is the diversity [31,32] of the recommended exercises at a time. In the LFCKT-ER model, we learn the representation vector of each exercise, which can be understood as an embedded representation of the knowledge concept since the exercises considered in this paper contain only one knowledge concept. The variance of the diversity representation recommended exercises is expressed quantitatively by the cosine similarity between the knowledge concepts of the two exercises. The degree of difference in knowledge concepts between each exercise in the recommended list is first calculated, and then averaged to obtain the diversity value of the exercise as in Eq. (12):

Diversity=∑i=1,j=1,i≠jlen(REL)1−Cossim(ei,ej)len(REL)(12)

where e(i),e(j) denote the different exercises in the recommended list, Cossim means the calculation of cosine similarity between the exercises, REL denotes the recommended list of exercises, and len(REL) denotes the number of recommended exercises.

4) Knowledge state improvement

The fourth evaluation metric uses improving the student’s knowledge state [14] to indicate that the student wants to do the least number of exercises to get the maximum improvement in learning performance. When the number of recommended exercises is fixed, the more the student’s knowledge state improves, the better the performance of the recommendation algorithm. In this experiment, if the probability of a student answering an exercise is more significant than 0.7 [13], then we assume that the student answered the exercise; otherwise, the student answered the exercise incorrectly. After one round of recommendations, the model simulates the student’s behavior to determine how much the student’s knowledge state has improved.

4.5 Experiments and the Analysis of the Results

4.5.1 Analysis of the Results of Ability Computation

As shown in Table 2 above, our model has the best AUC and ACC values as opposed to the others, which means that our model performs better than the other three models in terms of prediction. In particular, on the ASSISTment2015 dataset, the AUC is increased by nearly 10% over DKVMN. It indicates that combining learning and forgetting behaviors in the ability computing has better prediction performance. For the internal validity of the algorithm, we employed several methods to avoid vanishing gradients and network degradation. For example, we introduced gated linear units [33] in the convolutional layers to avoid vanishing gradients and added residual connections between convolutional layers to accelerate training and avoid network degradation. For the external validity of the algorithm, we used widely used educational datasets and evaluated the algorithm’s performance by comparing it with multiple evaluation metrics and baseline methods. We found that our algorithm performed better than other methods on all three datasets in the experiments, indicating its high external validity.

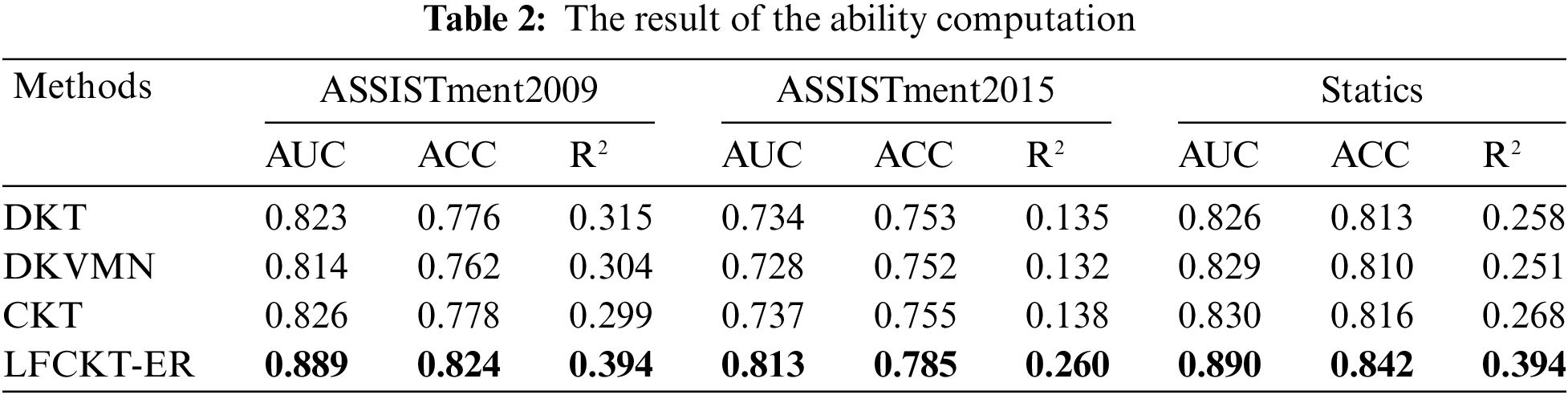
Fig. 6 below visualizes the cosine similarity of some knowledge concepts in the datasets ASSISTment2009. A darker green color indicates a higher similarity between two knowledge concepts, and a lighter green color indicates that two knowledge concepts are less similar. The numbers on the horizontal and vertical axes represent the knowledge concepts, and the knowledge concepts are illustrated at the top of Fig. 6. It can be seen that LFCKT can learn the embedding representation of different knowledge concepts better. 86 and 75 related to Volume have a higher similarity with 0.65; 89 and 99 associated with Line Equations have a higher similarity with 0.48; the others have a lower similarity.

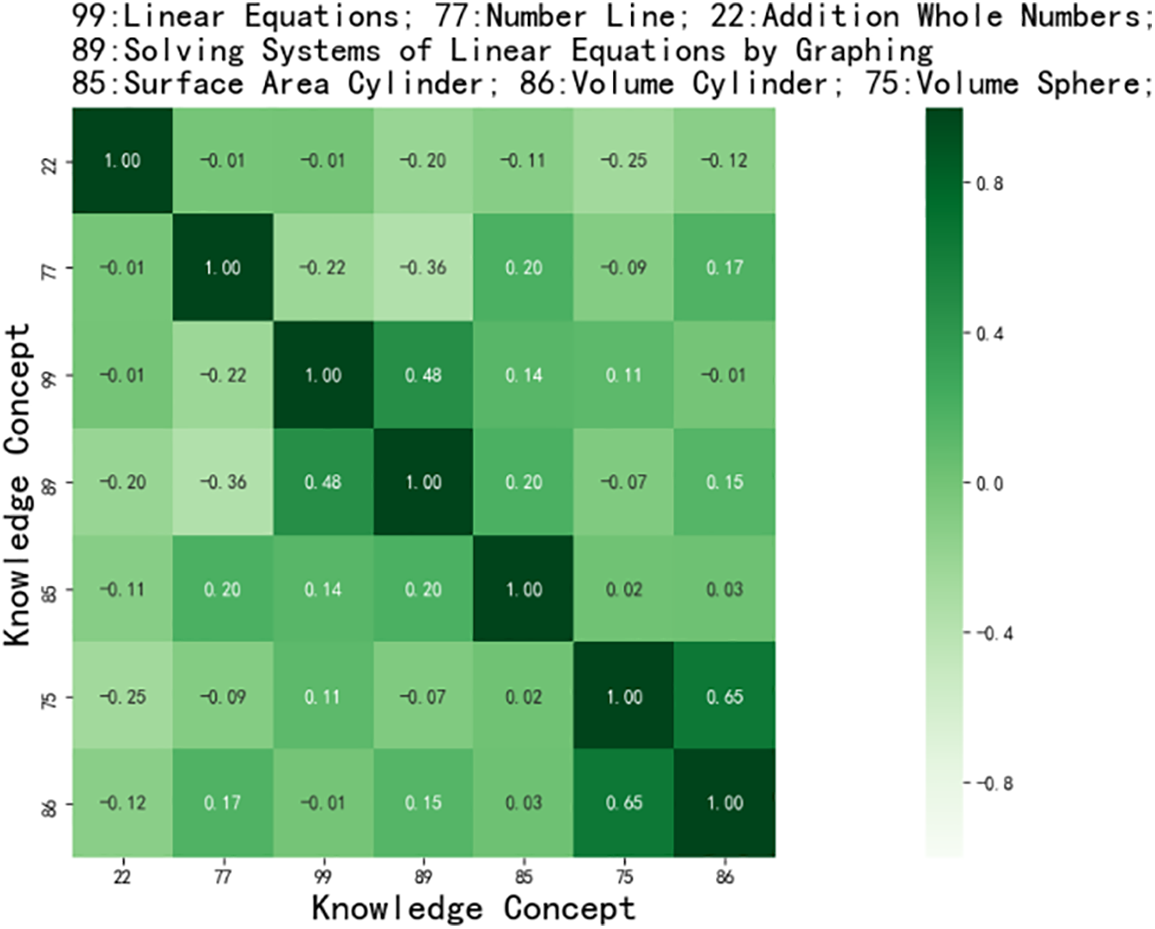
Figure 6: Similarity between exercises

4.5.2 Analysis of the Results of Exercise Recommendation

To compare each exercise recommendation model’s effectiveness, the experiment uses those mentioned three public datasets, in which 20% of the student data can test the efficacy of the recommendation model. In the exercise selection stage, the exercises can rank according to students’ knowledge mastery and students’ expectations, and the set of exercises closest to students’ expectation difficulty is selected. Then the most diverse collection of exercises is optimized using a simulated annealing algorithm for combination. The most varied group of exercises is then optimized using a simulated annealing algorithm.

Fig. 7 shows the accuracy of the recommended exercises, Fig. 8 shows the diversity, Fig. 9 shows the novelty of the exercises, and Fig. 10 shows the improvement of the student’s knowledge state.

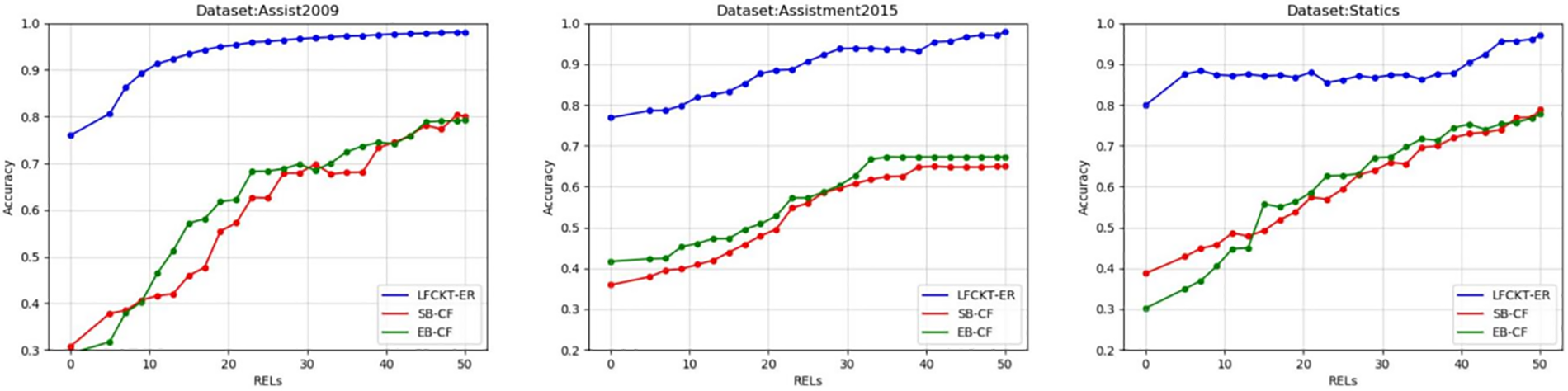
Figure 7: Accuracy of exercise recommendations

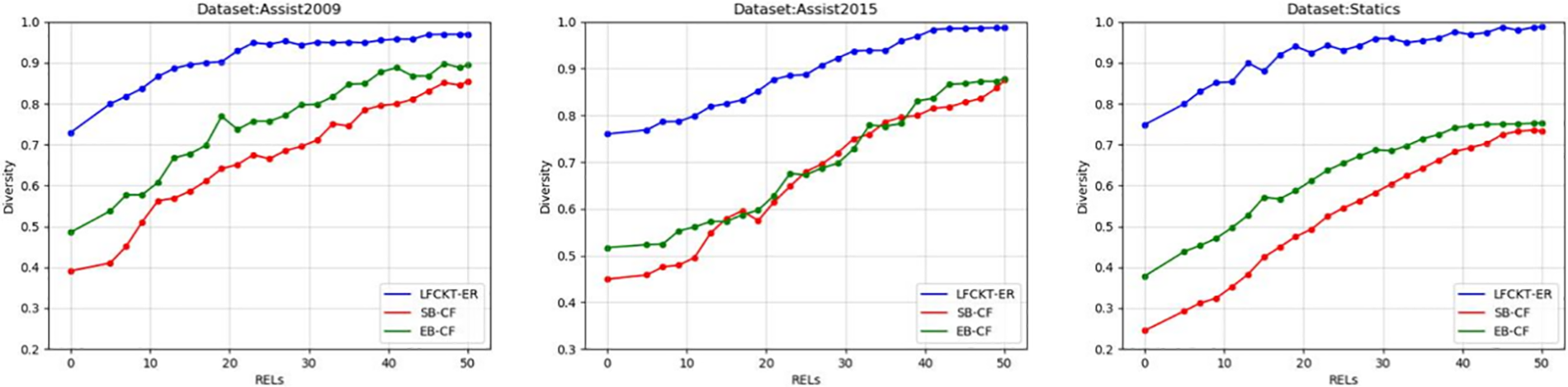
Figure 8: Diversity of exercise recommendations

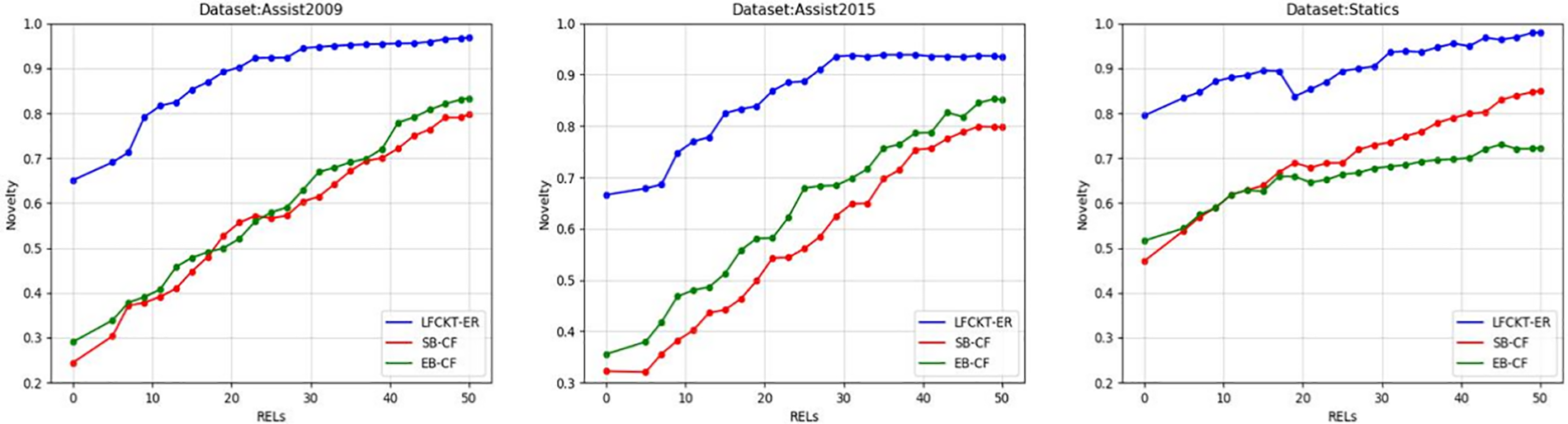
Figure 9: Novelty of exercise recommendations

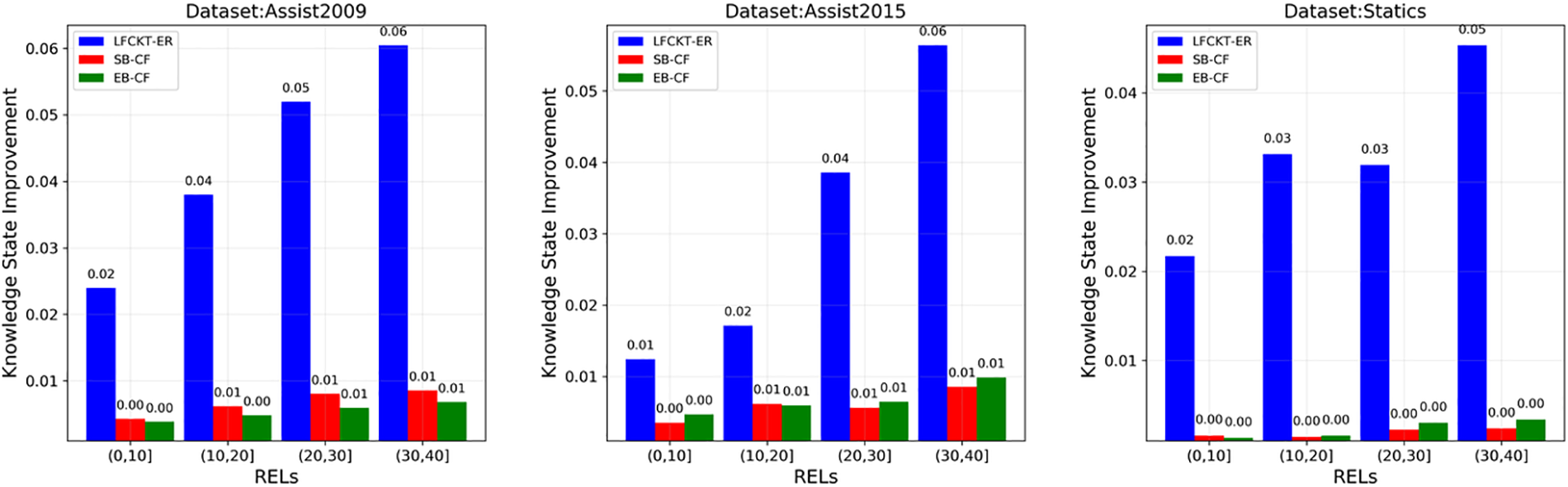
Figure 10: Knowledge state improvement after exercise recommendations

The experimental results show that the traditional exercise recommendation algorithms SB-CF and EB-CF could improve recommendation accuracy. In contrast, the accuracy of the method LFCKT-ER model proposed in this paper has significantly enhanced, proving the LFCKT model’s effectiveness in enhancing recommendation accuracy. LFCKT-ER uses cognitive computation based on a convolutional neural network, which can more accurately calculate the mastery level of students’ knowledge. Hence, the accuracy of the exercise recommendation is significantly better than the other two models.

Fig. 8 shows the recommended diversity of the exercises. The diversity results of the LFCKT-ER model proposed in this paper are about 20% higher than the other two models for the three datasets, which is due to the simulated annealing algorithm used in this paper to optimize the combination of the filtered exercises, intending to minimize the similarity between the combined exercises and maximizing the diversity of the exercises to improve student’s learning interest.

Fig. 9 shows the novelty of the recommended exercises, which shows that the LFCKT-ER model performs better in recommending the novelty of the exercises when the students’ learning stage preferences is exploration. LFCKT incorporates the attribute of a student forgetting in the cognitive computation, and the cognitive state of students changes during the problem-solving process. In the recommendation process, students are given more weight to exercises that have not been done or have a high error rate to satisfy their exploration preferences. Therefore, this model is higher than the traditional exercise recommendation algorithm in terms of the novelty of recommended exercises.

Fig. 10 shows the improvement student’s ability after doing the recommended exercises. We simulate the students’ behavior in doing the exercises. Inputting the exercises into the cognitive computational model LFCKT gives the probability that the student will answer the exercises correctly. In the simulation, we consider that a student’s likelihood is more significant than 0.7, which means the student can answer rightly. Otherwise, the student can not answer the exercise correctly. Fig. 10 shows that LFCKT-ER is much better than the traditional recommendation algorithm in improving the student’s knowledge state. This is because, in the recommendation process, LFCKT-ER considers the students’ perceptions and expectations. In the recommendation, the model will evaluate whether the students’ expectations are reasonable and help them understand themselves correctly to promote efficient learning.

We visualize the recommendations for each student, select 125 students in the datasets for recommendations, and record the comparison between our model and the other two models. Our model is much better than SB-CF and EB-CF regarding accuracy, novelty, and complexity. The model of LFCKT-ER is mainly in the ideal region. Fig. 11 shows the performance of the recommendation algorithm in terms of accuracy and diversity, Fig. 12 shows the performance of the recommendation algorithm in terms of accuracy and novelty, and Fig. 13 shows the performance of the recommendation algorithm in terms of diversity and novelty, with the points in the figure closer to the top right indicating the better performance of the model. Our model’s recommendation performance for students is closer to the upper right corner than the other two models.

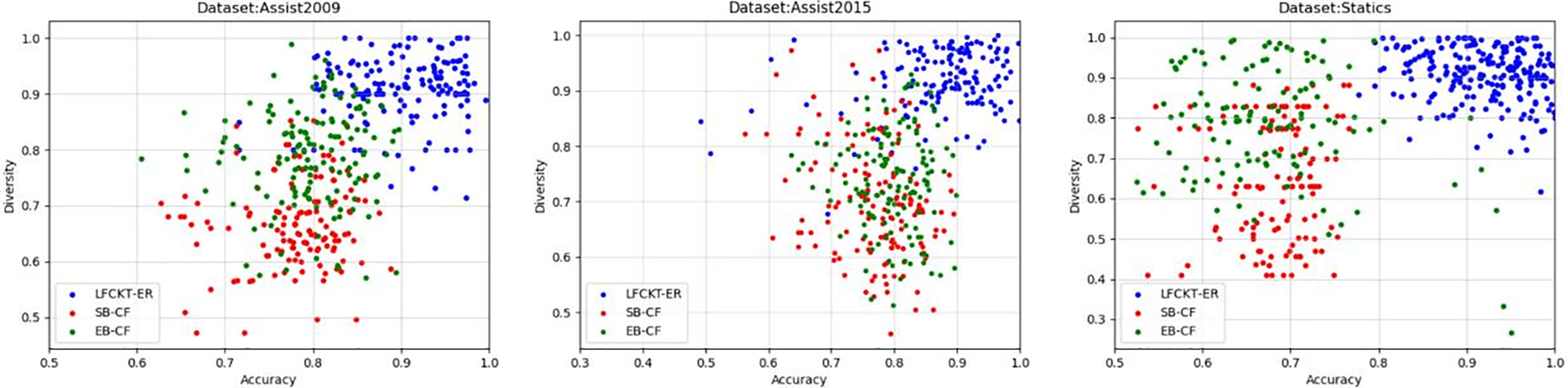
Figure 11: Accuracy and diversity compared

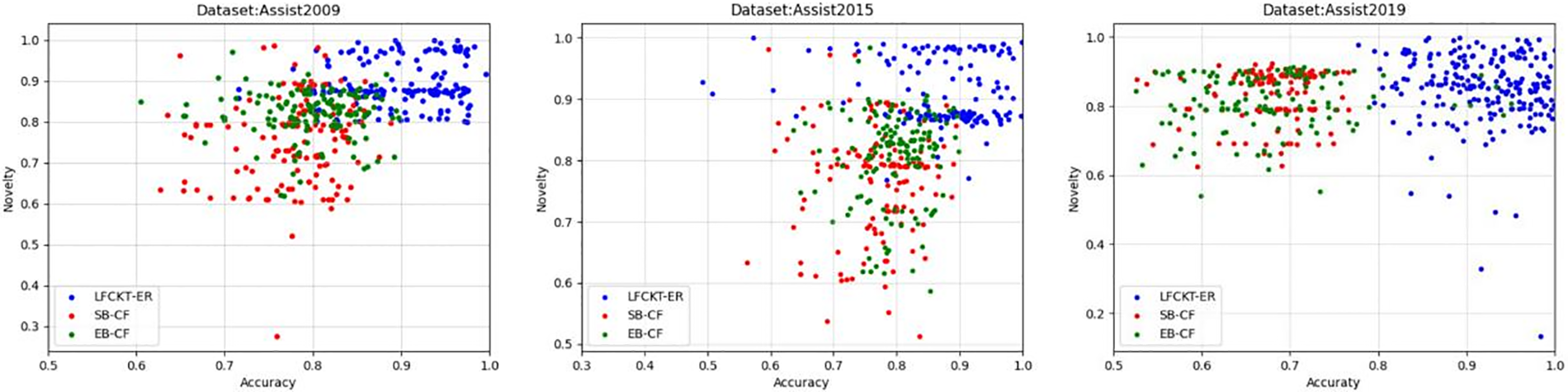
Figure 12: Accuracy and novelty compared

Figure 13: Diversity and novelty compared

4.5.3 The Results of Tune Parameters

Then, we try to discuss the effect of students’ expectations E and learning stage preferences on the recommendation performance to maximize the student’s learning efficiency at each recommendation. Accuracy, Novelty, Diversity, and Knowledge State Improvement (KSI) were metrics. When changing preferences and E, we also used other parameters REL for experiments on dataset ASSISTment2009, where Z denotes the average of the cognitively calculated student knowledge point mastery. The results are shown in Table 3:

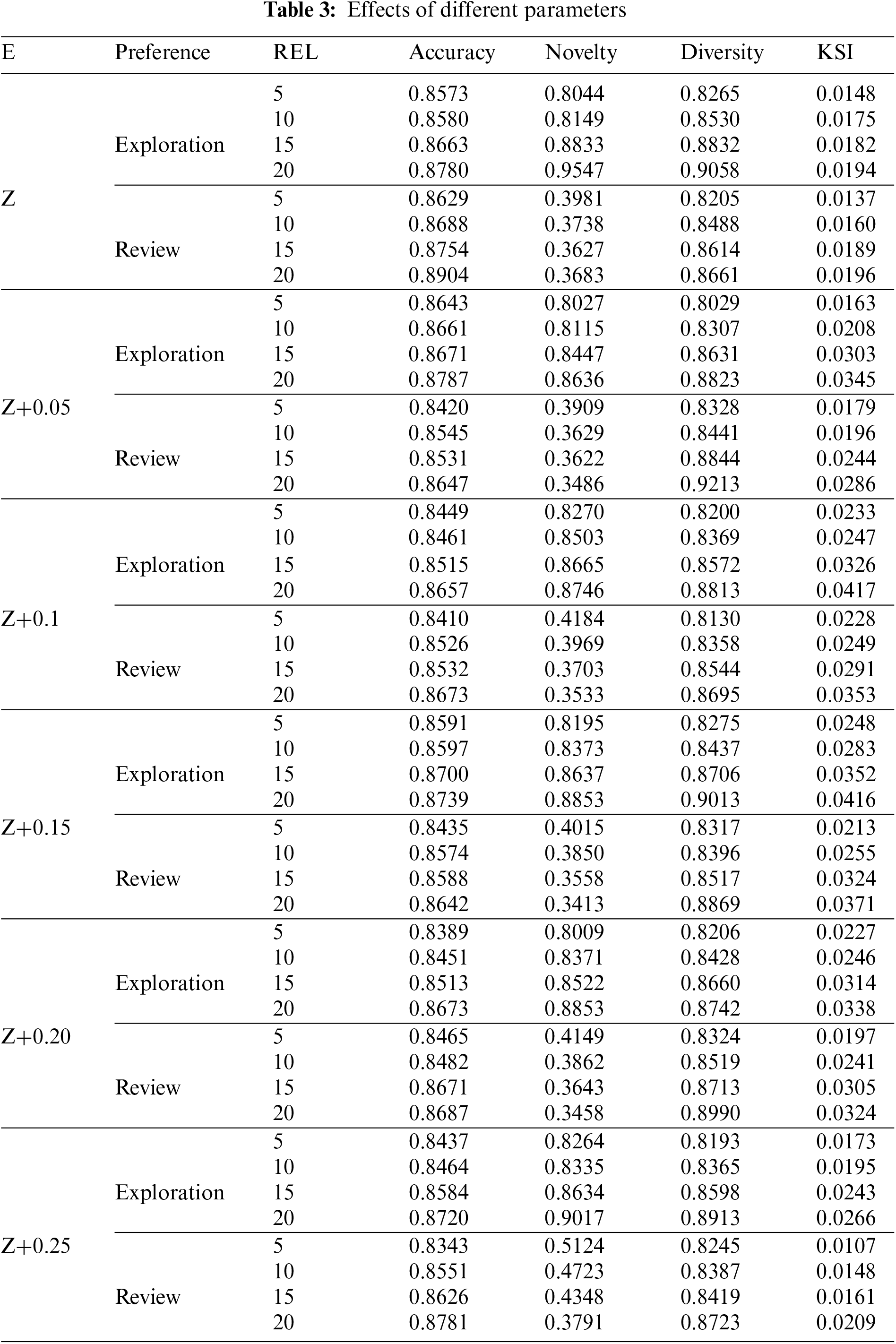
Table 3 shows that students’ expectations of the difficulty of the exercises are lower than they are. When exceeding 0.2 of their knowledge level, it was found that all four of our evaluation indicators decreased. Students’ knowledge states are steadily increasing within the vicinity of their knowledge state. This is why we have a basis for evaluating whether students’ expectations are reasonable in Eq. (7). Students will see their ability values and then adjust their expectations appropriately according to the system’s prompts to achieve an effect of improving their ability the fastest.

5  Conclusion

This paper proposes an exercise recommendation algorithm specifically designed for online learning platforms. Using students’ exercise records, the proposed algorithm calculates their ability and learning progress and incorporates their exercise learning stage preferences and students’ expectations of difficulty to generate personalized exercise recommendations. The ultimate goal of the proposed algorithm is to enhance students’ interest and competence in learning. To demonstrate the effectiveness of the proposed algorithm, we conducted simulation experiments and compared its performance with several baseline methods. The results show that the proposed algorithm outperforms the recommendation accuracy and knowledge state improvement baselines. The proposed algorithm addresses the challenge of providing appropriate exercise recommendations to students who need to complete exercises to test their mastery of knowledge points and who also need to choose the appropriate exercises based on their learning progress, students’ expectations of difficulty, and learning stage preferences. By providing tailored exercise recommendations, the proposed algorithm can better meet students’ exercise needs and help them achieve better learning outcomes. Therefore, the proposed exercise recommendation algorithm has practical value in online learning platforms and can benefit students by improving their learning experience and results.

This paper studies the effect of students’ forgetting behavior on their state of knowledge. It calculates their learning progress, learning stage preferences, and expected difficulty of the exercises in the recommendation to build a dynamic exercise recommendation system. The proposed algorithm enriches the diversity of exercises in the recommendation to meet students’ learning needs and interests to the maximum. However, there are still some rooms to improve. For example, this paper just utilized knowledge concepts instead of exercises. Although it could solve the cold exercise start [34–36] problem, limited information involved in the exercises cannot provide more accurate recommendation results. Also, this paper only utilized a limited number of tags, e.g., the number of questions answered, knowledge points, and correctness. In future work, other types of labels could also be utilized for the recommendation, e.g., the number of attempts to answer questions and the number of a student’s reviews of reference solutions.

Acknowledgement: The authors extend their appreciation to the anonymous reviewers for their constructive comments, and wish to thank Ms. Shuo Liu for her helpful suggestions in writing this paper.

Funding Statement: This research is partially supported by the National Natural Science Foundation of China (No. 62006090), and Research Funds of Central China Normal University (CCNU) under Grants 31101222211 and 31101222212.

Author Contributions: Study conception and design: Mengjuan Li, Lei Niu; analysis and interpretation of results: Mengjuan Li, Lei Niu; draft manuscript preparation: Mengjuan Li. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: Data not available due to commercial restrictions. Due to the nature of this research, participants of this study did not agree for their data to be shared publicly, so supporting data is not available.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. E. H. Chen, Q. Liu and S. J. Wang, “Key techniques and application of intelligent education oriented adaptive learning,” CAAI Transactions on Intelligent Systems, vol. 16, no. 5, pp. 886–898, 2021. [Google Scholar]

2. S. Markovitch and P. D. Scott, “The role of forgetting in learning,” in Proc. of ICML, Ann Arbor, USA, pp. 459–465, 1988. [Google Scholar]

3. J. Papoušek, V. Stanislav and R. Pelánek, “Impact of question difficulty on engagement and learning,” in Proc. of ITS2016, Osaka, Japan, pp. 267–272, 2016. [Google Scholar]

4. Z. Wu, M. Li and Y. Tang, “Exercise recommendation based on knowledge concept prediction,” Knowledge-Based Systems, vol. 210, no. 4, pp. 106481, 2020. [Google Scholar]

5. T. Y. Zhu, Z. Y. Huang, E. H. Chen, Q. Liu, R. Z. Wu et al., “A personalized test recommendation method based on cognitive diagnosis,” Journal of Computer Science, vol. 40, no. 1, pp. 176–191, 2017. [Google Scholar]

6. M. H. Shan, R. Y. Zhang and Z. Shi, “Research on cognitive computing and educational applications in the “Smart+” educational field,” Journal of Distance Education, vol. 39, no. 2, pp. 21–23, 2021. [Google Scholar]

7. G. Linden, B. Smith and J. York, “Amazon. com recommendations: Item-to-item collaborative filtering,” IEEE Internet Computing, vol. 7, no. 1, pp. 76–80, 2003. [Google Scholar]

8. D. L. Torre and Jimmy, “DINA model and parameter estimation: A didactic,” Journal of Educational and Behavioral Statistics, vol. 34, no. 1, pp. 115–130, 2009. [Google Scholar]

9. C. Z. Xing, Y. H. Liu, Y. L. Guo and J. L. Guo, “Knowledge graph convolution networks recommendation algorithm based on distance strategy,” Computer Engineering and Applications, pp. 1–11, 2023. [Online]. Available: http://kns.cnki.net/kcms/detail/11.2127.TP.20230328.1800.033.html [Google Scholar]

10. L. H. Chen and X. H. Pan, “Research on recommendation and retrieval of books based on knowledge graph and reader portrait,” Data Analysis and Knowledge Discovery, pp. 1–16, 2023. [Online]. Available: http://kns.cnki.net/kcms/detail/10.1478.g2.20230317.1312.006.html [Google Scholar]

11. R. Y. Zhang, L. Jin and H. F. Ma, “A knowledge graph recommendation model incorporating similar user influence effects,” Computer Engineering and Science, vol. 45, no. 3, pp. 520–527, 2023. [Google Scholar]

12. X. R. Ma, “Personalized exercise recommendations with deep knowledge tracking,” M.D. dissertation, Beijing University of Chemical Technology, China, 2020. [Google Scholar]

13. G. B. Zhu, Z. H. Yin, W. W. Si, L. Yan, L. G. Dong et al., “A multi-metric exercise recommendation algorithm based on student knowledge tracking,” Telecommunications Science, vol. 38, no. 9, pp. 129–143, 2022. [Google Scholar]

14. Y. He, H. L. Wamg, Y. G. Pan, Y. H. Zhou and G. Z. Sun, “Exercise recommendation method based on knowledge tracing and concept prerequisite relations,” CCF Transactions on Pervasive Computing and Interaction, vol. 4, no. 4, pp. 452–464, 2022. [Google Scholar]

15. S. Hochreiter and J. Schmidhuber, “Long short-term memory,” Neural Computation, vol. 9, no. 8, pp. 1735–1780, 1997. [Google Scholar] [PubMed]

16. Q. Shen, W. B. Guo and J. G. Lou, “Personalized recommendation model with multi-level latent features,” Telecommunications Science, vol. 38, no. 2, pp. 71–83, 2022. [Google Scholar]

17. M. J. Li, L. Niu, J. H. Zhao and Y. C. Wang, “LFCKT: A learning and forgetting convolutional knowledge tracking model,” in Proc. of IEIR, Wuhan, China, pp. 148–155, 2022. [Google Scholar]

18. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, 1983. [Google Scholar] [PubMed]

19. R. A. Rutenbar, “Simulated annealing algorithms: An overview,” IEEE Circuits and Devices Magazine, vol. 5, no. 1, pp. 19–26, 1989. [Google Scholar]

20. D. Bertsimas and J. Tsitsiklis, “Simulated annealing,” Statistical Science, vol. 8, no. 1, pp. 10–15, 1993. [Google Scholar]

21. Y. Huo, D. F. Wong and L. M. Ni, “Knowledge modeling via contextualized representations for LSTM-based personalized exercise recommendation,” Information Sciences, vol. 523, no. 7, pp. 266–278, 2020. [Google Scholar]

22. C. Piech, J. Bassen and J. Huang, “Deep knowledge tracing,” Advances in Neural Information Processing Systems, vol. 28, pp. 505–513, 2015. [Google Scholar]

23. J. Zhang, X. Shi and I. King, “Dynamic key-value memory networks for knowledge tracing,” in Proc. of Web3, Perth, Australia, pp. 765–774, 2017. [Google Scholar]

24. S. Shen, Q. Liu and E. Chen, “Convolutional knowledge tracing: Modeling individualization in student learning process,” in Proc. of SIGIR, Beijing, China, pp. 1857–1860, 2020. [Google Scholar]

25. S. Wei, N. Ye and S. Zhang, “Item-based collaborative filtering recommendation algorithm combining item category with interestingness measure,” in Proc. of CSSS, Nanchang, China, pp. 2038–2041, 2012. [Google Scholar]

26. G. Liu and T. Hao, “User-based question recommendation for question answering system,” International Journal of Information and Education Technology, vol. 2, no. 3, pp. 243–246, 2012. [Google Scholar]

27. J. L. Herlocker, J. A. Konstan, L. G. Terveen and J. T. Riedl, “Evaluating collaborative filtering recommender systems,” ACM Transactions on Information Systems, vol. 22, no. 1, pp. 5–53, 2004. [Google Scholar]

28. T. Murakami, K. Mori and R. Orihara, “Metrics for evaluating the serendipity of recommendation lists,” in Proc. of JSAI, Miyazaki, Japan, pp. 40–46, 2008. [Google Scholar]

29. M. Ge, C. Delgado-Battenfeld and D. Jannach, “Beyond accuracy: Evaluating recommender systems by coverage and serendipity,” in Proc. of RecSys, San Francisco, USA, pp. 257–260, 2010. [Google Scholar]

30. S. Niwattanakul, J. Singthongchai and E. Naenudorn, “Using of Jaccard coefficient for keywords similarity,” in Proc. of IMECS, Hong Kong, China, pp. 380–384, 2013. [Google Scholar]

31. C. N. Ziegler, S. M. McNee and J. A. Konstan, “Improving recommendation lists through topic diversification,” in Proc. of Web3, Tokyo, Japan, pp. 22–32, 2005. [Google Scholar]

32. M. Kaminskas and D. Bridge, “Diversity, serendipity, novelty, and coverage: A survey and empirical analysis of beyond-accuracy objectives in recommender systems,” ACM Transactions on Interactive Intelligent Systems, vol. 7, no. 1, pp. 1–42, 2016. [Google Scholar]

33. Y. N. Dauphin, A. Fan and M. Auli, “Language modeling with gated convolutional networks,” in Proc. of ICML, Sydney, Australia, pp. 933–941, 2017. [Google Scholar]

34. A. I. Schein, A. Popescul and L. H. Ungar, “Methods and metrics for cold-start recommendations,” in Proc. of SIGIR, Fribourg, Switzerland, pp. 253–260, 2002. [Google Scholar]

35. B. Lika, K. Kolomvatsos and S. Hadjiefthymiades, “Facing the cold start problem in recommender systems,” Expert Systems with Applications, vol. 41, no. 4, pp. 2065–2073, 2014. [Google Scholar]

36. J. Zhao, S. Bhatt and C. Thille, “Cold start knowledge tracing with attentive neural turing machine,” in Proc. of the Seventh ACM Conf. on Learning @ Scale, Berlin, Germany, pp. 333–336, 2020. [Google Scholar]