PAN-DeSpeck: A Lightweight Pyramid and Attention-Based Network for SAR Image Despeckling

1  Introduction

Synthetic Aperture Radar (SAR) is a powerful remote sensing technology that uses microwave frequencies to produce high-resolution images of the Earth’s surface. One of the challenges of using SAR is the presence of speckle noise, a random, granular pattern that appears on the images due to the interference of multiple reflections. This noise can significantly affect the quality and interpretability of SAR images, making it difficult to extract useful information [1–3]. Speckle noise is a granulated pattern that is multiplicative and can be modeled using a product model that can be represented as:

Yi=nXi 

In the above expression, Y represents the speckled degraded image, X is the clean image, n represents the noise, and I represents the pixel coordinates. During the image acquisition process, constant interference of electromagnetic waves creates speckle noise [2]. This kind of noise creates image distortion. Consequently, it is challenging to extract useful information from SAR images for various tasks like image classification, segmentation, recognition, and feature extraction [4,5]. Therefore despeckling is a necessary process for image restoration in remote sensing.

Recently, many methods based on deep learning (DL) have been proposed, and most of them have shown state-of-the-art performance in suppressing speckle noise in SAR images. DL is a new generation of algorithms that can leverage the powerful representational capabilities of neural networks. One is the convolutional neural network (CNN) which has shown state-of-the-art performance in object recognition, object classification, and many other image restoration tasks. CNN is also adopted for image-denoising tasks, and attention-guided denoising convolutional neural network (ADNET) [6] is a commonly used algorithm. Although CNN-based approaches [7] perform exceptionally well, a few limitations hinder their application in various low and high-level vision tasks. Firstly, most CNN-based methods used single-scale decomposition or single-stream CNN structure for training [8].

In the real world, images contain objects of different sizes, and their respective features are also at different scales; however, in the case of single-scale analysis, important information at other scales may be missed. Secondly, some CNN-based approaches have many parameters that limit their application for various computer vision tasks as they require more storage space [9]. Moreover, earlier CNN-based approaches adopted fixed-size receptive fields and looked for similar patterns in images, extracting global features of an image. A receptive field with different sizes can get more context information, which may be helpful in complex or heavy, noisy images. Furthermore, a complex background in an image can obscure significant features, making it difficult to extract valuable information from a noisy image [6,10]. To tackle this challenging problem, researchers have developed an innovative approach, the attentive idea aimed at extracting salient features for image applications [6,11]. The attentive idea leverages the current stage to guide the previous stage, allowing for extracting noteworthy crucial features.

Moreover, the above deep models [5,12] use the single-stream CNN structure for training. These structures cannot capture image features at various scales and hence cause loss of texture and edge details during despeckling. Also, scale variation of objects is the most frequently seen problem in low and high-level vision tasks. CNN-based approaches may encounter limitations due to their single-scale analysis, which might fail to capture crucial image details across various scales. To address this challenge, leveraging multiscale images or feature pyramids has proven effective [9,13,14]. The multiscale analysis involves processing images at multiple scales to extract local and global information, enhancing image restoration quality. This study presents a lightweight network that addresses the despeckling of SAR images. The proposed PAN-DeSpeck approach combines the benefits of pyramid-based representations for multiscale decomposition [9] with an attention mechanism [6,11]. The approach effectively removes complex background noise by focusing on the most prominent noise features, utilizing the attention mechanism. Integrating these ideas into a single network structure results in a multiscale Gaussian-Laplacian pyramid attention-based network. This network utilizes a multiscale decomposition strategy to capture local and global image features at different scales. The proposed PAN-DeSpeck network offers an effective solution for SAR image despeckling by leveraging the strengths of multiscale analysis and attention mechanisms. It enhances the restoration quality by considering local and global features and addresses the challenges of single-scale analysis.

The proposed method is composed of multiple subnetworks. First, a speckled image is decomposed into various levels using Laplacian pyramids. After the decomposition of an image at multiple levels, multiple independent subnetworks are designed. Each subnetwork comprises feature enhancement blocks (FEB) to extract local and global features of an image at various scales. Then, using an attention mechanism, the most critical components are selected to remove noise information. In each subnetwork structure, residual and recursive blocks are used to reconstruct a Gaussian pyramid for each level in a recursive manner. Each subnetwork is trained using its loss function based on its desired physical properties.

Furthermore, the review of past work within the domain of despeckling reveals that no method utilizes Laplacian Gaussian pyramids for multiscale decomposition, unlike the Feature Enhancement Block (FEB) and Attention Block (AB) for extracting multiscale features.

A lightweight PAN-DeSpeck network is proposed to overcome the limitations mentioned earlier and harness the advantages of multiscale decomposition and feature enhancement. This network is designed with reduced parameters to enhance the despeckling performance. Fig. 1 illustrates the effectiveness of the proposed PAN-DeSpeck network in SAR image despeckling.

Figure 1: Despeckling result for PAN-DeSpeck network

The result of the proposed PAN-DeSpeck network for SAR image despeckling is illustrated in Fig. 1.

The main contributions of the proposed PAN-DeSpeck network are as follows:

•   A lightweight multiscale image decomposition strategy based on a mature Gaussian-Laplacian pyramid and attention network is proposed to perform multiscale image analysis of a speckle image with only 7 K parameters achieving high despeckling performance.

•   Feature enhancement using Feature Enhancement Block (FEB) is performed to increase the expressive ability of the despeckling model.

•   Multiscale feature extraction for each pyramid level using Attention Block (AB) is performed. AB is used to extract speckle information hidden due to the complex background of the image.

•   Residual and Recursive blocks are incorporated in each subnetwork to share weights among each level to accelerate training speed.

•   Extensive experiments have been conducted on the virtual SAR dataset using various image restoration techniques. The proposed study stands out as no benchmark scheme has ever performed despeckling on this dataset.

The remainder of the paper is organized as follows. Section 2 provides a detailed summary of the literature on image denoising/despeckling problems. Section 3 presents the proposed methodology. Section 4 explains the experimental setup, including quantitative and visual comparisons with State-of-the-art image restoration methods. Additionally, this section presents significant research findings derived from the comparisons.

2  Literature Review

This section reviews the literature on image despeckling, encompassing image denoising and other image restoration domains. The weaknesses and limitations of existing approaches are discussed, which are the focus of this work.

2.1 CNN-Based Approaches for Image Denoising/Despeckling

In digital image processing and computer vision, image denoising is considered an ill-posed inverse problem [15–20]. Image denoising aims to remove the noise from an image and restore a latent clean image. Many algorithms in literature have been proposed for machine learning and DL [21–23] that promise a new generation of algorithms that can leverage the powerful representational capabilities of CNN [24–26] to recover the underlying ground reflectivity more faithfully. Inspired by DL’s powerful stuff, many researchers used DL in the image despeckling domain to avoid handcrafted features, producing well-optimized algorithms. In [5], a U-Net-based encoder-decoder architecture is proposed explicitly for SAR images. The proposed method is highly capable of preserving spatial details of images by extracting features at various scales. However, as the model is trained on a synthetic dataset with few noise levels, it may hinder its applications for blind noise. Irrespective of features extracted by the network for high-level vision tasks, image despeckling [26] requires full texture detail of the image to make network propagation more accurate.

2.2 Attention Mechanism

Recently, several innovative methods have adopted attention mechanisms to extract essential features of an image. Initially, attention was designed in a non-local way where each image’s global dependencies can be drawn via each pixel in an image. Inspired by the fact that attention can focus on crucial features while ignoring others, attention has been applied in the image processing domain to extract relevant features and improve network performance. An attention mechanism is introduced to enhance the features and improve expressive ability, as described in [6]. This mechanism involves utilizing a single attention layer in the current stage to train the previous stage in learning noise distribution.

The proposed PAN-DeSpeck network uses FEB to enhance the expressive ability of the denoising model via feature enhancement block and then extracts relevant features via AB. However, specific noise levels and an enormous number of parameters are a few limitations of the current study. Moreover, when trained on a virtual SAR training set, this technique creates blurry artifacts in some regions. Another attention-based method, called hybrid dilated residual attention network (HDRANet), is proposed in [11], which introduced a convolutional block attention module (CBAM) combined with residual learning and dilated convolution. In [27], image classification based on squeeze and excitation (SE) block using channel-wise attention is proposed. To collect global information, the global pooling layer, followed by convolution layers, is used to compute channel attention weight. In [28], residual channel attention networks (RCAN) are introduced to tackle the problem of image super-resolution. In [29], dilated convolution combined with channel-wise attention was used to tackle the problem of vanishing gradient that originates due to the increase in network depth.

A deep residual non-local attention network (RNAN) was proposed in [30] to improve the representation ability of the network. This method aims to tackle the flaws of existing image restoration methods, where channel and spatial features are equally treated. Also, these methods have strict restrictions on local convolutional operation. In [30], regional, non-local, and attention-based methods are introduced to capture long-range dependencies. In [31], the single-image dehazing problem is resolved based on channel-wise and pixel-wise attention, which significantly improves the overall performance of the dehazing network. In [32], a channel attention module was proposed to extract information from multiple receptive fields and local and global features aggregated inside channels to address the scale variation problem.

2.3 Pyramid Networks

Since images contain objects of varying spatial complexity, the most flexible way is to incorporate image pyramids [9,32] in a learning framework. In pyramid representations, input images are decomposed into multiscale representations, and the desired task is performed against a specific scale. Pyramid representations involve decomposing input images into multiscale representations, allowing the desired task to be performed at a specific scale. Different pyramids, such as Gaussian, Laplacian, and ratio pyramid networks, can be constructed using various kernels. This multiscale decomposition is adapted to preserve spatial scales of images. In [33], the pansharpening problem using pyramid networks and a shallow CNN with fewer parameters is proposed to get high-frequency components of images. For low-light image enhancement, a lightweight pyramid-based network structure [34] is proposed that uses a fine-to-coarse strategy to mimic natural lighting. Likewise, reference [35] adopted CNN using Laplacian pyramids for image super-resolution at scale.

A unique pyramid-based attention network is proposed in [36] for Image restoration to adapt better generalization capability, where spatial image information is processed at each scale to capture long-range dependencies. In [37], a solution is presented to tackle the issue of blind denoising. The proposed approach is called the pyramid real image denoising network (PRIDNet), which encompasses key components such as channel attention, pyramid pooling, and a feature fusion stage. The first stage employs noise estimation using channel attention; in the second stage, multiscale features are extracted, and then feature fusion is performed using kernel selecting operation. In [15], to tackle the problem of various noise levels, a CNN auto-encoder network with a feature pyramid is proposed for additive white Gaussian noise (AWGN) suppression. A pyramid-aware network was proposed in [32] for blurry image restoration. The network exploited both self and cross-scale similarities. The proposed network comprises two modules: Self-Attention and Pyramid Progressive Transfer. The latter is used for feature fusion using spatial and self-attention modules.

3  Proposed Methodology

This section presents the speckle noise model and the proposed PAN-DeSpeck network for SAR image despeckling. The proposed PAN-DeSpeck network comprises a mature Laplacian-Gaussian pyramid network, which uses an additional subnetwork structure consisting of a feature enhancement block (FEB) and attention block (AB). The residual and recursive blocks are significant components of this proposed system. The details of features used in the proposed approach are discussed below.

3.1 Speckle Noise Model

From an image processing perspective, speckle noise can be regarded as multiplicative noise, where the resultant signal is the product of noise and speckle-free signal. The multiplicative nature of speckle noise can be stated as a multiplicative noise model [5,26]. The speckle noise model can be defined as:

Yi=nXi

where “Y” represents a speckled degraded image, “X” represents a clean image, “i” represents SAR image pixel coordinates, and n represents speckle noise. The speckle noise model can help smooth images in uniform regions depending on the signal. The local variance-to-mean ratio checks whether the improved pixel is within a uniform area. When the speckle is less than the local variance to the mean ratio, that pixel is usually regarded as a resolvable object, else it is assumed to be in the uniform region and will be smoothed. The overall speckle noise model follows a gamma distribution with mean and variance of (1 and 1/L), which can be defined as:

 P(N)=1Nτ(L) (NL)L ϵ−NL , N≥0,L≥1(1)

In Eq. (1), Γ(L) represents the function of the gamma distribution, and “L” means the number of looks of the SAR images.

3.2 System Model of PAN-Despeck Network

This section presents the proposed methodology and the system model, encompassing various components of the proposed method. Fig. 2 illustrates the system model specifically designed for speckle noise removal. The primary workflow of this system involves taking a speckle noise as input and applying a pyramid-based structure to divide it into multiscale representations. Subsequently, a subnetwork is depicted at each image scale, which is further expanded upon. Detailed workings of the subnetwork are illustrated in Fig. 3.

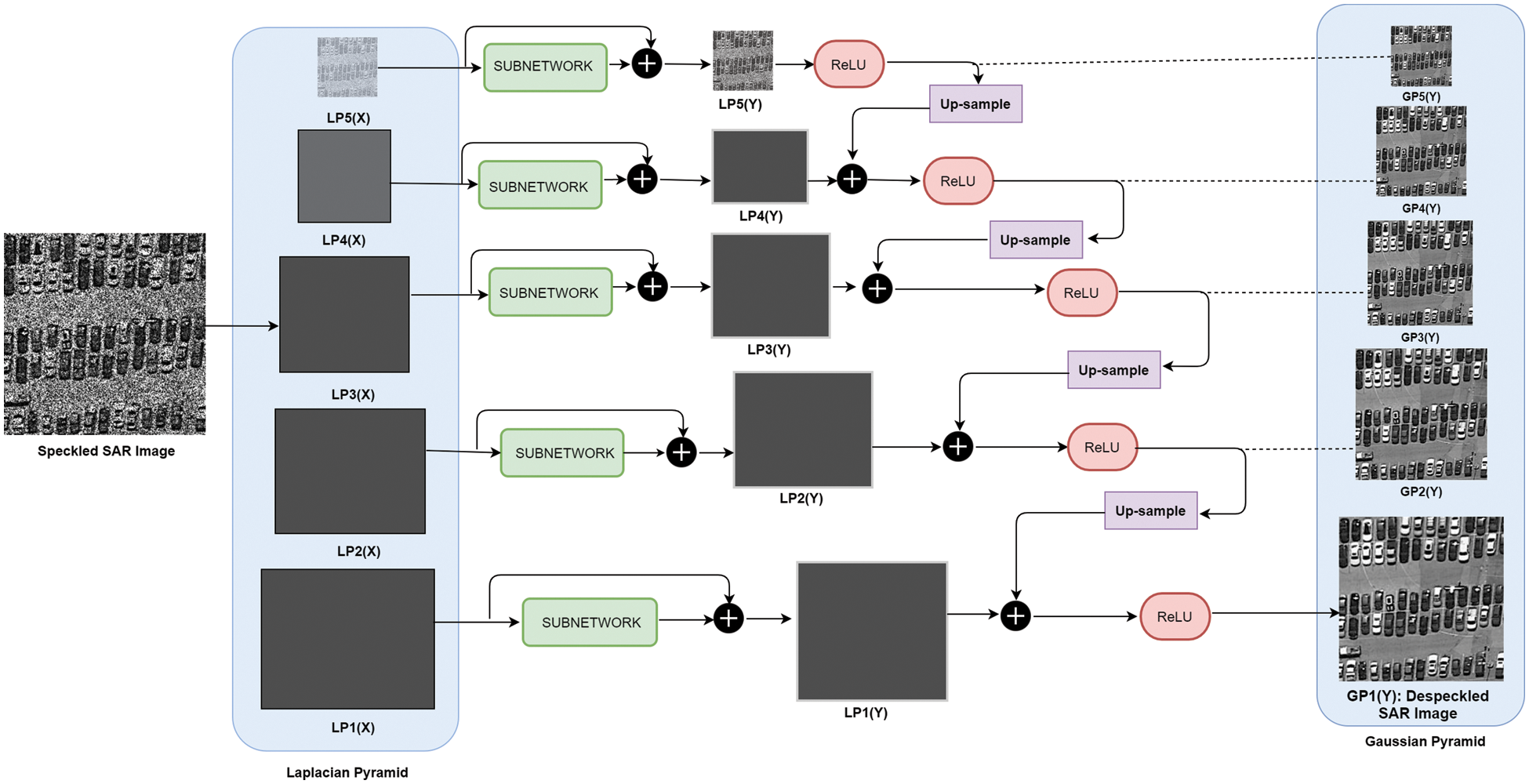
Figure 2: System model of PAN-DeSpeck network

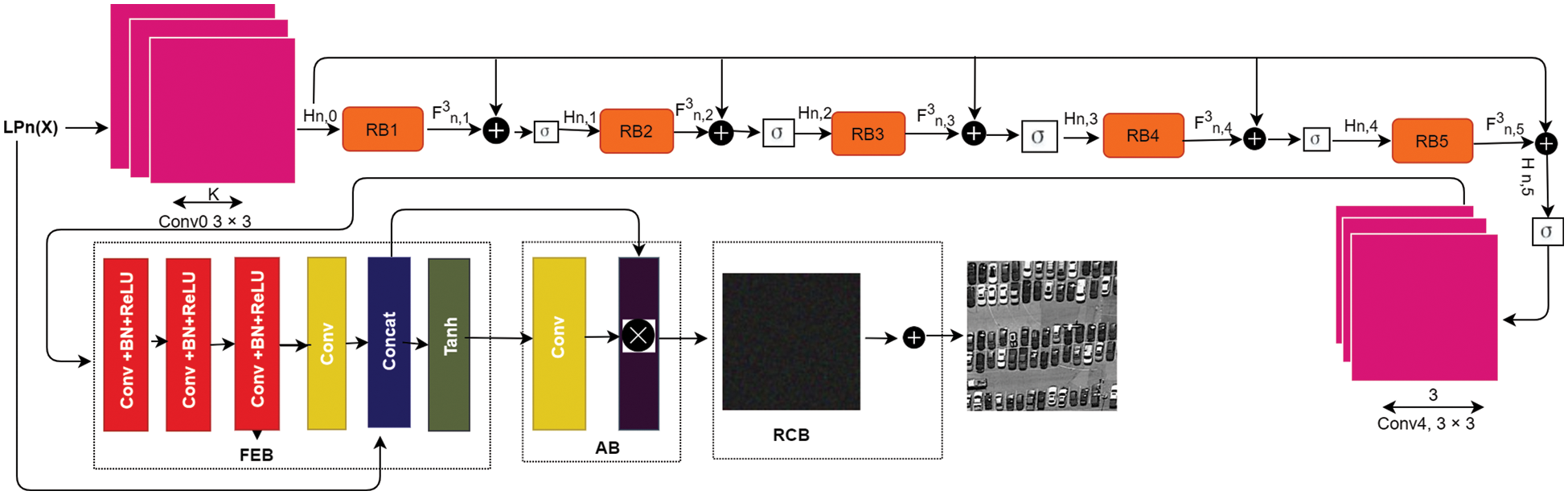
Figure 3: PAN-DeSpeck subnetwork structure

3.2.1 Laplacian Pyramid

In general, images are scale variants; objects and features in an image (patterns, shapes, edges) are located at different scales and spatial locations. Hence, there is a need for multiscale feature fusion techniques that can be applied using pyramid representations. The pyramid representations divide an image into different scales and levels, where the top level represents the original image, and the bottom level stores the image details. The Laplacian pyramid is a multiscale decomposition technique; the main idea is to decompose images into their respective low and high-frequency band to reconstruct an original image. It is similar to the Gaussian pyramid; however, the different images or blurred versions can be saved at each level. A speckle image X is decomposed into its Laplacian pyramids. The decomposed image comprises a set of images L with N levels, which can be defined in Eq. (2).

LPn (X)=GPn (X)−GPn−1 (X)∀ GPn−1 (X)=↑(↓GPn ′(X))(2)

Unlike previous image restoration methods, the Laplacian pyramid adopts a multiscale decomposition strategy using fixed smoothed kernels. The top level contains detailed background information of a given speckle image, while other levels have spatial information of an image at multiple scales. Performing a multiscale decomposition of the image helps simplify the problem and take advantage of sparsity. Additionally, in the Laplacian pyramid, the computational cost is reduced by predominantly utilizing Gaussian filtering.

3.2.2 Subnetworks

A set of independent subnetworks is built for each pyramid level to generate a clean Gaussian pyramid against each input Laplacian pyramid level. The proposed subnetwork structure comprises FEB, AB, recursive, and residual blocks. The detail of each component of the subnetwork is described below:

Feature Enhancement Block (FEB)

According to [6], the effect from shallow to deep layers is weakened as the network depth increases. A proposed solution is a simple network structure composed of four layers. Inspired by this, the proposed approach utilizes four layers of Feature Extraction Block (FEB) in each subnetwork to combine local and global features of an image, aiming to improve the despeckling performance. The FEB takes input from the nth level of an image and concatenates the extracted features with the original input image to extract both local and global features. The FEB block consists of four layers: three convolutional layers, Batch Normalization (BN), ReLU activation, and one convolutional layer.

The convolution operation is mathematically represented as follows in Eq. (3):

Yi,j,k=σ(∑m=1M∑n=1N∑c=1CXi+m−1,j+n−1,c⋅Wm,n,c,k+bk)(3)

where:

•   Yi, j, k represents the kth filter’s output feature map at position (i, j).

•   σ represents the activation function.

•   Xi + m − 1, j + n − 1, c denotes the pixel intensity of the input image at position (i + m − 1, j + n − 1).

•   Wm, n, c, k represents the weight of the filter at position (m, n).

•   bk is the bias term associated with the kth filter.

The main objective of the PAN-DeSpeck network is to enhance the expressive ability of the despeckling model by combining local and global features through a long path. In the proposed study, this objective is accomplished by integrating the speckled image (representing global features) with the output of the convolution layer (representing local features), forming a long path.

Attention Block (AB)

Due to its limited size, the convolution kernel can only compute target pixels based on local information. Consequently, there is a risk of information loss due to the absence of global data. Based on its paring covariance, if each pixel in the feature map is treated as a random variable and the paring covariance is determined, the predicted pixel’s value can be increased or decreased. Each pixel’s value may be increased or reduced depending on its closeness to other pixels in the image. Self-attention employs identical pixels in training and prediction while ignoring distinct pixels. A complex background in real noisy images or blind noisy images like speckle noise can hide essential features of an image, which may create additional difficulty in training [6].

Earlier CNN-based approaches calculate target pixel information using local neighborhoods so that they may miss important details of an image. Different variants of attention modules are used to tackle this issue in the literature. In literature, the attention module [6,11] is used to get important noise information for an image in case of real or blind noise. Motivated by this idea, we independently use the attention module in each subnetwork for SAR image despeckling and the Laplacian pyramid. The proposed attention mechanism works in two steps; the proposed convolution layer of the attention block takes the output of FEB as input. Then feature vector (weights) for obtained features is constructed to help guide the current stage via the previous stage. Then the obtained weights in the second step are multiplied with the output of the convolution layer of FEB to extract more dominant speckle features.

Recursive Blocks

Deeper networks are of prime importance in neural network (NN) architectures. However, very deep networks are more challenging to train with more stacked layers. Moreover, an intense network faces the problem of vanishing gradient during backpropagation. The recursive and residual blocks concept was introduced in [9,37] to tackle the problems mentioned above. Using residual and recursive blocks accelerates the training speed, resolves the vanishing gradient problem using skip connections [9], and reduces the number of parameters using parameter sharing between blocks. Although mapping problems have already become more manageable using the Laplacian pyramid. However, image information may need to be recovered during feed-forward convolution operation. Skip connections are used in each recursive block for this purpose.

The proposed approach adopts recursive blocks to create a lightweight network and introduces an intermediate layer that operates recursively. This design choice ensures a reduction in network complexity while maintaining its effectiveness.

3.2.3 PAN-DeSpeck Sub-Network Structure Details

In the proposed subnetwork, first, the speckled image is decomposed into different levels LPn(X), using the Laplacian pyramid, and then to reconstruct the despeckled Gaussian pyramid GPn(Y), an independent subnetwork structure is designed for each level, and then features are extracted from the nth input level for each scale. After removing features, recursive and residual blocks are used in each subnetwork, where an intermediate inference layer is used recursively to share and reduce the number of parameters. The proposed approach utilizes five recursive blocks within each subnetwork, and the number of parameters stays the same with an increase in the number of blocks due to parameter sharing.

In each recursive block, three convolutions operations are introduced, and the output feature map for the ith recursive block can be calculated by adding the output feature map of Hn,o. After getting the features from the nth input level, those features are fed to the FEB. As proposed, the FEB block consists of four layers of architecture. The first three layers are CON, BN, and ReLu, respectively, while the last layer is composed of a convolution layer followed by the Tanh activation function. After applying the nonlinear function Tanh, the output of FEB becomes the input of the proposed one-layer attention block where 1 × 1 convolution operation is used, and hence obtained features are transformed into a weight vector to adjust the previous despeckling stage that may help in improving the despeckling performance.

After compressing obtained features into a weight vector, those weights are multiplied by the output of the convolution layer of FEB to get robust feature representation LPn(X).

GPn(Y )=LPgn(X)+↑ GPn−1(Y )(4)

Finally, the synthesis operation recursively produces the clean image at each scale depicted via Eq. (4).

3.2.4 Loss Function

Mean square error (MSE) loss [6,38,39] is the most popular loss function for image restoration problems. However, MSE-based losses impose a squared penalty [9] on pixel values, due to which over-smoothed results are generated. To tackle this problem and learn semantic dependencies between pixels, Structural Similarity (SSIM) and L1 losses are introduced in [9]. The proposed study has adopted the same loss functions for each image scale as most research studies have used this function. Finer levels are trained using SSIM and L1 loss, while coarser pyramid levels are trained using L1 loss. Each subnetwork comprises AB and FEB, which helps to enhance and extract local and global features. Moreover, in the backpropagation step, the finer-level gradient can flow toward coarser pyramid levels, which helps to update the desired parameters. Thus, the proposed lightweight PAN-DeSpeck network, while using SSIM and L1 losses, can achieve better performance than other deep models with enormous parameters and MSE loss.

3.2.5 Pseudocode of PAN-Despeck Network

In Algorithm 1, the pseudocode of the PAN-Despeck network is represented. A speckled image is input to the model. The input image is then decomposed into multiple scales and levels using LP. Once this decomposition is done, a subnetwork is defined for each scale. The subnetwork structure uses AB, FEB, and reconstruction block (RB) to reconstruct a clean LP version at each scale. Finally, the synthesis process reconstructs the Gaussian pyramid of the despeckled SAR image.

4  Experimental Setup

4.1 Dataset

The IEEE data port’s Virtual SAR dataset [40] is utilized, which consists of 31500 images, each with a size of 256 × 256 pixels. The dataset comprises clean and noisy references for training with variable kinds of speckle noise instead of fixed noise levels. Varying levels of noise are added to generalize the dataset well. The SAR training data set is divided into patches of 80 × 80. Dividing images into patches helps get more robust features and helps in improving the efficiency of despeckling [41]. As the entire dataset contains 31500 images, we have divided the dataset into training and testing sets, among which 22,050 images are used for training and 9,450 for testing. Data augmentation is also performed to train the model better, and images are flipped and rotated at various angles. Furthermore, since the proposed approach utilizes multiscale decomposition, the proposed model is trained separately for each scale to ensure the preservation of the spatial scale of an image.

4.2 Training Details

The proposed model is trained using TensorFlow GPU 1.14 on the NVIDIA Tesla P4 GPU of Google Colab. The Adam optimizer with a learning rate 0.001 and a batch size of 10 is employed. The number of training epochs is set to 50.

5  Experiments

PAN-DeSpeck results are compared with various image restoration techniques to validate the results effectively. The virtual SAR dataset is used for training and testing. The results of the proposed method are compared to the following five image restoration methods ADNET [6], lightweight pyramid network (LPNET) [9], Non-local CNN [12], AEFPNC [15], and batch renormalization using deep CNN (BRDNET) [38]. The proposed PAN-DeSpeck and all comparison schemes share the same training dataset (Virtual SAR) and use the nonlinear function Leaky ReLU with a batch size of 10 and a learning rate of 0.0001. The dataset used in the proposed method already contains clean and speckle image pairs with variable kinds of speckle noise. Hence, noise models for comparison schemes are slightly modified for the approaches above. For a fair comparison, all methods are retrained on the virtual SAR dataset.

Fig. 4 shows visible results for the proposed scheme on the SAR dataset. The results suggest that the proposed system achieves an outstanding performance in removing speckle noise and restoring an image with sharp edges and fine texture details.

Figure 4: Visual results for the proposed network

In Figs. 5–7, comparisons of the proposed scheme are shown with other state-of-the-art methods. The first image represents a noisy input image; the rightmost image is the ground truth image. In [6], the despeckling performance is very close to the ground truth image. It removed the speckle from the image entirely, and the restored image is sharp. However, in contrast with ground truth and the proposed scheme, it hides the necessary details in a few parts of images by creating a blur effect. In [38], the despeckling performance regarding artifacts reduction and sharpness could be better. The performance of AEFPNC [15] is average; the image’s resolution is low, while blurriness is also noted. Another non-local method [12] creates bluer artifacts in the despeckled images. Another reason behind the average performance of the approaches mentioned above is the use of MSE-based loss, which makes edges seem over-smoothed.

Figure 5: Comparison of various image restoration methods on the SAR dataset with the proposed network

Figure 6: Comparison of various image restoration methods on the SAR dataset with the proposed network

Figure 7: Comparison of various image restoration methods on the SAR dataset with the proposed network

With fewer parameters, the baseline approach [9] shows excellent performance in suppressing speckles using multiscale decomposition of images; however, it creates a blur effect in a few images while despeckling. In contrast, with the comparison above, the proposed PAN-DeSpeck performs visually and quantitatively outstandingly.

The advantage of the proposed scheme is twofold. The CNN-based approaches [39,40] used MSE loss, whereas we used combined SSIM and L1 loss that helps in addressing the over-smooth issue created due to squared penalty in MSE. Another reason is using FEB at multiscale pyramid levels, which helps extract local and global information at each level. Later from these extracted features, the most prominent noise features are extracted using an attention module that may be hidden due to the complex background. The multiscale attention modules also help in getting similar patterns in an image. Using residual and recursive blocks helps increase training speed and reduce the number of parameters. Hence, the proposed network, with fewer parameters than the approaches above, which have many parameters, shows state-of-the-art performance in suppressing speckle noise from SAR images. At the same time, a nice balance is maintained between despeckling performance and texture preservation.

5.1 Quantitative Measures

The most widely used measures for quantitative analysis are peak signal-to-noise ratio (PSNR) and SSIM [9,39,41]. The higher values of the Structural Similarity Index (SSIM) and PSNR [42–44] represent the better quality of the restored or despeckled image.

Table 1 compares the proposed approach results with other state-of-the-art image restoration approaches, where PSNR and SSIM-based fair comparison is performed on a virtual SAR dataset.

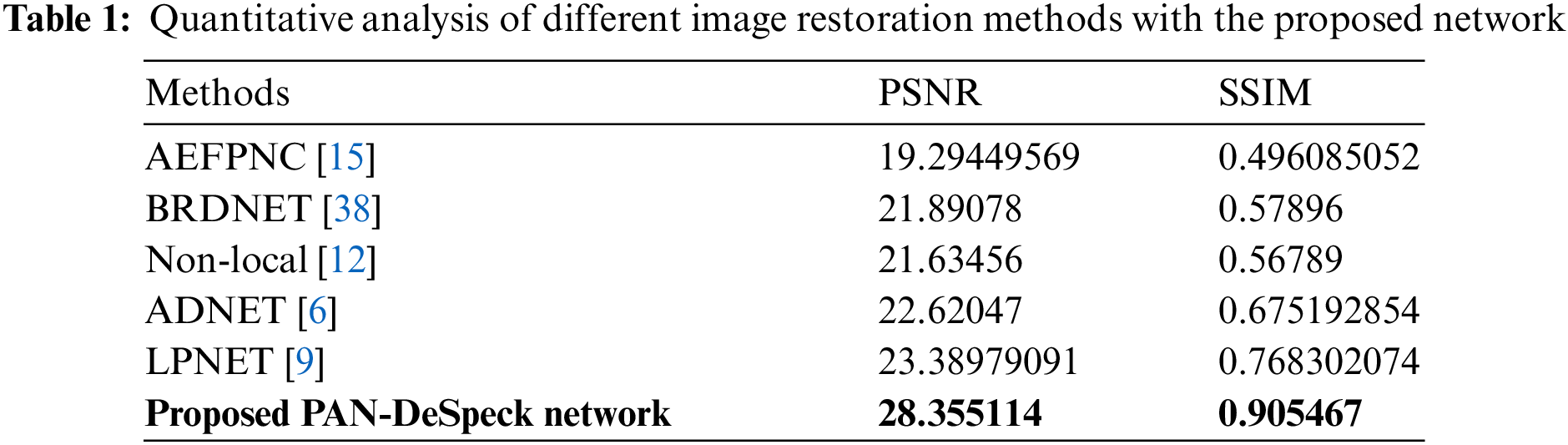
Table 2 also analyzes the proposed approach with and without recursive blocks. From the comparison, it has been interpreted that the use of recursive blocks in a network can share parameters among each level. As a result, several parameters can be reduced. The proposed scheme is also trained without the usage of recursive blocks. Instead of recursive blocks, eight layers of sparse blocks are adopted in each subnetwork. As pyramids also enlarge the receptive fields, the concept of pyramids is used instead of dilated convolution layers. The results with and without recursive blocks differ in performance. Still, without recursive blocks, there is a massive increase in the number of parameters compared with recursive blocks, directly or indirectly increasing storage costs.

Table 3 compares the proposed scheme with other approaches regarding several trainable parameters. The proposed scheme performs better and does this with fewer parameters.

5.2 Parameter Settings

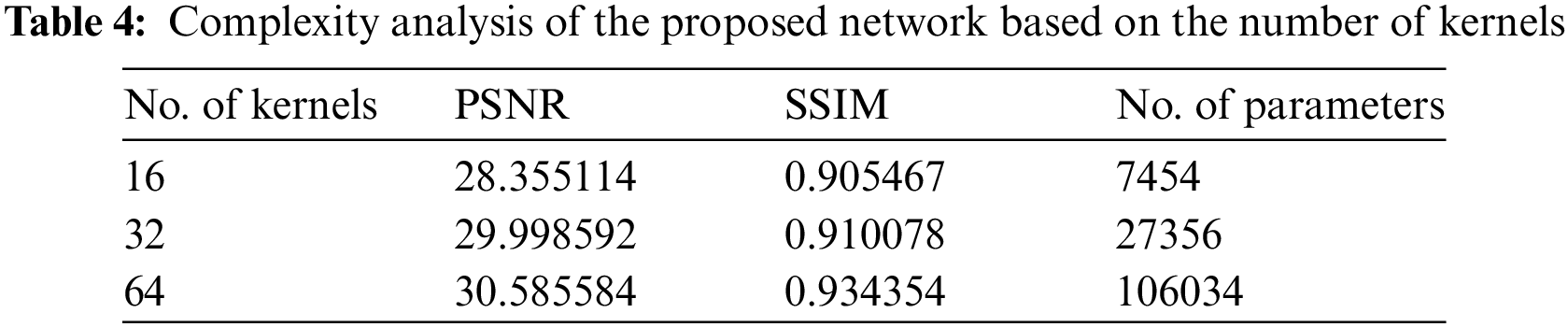
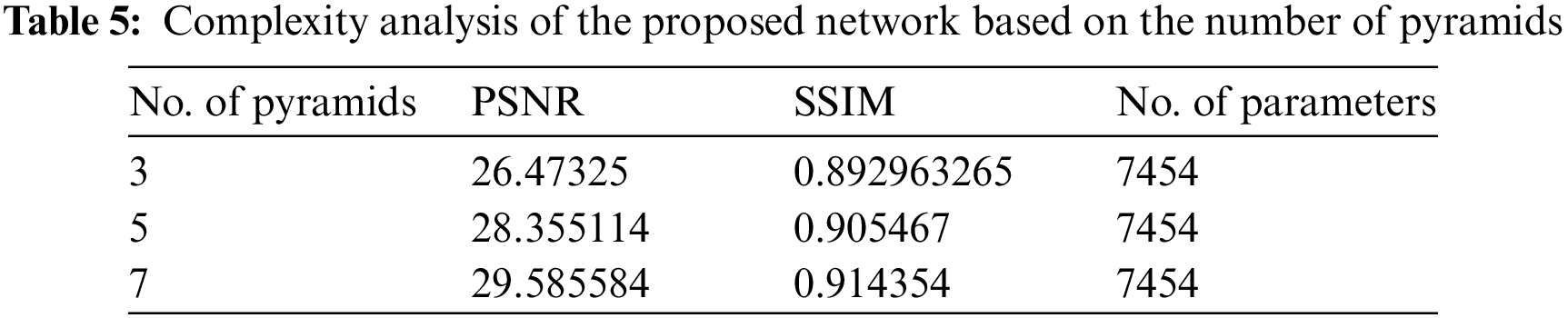
A given grayscale SAR image is decomposed into its respective five-level Laplacian pyramid using a fixed cubic interpolating kernel with coefficients [0.0625, 0.25, 0.375, 0.25, 0.625]. The same smoothing kernel is reused to reconstruct a clean Gaussian pyramid. We use five recursive blocks and five pyramid levels. The number of feature maps in each convolution layer is 16, the default setting for the proposed despeckling network. This results in 7 K parameters for the proposed despeckling network, which makes the proposed network lightweight in terms of storage and computational cost. Despeckling performance can be further improved if the number of kernels, pyramid levels, and recursive blocks increases. Extensive experiments were conducted to evaluate the performance, examining various factors such as the number of feature maps (16, 32, 64), pyramid levels (3, 5, 7), and recursive blocks (3, 5, 7). Although there is a minor improvement in PSNR and SSIM values, visual image quality remains the same. Moreover, increasing the number of recursive and pyramid levels does not increase parameters as parameters are shared; however, increasing the number of feature maps may improve model performance at the cost of a huge increase in model parameters.

In Table 4, the PSNR and SSIM results for various kernel numbers, and in Table 5 number of pyramids is shown against their respective number of parameters, which shows that a higher number of maps have a minor increase in PSNR and SSIM metrics at the cost of an enormous increase in several parameters. In the case of increasing pyramid levels, there is no increase in the number of parameters, although PSNR and SSIM metrics may increase with the increase in the number of levels.

6  Discussion

The suggested PAN-DeSpeck approach outperforms other cutting-edge image restoration methods in the context of SAR image despeckling, according to the evaluation findings for the method. The visual results in Fig. 4 show how well the suggested approach eliminates speckle noise and restores images with crisp edges and fine texture features. Figs. 5–7 show comparisons that highlight the shortcomings of current techniques, including blurring effects, lost features, and bluer artifacts. Higher PSNR and SSIM values in Table 1 demonstrate the suggested PAN-DeSpeck’s exceptional despeckling performance, which is statistically and qualitatively impressive.

Additionally, Table 2 compares recursive and non-recursive blocks, showing how using recursive blocks can improve efficiency while requiring fewer parameters. Tables 4 and 5’s complexity analysis also emphasize the trade-off between parameter number and performance indicators like PSNR and SSIM. Overall, the suggested PAN-DeSpeck method employs an attention module, multiscale pyramids, and an optimized loss function to satisfactorily handle the issues related to speckle noise removal in SAR images. It is appealing for SAR image restoration applications because it balances despeckling performance and texture retention.

7  Future Work

Even though the PAN-DeSpeck approach under consideration has shown exceptional effectiveness in despeckling SAR images, there is still potential for improvement and progress in subsequent studies. Although the proposed method performs better than existing methods, there are certain drawbacks and possible areas for improvement. For instance, the proposed strategy might benefit from investigating new loss functions or regularization strategies to enhance edge retention and texture features in the despeckled images. Speckle noise reduction may also become even more efficient by looking into the possibility of adding advanced deep-learning architectures or by examining new attention techniques.

Also, examining different data augmentation techniques or investigating the effects of various network architectures for specific SAR imaging settings may help to design more adaptable and reliable despeckling methods. Additionally, the effectiveness of the suggested technique might be further assessed and confirmed using various SAR datasets, including those with more intricate backgrounds and speckle noise properties. Future research projects can progress the state-of-the-art in SAR picture despeckling by tackling these issues and paving the way for better image quality and information extraction in various applications.

Additionally, various image restoration tasks can be adapted to the proposed method’s lightweight and multiscale decomposition characteristics. Furthermore, more modern image restoration methods would be beneficial for thorough comparison and evaluation.

8  Conclusion

A lightweight multiscale PAN-DeSpeck network is proposed based on attention and the Laplacian pyramid for SAR image despeckling. The proposed method comprises multiple independent subnetworks. Each subnetwork takes the input from the Laplacian pyramid, enhances the features of a decomposed image using FEB, extracts key features using multiscale attention, and predicts the corresponding clean Gaussian pyramid at each scale using recursive blocks. The approach utilizes residual blocks and implements recursive blocks with a parameter-sharing strategy to accelerate the training speed, effectively reducing the number of parameters. The proposed PAN-DeSpeck model has approximately 7 k parameters and shows outstanding performance compared to various other image restoration methods used for comparison in terms of visual and quantitative analysis. The proposed method is also trained without the usage of recursive blocks. It was observed that without recursive blocks, the number of parameters increased to 46 K with negligible gain in performance. Since the virtual SAR dataset contains images with very complex backgrounds; consequently the trained model may not produce sharp edges in some cases, resulting in performance degradation. As a future direction, increasing the number of training samples using generative models can be an excellent choice to improve the despeckling performance. Moreover, the proposed method’s lightweight and multiscale decomposition nature can be adapted to other image restoration tasks like image dehazing, denoising, and low-light image enhancement.

Acknowledgement: The authors would like to thank Prince Sultan University (PSU) and Smart Systems Engineering Lab for their valuable support.

Funding Statement: The authors would like to thank Prince Sultan University (PSU) for paying the Article Processing Charges (APC) of this publication.

Author Contributions: Study conception and design: Saima Yasmeen, Muhammad Usman Yaseen, Syed Sohaib Ali, Sohaib Bin Altaf Khattak, and Moustafa M. Nasralla; data collection: Syed Sohaib Ali; analysis and interpretation of results: Saima Yasmeen, Muhammad Usman Yaseen, Syed Sohaib Ali, and Moustafa M. Nasralla; draft manuscript preparation: Syed Sohaib Ali, Sohaib Bin Altaf Khattak, and Moustafa M. Nasralla. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The source code and used dataset for this study are available on GitHub.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Passah, K. Amitab and D. Kandar, “SAR image despeckling using deep CNN,” IET Image Processing, vol. 15, no. 6, pp. 1285–1297, 2021. [Google Scholar]

2. M. Zhang, L. D. Yang, D. H. Yu and J. B. An, “Synthetic aperture radar image despeckling with a residual learning of convolutional neural network,” Optik, vol. 228, pp. 165876, 2021. [Google Scholar]

3. H. Salehi, J. Vahidi, T. Abdeljawad, A. Khan and S. Y. B. Rad, “A SAR image despeckling method based on an extended adaptive Wiener filter and extended guided filter,” Remote Sensing, vol. 12, no. 15, pp. 2371, 2020. [Google Scholar]

4. P. Singh, M. Diwakar, A. Shankar, R. Shree and M. Kumar, “A review on SAR image and its despeckling,” Archives of Computational Methods in Engineering, vol. 28, pp. 4633–4653, 2021. [Google Scholar]

5. F. Lattari, B. Gonzalez, F. Asaro, A. Rucci, C. Prati et al., “Deep learning for SAR image despeckling,” Remote Sensing, vol. 11, no. 13, pp. 1532, 2019. [Google Scholar]

6. C. Tian, Y. Xu, Z. Li, W. Zuo, L. Fei et al., “Attention-guided CNN for image denoising,” Neural Networks, vol. 124, pp. 117–129, 2020. [Google Scholar] [PubMed]

7. R. Chaurasiya and D. Ganotra, “Deep dilated CNN based image denoising,” International Journal of Information Technology, vol. 15, no. 1, pp. 137–148, 2023. [Google Scholar]

8. G. Liu, H. Kang, Q. Wang, Y. Tian and B. Wan, “Contourlet-CNN for SAR image despeckling,” Remote Sensing, vol. 13, no. 4, pp. 764, 2021. [Google Scholar]

9. X. Fu, B. Liang, Y. Huang, X. Ding and J. Paisley, “Lightweight pyramid networks for image deraining,” IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 6, pp. 1794–1807, 2019. [Google Scholar] [PubMed]

10. Y. Li, X. Chen, Z. Zhu, L. Xie, G. Huang et al., “Attention-guided unified network for panoptic segmentation,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 7026–7035, 2019. [Google Scholar]

11. J. Li, Y. Li, Y. Xiao and Y. Bai, “HDRANet: Hybrid dilated residual attention network for SAR image despeckling,” Remote Sensing, vol. 11, no. 24, pp. 2921, 2019. [Google Scholar]

12. D. Cozzolino, L. Verdoliva, G. Scarpa and G. Poggi, “Nonlocal CNN SAR image despeckling,” Remote Sensing, vol. 12, no. 6, pp. 1006, 2020. [Google Scholar]

13. N. Martinel, G. L. Foresti and C. Micheloni, “Aggregating deep pyramidal representations for person re-identification,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition Workshops (CVPRW), Long Beach, CA, USA, pp. 1544–1554, 2019. [Google Scholar]

14. S. Liu, Y. Lei, L. Zhang, B. Li, W. Hu et al., “MRDDANet: A multiscale residual dense dual attention network for SAR image denoising,” IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1–13, 2021. [Google Scholar]

15. E. Çetinkaya and M. F. Kiraç, “Image denoising using deep convolutional autoencoder with feature pyramids,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 28, no. 4, pp. 2096–2109, 2020. [Google Scholar]

16. Y. Zhou, J. Shi, X. Yang, C. Wang, D. Kumar et al., “Deep multi-scale recurrent network for synthetic aperture radar images despeckling,” Remote Sensing, vol. 11, no. 21, pp. 2462, 2019. [Google Scholar]

17. F. Gu, H. Zhang and C. Wang, “A Two-component deep learning network for SAR image denoising,” IEEE Access, vol. 8, pp. 17792–17803, 2020. [Google Scholar]

18. A. E. Ilesanmi and T. O. Ilesanmi, “Methods for image denoising using convolutional neural network: A review,” Complex Intelligent Systems, vol. 7, no. 5, pp. 2179–2198, 2021. [Google Scholar]

19. S. Gu and R. Timofte, “A brief review of image denoising algorithms and beyond,” Inpainting and Denoising Challenges, Gjøvik, Norway, pp. 1–21, 2019. [Google Scholar]

20. B. Goyal, A. Dogra, S. Agrawal, B. S. Sohi and A. Sharma, “Image denoising review: From classical to state-of-the-art approaches,” Information Fusion, vol. 55, pp. 220–244, 2020. [Google Scholar]

21. H. Saki, N. Khan, M. G. Martini and M. M. Nasralla, “Machine learning based frame classification for videos transmitted over mobile networks,” in 2019 IEEE 24th Int. Workshop on Computer Aided Modeling and Design of Communication Links and Networks (CAMAD), Berlin, Germany, pp. 1–6, 2019. [Google Scholar]

22. M. M. Nasralla, I. U. Rehman, D. Sobnath and S. Paiva, “Computer vision and deep learning-enabled UAVs: Proposed use cases for visually impaired people in a smart city,” in Computer Analysis of Images and Patterns: CAIP 2019 Int. Workshops, ViMaBi and DL-UAV, Salerno, Italy, pp. 91–99, 2019. [Google Scholar]

23. Y. Tang, J. Huang, W. Pedrycz, B. Li and F. Ren, “A fuzzy clustering validity index induced by triple center relation,” IEEE Transactions on Cybernetics, vol. 53, no. 8, pp. 5024–5036, 2023. [Google Scholar] [PubMed]

24. S. A. Kumar, M. M. Nasralla, I. García-Magariño and H. Kumar, “A machine-learning scraping tool for data fusion in the analysis of sentiments about pandemics for supporting business decisions with human-centric AI explanations,” PeerJ Computer Science, vol. 7, pp. e713, 2021. [Google Scholar] [PubMed]

25. Q. Zhang, Q. Yuan, J. Li, Z. Yang and X. Ma, “Learning a dilated residual network for SAR image despeckling,” Remote Sensing, vol. 10, no. 2, pp. 196, 2018. [Google Scholar]

26. A. G. Mullissa, D. Marcos, D. Tuia, M. Herold and J. Reiche, “DeSpeckNet: Generalizing deep learning-based SAR image despeckling,” IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1–15, 2020. [Google Scholar]

27. J. Hu, L. Shen and G. Sun, “Squeeze-and-excitation networks,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 7132–7141, 2018. [Google Scholar]

28. Y. Zhang, K. Li, K. Li, L. Wang, B. Zhong et al., “Image super-resolution using very deep residual channel attention networks,” in Proc. of the European Conf. on Computer Vision (ECCV), Munich, Germany, pp. 286–301, 2018. [Google Scholar]

29. S. Anwar and N. Barnes, “Real image denoising with feature attention,” in Proc. of the IEEE/CVF Int. Conf. on Computer Vision, Seoul, South Korea, pp. 3155–3164, 2019. [Google Scholar]

30. Y. Zhang, K. Li, K. Li, B. Zhong and Y. Fu, “Residual non-local attention networks for image restoration,” arXiv preprint arXiv:1903.10082, 2019. [Google Scholar]

31. X. Qin, Z. Wang, Y. Bai, X. Xie and H. Jia, “FFA-Net: Feature fusion attention network for single image dehazing,” in Proc. of the AAAI Conf. on Artificial Intelligence, vol. 34, no. 7, pp. 11908–11915, 2020. [Google Scholar]

32. R. Xu, Z. Xiao, J. Huang, Y. Zhang and Z. Xiong, “EDPN: Enhanced deep pyramid network for blurry image restoration,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Virtual, pp. 414–423, 2021. [Google Scholar]

33. W. Dong, T. Zhang, J. Qu, S. Xiao, J. Liang et al., “Laplacian pyramid dense network for hyperspectral pansharpening,” IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1–13, 2021. [Google Scholar]

34. J. Li, J. Li, F. Fang, F. Li and G. Zhang, “Luminance-aware pyramid network for low-light image enhancement,” IEEE Transactions on Multimedia, vol. 23, pp. 3153–3165, 2020. [Google Scholar]

35. Y. Tang, W. Gong, X. Chen and W. Li, “Deep inception-residual laplacian pyramid networks for accurate single-image super-resolution,” IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 5, pp. 1514–1528, 2019. [Google Scholar] [PubMed]

36. Y. Mei, Y. Fan, Y. Zhang, J. Yu, Y. Zhou et al., “Pyramid attention networks for image restoration,” Computers, Materials & Continua, vol. 65, no. 1, pp. 1–17, 2020. [Google Scholar]

37. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]

38. C. Tian, Y. Xu and W. Zuo, “Image denoising using deep CNN with batch renormalization,” Neural Networks, vol. 121, pp. 461–473, 2020. [Google Scholar] [PubMed]

39. C. Tian, Y. Xu, W. Zuo, B. Du, C. Lin et al., “Designing and training a dual CNN for image denoising,” Knowledge-Based Systems, vol. 226, pp. 106949, 2021. [Google Scholar]

40. S. Dabhi, K. Soni, U. Patel, P. Sharma and M. Parmar, “Virtual SAR: A synthetic dataset for deep learning-based speckle noise reduction algorithms,” arXiv preprint arXiv:2004.11021, 2020. [Google Scholar]

41. H. Shen, C. Zhou, J. Li and Q. Yuan, “SAR image despeckling employing a recursive deep CNN prior,” IEEE Transactions on Geoscience and Remote Sensing, vol. 59, no. 1, pp. 273–286, 2020. [Google Scholar]

42. D. Setiadi and I. M. Rosal, “PSNR vs SSIM: Imperceptibility quality assessment for image steganography,” Multimedia Tools and Applications, vol. 80, no. 6, pp. 8423–8444, 2021. [Google Scholar]

43. Y. Zhao, Z. Jiang, A. Men and G. Ju, “Pyramid real image denoising network,” in 2019 IEEE Visual Communications and Image Processing (VCIP), Taipei, Taiwan, IEEE, pp. 1–4, 2019. [Google Scholar]

44. W. El-Shafai, A. A. Mahmoud, E. S. M. El-Rabaie, T. E. Taha, O. F. Zahran et al., “Efficient deep CNN model for COVID-19 classification,” Computers, Materials & Continua, vol. 73, no. 15, pp. 4373–4391, 2022. [Google Scholar]