 Open Access
Open Access
ARTICLE
Efficient Multi-Authority Attribute-Based Searchable Encryption Scheme with Blockchain Assistance for Cloud-Edge Coordination
1 School of Computer and Information Security, Guilin University of Electronic Technology, Guilin, 541004, China
2 School of Computer Science, National University of Defense Technology, Changsha, 410073, China
* Corresponding Author: Qian He. Email:
(This article belongs to the Special Issue: Innovative Security for the Next Generation Mobile Communication and Internet Systems)
Computers, Materials & Continua 2023, 76(3), 3325-3343. https://doi.org/10.32604/cmc.2023.041167
Received 13 April 2023; Accepted 26 June 2023; Issue published 08 October 2023
Abstract
Cloud storage and edge computing are utilized to address the storage and computational challenges arising from the exponential data growth in IoT. However, data privacy is potentially risky when data is outsourced to cloud servers or edge services. While data encryption ensures data confidentiality, it can impede data sharing and retrieval. Attribute-based searchable encryption (ABSE) is proposed as an effective technique for enhancing data security and privacy. Nevertheless, ABSE has its limitations, such as single attribute authorization failure, privacy leakage during the search process, and high decryption overhead. This paper presents a novel approach called the blockchain-assisted efficient multi-authority attribute-based searchable encryption scheme (BEM-ABSE) for cloud-edge collaboration scenarios to address these issues. BEM-ABSE leverages a consortium blockchain to replace the central authentication center for global public parameter management. It incorporates smart contracts to facilitate reliable and fair ciphertext keyword search and decryption result verification. To minimize the computing burden on resource-constrained devices, BEM-ABSE adopts an online/offline hybrid mechanism during the encryption process and a verifiable edge-assisted decryption mechanism. This ensures both low computation cost and reliable ciphertext. Security analysis conducted under the random oracle model demonstrates that BEM-ABSE is resistant to indistinguishable chosen keyword attacks (IND-CKA) and indistinguishable chosen plaintext attacks (IND-CPA). Theoretical analysis and simulation results confirm that BEM-ABSE significantly improves computational efficiency compared to existing solutions.Keywords
The widespread use of the Internet of Things (IoT) and 5G have led to a surge in the number of network edge devices, resulting in a rapid growth in edge data [1,2]. The centralized data processing approach based on cloud computing is facing challenges in efficiently processing the vast amount of data generated by edge devices. Edge computing has emerged as a promising solution to the challenges faced by traditional cloud computing in processing the massive amounts of data generated by IoT devices. The fundamental concept of edge computing is to perform computing tasks close to the data source, which reduces network transmission bandwidth and response delay compared to traditional cloud computing [3]. However, the untrusted or partially trusted nature of cloud service providers (CSP) and edge nodes (ENs) poses a significant risk to the privacy of sensitive data. Tampering and abusing data by these entities can leak user privacy information [3–5]. Although symmetric encryption can be used by the data owner (DO) to maintain data confidentiality, the use of encryption prevents the ability to perform plaintext keyword retrieval. It creates challenges for fine-grained access control and data sharing.
To mitigate the potential risks of private data leakage, it is crucial to prioritize both data confidentiality and accessibility for effective access control. While symmetric encryption can provide data confidentiality, it makes information on encrypted data difficult to retrieve. Identity-based encryption (IBE) and attribute-based encryption (ABE) provide distinct access control mechanisms, with IBE offering coarse-grained access control and ABE providing fine-grained access control capabilities [6,7]. It is critical in practice to have an effective keyword search and to have fine-grained access control over encrypted data. The technique of searchable encryption (SE) enables data users (DUs) to conduct searches on ciphertext data using specific keywords [8]. To provide even more precise access control, the gradually popular solution in both industrial and academic domains is ciphertext-policy attribute-based searchable encryption (CP-ABSE) with flexible access control policies [9,10]. The high computational and storage requirements of CP-ABSE prevent its deployment on resources-constrained IoT devices, despite its promise as a SE scheme for fine-grained access control. Therefore, the lightweight CP-ABSE scheme is a prerequisite for its implementation on resource-constrained terminal devices. Additionally, many existing CP-ABSE schemes [9–13] that employ single-attribute authorization for attribute management and key distribution may encounter challenges in efficiently and securely handling attributes from a vast network of interconnected IoT devices and are prone to single-point failures and central corruption. Furthermore, trust in CSP is often weakened due to the risk of malicious access to data and tampering with query results. In contrast, blockchain technology provides a safer and more trustworthy option [14]. As a decentralized ledger with multi-party consensus and a chain structure, blockchain offers an unparalleled guarantee of data integrity and trustworthiness compared to centralized systems.
This paper proposes an efficient multi-authority attribute-based searchable encryption scheme with blockchain assistance (BEM-ABSE) for cloud-edge collaboration. This BEM-ABSE scheme aims to provide secure and reliable searching while protecting privacy through blockchain, ciphertext searching, and ABE. To address the efficiency limitations and security vulnerabilities associated with Certificate Authorities (CAs), the BEM-ABSE scheme employs a consortium blockchain, enabling multiple attribute authorities to autonomously manage user attributes and key assignments. Furthermore, this scheme facilitates online/offline hybrid encryption and edge-assisted verifiable decryption, effectively minimizing the computational overhead involved in encryption and decryption operations. The main contributions of the scheme are as follows:
(1) Taking advantage of multi-authority ABE and blockchain, this paper proposes a searchable encryption scheme with fine-grained access control for cloud-edge collaboration. BEM-ABSE supports ciphertext keyword search based on smart contracts, online/offline hybrid encryption, and edge-assisted verifiable outsourcing decryption. This paper also proves this scheme can resist IND-CPA and IND-CKA under the random oracle model.
(2) Consortium blockchain is designed to replace the trusted CA in the traditional CP-ABSE scheme, allowing for the generation of global public parameters and the execution of ciphertext searches. The dependence on single-centre authorization is broken, and the reliability of ciphertext searches is improved.
(3) An online/offline hybrid encryption mechanism is utilized to reduce the time overhead during the encryption phase by performing pre-encryption computation and generating intermediate ciphertext. The decryption tasks are offloaded to ENs, effectively decreasing the computational burden of decryption for resource-constrained IoT devices.
The remainder of this paper is organized as follows. Section 2 provides a review of the related work. Section 3 demonstrates the background knowledge in the understanding of the BEM-ABSE. In Section 4, Formalize the system and security model. Then, the formal construction of the BEM-ABSE scheme is presented in Section 5. In Section 6 and 7, separate analyses of safety and performance are presented. Finally, The work of this paper is concluded in Section 8.
SE enables search on encrypted data using specified keywords, while ABSE provides detailed permissions control for data ciphertext retrieval, with significant research having been conducted in this field. Searchable symmetric encryption was first proposed by Song et al. [8] in 2000. However, using a single shared key for encryption and decryption in symmetric cryptography makes it impractical for complex multi-user applications. ABSE provides a flexible way to execute access control policies, ensuring that only users with the required policy attributes can access data. This one-to-many access control model enables secure and convenient data sharing. To reduce the computational overhead during the search process, Zheng et al. [9] proposed an ABSE scheme with verifiable results, which uses verifiable attribute-based encryption, but it also has some drawbacks, such as requiring a secure channel and high costs. Huang et al. [15] introduced a rapid and privacy-preserving attribute-based keyword search system designed for cloud document services. This system exhibits improved stability and efficiency during the search phase, but it does entail additional computational costs in other phases. Zhang et al. [16] designed a distributed and scalable, searchable encryption access control scheme that utilizes cloud services to achieve lightweight decryption processes, resulting in lower computational complexity and improving security against selected keyword attacks and selected plaintext attacks, but not suitable for resource-constrained devices due to high encryption time overhead. Considering the limitations of resource-constrained devices, Miao et al. [17] proposed a constant-sized trapdoor-based online/offline SE for cloud-assisted industrial IoT, where the overall encryption burden on DO is still heavy, but the cost of generating DU's trapdoor is reduced through an elegant technique. Zhou et al. [18] proposed a general searchable encryption scheme for cloud-assisted industrial IoT systems, with the lightweight generation of both index and query trapdoors. Liu et al. [5] proposed an efficient ABSE scheme for cloud-edge collaborative computing, reducing the computational cost of resource-constrained terminals by allowing EN to simultaneously perform text-based search and pre-decryption algorithms and save keyword indexes.
However, these schemes risk privacy data leakage as the CSP and ENs are either untrusted or semi-trusted. The combination of searchable public key encryption with blockchain technology is gaining popularity among scholars to enhance ciphertext security. This approach benefits from blockchain technology's decentralized, transparent, traceable and tamper-proof characteristics. Yang et al. [19] presented a scheme allowing encrypted file upload to the cloud while placing the encrypted index on the blockchain. This scheme ensures the encrypted index is tamper-proof, integrity, and traceability and enables users to obtain accurate search results without needing third-party verification. However, these schemes have limitations, such as scalability difficulties, security and performance bottlenecks, and the potential for excessive permissions, as they rely on a single authorization center. Niu et al. [20] proposed a policy hide and verifiable blockchain-assisted ABSE scheme. This scheme stores the index is stored on the blockchain, and searches are performed using smart contracts, which reduces the computational load on the service. With the growth of the Internet of Things and the widespread adoption of 5G wireless networks, the cloud-edge collaborative data-sharing model has become more prevalent, and the number of IoT devices requiring authorization has increased significantly. However, relying on a single authorization center can result in significant losses if it crashes or is compromised.
2.2 Multi-Authority Attribute-Based Encryption
There are significant security risks in the current ABE schemes, as they rely on one attribute authority to manage attributes and keys. This authority may be able to decrypt any ciphertext within its control. To address this issue, researchers have proposed a variety of multi-authority ABE schemes (MA-ABE). The MA-ABE scheme was first proposed by Chase [21], but managing attribute authorities requires a trusted certificate authority, which may prove costly and have backward security challenges. Subsequently, Lewko et al. [22] proposed a distributed multi-authority ABE where attribute authorities are solely responsible for creating initial public parameters. The scheme utilizes a linear secret sharing scheme (LSSS) matrix to represent access policies, offering greater expressive capabilities compared to AND gates. However, the scheme lacks post-quantum security assurance. Tu et al. [23] suggested using attribute-group keys for large attribute domains in distributed computing systems using fog computing. To improve user privacy and security, Guo et al. [24] developed an encrypted data access control solution that utilizes smart contracts to define interactions between DOs, users and attribute authorities. However, DOs using symmetric encryption for data encryption can lead to heavy key management overhead. Qin et al. [25] utilized a consortium blockchain to establish trust bridges between attribute authorities and designed an MA-ABE based on blockchain. However, the existence of certificate authorities raises concerns about potential single-point failures. According to Xiao et al. [26], their blockchain-based MA-ABE scheme incorporates flexible attribute revocation; It can be applied to data publishing services and payment platforms for Dos. To manage dynamic users and improve search result credibility, Yu et al. [27] proposed an efficient multi-authority SE scheme using blockchain technology for keyword-based search and dynamic user management. Multiple-cloud block storage technology was used by Wu et al. [28] to address the problems with unstable cloud servers and to guard against malicious actions, including the leakage of private information, tampering with ciphertext, and malicious deletion of ciphertext. The security of keyword indexes and the impartiality of search results are guaranteed by the blockchain's immutability. Utilizing online/offline encryption and outsourced decryption processes, Xu et al. [29] distributed ABSE approach with shared keyword search was suggested. Although the key delegation problem is resolved inside a single authority, the approach has a somewhat high total computation cost.
While these schemes address the attribute and key management issue a single authority brings, current multi-authority systems still face some challenges. Some schemes rely on a central authority for management [30], generating complete private keys through the CA to avoid single-point of failure of attribute authorities. However, this approach also involves high trust costs for the CA. Additionally, there is over-reliance on the cloud service when users send encryption requests to the cloud. The CSP usually performs encryption search and pre-decryption processes [31], meaning they can arbitrarily modify the search results or encryption data.
Assume that G and
(1) Biplanarity:
(2) Nondegeneracy:
(3) Computability: an efficient algorithm exists to calculate
Definition 1 (access structure): Given that there are n participants
3.3 Pedersen (t, n) Secret Sharing Algorithm
Each participant is both a distributor and a participant in the Pedersen (t, n) [27]. Given that there are n participants
(1) Generating the master secret
(2) Producing the sub-share value
(3) Producing the master share
(4) Recovering the master secret: If any t participants can recover the master secret, it may be assumed that
The Pedersen (t, n) algorithm achieves secure sharing of secrets among multiple participants without revealing any information about the secret without a trust center. Therefore, it is executed by blockchain nodes in the BEM-ABSE scheme to produce global parameters and accomplish ciphertext search.
Definition 2 (Bilinear Diffie-Hellman (BDH) assumption). Let
Definition 3 (Decisional q-parallel Bilinear Diffie-Hellman Exponent (BDHE) assumption). Let
Even though the adversary has a tuple y, the tuple
When the inequality Eq. (3) is satisfied, the algorithm demonstrates an advantage E in solving the q-BDHE problem. This implies that it is not possible for any algorithm to successfully solve the decisional q-BDHE problem with non-negligible advantage.
The system architecture of the suggested strategy is displayed in Fig. 1. It comprises five entities: DO, EN, CSP, AAs, DU and BC. The BEM-ABSE scheme system model is depicted in Fig. 1, demonstrating the scheme's fundamental structure.

Figure 1: System architecture
1) DO. Any IoT device capable of generating data. DO sets access policies, encrypts files and keyword indexes, and uploads the encrypted data and keyword indexes over a wireless network to EN.
2) EN. ENs are located at the edge of the network and possess strong computing and storage capabilities. They are able to dutifully store the ciphertext in the CSP and embed the keyword index and ciphertext address into the keyword index storage transaction, which is then submitted to the blockchain. In addition, ENs assist DU in partially decrypting the ciphertext, but they cannot obtain any information during the decryption process.
3) CSP. CSP is responsible for providing storage services for the encrypted data uploaded by legitimate DO through EN. In addition, it allows EN to access the ciphertext data associated with search results.
4) AAs. The BEM-ABSE has a number of attribute authorities. Each AA manages multiple attributes in an attribute domain and generates user attribute keys based on its user attributes.
5) DU. DUs create search trapdoors using keywords of their interest and embed them into search transactions, which are then submitted to the blockchain for subsequent encrypted file searching. After receiving partially decrypted ciphertext associated with search results from the EN, DUs can fully decrypt the data using their identity private keys.
6) BC. BC consists of trusted nodes responsible for global parameter generation and user registration. Search smart contracts (SSC) and validation smart contracts (VSC) are deployed on the blockchain. SSC conducts encrypted file searching on the blockchain through search trapdoors submitted by users, while VSC verifies the integrity of the data associated with user search results.
EN serves as a crucial link between users and the cloud in the BEM-ABSE. DO encrypts and transmits a large amount of generated data to the cloud through EN, reducing the cost of local storage management. Moreover, in order to lessen the computing burden of the decryption process, the EN nearest to DU is in charge of partly decrypting the ciphertext. CSP is solely responsible for storing a large amount of encrypted data. A permission blockchain composed of pre-selected trusted nodes is accountable for storing encrypted indices, conducting ciphertext searches, and verifying decryption results to achieve secure and controllable encrypted retrieval.
The BEM-ABSE scheme includes the following nine algorithms. Assuming there are N attribute authorities
(1) Setup
1)
2)
(2) Key Generation
1)
2)
(3) Encryption
1)
2)
(4) Trapdoor Generation
(5) Search
(6) Decryption
1)
2)
The security of BEM-ABSE is based on the BDH assumption and q-BDHE assumption. This paper design two security games to demonstrate that the BEM-ABSE system is secure in the IND-CKA and IND-CPA models.
(1) IND-CKA mode.
The BEM-ABSE scheme is IND-CKA secure. A pre-selected group of reliable and secure nodes serves as the consensus node in a blockchain, albeit these nodes might be unavailable or infected. As long as the Pedersen (t, n) secret sharing method remains safe, no one node can independently complete the reconstruction of the system's secret parameters, keeping the entire blockchain secure. The IND-CKA of the BEM-ABSE is defined as a game between challenger
Setup: The challenger
Phase 1: In polynomial-time many times (PPT),
Challenge:
Phase 2:
Guess:
Definition 4: If the bilinear Diffie-Hellman assumption holds, the BEM-ABSE scheme achieves IND-CKA security.
(2) IND-CPA mode.
The BEM-ABSE scheme is IND-CPA secure. Assume that
Init: The adversary
Setup:
Phase 1:
Challenge:
Phase 2:
Guess:
Definition 5: The BEM-ABSE scheme achieves IND-CPA security if no PPT adversary has a significant advantage in the security game described above.
(1) Setup
1) GlobalSetup: This algorithm runs through the primary node with inputs of security parameter
2) AuthoritySetup: Each attribute authority
(2) Key Generation
1) IdKeyGen: DU is assigned a unique identifier
2) SKGen: When the DU is successfully registered, each
(3) Encryption
1) Offline.Enc: DO perform offline encryption on computationally capable devices before determining the access structure and extracting keywords. First, DO selects
Leveraging
2) Online.Enc: After obtaining the intermediate ciphertext
Then, the DO protects m with the specified access policy
Next, the DO extracts keywords set
(4) Trapdoor Generation
TrapGen: When a DU searches for data files according to his keyword
(5) Search
Search: After receiving the search transaction from DU, the SSC checks whether
(6) Decryption
1) EN.Dec: When EN receives the
2) User.Dec: After receiving the transform ciphertext from EN, the DU utilizes its private key
Theorem 1: If the decisional q-BDHE assumption holds, the BEM-ABSE scheme achieves IND-CPA security.
Proof: Assume there is a game that can be won in PPT by the adversary
Init:
Setup:
Phase 1:
Challenge:
Phase 2:
Guess:
Because of the hardness of the q-BDHE problem, the advantage
Theorem 2: If the bilinear Diffie-Hellman assumption holds, the BEM-ABSE scheme achieves IND-CKA security.
Proof: Assume there is a game that can be won in PPT by the adversary
Init: Assume that given a BDH tuple
Setup:
Phase 1:
Challenge:
Phase 2:
Guess:
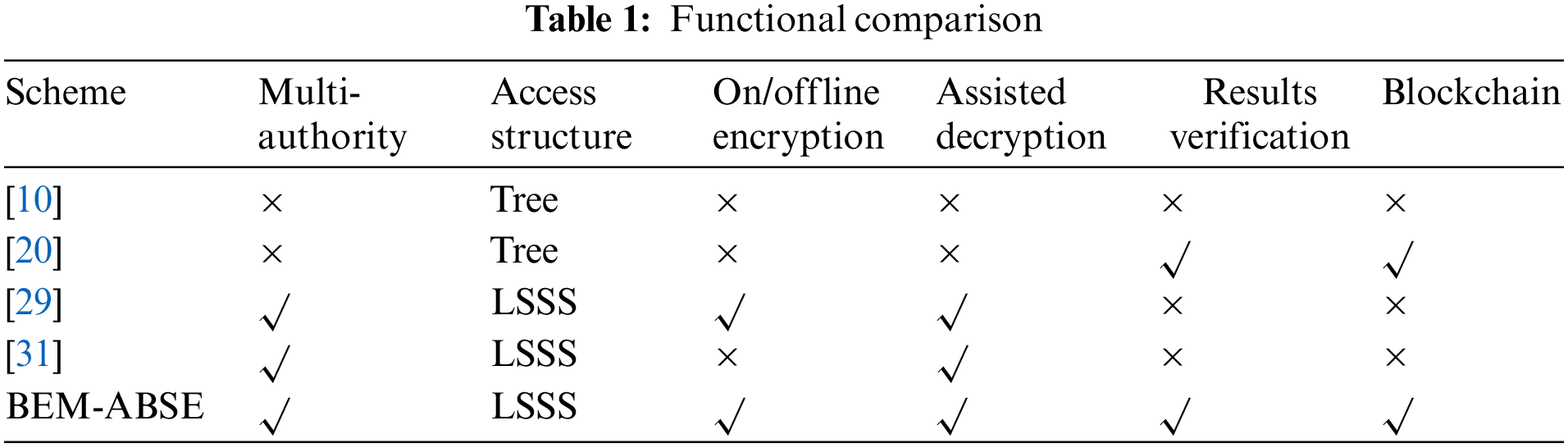
BEM-ABSE supports multi-authority, LSSS, on/offline encryption, assisted decryption, results verification and blockchain. The functional features are compared in Table 1. Schemes [29,31] and BEM-ABSE are all SE schemes based on multiple authorization centers. The access policy is based on LSSS, which can effectively avoid single-point failures and improve the system's security. However, A significant computational cost is placed on the client by other systems, with the exception of the BEM-ABSE scheme, which does not have the design of online/offline procedures or edge-assisted decryption throughout the encryption and decryption stages. Despite the fact that the scheme [29] outsources encryption and decryption to save costs for the client, its overall computing cost is significant, and its impact is poor. Schemes [20] and BEM-ABSE support data integrity verification. Furthermore, BEM-ABSE runs ciphertext search via a smart contract and uploads the ciphertext index to the blockchain, which can better safeguard user privacy and data security.
In theoretical computations, the computational complexity is primarily evaluated by considering the pairing P and the exponentiation
The computational complexity of the selected method was analyzed, and a detailed study was conducted on the differences in computational costs. The results were compared in Table 2, where

The storage cost comparison results of these schemes are shown in Table 3. Where

The experiment simulated the deployment of a Hyperledger Fabric on a server with an Inter® Xeon® E5-2630 CPU @2.3 GHz 16-core and 64 GB RAM. We instantiated an edge node on a laptop with a 2.8 GHz Intel® Core™ i7-1165 and 16 GB of RAM and instantiated a resource-constrained device on a Raspberry Pi 3B with a Quad-Core ARMv8 CPU @1.2 GHz 4-core processor and 1 GB of RAM. The Fabric network is made up of three order nodes and four peer nodes that use the Raft consensus mechanism. Note that the experiment used the Pairing-Based Cryptography Library (PBC) to implement cryptographic operations and chose an elliptic curve group with type A:
Fig. 2 describes the computation and storage cost of BEM-ABSE. The comparison of computation costs is given in Figs. 2a–2d. In Fig. 2a, we noticed that the time cost for all three methods has a direct correlation with the number of attributes during the key generation procedure. Notably, when compared to the other two systems, the BEM-ABSE method has reduced computing costs. In Fig. 2b, scheme BEM-ABSE adopts an online/offline encryption mechanism. Note that although the BEM-ABSE scheme's computational cost during the encryption phase is larger than that of the scheme [20], the BEM-ABSE scheme uses intermediate ciphertexts for online encryption during DO usage in the encryption process rather than performing offline encryption every time during encryption. When we set

Figure 2: Algorithm time and storage cost
Next, the comparison of storage costs is given in Figs. 2e and 2h. As illustrated in Fig. 2e, the key generation stage storage costs in schemes [29] and BEM-ABSE are similar. When the number of attributes reaches 50, the scheme [20] has a storage cost that is almost double that of the BEM-ABSE. In Fig. 2f, it can be observed that in the encryption stage, the storage cost of the scheme [29] escalates significantly as the number of attributes increases, surpassing the storage cost of the schemes [20] and BEM-ABSE by a significant margin. Figs. 2g and 2h demonstrate that the storage costs associated with trapdoor generation and search stages in BA-ABSE are denoted as
In Fig. 3, the decryption time overhead is depicted. It can be observed that both the BME-ABSE scheme and [29] exhibit a linear increase in decryption time overhead as the number of attributes in the ciphertext policy grows. The BME-ABSE scheme has a total decryption time of 282 ms when there are 50 attributes which is much less than the 423 ms of the scheme [29]. In order to further lower the DU's computing expense during the decryption stage, the BME-ABSE scheme delegates the task of converting ciphertext with higher computational cost to ENs. At the same time, DU only needs to perform consistent operations regardless of the access policy. The utilization of computational resources on ENs simplifies the decryption process, reduces complexity, and shortens the time cost of decryption. In order to increase the decryption efficiency of IoT devices with limited resources, a lightweight decryption procedure is advantageous.
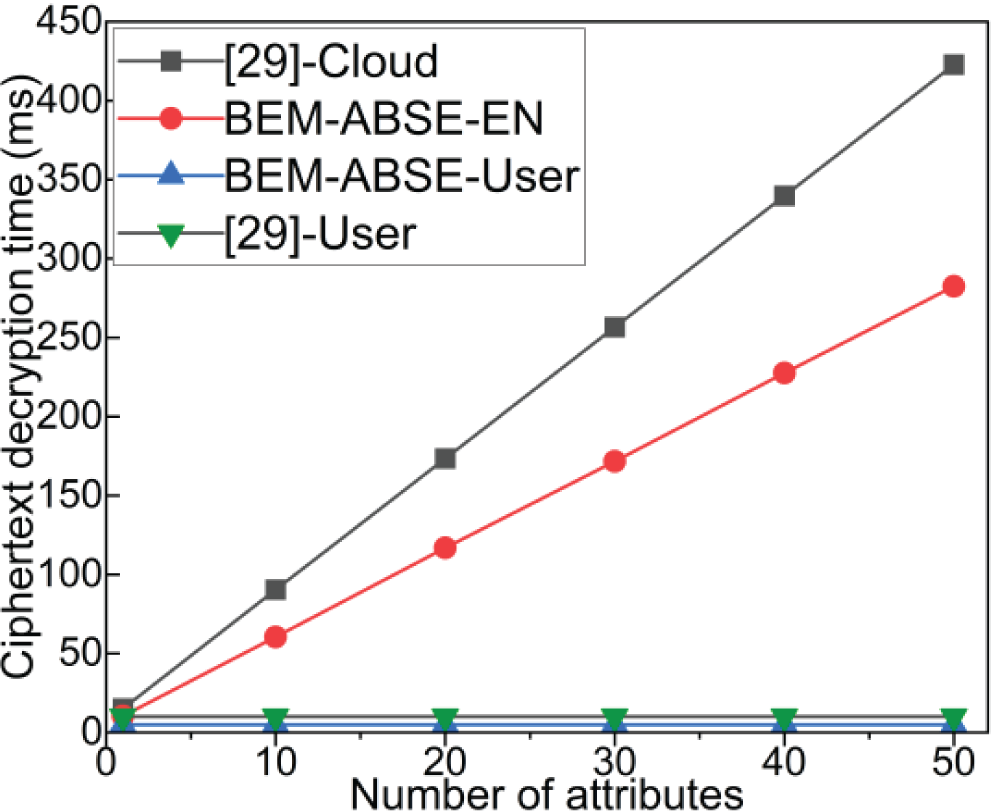
Figure 3: Decryption time cost
This paper presents an efficient multi-authority attribute-based searchable encryption scheme with blockchain assistance (BEM-ABSE) for cloud-edge collaborative scenarios. The BEM-ABSE scheme introduces an online/offline hybrid encryption mechanism. It adopts an edge-assisted outsourcing decryption mechanism, significantly improving the efficiency of encryption and decryption and effectively reducing the computation overhead of resource-limited IoT devices. The consortium blockchain serves as a trusted authentication center for global parameter generation and management, and the introduction of smart contracts realizes trusted and fair ciphertext keyword search and decryption result verification. BEM-ABSE has been rigorously analyzed for security and shown to be secure against IND-CPA and IND-CKA attacks. Performance analysis confirms its efficiency and practicality. However, a major limitation of the BEM-ABSE is its lack of support for expressive search queries such as fuzzy search and multi-keyword search and its inability to revoke permissions for malicious users. Future work will focus on designing a flexible indexing and efficient permission revocation scheme, enabling the BEM-ABSE to support various controllable search requests.
Acknowledgement: We thank the anonymous reviewers and editors for their very constructive comments.
Funding Statement: This work is supported by the National Natural Science Foundation of China (Nos. 62162018, 61972412), the Natural Science Foundation of Guangxi (No. 2019GXNSFGA245004), the Guilin Science and Technology Project (20210226-1) and the Innovation Project of Guangxi Graduate Education (No. YCSW2022296).
Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: Peng Liu, Qian He; data collection: Peng Liu; analysis and interpretation of results: Peng Liu, Biao Guo; draft manuscript preparation: Peng Liu. All authors reviewed the results and approved the final version of the manuscript.
Availability of Data and Materials: The data used to support the findings of this study are included within the article.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. K. Yu, J. Yu and C. Luo, “The impact of mobility on physical layer security of 5G IoT networks,” IEEE/ACM Transactions on Networking, vol. 1, pp. 1–14, 2022. [Google Scholar]
2. S. Jiang, J. Cao, H. Wu, K. Chen and X. Liu, “Privacy-preserving and efficient data sharing for blockchain-based intelligent transportation systems,” Information Sciences, vol. 635, pp. 72–85, 2023. [Google Scholar]
3. Y. Chiang, Y. Zhang, H. Luo, T. Y. Chen, G. H. Chen et al., “Management and orchestration of edge computing for IoT: A comprehensive survey,” IEEE Internet of Things Journal, vol. 1, pp. 1–30, 2023. [Google Scholar]
4. L. Zhang, H. Xiong, Q. Huang, J. G. Li, K. K. R. Choo et al., “Cryptographic solutions for cloud storage: Challenges and research opportunities,” IEEE Transactions on Services Computing, vol. 15, no. 1, pp. 567–587, 2022. [Google Scholar]
5. J. Liu, Y. Li, R. Sun, Q. Pei, N. Zhang et al., “EMK-ABSE: Efficient multikeyword attribute-based searchable encryption scheme through cloud-edge coordination,” IEEE Internet of Things Journal,vol. 9, no. 19, pp. 18650–18662, 2022. [Google Scholar]
6. F. Guo, Y. Mu, W. Susilo, W. Hsing, D. S. Wong et al., “Optimized identity-based encryption from bilinear pairing for lightweight devices,” IEEE Transactions on Dependable and Secure Computing, vol. 14, no. 6, pp. 211–220, 2015. [Google Scholar]
7. V. Goyal, O. Pandey, A. Sahai and B. Waters, “Attribute-based encryption for fine-grained access control of encrypted data,” in Proc. of the 13th ACM Conf. on Computer and Communications Security, New York, NY, USA, pp. 89–98, 2006. [Google Scholar]
8. D. X. Song, D. Wagner and A. Perrig, “Practical techniques for searches on encrypted data,” in Proc. of the 2000 IEEE Symp. on Security and Privacy, Washington DC, USA, pp. 44–55, 2000. [Google Scholar]
9. Q. Zheng, S. Xu and G. Ateniese, “VABKS: Verifiable attribute-based keyword search over outsourced encrypted data,” in Proc. of the IEEE INFOCOM 2014, Toronto, ON, Canada, pp. 522–530, 2014. [Google Scholar]
10. Y. Miao, X. Liu, K. K. R. Choo, R. H. Deng, J. Li et al., “Privacy-preserving attribute-based keyword search in shared multi-owner setting,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 3, pp. 1080–1094, 2021. [Google Scholar]
11. M. Ali, M. R. Sadeghi, X. Liu, Y. Miao and A. V. Vasilakos, “Verifiable online/offline multi-keyword search for cloud-assisted industrial internet of things,” Journal of Information Security and Applications, vol. 65, pp. 103101, 2022. [Google Scholar]
12. Y. Miao, Q. Tong, R. H. Deng, K. K. R. Choo, X. Liu et al., “Verifiable searchable encryption framework against insider keyword-guessing attack in cloud storage,” IEEE Transactions on Cloud Computing, vol. 10, no. 2, pp. 835–848, 2020. [Google Scholar]
13. X. Xiang and X. Zhao, “Blockchain-assisted searchable attribute-based encryption for e-health systems,” Journal of Systems Architecture, vol. 124, pp. 102417, 2022. [Google Scholar]
14. M. Zhang, J. Cao, Y. Sahni, Q. Chen, S. Jiang et al., “Blockchain-based collaborative edge intelligence for trustworthy and real-time video surveillance,” IEEE Transactions on Industrial Informatics, vol. 19, no. 2, pp. 1623–1633, 2022. [Google Scholar]
15. Q. Huang, Q. Wei, G. Yan, L. Zou and Y. Yang, “Fast and privacy-preserving attribute-based keyword search in cloud document services,” IEEE Transactions on Services Computing, vol. 1, pp. 1–13, 2023. [Google Scholar]
16. K. Zhang, J. Long, X. Wang, H. N. Dai, K. Liang et al., “Lightweight searchable encryption protocol for industrial internet of things,” IEEE Transactions on Industrial Informatics, vol. 17, no. 6, pp. 4248–4259, 2020. [Google Scholar]
17. Y. Miao, Q. Tong, K. K. R. Choo, X. Liu, R. H. Deng et al., “Secure online/offline data sharing framework for cloud-assisted industrial internet of things,” IEEE Internet of Things Journal, vol. 6, no. 5, pp. 8681–8691, 2019. [Google Scholar]
18. R. Zhou, X. Zhang, X. Wang, G. Yang, H. N. Dai et al., “Device-oriented keyword-searchable encryption scheme for cloud-assisted industrial IoT,” IEEE Internet of Things Journal, vol. 9, no. 18, pp. 17098–17109, 2021. [Google Scholar]
19. X. Yang, G. Chen, M. Wang, T. Li and C. Wang, “Multi-keyword certificateless searchable public key authenticated encryption scheme based on blockchain,” IEEE Access, vol. 8, pp. 158765–158777, 2020. [Google Scholar]
20. S. Niu, M. Song, L. Fang, S. Han and C. Wang, “Keyword search over encrypted cloud data based on blockchain in smart medical applications,” Computer Communications, vol. 192, pp. 33–47, 2022. [Google Scholar]
21. M. Chase, “Multi-authority attribute-based encryption,” in Proc. of the TCC 2007, Amsterdam, Netherlands, pp. 515–534, 2007. [Google Scholar]
22. A. Lewko and B. Waters, “Decentralizing attribute-based encryption,” in Proc. of the EUROCRYPT 2011, Tallinn, Estonia, pp. 568–588, 2011. [Google Scholar]
23. S. Tu, M. Waqas, F. Huang, G. Abbas and Z. H. Abbas, “A revocable and outsourced multi-authority attribute-based encryption scheme in fog computing,” Computer Networks, vol. 195, pp. 108196, 2021. [Google Scholar]
24. H. Guo, W. Li, M. Nejad and C. C. Shen, “A hybrid blockchain-edge architecture for electronic health record management with attribute-based cryptographic mechanisms,” IEEE Transactions on Network and Service Management, vol. 1, pp. 1–16, 2022. [Google Scholar]
25. X. Qin, Y. Huang, Z. Yang and X. Li, “A blockchain-based access control scheme with multiple attribute authorities for secure cloud data sharing,” Journal of Systems Architecture, vol. 112, pp. 101854, 2021. [Google Scholar]
26. M. Xiao, Q. Huang, Y. Miao, S. Li and W. Susilo, “Blockchain based multi-authority fine-grained access control system with flexible revocation,” IEEE Transactions on Services Computing, vol. 15, no. 6, pp. 3143–3155, 2021. [Google Scholar]
27. J. Yu, S. Liu, M. Xu, H. Guo, F. Zhong et al., “An efficient revocable and searchable MA-ABE scheme with blockchain assistance for C-IoT,” IEEE Internet of Things Journal, vol. 10, no. 3, pp. 2754–2766, 2022. [Google Scholar]
28. Q. Wu, T. Lai, L. Zhang and F. Rezaeibagha, “Blockchain-enabled multi-authorization and multi-cloud attribute-based keyword search over encrypted data in the cloud,” Journal of Systems Architecture, vol. 129, pp. 102569, 2022. [Google Scholar]
29. Q. Xu, C. Tan, W. Zhu, Y. Xiao, Z. Fan et al., “Decentralized attribute-based conjunctive keyword search scheme with online/offline encryption and outsource decryption for cloud computing,” Future Generation Computer Systems, vol. 97, pp. 306–326, 2019. [Google Scholar]
30. N. Gorasia, R. R. Srikanth, N. Doshi and J. Rupareliya, “Improving security in multi authority attribute based encryption with fast decryption,” Procedia Computer Science, vol. 79, pp. 632–639, 2016. [Google Scholar]
31. Y. Miao, R. H. Deng, X. Liu, K. K. R. Choo, H. Wu et al., “Multi-authority attribute-based keyword search over encrypted cloud data,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 4, pp. 1667–1680, 2019. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools