Multi-Agent Deep Reinforcement Learning for Efficient Computation Offloading in Mobile Edge Computing

1  Introduction

With the development of emerging fifth-generation (5G) networks and sixth-generation (6G) networks, a wide variety of Internet of Things (IoT) devices for computation-intensive applications is increasing year by year. These devices form a vast network consisting of various information-sensing devices and networks. The flourishing IoT devices always need to provide a high level of Quality of Service (QoS) to get a better range of services. However, the current user devices (UDs) are limited by computing capabilities and energy power, which cannot provide sufficient resources for the user with intense service requirements [1,2]. Mobile edge computing (MEC) has emerged as a promising technology to address the aforementioned problems at the edges of networks [3–5]. MEC is extremely effective in dealing with computing-intensive applications and is considered a crucial technology in 5G networks [6,7]. It allocates computing and storage resources to assist mobile devices in speeding up task processing [8,9]. MEC offloads the computing task of mobile devices to the nearby edge server by utilizing base stations or access points (APs) according to given rules (e.g., proximity principle) to complete the task calculations.

Although MEC has better performance in terms of bearing capacity and latency, with the increase of devices in the access MEC network, the channel interference between devices and MEC servers brings computational pressure that will seriously affect the quality of service. Moreover, in a dynamic environment, the strategy of the MEC system is hard to adjust correspondingly according to the change in the current operating environment. Therefore, it is important to formulate corresponding offloading decisions and resource allocation strategies to overcome the MEC performance bottleneck and improve the effectiveness of resource utilization. However, MEC also encounters many challenges. The dynamic nature of wireless communication and computation technologies has led to increasingly complex offloading decision and resource allocation problems. Traditional methods require complex iterative computations and the collection of statistical information about the known environment, which is difficult to obtain in real MEC systems. Traditional methods generate high costs but only provide approximate optimal solutions.

Machine Learning (ML) is a popular technology for searching for asymptotically optimal solutions, which can learn future directions from data. Specifically, Reinforcement Learning (RL) [10] is an optimization method based on interaction with the environment without labeled data. Deep reinforcement learning (DRL) [11,12] combines reinforcement learning and deep learning, which can capture the hidden dynamics of the current environment without prior knowledge, and neural networks in deep learning methods have a powerful perceptual capacity. The complex offloading decision and resource allocation problems can be solved more effectively by combining the decision-making capability of reinforcement learning with the perceptual capacity of neural networks in deep learning [13,14]. However, in our proposed system, we consider the scenarios of multiple UDs under a MEC network, which is a multi-agent environment. The traditional single-agent reinforcement learning method mentioned above cannot be applied in this scenario due to the instability of the multi-agent environment [15]. Thus, we further introduce multi-agent deep reinforcement learning (MADRL), which determines more optimized action strategies than the single-agent one, and it can effectively adapt to the dynamic changes in the multi-agent environment [16]. Moreover, it can learn the cooperation policy with each agent to realize the best long-term goal in the entire MEC system.

In this work, the key research topic is coordinated optimizing the offloading decision and resource allocation for latency-aware and energy-efficient offloading applications by a multi-agent deep reinforcement learning method to adapt to the dynamic changes of the MEC system. We aim to minimize the energy consumption with the maximum tolerated latency constraint. To this end, we first formulate this problem as a Markov game to find the Stackelberg equilibrium (SE). This is because Stackelberg equilibrium is a potentially better convergence point than Nash equilibrium, especially in cooperative environments [16]. Secondly, we propose a bi-level actor-critic (Bi-AC)-based method to address the above-mentioned problem. We consider a scenario with n UDs and one AP and allocate one agent for each UD. The agent takes action by observing the current state and the actions of the other agent, and it can effectively reduce the occurrence of the resource preemption problem. The main contributions of this paper are as follows:

(1)   We jointly optimize the offloading decision and resource allocation in a dynamic time-varying system and consider minimizing long-term energy consumption with the maximum tolerated latency constraint in the entire offloading process.

(2)   We approximate the optimization problem as a Markov game, which finds the Stackelberg equilibrium to address the problem of energy consumption minimization.

(3)   To tackle the combinatorial optimization problem, we propose a Bi-AC-based method, which learns the cooperative policy of multi-agent and can significantly reduce the occurrence of the resource preemption problem by fully considering the other agents’ actions. The proposed method can effectively adapt to dynamic environments compared to single-agent methods and capture the distribution of resource allocation.

(4)   Simulation results demonstrate that the proposed method consumes less energy than the various baseline approaches under the different scenarios.

The remainder of this paper is organized as follows. Section 2 introduces the related work. Section 3 describes the system model. Section 4 presents the problem formulation for task offloading. In Section 5, we formulate the problem as a Markov game problem and describe the Bi-AC-based model. The simulation results analysis and performance evaluation are discussed in Section 6. Finally, we conclude this work in Section 6.

2  Related Work

The research of computation offloading in the MEC system has been widely studied. Currently, most studies consider the following essential metrics: energy, latency, and both. For instance, Mao et al. [17] focused on joint computation offloading and utilize a downloading strategy to minimize long-term energy consumption throughout the offloading process. Similarly, Tran et al. [18] coordinately optimized the offloading decision and resource allocation to maximize the users’ task offloading gains using convex and quasi-convex optimization techniques and a novel heuristic algorithm. Unlike the research mentioned above, Ning et al. [19] comprehensively considered the cooperation of cloud computing and mobile edge computing in IoT and allow partial computation offloading that can effectively reduce latency. Some of the computation tasks can be executed on the local terminal, while the remaining computation tasks are offloaded to the edge servers to complete the calculation. However, the above research rarely considers time-varying environment conditions, which can cause performance degradation during computation offloading.

Some research has utilized ML-based methods to address the above issues in the MEC system. The ML-based methods can effectively predict the current environment state to help address the above issues, which can be divided into three categories: supervised learning-based, reinforcement learning-based, and unsupervised learning-based. The supervised learning-based methods map the original input to the classification output [20–22]. Chen et al. [20] designed an offloading mechanism, DNNOff, to extract the structure and parameters of the DNN model and then use a random forest regression model to predict the execution cost of each layer for offloading automatically and dynamically in the MEC environment. Mohammed et al. [21] proposed a technique to divide a DNN into multiple partitions, which can be processed locally by a mobile device or offloaded to one or multiple powerful nodes to complete the calculation. This method can efficiently exploit extra computing power and reduce latency. The reinforcement learning-based methods are a trial-and-error learning method that modifies the agent's policy through rewards and penalties [23–25]. Zhang et al. [24] applied a deep Q-Learning algorithm aimed at minimizing task offloading time as well as computational offloading and proposed a processing time minimization problem. Li et al. [25] designed a multilayer data hierarchical offloading strategy to optimize the performance of IoT devices, using offline and online algorithms to optimize the serviceability of edge computing models and identify the final output by a classifier. The unsupervised learning-based method is used to detect hidden structures in unlabeled data [26–28]. Jia et al. [27] used a decentralized coordination model in MEC networks when solving the multiplayer coordination problem and built an iterative algorithm to reduce the game frame durations between players. Table 1 classifies machine learning-based computational offloading decisions according to learning paradigms and expresses the advantages and disadvantages of each approach.

According to the above research, the primary research on computation offloading focuses on the following two aspects: one is the offloading decision of each UD, and the other is the resources allocated on demand. Especially, resources allocated have become an essential factor for task offloading gains in the MEC system. In the multi-agent environment, however, the above studies do not fully consider the resource conflict problem, and resource conflict is one of the important factors that directly affect performance. Moreover, the optimized resource allocation requires a clear understanding of time-varying environmental conditions. Thus, we propose a multi-agent deep reinforcement learning method combined with the Markov game to find the Stackelberg equilibrium (SE) for designing the scheme of offloading decisions and resources allocated in the MEC system. This allows the MEC system to dynamically assign the resources, and it can effectively reduce the resource conflict problem among UDs by fully considering the actions of other agents in the multi-agent environment.

3  System Model

In this section, we introduce the system model of our scheme. Firstly, we introduce the network architecture with an AP and n UDs. Then, we analyze the details of the communication model, computation model, and energy consumption model, respectively.

3.1 Network Model

In this work, we propose a network model with n user devices and an AP and denote the ith UD by ui. Meanwhile, we assume that the task execution time can be divided into multiple time slots, and the set of time slots is denoted by T = <0, 1, . . . , t, . . .>. In each time slot, each UD can generate multiple computation-intensive tasks and allow partial computation offloading. If UD offloads the tasks to the edge server to complete the calculation, we can offload some of the tasks or offload all the tasks according to the current offloading strategy. It is noteworthy that each task cannot be divided into smaller segments, which means a task is either executed locally or offloaded to the edge server for calculation. Then we consider the importance of each computation task by using a queue to store the task priorities to limit the sequence of task calculation. Under the dynamic changes of the MEC system, we are responsible for allocating the channel resources and computation resources when multiple tasks need to be offloaded to the edge server to complete the calculation according to the current task status and the rest of the available resources. The purpose is to effectively reduce latency and energy consumption generated during the task calculations through optimized resource allocation.

As mentioned earlier, we assume that each UD can generate more than one computation task in each time slot, and the number of tasks between UDs is always identical. Thus, we describe the task queue of each UD as Bit = <bi1t, bi2t, . . . , bijt, . . .>, where Bit represents all tasks generated by the ith UD ui in time slot t. We build all the following models focused on the time slot t. Thus, we omit the symbol t during the modeling process to simplify our description. For example, Bit can be expressed as Bi = <bi1, bi2, . . . , bij, . . ., bim>. Here, sij and zij stand for the data size of the computation task bij and the requested CPU cycles for processing the task bij. Thus, the total data size of Bi can be expressed as si = ∑sij, and the total requested CPU cycles for processing the task queue Bi can be expressed as zi = ∑zij. Δ stands for the maximum tolerable latency of the task queue Bi and is designed to confine the task execution time, which means that the task queue Bi is successfully executed when the total running time is less than its maximum tolerable latency.

In this work, we aim to minimize the total energy consumption and latency in the entire offloading process, and we only consider the computation tasks executed locally or offloaded to the edge server without the cloud server. We assume that each UD can generate more than one task in each time slot. Thus, we define the offloading decision of the ui as φi = {φi1, φi2, . . . , φij, . . . , φim }, where φij ∈ {0, 1} and φij corresponds to task bij. φij = 0 denotes that computation task bij is executed locally, and φij = 1 denotes that computation task bij is offloaded to the edge server to complete the calculation. Thus, for the computation offloading problem, we allow the tasks of each UD to be partially offloaded according to the current strategy in time slot t. We denote the offloading decision of all the UDs as Φ(t) = {φ1, φ2, . . ., φi, . . ., φn}.

3.2 Communication Model

In this section, we introduce the communication model in detail. The MEC system needs a better communication environment to reduce latency when the computation task is offloaded to the edge server. The mobile device communicates with the MEC server through the wireless AP, and we do not consider the communication cost between the MEC server and the AP. Similarly, the interference among APs is not considered because we assume that there is only one AP in the network architecture. We assume that the wireless channel remains constant in each same time slot but varies among different time slots.

C(t)=[c11c12…c1p…c1qc21c22…c2p…c2q⋮⋮⋮⋮ci1ci2…cip…ciq⋮⋮⋮⋮cn1cn2…cnp…cnq](1)

It is noteworthy that we divide the spectrum into q channels and denote the set of channels by C = {c1, c2, . . . , cp , . . . , cq}. In each time slot, each channel has two states. If the channel state is equal to 0, the channel is idle. If the channel state is equal to 1, the channel changes from the status of idle to busy. We denote the channel state and channel allocation of all the UDs as matrix C(t).

In (1), the row vectors of C(t) correspond to the state of each channel cp, and the column vectors of C(t) correspond to the set of UDs. Here, ∀p∈[1,q]∑i=1ncip≤1 and ∀i∈[1,n]∑p=1qcip≤1 stand for each ui occupying the channel cp, which means each channel can be selected by only one UD, and each UD can occupy only one channel at the same time. ∑i=1ncip = 0 denotes that the state of channel cp is idle. ∑p=1qcip = 0 denotes that task queue Bi generated by ui is to be executed locally, and the channel resources will not be used. cip = 1 denotes that ui selects the channel cp to communicate with the edge server. When the mobile device offloads the tasks to the edge server to complete the calculation, the uplink transmission rate of ui is denoted by ξi and calculated by Eq. (2) [29].

ξi=Blog2⁡(1+pigi,cpσ2)(2)

where B denotes the channel bandwidth and pi is the transmission power of UD ui. Here, σ2 is the additive white Gaussian noise power spectral density. gi,cp represents the channel gain of UD ui with channel cp.

3.3 Computing Model

In our network architecture, the task can be executed locally on the mobile device or offloaded to the edge server via the AP. Here, we introduce the local computing model and Mobile Edge Execution Model in detail.

In practice, different sorts of UDs may have distinct configurations. Here, we denote filoc as the computing capability of UD ui (CPU-cycles/second), and zij reflects the requested CPU cycles for processing the task bij. Thus, when the mobile device processes the computing task locally, we denote the local execution time of UD ui as

liloc=∑j=1m(1−φij∑p=1qcip)zijfiloc(3)

here, ∑p=1qcip is used to represent whether or not the channel selection is successful. When φij = 1 and ∑p=1qcip = 1, it means that ui can be assigned an idle channel, and the task bij will complete the calculation on the remote server. When φij = 1 and ∑p=1qcip = 0, the channel selection of ui is failed, which means that the selected channel is busy. Next, when the computation task is executed locally, the energy consumption of UD ui is calculated as

eiloc=∑j=1m(1−φij∑p=1qcip)zijk(filoc)2(4)

where k(filoc)2 is the model of energy consumption per computing cycle [30]. Here, k is an energy coefficient, and it is directly affected by the hardware architecture.

Next, when the mobile device offloads the computing task to the nearby edge server to complete the calculation, we only consider the overhead of both uploading transmission and remote computing. In most instances, the size of the task computation results is small, and the speed of data transmission between the edge server and mobile devices is fast because of the higher downlink rate. Thus, we neglect energy consumption and latency during the process of returning the result. The total processing overhead of the task queue Bi includes two parts: one is the cost of sending the data from the mobile device to the edge server via the AP, and the other is the cost of the task execution time on the edge server.

In each time slot, we denote the percentage of computation resources assigned for the edge server to process the task queue Bi by β(t) = <γ1, γ2, . . . , γi,. . . , γn>, where γi ∈ [0,1] and ∑i=1nγi≤1. According to the above description, the total latency of the mobile edge execution model is calculated as

liMEC=litra+liap(5)

where litra stands for the transmission latency of task queue Bi and liap is the computing time of the edge server. We furthermore denote the litra and liap as

litra=∑j=1mφij∑p=1qcipsiξiandliap=∑j=1mφij∑p=1qcipziγi fMEC(6)

where we denote fMEC as the computing capability of the edge server (CPU-cycles/second). In each time slot, the corresponding overall energy consumption for UD ui to offload the task to the edge server can be expressed as

eiMEC=eitra+eiap(7)

Similarly, he total energy consumption includes the energy consumption for transmission and computation. eitra denotes the energy consumption for transmission and eiap is the energy consumption for computation. We furthermore denote the eitra and eiap as

eitra=∑j=1mφij∑p=1qcipsiξipiandeiap=∑j=1mφij∑p=1qcipzik(γifMEC)2(8)

where the energy coefficient k = 10−27, we adopt the measurement result of reference [30].

3.4 Energy Consumption

Through the above analysis, when multiple tasks are generated by the UD ui, each computation task can be offloaded to the edge server or executed locally to complete the calculation. We can calculate the latency of the task queue Bi through the offloading decision, and the latency can be described as

li=max(liloc,liMEC)=max(∑j=1m(1−φij∑p=1qcip)zijfiloc,∑j=1mφij∑p=1qcipsiξi+∑j=1mφij∑p=1qcipziγi fMEC)(9)

where li is equal to the higher value among liloc and liMEC. The task queue Bi can simultaneously offload to the edge server and execute locally to complete the calculation. Thus, the latency equals the time value for completing all tasks. In each time slot, we can denote the total latency in the entire MEC system as

l=∑i=1nli=∑i=1nmax(liloc,liMEC)(10)

Then, the corresponding energy consumption for completing the task queue Bi is given by

ei=eiloc+eiMEC=∑j=1m(1−φij∑p=1qcip)zijk(filoc)2+∑j=1mφij∑p=1qcipsiξipi+∑j=1mφij∑p=1qcipzik(γifMEC)2(11)

In each time slot, we can denote the sum of energy consumption in the entire MEC system as

e=∑i=1nei=∑i=1n(eiloc+eiMEC)(12)

3.5 Problem Formulation

In this work, we aim to maximize the energy efficiency of the entire MEC system under the latency constraint by investigating the joint optimization problem of offloading decisions and resource allocation in time-varying environmental conditions. We can describe the joint optimization problem as

minC(t),Φ(t),β(t)∑i=1n[(1−α)li+αei]s.t.    γi∈[0,1]          li≤Δ          φij∈{0,1}(13)

We focus on the coordinated optimization problem for latency-aware and energy-efficient offloading applications. In (13), α denotes the weight parameters for latency and energy consumption, and α ∈ [0,1], which can be adjusted by the demand of the application. We assume that the multiple tasks generated by a UD can select the local or edge server to execute the computation task. Thus, given an offloading decision, the computation tasks can be divided into several subtasks for parallel execution with the mobile device or edge server. li ≤ Δ is designed to confine the task execution time. li is equal to the higher value between liloc and liMEC, and it is no more than the maximum tolerable latency. Φ(t) denotes the offloading decision of all the UDs. φij = 0 denotes that the computation task bij is executed locally, and φij = 1 denotes that the computation task bij is offloaded to the edge server.

We aim to minimize long-term energy consumption within the maximum tolerated latency constraint in the entire offloading process. As we all know, the above problem is essentially an NP-hard problem, and it requires exponential time complexity to find the optimal solution. The existing research provides efficient methods to address the NP-hard optimization problem, such as heuristic and meta-heuristic algorithms [31]. However, these methods are prone to finding local optimal results or require too many parameters. In contrast, deep reinforcement learning can be an effective solution to solve this problem, as it combines the advantages of reinforcement learning and deep learning. It can capture the hidden dynamics of the current environment and leverage the efficiency of self-learning and self-adaptation capabilities. In this paper, we further propose a multi-agent deep reinforcement learning method to tackle the combinatorial optimization problem, which can effectively adapt to a dynamic environment during data transmission compared to the single-agent approach.

4  MADRL Approach

In this section, we approximate the optimization problem as a Markov game, and our objective is to minimize the long-term energy consumption within the maximum tolerated latency constraint in a dynamic MEC system. We propose a bi-level actor-critic (Bi-AC)-based method to solve the combinatorial optimization problem. The Bi-AC optimization method [16] is based on the actor-critic learning structure, which allows agents to have different knowledge bases, and it can effectively optimize the energy consumption of the entire MEC system by reducing the resource preemption problem significantly. First, we describe the details of the Markov game problem. Second, we further propose a multi-agent deep reinforcement learning algorithm for our problem.

4.1 RL Problem Formulation

In the multi-agent environment, agents can learn cooperation policies with other agents to better solve resource allocation and task offload problems. At each time slot, the agent selects an action and interacts with the environment by observing the current environment and other agents’ actions. We formulate the optimization problem as an n-player Markov game, which is described as a tuple <Si, Ai, p, Ri, λ> for agent i, where S denotes the set of finite state space, Ai denotes the set of finite action space, and p denotes the transition function, which represents the transition probability from the current state to the next state. Ri and λ stand for the reward function for agent ui and the discount factor, respectively. Here, λ ∈ [0,1]. λ represents the importance of future rewards. The agent ui aims to maximize the cumulative discounted reward value Gt=∑t=0∞λtRit+1. Next, we define the state space, action space, and reward functions as S(t), A(t), and R(t), respectively.

4.1.1 State Space

The state space of the network environment includes the state of channel resources and computation offloading tasks. Thus, the state space Si(t) at each time slot can be formulated as

Si(t)={1−∑i=1nγi,C(t),si,zi,pr}(14)

where 1−∑i=1nγi stands for the percentage of spare computation resources, where γi ∈ [0,1] is the percentage of computation resources assigned to the edge server to process the task queue Bi. C(t) represents the current channel state under the MEC system. pr is the priority of the task to match the practical situations, and pr ∈ {1, 2, 3} stands for the importance of the task. The maximum value represents the highest priority.

4.1.2 Action Space

The agent aims to determine optimized action strategies to realize the best long-term goal by interacting with the environment. In our proposed method, the action space for the MEC system is composed of the task offloading decision Φ(t), the channel selection C(t), and the computation resources allocation policy β(t). Therefore, the action space at for agent i can be given as follows:

Ai(t)={φi,γi}(15)

here, if ∑j=1mφij = 0, we do not allocate the channel resource to ui. If ∑j=1mφij > 0, we traverse the matrix C(t) to allocate a channel. For example, when ∑j=1mφij > 0, we allocate the channel resource to ui by traversing C(t) of each column in sequence. Once we find the expression ∑i=1ncip = 0, we allocate the idle channel cp to ui. If all the result of ∑i=1ncip is equal to 1, the channel allocation will fail, which means the task queue Bi are executed locally.

4.1.3 Reward Function

In general, the performance of the MEC system mainly depends on energy consumption and latency, and the total reward is the sum of the reward of all UDs. We utilize these two crucial metrics to formulate the reward function Ri(t) as follows:

Ri(t)=∑i=1n(pri((1−α)Ril(t)+αRie(t)))(16)

where Ril(t) is the reward of the latency and Rie(t) is the reward of the energy consumption. α denotes the weight factors of the latency reward and the energy consumption reward for the task queue Bi in each time slot. In addition, pr stands for the task priority to indicate the importance of the task. In the following, we furthermore denote the reward of the latency Ril(t) in detail.

Ril(t)=−lit(17)

In (20), it should be noted that the total task executing time is less than the maximum tolerable latency Δ. If the execution time exceeds the Δ, we set the reward as a punitive negative. Next, we describe the reward of latency Rie(t)

Rie(t)=−eit=−(eiloc,t+eiMEC,t)(18)

In this combinatorial optimization problem, we aim to minimize the energy consumption within the maximum tolerated latency constraint in the entire MEC system. However, the goal of reinforcement learning is to maximize cumulative discounted rewards. Therefore, we use the negative ratio of the energy consumption function as the reward function. Through the above analysis, our objective can convert to maximize long-term reward expectations by achieving a series of strategies, which can be expressed as

π∗=arg maxπ Eπ[∑t=0∞λtRt+1](19)

where π = {π1, π2, . . . , πi, . . ., πn} is the action strategy of all UD, and πi denotes the policy of UD ui, which is composed of task offloading decision, channel selection policy, and computation resources allocation policy.

4.2 Bi-AC-Based Solution

In this section, we introduce the bi-level actor-critic algorithm [16], which is based on the actor-critic learning structure and can perform well in the combinatorial optimization problem. The Bi-AC algorithm consists of two components: upper-level optimizer and lower-level optimizer. The upper-level optimizer is the critic network that outputs the approximate Q-value and takes actions by observing the current environment. The lower-level optimizer consists of the actor and critic networks, which take action by observing the current environment and the actions of the upper-level optimizer. To adapt to the MEC system, we assign one agent for each UD. Thus, we extend the bi-level actor-critic algorithm to the multi-level actor-critic algorithm, where each level includes one agent, and the lower-level agents take action by observing the actions of all the upper-level agents. In this way, we can effectively reduce the problem of resource preemption by observing the actions of each other, such as channel and computing resources. It is noteworthy that the convention of multi-agent deep reinforcement learning methods is to address the Markov game by finding a Nash equilibrium (NE). However, our method treats agents unequally, and the object is to find the Stackelberg equilibrium (SE) because SE can yield a better payoff compared to the average NE in cooperative environments [16].

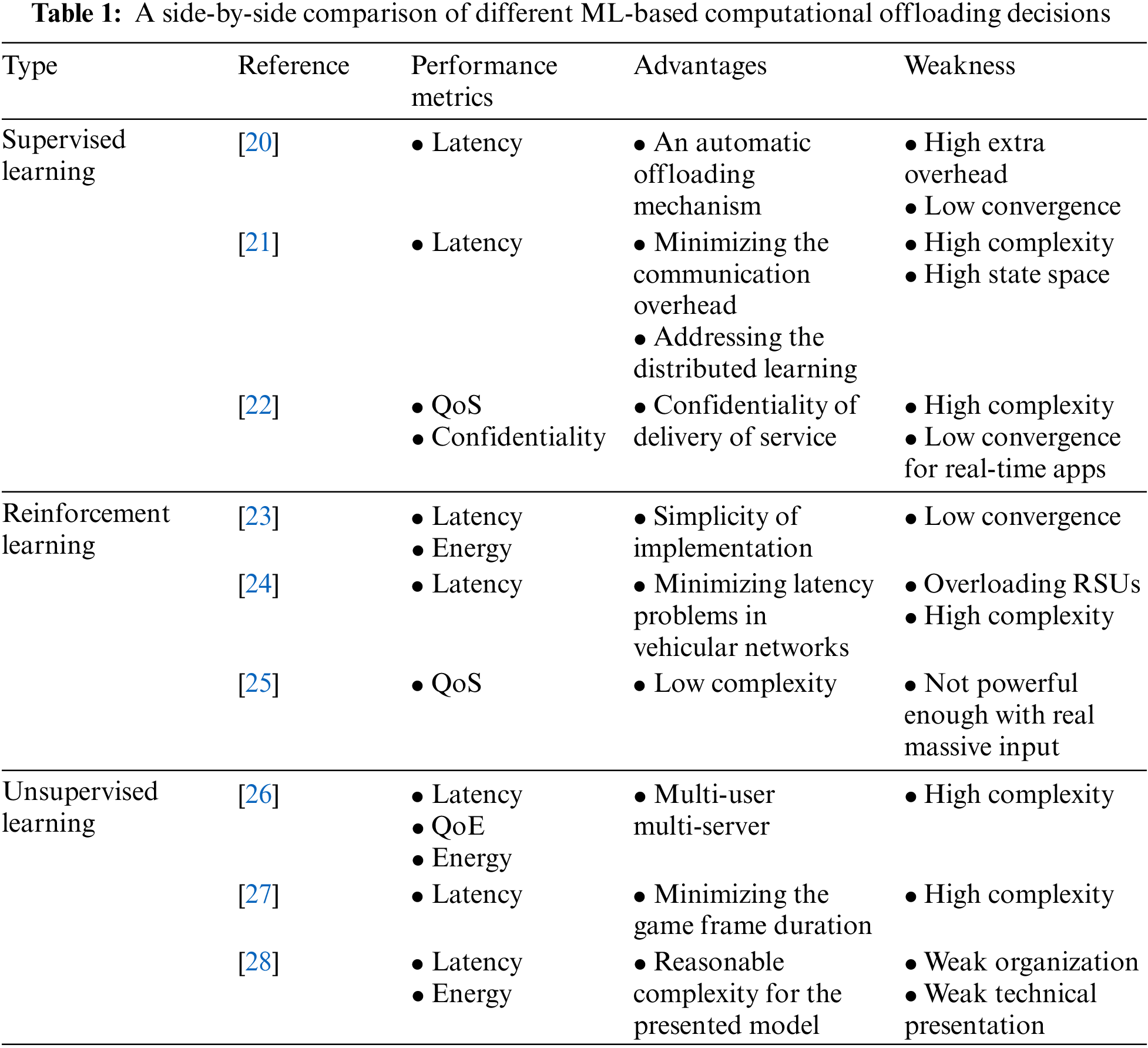
Fig. 1 shows the network structure of the Bi-AC-based method and more specific detail. ui first obtains the initial state by observing the initial MEC system, which includes channel conditions, computation resources, and the attribute of the corresponding tasks, and then inputs the current state into the actor network. The actor network will output the action Ai with the initial parameters. Next, the agent executes the action Ai to interact with the current environment to get the reward Ri, and then the current state is updated to the next state. Thus, we can get the experience tuple (Sit, Ait, Rit, Sit+1), which will be stored in the local experience replay buffer of UD ui at each time step t.

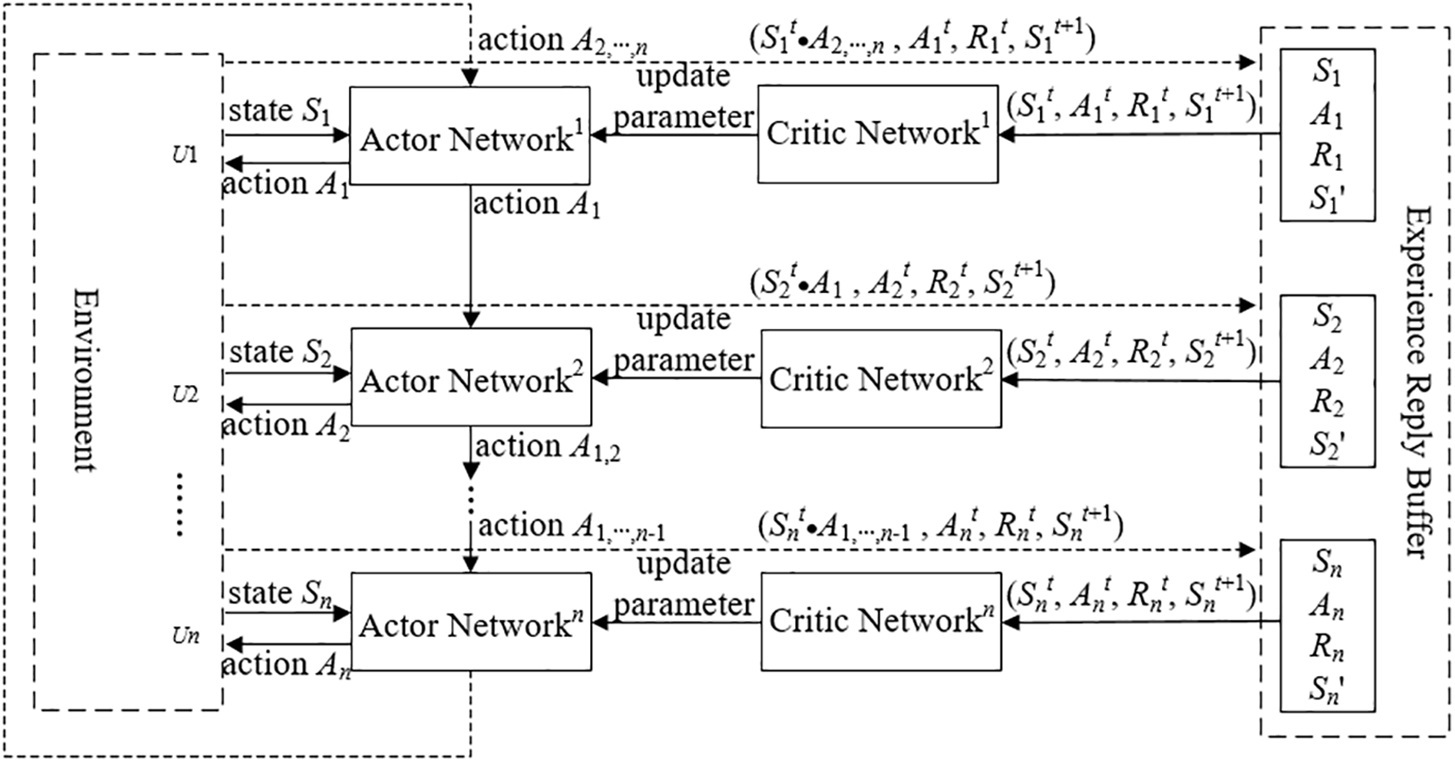
Figure 1: Network structure applied to task offloading

Then, we use the local experience replay buffer to train the critic network using the TD error method [10]. The critic network is an approximate value function that can output the Q-value of the current action of ui by inputting Si and Ai. It is noteworthy that the agent i require to consider the actions of all the upper-level agents to make a decision. This operation can effectively reduce resource competition, such as channel and computing resources. Thus, the state Si includes the current state and all the upper-level agents’ actions taken. For example, the three-level agent will take the action of the one-level agent and two-level agent as its input in addition to the current state, and it can be denoted by Sit = Sit • A1,…,i−1 as Fig. 1 shows, where “•” represents merging operation, which merge these two vectors into one. Next, we can update the weights of the actor network to minimize the overall losses using the sampled gradient method. In the training phase, all the networks are updated accordingly from the upper-level to the lower-level. In the execution phase, as Fig. 2 shows, we assign one agent to each UD, and each agent has all the trained n actor networks. Then, all the agents independently perform Stackelberg equilibrium.

Figure 2: The execution phase of the Bi-AC-based method

The output of the actor network is the action value, and the critic network can output the Q-value to evaluate the action produced by the actor network. For each ui, the output of actor network consists of two parts, which contain φi and γi. φi is the one-dimensional vector with m elements. γi ∈ [0,1] represents the computation resources assigned to the edge server for task queue Bi. Next, we will describe the detail of the actor network and the critic network.

The actor network consists of a two-layer fully connected network with the ReLU activation function and an output layer with m + 1 node. The first m nodes denote the offloading decision for task queue Bi. The m + 1th node stands for the computation resources assigned. The output layer goes through the sigmoid activation function. This results in a series of probability values. If the probability values of the first m + 1 rows are greater than 0.5, we set the task φij to 1, indicating that task φij is executed on the remote server. If ∃ φij = 1, we will allocate the channel resource to ui. Additionally, it is important to consider the randomness of the actor network to generate more diverse data. Therefore, we combine the output probability with the ɛ-greedy approach to choose the output action and determine whether to offload the task. The critic network also consists of a two-layer fully connected network with the ReLU activation layer and an output layer with one node. The critic network can output the Q-value of the current action of ui by inputting the state Si and action Ai, and the Q-value Qπ(St, At) can be described as

Qπ(St,At)=R(St,At)+λ∑St+1p(St+1|St,At)V∗(St+1)=R(St,At)+λ∑St+1p(St+1|St,At)maxAt+1Qπ(St+1,At+1)(20)

At the beginning of the training phase, each UD will randomly select a minibatch of W samples from the local experience replay buffer to train the network. We denote the policy model as follows:

Ai=πi(Si,A1..i−1;θi)(21)

where θi stands for the policy parameter. For the environments with discrete action space, we utilize the sampled gradient method to update the actor network, which is denoted as

∇θiJ=1W∑∇θilog⁡πi(Si,A1..i−1)×Qπi(Si,A1..n)(22)

Next, the critic network updates the weight using the TD error method. The TD error is represented as follows:

δi=Ri+λQπ′i(Si,A1..n′)−Qπi(Si,A1..n)(23)

At each iteration, we achieve the target value by minimizing the loss function Loss(θi), which can be expressed as follow:

Loss(θi)=1W∑(Ri+λQπ′i(Si,A1..n′)−Qπi(Si,A1..n))2(24)

In this paper, we extend the bi-level actor-critic algorithm to the multi-level actor-critic algorithm to adapt to the MEC system. The Bi-AC-based method can effectively reduce the occurrence of the resource preemption problem by observing the actions of the upper-level agents, and it can reduce energy consumption while satisfying the maximum tolerated latency constraint.

5  Simulation Results

In this section, we illustrate the performance of the proposed method through the simulations in dynamic cooperative environments and use Python as the programming language and compare the performance of various methods through TensorFlow. We premeditate a scenario with n UDs and one AP.

5.1 Experiment Settings

Here, we set the computation capabilities of the MEC server fMEC to be randomly distributed between 10 and 20 GHz, and the computation capabilities of each UD are uniformly distributed between 0.5 and 1.5 GHz. We set the channel bandwidth B = 10 MHz. Similar to the relevant paper [32], the path loss is modeled as 128.1 + 37.6log(l), where l is the distance from MEC to UD. The data size of computation tasks for a UD is randomly distributed between 1000 and 2000 KB, and the number of subtasks for a task queue Bi is randomly distributed between 5 and 10. The corresponding number of CPU cycles required for the UD’s tasks are randomly distributed between 0.5 and 3 GHz, and we set the transmission power of each UD to 20 dBm. The capacity of the global experience replay buffer is equal to 1000, and the selected minibatch sample is equal to 32. For the reinforcement learning algorithm, the learning rate parameter is set to 0.01, and the discount factor is set to 0.9.

In addition, we provide the following four representative benchmark methods to compare the performance of our method, and the details are as follows:

(1)   Actor–critic: Actor–critic is a policy gradient algorithm, and it is different from our method. In the training phase, the actor–critic algorithm only utilizes local information, which means the UD cannot communicate with each other.

(2)   Random offloading: The UDs randomly select whether the computation tasks offload to the edge server to complete the calculation or can be executed locally.

(3)   All local execution: All the computation tasks of UDs are executed locally under the maximum tolerant latency, or else UDs will offload the computation tasks to the edge server.

(4)   All offloading execution: All the computation tasks of UDs are offloaded to the edge server to complete the calculation. When the resource of the edge server is occupied entirely, the new tasks will be waiting.

(5)   Exhaustion: The exhaustion method can obtain the approximate optimal solution by brute-force search, but it is difficult to be used in practical situations because of the substantial overhead.

In each time slot, we assume that the wireless channel remains constant, but the resource requirements of computation tasks are different. Thus, it is important to capture the current environment’s hidden dynamics to make a policy.

5.2 Numerical Results

We utilize the multi-agent deep reinforcement learning method to effectively adapt to the dynamic changes, which can learn the cooperation policy and allocate resources dynamically compared with the baseline methods. Next, we illustrate the convergence performance of the proposed method and compare the performance of the proposed method with the baseline methods.

Fig. 3 shows the convergence performance of the proposed Bi-AC-based method and actor-critic-based method, which illustrates the changing trend of average system reward with the increase of training episodes. This is the two-level Bi-AC-based method with two agents. Leader and follower are expressed as the upper-level agent and the lower-level agent, respectively. The leader is converged before the follower because of the difference in learning rate. From the figure, we can see that Bi-AC can obtain better performance and greater stability than the actor-critic method. In a single-agent environment, the actor-critic algorithm can provide clear performance benefits, but its performance will continually decline due to the rising number of agents. The actor-critic algorithm can only utilize the local information of a single agent to train the model, which cannot learn the cooperative policy with each other. In contrast, the proposed Bi-AC-based method can effectively reduce the occurrence of the resource preemption problem by observing the action of other agents, and it can utilize the global information to learn the cooperative policy to maximize the global reward in the multi-agent environment.

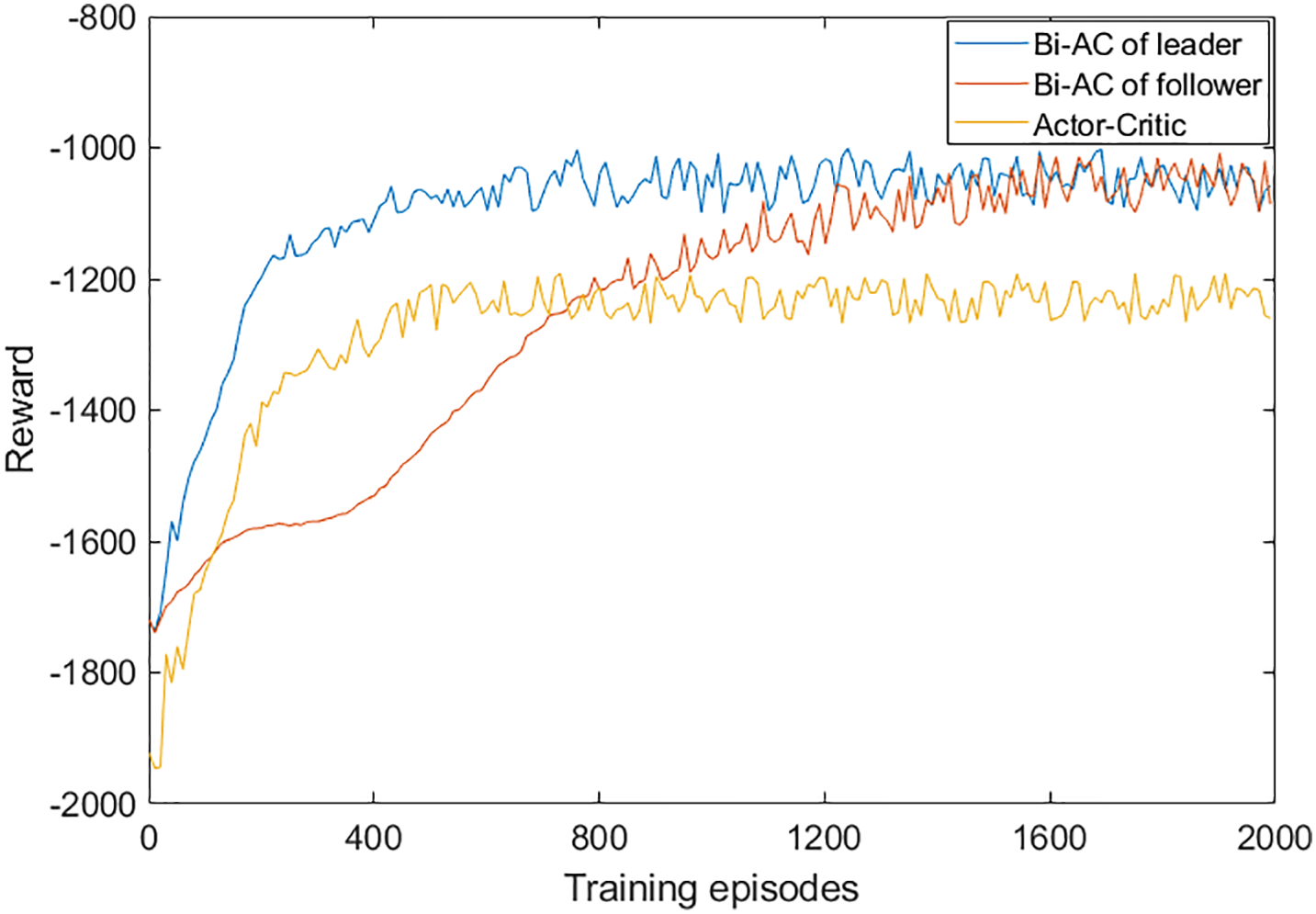
Figure 3: System reward with training episodes

Fig. 4 describes the total computational overhead of the six methods with the difference in the number of UDs. We fix the corresponding number of CPU cycles required for the UD’s tasks to 0.5 Megacycles, and the total MEC computing resource is 10 GHz. The total computational overhead o = ∑i=1n[(1−α)li+αei] includes energy consumption and computation latency, which is mentioned in Eq. (13). From the figure, we can find that the exhaustion method can achieve less computational overhead than other methods throughout the process. This is because the exhaustion method adopts the optimal action by filtering all the action space of the agent, but the brute-force search cannot be implemented in the practical situation due to the more time-consuming. The computational overhead of our method is closer to the exhaustion method than other methods, which has better performance for the offloading decision and resource allocation.

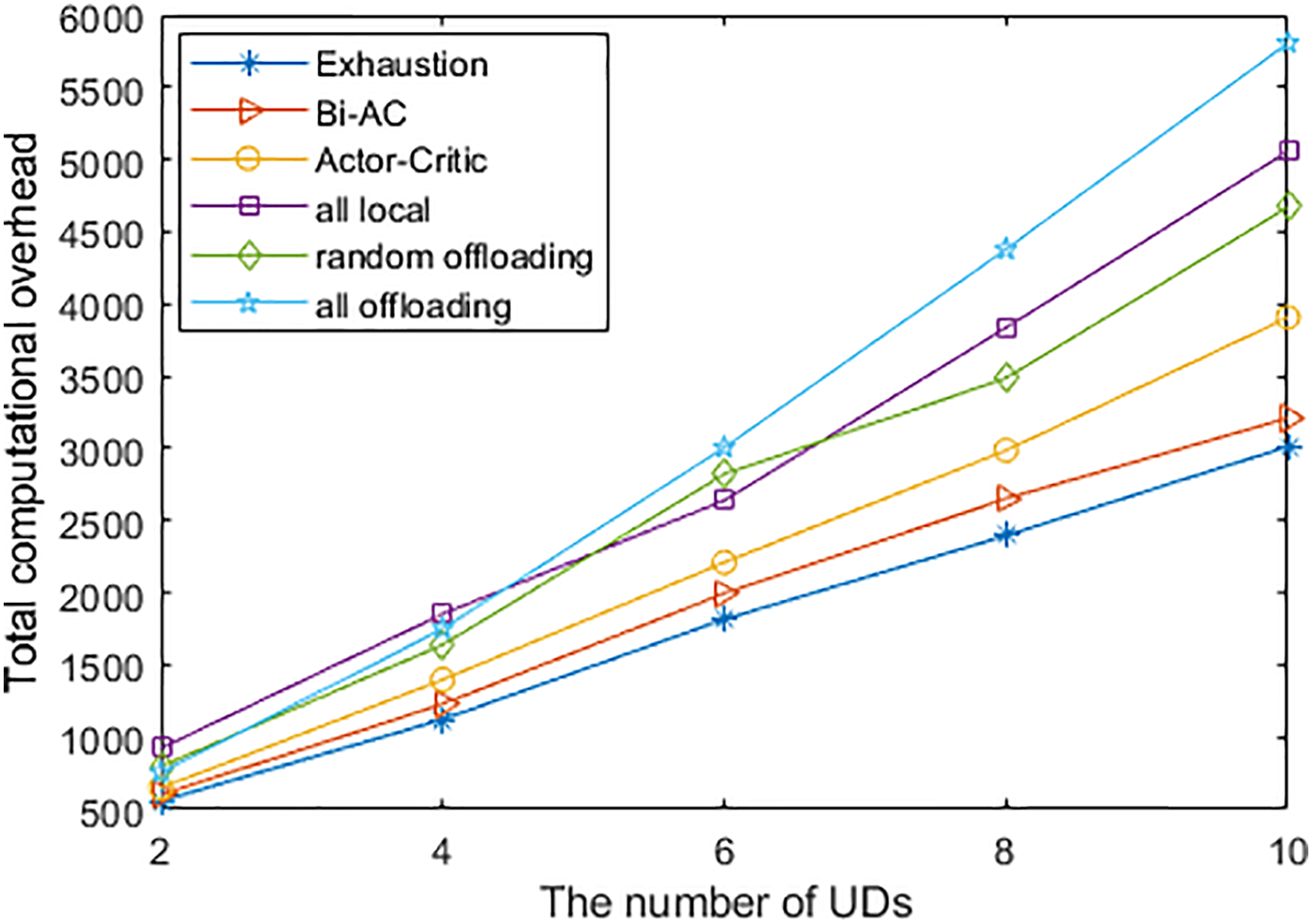
Figure 4: Total computational overhead with different numbers of UDs

When the number of UDs is 6, the total computational overhead of all offloading execution exceeds all local execution. This is because all offloading execution are not fully considered resource allocation. With the increase of UDs, a larger number of tasks will offload to the edge server to complete the calculation. The resource will be fewer for each UD, and the computational overhead of transmission and computation will increase significantly. When the number of UDs is 10, the proposed Bi-AC-based method can reduce 17.8%, 36.5%, 31.3%, and 44.7% total computational overhead compared with the actor-critic-based method, all local execution, random offloading, and all offloading execution, respectively. In addition, the computational overhead of our method increases slowly compared with the baseline methods. This is because the baseline methods cannot allocate the communication and computation resources intelligently. As the number of UDs increases, the available resources of computing services become more and more inadequate to process the task in real-time, and the problem of resource preemption becomes more significant. At this point, the advantage of the optimized resource allocation will emerge, and our method can excel in solving this problem.

In this experiment, we fix the number of UDs to 6, and the total MEC computing resource is 10 GHz. Fig. 5 compares the total computational overhead of the six methods with the number of CPU cycles required by the task in Fig. 5. It is not difficult to see that with the gradual increase in the number of CPU cycles required by the task, the total computational overhead of the six methods also grows, and it can be seen from the Eqs. (10) and (12). Except for the Exhaustion method, the proposed Bi-AC-based method remains superior to the performance due to the optimized resource allocation policy. As can be seen from the figure, the computational overhead of the all-local execution method exceeds the all-offloading execution method when the CPU cycles required by the task are equal to 2 Megacycles. This is because the local terminal cannot complete all the calculation tasks under the maximum tolerant latency, and the remaining tasks need to be transported to edge servers to complete the calculation, which will generate more energy consumption for transmission. Therefore, the all-local execution method will lead to more computational overhead when the required computation resources of the task go beyond a certain range.

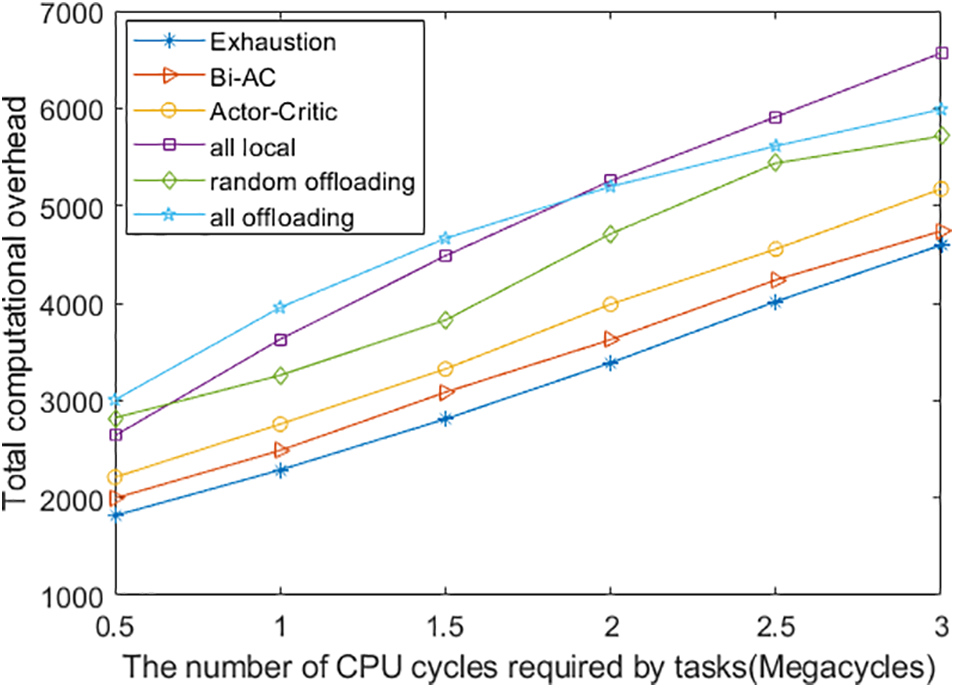
Figure 5: Total computational overhead with different numbers of required CPU cycles

Finally, Fig. 6 shows the relationship between the total computational overhead and the total MEC computing resources. For this experiment, we vary the allocated MEC computing resources from 10 to 20 GHz. We also fixed the number of UDs to 6, and the corresponding number of CPU cycles required for the UD’s tasks is 0.5 Megacycles. We can see that the performance of the proposed Bi-AC-based method is also better than the other methods, except for the exhaustion method. The all-offloading method consumes more computational overhead than other methods at 10 GHz. However, with the increase of the allocated MEC computing resources, the computational overhead of the all-offloading method becomes smaller than that of the all-local method. This is because as the execution capacity of the edge server increases, the remote computation latency will decrease significantly. In summary, the Bi-AC-based method outperforms other baseline methods in different scenarios by learning the cooperation policy with each agent.

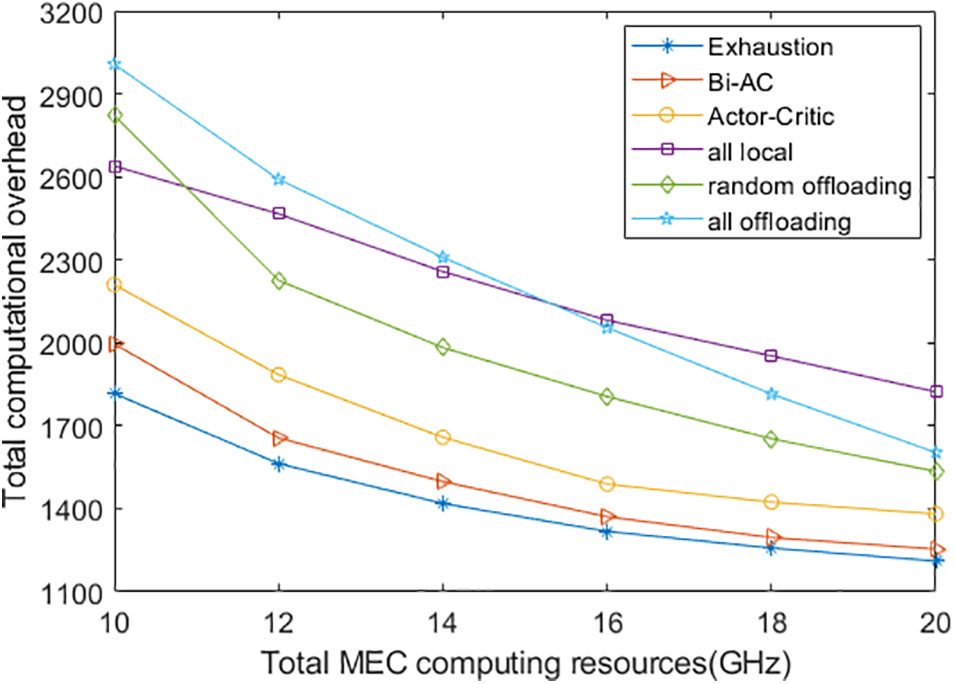
Figure 6: Total computational overhead with different total MEC computing resources

6  Conclusion and Future Work

In this paper, we investigate the computation offloading problem, which aims to maximize the performance in terms of energy consumption and latency of the entire MEC system. In the multi-agent environment, existing studies do not fully consider the resource conflict problem, and resource conflict is an important factor that directly affects performance. We propose the Bi-AC-based method to significantly reduce the resource conflict problem among agents by fully considering the actions of other agents, which is a multi-level structure optimization design. The proposed method can select the optimal offloading decision and resource allocation policy to achieve the best long-term goal using an asymmetric method. The simulation results show that the proposed method could decrease total computational overhead by 17.8% compared to the actor-critic-based method and reduce the total computational overhead by 31.3%, 36.5%, and 44.7% compared to random offloading, all local execution, and all offloading execution, respectively. For future work, we will expand the number of edge servers and coordinately optimize the offloading decision and resource allocation for latency-aware and energy-efficient offloading applications in a dynamic environment.

Acknowledgement: The authors are grateful to all the editors and anonymous reviewers for their comments and suggestions.

Funding Statement: This work was supported by the National Natural Science Foundation of China (62162050), the Fundamental Research Funds for the Central Universities (No. N2217002), and the Natural Science Foundation of Liaoning Provincial Department of Science and Technology (No. 2022-KF-11-04).

Author Contributions: Study conception and design: T. Jiao, J. Song; Data collection: T. Jiao; Analysis and interpretation of results: T. Jiao, X. Feng, C. Guo, and D. Wang; Draft manuscript preparation: T. Jiao, C. Guo. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The data that support the findings of this study are available from the corresponding authors upon reasonable request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. G. Premsankar, M. D. Francesco and T. Taleb, “Edge computing for the Internet of Things: A case study,” IEEE Internet Things Journal, vol. 5, no. 2, pp. 1275–1284, 2018. [Google Scholar]

2. Y. Chen, F. Zhao, X. Chen and Y. Wu, “Efficient multi-vehicle task offloading for mobile edge computing in 6G networks,” IEEE Transactions on Vehicular Technology, vol. 71, no. 5, pp. 4584–4595, 2022. [Google Scholar]

3. Y. Mao, C. You, J. Zhang, K. Huang and K. B. Letaief, “A survey on mobile edge computing: The communication perspective,” IEEE Communications Surveys & Tutorials, vol. 19, no. 4, pp. 2322–2358, 2017. [Google Scholar]

4. W. Shi, J. Cao, Q. Zhang, Y. Li and L. Xu, “Edge computing: Vision and challenges,” IEEE Internet of Things Journal, vol. 3, no. 5, pp. 637–646, 2016. [Google Scholar]

5. S. Bi and Y. J. Zhang, “Computation rate maximization for wireless powered mobile-edge computing with binary computation offloading,” IEEE Transactions on Wireless Communications, vol. 17, no. 6, pp. 4177–4190, 2018. [Google Scholar]

6. N. Abbas, Y. Zhang, A. Taherkordi and T. Skeie, “Mobile edge computing: A survey,” IEEE Internet of Things Journal, vol. 5, no. 1, pp. 450–465, 2018. [Google Scholar]

7. S. Wang, X. Zhang, Y. Zhang, L. Wang, J. Yang et al., “A survey on mobile edge networks: Convergence of computing caching and communications,” IEEE Access, vol. 5, pp. 6757–6779, 2017. [Google Scholar]

8. Y. Chen, N. Zhang, Y. Zhang and X. Chen, “Dynamic computation offloading in edge computing for Internet of things,” IEEE Internet of Things Journal, vol. 6, no. 3, pp. 4242–4251, 2019. [Google Scholar]

9. A. Asheralieva and D. Niyato, “Bayesian reinforcement learning and Bayesian deep learning for blockchains with mobile edge computing,” IEEE Transactions on Cognitive Communications and Networking, vol. 7, no. 1, pp. 319–335, 2021. [Google Scholar]

10. R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction, 2nd ed., Cambridge, MA, USA: MIT Press, 2018. [Google Scholar]

11. M. Riedmiller, “Neural fitted Q iteration-first experiences with a data efficient neural reinforcement learning method,” in Proc. of European Conf. on Machine Learning, Porto, Portugal, pp. 317–328, 2005. [Google Scholar]

12. V. Mnih, “Human-level control through deep reinforcement learning,” Nature, vol. 518, no. 7540, pp. 529–533, 2015 [Google Scholar] [PubMed]

13. H. Zhou, K. Jiang, X. Liu, X. Li and V. C. M. Leung, “Deep reinforcement learning for energy-efficient computation offloading in mobile edge computing,” IEEE Internet of Things Journal, vol. 9, no. 2, pp. 1517–1529, 2022. [Google Scholar]

14. X. Zhou, W. Liang, K. Yan, W. Li, K. I. Wang et al., “Edge enabled two-stage scheduling based on deep reinforcement learning for Internet of everything,” IEEE Internet of Things Journal, vol. 10, no. 4, pp. 3295–3304, 2023. [Google Scholar]

15. J. Foerster, N. Nardelli and G. Farquhar, “Stabilising experience replay for deep multi-agent reinforcement learning,” in Proc. of the 34th Int.Conf. on Machine Learning, NSW, Australia, pp. 1146–1155, 2017. [Google Scholar]

16. H. Zhang, W. Chen, Z. Huang, M. Li and Y. Yang, “Bi-level actor-critic for multi-agent coordination,” in Proc. of the AAAI Conf. on Artificial Intelligence, NY, USA, pp. 7325–7332, 2020. [Google Scholar]

17. S. Mao, S. Leng and Y. Zhang, “Joint communication and computation resource optimization for NOMA-assisted mobile edge computing,” in Proc. of IEEE Int. Conf. on Communications, MO, USA, pp. 1–6, 2019. [Google Scholar]

18. T. X. Tran and D. Pompili, “Joint task offloading and resource allocation for multi-server mobile-edge computing networks,” IEEE Transactions on Vehicular Technology, vol. 68, no. 1, pp. 856–868, 2019. [Google Scholar]

19. Z. Ning, P. Dong, X. Kong and F. Xia, “A cooperative partial computation offloading scheme for mobile edge computing enabled Internet of Things,” IEEE Internet of Things Journal, vol. 6, no. 3, pp. 4804–4814, 2019. [Google Scholar]

20. X. Chen, M. Li, H. Zhong, Y. Ma and C. H. Hsu, “DNNOff: Offloading DNN-based intelligent IoT applications in mobile edge computing,” IEEE Transactions on Industrial Informatics, vol. 18, no. 4, pp. 2820–2829, 2021. [Google Scholar]

21. T. Mohammed, C. J. Wong, R. Babbar and M. D. Francesco, “Distributed inference acceleration with adaptive DNN partitioning and offloading,” in Proc. of IEEE Conf. on Computer Communications, ON, Canada, pp. 854–863, 2020. [Google Scholar]

22. A. K. Sangaiah, D. V. Medhane, T. Han, M. S. Hossain and G. Muhammad, “Enforcing position-based confidentiality with machine learning paradigm through mobile edge computing in real-time industrial informatics,” IEEE Transactions on Industrial Informatics, vol. 15, no. 7, pp. 4189–4196, 2019. [Google Scholar]

23. J. Wang, K. Liu, M. Ni and J. Pan, “Learning based mobility management under uncertainties for mobile edge computing,” in Proc. of IEEE Global Communications Conf. (GLOBECOM), Abu Dhabi, United Arab Emirates, pp. 1–6, 2018. [Google Scholar]

24. J. Zhang, H. Guo and J. Liu, “A reinforcement learning based task offloading scheme for vehicular edge computing network,” in Proc. of Artificial Intelligence for Communications and Networks, Harbin, China, pp. 438–449, 2019. [Google Scholar]

25. H. Li, K. Ota and M. Dong, “Learning IoT in edge: Deep learning for the Internet of Things with edge computing,” IEEE Network, vol. 32, no. 1, pp. 96–101, 2018. [Google Scholar]

26. J. Sheng, J. Hu, X. Teng, B. Wang and X. Pan, “Computation offloading strategy in mobile edge computing,” Information, vol. 10, no. 6, pp. 191, 2019. [Google Scholar]

27. M. Jia and W. Liang, “Delay-sensitive multiplayer augmented reality game planning in mobile edge computing,” in Proc. of the 21st ACM Int. Conf. on Modeling, Analysis and Simulation of Wireless and Mobile Systems, NY, USA, pp. 147–154, 2018. [Google Scholar]

28. A. Samir and C. Pahl, “DLA: Detecting and localizing anomalies in containerized microservice architectures using markov models,” in Proc. of the 7th Int. Conf. on Future Internet of Things and Cloud (FiCloud), Istanbul, Turkey, pp. 205–213, 2019. [Google Scholar]

29. R. Bultitude, “Measurement, characterization and modeling of indoor 800/900 MHz radio channels for digital communications,” IEEE Communications Magazine, vol. 25, no. 6, pp. 5–12, 1987. [Google Scholar]

30. X. Chen, “Decentralized computation offloading game for mobile cloud computing,” IEEE Transactions on Parallel and Distributed Systems, vol. 26, no. 4, pp. 974–983, 2015. [Google Scholar]

31. O. Skarlat, M. Nardelli, S. Schulte, M. Borkowski and P. Leitner, “Optimized IoT service placement in the fog,” Service Oriented Computing and Applications, vol. 11, no. 4, pp. 427–443, 2017. [Google Scholar]

32. L. Xiao, X. Lu, T. Xu, X. Wan, W. Ji et al., “Reinforcement learning-based mobile offloading for edge computing against jamming and interference,” IEEE Transactions on Communications, vol. 68, no. 10, pp. 6114–6126, 2020. [Google Scholar]