FedTC: A Personalized Federated Learning Method with Two Classifiers

1  Introduction

Machine learning mines experience and knowledge from large amounts of data, allowing computers to think more innovatively. However, data is often distributed across different devices or departments, which causes training of machine learning models prone to overfitting due to insufficient local data. Therefore, collecting data from multiple parties to the computing center is often necessary for centralized model training. However, people have become increasingly concerned about personal data privacy in recent years. Relevant regulations have also been issued in some countries and regions to protect personal data, such as the General Data Protection Regulation (GDPR) [1] in Europe and the Personal Information Protection Law [2] in China. Due to privacy and security concerns and regulatory prohibitions, data owners are no longer willing to share their source data with the computing center.

Federated learning (FL) [3] has been proposed to solve the privacy issue in centralized model training. FL allows multiple clients to train a deep learning model collaboratively by exchanging model parameters with the server and avoiding the direct sharing of raw data. Currently, federated learning is a crucial privacy computing technology widely used in finance [4], healthcare [5], telecommunications [6], and other fields [7–10]. However, since the data are usually generated locally, the distribution is non-independently and homogeneously distributed (Non-IID) across clients, also known as heterogeneous data. For example, the data held by different hospitals are often distributed differently due to their areas of expertise and geographical location. The study [11] has demonstrated that conventional federated learning algorithms struggle to achieve stable convergence when dealing with Non-IID data, resulting in a substantial decrease in model quality.

Traditional federated learning algorithms train only one global model. However, the study in [12] showed that the local optimal point for individual client data and the global optimal point for all data are inconsistent, especially when the data are Non-IID. Therefore, some personalized federated learning algorithms have recently been proposed to train a personalized model for each client rather than a single global model. For example, studies such as Per-FedAvg [13], Ditto [14], and FedAMP [15] introduced a local regularization term to allow clients to focus more on local objectives and train personalized local models. However, introducing the regularization term has brought a lot of additional computational load. To achieve personalization in a more lightweight manner, the approach of partial layer sharing has been proposed in studies such as FedPer [16], FedRep [17], FedBABU [18], and LG-FedAvg [19]. These studies divide the neural network layers of the model into two parts: the shared and personalized layers. In their methods, only the shared layers are uploaded to the server for aggregation in each training round, while the personalized layers are always trained locally. In this way, the personalized information of the classifier is retained, and thus the model performs better on local data. However, in these approaches, the shared model loses the information of the personalized layers that might benefit most clients [20].

Through our observations, we have found another reason for the loss of client personalization information: the client discarded old local models from each client in every federated training round. Specifically, within each training round in the traditional federated learning algorithm, the client performs the following steps after receiving the global model from the server. The client first discards the old local model and uses the received global model as the initialized model for local training. The client then independently updates the model in several steps on the local data and uploads the updated local model to the server for aggregation. However, it is important to note that the old local model contains valuable personalized information specific to the client’s data distribution. Discarding this information can negatively impact the test performance of the model on the client’s data, particularly at the classifier layer, which plays a crucial role in making final predictions based on the learned features from the input data.

Based on the aforementioned observations, we propose FeTC, a federated learning algorithm method with two classifiers. Unlike traditional federated learning algorithms, FeTC does not introduce regularization terms, which significantly reduces computational loads. Additionally, FeTC allows all layers to be shared, ensuring that no layer information is lost in the shared model. To achieve personalization, we employ a two-classifier training strategy in FeTC. Specifically, we define the last layer of the neural network as the classifier and the other neural network layers as the extractor. FedTC requires the client to upload the entire local model (extractor and classifier) to the server in each training round, as with FedAvg, to ensure that no information is left out. To ensure personalization, FedTC allows the local classifier to remain instead of discarded when obtaining the initial model for local training. To effectively use the global classifier, FedTC designs a two-classifier training strategy, where the global classifier acts as a second classifier to guide the update of the local model. Empirically, in the Non-IID setting, we demonstrate that FedTC performs better than FedAvg, FedPer, and Local.

Our paper makes the following contributions:

(1)   We analyzed the training process of federated learning. We discovered that personalized information in the model is lost due to the discarding of old local models in each round of training.

(2)   We propose a novel federated learning method called FedTC. FedTC does not use any regularization terms, thereby avoiding excessive computational overhead. Furthermore, FedTC allows all layers of the local model to be shared, ensuring that valuable information is not lost in the shared model. We also introduce a dual classifier training strategy into FedTC, which ensures personalization in federated learning and enhances its ability to handle heterogeneous data.

(3)   Our experiments on the Cifar10 and Cifar100 datasets demonstrate that FedTC can improve model accuracy on Non-IID data. In three Non-IID settings, FedTC outperforms FedAvg, FedPer, and local training. Notably, in extremely Non-IID cases, FedTC achieves a classification accuracy of 27.95% higher than that of FedAvg.

The structure of this paper is as follows. In Section 2, we review relevant literature on federated learning. Section 3 formally describes of classical federated learning algorithms and highlights their limitations. In Section 4, we propose the FedTC algorithm and describe it in detail, emphasizing the local training strategy that utilizes two classifiers. We evaluate our approach using the widely used Cifar10 and Cifar100 datasets in Section 5. Finally, in Section 6, we conclude and discuss future work.

2  Related Work

The first federated learning algorithm is FedAvg [3], proposed by Google, which is used to train word prediction models without collecting data on the user. In FedAvg, the client uploads model parameters instead of original data to the server in each training round. FedAvg can achieve the same effect as the centralized model training when the participants’ data are independent and identically distributed (IID). However, when the data is Non-IID, FedAvg is challenging to converge stably, and the trained global model performs poorly on the local data. Thus, many studies have made efforts to improve the performance of FedAvg on Non-IID data. Li et al. [21] introduced an L2 regularization term into the local objective function to limit the distance between the local and global models, making the model convergence more stable. According to the study [22], “client drift” is a significant factor contributing to the deterioration of joint learning performance. To address this problem, they propose SCAFFOLD, which utilizes control variables to correct client drift and improve federated learning performance. They also prove the effectiveness and convergence of SCAFFOLD through rigorous mathematical proof and experimental analysis. Zhao et al. [11] used Earth’s Mover’s Distance (EMD) to measure the difference in data distribution among clients. They found that the model accuracy would drop sharply when EMD reached a certain threshold. Therefore, they reduce EMD by sending clients a subset of global data. Experiments on the Cifar10 dataset show that only 5% of globally shared data can improve accuracy by about 30%. Also, to make clients’ data more IID, Jeong et al. [23] proposed a data enhancement strategy FAug based on Generative Adversarial Network (GAN). In this method, each client uploads seed data of the labels lacking samples to the server. The server then oversamples these seed data and uses them to train a GAN model. Finally, the client downloads the GAN model from the server and generates the missing data locally. Overall, although these studies improved FedAvg, only one global model was trained in their approach during the entire training process, which resulted in every client getting the same model at the end of the training. However, in the case of Non-IID local data distributions among clients, training a single global model may not meet the diversified local data [24].

To address the issue of Non-IID local data distributions among clients, personalized federated learning has been proposed as an alternative approach. Specifically, custom models are trained for each client instead of using the same model for all clients. This approach allows for greater flexibility and can better accommodate the diverse local data distributions. Researchers in [25] clustered clients according to the channel sparse vector uploaded by clients. Through clustering, the local data distribution of the same cluster client is more IID. In addition, Fallah et al. [13] introduced meta-learning into federated learning, where all clients work together to train a good initialization model. The client then fine-tunes the model on the local data to get a personalized model suitable for its local data. Li et al. [26] used model distillation in federated learning and assume that there was a large common dataset. During each training round, each client calculates the class scores on the common dataset and sends the class scores to the server for average aggregation to get the global average class score. Each client then downloads the global average class scores and performs model distillation to make the local class scores fit the global class scores. After receiving the trained model, the client continues training on their local dataset for several steps to obtain the final personalized model. However, these methods come with additional computational costs. In contrast, researchers in [16–19] proposed personalized federated learning methods based on partial layer sharing. In their methods, only a part of the neural network layers are uploaded to the server for aggregation, and the other parts only perform local updates. Although these methods are more lightweight, they lead to the information of some layers not being shared. Our method, FedTC, is also a personalized federated learning algorithm because the client ultimately obtains a personalized local model. However, it is worth noting that our method does not introduce additional computational load and ensures that all neural network layers are shared.

3  Preliminaries

3.1 Notations

In this paper, we consider a simple federated learning setup. Suppose there are N clients whose local training data are D1,D2,…,DN, respectively. In each training round, fN clients will be selected to participate in federated learning, where f is the client sampling rate.

3.2 Classical Federated Learning

In classic federated learning algorithms such as FedAvg [3], a single shared model with parameters w is trained by all clients in coordination with the server. In each training round t, The training process of the classic federated learning algorithm can be divided into the following four stages:

(1) Client selection stage: The server selects fN clients to participate in the training round;

(2) Model distribution stage: The server distributes the latest global model w¯t to the selected clients;

(3) Local training stage: First, each client i initializes the local model after receiving the global model. The local model is initialized with the parameters of the global model, that is, wit=w¯t. Then, the client i performs several local updates to the model on local training data. Suppose a batch of mini-batch data ξ⊆Di is fed into the local model of client i, and then the following parameter updates are performed as Eq. (1):

wit=wit−ηΔwitLi(wit;ξ)(1)

where wit is the model parameter of the client i in training round t, L(.) is the loss function, Li(wit;ξ) is local empirical loss on mini-batch data ξ, and η(η>0) is the learning rate.

(4) Model aggregation stage: After all clients complete local training, they upload the local model to the server. The server collects these models and averages them to get the global model of the next round as Eq. (2):

w¯t+1=∑i=1fNninwit(2)

where w¯t+1 is the model parameter of the client i in training round t.

The goal of classic federated learning algorithms is to get a global model w∗ training over the global dataset D=∪i∈[N]Di that solves the objective as Eq. (3):

w∗=argminwL(w;D)=argminw∑i=1N|Di||D|Li(wi;Di)(3)

where L(w;D) is global empirical loss on global training data D, Li(wi;Di) is local empirical loss on local training data Di. |Di| is the number of samples on Di, |D| is the number of samples on D, wi is the model parameter of the client i.

However, when the local data is Non-IID, the above equation is not valid. That is, the optimal model on the global data may not be optimal on the local data. The study [11] indicates that the convergence of federated learning is unstable, and the accuracy decreases significantly when training on heterogeneous data.

4  Method

Classical federated learning aims to train an optimal model on global data. However, when data is heterogeneous, global data distribution cannot represent local data distribution. Therefore, the global model may perform poorly on local data. Observing the whole training process of classical federated learning in the previous section, it can be found that after receiving the global model, the client will discard the entire local model and adopt the parameter of the latest global model. However, the local model retains personalized information that reflects the distribution of client data. Especially when the local data distribution is Non-IID, personalized information often determines whether the model can perform well on the local dataset. Recently, some personalized federated learning (PFL) algorithms have been proposed. The goal of PFL is to collaboratively learn individual local models w1∗,w2∗,…,wN∗ using D1,D2,…,DN for each client. As shown in Eq. (4), PFL is trained to minimize the following objective:

w1∗,w2∗,…,wN∗=argminw1,w2,…,wNL(w;D)=argminw1,w2,…,wN∑i=1N|Di||D|Li(wi;Di)(4)

where w1∗,w2∗,…,wN∗ are the optimal models on local training data and are trained simultaneously.

In particular, researchers in [16] realized personalization through partial layer sharing. Unlike classic federated learning, each client finally obtains a customized model due to the presence of the personalized layer in their methods. However, these approaches also result in the shared model lacking information about the personalized layers. To ensure the personalization of the local model while effectively sharing information from all layers, we propose FedTC, a personalized federated learning method with two classifiers.

Similar to the personalized federated learning method based on partial layer sharing, we consider the deep neural network to consist of two components: the extractor and the classifier. In our work, the last linear layer of the deep learning model acts as the classifier, while the other layers make up the extractor. In our proposed approach, the local model’s classifier is always updated locally. To efficiently utilize the information of the classifier, the parameters of the classifier and extractor will be uploaded to the server for aggregation in the model aggregation stage. Then the server aggregates the local models uploaded by the client to get the latest global model. The entire global model is distributed to the clients during the model distribution stage. The study [27] indicated that the extractor usually contains more beneficial information, so the global extractor will replace the local extractor before local training in FedTC. The global model classifier serves as the client’s second classifier to guide the local model’s training. Fig. 1 shows the basic training steps of FedTC, the classical federated learning algorithm FedAvg and a partial layer sharing-based federated learning algorithm FedPer. For FedAvg, FedPer, and FedTC, each training round is divided into four steps: ① The server distributes the global model to selected K clients. ② The client initializes the local model (FedAvg replaces all local model parameters with global model parameters, FedPer replaces the parameters of shared layers with global model parameters, and FedTC replaces the parameters of the local extractor with the parameters of the global extractor). ③ Local training (FedAvg and FedPer use one-classifier mode for local update training, FedTC uses two-classifier mode for local update training). ④ Central server aggregates models (FedAvg and FedTC aggregate the parameters of the entire model, while FedPer aggregates only the parameters of the personalized layers).

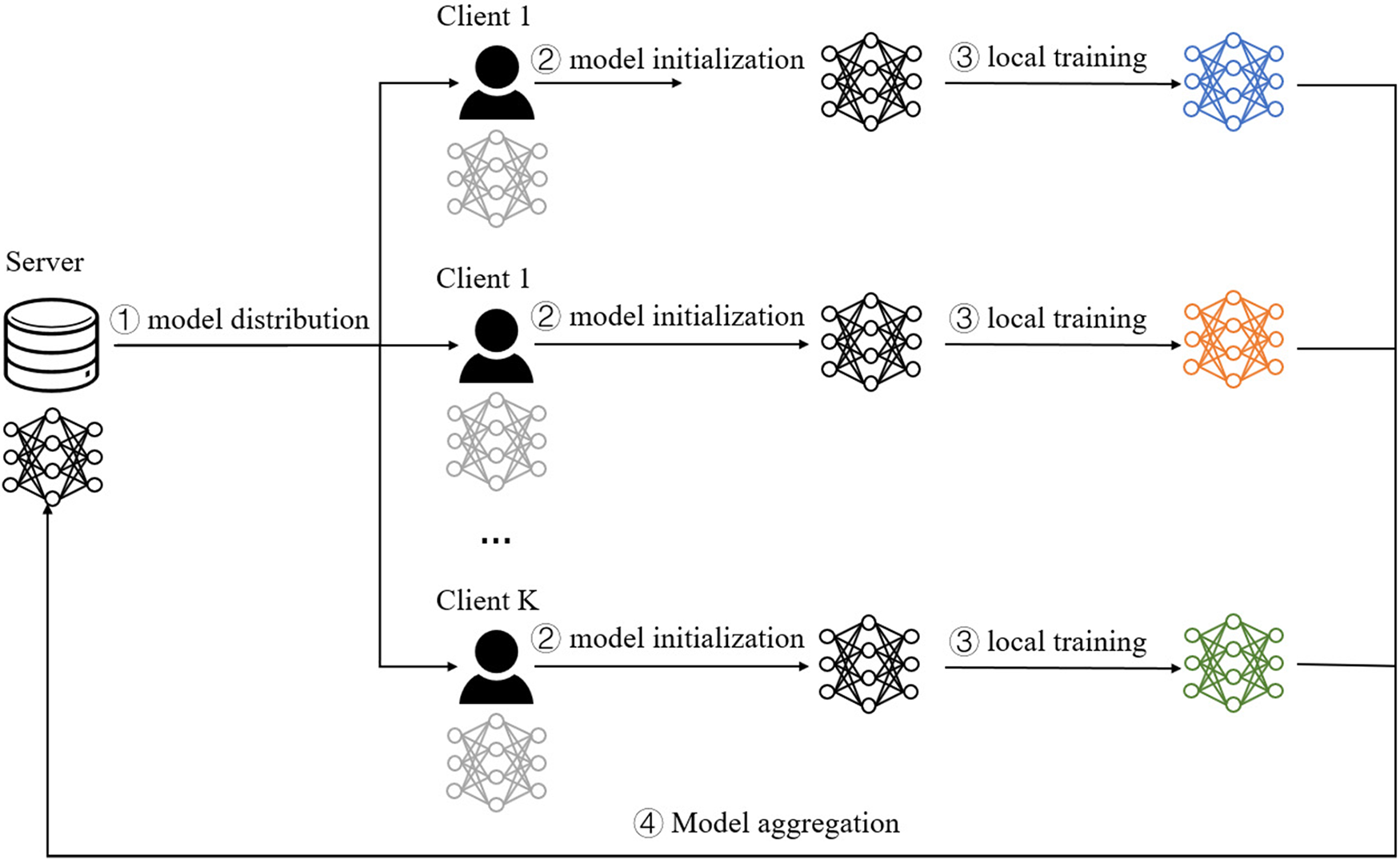
Figure 1: The overview of the training process for each round of FedAvg, FedPer, and FedTC

Algorithm 1 provides the pseudo code for FedTC. First, before the federated learning starts, the server selects a portion of the clients (in this paper, the portion is set to 100% by default), and then the initialized global model is distributed to the selected clients. Then, client and server updates are executed alternately in the following manner.

Client updates. In the tth round of federated training, client i receives the global model from the server with the global extractor parameters θ¯t and the global classifier parameters ϕ¯t. As shown in Fig. 2, before starting local training, the local extractor of the local model will be replaced with the latest global extractor. The local model contains three parts: (1) shared extractor: the shared extractor is the local extractor replaced by the latest global extractor with parameters θit=θ¯t. (2) local classifier: the local classifier is always kept local and its parameters are obtained after the last round of local training, i.e., ϕit=ϕit−1. (3) shared classifier: the shared classifier is the classifier in the latest global model, which has the parameters ϕ¯t. Based on these initialized model parameters, the client performs local updates on the local data. Suppose that the client samples the mini-batch data for a particular time as ξ, and we note that L(θ,ϕ;ξ) is the loss function. The client will perform the following operations to update the local feature extractor parameters θit and the local classifier parameters ϕit, respectively.

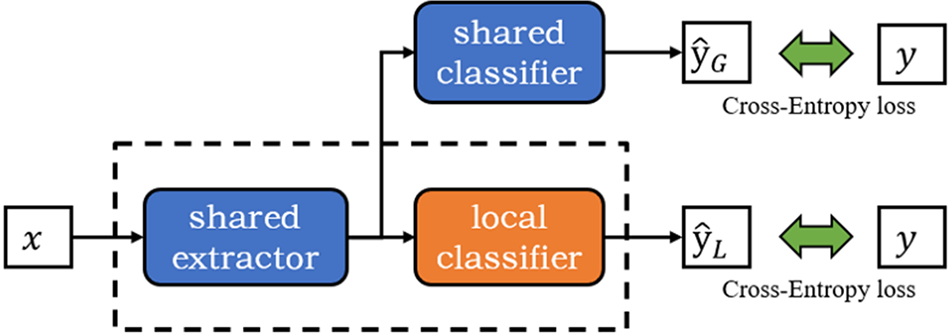
Figure 2: The local model consists of three parts: shared extractor, shared classifier, and local classifier

The local classifier parameters ϕit are first updated. The local extractor parameters θit will be fixed before forward propagation is performed. The sampled data ξ is fed to the local extractor and the shared classifier successively to obtain the predicted values. Then the loss function Li(θit,ϕit;ξ) is calculated, and backpropagation is performed to update the local classifier parameters ϕit as Eq. (5):

ϕit=ϕit−ηcΔϕitLi(θit,ϕit;ξ)(5)

where ηc is the learning rate for the local classifier.

Then, the local extractor parameters θit are updated. At this point, the shared classifier parameters ϕit will be fixed before forward propagation is performed. The sampled data ξ is fed to the local extractor and the shared classifier successively to obtain the predicted values. Then, the loss function Li(θit,ϕ¯t;ξ) is calculated, and backpropagation is performed to update the local extractor parameters θit as Eq. (6):

θit=θit−ηeΔθitLi(θit,ϕ¯t;ξ)(6)

where ηe is the learning rate for the shared extractor.

As mentioned above, the local extractor parameters do not change when the shared classifier is updated, so the local extractor only needs to be forward propagated once. When updating the local extractor, the output of the local extractor obtained when updating the local classifier can be fed directly into the shared classifier without the need to compute it again.

Server executes. After all the clients have completed the local updates, they will upload their local model parameters (θit,ϕit) to the server. Assume that there are K clients participating in the tth round of training, where K=fN. The number of local samples for each client is nk, and the total number of local samples is n. After receiving the model parameters uploaded by the client, the server will aggregate these parameters to get the global model of the next round as Eqs. (7) and (8):

θ¯t+1=∑i=1Kninθit(7)

ϕ¯t+1=∑i=1KninΦit(8)

where θ¯t+1 is the global extractor for the next training round, and ϕ¯t+1 is the global classifier for the next training round.

After computing the global model for the next round, the server will select a portion of the clients to perform the next round of federated training.

5  Test Experimental Results and Discussion

5.1 Datasets and Settings

Federated Datasets. To validate the effectiveness of the method proposed in this paper, we perform simulated federated learning experiments on Cifar10 and Cifar100, which are two popular public datasets for the image classification task. To better simulate the Non-IID distribution of client datasets, we use the popular data partitioning method based on Dirichlet distribution to allocate data for each client [28–30]. We use Dir(α) to denote such a partitioning strategy for convenience. Here α is a hyperparameter used to control the Non-IID degree of data distribution. When α is larger, the local data distribution tends to be IID, while when α is smaller, the local data distribution tends to be Non-IID. We randomly divide the data on each local device into 75% of the training set and 25% of the test set.

Implementation. All our algorithms are implemented based on the open-source project PFL-Non-IID from Zhang et al. [31]. We used Pytorch to perform our experiments on NVIDIA GeForce RTX 3090 GPUs. For the Cifar10 dataset, we used the same convolutional neural network (CNN) model setup as the study [3], while for the Cifar100 dataset, we used the ResNet18 network [32]. In all experiments, We set the client sampling rate to 1.0 for each round of federated learning, similar to recent works [33–35], i.e., all clients are involved in each round of federated learning. In all experiments, the number of local training iterations is set to 5, and the local batch size is set to 64 by default. We used stochastic gradient descent (SGD) to optimize the neural network parameters, with the weight decay set to 1e-5 and the momentum parameter set to 0.9. In FedTC, the learning rate of the extractor is set to 0.01, and the learning rate of the classifier is set to 1e-4. The learning rate of FedAvg, FedPer, and Local is set to 0.01 for fairness. Li et al. [36] proved that the learning rate decay is necessary, so we set the learning rate decay to 0.9 in all experiments. We set the number of clients for all datasets to 10 in all experiments [37].

Evaluation Metrics. As we are conducting an image classification experiment, we have chosen image classification accuracy as our evaluation metric. In each round of training, when a client receives the global model and initializes its local model, the client will test the initialized local model on its local test dataset. Then, for each of the selected clients in a round, client i will calculate the total number of test samples Tsi and the number of correctly classified samples Tci. The local test accuracy Acci is calculated using Eq. (9). For the global test accuracy, we count the sum of correctly classified samples for all clients ∑i=1KTci, as well as the total number of test samples for all clients ∑i=1KTsi, and then calculate the overall test accuracy ACC using Eq. (10):

Acci=TsiTci(9)

Acc=∑i=1KTsi∑i=1KTci(10)

where K represents the number of selected clients, Tci represents the number of correctly classified samples for client i, and Tsi represents the total number of test samples for client i.

5.2 Evaluate the Test Performance of the FedAvg Algorithm on Local Test Dataset

Since all clients share a unique global model throughout the FedAvg training process, many previous researchers have typically assumed that the server has a portion of test data that matches the global data distribution. In their research, the global model is evaluated on the global test data after the model aggregation stage, but the model’s performance on local datasets is not considered. When the client data distribution is IID, the data distribution of each client matches the global data distribution, so the accuracy of the global test data is usually similar to the accuracy of the local test data. However, when the local data distribution is Non-IID, the global data distribution does not represent the data distribution of each client. Therefore, the accuracy of the global model is not representative of its performance on each client’s local data.

We conducted experiments on the Cifar10 dataset to verify the above claims, training a classification model using the FedAvg algorithm and performing local tests. We considered different values of the hyperparameter α, namely 0.1, 0.5, and 5.0. As shown in Table 1, we tested the trained model on the local datasets of 10 clients and computed the standard deviation δ of their local test accuracies. The “global” entry in the table indicates the model’s test accuracy on the entire dataset. We observed that Non-IID data leads to a decrease in both the global and local test accuracies of the FedAvg algorithm. Specifically, when α = 0.1, the global test accuracy drops by 7.73% compared to when α = 5.0. Additionally, we noticed that as the Non-IID degree increases, the differences in the local test accuracies among the clients become more pronounced. In particular, when α = 0.1, the local test accuracy of client 2 differs from client 8 by 22.12%. Therefore, a single model trained using FedAvg may not be suitable for scenarios where the client data is highly Non-IID.

5.3 Compare the Performance of FedAvg and Local Training

Local training can be viewed as a highly personalized setup of federated learning, where each client trains the model only on its local dataset, and no data is shared between the clients. Traditional federated learning algorithms that train a single model are rarely compared to local training, as the test data is usually on the server side. However, the performance improvement on local data may affect the client’s interest in participating in federated learning. Therefore, we also compared FedAvg and Local on the Cifar10 dataset.

The experimental results are presented in Fig. 3, where the x-axis represents the value of α, and the y-axis represents the global testing accuracy of the corresponding algorithm. It can be observed that the global model trained by FedAvg outperforms the Local when α=5.0. As the Non-IID level increases, the accuracy of FedAvg’s model decreases, but the accuracy of the locally trained model gradually increases. At α values of 0.5 and 0.1, the accuracy of the model trained by FedAvg decreases significantly and is lower than that of the locally trained model for each client. To further investigate the reasons for the accuracy fluctuations of these two algorithms, we visualize the local data distribution of clients. As shown in Fig. 4, the bar chart shows the local data distribution of each client when Cifar10 is partitioned into 10 clients based on α values of 0.1, 0.5, and 5.0, where the height of each bar represents the number of samples. When the α is large, the sample quantity of each label is uniform among clients, enabling FedAvg to perform better. However, as α decreases, data distribution across clients becomes more and more different. The single model trained by FedAvg is no longer applicable to all clients’ local data. However, the decreasing value of α allows clients to have more samples of a specific class. For example, when α=0.1, the data of label 3, label 8, and label 9 make up a large proportion of the local data samples of client 9, which is a simple classification task for the client. Thus, in the case of highly Non-IID client data distribution, a good model can be obtained solely through local training, which may outperform the model trained through FedAvg. Therefore, it is crucial to enhance the performance of FedAvg on Non-IID data to prevent potential discouragement of user participation in federated learning. In addition, we found that local training may outperform FedAvg in some extremely Non-IID scenarios, indicating that local models may contain personalized information that enables them to perform better on local data.

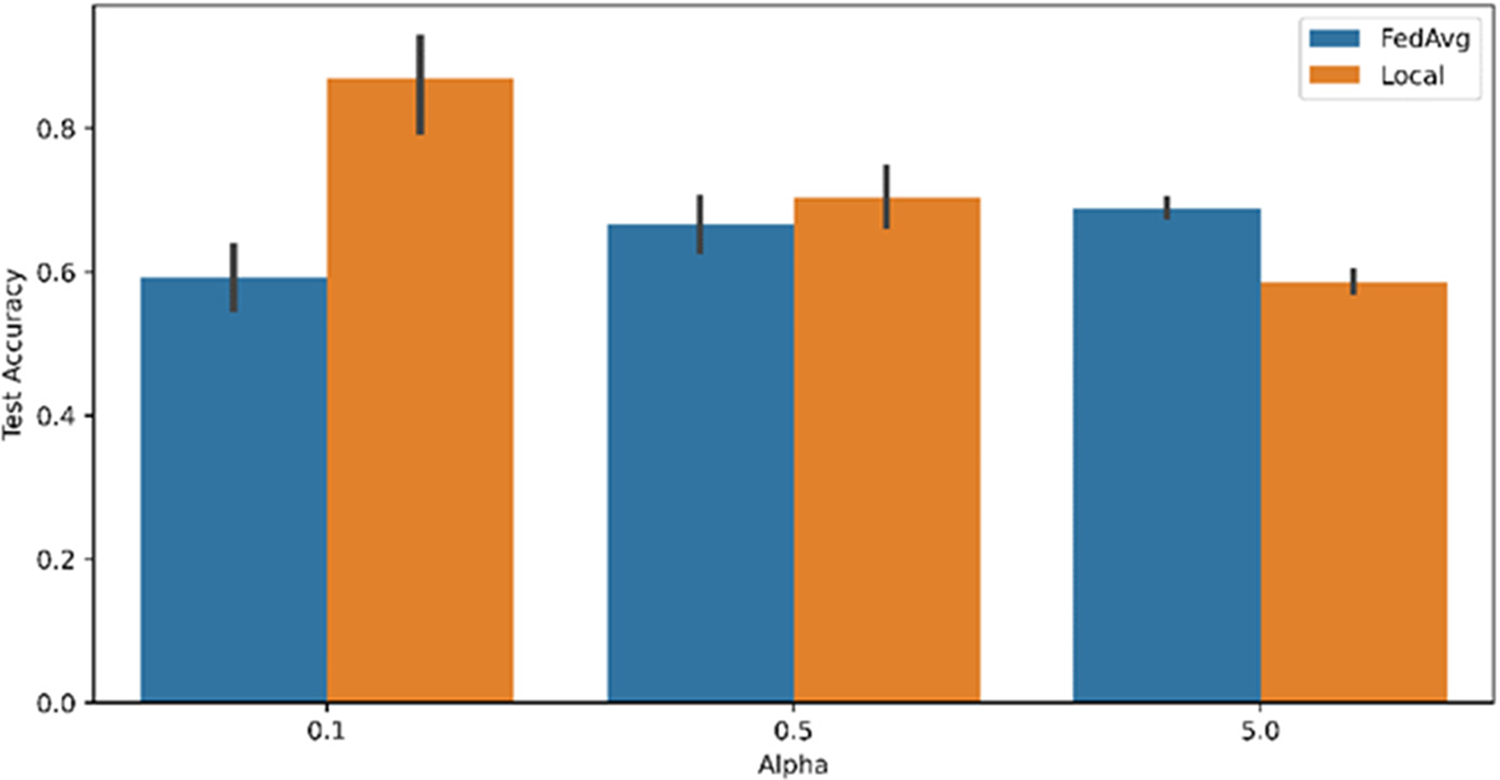
Figure 3: Test accuracy of FedAvg and Local on Cifar10 when α values of 0.1, 0.5 and 5.0

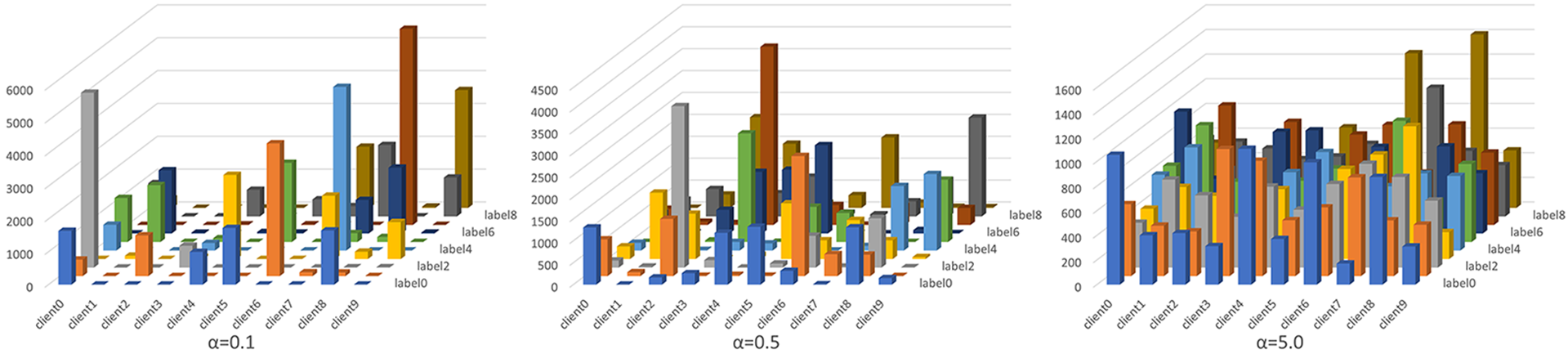
Figure 4: The local data distribution of each client when Cifar10 is divided into 10 clients according to α values of 0.1, 0.5 and 5.0

5.4 Evaluation of FedTC

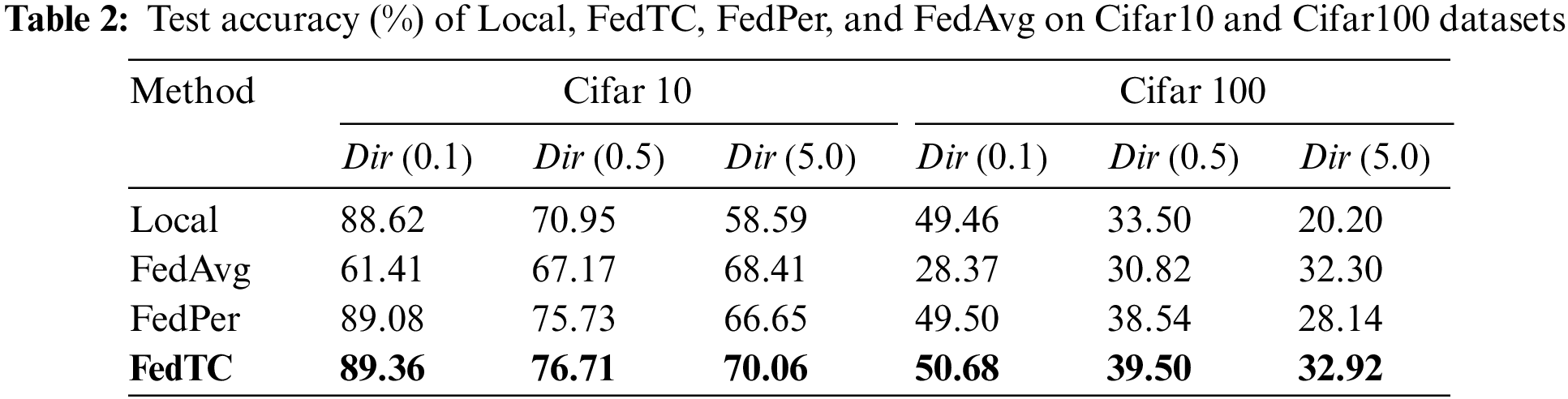
To demonstrate the effectiveness of our proposed method, we compare FedTC with FedAvg, FedPer, and Local (local training). FedAvg is a classic federated learning algorithm and the baseline for comparison in many studies. FedPer is a personalized federated learning algorithm based on partial layer sharing, which proposes keeping the client model’s classifier parameters local and uploading only the feature extractor parameters to the server for aggregation to ensure local personalization. Local is implemented the same way as FedAvg, except that model aggregation and model distribution are removed. In our experiment, the number of clients was 10. We divided the Cifar10 and Cifar100 datasets into 10 parts as the local data of each client according to the α values of 0.1, 0.5, and 5.0.

The experimental results are presented in Table 2. As the Non-IID degree increases, all algorithms except for Local exhibit a decrease in accuracy, which is expected as a higher Non-IID degree reduces the difficulty of local tasks. FedAvg performs worse than Local in all cases except for α=5.0, indicating that FedAvg is not proficient in handling Non-IID data. FedPer preserves the personalized information of local models through partial layer sharing. Hence its accuracy is significantly higher than FedAvg at α=0.1 or 0.5. This indicates that preserving personalized information is an effective way to improve model performance in Non-IID scenarios. However, FedPer’s accuracy is slightly lower than FedAvg at α=5.0 because some layers’ information is not shared. FedTC, proposed in this work, preserves personalized information of local models through a two-classifier training strategy while retaining all layer information in the shared model. Therefore, from the experimental results, FedTC achieves the highest accuracy in all scenarios. Notably, in the extreme Non-IID scenario where α=0.1, where FedAvg performs the worst, FedTC achieves up to 27.95% higher test accuracy than FedAvg.

6  Conclusion and Future Work

In this study, we propose FedTC, a personalized federated learning algorithm that handles the problem of Non-IID local data distribution. FedTC introduces almost no additional computational complexity compared to previous methods and ensures that all layers of the client’s local model are shared. To maintain personalization, we present a two-classifier training strategy that ensures the classifier of the local model is not discarded before each round of local training. Our extensive experiments show that FedTC outperforms many federated learning algorithms in Non-IID scenarios. However, we acknowledge that our current work only considers simple federated learning settings and future work will need to address the challenge of applying it to complex experimental scenarios. Additionally, techniques such as generative adversarial networks and model compression can be considered to improve model accuracy further and reduce communication costs.

Acknowledgement: The authors thank Lu Shi and Weiqi Qiu for discussions that helped to improve this work.

Funding Statement: This research was funded by Shenzhen Basic Research (Key Project) (No. JCYJ20200109113405927), Shenzhen Stable Supporting Program (General Project) (No. GXWD2020 1230155427003-20200821160539001), Guangdong Provincial Key Laboratory of Novel Security Intelligence Technologies (2022B1212010005), and Peng Cheng Laboratory Project (Grant No. PCL2021A02), Ministry of Education's Collaborative Education Project with Industry Cooperation (No. 22077141140831).

Author Contributions: The authors confirm their contribution to the paper as follows: study conceptionand design: Y. Liu, J. Wang; data collection: J. Wang, W. Xu, J. Zhang; analysis and interpretation of results: J. Wang, Y. Liu, Z. L. Jiang; draft manuscript preparation: Y. Liu, J. Wang, Q. Liu, M. Gheisari. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: All data incorporated in this study can be accessed by contacting the corresponding author upon request.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Datoo, “Data in the post-GDPR world,” Computer Fraud & Security, vol. 2018, no. 9, pp. 17–18, 2018. [Google Scholar]

2. L. Determann, Z. J. Ruan, T. Gao and J. Tam, “China’s draft personal information protection law,” Journal of Data Protection & Privacy, vol. 4, no. 3, pp. 235–259, 2021. [Google Scholar]

3. H. B. McMahan, E. Moore, D. Ramage, S. Hampson and B. A. Arcas, “Communication-efficient learning of deep networks from decentralized data,” in Proc. of the 20th Int. Conf. on Artificial Intelligence and Statistics (AISTATS), Fort Lauderdale, FL, USA, pp. 1273–1282, 2017. [Google Scholar]

4. B. Dash, P. Sharma and A. Ali, “Federated learning for privacy-preserving: A review of PII data analysis in fintech,” International Journal of Software Engineering & Applications (IJSEA), vol. 13, no. 4, pp. 1–13, 2022. [Google Scholar]

5. N. Rieke, J. Hancox, W. Li, F. Milletarì, H. R. Roth et al., “The future of digital health with federated learning,” NPJ Digital Medicine, vol. 3, no. 1, pp. 1–7, 2020. [Google Scholar]

6. T. T. Vu, D. T. Ngo, N. H. Tran, H. Q. Ngo, M. N. Dao et al., “Cell-free massive MIMO for wireless federated learning,” IEEE Transactions on Wireless Communications, vol. 19, no. 10, pp. 6377–6392, 2020. [Google Scholar]

7. A. Hammoud, H. Otrok, A. Mourad and Z. Dziong, “On demand fog federations for horizontal federated learning in IoV,” IEEE Transactions on Network and Service Management, vol. 19, no. 3, pp. 3062–3075, 2022. [Google Scholar]

8. A. Hammoud, H. Otrok, A. Mourad and Z. Dziong, “Stable federated fog formation: An evolutionary game theoretical approach,” Future Generation Computer Systems, vol. 124, no. 5, pp. 21–32, 2021. [Google Scholar]

9. H. Shamseddine, J. Nizam, A. Hammoud, A. Mourad, H. Otrok et al., “A novel federated fog architecture embedding intelligent formation,” IEEE Network, vol. 35, no. 3, pp. 198–204, 2021. [Google Scholar]

10. Z. Zheng, Y. Zhou, Y. Sun, Z. Wang, B. Liu et al., “Applications of federated learning in smart cities: Recent advances taxonomy and open challenges,” Connection Science, vol. 34, no. 1, pp. 1–28, 2022. [Google Scholar]

11. Y. Zhao, M. Li, L. Lai, N. Suda, D. Civin et al., “Federated learning with non-IID data,” arXiv preprint, arXiv:1806.00582, 2018. [Google Scholar]

12. L. Gao, H. Fu, L. Li, Y. Chen, M. Xu et al., “FedDC: Federated learning with non-IID data via local drift decoupling and correction,” in 2022 IEEE/CVF Conf. on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, pp. 10102–10111, 2022. [Google Scholar]

13. A. Fallah, A. Mokhtari and A. Ozdaglar, “Personalized federated learning with theoretical guarantees: A model-agnostic meta-learning approach,” in Proc. of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, pp. 3557–3568, 2020. [Google Scholar]

14. T. Li, S. Hu, A. Beirami and V. Smith, “Ditto: Fair and robust federated learning through personalization,” in Proc. 38th Int. Conf. Mach. Learn., Vienna, VIE, Austria, pp. 6357–6368, 2021. [Google Scholar]

15. Y. Huang, L. Chu, Z. Zhou, L. Wang, J. Liu et al., “Personalized cross-silo federated learning on non-IID data,” in Proc. of the AAAI Conf. on Artificial Intelligence, Vancouver, BC, Canada, pp. 7865–7873, 2021. [Google Scholar]

16. M. G. Arivazhagan, V. Aggarwal, A. K. Singh and S. Choudhary, “Federated learning with personalization layers,” arXiv preprint, arXiv:1912.00818, 2019. [Google Scholar]

17. L. Collins, H. Hassani, A. Mokhtari and S. Shakkottai, “Exploiting shared representations for personalized federated learning,” in Proc. of the 38th Int. Conf. on Machine Learning, Vienna, VIE, Austria, pp. 2089–2099, 2021. [Google Scholar]

18. J. Oh, S. Kim and S. Y. Yun, “Fedbabu: Towards enhanced representation for federated image classification,” arXiv preprint, arXiv:2106.06042, 2021. [Google Scholar]

19. P. P. Liang, T. Liu, L. Ziyin, N. B. Allen, R. P. Auerbach et al., “Think locally, act globally: Federated learning with local and global representations,” arXiv preprint, arXiv:2001.01523, 2020. [Google Scholar]

20. M. Luo, F. Chen, D. Hu, Y. Zhang, J. Liang et al., “No fear of heterogeneity: Classifier calibration for federated learning with non-IID data,” in Advances in Neural Information Processing Systems, Vancouver, BC, Canada, pp. 5972–5984, 2021. [Google Scholar]

21. T. Li, A. K. Sahu, M. Zaheer, M. Sanjabi, A. Talwalkar et al., “Federated optimization in heterogeneous networks,” in Proc. of the 1st Adaptive & Multitask Learning Workshop, Austin, TX, USA, pp. 429–450, 2020. [Google Scholar]

22. S. P. Karimireddy, S. Kale, M. Mohri, S. Reddi, S. Stich et al., “SCAFFOLD: Stochastic controlled averaging for federated learning,” in Proc. of the 37th Int. Conf. on Machine Learning, Vienna, VIE, Austria, pp. 5132–5143, 2020. [Google Scholar]

23. E. Jeong, S. Oh, H. Kim, J. Park, M. Bennis et al., “Communication-efficient on-device machine learning: Federated distillation and augmentation under non-IID private data,” arXiv preprint, arXiv:1811.11479, 2018. [Google Scholar]

24. Y. Deng, M. Mahdi Kamani and M. Mahdavi, “Adaptive personalized federated learning,” arXiv preprint, arXiv:2003.13461, 2020. [Google Scholar]

25. B. Liu, Y. Guo and X. Chen, “PFA: Privacy-preserving federated adaptation for effective model personalization,” in Proc. of the Web Conference 2021, Ljubljana, Slovenia, pp. 923–934, 2021. [Google Scholar]

26. D. Li and J. Wang, “Fedmd: Heterogenous federated learning via model distillation,” arXiv preprint, arXiv:1910.03581, 2019. [Google Scholar]

27. Z. Zhu, J. Hong and J. Zhou, “Data-free knowledge distillation for heterogeneous federated learning,” in Proc. of the 38th Int. Conf. on Machine Learning, Vienna, VIE, Austria, pp. 12878–12889, 2021. [Google Scholar]

28. M. Yurochkin, M. Agarwal, S. Ghosh, K. Greenewald, N. Hoang et al., “Bayesian nonparametric federated learning of neural networks,” in Proc. of the 36th Int. Conf. on Machine Learning, Long Beach, CA, USA, pp. 7252–7261, 2019. [Google Scholar]

29. H. Wang, M. Yurochkin, Y. Sun, D. Papailiopoulos and Y. Khazaeni, “Federated learning with matched averaging,” arXiv preprint, arXiv:2002.06440, 2020. [Google Scholar]

30. T. Lin, L. Kong, S. U. Stich and M. Jaggi, “Ensemble distillation for robust model fusion in federated learning,” in Proc. of the 34th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, pp. 2351–2363, 2020. [Google Scholar]

31. J. Zhang, Y. Hua, H. Wang, T. Song, Z. Xue et al., “FedALA: Adaptive local aggregation for personalized federated learning,” arXiv preprint, arXiv:2212.01197, 2022. [Google Scholar]

32. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in IEEE Conf. on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]

33. S. Wang, T. Tuor, T. Salonidis, K. K. Leung, C. Makaya et al., “Adaptive federated learning in resource constrained edge computing systems,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 6, pp. 1205–1221, 2019. [Google Scholar]

34. J. Wang and G. Joshi, “Cooperative SGD: A unified framework for the design and analysis of local-update sgd algorithms,” Journal of Machine Learning Research, vol. 22, no. 213, pp. 1–50, 2021. [Google Scholar]

35. H. Yu, S. Yang and S. Zhu, “Parallel restarted SGD with faster convergence and less communication: Demystifying why model averaging works for deep learning,” in Proc. of the Thirty-Third AAAI Conf. on Artificial Intelligence, Honolulu, Hawaii, USA, pp. 5693–5700, 2019. [Google Scholar]

36. X. Li, K. Huang, W. Yang, S. Wang and Z. Zhang, “On the convergence of fedavg on non-IID data,” arXiv preprint, arXiv:1907.02189, 2019. [Google Scholar]

37. J. Zhang, Z. Li, B. Li, J. Xu, S. Wu et al., “Federated learning with label distribution skew via logits calibration,” in Proc. of the 39th Int. Conf. on Machine Learning, Baltimore, MD, USA, pp. 26311–26329, 2022. [Google Scholar]