AI-Driven FBMC-OQAM Signal Recognition via Transform Channel Convolution Strategy

1  Introduction

In the upcoming fifth industrial revolution (Industry 5.0) era, the industrial Internet of Things will require low-latency and high-rate data communications transmissions [1] due to the intensive interaction between the industrial information center and manufacturing machine nodes. The 5G (fifth generation) and B5G wireless communications techniques have been proposed as viable enablers for meeting data transmission requirements in industrial IoT networks [2]. As a B5G candidate wireless transmission approach, the FBMC-OQAM multicarrier technique develops a non-orthogonal prototype filter to achieve high spectrum utilization and data transmission rate. In recent years, some works [3,4] have integrated the FBMC-OQAM technique into the industrial IoT network. However, considering its open connection traits, the FBMC-OQAM industrial IoT network is susceptible to vicious attacks from malicious nodes. As depicted in Fig. 1, the malicious attack will disturb the order of the industrial IoT network and deteriorate the data transmission performance between the industrial information center and legitimate nodes [5]. These attacks might deactivate industrial manufacturing and wiretap the industrial information of legitimate nodes. Therefore, it is imperative to deploy the FBMC-OQAM ICRNet to recognize malicious attacks and improve the physical layer security of the FBMC-OQAM ICRNet.

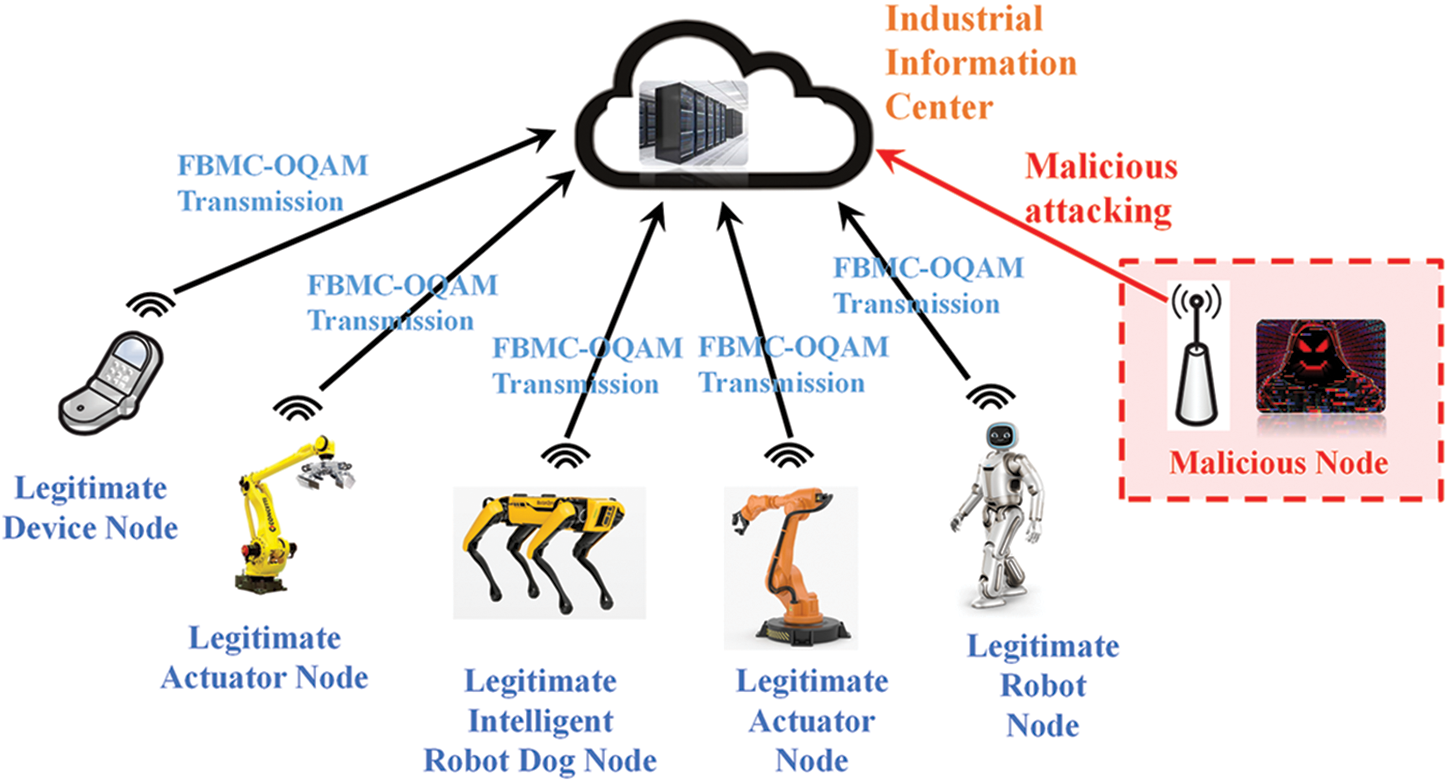
Figure 1: The application illustration of the FBMC-OQAM industrial cognitive radio networks

Blind modulation recognition (BMR) technology plays a pivotal role in the FBMC-OQAM ICRNet. It can recognize the modulation schemes of intercepted signals to judge whether it is a legitimate node or an illegal threat in complex electromagnetic scenarios. BMR has excellent promise in civilian and military applications [6] in ICRNet, such as spectral monitoring, situation awareness, and spectrum sensing. According to the latest survey in [7], the traditional BMR techniques can be grouped into two pillars: 1) likelihood-based (LB) and 2) feature-based (FB) methods. Compared with likelihood-based methods, feature-based methods have a better generality for different wireless environments and reduce the need for prior information. In FB methods, various expert features are extracted as the model input of a machine learning classifier to perform the BMR tasks, such as support vector machine (SVM) [8]. Up to now, deep learning has been a promising technology. It has been applied to many scenarios, such as climate change forecasting [9], groundwater storage change [10], forest areas classification [11], nanosatellites image classification [12], and the sustainable agricultural water practice [13]. With the prosperity of artificial intelligence (AI), the BMR approach based on deep learning (DL) has become a game changer due to its powerful capability for feature extraction and recognition [7].

Notably, the existing DL-based approaches can be broadly summarized into two aspects: single-carrier and multi-carrier systems. For the single-carrier case, Liu et al. [14–16] explored BMR technology in the context of industrial cognitive radio networks. In [14], the time-frequency feature was converted from the received signals and fed into the stack hybrid autoencoders to infer the modulation types. To further improve the signal feature representation, the cyclic spectrum method was employed in [15] to preprocess the received node signal and the federated learning strategy was applied to protect the privacy of industrial IoT networks. In [16], the author integrated the signal SNR estimation and modulation recognition to form a unitary framework of signal estimation in the satellite-based ICRNet. Up to now, many prior DL-based BMR methods have been widely investigated in multi-carrier systems, especially for the Orthogonal Frequency Division Multiplexing (OFDM) system [17,18]. For instance, Zhang et al. [17] proposed a real-time DL-based BMR method for the OFDM system to identify six modulation types of OFDM signal subcarriers, yielding 100% accuracy at 6dB with a sampling length of 1024. In [18], the blind signal separation technique is employed to reconstruct the damaged OFDM signal and a multi-modal learning network based on the constellation and series features is proposed to recognize low-order phase shift keying (PSK) and quadrature amplitude modulation (QAM) signals.

Unlike the traditional OFDM technology, the FBMC-OQAM method can prevent the cyclic prefix (CP) insertion to improve spectral efficiency and reduce out-of-band leakage. Using a great localized frequency/time prototype filter, the FBMC-OQAM technique can relax the strict orthogonality limits of the OFDM method to tackle the carrier frequency offset. However, few BMR works have been presented for the FBMC-OQAM system, which is a promising multicarrier technology due to its low spectrum sidelobe and total spectral efficiency [19]. Most BMR methods in OFDM systems cannot be directly applied to the new FBMC-OQAM system since two multi-carrier systems employ different modulation types in corresponding subcarriers. Specifically, the OFDM system adopts QAM, whereas the FBMC system utilizes OQAM, which is used to achieve imaginary interference cancellation [20].

Consequently, it is necessary to redesign the BMR method for FBMC-OQAM ICRNet. From a significant survey of Dobre’s literature [21], it has been illustrated that the new signal recognition task in the promising FBMC-OQAM systems should be listed on the agenda. It is illustrated in Fig. 2 for the difference in the gridding constellation matrix between OFDM and FBMC modulation at SNR = 26dB. It is evident that the OFDM scheme has square-shaped QAM modes, but the FBMC scheme presents cross-shaped OQAM modes. Therefore, the novel BMR methods are needed to update by considering the modulation type gap between FBMC-OQAM and OFDM-QAM types. There are currently no algorithms in previous work that can perform the BMR task of FBMC-OQAM signals in ICRNet nodes.

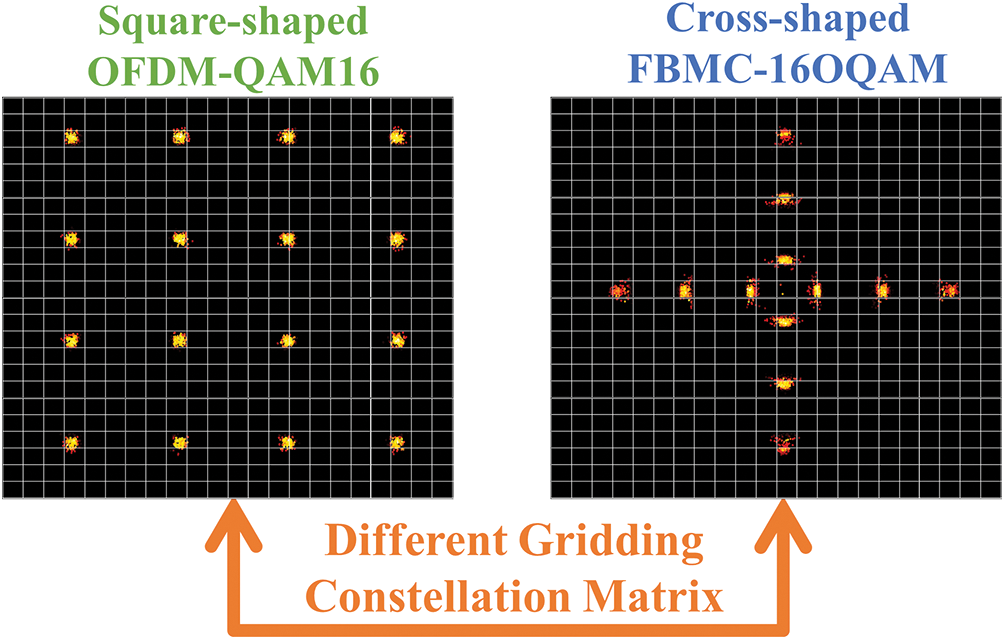
Figure 2: The difference between the FBMC-OQAM and traditional OFDM-QAM modulation modes

Inspired by [21], a novel BMR network is proposed with a transform channel convolution strategy (called TCCNet) for current FBMC-OQAM ICRNet systems to recognize nine modulation types, containing Binary Phase Shift Keying (BPSK), Quadrature Phase Shift Keying (QPSK), Eight Phase Shift Keying (8PSK), 16OQAM, 32OQAM, 64OQAM, 128OQAM, 256OQAM, and 512OQAM. This FBMC-OQAM BMR framework aims to calculate the posterior probability of modulation schemes using the binary constellation diagram and the lightweight TCCNet model. Notably, the proposed FBMC-OQAM BMR algorithm has several significant contributions, as follows:

•   As previously mentioned, this work is the first attempt at leveraging the DL technique to address the issue of BMR in the FBMC-OQAM system. Specifically, this work focuses on recognizing the new OQAM rather than the traditional QAM in previous OFDM systems, which has not been investigated in previous works.

•   To achieve the low-latency BMR in industrial FBMR-OQAM scenarios, this work develops a low-complexity binary constellation diagram gridding matrix, rather than the complicated colorful constellation diagram tensor produced by the lightweight binary image preprocessing.

•   Unlike previous BMR works using the two-dimensional (2D) convolution, this work proposes a transform channel convolution (TCC) strategy to transform the 2D constellation image matrix into the one-dimensional (1D) series-like format. In this way, this work can leverage the 1D convolution operation to perform the recognition task of the 2D constellation diagram. The proposed TCCNet can achieve low-latency recognition in the FBMC-OQAM ICRNet.

•   The proposed approach does not need prior channel state information (CSI) to perform channel equalization in advance. This method is more suitable for the FBMC-OQAM industry cognitive radio network, where it is difficult to obtain prior knowledge of malicious nodes.

2  System Model and Problem Formulation

2.1 FBMC-OQAM System Model

As depicted in Fig. 3, this paper considers an FBMC-OQAM communications transmission system [20] with an antenna setup of single input and output. In the transmitting terminal, the data bits are first mapped into the digital modulation signal, such as QAM. The aliasing interference between the QAM adjacent carriers exists since the FBMC technique is a non-orthogonal multicarrier scheme [22], which differs from OFDM schemes with orthogonal adjacent subcarrier transmission. To avoid this aliasing interference, the real and imaginary parts of QAM complex symbols are offset by half symbol period and formed as the OQAM symbols. As illustrated in Fig. 4, the OQAM modulation scheme can segment the complex-value signal into the real and imaginary parts fed into the adjacent subcarrier to transmit information. The original aliasing interference can be transferred into the imaginary domain by performing the appropriate phase shift φk,n. Due to the transferred imaginary interference, FBMC techniques only need to transmit real-value symbols, which facilitates the relaxed real orthogonality condition to replace the strict complex orthogonality condition. Meanwhile, a complex-value FBMC symbol is transmitted by transmitting two real-value symbols, achieving the identical information rate with the no CP-aided OFDM multicarrier.

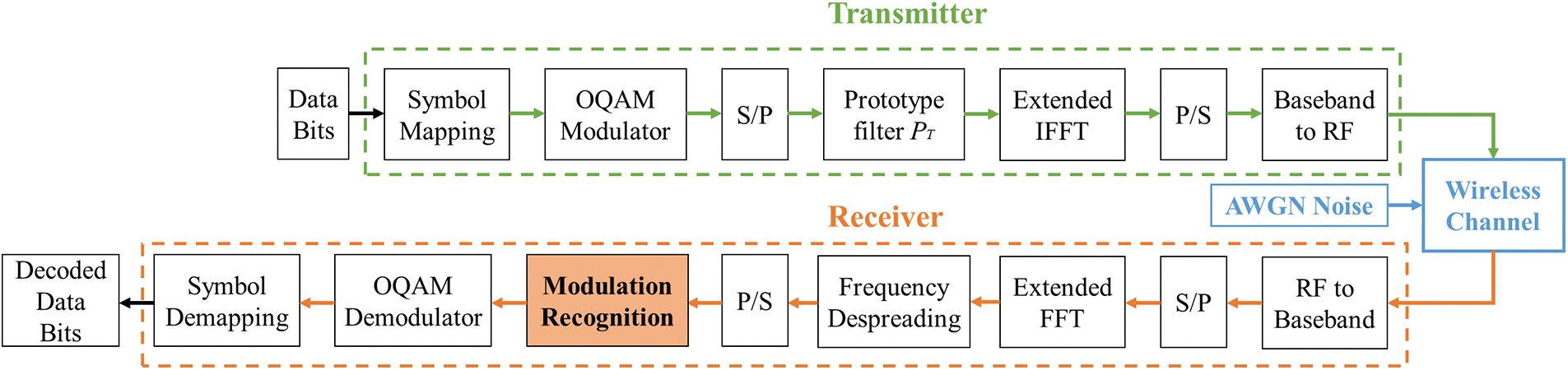
Figure 3: The framework of the FBMC-OQAM communications transmission systems

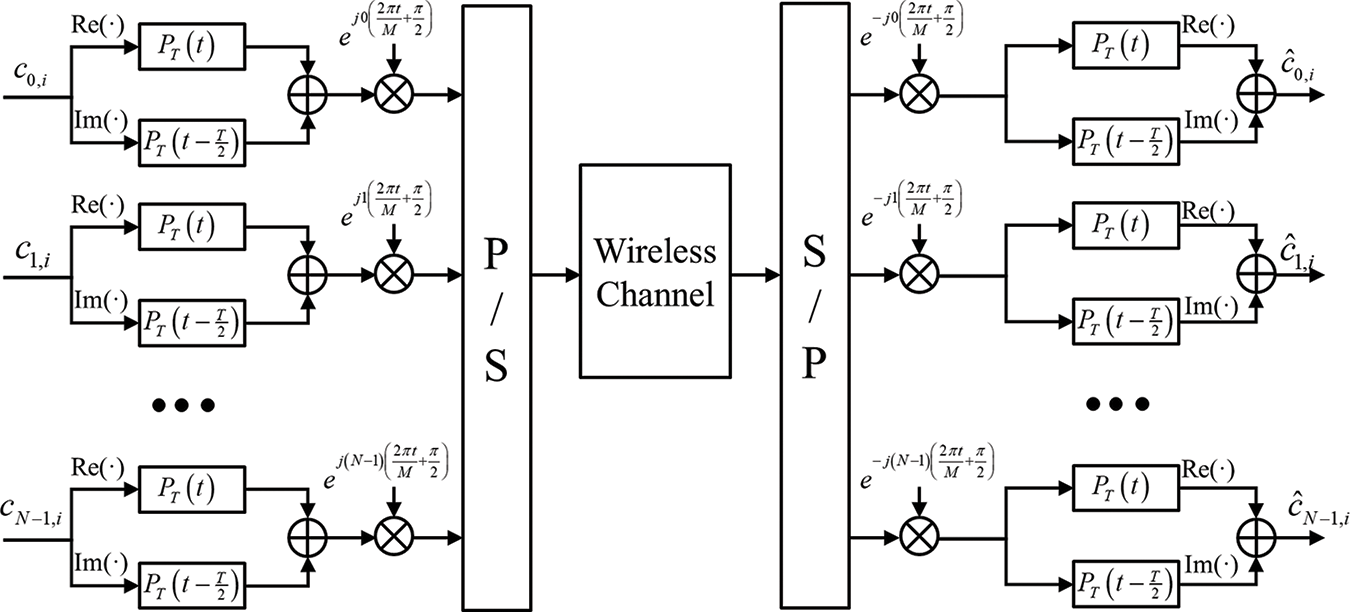
Figure 4: The framework of the OQAM modulation scheme

In Fig. 3, the prototype filter PT(⋅) and IFFT operation are employed to filter the OQAM symbols in the frequency domain. As such, the FBMC transmitting signal x(t) can be presented as follows:

x(t)=∑k=0M−1∑n=−∞+∞ck,n⋅pT,k(t−nM),(1)

pT,k(t)=pT(t)ej2πMk(t−KM+1),(2)

pT(t)=1+2∑k=1K−1(−1)kHkcos⁡(2πktKM),(3)

where M denotes the number of subcarriers, K denotes the overlapping factor, pT,k(t) denotes the offset version of prototype filter PT(⋅) with a constant sampling interval of T/M and has a non-zero coefficient during the range [0,KM−1]. According to the PHYDYAS project [23], the overlapping factor of the FBMC prototype filter K is set as 4 with the frequency-domain coefficients H=[H0,H1,H2,H3]=[1,0.97196,2/2,0.235147]. In formula (1), 𝒞k,n denotes the n-th OQAM modulation symbol in the k-th subcarrier as:

ck,n=dk,2nejφk,2n+dk,2n+1ejφk,2n+1,(4)

φk,n=π2(k+n),(5)

where dk,n is the real-value symbol, φk,n is the additional phase. It can beused to generate the OQAM symbols by alternately adding the real and imaginary parts in the time and frequency domains, as shown in Fig. 4. Finally, the received FBMC signal r(t) is corrupted by the additive white Gaussian noise (AWGN) channel. Its mathematical expression can be expressed as follows:

r(t)=x(t)+w(t)=∑k=0M−1∑n=−∞+∞dk,nejφk,n⋅ej2πkM(t−KM+1)−1PT(t−nM2)−1+w(t),(6)

where w(t) represents the complex AWGN noise with zero mean and variance δw2=1.

2.2 BMR Problem Formulation

With the help of AI, this paper can consider the FBMC BMR task as a pattern recognition problem. Specifically, this paper needs to recognize the modulation types of received FBMC signals in the receiver. In formula (1), 𝒞n,i denotes the modulated signal by implementing the modulation schemes on signal bits s. It is worth noting that 𝒞n,i and s have a close relationship of 𝒞n,i=F(s). Consequently, this research can reformate the formula (6) as follows:

r(t)=∑k=0M−1∑n=−∞+∞F(s)⋅ej2πkM(t−KM+1)−1PT(t−nM2)−1+w(t),(7)

where F(s) represents the modulation functions, entailing PSK and Offset Quadrature Amplitude Modulation (OQAM). As such, the proposed AI-based BMR task aims to identify modulation format F(⋅) from the candidate modulation set BPSK, QPSK, 8PSK, 16OQAM, 32OQAM, 64OQAM, 128OQAM, 256OQAM, and 512OQAM. Based on the maximum a posterior (MAP) criterion, the final recognition decision FLast relies on the modulation modes with the maximum probability between the i-th predicted label FP and the true label FT. And its mathematical expression is given by:

FLast=argmax1≤i≤NmP(FPi=FT∣r(t)),(8)

where P(⋅∣r(t)) denotes the posterior probability and Nm denotes the number of all modulation types.

3  Proposed FBMC-OQAM BMR Algorithm

In the following, the system architecture of the proposed FBMC-OQAM modulation recognition algorithm is presented in Fig. 5. The proposed FBMC-OQAM BMR algorithm mainly consists of two key modules: 1) FBMC signal constellation diagram preprocessing and 2) the proposed TCCNet recognizer based on transform channel convolution strategy.

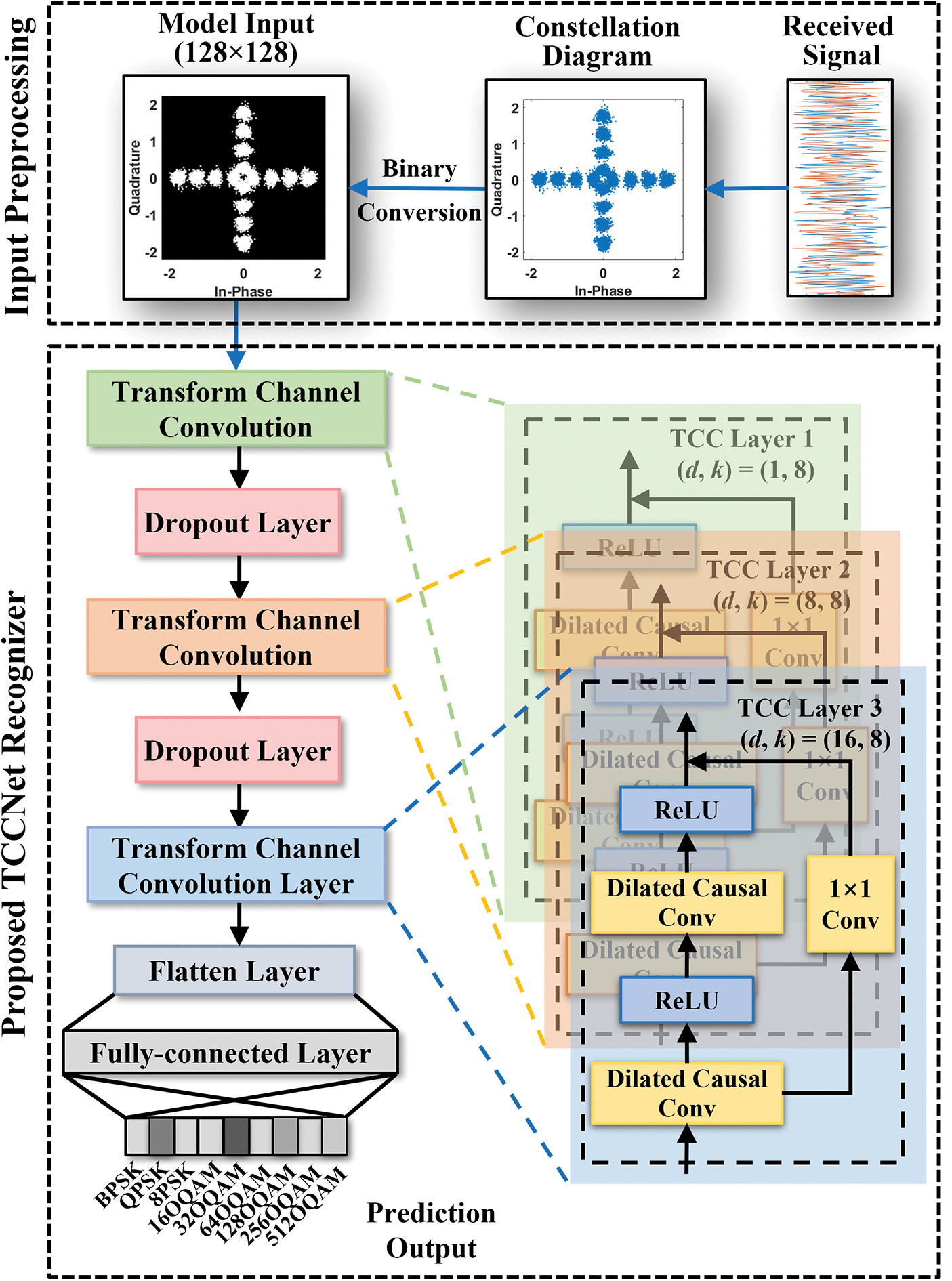
Figure 5: The architecture of the proposed FBMC-OQAM BMR algorithm

3.1 FBMC Signal Constellation Diagram Preprocessing

Existing BMR works based on constellation diagrams [24] usually utilize the three-channel colourful image, which will inevitably increase the computation complexity and trainable parameters of DL-based models. To better balance the signal representation and model complexity, this paper transforms the received signal r(t) into new representations using binary image preprocessing. Specifically, the above transformation process can be divided into two steps, as follows:

Firstly, this paper maps the input FBMC signal r(t) into scattering points on the two-dimensional I/Q plane to generate the raw constellation diagram (RCD). Here, this paper puts each element in r(t) into the corresponding pixel, yielding the constellation coordinate (ImgXm;ImgYm) as follows:

ImgXm(l,w)=round{Lc⋅(2⋅SC)−1SC+Re[γ(l,w)]},(9)

ImgYm(l,w)=round{Lc⋅(2⋅SC)−1SC−Im[γ(l,w)]},(10)

where SC=Max{abs[Re(γ)]}⋅1.5 denotes the boundary value of FBMC signal element, Lc denotes the size of preprocessed constellation diagram and γ denotes the raw constellation diagram. Then, this paper standardizes every pixel value of the above constellation diagram into the binary value with 0 or 255. After that, this paper can obtain the final binary constellation diagram. Mathematically, the above binary image preprocessing can be described as follows:

γB={255, if (ImgXm<SC)‖(ImgYm<SC)0, else (11)

To conduct the visualization analysis, the BCD feature of nine modulation signals at SNR = 20 dB is presented in Fig. 6. As shown in Fig. 6, it is evident that nine modulation schemes have different constellation clustering characteristics in terms of BCD features. Specifically, the OQAM signal displays the cross-shaped constellation layout, which differs from PSK signals with sparse constellation points. In other words, the higher-order OQAM signals correspond to the more intensive cross-shaped constellation. Moreover, different orders of OQAM signals present the different cluster densities of the constellation points. Therefore, the above diversity of various BCD features facilitates the following FBMC modulation recognition task.

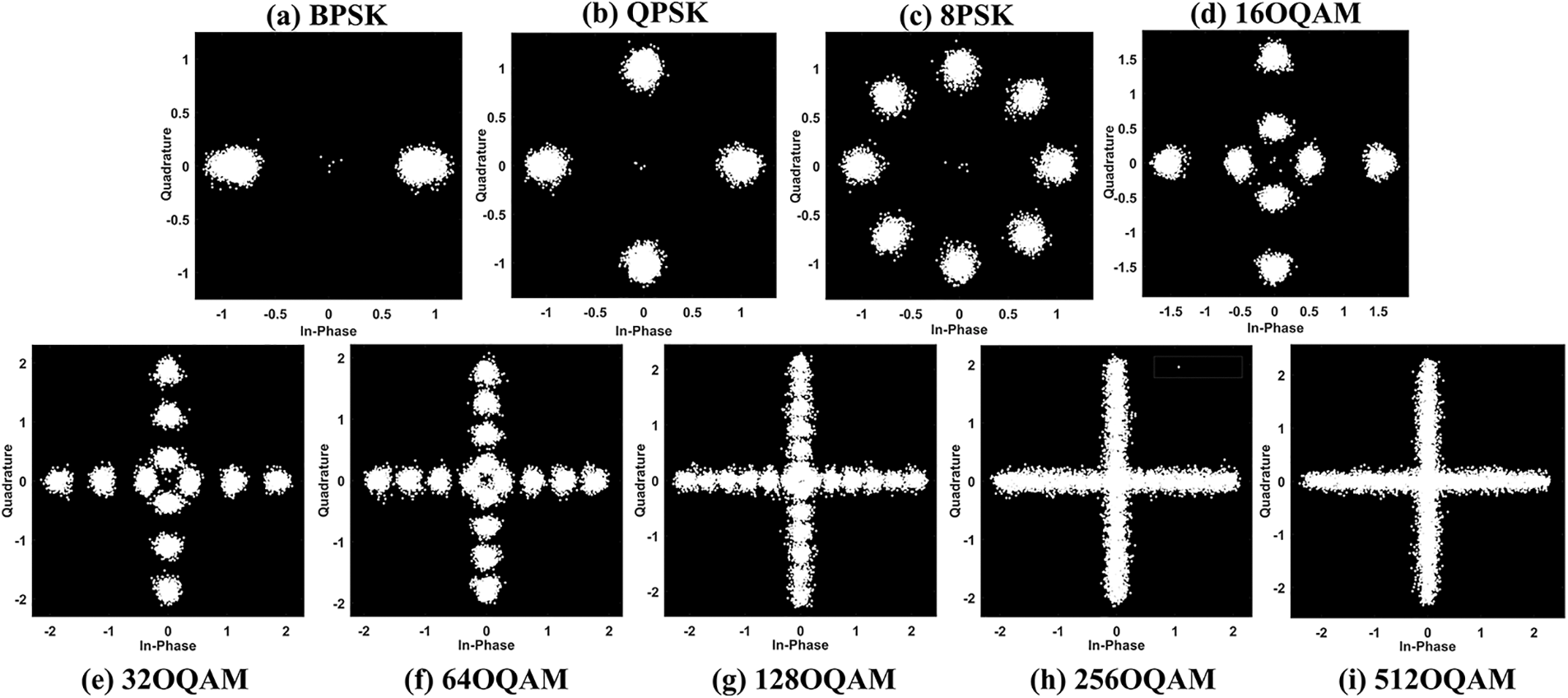
Figure 6: Binary constellation diagram of nine modulation types in FBMC-OQAM systems

3.2 TCCNet Recognizer Based on Transform Channel Convolution Strategy

With the input of BCD features, this paper develops a TCCNet modulation recognition model using the 1D transform channel convolution strategy to accelerate the BMR recognition process, as shown in Fig. 5. Specifically, this research transforms the Q channel axis of the BCD image into the convolution channel axis, which promotes the application of 1D convolutional operation to calculate the 2D image feature. As such, the BCD image recognition task can be shifted into a series recognition task, which can significantly reduce the computational complexity. This work will detail the principle and advantages of the proposed 1D TCC strategy compared with the traditional 2D convolution.

For the case of traditional 2D convolution, the current work [24] directly leverages the 2D constellation diagram as an input feature of AlexNet and Google-Inception-Network (GoogleNet) models, which will induce high complexity and time consumption. As presented in Fig. 7a, this paper sets the input map of a single BCD image as X2D∈RI×Q×1, where I=128 and Q=128 are image length and height, respectively. Additionally, the weight of 2D convolution can be expressed as W2D∈Rlω×lh×c×p where lw=lh=2 denotes the size of the convolutional kernel, c=1 denotes the input channel, p denotes the kernel number. As shown in Fig. 7a, the 2D convolution utilizes the sliding window to implement multiply addition calculation on the input map X2D, yielding the output feature map as Y2D∈RI×Q×p. As a note, the trainable parameter of 2D convolution is given by MACs-2D=2×2×1×I×Q×p=134,217,728.

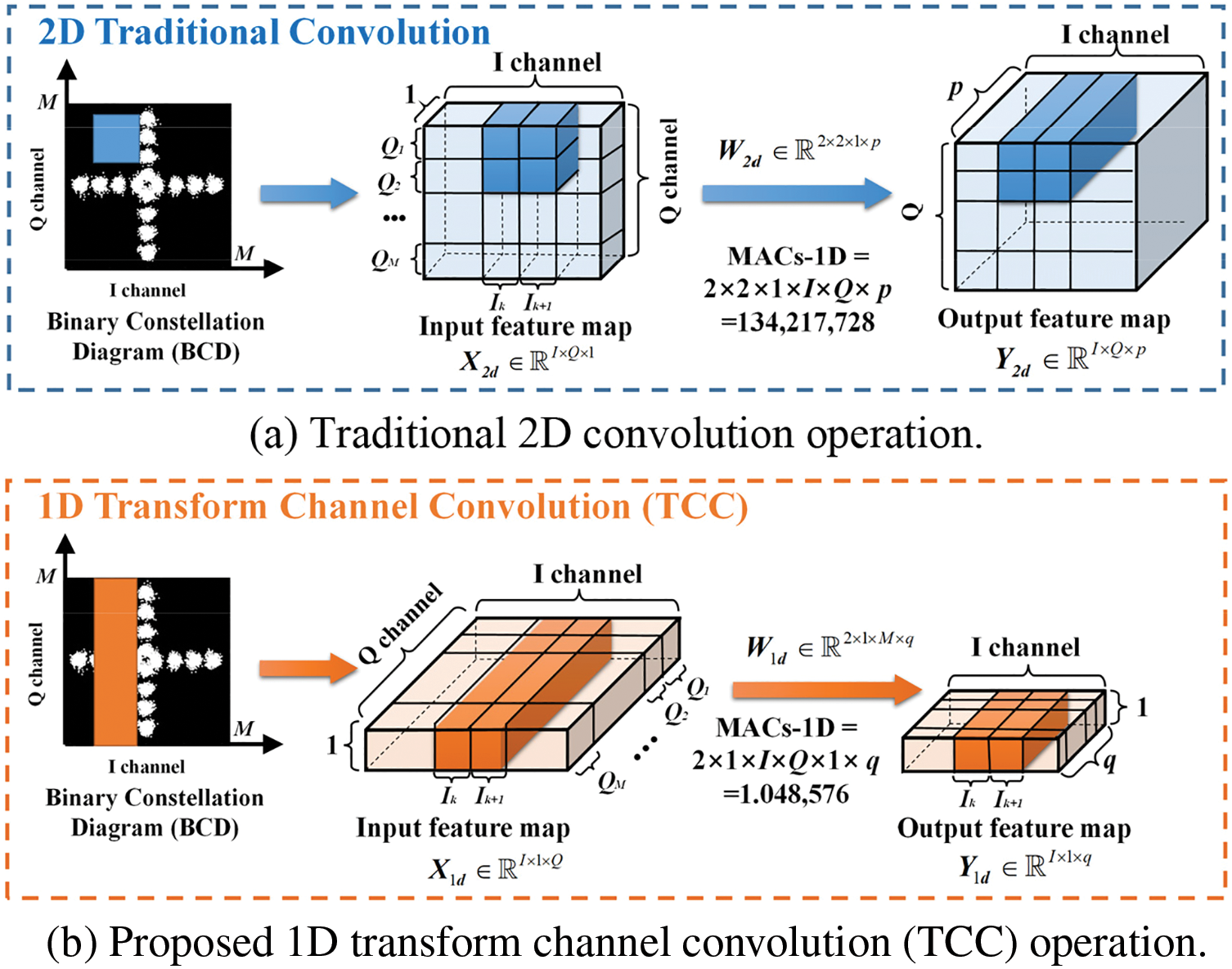
Figure 7: The illustration of the comparison between the proposed 1D TCC convolution and traditional 2D convolution. (Note that two convolution schemes have the same size of convolution kernel size by setting I=128, Q=128, p=2048 and q=32)

For the case of the 1D TCC convolution in Fig. 7b, this work recognizes each column of the BCD image as the 1D temporal feature rather than the 2D grayscale matrix. This feature facilitates the lightweight 1D convolution operation rather than complicated 2D convolution. In detail, this paper exchanges the Q channel and input channel in the BCD feature map X2D∈RI×Q×1 to produce the transformed feature map X1D∈RI×1×Q. To achieve a fair comparison, this paper sets that two convolutions schemes have the same convolution weight, where W1D∈Rlω×c×Q×q with q=(2×p)/Q=32. After the convolution between X1D and W1D, its final output feature map can be expressed as Y1D∈RI×1×q. Accordingly, the trainable parameter of 1D TCC convolution can be presented as MACs-1D=2×1×Q×I×1×q=1,048,576.

Compared with traditional 2D convolution, it is obvious that the 1D TCC convolution can reduce the training parameter of 133,169,152. Therefore, the 1D TCC convolution is a lightweight way to deal with the image recognition task since it possesses a lower computation complexity than traditional 2D convolution methods. This advantage facilitates its application in low-latency scenarios.

As shown in Fig. 5, the proposed TCCNet model mainly consists of three TCC units, two Dropout layers, two Dense layers, and one Flatten layer. Specifically, each TCC unit contains one 1 × 1 residual convolution layer, two rectified linear unit (ReLU) activation layers, and three dilated causal convolution layers. The function of TCC units is to leverage the residual connection and dilated causal convolution for faster recognition speed. Because the dilated causal convolution can learn more prominent features with the exponential information expansion. The 1 × 1 residual convolution, inspired by the ResNet structure, can prevent the vanishing gradient. Mathematically, the dilated causal convolution and the 1 × 1 residual convolution can be presented as follows:

ψ(s)=xd∗ξ(s)=∑ker=0m−1ξ(ker)⋅xs−d⋅ker,(12)

Y=ReLU(x+Psi(s)),(13)

where d and ker are the dilation factor and filter size, respectively. This paper sets that the dilation factor of three dilated causal convolution layers are d1=1, d2=8 and d3=16 to fit the traits of dilated causal convolution. However, all filter size in three layers is ker=8.

For the deployment of TCCNet into the FBMC industrial cognitive radio networks, the overall BMR process can be divided into two parts: the offline training phase and the online testing phase, as depicted in Fig. 8. Note that the offline training is performing the model training before the model testing, regardless of the local Graphic Processing Units (GPU) or the website GPU. Forthe TCCNet model training, the stochastic gradient descent (SGD) algorithm is adopted to perform the backpropagation, namely, to update the model weight and bias parameters Wand b, as follows:

Wl=Wl−η∂L(W,b)∂Wl,(14)

bl=bl−η∂L(W,b)∂bl,(15)

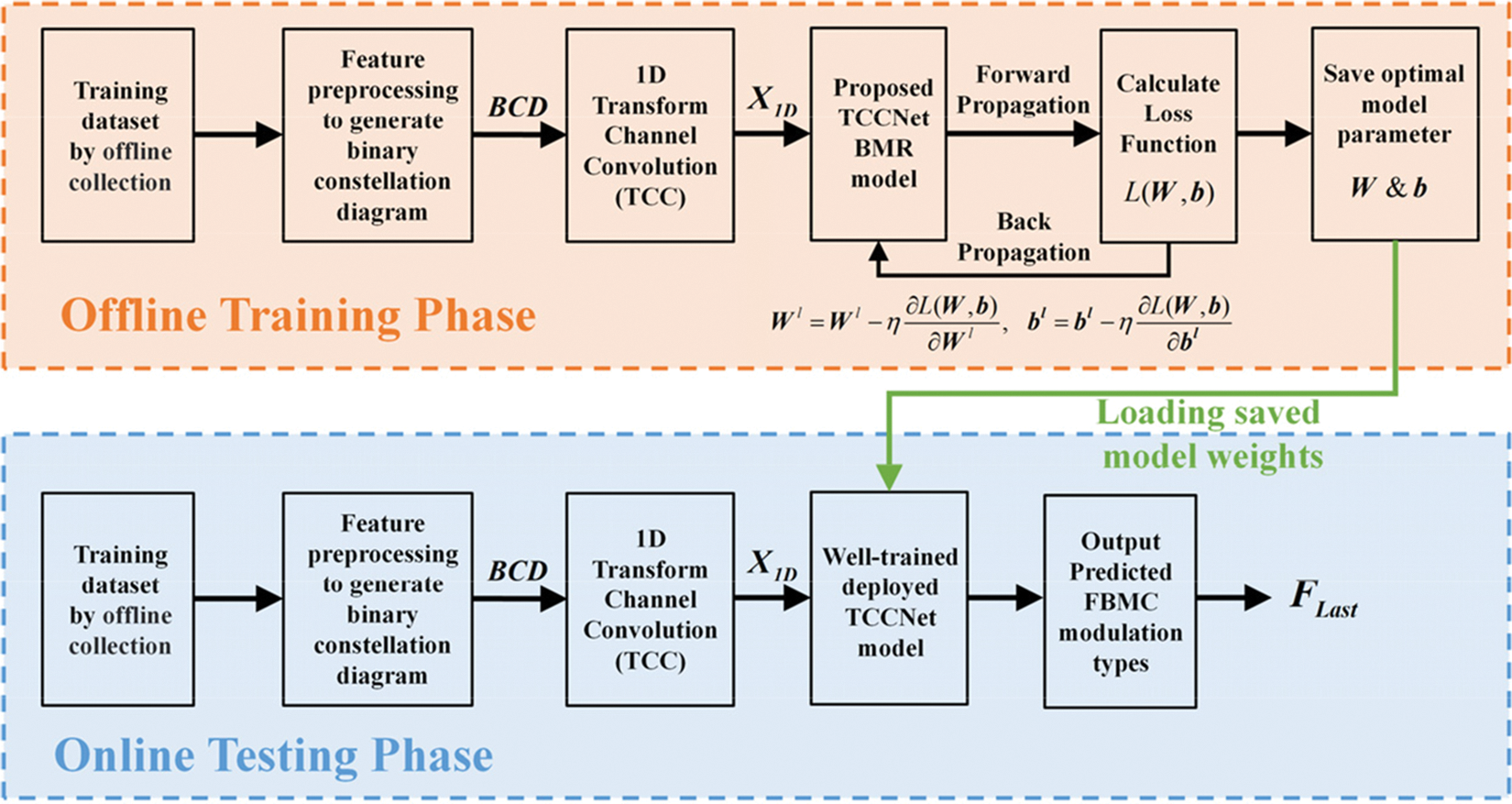
Figure 8: The implementation of offline training and online testing in the proposed TCCNet BMR model

where Kb denotes the sample number in one batch and log⁡(⋅) denotes the logarithmic operation. For the online testing phase, this paper loads the well-trained model parameters W and b into the TCCNet model to perform the FBMC BMR task.

L(W,b)=∑j=1Kb⁡[FTjlog⁡(FPj)+(1−FTj)log⁡(1−rj)FPj]−Kb,(16)

4  Experiments and Simulation Results

In this section, this paper implements several experiments to validate the BMR performance of the proposed TCCNet algorithm in the FBMC-OQAM systems.

4.1 Datasets and Implementation Details

This paper considers a modulation candidate pool of nine modulation types P = {BPSK, QPSK, 8PSK, 16OQAM, 32OQAM, 64OQAM, 128OQAM, 256OQAM, 512OQAM}. The whole SNR ranges from −10 dB to 30 dB with a 2 dB gap. After the binary transformation of the constellation diagram, 600, 200 and 200 images per SNR per mode are generated as the training, validating and testing datasets, respectively. The datasets used in this letter are generated through the matrix laboratory (MATLAB) platform. The key simulation parameters in FBMC systems can be summarized as follows: the overlap factor of the prototype filter is four, the carrier frequency is 6 kHz, the number of subcarriers is 128, the carrier spacing is 100 Hz, and the sampling frequency is 8 kHz.

For the algorithm evaluation, the hardware configuration contains an Intel i7-9700K Center Processing Unit (CPU) and an RTX2060 graphics card. This paper employs the DL framework of Tensorflow 2.4 as the software platform for model training and testing. The number of total epochs in the training process is 50, with an initial learning rate of 0.001. In the model training, this paper adopts the Adam optimizer and the loss function of categorical cross-entropy with a mini-batch step of 128. For the dropout rate, we choose a moderate parameter value of 0.3. In the testing process, the average correct recognition accuracy per SNR PcrSNR=(NrSNR/NAllSNR)×100% is employed as the evaluation index by 1800 Monte Carlo trials per SNR, where NrSNR and NAllSNR denote the number of correct recognized trials and the total trials at each SNR, respectively. As a note, the source FBMC-OQAM signal and AWGN noise are realized randomly in every trial, which is conducive to enhancing the generalization ability of TCCNet in various experimental scenes. The k-fold cross-validation strategy (k = 5) is adopted to perform numerous training and testing procedures to obtain a mean value of recognition accuracy.

4.2 Performance Analysis of Proposed TCCNet

4.2.1 Accuracy Comparisons with Other Existing Methods

To evaluate the proposed TCCNet, this paper calculates the recognition accuracy of six BMR algorithms, containing the SVM-RBF [8] (SVM using the nine expert features), the I/Q-CLDNN [25] (CLDNN using the I/Q feature), the I/Q-ResNet [26] (Residual Network (ResNet) using the I/Q feature), the A/P-LSTM [27] (Long Short Term Memory (LSTM) using the amplitude-phase (A/P) feature), the A/P-GRU [28] (Gate Recurrent Unit (GRU) using the A/P feature) and the CD-AlexNet [24] (AlexNet using the CD feature). An identical amount of signal samples implements all experiments. As illustrated in Fig. 9, this paper observes that the TCCNet performs better than other BMR methods with the SNR ranges distributed from 0 dB to 30 dB. Specifically, compared with baseline CD-AlexNet, the proposed TCCNet can obtain an SNR gain of around 2 dB when the recognition accuracy is 88%. In addition, the previous I/Q-CLDNN, I/Q-ResNet, A/P-LSTM, A/P-GRU and SVM-RBF fail to exceed the maximum recognition accuracy of 80% at the SNR of 30 dB. It also can be observed from Fig. 9 that TCCNet model can obtain an approximate 8% accuracy improvement over the subprime CD-AlexNet model when the SNR is 12 dB, which can be explained by the fact that the TCCNet adopt the transform channel convolution to reduce the effects of interference pixels and AWGN noise. However, when the SNR is below 0 dB, CD-AlexNet outperforms TCCNet with around 4% performance advantages. Because the constellation diagram is too obscure to represent the signal feature under the low SNR cases, which limits the TCCNet. This can be accepted since CD-AlexNet, and other models only obtain a recognition accuracy below 60%.

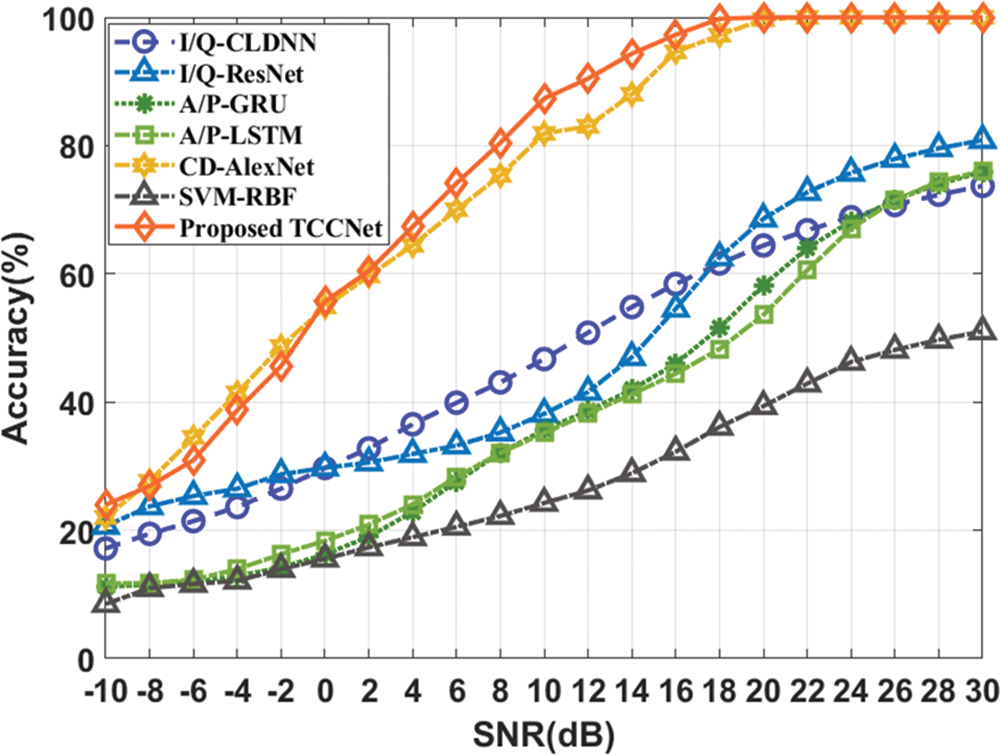
Figure 9: The recognition accuracy among different methods

4.2.2 Complexity Comparisons with Other Existing Methods

Furthermore, this paper evaluates the computational complexity between the proposed TCCNet and other previous methods regarding the total training time (s) and average testing time per sample (ms). Note that all algorithms are trained and tested on the same hardware platform, with GTX1660Ti GPU, 32 GB RAM and Intel i7-9700K CPU. In Fig. 10a, the proposed TCCNet obtains the lowest training time among other methods besides SVM-RBF. However, the recognition accuracy of SVM-RBF could be better to qualify for the BMR task. Thus this paper cannot select SVM-RBF as the final recognizer. The proposed TCCNet can achieve around 29.682 and 2.356 times faster than the suboptimal CD-AlexNet and I/Q-CLDNN, respectively. Moreover, as shown in Fig. 10b, the TCCNet has a similar testing time per sample with the RCD-AlexNet and performs faster than other models based on time-series I/Q and A/P features. Therefore, those indicate that the proposed TCCNet is attractive since it can have a shorter inference time and the best recognition accuracy.

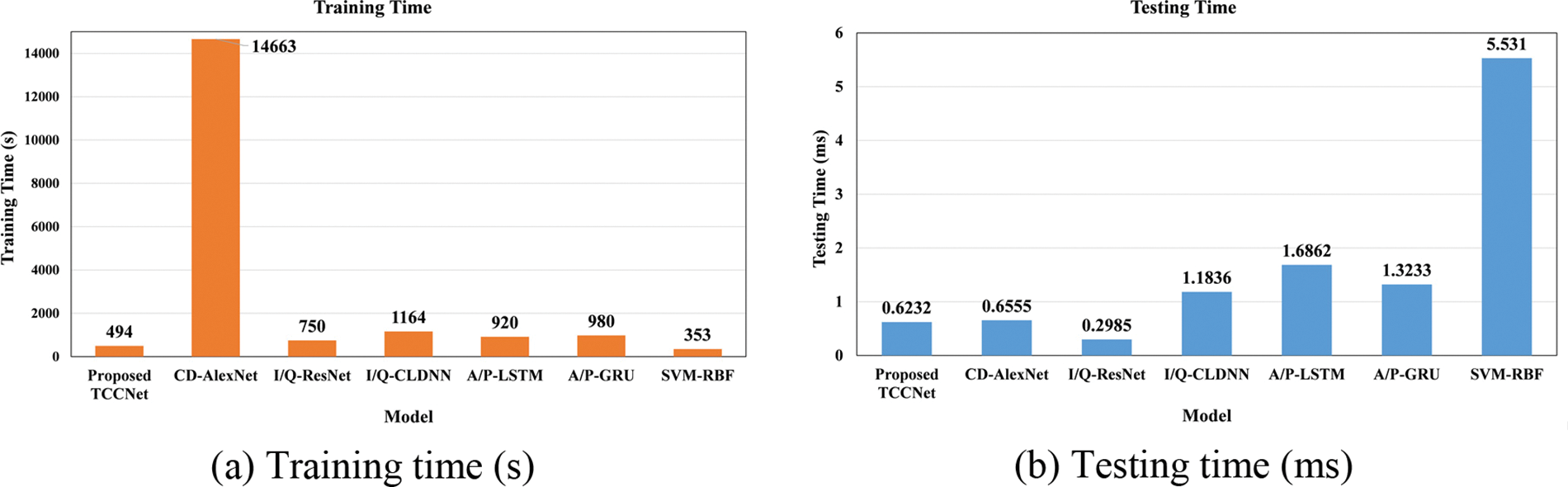
Figure 10: Complexity comparison among existing BMR methods

4.2.3 Recognition Accuracy among Different Modulation Types

In Fig. 11, this paper explores the BMR performance of nine modulation types with the proposed TCCNet. This paper can observe in Fig. 11 that the accuracy of most modulation signals can be improved by increasing the SNR. Note that the 512OQAM type presents an accuracy trend of reducing after improving in the entire SNR range. Because 512OQAN has the inevitable feature confusion with the 128OQAM type at the SNR range from 2 dB to 16 dB, which also can be found in the confusion matrix of Fig. 12. In addition, the low-order modulation types display a higher recognition accuracy than the counterpart of high-order cases. Because the high-order modulated signal has overcrowded constellation points, which inevitably reduces signal representation and deteriorates the BMR accuracy. Moreover, the performance of all modulation modes tends to be stable when SNR≥18 dB since the signal energy is enough to distinguish various modulation types at high SNRs.

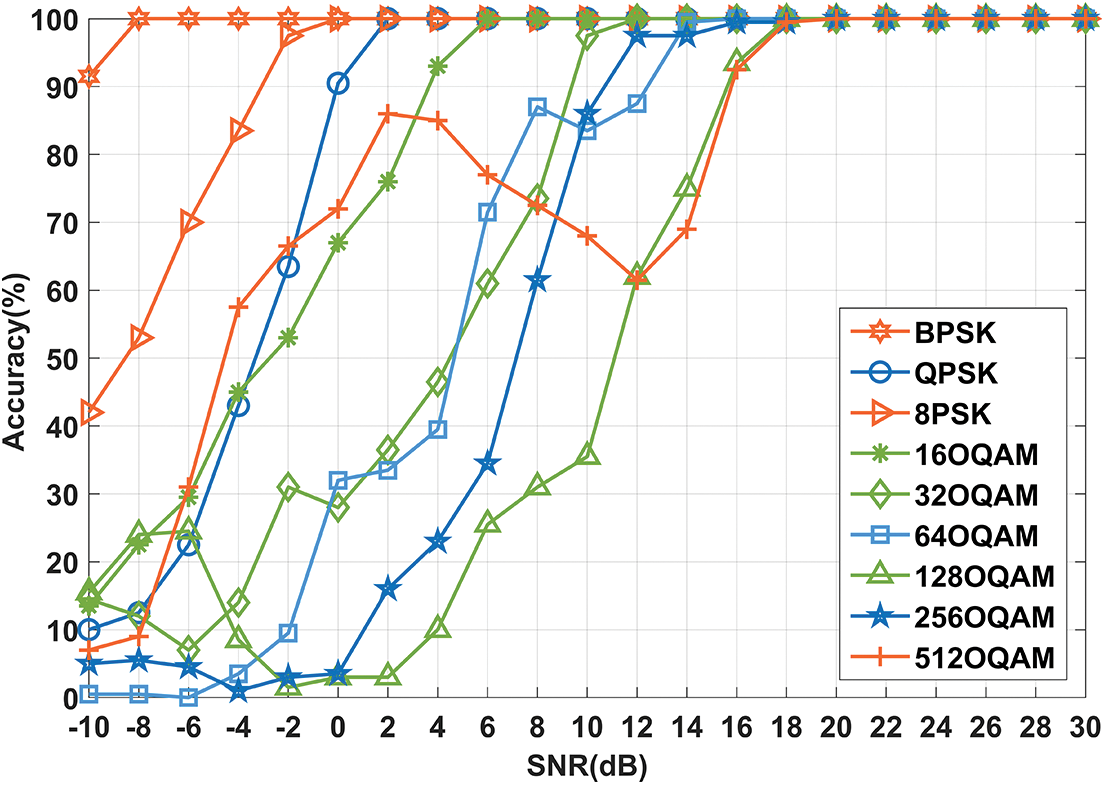
Figure 11: The recognition accuracy of nine modulation types

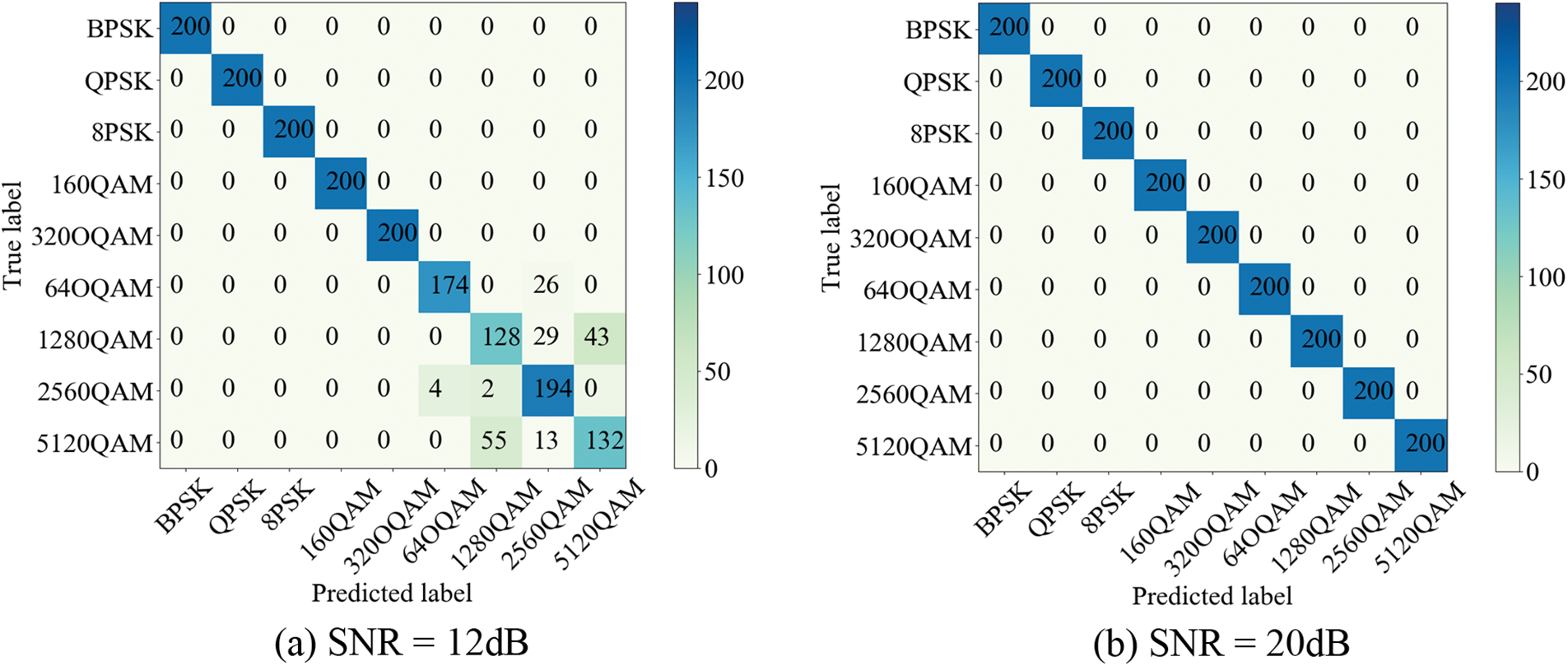
Figure 12: Confusion matrices of the proposed TCCNet under two SNR cases of 12 dB and 20 dB

4.2.4 Confusion Matrices

To illustrate the recognition performance intuitively, the confusion matrices of the proposed TCCNet recognizer are visualized in Fig. 12 at SNR = 12 dB and 20 dB. From Fig. 12a, this paper can observe that the proposed TCCNet presents an apparent confusion between two pairs of high-order classes (64OQAM/256OQAM and 128OQAM/512OQAM) because these OQAM signals have numerous overlapped constellation points in the I/Q plane. Especially for the high-order modulation, the AWGN noise will easily induce feature interference and increase the similarity between 64OQAM/256OQAM and 128OQAM/512OQAM. With the increase of SNR, the confusion problem of high-order modulation schemes can be eliminated in Fig. 12b, where TCCNet can remarkably achieve a 100% recognition accuracy when SNR = 20 dB. Generally, these confusion matrices in Fig. 12 are consistent with the simulation results in Fig. 9. This result means that the high-order modulation recognition is a big challenge for the proposed TCCNet and existing models, which still needs to be solved in the future.

4.2.5 Visualization of Learned Modulation Features

In Fig. 13, this paper visualizes the learned feature distribution of the proposed TCCNet by the T-SNE (T-Distributed Stochastic Neighbor Embedding) tool. It is visible that the overlapping problem can be alleviated effectively with the increase of SNR values. Specifically, a two-pair overlapping problem mainly occurs between 64OQAM/256OQAM and 128OQAM/512OQAM at SNR = 12 dB, which aligns with the confusion matrix results in Fig. 12. At SNR = 20 dB, different modulation types can converge to tighter clusters independently, which improves the differentiation among different modulation types and constructs the visible division border for the deep neural network. From the above results, it can be validated that the 100% accuracy of TCCNet comes from effective feature selection and extraction.

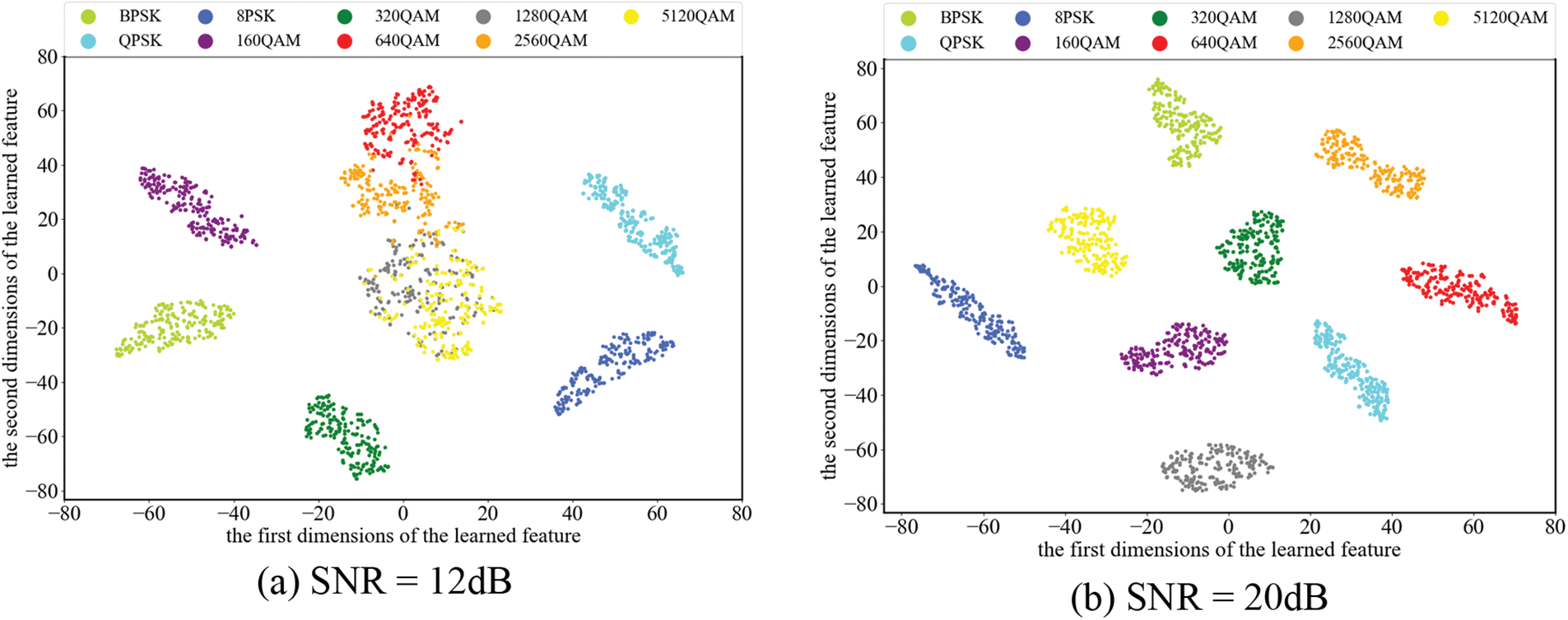
Figure 13: The feature distribution of different modulation types extracted from the proposed TCCNet

4.2.6 Effects of Model Parameters

Fig. 14 explores the impacts of the number of convolution filters in the range [8, 64] and the input image pixel values from to (128 × 128). Generally, the recognition accuracy improves along with the increment of filter numbers and image pixel values. For the SNR of 10 dB, the Filters = 32, 16, and 8 cases achieve around 87.33%, 83.83% and 77.89% accuracy, respectively, where the Filters = 32 has an advantage of 3.5% over Filters = 16 cases and 9.44% over Filters = 8 cases. However, the endless increase of filters will cause an adverse influence on TCCNet performance, with a slight 2.15% performance deterioration from Filters = 32 to Filters = 64. Moreover, the proposed TCCNet can obtain the best performance with pixel = (128 × 128). These results imply that the bigger pixel value contains more conducive information to capture more discriminative features.

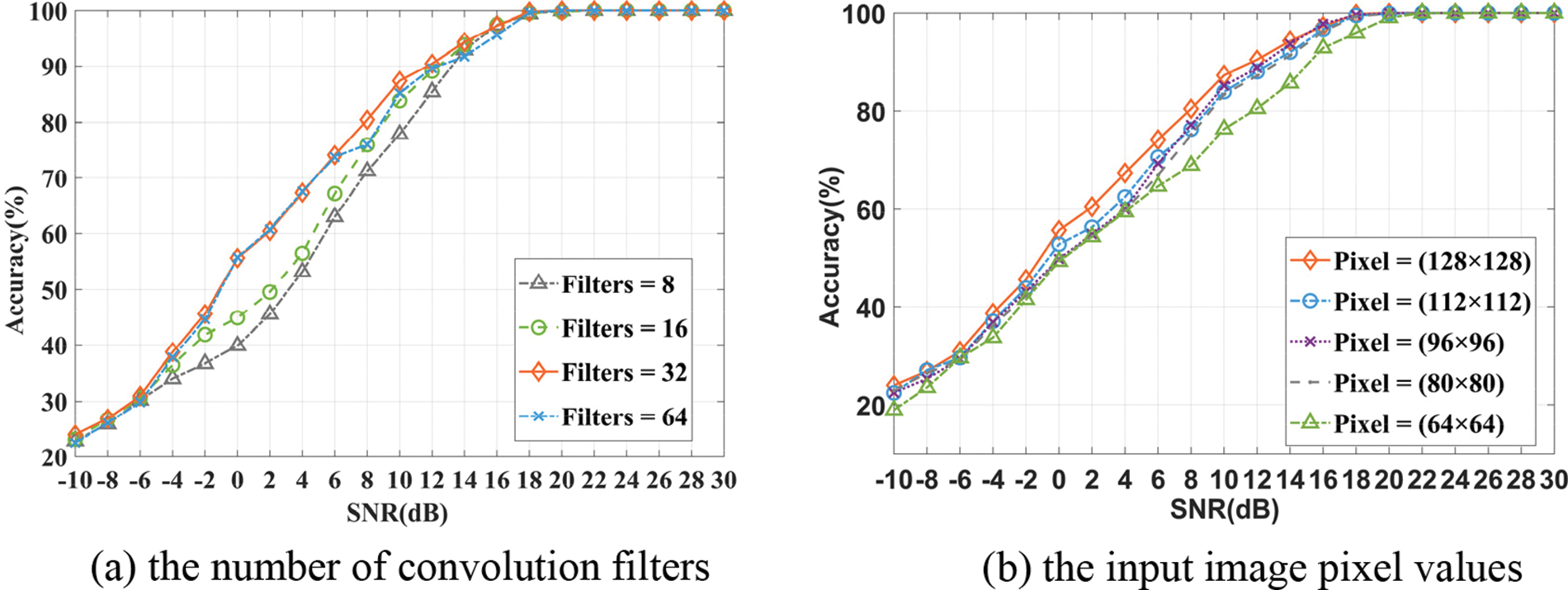
Figure 14: Effects of the different convolution filters and image pixel values on the recognition accuracy of the proposed TCCNet

5  Conclusion

This article proposes a viable BMR framework using transform channel convolution, TCCNet, to identify new OQAM modulation types in the emerging FBMC-OQAM industry cognitive radio network. To maximize the discrimination among various OQAMs, this paper generates the BCD image as the learning content of TCCNet. The novel transforms channel convolution strategy is presented to convert the 2D BCD into 1D series-like format, which supports faster recognition speed and lower network complexity. Another advantage of the TCCNet is that it does not rely on the prior channel knowledge of the receiver. Simulation results verify the efficacy of the proposed TCCNet to recognize nine modulation signals with a recognition accuracy of 100% at SNR=18 dB.

This work contributes to the future B5G intelligent receiver design and opens up new BMR research directions for the emerging FBMC-OQAM ICRNet. For the research limitation of this paper, supervised learning with enough samples is employed to perform the FBMC modulation recognition. However, this paper has yet to consider the small sample learning technique in FBMC BMR research to reduce the need for a massive sample. In the future, more powerful prepossessing features can be further investigated to improve recognition accuracy and more challenging generalization ability. Additionally, this paper will explore meta-learning technologies to reduce the needs of the labelled training dataset and achieve a BMR method driven by small-scale labelled data samples. Cyclostationary theory can be a promising solution to investigate further to improve the performance of high-order modulation schemes.

Acknowledgement: Thanks for the contributors of the editing and planning from Abdullah Tahir and Martin Hedegaard Nielsen.

Funding Statement: This work is supported by the National Natural Science Foundation of China (Nos. 61671095, 61371164), the Project of Key Laboratory of Signal and Information Processing of Chongqing (No. CSTC2009CA2003).

Author Contributions: The authors confirm contribution to the paper as follows: conceptualization, methodology, software, writing original draft: Zeliang An, Tianqi Zhang, Debang Liu and Yuqing Xu; formal analysis, investigation, methodology, supervision: Gert Frølund Pedersen and Ming Shen. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The relevant data and materials are utilized in the following research for our group.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. Zong, F. H. Memon, X. Li, H. Wang and K. Dev, “End-to-end transmission control for cross-regional industrial internet of things in Industry 5.0,” IEEE Transactions on Industrial Informatics, vol. 18,no. 6, pp. 4215–4223, 2022. [Google Scholar]

2. A. Mahmood, L. Beltramelli, S. Fakhrul Abedin, S. Zeb, N. Mowla et al., “Industrial IoT in 5G and beyond networks: Vision, architecture, and design trends,” IEEE Transactions on Industrial Informatics, vol. 18, no. 6, pp. 4122–4137, 2022. [Google Scholar]

3. H. Wang, L. Xu, Z. Yan and T. A. Gulliver, “Low-complexity MIMO-FBMC sparse channel parameter estimation for industrial big data communications,” IEEE Transactions on Industrial Informatics, vol. 17, no. 5, pp. 3422–3430, 2021. [Google Scholar]

4. H. Wang, X. Li, R. H. Jhaveri, T. R. Gadekallu, M. Zhu et al., “Sparse Bayesian learning based channel estimation in FBMC/OQAM industrial IoT networks,” Computer Communications, vol. 176, no. 1, pp. 40–45, 2021. [Google Scholar]

5. K. Wang, X. Liu, C. M. Chen, S. Kumari, M. Shojafar et al., “Voice-transfer attacking on industrial voice control systems in 5G-aided IIoT domain,” IEEE Transactions on Industrial Informatics, vol. 17, no. 10, pp. 7085–7092, 2021. [Google Scholar]

6. Y. Zhuo and Z. Ge, “Data guardian: A data protection scheme for industrial monitoring systems,” IEEE Transactions on Industrial Informatics, vol. 18, no. 4, pp. 2550–2559, 2022. [Google Scholar]

7. S. Peng, S. Sun and Y. Yao, “A survey of modulation classification using deep learning: Signal representation and data preprocessing,” IEEE Transactions on Neural Networks and Learning Systems, vol. 33,no. 12, pp. 1–19, 2021. [Google Scholar]

8. H. Tayakout, I. Dayoub, K. Ghanem and H. Bousbia-Salah, “Automatic modulation classification forD-STBC cooperative relaying networks,” IEEE Wireless Communications Letters, vol. 7, no. 5, pp. 780–783, 2018. [Google Scholar]

9. M. Anul Haq, “Cdlstm: A novel model for climate change forecasting,” Computers, Materials & Continua, vol. 71, no. 2, pp. 2363–2381, 2022. [Google Scholar]

10. M. Anul Haq, A. Khadar Jilani and P. Prabu, “Deep learning based modeling of groundwater storage change,” Computers, Materials & Continua, vol. 70, no. 3, pp. 4599–4617, 2022. [Google Scholar]

11. M. Anul Haq, G. Rahaman, P. Baral and A. Ghosh, “Deep learning based supervised image classification using UAV images for forest areas classification,” Journal of the Indian Society of Remote Sensing, vol. 49, no. 3, pp. 601–606, 2021. [Google Scholar]

12. M. Anul Haq, “Planetscope nanosatellites image classification using machine learning,” Computer Systems Science and Engineering, vol. 42, no. 3, pp. 1031–1046, 2022. [Google Scholar]

13. M. Anul Haq, “Intellligent sustainable agricultural water practice using multi sensor spatiotemporal evolution,” Environmental Technology, vol. 1, no. 1, pp. 1–14, 2021. [Google Scholar]

14. M. Liu, G. Liao, N. Zhao, H. Song and F. Gong, “Data-driven deep learning for signal classification in industrial cognitive radio networks,” IEEE Transactions on Industrial Informatics, vol. 17, no. 5, pp. 3412–3421, 2021. [Google Scholar]

15. M. Liu, K. Yang, N. Zhao, Y. Chen, H. Song et al., “Intelligent signal classification in industrial distributed wireless sensor networks based industrial internet of things,” IEEE Transactions on Industrial Informatics, vol. 17, no. 7, pp. 4946–4956, 2021. [Google Scholar]

16. M. Liu, N. Qu, J. Tang, Y. Chen, H. Song et al., “Signal estimation in cognitive satellite networks for satellite based industrial internet of things,” IEEE Transactions on Industrial Informatics, vol. 17, no. 3, pp. 2062–2071, 2021. [Google Scholar]

17. L. Zhang, C. Lin, W. Yan, Q. Ling and Y. Wang, “Real-time OFDM signal modulation classification based on deep learning and software-defined radio,” IEEE Communications Letters, vol. 25, no. 9, pp. 2988–2992, 2021. [Google Scholar]

18. Z. An, T. Zhang, M. Shen, E. D. Carvalho, B. Ma et al., “Series-constellation feature based blind modulation recognition for beyond 5G MIMO-OFDM systems with channel fading,” IEEE Transactions on Cognitive Communications and Networking, vol. 8, no. 2, pp. 793–811, 2022. [Google Scholar]

19. D. Kong, X. Zheng, Y. Yang, Y. Zhang and T. Jiang, “A novel DFT-based scheme for PAPR reduction in FBMC/OQAM systems,” IEEE Wireless Communications Letters, vol. 10, no. 1, pp. 161–165, 2021. [Google Scholar]

20. B. Q. Doanh, D. T. Quan, T. C. Hieu and P. T. Hiep, “Combining designs of precoder and equalizer for MIMO FBMC-OQAM systems based on power allocation strategies,” AEU-International Journal of Electronics and Communications, vol. 130, no. 3, pp. 153572, 2021. [Google Scholar]

21. Y. A. Eldemerdash, O. A. Dobre and M. Öner, “Signal identification for multiple-antenna wireless systems: Achievements and challenges,” IEEE Communications Surveys Tutorials, vol. 18, no. 3, pp. 1524–1551, 2016. [Google Scholar]

22. R. Nissel and M. Rupp, “OFDM and FBMC-OQAM in doubly-selective channels: Calculating the bit error probability,” IEEE Communications Letters, vol. 21, no. 6, pp. 1297–1300, 2017. [Google Scholar]

23. PHYDYAS, Phydyas european project, 2010. [Google Scholar]

24. S. Peng, H. Jiang, H. Wang, H. Alwageed, Y. Zhou et al., “Modulation classification based on signal constellation diagrams and deep learning,” IEEE Transactions on Neural Networks and Learning Systems, vol. 30, no. 3, pp. 718–727, 2019. [Google Scholar] [PubMed]

25. X. Liu, D. Yang and A. E. Gamal, “Deep neural network architectures for modulation classification,” in 2017 51st Asilomar Conf. on Signals, Systems, and Computers, Pacific Grove, CA, USA, pp. 915–919, 2017. [Google Scholar]

26. T. J. O’Shea, T. Roy and T. C. Clancy, “Over-the-air deep learning based radio signal classification,” IEEE Journal of Selected Topics in Signal Processing, vol. 12, no. 1, pp. 168–179, 2018. [Google Scholar]

27. S. Rajendran, W. Meert, D. Giustiniano, V. Lenders and S. Pollin, “Deep learning models for wireless signal classification with distributed low-cost spectrum sensors,” IEEE Transactions on Cognitive Communications and Networking, vol. 4, no. 3, pp. 433–445, 2018. [Google Scholar]

28. D. Hong, Z. Zhang and X. Xu, “Automatic modulation classification using recurrent neural networks,” in 2017 3rd IEEE Int. Conf. on Computer and Communications (ICCC), Chengdu, China, pp. 695–700, 2017. [Google Scholar]