An Air Defense Weapon Target Assignment Method Based on Multi-Objective Artificial Bee Colony Algorithm

1  Introduction

In the modern complex battlefield environment, with the emergence of high-tech and high-speed aerial weapon platforms, intelligent decision-making and scheduling of air defense weapon resources are particularly important. In air defense and anti-missile operations, weapon target assignment (WTA) is an important issue that needs to be resolved in the battlefield fire attack decision [1–4]. Our maximum effectiveness is the target of air defense operations. Developing a rational air defense WTA planning by determining the threat of target attack is an important topic in the field of military combat research. The design of WTA models and the selection of accurate and efficient intelligent optimization algorithms in a given situation is the focus and difficulty. Based on the destruction area of multiple target passage numbers for ground-to-air missile defense systems, Liu et al. [3] studied the WTA problem of maximizing the interception of enemy targets and satisfying the time constraint, space constraint, and resource constraint. Davis et al. [4] studied the ballistic missile defense problem based on a dynamic perspective with an uncertainty of multiple rounds of flanking fire to maximize the protection of own resources. The single-objective WTA model suffers from the obvious shortcomings of resource wastage and inconsistency, and the current mainstream studies are generally multi-objective WTA models. Given the new characteristics of defense strategies during group target attacks, Nie et al. [5] established a WTA model with principles that aim at the maximum attack effectiveness, the maximum own remaining effectiveness, and the minimum total weapon consumption. Based on the above research, we design the air defense weapon target assignment as a multi-objective optimization model, taking defensive resource loss, total weapon consumption, and target residual effectiveness as optimization objectives.

The intelligent optimization algorithm is an effective method to solve the NP-hard problems, such as the immune-based ant colony optimization (ACO) algorithm [6,7], genetic algorithm (GA) [8], discrete particle swarm optimization (DPSO) [9], etc. All belong to the meta-heuristic algorithm, which can simulate the foraging and reproduction of biological populations. However, these methods can only deal with single-objective WTA issues and cannot be applied to multi-objective optimization models. Nie et al. [5] proposed an optimization framework and specific process based on the NSGA-III algorithm and conducted simulation experiments under specific combat missions. Zhou et al. [10] proposed a D-NSGA-III algorithm to achieve high-dimensional multi-target task assignment for UAV swarms. Long et al. [11] used the data set to train a decision-making neural network to realize air defense weapons intelligent scheduling. As mentioned above, an important issue in air defense weapon target assignment is the selection of an appropriate performance metric. In the modeling that follows, we should optimize the performance metric for the mission WTA scenario under a set of operational constraints.

The targets move fast and can only be destroyed in a short time window. For air defense operations, the requirement of timeliness is high. Considering the short time window of the weapon’s striking, it is still necessary to further improve the real-time performance. The computational efficiency and global convergence of NSGA-III algorithm for WTA solving are insufficient. In addition, the actual data samples for combat are small, and it is difficult to obtain an effective decision model through neural network training. The rationality of input simulated data training cannot be verified.

The artificial bee colony (ABC) algorithm, proposed by Turkey scholar Karaboga in 2005, is a swarm intelligence optimization method simulating bees’ foraging behaviors [12]. It completes a series of optimization processes by simulating bees foraging. Compared with the above algorithms, it has fewer parameters and is easy to implement. It is widely used in production scheduling, path planning, system optimization, and other fields, and its algorithm research is relatively mature. The multi-objective bee colony algorithm first proposed in the reference [13] is a milestone. It further extends the ability of the algorithm to achieve multi-objective optimization by constructing an external file on the standard ABC algorithm and using better individuals to guide the evolution. The MOABC algorithm has great adaptability to high-dimensional multi-objective optimization, and has significant advantages in improving operating efficiency, increasing the diversity of solution spaces, and reducing computational complexity, effectively compensating for many shortcomings.

To summarize, the contributions of this work are presented in the following list:

The effectiveness of air defense operations is evaluated through indicators including defensive resource loss, total weapon consumption, and target residual effectiveness based on the characteristics of the battlefield environment and operational tasks. A 0–1 integer-constrained multi-objective WTA optimization model is developed.

The MOABC algorithm for air defense weapon target assignment is presented. One-to-one and many-to-one scenarios weapon and target mapping relationships are established by cleverly designed coding rules, respectively. The effectiveness of the algorithm is verified by establishing Archive update non-dominated solutions.

2  Related Work

Recently, as one type of the most effective algorithms for solving non-deterministic polynomial hard (NP-hard) problems like MOPs, multi-objective artificial bee colony (MOABC) algorithm have been proved successfully in practice and demonstrated powerful competitiveness. due to its ease of implementation, it has been successfully applied to many real-world problems, such as industrial systems, image processing, and so on. Compared with other evolutionary algorithms, such as particle swarm optimization (PSO) and NSGA, ABC shows strong global search ability. Zhao et al. [14] used the MOABC algorithm based on the limit search strategy. With the bees searching according to individual limits, the search radius is dynamically adjusted to improve the search accuracy and convergence speed, which improves the search accuracy and convergence speed. The proposed algorithm performs well in convergence and distribution. To reduce the number of casualties and damages in disaster management, Niyomubyeyi et al. [15] used the MOABC algorithm for evacuation planning and provided a better evacuation solution. In addition, they compared and studied four meta-heuristic algorithms, AMOSA, MOABC, MSPSO, and NSGA-II, and found that the MOABC algorithm achieves higher quality solutions and a higher level of repeatability [16]. Zhang et al. [17] proposed a multi-objective artificial bee colony optimization (MOABCO) algorithm and applied it to solve the Multi-Objective Test Case Prioritization (MOTCP) problem to improve the efficiency of regression testing.

The MOABC algorithm has unique advantages for solving mission planning and intelligent decision-making in the military field, but its related research in the air defense combat WTA problem is rare. Mao et al. [18] used the ABC algorithm to solve the weapon target assignment problem, but their optimization objective considered only one optimization objective, i.e., the maximum mathematical expectation of all weapon system destruction targets. Gu et al. [19] used the MOABC algorithm to optimize the UAV formation topology based on the formation communication chain length, considering the network delay influence factor and the residual energy imbalance degree, etc. The study showed that the optimization result of MOABC algorithm can improve the formation range. In order to solve the problem of troop deployment and firepower coordination of tank detachments in offensive combat, Chu et al. [20] first put forward the model of tank position deployment and the model of tank firepower allocation. Then, the two-layer iteration strategy was adopted and the bottom iteration was used to solve the firepower allocation model. Finally, the ABC algorithm was used to optimize the tank position deployment scheme. The experimental results show that the convergence speed and convergence accuracy of the ABC algorithm on a specific model are significantly improved. Under the same fitness evaluation, it can significantly improve the timeliness and scientificity of command decision-making in combat.

At present, there is no research on solving multi-objective air defense WTA with MOABC. Inspired by the above research, we design multi-objective-driven WTA models and use the MOABC algorithm for the optimization of air defense WTA schemes to meet the requirements of rapidity and accuracy.

3  System Model and Problem Description

3.1 Descriptions of Multi-Objective Programming

The multi-objective programming (MOP) is composed of multiple objective functions, decision variables, and constraints, and there are generally conflicting relationships between objective functions. The model can be described as Eq. (1).

minF(x)=[f1(x),f2(x),⋯,fm(x)]Ts.t.gi(x)≤0,i∈Ihj(x)=0,j∈I(1)

In Eq. (1), x is a feasible solution, f(x) is an objective function, g(x) and h(x) are inequality constraints and equality constraints, respectively.

The solution of multi-objective optimization is not unique, but a set of solutions. Pareto dominance is the most common multi-objective solving mechanism. In the case of multiple objective functions, there may be conflicts and incomparable phenomena between objective functions. For example, a solution that is best for one objective function may be the worst for another. While improving any objective function, these solutions called the Pareto solutions will inevitably weaken at least one other objective function, which is also called non-dominated solutions. The set of optimal solutions for multi-objective functions is called the Pareto optimal set. The optimal set forms a Pareto front in the solution space. Pareto proposed the concept of a non-dominated set of multi-objective solutions in 1986, whose basic definition is as follows.

For a multi-objective programming problem, its variable feasible region is denoted by S, and the corresponding objective function feasible region is Z=f(S). Given a feasible point x∗∈S, for ∀x∈S, if f(x∗)<f(x), x∗ is called the absolute optimal solution. If there is no x∈S, resulting in f(x∗)<f(x), x∗ is called the effective solution, which is the Pareto optimal solution of the multi-objective programming problem.

3.2 A Multi-Objective Programming WTA Model

3.2.1 Model Assumptions

In this paper, the optimization goal is to minimize the target residual effectiveness, minimize the defensive resource loss, and minimize the weapon resource consumption, which is also in line with the experience of battlefield commanders. Then the air defense WTA model is constructed to quickly form a strike decision plan. The specific combat scenario is an air defense combat mission. Suppose we have K important ground defensive resources (D={d1,d2,…,dn}), and the enemy has a task formation composed of N potential aerial targets (T={t1,t2,…,tn}). We deploy M available weapons to strike the targets (W={w1,w2,…,wm}). The cost of firing a weapon to strike a target is C={c1,c2,…,cm}, the target unit value vector is V={v1,v2,…,vn}, and the value vector of our defense resources is L={l1,l2,…,lk}.

The deployed firepower resources of M defense weapons to N air targets are allocated by setting a Boolean variable xij, which xij=1 means that the weapon wi strikes the target tj, and xij=0 means that the weapon wi does not strike the target tj. Therefore, it can be represented by the “0–1” integer programming model.

3.2.2 Objective Functions

(1)   Defensive resource loss

The purpose of air defense weapons is to destroy aerial targets to secure defense resources from attack. However, in actual air defense operations, the enemy air combat units will attack or even destroy important defense resources, so combat losses are inevitable. Assuming that each aerial target has penetration capability, the target’s ability to strike and destroy is positively correlated to the weapon’s damage probability and the target’s threat level.

f1=∑k=1Klk∑j=1Nqkj∏i=1M(1−pij)xij(2)

In Eq. (2): pij(0≤pij≤1) is the damage probability of the i-th weapon against the j-th target, qjk is the threat of the j-th target to the k-th one’s defense resource, and lk is the value of the k-th defense resource (task contribution).

(2)   Total weapon consumption

Assuming that each surface-to-air weapon can only hit one target when weapons attack the opponent’s targets, the total weapon consumption is shown in Eq. (3).

f2=∑i=1Mci∑j=1Nxij(3)

(3)   Target residual effectiveness

The target residual effectiveness is an important indicator to measure the strike and destroy the capability of surface-to-air weapons. The higher the damage probability of the surface-to-air weapon, the lower the target’s residual effectiveness. In the adversarial battlefield scenario, the damage probability of air defense weapons is used to characterize the damage capability, and the target residual effectiveness function is designed as Eq. (4).

f3=∑j=1Nvj∏i=1M(1−pij)xij(4)

To efficiently destroy enemy targets, protect our battlefield defensive resources from attacks, and reduce weapon consumption, the MOP model of WTA shown in Eq. (5) is obtained.

minF=(f1,f2,f3)(5)

{M≥N∑j=1Nxij=1,i=1,2,⋯M1≤∑i=1Mxij≤M−N+1,j=1,2,⋯Nxij∈{0,1}(6)

Constraints in Eq. (6): ① The number of weapon resources M is more than that of aerial targets N; ② Each weapon can strike at most one target when performing fire strike missions; ③ The number of weapons allocated to the same target is no more than M−N + 1.

4  A Multi-Objective Artificial Bee Colony Algorithm for WTA

4.1 The Mechanism of Seeking Nectar

The multi-objective artificial bee colony algorithm (ABC) is a swarm intelligence optimization algorithm based on the nectar-collecting mechanism of bees. The ABC algorithm has the advantages of few parameters, fast convergence, and simple operation. The description of the ABC algorithm is as follows: The candidate solution of the problem is regarded as a nectar source, and bees are divided into three types according to the division of labor, including employed bees, onlooker bees, and scout bees. Employed bees are responsible for the initial search for nectar source and sharing information. Onlooker bees are responsible for staying in the hive to collect nectar according to the information provided by the employed bees. After the original nectar source is abandoned, the scout bees randomly search for a new nectar source to replace the original one. After initializing the bee colony and nectar source, the three operations, including the phase of employed bees, onlooker bees, and scout bees, are performed repeatedly to find the optimal solution.

(1)   Initialize the bee colony

Initialize the algorithm parameters and randomly generate a certain amount of nectar source X=(x1,x2,…,xN) as feasible solutions within the feasible region, where xi=(xi1,xi2,…,xiD)T. D is the dimension of the solution vector, and Eq. (7) represents randomly generated nectar source.

xij=xminj+rand[0,1]×(xmaxj−xminj)i={1,2,…,N}j={1,2,…,D}(7)

In Eq. (7), xij is the j-th dimension of the i-th nectar source. rand[0,1] is a random number of [0, 1]. xmaxj and xminj are the maximum and minimum values of the j-th dimension of all nectar source, respectively.

(2)   Employed bees phase

Employed bees find new nectar source according to Eq. (8). The value of the nectar source is evaluated by comparing the nectar quality (fitness value) of each nectar source. The larger the value, the better the quality of the feasible solution. The greedy mechanism is used to select the nectar source and retain the better nectar source.

vij=xij+ϕij(xij−xkj)(8)

In Eq. (8), xk (k={1,2,…,N}) is the nectar in the neighborhood of xi. ϕij is a random number from −1 to 1, which affects the convergence speed of the algorithm.

(3)   Onlooker bees phase

After the employed bees find a new source of nectar, the employed bees select onlooker bees to follow based on a roulette strategy and then track and develop the nectar source. Like employed bees, a new nectar source location is locally searched according to Eq. (9), and the better nectar source is retained following the principle of the greedy mechanism. If the quality of the nectar source is better than the original nectar source, the existing nectar source is replaced with a count of the trial(i) = 0, otherwise trial(i) = trial(i)  +1. The selection probability of onlooker bees is shown in Eq. (10) and Fi is the fitness value of the i-th nectar source.

pi=Fi/∑n=1NFnn={1,2,…,N}(9)

Fi={11+fi,fi≥01+|f|,fi<0(10)

(4)   Scout bees phase

If the nectar source has not been updated when the number of searches reaches the upper limit of Gmax, the current nectar source is discarded. The corresponding employed bees and onlooker bees act as scout bees. In the scout bees phase, the scout bees randomly search for new nectar source to replace the current nectar source according to Eq. (7). The scout bees phase effectively avoids falling into the local optimum prematurely and improves the global search capability of the algorithm.

4.2 Archive Update

In order to apply the artificial bee colony algorithm to multi-objective optimization, it is necessary to improve the original algorithm and set up an external file-handling mechanism. The high-quality solutions generated in each iteration are stored in the Archive [15], and the internal nectar source is constantly updated during the iteration. The detailed steps are as follows:

1.    The solution generated during the iteration is discarded if it is dominated by the solution in the Archive.

2.    If the new solution dominates one or more solutions in the Archive, the solutions dominated in the Archive are replaced by the new solution.

3.    All the solutions in the Archive are independent of each other, and a new solution is added to the Archive.

The addition of new non-dominated solutions to the Archive can effectively maintain group diversity. When the number of solutions in the Archive reaches the limit, similar individuals need to be eliminated according to the dominance level and crowdedness distance to satisfy the Archive space.

1.    Calculate the objective function f (f1, f2,…, fn) of all solutions, and find the maximum fimax and minimum fimin of each objective function.

2.    Calculate the crowdedness distance Dc(i) of each solution according to Eq. (11).

Dc(i)=∑i=1kfi(j+1)−fi(j−1)fimax−fimin(11)

In Eq. (11) and Fig. 1, fi(j + 1) and fi(j−1) are the values of the i-th objective function corresponding to the two adjacent nectar source of the j-th nectar source.

3.   If the number of solutions in the Archive exceeds the limit, the solution with a higher degree of congestion is preferred, that is, the solution with a smaller Dc is removed from the Archive.

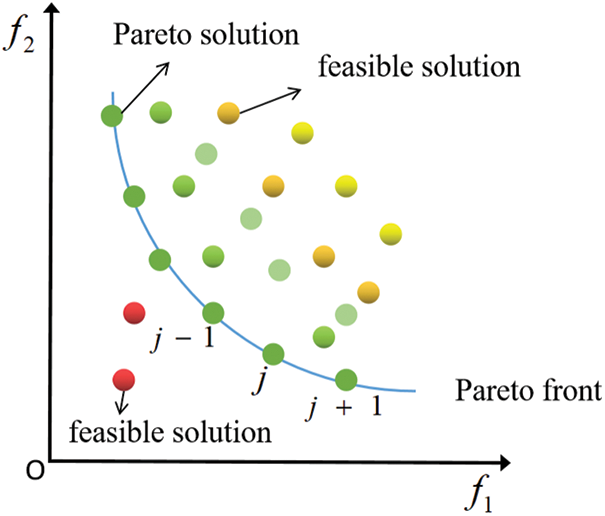
Figure 1: Congestion diagram

4.3 Encoding and Constraint Processing

In this paper, real number vectors are used to encode individuals in the population. For a scenario where M air defense weapons strike N aerial targets, the dimension D = M. Each dimension is represented by a random real number in the interval (0, N + 1). The integer represents the target number (except when the integer part is 0), and the order of decimals represents the weapon serial number of the corresponding target. M air defense weapons are numbered in descending order. Each weapon strike at most one opponent’s target, so not all weapons are assigned. When the integral part of a dimension is 0, the corresponding air defense weapon is not assigned. For example, it is supposed that 5 air defense weapons strike 4 aerial targets in a combat scenario, and the individual positions of the population are represented by random real numbers in [0, 5]. In Fig. 2, x1 = 2.91, x3 = 2.46, the integer part is 2, and the decimal part in descending order is 1st and 5th, which means that w1 and w5 jointly attack the second target. Compared with binary encoding, real number encoding effectively utilizes the characteristics of the bee colony and greatly reduces the dimensionality of the computation.

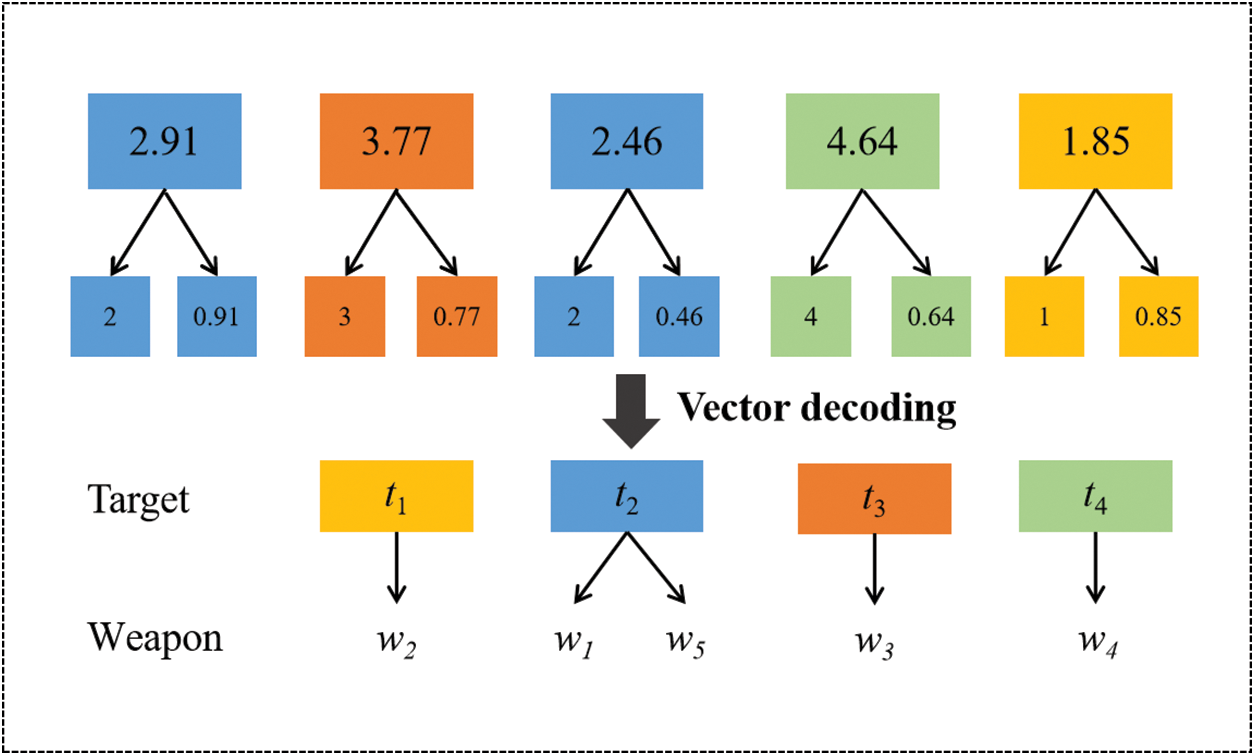
Figure 2: An example diagram of correspondence between coding and weapon target assignment scheme

Generally, multi-objective optimization algorithms only focus on the domain of variables, in other words, all dimensions of the solution are within the boundary. However, in the process of searching for new nectar source, infeasible solutions that do not meet the constraints may be generated. In this regard, it is necessary to adopt a repair strategy for individuals who do not meet the constraints to ensure the feasibility of the solution. There are two principles of repair. 1. The decimals of each dimension are different. 2. The integers contain the number of all targets.

For example, the position of the nectar source after one update is represented by the vector in Eq. (12).

J=[x1,x2,…,xd](12)

If the integers of two or more elements in J are equal, there must be some integers in the interval (0, N + 1) that do not exist, which means that these solutions do not satisfy the second constraint. Because there are unassigned targets, these solutions are infeasible and must be fixed.

1.    If there are as many weapons as targets, select elements with the equivalent integer, and change the integers of these elements to the serial numbers of unassigned targets.

2.    If there are more weapons than targets and there are unassigned targets, the repairing strategy is the same as 1, otherwise, no repair is required.

4.4 The Pseudo-Code of MOABC Algorithm

Based on the above principle, the pseudo-code of the MOABC algorithm is as follows.

5  Simulation and Discussion

The experiment in this paper is conducted on the Windows 10 operating system with the main frequency of 2.9 GHz, and 8 GB of memory. Suppose that several enemy targets attack our important ground defensive resources. To implement effective defensive measures, we deploy several air defense weapons to strike and destroy opponents’ targets. Target types include bombers, fighter planes, electronic jammers, unmanned jammers, air-to-surface missiles, etc. Due to the confidentiality of real battlefield data, we simulated the data based on operational scenarios. For the construction of the WTA model, two operational scenarios are designed in the experiment. ① Weapon-target one-to-one assignment. ② Weapon-target many-to-one assignment.

Algorithm parameter settings: Population size 2 N = 100, Archive size Im = 100, maximum repetition number Limit = N * D, and maximum fitness evaluations Gmax = 200 D.

5.1 Operational Scenario 1: Weapon-Target One-to-One Assignment

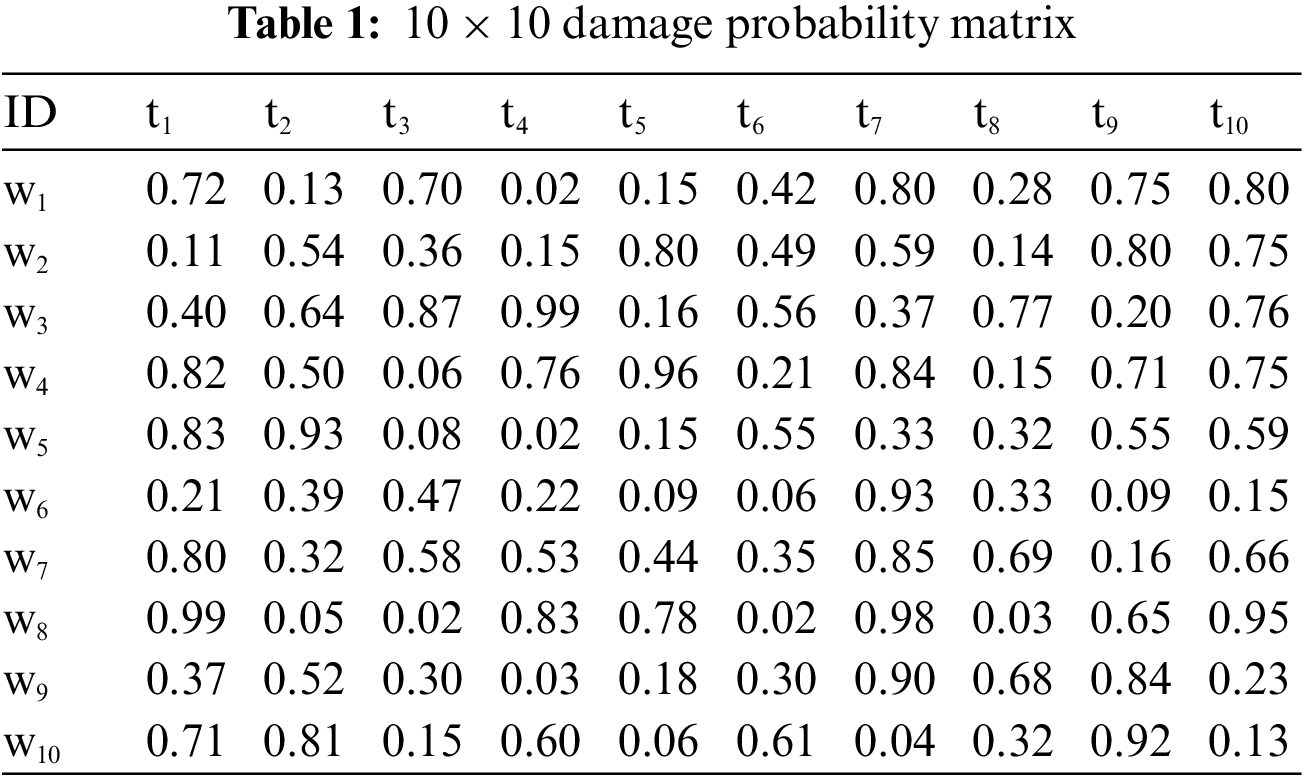
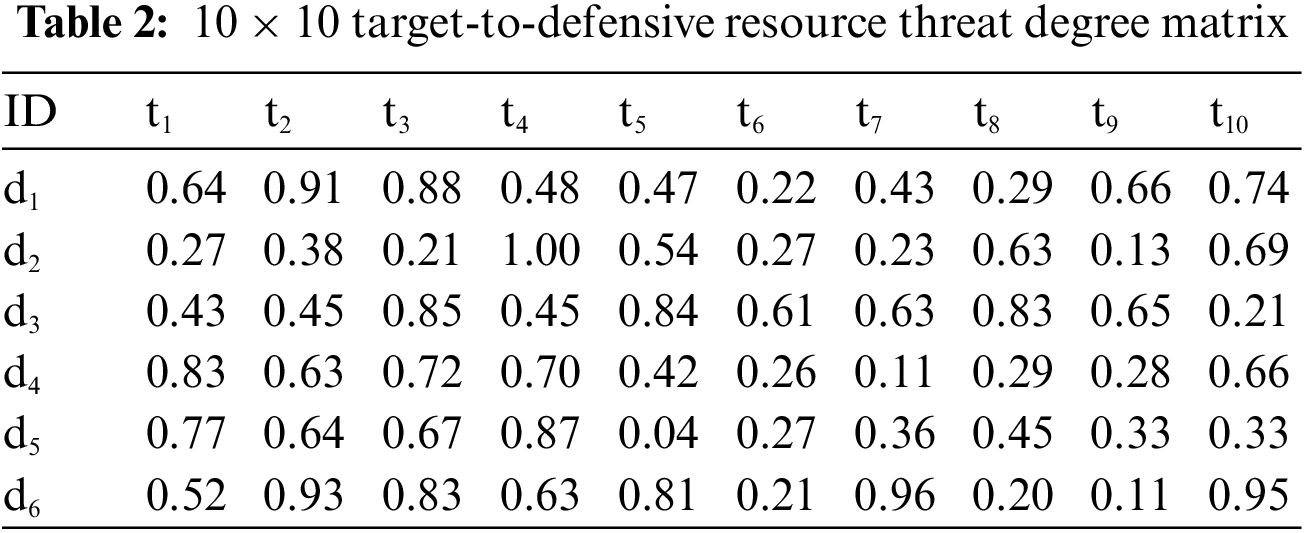
It is supposed that there are 10 enemy assault targets, 10 air defense weapons, and 6 important ground resources on the battlefield. The target damage probability, target threat level, defensive resource value, target value, and weapon consumption are shown in Tables 1–5.

The distribution plan is solved by the MOABC algorithm. In Fig. 3, the three coordinate axes represent three objective function values. The scattered marks are non-dominated solutions. It can be seen that the distribution of the entire non-dominated solution set is relatively scattered. Because, during the iteration, similar solutions with smaller crowding distances will be continuously eliminated, making the solution set more diverse. It is for decision-makers to consider and choose an assignment plan from different requirements.

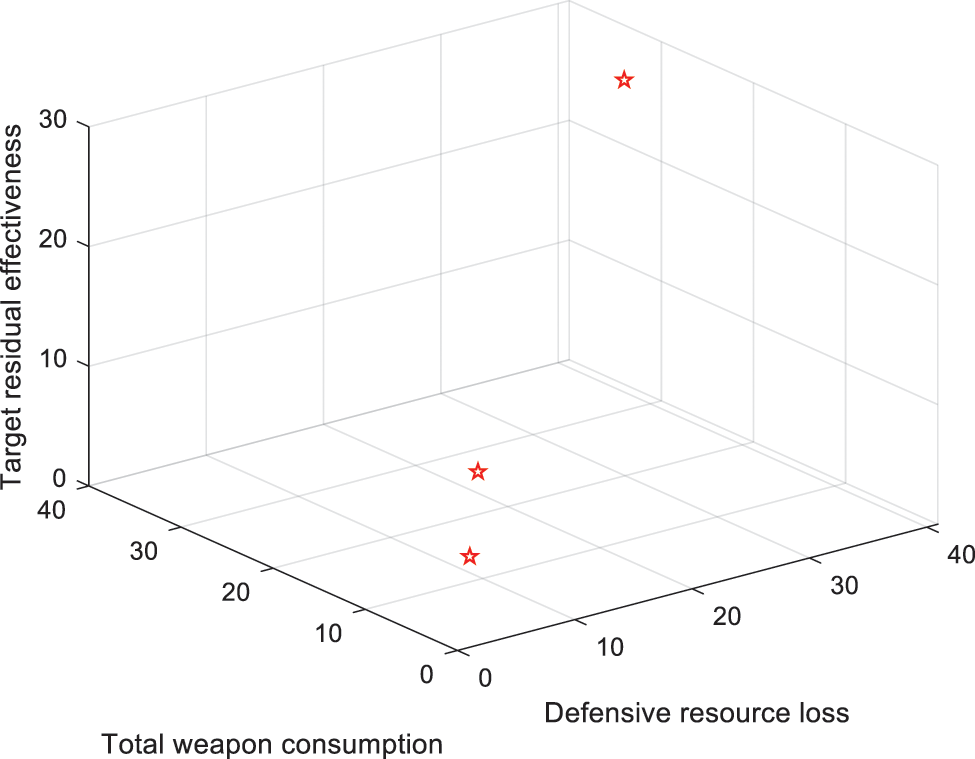
Figure 3: Weapon-target one-to-one distribution of non-dominated solutions

The MOABC algorithm has good convergence. Since the non-dominated sorting algorithm has a strict selection principle, the Archive has a forced ability to reserve better solutions. In Fig. 4, the defensive resource loss converges to about 46, the target residual effectiveness converges to approximately 12.3, and the total weapon consumption is always the same at 4.90. Since the number of targets is the same as the weapons, all weapons are involved in the strike.

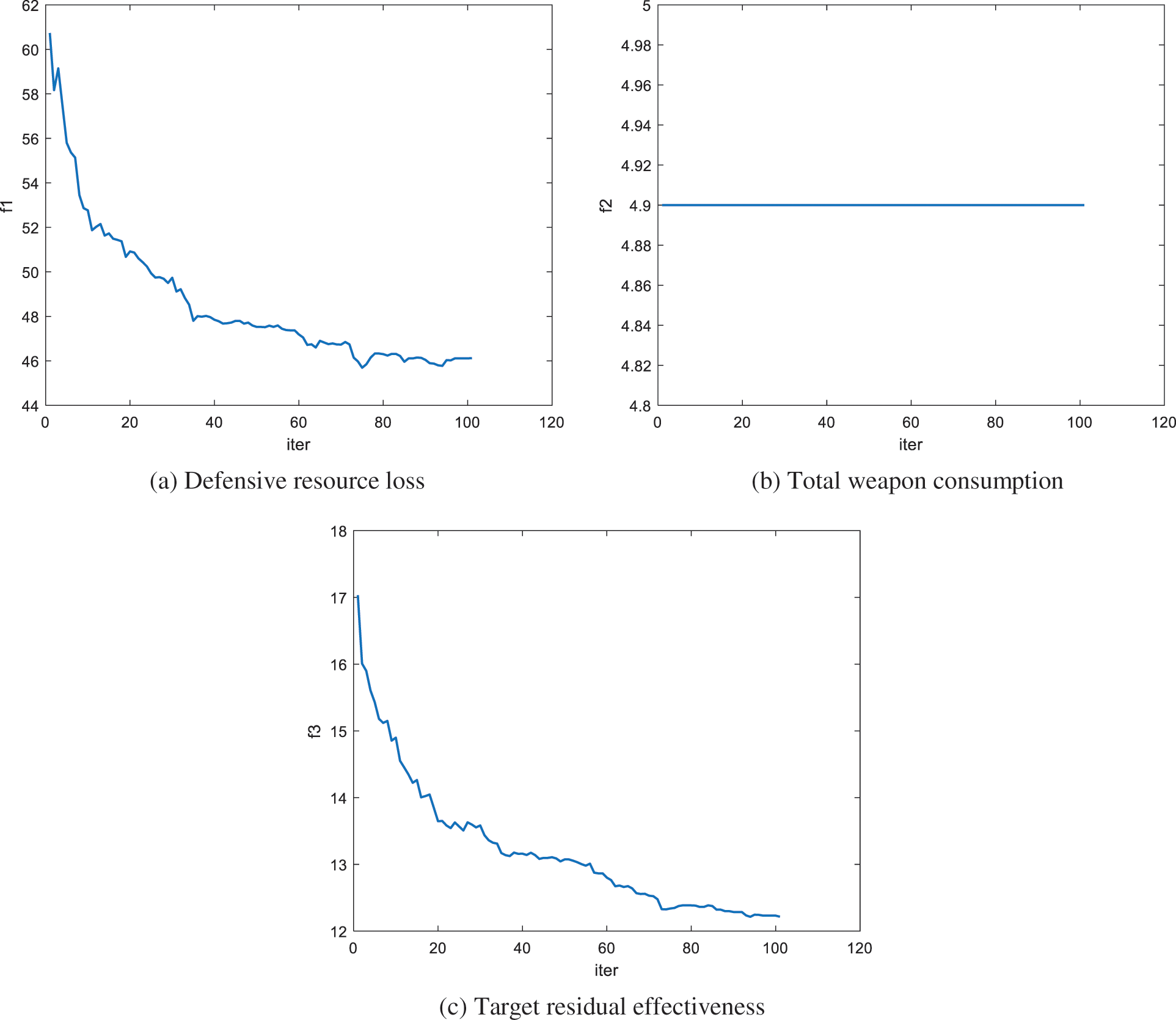
Figure 4: Mean values of the objective function value obtained by solving scenario 1 over 20 independent runs in 1 to 100 generations

Table 6 shows each objective function value corresponding to the non-dominated solution. It can be seen that the non-dominated solutions sought are independent of each other. The decision-maker further selects the best plan from the alternatives based on the operational needs. Table 7 shows the WTA plan optimized corresponding to each non-dominated solution.

5.2 Operational Scenario 2: Weapon-Target Many-to-One Assignment

It is supposed that there are 7 enemy assault targets. Other settings are consistent with operational scenario 1. The enemy’s target damage probability, target threat degree, and target value are shown in Tables 8–10.

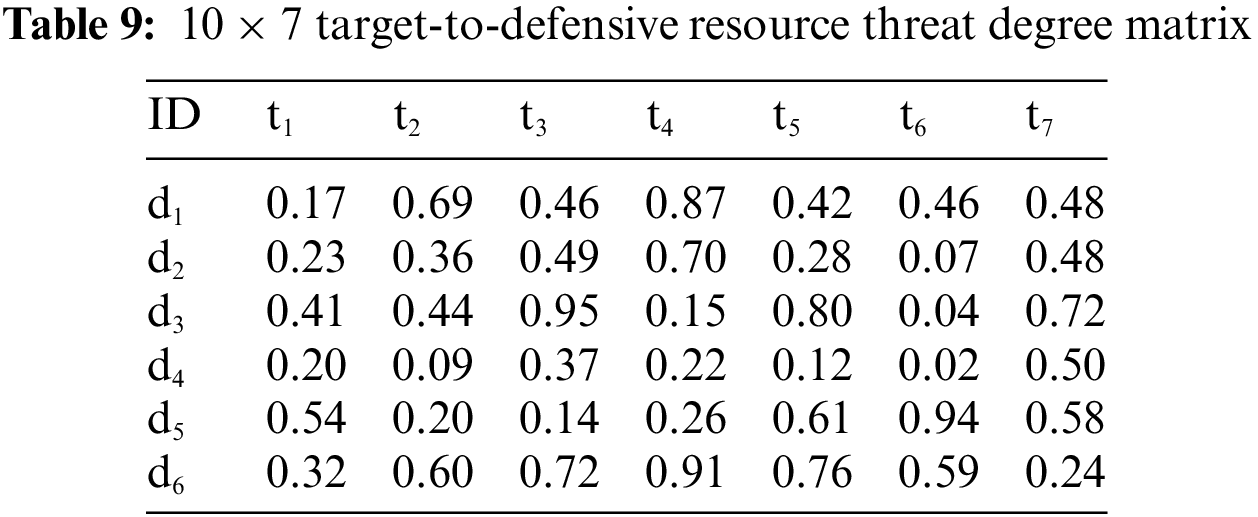
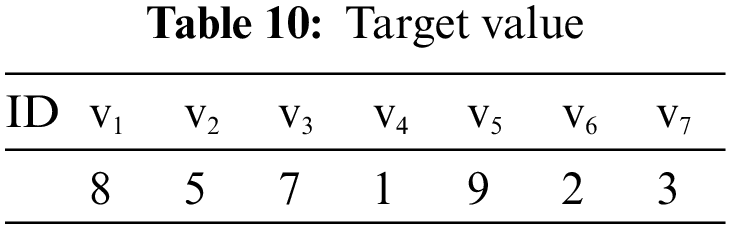
Fig. 5 shows the 15 non-dominated solutions obtained after running. Table 11 shows the objective function values corresponding to the solutions. Compared with operation scenario 1, more non-dominated solutions are obtained, demonstrating that the Pareto solution space is larger and the solution set is more diverse when the weapons are more than enemy targets. Table 12 shows the WTA plan optimized corresponding to each non-dominated solution.

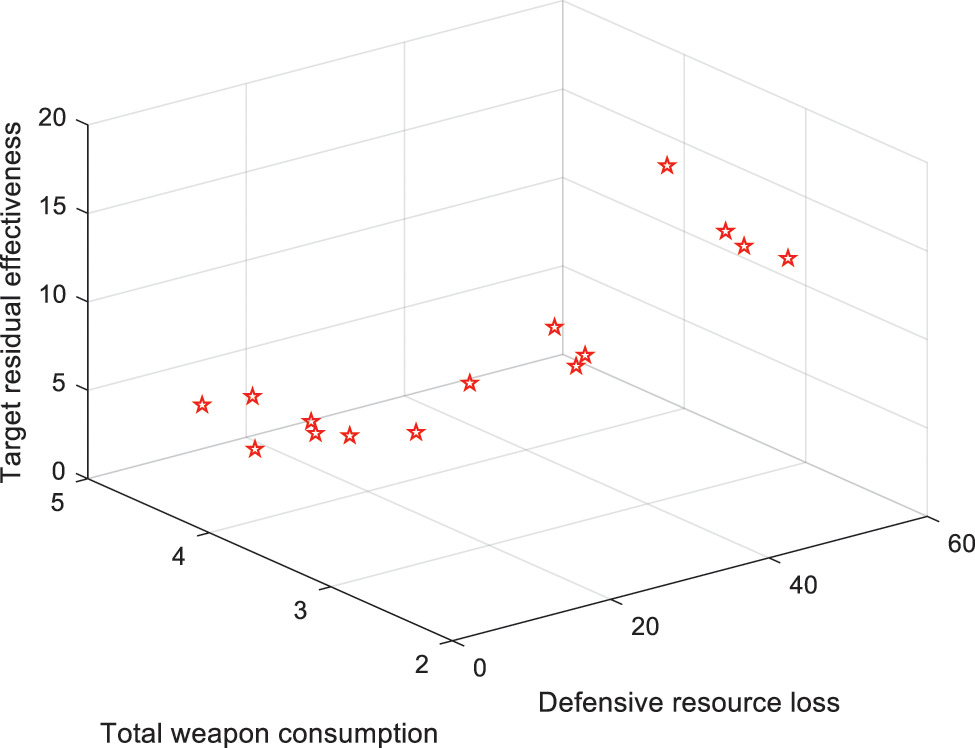
Figure 5: Weapon-target many-to-one distribution of non-dominated solutions

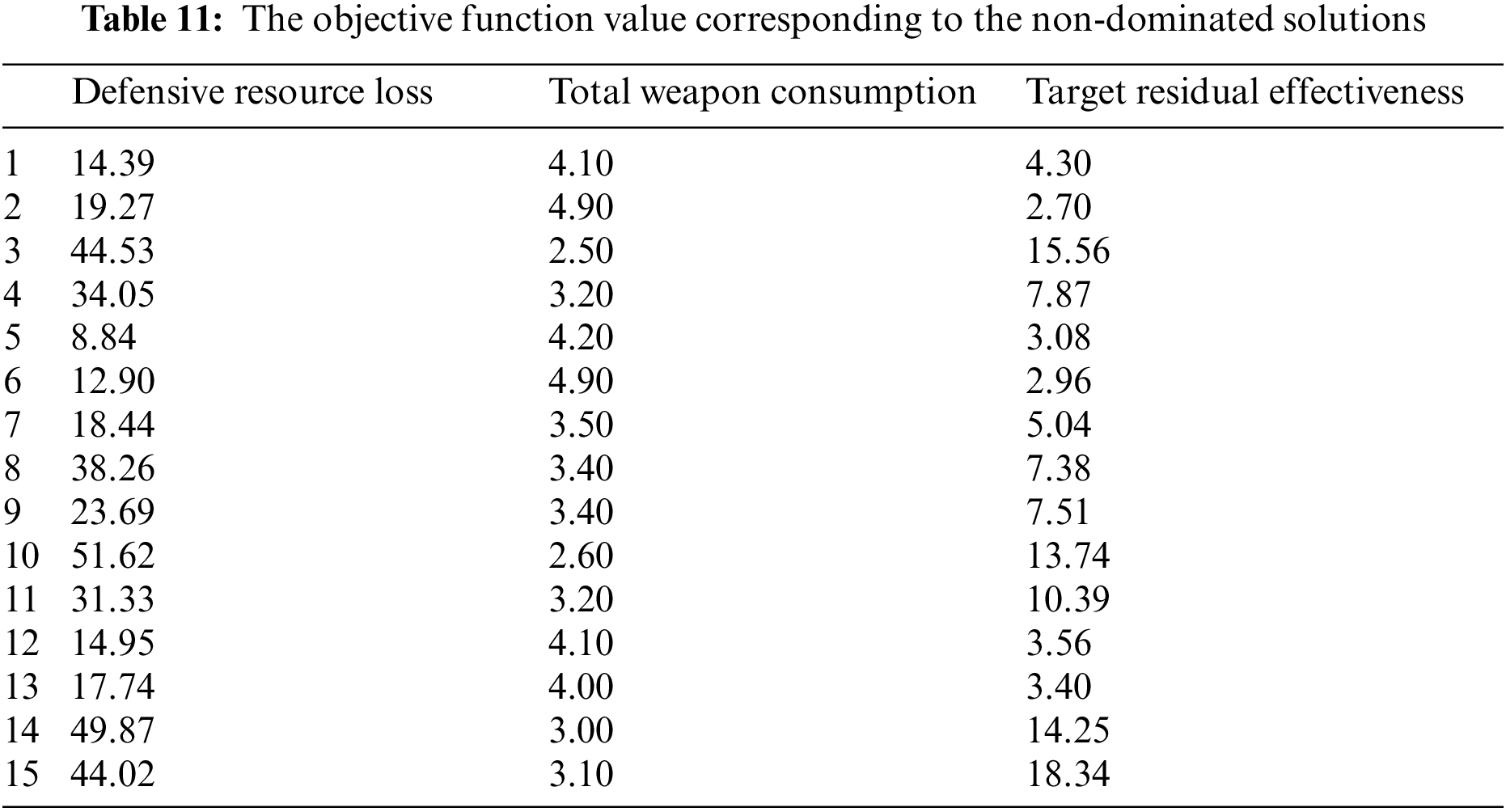
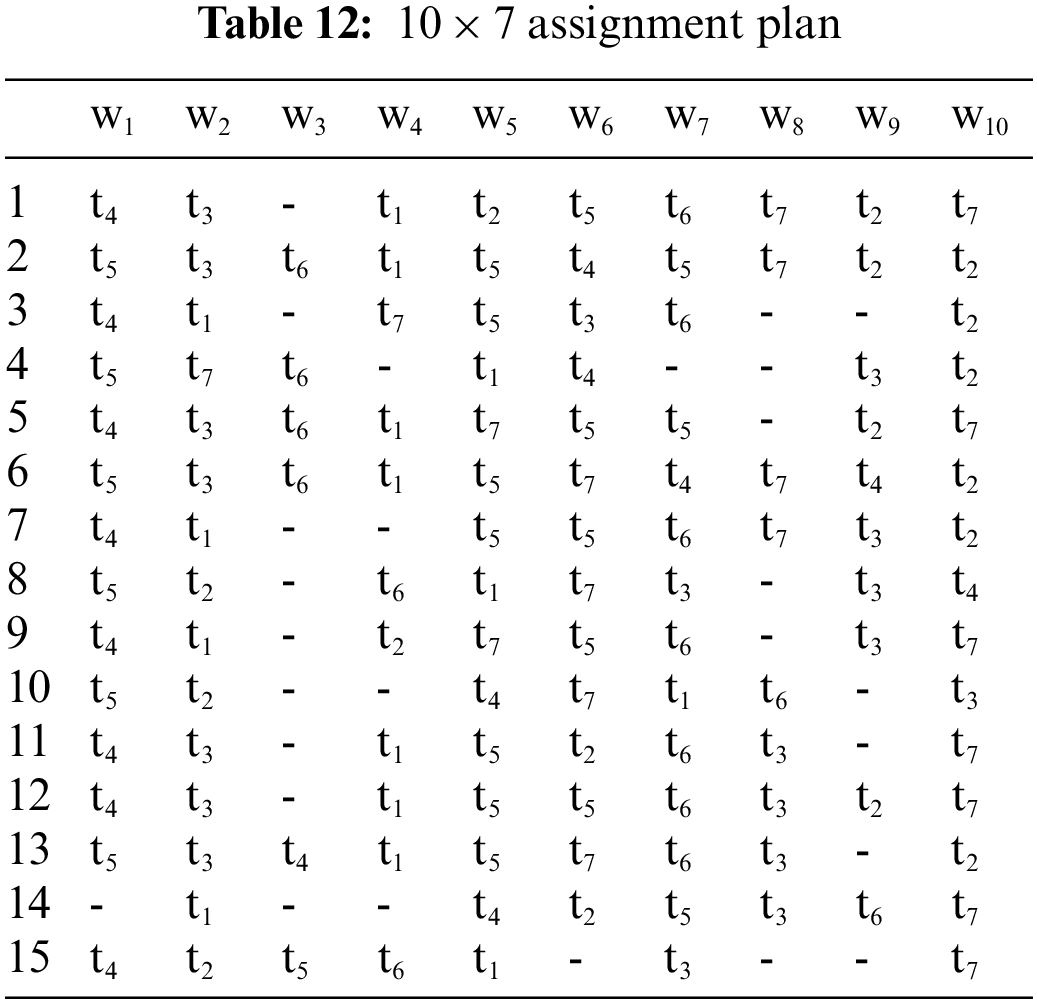
In Fig. 6, each objective function value of scenario 2 is converged, the defensive resource loss converges to about 25, and the target residual effectiveness converges to about 6.2. Unlike scenario 1, some weapons are not assigned targets due to the surplus of weapons. The total weapon consumption decreases while searching for a better solution, eventually converging to about 3.62. Overall, the convergence values of all three metrics are better than the results of scenario 1, indicating that the assignment plan not only improves operational effectiveness but also reduces total weapon consumption when increasing the number of air defense weapons.

Figure 6: Mean values of the objective function value obtained by solving scenario 2 over 20 independent runs in 1 to 100 generations

5.3 Algorithm Performance Comparison

Nie et al. [5] proposed firepower strike assignment for cluster UAV targets based on the NSGA-III algorithm. As a typical representative of multi-objective optimization algorithms, NSGA-III has a wide range of applications and strong practicability. In reference [5], WTA optimization model and framework are close to the current research solution. To better verify the effectiveness of the MOABC algorithm, the global optimization capabilities of the NSGA-III algorithm and the MOABC algorithm are compared. The initial parameter settings of both algorithms are as follows.

NSGA-III algorithm: population size 2 N = 100, Archive size Im = 50, maximum repetition number Limit = N * D, and maximum fitness evaluations Gmax = 200D, the crossover probability is 0.8, and the mutation probability is 0.05.

MOABC algorithm: population size 2 N = 100, Archive size Im = 50, maximum repetition number Limit = N * D, and maximum fitness evaluations Gmax = 200D.

The performance is evaluated by inverse generation distance (IGD) [21] and running time. IGD is a comprehensive performance evaluation index that assesses the convergence and diversity of the solutions. IGD can calculate the sum of the minimum distance between each solution on the real Pareto frontier and the solution set obtained. IGD is defined as Eq. (13).

IGD(P,Q)=∑v∈Pd(v,Q)|P|(13)

In Eq. (13), P is the solution set uniformly distributed on the real Pareto frontier. |P| is the number of solutions distributed on the real Pareto frontier. Q is the obtained Pareto optimal solution set. d(v,Q) is the minimum Euclidean distance from the solution v to the solution set Q. IGD evaluates the convergence and distribution uniformity of the algorithm by calculating the average minimum distance from the solution set on the real Pareto frontier to the solution set obtained. From Eq. (13), the smaller d(v,Q) indicates that the closer the solution v is to solution set Q, the better the convergence performance of the algorithm. However, the larger d(v,Q) indicates that most of the solutions obtained are concentrated in a narrow region, and the worse the distribution performance of the algorithm. In this paper, some non-dominated solutions with uniform distribution are selected from the solution sets obtained by multiple experiments, and their objective function values are approximated to the real Pareto frontier. The real Pareto frontier is filtered. Next, the solution set obtained by the algorithm is compared with the real Pareto frontier. The results of IGD values and average running time after 30 runs are summarized in Table 13. NSGA-III algorithm can not obtain the feedback information of the population in time, so its search speed is relatively slow, and more time is required to obtain more accurate solutions. For the two scenarios, the search efficiency of MOABC algorithm is better than that of NSGA-III algorithm, which reflects the advantages of the algorithm for solving the model in this paper.

Figs. 7a and 7b are the IGD box diagrams of the two operational scenarios, respectively. Comparing the results of both algorithms, the IGD value of the MOABC algorithm is superior to that of the NSGA-III algorithm, which shows that the approximate Pareto optimal solution obtained by the MOABC algorithm has better convergence and the solutions are more uniformly distributed in the solution space.

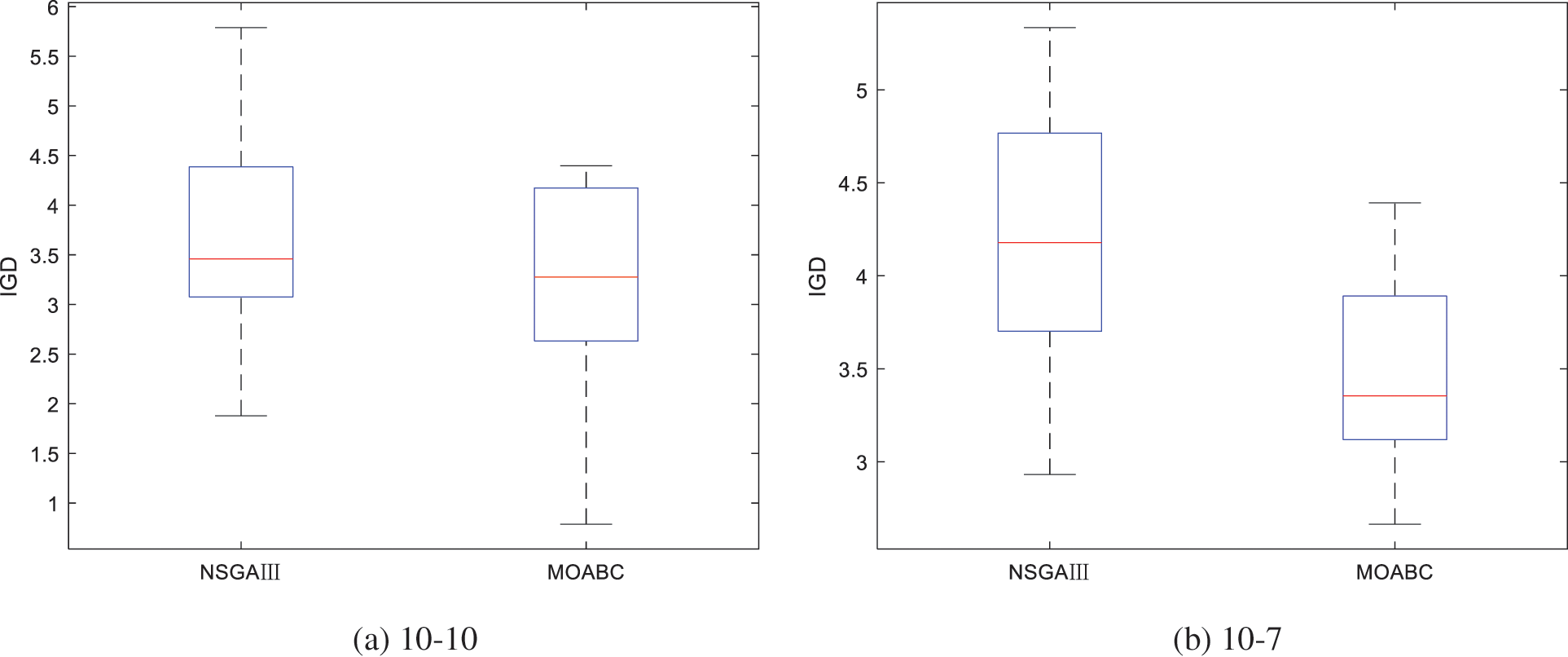
Figure 7: IGD box diagrams of NSGA-III and MOABC algorithm

6  Conclusion

It is of great military significance to study the issue of WTA in air defense operations. From the perspective of both opposing sides, we evaluated the results of air defense WTA with three indicators, including defensive resource loss, total weapon consumption, and target residual effectiveness. A multi-objective and multi-constrained air defense WTA model is constructed. The MOABC algorithm is used to realize the optimal solution of air defense weapon scheduling at different countermeasure scales, and the efficiency of the algorithm is verified. The performance of MOABC algorithm and NSGA-III algorithm is compared. The former has a lower IGD value of the Pareto solution set than the latter, and the overall quality of the solutions is higher and more uniformly distributed. The running time of the former is less than that of the latter, and the search efficiency of the algorithm is higher. This work provides certain ideas and means for air defense for group targets. Firstly, the applicability of the model has been improved. Multi-objective programming is established to objectively select the optimal assignment scheme, avoiding the commander’s personal preference affecting the decision-making results. Secondly, the scientific and reasonable evaluation indicators are designed to compare and verify the optimization results, and closed-loop research is realized. Finally, the Pareto optimal solution set can be regarded as an important reference to assist decision-making, which may also provide the best plan for decision-making commanders.

Acknowledgement: The authors are very grateful to the referees for their valuable remarks, which improved the presentation of the paper.

Funding Statement: This work was supported by the National Natural Science Foundation of China (71771216).

Author Contributions: The authors confirm contribution to the paper as follows: study conception and design: H. Xing, Q. Xing; data collection: H. Xing; analysis and interpretation of results: H. Xing, Q. Xing; draft manuscript preparation: H. Xing. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The authors confirm that the data supporting the findings of this study are available within the paper.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. Y. Lu and D. Z. Chen, “A new exact algorithm for the weapon-target assignment problem,” Omega, vol. 98, no. 1, pp. 102–138, 2021. [Google Scholar]

2. A. Shojaeifard, A. N. Amroudi, A. Mansoori, A. Mansoori and M. Erfanian, “Projection recurrent neural network model: A new strategy to solve weapon-target assignment problem,” Neural Processing Letters, vol. 50, no. 3, pp. 3045–3057, 2019. [Google Scholar]

3. F. X. Liu, Y. L. Wang and Q. H. Xing, “Study on problems of optimized target assignment in ground to air defense,” Fire Control ＆Command Control, vol. 28, no. 4, pp. 45–48, 2003. [Google Scholar]

4. M. T. Davis, M. J. Robbins and B. J. Lunday, “Approximate dynamic programming for missile defense interceptor fire control,” European Journal of Operational Research, vol. 259, no. 3, pp. 873–886, 2017. [Google Scholar]

5. J. F. Nie, X. J. Chen and Q. Su, “Modeling and optimization of weapon target assignment for the group targets attacking defense based on NSGA-III algorithm,” Acta Armamentarii, vol. 42, no. 8, pp. 1771–1779, 2021. [Google Scholar]

6. Y. F. Zhang, D. H. Yan, J. Y. Wang and Z. Cao, “A quasi dynamic defense weapon assignment algorithm based on ant-colony optimization,” Fire Control & Command Control, vol. 41, no. 9, pp. 1614–1619, 2016. [Google Scholar]

7. Y. Li, Y. Kou, Z. Li, A. Xu and Y. Chang, “A modified pareto ant colony optimization approach to solve biobjective weapon-target assignment problem,” International Journal of Aerospace Engineering, vol. 33, no. 2, pp. 1–14, 2017. [Google Scholar]

8. Z. J. Lee, S. F. Su and C. Y. Lee, “Efficiently solving general weapon-target assignment problem by genetic algorithms with greedy eugenics,” IEEE Transactions on Systems, Man and Cybernetics, Part B (Cybernetics), vol. 33, no. 1, pp. 113–121, 2003. [Google Scholar]

9. C. L. Fan, Q. H. Xing, M. F. Zheng and Z. J. Wang, “Weapon-target allocation optimization algorithm based on IDPSO,” Systems Engineering and Electronics, vol. 37, no. 2, pp. 336–342, 2015. [Google Scholar]

10. J. Zhou, X. Z. Zhao, Z. Xu, Z. Lin and X. P. Zhang, “Many-objective task allocation method based onD-NSGA-III algorithm for multi-UAVs,” Systems Engineering and Electronics, vol. 43, no. 5, pp. 1240–1247, 2021. [Google Scholar]

11. T. Long, Z. Y. Liu, R. H. Shi and S. Y. Wang, “Neural network based air defense weapon target intelligent assignment method,” Air & Space Defense, vol. 4, no. 1, pp. 1–7, 2021. [Google Scholar]

12. D. Karaboga and B. Basturk, “A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm,” Journal of Global Optimization, vol. 39, no. 3, pp. 459–471, 2007. [Google Scholar]

13. R. Hedayatzadeh, B. Hasanizadeh and R. Akbari, “A multi-objective artificial bee colony for optimizing multi-objective problems,” in Proc. ICACTE,, Chengdu, China, pp. 277–281, 2010. [Google Scholar]

14. X. Q. Zhao, S. Y. Duan and X. M. Ma, “A multi-objective artificial bee colony based on limit search strategy,” Control and Decision, vol. 35, no. 8, pp. 1793–1802, 2020. [Google Scholar]

15. O. Niyomubyeyi, P. Pilesjö and A. Mansourian, “Evacuation planning optimization based on a multi-objective artificial Bee colony algorithm,” International Journal of Geo-Information, vol. 8, no. 3, pp. 110, 2019. [Google Scholar]

16. O. Niyomubyeyi, T. E. Sicuaio, J. I. Díaz González, P. Pilesjö and A. Mansourian, “A comparative study of four metaheuristic algorithms, AMOSA, MOABC, MSPSO, and NSGA-II for evacuation planning,” Algorithms, vol. 13, no. 1, pp. 1–16, 2020. [Google Scholar]

17. N. Zhang, W. Zhang, B. Wu and X. A. Bao, “Multi-objective test case prioritization based on MOABCO,” Journal of Test and Measurement Technology, vol. 33, no. 2, pp. 93–98, 2019. [Google Scholar]

18. Y. F. Mao and D. L. Zhang, “Improved artificial bee colony algorithm for solving weapon target assignment problem,” Military Operations Research and Systems Engineering, vol. 29, no. 1, pp. 30–33, 2015. [Google Scholar]

19. X. Y. Gu, L. Chen and X. P. Deng, “Multi-objective optimization of UAV formation information interaction topology,” Electronics Optics ＆ Control, vol. 29, no. 9, pp. 27–31+52, 2022. [Google Scholar]

20. K. X. Chu, T. Q. Chang, D. P. Kong, L. Zhang and H. Z. Sun, “Bee colony algorithm based model of tank troop deployment and firepower allocation,” Systems Engineering and Electronics, vol. 44, no. 2, pp. 546–556, 2022. [Google Scholar]

21. H. X. Xing, H. Wu, Y. Chen and X. Zhang, “Multi-efficiency optimization method of jamming resource based on multi-objective grey wolf optimizer,” Journal of Beijing University of Aeronautics and Astronautics, vol. 46, no. 10, pp. 1990–1998, 2020. [Google Scholar]