 Open Access
Open Access
ARTICLE
3-D Gait Identification Utilizing Latent Canonical Covariates Consisting of Gait Features
Department of Computer Engineering, Istanbul University, Cerrahpasa, Istanbul, 34300, Turkey
* Corresponding Author: Ramiz Gorkem Birdal. Email:
Computers, Materials & Continua 2023, 76(3), 2727-2744. https://doi.org/10.32604/cmc.2023.032069
Received 05 May 2022; Accepted 30 January 2023; Issue published 08 October 2023
Abstract
Biometric gait recognition is a lesser-known but emerging and effective biometric recognition method which enables subjects’ walking patterns to be recognized. Existing research in this area has primarily focused on feature analysis through the extraction of individual features, which captures most of the information but fails to capture subtle variations in gait dynamics. Therefore, a novel feature taxonomy and an approach for deriving a relationship between a function of one set of gait features with another set are introduced. The gait features extracted from body halves divided by anatomical planes on vertical, horizontal, and diagonal axes are grouped to form canonical gait covariates. Canonical Correlation Analysis is utilized to measure the strength of association between the canonical covariates of gait. Thus, gait assessment and identification are enhanced when more semantic information is available through CCA-based multi-feature fusion. Hence, Carnegie Mellon University’s 3D gait database, which contains 32 gait samples taken at different paces, is utilized in analyzing gait characteristics. The performance of Linear Discriminant Analysis, K-Nearest Neighbors, Naive Bayes, Artificial Neural Networks, and Support Vector Machines was improved by a 4% average when the CCA-utilized gait identification approach was used. A significant maximum accuracy rate of 97.8% was achieved through CCA-based gait identification. Beyond that, the rate of false identifications and unrecognized gaits went down to half, demonstrating state-of-the-art for gait identification.Keywords
In parallel with the growing advantages of high-performance computers, technological advancement in biometric systems is accelerating. In today’s society, biometric systems are used in many areas, such as the advertising sector, access control units, and identification documents such as passports and driver’s licenses. These areas utilize biometric identifiers to categorize and identify individuals based on their distinctive measurable characteristics. Gait is a characteristic behavior of humankind and is one of these distinctive characteristics. A closer analysis of this behavior provides valuable insight into individual identification.
The correct measurement of gait characteristics begins with an accurate gait assessment. On the other hand, due to the complexity of human gait, gait analysis generates large quantities of data, and its interpretation is time-consuming. Therefore, human gait assessment begins with identifying the exact features and then analyzing them according to the appropriate methodology.
Psychophysics shows that [1] people can recognize one another in low-quality environments, indicating that the gait characteristics contain identity information. The purpose of Lee et al.’s study [2] was to explore this identity information in gait using simple features such as patterns extracted from orthogonal view video silhouettes of humans walking. Researchers such as Wang et al. [3] also focused on spatial-temporal silhouette analysis in gait recognition. They tracked the moving silhouettes of a walking figure. Then, eigenspace transformation based on Principal Component Analysis (PCA) is applied to time-varying distance signals derived from a sequence of silhouette images. Wang et al. [4] developed a statistical shape analysis-based gait recognition system as the next step. Over time, the methods in gait recognition are improved and diversified. In Ekinci et al.’s study [5], in order to recognize patterns in the lower dimensional eigenspace, four projections were concatenated and transformed into one vector. In another paper [6], kernel principal component analysis is utilized to extract higher-order relations among the gait patterns for feature recognition in the CMU and USF gait databases. Moreover, eigenspace transformation based on PCA is applied to time-varying distance vectors [7]. Also, Mahalanobis distance-based supervised pattern classification is then performed in the lower dimensional eigenspace for human identification. In another way, some research focuses on specific parts of the body. Some researchers [8] developed a method for analyzing inter-leg dynamics by comparing local features. They examined the influence of walking speed on the synchronization dynamics of stride intervals. Afendi et al. [9] also focused on the leg movements. Characteristics of leg movements depend on human physical conditions and age, so it tends to vary easily. On the other hand, Afendi et al. [10] aimed to add depth information to 2D images. Therefore, they utilized a 3D time-of-flight camera to capture depth data. Gait Depth Energy Image (GDE), Partial Gait Depth Energy Image (PGDE), Discrete Gait Depth Energy Image (DGDE), and Partial Discrete Cosinus Converted Gait Energy Image (Partial DCCGE) are obtained from gait images. Some researchers conducted health-related research as well. Toebes et al. [11] showed that gait parameters captured by sensors might hold promise for identifying individuals at risk of falling. They implied that Local Dynamic Stability (LDS) of gait might be a predictor of fall risk. In their study, Terrier et al. [12] attempted to determine the effect of aging on gait variability. They evaluated the walk ratio (step length normalized by step frequency) and gait instability with acceleration variability. Mapelli et al. [13] concluded that the kinematics of the center of mass is important in sports surveys. Another approach that focuses on energy image comes from literature. The specific method [14] identified 20 basic gait kinetic data features using singular value decomposition, which yielded a 91% accurate reconstruction. Utilizing shape analysis is another area as Choudhury et al. [15] studied Procrustes Shape Analysis (PSA) and Elliptic Fourier Descriptors (EFD) to identify human gait silhouettes. There are also several up-to-date studies on gait recognition. Human shadows were used by Iwashita et al. [16] among the other features in their study. Choudhury et al. [17] examined human body shapes and the correlation between these shapes. As well as gait signal analysis, Li et al. [18] used an IMU to gather information about the gait and pursue it. Some researchers [19] applied Uncorrelated Multilinear Principal Component Analysis (UMPCA) to analyze the variation of human movement patterns. Wavelet-based schemes were used by Baratin et al. [20] in their study for characterizing gait signals associated with neurological disorders. Some researchers [21] showed that artificial walking patterns are easier to be identified when aligned with egocentric referential. Health and sports issues continued with Zeng et al. [22], who showed that deterministic learning theory could diagnose Parkinson’s disease patients and healthy control subjects based on their gait patterns. In addition, radial basis functions in neural networks are locally accurate in estimating gait dynamics underlying gait patterns of healthy controls and patients with Parkinson’s disease. Also, the collaborative healthcare framework utilizing novel activity recognition explained by Javed et al. [23] helps to capture better accuracy. Deng et al. [24] demonstrated that gait could be recognized using the principle of the smallest error with spatial-temporal and kinematic cues. Ardestani et al. [25] used gait analysis scores to treat osteoarthritis. Some other researchers focus on gender recognition by gait analysis. Zhang et al. [26] studied gait recognition and gait-based soft biometrics in a joint CNN-based framework. Zakaria et al. [27] presented the application of the ANN-SCG (Scaled Conjugate Gradient) model with nine hidden neurons in gender classification for children in Malaysia. Solano et al. [28] aimed to assess gender-related differences in gait spatiotemporal and quality parameters. Sun et al. [29] proposed a gait template synthesis method to reduce the intra-subject gait fluctuation of elderly users. The study of distinguishing between normal and pathological gait variability in older adults was conducted by Bogen et al. [30]. Regarding CCA, it is beneficial to look at Barcikowski et al. Carlo study [31] on canonical coefficients. Zulcaffle et al. [32] utilized a classification approach based on an Adaptive Multi-Stage Fusion Classifier, showing distinct improvements over recognition rates. Xing et al. [33] utilized CCA (Canonical Correlation Analysis) for gait recognition. First, they reformulate the traditional CCA so that they can avoid the computing of the inverse of a high-dimensional matrix. Through this, a novel C3A method converts two stable eigenvalue decomposition problems from the singular generalized eigensystem computation of the CCA method. Also, there is a study about discoveries of biological significance by Manipur et al. [34] to find a solution that could consist of the representation of a graph model of the body with the various points and related features. Numerous studies have obtained results by working one by one with features without utilizing linear combinations. The lack of stand-alone feature details causes low identification of individuals, and finding other distinctive components is the optimal solution to overcome this. The presence of certain components guarantees better recognition clues, thus ensuring much more accurate identification. This weighted component-based approach shows 6%–7% higher achievement performance [35], which is an important indicator for comparing the success of our study. One of the major difficulties in optimizing continuous complex data is premature convergence and recognition. The proposed algorithms provide stable support for solving optimization problems through their ability to adjust according to their experiences. This algorithm’s 94% maximum accuracy is also an important indicator for our novel approach [36]. Hybridization and adaptive parameter selection approaches lead to higher success rates and find solutions to slow and premature convergence. The ability to obtain higher accuracy shows the importance of this method for analyzing complexdata [37].
This study improves gait identification in 3D by taking advantage of a unique perspective. The new method captures the surprising harmony between canonical covariates that describe gait through multivariate data analysis in separate body halves. Following is the remainder of this paper: Sections 2 & 3 present the materials and the methods used in this work. The Materials and methods sections consist of the dataset, runtime environment, and the Canonical Correlation Analysis (CCA) method. Section 4 describes the methodology for selecting features in this study. Experimental results and performance comparison in terms of the feature selection approach are also provided in Section 4. Section 5 includes a discussion, concluding remarks, and the contributions of this study.
This section discusses the database and the runtime environment.
The study uses data from Carnegie Mellon University’s motion capture library [38]. The data is collected from healthy subjects without joint pain or musculoskeletal disorders. These gait videos are captured using 41 retro-reflective markers seen in Table 1. Moreover, the system includes 12 Vicon MX-40 infrared cameras, each capable of recording images at 120 Hz with a four-megapixel resolution. The cameras are placed around a rectangular area of approximately 3 m × 8 m in the center of the room.

These markers are placed all over the human body, particularly at the ends and medial sides of the extremities. In addition to this, they are fitted to the body’s torso, head, and backbone. Our gait records have 32 subjects’ gait sequences, and each sequence contains at least 300–500 frames with a length of 3 to 6 s. This 3D marker data spots changes on X, Y, and Z coordinates, as seen in Fig. 1.
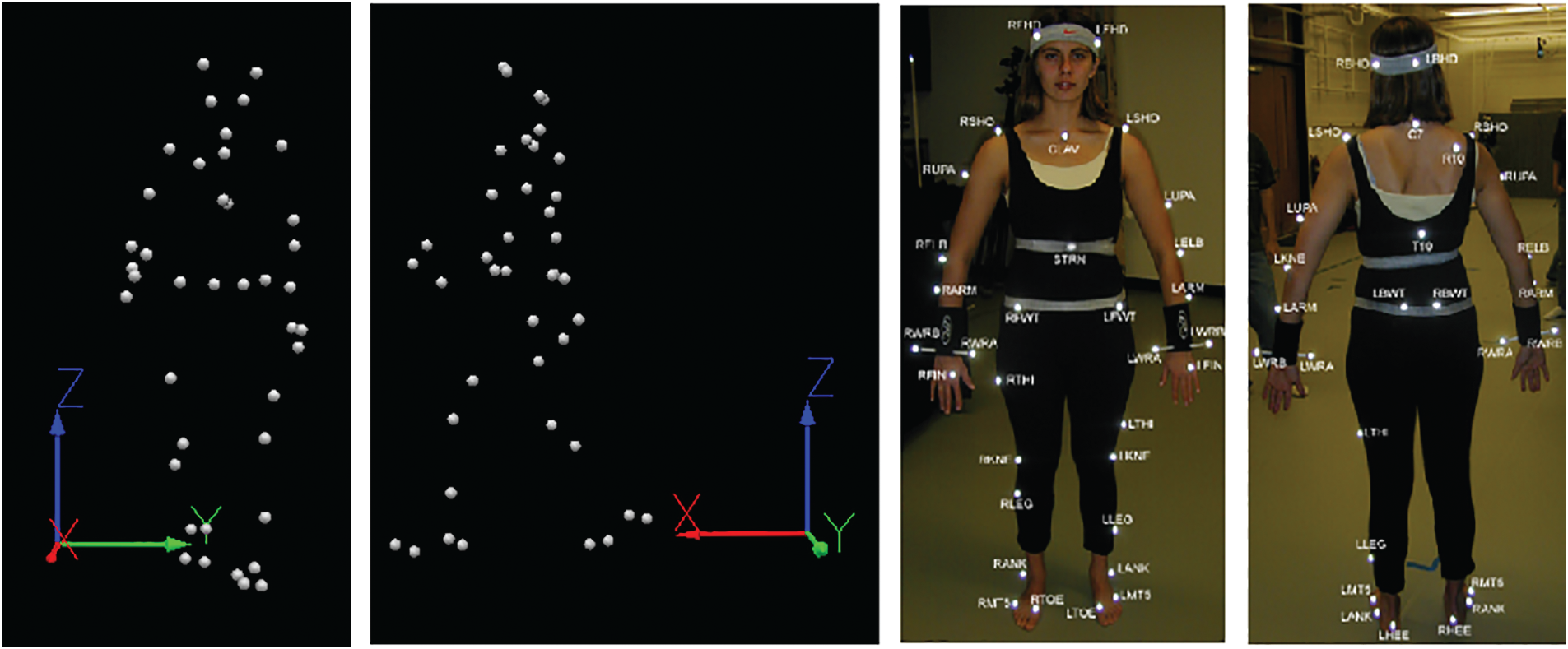
Figure 1: An aspect of the human body with retro-reflective markers
In the chosen gait sequences, subjects walk in the same direction and do not perform any reversing, jumping, or turning actions during the records. Hence, the characteristics of gait are preserved as much as possible.
Our runtime environment system is MATLAB R2020b, which allows matrix manipulations, plotting functions, implementing algorithms, creating user interfaces, and integrating with other computer programs. Its numerical computing ability is another criterion for choosing MATLAB for gait analysis.
This section discusses the methods used in this study. This novel approach aims to group features according to whether they are relevant or irrelevant and structures canonical covariates to allow multiple feature analyses.
3.1 Canonical Correlation Analysis
CCA (Canonical Correlation Analysis) is a well-known method to analyze the relationship between two groups. Consider two sets of zero-mean random vectors, X = [X1, X2, …, XN] ∈RdxxN and Y = [Y1, Y2, …, YN] ∈RdyxN, which are data matrices with N gait instances, dx and dy features selected from our gait features. CCA aims to seek the projection pairs for two sets of vectors such that the transformed vectors are maximally correlated in the dimensionality-reduced space. CCA targets to capture K pairs of linear projections, called canonical vectors, so that the correlations between WTXX and WTYX are maximized.
Wx=[wx,1,wx,2,…,wx,K]∈RdxXKandWy=[wy,1,wy,2,…,wy,K]∈RdyXK(1)
As an example, consider a canonical vector consisting of features relating to head position in gait wx∈RdxX1 for X and a canonical vector wy∈RdyX1 for Y. CCA maximizes the correlation coefficient p between XTwx and YTwy.
p=wTxXYTwy√(wTxXXTwx)(wTyYYTwy)(2)
is maximized. Since p is invariant to the scaling of wx and wy, CCA is formulated as the following constrained form:
argmaxwx,wywTxXYTwy(3)
s.t. wTxXXTwx = 1, wTyXXTwy = 1
Using the method of Lagrange multipliers to solve the objection function,
ℒ=wTxXYTwy+λx(1−wTxXXTwx)+λy(1−wTyYYTwy)(4)
The derivative of ℒ concerning px and py to zero is seen below:
∂ℒ∂wx=YTwy−λxXXTwx=0∂ℒ∂wy=XTwX−λYYYTwy=0(5)
For the constraints with wTxXXTwX=1 and wTyYYTwy=1, the equation of λx−λy=0 is obtained. By solving the following generalized eigenvalue problem:
XYT(YYT)−1YXTwX=λ2XXTwX(6)
wX and wy are obtained. Suppose X ∈ RDxXN and Y ∈ RDyXN, the size of YYT is DyXDy, and the size of the Eigen matrices XYT(YYT)−1YXTwX and XXT is DxXDx. Not to be forgotten in the equations, both DX and Dy are very large because of the video frame number and 3D coordinate information of many sensors, which takes high time and space costs. Hence, the study utilizes the generalized Eigendecomposition.
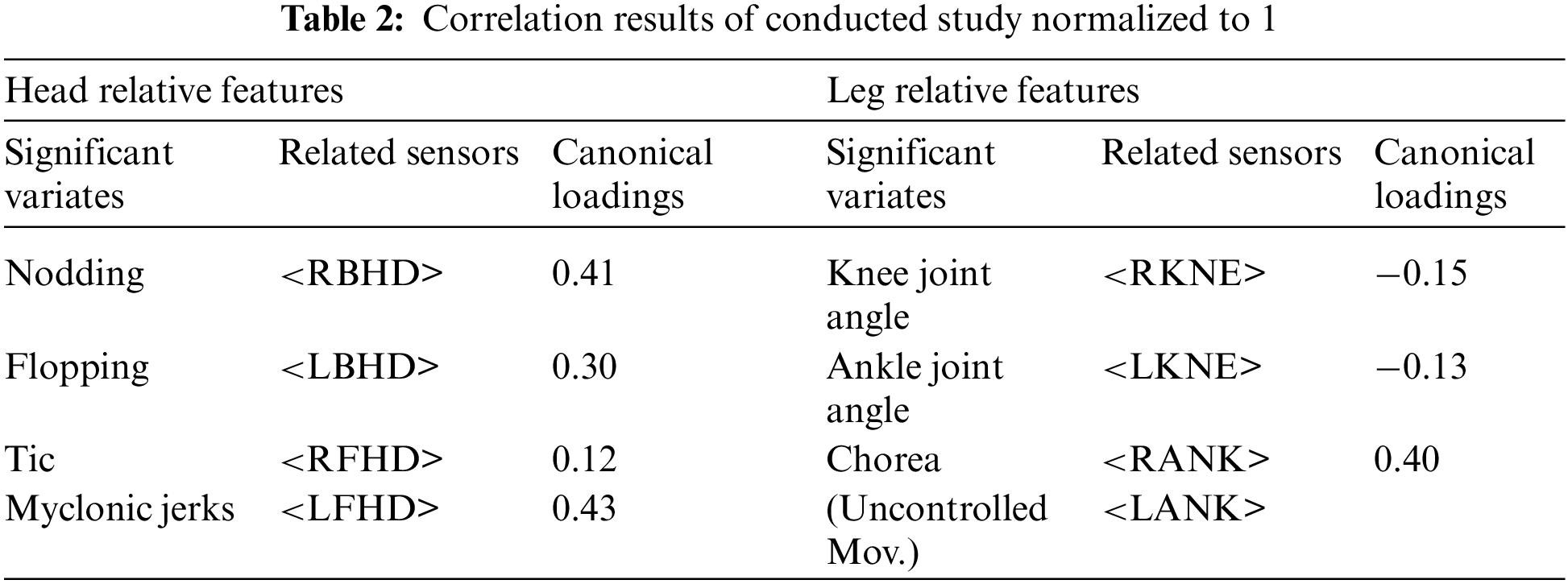
We explain our approach: our dX consists of head relative feature groups, and dy consists of leg relative features. Table 2 shows dX features such as nodding, flopping, tics, and myoclonic jerks and dy features such as knee joint angle, ankle joint angle, and chorea. A canonical loading measures the simple linear correlation between the original observed variable in dX and dX variable set and that set’s canonical variate. The scores show a significant correlation between nodding, myoclonic jerks, and chorea. These additional CCA-utilized features will be our unique key in gait identification.
A canonical correlation is a correlation between two canonical or latent types of variables. This feature extraction approach for identifying subjects includes collecting the gait feature sets (forming groups), then exploring associations between factors from two multidimensional feature groups. This step will lead to distinctive gait CCA features, as seen in Fig. 2.
Figure 2: A way of inferring information from cross-covariance matrices
3.2 Extracting Canonical Variates
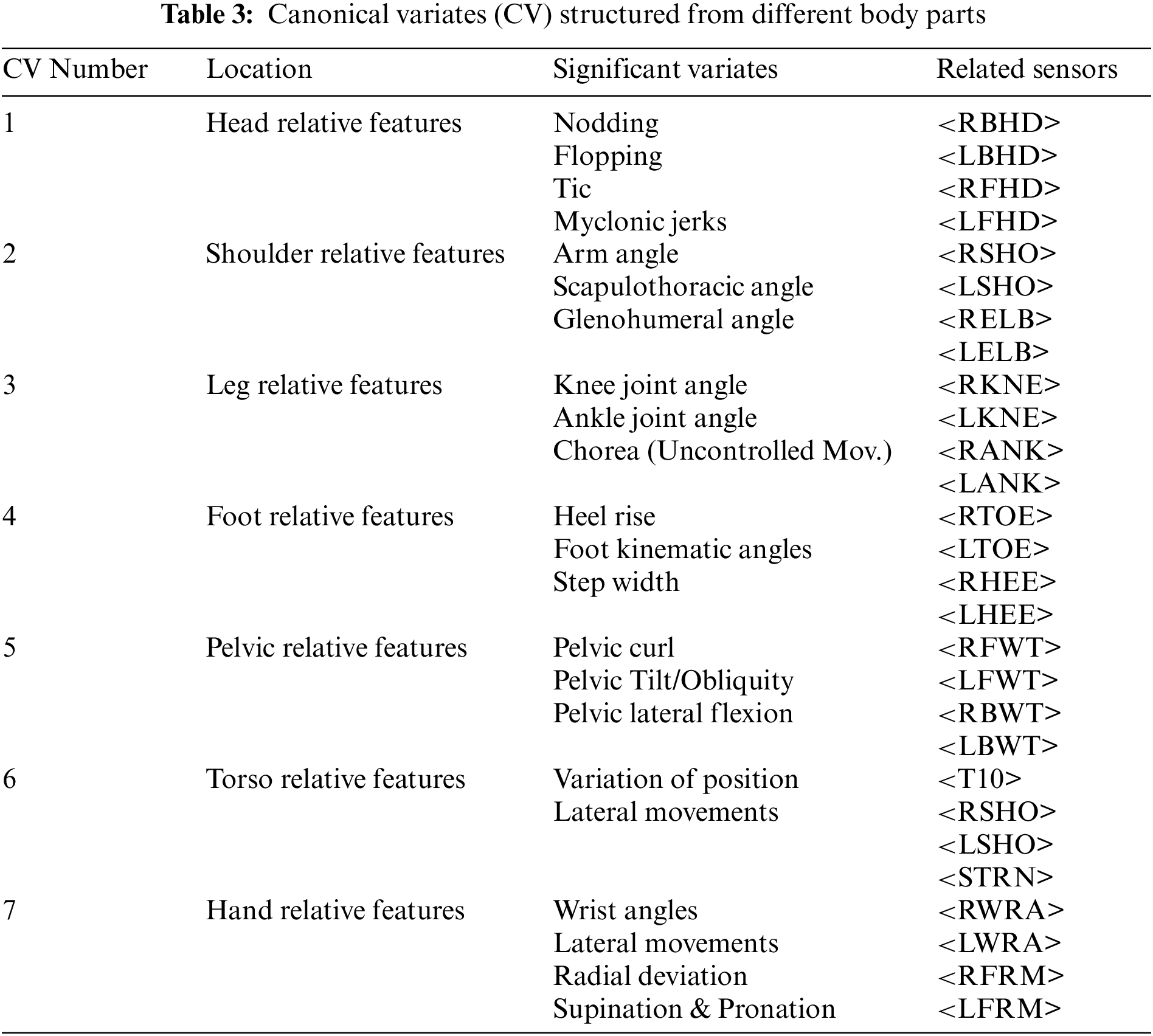
Multivariate data analysis uses canonical variates, the weighted sums of the variables. The quality of extracting these components has a significant impact on gait analysis. The study goes beyond the traditional approach by grouping these local features into seven feature sets to capture covariance between these sets of local features.
The analysis of the gait character contains extracting as many valuable features as possible to understand the complexity of human gait variability. With this aim, analyzing all parts of the human body comes first to detect the best local features. Initially, it is focused on head-related features (nod ratio, flopping ratio, tic) and then advanced to shoulder-related features. Leg-related features (knee joint angle, ankle joint angle, abnormal movements like chorea) and foot-related features (heel rise, foot kinematic angles) come after them. Afterward, pelvic-related features (pelvic curl, pelvic tilt, pelvic lateral flexion) and torso-related features (variation of the center position, lateral movement ratio) are obtained. The final step is to identify hand-related features (wrist angles, lateral movements, radial deviations, pronation, and supination).
In our approach, as an example, knee joint angle in flexion and ankle joint angle in plantarflexion construct canonical covariates. Similarly, abduction motions of arms contribute significantly to the construction of relative canonical covariates for shoulders, as seen in Table 3. As a result of using this covariation, it becomes possible to summarize the relationships into a smaller number of statistics while maintaining the most significant aspects of the relationships. This approach captures captured unobservable human gait harmonies that lead the way to identify the subjects based on latent covariance, thus, gait characteristics.
The key to our approach is identifying the most distinctive gait features, as shown in Figs. 3 & 4. Following classifying these traits by location on the body, it is possible to generate CCA covariates using anatomical planes. Afterward, ML (Machine Learning) methods harness these covariate harmonies as gait determinants to enhance gait identification.
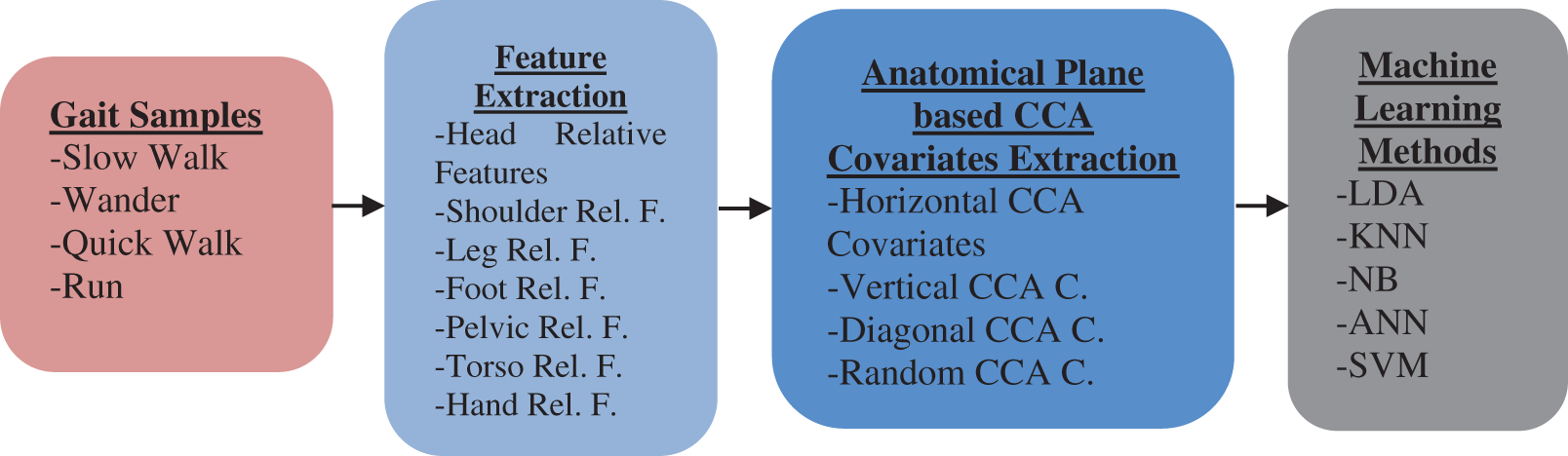
Figure 3: Our proposed approach to strengthening the success of gait identification utilizing CCA
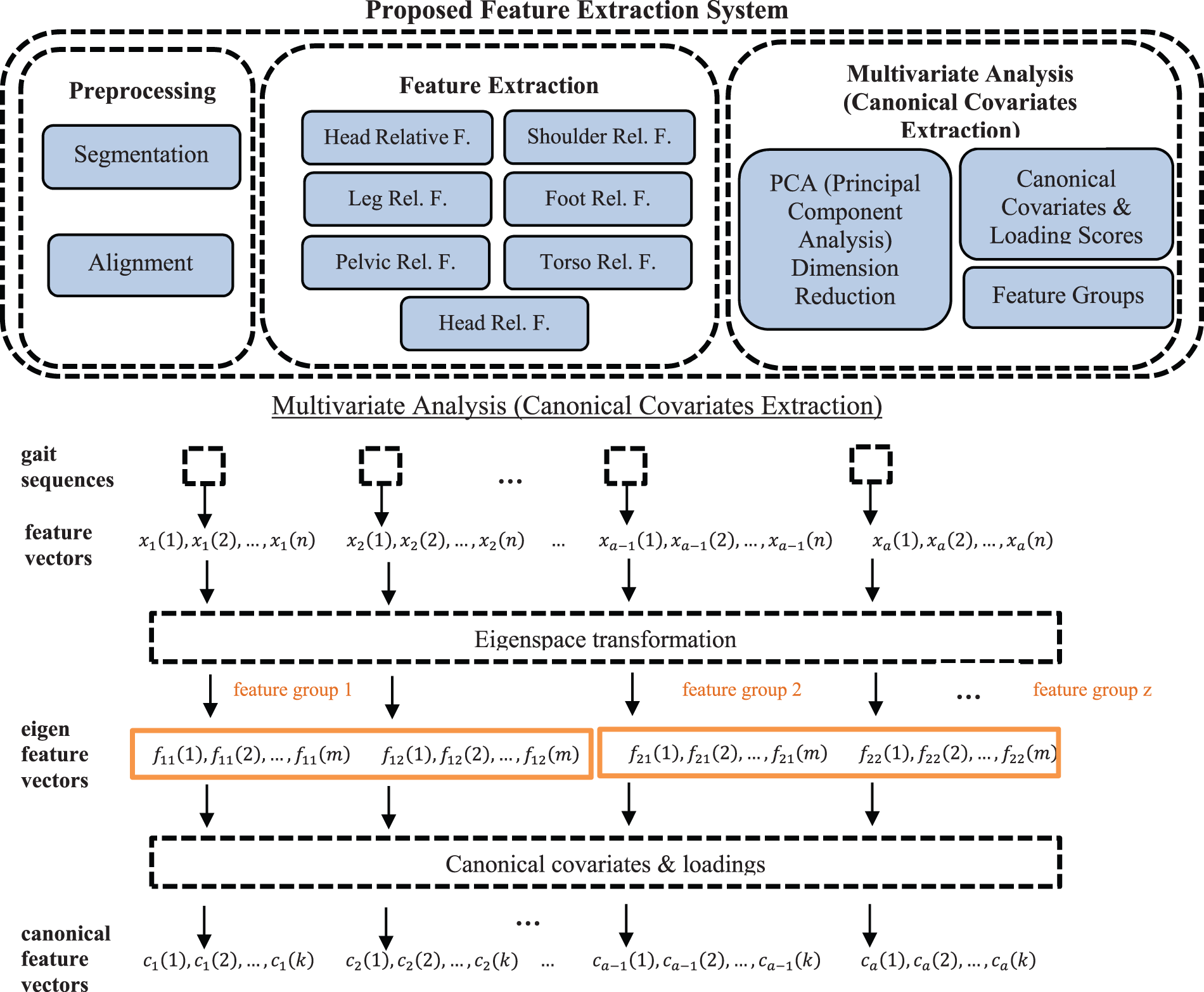
Figure 4: Proposed feature extraction system
As shown in Fig. 5, the graphs have normalized coordinate values of the markers on the X, Y, and Z-axis for the first three subjects. Our first observation is that some body parts are inversely proportional to one another (Fig. 5a). It should be noted that the intensity of this ratio varies between the other two subjects (Figs. 5b and 5c). In regards to the correct ratio, there are some values of the left and right wrists of the same subjects (Figs. 5d–5f). Also, it appears their harmony ratios are not at that level on the left and right wrists; either the first or the second subject’s wrist motions are smoother than the third one (Figs. 5g–5i).
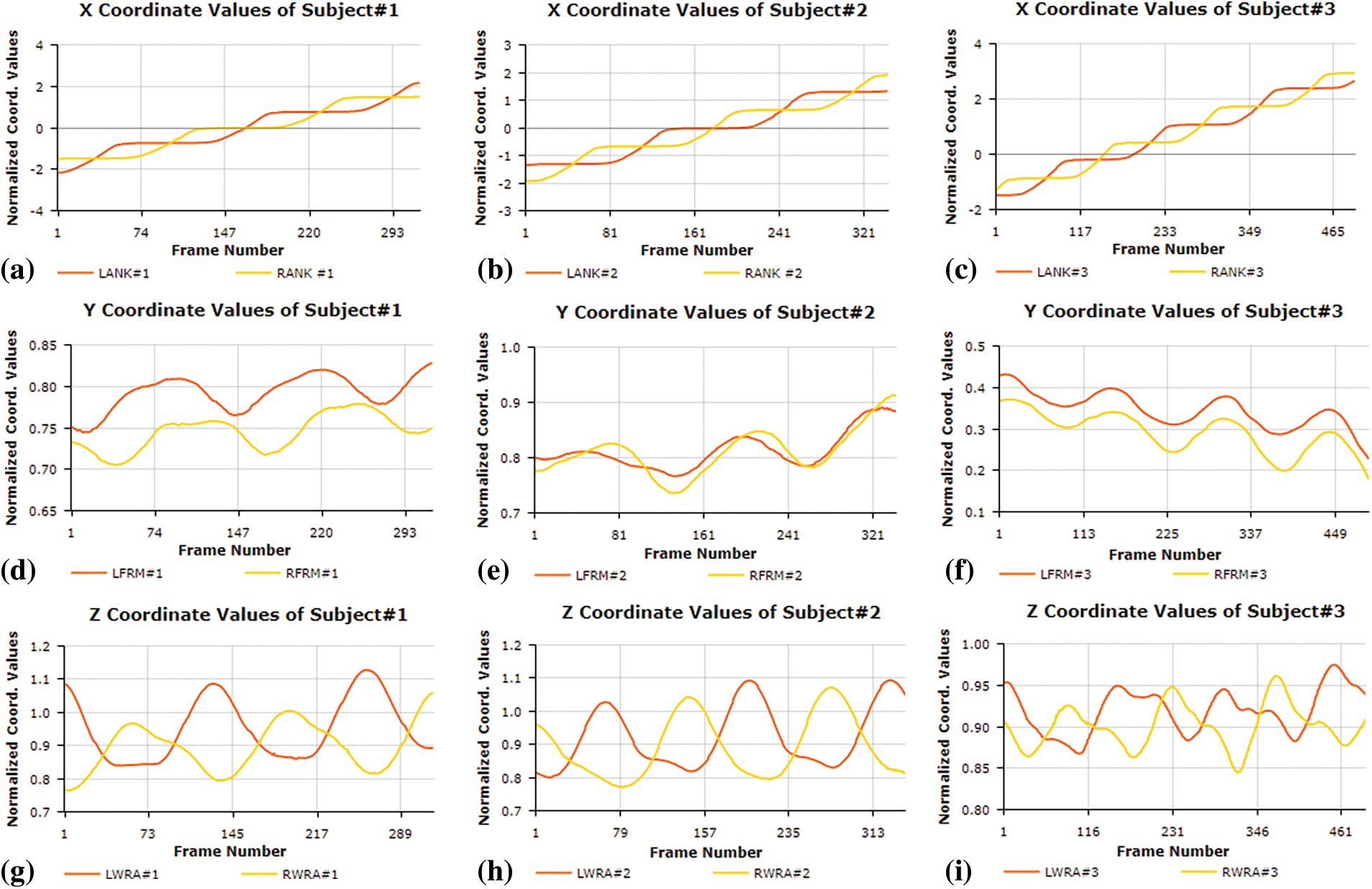
Figure 5: (a) Example of high correlation value (inverse-ratio) between ankles of Subject#1, which is usually in a rising trend due to approaching. (b) Example of high correlation value (inverse-ratio) between ankles of Subject#2. (c) Example of high correlation value (inverse-ratio) between ankles of Subject#3. (d) Middle-level correlated left and right forward arms of Subject#1, which is both in rising and decreasing trend up to subjects’ variation. (e) Middle-level correlated left and right forward arms of Subject#2. (f) Middle-level correlated left and right forward arms of Subject#3. (g) Example of middle-level correlation of left and right wrists of Subject#1, which has more variation than previous graphs. (h) Example of middle-level correlation of left and right wrists of Subject#2. (i) Example of middle-level correlation of left and right wrists of Subject#3
Several distinct features were determined by cross-checking throughout the body. All markers and dimensions are taken into consideration when analyzing the gait features. This step includes focusing on head movements such as nodding or flopping, arm angles, heel rise, radial deviation of hands, etc. For example, the rotation of hands and limbs from lateral to medial is a significant feature for us. The extension and flexion of the arms are also remarkable. Observing other body parts also reveals valuable information.
As a next step, structuring canonical variates for CCA comes. CCA has two specific purposes, explaining covariance between two sets of variables using a few linear combinations and identifying contributing variables. Two points of view are needed to evaluate the importance of each variate in CCA. First, it is necessary to determine the strength of the relationship between the variate and the variables used to create it. It is also required to study the strength of the relationship between the corresponding X and Y variates. Therefore, our objective is to find meaningful relationships among the covariates to improve the identification scores of the covariates.
The proposed method of identifying human gaits focuses on the canonical correlation coefficients, which measure the correlation between different types of canonical variates in different body halves. These body halves are separated by anatomical planes, which consist of four imaginary flat surfaces or planes that pass through the body in the anatomical position: the median plane, sagittal planes, frontal (coronal) planes, and horizontal (transverse) planes, as shown in Fig. 6. Extracting bilateral harmony leads a way to identify the relevance of gait samples. The study focuses on identifying gait samples utilizing canonical variates formed by the features in opposite horizontal halves-the right and left halves, the features in opposite vertical halves-the upper and lower halves, the features in cross halves-;cross upper and lower halves. During the last forming process, gait samples are identified with the help of canonical variates made up of randomly selected features distributed throughout the body, which aims to spot unexpected harmony between body parts.
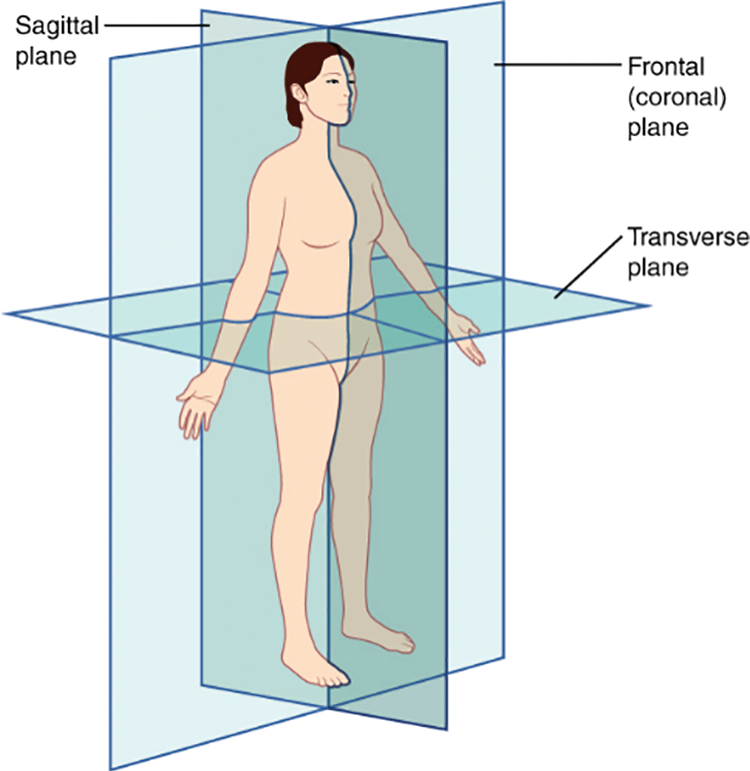
Figure 6: Anatomical planes
4.1 Benchmarking ML Methods for CCA Contribution
At first, the study reveals identification results utilizing classical machine learning methods. The findings are displayed in Table 4; all types have four different gait speed categories. SVM (Support Vector Machines) captured the best mean identification scores among quick walk-and-run sections. In all, SVM (Support Vector Machines) 92.5% identification rate improves to 96%, which is close to a 4% improvement, demonstrating the success of the CCA’s additional features. Also proposed approach improves identification scores by 3% over all other methods.
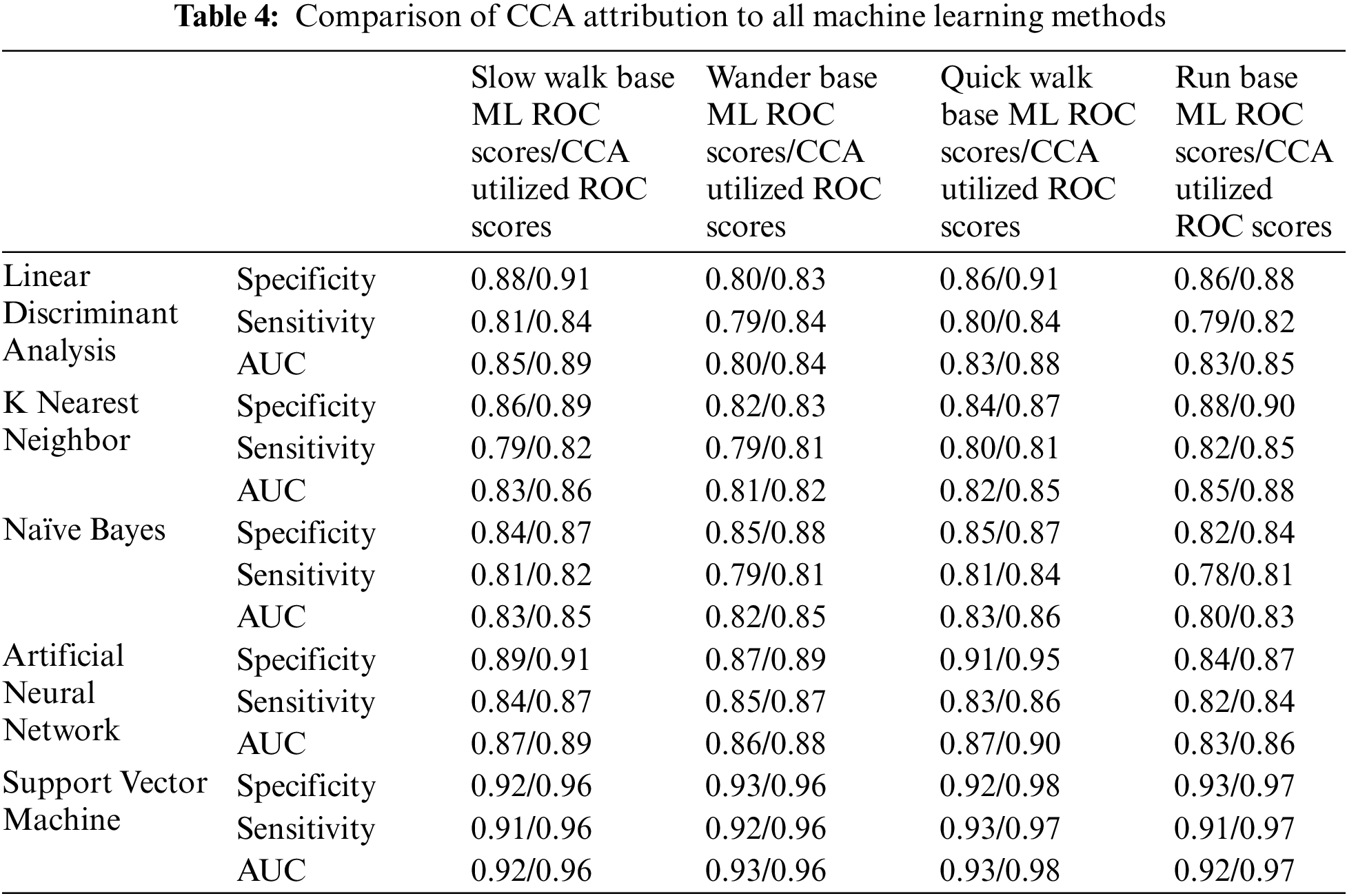
4.2 Evaluation of Performance Based on the Different Classes of Walking
Further analysis of our gait identification approach also emphasizes the importance of anatomical planes. Analyzing the identification ROC (Receiver Operating Characteristic) curve scores seen in Table 5, the CCA utilized identification score for all machine learning methods are higher 2.7% in horizontal comparison, 3.2% in vertical comparison, 3.8% in diagonal comparison, 3% in random comparison than without CCA. As a result of using canonical covariates as gait determinants, our approach to gait identification contributes about 3.5 points to ROC scores. The diagonal cross-correlation of CCA covariates, based on the CCA covariates in the diagonal body halves, shows the most remarkable improvement. This result shows a key clue for gait identification with CCA; if there is some significance between two canonical variates located diagonally, then identification of that person becomes straightforward. As for speed categories, the gait pace could be more effective. However, a quick walk is a step ahead regarding the improvement rate. It is the top category for SVM-CCA utilized identification by the rate of 97,11%. Concerning comparison in the body halves approach, the diagonal comparison approach also has the highest identification score of 97,8% related to mean scores. This high identification score tells us that if there is some significant strength of association between two canonical variates located in diagonal halves while walking quickly, the identification becomes more successful than other types.
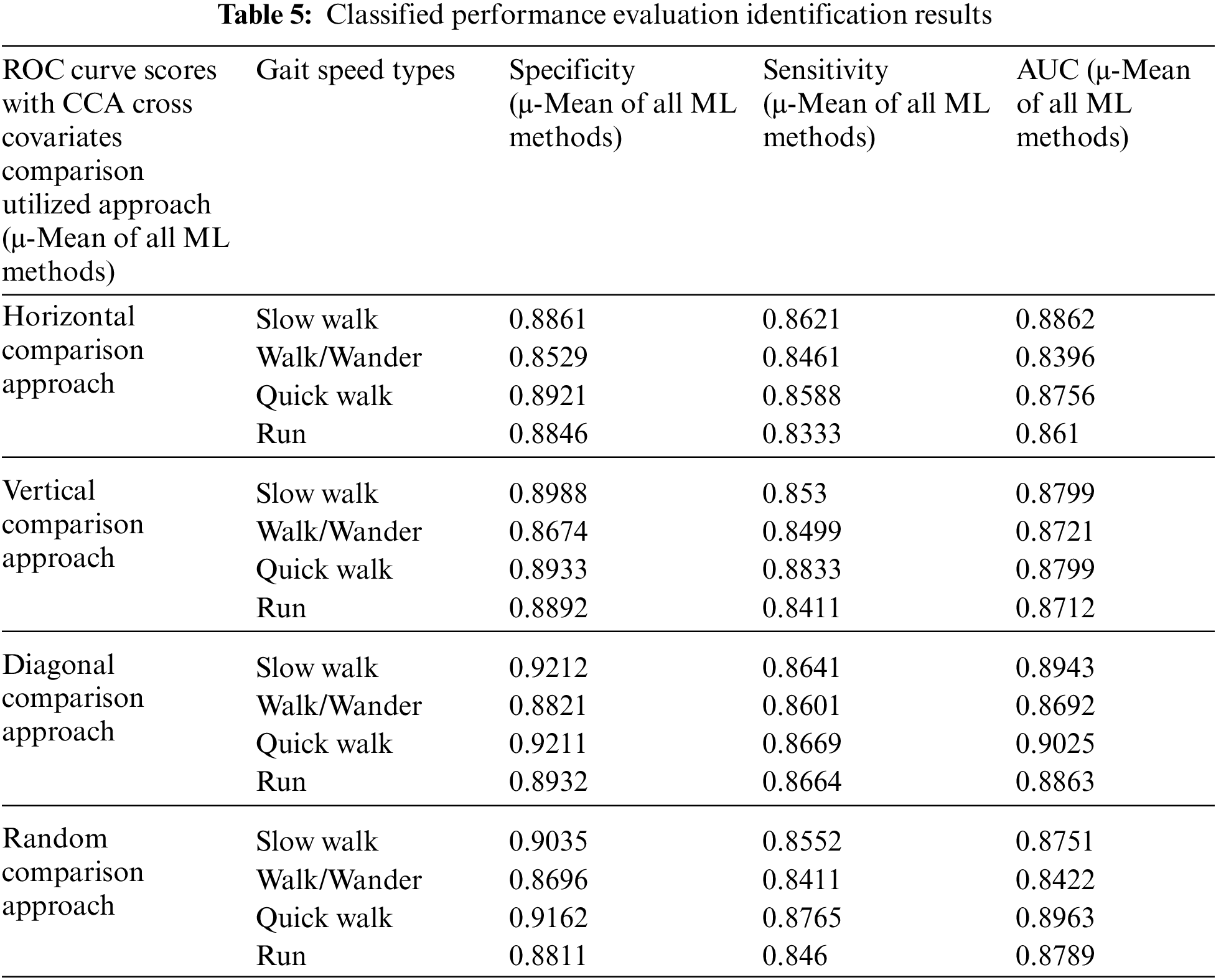
Biometric identification systems also request low false-negative and false-positive scores as much as accurate recognized scores. As for our proposed algorithm, SVM-CCA utilized a diagonal comparison approach with an average false detection rate of 0.03. The result of the study discovers that the minimum false rate is 0.02 using a diagonal comparison methodology. The other comparisons are as high as 0.04. The most considerable improvement in gait identification utilizing CCA in this section is the diagonal comparison approach, with a drop from 0.08 to 0.03.
Even though biometric identification systems can tolerate unidentified samples, false identification is a danger that must be avoided and minimized due to their security. Therefore, minimizing this undesirable situation is also a critical evaluation criterion with the improvement of successful identification scores for the assessment of our study. Beyond the 4% positive contribution to gait identification scores, there is also almost 50% improvement in both unidentified and falsely identified samples, which shows the success of Canonical Correlation Analysis in gait identification. In addition to improving identification scores, these ROC results also show that the CCA-oriented approach reduces unwanted identification results that may compromise security.
4.3 Comparison with Existing Methods
The section presents a comparative evaluation of the proposed approach against related works. All studies in the Table 6 use the positions of the markers obtained from 3D human gait data. This table lists the number of markers and the methods used in the studies. The proposed system outperforms state-of-the-art works in human identification. The paper utilizes CCR (Correct Classification Rate) to obtain a more applied performance evaluation. According to Table 6, the study indicates that there is, on average, 10.84% better accuracy than the related works. Beyond that, our proposed system contains more marker data and, in this way, more feature information than most.
This paper uses a way of inferring information from the cross-covariance group of features to improve identification success in 3D gait analysis. The fundamental concept behind the suggested approach is the use of complicated labels to direct feature selection toward the underlying semantics, which includes multivariate data harmony between irrelevant human body parts and the ratio of this relationship between often relevant parts. This method has improved the gait identification ROC score to attain a positive rise of around 4% and a success rate of 97.8%, as shown in Fig. 7. It is also remarkable that unidentified and misidentified gait samples have declined to nearly half of the previous score without utilizing CCA. Another effective, resilient barrier against deceit is the identification’s low rate of false-negative and false-positive results. The analysis also shows that quick walk (speed type) and diagonal comparison approach (includes canonical covariates from cross halves) significantly enhance gait identification performance. It is evident from all of these results that the model is adequate. Further work will be using a more extensive database to confirm the effectiveness of the proposed model with different factors of a gait such as clothing, health, and age conditions which can improve the robustness of the systems for unimagined gait conditions.
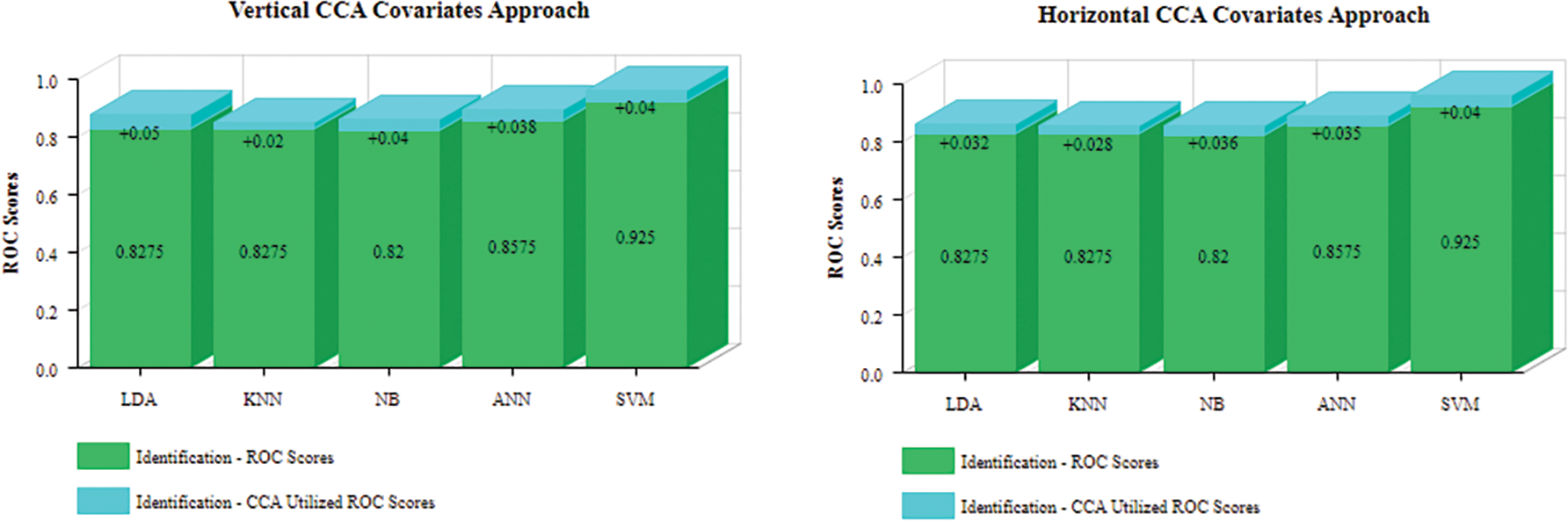
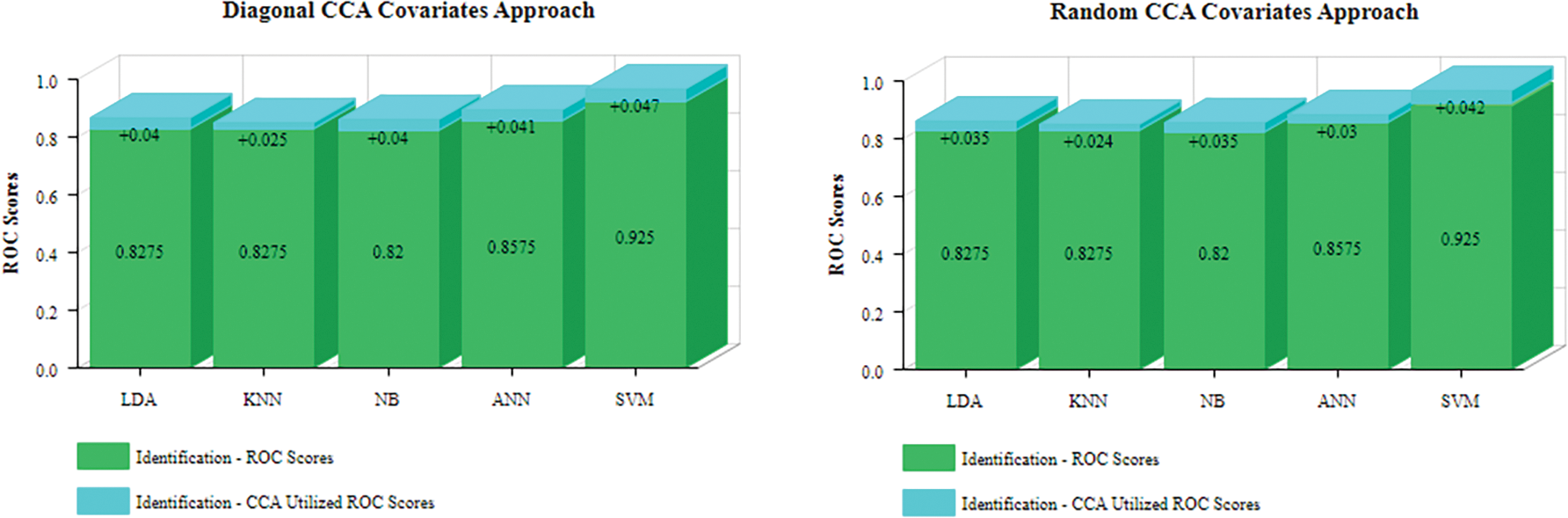
Figure 7: Graphical representation of positive contributions of CCA to gait identification
Acknowledgement: None.
Funding Statement: This study was supported by Istanbul University Scientific Research Project Department with IRP-51706 Project Number.
Author Contributions: Ramiz Gorkem Birdal: Conceptualization, Methodology, Software, Investigation, Writing, Visualization. Ahmet Sertbas: Supervision, Writing–Review & Editing.
Availability of Data and Materials: The authors do not have permission to share data.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. J. Cutting and L. Kozlowski, “Recognizing friends by their walk: Gait perception without familiarity cues,” Bulletin of the Psychonomic Society, vol. 9, no. 1, pp. 353–356, 1977. [Google Scholar]
2. L. Lee and W. E. L. Grimson, “Gait analysis for recognition and classification,” in Proc. of the IEEE Conf. on Face and Gesture Recognition, Washington DC, USA, pp. 155–161, 2002. [Google Scholar]
3. L. Wang, T. Tan, H. Ning and W. Hu, “Silhouette analysis-based gait recognition for human identification,” IEEE Transactions on Pattern Analysis and Machine Intelligence Archive, vol. 25, no. 12, pp. 1505–1518, 2003. [Google Scholar]
4. L. Wang, T. Tan, W. Hu and H. Ning, “Automatic gait recognition based on statistical shape analysis,” IEEE Transactions on Image Processing, vol. 12, no. 9, pp. 1120–1131, 2003. [Google Scholar] [PubMed]
5. M. Ekinci and M. Aykut, “Improved gait recognition by multiple-projections normalization,” Machine Vision and Applications, vol. 21, no. 2, pp. 143–161, 2010. [Google Scholar]
6. M. Ekinci and M. Aykut, “Human gait recognition based on kernel PCA using projections,” Journal of Computer Science and Technology, vol. 22, no. 6, pp. 867–876, 2007. [Google Scholar]
7. M. Ekinci, “Human identification using gait,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 14, no. 2, pp. 267–291, 2006. [Google Scholar]
8. M. Weuher, C. Pradhan, T. Brandt, K. Jahn and R. Schniepp, “Patterns of optimization in single and inter-leg gait dynamics,” Gait & Posture, vol. 39, no. 2, pp. 733–738, 2014. [Google Scholar]
9. T. M. Afendi, F. Kurugollu and D. Crookes, “Gait period estimation algorithm based on the angles of extremities,” in European Workshop on Visual Information Processing (EUVIP), Paris, France, pp. 160–165, 2013. [Google Scholar]
10. T. Afendi, F. Kurugollu, D. Crookes and A. Bouridane, “A frontal view gait recognition based on 3D imaging using a time of flight camera,” in 22nd European Signal Processing Conf., Lisbon, Portugal, pp. 2435–2439, 2014. [Google Scholar]
11. M. J. Toebes, M. J. Hoozemans, R. Furrer, J. Dekker and J. H. van Dieën, “Local dynamic stability and variability of gait are associated with fall history in elderly subjects,” Gait & Posture, vol. 36, no. 3, pp. 527–531, 2012. [Google Scholar]
12. P. Terrier and F. Reynard, “Effect of age on the variability and stability of gait: A cross-sectional treadmill study in healthy individuals between 20 and 69 years of age,” Gait & Posture, vol. 41, no. 1, pp. 170–174, 2015. [Google Scholar]
13. A. Mapelli, M. Zago, L. Fusini, D. Galante, A. Colombo et al., “Validation of a protocol for the estimation of three-dimensional body center of mass kinematics in sport,” Gait & Posture, vol. 39, no. 1, pp. 460–465, 2014. [Google Scholar]
14. V. Cimolin and M. Galli, “Summary measures for clinical gait analysis: A literature review,” Gait & Posture, vol. 39, no. 4, pp. 1005–1010, 2014. [Google Scholar]
15. S. D. Choudhury and T. Tjahjadi, “Silhouette-based gait recognition using Procrustes shape analysis and elliptic Fourier descriptors,” Pattern Recognition, vol. 45, no. 9, pp. 3414–3426, 2012. [Google Scholar]
16. Y. Iwashita, A. Stoica and R. Kurazume, “Gait identification using shadow biometrics,” Pattern Recognition Letters, vol. 33, no. 16, pp. 2148–2155, 2012. [Google Scholar]
17. S. D. Choudhury and T. Tjahjadi, “Gait recognition based on shape and motion analysis of silhouette contours,” Computer Vision and Image Understanding, vol. 117, no. 12, pp. 1770–1785, 2013. [Google Scholar]
18. X. Li, H. Ju and J. Cheung, “Gait force model and inertial measurement unit-based measurements: A new approach for gait analysis and balance monitoring,” Journal of Exercise Science and Fitness, vol. 14, no. 2, pp. 60–66, 2016. [Google Scholar] [PubMed]
19. H.İ. Masoud, Y. Zerehsaz and J. Jin, “Analysis of human motion variation patterns using UMPCA,” Applied Ergonomics, vol. 59, no. 1, pp. 401–409, 2016. [Google Scholar] [PubMed]
20. E. Baratin, L. Sugavaneswaran, K. Umapathy, C. Loana and S. Krishnan, “Wavelet-based characterization of gait signal for neurological abnormalities,” Gait & Posture, vol. 41, no. 2, pp. 634–639, 2015. [Google Scholar]
21. G. Barbieri, F. Fauque, T. Pozzo and D. Perennou, “A biological walker is faster and better recognized when aligned with body axis observer,” Gait & Posture, vol. 38, no. 4, pp. 981–986, 2013. [Google Scholar]
22. W. Zeng, F. Liu, Q. Wang, Y. Wang, L. Ma et al., “Parkinson’s disease classification using gait analysis via deterministic learning,” Neuroscience Letters, vol. 633, no. 6, pp. 268–278, 2016. [Google Scholar] [PubMed]
23. A. R. Javed, M. U. Sarwar, M. O. Beg, M. Asim, T. Baker et al., “A collaborative healthcare framework for shared healthcare plan with ambient intelligence,” Human-Centric Computing and Information Sciences, vol. 10, no. 1, pp. 1–21, 2020. [Google Scholar]
24. M. Deng, C. Wang, F. Cheng and W. Zeng, “Fusion of spatial-temporal and kinematic features for gait recognition with deterministic learning,” Pattern Recognition, vol. 67, pp. 186–200, 2017. [Google Scholar]
25. M. M. Ardestani and M. A. Wimmer, “Can a linear combination of gait principal component vectors identify hip OA stages,” Journal of Biomechanics, vol. 49, no. 10, pp. 2023–2030, 2016. [Google Scholar] [PubMed]
26. Y. Zhang, Y. Huang, L. Wang and S. Yu, “A comprehensive study on gait biometrics using a joint CNN-based method,” Pattern Recognition, vol. 93, no. 3, pp. 228–236, 2019. [Google Scholar]
27. K. N. Zakaria, R. Jailani and N. M. Tahir, “Application of ANN in gait features of children for gender classification,” Procedia Computer Science, vol. 76, no. 4, pp. 235–242, 2015. [Google Scholar]
28. S. P. Solano and L. F. A. Vargas, “Gait characteristics and sensory abilities of older adults are modulated by gender,” Gait & Posture, vol. 42, no. 1, pp. 54–59, 2015. [Google Scholar]
29. F. Sun, W. Zang, L. Gravina, G. Fortino and Y. Li, “Gait-based identification for elderly users in wearable healthcare systems,” Information Fusion, vol. 53, no. 4, pp. 134–144, 2019. [Google Scholar]
30. B. Bogen, M. K. Aaslund, A. H. Ranhoff and R. M. Nilssen, “Two-year changes in gait variability in community-living older adults,” Gait & Posture, vol. 72, no. 9, pp. 142–147, 2019. [Google Scholar]
31. R. S. Barcikowski and J. P. Stevens, “A monte carlo study of the stability of canonical correlations, canonical weights, and canonical variate correlations,” Multivariate Behavioral Research, vol. 10, no. 3, pp. 353–364, 2010. [Google Scholar]
32. T. M. A. Zulcaffle, F. Kurugollu, D. Crookes, A. Bouridane and M. Farid, “Frontal view gait recognition with a fusion of depth features from a time of flight camera,” IEEE Transactions on Information Forensics and Security, vol. 14, no. 4, pp. 1067–1082, 2019. [Google Scholar]
33. X. N. Xing, K. N. Wang, T. Yan and L. V. Zhuowen, “Complete canonical correlation analysis with application to multi-view gait recognition,” Pattern Recognition, vol. 50, no. 19, pp. 107–117, 2016. [Google Scholar]
34. I. Manipur, M. Manzo, I. Granata, M. Giordano and L. Maddalena, “Netpro2vec: A graph embedding framework for biomedical applications,” IEEE/ACM Transactions on Computational Biology and Bioinformatics, vol. 19, no. 2, pp. 729–740, 2022. [Google Scholar] [PubMed]
35. F. U. Mangla, M. Shahzad, M. I. Lali and S. A. C. Bukhari, “Sketch-based facial recognition, a weighted component-based approach (WCBA),” Multimedia Tools Applications, vol. 79, no. 37, pp. 27533, 2020. [Google Scholar]
36. H. T. Rauf, S. Malik, U. Shoaib, M. Naeem Irfan and M. Ikramullah Lali, “Adaptive inertia weight bat algorithm with Sugeno-function fuzzy search,” Applied Soft Computing, vol. 90, no. 2, pp. 106–159, 2020. [Google Scholar]
37. H. T. Rauf, W. H. K. Bangyal and M. I. Lali, “An adaptive hybrid differential evolution algorithm for continuous optimization and classification problems,” Neural Computing and Applications, vol. 33, no. 17, pp. 10841–10867, 2021. [Google Scholar]
38. Carnegie Mellon University Motion Capture DB, viewed 2 February 2021, Locomotion Category Walking DB. CMU Graphics Lab Motion Capture Database. 2021. [Online]. Available: http://mocap.cs.cmu.edup [Google Scholar]
39. F. Bobillo, L. Dranca and J. Bernad, “A fuzzy ontology-based system for gait recognition using Kinect sensor,” in Int. Conf. on Scalable Uncertainty Management, Granada, Spain, vol. 1, pp. 397–404, 2017. [Google Scholar]
40. N. Hosni, H. Drira, F. Chaieb and B. B. Amor, “3D gait recognition based on functional PCA on Kendall’s shape space,” in 24th Int. Conf. on Pattern Recognition, Beijing, China, pp. 2130–2135, 2018. [Google Scholar]
41. B. Dikovski, G. Madjarov and D. Gjorgjevikj, “Evaluation of different feature sets for gait recognition using skeletal data from Kinect,” in 37th Int. Convention on Information and Communication Technology, Electronics and Microelectronics (MIPRO), Opatija, Croatia, pp. 1304–1308, 2014. [Google Scholar]
42. M. Balazia and P. Sojka, “Learning robust features for gait recognition by maximum margin criterion,” in 23rd Int. Conf. on Pattern Recognition (ICPR), Cancún, Mexico, pp. 901–906, 2016. [Google Scholar]
43. B. Kwolek, T. Krzeszowski, A. Michalczuk and H. Josinski, “3D gait recognition using Spatio-temporal motion descriptors,” in Asian Conf. on Intelligent Info and DB Systems, Bangkok, Thailand, pp. 595–604, 2014. [Google Scholar]
44. A. Sinha, K. Chakravarty and B. Bhowmick, “Person identification using skeleton information from Kinect,” in Proc. of Intl. Conf. on Advances in Computer-Human Interactions, Nice, France, pp. 101–108, 2013. [Google Scholar]
45. V. O. Andersson and R. M. Araujo, “Person identification using anthropometric and gait data from Kinect sensor,” in Twenty-Ninth AAAI Conf. on Artificial Intelligence, Austin, Texas, USA, 2015. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF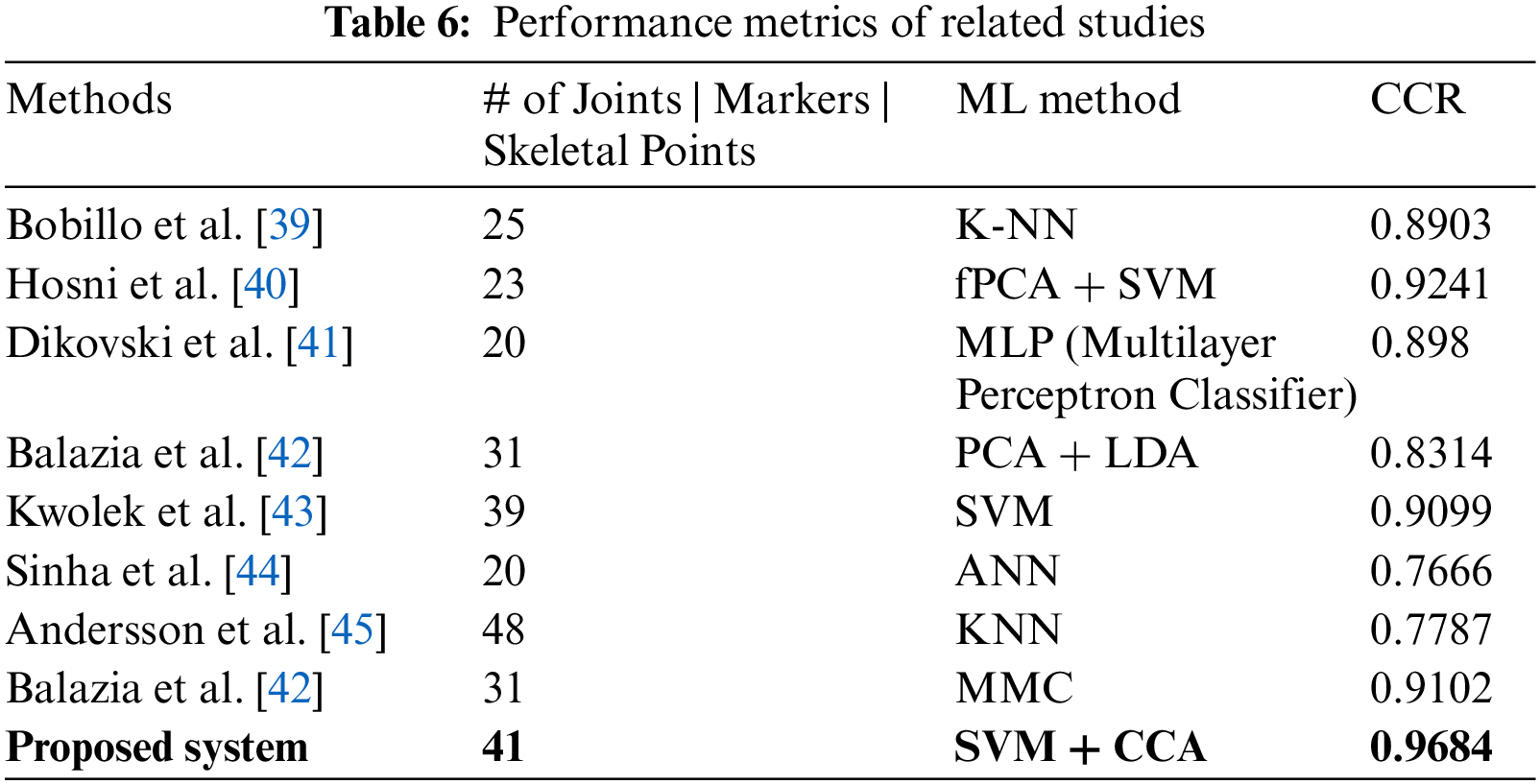
 Downloads
Downloads
 Citation Tools
Citation Tools
