A Positive Influence Maximization Algorithm in Signed Social Networks

1  Introduction

Social networks such as TikTok and Twitter have grown rapidly in recent years. These networks connect individuals such as friends and enemies, and provide personalized services according to individual needs, enabling them to communicate and exchange information. Due to the development of social networks, influence maximization has become one of the most popular research directions. The IM problem is first proposed by Domingos et al. [1]. Its goal is to select a set of seeds to propagate influence so that their influence can be spread as much as possible in the network. IM has numerous applications, i.e., viral marketing and rumor control. However, current studies on IM usually focus on unsigned social networks where users only have positive relationships with others, i.e., users are friends. In real-world social networks, the networks are signed and users have positive and negative relationships, and information decay should also be considered. Traditional IM algorithms do not account for these situations, which may lead to inaccurate calculation of the positive influence.

Considering Fig. 1 as an example. Fig. 1a shows an unsigned social network without information decay, where all users are connected in positive relationships, i.e., all connected users are friends. Fig. 1b depicts a signed social network with information decay, where users with the same color are friends, and different colors indicate they are enemies. Suppose user A wants to recommend a great product to other users. If neighbors are friends, positive information will be propagated, but negative information will be spread if they are enemies. In Fig. 1a, since all users are friends, all users think this product is great when the information propagation is finished. So the positive influence of A is 4. However, in Fig. 1b, since D and E are enemies, E will receive the message that this product is bad from D, leading to A’s positive influence being 3. Additionally, there are gaps in influence propagation over time due to information decay, so the information C received about the product is not entirely accurate, e.g., the information C received is “good” rather than “great”.

Figure 1: Two examples of social networks where users communicate with others. (a) An unsigned social network without information decay. (b) A signed social network with information decay

For signed social networks, several studies have researched the PIM problem and presented various solutions. However, some of these studies do not consider the possibility of negative nodes causing positive influence and information decay during influence propagation when modeling the PIM problem, which finally caused inaccurate calculation of the positive influence as mentioned in the previous example. Moreover, some of these studies are obtained by greedy strategies, which will undoubtedly cause a significant time overhead due to time-consuming simulations. To address these limitations, this paper proposes a new IC-PD model that captures the influence propagation and information decay in signed social networks, which is more similar to real-world social networks. Furthermore, to avoid extensive Monte Carlo simulations for seeds selection, this paper proposes the SRIS algorithm based on the PRR set to solve the PIM problem, inspired by the state-of-the-art reverse influence sampling (RIS) method [2] in the IM problem. The algorithm incorporates the famous saying “friends of my enemies are my enemies” and “enemies of my enemies are my friends” into its design. In conclusion, the contributions of this paper are as follows:

1.    This paper proposes a new model IC-PD for signed social networks. It considers the possibility of negative nodes causing positive influence and information decay during influence propagation.

2.    This paper proposes the concept of the PRR set and devises the SRIS algorithm to solve the problem of PIM. The algorithm uses PRR sets to select seed nodes under the IC-PD model.

3.    Experiments are conducted on three real-world signed social network datasets, and the results demonstrate that SRIS has better performance in effectiveness than other baseline algorithms.

The rest of the paper is structured as follows: Section 2 provides an overview of related work. Section 3 gives a detailed explanation of the IC-PD model and the PIM problem. Further, the PRR set is defined and the SRIS algorithm is presented in Section 4, and experiments are conducted in Section 5. Finally, Section 6 concludes the paper.

2  Related Work

This section briefly summarizes the related work on solutions to the IM problem, including influence maximizing in traditional and signed social networks.

2.1 Influence Maximizing in Traditional Social Networks

A majority of algorithms use greedy based Monte Carlo simulations to solve the IM problem in traditional social networks. Domingos et al. [1] first proposed an influence model based on Markov random fields. On this basis, Kempe et al. [3] defined the IM problem for the first time and proposed influence propagation models called independent cascade (IC) and linear threshold (LT). A large number of related studies have emerged based on these models.

Chen et al. [4] improved the efficiency of greedy based IM algorithm and devised an improved greedy algorithm called New-Greedy. The algorithm removes the unsuccessfully propagated edges from the network in each iteration and obtains a new network to select the next seed. Further, they proposed an improved algorithm called degree discount (DD) to solve the IM problem. Experiments show that DD can achieve a wider spread than degree based and distance based heuristics. Leskovec et al. [5] further proposed the cost effective lazy forward (CELF) algorithm to improve the performance of the greedy algorithm under the IC model. Experiments demonstrate that CELF is about three magnitudes faster than the original algorithm and has similar effects. Based on this algorithm, Goyal et al. [6] presented the CELF++ algorithm to improve the efficiency of the CELF algorithm further.

The algorithms based on the reverse reachable (RR) set [7] have also aroused extensive research. Borgs et al. [2] were the first to propose the RIS algorithm, which collects enough RR sets and selects the nodes with the most influence. Tang et al. [7] presented a martingale based influence maximization (IMM) algorithm based on RIS, which improves the efficiency of the algorithm while satisfying the theoretical guarantee of an approximate ratio of 1−1e−ε, where e is a mathematical constant that represents the base of the natural logarithm function, and ε represents the error control parameter.

There are also a series of extensive algorithms for the traditional IM problem. Huang et al. [8] proposed the community based IM problem. They established a comprehensive hidden variable model and algorithm to infer potential topic information in influence propagation. Chen et al. [9] presented the problem of maximizing social influence by fusing topic perception, and devised a general RR set algorithm to support different sampling strategies. Further, three different sampling strategies are proposed to construct the RR set to improve the performance. Liu et al. [10] devised a maximum likelihood algorithm, which graded the existing graph according to the degree of nodes, and obtained seed nodes by likelihood calculation, avoiding Monte Carlo simulations. Li et al. [11] presented an algorithm based on the Gaussian propagation model, which likens influence diffusion to the concentration of pollutants in space. There’s no need for Monte Carlo simulations with Gaussian propagation, so the algorithm runs faster.

2.2 Influence Maximization in Signed Social Networks

In signed social networks, the problem of IM aims to select the most influential seed set under the polar relationship of nodes so that the information propagation of seeds is the most. Therefore, it is essential to focus not only on topological features but also on signed features.

Li et al. [12] introduced a new independent cascade propagation (IC-P) model for signed social networks. They also proposed the polarity-related influence maximization (PRIM) problem and devised a greedy based algorithm to solve it. Further, they presented the PIM problem in ref. [13] for the first time and devised a simulated annealing based algorithm to solve it. Hosseini et al. [14] presented a sign aware cascade model in polar social networks. A stochastic secret key technique was proposed to solve the PIM problem using continuous particle swarm optimization. Liu et al. [15] defined an independent cascade diffusion model to simulate influence propagation in signed social networks. They devised an independent propagation path algorithm to maximize the number of positive active nodes in the path. Yin et al. [16] proposed a new framework to describe influence propagation for advertisement recommendations in signed social networks. They devised a page rank based algorithm to select seed nodes with positive effects. Ju et al. [17] presented an independent path based algorithm to solve the PIM problem, which included a propagation increment function for accelerating the seeds selection phase.

There are also some issues concerning with PIM problem in recent years. e.g., Sheng et al. [18] considered two different views spread simultaneously and that negative views can reverse the polar relations of nodes. Further, they proposed a positive influence maximization algorithm based on the IC model in signed social networks. He et al. [19] presented the positive opinions maximization (POM) problem and modeled it as an optimization model. Further, they devised an activated opinion maximization framework (AOMF) that considers the dynamic opinion formation process and user preferences. Li et al. [20] formulated the net positive influence maximization (NPIM) problem. They proved that the NPIM problem is non-monotone and non-submodule in the polarity dependent independent cascade diffusion model. Therefore, an improved greedy algorithm was proposed for solving the NPIM problem. Alla et al. [21] proposed three heuristic methods based on centrality measures and clustering to solve the opinion maximization problem in signed social networks. Besides, there are also some studies [22–25] related with maximize influence in signed social networks.

Based on the review above, it is clear that polarities play an essential role in IM. The research of IM has been extended from unsigned to signed social networks to find seeds with the greatest polar influence. In contrast to the previous works, this paper considers the possibility of negative nodes causing positive influence and information decay during influence propagation. Compared to existing studies, this research is more grounded in reality and can perform better in some actual cases.

3  Preliminaries

First, some notations frequently used throughout the paper are presented in Table 1 to clearly introduce the preliminaries.

3.1 Influence Propagation Model

This paper proposes a new model IC-PD to describe the influence propagation of nodes and the decay of information during the influence propagation. The model is based on the polarity related independent cascade model [12] and considers information decay.

In the IC-PD model, let G = (V, E) be a signed social network, and each node has three states: positive, negative, or inactive, denoted as Sta(u)∈{+1,−1,0}. Given a node u, the positive state refers to the corresponding user receiving and trusting the information. The negative state indicates that the corresponding user receives the information but does not trust it. The inactive state means that the corresponding user does not accept the received information or has not received information at all. In addition, the edges between nodes have different polarities: positive polarity or negative polarity, denoted as rel(u,v)∈{+1,−1}. The positive polarity relationship indicates a friend or trust relationship between these two nodes, and a negative polarity relationship suggests that the two nodes have an enemy or distrust relationship. On this basis, the influence diffusion process of IC-PD is formulated as follows.

1) Let S be an initial set of active nodes consisting of positive nodes; the other nodes not in S are inactive. At time step 0, for each u in S, it has one and only one chance to try to activate its each inactive neighbor v with probability pu,v. If v is activated, the state of v is assigned according to Eq. (1).

Sta(v)=Sta(u)⋅rel(u,v)(1)

2) For a node u first activated at time step t, it will become either positively or negatively active at time step t + 1. The state of u is decided by Eq. (1); then u will have one and only one chance to try to activate each inactive neighbor v with probability pu,v.

3) The process of Step 2 will continue until no new nodes are activated at some time step.

The IC-PD model takes into account that the information will gradually decay in the process of influence diffusion, which can be treated as the influence probability pu,v is sensitive to the influence propagation step. Let Nat(v) be the set of in-neighbors of node v that become positively active or negatively active at step t. At step t + 1, each u∈Nat(v) will try to activate v with probability pu,vt in arbitrary order. Once v is activated by one of the nodes in Nat(v), other nodes in Nat(v) will no longer try to activate v. This paper tries to capture the information decay from the influence diffusion over time. The formula of pu,vt is defined as follows:

pu,vt+1=α⋅pu,vtt+1+(1−α)⋅pu,vt⋅Cu,(2)

where α is the weight parameter used to measure the decay of information in time steps and the importance of nodes themselves, t is the time step of the influence propagation, and Cu is the degree centrality of u, i.e., Cu=Dun−1, where Du represents the out degree of u, and n is the number of nodes in the network.

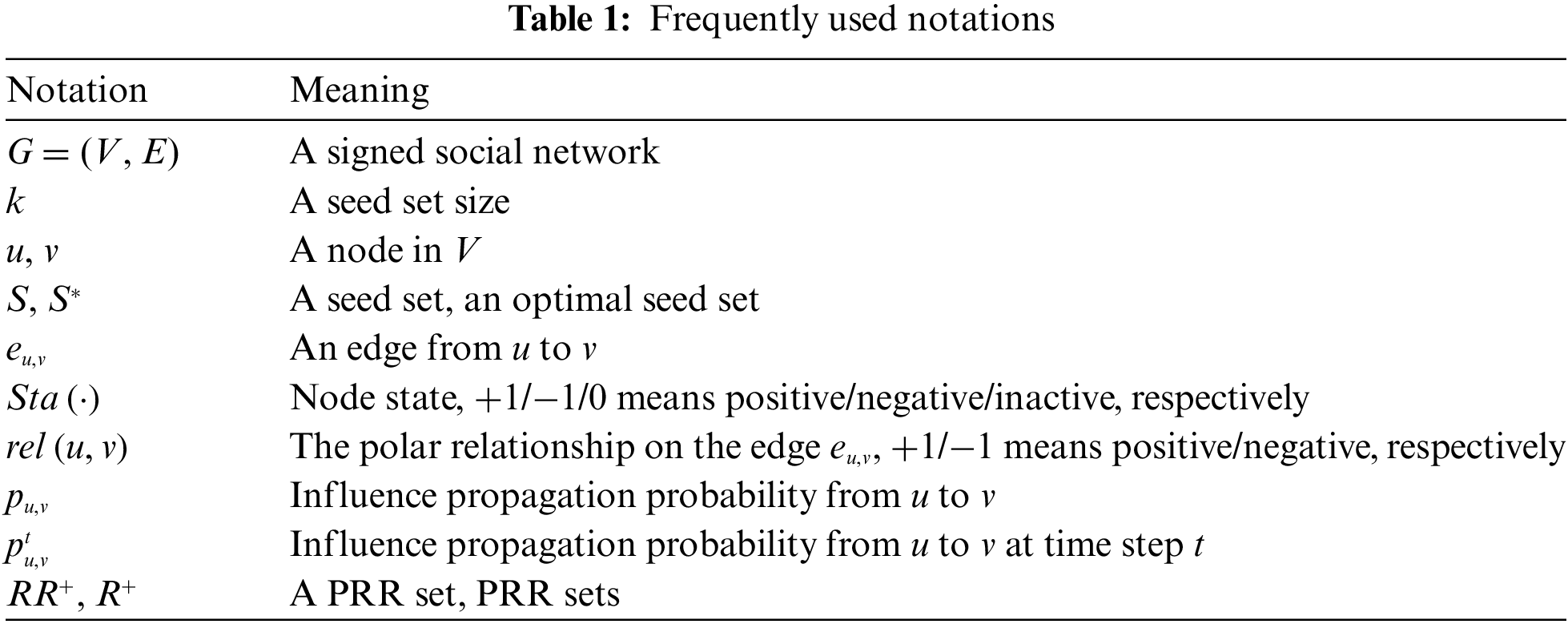
Fig. 2 shows an example of the influence diffusion in the IC-PD model with α = 0.5 and the initial influence probability of each node pair pu,v0=0.1. The red color means the corresponding node has a positive state, yellow means a negative state, and white means an inactive state. Solid squares represent seed nodes, while empty and solid circles represent nodes that are not activated and activated, respectively. The numbers on the edges represent the probability of influence spreading and the polarities between node pairs, respectively. The influence probability changes over time due to the decay of information. When a node is positively activated, the color of the node is the same as its parent node which activates it. Otherwise, their colors are different. When the propagation ended at time t, solid lines represent successful propagation of influence along that edge, while dotted lines represent unsuccessful propagation. At time t = 0, let nodes 1 and 2 be the positive seeds, and all other nodes are inactive. At t = 1, node 1 positively activates node 3, and node 2 negatively activates node 5, but node 1 does not activate node 4. At t = 2, node 3 positively activates node 7 but does not activate node 6, while node 5 successfully activates node 8 with a negative polarity. At t = 3, node 7 successfully activates nodes 4 and 9 in a negative relation, and node 8 positively activates node 10. The propagation ends here, and node 6 is not activated; nodes 3, 7, 8 and 10 are positively activated; nodes 4, 5 and 9 are negatively activated in this propagation.

Figure 2: An example of the influence diffusion in the IC-PD model

3.2 The Positive Influence Maximization Problem

The IM problem focuses on selecting seeds with the largest non-polar influence, disregarding that user influence can be positive or negative. In contrast, the PIM problem considers the positive influence resulting from the polar relationships between users, making it more applicable to real-world social networks.

To formalize the PIM problem, let σ+ (⋅) be the positive influence functions. Given a seed set S, σ+ (S) represent the positive influence spread value of S. Then, the PIM problem can be formalized as follows:

Definition 1: (The positive influence maximization problem). Given a signed social network G and an influence diffusion model such as IC-PD, for a non-negative parameter k, the PIM problem is to find an optimal seed set S∗ of size k, such that the positive influence propagation of this set can be as much as possible, i.e.,

S∗=argmaxS⊆V,|S|=kσ+(S)(3)

To solve the PIM problem, the traditional solutions follow the idea of the greedy based algorithm, which mainly divides the problem into two sub-processes. One process is calculating the marginal gain of nodes by Monte Carlo simulations under the IC-PD model. The other process is selecting the top k most influential nodes using the greedy approximation algorithm. The pseudocode of the algorithm called ICPD-Greedy is shown in Algorithm 1.

Assuming that the network has n nodes and m edges, the algorithm runs for k iterations with R simulations in each iteration. In each iteration, the algorithm needs to search through all nodes u∈V\S to identify the node with the maximum marginal influence. For each node, R simulations are run to determine its marginal gain after it is added to the seed set. Since each simulation may require traversing all edges, the time complexity of Algorithm 1 is O (knRm). As the network size increases, the algorithm becomes computationally complex, making the Monte Carlo based ICPD-Greedy algorithm impractical for real world applications. In the next section, the state-of-the-art RIS technique for the IM problem will be introduced, which inspired this work.

4  The Signed Reverse Influence Sampling Algorithm

In this section, the SRIS algorithm is proposed. It incorporates the famous saying “friends of my enemies are my enemies” and “enemies of my enemies are my friends” into its design, and considers the possibility of negative nodes causing positive influence and the information decay during the influence propagation.

4.1 Polar Reverse Reachable Set

Reverse influence sampling is an effective method to accelerate influence estimation. The core of RIS technology is to construct a set of sampling result sets, namely the RR set to make an unbiased estimation of the influence of seeds. The concept of the RR set is defined in [7], and can be formulated as follows:

Definition 2: (Reverse Reachable Set). Given a social network G = (V, E), the RR set of each node v∈V can be obtained in two steps. First, v is chosen as the sampling source randomly and uniformly. Then, starting from v, a random reverse breadth-first search is performed on G. In this process, an activation attempt is made for each node belonging to the visited edge e using the probability p(e), and all activated nodes on visited edges are added to the RR set, where v is called the root node of this RR set.

Tang et al. [7] proved that nodes with great influence frequently appear when the number of sampled RR sets R reaches a specific scale. The coverage probability of RR sets in R of a seed set S can be used as an unbiased estimate of the influence spread of it in the original network G. This can be formulated as follows:

E[σ(S,R)]=θn⋅E[∑i=1θxi],(4)

σ(S,R) is the influence of S in the original network, R is the set consisting of θ random RR sets with R={R1,R2,…,Ri,…,Rθ}, Ri is a random RR set and xi is a random variable that equals 0 if S∩Ri=∅, and 1 otherwise.

However, the RIS algorithm is unsuitable for the PIM problem because it does not consider the polar relationships of nodes, making it incorporate to select the optimal seeds. As shown in Fig. 3, assume that node 9 is randomly selected as the root node, and then a random reverse breadth-first search is run from it. After the process is finished, the RR set consists of nodes with colors. A RR set containing nodes 9, 7, 4, 3, and 2 can be obtained, i.e., any of these nodes can be chosen as a seed, which can influence node 9. However, if the polar relations of nodes are considered and the numbers on the edges represent the polarities between nodes, the red color means the corresponding node has a positive state, and yellow means a negative state. It can be seen that nodes 2, 3 and 7 cannot positively influence node 9 since their relations are negative, while the RIS algorithm takes these nodes to consist of a RR set rooted from node 9, so the result is not accurate.

Figure 3: An example of the RR set

Inspired by the RIS method, considering the polarity relationship in signed social networks, this paper proposes the SRIS algorithm to solve the PIM problem. SRIS aims to efficiently find the seeds to maximize the positive influence in signed social networks. It uses sampled PRR sets to estimate influence and selects seeds. The definition of the PRR set is as follows:

Definition 3: (Polar Reverse Reachable Set). Given a social network G = (V, E), the PRR set of each node v∈V can be generated in two steps. First, v is chosen as the sampling source randomly and uniformly. Then, starting from v, a random reverse breadth-first search is performed on G. In this process, the IC-PD model is used to simulate the influence diffusion in G with the initial set S={v}, and each activated u with Sta(u)=+1 on visited edges is added to the PRR set.

Algorithm 2 describes the pseudocode of the construction of a PRR set. In the algorithm, lines 3–13 simulate the process of influence diffusion in the IC-PD model.

4.2 Signed Reverse Influence Sampling Algorithm

On this basis, this paper proposes the SRIS algorithm. It consists of two phases: sampling and node selection. The pseudocode of the algorithm is given below.

Given G, k, ε, and l, the SRIS algorithm first determines the lower bound of the number of PRR sets, and generates the corresponding PRR sets R+ using Algorithm 2 in the sampling phase. Then, in the node selection phase, the algorithm iteratively selects a seed set S* of size k that covers a large number of PRR sets based on the greedy coverage method. Finally, the algorithm returns S* as the final result. Since the node selection algorithm is used in the sampling phase, this paper first introduces the node selection algorithm. Algorithm 4 describes its pseudocode.

Given G,k and the PRR sets R+, The node selection algorithm first calculates the count of each node that covered PRR sets in R+ (lines 2–4). A node ν covered a PRR set RR+ means that ν∩RR+≠∅. In each iteration, it selects a node ν that covers the largest number of PRR sets in R+ as a seed (lines 6–7), removes the PRR sets that ν covered and discounts the count of nodes in the corresponding PRR sets (lines 8–13). Finally, the algorithm returns S* as the final result.

Algorithm 5 describes the pseudocode of the sampling phase of the SRIS algorithm. Given G, k, ε, and l, the algorithm first initializes a PRR set R+ = ∅ and utilizes the binary search algorithm in [26] to calculate the number of necessary PRR sets θ during the sampling phase (lines 1–14). The variable i is used to record the number of times the binary search is performed and xi to store the guessed value. In each binary search iteration, the algorithm calculates the value of θi, and uses Algorithm 2 to generate the corresponding PRR sets R+ (lines 3–8), then utilizes Algorithm 3 to find a seed set S (line 9) and Eq. (4) to calculate the coverage probability of PRR sets in R+ of a seed set S (line 10). Then, the algorithm checks whether the guess is successful (lines 10–13). Once the condition in line 10 holds, the algorithm terminates the iteration and identifies the lower bound of xi, denoted as LB, and calculates the final needed number of PRR set θ. Finally, the algorithm constructs θ PRR set based on Algorithm 2 for the node selection phase (lines 15–20).

5  Experiment and Evaluation

Experiments are conducted on three real signed social networks. These experiments aim to evaluate the performance of the proposed SRIS algorithm for the PIM problem.

5.1 Experimental Setup

Datasets. Three real-world signed social networks are used: WikiElec, Epinions, and Slashdot. All of them can be downloaded from http://snap.stanford.edu/data. WikiElec is a management election dataset that includes historical data on the administrator elections and votes of Wikipedia users. Epinions is a popular product review website where users can trust or not trust other users. Slashdot is a popular technology news website where users can mark other users as friends or enemies. The details of the datasets are shown in Table 2.

Evaluated algorithms. This paper compares the SRIS algorithm with some baseline algorithms. The following list of the methods compared in experiments:

• IC-PD: Algorithm 1 in this paper utilizes the CELF algorithm in [5] to speed up the process.

• IMM: The state-of-the-art algorithm based on RIS [7], selecting the optimal seeds without considering the polar relations of nodes.

• POD: The positive out degree (POD) algorithm selects the top k nodes based on the positive out degrees of nodes.

• DD: This algorithm [4] is based on the degree of nodes and does not consider the nodes’ polar relationships. Once a node is selected as a seed, its neighbors’ degree should be discounted.

• Random: This algorithm randomly selects k nodes as seeds from signed social networks.

Experimental environment. The experimental platform is 64-bit Windows 10, the CPU is AMD R7 2.9 GHz, the memory is 16 GB, the programming environment is Pycharm, and all compared algorithms are written in Python.

Parameter settings. All of the algorithms simulate the influence propagation under the IC-PD model. Since the initial influence propagation probability pu,v is unknown, this paper uses two classical probability models to generate it. One is the uniformly (UN) model. In this model, all edges are uniformly assigned the same influence propagation probability pu,v= 0.02 in experiments. The other is the weighted cascade (WC) model, in which pu,v is set to 1/dv, dv is the in-degree of node v. The parameter ε is set to 0.1 and the parameter l is set to 1 for SRIS and IMM, and the simulations of IC-PD are set to 10000. Since the running time of simulations increases with the number of nodes, this performance is unacceptable in practical applications. So the IC-PD algorithm is not compared in the Epinions and Slashdot datasets. To evaluate the effectiveness, after an algorithm returns the final seed set, 10,000 Monte Carlo simulations are performed on the selected seed set to obtain the average positive influence spread value as the final result.

5.2 The Results on the WikiElec Dataset

In this section, the effectiveness of the compared algorithms is evaluated on the WikiElec dataset under the UN and WC models, respectively. The results are shown in Figs. 4 and 5. The seed set size is 50 to 300, and the step is 50.

Figure 4: The results on the WikiElec dataset under the UN model

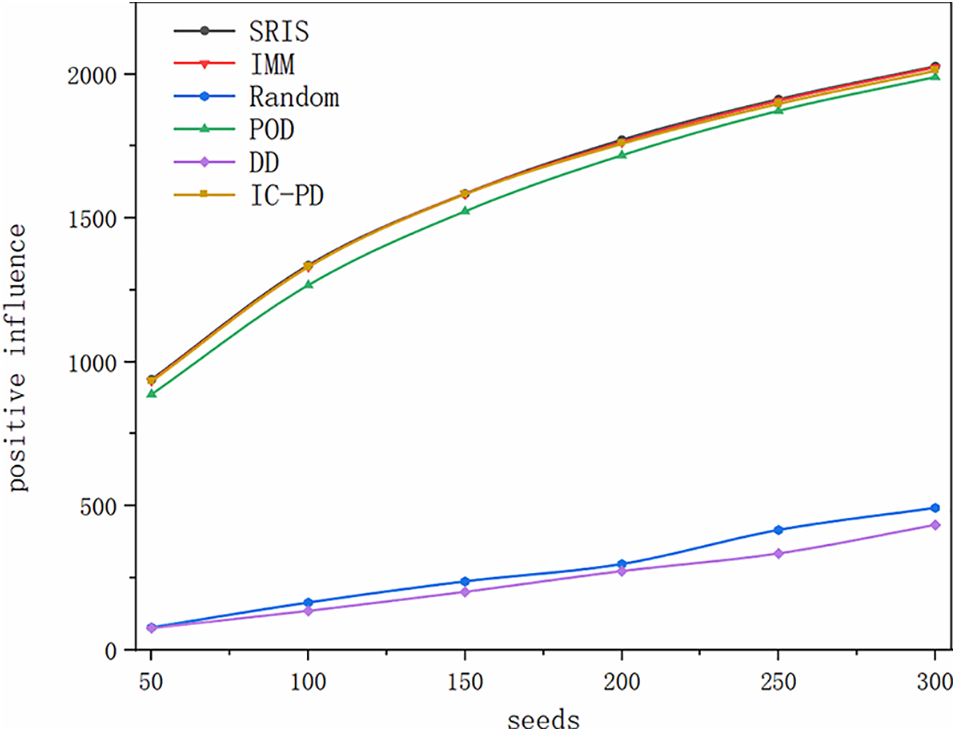
Figure 5: The results on the WikiElec dataset under the WC model

From Fig. 4, the observations are as follows. First, SRIS performs best, and DD and Random perform worst in all of the algorithms. Then, the positive influence increases as the increase of seed set size. The performance of SRIS, POD, IMM, and IC-PD almost overlap when the seed set size is 50, and differences gradually appear as the number of seeds increases. When the number of seeds is enlarged to 300, the performance of SRIS is the highest among all algorithms.

Fig. 5 shows that the results are similar to those under the UN model. Besides, due to the non-uniform probabilities on the edges between nodes, the performance of the POD algorithm is inferior to the SRIS, IC-PD, and IMM algorithms. Although the curves of the SRIS, IC-PD, and IMM algorithms overlap significantly, the SRIS algorithm has the highest performance among all algorithms when the number of seeds is 300.

5.3 The Results on the Epinions Dataset

In this section, the effectiveness of the compared algorithms is evaluated on the Epinions dataset under the UN and WC models, respectively. The seed set size is 5 to 25, and the step is 5. Figs. 6 and 7 show the results under the UN and WC models, respectively.

Figure 6: The results on the Eponions dataset under the UN model

Figure 7: The results on the Eponions dataset under the WC model

As shown in Fig. 6, the RIS algorithm has the best performance, followed by the POD algorithm. Although the IMM algorithm is a RIS based algorithm, the positive influence spread of RIS is much lower than that of the SRIS algorithm. The reason is that the IMM algorithm does not consider the polar relations of nodes, and the selected seeds with the most influence may not have the most positive influence. The DD algorithm has lower performance than the IMM algorithm, since it is heuristic and cannot guarantee the quality of the selected seeds. The Random algorithm is the worst since it has too much randomness and cannot ensure that the selected seeds have a largely positive influence.

It can also be seen that the SRIS algorithm performs best in Fig. 7. Although the POD algorithm performs better than IMM in the UN model, it performs worse than IMM in the WC model. The reason lies in that the POD algorithm is a heuristic algorithm that selects the seeds with the maximum out degree, so it is not robust and sensitive to the network structure. So, the performance of the POD algorithm decreases quickly as the increase of the number of seeds.

5.4 The Results on the Slashdot Dataset

In this section, the same parameters are set on the Slashdot dataset as on Epinions. The performance of compared algorithms is shown in Figs. 8 and 9 under the UN and WC models, respectively.

Figure 8: The results on the Slashdot dataset under the UN model

Figure 9: The results on the Slashdot dataset under the WC model

Fig. 8 shows that the results are similar to those on the Epinions dataset under the UN model. The POD algorithm performs similarly to the SRIS algorithm and outperforms the IMM algorithm. The Random algorithm performs worst due to the high randomness of selecting seed nodes. The DD algorithm did not consider the polarity relationship on the edges and only achieved better results than the Random algorithm. From Fig. 9, it is further confirmed the effectiveness of the SRIS algorithm, e.g., its positive influence value is about 24.7% larger than POD and 32.1% larger than IMM when the number of seed set size is 25.

In conclusion, it is clear from the above analysis that the SRIS algorithm has a better performance in effectiveness than other baseline algorithms. Although the IMM is also a RIS based algorithm, its performance is lower than SRIS. Since it does not consider the polar relations of nodes in the signed social network, i.e., the seeds with the largest influence for IM may not be the optimal seeds with the largest positive influence for PIM. POD performs similarly to SRIS under the UN model, but its performance is much lower than that of the WC model. Although it selects seeds with maximum out degrees of nodes, the initial influence propagation probability on edges is different for the UN and WC models, so the performance POD is sensitive to the structure of the network. It can also be seen that the effectiveness of DD and Random algorithms is much lower than other compared algorithms in all experiments because these two algorithms are too simple to guarantee the performance of the selected seeds.

6  Conclusion

This paper focuses on solving the PIM problem in signed social networks. Firstly, a new influence propagation model called IC-PD is proposed, which incorporates the positive influence caused by negative nodes and accounts for information decay during influence propagation. This approach aligns with the intuition that “friends of my enemies are my enemies” and “enemies of my enemies are my friends.” To solve the PIM problem, this paper presents a greedy based algorithm, and further proposes the SRIS algorithm to overcome the low efficiency of the greedy algorithm. The SRIS algorithm consists of two phases: sampling and node selection. In the sampling phase, the IC-PD model is used in conjunction with the RIS method to generate a PRR set. A binary search algorithm is then performed to determine the number of necessary PRR sets. In the node selection phase, the greedy coverage method is used to select the optimal seeds. Experiments on three real-world signed social datasets demonstrate the SRIS algorithm has better performance in effectiveness than other baseline algorithms, and is suitable for solving the PIM problem.

Although the SRIS algorithm currently only runs on signed social networks, it can be easily extended to multi-entity competitive networks. Additionally, SRIS still has some limitations that deserve future studies. Firstly, it is important to investigate the support of dynamic networks since real-world social networks are continually changing. Secondly, since the SRIS algorithm currently only works on the IC-PD model, it will be investigated in other influence propagation models in the future. Finally, additional attributes such as location or time will be considered to better align with real-world applications.

Funding Statement: This work is supported by the Youth Science and Technology Innovation Personnel Training Project of Heilongjiang (No. UNPYSCT-2020072), the Fundamental Research Funds for the Universities of Heilongjiang (Nos. 145109217, 135509234), the Education Science Fourteenth Five-Year Plan 2021 Project of Heilongjiang (No. GJB1421344) and the Innovative Research Projects for Postgraduates of Qiqihar University (No. YJSCX2022048).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. P. Domingos and M. Richardson, “Mining the network value of customers,” in Proc. of the 7th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, New York, NY, USA, pp. 57–66, 2001. [Google Scholar]

2. C. Borgs, M. Brautbar, J. Chayes and B. Lucier, “Maximizing social influence in nearly optimal time,” in Proc. of the 25th Annual ACM-SIAM Symp. on Discrete Algorithms, Portland, Oregon, USA, pp. 946–957, 2014. [Google Scholar]

3. D. Kempe, J. Kleinberg and É. Tardos, “Maximizing the spread of influence through a social network,” in Proc. of the 9th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, New York, NY, USA, pp. 137–146, 2003. [Google Scholar]

4. W. Chen, Y. Wang and S. Yang, “Efficient influence maximization in social networks,” in Proc. of the 15th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, New York, NY, USA, pp. 199–208, 2009. [Google Scholar]

5. J. Leskovec, A. Krause, C. Guestrin, C. Faloutsos, J. VanBriesen et al., “Cost-effective outbreak detection in networks,” in Proc. of the 13th ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, New York, NY, USA, pp. 420–429, 2007. [Google Scholar]

6. A. Goyal, W. Lu and L. Lakshmanan, “CELF++: Optimizing the greedy algorithm for influence maximization in social networks,” in Proc. of the 20th Int. Conf. Companion on World Wide Web, New York, NY, USA, pp. 47–48, 2011. [Google Scholar]

7. Y. Tang, Y. Shi and X. Xiao, “Influence maximization in near-linear time: A martingale approach,” in Proc. of the 2015 ACM SIGMOD Int. Conf. on Management of Data, New York, NY, USA, pp. 1539–1554, 2015. [Google Scholar]

8. H. M. Huang, H. Shen, Z. Q. Meng, H. J. Chang and H. W. He, “Community-based influence maximization for viral marketing,” Applied Intelligence, vol. 49, no. 6, pp. 2137–2150, 2019. [Google Scholar]

9. Y. P. Chen, Q. Qu, Y. X. Ying, H. Y. Li and J. L. Shen, “Semantics-aware influence maximization in social networks,” Information Sciences, vol. 513, no. 1, pp. 442–464, 2020. [Google Scholar]

10. W. Liu, Y. Li, X. Chen and J. He, “Maximum likelihood-based influence maximization in social networks,” Applied Intelligence, vol. 50, no. 11, pp. 3487–3502, 2020. [Google Scholar]

11. W. M. Li, Z. Li, A. Onjeniko and C. Yang, “Influence maximization algorithm based on Gaussian propagation model,” Information Sciences, vol. 568, pp. 386–402, 2021. [Google Scholar]

12. D. Li, Z. M. Xu, N. Chakraborty, A. Gupta, K. Sycara et al., “Polarity related influence maximization in signed social networks,” PLoS One, vol. 9, no. 7, pp. 238–248, 2014. [Google Scholar]

13. D. Li, C. H. Wang, S. P. Zhang, G. L. Zhou, D. H. Chu et al., “Positive influence maximization in signed social networks based on simulated annealing,” Neurocomputing, vol. 260, no. 6, pp. 69–78, 2017. [Google Scholar]

14. M. Hosseini-Pozveh, K. Zamanifar, A. R. Naghsh-Nilchi and P. Dolog, “Maximizing the spread of positive influence in signed social networks,” Intelligent Data Analysis, vol. 20, no. 1, pp. 199–218, 2016. [Google Scholar]

15. W. Liu, X. Chen, B. Jeon, L. Chen and B. Chen, “Influence maximization on signed networks under independent cascade model,” Applied Intelligence, vol. 49, no. 3, pp. 912–928, 2019. [Google Scholar]

16. X. Y. Yin, X. Hu, Y. J. Chen, X. Yuan and B. C. Li, “Signed-PageRank: An efficient influence maximization framework for signed social networks,” IEEE Transactions on Knowledge and Data Engineering, vol. 33, no. 5, pp. 2208–2222, 2019. [Google Scholar]

17. W. J. Ju, L. Chen, B. Li, W. Liu, J. Sheng et al., “A new algorithm for positive influence maximization in signed networks,” Information Sciences, vol. 512, no. 1, pp. 1571–1591, 2020. [Google Scholar]

18. J. Sheng, L. Chen, Y. X. Chen, B. Li and W. Liu, “Positive influence maximization in signed social networks under independent cascade model,” Soft Computing, vol. 24, no. 19, pp. 14287–14303, 2020. [Google Scholar]

19. Q. He, L. H. Sun, X. W. Wang, Z. K. Wang, M. Huang et al., “Positive opinion maximization in signed social networks,” Information Sciences, vol. 558, no. 2, pp. 34–49, 2021. [Google Scholar]

20. D. Li, Y. J. Wang, M. H. Li, X. Sun, J. C. Pan et al., “Net positive influence maximization in signed social networks,” Journal of Intelligent & Fuzzy Systems, vol. 41, no. 2, pp. 3821–3832, 2021. [Google Scholar]

21. L. S. Alla and A. S. Kare, “Opinion maximization in signed social networks using centrality measures and clustering techniques,” in Proc. of the 19th Int. Conf. of Distributed Computing and Intelligent Technology, Bhubaneswar, India, pp. 125–140, 2023. [Google Scholar]

22. S. Tu, S. U. Rehman, S. M.Waqas, O. U. Rehman, Z. Yang et al., “Optimisation-based training of evolutionary convolution neural network for visual classification applications,” IET Computer Vision, vol. 14, no. 5, pp. 259–267, 2020. [Google Scholar]

23. S. Iqbal and Z. Halim, “Orienting conflicted graph edges using genetic algorithms to discover pathways in protein-protein interaction networks,” IEEE Transactions on Computational Biology and Bioinformatics, vol. 18, no. 5, pp. 1970–1985, 2021. [Google Scholar] [PubMed]

24. S. Tu, M. Waqas, S. U. Rehman, T. Mir, Z. Halim et al., “Social phenomena and fog computing networks: A novel perspective for future networks,” IEEE Transactions on Computational Social Systems, vol. 9, no. 1, pp. 32–44, 2022. [Google Scholar]

25. H. Peng, C. Qian, D. Zhao, M. Zhong, J. Han et al., “Targeting attack hypergraph networks,” Chaos, vol. 32, no. 7, pp. 073121, 2022. [Google Scholar] [PubMed]

26. W. Chen, Network diffusion models and algorithms for big data. Beijing, China: Tech Science Press, pp. 78–96, 2020. [Google Scholar]