 Open Access
Open Access
ARTICLE
A Novel Parallel Computing Confidentiality Scheme Based on Hindmarsh-Rose Model
1 School of Computing, Engineering and the Built Environment, Edinburgh Napier University, Edinburgh, EH10 5DT, UK
2 Department of Information Systems, College of Computer Science and Information Systems, Najran University, Najran, 61441, Saudi Arabia
3 Department of Computer Science, College of Computer Science and Information Systems, Najran University, Najran, 61441, Saudi Arabia
4 Department of Computer Science, Al Ain University, Abu Dhabi, 112612, United Arab Emirates
5 School of Science, Technology and Health, York St John University, York, YO31 7EX, UK
6 Research Centre for Intelligent Healthcare, Coventry University, Coventry, CV1 5FB, UK
* Corresponding Author: Jawad Ahmad. Email:
Computers, Materials & Continua 2023, 76(2), 1325-1341. https://doi.org/10.32604/cmc.2023.040858
Received 01 April 2023; Accepted 29 May 2023; Issue published 30 August 2023
Abstract
Due to the inherent insecure nature of the Internet, it is crucial to ensure the secure transmission of image data over this network. Additionally, given the limitations of computers, it becomes even more important to employ efficient and fast image encryption techniques. While 1D chaotic maps offer a practical approach to real-time image encryption, their limited flexibility and increased vulnerability restrict their practical application. In this research, we have utilized a 3D Hindmarsh-Rose model to construct a secure cryptosystem. The randomness of the chaotic map is assessed through standard analysis. The proposed system enhances security by incorporating an increased number of system parameters and a wide range of chaotic parameters, as well as ensuring a uniform distribution of chaotic signals across the entire value space. Additionally, a fast image encryption technique utilizing the new chaotic system is proposed. The novelty of the approach is confirmed through time complexity analysis. To further strengthen the resistance against cryptanalysis attacks and differential attacks, the SHA-256 algorithm is employed for secure key generation. Experimental results through a number of parameters demonstrate the strong cryptographic performance of the proposed image encryption approach, highlighting its exceptional suitability for secure communication. Moreover, the security of the proposed scheme has been compared with state-of-the-art image encryption schemes, and all comparison metrics indicate the superior performance of the proposed scheme.Keywords
Chaos is a ubiquitous phenomenon in nature, and nonlinear science heavily relies on the study of chaos. Chaos theory, with its fundamental characteristics such as system unpredictability, parameter sensitivity, pseudo-randomness, and others, has found applications in various precise disciplines. In recent years, the practical advantages of chaos theory have gained significant attention. Chaos theory has numerous practical uses, including in the secure transmission of multimedia data. Specifically, when data is exchanged over the Internet. Images of national defense and private information are just two examples of a few private images that must be communicated securely [1–3]. When it comes to protecting sensitive data, encryption is crucial. The two most common older methods for encrypting data are the Data Encryption Standard (DES) and the Advanced Encryption Standard (AES). The high correlation among neighbouring pixels in digital images is one distinguishing feature; the relative insensitivity to change is another; minor adjustments to pixel values do not lead to noticeably different images from those already in the database [4–6]. Hence, standard encryption approaches are unsuitable for image data encryption due to their time complexity etc. A plethora of image security solutions has been proposed in the literature [7–9] to address the aforementioned issue. High-speed encryption, complexity, strong security, and a manageable computer resource overhead are all features of chaos-based secure communication. For real-world use cases, it can be adopted for image and text encryption.
Ye et al. [10] proposed that diffusion and confusion are the two main building blocks of image encryption. Diffusion refers to the connection between the unencrypted text and the encrypted representation of it. The efficacy of an encryption method increases if even a small shift in the initial image falls out into a noticeable shift in the enciphered image. In this context, “confusion” refers to the connection between the hidden key and the ciphertext representation. When making slight changes to the encryption key, resulting in noticeably different encrypted images, it is generally accepted that the encryption is highly secure.
The role that chaos plays in cryptography is also influenced by its characteristics. Mutually continuous-time and discrete-time chaotic maps can be distinguished from the mathematical model description of chaotic systems. There are many common models of continuous-time chaotic systems, but two of the most common are the Lorenz system and the Chen system. Arnold maps, logistic maps, sine maps, and Henon maps are examples of models for discrete chaotic systems. Another methodology for categorizing chaotic systems distinguishes between systems with integer forms and systems with fractional forms. The model of a fractional system is more general. Hénon-Lozi type maps [11], for example, are examples of recently proposed typical fractional chaotic maps that display a rich complicated dynamic behaviour. After proposing a hyperchaotic fractional Grassi-Miller map in [12], the authors proceed to implement it in hardware. A chaotic map with fractional order is presented and investigated in [13]. Several books and articles discuss the utilization of chaos for image encryption.
A fast and secure image encryption system was proposed by Khennaoui et al. [14], and it makes use of a 1D chaotic map. The composition of a 1D chaotic system is straightforward, even though the key space is very small. When it comes to protecting images, 1D chaotic maps provide advantages such as increased speed and simpler hardware implementation. Chaotic encryption research excels in the field of image encryption due to the synergy between effective chaotic systems and challenging encryption approaches. In [9], a sine trigonometric function and tent map are utilized to propose a discrete chaotic system. The statistical behaviour is consistent over a large range of parameter values. Piecewise linear chaotic mapping and a trigonometric function were used by Liu et al. [15] to create the chaotic mapping. Li et al. [16] discussed a nonlinear dynamic system that includes a cosine function and finds that it has a lengthy chaotic interval and resilient chaotic qualities. The inverse of a trigonometric function is likewise a trigonometric function because trigonometric functions have unique qualities such as periodicity and boundedness. A 1D piecewise chaotic map and the bisection approach were presented for image encryption in [17]. Elghandour et al. [18] employed a hyperchaotic model to produce a pseudo-random sequence, which they subsequently encrypted using a combination of scrambling and diffusion. Gopalakrishnan et al. [19] generated a new 1D chaotic model using the Beta function and applied it to image encryption; they called their proposal the Beta chaotic map. Zahmoul et al. [20] proposed an innovative image cryptosystem that employs a hybrid chaotic system by combining two 1D chaotic maps. The pseudo-orbits of one-dimensional chaotic systems are employed as the key in an innovative encryption method presented by Alawida et al. [21]. Nepomuceno et al. [22] designed and implemented a one-dimensional sine-powered chaotic map for image encryption. As part of an effective symmetric image encryption scheme, Mansouri et al. [23] proposed a novel 2D chaotic map to expand the available key space. Using a 2D economic chaotic map and a logistic map, Huang et al. [24] devised a method for encrypting images. Askar et al. [25] propose an innovative method of encryption that uses keys generated from either DNA or an image of plaintext. Khan et al. [26] introduced an S-Box and logistic-sine scheme for image encryption.
The research discussed above has led to the proposal of secure cryptosystems. However, it is worth noting that many of these proposals may suffer from either insecurity or impracticality issues, primarily related to time complexity. Therefore, considering the time cost as a crucial factor, we focused on improving the efficiency of the system. To achieve better security, we employed a simple chaotic map available, which exhibits high randomness.
Many encryption algorithms do not offer strong security against classical cryptographic attacks [27–29]. The cryptanalysis of many recently proposed cryptosystems has increased the risk of sensitive information being lost. Therefore, by considering all the weaknesses carefully, we have constructed a secure encryption algorithm to provide image security. We have proposed a multiplication and diffusion-based encryption strategy based on the Hindmarsh-Rose chaotic model [1]. The key generation process is secured by the SHA-256 hashing algorithm. The proposed technique employs an image’s associated encryption key as a substitute for the traditional encryption key, which increases security and reduces the amount of time it takes to decrypt data [30,31]. The encryption method combines a scrambling process with a diffusion process.
The subsequent sections of this manuscript are organised as follows: Section 2 offers a comprehensive analysis of the Hindmarsh-Rose model; Section 3 discusses the construction of the proposed model. In the next two sections, we have shown simulation outcomes and performance analysis, respectively. Finally, the conclusion with some future recommendations is presented in the last section.
The Hindmarsh-Rose model is a mathematical representation of the spiking-bursting behaviour detected in research with single neurons [1]. It focuses on the membrane potential, represented by the dimensionless variable
where
To find the equilibrium points, we set the derivatives in the above equations to zero and solve for
where x is the membrane potential, y and z are the gating variables for the two potassium currents, a, b, c, d,
We will use the following parameter values for the stability analysis:
To determine the fixed points of the model, we solve the equations
To examine the stability of the fixed points, compute the Jacobian matrix J evaluated at each fixed point. The Jacobian matrix is given by:
where
Fixed point 1:
The real part of all eigenvalues is negative, so the fixed point is stable.
Fixed point 2:
One eigenvalue has a positive real part, so the fixed point is unstable.
Fixed point 3:
The real part of both eigenvalues is negative, so the fixed point is stable.
Therefore, we have one unstable fixed point and two stable fixed points. This means that the system can exhibit different types of behaviour depending on the initial conditions. If the initial conditions are near the unstable fixed point, the system will diverge and exhibit chaotic behaviour. If the initial conditions are instead near a stable fixed point, the system will converge towards that point and exhibit stable behaviour. The behaviour of a dynamical system is largely determined by its fixed points, which are values of the system’s variables that do not change over time. Stable fixed points act as attractors, pulling the system towards them, while unstable fixed points act as repellers, pushing the system away from them.
2.2 Simulation of Hindmarsh–Rose Neuron
To examine the execution of the Hindmarsh-Rose model we have performed simulations based on different times. The spiking-bursting behaviour findings are explained in Fig. 1.
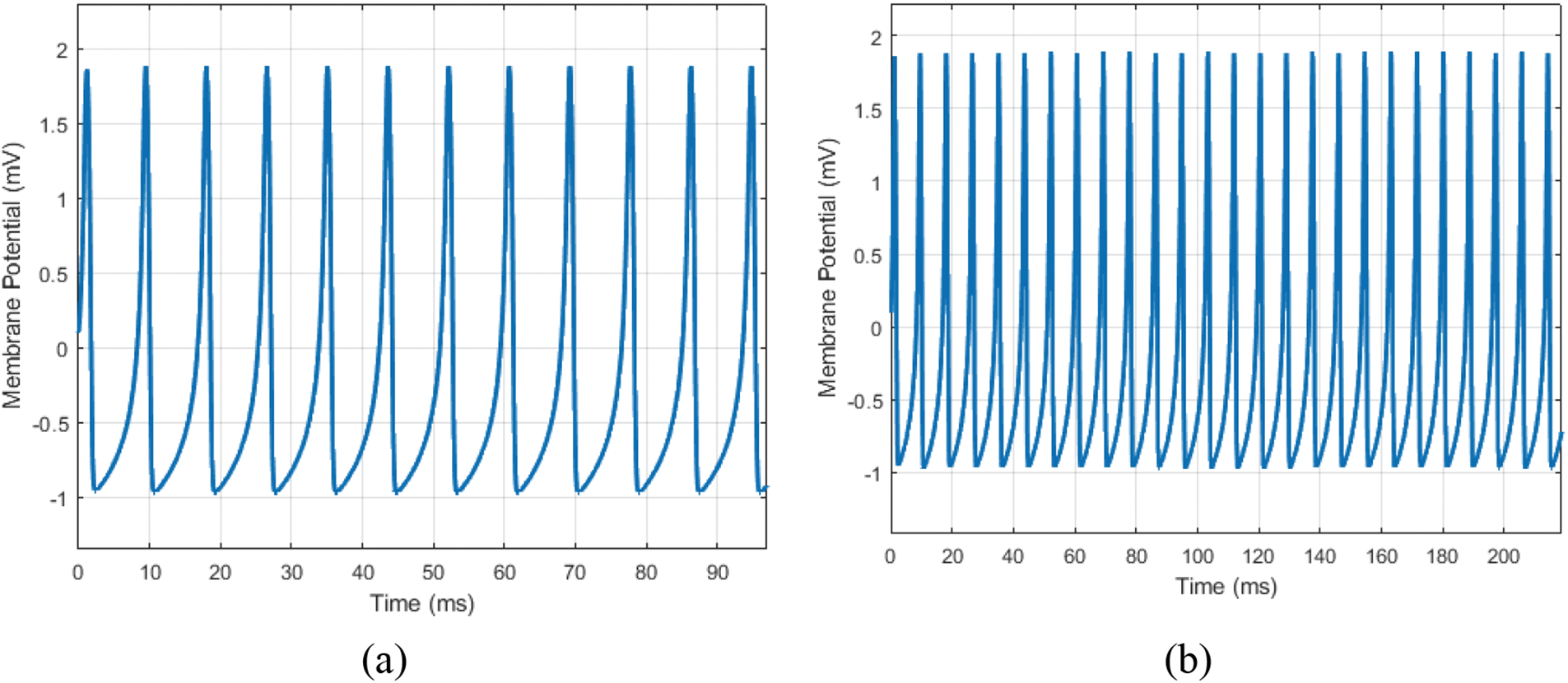
Figure 1: Hindmarsh-Rose neuron model for (a) 100-time span; (b) 220-time span
The National Institute of Standards and Technology (NIST) developed a widely used suite of tests for measuring the random behaviour of time series. Each sequence being evaluated is 1,000,000 bits in length, hence testing many sequences is necessary. Random performance of time series may be measured with the help of the p-value. The standard deviation is set to = 0.01. We produced 500 chaotic real number categorizations, individually with a length of 125,000 real numbers, to assess the stochastic recital of sequences produced using the chaotic map. For the NIST evaluation, one hundred sequences of length one million bits are obtained. Table 1 summarizes our experimental findings and comparative results with the existing chaotic map. Each p-value is bigger than 0.01, and the run test has a minimum pass rate of 96%, as can be seen from the test outcome. All chaotic sequences created by system (1) have been shown to pass the NIST test in experiments.
In this section, we have proposed a novel image encryption scheme. The security of the encryption entirely varies on the input of the encryption algorithm. The proposed encryption approach comprises two sub-algorithms named key generation and encryption/decryption processes defined in detail below:
The initial conditions and the key parameters of the proposed encryption algorithm are generated by inserting the input image in the SHA-256 algorithm. The results generated from SHA-256 are utilized as key parameters of the Hindmarsh-rose chaotic model. The first step was using the SHA-2 256 hash method to get the encryption key from the hash of the plaintext picture. The initial state value of the chaotic Hindmarsh-Rose system was determined by dividing the hash string into four parts, each of which was then mapped to a decimal larger than 0 and less than 1.
3.2 Encryption/Decryption Process
In this study, the colour digital image is encrypted by combining the operation of diffusion and invertible matrix multiplication generated from the Hindmarsh chaotic map. The notion of secure key generation from SHA-256 makes the encryption secure against statistical attacks. The major operations involved in the cryptosystem are matrix multiplication and diffusion. The array for diffusion is generated from the Hindmarsh-Rose model. The arrays constructed for the matrices are filtered through the inverse operation to make the decryption possible. The steps of the proposed encryption are as follows:
Step 1: The size of the input image is
Step 2: The layers of the plain image are separated into red, green, and blue channels.
Step 3: Each layer is divided into blocks of
Step 4: The invertible matrices generated from the Hindmarsh-rose model are then multiplied with the plain image matrices, respectively.
Step 5: The multiplicated results are then diffused with the key arrays generated from the Hindmarsh-Rose model.
Step 6: The resultants are then concatenated as cipher images.
The decryption of the ciphertext is performed in the same step in a reverse manner. The detailed working strides of the decryption process are as follows:
Step 1: The cipher image of size
Step 2: Inverse diffusion is applied to the layer of the cipher image.
Step 3: The resultant from Step 2 is then multiplied with the inverse of the private key constructed from the Hindmarsh-Rose model.
Step 4: The outcome layers from Step 3 are then combined into one plain image.
The working mechanism of the proposed encryption work is shown in Fig. 2.
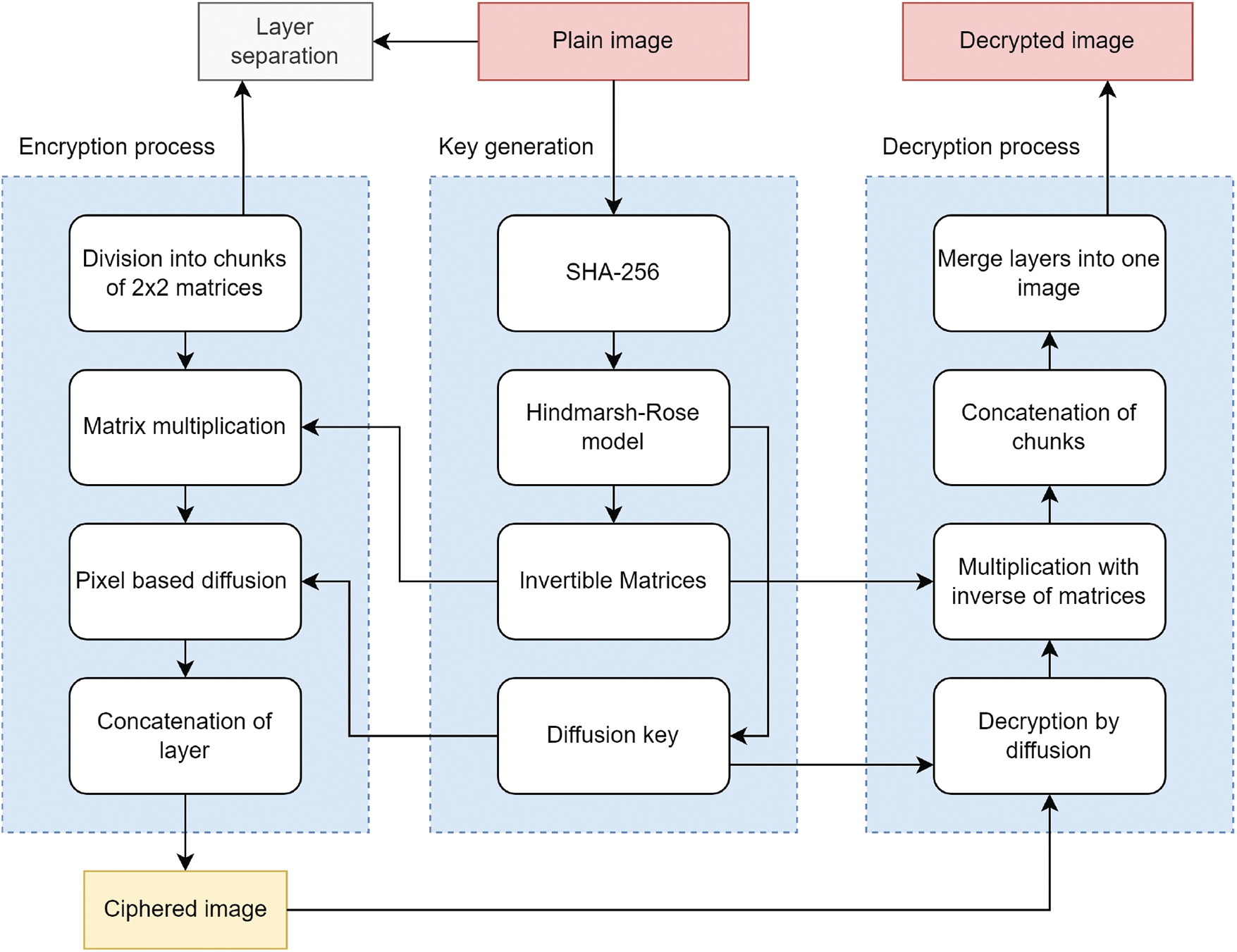
Figure 2: The flowchart of the proposed scheme
To examine the implementation of the proposed cryptosystem, we have applied the encryption process over some standard colour images. The images of Baboon, Parrots, Peppers, and Tulip with sizes

Figure 3: Plain images of (a) Baboon; (b) Parrots; (c) Peppers; (d) Tulip; (e–h) respective cipher images
5 Security Performance Analyses
The security evaluation of any cryptosystem is essential to claim the quality performance of an image encryption scheme. Therefore, to assess the robustness, we analysed several image encryption metrics. The results of several metrics are listed below.
The histogram of an image provides a visual representation of how the image’s pixel values are distributed. Plaintext images typically exhibit non-normal distribution shapes in their histograms. The histograms of an encrypted image should be uniformly distributed for higher security. The statistical histograms of Baboon, Parrots, Peppers, and Tulip test images and their enciphered counterparts are displayed in Fig. 4.
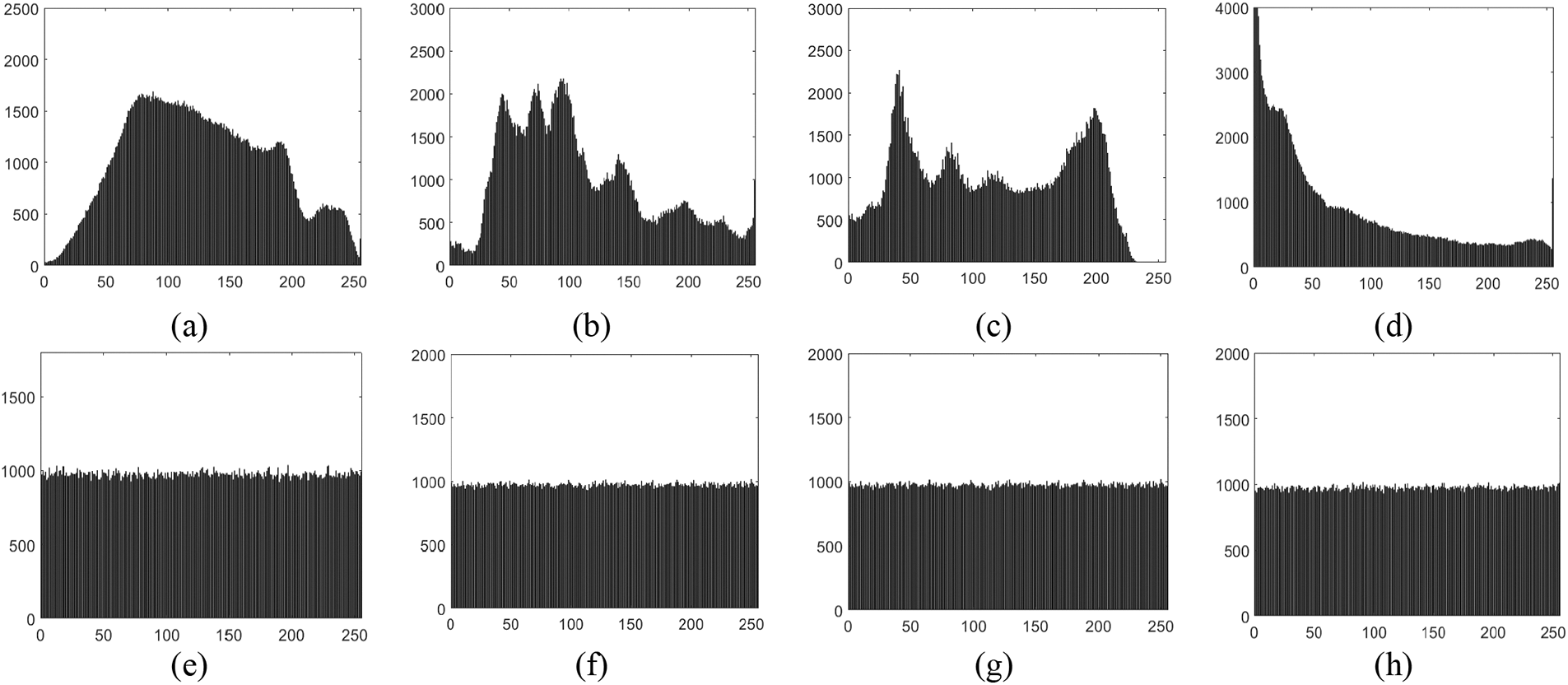
Figure 4: Histogram of Baboon, Parrots, Peppers, Tulip (a–d) original (e–h) encrypted images correspondingly
The horizontal coordinates in Fig. 4 represent pixel value and the vertical coordinate denotes the frequency occurrence of each pixel. The histograms of the encrypted and plaintext versions of the image are very different from one another. The histogram of the enciphered ciphertext image is normally dispersed, even though the histogram of the plain image was not. Consequently, the encrypted image is secure against attacks based on statistical analysis.
Furthermore, we can use the Chi-square test to quantify the histogram’s uniformity distribution. The Chi-square
where n denotes the number of grayscale levels in the image,
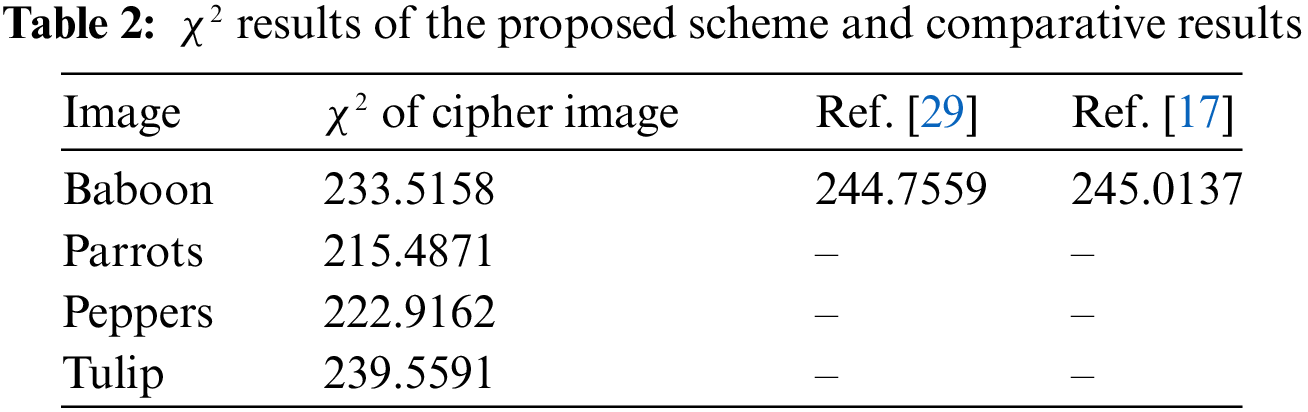
From Table 2, the Chi-square results of all the enciphered images are smaller than the crucial value. However, the Chi-square estimate of enciphered images produced by our proposed work is lower than that of similarly prepared images from other encryption schemes.
There is a strong correlation among neighbouring pixels in meaningful plaintext images. As such, a strong encryption method needs to be able to break the link among adjacent pixels. A correlation coefficient provides a quantitative calculation of the degree to which neighbouring pixels are correlated with one another. In this work, we used the correlation coefficient, a measure for examining the degree to which neighbouring image pixels share common characteristics.
where
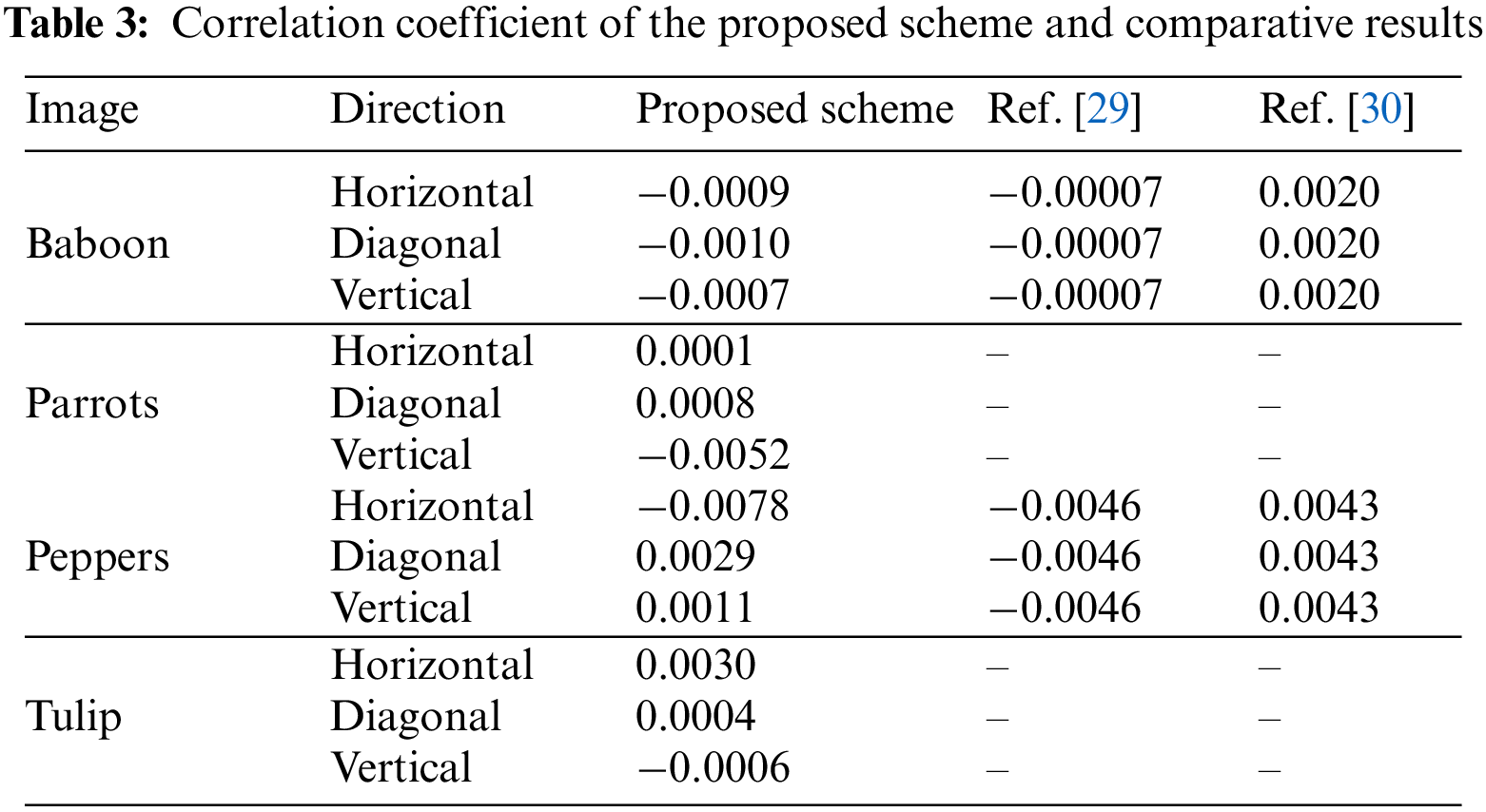
The comparison outcomes are shown in Table 3. The proposed approach yields good results, especially when compared to state-of-art techniques. In this study, we present a method that utilizes the Hindmarsh Rose model to create confusion and diffusion among pixels.
Fig. 5 plots the distribution of neighbouring pixel values for the Parrots, making it easy to see how their values are related to one another. Fig. 5 shows that, in the original Parrots image, neighbouring points are typically distributed along or around the 45-degree line, signifying that the estimates of nearby pixels are the same or very similar. Yet, there is a significant variance in value between neighbouring pixels, as seen by the fact that the ciphertext image’s adjacent points are not centred on the 45-degree line. As a result, the image’s pixel correlation is essentially broken by the encryption technique.
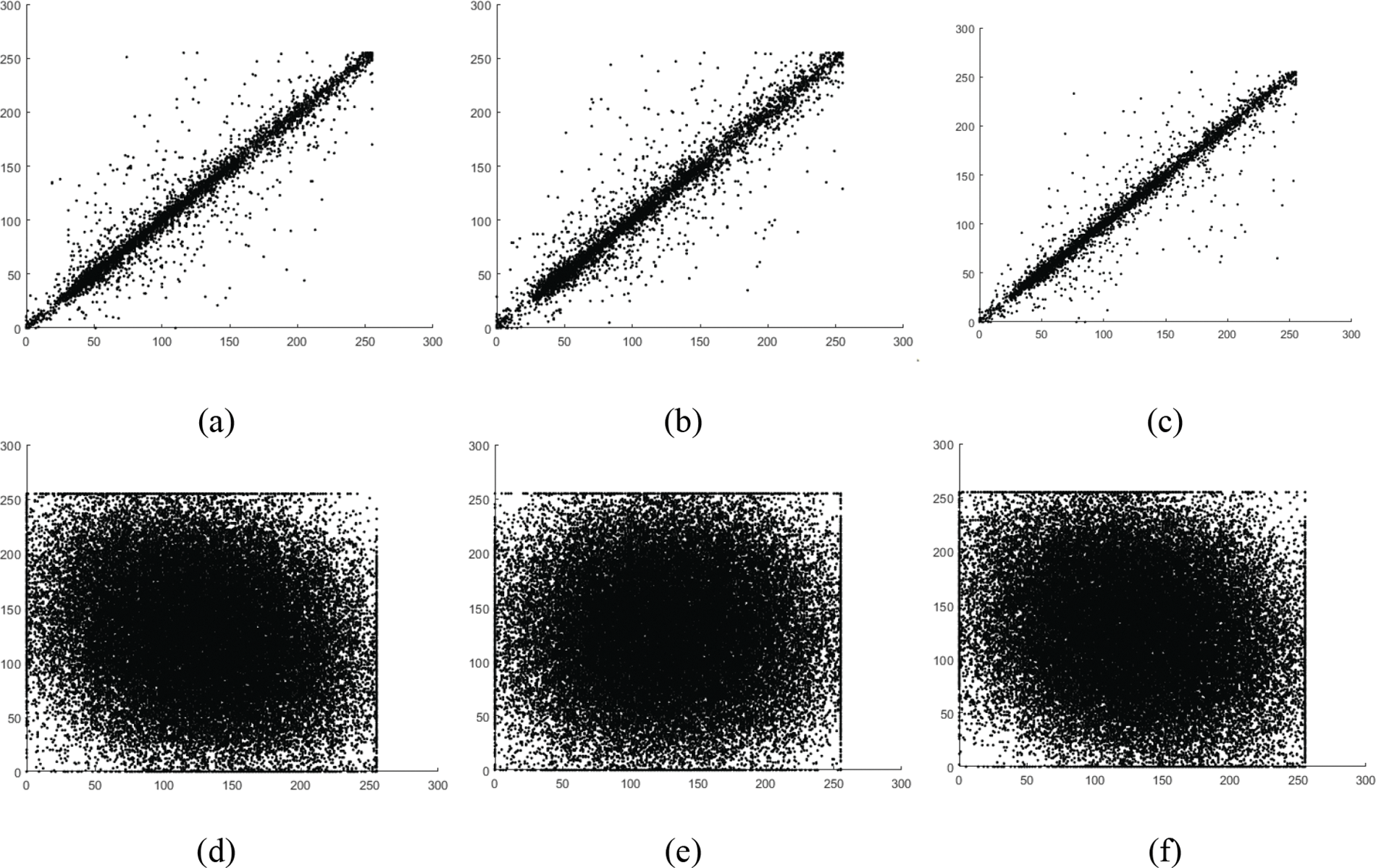
Figure 5: Parrots image correlation diagram (a–c) plain; (d–f) enciphered in horizontal, diagonal, and vertical paths correspondingly
Information entropy can be utilized to calculate how unpredictable or random data is. The greater the information entropy, the more difficult it is to forecast or understand the underlying information. The following formula may be used to determine an information source’s entropy:
where
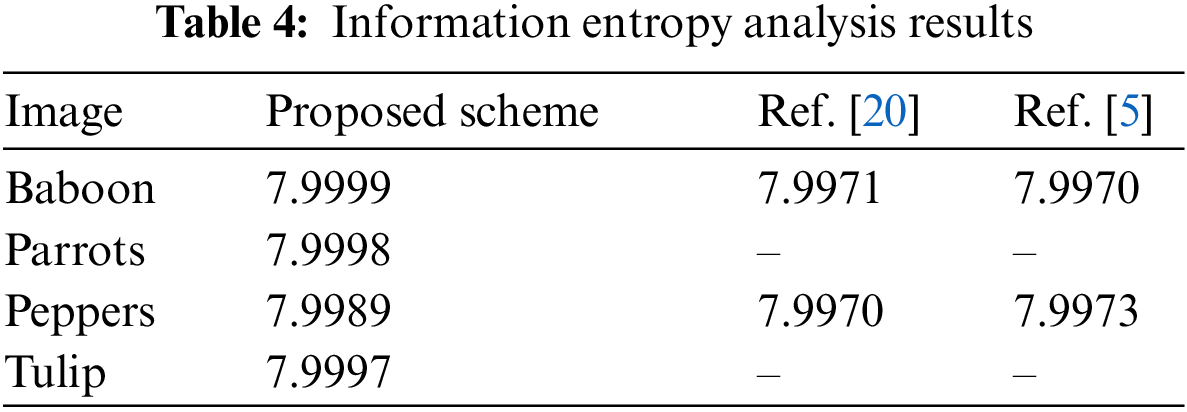
The results demonstrate that ciphertext image information entropy is quite near to the maximum value and hence the proposed scheme is secure against entropy attack.
5.5 Differential Attack Analysis
The strong sensitivity of the ciphertext to the plaintext and the secret keys is a feature of an effective encryption algorithm. A comparison of the enciphered image’s sensitivity to the original image or secret keys can be carried out with either NPCR or UACI. Mathematically, NPCR and UACI are written as:
where M and N refer to the image’s row and column coordinates. The sensitivity of the encryption technique is relative to the square root of the product of NPCR and UACI. An NPCR of 99.6094% and a UACI of 33.4635% are considered good for image encryption.
After comparing the UACI and NPCR values of two different enciphered images for the key sensitivity study, we found that the respective encryption keys differed by just one parameter on the order of

Through, key space analysis, one can analyse the total number of possible keys. In this study, the parameters and starting results of the chaotic model are the original keys to the algorithm. Eleven parameters of double precision
In evaluating our algorithm’s efficacy, we utilize MSE and PSNR. The MSE shows how far off the target image is from the original. MSE is measured as:
where
where

While transmitting encrypted images, a good encryption technique should be able to deal with a certain amount of data loss. A visually recognizable decrypted image may be recovered even when noise or data loss corrupts the encrypted image, demonstrating the algorithm’s resilience.
To evaluate the algorithm’s robustness against data loss, we first encrypt a

Figure 6: Cipher image of Baboon with a black chunk of (a)
The proposed approach encrypts data in three distinct steps: generating Hindmarsh-Rose chaotic secret key streams, encryption of pixels using invertible matrices, and pixel diffusion carried by bitwise XOR operation. As part of the algorithm’s time-cost analysis, we encrypt and decrypt a 256-by-256 grayscale Baboon image. Table 7 displays the average encryption and decryption times (in seconds) from some different studies. Table 7 also includes statistics on the time cost of several chaos-based algorithms taken from recently published work. The outcomes show that the proposed method is quicker at both encrypting and decrypting than the methods discussed in [30,31].

5.10 Classical Cryptanalysis Attack
The strength of the proposed encryption scheme can be measured by evaluating it against classical cryptanalysis attacks. When the system is subjected to the chosen plaintext or chosen ciphertext attack then the attacker might try to insert some images trying to recover the private keys from the system. As the proposed encryption scheme utilized the algorithm of SHA-256 based on the input of the algorithm, therefore, the output against each image would be different. Therefore, the proposed structure can resist all types of classical attacks due to its nature of the complex design.
In this study, we present a novel three-dimensional Hindmarsh-Rose model-based cryptosystem that demonstrates significant chaotic behaviour across a wide range of parameters. The proposed encryption method is mainly based on chaos theory and offers suitability for real-time encryption. To assess the effectiveness of the model, we utilized standard measures commonly employed in chaos theory. During the testing phase of our proposed scheme, we observed robust chaotic behaviour across various parameter values. Furthermore, we employed the chaotic map to create a faster and more secure image encryption technique. This proposed image encryption approach combines multiplication and diffusion operations, effectively merging permutation and substitution into a single step. As a result, the proposed scheme achieves efficiency and enhanced security compared to the conventional encryption algorithms. Performance analysis of the proposed encryption algorithm demonstrates that it satisfies numerous ideal values across different measures. Moreover, the algorithm successfully passes all security tests along with low computational complexity. We tested the proposed image encryption technique using extensive simulation and experimental tests, which confirmed its suitability for real-time applications. Additionally, we plan to apply the proposed method to encrypt audio and video data in the future. Our forthcoming research will focus on evaluating the effectiveness of the proposed encryption method on videos and audio.
Acknowledgement: The authors are thankful to the Deanship of Scientific Research at Najran University for funding this work under the Research Groups Funding Program Grant Code (NU/RG/SERC/12/3).
Funding Statement: The authors are thankful to the Deanship of Scientific Research at Najran University for funding this work under the Research Groups Funding Program Grant Code (NU/RG/SERC/12/3).
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. R. Barrio, S. Ibáñez and L. Pérez, “Hindmarsh–Rose model: Close and far to the singular limit,” Physics Letters A, vol. 381, no. 6, pp. 597–603, 2017. [Google Scholar]
2. A. Atangana and I. Koca, “Analytical and numerical investigation of the Hindmarsh-Rose model neuronal activity,” Mathematical Biosciences and Engineering, vol. 20, no. 1, pp. 1434–1459, 2023. [Google Scholar] [PubMed]
3. S. Zhang, L. Liu and H. Xiang, “A novel plain-text related image encryption algorithm based on LB compound chaotic map,” Mathematics, vol. 9, no. 21, pp. 1–25, 2021. [Google Scholar]
4. D. S. Malika and T. Shah, “Color multiple image encryption scheme based on 3D-chaotic maps,” Mathematics and Computers in Simulation, vol. 178, pp. 646–666, 2020. [Google Scholar]
5. I. Ö. Ztürk and R. Kılıç, “Utilizing true periodic orbits in chaos-based cryptography,” Nonlinear Dynamics, vol. 103, pp. 2805–2818, 2021. [Google Scholar]
6. C. X. Zhu, “A novel image encryption scheme based on improved hyperchaotic sequences,” Optics Communications, vol. 285, pp. 29–37, 2012. [Google Scholar]
7. S. Zhu, G. Wang and C. Zhu, “A secure and fast image encryption scheme based on double chaotic S-boxes,” Entropy, vol. 21, pp. 790, 2019. [Google Scholar] [PubMed]
8. X. Chai, J. Fu, Z. Gan, Y. Lu and Y. Zhang, “An image encryption scheme based on multi-objective optimization and block compressed sensing,” Nonlinear Dynamics, vol. 108, pp. 2671–2704, 2022. [Google Scholar]
9. G. Ye, M. Liu and M. Wu, “Double image encryption algorithm based on compressive sensing and elliptic curve,” Alexandria Engineering Journal, vol. 61, pp. 6785–6795, 2022. https://doi.org/10.1016/j.aej.2021.12.023 [Google Scholar] [CrossRef]
10. G. Ye, H. Wu, M. Liu and Y. Shi, “Image encryption scheme based on blind signature and an improved lorenz system,” Expert Systems with Applications, vol. 205, pp. 117709, 2022. https://doi.org/10.1016/j.eswa.2022.117709 [Google Scholar] [CrossRef]
11. C. E. Shannon, “A mathematical theory of communication,” Bell System Technical Journal, vol. 27, pp. 379–423, 1948. [Google Scholar]
12. A. Ouannas, A. A. Khennaoui, X. Wang, V. T. Pham, S. Boulaaras et al., “Bifurcation and chaos in the fractional form of Hénon-Lozi type map,” The European Physical Journal Special Topics, vol. 229, pp. 2261–2273, 2020. [Google Scholar]
13. A. Ouannas, A. A. Khennaoui, T. E. Oussaeif, V. T. Pham, G. Grassi et al., “Hyperchaotic fractional Grassi–Miller map and its hardware implementation,” Integration, vol. 80, pp. 13–19, 2021. [Google Scholar]
14. A. A. Khennaoui, A. Ouannas, S. Boulaaras, V. T. Pham and A. T. Azar, “A fractional map with hidden attractors: Chaos and control,” The European Physical Journal Special Topics, vol. 229, pp. 1083–1093, 2020. [Google Scholar]
15. L. Liu and S. Miao, “A new simple one-dimensional chaotic map and its application for image encryption,” Multimedia Tools and Applications, vol. 77, pp. 21445–21462, 2018. [Google Scholar]
16. Y. Li, X. Li and X. Liu, “A fast and efficient hash function based on generalized chaotic mapping with variable parameters,” Neural Computing and Application, vol. 28, pp. 1405–1415, 2016. [Google Scholar]
17. W. Yu and T. Yu, “Analysis of chaotic characteristics of trigonometric function system,” Modern Physics Letters B, vol. 34, pp. 2050210, 2020. [Google Scholar]
18. A. N. Elghandour, A. M. Salah, Y. A. Elmasry and A. A. Karawia, “An image encryption algorithm based on bisection method and one-dimensional piecewise chaotic map,” IEEE Access, vol. 9, pp. 43411–43421, 2021. [Google Scholar]
19. T. Gopalakrishnan and S. Ramakrishnan, “Image encryption using hyper-chaotic map for permutation and diffusion by multiple hyper-chaotic maps,” Wireless Personal Communications, vol. 109, pp. 437–454, 2019. [Google Scholar]
20. R. Zahmoul, R. Ejbali and M. Zaied, “Image encryption based on new beta chaotic maps,” Optics and Lasers in Engineering, vol. 96, pp. 39–49, 2017. [Google Scholar]
21. M. Alawida, A. Samsudin, J. S. The and R. S. Alkhawaldeh, “A new hybrid digital chaotic system with applications in image encryption,” Signal Processing, vol. 160, pp. 45–58, 2017. [Google Scholar]
22. E. G. Nepomuceno, L. G. Nardo, J. A. Garcia, D. N. Butusov and A. Tutueva, “Image encryption based on the pseudo-orbits from 1D chaotic map,” Chaos, vol. 29, pp. 061101, 2019. [Google Scholar] [PubMed]
23. A. Mansouri and X. Wang, “A novel one-dimensional sine powered chaotic map and its application in a new image encryption scheme,” Information Science, vol. 520, pp. 46–62, 2020. [Google Scholar]
24. H. Huang, S. Yang and R. Ye, “Efficient symmetric image encryption by using a novel 2D chaotic system,” IET Image Processing, vol. 14, pp. 1157–1163, 2020. [Google Scholar]
25. S. Askar, A. Karawia, A. A. Khedhairi and F. A. Ammar, “An algorithm of image encryption using Logistic and two-dimensional chaotic economic maps,” Entropy, vol. 21, pp. 44, 2019. [Google Scholar] [PubMed]
26. J. S. Khan, W. Boulila, J. Ahmad, S. Rubaiee, A. U. Rehman, et al., “DNA and plaintext dependent chaotic visual selective image encryption,” IEEE Access, vol. 8, pp. 159732–159744, 2020. [Google Scholar]
27. Q. Lu, C. Zhu and X. Deng, “An efficient image encryption scheme based on the LSS chaotic map and single S-Box,” IEEE Access, vol. 8, pp. 25664–25678, 2020. [Google Scholar]
28. S. Zhu and C. Zhu, “Security analysis, and improvement of an image encryption cryptosystem based on bit plane extraction and multi chaos,” Entropy, vol. 23, pp. 505, 2021. [Google Scholar] [PubMed]
29. S. Zhu and C. Zhu, “An efficient chosen-plaintext attack on an image fusion encryption algorithm based on DNA operation and hyperchaos,” Entropy, vol. 23, pp. 804, 2021. [Google Scholar] [PubMed]
30. S. Zhu, X. Deng, W. Zhang and C. Zhu, “Image encryption scheme based on newly designed chaotic map and parallel DNA coding,” Mathematics, vol. 11, pp. 231, 2023. [Google Scholar]
31. H. Zang, M. Tai and X. Wei, “Image encryption schemes based on a class of uniformly distributed chaotic systems,” Mathematics, vol. 10, no. 7, pp. 1–27, 2022. [Google Scholar]
32. S. Zhu, X. Deng, W. Zhang and C. Zhu, “A new one-dimensional compound chaotic system and its application in high-speed image encryption,” Applied Sciences, vol. 11, no. 23, pp. 11206, 2021. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF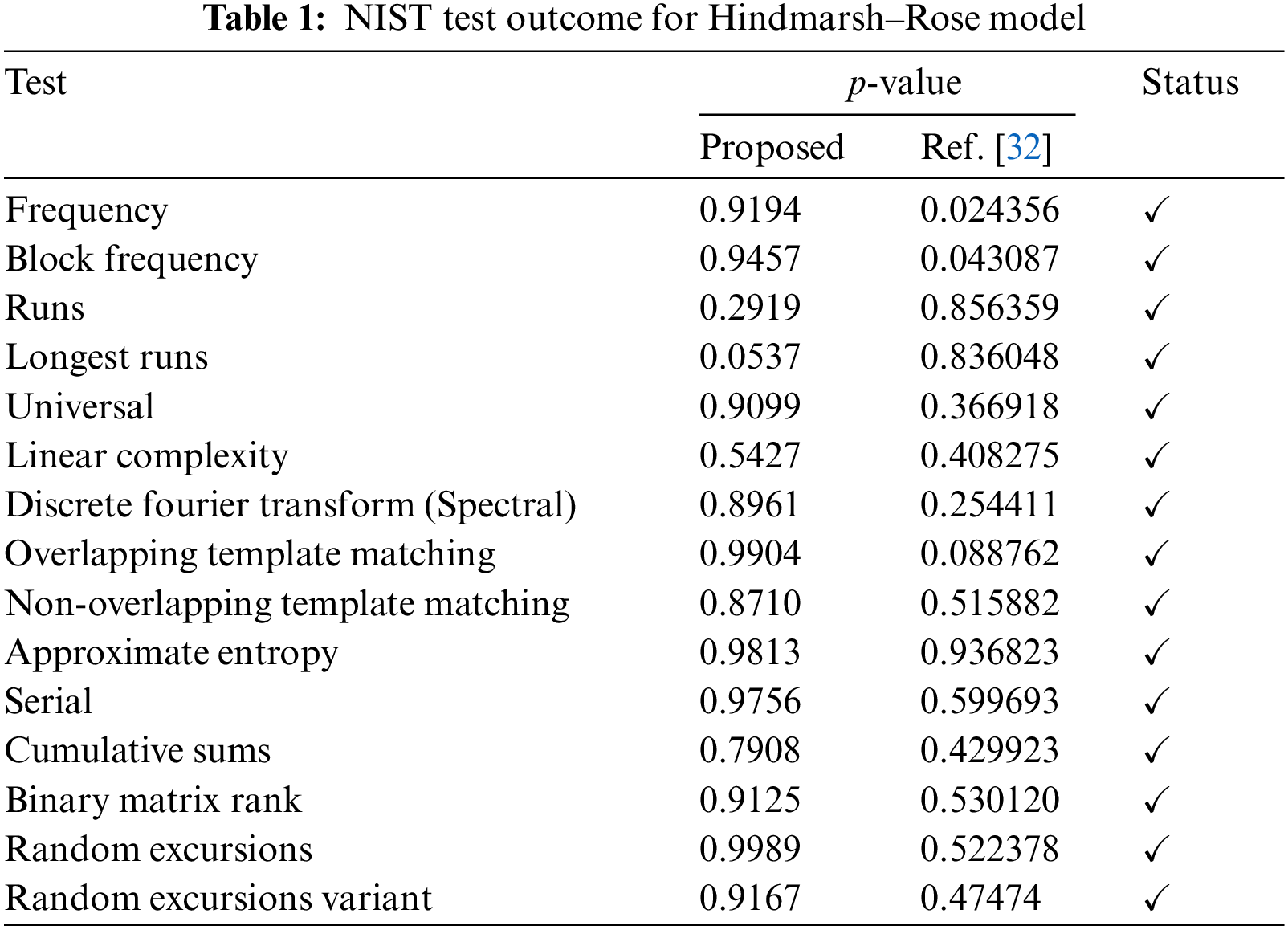
 Downloads
Downloads
 Citation Tools
Citation Tools