A Hybrid Heuristic Service Caching and Task Offloading Method for Mobile Edge Computing

1  Introduction

The boom in IoT technology has led to significant demand for managing a large number of devices and a massive amount of data. The total number of mobile subscribers exceeded 7 billion in 2016 around the world [1]. The IoT Analytics report on IoT platforms released in 2019 predicts that there will be more than 22 billion active IoT devices worldwide by 2025. At the same time, more and more advanced IoT applications are emerging, such as artificial intelligence [2], federal learning [3], and autonomous driving [4], and they are confronted with a huge amount of data needed to be processed every moment. By using traditional cloud computing for serving user requests, first, services are deployed on the cloud. Then, IoT devices collect data and transmit collected data to the cloud for centralized processing, and eventually receive processed results from the cloud [5]. This centralized service mode tends to spend a lot of time on data transmission, which will inevitably cause prolonged user response time and thus reduce the quality of service (QoS) and quality of experience (QoE) [6].

To address these issues, mobile edge computing (MEC) has been proposed as a new paradigm. The core idea of MEC is to deploy small service nodes (i.e., edge servers, edge for short) with a certain storage capacity and computing power close to the data sources, to improve the efficiency of system operation. Relying on service applications cached at edge servers, tasks generated by mobile devices can be partially assigned to the edge servers for execution. Such a working model greatly extends the caching and computing capabilities of traditional cloud computing and increases the flexibility and security of the system. Meanwhile, the close physical communication distance can provide a high-bandwidth and low-latency network environment for data transfers between devices and processing nodes, which can largely help some latency-sensitive tasks avoid high network latency caused by long-distance communication. Based on these advantages, MEC is considered as one of the key technologies that can solve the challenges faced by future hyper-scale networks [7].

As a core problem of MEC, the task offloading problem has been extensively and profoundly studied by many scholars. The optimal task offloading problem can be attributed to offloading the proper task to the proper computational node at the proper time. The task offloading problem has been proven as an NP-hard problem [8]. An unreasonable task offload strategy has the potential to cause a series of problems such as computational conflicts, wasted resources, and increased task response times, which will irreparably affect the QoS and QoE. A well-designed task offloading scheme helps to improve the efficiency of MEC [9], but has some challenges. In a MEC environment, edge servers are geographically distributed and usually have large-scale. In addition, each edge server has limited computational capacity and storage capacity of these servers. These realities increase the complexity of task offloading. Besides, load balancing is also a key issue in task offloading due to the varying number and location of mobile devices [10]. Task allocation needs to consider the workload of edge servers, and a balanced workload helps to fully utilize the computational resources of the MEC.

To address the above challenges, in [11], the researchers focused on a joint optimization strategy for task scheduling and resource utilization in a distributed training environment. They first formally defined the joint optimization problem as a mixed nonlinear integer optimization problem, and then solved it using a random rounding approximation algorithm to maximize the system throughput. Wang et al. [12] proposed a particle swarm optimization algorithm based on integer coding to search for the optimal scheduling decision to maximize the number of tasks to be completed within the deadline and the resource utilization. Kong et al. [13] proposed a classification-based task offloading method. Firstly, the service level information of all servers is integrated into global information. Then, these servers were classified by the K-means method. Finally, based on the classification results, a suitable server was filtered for the latest requests to provide a secure, low-energy, and low-latency computing environment. Chen et al. [14] proposed a task offloading method for ultra-dense networks, to optimize energy consumption and latency. They formulated the problem as a mixed integer nonlinear programming, and solved it by decomposing it into two subproblems, task allocation, and resource allocation. Gao et al. [15] investigated computational task offloading strategies for deep neural networks in MEC environments, to reduce energy consumption. They established an evaluation model for time and energy consumption, and used a particle swarm optimization algorithm to solve the problem. This work was able to fully optimize the end device energy consumption while satisfying the time constraints.

These above studies have an assumption that all services are available at the edge, which requires edge servers have unlimited cache capacity, which is not possible in reality. User requests can only be processed by edge servers that have cached their required services [16]. Therefore, ignoring the service caching when seeking a task offloading solution will potentially lead to problems such as task execution blocking or failure of the offloading solution.

Therefore, some works studied the service caching problem of MEC. Zhang et al. [17] and Wei et al. [18] focused on the caching strategy that pre-cached services by a predictive approach to improve the cache hit rate. Xia et al. [19] quantified the gain of one decision by comparing the hops of obtaining the data, and selecting the decision with the greater gain among the candidate decisions as the caching decision. However, when there are too many services, the method of selecting candidate decisions is not flexible enough, which may affect the performance of the system. Liu et al. [20] modeled the service placement problem in a MEC environment as a multi-objective optimization problem, and used the cuckoo search algorithm to solve the problem. Their work achieved a good performance in terms of energy consumption and response time. Reference [21] searched for a service placement strategy in MEC environments by using genetic algorithm, to improve network utilization, energy consumption and cost. Reference [22] used the whale optimization algorithm to find an efficient service placement solution, trying to increase the throughput and reduce the energy consumption of MEC. Reference [23] proposed a two-stage edge caching strategy. They used a deep neural network to predict the services in the cache selection stage to improve the cache hit rate, and used the branch and bound algorithm in the service placement stage to obtain the optimal solution for the reduction of power consumption and latency. References [17–23] only considered the solution for cache prediction and service placement, without concerning the task offloading.

In this paper, we focus on task offloading for MEC. In addition, we consider the impact of MEC’s caching mechanism on the task processing, to improve the efficiency of MEC and ensure the availability of task offloading decisions. Our main contributions are as follows.

•   We propose a task offloading model considering edge caching mechanisms. We incorporate the caching information of the edge servers into the task offloading model, with the cache space constraints of these edge servers. We model the task offloading problem as a mixed integer nonlinear programming problem to minimize the execution time of the tasks.

•   We design an integer particle swarm optimization and improved genetic algorithm (IPSO_IGA). In IPSO_IGA, a task offloading solution, i.e., a set of tasks offloading decisions, corresponds to a particle position. The particles update their positions using the crossover operator. In addition, IPSO_IGA maintains the particle diversity by an improved mutation operator.

•   We conduct simulation experiments to evaluate our proposed task offloading method. The parameters of IPSO_IGA were set referring to recent related works and realities. The experimental results show that our method can save 20%–82% of the response time, compared with other algorithms. In addition, our method achieves the highest cache hit ratio and the best load balance and can be applied to scenarios with a large number of users.

The rest of this paper is organized as follows. Section 2 formulates the task offloading problem we concern about. Section 3 describes the IPSO_IGA based task scheduling method in detail. Section 4 evaluates the performance of IPSO_IGA by simulated experiments and analyses the experimental results. Section 5 concludes the paper and presents our outlook.

2  Problem Formulation

2.1 Resource and Task Model

The MEC environment consists of a device tier, an edge tier, and a cloud tier [24], as shown in Fig. 1. In MEC, users offload their tasks from their local devices to the edge and cloud tiers. Different types of tasks require different services, such as, image rendering tasks are processed by corresponding image rendering applications. If the service application required for a task is not cached at an edge server, the task cannot be processed by the edge server. In this paper, we focus on independent tasks, which are commonly found in parallel distributed systems [25]. The notations used in this paper are shown in Table 1.

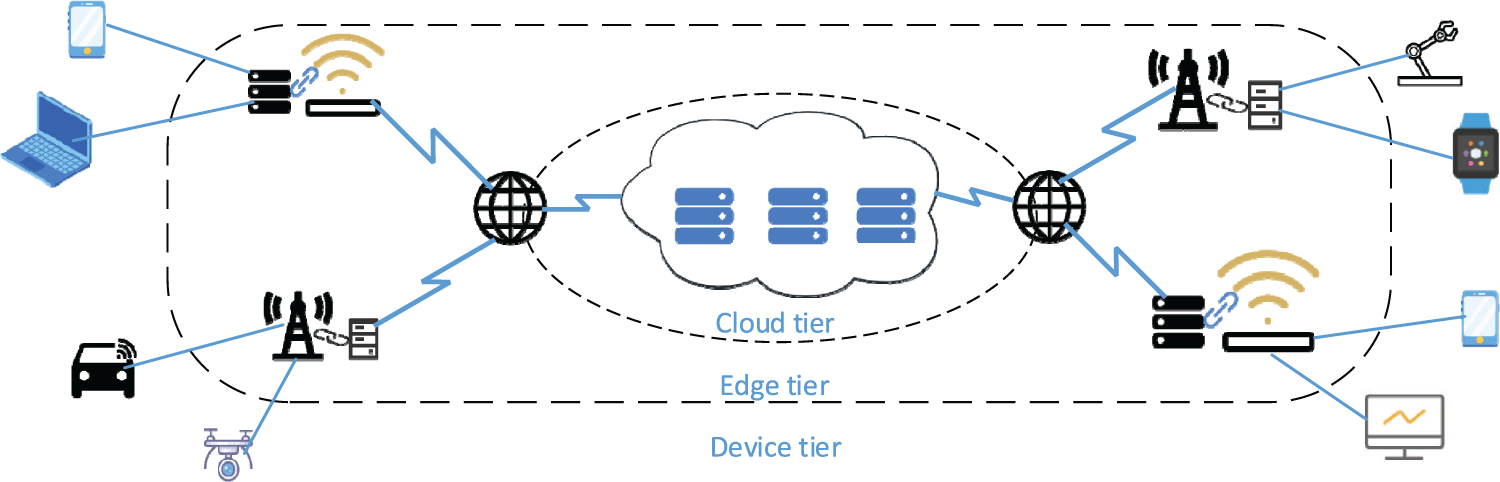
Figure 1: The architecture of MEC

Assume that there are p services provided in the MEC, expressed by the set 𝒯𝒴, 𝒯𝒴={P1,P2,⋯,Pp}. The cache space occupied by each service can be mapped one-to-one to the set 𝒫𝒮={H1,H2,⋯,Hp}, where the function h(Px)=Hx is used to describe the mapping. For example, the cache space occupied by the service P1 is H1 (in MB), which can be expressed as h(P1)=H1. There are e edge servers in MEC. All edge servers form the set ℰ𝒮, ℰ𝒮={E1,E2,⋯,Ee}.Use Ei=⟨si,ni,gi⟩ to define the parameters of the ith edge server, where si denotes the storage capacity of the edge server (in GB), ni denotes the core number of this edge server, and gi denotes the computing power of each core (quantified in the form of frequency, GHz). The computing power of the edge server is denoted by W. Then

Wi=ni×gi(1)

Use a queue ℒi to represent the cache list of Ei. At a certain moment, Ei caches a certain number of services, which can be denoted as ℒi=(Pxhead,Py,⋯,Pztail), where x,y,⋯,z∈[1,p] and x≠y≠⋯≠z (x,y,⋯,z is a local variable for each edge server). The superscript head and tail indicate the head and tail elements of the queue, respectively. In addition, ℒi should also satisfy the following constraints:

∀Ei∈ℰ𝒮,Hx+Hy+⋯+Hz≤si(2)

Which indicates that the total space occupied by all cached services cannot exceed the physical storage space for each edge server.

The cloud servers are usually deployed as a cluster or data center far away from users, over the internet. So, they can be considered as one node/server to simplify the model. The cloud server is defined as C=⟨sc,nc,gc⟩, where nc and gc represent the number of cores and the frequency of each core, respectively. Similar to edge servers, the computing power of the cloud server can be expressed as

Wc=nc×gc(3)

The cloud server can be assumed that has ∞ cache space for deploying all services in the MEC, so the cache list of the cloud server can be expressed as ℒc=(P1,P2,⋯,Pp).

There are d mobile devices in the MEC, which are represented by ℳ𝒟={D1,D2,⋯,Dd}. At the initial time, each mobile device generates a set of tasks waiting to be processed. The jth mobile device generates ρj tasks, denoted by ℛ={rj,1,rj,2,⋯,rj,ρj}. Each task requires a certain service for its processing, where f(r)=P is given to reflect this requirement information. For example, f(rj,k)=Pi means that the kth task of the jth mobile device requires service Pi.

2.2 Network and Computational Model

Data is transmitted between mobile devices and servers over various communications and networks, and the bandwidth between them is denoted as

DS=(a1,1⋯a1,e+1⋮⋱⋮ad,1⋯ad,e+1)(4)

where the row subscripts of the matrix elements indicate mobile devices, and the column subscripts indicate edge and cloud servers. When the column subscript is e + 1, the elements indicate the bandwidth between mobile devices and the cloud server. For example, aj,i(i≤e) denotes the bandwidth between Dj and Ei, aj,e+1 denotes the bandwidth between Dj and the cloud server C. If aj,i=0, it means that the current mobile device is not covered by the signal of Ei, and thus has no connection with the server.

The bandwidth between the edge servers and the cloud server is represented by a vector ℰ𝒞, expressed as ℰ𝒞=[b1b2⋯be]⊤, where bi denotes the bandwidth between Ei and the cloud server C.

When a mobile device generates k tasks to be offloaded, the kth task can start offloading only after the k-1th task complete its offloading. Then when task rj,k is offloaded to Ei for execution, the offloading completion time Uj,k of the task can be expressed as

Uj,k=Tj,k+ζj,kaj,i(5)

where Tj,k denotes the start offloading time of task rj,k, ζj,k denotes the input size of the task. Meanwhile, the start offloading time between adjacent tasks has to meet the constraint of the following formula

Tj,k=Tj,k−1+ζj,k−1aj,i∗(6)

The above formula indicates that the start offloading time of the kth task is the offloading completion time of the k-1th task. aj,i∗ denotes the transmission bandwidth of the k-1th task. A task will start waiting to be executed after it has been offloaded to the server. As servers are usually multi-in and multi-out, they can receive multiple tasks’ requests simultaneously. To minimize the waiting time of the servers, the servers process tasks on a first in first out (FIFO) basis. The current task can only be carried out once the tasks that arrive earlier have been processed. Note that pre(rj,k) is the task that arrives at the server before the task rj,k, and the execution completion time of pre(rj,k) can be recorded as pre(Qj,k). Therefore, the starting execution time Vj,k of the task rj,k can be expressed as

Vj,k=max{pre(Qj,k),Uj,k}(7)

The above formula indicates that the execution start time of a task is the later one of the execution completion time of its previous task and its offloading completion time.

When a task reaches the executable time, we consider two different scenarios that the task is executed by the cloud server and an edge server, respectively. The cloud server works as a storage repository and distribution source for all services, and can cache all services. In other words, if a task is offloaded to the cloud, the service corresponding to the task can be provided directly by the cloud. So, there is no need to consider whether the cache is hit or not. Therefore, the execution completion time of a task when it is offloaded to the cloud can be expressed as

Qj,k=Vj,k+ηj,kWc(8)

where ηj,k denotes the computational length of the task (quantified in clock cycles) and Wc denotes the computing capacity of the cloud server.

When a task is offloaded to an edge server, there are two cases, which are the service has or not cached on the edge server. If the service cache does not hit or a version update is required, the edge server has to download the service from the cloud before executing the task. A binary variable N is used to indicate whether the cache hits.

Nj,k={1,f(rj,k)∈ℒi0,otherwise(9)

The above formula indicates that the task rj,k is offloaded to the edge server Ei for execution. If the service required by rj,k exists in the cache list of the edge server, then Nj,k=1 and the edge can execute the task directly. Otherwise, Nj,k=0, the edge downloads the service from the cloud server, and executes the task when the download finishes. Because of the limited cache space, edge Ei must consider whether the remaining cache space is sufficient when downloading the service. The server downloads the service directly if the cache space is sufficient (as in formula (10)).

si−∑P∈ℒih(P)≥h(f(rj,k))(10)

∑P∈ℒih(P) in the above formula represents the total storage space occupied by all services that Ei has cached. Newly downloaded services will be placed at the head of the cache list according to the least recently used (LRU) algorithm, i.e.,

f(rj,k)→f(rj,k)head(11)

When the remaining cache space on the edge server is not enough to place the new service, i.e.,

si−∑P∈ℒih(P)<h(f(rj,k))(12)

The LRU algorithm will iteratively remove the service Ptail at the tail of the cache list until the cache space satisfies formula (8) again. The time Mi,j,k consumed by Ei to download service f(rj,k) can be expressed by the following formula:

Mi,j,k=h(f(rj,k))bi(13)

where bi denotes the bandwidth between the edge server and the cloud server. Therefore, the total execution time of task rj,k can be expressed as

(1−Nj,k)×Mi,j,k+ηj,ksi(14)

Now, the execution completion time of task rj,k can be calculated by

Qj,k=Vj,k+(1−Nj,k)×Mi,j,k+ηj,ksi(15)

A server completed all the tasks assigned to it by the task offloading decision when it has executed the last task in the task list. We denote ri as the last task arriving at Ei. The time for Ei to complete all tasks is represented as Qi. The time taken by the cloud server to complete all tasks is represented as Qc. We use set ψ to represent the working time of all servers, ψ={Q1,Q2,⋯,Qe,Qc}. The maximum value in the set ψ is the time for all servers to complete all tasks, denoted by ψmax.

2.3 Problem Model

For the task rj,k, the symbol ωj,k is used to indicate the server it will be offloaded to. For example, ωj,k=Ei can be represented as task rj,k will be offloaded to edge server Ei for execution. As one of the most crucial factors affecting QoS, the task execution time is tried to be optimized as much as possible in this paper. Therefore, the task offloading problem solved in this paper can be summarized as follows: finding a suitable server for each task to be executed, and making the completion time ψmax as early as possible. A complete set of offloading decisions is represented by vector Ω=(ω1,1⋯ω1,ρ1⋯ωd,1⋯ωd,ρd)⊤, where the subscript d denotes the number of mobile devices and ρd denotes the number of tasks generated by mobile device Dd. Based on the definitions and formulas mentioned in this section, the formal definition of the problem is given as

min(ψmax)(16)

s.t.Formula (1)–(15)

This problem is a mixed integer nonlinear programming problem. When the problem scale is large, exact algorithms cannot solve the problem within a reasonable time complexity. In recent research progress, for solving such problems, most scholars have focused on swarm intelligence and evolutionary algorithms. In the next section, we design a hybrid metaheuristic algorithm IPSO_IGA to solve the problem.

3  IPSO_IGA Based Task Offloading Algorithm

IPSO_IGA is based on the framework of particle swarm optimization (PSO) algorithm, and combines the crossover and mutation operations of genetic algorithm (GA). Firstly, IPSO_IGA initializes the particle swarm using integer encoding. Then, the crossover operator is used to move each particle toward the personal best position (pBest) and the global best position (gBest). Finally, a mutation operator based on gene frequency improvement is used for the particles to further optimize the algorithm performance.

3.1 Integer Encoding and Decoding

In IPSO_IGA, a task offloading solution Ω corresponds to a particle position. The number of dimensions of a particle is Dim. Firstly, all mobile devices in the MEC are encoded as integers, starting from 1 to d. Then, all tasks are also encoded by integers. The tasks of the 1st mobile device are encoded from 1 to ρ1 (the 1st mobile device generated ρ1 tasks), the tasks of the 2nd mobile device are encoded from ρ1+1 to ρ1+ρ2 (the 2nd mobile device generated ρ2 tasks), and so on. The last task is encoded as ∑i=1dρi=dim. That is, the number of tasks is equal to the number of dimensions Dim for each particle.

Then, all servers in the MEC are encoded. The coding for the cloud server is 0, and the coding for edge servers are from 1 to e. An illustration of how the devices and tasks are encoded is shown in Fig. 2. The squares next to the mobile devices represent the tasks they generated.

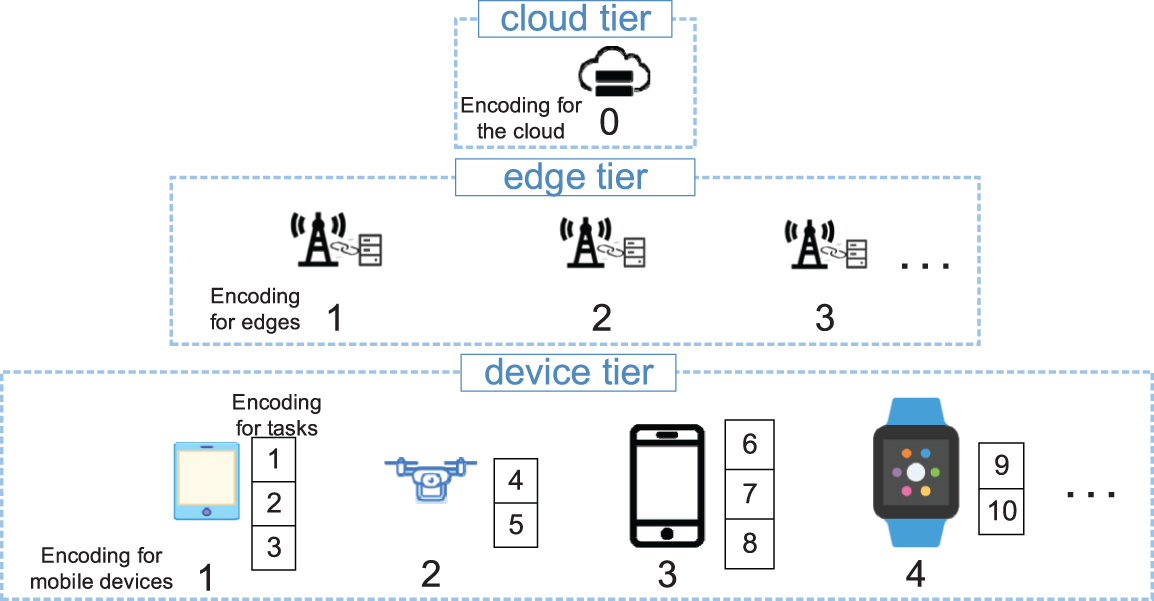
Figure 2: Integer encoding for devices and tasks

The value of each dimension (i.e., each task) in a particle is the code of the server. For example, if a task encoded as 5 is offloaded to a server encoded as 3, the value of the 5th dimension of the particle is 3 (note that if a mobile device is not covered by the signal of an edge server, the task cannot be offloaded to this edge server, and the code of this edge is an illegal value for this dimension). An illustration of particle encoding and decoding is shown in Fig. 3.

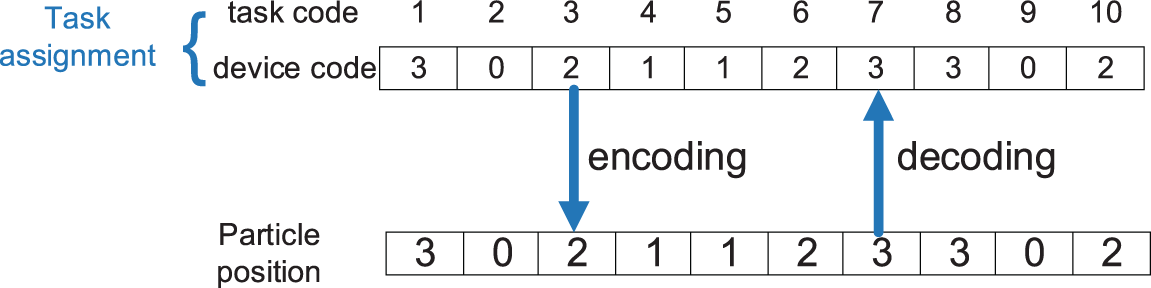
Figure 3: An illustration of a particle encoding

3.2 Initialization and Update of Particles

Based on the above encoding approaches, IPSO_IGA first generates a random set of particles and calculates the fitness of each particle. The particle fitness fit is represented by the execution time spent on task offloading decisions, i.e.,

fit=ψmax(17)

Our goal is to minimize the fit. For each particle, pBest is used to record the personal best position of the particle. When a particle is initialized, pBest records the current position of the particle. gBest is recoding the best position among all particles. During the particle movement, if a particle moves to a position better than its pBest, update its pBest. After all of the particles have moved once (called one iteration), the gBest is updated as the new best position of all pBest. Traditional PSO uses algebraic calculations to optimize the particle positions. However, in the problem studied in this paper, the value of each dimension of the particle is a code and has no numerical significance. Therefore, the algebraic calculation may not move a particle to a better position. Based on the above considerations, IPSO_IGA takes inspiration from the genetic algorithm and uses the crossover operator to move the particles toward pBest and gBest. Specifically, a particle is first compared with pBest to find all the different points (i.e., dimensions or genes) and records them. Among these points of pBest, the particle selects a part of them randomly to copy from pBest to itself. Then, in the same way, the particle is compared with gBest and a part of the genes from gBest is copied to itself. The crossover operator is shown in Fig. 4, where the blue shading marks the different points.

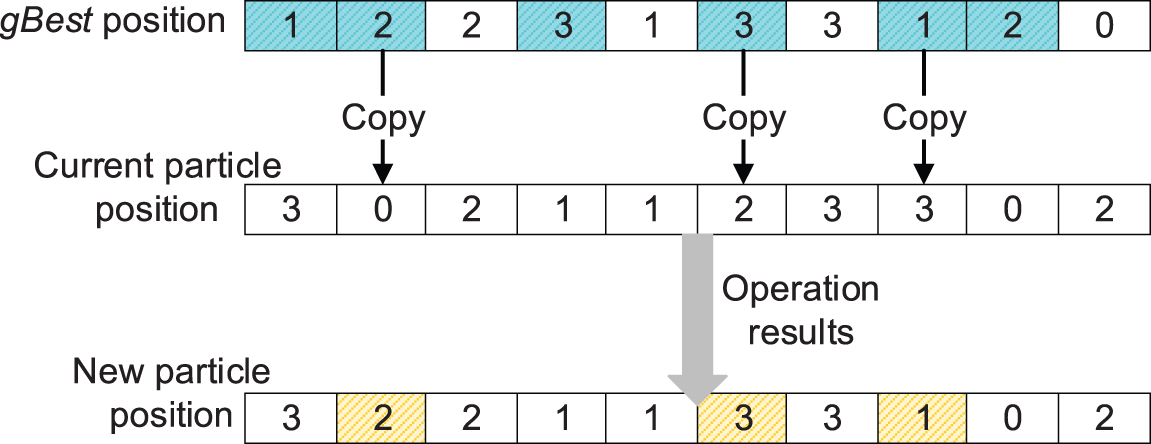
Figure 4: An illustration of the crossover operator

To avoid the situation that the particles trap into local optimal solutions too quickly, the number of copied genes should not be too many. IPSO_IGA sets the copiable genes not to exceed half of all different points, and the worse particle should copy more genes than the better particle. Assuming that there are diff points where the current particle differs from the gBest, the number of copyable genes copyNum should satisfy the following formula:

copyNum=12×diff×fitcurrent−fitgBestfitgWorst−fitgBest(18)

where fitcurrent denotes the fitness of the current particle, and fitgWorst denotes the fitness of the worst particle. If the current particle is the worst, copyNum is exactly half of diff. If the current particle is the global optimal particle, copyNum = 0 and there is no need to copy any genes.

After the particle performed the crossover operator with pBest and gBest respectively, it starts to perform the mutation operator. The mutation operator can maintain the diversity of particles and prevent premature convergence of particles. The mutation operator of the traditional genetic algorithm is selecting a gene and mutates it randomly [24]. However, a completely random mutation would have a high probability to move the particle to a worse position. To solve this problem, IPSO_IGA has made improvements to the mutation operator.

IPSO_IGA uses a gene frequency-based approach to optimize the mutation operator. First, select a gene in the particle randomly. Then, count the frequency of occurrence of each legal value in gBest and pBest (without counting current and illegal values). Finally, based on the statistical results, make the gene mutates with unequal probability. The more times a gene is counted, the greater the probability that the mutation will be in that gene. The illustration of the mutation operator is shown in Fig. 5.

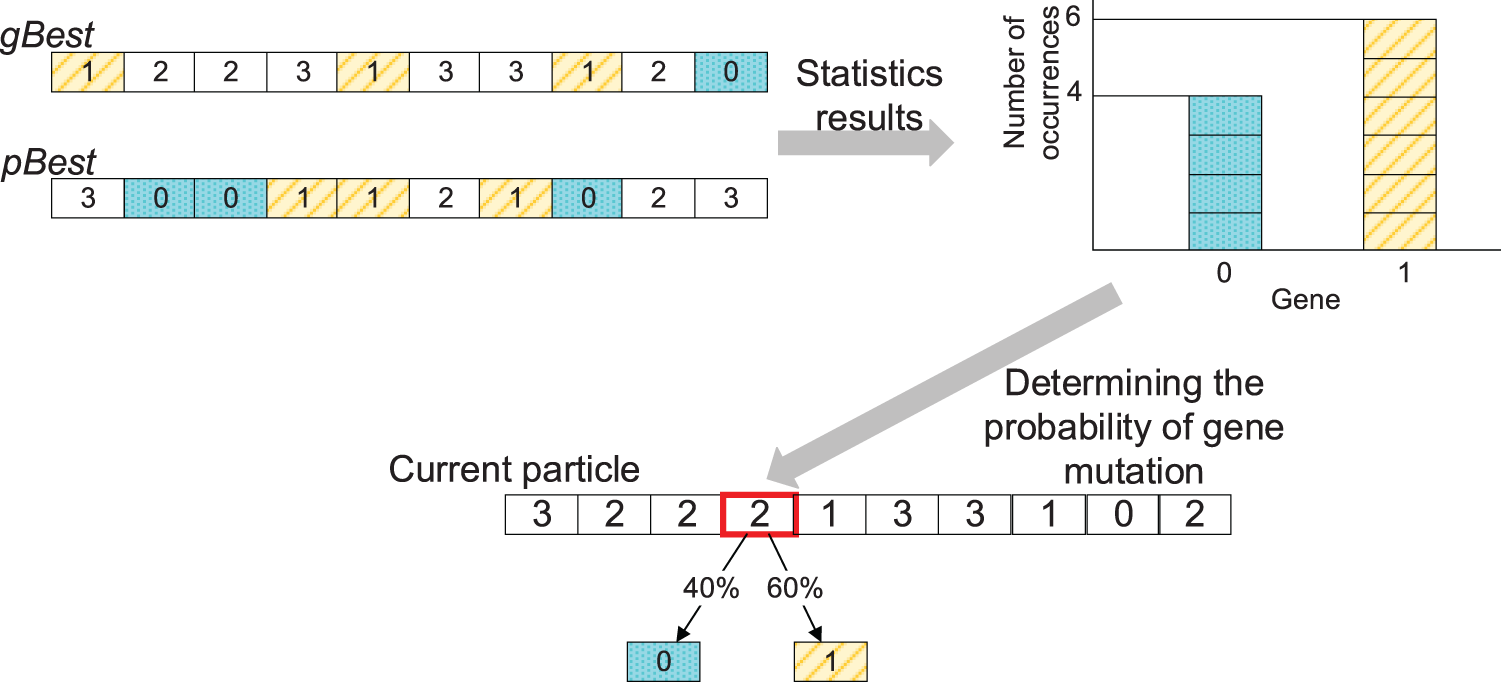
Figure 5: The illustration of the mutation operator

In Fig. 5, the gene marked by a red frame in the current particle is a randomly selected gene that will be mutated. The mobile devices that generate this task are only covered by cloud servers 0 and the edge server 1 (excluding the edge before the mutation), so only count 0 and 1 in pBest and gBest. There are 4 “0s” and 6 “1s”, so the mutation has a 40% probability of being “0” and a 60% probability of being “6”. Algorithm 1 shows the procedure of IPSO_IGA.

3.3 IPSO_IGA Time Complexity Analysis

In IPSO_IGA, there are two main layers of loops. The number of loops in the first layer is determined by the number of iterations ite, and the number of loops in the second layer is determined by the number of particles pop. In the second loop, the most complex part is the computation of fit, which is determined by the complexity of computing ψmax. The number of mobile devices is denoted by MN, and EN denotes the average number of tasks generated per mobile device. Therefore, there are a total of MN×EN tasks that need to be offloaded to the servers, and it also means that each particle has MN×EN dimensions. For each task, an LRU algorithm needs to be executed to ensure that the corresponding service is supported. Assuming that each edge server can cache CH services on average, its complexity can be expressed as O(CH). In summary, the average time complexity of IPSO_IGA can be denoted as O(ite×pop×MN×EN×CH), where ite and pop are preset variables and CH is a constant. The time complexity of IPSO_IGA grows linearly with the total number of tasks.

4  Simulation Experiments and Performance Analysis

This section examines the performance of IPSO_IGA through simulation experiments. At first, we prove that applying the crossover operator and the improved mutation operator to PSO is effective. Then, IPSO_IGA is compared with some classical and state-of-the-art algorithms in several aspects. In the simulated MEC environment, there is 1 cloud server, 10 edge servers, and 20 mobile devices. Each mobile device is covered by 2–5 edge servers and generates approximately 50 tasks. For the parameter setting of IPSO_IGA, the number of particles is set to 50, the number of iterations is set to 50, and the mutation probability is taken in the range of [0.1,0.001]. In this section, the algorithms compared with IPSO_IGA are the following.

•   Genetic Algorithm (GA) [26] mimics the laws of biological evolution. Chromosomes in a population cross over each other, mutate spontaneously, and enter the next generation on a selective basis, thus iterating until the termination condition is reached.

•   Cuckoo algorithm (CS) [20] simulates cuckoo breeding behavior to retain better eggs with higher probability. The born chicks continue to search for new nests using Levi’s flight and breed, thus iterating until the termination condition.

•   Integer particle swarm algorithm (IPSO) [12] first randomly generates a set of particles with an integer encoding, and then moves each particle by a random distance to pBest and gBest to search for the optimal particle position.

•   Simulated annealing algorithm (SA) randomly generates an offloading solution and randomly changes the partial task assignment of this offloading solution. If the changed solution is better than the current offloading solution, the current offloading solution is replaced. Otherwise, it will decide whether to replace the current solution with a certain probability. When the preset number of iterations is reached, the final offload solution is returned.

•   Greedy algorithm (Greedy) greedily sends tasks to the server with the fastest execution speed based on the initial device information and cache information of the MEC.

•   Even algorithm (Even) distributes tasks equally to all accessible servers.

4.1 Effectiveness of Crossover Operator and Improved Mutation Operator

In this subsection, we compare IPSO_IGA with the PSO and PSO_GA algorithms to demonstrate the effectiveness of the crossover operator and the mutation operator, where PSO optimizes particles using only algebraic computation and PSO_GA optimizes particles using the crossover operator and the traditional mutation operator. Fig. 6 shows the trend of the optimal particle fitness after each iteration of each algorithm in one experiment.

Figure 6: The trend of the optimal particle fitness after each iteration of each algorithm

In this experiment, all three algorithms use the same particle swarm. The two algorithms using the crossover operator have an obvious advantage over PSO. This is because the values of each dimension do not have algebraic significance and the algebraic calculation of PSO does not bring the particles closer to pBest and gBest. After one iteration of PSO, the particles are not guaranteed to move to a better position, and pBest and gBest are not updated. This affects the convergence speed of the algorithm and is the reason why PSO shows step-shape convergence. The particle can obtain excellent genes from pBest and gBest after using the crossover operator, which makes the particle move to a better position in the solution space. The generality of the metaheuristic algorithm is well recognized, but for specific problems, a rationally designed metaheuristic algorithm will achieve higher performance.

Compared to IPSO_GA, IPSO_IGA uses a mutation operator based on gene frequency improvement instead of the traditional mutation approach. This improvement makes the completely random mutation directional and the particles will move to a better position with a higher probability. This explains the phenomenon that IPSO_IGA converges fastest at the beginning. In addition, the improved mutation operator still maintains the fastest optimization speed at the end of the iteration. The relevance of the improved mutation operator based on genetic frequency is that in a good offloading decision if more tasks are offloaded to a particular server, this server may have more computational power and cache space. Therefore, that server should take on more tasks.

4.2 Completion Time for Different Offloading Solutions

Figs. 7–9 compare the task completion times of task offloading solutions generated by different algorithms in different environments, which is the main optimization goal of IPSO_IGA. In the experimental environment corresponding to Fig. 7, there are 1 cloud server, 5 edge servers, and 10 mobile devices (a scenario with a small number of devices). In the experimental environment corresponding to Fig. 8, there is 1 cloud server, 10 edge servers, and 20 mobile devices (a scenario with a moderate number of devices). In the experimental environment corresponding to Fig. 9, there is 1 cloud server, 20 edge servers, and 40 mobile devices (scenario with a high number of devices).

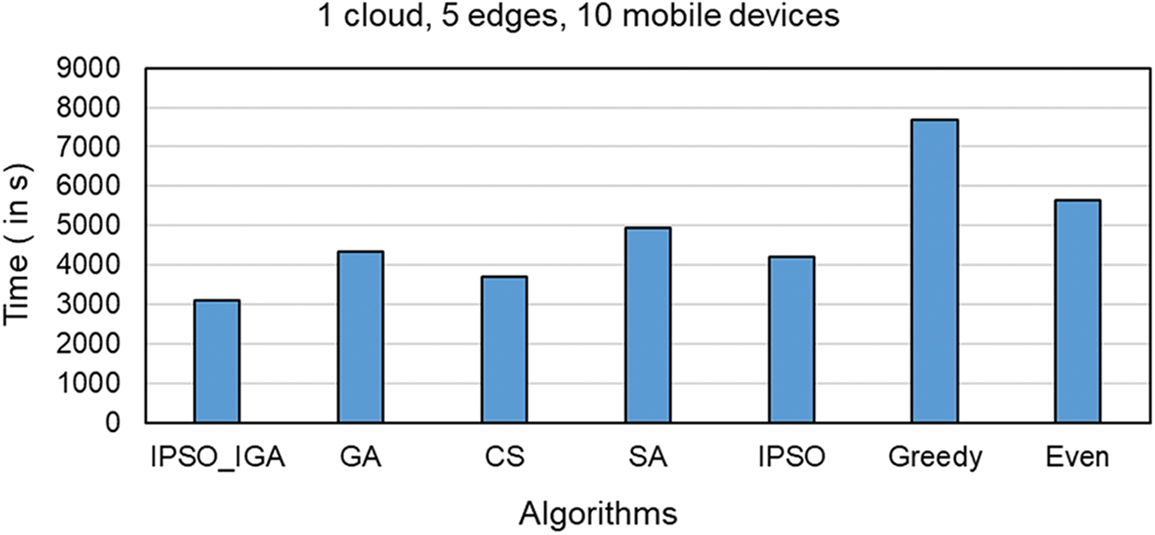
Figure 7: Scenarios with a low number of devices

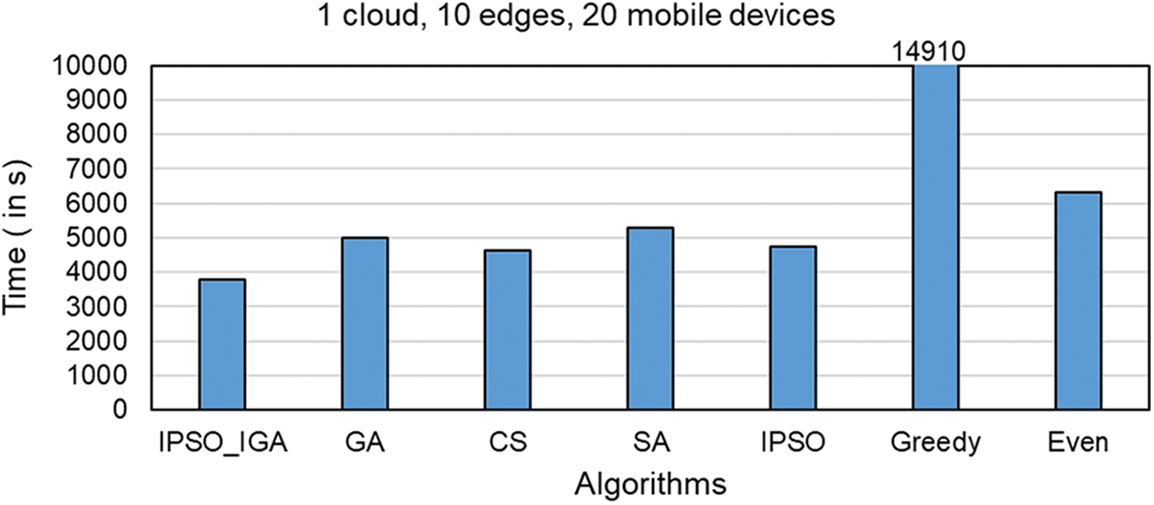
Figure 8: Scenarios with a moderate number of devices

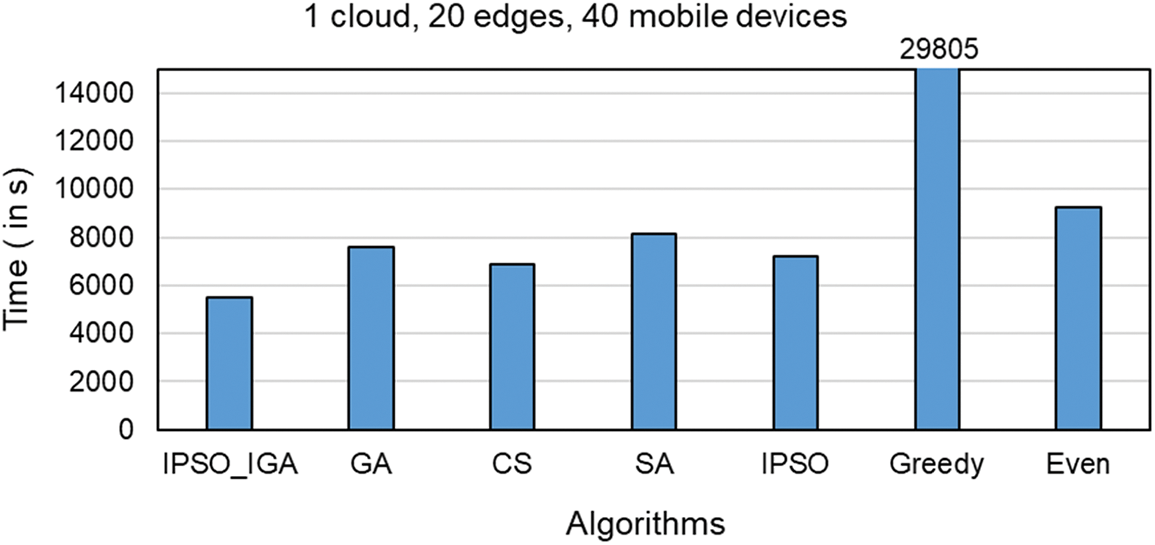
Figure 9: Scenarios with a high number of devices

In these three scenarios with a low to a high number of devices, the performance of IPSO_IGA is higher than the other algorithms by 16%–60%, 18%–75%, and 20%–82%, respectively. As the number of devices continues to increase, the problem becomes more complex and the solution space grows geometrically. But IPSO_IGA can achieve the best performance compared to other algorithms, which indicates that IPSO_IGA can be adapted to solve complex problems. In each iteration of the genetic algorithm, the excellent genes cannot be replicated in all individuals. The excellent genes can only spread by way of higher probability into the next generation, which makes it converge slowly. The cuckoo algorithm relies mainly on Lévy flight to optimize, and this optimization can show good performance in continuous space, but cannot completely exploit its advantages in a discrete space [27]. The convergence speed of the simulated annealing algorithm is relatively slow when solving large-scale problems. It has a poorer optimization solution search capability than IPSO_IGA [28] at the same number of iterations. The IPSO algorithm has powerful capabilities in both global search and convergence, but its search method does not apply to the problem studied in this paper. The greedy algorithm pursues locally optimal solutions, which is contrary to the idea of global optimization search. The even algorithm has a simple structure but does not have any self-optimization capability and has moderate performance in any scenario.

4.3 Cache Hit Rate

The cache hit rates of different task offloading algorithms are shown in Fig. 10. The greedy algorithm has the highest cache hit ratio and the IPSO_IGA algorithm is the second highest. This is because the greedy algorithm always prefers to offload the tasks to the cloud server, which will save a lot of services download time due to the cache not hitting. However, such an unreasonable allocation will cause the cloud server to take too much load and eventually make the task execution time longer. When the cache does not hit, the service resource download usually occupies a portion of the task response time as well. Therefore, the metaheuristic algorithm spontaneously looks for solutions with a higher cache hit rate and reduces the execution time by increasing the cache hit rate. Among all these metaheuristics, IPSO_IGA has the highest cache hit ratio. The even algorithm assigns tasks without considering cache hits and thus has the lowest cache hit rate.

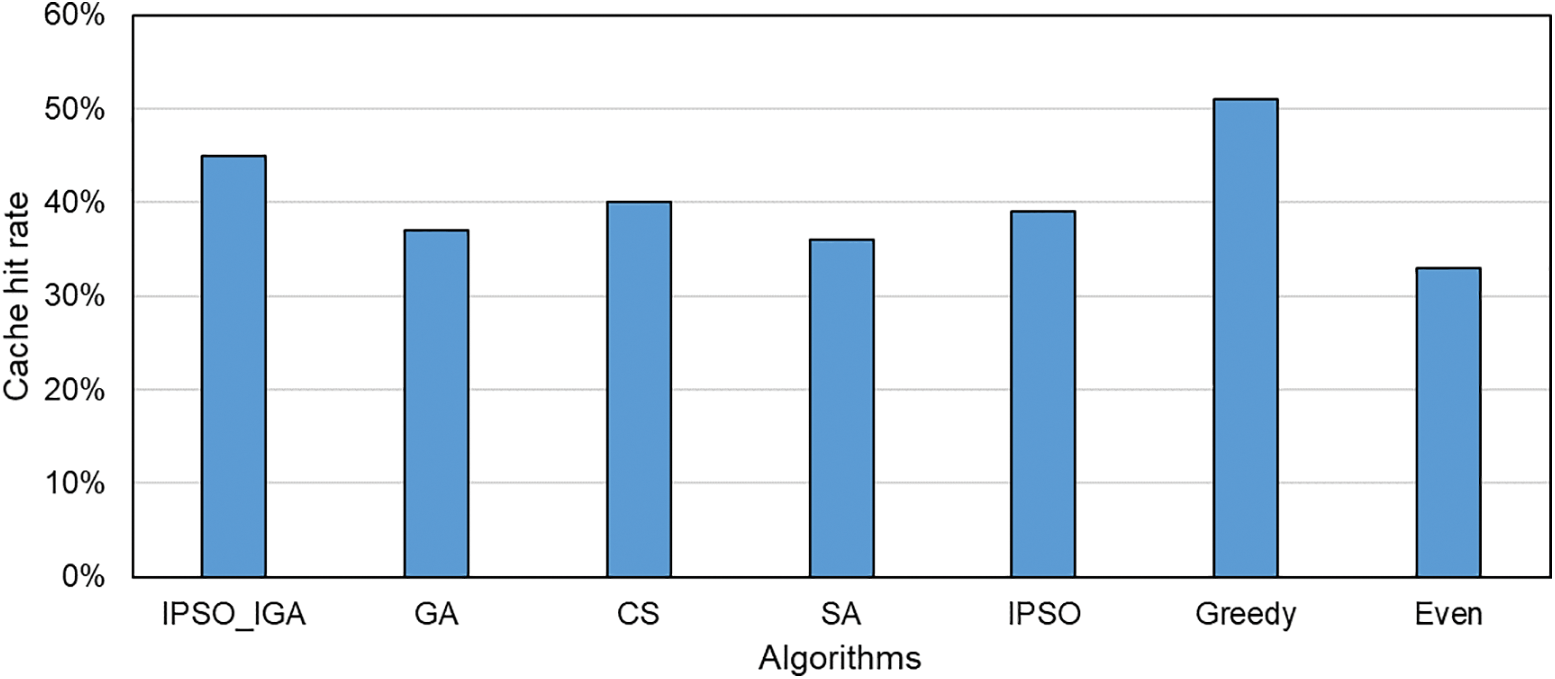
Figure 10: Cache hit rate

4.4 Throughput of MEC Systems

The trend of throughput with an increasing number of tasks for different task offloading algorithms is shown in Fig. 11, which is a direct indicator of processing efficiency and resource utilization. The throughput of IPSO_IGA is consistently at the highest level, which is 38%–244% higher than others. Although we do not consider resource utilization as the optimization goal of IPSO_IGA, the algorithm can spontaneously find the solution with the highest resource utilization to reduce the task execution time, which is one of the advantages of the metaheuristic algorithm. The performance of the cuckoo algorithm and IPSO are close, which have the second and third highest throughputs, respectively. The genetic algorithm and simulated annealing algorithm are more volatile, which may be caused by their slower convergence rate. They cannot converge close to the optimal solution in the same number of iterations. The even algorithm is the most stable but has poor performance. With the increasing number of tasks, the performance of the greedy algorithm decreases rapidly, and thus resource utilization keeps decreasing.

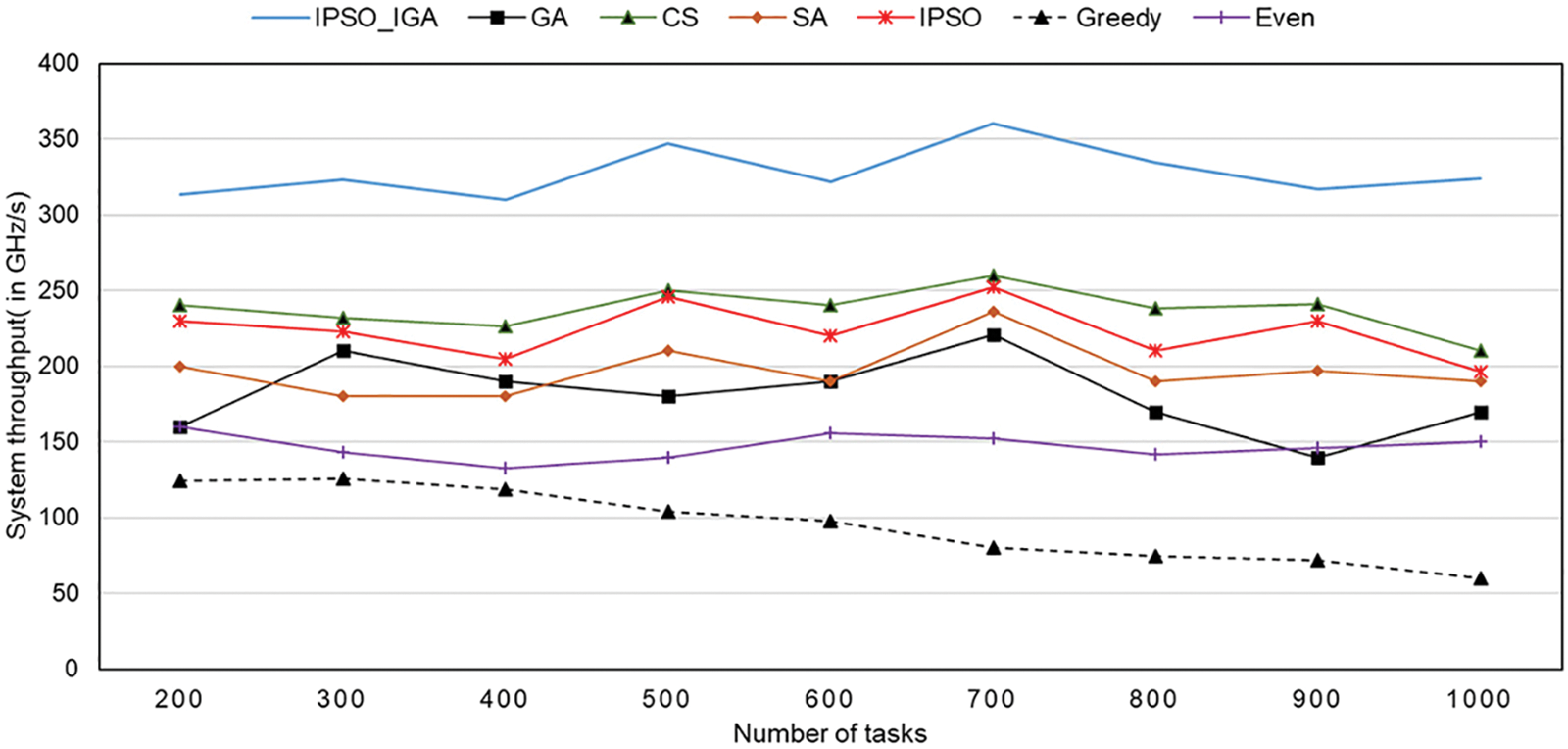
Figure 11: The trend of throughput with an increasing number of tasks

4.5 Load Balancing

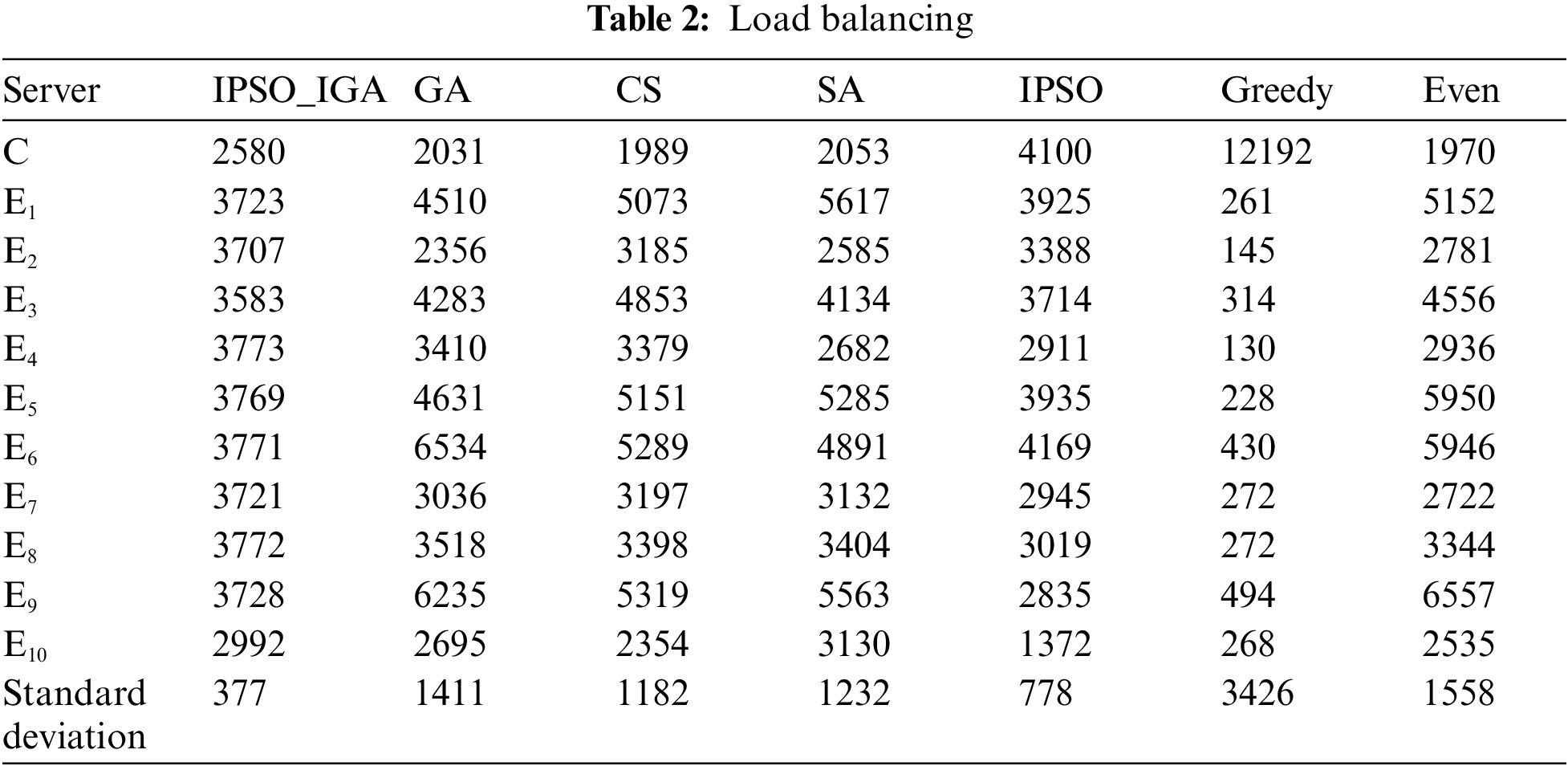
In this subsection, we compare the differences in load balancing between different task offloading schemes. In the study of load balancing methods for MEC, Yao et al. [29] used the number of tasks assigned to a server as a metric for calculating load balancing. However, in a real MEC environment, the computation length of each task and the computing power of each server are not the same. Even the same number of tasks brings different loads to different servers. Therefore, we consider the dispersion of the time taken by the servers for task executions as a metric for load balancing (quantified by standard deviation). We designed a set of experiments that tracked the task execution time of each server. The data is presented in Table 2. IPSO_IGA has the best load balancing performance. Compared with other algorithms, IPSO_IGA can reduce the imbalance by 52%–89%. Greedy algorithm offloads most tasks to the cloud server. The computing time of the cloud server is prolonged due to excessive workload. Even though the tasks will definitely cache hits in the cloud server, IPSO_ IGA still offloads most tasks to the edges for execution, which is in line with the idea of edge computing. Moreover, IPSO_IGA will assign tasks to each service device as much as possible based on the principle that assigning more tasks to edges with more capacity, so that the difference in computation time between servers is not too large. The higher cache hit rate, resource utilization, and balanced task load are the main factors that make IPSO_IGA better than other algorithms.

4.6 Impact of the Number of Users on Task Execution Time

The increase in the number of mobile devices can rapidly increase the complexity of the network structure of the MEC environment. In this subsection, we test the performance of the algorithm in complex networks by increasing the number of mobile devices. As shown in Fig. 12, IPSO_IGA saves 24%–76% of the time compared with other algorithms when the number of mobile devices reaches 40. When the number of mobile devices exceeded 30, the genetic algorithm and simulated annealing algorithm execution time increase rapidly, surpassing the even algorithm. This may be due to their slow convergence rates, and to maintain their original performance, it is necessary to adjust their parameters, such as increase the number of populations or the number of iterations. However, these approaches will greatly increase the computational cost of the algorithms. The slope of IPSO_IGA is relatively stable, indicating that the increase in the number of mobile devices has little impact on its performance. IPSO_IGA can be applied to scenarios with a high density of mobile devices.

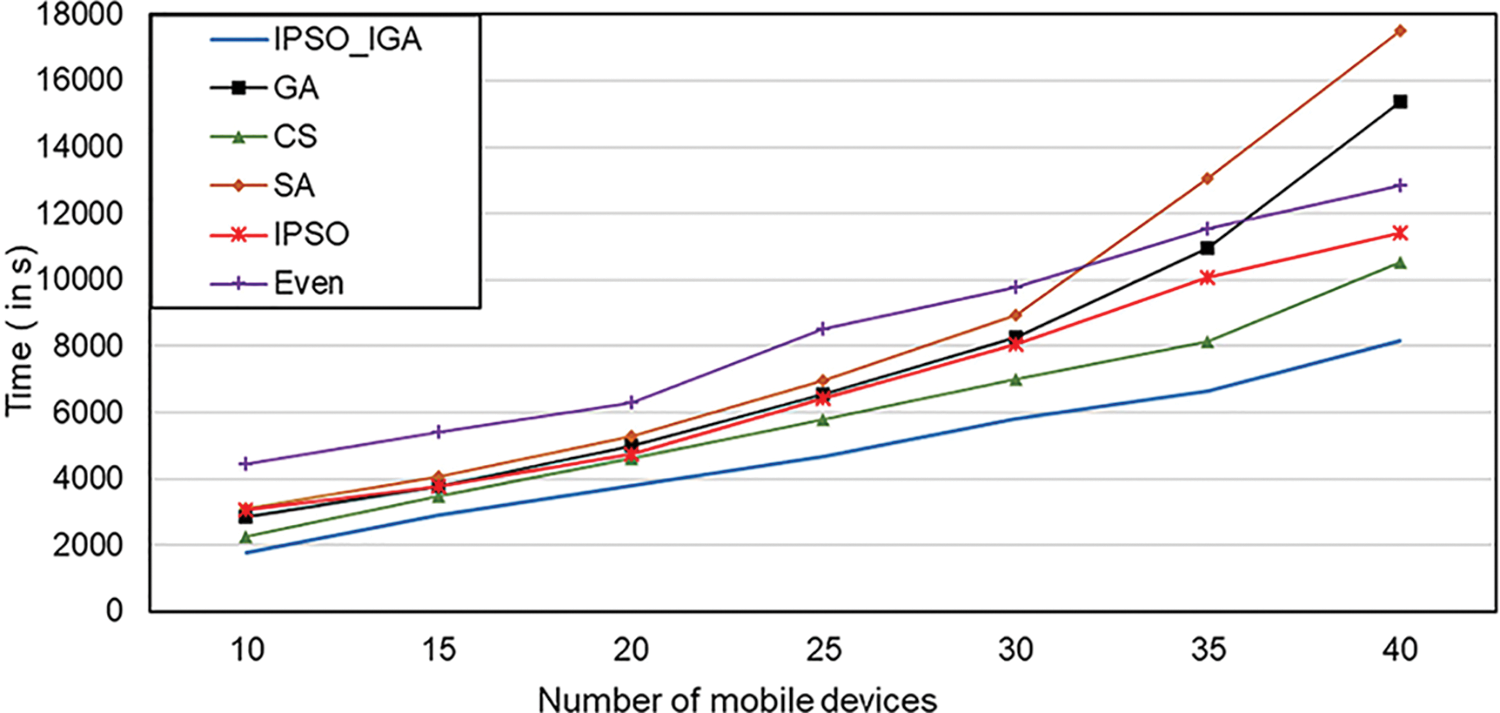
Figure 12: Impact of the number of mobile devices on execution time

4.7 Impact of Different Task Types on Task Execution Time

In this subsection, we compare the performance of each algorithm when executing different types of tasks. Three task types are considered in the experiments, as follows.

•   Type 1: High transfer, low computation, and high cache task type. This type of task mainly includes streaming media transfer, etc.

•   Type 2: Medium transfer, medium computation, and medium cache task types. This type of task mainly includes regular tasks.

•   Type 3: Medium transfer, high computation, and medium cache task type. This type of task mainly includes tasks such as deep learning.

The experimental results are shown in Fig. 13. When executing the first type of task, the greedy algorithm has the best performance. IPSO_IGA has the second-best performance, which saves 10%–29% of the time compared with other algorithms. When executing the second type of task, IPSO_IGA has the best performance and it saves 22%–73% of the time. IPSO_IGA saves 27%–73% of the time compared with other algorithms when executing the third type of task. We can conclude that the more computationally intensive the tasks are, the better the performance of IPSO_IGA, and IPSO_IGA is more suitable for computationally intensive MEC environments.

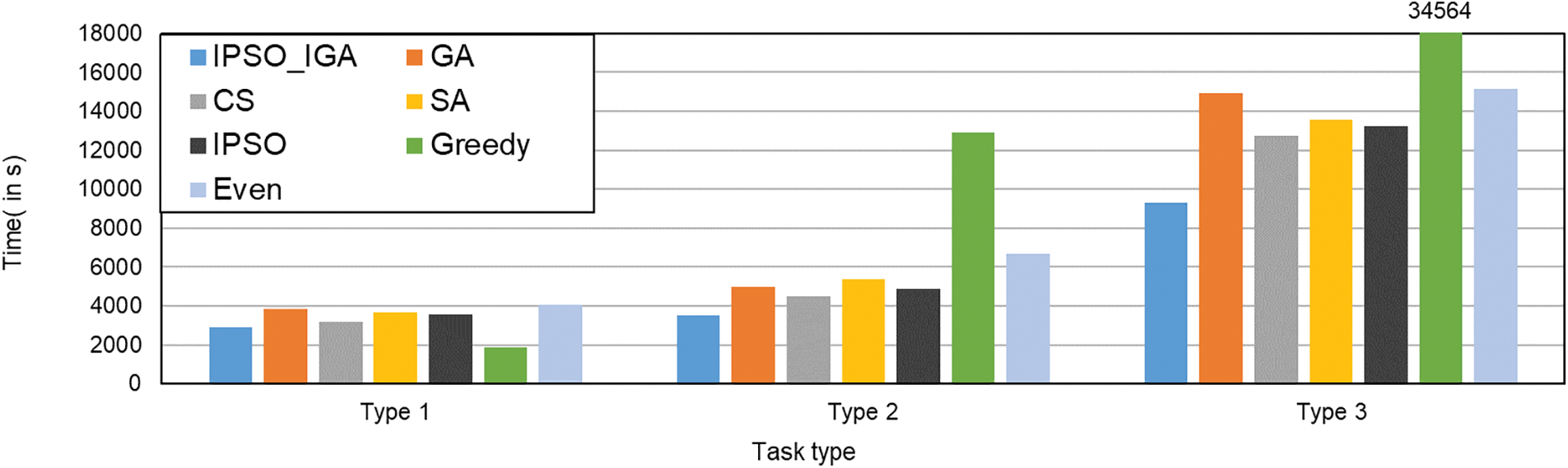
Figure 13: Impact of different task types on task execution time

5  Summary and Outlook

In this paper, we study a task offloading algorithm to reduce the maximum task response time. Different from previous studies, this paper models the problem as a mixed integer nonlinear programming problem by using the caching mechanism in MEC as a constraint. For solving the problem, a mixed metaheuristic algorithm, IPSO_IGA, is proposed, which can search for an efficient task offloading solution within a reasonable time complexity. Finally, this paper compares IPSO_IGA with the state-of-the-art and the most classical algorithms. The results show that IPSO_IGA can improve the performance in terms of the task response time by 20%–82%. In our future work, we will continue to focus on and investigate more efficient metaheuristic algorithms to solve the problems in MEC for a better service quality.

Funding Statement: The research was supported by the Key Scientific and Technological Projects of Henan Province with Grant Nos. 232102211084 and 222102210137, both received by B.W. (URL to the sponsor’s website is https://kjt.henan.gov.cn/). And the National Natural Science Foundation of China with grant No. 61975187, received by Z.Z (the URL to the sponsor’s website is https://www.nsfc.gov.cn/).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Satyanarayanan, “The emergence of edge computing,” Computer, vol. 50, no. 1, pp. 30–39, 2017. [Google Scholar]

2. C. I. Nwakanma, J. W. Kim, J. M. Lee and D. S. Kim, “Edge AI prospect using the NeuroEdge computing system: Introducing a novel neuromorphic technology,” ICT Express, vol. 7, no. 2, pp. 152–157, 2021. [Google Scholar]

3. R. Wang, J. Lai, Z. Zhang, X. Li, P. Vijayakumar et al., “Privacy-preserving federated learning for internet of medical things under edge computing,” IEEE Journal of Biomedical and Health Informatics, vol. 27, no. 2, pp. 854–865, 2023. [Google Scholar] [PubMed]

4. W. Schwarting, J. Alonso-Mora and D. Rus, “Planning and decision-making for autonomous vehicles,” Annual Review of Control, Robotics, and Autonomous Systems, vol. 1, no. 1, pp. 187–210, 2018. [Google Scholar]

5. J. Zeng, T. Wang, W. Jia, S. L. Peng and G. J. Wang, “A survey on sensor-cloud,” Journal of Computer Research and Development, vol. 54, no. 5, pp. 925–939, 2017. [Google Scholar]

6. S. Wang, Y. Zhao, L. Huang, J. Xu and C. H. Hsu, “QoS prediction for service recommendations in mobile edge computing,” Journal of Parallel and Distributed Computing, vol. 127, pp. 134–144, 2019. [Google Scholar]

7. H. Guo, J. Liu and J. Zhang, “Computation offloading for multi-access mobile edge computing in ultra-dense networks,” IEEE Communications Magazine, vol. 56, no. 8, pp. 14–19, 2018. [Google Scholar]

8. Q. V. Pham, L. B. Le, S. H. Chung and W. J. Hwang, “Mobile edge computing with wireless backhaul: Joint task offloading and resource allocation,” IEEE Access, vol. 7, pp. 16444–16459, 2019. [Google Scholar]

9. X. Chen, T. Gao, H. Gao, B. Liu, M. Chen et al., “A multi-stage heuristic method for service caching and task offloading to improve the cooperation between edge and cloud computing,” PeerJ Computer Science, vol. 8, no. 7, pp. e1012, 2022. [Google Scholar] [PubMed]

10. Z. Li and E. Peng, “Software-defined optimal computation task scheduling in vehicular edge networking,” Sensors, vol. 21, no. 3, pp. 955–967, 2021. [Google Scholar] [PubMed]

11. H. Wang, X. Chen, H. Xu, J. Liu and L. Huang, “Joint job offloading and resource allocation for distributed deep learning in edge computing,” in Proc. HPCC, Zhang Jiajie, China, pp. 734–741, 2019. [Google Scholar]

12. B. Wang, J. Cheng, J. Cao, C. Wang and W. Huang, “Integer particle swarm optimization based task scheduling for device-edge-cloud cooperative computing to improve SLA satisfaction,” PeerJ Computer Science, vol. 8, no. 5, pp. e893, 2022. [Google Scholar] [PubMed]

13. W. Kong, X. Li, L. Hou, J. Yuan, Y. Gao et al., “A reliable and efficient task offloading strategy based on multi feedback trust mechanism for IoT edge computing,” IEEE Internet of Things Journal, vol. 9, no. 15, pp. 13927–13941, 2022. [Google Scholar]

14. M. Chen and Y. Hao, “Task offloading for mobile edge computing in software defined ultra-dense network,” IEEE Journal on Selected Areas in Communications, vol. 36, no. 3, pp. 587–597, 2018. [Google Scholar]

15. H. Gao, X. Li, B. Zhou, X. Liu and J. Xu, “Energy efficient computing task offloading strategy for deep neural networks in mobile edge computing,” Computer Integrated Manufacturing Systems, vol. 26, no. 6, pp. 1607–1615, 2020. [Google Scholar]

16. K. Peng, J. Nie, N. Kumar, C. Cai, J. Kang et al., “Joint optimization of service chain caching and task offloading in mobile edge computing,” Applied Soft Computing, vol. 103, no. 3, pp. 107142, 2021. [Google Scholar]

17. S. Zhang and L. Jiang, “Cloud edge end collaborative offloading strategy based on active caching,” Computer Engineering and Design, vol. 42, no. 8, pp. 2124–2129, 2021. [Google Scholar]

18. X. Wei, J. Liu, Y. Wang, C. Tang and Y. Hu, “Wireless edge caching based on content similarity in dynamic environments,” Journal of Systems Architecture, vol. 115, no. 2, pp. 102000, 2021. [Google Scholar]

19. X. Xia, F. Chen, J. Grundy, M. Abdelrazek, H. Jin et al., “Constrained app data caching over edge server graphs in edge computing environment,” IEEE Transactions on Services Computing, vol. 15, no. 5, pp. 2635–2647, 2022. [Google Scholar]

20. C. Liu, J. Wang, L. Zhou and A. Rezaeipanah, “Solving the multi-objective problem of IoT service placement in fog computing using cuckoo search algorithm,” Neural Processing Letters, vol. 54, no. 3, pp. 1823–1854, 2022. [Google Scholar]

21. N. Sarrafzade, R. Entezari-Maleki and L. Sousa, “A genetic-based approach for service placement in fog computing,” The Journal of Supercomputing, vol. 78, no. 8, pp. 10854–10875, 2022. [Google Scholar]

22. M. Ghobaei-Arani and A. Shahidinejad, “A cost-efficient IoT service placement approach using whale optimization algorithm in fog computing environment,” Expert Systems with Applications, vol. 200, no. 4, pp. 117012, 2022. [Google Scholar]

23. C. Li, Y. Zhang, X. Gao and Y. Luo, “Energy-latency tradeoffs for edge caching and dynamic service migration based on DQN in mobile edge computing,” Journal of Parallel and Distributed Computing, vol. 166, no. 4, pp. 15–31, 2022. [Google Scholar]

24. H. A. Alameddine, S. Sharafeddine, S. Sebbah, S. Ayoubi and C. Assi, “Dynamic task offloading and scheduling for low-latency IoT services in multi-access edge computing,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 3, pp. 668–682, 2019. [Google Scholar]

25. B. Wang, C. Wang, W. Huang, Y. Song and X. Qin, “Security-aware task scheduling with deadline constraints on heterogeneous hybrid clouds,” Journal of Parallel and Distributed Computing, vol. 153, no. 1, pp. 15–28, 2021. [Google Scholar]

26. B. Wang, J. Wei, B. Lv and Y. Song, “An improved genetic algorithm for the multi-temperature food distribution with multi-station,” International Journal of Advanced Computer Science and Applications, vol. 13, no. 6, pp. 24–29, 2022. [Google Scholar]

27. J. Yang, Y. Cai, D. Tang and Z. Liu, “A novel centralized range-free static node localization algorithm with memetic algorithm and lévy flight,” Sensors, vol. 19, no. 14, pp. 3242–3271, 2019. [Google Scholar] [PubMed]

28. J. Kang, I. Sohn and S. H. Lee, “Enhanced message-passing based LEACH protocol for wireless sensor networks,” Sensors, vol. 19, no. 1, pp. 75–91, 2019. [Google Scholar]

29. Z. Yao, J. Lin, J. Hu and X. Chen, “PSO-GA based approach to multi-edge load balancing,” Computer Science, vol. 48, pp. 456–463, 2021. [Google Scholar]