A New Privacy-Preserving Data Publishing Algorithm Utilizing Connectivity-Based Outlier Factor and Mondrian Techniques

1  Introduction

Today, many institutions collect and store large amounts of personal data from various sources connected to the Internet for business and research purposes [1]. These data can be used to make future predictions about the sectors and develop decision-making mechanisms. It is vital to share the processed data with other individuals, institutions, and organizations in order to generate a high level of value from it. However, because this data may contain various personal data that can directly or indirectly identify the individual, sharing such data without adequate protection will result in significant problems, such as attackers revealing the identities of data owners over the shared dataset [2,3]. On the other hand, if data privacy safeguards are overly stringent, data utility will suffer. For all these reasons, it is very important to maintain a trade-off between data privacy and utility [4].

There are numerous approaches in the literature for ensuring data privacy. De-identification is the most basic of these methods [5]. Although this method is a privacy-preserving approach, Sweeney’s research revealed that it did not provide a sufficient level of protection. Because the de-identification method cannot meet the data privacy requirements, stronger privacy-preserving models such as k-anonymity [6,7], l-diversity [8,9], and differential privacy [10,11] have been developed in the literature. As each model is vulnerable to different privacy threats, k-anonymity was chosen as the privacy model for our study. The study additionally examined the algorithms that deal with data privacy using the k-anonymity model.

Microdata can contain outliers that do not fit the overall pattern of the population. Many publicly published real datasets contain outliers [12]. Assume you have a dataset containing information about people’s income levels. Suppose there are two separate individuals in this dataset, one young and one old, and that these individuals are famous personalities with large annual revenues. These individuals are considered outliers in the dataset. In every society, the recognition of such individuals is higher than that of other normal people. It goes without saying that an adversary knows more about these people than the average person. As a result, adversaries can simply manipulate datasets using outliers. Outliers are also known to diminish data utility, in addition to having negative effects on data privacy. As a consequence, while some research in the literature handles this problem by deleting outliers from the entire dataset, others attempt to gain from outliers.

In this study, an outlier detection mechanism was added to the Mondrian local recoding algorithm. In this way, a major contribution has been made to the Mondrian algorithm’s weakness, which was its inability to find a solution to the negative impacts of outliers. As a result of this study, a new model based on the Mondrian algorithm reduces the losses caused by outliers has been introduced. Extensive experiments on real-world data demonstrate the success of the proposed algorithm.

The contributions of this study are listed below:

•   A new model based on the Mondrian algorithm has been proposed, and the data utility of the algorithm has been increased.

•   Significant improvements have been made to the Mondrian algorithm’s information loss problems based on outlier data.

•   Unlike existing approaches to outlier management, the proposed algorithm discovers outlier data before anonymizing equivalence classes. The significant computational cost of removing outlier data from the dataset after anonymization is also lowered in this manner.

•   It has an edge over other algorithms in the field because it can be used with both categorical and numerical data.

•   On a real-world dataset, experimental comparisons are carried out with commonly used k-anonymity algorithms to illustrate the efficacy of the proposed algorithm in terms of data utility.

The organization of the rest of the paper is as follows: In Section 2, data privacy and recoding concepts, k-anonymity-based anonymization models, and existing outlier data methods are mentioned. In Section 3, the privacy-preserving data publishing algorithm proposed in the paper is introduced. In Section 4, the dataset and information metrics utilized in the study are detailed. In addition, the results of the experiments conducted are shown, and the success of the algorithms in terms of data utility is presented. Finally, Section 5 concludes the study and makes recommendations for further research.

2  Background and Related Work

k-anonymity is a recommended mechanism for privacy-preserving data publishing and is still used for a variety of purposes [13]. The transformation operations conducted on the data are known as recoding. They are undertaken to safeguard the information of individuals on the datasets or prevent it from being disclosed. Numerous recoding models have been proposed for k-anonymity implementation. In recoding operations, there are two major models: global and local recoding [14]. Global recoding happens when a particular detailed value is mapped to the same generalized value in all records [15]. There should be just one generalization rule for records in global recoding. For example, given Fig. 1, consider two records whose quasi-identifiers (QIDs) are the same as {43, female}. When the global recoding process is finished, all records will have the same generalized values in that attribute group {40–45, female}. Local recoding allows the same detailed value to be mapped to different generalized values in each anonymized group [15]. Multiple registration rules for the same attribute values are provided by local recoding [16]. For instance, for a value of 43, female, two generalization rules are mapped (i.e., {40–43, female}, or {43–45, female}) in Fig. 1.

Figure 1: Example of two recoding models

2.1 k-Anonymity Algorithms

While there are many k-anonymization algorithm proposals in the literature [17–19], [20–22] only a few are implemented. Although it appears to be a simple problem at first glance, providing optimum k-anonymity has been shown to be an NP-hard problem [20], and approximate solutions have been attempted. Datafly [23], Incognito [24], Mondrian [14], Basic Mondrian [25], the Top-Down greedy data anonymization [26], and clustering-based k-anonymization algorithms [27,28] are the most widely used methods. In this study, Mondrian, a Top-Down greedy data anonymization algorithm for relational datasets described by Kristen LeFevre [14], is used as a reference algorithm in this study. It uses the k-dimensional tree (KD-tree), which is a special type of binary space partitioning tree, to split all the data into small pieces and then generalize [29]. It is also known as one of the fastest local recording algorithms with high data utility.

2.2 Outlier Methods

Datasets preserved by algorithms based on k-anonymity have significant weaknesses against outlier data. If an adversary even has a rudimentary understanding of whether a specific individual is an outlier, this individual can be easily identified within the sample. For example, in equivalence classes of three different individuals aged 20 to 25 with annual incomes of [10, 30, 500 K], the adversary could easily conclude the person they are looking for is this young person whose income is unusually high compared to other young people. Other information about the person in the dataset can be accessed in this manner. This example demonstrates that outliers with additional external information are easier to attack than typical ones. Unfortunately, simply removing these outliers from the dataset alone can result in high information loss [30]. Therefore, it is necessary to preserve the properties of the outliers so that they can be safely hidden in the crowd. The majority of the privacy-preserving data publishing studies in the literature does not take into account the potential hazards of outliers, which might cause substantial harm to data privacy due to their uniqueness. Studies examined in this paper both ensure data privacy by taking outliers into account and regard the data utility.

There are numerous ways in the literature on privacy-preserving data publishing detect outlier data, including distance-based [12,31,32], taxonomy tree-based [33,34], and density-based [10] methods. Each of these approaches in the papers includes different methods. In taxonomy tree-based methods, the use of taxonomy trees that do not consider the data and its distribution reduces the data utility [10]. Distance-based methods measure the proximity between objects by calculating distances. Because distance-based methods are easily influenced by a dataset’s local density, density-based methods have been developed [35]. In [10], a density-based approach was adopted using the local outlier factor (LOF) algorithm [36] for outlier data detection. The LOF algorithm’s operating technique involves scoring data based on density. Data with a LOF score higher than 1 are more likely to be outliers [35]. Other studies using the LOF algorithm to detect outliers are [37–39]. Huang et al. [37] rejected the notion that identifying low-density data as outliers was a sufficient prerequisite. Therefore, a COF was proposed [40]. It works by choosing a set of nearest neighbors using the cluster-based shortest path. When outliers are located in the center of two clusters of similar density, the COF method performs better. The COF technique was used in this paper to detect outliers in the dataset.

The COF algorithm is an advanced version of the LOF algorithm. The different task of COF density estimation for data points distinguishes COF from LOF. LOF is similar to the k-nearest neighbor (KNN) algorithm in terms of its working principle. The distinction is that while certain observations in KNN are close to one another, some attempts are made in the LOF to identify dissimilar observations. The COF algorithm also uses the KNN algorithm, like LOF. While LOF determines the KNN using Euclidean distance. The COF determines the KNN using the chaining distance [41]. COF is a better algorithm than LOF. Because it performs better than LOF on datasets with linear correlation. Besides, COF works by creating a set of ways to detect the outlier [42]. COF identifies outliers based on neighborhood density and neighborhood connectivity [39]. COF computes the mean chaining distance and identifies data points as outliers with a sufficiently large COF factor.

Definition 1 (The connectivity-based outlier factor). The COF is defined as the ratio of the average chaining distance (ac-dist) at a point and the ac-dist at its KNN [39]. We use o and p to denote objects in a dataset. Assuming k is a positive integer and p ∈ D. The COF at p is calculated concerning the k-neighborhood as follows.

COFk(p)=|NkP|.ac−distnk(p)(p)∑o∈Nk(p)ac−distN(k)(o)(1)

2.3 Comparison of Recent Studies

Some studies that aim to improve the existing problems of Mondrian-based algorithms in the literature and some studies that address the outlier problem besides being Mondrian-based are shown in Table 1. The studies in the table are compared based on various criteria, such as data type, enhancement target, outlier approach, and outlier algorithm. The data type column in the table provides information on whether the algorithms were applied to datasets containing categorical or numerical data. Enhancement target indicates which of the problems of the Mondrian algorithm that the researchers addressed while developing their algorithms. The study [43] in the table addresses the outlier problem in equivalent classes obtained by applying k-anonymity and l-diversity privacy models to datasets, whereas the studies [10] and [29] focus on the outlier problem in the Mondrian algorithm. These recent studies served as inspiration for the proposed algorithm. When we examine the table, it can be observed that the proposed algorithm can be implemented on both nominal and continuous data types, whereas other algorithms in their research area that focus on the outlier problem can only be realized on continuous data types. As a result, when compared to other studies, the proposed algorithm stands out in this regard. In addition, the proposed algorithm uses the COF algorithm to decide which records in the equivalence classes are outliers. COF finds the local outlier using chaining distance, whereas other techniques use the LOF algorithm and thus Euclidean distance to evaluate proximity between data points. Chaining distance is better for working with categorical data. Therefore, it can be said that the proposed method may be better for working on real-world datasets that contain both nominal and continuous data types.

3  Proposed Privacy-Preserving Data Publishing Algorithm

The proposed algorithm within the scope of the paper is based on Mondrian, a multidimensional k-anonymity algorithm. The basic workflow of the Mondrian algorithm consists of two main parts. These parts are the partition and generalization phases presented in Fig. 2. In the first part, partitions containing at least k values are obtained by using the KD-tree algorithm. In the second part, these k groups created in the partition part are anonymized using the generalization method. The proposed algorithm, on the other hand, uses an outlier data detection mechanism to eliminate its most important weakness in addition to these two main parts of the Mondrian algorithm. In this way, a more successful greedy data anonymization algorithm has been obtained in terms of data utility. The workflow of the proposed method, consisting of three main parts, is presented in Fig. 2.

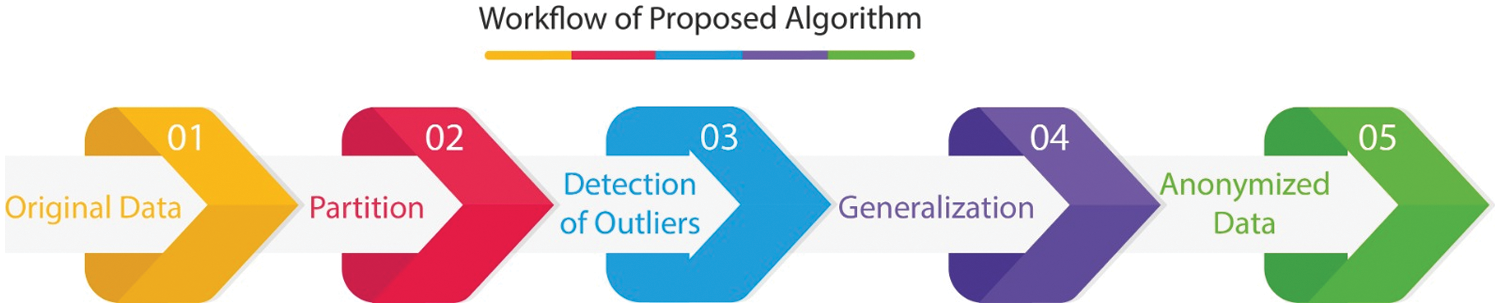
Figure 2: Workflow of the proposed algorithm

Within the scope of the study, it was decided that the most suitable anonymization algorithm to be used as a reference for the proposed algorithm is Mondrian, and the outlier detection algorithm to be used is COF, and the reasons for this decision are presented below:

•   The Mondrian algorithm provides solutions close to optimal.

•   Compared to many k-anonymization models in the literature, Mondrian’s ability to perform anonymization on multidimensional data and its suitability for real-world data needs make it a preferred option.

•   Because the Mondrian method employs a fractional partitioning strategy, the feature space can be partitioned more effectively. This method allows for more precise division of data features, resulting in improved anonymization.

•   The COF algorithm is designed to find outliers in high-dimensional datasets with complicated structures.

•   COF using the chaining distance method is more advantageous for determining the proximity of data points in real-world datasets that consist of both nominal and continuous data types.

The pseudo-code of the proposed method is given in Algorithm 1.

The stages in the 3 main sections in the proposed effective privacy-preserving algorithm are explained in detail below.

(1) Part: Partitioning Phase

Step 1: Input the dataset to be anonymized,

Step 2: Check the dataset for up to or more than k data, if there is, continue to

Step 3: If not, return the incoming data as partition,

Step 4: Declare the result set as an empty set presult (array of n partition for generalization) = { },

Step 5: Create a partition containing all the data,

Step 6: Preprocessing steps are started for all dimensions and the frequency of data is calculated,

• Digitize all categorical data on the entire dataset,

• Define range list (2 dimensional), QID index list (1 dimensional), value list (2 dimensional),

• Add all values for each attribute to the value list once, without data duplication,

• For each attribute, the data spread is calculated by finding the difference between the largest and the smallest value of that attribute and add to the range list. Sort values by range list,

Step 7: The size selection process for the partition is done by checking the data spreads in the QID index list and the range list,

Step 8: The division value is calculated by taking the median of the partition’s size,

Step 9: Using the calculated median value, current partition is divided into two parts as left and right,

Step 10: If there is an element to be split in the left or right lower parts, go to Step 6, if there are no more, an array list of partitions is obtained,

(2) Part: Detection of Outliers Phase

Step 11: Declare the outlier set as an empty set poutlier (array of n row data) = { },

Step 12: Detect outliers for each partition returned through array list,

Step 13: Outliers in the partition are separated and collected in the poutlier array,

Step 14: Add outlier-free data to presult set,

Step 15: Consider the poutliers set as the new dataset to be anonymized and submit to Step 1,

Step 16: If processing the first invoked (first dataset that does not free of outliers) dataset, continue with the Generalization Phase, otherwise return the presult set and finish,

(3) Part: Generalization Phase

Step 17: Generalize presult,

Step 18: Restore digitized data to categorical and return presult.

The flowchart of the proposed algorithm is shown in Fig. 3 to explain the algorithm more clearly.

Figure 3: Flowchart of the proposed algorithm

4  Experimental Results and Discussion

The experimental evaluation of the proposed method is presented in this part. All test and analysis studies were conducted on a notebook with 16 GB RAM and a 9th generation i7 CPU in order to develop a model that will ensure privacy preservation. In the experiments conducted in the paper, PyCharm was used as the integrated development environment and Python as the programming language. To assess the performance of the proposed algorithm in terms of data utility, the following metrics are used: DM, Cavg, GCP, query error rate, CA, and F-measure. The Adult dataset was used as the dataset.

4.1 Dataset

On the Adult dataset, the capabilities of the proposed privacy-preserving data publishing algorithm were tested [45]. The Adult dataset was used for our investigation since it is frequently utilized in the literature. Thus, we could simply compare the success of our proposed algorithm to that of other methods. The Adult dataset is available online at the University of California-Irvine, Machine Learning Repository [46]. Despite the fact that the dataset comprises 32561 records, the number of records without missing values employed during the experimental research is 30162. The dataset contains 15 attributes, 6 of which are numerical and 9 of which are categorical.

4.2 Information Loss Metrics

In this section, the information loss metrics on which the proposed privacy-preserving algorithm is evaluated are explained in detail. The proposed algorithm’s performance results against these measures are shown. Furthermore, in order to better understand the success of the proposed algorithm, various comparisons were made with commonly used algorithms in the literature, and the results were reflected in the graphics.

4.2.1 Discernibility Metric

The DM is used to measure how indistinguishable a record is from the others, with equal penalty scoring assigned to each record within the equivalence classes [47,48]. The size of the equivalence class T in the Z table |T| if we accept it as; penalty value of the record belonging to the related equivalence class is also |T| taken as. The DM metric can be expressed mathematically as:

DM(Z)=∑EquivClassesT|T|2(2)

In Fig. 4, the comparison of the DM results of the proposed algorithm with other studies is presented. The DM values of all algorithms grow as the k value increases. It is seen that our proposed algorithm in the study gives the best results for almost all k values. Only the cluster algorithm has obtained results close to our proposed algorithm for some k values. However, our algorithm showed more successful performances than the cluster algorithm for k parameter values such as 10 and 50. As a consequence, DM clearly demonstrates that our suggested method outperforms other algorithms in terms of data utility.

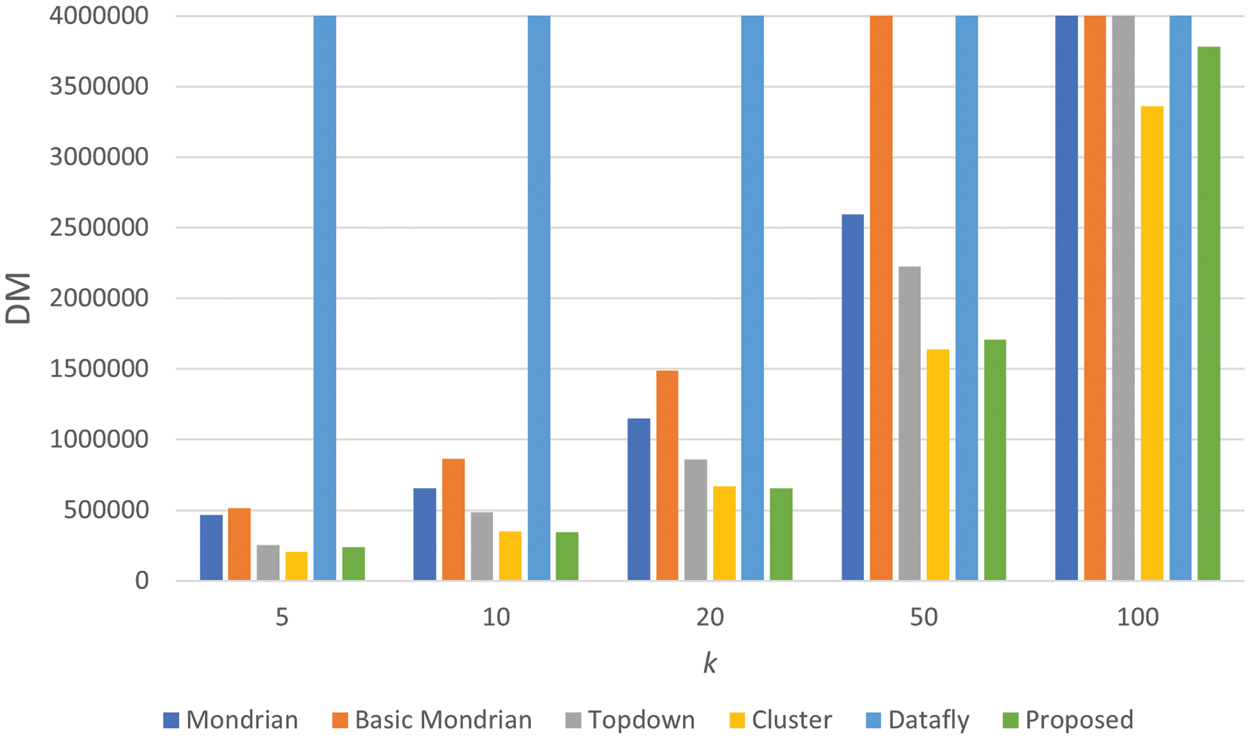
Figure 4: Comparison of discernibility metric results

4.2.2 The Normalized Average Equivalence Class Size

The Cavg was first introduced in [14], and used in [26] as an information metric. The average size of the created equivalence classes is used to calculate the extent to which the k-anonymization model used on the datasets causes data loss [49]. The Cavg metric measures how well the partitioning approaches the optimal state when each equivalence class is generalized to a group of similar equivalence classes. The Cavg score of an anonymized table is calculated as follows [c]:

Cavg=total_recordstotal_equiv_classes/(k)(3)

In the formula, total records is the number of records in the dataset, total_equiv_classes is the number of created equivalence classes, and k is the privacy level [49]. The degree of similarity between the equivalence classes generated by this algorithm and the best situation, where each equivalence class has k records, is calculated. The ideal score for the Cavg metric is 1 [49]. In Fig. 5, the performances of the algorithms against the Cavg metric are presented.

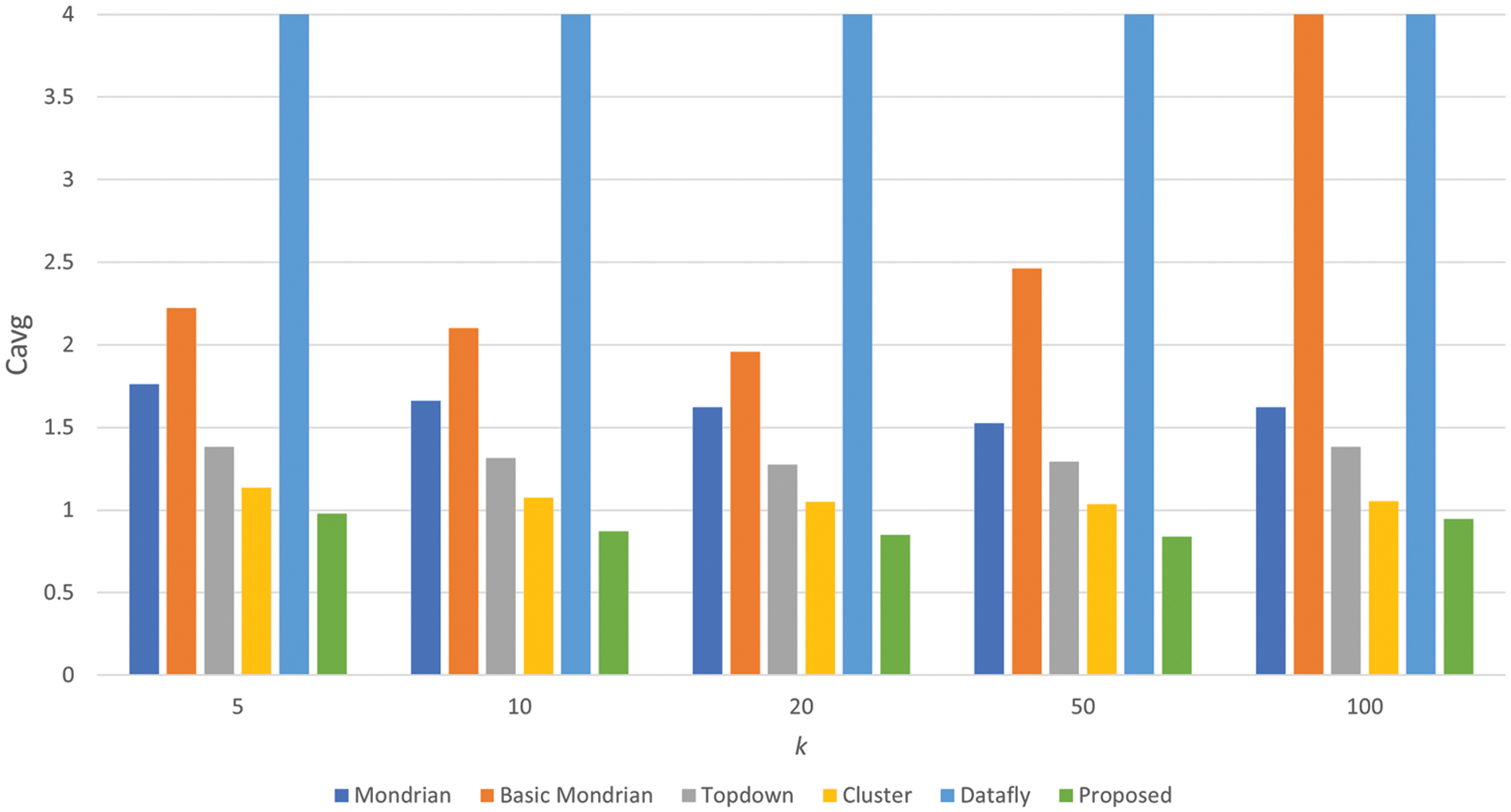
Figure 5: Comparison of normalized average equivalence class size results

Cavg measures data utility based on the dimensions of the equivalence classes. In terms of the Cavg metric, a 1 value is a baseline, and algorithms close to this value performed better. The graph shows that the proposed approach outperforms other algorithms at all parameter values.

4.2.3 Global Certainty Penalty

The normalized certainty penalty (NCP) metric is used to evaluate the loss of accuracy in the definition of equivalence classes [15]. It is a metric that measures the proximity of elements in equivalence classes to each other. In other words, NCP is a measurement used to measure the quality of anonymization applied to the dataset. The working principle of NCP is to characterize the information loss of an entire partition by summing over all equivalence classes in each group. The information metric known as GCP [50], which is a normalized formulation of the aggregated version of NCP, was used in this paper.

Assuming T is an equivalence class and Q is a QID attribute contained in the equivalence class. In such a case, the NCP of an equivalence class T for numerical attributes is defined as:

NCPQNum(T)=maxQNumT−minQNumTmaxQNum−minQNum(4)

In the above formula, the numerator is obtained by subtracting the smallest QID value from the largest QID value in the T equivalence class. The denominator is calculated by subtracting the smallest QID value from the greatest in the total dataset. When it comes to categorical attributes, NCP is defined concerning the taxonomy tree of the attribute.

where u is the lowest common ancestor of all QCat values included in T, card(u) is the number of leaves (i.e., attribute values) in the subtree of u, and |QCat| is the total number of distinct QCat values. The NCP of class T over all QID attributes is:

NCPQNum(T)={0,card(u)=1card/|QCat|,otherwise(5)

d is the number of attributes (i.e., the dimensionality) in a dataset, Qi is either a numerical or categorical attribute, and weights wi if we assume that where Σ wi = 1; the NCP value of all QIDs within a T equivalence class is calculated as follows:

NCP(T)=∑i=1dwi.NCPQi(T)(6)

As a result, |T| is the cardinality of group T, if we accept the value of M for all equivalence classes in the anonymized dataset and the total number of records in the dataset as N; the GCP value of this table is calculated as follows:

GCP(M)=∑G∈M|T|.NCP(T)d.N(7)

This formulation’s most significant addition is its benefit in evaluating information loss between tables of varied size and cardinality. The advantage of this formulation is its ability to measure information loss among tables with varying cardinality and dimensionality. The GCP score must be between 1 and 0. Being close to 0 as a GCP score means that there is no or little loss of information; a value close to 1 indicates that there is a serious loss of information. In Fig. 6, the results of the GCP metric that we used to measure the loss of information in the anonymized dataset are presented.

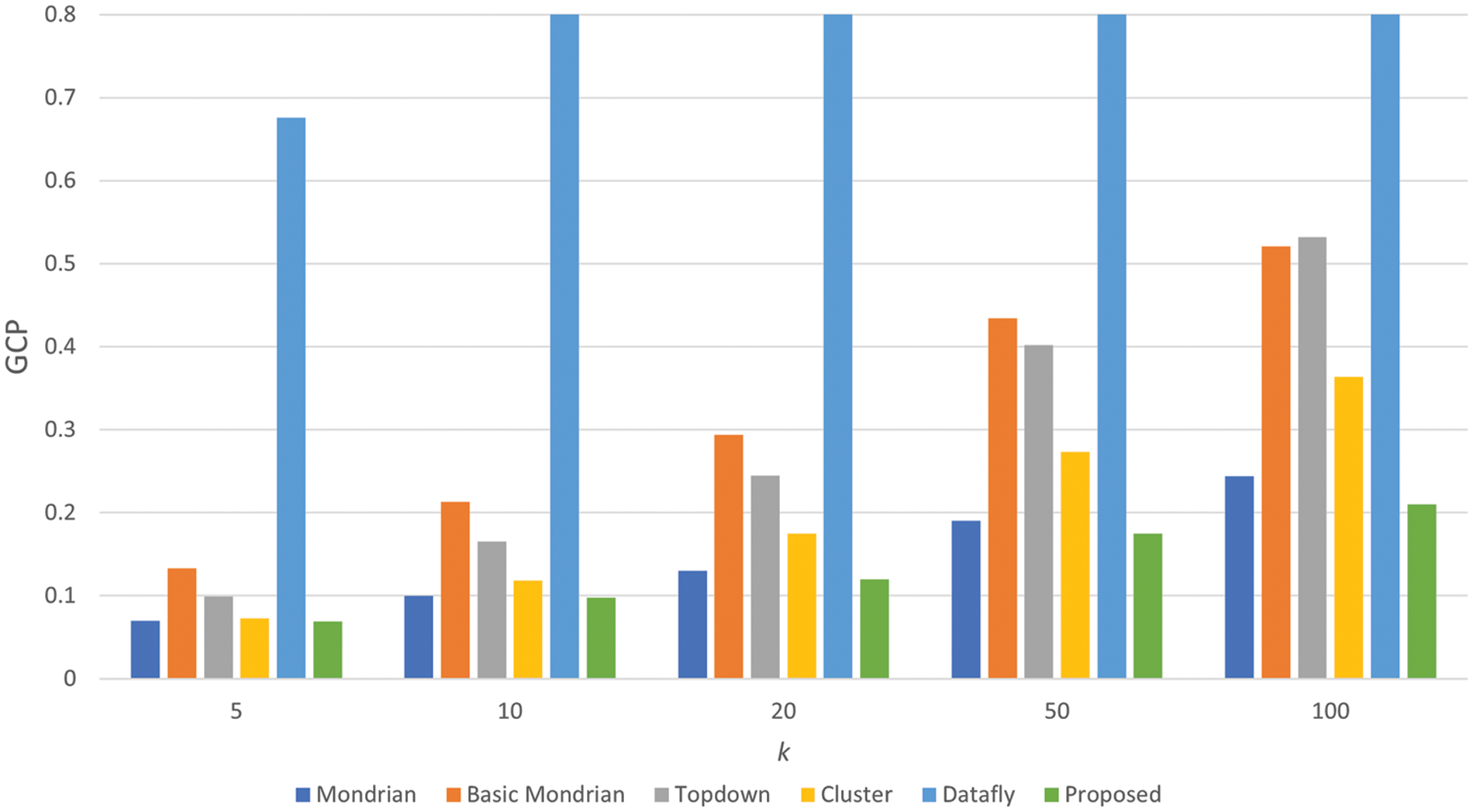
Figure 6: Comparison of global certainty penalty results

The performance of the proposed method under different k parameter values was assessed using algorithms commonly utilized in the literature. In Fig. 6, algorithms with lower GCP scores performed better. According to these results, as the k value increases, the GCP of all algorithms gradually increases. Because as the value of k grows larger, all algorithms distort more information to obtain k-anonymity. In this case, it negatively affects and increases the GCP value. When we examine the performance of the proposed algorithm, we observe that it performs better than other algorithms for all k parameters.

4.2.4 Query Error Rate

The query error rate is a study of the utility of a data processing method based on data re-accessibility. Structured query language (SQL) queries are applied to raw and processed data in this manner. The resulting difference is calculated using the relative error method, and it indicates how far the method departed from the predicted outcome. The relative error is a type of error that shows how close results are obtained proportionally to the true value. Because the size of the results can vary depending on the circumstances, relative error is more meaningful than absolute error. If A is the genuine value and a is the estimated approximation value, the relative error is calculated as shown in the formula below.

δa=|A−aA|(8)

Some SQL queries were run on raw and anonymized data to demonstrate the success of the proposed algorithm in terms of query error rate. The implemented queries are shown below. The results obtained as a result of these queries are presented in Fig. 7.

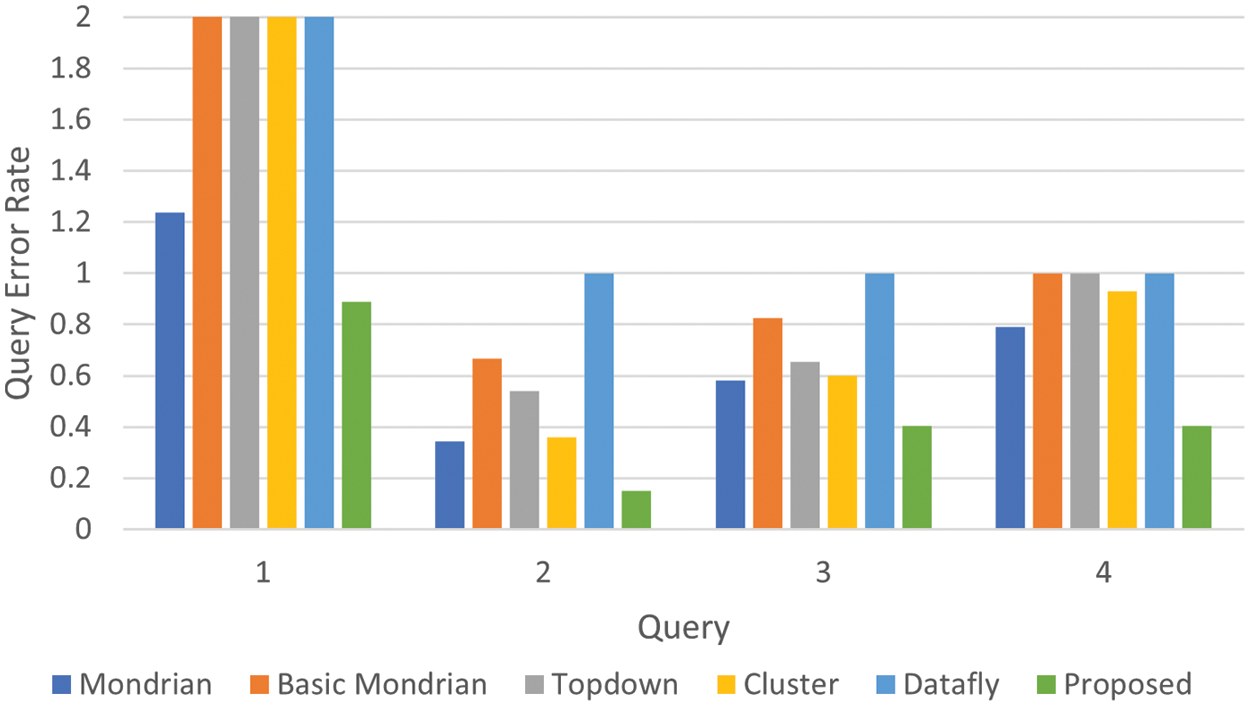
Figure 7: Comparison of query error rate results

•   Query1: Select Count (*) From Data_Set Where (Workclass = “Private” or Workclass = “Self-Emp-Not-Inc” Or Workclass = “Self-Emp-Inc”) and Age_Min = 35;

•   Query2: Select Count (*) From Data_Set Where Race = “Black” and Nativecountry = “United-States”;

•   Query3: Select Count (*) From Data_Set Where (Workclass = “Private” or Workclass = “Self-Emp-Not-Inc” or Workclass = “Self-Emp-Inc”) And Age_Min > 55 And Race = “White”;

•   Query4: Select Count (*) From Data_Set Where (Workclass = “Private” or Workclass = “Self-Emp-Not-Inc” or Workclass = “Self-Emp-Inc”) And Age_Min > 70 And Race = “White”;

According to the results presented in Fig. 7, the algorithms must be near zero to be considered successful in terms of the error rate metric. In this context, our proposed algorithm outperformed all other algorithms in simple queries like Query2, hierarchical queries like Query1, and sensitive queries like Query3, and Query4. The types of queries for more specific fields are Query3 and Query4. These queries were made on the values that are numerically less than the others on the dataset. As a result, the fact that the proposed algorithm gives similar results in the Query3 and Query4 graphs demonstrates the algorithm’s success in terms of data utility more clearly.

4.2.5 Classification Accuracy

The CA is the percentage of correctly classified test set equivalence classes. P is the number of positive equivalence classes. N is the number of negative equivalence classes. True positives (TP) are correctly labeled positive groups. True negatives (TN) are negative groups that are correctly labeled [51]. CA is determined using the following formula considering this information:

CA=TP+TNP+N(9)

The proposed algorithm’s CA was evaluated using four different classifiers: KNN, support vector machine (SVM), random forest (RF), and Naive Bayes (NB). The performances of the proposed algorithm at different k values are shown in Figs. 8 and 9. According to the results presented in the graphics, it is known that the algorithm with a higher CA is the most successful. The results obtained from the original dataset are reflected in the graph. CA values close to the baseline indicate little information loss. In other words, it indicates that it has high data utility.

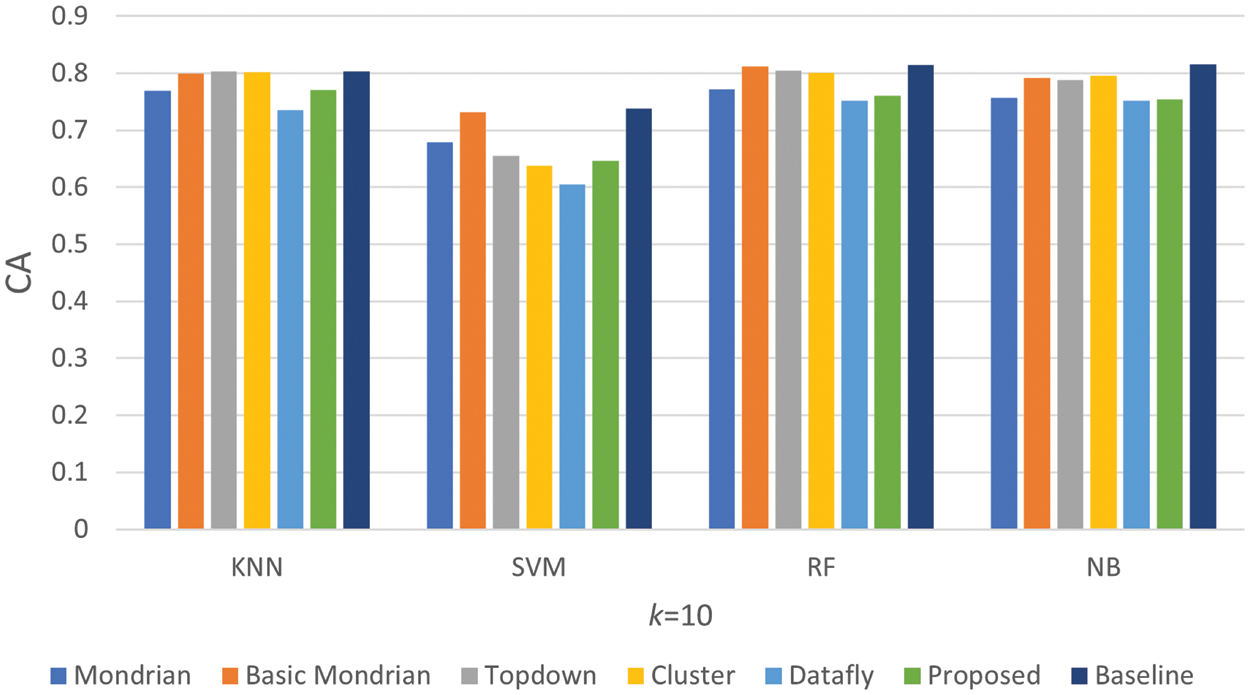
Figure 8: Comparison of classification accuracy k = 10 results

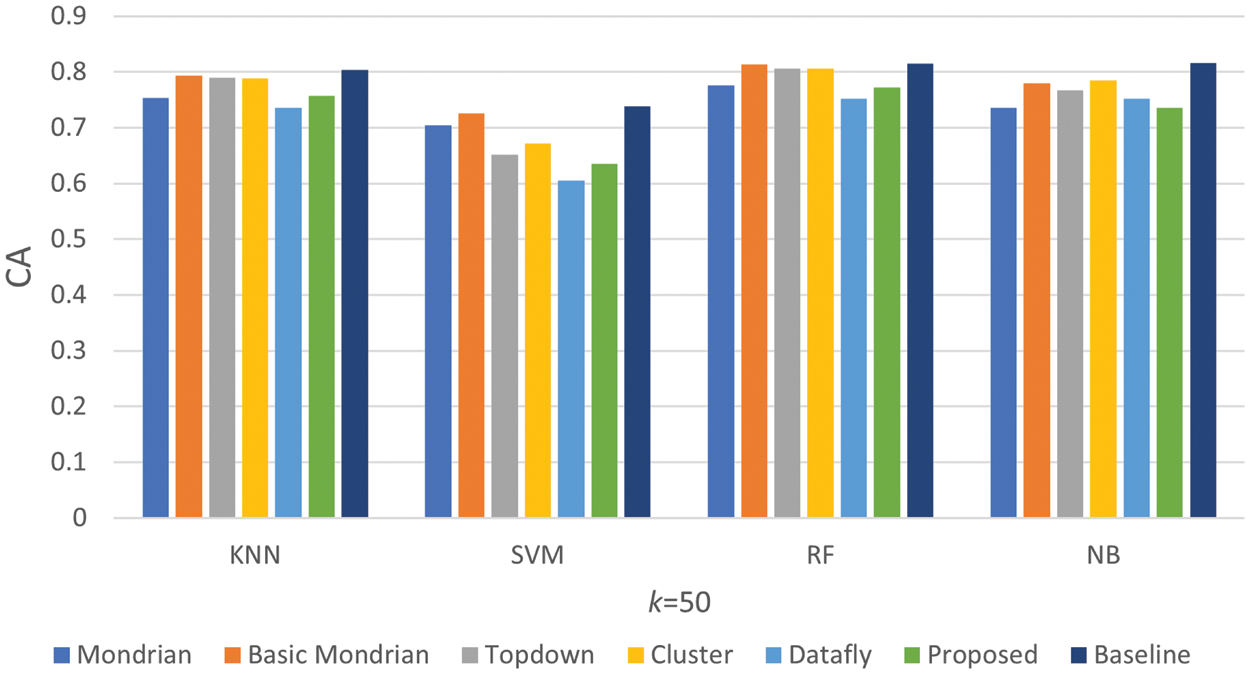
Figure 9: Comparison of classification accuracy k = 50 results

In Fig. 8, the CA of the anonymized dataset forms of each algorithm obtained by applying it to the Adult dataset and the original Adult dataset form are compared. The CA result of the Adult dataset’s original version is shown as a baseline in the graph. Among the algorithms, the Datafly algorithm has the worst result. Another situation observed in the graph is that the proposed algorithm obtained results similar other algorithms. When the findings in Fig. 9 are reviewed, it is clear that the algorithms’ performances under 10 and 50 k values are not far apart. The proposed algorithm has achieved successes similar other algorithms with this parameter value. Consequently, the proposed algorithm performed well in terms of data utility in this metric.

4.2.6 F-Measure

The F-measure, also known as the F-score or F1 score, is a measure of the accuracy of a test and is used to evaluate classification techniques [52]. We use precision and recall measurements when calculating the F-measure. These measurements are calculated as [51]:

Precision=TPTP+FP(10)

Recall=TPTP+FP=TPP(11)

The F-measure is defined as:

F−measure=2 × precision × recallprecision+recall(12)

As in the CA section, four different classification methods are used to analyze the F-measure performance of the proposed algorithm. To evaluate the performance of the proposed algorithm, the F-measure values of the original and anonymized versions of the Adult dataset produced by applying each algorithm are shown in Figs. 10 and 11. The results obtained from the original dataset are reflected in the graph as a baseline. When examining the values presented in the graph, it should be noted that the algorithm with the highest F-score achieves the best result. F-measure values closer to the baseline are also better.

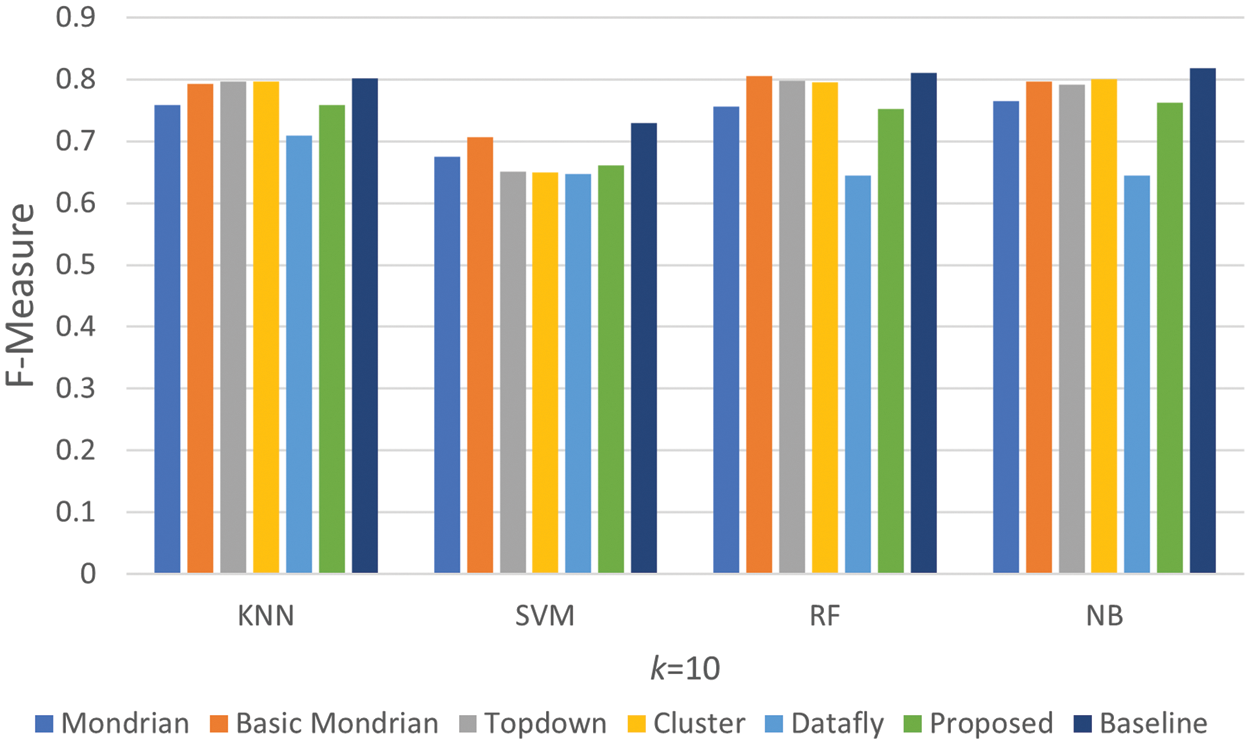
Figure 10: Comparison of F-measure k = 10 results

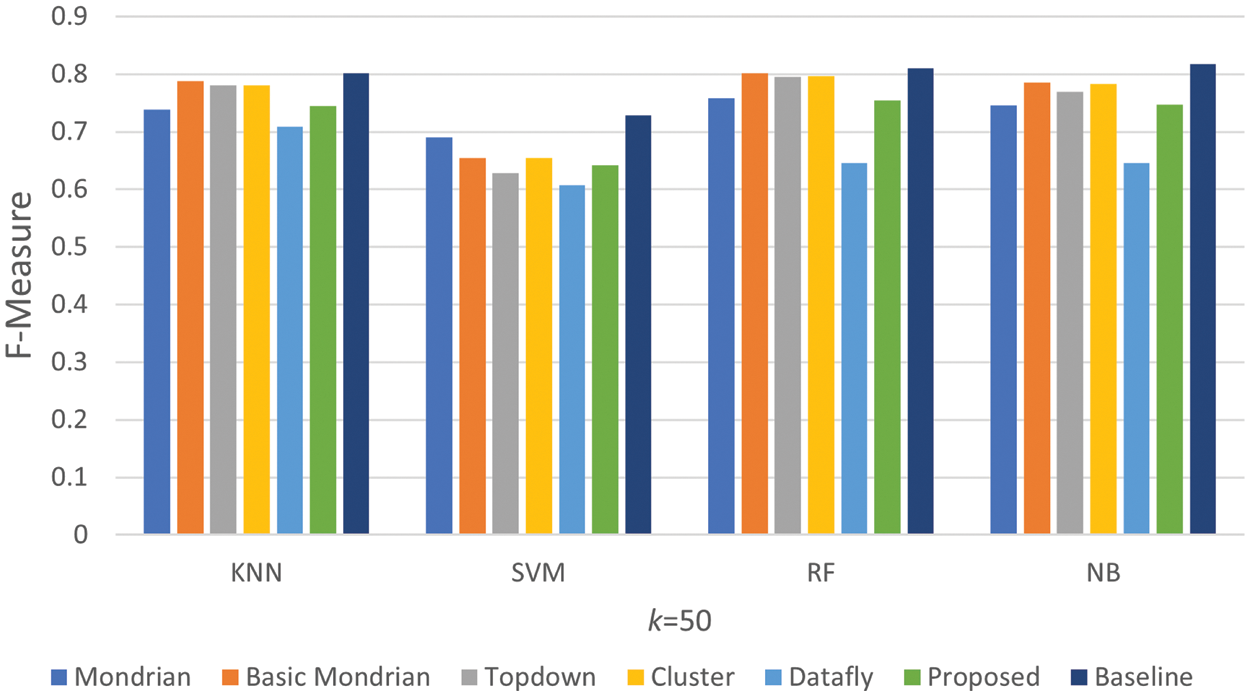
Figure 11: Comparison of F-measure k = 50 results

Except for the Datafly, all algorithms performed well in the findings shown in Fig. 10. The graph shows that our proposed algorithm produced results that were close to the baseline value in the tests that were run. When the findings in Fig. 11 are reviewed, it is discovered that the algorithms perform similarly to the results in Fig. 10 at this k value. As a consequence of examining the F-measure findings in two graphs, it is clear that the proposed algorithm is successful in terms of all four classifiers.

4.3 Discussion

In this section, a general evaluation of the results obtained by the proposed algorithm and other k-anonymization based algorithms is presented. In order to have a clearer understanding of the performance of the proposed algorithm in experiments, success rates against other k-anonymization-based algorithms are presented in a Table 2. Additionally, the time complexity calculations and industrial benefits of the proposed algorithm are also provided in this section.

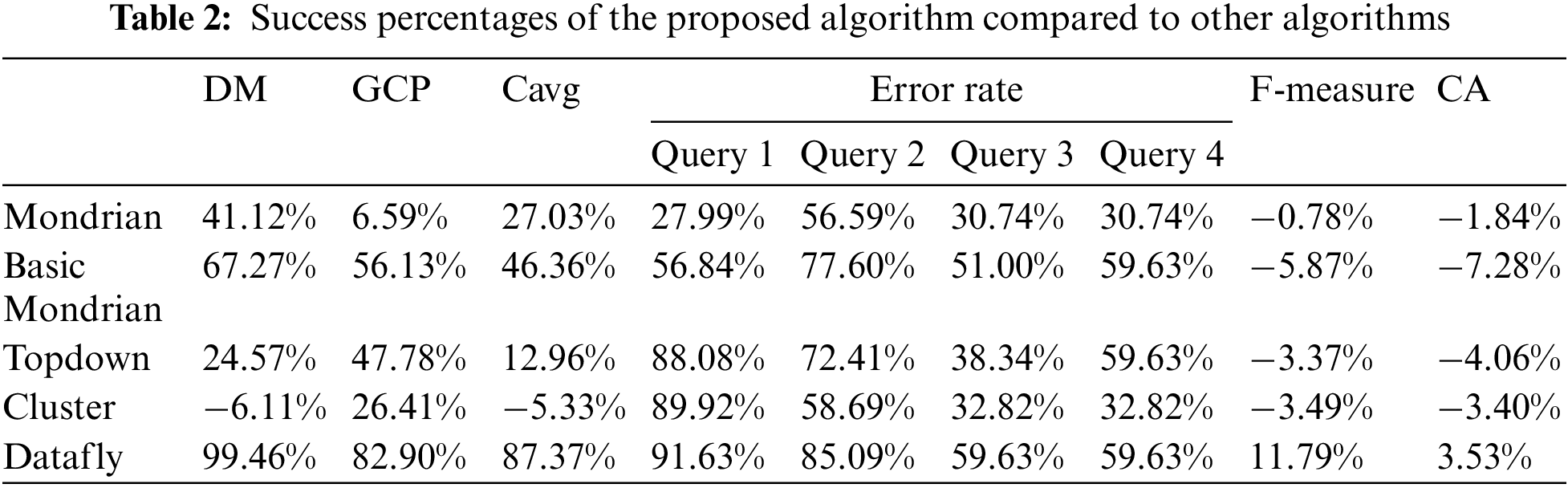
•   The proposed algorithm generates more equivalence classes than the Mondrian algorithm. This has a positive effect on the data utility.

•   The proposed algorithm has achieved more successful results in terms of DM, Cavg, GCP, query error rate, CA and F-measure metrics compared to other algorithms based on k-anonymization.

•   The proposed algorithm offers higher data utility than other algorithms based on k-anonymization.

•   Considering all algorithms in Table 1, the proposed algorithm differs from other algorithms in that it can be applied to both categorical and numerical data.

•   The proposed algorithm’s ability to group similar data points together has been demonstrated through its positive impact on the GCP metric and error rate values, resulting in an increased level of data utility compared to other algorithms.

4.3.1 Time Complexity

In this study, a new data anonymization algorithm was proposed using the Mondrian and COF algorithms. Assuming n is the number of elements in the dataset and k is the parameter for k-anonymity. The time complexity of the Mondrian is O(n log n) [14]. The time complexity of the COF is O(n) for low-dimensional datasets, O(n log n) for medium-dimensional datasets, and O(n2) for high-dimensional datasets. Therefore, the worst-case time complexity of the COF algorithm is O(n2) [39]. For small and medium-dimensional datasets, our proposed algorithm operates with a time complexity of O(n log n), while for large high-dimensional datasets, the time complexity is O(n log n + n2/k). This variability is due to the performance of the outlier algorithm used, and the verifications made from the obtained runtime results confirm this situation. As a result, although the time complexity of the proposed algorithm is higher than Mondrian’s, the difference that arises in very high-dimensional datasets can be negligible considering the high data quality it offers.

4.3.2 Industrial Benefits

The industrial benefits of the proposed privacy-preserving data publishing algorithm are as follows:

•   Publishing of preserved data: The proposed algorithm ensures the protection of personal data, making it easier for data owners to share their data. This can help businesses or researchers access a larger data set and achieve better results.

•   Customer privacy: The proposed algorithm can protect customer data and ensure customer privacy for businesses. This can increase customer trust, enhance customer satisfaction, and promote customer loyalty.

•   Legal compliance: The proposed algorithm ensures compliance with laws such as general data protection regulation (GDPR) regarding the protection of personal data. This enables businesses to act in compliance with the law and prevent legal issues.

•   Data analysis: The algorithm ensures that the protected data is available. This can help businesses make better business decisions by analyzing data.

•   Competitive advantage: The algorithm can provide businesses with a competitive advantage. By using this algorithm to ensure customer privacy and legal compliance, businesses can gain their customers’ trust and differentiate themselves from their competitors.

5  Conclusion and Future Work

The presence of outlier data causes various data utility challenges for algorithms used to ensure data privacy. This work introduces a new privacy-preserving data publishing algorithm that improves data utility via an outlier detection mechanism. Various performance metrics with different evaluation criteria were applied and tested to demonstrate the success of the proposed algorithm. The findings of the experiments clearly illustrate that the outlier detection technique boosts the overall data utility of anonymizations. The proposed algorithm has important implications for industry as it offers several benefits, such as making it easier to share protected data, ensuring customer privacy, complying with legal requirements, and providing data for analysis, as well as providing a competitive advantage. Additionally, the proposed algorithm introduces a novel approach for protecting privacy by detecting outliers before anonymization, reducing the computational cost, and increasing the overall data utility. The proposed algorithm’s time complexity is O(n log n) for small and medium-dimensional datasets and O(n log n + n2/k) for large high-dimensional datasets. The results of this study suggest that the proposed algorithm can be a valuable tool for organizations that require privacy-preserving data publishing while maintaining high data utility.

As a possible future work, the outlier detection mechanism proposed in this paper can be further developed and algorithms with superior performance in terms of data utility can be designed. Furthermore, the developed algorithm’s success can be demonstrated not only in terms of data utility but also in terms of data privacy.

Acknowledgement: This study is based on previous works in the field of privacy-preserving data publishing. In this context, we are grateful to all the researchers who led us to develop a new privacy-preserving data publishing algorithm.

Funding Statement: This work was supported by the Scientific and Technological Research Council of Türkiye, under Project No. (122E670).

Author Contributions: Study conception and design: B. C. Kara, C. Eyupoglu; methodology: B. C. Kara, C. Eyupoglu; software: B. C. Kara; data curation: B. C. Kara; analysis and interpretation of results: B. C. Kara; draft manuscript preparation: B. C. Kara; writing, review and editing: B. C. Kara, C. Eyupoglu; supervision: C. Eyupoglu. All authors reviewed the results and approved the final version of the manuscript.

Availability of Data and Materials: The Adult dataset used in this study is available online at the University of California-Irvine, Machine Learning Repository.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. N. L. Raju, M. Seetaramanath and P. S. Rao, “An enhanced dynamic KC-slice model for privacy preserving data publishing with multiple sensitive attributes by inducing sensitivity,” Journal of King Saud University-Computer and Information Sciences, vol. 32, no. 10, pp. 1394–1406, 2022. [Google Scholar]

2. M. Kumar, P. Mukherjee, S. Verma, Kavita, J. Shafi et al., “A smart privacy preserving framework for industrial IoT using hybrid meta-heuristic algorithm,” Scientific Reports, vol. 13, no. 1, pp. 1–17, 2023. [Google Scholar]

3. Y. Liang, Y. Liu and B. B. Gupta, “PPRP: Preserving-privacy route planning scheme in VANETs,” ACM Transactions on Internet Technology, vol. 22, no. 4, pp. 1–18, 2022. [Google Scholar]

4. J. J. V. Nayahi and V. Kavitha, “Privacy and utility preserving data clustering for data anonymization and distribution on Hadoop,” Future Generation Computer Systems, vol. 74, no. 1, pp. 393–408, 2017. [Google Scholar]

5. L. Sweeney, “Simple demographics often identify people uniquely,” Health (San Francisco), vol. 671, pp. 1–34, 2000. [Google Scholar]

6. L. Sweeney, “k-Anonymity: A model for protecting privacy,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, vol. 10, no. 5, pp. 557–570, 2002. [Google Scholar]

7. A. Machanavajjhala, J. Gehrke, D. Kifer and M. Venkitasubramaniam, “ℓ-Diversity: Privacy beyond k-anonymity,” ACM Transactions on Knowledge Discovery from Data, vol. 1, no. 1, 3-es, 2007. [Google Scholar]

8. N. Li, T. Li and S. Venkatasubramanian, “t-Closeness: Privacy beyond k-anonymity and l-diversity,” in IEEE 23rd Int. Conf. on Data Engineering, Istanbul, Turkey, pp. 106–115, 2007. [Google Scholar]

9. C. Dwork, “Differential privacy,” in Proc. Conf. on Automata, Languages and Programming: 33rd Int. Colloquium, Berlin, Germany, pp. 1–12, 2006. [Google Scholar]

10. Y. Canbay, Y. Vural and Ş. Sağıroğlu, “Oan: Outlier record-oriented utility-based privacy preserving model,” Journal of the Faculty of Engineering and Architecture of Gazi University, vol. 35, no. 1, pp. 355–368, 2020. [Google Scholar]

11. B. C. Kara and C. Eyupoglu, “Anonymization methods for privacy-preserving data publishing,” Smart Applications with Advanced Machine Learning and Human-Centred Problem Design, vol. 1, pp. 145–159, 2023. [Google Scholar]

12. H. W. Wang and R. Liu, “Hiding distinguished ones into crowd,” in Proc. Conf. on Extending Database Technology: Advances in Database Technology, Saint Petersburg, Russia, pp. 624–635, 2009. [Google Scholar]

13. S. Zhang, B. Hu, W. Liang, K. -C. Li and B. B. Gupta, “A caching-based dual k-anonymous location privacy-preserving scheme for edge computing,” IEEE Internet of Things Journal, vol. 10, no. 11, pp. 9768–9781, 2023. [Google Scholar]

14. K. LeFevre, D. J. DeWitt and R. Ramakrishnan, “Mondrian multidimensional k-anonymity,” in Proc. Conf. on Data Engineering, Atlanta, GA, USA, pp. 25, vol. 2006, 2006. [Google Scholar]

15. M. Terrovitis, N. Mamoulis and P. Kalnis, “Local and global recoding methods for anonymizing set-valued data,” The VLDB Journal, vol. 20, no. 1, pp. 83–106, 2011. [Google Scholar]

16. S. Kim, H. Lee and Y. D. Chung, “Privacy-preserving data cube for electronic medical records: An experimental evaluation,” International Journal of Medical Informatics, vol. 97, no. 1, pp. 33–42, 2017. [Google Scholar] [PubMed]

17. H. Park and K. Shim, “Approximate algorithms for k-anonymity,” in Proc. Conf. on Management Data, Beijing, China, pp. 67–78, 2007. [Google Scholar]

18. M. E. Nergiz and C. Clifton, “Thoughts on k-anonymization,” Data & Knowledge Engineering, vol. 63, no. 3, pp. 622–645, 2007. [Google Scholar]

19. A. Gionis and T. Tassa, “k-Anonymization with minimal loss of information,” IEEE Transactions on Knowledge and Data Engineering, vol. 21, no. 2, pp. 206–219, 2009. [Google Scholar]

20. B. Kenig and T. Tassa, “A practical approximation algorithm for optimal k-anonymity,” Data Mining and Knowledge Discovery, vol. 25, no. 1, pp. 134–168, 2012. [Google Scholar]

21. J. Soria-Comas, J. Domingo-Ferrer, D. Sánchez and S. Martínez, “t-Closeness through microaggregation: Strict privacy with enhanced utility preservation,” IEEE Transactions on Knowledge and Data Engineering, vol. 27, no. 11, pp. 3098–3110, 2015. [Google Scholar]

22. A. Anjum, N. Ahmad, S. U. Malik, S. Zubair and B. Shahzad, “An efficient approach for publishing microdata for multiple sensitive attributes,” The Journal of Supercomputing, vol. 74, no. 10, pp. 5127–5155, 2018. [Google Scholar]

23. L. Sweeney, “Datafly: A system for providing anonymity in medical data,” in Database Security XI: Status and Prospects. Boston, MA, USA: Springer, pp. 356–381, 1998. [Google Scholar]

24. K. LeFevre, D. J. DeWitt and R. Ramakrishnan, “Incognito: Efficient full-domain k-anonymity,” in Proc. Conf. on Management Data, Baltimore, MD, USA, pp. 49–60, 2005. [Google Scholar]

25. K. Lefevre, D. J. Dewitt and R. Ramakrishnan, “Workload-aware anonymization,” in Proc. Conf. on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, vol. 2006, pp. 277–286, 2006. [Google Scholar]

26. J. Xu, W. Wang, J. Pei, X. Wang, B. Shi et al., “Utility-based anonymization using local recoding,” in Proc. Conf. on Knowledge Discovery and Data Mining, Philadelphia, PA, USA, vol. 2006, pp. 785–790, 2006. [Google Scholar]

27. J. Byun, A. Kamra, E. Bertino and N. Li, “Efficient k-anonymization using clustering techniques,” in Proc. Conf. on Database Systems for Advanced Applications, Berlin, Germany, pp. 188–200, 2007. [Google Scholar]

28. J. L. Lin and M. C. Wei, “An efficient clustering method for k-anonymization,” in Proc. Conf. on Privacy and Anonymity in Information Society, Nantes, France, vol. 331, pp. 46–50, 2008. [Google Scholar]

29. Y. Canbay, S. Sagiroglu and Y. Vural, “A new utility-aware anonymization model for privacy preserving data publishing,” Concurrency and Computation: Practice and Experience, vol. 34, no. 10, pp. 1–19, 2022. [Google Scholar]

30. F. Prasser, R. Bild, J. Eicher, H. Spengler, F. Kohlmayer et al., “Lightning: Utility-driven anonymization of high-dimensional data,” Transactions on Data Privacy, vol. 9, no. 2, pp. 161–185, 2016. [Google Scholar]

31. B. Yu, M. Song and L. Wang, “Local isolation coefficient-based outlier mining algorithm,” in Proc. Conf. on Information Technology and Computer Science, Long Beach, CA, USA, vol. 2, pp. 448–451, 2009. [Google Scholar]

32. H. Wang and R. Liu, “Hiding outliers into crowd: Privacy-preserving data publishing with outliers,” Data & Knowledge Engineering, vol. 100, no. 5, pp. 94–115, 2015. [Google Scholar]

33. H. Lee, S. Kim, J. W. Kim and Y. D. Chung, “Utility-preserving anonymization for health data publishing,” BMC Medical Informatics and Decision Making, vol. 17, no. 1, pp. 1–12, 2017. [Google Scholar]

34. M. E. Nergiz and M. Z. Gök, “Hybrid k-anonymity,” Computers & Security, vol. 44, no. 2, pp. 51–63, 2014. [Google Scholar]

35. L. Sun, K. Zhou, X. Zhang and S. Yang, “Outlier data treatment methods toward smart grid applications,” IEEE Access, vol. 6, pp. 39849–39859, 2018. [Google Scholar]

36. M. M. Breunig, H. P. Kriegel, R. T. Ng and J. Sander, “LOF: Identifying density-based local outliers,” in Proc. Conf. on Management Data, Dallas, TX, USA, pp. 93–104, 2000. [Google Scholar]

37. T. Huang, Y. Zhu, Y. Wu, S. Bressan and G. Dobbie, “Anomaly detection and identification scheme for VM live migration in cloud infrastructure,” Future Generation Computer Systems, vol. 56, no. 4, pp. 736–745, 2016. [Google Scholar]

38. S. Kim, N. W. Cho, B. Kang and S. H. Kang, “Fast outlier detection for very large log data,” Expert Systems with Applications, vol. 38, no. 8, pp. 9587–9596, 2011. [Google Scholar]

39. J. Tang, Z. Chen, A. W. Fu and D. Cheung, “A robust outlier detection scheme for large data sets,” in Proc. Conf. on Advances in Knowledge Discovery and Data Mining, Taipei, Taiwan, 2002. [Google Scholar]

40. J. Tang, Z. Chen, A. W. Fu and D. Cheung, “Enhancing effectiveness of outlier detections for low density patterns,” in Proc. Conf. on Advances in Knowledge Discovery and Data Mining, Taipei, Taiwan, pp. 535–548, 2002. [Google Scholar]

41. O. Alghushairy, R. Alsini, T. Soule and X. Ma, “A review of local outlier factor algorithms for outlier detection in big data streams,” Big Data and Cognitive Computing, vol. 5, no. 1, pp. 1–24, 2020. [Google Scholar]

42. Y. Wang, K. Li and S. Gan, “A kernel connectivity-based outlier factor algorithm for rare data detection in a baking process,” IFAC-PapersOnLine, vol. 51, no. 18, pp. 297–302, 2018. [Google Scholar]

43. Y. Vural and M. Aydos, “ρ-Gain: A utility based data publishing model,” Journal of the Faculty of Engineering and Architecture of Gazi University, vol. 33, no. 4, pp. 1355–1368, 2018. [Google Scholar]

44. R. Padmaja and V. Santhi, “An extended mondrian algorithm-XMondrian to protect identity disclosure,” Smart Intelligent Computing and Communication Technology, vol. 38, pp. 480–490, 2021. [Google Scholar]

45. R. Kohavi and B. Becker, “Adult data set,” Data Mining and Visualization Silicon. Graphics, 1996. [Online]. Available: https://archive.ics.uci.edu/ml/datasets/adult [Google Scholar]

46. M. Lichman, “UCI machine learning repository,” 2013. [Online]. Available: https://archive.ics.uci.edu [Google Scholar]

47. R. J. Bayardo and R. Agrawal, “Data privacy through optimal k-anonymization,” in Proc. Conf. on Data Engineering, Tokyo, Japan, pp. 217–228, 2005. [Google Scholar]

48. J. Li, R. C. W. Wong, A. W. C. Fu and J. Pei, “Anonymization by local recoding in data with attribute hierarchical taxonomies,” IEEE Transactions on Knowledge and Data Engineering, vol. 20, no. 9, pp. 1181–1194, 2008. [Google Scholar]

49. M. Djoudi, L. Kacha and A. Zitouni, “KAB: A new k-anonymity approach based on black hole algorithm,” Journal of King Saud University-Computer and Information Sciences, vol. 34, no. 7, pp. 4075–4088, 2021. [Google Scholar]

50. G. Ghinita, P. Karras, P. Kalnis and N. Mamoulis, “A framework for efficient data anonymization under privacy and accuracy constraints,” ACM Transactions on Database Systems, vol. 34, no. 2, pp. 1–47, 2009. [Google Scholar]

51. J. Han, J. Pei and M. Kamber, Data Mining: Concepts and Techniques, 3rd eds., San Francisco, CA, USA: Morgan Kaufmann Publisher, Elsevier, 2012. [Google Scholar]

52. C. Eyupoglu, M. A. Aydin, A. H. Zaim and A. Sertbas, “An efficient big data anonymization algorithm based on chaos and perturbation techniques,” Entropy, vol. 20, no. 5, pp. 1–18, 2018. [Google Scholar]