 Open Access
Open Access
ARTICLE
Double-Layer-Optimizing Method of Hybrid Energy Storage Microgrid Based on Improved Grey Wolf Optimization
1 College of Intelligent Science and Engineering, Hubei Minzu University, Enshi, 445000, China
2 College of Automation Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210000, China
* Corresponding Author: Xianbo Sun. Email:
Computers, Materials & Continua 2023, 76(2), 1599-1619. https://doi.org/10.32604/cmc.2023.039912
Received 24 February 2023; Accepted 27 April 2023; Issue published 30 August 2023
Abstract
To reduce the comprehensive costs of the construction and operation of microgrids and to minimize the power fluctuations caused by randomness and intermittency in distributed generation, a double-layer optimizing configuration method of hybrid energy storage microgrid based on improved grey wolf optimization (IGWO) is proposed. Firstly, building a microgrid system containing a wind-solar power station and electric-hydrogen coupling hybrid energy storage system. Secondly, the minimum comprehensive cost of the construction and operation of the microgrid is taken as the outer objective function, and the minimum peak-to-valley of the microgrid’s daily output is taken as the inner objective function. By iterating through the outer and inner layers, the system improves operational stability while achieving economic configuration. Then, using the energy-self-smoothness of the microgrid as the evaluation index, a double-layer optimizing configuration method of the microgrid is constructed. Finally, to improve the disadvantages of grey wolf optimization (GWO), such as slow convergence in the later period and easy falling into local optima, by introducing the convergence factor nonlinear adjustment strategy and Cauchy mutation operator, an IGWO with excellent global performance is proposed. After testing with the typical test functions, the superiority of IGWO is verified. Next, using IGWO to solve the double-layer model. The case analysis shows that compared to GWO and particle swarm optimization (PSO), the IGWO reduced the comprehensive cost by 15.6% and 18.8%, respectively. Therefore, the proposed double-layer optimization method of capacity configuration of microgrid with wind-solar-hybrid energy storage based on IGWO could effectively improve the independence and stability of the microgrid and significantly reduce the comprehensive cost.Keywords
Nomenclature
| PPV (t) | Output power of the photovoltaic array at time t |
| CPV | Rated output power of photovoltaic array |
| GAC | Current light intensity |
| Power temperature coefficient of photovoltaic array | |
| T | Current surface temperature of photovoltaic array |
| Tr | Reference temperature |
| GSTC | Light intensity under standard environment |
| PWT (t) | Output power of the wind turbine at time t |
| PEbuy (t) | Power of microgrid purchasing electricity from utility grid at time t |
| v (t) | Wind speed at time t |
| vr | Rated speed of wind turbine |
| vin | Rated cut-in speed of wind turbine |
| PES,c (t) | Charging power of the electric energy storage at time t |
| EES (t) | Electric energy storage at time t |
| Self-discharge efficiency of electrical energy storage | |
| vout | Rated cut-out speed of wind turbine |
| PES,d (t) | Discharge power of electric energy storage at time t |
| PEsell-max | The maximum selling power of the microgrid to utility grid |
| Discharge efficiency of electric energy storage | |
| Converter efficiency | |
| PEL-HT (t) | Output power from the electrolyzer to the hydrogen storage tank at time t |
| Efficiency of electrolyzer | |
| PEL (t) | Output power of electrolyzer at time t |
| EHT (t) | Capacity of hydrogen energy storage tank at time t |
| PHT-FC (t) | Output power from the hydrogen storage tank to the fuel cell at time t |
| Efficiency of hydrogen storage tank | |
| Efficiency of fuel cell | |
| PFC (t) | Output power of fuel cell at time t |
| CWT | Rated output power of wind turbine |
| PEsell (t) | Power of microgrid selling electricity to utility grid at time t |
| PLOAD (t) | Load power of microgrid at time t |
| Pi-max | Maximum output power of device i |
| Charging efficiency of electric energy storage | |
| PEbuy-max | The maximum purchasing power of the microgrid from utility grid |
| Ej-max | Maximum service capacity depth of equipment j |
| Ej-min | Minimum service capacity depth of equipment j |
| Pi,max | Power configuration upper limit of device i |
| Ej-max | Capacity configuration upper limit of device j |
| kmax | Upper limit of the ratio of electric energy storage power to capacity |
| kmin | Lower limit of the ratio of electric energy storage power to capacity |
Renewable energy generation has recently attained greater penetration and larger-scale grid connection benefits from the vigorous growth of distributed generation (DG). However, DG’s intermittent and fluctuating nature seriously influences the safe and stable microgrid (MG) operation. This impact affects the power quality and raises the difficulty of optimizing the operation of MG [1]. It is vital to find the optimal capacity configuration of each device in the MG to enhance the stability and quality of the system’s electrical energy.
The advancement of the economy and reliability of MG depends heavily on the energy storage system, which is necessary hardware for electrical energy transfer and load peak adjustment [2,3]. For systems that use a substantial amount of renewable energy, adding an energy storage system with a specific capacity could boost the ability to use renewable energy while maximizing overall economic benefits, achieving limitation of the amount of abandoned wind, solar, and electricity. From this, Suppressing the power fluctuation and reducing the difficulty of peak regulation of the grid, making the power output of the DG system more stable [4].
To address the problems of energy storage systems currently, this paper proposes building a hybrid energy storage system (HESS) with electric energy storage as short-duration energy storage (SDES); hydrogen energy storage as long-duration energy storage (LDES). The HESS fully uses electrical energy storage’s substantial flexibility and fast response characteristics. Meanwhile, hydrogen energy storage, used as LDES, has a large storage capacity, a low unit cost of energy storage, long service life, and high energy conversion efficiency. It can adjust the electric power in a long timescale and an ample space, realizing the energy transfer (exchange) in a wide area and time range, effectively coping with the seasonal output fluctuations of a high proportion of renewable energy. Therefore, the Electric SDES–Hydrogen HLDES (ESDES-HLDES) HESS proposed promotes the load response of different frequencies and the economic absorption of renewable energy, improves the system’s environmental protection, effectively promotes the power system’s stability and the ability to cope with extreme events to a certain extent.
After selecting the effective energy storage devices and building the topology of the MG model, the double-layer planning method is currently used as a faster and more effective solution for the MG capacity optimization allocation model. The outer layer algorithm tends to be an intelligent heuristic algorithm, and the inner layer algorithm varies according to different optimization objectives [5]. Therefore, this paper’s outer and inner layer objectives are constructed separately, considering the economy and system stability. The IGWO is used to solve the goal of obtaining the optimal configuration results that consider planning and operation.
Overall, this paper proposes a double-layer optimal configuration method of HESS in wind-solar MG based on IGWO. The introduction presents the context of the study. Section 2 analyzes the current research status and representative literature. Section 3 establishes the MG model containing a Wind Turbine (WT) and Photovoltaic array (PV) system coupled with ESDES-HLDES. In Section 4, the comprehensive cost of MG is taken as the outer objective function and the daily output fluctuation rate of the power generation system as the inner objective function. The relevant constraints are the characteristics and operation of DG. Then, a double-layer model for the optimal capacity of the MG is constructed. Aiming at the problems of slow convergence rate in the later period and easily falling into a local optimum of GWO, Section 5 proposes IGWO. Introducing the nonlinear convergence factor and Cauchy mutation operator improves the convergence and global optimization performance of GWO effectively. After the benchmark test function is used to test IGWO, GWO, and PSO, the advantages of IGWO are verified. Then it is used to solve this model. In Section 6, simulation analysis is carried out with the data of the scenery resources and a load of a certain scenery station in Belgium as the input. Comparison analysis is carried out with different scenes to verify the stability and superiority of the model proposed in this paper.
The optimal configuration of MG is a complex problem that involves the construction of distributed energy systems and the selection of optimal solution methods. Previous studies have focused on the selection and capacity deployment of the energy storage system. For instance, a day-ahead economic dispatching method was proposed for the integrated energy system of the park [6]. It has been demonstrated by the simulation results that the participation of energy storage devices could increase the operating flexibility of the generating units and, consequently, the efficiency of the system.
Several studies have noted HESS instead of the single energy storage technique mentioned above. Considering the thermal energy storage part of solar PV, Zhao et al. built a HESS with electric-thermal coupling, which improved the utilization rate of solar energy and elevated the economic benefits to a certain extent [7]. However, most of these methods used batteries as energy storage. With the high proportion of new energy generation with prominent seasonal supply characteristics connected to the grid, the mismatch of other power loads increases. The power system’s seasonal power and energy imbalance becomes increasingly apparent [8,9]. To alleviate this issue, Wang et al. proposed an improved HESS with a supercapacitor and battery coupled, which has the merits of processing speed and reaction time and could realize high and low-frequency power distribution. However, it is power-based SDES, which is difficult to adjust to the actual needs of the grid and rarely able to supply the need for electricity with a high energy density [10]. To address the seasonal imbalance between the supply and demand of power systems, Fang et al. conducted a refined analysis of the cost-benefit impact of LDES technology. According to the analysis, the adoption of LDES would result in a 40% decrease in the overall cost of the power system. However, the response speed of such technology could be faster, and the peaking ability to cope with the sudden load consumption behavior could be more vital [11]. As a result, the main focus of current research is developing an ESDES-HLDES HESS that combines the benefits of both types of energy storage. This strategy can successfully handle the seasonal power and energy imbalance while enhancing the power system’s overall effectiveness and adaptability.
After developing an effective model for MG, researchers have conducted studies on the optimal capacity of MG. Based on generative adversarial networks, Li et al. suggested a reliable technique for independent MG optimization of optical storage capacity allocation. This method ensures the efficient solution of the optimal configuration through robust optimization methods such as variable difference distance and sampling average approximation principle. The objective is to balance the economics of power allocation with the risk of operation. However, the results obtained by this method are more conservative, and deviations may occur between the preset scenarios and the actual scenarios. This could lead to the difficulty of failing to meet the operational reliability of the system [12]. For the MG with electric-hydrogen energy storage, Nguyen et al. considered the different response times and the influence of the uncertainty of power and load to optimize the capacity of the MG. However, when considering the uncertainty, the determined smooth average load is adopted during the solution, which weakens the response-ability of the system to cope with the mutation load [13]. In 2022, Zhang et al. used the optimization objective of minimizing the annual value of the initial investment cost and the annual operating cost to optimize the capacity allocation of a cogeneration MG based on hydrogen energy storage. The feasibility of replacing battery energy storage with hydrogen energy storage is demonstrated at the application level, and the economy of the system is greatly improved. However, the authors did not address the disadvantages of PSO, which led to slow convergence and tended to fall into local optimal [14]. To cope with the impact of renewable energy and load uncertainty on the grid system, Chao et al. proposed a method to optimize the capacity allocation of Water-Wind-Photovoltaic complementary schemes into the system to deal with the impact of renewable energy and load uncertainty on the grid system. They also established a nested mathematical model for capacity allocation and coordinated operation optimization of renewable energy systems. However, the carrying capacity of the system is weak in spring and winter, and further engineering practicality needs to be considered when planning and operating the system [15].
The current mainstream methods for solving the optimal allocation model of MG capacity are robust algorithms and intelligent algorithms. Luo et al. proposed a two-stage robust optimal-scheduling method based on a combined Wind-Photovoltaic-Fire-Storage system, considering the pollutant emission penalty. The method uses the Column-and-Constraint Generation (C&CG) algorithm, which is easy to converge and solve quickly. The model is transformed into an alternating main problem and subproblem with mixed integer linear form. The model has been verified by arithmetic examples to significantly improve system operation economy, smooth scenery fluctuations, and reduce pollutant emissions. However, the optimal configuration results of the method suffer from the problem that they are too conservative [16]. Because of their advantages of high efficiency and wide application scenarios when solving complex and multi-parameter problems [17–19], intelligent algorithms such as PSO, Tree-seed Algorithm, and GWO are widely used in MG capacity optimization [20–22].
For the specific methods to solve the problem of the equipment capacity of the MG, the current methods are mainly divided into single-layer and double-layer solution methods [23,24]. Previous work [23] constructed a photovoltaic-biogas on-grid energy system with the Levelized Cost of Energy, total net present cost, and the annualized cost of the system as the objective functions. It proposed a single-layer multi-objective MG capacity optimization method. However, this method is fundamentally a multi-objective optimization problem, and the optimal solution is theoretically too ideal, ignoring the system operation problem, which often makes it difficult to be applied in engineering. The two-layer solution method has been gradually researched by scholars in recent years because of its better solution effect. Mansouri et al. predicted the demand for electricity, heating, and cooling loads. They used Monte Carlo simulation and backward scenario reduction techniques to generate representative scenarios and construct an integrated energy system hub. A two-stage optimization method was completed. The first stage uses a particle swarm algorithm for planning and design, and the second stage is a mixed-integer non-linear programming model. The comparison shows that the method makes the entities of the planning architecture more accurate and effectively improves effectiveness and efficiency [25]. Previous work [26] established a two-layer model for the optimal allocation of energy storage and solved this model using an improved multi-objective PSO. By enhancing the model architecture, the double-layer model outperforms the single-layer model in terms of the distribution of the solution set and the effectiveness of the smoothing effect of energy storage on load variations. However, the influence of the system grid structure on the integrated loss sensitivity needs to be considered, and the stability of the model should be visually verified. In 2022, by considering three states of WT and PV, Wang et al. suggested a two-layer optimal model for enhancing the configuration of HESS capacity in MG. The upper layer of this model establishes a three-state model for WT and PV units, and the lower layer calculates the output capacity based on the initial capacity of the units imported from the upper layer, taking into account the reliability and establishing a configuration model to minimize the total cost of MG. The findings of the algorithm study demonstrate that this model significantly boosts the system’s economy while preserving its self-stability. However, this model does not examine the energy storage design or how the system is affected by the location of the energy storage installation [27].
After a comprehensive analysis of the literature above, it is evident that there needs to be more research on MGs for configuring hybrid energy storage systems. Hydrogen energy storage systems could transfer large capacity, zero pollution energy for extended periods, which is crucial in enhancing the economy and stability of the power grid. The double-layer planning approach can account for system economy and scheduling issues compared to the single-layer model, which significantly enhances the application performance of the configuration outcomes. Furthermore, while intelligent algorithms are often used for solving, their solution drawbacks should be studied more. Therefore, there is room for improvement as the traditional algorithms need more solving capabilities.
3 Wind-Solar-Hybrid Energy Storage Microgrid Model
The wind-solar-hydrogen HESS MG primarily comprises the wind-turbine power generation system, photovoltaic array power generation system, ESDES-HLDES, load, and related power electronic conversion devices. The system structure is shown in Fig. 1.
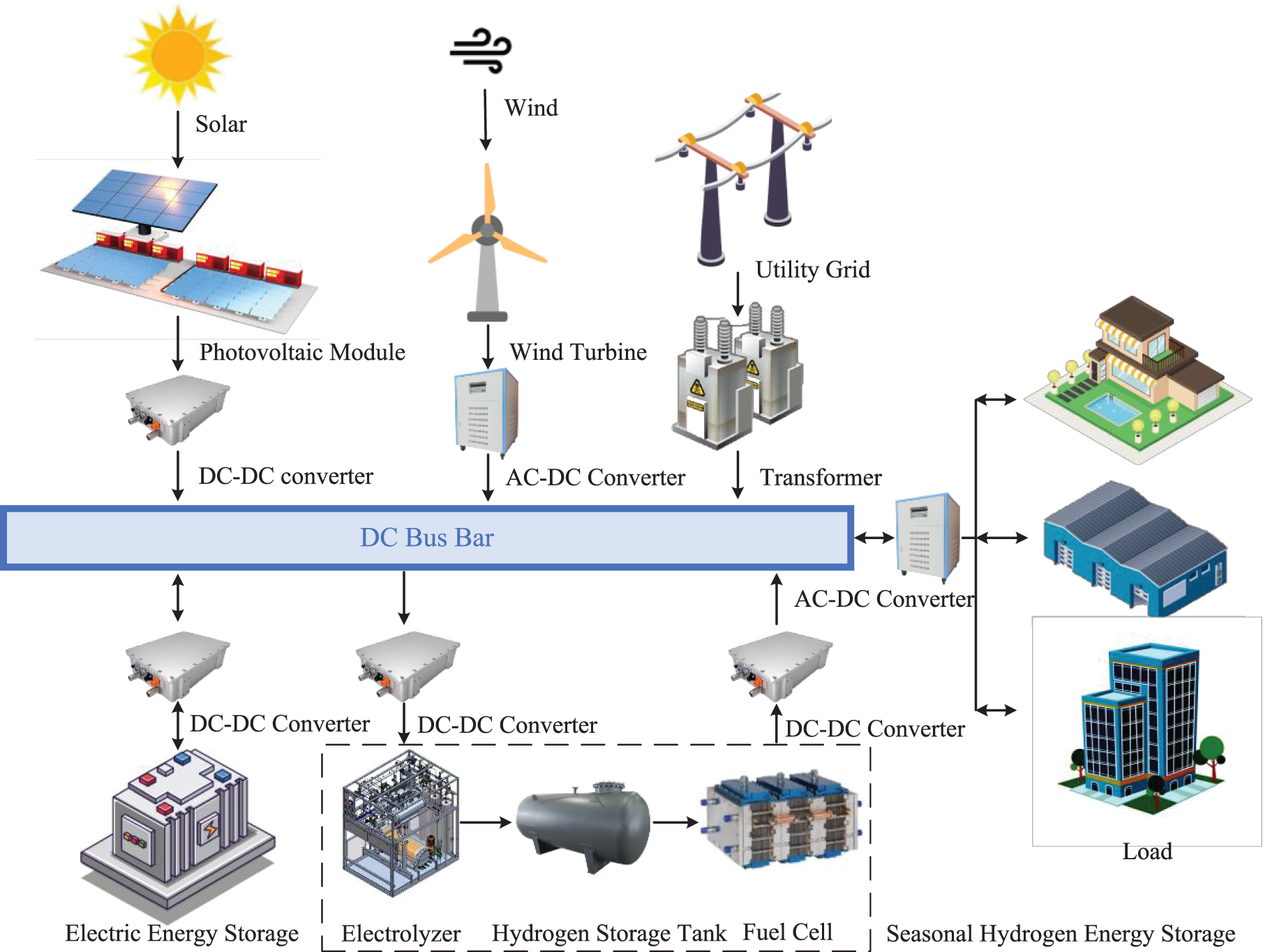
Figure 1: Microgrid topology diagram
The expression for the output power of photovoltaic power generation is shown in Eq. (1):
1
The expression of the output power of the wind turbine is shown in Eq. (2):
2
3.3 Hybrid Energy Storage Model
In a grid-connected MG system, coupling electric energy storage with seasonal hydrogen storage can achieve a more balanced distribution of supply loads and energy buffering than using a single energy storage system.
3.3.1 Electric Energy Storage Model
Despite its limited storage capacity, electric energy storage is utilized to smooth out oscillations brought on by abrupt load demand on the grid because of its quick reaction and high cycle efficiency [28]. Considering the charging and discharging states, the specific expressions for the change in the stored energy of the battery during charging and discharging are as follows:
(1) When the battery is charged, the electric storage energy is stored as shown in Eq. (3):
3
(2) When the battery is discharged, the electric storage energy is stored as shown in Eq. (4):
4
3.3.2 Seasonal Hydrogen Energy Storage Model
To cover the grid’s long-term loss of electricity, hydrogen energy storage is employed as a seasonal long-term energy storage solution. This is due to its high energy density, high conversion efficiency, and low loss rate during long-term storage [29]. The electrolyzer, hydrogen storage tank, and fuel cell are the three parts of the hydrogen energy storage system, and they are expressed as follows.
(1) Electrolyzer Model
The electrolysis tank achieves energy conversion and storage by the electrolyzer. The output power is modeled by Eq. (5):
5
(2) Hydrogen Storage Tank Model
The bidirectional hydrogen storage tank can hold the hydrogen created by the electrolysis of water in the electrolyzer. Simultaneously, it can provide hydrogen for electricity production in the fuel cell to improve the flexibility of the system. Its mathematical model of energy storage is shown in Eq. (6):
6
(3) Fuel Cell Model
The fuel cell uses hydrogen and oxygen as fuel and converts the chemical energy inside the fuel into electrical energy for storage. Its output power is shown in Eq. (7):
7
The meaning of the design parameters and the critical parameters taken in this section are shown in the Nomenclature.
4 Double-Layer Optimization Model
The double-layer optimization model is a double-layer structure with a coupling relationship. Each layer has a corresponding objective function and constraints; the inner and outer layers interact and influence each other in the optimization solution process [30]. The economy is regarded as the outer layer objective, and system stability is the inner layer target in the double-layer optimization model. The decision variables include photovoltaic module power, wind turbine power, electric storage power and capacity, fuel cell power, electrolyzer power, and hydrogen storage tank capacity. The double-layer optimization model proposed in this paper is shown in Fig. 2.
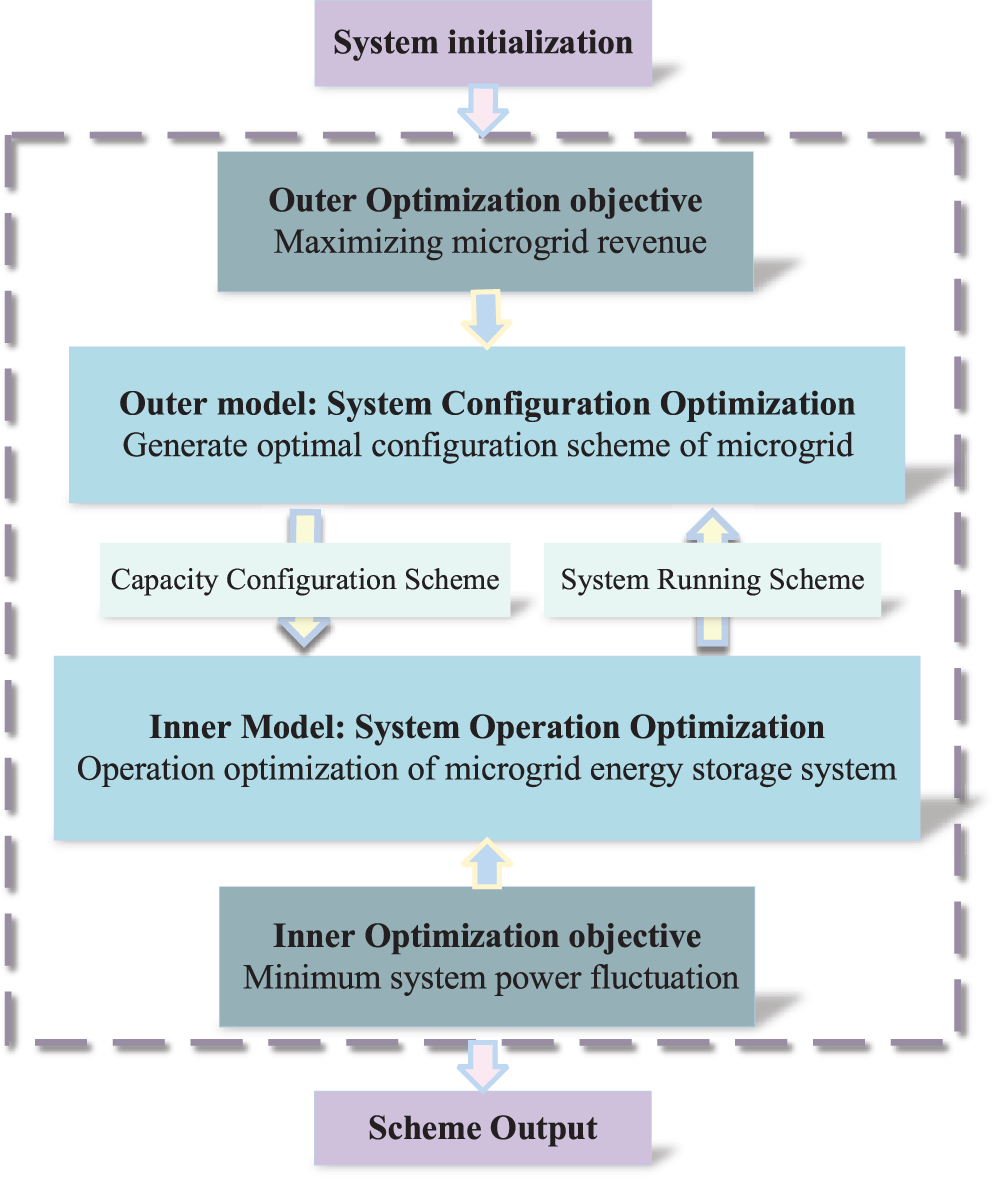
Figure 2: Double-layer optimization model architecture diagram
4.1 Objective Function of the Outer Model
In this paper, the objective function of the outer model is to minimize the lowest annual integrated cost of the MG system. This cost includes the initial investment cost, replacement cost, operation and maintenance cost of the system, and the cost of grid exchange with the utility grid. The specific expression is shown in Eq. (8):
8
The expressions in the formula are shown in Eq. (9):
9
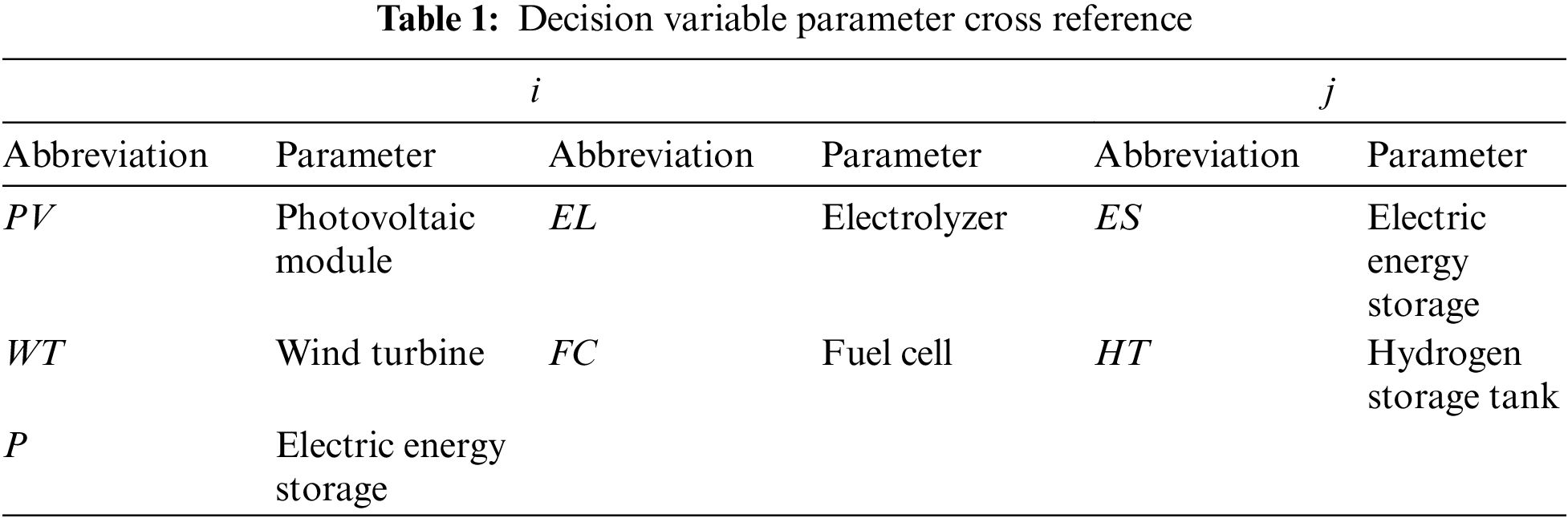
where kCRF = r(1 + r)N/(1 + r)N−1, r is the discount rate. The parameters related to i and j are shown in Table 1. The values of the vital related parameters in the above are shown in Table 2.

4.2 Outer Model Constraint Conditions
When solving the capacity optimization configuration scheme of the connection microcomputers, it is necessary to consider the restrictions of the system, including the restrictions of system electrical energy supply and demand balancing constraints and restrictions on the output power of each distributed power supply and investment.
(1) Power Balance Constraint
During normal MG operation, each components power balance must be ensured, and this is restricted by Eq. (10):
10
(2) Linking Line Exchange Power Constraints
The interaction power on the contact line must be within the exchange restrictions allowed by the system operation to ensure stable MG operation. This constraint is shown in Eq. (11):
11
(3) Each Equipment Capacity and Power Constraints
The power and equipment capacity generated by each device must be satisfied within a certain up-and-down power range, so constraints are made, as shown in Eq. (12):
12
(4) Investment Constraints
Due to restrictions on the construction venue, the capacity of each equipment configuration of the MG needs to be restricted within a reasonable range. This constraint is shown in Eq. (13):
13
4.3 Objective Function of the Inner Model
Minimizing the peak-to-valley in the MG’s daily output is the aim function of the inner objective. The energy storage charging and discharging behavior is optimized for the power generation system output by simulating 365 days of operation, as shown in Eq. (14):
14
maxP(H) and minP(H) are the maximum and minimum values, respectively, of the output of the MGs’ complementary power generation system on day h.
4.4 Inner Model Constraint Conditions
In the optimization of MG operation, it is necessary to consider the state and situation of the energy storage operation. Therefore, the following constraints are implemented:
(1) ESDES’ Constraints
As electric energy storage is employed to address the issue of electric energy supply and demand daily and since the charging and discharging of electric energy storage are staggered, the operation constraint shown in Eq. (15) is imposed:
15
where N1 = min{Zp, Mμ1}, N2 = min{Zp, M(1-μ1)}. M is a large positive number. μ1 = {0, 1}, charging when μ1 = 1; discharging when μ1 = 0.
(2) HLDES’ Constraints
Hydrogen storage is used as seasonal, long-term energy storage, and the electrolyzer is staggered with fuel cell operation. As a result, the following constraint, shown in Eq. (16), is imposed:
16
where O1 = min{ZEL,Mμ2}, O2 = min{ZFC,M(1-μ2)}. μ2 = {0, 1}, electrolyzer operating when μ2 = 1; fuel cell operating when μ2 = 0.
In the solution of the double-layer optimization model, the outer layer generates the capacity allocation scheme and passes it to the inner layer. The inner layer then finds the optimal local solution for the operation and passes it back to the outer layer. The outer layer optimizes the scheme again based on the feedback received from the inner layer and passes it back to the inner layer for further processing. Through multiple iterations of the inner and outer layers, a globally optimal solution is ultimately found that considers both layers’ objectives.
4.5 Evaluation Index of Microgrid System
Energy self-smoothness (ESS) reflects the self-sufficiency of the microgrids. Calculating by determining the ratio of the self-generated electricity to the total load supply in a statistical time. Shown in Eq. (17):
17
where EtExchange represents the interaction power between the MG and the distribution network at time t. The interaction power is negative when the microgrid delivers power to the distribution network, and vice versa is positive. EtLoad refers to the electricity consumption of the load at time t.
5 Capacity Optimization Configuration Method of Microgrid System Based on IGWO
This section aims to address the drawbacks of GWO, namely its’ slow convergence speed and tendency to fall into local optimal. The proposed solution is the improved IGWO, which boasts global solid search ability and fast convergence speed. The authors conducted experiments using Benchmark test functions to compare the performance of IGWO, GWO, and PSO. Based on the results, they selected IGWO as the superior optimizer and used it to solve the model.
Wu et al. introduced the meta-heuristic algorithm GWO in 2014. It is inspired by the leadership level and hunting mechanism of gray wolf populations in nature [31]. The basic theory of GWO is as follows:
(1) Hierarchy
The GWO hierarchy forces wolves to rigorously adhere to the direction of the α, β, and δ wolves during the iteration, enabling a well-organized hunt. Fig. 3 shows the distribution of wolf pack levels.
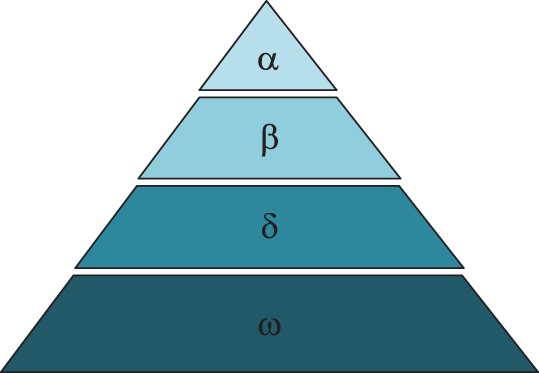
Figure 3: Gray wolf population distribution
In the figure, α > β > δ and the common gray wolf is ω, which follows α, β, δ and is guided by them to perform optimization.
(2) Encircling Prey
Searching for prey, the gray wolf population slowly moves closer and encircles it. Here is the mathematical model:
18
19
where t denotes the number of iterations of the current population, A and C denote the coefficient phasor, Xp denotes the location phasors of the prey, and X denotes the location phasors of the gray wolf, and the specific equations of A and C are as follows.
20
21
where α is the convergence factor, which decays linearly from 2 to 0 with an increasing number of iterations; r1 and r2 are the random numbers in [0, 1].
(3) Hunting
During each iteration, GWO selects the three optimal gray wolves as α, β, δ. Then update the remaining gray wolf positions according to the optimal gray wolf positions, as follows.
22
23
24
where Dα, Dβ, Dδ represent the distance between the wolf and the current candidate wolf; X represents the current candidate wolf position; C1, C2, C3 are random phase quantities; Xα, Xβ, Xδ represent the current position of the wolf; X1, X2, X3 represent the three best positions of the wolf; A1, A2, A3 represent the coefficient phase quantities of the three best positions of the wolf; X(t + 1) is the position of the wolf after iteration.
(4) Attacking Prey
Eq. (20) shows that A fluctuates with changes in α. As the number of iterations increases, the corresponding A value varies within the interval [–α, α].
25
when |A| < 1, wolves attack the prey, t is the current number of iterations, and T is the maximum number of iterations.
(5) Searching for Prey
The position that wolves rely on primarily to find prey is affected by A. When |A| > 1, gray wolves perform a global search for prey, and when |A| < 1, gray wolves perform a local search. The random coefficient C also affects the prey position, causing gray wolves to exhibit random search behavior when searching for prey.
5.2.1 Convergence Factor Nonlinear Adjustment Strategy
In GWO, the convergence factor α linearly decreases with the number of iterations. It can be challenging to maintain equilibrium between the local and global search processes in this variant. The linear decay is altered to nonlinear decay to speed up convergence and increase the scope of the GWO’s global search capacity. The trend of nonlinear dynamic changes with the increase in the number of iterations, which can better balance the search capability of the algorithm. The improvement is as follows:
26
The image of the improvement is shown in Fig. 4.
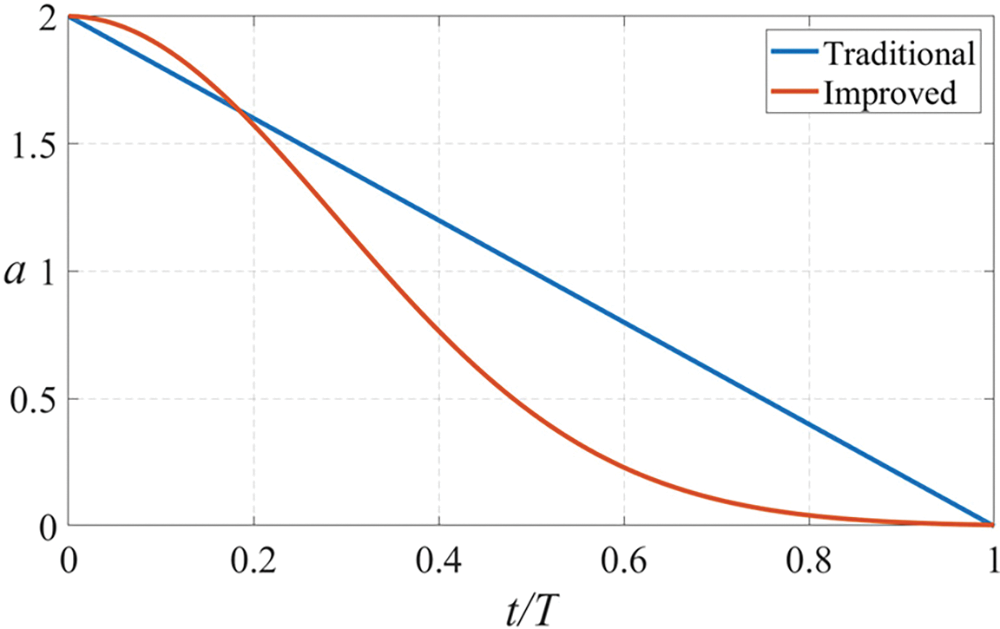
Figure 4: Improved adaptive parameter curve
By analyzing Fig. 4, it is found that in the early iteration, t/T starts to decrease slowly before 0.2. This ensures the global exploration ability of the algorithm. Then, it rapidly decreases and falls below 1 in the middle of the iteration. This significantly accelerates the algorithm’s rate of convergence. In the late iteration, t/T slowly decreases to 0 before increasing to 0.6. This improves the algorithm’s capacity for local search.
5.2.2 Cauchy Mutation Operator
The introduction of the Cauchy mutation operator enhances the GWO algorithm’s capacity to depart from the optimal local solution. This is because the GWO algorithm is prone to falling into local extreme values during the late iterations. The variation formulas are Eqs. (27) and (28):
27
28
where Xg(t) represents the optimal global solution of generation t, η is the variation weight, and C (0, 1) is the standard Cauchy random distribution when t = 1, λ is an adjustment parameter with a value range of [30,100].
The effectiveness of IGWO’s optimization was examined using Table 3. Three typical test functions were employed to compare the optimization performance of IGWO, GWO, and PSO. The population size of all three methods was 50, and the number of iterations was 1000. The optimization process is shown in Fig. 5, and the test results of IGWO are presented in Fig. 6.
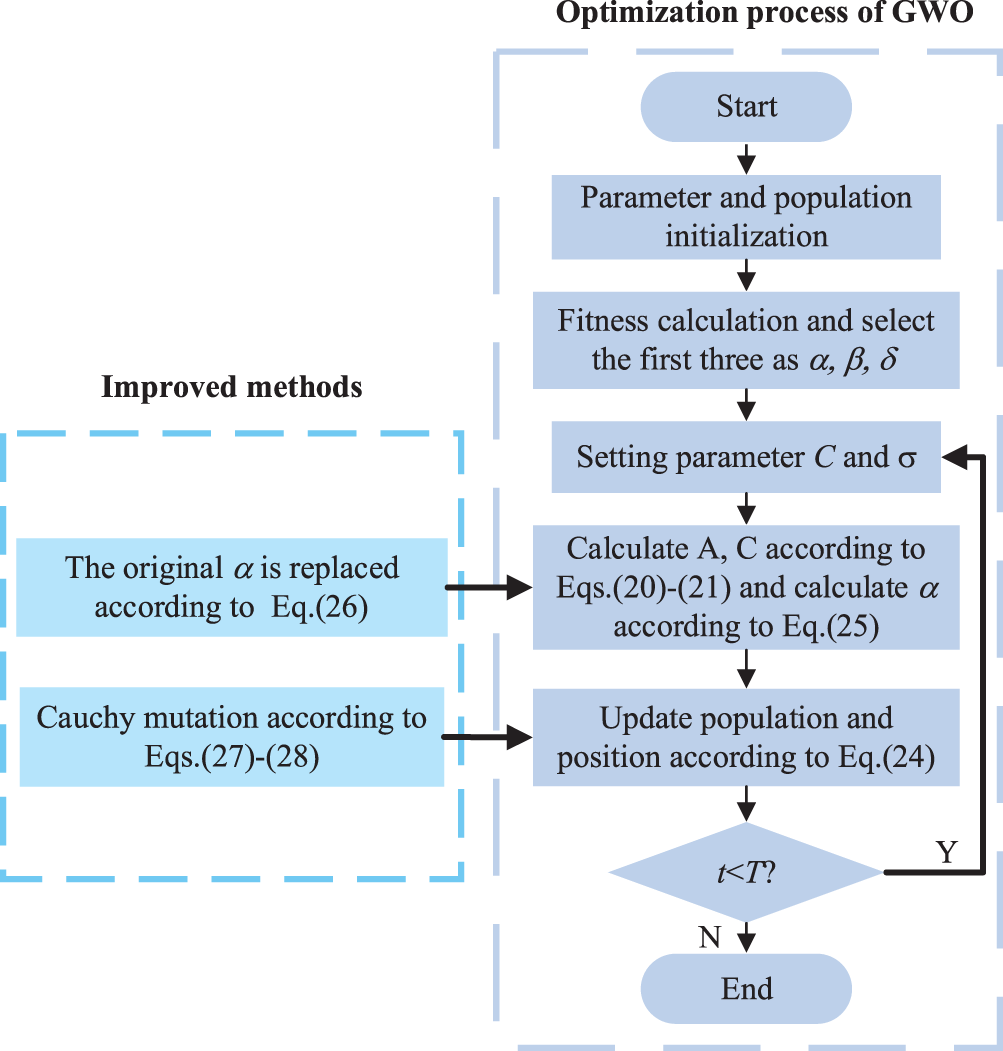
Figure 5: IGWO optimizes flow charts
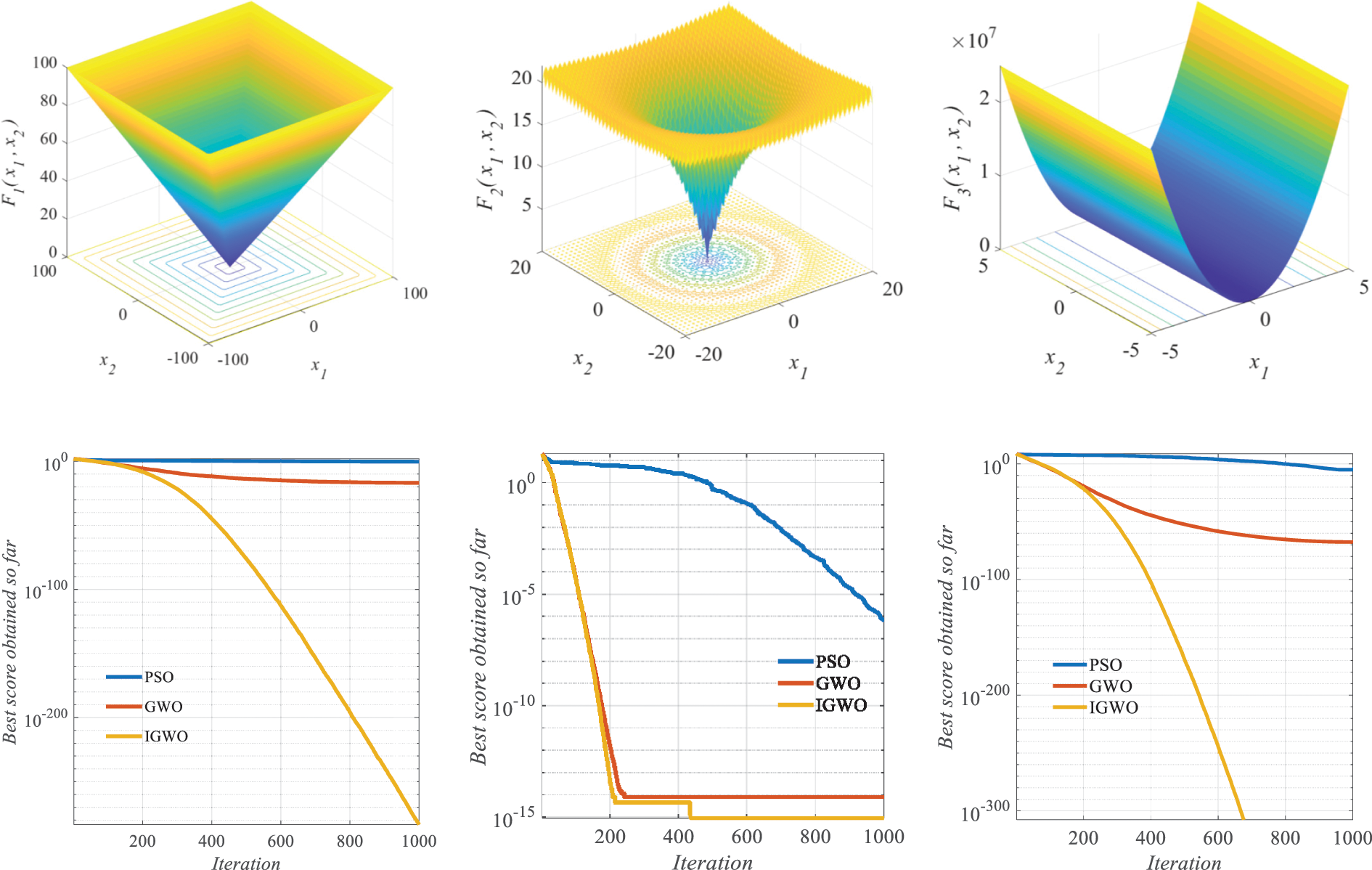
Figure 6: Test function results
After analyzing Fig. 6, it can be concluded that IGWO’s convergence speed is faster than that of PSO and GWO in unimodal test functions F1 and F2. IGWO can find a better solution with stronger local optimization ability under the same number of iterations, proving that the improved method in this paper effectively enhances GWO’s convergence speed and local optimization ability. Furthermore, by analyzing the multimodal test function F3, it was found that IGWO exhibits better global optimization ability in the early stage of iteration. The Cauchy mutation operator effectively avoids the problem of falling into local optimization. In the middle of the iteration, the dynamic boundary setting dynamically changes the search range, enabling the algorithm to jump out of local extreme values and continue global optimization when the curve falls into a local optimum. At the end of the iteration, IGWO can find a better value through global optimization. In conclusion, the test function results strongly demonstrate IGWO’s superior optimization ability.
This section aims to verify and analyze the proposed model and algorithm through experiments. The context of the simulation as well as the pertinent data and sources of model input are presented in Section 6.1. Then, four distinct scenarios are built. Section 6.2 evaluates the effectiveness of IGWO. Finally, in Section 6.3, GWO is applied to the above four scenarios to verify the effectiveness of the model.
6.1 Basic Data and Parameter Settings
The MG-related data of Belgium’s wind and photovoltaic integrated power station is taken as the input data [32]. The annual actual load data of the MG and the per unit value of wind and light power generation power with the hourly resolution are shown in Fig. 7. Additionally, the unit price of power acquired from the main network and the investment criteria for each piece of microgrid equipment are also included in Tables 4 and 5, respectively as [33]. Four scenarios are set to analyze and verify the model’s effectiveness in this paper, as shown in Table 6.
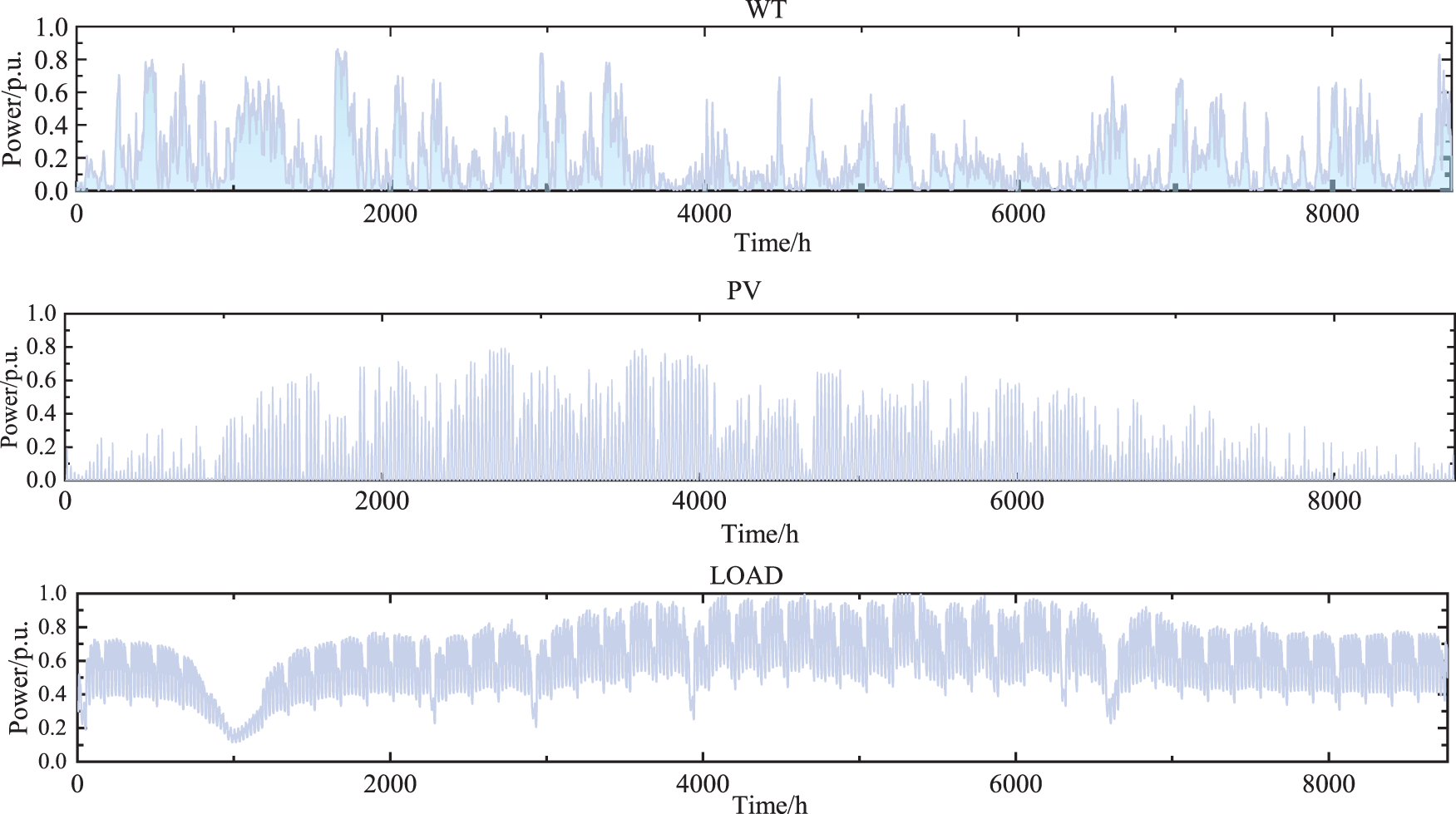
Figure 7: Annual wind, photovoltaic and load power data

6.2 Comparison and Analysis of IGWO and Others
The solution outcomes of IGWO, GWO, and PSO are compared for the MG capacity optimization problem in Scenario 4 to evaluate the effectiveness of the IGWO proposed further. In the solution process, the population size of the three algorithms is set to 30, and the maximum number of iterations is 200. The convergence curves of the three algorithms are shown in Fig. 8.
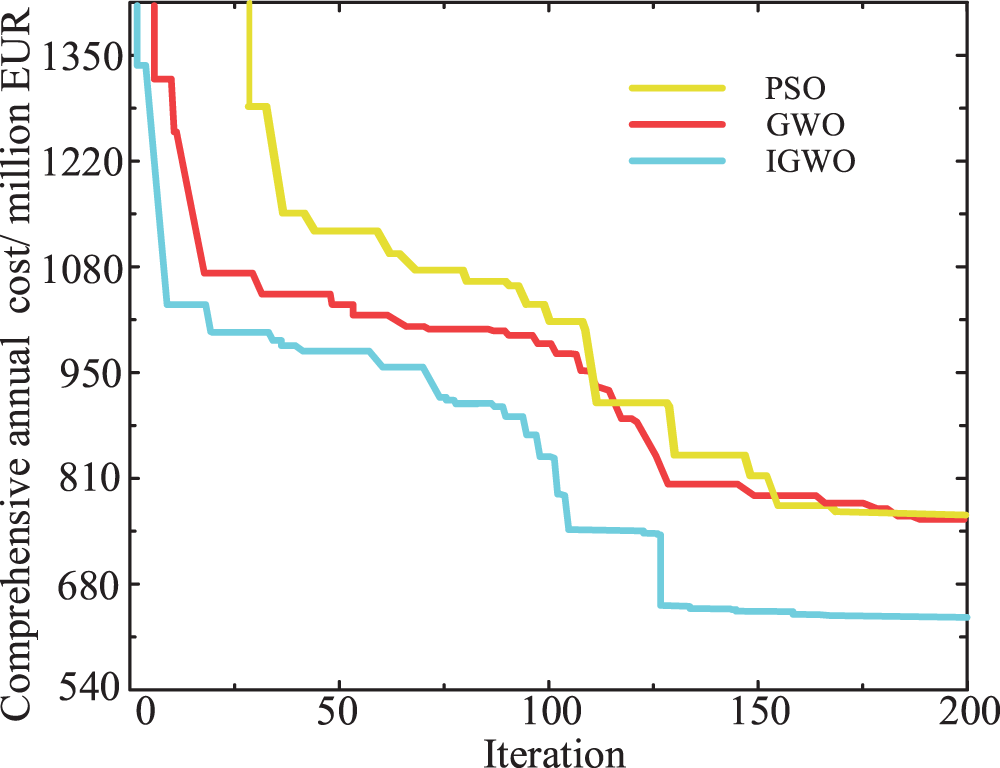
Figure 8: Comprehensive annual cost curve of three algorithms
As seen in Fig. 8, the convergence speed of IGWO is faster than that of the other two algorithms, and it reaches the convergence state in fewer iterations. This faster convergence is since compared to PSO, the α, β, δ (optimal solution, superior solution, and suboptimal solution) parameters in IGWO determine the direction and scope of the next solution, resulting in a wider search scope. Additionally, compared to the GWO, the introduction of nonlinear convergence factor α and the Cauchy mutation operator in IGWO also helps to expand its search scope. Therefore, the proposed IGWO algorithm has a faster convergence speed and stronger optimization ability in solving the double-layer capacity allocation model of electric seasonal hydrogen hybrid energy storage MG compared to the other two algorithms.
6.3 Comparison and Analysis of Different Schemes
In this section, the effectiveness of the proposed model is analyzed through experimental analysis. The MG system capacity configuration schemes and results obtained by solving scenarios 1–4 through IGWO are presented in Table 7. The effectiveness of different scenarios is compared to conclude.
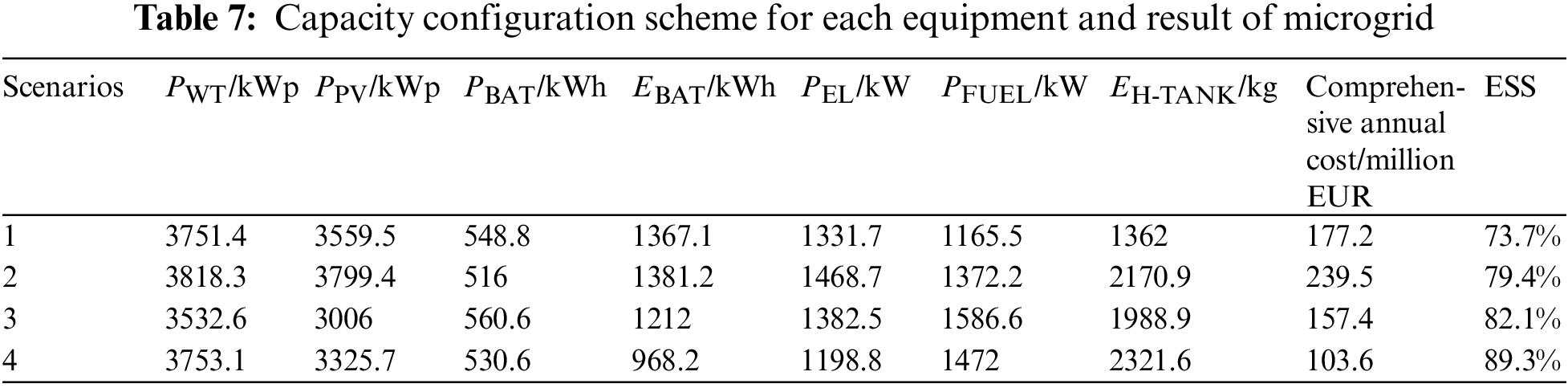
When comparing Scenario 1 with Scenario 2, and Scenario 3 with Scenario 4, it is found through analysis that, compared with configuring the ESDES, the HLDES in the grid-connected MG can improve the ESS and help to enhance the capacity of the MG to be self-sufficient in electricity. However, it is also discovered that using HLDES as the only energy storage technology would cause a high system total cost and significant investment issues. In Scenario 4, electric energy storage is added as ESDES, which effectively solves this problem. By building a HESS ESDES- HLDES, the economy and self-sufficiency of the MG are optimized. This proves the practicability of the proposed model.
This paper proposes a double-layer optimal capacity method of wind-solar-HESS microgrid, based on improved gray wolf optimization, to improve the economy and stability of the microgrid. By comparing different Scenarios and solving algorithms, the effectiveness and superiority of the proposed model and algorithm are demonstrated. The specific conclusions are as follows:
(1) The ESDES-HLDES model established can adapt to the seasonal fluctuations of renewable energy and achieve efficient utilization of electric energy, leading to high economic feasibility. By analyzing the output characteristics of each power source in the microgrid, the double-layer programming model could better coordinate different optimization objectives within the microgrid, formulate reasonable strategies and microgrid optimization operation schemes, and is conducive to solving complex planning problems.
(2) By introducing the nonlinear convergence factor and Cauchy mutation operator to improve GWO, an IGWO is proposed to solve the double-layer model of capacity optimal allocation in this paper. The test function and simulation results show that IGWO has substantial advantages in convergence speed and optimization performance.
The double-layer optimal configuration method proposed in this paper has shown effectiveness in quickly obtaining an economical and stable MG configuration. However, the research mainly focuses on electricity-hydrogen coupling. In the future study, the power output characteristics of each device should be further analyzed, and thermal energy should be considered to achieve further utilization of energy and meet multiple energy demands. This could achieve the developing of the microgrid-integrated energy system and other research on configuration and dispatch.
Funding Statement: This research was supported by the National Natural Science Foundation of China Under Grant 61961017 and Key R&D Plan Projects in Hubei Province 2022BAA060.
Availability of Data and Materials: Publicly available datasets were analyzed in this study. This data is found here: https://www.elia.be/, accessed on 1 January 2020.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. A. T. Àlex, M. Helena, C. Sergio and I. H. Jordi de, “Optimization models under uncertainty in distributed generation systems: A review,” Energies, vol. 15, no. 5, pp. 1932, 2022. [Google Scholar]
2. E. Dogan and D. Ibrahim, “Development and assessment of a novel hydrogen storage unit combined with compressed air energy storage,” Applied Thermal Engineering, vol. 219, pp. 119524, 2023. [Google Scholar]
3. Z. Zhang, K. Wen and W. Sun, “Optimization and sustainability analysis of a hybrid diesel-solar-battery energy storage structure for zero energy buildings at various reliability conditions,” Sustainable Energy Technologies and Assessments, vol. 55, pp. 102913, 2023. [Google Scholar]
4. Y. Cui, J. Zhang, Z. Wang, T. Wang and Y. Zhao, “Day-ahead scheduling strategy of Wind-PV-CSP hybrid power generation system by considering PDR,” Proceedings of the CSEE, vol. 40, no. 10, pp. 3103–3114, 2020. [Google Scholar]
5. X. Wang, P. Dong, L. Zhao, Y. Xue, K. Lin et al., “A two-layer optimization model for energy storage system configuration considering life cycle cost,” Journal of Physics: Conference Series, vol. 2418, no. 1, pp. 12017, 2023. [Google Scholar]
6. R. Yang, K. Li, J. Liu, J. Liu and Y. Xiang, “Day-ahead economic dispatch model of park integrated energy system considering reserve allocation of energy storage,” Electric Power Construction, vol. 43, no. 12, pp. 103–111, 2022. [Google Scholar]
7. Z. Ma, M. Li, K. Zhang and F. Yuan, “Novel designs of hybrid thermal energy storage system and operation strategies for concentrated solar power plant,” Energy, vol. 216, pp. 119281, 2021. [Google Scholar]
8. O. Marchenko and S. Solomin, “Modeling of hydrogen and electrical energy storages in Wind/PV energy system on the Lake Baikal coast,” International Journal of Hydrogen Energy, vol. 42, no. 15, pp. 9361–9370, 2017. [Google Scholar]
9. A. Lyden, C. Brown, I. Kolo, G. Falcone and D. Friedrich, “Seasonal thermal energy storage in smart energy systems: District-level applications and modelling approaches,” Renewable and Sustainable Energy Reviews, vol. 167, pp. 112760, 2022. [Google Scholar]
10. T. Wang, X. Zhang, Y. Wang, P. Zhou, Y. Cheng et al., “Energy management control strategy of hybrid energy storage system based on second-order filtering,” Acta Energiae Solaris Sinica, vol. 43, no. 11, pp. 399–405, 2022. [Google Scholar]
11. K. Fang, M. Zhou, Z. Wu, Z. Zhao, H. Zhao et al., “Optimal planning and cost-benefit analysis of long-duration energy storage for low-carbon electric power system,” Proceedings of the CSEE, pp. 1–17, 2022. [Online]. Available: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=ZGDC20221125008&DbName=DKFX2022 [Google Scholar]
12. Y. Li, X. Xu and Y. Zheng, “Distributionally robust optimal allocation for capacity distribution of photovoltaic and energy storage units in standalone microgrid based on generative adversarial network,” Automation of Electric Power Systems, pp. 1–14, 2022. [Online]. Available: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=DLXT20221021002&DbName=CAPJ2022 [Google Scholar]
13. N. Thi Hoai Thu, N. Tomonori and I. Masayoshi, “Optimal capacity design of battery and hydrogen system for the DC grid with photovoltaic power generation based on the rapid estimation of grid dependency,” International Journal of Electrical Power and Energy Systems, vol. 89, pp. 27–39, 2017. [Google Scholar]
14. J. Zhang, S. Kan, Y. Hua, X. Zhang, G. You et al., “Capacity optimization of CHP microgrid based on hydrogen energy storage,” Acta Energiae Solaris Sinica, vol. 43, no. 6, pp. 428–434, 2022. [Google Scholar]
15. C. Ma and L. Liu, “Optimal capacity configuration of Hydro-Wind-PV hybrid system and its coordinative operation rules considering the UHV transmission and reservoir operation requirements,” Renewable Energy, vol. 198, pp. 637–653, 2022. [Google Scholar]
16. Y. Luo, Y. Wang, C. Liu and L. Fan, “Two-stage robust optimal scheduling of wind power-photovoltaic-thermal power-pumped storage combined system,” IET Renewable Power Generation, vol. 16, no. 13, pp. 1–11, 2022. [Google Scholar]
17. M. Sharma, G. Singh and R. Singh, “Stochastic analysis of DSS queries for a distributed database design,” International Journal of Computer Applications, vol. 83, no. 5, pp. 36–42, 2013. [Google Scholar]
18. E. Ngozi and N. Clara, “Applications of artificial intelligence in agriculture: A review,” Engineering Technology and Applied Science Research, vol. 9, no. 4, pp. 4377–4383, 2019. [Google Scholar]
19. M. Sharma and K. Prableen, “A comprehensive analysis of nature-inspired meta-heuristic techniques for feature selection problem,” Archives of Computational Methods in Engineering, vol. 28, pp. 1103–1127, 2021. [Google Scholar]
20. G. Jin, Y. Liu, G. Li, Y. Xin and S. Li, “Collaborative optimization planning of an AC/DC hybrid distribution network frame and distributed power generation considering reliability,” Power System Protection and Control, vol. 50, no. 22, pp. 59–70, 2022. [Google Scholar]
21. Q. Xu, W. Teng, X. Wu, Y. Liu and S. Liang, “Capacity configuration method of flywheel storage system for suppressing power fluctuation of wind farm,” Energy Storage Science and Technology, vol. 11, no. 12, pp. 3906–3914, 2022. [Google Scholar]
22. C. Zhao, B. Wang, Z. Sun and X. Wang, “Optimal configuration optimization of islanded microgrid using improved grey wolf optimizer algorithm,” Acta Energiae Solaris Sinica, vol. 43, no. 1, pp. 256–262, 2022. [Google Scholar]
23. H. Al-Masri, A. Al-Sharqi, S. Magableh, A. Al-Shetwi, M. Abdolrasol et al., “Optimal allocation of a hybrid photovoltaic biogas energy system using multi-objective feasibility enhanced particle swarm algorithm,” Sustainability, vol. 14, no. 2, pp. 685, 2022. [Google Scholar]
24. P. Li, Z. Wang, H. Liu, J. Wang, T. Guo et al., “Bi-level optimal configuration strategy of community integrated energy system with coordinated planning and operation,” Energy, vol. 237, pp. 121539, 2021. [Google Scholar]
25. S. Mansouri, A. Ahmarinejad, M. Javadi and J. Catalão, “Two-stage stochastic framework for energy hubs planning considering demand response programs,” Energy, vol. 206, pp. 118124, 2020. [Google Scholar]
26. L. Lu, G. Zhu, T. Zhang and Z. Yang, “Optimal configuration of energy storage in a microgrid based on improved multi-objective particle swarm optimization,” Power System Protection and Control, vol. 48, no. 15, pp. 116–124, 2020. [Google Scholar]
27. P. Wang, X. Deng and K. Wang, “Double-layer capacity configuration method of hybrid energy storage in microgrid considering three states of wind turbines and photovoltaic units,” Modern Electric Power, pp. 1–10, 2023. [Online]. Available: https://kns.cnki.net/kcms/detail/detail.aspx?FileName=XDDL20220811003&DbName=CAPJ2022 [Google Scholar]
28. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, no. 3, pp. 46–61, 2014. [Google Scholar]
29. J. Brauns and T. Turek, “Alkaline water electrolysis powered by renewable energy: A review,” Processes, vol. 8, no. 2, pp. 248, 2020. [Google Scholar]
30. C. Yu, W. Li, N. Liu, L. Yang, S. Zhang et al., “Double-layer optimization study of virtual power plants with source-load-storage,” Journal of Physics: Conference Series, vol. 2401, no. 1, pp. 12056, 2022. [Google Scholar]
31. Y. Wu, X. Sun, B. Dai, P. Yang and Z. Wang, “A transformer fault diagnosis method based on hybrid improved grey wolf optimization and least squares-support vector machine,” IET Generation, Transmission & Distribution, vol. 16, no. 10, pp. 1950–1963, 2022. [Google Scholar]
32. https://www.elia.be/ [Google Scholar]
33. X. Zhong, B. Sun and Y. Wu, “A capacity optimization method for a hybrid energy storage microgrid system based on an augmented ε-constraint method,” Energies, vol. 15, no. 20, pp. 7593, 2022. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF Downloads
Downloads
 Citation Tools
Citation Tools