A Lightweight ABE Security Protection Scheme in Cloud Environment Based on Attribute Weight

1  Introduction

The development of big data, cloud environment, and multi-user ecological environment makes the traditional access control and encryption system no longer applicable, and ABE came into being. ABE is an extension of the traditional public key encryption system, and it was originally proposed by Sahai and Waters in 2005. ABE is a new way to achieve access control on ciphertext, it has access control capability and enhances the flexibility of access control, and has been applied in building a variety of security systems.

ABE is different from conventional access control, its characteristics are as follows: 1) the information processed in the ABE is always stored in ciphertext, and they can be used in a completely dangerous hostile environment, even if attacked, and the information will not be obtained. 2) The data owner encrypts information according to attributes, and it restricts the users’ access and decryption capabilities to ciphertext through access policies, ensuring the flexibility of data sharing. 3) In ABE, the user keys are related to the random polynomials, and it effectively prevents collusion attacks.

At present, ABE is widely used in the field of access control, which greatly guarantees the confidentiality, integrity, availability, and sharing security of data in cloud storage. However, there are still the following disadvantages: 1) Low efficiency: A large number of bilinear mappings are used in ABE, and it is time-consuming; 2) No accountability: The decryption key is not uniquely associated with personal identification information. Since multiple users share the same attributes, if the decryption key is maliciously sold, ABE is unable to achieve accountability for the user; 3) Heavy burden on users: The general ABE scheme has a large amount of computation, and the authorized user downloads the ciphertext to the local for decryption, which is a burden for the user. 4) Ignore the hierarchy of shared messages: Most of the current solutions focus on access control, but the shared messages have the multilevel hierarchy characteristic, the hierarchy structure hasn’t been explored in ABE.

Given the above problems in ABE, in this work, we provide a message security hierarchy ABE scheme based on attribute weight, which not only considers the efficiency, accountability, and the user’s computing power but also considers the fine-grained access needs of the message itself.

Its main contributions are as follows:

(1)   Propose a new ABE scheme for the scenario where the shared message requires hierarchical access.

(2)   Construct an access structure based on a threshold tree and attribute weight.

(3)   Provide a two-stage decryption approach. It greatly reduces the burden on users.

(4)   Design a series of experiments to test its performance.

Organization: The rest of the paper is organized as follows. Section 2 is the related work. Section 3 is the preliminaries. Section 4 describes the construction, and then the implementation and performance are shown in Section 5. Finally, we conclude in Section 6.

2  Related Work

2.1 Related Research of ABE

In literature [1], Shamir first proposed Identity-Based Encryption (IBE), it is assumed that there is a trusted key generation center to perform the work of issuing and verifying the legal identity of users. Later, people use biometrics to represent IBE’s functions, but existing IBE cannot be used due to noise issues, so in 2005, Sahai and Waters proposed the vague concept of IBE, named Fuzzy Identity-Based Encryption (FIBE) [2,3], and this paper proposed the concept of ABE for the first time. In FIBE, the identity is regarded as a set of attributes, the idea of a threshold scheme is introduced, and multiple public keys of users are constructed into a threshold structure with a logical relationship. It has strong fault-tolerance and anti-collusion attack abilities.

As the research goes deeper, Sahai and Waters further clarified and divided the ABE into Key Policy ABE (KP-ABE) and Ciphertext Policy ABE (CP-ABE). In 2007, Bethencourt, Sahai, and Waters proposed attribute encryption based on ciphertext strategy for the first time [4] (named CP-ABE). In this scheme, the structure of the access tree was used to hide the key of source data. The attributes and attribute values set by the leaf node for the data owner, as well as the secret values passed to the node by the parent node, are encrypted and processed. Users need to have the specific attributes of the leaf node to get the secret value S of this node. The non-leaf node is the threshold node, and the user needs to have the minimum attribute set that meets the threshold to decrypt the secret value of the threshold node. CP-ABE has a wide application that is generally used for encrypted data storage and fine-grained sharing on public clouds. The schemes or models based on CP-ABE include the CP-ABE model of the hidden access structure, ABE scheme with multiple authorization centers, ABEs that can be held accountable: white-box ABEs and black-box ABEs, etc. [5]. In KP-ABE scheme [6], ciphertexts are associated with sets of attributes, and private keys are associated with access structures.

Next, in 2012, Bonch proposed the concept of Functional Encryption (FE) [7], FE is an extension of traditional encryption, which allows a third party to calculate the function value of the output plaintext without decrypting the ciphertext. In literature [8], Garg used indistinguishable obfuscator early enough for general FE; later, many schemes improved the efficiency of FE: Abdalla first proposed a public key-based inner product function encryption scheme, and Boneh proposed the Order Revealing Encryption (ORE) system. Deng proposed Process Based Encryption (PBE) [9].

At present, almost all algorithms of ABE focus on access control of the user [10,11], but the decryption process of the ABE algorithm is coarse-grained control, and the user can either decrypt it, or cannot decrypt it at all. In practical applications, we always focus on the access control of the files, and need to perform fine-grained control over the decryption process, in recent years, some scholars have shifted the focus to access control of the shared messages, because the message is the purpose of users.

In 2012, Hierarchical Attribute-Set-Based Encryption (HASBE) was proposed by extending CP-ABE scheme with a hierarchical structure. This scheme employs multiple value assignments for access expiration time to deal with user revocation more efficiently than existing schemes. In 2013, Rouselakis and Waters proposed two large-scale ABE structures. This is a new large-scale ciphertext policy attribute encryption scheme on first-order bilinear groups, and significantly improves the efficiency of the KP-ABE system. It brings “program and cancel” techniques to address this problem, aiming to provide practical large-scale implementations of attribute encryption.

In 2016, File Hierarchy CP-ABE (FH-CP-ABE) [12] scheme is proposed. In this scheme, at different access levels, the shared messages are divided into many hierarchy subgroups, and the layered access structures are integrated and encrypted with the integrated access structure. The messages in the same hierarchical structure could be encrypted by an integrated access structure. In 2021, Extended File Hierarchy CP-ABE (EFH-CP-ABE) scheme [13] is proposed, which can encrypt multiple files on the same access level in the existing FH-CP-ABE scheme. It greatly saves storage space and computation costs on the cloud servers.

2.2 The Existing Problem

Throughout the development process of ABE, it has experienced a series of upgrades and improvements [14–17]. But access control for shared files is popular from a practical standpoint, especially since it is suitable for those big institutions or companies which have many hierarchical sectors.

At present, although the existing file hierarchy ABE schemes have saved time for encryption and decryption, and reduced the burden of storage, there are still some important factors not taken into account. For example, 1) Lack of accountability. If the decryption key is maliciously sold, ABE is unable to achieve accountability for the user. 2) Low efficiency. At present, the biggest burden of ABE is on the user. When the ciphertext files become larger and larger, ciphertext files must be downloaded to the user for decryption, which meets a challenge to the storage and computing power of the user. All of these are lack of in the above file hierarchy ABE. So, in this paper, we propose a new message hierarchy ABE scheme.

In this work, a new ABE scheme was proposed for the application scenario where the shared message requires hierarchical access. It makes up for the shortcomings of previous ABE programs.

3  Basic Theoretical Knowledge

To elaborate the proposed scheme in this paper, some relevant knowledge will be introduced.

3.1 Hash Function

A hash function is any function that converts an input of any length into a fixed-length output, and the output is the hash value. The values are called hash values, hash codes, checksums, or simply hashes. This transformation is a compression map. Some famous hash algorithms are MD5, SHA-256, SHA-512, et al.

3.2 Elliptic Curve Cryptography

Elliptic Curve Cryptography (ECC) is the theoretical basis of bilinear pairing. Generally, an elliptic curve refers to the curve determined by the Weierstrass equation. In cryptography, the elliptic curve on the finite field is used, that is, the variables and coefficients are all elements on the finite field, and the elliptic curve satisfies Eq. (1):

y2=x3+ax+b(mod p)(1)

All points (x, y) satisfied the Eq. (1), plus an infinite point O constitutes a set, where a, b, x, y are all on the finite field GF(p), and p is a prime number. Here the elliptic curve is denoted as: Ep(a,b). The elliptic curve has a finite number of points.

While 4a3+27b2≠0, based on the set Ep(a,b), it can define an Able groups. Assume that: P,Q∈Ep(a,b), then: P + O = P; If P = (x, y), then (x, y) + (x,−y) = O, that point (x,−y) is the additive inverse of P’s, which means −P.

Assume that P = (x1, y1) and Q=(x2,y2), P is not equal to Q, S=P+Q=(x3,y3), the value of S is determined by the following rules:

x3≡λ2−x1−x2(mod p)

y3≡λ(x1−x3)−y1(mod p)

λ≡{y2−y1x2−x1(mod p),P≠Q3x12+a2y1(mod p),P=Q

Point doubling operation is defined as repeated addition, for example, 3P = P + P + P.

3.3 Weil Pairing

The definition of Weil pairing: Suppose E (Fq) is an elliptic curve defined in a finite field Fq, P∈E(Fq) and Q∈E(Fq), there is a function that satisfies div(fQ)=nDQ, then the definition of P and Q’s Weil pairing is Eq. (2). Here, div(fQ) is the divisor of function fQ.

e∧(P,Q)=fP(DQ)fQ(DP)(2)

3.4 Bilinear Maps

The bilinear map is e:G0×G0→G1 implemented via the Weil pairing or Tate pairing. Suppose that k is the secure parameter, and prime order p is k-bits long. Let G0 and G1 be two multiplicative cyclic groups of prime order p, and let g be a generator of G0.

A map e:G0×G0→G1 is an admissible bilinear map if it satisfies the three following properties:

•   Computable. ∀P,Q∈G0, there exists an efficient algorithm to compute e(P,Q);

•   Bilinearity. For all a,b∈Zp, we have e(ga,gb)=e(g,g)ab.

•   Non-degeneracy. The map is non-degenerate, it must be e(g,g)≠1.

3.5 Shamir’s Secret Share

Secret distribution: first, the secret sharer needs to construct a t − 1th polynomial, assuming that the secret value to be shared is s. The polynomial f(x)=s+a1x+a2x2+⋯anxn−1 is constructed by randomly selecting t − 1 elements a1,a2,…at−1, and then the secret sharer calculates the secret share si=f(i)(mod p),i=1,2,…n, and sends it to the n participants. If a user has t secret shares at least, then he can calculate the shared secret value s.

Secret reconstruction: Assume that Dn={0,1,…,n−1}, we define the Lagrange coefficient pk(x) in Eq. (3):

pk(x)=Πi∈Bkx−xixk−xi(3)

Here, Bk={i|i≠k,i∈Dn}, pk(x) is a polynomial of n − 1 degree, which is satisfied ∀m∈Bk,pk(xm)=0 and pk(xk)=1. At last, we can get the Lagrange interpolation polynomial formula (5) and the expansion of Lagrange interpolation polynomial Eq. (4):

f(x)=∑j=0n−1⁡yjpj(x)(4)

fn(x)=yi∗(x−x2)(x−x3)…(x−xn)(x1−x2)(x1−x3)…(x1−xn+1)(5)

Using Eq. (5), the secret value can be calculated, here s=f(0).

4  Access Control Policy and Model

The access policy, named access structure, is the core of ABE, which is exactly a set of data elements authorized to access. In pieces of ABE literature [18–22], it was introduced. To summarize, access structure is mainly divided into the following categories.

4.1 Simple Attribute Set

Assume that S is the attribute set and the threshold value is 2, if someone owns the set S1, if S1∩S >= threshold, then the person can access this document. For example, S = {Computer, Professor, High-eve}, threshold is 2. S1 = {Computer, Professor}, S1∩S = |{Computer, Professor}| = 2. This value is satisfied the threshold, so the person can decrypt the document. But in practical application, this solution based on preset thresholds is not universal.

4.2 Bool Algebra

The access control policy is expressed by Boolean algebra, policies are AND-OR relationships between these attributes. A policy is a logical expression consisting of attributes and their relationships. For example, S = ((A and B) and (C or D or E) and (F and G), S1 = {A, B, D, F, G}. S1 meets the conditions of access control policy S, so the person with attribute S1 has the right to access the document.

4.3 Access Tree

In this model, access control policy is represented by an access tree. Therefore, an access tree implies an authorization set.

(1)   Access tree = threshold nodes + leaf nodes.

An access tree is used to represent an authorization set. The leaf nodes are the attribute values, and the non-leaf nodes are the threshold nodes. The user needs to meet the minimum value of this threshold. For example, if the threshold is (3, 2) and the node has 3 children, the user needs to satisfy at least 2 children. For example 3: According to the access tree in Fig. 1. The attribute set S1 = {A, C, D, I, J}, it satisfies the conditions of the access tree, so this user with this set of attributes meets the access conditions.

(2)   Linear Secret Sharing Scheme

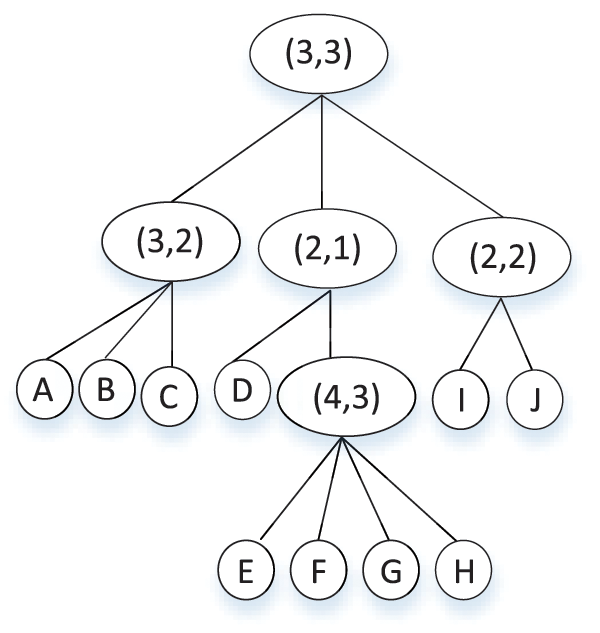
Figure 1: Access tree with threshold node

Linear Secret Sharing Scheme (LSSS) is a rule for transforming the access threshold tree, and the access tree can be transformed into a matrix. The conversion method is for each non-leaf node starting from the root node, the nodes are numbered by top-down hierarchical traversal, in order of 0, 1, 2…; For each leaf node from left to right, top to bottom, numbered from −1, in order of −1, −2 …; Each row of the matrix is used to store the threshold information and child node numbers of non-leaf nodes. The non-leaf node is stored sequentially in the top-down hierarchical traversal order. To satisfy the neatness of the matrix, insufficient information is filled with 0 to supplement.

For example 4: take Fig. 1 as an example. In this tree, it has 5 non-leaf nodes, (3, 3) is number 0, (3, 2) is number 1,… (4, 3) is number 4, and it has 11 leaf nodes, their numbers are A (−1), B (−2), C (−3) … J(−10). The corresponding LSSS matrix of Fig. 1 is below. According to the conversion method, the first row represents the root node: its threshold information (3, 3) and its children’s numbers: 1, 2, 3, and so on. The second row is the non-leaf node (3, 2), and its children’s numbers are −1, −2, −3.

[33123032−1−2−3021−440032−9−100043−5−6−7−8]

(3)   Access tree = threshold nodes + leaf nodes + polynomials

Neither the above access tree nor the access tree represented by the LSSS matrix is resistant to user collusion attacks. Here, the introduction of random polynomials solves the collusion attack problem. Shamir’s secret sharing cannot solve the collusion attack problem, so it must resort to bilinear mapping and cryptography.

For each threshold node, we construct a random polynomial, use a secret sharing scheme to distribute the encryption key layer by layer, and finally go to the leaf node. When accessing, as long as the attribute set makes the root node satisfy the conditions, it can be decrypted. Here, the number of the random polynomial is determined by t in (s, t). For example, for a node with a threshold (3, 2), the number of randomly assigned polynomial terms is 2. For example: Assume the encryption key is 5. For a user, according to the access tree in Fig. 2.

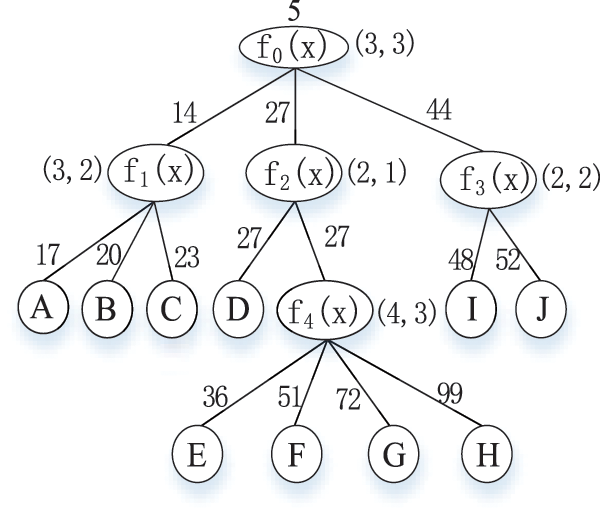
Figure 2: Access tree with threshold and polynomial

Four polynomials f0, f1, f3 and f4 are generated at random. Assume that the corresponding thresholds and polynomials are shown in Table 1.

For different users, the root encryption key is the same key (the root secret value is 5), but the polynomial is random. For example, in Table 1, the user’s random polynomial is f0(x)=5+7x+2x2, and another user has a different random polynomial f0(x)=5+3x+4x2. Although they have the same root secret value, they each have different polynomials, and naturally, their secret share is distributed differently from the top to down. So, the different user has different private key components. Since the private key components are bound to random polynomials, users cannot implement collusion attacks.

4.4 Selective-Set Model for ABE

Init. Define the adversary A and the challenger B. A declares the attribute set S.

Phase 1. A sends the queries for many access structures Aj, where S∉Aj for all j.

Challenge. A submits two messages M0 and M1 with equal length. B flips a random coin b, and encrypts Mb with S. The ciphertext is passed to A.

Phase 2. Phase 1 is repeated.

Guess. A outputs a guess b0 of b. The advantage of A is defined as Pr [b0 = b] − 1/2.

5  ABE Scheme with Message Hierarchy

In practice, the message has different levels of security, and users with different attributes are expected to have different access rights. Here, an ABE scheme with a message security hierarchy was proposed. A message is divided into many blocks according to the security level, and the users with different attribute set keys can decrypt the part of the message with different security levels by access policies.

5.1 Access Structure

In this part, a new access structure based on a threshold tree and attribute hierarchy was proposed. The threshold tree is similar to the Huffman tree, and the difference is that it allows each node to have many children greater than 2, and each threshold node saves the corresponding key of encrypting every message block. The higher the level of the threshold node in the tree, the higher the security level of the message block encrypted with it. The structure of child nodes from left to right is the threshold node with message level n − 1, attribute 1, attribute 2, … The detailed access tree is shown in Fig. 3.

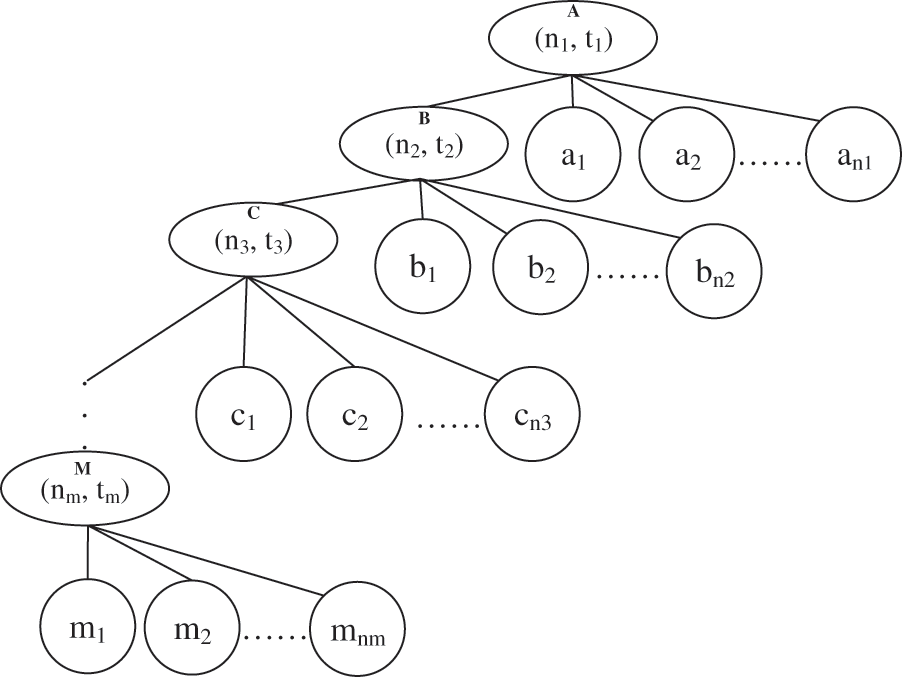
Figure 3: Threshold tree structure for multiple security levels

Similar to the access tree with threshold node and polynomial, this kind of access structure is also resistant to collusion attacks by assigning different random polynomials to users with the help of thresholds and polynomials. To achieve this access with hierarchy, it is necessary to sort the attributes by weight. According to Fig. 3, the weight set is shown in Table 2. The higher the weight value of the attribute set, the lower its privilege.

5.2 The Design and Construction

In our construction, the architecture of the hierarchy ABE is shown in Fig. 4.

•   Data Owner (DO): The data owner is the one who stores and shares the data in the ciphertext in the cloud server environment. It is responsible for defining the access structure, encrypting, and uploading the generated ciphertext to the cloud server.

•   Key Generating Center (KGC): It is a fully trusted entity and can provide the registration of users. He can also perform a series of initialization operations, generate the secret key and save critical information.

•   Cloud Server: It is a not fully trusted entity that can only perform the tasks assigned to him and return the corresponding results. It has computing and storage resources and can be responsible for providing partial decryption for the user.

•   Data Users (DU): The users are the people who access the cloud server to download and decrypt the interested ciphertext from the cloud server.

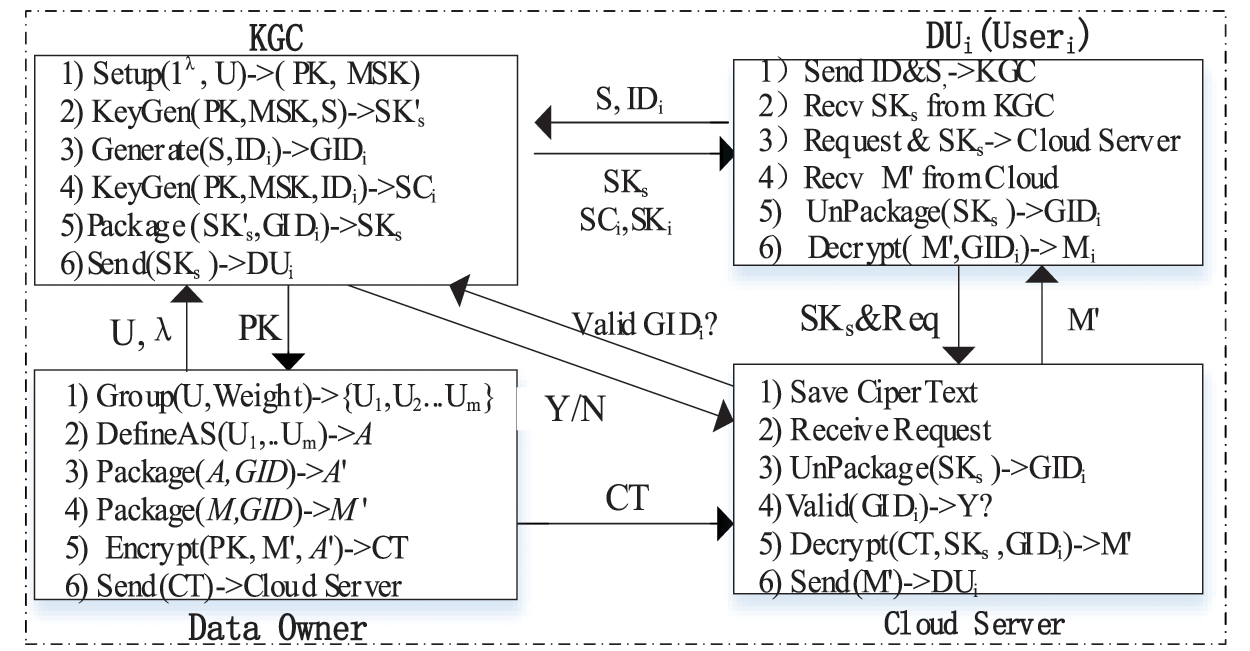
Figure 4: The architecture of the CP-ABE and data flow

5.3 Security Model

(1)   DefineAS (U)

For the data owners, the important task is to define an access structure that explicitly shows the attributes available to users who have access rights. More specifically, first, associating the specified weight to an attribute based on its importance. Second, dividing the attribute set U into several attribute groups U1, U2 … and Um according to their weights, the result shows in Table 1. Finally, completing the creation of an access structure A with threshold and multiple security levels. The detailed access tree is shown in Fig. 3.

(2)   Setup(1λ,U)

For the trusted KGC, first, enter security parameter λ and attribute set U, the set U is related to the attribute groups U1, U2 … and access structure. The setup algorithm will choose a bilinear group G1 of prime order p with generator g. The size of the bilinear group G0 determines the security parameter λ. In addition, let e:G0×G0→G1 denote the bilinear map, it has the properties of bilinearity and non-degeneracy, as described in Section 3.

In this algorithm, it chooses α,β at random, α,β∈Zp. It outputs the Public Key (PK) and a Master Secret Key (MSK). Here, PK is public, and MSK is kept secret, which is used when productizing the user attribute group key.

Setup(1λ,U)→PK,MSKPK:G0,g,e(g,g),αgβMSK:gα,β

(3)   KeyGen (PK, MSK, S)

In this phase, the system will generate the user’s decryption key SKs. This algorithm takes as input the public parameters PK, the master secret key MSK and a set of attributes S. It outputs the user’s secret key SKs. The steps of key generation and distribution are as follows:

First, according to the user’s attribute set S, the system provides its group GIDi based on its attribute weight. And then choose a polynomial for each threshold node tx in the tree, sending the degree dx of the polynomial qx to be one less than the threshold value tx of that node, that is, dx = tx − 1. Then, start with the root node R(n1, t1), choose a random value y, and set qR(0) = y. It chooses dR other nodes of the polynomial qR randomly to define it completely. For node x, it sets qx(0) = qparent(x) (index(x)) and chooses dx other nodes randomly to completely define qx. Next, choose a random value r for the user DUi with attribute set S, and then choose a random rj for each valid attribute of this user. At last it computes the key set SKS′ as Eq. (6):

SKS′=(D=gαβgrβ,∀j∈S,Dj=gr⋅H(att(j))rj,Dj′=grj)(6)

In this part, and then, designing an embedding algorithm. It takes SKS′ and GIDi as the input parameters, and the final secret keys SKS are formed.

Package(SKS′,GIDi)→SKS

Finally, the system will distribute the key SKs to the user DUi.

(4)   Encrypt (PK, M, A)

This algorithm takes the PK (public parameters), M (shared message), and A (an access structure) as the input parameters, and it outputs the ciphertext CT. Encryption with PK and M proceeds as follows. First, to prevent information leakage in access structure A, the group keys GID are integrated into the access structure. In this way, it not only achieves a hidden access structure but also carries the group key to complete the secondary decryption by the user. Then, a random value t is chosen, and let attribute set U be the set of leaf nodes in source access structure A. The ciphertext constructed by giving the tree access structure A’ is published below Eq. (7):

Package(A,GID)→A′ Package(M,GID)→M′

CT=(A′,C~=M′e(g,g)αt,C=gβt,∀x∈U,Cx=gqx(0),Cx′=H(att(x))qx(0))(7)

(5)   Decrypt (PK, CT, SKs)

The decryption algorithm consists of two sub-algorithms, one runs in the cloud server, and it completes the partial decryption of the ciphertext, and the other runs in the DU, and decrypts the whole by the users. It takes as input the public parameters PK, a secret key SKs and a ciphertext CT. It outputs the message M’. If the attribute set S satisfies the access structure A, then Decrypt (PK, CT, SKs)→M’. Otherwise, with overwhelming probability, Decrypt (.) outputs a random message. In this phase: the decryption user gets the corresponding ciphertext, and the user decrypts it with his own key SKs to get the plaintext message M.

For the overall encryption process, we first choose an arbitrary d-element subset. In Fig. 3, assume that: the threshold of node A is n1 = 5 and t1 = 3, that is A (5, 3). We assume that the user’s attribute key set contains the keys for attribute nodes a1, a2 and a4, which means that we can compute: e(g,g)rqa1(0), e(g,g)rqa2(0) and e(g,g)rqa4(0).

Further, based on the secret sharing and the bilinear map operation, we know that Eqs. (8)–(10):

e(g,g)rqa1(0)=e(g,g)rqA(1)(8)

e(g,g)rqa2(0)=e(g,g)rqA(2)(9)

e(g,g)rqa4(0)=e(g,g)rqA(4)(10)

Suppose Lagrange coefficients of node A at x = 1 and x = 2 are Δ1(x), Δ2(x) and Δ4(x), then the Eq. (11) is below:

Δ1(x)=x−21−2⋅x−41−4Δ2(x)=x−12−1⋅x−42−4Δ4(x)=x−14−1⋅x−24−2(11)

Based on the Lagrange interpolation polynomial (5), we can get Eq. (12):

qA(x)=qA(1)Δ1(x)+qA(2)Δ2(x)+qA(4)Δ4(x)(12)

Then put x = 0 into the above equation, and the result is Eq. (13):

qA(0)=qA(1)Δ1(0)+qA(2)Δ2(0)+qA(4)Δ4(0)(13)

Therefore, Eq. (14) is

(e(g,g)rqA(1))Δ1(0)⋅(e(g,g)rqA(2))Δ2(0)⋅(e(g,g)rqA(4))Δ4(0)=e(g,g)rqA(1)Δ1(0)+rqA(2)Δ2(0)+rqA(4)Δ4(0)=e(g,g)rqA(0)=e(g,g)s(14)

Next step:

UnPackage(A′)→A,GID

UnPackage(SKS)→GIDi

Separating the GIDi from the user group key SKS, if GIDi∉GID, then the decryption is terminated, otherwise using the secret value y of root node and access structure A, take C, D and A into the Eq. (15), we can get M’ according to Eq. (16).

C~/(e(C,D)/(∏i∈Sx⁡(e(Cx,Di)/e(Cx′,Di′))Δi,s(0))=C~/(e(C,D)/(∏i∈Sx⁡(e(gqx(0),gr⋅H(att(x))ri)/e(H(att(x))qx(0),gri))Δi,s(0))=C~/(e(C,D)/(∏i∈Sx⁡(e(gqx(0),gr)⋅e(gqx(0),H(att(x))ri)/e(H(att(x))qx(0),gri))Δi,s(0))=C~/(e(C,D)/(∏i∈Sx⁡(e(gqx(0),gr)⋅e(gqx(0),H(att(x))ri)/e(gqx(0),H(att(x))ri))Δi,s(0))=C~/(e(C,D)/(∏i∈Sx⁡e(g,g)r⋅qx(0)⋅Δi,s(0))=(C~/(e(C,D))⋅e(g,g)rqx(0))=(C~/(e(C,D))⋅e(g,g)rs)=C~⋅e(g,g)rse(C,D)(15)

C~⋅e(g,g)rse(C,D)=M′e(g,g)αs⋅e(g,g)rse(gβs,gαβgrβ)=M′e(g,g)αs⋅e(g,g)rse(gβs,gα+rβ)=M′e(g,g)αs⋅e(g,g)rse(g,g)βs⋅α+rβ=M′e(g,g)αs⋅e(g,g)rse(g,g)αs⋅e(g,g)rs=M′(16)

At last, Message M′ is sent to the user DUi, by his group secret key SKS, the unpacked and decryption function is used, and he can get the corresponding plaintext message Mi.

UnPackage(SKS)→GIDiDecrypt(M′,GIDi)→Mi

In the tradition ABE decryption algorithm, using the secret value y of the root node and access structure A, take C, D and A to decrypt the ciphertext, it needs to distinguish different nodes. If node x is a leaf node, then we can decrypt the nodes by Eq. (15), if x is a non-leaf node, it calls a recursive decryption algorithm to proceed with the process. For all nodes z that are children of x, it calls DecrptNode(CT, SK, z) and stores the output as Fz.

5.4 Proof of Security

In this section, we prove the security of our scheme. The security game is between a simulator W and an adversary P, the game proceeds as follows:

Init. W runs the algorithm and P chooses the attribute set S. This challenge is divided into two phases: one is the acquisition of legitimate GIDs, and the other is the access structure. Assume that the system provides the adversary the attribute group GIDs based on its attribute weight, and satisfied Pr[GIDs∈GID] = 1/2.

Setup. The simulator assigns the public key parameters as follows. It chooses random α,β∈Zp, which we associate with the integers from 0 to p − 1, (p is the prime order of the bilinear group G0 with generator g), and the public parameter Y=e(g,g)a, gβ are sent to the adversary. From the view P all parameters are chosen at random as in the construction.

When the adversary P calls for the evaluation of H (attri). (Hash on any attribute string attri), a new random value ti∈Zp is chosen, the simulator uses gti to response the H (attri).

Phase 1. When the adversary makes its jth key generation query for the set Sj of attributes, a new random value r(j) is chosen from Zp and for every i < Sj, new random values ri(j) are chosen from Zp. The simulator computes: D=gαβgr(j)β and for each i < Sj, we have Di=gr(j).gti.ri(j) and Di′=gri(j), these values are passed onto the adversary.

Suppose P makes a request for an access structure T where T(S) = 0. To generate the secret key, W needs to assign a polynomial Qx of degree dx for every node in T. We define two function Satisfy and Unsatisfied. Satisfy (Tx, S, λx) sets up the polynomials for the nodes of an access sub-tree with satisfied root node, that is, Tx(S) = 1; Unsatisfy (Tx, S, gλx) sets up the polynomials for the nodes of an access tree with unsatisfied root node, that is, Tx(S) = 0.

For each child node x’ of x, the algorithm calls: Satisfy (Tx’, S, qx(index(x’))), if x’ is a satisfied node. Unsatify (Tx, S, gqx(index(x′))), if x’ is not a satisfied node. To give keys for access structure T, the simulator runs Unsatify (T, S, P) to define a polynomial qx for each node x of T. For each leaf node x of T, we know qx completely if x is satisfied, if x is not satisfied, then at least gqx(0) is known.

Simulator now defines the final polynomial Qx(⋅) = bqx(⋅) for each node x of T . Notice that this sets y = Qs(0) = ab. The key corresponding to each leaf node is given using its polynomial as follows. Let i = att(x).

If i ∈ S, Dx=gQx(0)ti=gbqx(0)ti, and if i∉S, Dx=gQx(0)ti=gbqx(0)bβi=gqx(0)βi.

Here, constructing the private keys for the access structure T and distributing the private keys for T are identical to that in the original scheme.

Challenge. The adversary P submits two equal length messages m1, m0 to the simulator W. The simulator flips a fair binary coin v, and encrypts mv. The ciphertext is passed to P.

Phase 2. The simulator repeated it as in Phase1.

Guess. Assume that the adversary’s advantage in this situation is ε. A submits a guess v’ of v. If v’ = v the simulator outputs u’ = 0, otherwise output μ’ = 1. The probability analysis under different circumstances is shown in Table 3.

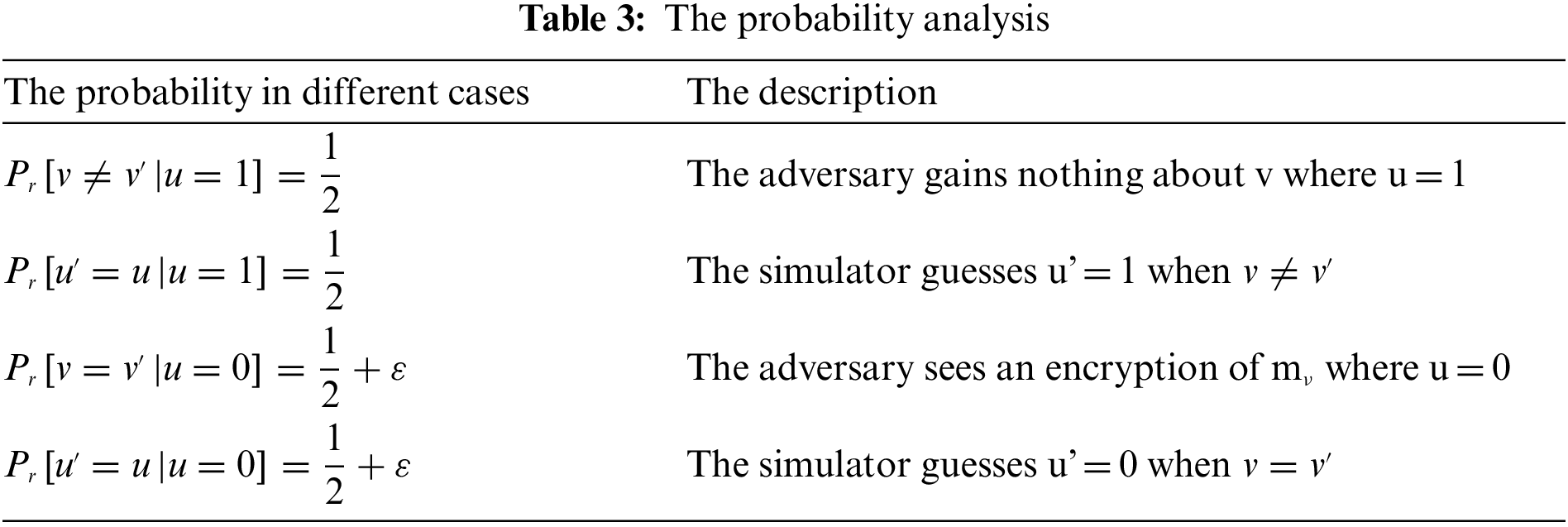
Synthesize the above conditions, in the second phase, the advantage of the simulator is (12Pr[u′=u|u=0]+12Pr[u′=u|u=1]−12)=ε2. So in two-stage process, the overall advantage of the simulator in the game is 12∗(12Pr[u′=u|u=0]+12Pr[u′=u|u=1]−12)=12∗ε2=ε4.

5.5 Experimental Results and Discussion

To evaluate the performance, this paper implements it based on CP-ABE, and selects different security levels to test. The test was conducted on a computer with Inter (R) Core (TM) i5-6500 CPU 3.20 GHz and 16 GB of RAM. We use IntelliJ IDEA as the integrated development environment. Java is used as the programming language, and JPBC libraries are used to implement the operation (https://crypto.stanford.edu/pbc/). PBC library classifies the pairs into type A, B∼G seven categories, and we use an elliptic curve group constructed on the curve y2 = x3 + x based on type A.

Here, the safety coefficient is 80, 160, and 320 bits, respectively, and the prime order of base point is 256, 512, and 512 bits, respectively, so there are three groups to test the performance: type A-80-256, type A-160-512, type A-320-512. The hash function is implemented using SHA-256. The number of given attributes (according to the attribute weight, the message hierarchy was set from 1 to 5) increases from 1 to 10. The testing went through 20 rounds, and the average value was as the final time consumption.

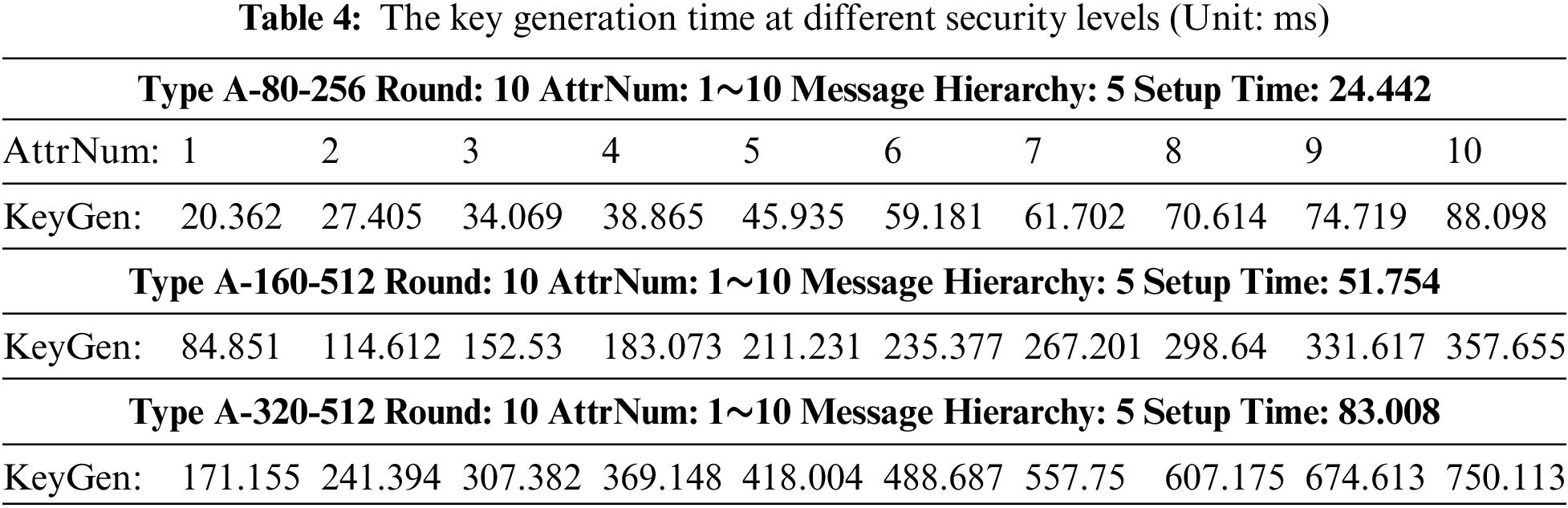
(1) Key generation time at different security levels

In this experiment, we set the access policy as below: set the message hierarchy as 5, in every level, its number of attributes changed from 1 to 10, and all the threshold is AND gate.

① Testing the setup time in different security conditions. From the test result we know that when we select type A, the safety coefficient is 80, and the prime order is 256 bits, its setup time is 24.442 ms, when we select type A-160-512, the setup time is 51.754 ms, and when we select type A-320-512, the setup time is 83.008 ms. With the increase in security level, its setup time is increasing.

② Testing the key generated time in different conditions. We set an access policy with 5 message hierarchies, and each message hierarchy has the same number of attributes. When each message level has 1 attribute node, its key generation time is 20.362 ms in type A-80-256, and when each message level has 2 attribute nodes, its key generation time is 27.405. With the increase of attribute number in every message hierarchy, the key generation time is gradually linear increasing. In the same way, at different security levels, the key generation time is different, the detailed information is shown in Table 4.

(2) Encryption time at different security levels

In this part, we set the encryption time under different conditions. Similar to test (1), the setup time has not changed. We set an access policy with 5 message hierarchies, and each message hierarchy has the same number of attributes. When each message level has 1 attribute node, its encryption time is 43.567 ms in A-80-256, and when each message level has 2 attribute nodes, its key generation time is 49.414 ms. With the increase of attribute number, the encryption time is gradually linear increasing. In the same way, at different security levels, the encryption time is different, the information is shown in Table 5.

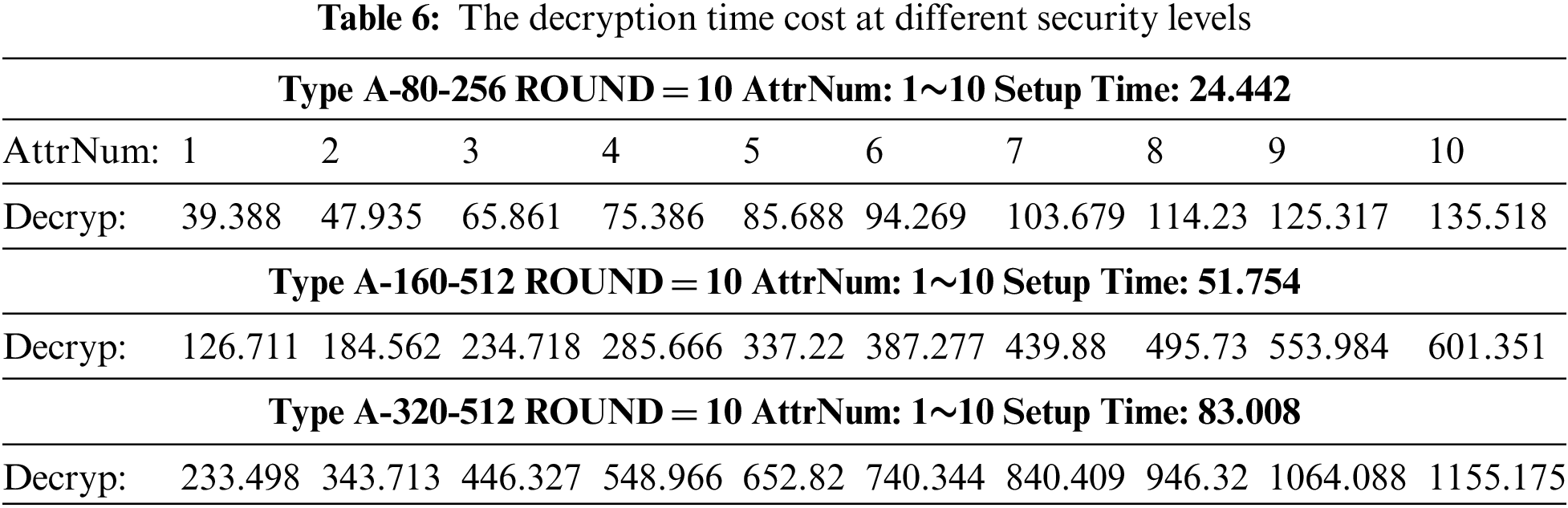
(3) Decryption time cost at different security levels

In this part, we set the decryption time in different conditions. Similar to test (1), the setup time hasn’t changed. We set an access policy with 5 message hierarchies, and each message hierarchy has the same number of attributes. When each message level has 1 attribute node, its decryption time is 39.388 ms in A-80-256, and when each message level has 2 attribute nodes, its key generation time is 47.935 ms. With the increase of attribute number, the decryption time is gradually linear increasing. In the same way, at different security levels, the decryption time is different, the detailed information is shown in Table 6.

(4) The discussion of the solution

In this part, we discuss the dataset, number of users, key size, and computation time. In the ABE scenario, the size of the data set is associated with the shared message, which mainly comes from the data owner, and the number of users is linked with the attribute set. In our scheme, the access rights are refined so that users have different access perspectives to the same shared message. Regarding ciphertext size and private key size, let G0 and G1 be two multiplicative cyclic groups of prime order p. Let g be a generator of G0, Zp be the group {0, 1, …, p − 1}, and the attributes can be denoted as {AU1, AU2, … AUm}. Assume that L* is the bit-length of the element in *, then the size of PK is 3LG0 + LG1, the size of MSK is Lzp + LG0, and the length of the user key SKUi is |AUi| * LG0 + LGid. The number of group elements grows linearly with the number of attributes associated with her identity. In terms of time complexity, attributes were grouped and weighted according to their importance of attributes, and the access structure based on a threshold tree was constructed according to attribute weight. Suppose there are n threshold nodes in the access structure tree, and the average operation time to compute a threshold node is t, then in the previous ABE, the time to decrypt the root node is n * t, while in our scheme, the decryption time is t. So there is a significant improvement in the process of getting the decryption key.

6  Conclusion

At present, CP-ABE is considered to be the ideal high-security data protection solution with protection against collusion or malicious attacks in a shared environment. But in practical applications, the shared message needs different access perspectives for users with different permissions, for this scenario, we proposed a lightweight new ABE scheme.

First, we presented our construction of a message security hierarchy CP-ABE scheme that uses attribute weight as the access rank of the message, which makes the users get different levels of messages. And then, the two-step decryption method is used in this scheme, which reduces the computational and storage burden of the users by leveraging the computing power of the cloud. In addition, in this scheme, the introduction of the group ID and user ID makes it possible for the audit to track malicious users. Finally, the security proof and the experiment result show that this scheme has good performance. ABE schemes in cloud environments have broad prospects for development [23,24], therefore, we will continue to study how to better play the role of ABE in different application scenarios.

Funding Statement: This work was funded by the Funding of Nanjing Institute of Technology No. JXGG2021017, the National Natural Science Foundation of China No. 61701221.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Shamir, “Identity-based cryptosystems and signature schemes,” in Proc. of CRYPTO 84 on Advances in Cryptology, Berlin, Germany, vol. 196, pp. 47–53, 1985. [Google Scholar]

2. D. Boneh and M. Franklin, “Identity-based encryption from the weil pairing,” SIAM Journal on Computing, vol. 32, no. 3, pp. 586–615, 2003. [Google Scholar]

3. A. Sahai and B. Waters, “Fuzzy identity based encryption,” in Advances in Cryptology EUROCRYPT, Heidelberg, Springer, vol. 3494, pp. 457–473, 2005. [Google Scholar]

4. J. Bethencourt, A. Sahai and B. Waters, “Ciphertext-policy attribute-based encryption,” in IEEE Symp. on Security and Privacy, Berkeley, USA, pp. 321–334, 2007. [Google Scholar]

5. B. Waters, “Ciphertext-policy attribute-based encryption: An expressive, efficient, and provably secure realization,” in Int. Workshop on Public Key Cryptography (PKC), Berlin, Germany, pp. 53–70, 2011. [Google Scholar]

6. V. Goya, O. Pandey, A. Sahai and B. Waters, “Attribute-based encryption for fine-grained access control of encrypted data,” in Proc. of the 13th ACM Conf. on Computer and Communications Security, Alexandria, VA, USA, pp. 89–97, 2006. [Google Scholar]

7. D. Boneh, A. Sahai and B. Waters, “Functional encryption: A new vision for public key cryptography,” Communications of the ACM, vol. 55, no. 11, pp. 56–64, 2012. [Google Scholar]

8. S. Garg, C. Gentry, S. Halevi and M. Zhandry, “Functional encryption without obfuscation,” in Proc. of the Theory of Cryptography Conf. (TCC), Berlin, Germany, pp. 1–40, 2016. [Google Scholar]

9. Y. Deng, C. Tang, G. Song and Y. Wen, “New cryptography primitive research: Process based encryption,” Journal of Software, vol. 28, no. 10, pp. 2722−2736, 2017. [Google Scholar]

10. Y. Ma, X. Cao, Z. Zheng, H. Guang and B. Wen, “Accountable CP-ABE with public verifiability: How to effectively protect the outsourced data in cloud,” International Journal of Foundations of Computer Science, vol. 28, no. 6, pp. 705–723, 2018. [Google Scholar]

11. S. Banerjee, S. Roy, V. Odelu, A. K. Das and Y. Park, “Multi-authority CP-ABE-based user access control scheme with constant-size key and ciphertext for IoT deployment,” Journal of Information Security and Applications, vol. 53, 102503, 2020. [Google Scholar]

12. S. Wang, J. Zhou and J. Liu, “An efficient file hierarchy attribute-based encryption scheme in cloud computing,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 6, pp. 1265–1277, 2016. [Google Scholar]

13. J. Li, N. Chen and Y. Zhang, “Extended file hierarchy access control scheme with attribute based encryption in cloud computing,” IEEE Transactions on Emerging Topics in Computing, vol. 9, no. 2, pp. 983–993, 2021. [Google Scholar]

14. W. Zhang, Z. Zhang and H. Xiong, “PHAS-HEKR-CP-ABE: Partially policy-hidden CP-ABE with highly efficient key revocation in cloud data sharing system,” Journal of Ambient Intelligence and Humanized Computing, vol. 13, no. 1, pp. 613–627, 2022. [Google Scholar]

15. H. Song, F. Yin, X. Han, T. Luo and J. Li, “MPLDS: An integration of CP-ABE and local differential privacy for achieving multiple privacy levels data sharing,” Peer-to Peer Networking and Applications,” vol. 15, no. 1, pp. 369–385, 2022. [Google Scholar]

16. N. Chen, J. Li, Y. Zhang and Y. Guo, “Efficient CP-ABE scheme with shared decryption in cloud storage,” IEEE Transactions on Computers, vol. 71, no. 1, pp. 175–184, 2022. [Google Scholar]

17. D. Kumar, M. Kumar and G. Gupta, “An outsourced decryption ABE model using ECC in internet of things,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, vol. 29, no. 6, pp. 949–964, 2021. [Google Scholar]

18. W. Y. Hwang and I. Y. Lee, “A study on data sharing system using ACP-ABE-SE in a cloud environment,” International Journal of Web and Grid Services, vol. 17, no. 3, pp. 201–220, 2021. [Google Scholar]

19. J. Zhang and H. Gao, “A compact construction for non-monotonic key-policy attribute-based encryption,” International Journal of High Performance Computing and Networking, vol. 13, no. 3, pp. 321–330, 2019. [Google Scholar]

20. E. Affum, X. Zhang, X. Wang and J. B. Ansuura, “Efficient lattice CP-ABE AC scheme supporting reduced-OBDD structure for CCN/NDN,” Symmetry, vol. 12, no. 1, pp. 166–178, 2020. [Google Scholar]

21. Z. Zhang, J. Zhang, Y. Yuan and Z. Li, “An expressive fully policy-hidden ciphertext policy attribute-based encryption scheme with credible verification based on blockchain,” IEEE Internet of Things Journal, vol. 9, no. 11, pp. 8681–8692, 2022. [Google Scholar]

22. S. Y. Tan, K. W. Yeow and S. O. Hwang, “Enhancement of a lightweight attribute-based encryption scheme for the internet of things,” IEEE Internet of Things Journal, vol. 6, no. 4, pp. 6384–6395, 2020. [Google Scholar]

23. F. Cheng, S. Ji and C. Lai, “Efficient CP-ABE scheme resistant to key leakage for secure cloud-fog computing,” Journal of Internet Technology, vol. 23, no. 7, pp. 1461–1471, 2022. [Google Scholar]

24. P. K. Premkamal, S. K. Pasupuleti and P. Alphonse, “Dynamic traceable CP-ABE with revocation for outsourced big data in cloud storage,” International Journal of Communication Systems, vol. 34, no. 2, pp. 1–21, 2021. [Google Scholar]