An Improved Honey Badger Algorithm through Fusing Multi-Strategies

1  Introduction

Meta-heuristic algorithms (MAs) gain wide attention in different science branches because of their higher efficiency and performance in recent years [1–3]. Little core knowledge is demanded to reach encouraging results, and it is effortless to transplant between different disciplines. Also, stochastic optimization techniques of MAs can effectively become retarded from getting stuck to the local optimum [4]. The uncertainty and randomness of MAs bring the possibility of finding better solutions while the algorithm searches in the global search space. Unfortunately, although most algorithms have been verified to be effective, the No-Free-Lunch theory (NFL) states that no one can deal with all real-world optimization problems [5]. This theory stimulates researchers to design a more versatile and efficient algorithms.

Generally, MAs consist of three main branches: evolutionary techniques, physics-based, and swarm-based methods [6]. The evolutionary algorithm (EA) makes use of the strategies of crossing, mutating, recombining, and selecting to obtain the superior offspring [7], such as Genetic Algorithm (GA) [8], Differential Evolution (DE) [9], which selecting high-quality individuals through population evolution and eliminating inferior individuals by the concept of survival of the fittest. The physics-based algorithm is based on natural phenomena and transforms the optimization process into a physical phenomenon. The main examples of this class are simulated annealing (SA) [10] and Equilibrium Optimizer (EO) [11]. The swarm-based algorithm imitates the behaviors of animals preying or searching for foods to update their positions in the population [6], as Particle Swarm Optimization (PSO) [12] and Grey Wolf Optimizer (GWO) [13]. The swarm-based algorithm simulates the mechanism of division of labor and collaboration among animal populations in nature and has good application prospects for realistic and complex problems [14,15]. For instance, Zhao et al. proposed the Manta Ray Foraging Optimization algorithm (MRFO) [16], which was inspired by the behaviors of the manta ray. There were three behaviors in MRFO, including chain foraging, cyclone foraging, and somersault foraging, which updated individual positions according to the global optimal individual position in a different state of behavior to solve optimization problems. The inspiration for the Reptile Search Algorithm (RSA) was based on the two steps of crocodile behavior, such as encircling which was performed by highly walking, and hunting which was performed by aggregating through cooperation [17]. Despite the basic version of the meta-heuristic algorithm being exciting, their variants are still instructive, which are broadly listed into three categories: optimizing the initial position of population or algorithm parameters [18], adding mutation factors [19], and blending other algorithms [20]. Although different MAs have distinguishing strategies for solving problems, they have two equivalent stages in the process of optimization: exploration and exploitation [6]. When the exploration is dominant, the algorithm can search in the solution space more widely, generating a more differentiated solution. When the exploitative is dominant, the algorithm can search more intensively. However, if the ability to explore is improved, it will reduce the ability to exploit, and vice versa [21]. Therefore, it is challenging to attain an acceptable balance between the two main stages.

Honey Badger Algorithm (HBA) is a novel swarm-based algorithm proposed recently, which is characterized by fewer adjustment parameters and better robustness performance [22]. Nassef et al. injected an efficient local search method which was called Dimensional Learning Hunting (DLH) into HBA and operated the photovoltaic systems cells as close as possible to the global value in maximum power point tracking problems [23]. Düzenli̇ et al. added Gauss mapping and oppositional-based Learning (OBL) strategy to control critical value in the exploration and exploitation stages [24]. However, it was still unevenly explored and exploited, which was also common in MAs [25].

With the aspiration of a more versatile and efficient algorithm, this paper proposes an improved HBA with fusing multi-strategies (IHBA) to balance the exploration and exploitation of HBA. Firstly, the Tent chaotic mapping is used to initialize individuals [26]. Secondly, the process of the parameters tuning of HBA is adjusted, which adds several random values to nonlinear parameters. Thirdly, three compound mutation factors are introduced to strengthen the ability of individuals to wander randomly. Finally, a modified position updating rules for individuals is introduced to improve the global optimization ability and avoid algorithm getting stuck in the local optimum. Simulation experiments are conducted on 10 benchmark functions and 5 engineering problems. The results show that the global search capability and convergence accuracy of the IHBA is improved effectively. The major contributions of this paper are given as follows:

•   Tent chaotic mapping, control parameters, and mutation factors are introduced to enhance the adaptability of the algorithm to different tasks.

•   An improved updating strategy of position to control the population search range has been proposed.

•   Compared with EO, MRFO, RSA, HBA, Nonlinear-based chaotic HHO (NCHHO) [26], improved GWO (IGWO) [27], and Differential Squirrel Search Algorithm (DSSA) [28], the Wilcoxon Rank-sum Test, Friedman Test, and Mann-Whitney U Test are performed on the benchmark functions and engineering problems and generate a series of comparative analyses.

The rest of this paper is organized as follows: The original HBA is described in Section 2. Section 3 outlines IHBA using multi-strategies fusion. Section 4 and Section 5 discusses the performance differences on benchmark functions and engineering problems. Finally, Section 6 concludes the work and suggests several future research directions.

2  The Basic Honey Badger Algorithm

Honey Badger Algorithm (HBA) is inspired by the foraging behavior of honey badgers. There are two phases of HBA: the digging phase and the honey phase. In the digging phase, the population of honey badgers is guided by the smell of bees or wanders around the bees. In the honey phase, the population is directly attracted to the bees until they locate the honeycomb [22]. In HBA, the fragrance is distributed by the bees (food), inducing honey badgers to congregate towards them. After sensing the smell, the honey badger moves toward the prey. HBA uses Eq. (1) to imitate the odor intensity (Ii).

Ii=r1×S4πdi2S=(xi−xi+1)2di=xprey−xi(1)

where r1 is a random number between 0 and 1, i∈[1,N], N is the size of the population, xprey indicates the position of prey, xi indicates the position of the current honey badger, di indicates the distance between the current honey badger and the prey, and S is the concentration intensity of the honey badger. The odor intensity Ii is proportional to S and inversely proportional to di. In Eq. (1), the greater the odor intensity, the denser the population of the honey badgers, and the closer the honey badgers are to their prey as well.

In the digging phase, the honey badger population needs to perceive the location of food in a global environment. The honey badger population is guided by the optimal individual to perform the search task. The digging mode is updated according to Eq. (2).

xnew=xprey+F×β×xprey+F×r2×α×di×|cos⁡(2π×r3)×[1−cos⁡(2π×r4)]|α=2×exp⁡(−ttmax)(2)

where F is an enumeration value of the set {−1,1} used to change the search direction. β denotes the ability of the honey badger to obtain food. r2, r3 and r4 are three random values between 0 and 1. α is a control parameter used to constrain the search range, t indicates the current search time, and tmax is the max iteration.

Different from the digging phase, the honey badgers are guided by the honeyguide bird to approach the prey during the honey phase, where the individuals hover around prey until they catch it. It can be simulated as Eq. (3), where r5 is a random number between 0 and 1.

xnew=xprey+F×r5×α×di(3)

In the basic HBA, the initial position of the individual is generated randomly, which provides an opportunity that the population to search in a wide area. The digging mode and honey mode provide detailed foraging behavior for the population. The honey badger, based on the odor intensity of the prey remaining in the air, identifies the approximate position of the prey and then approaches the prey until it locates. The Honey Badger Algorithm uses global sight to tackle the optimization and to achieve optimal solutions. Chen et al. applied HBA based energy management strategy to solve the problem of performance enhancement in the pressure retarded osmosis and photovoltaic/thermal system by maximizing the multi-variable functions [29]. Ashraf et al. applied HBA to optimally identify the seven ungiven parameters of the proton exchange membrane fuel cells steady-state model [30].

3  The Improved Honey Badger Algorithm

In response to the desire of designing a higher performance algorithm, an improved Honey Badger Algorithm with multi-strategy (IHBA) is proposed, which are detailed are following.

3.1 The Tent Chaotic Mapping

The original HBA obtains the initial solutions randomly, which are difficult to ensure the individuals covering over the entire solution space evenly. Chaotic mapping is often used in optimization algorithms to disperse the population and reduce aggregation. The main two classes of chaotic mappings are Logistic chaotic mapping and Tent chaotic mapping, while the latter creates a more uniform chaotic sequence and has a faster convergence speed [26], the Tent chaos mapping is used as Eq. (4).

xi+1={2xi+R×1Ndim0≤x<0.52(1−xi)+R×1Ndim0.5 < x ≤ 1(4)

where Ndim is the dimension of individuals in the Tent sequence. R is the random number between 0 and 1. The Tent chaotic mapping makes the population widespread and ensures that the population wanders randomly in the global range.

3.2 The Improved Control Parameter

With regard to Eq. (2), the change of control parameters is smooth. Once the population falls into the local optimum, it is difficult to maintain the diversity of the population, resulting in poor quality of solutions. In this paper, the control parameters with random perturbation are introduced. The improved control parameters are shown in Eq. (5).

A = [cos(2×R1)+1]×(1−ttmax)a = A×(2×R2−1)(5)

where t is the current search time, tmax is the max iteration. R1 and R2 are a random value between 0 and 1. The scope of A is between 0 and 2, and the scope of α is between −2 and 2. The search scope of the population can be expanded by α and A. The iterative curve of parameter α with time is shown in Fig. 1.

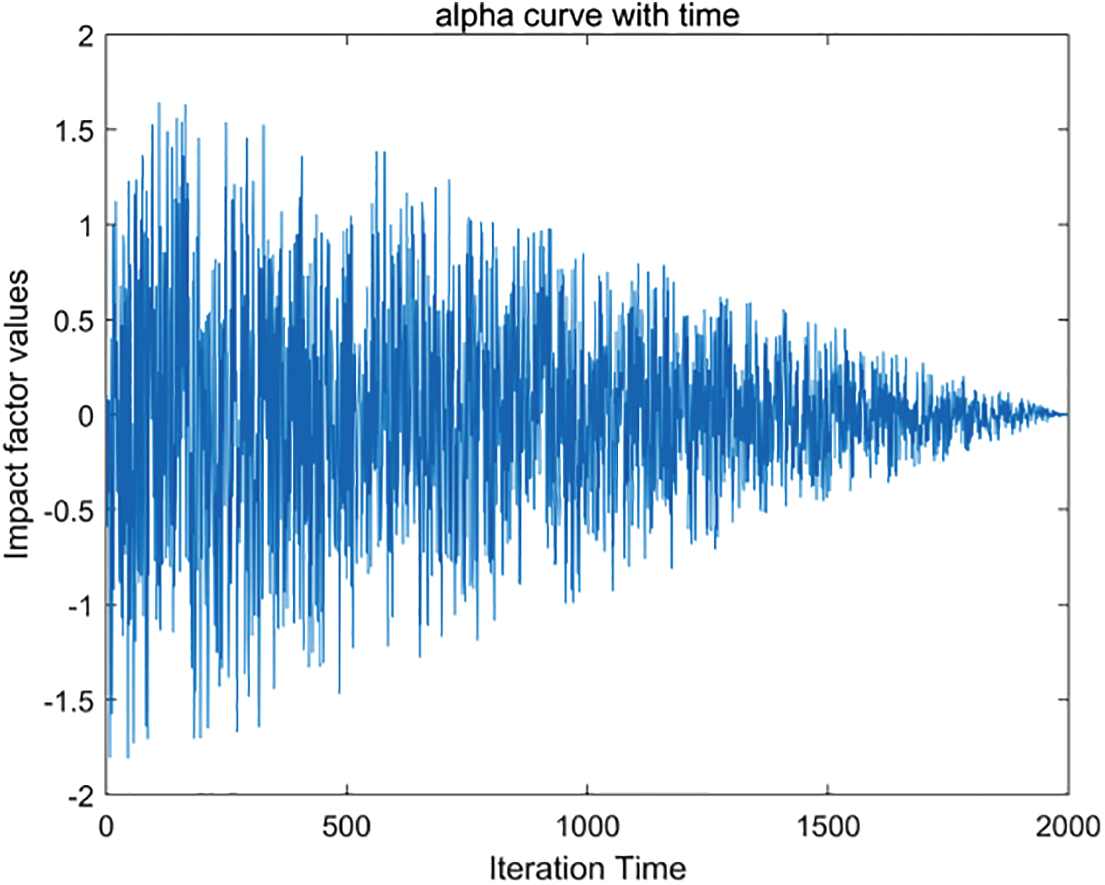
Figure 1: The iteration curve with time for parameter α

In Fig. 1, the control parameter α changes irregularly, indicating the ability of the population to escape the current local solution. When the absolute value of α is greater than 1, the individual could prey outside the scope of the population position. On the contrary, individuals search in a more intensive range. Meanwhile, α and A have randomness during the whole search process. When α changes more smoothly, the algorithm will perform a more refined exploration and exploitation.

3.3 The Composite Mutation Factors

Three hybrid mutation factors are utilized for multimodal problems as it is difficult to adapt complex and multivariate functions using simple parameters, which are defined as Eq. (6).

M1=a×A×xiM2=(a×R4−A)×xrandM3=a×[a×(xi−xrandi)+R5×(xi−xrandi)]xrandi=xi−xrand(6)

where α and A are control parameters, R4 and R5 are a random number between 0 and 1, and xrand indicates arbitrary individual of population, xrandi indicates the distance between xrand and xi. It is obvious that the randomness and nonlinearity of the composite factors become increasingly complex from M1 to M3. The detail range values of M1∼M3 as follows: α×A∈(−4,4), α×R4−A∈(−1,1) and α×(α+R5)∈(−2,6).

The three hybrid mutation factors could escape the local optimum. Since the definite value of these factors is uncontrollable, they have a better ability to adapt to different problems, and the probability of jumping out of the local solution may be higher. Meanwhile, xrand and xrandi expand the search range and enhance the diversity of the population.

3.4 An Improved Swarm-Based Strategy

The updating strategy of position is the core of the swarm-based algorithm. A diversified updating strategy of position is proposed to enhance the advantage between convergence and diversity.

3.4.1 The Proposed Exploration Strategy

To improve the diversity of population in exploration, an improved exploration strategy is defined. In detail, three mutation factors are added which can automatically adjust their values with the increasing of the iterations. During the stage of exploration, the IHBA updates the position of individuals according to Eq. (7).

xnew={g(xi)+M1+M2R3 > 0.5xi+F×r5×a×di+M3elsexrandi = xi−xrandg(xi)=|cos(2p×r3)×[1−cos(2p×r4)]|×F×r2×a×di+F×b×Ii×xprey(7)

where Eq. (7) is formed by Eq. (2) and Eq. (6), which expands the scope that the individuals preying on. It is known that the search scope is wider, the diversity of the population is better. At latter stage, the population is more aggregated, the distance di is shorter. Through Eq. (7), the range of the individuals is adjusted by the spatial information dynamically, which improves the diversity of the population.

3.4.2 The Proposed Exploitation Strategy

The population location information is introduced in the exploitation phase, which enhances the exploitation ability of IHBA and is defined as Eq. (8).

xnew={a×xmean×[xi−xprey]+xiA > 0.8xprey+(2R6−1)×(h×xi−xprey)else(8)

where xmean indicates the mean value of position in individuals, R6 is a random number between 0 and 1, and h is a number obeying normal distribution (µ=1,δ2=0). In Eq. (8), the search scope depends on xmean, xprey and xi when A>0.8. This operation transforms the exploration into exploitation, switching between the two phases. For other cases, IHBA updates the position of individuals relying on xprey and xi, which can expedite the population to the best individual xprey.

3.5 The Proposal of IHBA

IHBA ensures the global search under the dual pressure of fuzzy mapping and mutation factors after combining Tent chaotic mapping, self-adaption time parameters, and three mutation factors. According to the above description, the process of IHBA is as follows:

Step 1: Initialize the position of the population based on the Tent chaotic mapping.

Step 2: Calculate the control parameters α and A via Eq. (5).

Step 3: Calculate the odor intensity Ii of each individual by Eq. (1).

Step 4: Start to perform the exploration task according to Eq. (6) and calculates the fitness value.

Step 5: Update the best individual during the exploration stage. The elite selection is used to obtain the best individual among the original population and the honey badger group generated by step 4 and step 5.

Step 6: Start to perform the exploitation task via Eq. (7). After calculating the fitness value of the population and selecting the elite individual, the best individual xprey is updated.

Step 7: Rank the new population according to the fitness value of the individual.

Step 8: Record the global best value. Return to step 2 if the algorithm does not satisfy the termination condition. Otherwise, output the best position and best value.

On the whole, IHBA introduces the Tent chaotic mapping to disrupt the aggregation behavior of the population, which means that individuals can be distributed throughout the search space evenly. By modifying the time parameters and adding three mutation factors, the scope of population searching can be expanded, and the randomness of the algorithm can be greatly improved.

4  Simulation Experiments and Analysis

To verify the performance of the IHBA, simulation experiments are executed by solving 10 benchmark functions. The detail of the benchmark functions is shown in Table 1. IHBA is compared with EO [11], MRFO [16], RSA [17], HBA [22], NCHHO [26], IGWO [27] and DSSA [28]. The former 4 algorithms are basic versions, which are prominent and outstanding in relevant literature. The latter 3 algorithms are improved variants, which are novel and effective. For the fairness of the experiment, the 8 algorithms are run 30 times independently, the max of iterations is 2000, and the size of the population is 50. The specific parameters of algorithms are setting in Table 2. In addition, all experimental results in this paper are carried out on a personal computer with Intel (R) Core (TM) i7-8700 @3.2 GHz CPU, 16.0 GB RAM under Windows 10 system. All algorithms are achieved from MATLAB 2016.

The mean value (Mean) and standard deviation (STD) of the results are the evaluation metrics (Table 3). Meanwhile, to reveal significant differences between all algorithms, Wilcoxon Rank-sum Test, the Friedman Test and Mann-Whitney U Test are adopted. A significance level of the Wilcoxon Rank-sum Test is set to 0.05 and the p is the probability of overturning the hypothesis. When p ≤ 0.05, it indicates a significant difference between the algorithms. Wilcoxon Rank-sum Test, Friedman Test and Mann-Whitney U Test used 300 data to evaluate all the algorithms, which include 10 benchmark functions, each of which had 30 results.

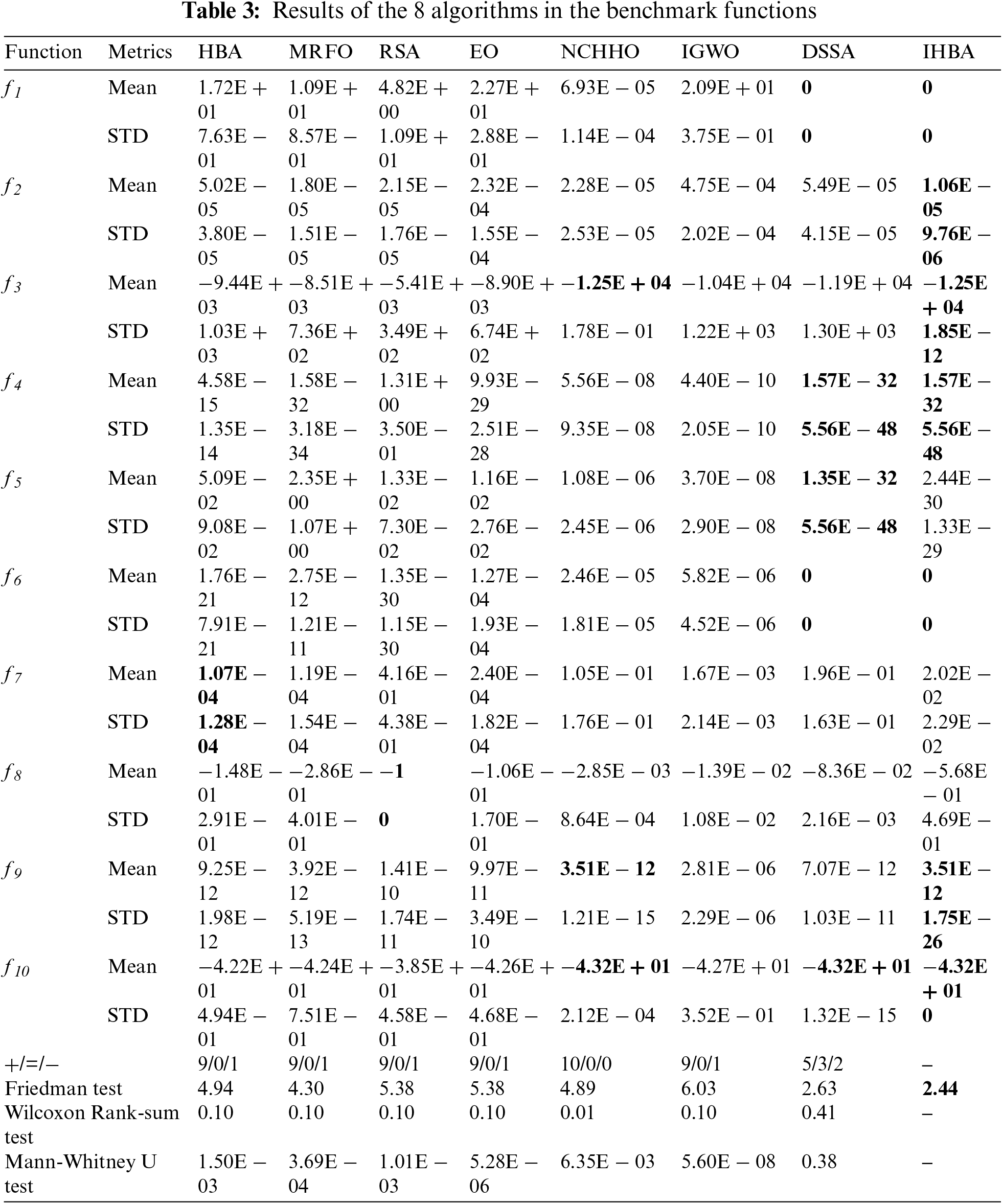
In Table 3, the metrics of Mean reflects the average optimization capability of the algorithm, and the STD reflects the stability of the algorithm. Under the same conditions, IHBA outperforms the others in the 10 benchmark functions. For the unimodal benchmark function f1, multimodal benchmark function f6 and f10, IHBA and DSSA locate the global optimal solution within the specified termination conditions. It is also outstanding in the stability of the algorithm. For the unimodal function f2 and multimodal function f3, all algorithms do not have the ability to locate the global optimal solution, but the values of Mean are 1.06E − 05 and −1.25E + 04 in IHBA, which is better in the same order of magnitude. For the multimodal functions f4 and f5, IHBA and DSSA have an advantage of several orders of magnitude or even tens of orders of magnitude compared with the others. For the multimodal functions f7,f8, and f9, there are a large number of local minima, which are close to the global optimum, and lead algorithms to trap into the local optimum. Specifically, although all the algorithms do not find the global optimal solution of the function in f7 and f9, the difference between all algorithms is not obvious. For multimodal function f8, IHBA can not compete with RSA, while performing better than other algorithms.

The last three rows of Table 3 show the results based on Wilcoxon Rank-sum Test and Friedman test. As for the symbols “+”, “=”, and “−”, denote that the performance of IHBA is better, the same good, and worse than the compared algorithm respectively. In Table 3, it could be seen that IHBA outperforms the others on the whole, which have comparable performance on 9 benchmark functions commonly. In the worst case, it outperforms the other algorithms on 5 functions with 3 approximate and 2 worse results. In the Friedman Test, the smaller the average ranking value, the better the overall optimization performance of the algorithm. IHBA has smaller sorting results. Furthermore, the p of NCHHO is 0.01 by the Wilcoxon Rank-sum Test, indicating that there is a significant difference between NCHHO with IHBA. The values of p in HBA, MRFO, RSA, and EO are 0.1, which is greater than 0.05, indicating that there was no significant difference between this compared algorithm and IHBA. The result of the Mann-Whitney U Test shows that there are significant differences between IHBA and the comparison algorithm, except for DSSA. All in all, the overall performance of IHBA is better than the compared algorithms.

Fig. 2 shows the convergence curves of different algorithms. IHBA and DSSA get better solutions than the others significantly in f1,f4,f5,f6, and f10, and they can converge to the final solution quickly in the early stage of the algorithm. It indicates that IHBA and DSSA have a more powerful exploration ability. In f2,f3,f9, the performance of IHBA is not significantly different from the others but still can obtain good solutions. In f7 and f8, the convergence trend of IHBA is weaker than most of the compared algorithms, reassuringly, it performs better than NCHHO and IGWO. In general, IHBA can converge faster than compared algorithms.

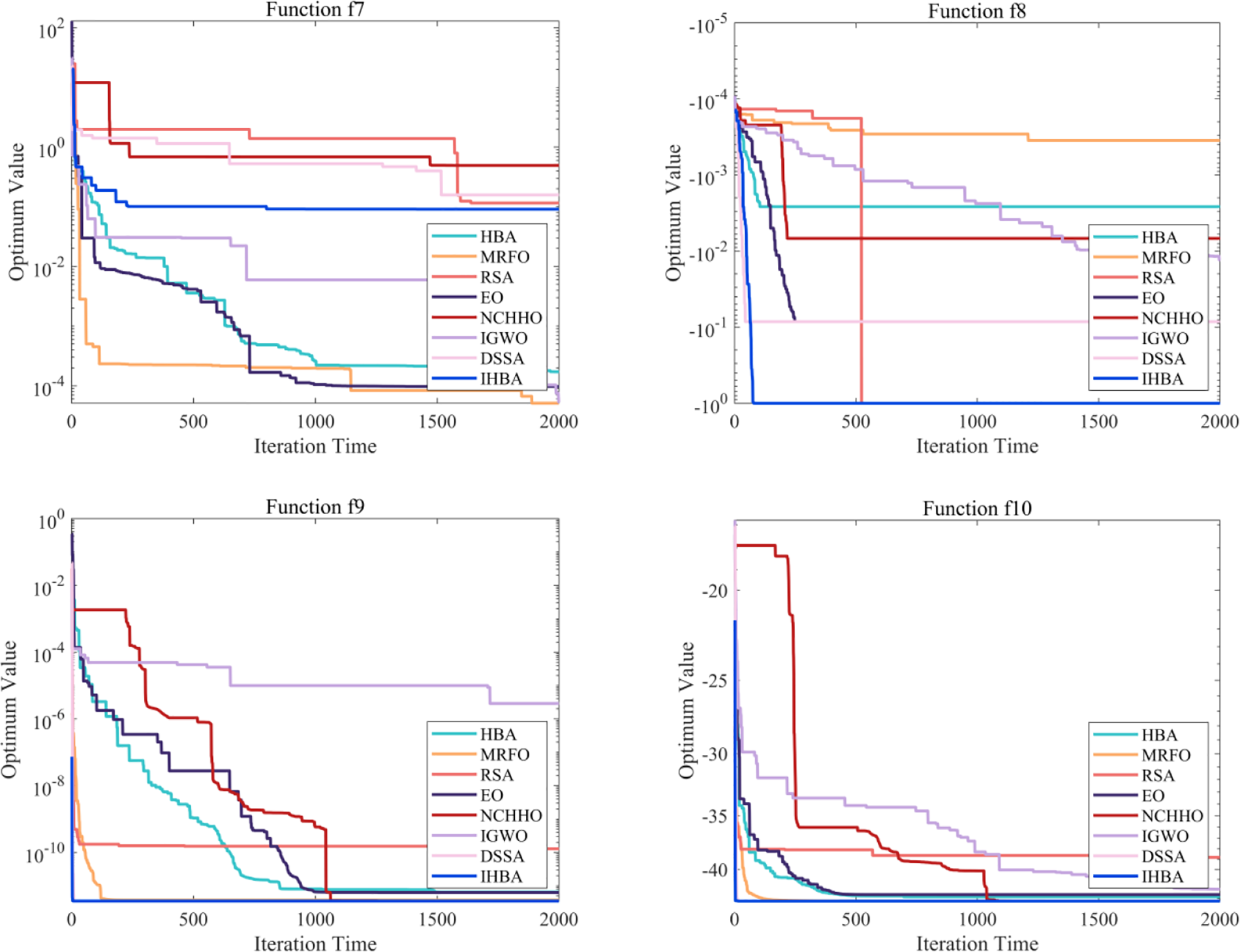
Figure 2: Convergence diagram of benchmark functions

5  Simulation in Engineering Optimization Problems

To compare the performance of algorithms involved in the paper on engineering problems, simulation experiments are performed on 5 engineering problems [31]. Specifically, F1 is the tension compression spring design problem, F2 is the three-bar truss design problem, F3 is the gear train design problem, F4 is the I-beam design problem, and F5 is the tubular column example. Parameters and indicators are the same as those set in Section 4.

In Table 4, it is clear that all algorithms can obtain acceptable solutions in 5 tasks. Specifically, in the F2 and F4 tasks, the mean values of 8 algorithms are 2.64E + 02 and 1.31E − 02. Moreover, the STD of IHBA is subtle, which indicates that there is better stability. For the F1 and F3 tasks, although IHBA does not gain the global optimal solution, there is a lower accuracy. For the F5 task, IHBA can obtain the global optimal solution in 30 runs as the STD is 0. In addition, there is no significant difference among RSA, NCHHO, and IHBA in the benchmark functions, but there is a gap in the constrained engineering problems when significance parameter is 0.05. It verifies the NFL again. Combining the Wilcoxon Rank-sum Test, Friedman Test and Mann-Whitney U Test, IHBA has a wider adaptability between the benchmark problem and the engineering problem compared.

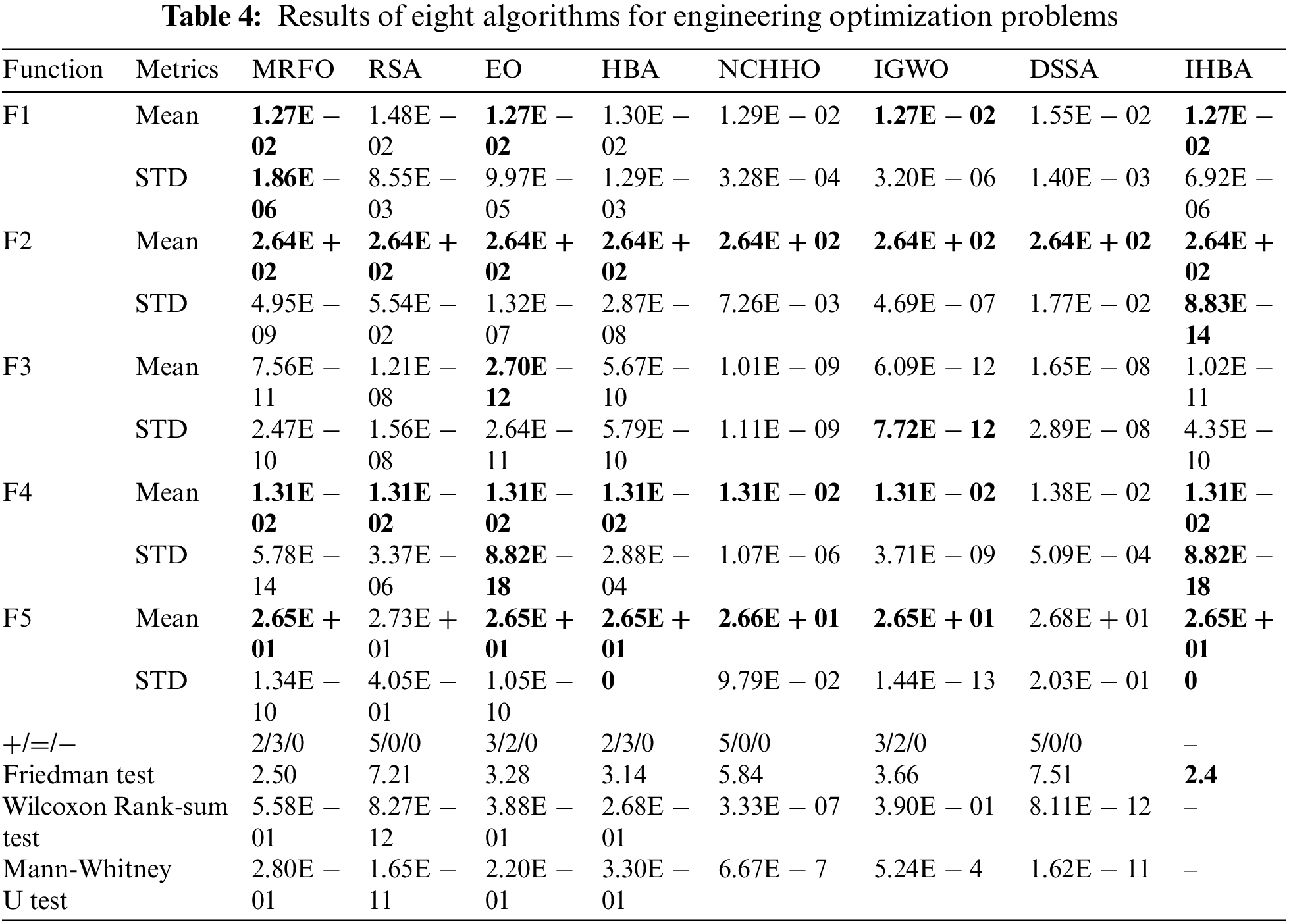
Fig. 3 shows the box plots of the solutions of different algorithms on 5 engineering problems. The blue box area is the scope of solutions. The smaller the box height indicates the better stability of the algorithm, and the lower the box signifies the superior solution accuracy of the algorithm. The solutions of IHBA are more concentrated in all five tasks, which denotes that IHBA has the advantage in the stability of the algorithm. Specifically, compared with the other algorithms, the box positions of MRFO and IHBA are lower in the F1. The box positions of MRFO, EO, HBA, IGWO, and IHBA are lower in F2, F4, and F5. The solutions of MRFO and EO are more attractive in F3 than others. In the mass, the performance of IHBA is not inferior to other novel algorithms in the above engineering problems. On the whole, IHBA uses a variety of strategies to enhance global search. Compared to other algorithms, IHBA performed better in terms of stability and optimization ability for the benchmark functions and engineering problems.

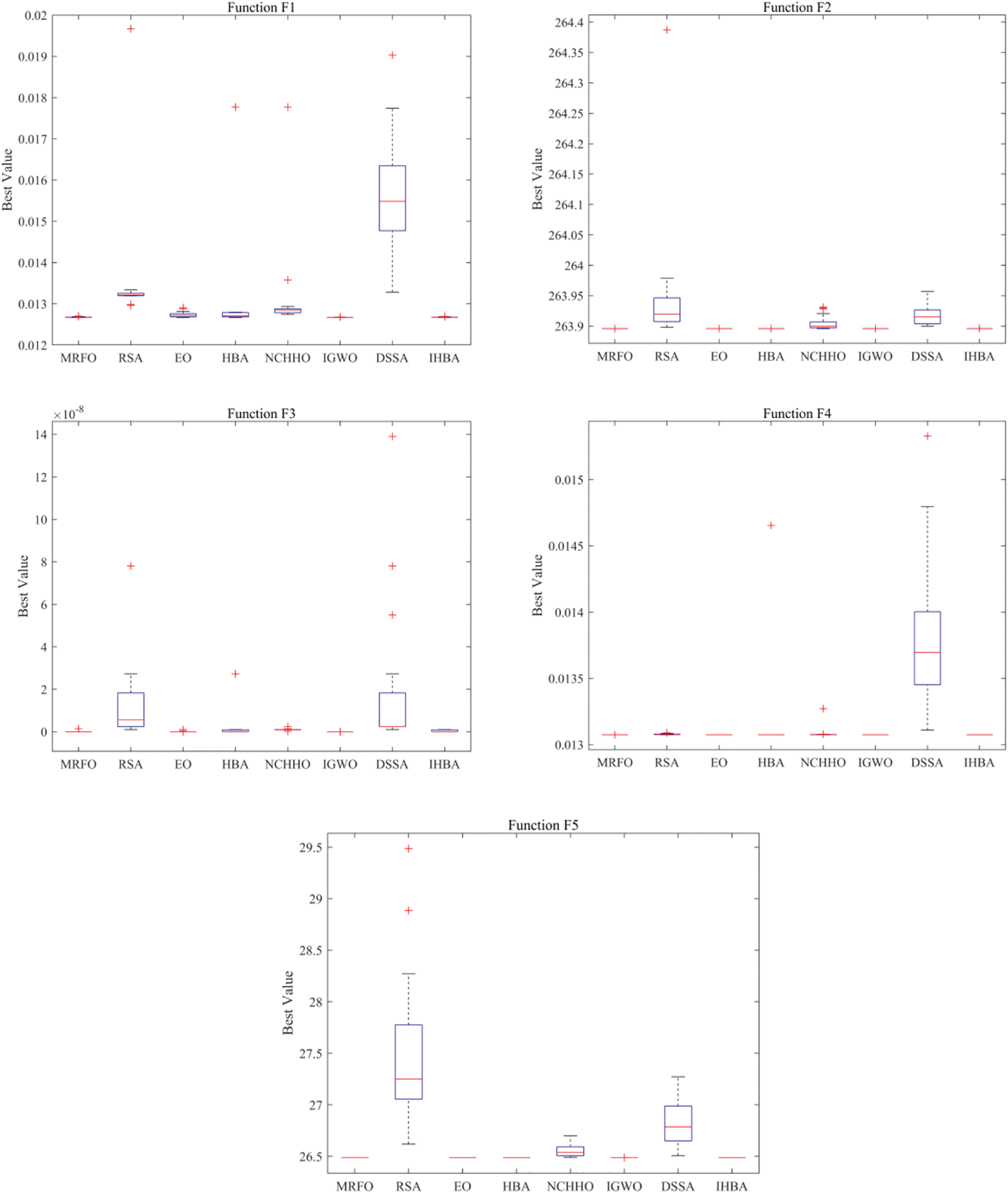
Figure 3: Solutions of engineering optimization problems

6  Conclusion and Future Work

HBA is a new MAs with good expansibility and high efficiency suffering from the local optimum and unbalanced exploration and exploitation. In this paper, we propose a hybrid approach using multi-strategies to improve the performance of HBA. It introduces Tent chaotic mapping and mutation factors to HBA, meanwhile, the random control parameter is improved, moreover, a diversified updating strategy of position is put forward to enhance the advantage between exploration and exploitation. IHBA is compared with EO, MRFO, RSA, HBA, NCHHO, IGWO and DSSA on 10 benchmark functions and 5 engineering problems. On 10 benchmark functions, the numerical results reflect that IHBA gets effective solutions for most functions. The Friedman test reveals that IHBA has a desirable average ranking on entire optimization problems. The Wilcoxon signed-rank test and Mann-Whitney U Test demonstrate that the performance of IHBA is dramatically different from other algorithms. The box plots show that IHBA achieves higher stability than other algorithms in engineering optimization problems. However, IHBA is attracted to local solutions and has difficulty finding global solutions for tasks with a large number of local minima.

In the future, we will continue to improve the exploration and exploitation capabilities of IHBA and apply IHBA to a wider range of issues, including multi-objective optimization, feature selection, and hyperparameter optimization in machine learning.

Funding Statement: The work is supported by National Science Foundation of China (Grant No. 52075152), and Xining Big Data Service Administration.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Mahdavi-Meymand and M. Zounemat-Kermani, “Homonuclear molecules optimization (HMO) meta-heuristic algorithm,” Knowledge-Based Systems, vol. 258, pp. 110032, 2022. [Google Scholar]

2. P. Lu, L. Ye, Y. Zhao, B. Dai, M. Pei et al., “Review of meta-heuristic algorithms for wind power prediction: Methodologies, applications and challenges,” Applied Energy, vol. 301, pp. 117446, 2021. [Google Scholar]

3. C. Renkavieski and S. R. Parpinelli, “Meta-heuristic algorithms to truss optimization: Literature mapping and application,” Expert Systems with Applications, vol. 182, pp. 115197, 2021. [Google Scholar]

4. W. Gao, S. Liu and L. Huang, “Particle swarm optimization with chaotic opposition-based population initialization and stochastic search technique,” Communications in Nonlinear Science and Numerical Simulation, vol. 17, no. 11, pp. 4316–4327, 2012. [Google Scholar]

5. H. D. Wolpert and G. W. Macready, “No free lunch theorems for optimization,” IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 67–82, 1997. [Google Scholar]

6. S. Li, H. Chen, M. Wang, A. A. Heidari and S. Mirjalili, “Slime mould algorithm: A new method for stochastic optimization,” Future Generation Computer Systems, vol. 111, pp. 300–323, 2020. [Google Scholar]

7. S. Mirjalili, “SCA: A sine cosine algorithm for solving optimization problems,” Knowledge-Based Systems, vol. 96, pp. 120–133, 2016. [Google Scholar]

8. P. Zhang, J. Wang, Z. Tian, S. Sun, J. Li et al., “A genetic algorithm with jumping gene and heuristic operators for traveling salesman problem,” Applied Soft Computing, vol. 127, pp. 109339, 2022. [Google Scholar]

9. Z. Zeng, M. Zhang, H. Zhang and Z. Hong, “Improved differential evolution algorithm based on the sawtooth-linear population size adaptive method,” Information Sciences, vol. 608, pp. 1045–1071, 2022. [Google Scholar]

10. C. Shang, L. Ma, Y. Liu and S. Sun, “The sorted-waste capacitated location routing problem with queuing time: A cross-entropy and simulated-annealing-based hyper-heuristic algorithm,” Expert Systems with Applications, vol. 201, pp. 117077, 2022. [Google Scholar]

11. A. Faramarzi, M. Heidarinejad, B. Stephens and S. Mirjalili, “Equilibrium optimizer: A novel optimization algorithm,” Knowledge-Based Systems, vol. 191, pp. 105190, 2020. [Google Scholar]

12. Q. Liu, J. Li, H. Ren and W. Pang, “All particles driving particle swarm optimization: Superior particles pulling plus inferior particles pushing,” Knowledge-Based Systems, vol. 249, pp. 108849, 2022. [Google Scholar]

13. S. Mirjalili, M. S. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]

14. D. Zhang, G. Ma, Z. Deng, Q. Wang, G. Zhang et al., “A self-adaptive gradient-based particle swarm optimization algorithm with dynamic population topology,” Applied Soft Computing, vol. 130, pp. 109660, 2022. [Google Scholar]

15. T. Si, B. P. Miranda and D. Bhattacharya, “Novel enhanced salp swarm algorithms using opposition-based learning schemes for global optimization problems,” Expert Systems with Applications, vol. 207, no. 8, pp. 117961, 2022. [Google Scholar]

16. W. Zhao, Z. Zhang and L. Wang, “Manta ray foraging optimization: An effective bio-inspired optimizer for engineering applications,” Engineering Applications of Artificial Intelligence, vol. 87, pp. 103300, 2020. [Google Scholar]

17. L. Abualigah, M. E. Abd, P. Sumari, Z. W. Geem and A. H. Gandomi, “Reptile search algorithm (RSAA nature-inspired meta-heuristic optimizer,” Expert Systems with Applications, vol. 191, pp. 116158, 2022. [Google Scholar]

18. Y. Luo, W. Dai and W. Y. Ti, “Improved sine algorithm for global optimization,” Expert Systems with Applications, vol. 213, pp. 118831, 2023. [Google Scholar]

19. H. Dong, Y. Xu, D. Cao, W. Zhang, Z. Yang et al., “An improved teaching-learning-based optimization algorithm with a modified learner phase and a new mutation-restarting phase,” Knowledge-Based Systems, vol. 258, pp. 109989, 2022. [Google Scholar]

20. H. Nenavath, K. R. Jatoth and S. Das, “A synergy of the sine-cosine algorithm and particle swarm optimizer for improved global optimization and object tracking,” Swarm and Evolutionary Computation, vol. 43, pp. 1–30, 2018. [Google Scholar]

21. K. J. Xue and B. Shen, “A novel swarm intelligence optimization approach: Sparrow search algorithm,” Systems Science & Control Engineering, vol. 8, no. 1, pp. 22–34, 2020. [Google Scholar]

22. A. F. Hashim, H. E. Houssein, K. Hussain, S. M. Mabrouk and W. Al-Atabany, “Honey Badger Algorithm: New metaheuristic algorithm for solving optimization problems,” Mathematics and Computers in Simulation, vol. 192, no. 2, pp. 84–110, 2022. [Google Scholar]

23. M. A. Nassef, H. E. Houssein, E. B. Helmy and H. Rezk, “Modified Honey Badger Algorithm based global MPPT for triple-junction solar photovoltaic system under partial shading condition and global optimization,” Energy, vol. 254, no. 3, pp. 124363, 2022. [Google Scholar]

24. T. Düzenli̇, K. F. Onay and B. S. Aydemi̇r, “Improved Honey Badger Algorithms for parameter extraction in photovoltaic models,” Optik, vol. 268, pp. 169731, 2022. [Google Scholar]

25. Z. Zhang and C. W. Hong, “Application of variational mode decomposition and chaotic grey wolf optimizer with support vector regression for forecasting electric loads,” Knowledge-Based Systems, vol. 228, pp. 107297, 2021. [Google Scholar]

26. A. A. Dehkordi, S. A. Sadiq, S. Mirjalili and K. Z. Ghafoor, “Nonlinear-based chaotic harris hawks optimizer: Algorithm and internet of vehicles application,” Applied Soft Computing, vol. 109, pp. 107574, 2021. [Google Scholar]

27. H. M. Nadimi-Shahraki, S. Taghian and S. Mirjalili, “An improved grey wolf optimizer for solving engineering problems,” Expert Systems with Applications, vol. 166, pp. 113917, 2021. [Google Scholar]

28. B. Jena, K. M. Naik, A. Wunnava and R. Panda, “A differential squirrel search algorithm,” Advances in Intelligent Computing and Communication, vol. 202, pp. 143–152, 2021. [Google Scholar]

29. Y. Chen, G. Feng, H. Chen, L. Gou, W. He et al., “A multi-objective honey badger approach for energy efficiency enhancement of the hybrid pressure retarded osmosis and photovoltaic thermal system,” Journal of Energy Storage, vol. 59, pp. 106468, 2023. [Google Scholar]

30. H. Ashraf, S. O. Abdellatif, M. M. Elkholy and A. A. El-Fergany, “Honey badger optimizer for extracting the ungiven parameters of PEMFC model: Steady-state assessment,” Energy Conversion and Management, vol. 258, pp. 115521, 2022. [Google Scholar]

31. H. Bayzidi, S. Talatahari, M. Saraee and C. Lamarche, “Social network search for solving engineering optimization problems,” Computational Intelligence and Neuroscience, vol. 2021, pp. 32, 2021. [Google Scholar]