Role-Based Network Embedding via Quantum Walk with Weighted Features Fusion

1  Introduction

Roles are sets of nodes with similar structural patterns and functions. Role-based network embedding aims to project role-similar nodes into a compact low-dimensional vector space. It is widely used in various downstream tasks such as role classification, etc. The first appearance of the concept of roles is in sociology [1] for mining potential social relationships, and it is gradually applied in complex networks like traffic network congestion [2]. By measuring the structural similarity [3], role-similar nodes can be found in distant locations, even in different subgraphs of disconnected networks.

Most previous studies mainly focus on the local context such as node structure, while rarely measuring their relevance globally, especially when nodes are far away so that ignoring their similarity in the global context. For example, Role-based graph embedding (Role2vec) [4] uses the classical random walk or its variants to extract structural information and aggregate role-based embedding. It selectively extracts the structural information from low-order neighborhoods, which ignores global information. However, the situation that role-similar nodes are far away from each other in the graph while showing high relevance in terms of node structural similarity may exist. As shown in Fig. 1, in the world-air-traffic network, landmarks with the same color indicate the same hub role, and landmarks with the same role may be far away. For example, two distant landmarks in Beijing and Washington D.C. airports. They are both capitals of their country and have the same status and role, which is reflected by global information. More recently, Role Embedding via Discrete-time quantum walk (RED) [5] considers the global role information and highlights the global role relevance of nodes, but ignores the effect of node features.

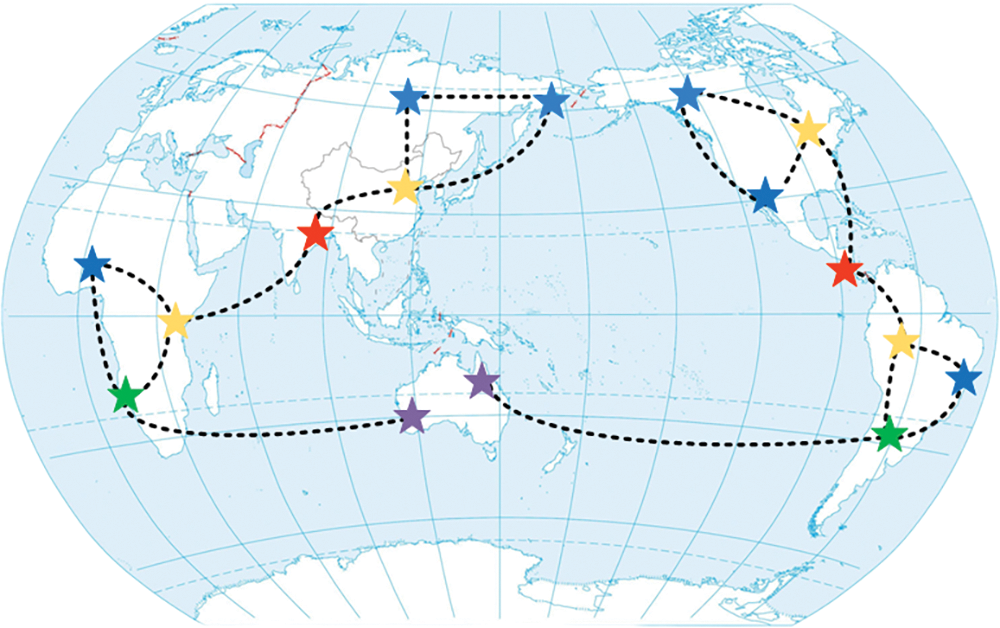
Figure 1: World-air-traffic network

In addition to the features of the node itself, its neighborhood nodes will also indeed affect the embedding of role-based networks. For example, a music teacher in the social network is interested in both music and photography, the role of which is more influenced by music than photography and its neighborhoods may be more music lovers than photography lovers. Most of the current methods based on features focus on linear aggregation [6] or manual [7] and recursive [8] feature extraction, which cannot represent the diverse information of neighborhood features. Characteristic functions on graphs: birds of a Feather (FEATHER) [9] considers this problem and proposes a characteristic function to make meaningful combinations of multiple node and neighborhood features.

Nevertheless, the extraction or aggregation of multiple features is extremely sensitive to noise that may interfere with the final embedding. VAE [10] assumes that the input follows an ideal data distribution by adding constraints to the encoder. Therefore, even if the noise disturbs networks to different degrees, a corresponding output can also be generated by using the coding within the disturbed range. Role-based network Embedding via Structural features reconstruction with Degree-regularized constraint (RESD) [11] uses VAE to reduce the effect of noise on the role-based network. It also proves the adverse effect of noise on embedding experimentally.

Above all, there are mainly three challenges in current role-based network embedding. 1) Role-similar nodes may be far away so we cannot capture global role information. 2) The varied distributions of nodes and their features are always ignored or simplified. 3) The noise may have an adverse influence on the embedding. To address these challenges, we propose a method called Role-based network Embedding via Quantum walk with weighted Features fusion (REQF).

Firstly, we superimpose all walk paths based on the superposition of the quantum walk to capture the global role information by multi-step evolution sequences and use the biased quantum walk to emphasize the local structure and learn role closeness. Secondly, we design a quantum walk weighted characteristic function to fuse features of nodes and their neighborhoods by different distributions. Finally, we use VAE to reduce the effects of noise and generate role-based network embedding. Extensive experiments on real-world networks demonstrate the effectiveness and stability of the proposed REQF.

Our main contributions are listed as follows:

▪   We propose a novel method REQF, which considers the influence of global and local role information, node features, and the effect of noise simultaneously for generating role-based network embedding.

▪   We utilize quantum walk to capture role information from global and local perspectives for solving the node distance problem, and we construct a quantum walk weighted characteristic function, that uses the quantum walk as probability weights of the characteristic function, to take node features into consideration for feature fusion.

▪   We use VAE to reduce the effect of noise in the network and get the optimal role-based network embedding.

The rest of the paper is organized as follows: In Section 2, we briefly review the related work. In Section 3, we introduce the proposed REQF in detail. In Section 4, we report experimental results on real-world networks. Finally, in Section 5, we conclude the paper.

2  Related Work

In graph networks, roles are sets of nodes with similar structural patterns and functions. It is first defined as classes of structurally equivalent nodes, and the structural equivalence is measured by the structural similarity of nodes [12]. Role-based network embedding aims to embed role-similar nodes into a compact embedding space.

Role-based networks are more concerned with the structural similarity of nodes and are independent of distance. To represent role information, Role-based graph embedding (Role2vec) [4] uses an attribute-based random walk to capture the role information of nodes. Learning structural Node Embeddings on Graphs via diffusion Wavelets (GraphWave) [13] learns structural node embedding by diffusion wavelets. Fast structural node embedding via role identification (RiWalk) [14] uses random walk to approximate graph kernels for role identification. Graph neural network with Local Structural Patterns (GraLSP) [15] incorporates local structure into sets of neighborhoods by anonymous walk. These methods based on the random walk are selective in obtaining the structural information and do not consider the global role information of nodes, which results in information loss. Thus, role-based network embedding needs a technique to overcome the limitations of distance and global information loss.

Quantum walk [16] is the quantization of walk based on the principle of random motion of particles. The generation of a walking path is determined by the walk position indicating the current location of the node and the walk state indicating the transfer process of walking to the next node. The classical random walk only generates one path for each walk, and no superposition is allowed. In contrast, the quantum walk has the property of coherent superposition that achieve randomness due to its superposition [17]. It can be described as the superposition of all walk states and it walks to all paths simultaneously. As shown in Fig. 2, quantum walk allows all nodes to interact with the whole network simultaneously.

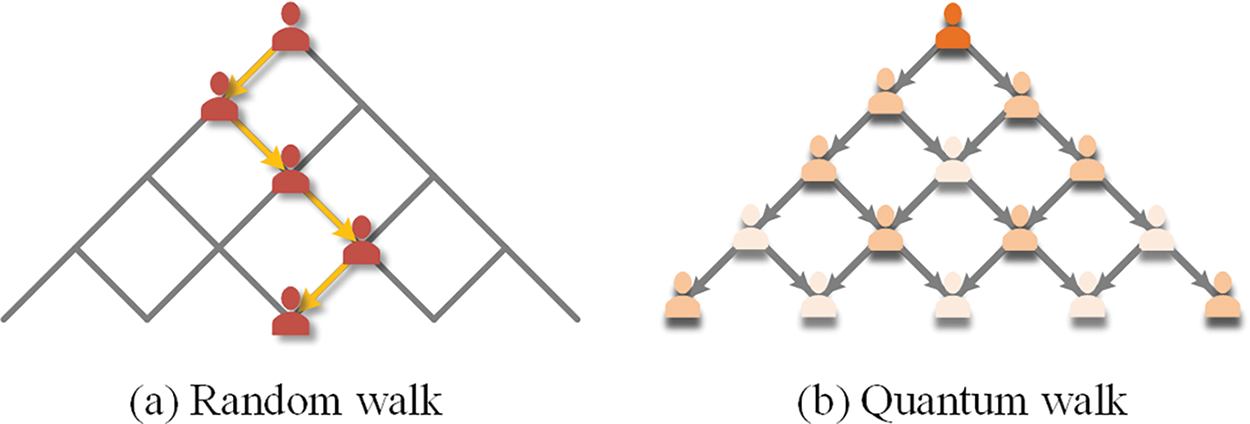
Figure 2: Illustration of comparison between random walk and quantum walk

Presently, the quantum walk has considerable research prospects in the field of role embedding. Most quantum walk of graphs is implemented by calculating the superposition of probability distributions. Fast Quantum Walk Kernel (FQWK) [18] uses quantum walk as the convolution kernel to measure the similarity of neighborhood substructures between node pairs. However, the method does not consider the structural influence of nodes from the global perspective. RED [5] uses quantum walk to capture the role information of nodes from global and local perspectives, but it ignores the feature information of nodes. It also proposes that role-similar nodes have similar evolution sequences, and the discrete-time quantum walk (DTQW) models are highly correlated with the structural information of nodes. Motivated by it, we introduce the DTQW model to learn the global and local structural patterns of nodes.

On the other side, most of the current feature-based network embedding methods generate embedding by simple extraction or linear aggregation of features. For example, Role eXtraction (RolX) [6] aggregates node features based on the matrix decomposition. Graph Auto-encoder guided by Structural information (GAS) [7] uses the manually extracted features as guidance to train the graph auto-encoder. Role Discovery-guided network embedding based on Autoencoder and Attention mechanism (RDAA) [8] uses recursive feature extraction and incorporates attention mechanisms to guide role discovery in auto-encoders. These methods view all neighborhood features of nodes as uniform distributions, ignoring the fact that different distributions of neighborhood features may have different effects on the central node. Thus, FEATHER [9] uses a complex-valued characteristic function to make meaningful combinations of multiple features and proves that characteristic functions can obtain effective neighborhood features at discrete evaluation points. But its probability weights are simply described by the power of the adjacency matrix, which cannot represent the correlated information well. Therefore, we try to use the quantum walk to appropriately represent the probability weights of the characteristic function that can implicitly highlight the role information and fuse various features in role-based network embedding.

Furthermore, noise affects the generation of high-quality network embedding. Due to the over-reliance on neighborhood information, the feature-based methods are sensitive to noise, causing side effects on the generation of embedding. RESD [11] uses VAE to reduce the effect of noise after extracting node features and preserve structural identity with degree regularization. Adversarial Variational Autoencoder Embedding (AVAE) [19] utilizes VAE to avoid noise from obstructing the convergence of generated data. Dual Adversarial Variational Embedding (DAVE) [20] proposes a model based on VAE for recommendations providing personalized noise reduction for different users and items. Purified Graph Generation (PGG) [21] also uses a variant of VAE to filter noise during graph generation. These methods indicate that the influence of noise can be reduced by using the approach of an encoder. Therefore, we attempt to use VAE to obtain a more accurate role-based embedding.

In this paper, we try to overcome the limitations of role-based embedding in terms of node distance and features via quantum walk and weighted characteristic function to capture the global role information and fuse node features, and we use VAE to effectively reduce the effect of noise, and finally obtain a more compact role-based network embedding.

3  The Proposed Method

In this section, we introduce the notation and the proposed method REQF. We first start with an overview and then present the detailed designs, including role information representation, feature information fusion, and noise effect reduction. Finally, we analyze the computational complexity of REQF.

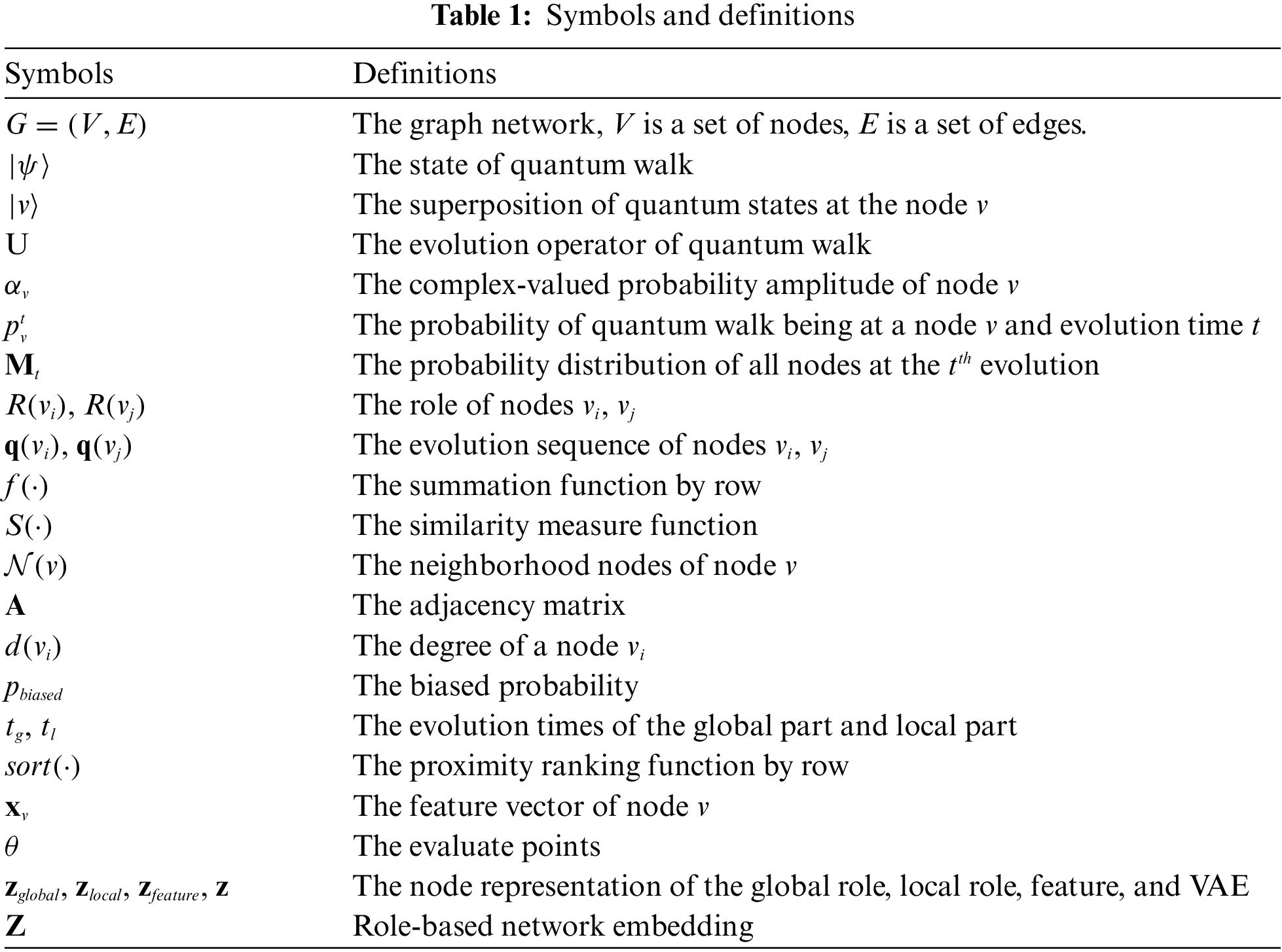
For clear clarification, the symbols and their definitions are listed in Table 1.

3.1 Notation and Problem Definition

Definition 1 Quantum Walk: Given an undirected and unweighted graph G=(V,E), where V={v1,v2,…vn} is the set of n nodes. Quantum walk consists of the state of quantum walk |ψ⟩ and the state evolution |ψ′⟩→U|ψ⟩. The state of quantum walk is described by a coordinate wave function |ψ⟩=∑vαv|v⟩, where |v⟩ denotes the superposition of quantum states at the node v, which is an n-dimensional column vector, and αv is the corresponding complex-valued probability amplitude. The state evolution process is usually described by |ψ′⟩→U|ψ⟩, where the evolution operator U is used to represent the position and direction of the quantum walk.

We define the probability of quantum walk being at a node v and evolution time t as pvt=∑v|αv(t)|2, where |αv(t)|2 is the complex-valued probability amplitude. The result of the quantum walk Mt is a n×n matrix, representing the probability distribution of all nodes at the tth evolution, that is Mt={p1t,p2t,…,pnt}T,t=1,2,…,n. The state evolution is defined as:

Mt=UMt−1(1)

Definition 2 Role Similarity: Roles are sets of nodes with similar structural patterns and functions in graph networks. The role similarity of nodes is defined by the evolution sequence that is formed by summing the probability distribution matrix of the quantum walk.

q={f(M1),f(M2),…,f(Mt)}(2)

S(R(vi),R(vj))→1⇔S(q(vi),q(vj))→1(3)

where q is the evolution sequence of quantum walks, R(vi), R(vj) represent the role of node vi, vj, f(⋅) is the summation function by row, and S(⋅) is the similarity measure function. Roles will get more similar if the value of S(⋅) reaches closer to 1.

Definition 3 Role-based Network Embedding: For a graph G, the neighborhood nodes of a node v are defined as 𝒩(v)={u∈V|(u,v)∈E}. Role-based network embedding Z∈Rn×d aims to generate the embedding that maximum reserves the role information contained in it, where d is the embedding dimension. zv∈Rd is the map for each node v into a low-dimensional vector space that contains role information.

Z={z1,z2,…,zn}T(4)

Role-similar nodes would be embedded into similar representations.

3.2 Overview of REQF

The illustration of our framework REQF is shown in Fig. 3. REQF consists of three parts: quantum walk, feature fusion, and VAE.

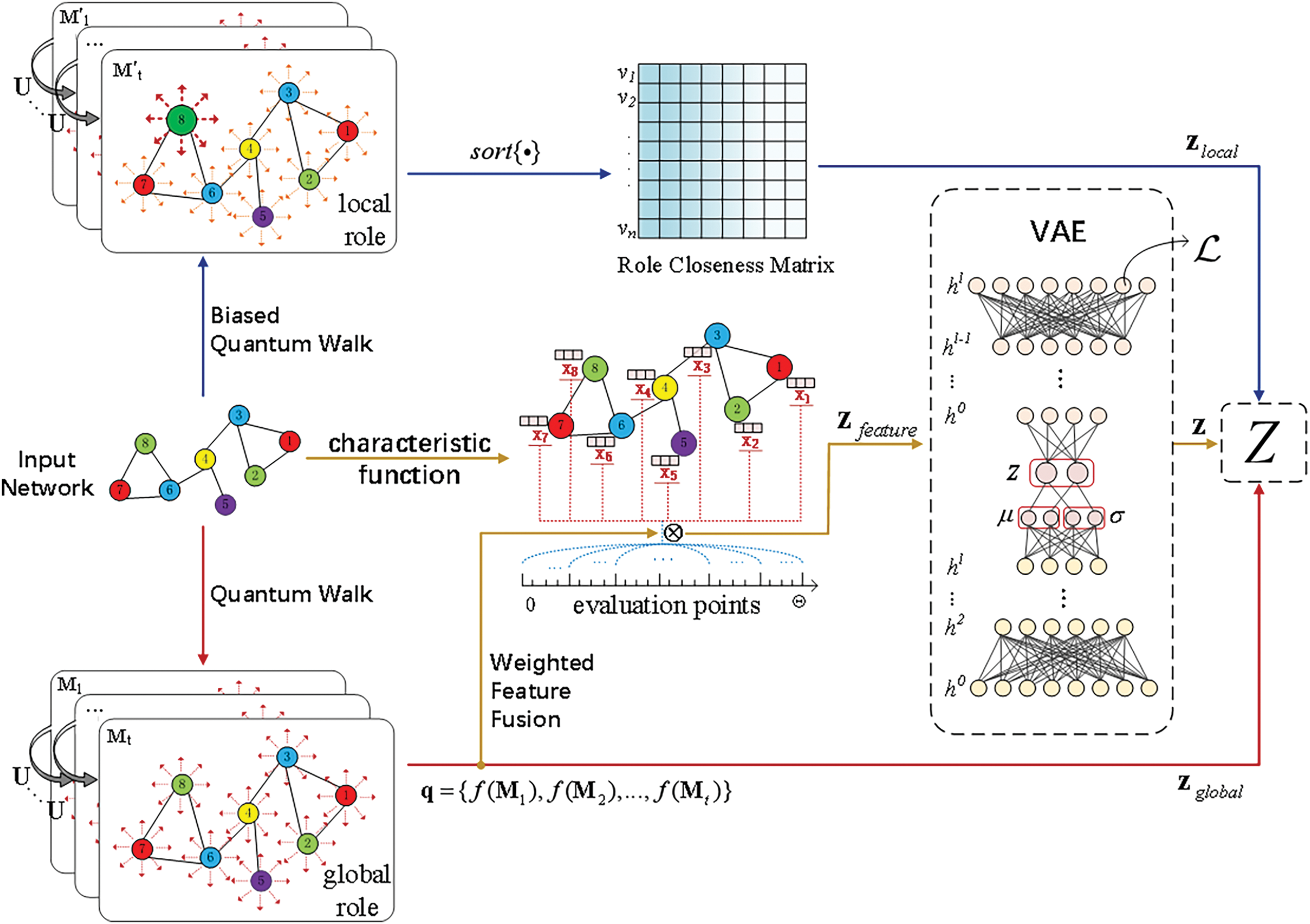
Figure 3: Illustration of our proposed framework REQF

First of all, we utilize quantum walk to capture the global role information zglobal (red arrow flow) and local role proximity zlocal (blue arrow flow) of nodes by the evolution sequence q. The block graphs represent the process of the quantum walk evolution as an operator U. The dotted arrows around nodes indicate that all nodes are involved in the evolution at the same time, and the thick dotted arrows indicate the biased process of the quantum walk with probability pbiased to make the node obtain a higher initial probability. Then, we use the quantum walk weighted characteristic function for feature fusion (yellow arrow flow), which uses Mt to weight characteristic function and is calculated at evaluation points θ to obtain the node neighborhood feature distribution zfeature with structural information. Finally, we leverage VAE to reduce the effect of noise z and generate the embedding Z.

3.3 Role Information Representation

REQF captures role information via quantum walk. It captures global role information and local role information by controlling the initial state probability. The global role information is the role relevance between nodes from the whole network. The local role information is the role proximity between nodes by the local structure of nodes, and it emphasizes more on the correlation between nodes and their neighborhoods.

3.3.1 Global Role Information

When all nodes have the same initial state probability, they evolve simultaneously over the entire network, and REQF simulates the global evolution by the probability distribution matrix Mt of quantum walk to represent the global role relevance of nodes and generate the global role representation zglobal. The formulated Grover operator [22] is shown in Eq. (5).

Mt(vi)=(2d(vi)−1)Mt−1(vi)+2d(vi)∑∀vj∈V,vj≠viMt−1(vj)(5)

M0(vi)=αvi(0)=An⋅d(vi)(6)

zglobal={f(M1),f(M2),…,f(Mtg)}(7)

where d(vi) is the degree of a node vi, A is the adjacency matrix, f(⋅) is the summation function by row, and tg is the evolution times of quantum walk.

3.3.2 Local Role Information

If the initial state probability of a particular node is higher, the evolution of the quantum walk should be biased to emphasize the similarity of the local structure of the node [23], and the probability distribution obtained can be viewed as the correlation between the node and the neighborhood. Thus, REQF use emphasizes the local structure of the node by biased quantum walk Mt to learn the role similarity of the node and generate a local role representation zlocal.

M0′(vi)=αvi(0)=A⋅pbiasedn⋅d(vi)(8)

zlocal=sort(f(M1′),f(M2′),…,f(Mtl′))(9)

where pbiased is the biased probability, tl is the evolution times of biased quantum walk, and sort(⋅) is the proximity ranking function by row to find other nodes with high role similarity to the central node.

3.4 Feature Information Fusion

Different distributions of neighborhood features may have different effects on nodes in real networks. FEATHER has theoretically demonstrated that graphs with the same structure have the same Characteristic Functions (CF). Therefore, considering the varied distributions of node neighborhood features, we use CF on the graph to describe the neighborhood feature distribution of the nodes, instead of fusing feature information in a simple linear aggregation way. The probability weights are defined by quantum walk to weight the CF which is to obtain feature information that highlights the structural property of the nodes.

According to the definition of the CF, we define the probability weights as the probability value of the quantum walk distribution matrix Mt between the source node vi and target node vj. REQF uses the quantum walk weighted CF to fuse features and obtain a better and richer node representation zfeature.

zfeature=∑vi,vj∈VMt(vi,vj)[cos⁡(θxvj)|sin⁡(θxvj)](10)

where xvj is the feature vector of the target node vj, θ is the value of evaluation points.

3.5 Noise Reduction and Embedding Generation

In reality, a lot of noise exists in extracting the role and feature information of nodes, and some node features unrelated to roles may interfere with the final role-based network embedding. To reduce the effect of noise, we use VAE to encode node role and feature information into the node embedding representation.

We use a Multi-Layer Perceptron (MLP) as our decoder and define it as follows:

hvil=tanh⁡(Wlhvil−1+bl),l=1,2,…,L(11)

where Wl and bl represent the weight vector and bias vector of the lth layer, L is the number of hidden layers in the encoder, and tanh⁡(⋅) is the hyperbolic tangent activation function. The vector zfeature(vi) contains the role and feature information of node vi, hvi0=zfeature(vi) is the input of the encoder.

The node embedding representation zvi of node vi follows a Gaussian distribution, that is, P(zvi)∼𝒩(μvi, diag(σvi2)). It can be obtained through a reparameterization trick [11] for learning the parameter μvi and σvi.

μvi=WμhviL+bμ(12)

log⁡σvi=WσhviL+bσ(13)

zvi=μvi+σvi⊙ι(14)

where Wμ, Wσ, bμ and bσ are respectively the weight and bias of the last layer of the encoder. ⊙ is the element-wise product, and ι follows a standard Gaussian distribution, ι∼𝒩(0,I).

Equally, we use an MLP as the decoder:

h^vil=tanh⁡(W^lh^vil−1+b^l),l=1,2,…,L(15)

where W^l and b^l are the weight and bias vector of the lth hidden layer in the decoder. h^vi0=zvi is the input of the decoder and h^viL is the reconstructed vector.

Finally, we define the loss function and the final embedding is obtained as follows:

ℒ=||h0−h^L||22=∑i=1n||hvi0−h^viL||22(16)

Z={zglobal,zlocal,z}(17)

The whole process of REQF is described in Algorithm 1.

3.6 Computational Complexity Analysis

The computational complexity of the proposed REQF mainly depends on the quantum walk and VAE, which are highly related to the number of nodes and feature dimensions.

Given a network G=(V,E), V is the set of nodes. REQF captures the global (lines 2–6) and local (lines 7–11) role information of nodes through the quantum walk, which takes O(tg + tl⋅|V|) time. In the quantum walk module, we simulate the quantum walk on classical computers, and the complexity is O(|V|3). The process of feature fusion (line 13) takes O(mtg⋅|V|), and m denote the dimension of the node feature. In the VAE module, the computational complexity is O(r2d), and r denotes the dimension of the input features, d denotes the output dimension. Therefore, the whole computational complexity of REQF is O(tl⋅|V|4+r2d).

The computational complexity of the REQF algorithm here is a bit high because the quantum walk is simulated with a conventional computer. But the complexity of the actual quantum walk is only O(1), so the theoretical complexity of REQF is only O(mtg⋅|V|+r2d), which indicates that the simulation of the quantum walk can be replaced by directly conducted in the future technologies, and make the present high complexity greatly reduced certainly.

4  Experiments

In this section, we evaluate the performance of REQF on real-world networks from the tasks of role classification, role detection and visualization, parameter sensitivity, and ablation study.

4.1 Datasets

We conduct experiments on seven real-world networks with unweighted undirected edges, the detailed statistics of the datasets are shown in Table 2.

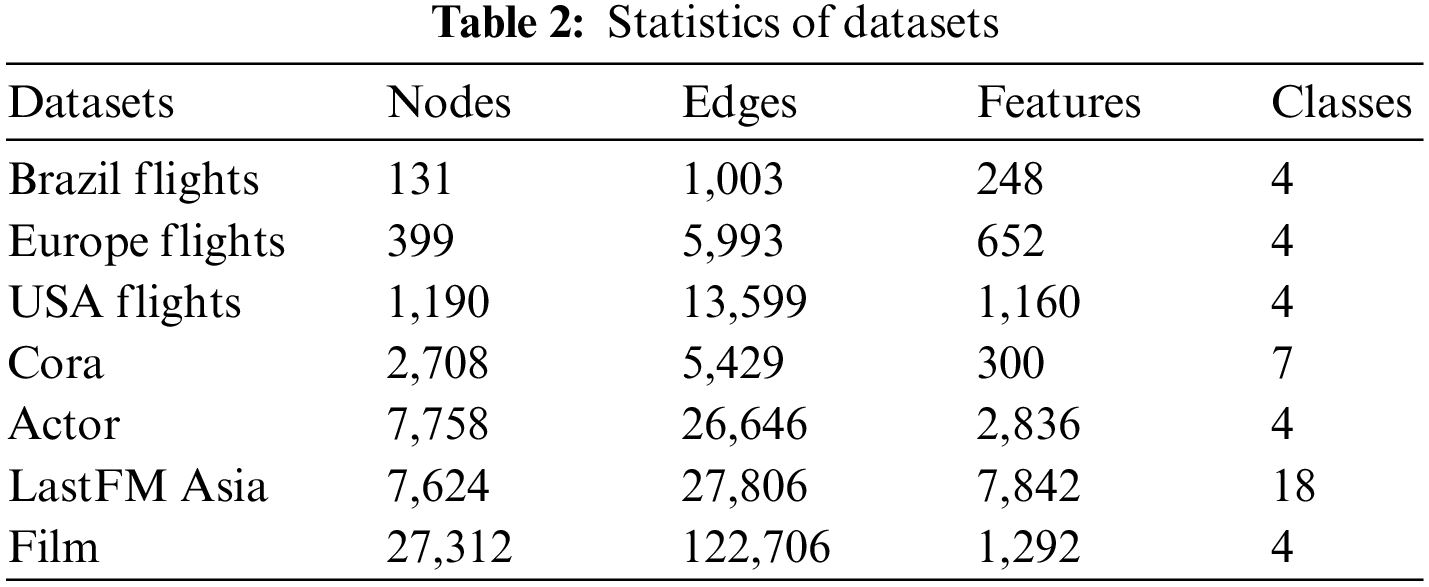
Air-traffic networks [11] is about air-traffic information network in different countries including America, Brazil, and Europe, Cora [15] is a citation network related to science, Actor [3] is a social network of American actors, LastFM Asia [9] is a social network of the LastFM music platform composed of Asian users, and Film [3] is English-language film network.

4.2 Experiment Setting

We compare REQF with classic and advanced role-based network embedding methods including Role2vec [4], FEATHER [9], RED [5], and RESD [11]. All the experimental parameters are set to the default values provided in their papers.

For the REQF, we set the final parameters in the parameter sensitivity experiment. We set quantum walk evolution times tg=16, biased evolution times tl=4, biased probability pbiased=0.9, and evaluation points θ=5. As for the datasets with missing features, like the Film dataset, we use ReFex [24] to extract the features of nodes. In VAE, we use a 1-layer MLP model with the ReLU activation function and set the number of hidden layers to 2, and set the number of epochs to 50.

4.3 Role Classification

We conduct the task of role-based node classification on seven real-world networks. In this experiment, we input the embedding into a linear logistic regression classifier, 70% of the data is randomly selected for training, and the rest is used for testing. We run all the methods 20 times, and compute their average F1 score to measure the accuracy of the classification, and the area under the curve (AUC) score to measure the quality of it. The results are shown in Tables 3–5.

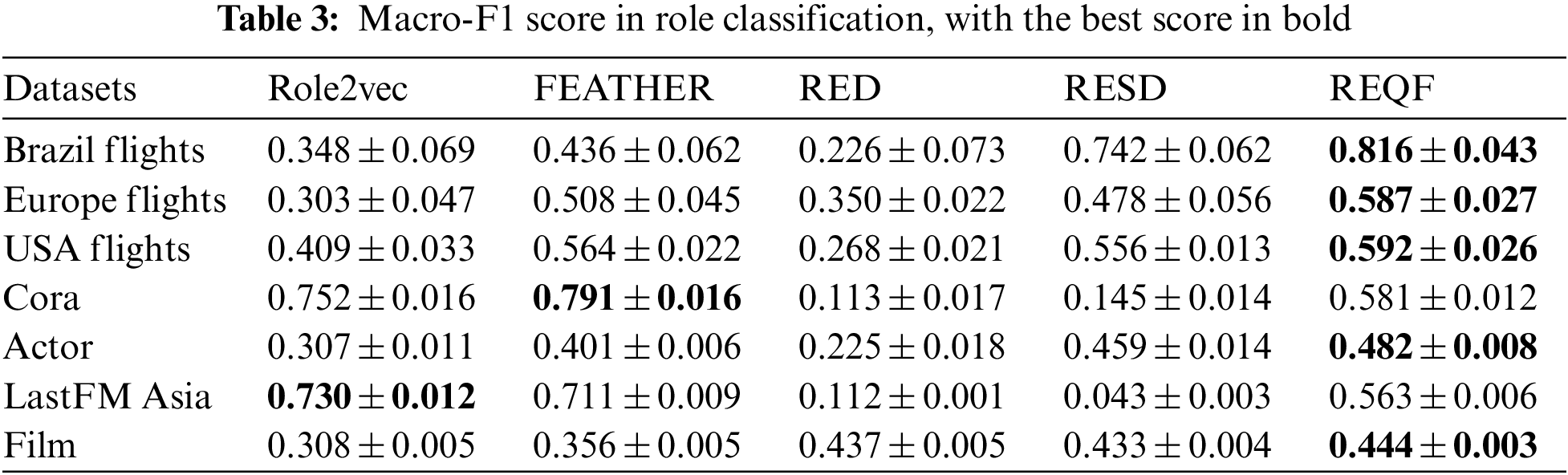
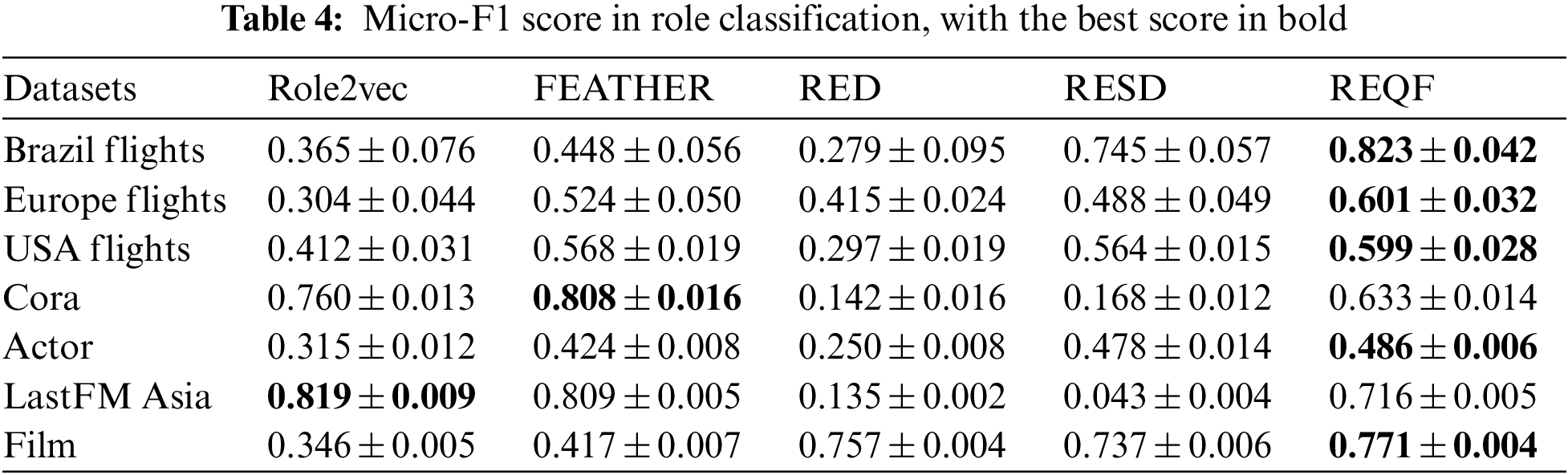
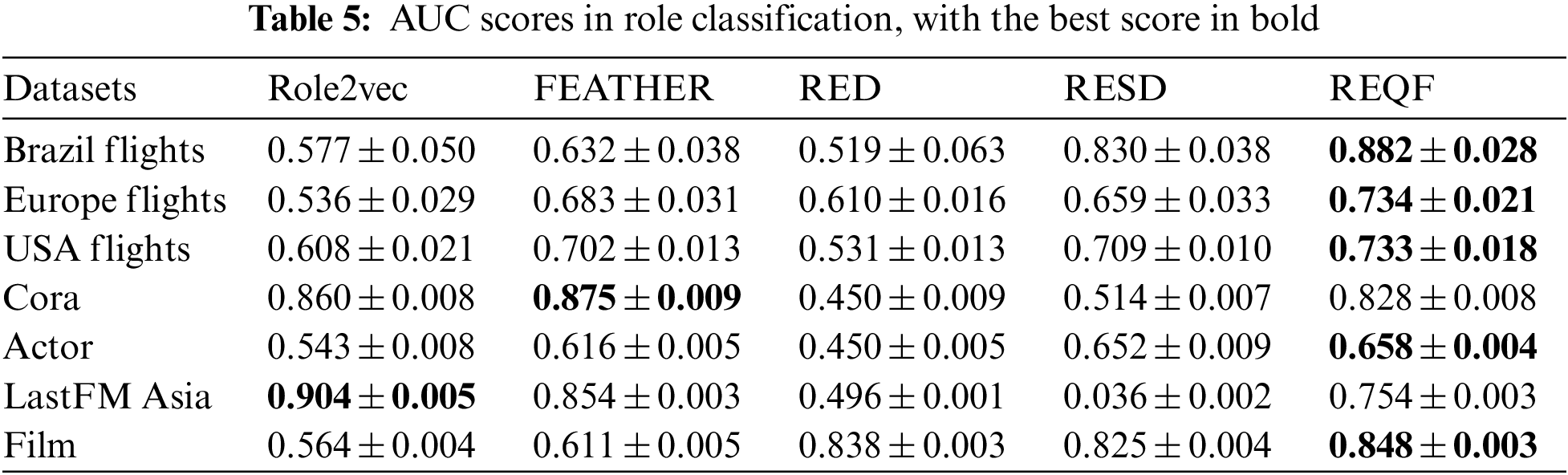
The results of role classification indicate that the proposed REQF has achieved the best performance in five networks, with 14.6% higher than the best baseline method. However, the performance of REQF on Cora and LastFM Asia networks is lower than FEATHER and Role2Vec separately. The reason may be that the users of these two social networks are mostly mutual strangers, with relatively equal interconnection and less obvious role characteristics, resulting in poor performance in role-based classification. It can be proved that both datasets also show low performance in the RED and RESD methods that are based on role embedding. So, the results demonstrate the effectiveness of REQF in the role classification task.

4.4 Role Detection

Role detection is one of the important tasks of role-based network embedding. It clusters the embedding into different existing classes to represent different roles in the real network. The experiment is conducted to K-means clustering method using Brazil fights dataset to observe the performances.

We evaluate the clustering extensively using four popular metrics: Adjusted Mutual Information (AMI) [25] to assess the closeness between the clustering results and the true classes of the samples, Adjusted Rand Index (ARI) [26] to measure the degree of fit between the two data distributions, V-measure [27] to indicate the closeness of the group divisions, and Silhouette score (Sil) [28] to indicate the closeness of each group class. The values of all metrics range from 0 to 1, and a value closer to 1 means a better effect.

The results are shown in Table 6, and REQF-means REQF without VAE to reduce the effect of noise. REQF significantly outperformed all other models in role detection due to considering node role information, features, and the effect of noise at the same time, which other methods ignore.

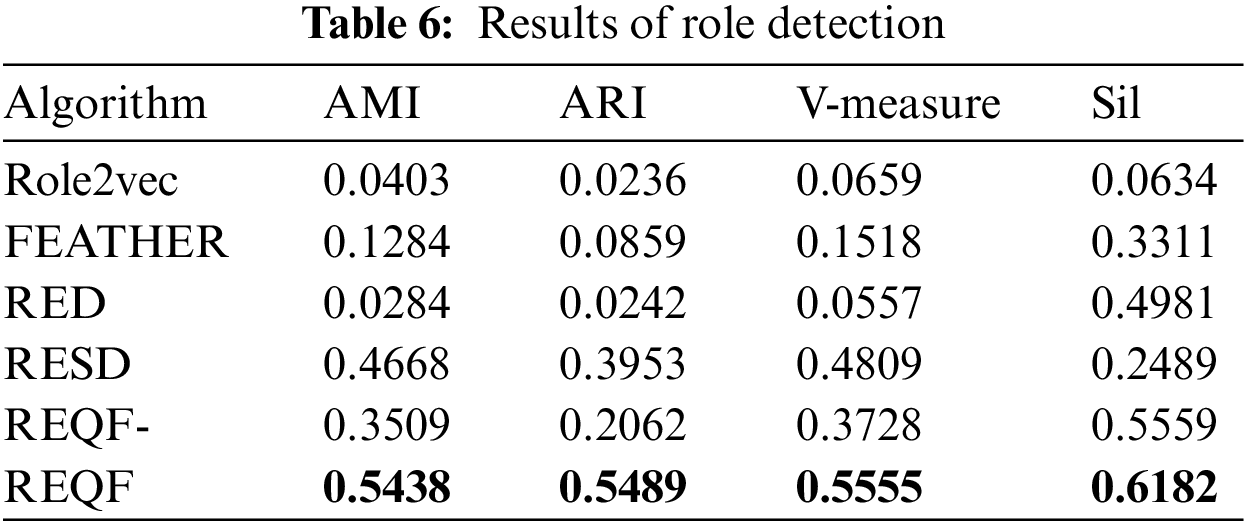
Compared with the best baseline, REQF is improved by 16.5% in AMI, 38.9% in ARI, 15.5% in V-measure, and 24.1% in Sil. An intuitive comparison is shown in Fig. 4. It is obvious that our REQF shows the best performance in role detection.

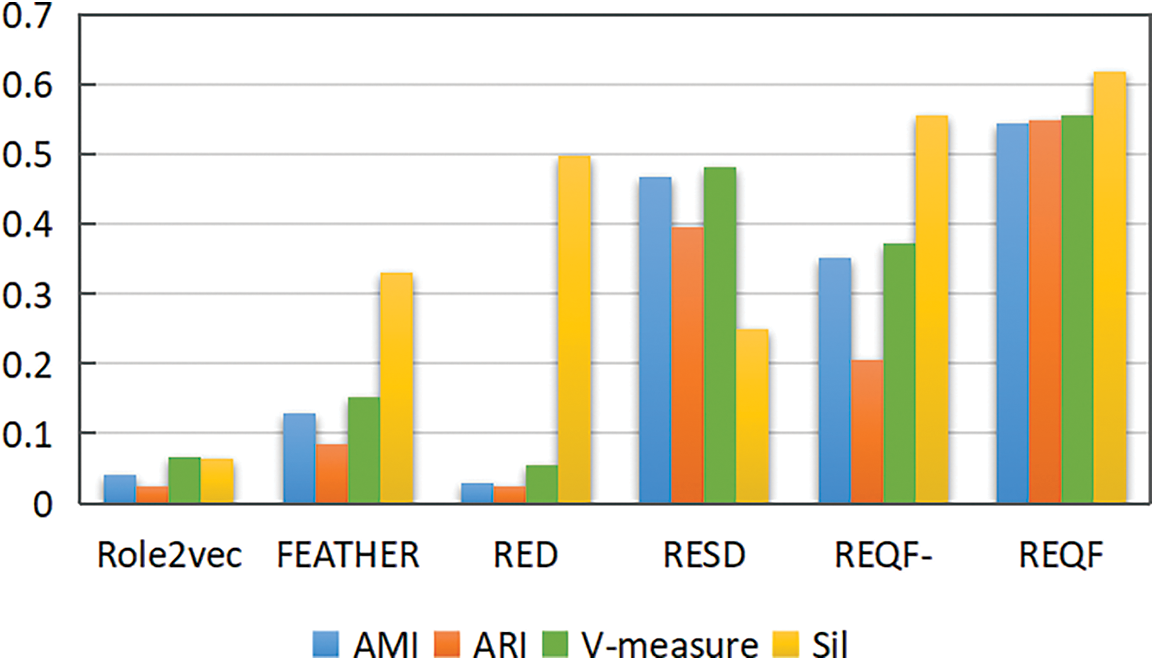
Figure 4: Histogram of role detection. REQF-means REQF without VAE

4.5 Parameter Sensitivity

For parameters of REQF, we conduct experiments to analyze the sensitivity of all parameters on the Brazil flights network. Fig. 5 plots the micro-F1 score of the role classification task with varying parameters.

▪   Effect of tg. As shown in Fig. 5a, when evolution times tg<16, the micro-F1 score fluctuates slightly, and with the increase of the evolution times, the model gradually tends to be stable. However, when tg>16, the model performance decreases significantly. Therefore, we can get the best model performance when tg=16.

▪   Effect of tl. Fig. 5b shows how the biased evolution times tl affects the performance. We can observe that REQF gets the best results with tl=4. When tl=2, although the average score is higher, it fluctuates more making the model more unstable, especially when tl=8 with the longest box. Thus, the performance does not become better as the biased evolution times increase, which indicates that quantum walk can capture network information and achieve better performance in short evolution times.

▪   Effect of pbiased. The results of varying biased probability pbiased are shown in Fig. 5c. We can get the optimal mean value when pbiased=0.2 and the second-best when pbiased=0.9, but it is more stable at pbiased=0.9. It confirms that the performance of our model is optimal when the biased probability is 0.9.

▪   Effect of θ. Fig. 5d shows the influence of evaluation points on REQF performance. When θ=1, we get the highest score but the length of the box is long, which means it fluctuates greatly. While when θ=7, the length of the box is the shortest and the model is the most stable. On the whole, varying θ has little effect on the mean value, so the appropriate parameter value can be set according to the demand for downstream tasks.

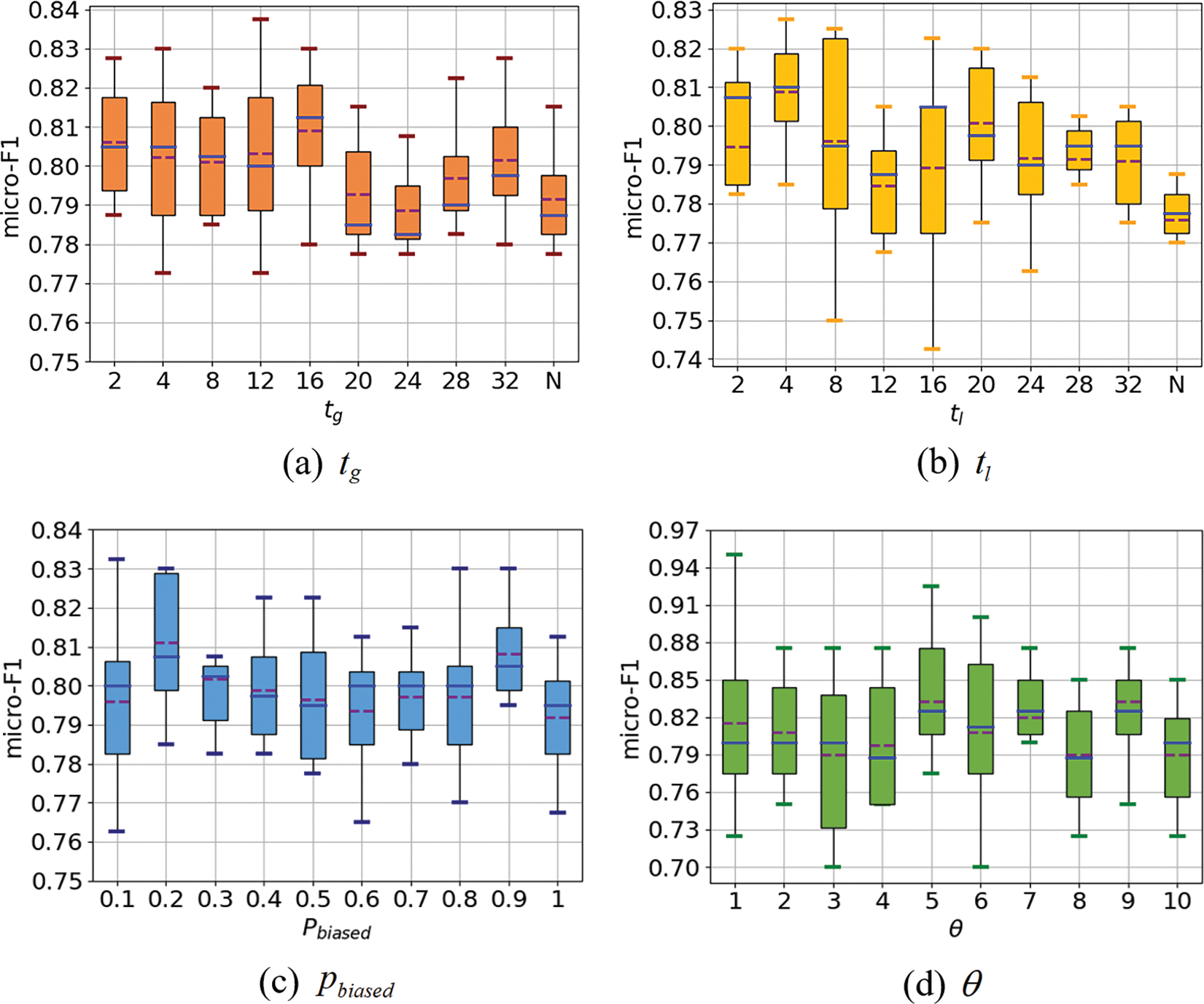
Figure 5: Parameters sensitivity on Brazil Network with varying (a) evolution times, (b) biased evolution times, (c) biased probability, and (d) evaluation points. The solid line denotes the median and the dotted line denotes the average

4.6 Ablation Study

To explore the influence of quantum walk, CF, and VAE modules on the REQF, we compare the performance between REQF and REQF without the quantum walk (REF), feature fusion (REQ), and VAE (REQF-). The results are shown in Fig. 6.

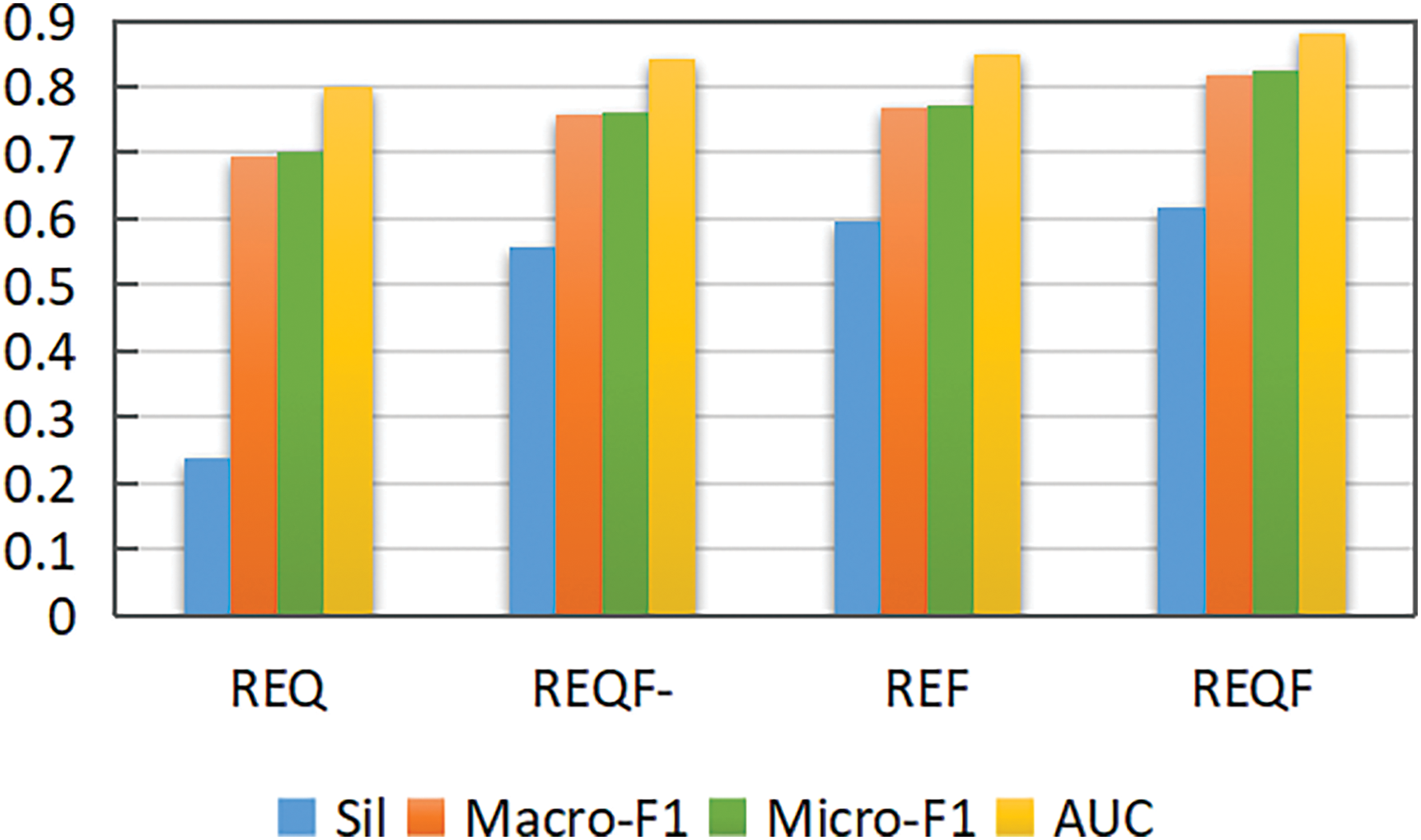
Figure 6: Ablation of REQF, REF, REQ, REQF-, which denote REQF without quantum walk (REF), feature fusion (REQ), and variational auto-encoder (REQF-), respectively

It is obvious that REQF significantly outperforms the other models, showing the best performance. REF is second-best, while it is still inferior to REQF, indicating the necessity of global role information and the effectiveness of the quantum walk module in capturing it. The results of REQF-and REF are close, which proves that noise reduction of VAE plays an important role same as the quantum walk. REQ has the worst results, especially the Sil metric, which is significantly lower than all the others. It indicates that the CF greatly affects the performance of REQF, especially in the clustering tasks, and it is necessary to consider the different distributions of node features and neighborhoods. Hence, all modules indeed play an important role in REQF, and all of them effectively improve the overall performance of REQF.

4.7 Visualization

In order to visualize the effect of role clustering, we compare REQF with baselines for visualization on the Brazil flights dataset due to its proper size and uniform classes of node roles. We use t-SNE [29] to get the dimensional reduction visualization, which is sensitive to the local structure of nodes and exhibits more stability than other visualization algorithms [30]. The roles are mapped into the color of points, points with the same color should be close to each other, while points with different colors should be far apart.

As shown in Fig. 7, each node is represented as a point with different colors, and the color indicates the node’s role. Points with the same role should be clustered together, that is, points with the same color should be close to each other, while points with different colors should be far apart. The visualization results show that the embedding of the REQF (Fig. 7f) can be well clustered in general, although there are a few individual nodes with incorrect clustering results. This is because REQF considers global and local role information, node features, and noise simultaneously. The points in different colors of Role2vec (Fig. 7a) are mixed up as it only considers the local structure of nodes and points cannot be classified well. RED (Fig. 7b) is better than Role2vec as it considers global role information. FEATHER (Fig. 7c) considers node features so it clusters closer while it still cannot effectively achieve role clustering. RESD (Fig. 7d) is more effective as the points of the same color are quite close to each other, but there is no obvious division of the different roles of nodes as it ignores global information. In addition, we conduct the experiment of REQF-(Fig. 7e) that REQF without VAE, and its visualization illustrates that the VAE indeed reduces the effect of noise and enables the model to have better role clustering ability. Therefore, REQF has the best visualization effect and the model can divide the roles of nodes well in the real network.

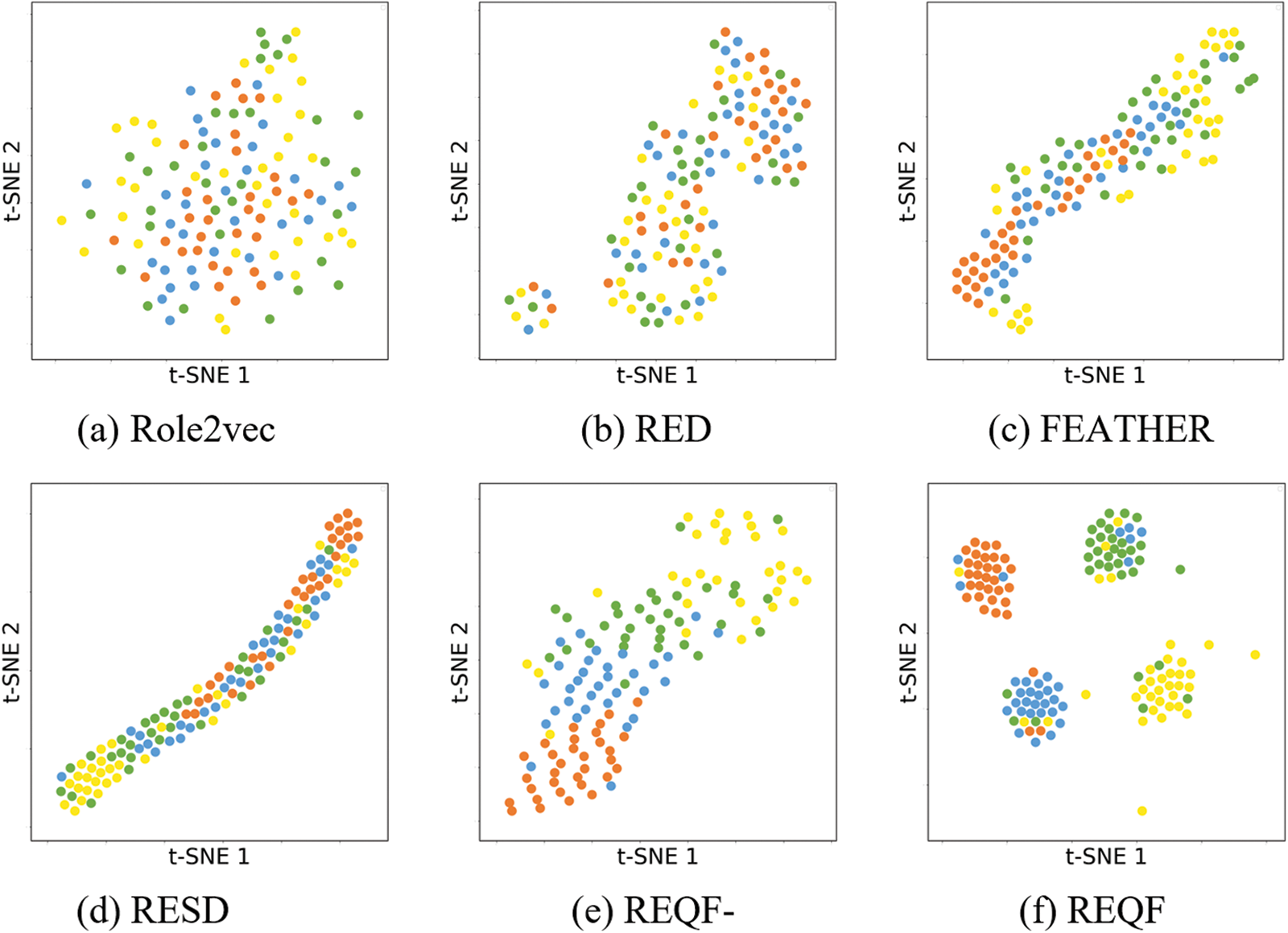
Figure 7: Visualization of different methods on Brazil network in 2D space

5  Conclusion

In this paper, we propose REQF to generate role-based network embedding via quantum walk and its weighted feature fusion, which simultaneously considers node role information, node features, and noise. REQF utilizes quantum walk to capture the global and local role information of nodes, leverage its weighted characteristic function for feature fusion, and finally use VAE to reduce the effect of noise. The experimental results demonstrate the effectiveness and stability of the REQF on real-world datasets for downstream tasks. We also demonstrate the importance of each module and explore optimal values of parameters. For the limitation of our work, on the one hand, we only use a simple multi-layer perceptron, which may not be able to reduce the effect of noise sufficiently. On the other hand, our proposed method only focuses on homogeneous networks, and it cannot be expanded to heterogeneous graph networks. For future work, we can try a more efficient deep-learning framework to obtain a better representation of the role-based network. We can also expand to explore the field of heterogeneous role-based graph networks.

Funding Statement: This work was supported in part by the National Nature Science Foundation of China (Grant 62172065) and the Natural Science Foundation of Chongqing (Grant cstc2020jcyj-msxmX0137).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. A. Rossi and N. K. Ahmed, “Role discovery in networks,” IEEE Transactions on Knowledge and Data Engineering, vol. 27, no. 4, pp. 1112–1131, 2015. [Google Scholar]

2. J. Ma, M. Li and H. J. Li, “Traffic dynamics on multilayer networks with different speeds,” IEEE Transactions on Circuits and Systems II: Express Briefs, vol. 69, no. 3, pp. 1697–1701, 2022. [Google Scholar]

3. P. Jiao, X. Guo, T. Pan, W. Zhang, Y. Pei et al., “A survey on role-oriented network embedding,” IEEE Transactions on Big Data, vol. 8, no. 4, pp. 933–952, 2022. [Google Scholar]

4. N. K. Ahmed, R. A. Rossi, J. B. Lee, T. L. Willke, R. Zhou et al., “Role-based graph embeddings,” IEEE Transactions on Knowledge and Data Engineering, vol. 34, no. 5, pp. 2401–2415, 2022. [Google Scholar]

5. X. Wang, S. Jian, K. Lu, Y. Zhang and K. Liu, “RED: Learning the role embedding in networks via discrete-time quantum walk,” Applied Intelligence, vol. 52, no. 2, pp. 1493–1507, 2022. [Google Scholar]

6. K. Henderson, B. Gallagher, T. Eliassi-Rad, H. Tong, S. Basu et al., “RoLX: Structural role extraction & mining in large graphs,” in Proc. KDD, New York, NY, USA, pp. 1231–1239, 2012. [Google Scholar]

7. X. Guo, W. Zhang, W. Wang, Y. Yu, Y. Wang et al., “Role-oriented graph auto-encoder guided by structural information,” in Proc. DASFAA, Jeju, South Korea, pp. 466–481, 2020. [Google Scholar]

8. P. Jiao, Q. Tian, W. Zhang, X. Guo, D. Jin et al., “Role discovery-guided network embedding based on autoencoder and attention mechanism,” IEEE Transactions on Cybernetics, vol. 53, no. 1, pp. 365–378, 2023. [Google Scholar] [PubMed]

9. B. Rozemberczki and R. Sarkar, “Characteristic functions on graphs: Birds of a feather, from statistical descriptors to parametric models,” in Proc. CIKM, New York, NY, USA, pp. 1325–1334, 2020. [Google Scholar]

10. D. P. Kingma and M. Welling, “Auto-encoding variational Bayes,” in Proc. ICLR, Banff, AB, Canada, pp. 14–16, 2014. [Google Scholar]

11. W. Zhang, X. Guo, W. Wang, Q. Tian, L. Pan et al., “Role-based network embedding via structural features reconstruction with degree-regularized constraint,” Knowledge-Based Systems, vol. 218, no. 3, pp. 106872, 2021. [Google Scholar]

12. R. A. Rossi, D. Jin, S. Kim, N. K. Ahmed, D. Koutra et al., “On proximity and structural role-based embeddings in networks: Misconceptions, techniques, and applications,” ACM Transactions on Knowledge Discovery from Data, vol. 14, no. 5, pp. 1–37, 2020. [Google Scholar]

13. C. Donnat, M. Zitnik, D. Hallac and J. Leskovec, “Learning structural node embeddings via diffusion wavelets,” in Proc. KDD, New York, NY, USA, pp. 1320–1329, 2018. [Google Scholar]

14. X. Ma, G. Qin, Z. Qiu, M. Zheng and Z. Wang, “Riwalk: Fast structural node embedding via role identification,” in Proc. ICDM, Beijing, China, pp. 478–487, 2019. [Google Scholar]

15. Y. Jin, G. Song and C. Shi, “GraLSP: Graph neural networks with local structural patterns,” in Proc. AAAI, New York, NY, USA, pp. 4361–4368, 2020. [Google Scholar]

16. S. E. Venegas-Andraca, “Quantum walks: A comprehensive review,” Quantum Information Processing, vol. 11, no. 5, pp. 1015–1106, 2012. [Google Scholar]

17. M. Islam Kamran, M. A. Khan, S. A. Alsuhibany, Y. Yasin Ghadi, Arshad et al., “A highly secured image encryption scheme using quantum walk and chaos,” Computers, Materials & Continua, vol. 73, no. 1, pp. 657–672, 2022. [Google Scholar]

18. Y. Zhang, L. Wang, R. C. Wilson and K. Liu, “An r-convolution graph kernel based on fast discrete-time quantum walk,” IEEE Transactions on Neural Networks and Learning Systems, vol. 33, no. 1, pp. 292–303, 2022. [Google Scholar] [PubMed]

19. X. Zhang, L. Yao and F. Yuan, “Adversarial variational embedding for robust semi-supervised learning,” in Proc. KDD, New York, NY, USA, pp. 139–147, 2019. [Google Scholar]

20. Q. Yi, N. Yang and P. Yu, “Dual adversarial variational embedding for robust recommendation,” IEEE Transactions on Knowledge and Data Engineering, vol. 35, no. 2, pp. 1421–1433, 2023. [Google Scholar]

21. Y. He, Y. Dong, P. Cui, Y. Jiao, X. Wang et al., “Purify and generate: Learning faithful item-to-item graph from noisy user-item interaction behaviors,” in Proc. KDD, New York, NY, USA, pp. 3002–3010, 2021. [Google Scholar]

22. V. Chauhan, S. Negi, D. Jain, P. Singh, A. K. Sagar et al., “Quantum computers: A review on how quantum computing can boom AI,” in Proc. ICACITE, Greater Noida, India, pp. 559–563, 2022. [Google Scholar]

23. X. Wang, K. Lu, Y. Zhang and K. Liu, “QSIM: A novel approach to node proximity estimation based on discrete-time quantum walk,” Applied Intelligence, vol. 51, no. 4, pp. 2574–2588, 2021. [Google Scholar]

24. K. Henderson, B. Gallagher, L. Li, L. Akoglu, T. Eliassi-Rad et al., “It’s who you know: Graph mining using recursive structural features,” in Proc. KDD, New York, NY, USA, pp. 663–671, 2011. [Google Scholar]

25. M. E. J. Newman, G. T. Cantwell and J. G. Young, “Improved mutual information measure for clustering, classification, and community detection,” Physical Review E., vol. 101, no. 4, pp. 042304, 2020. [Google Scholar] [PubMed]

26. M. J. Warrens and H. van der Hoef, “Understanding the adjusted rand index and other partition comparison indices based on counting object pairs,” Journal of Classification, vol. 39, no. 3, pp. 487–509, 2022. [Google Scholar]

27. J. Nowosad and T. F. Stepinski, “Spatial association between regionalizations using the information-theoretical v-measure,” International Journal of Geographical Information Science, vol. 32, no. 12, pp. 2386–2401, 2018. [Google Scholar]

28. K. R. Shahapure and C. Nicholas, “Cluster quality analysis using silhouette score,” in Proc. DSAA, Sydney, NSW, Australia, pp. 747–748, 2020. [Google Scholar]

29. F. Anowar, S. Sadaoui and B. Selim, “Conceptual and empirical comparison of dimensionality reduction algorithms (PCA, KPCA, LDA, MDS, SVD, LLE, ISOMAP, LE, ICA, t-SNE),” Computer Science Review, vol. 40, pp. 100378, 2021. [Google Scholar]

30. S. Kang and S. Kyun Kim, “Outlier behavior detection for indoor environment based on t-SNE clustering,” Computers, Materials & Continua, vol. 68, no. 3, pp. 3725–3736, 2021. [Google Scholar]