An Efficient Sleep Spindle Detection Algorithm Based on MP and LSBoost

1  Introduction

Sleep is essential, particularly in the early stages of life, for brain maturation and the development of the central nervous system [1]. The study of sleep is largely undertaken using a sleep EEG. In clinical practice, sleep spindles are often used to evaluate sleep phase abnormalities. As one of the markers of the second stage of NREM sleep, the sleep spindle, is one of the most important sleep events in the sleep microstructure, and is commonly generated in the thalamus cortex system [2,3]. The density, number and amplitude of spindle activity have been shown to be related to general cognitive ability, sleep disorders, learning and memory [4–8]. Furthermore, spindle activity can be used as one of the indicators to identify patients with a disorder of consciousness (DOC), that is, to identify patients with a minimal consciousness state and an unresponsive syndrome [9]. Spindle wave disorder is an important symptom of many early neurological diseases. Clinically, many mental diseases, such as Parkinson’s disease [3,10], Alzheimer’s disease [11,12], autism [13,14], schizophrenia [15] and epilepsy [16,17], have been proven to be closely related with abnormal spindles. Therefore, spindles are considered to be a biomarker of brain health and play an important role in clinical diagnosis and prognostic significance. It is crucial to detect sleep spindles rapidly and accurately for clinical diagnosis.

Traditional sleep spindle detection methods rely on manual annotation of the EEG by professionals, which is labor-intensive and inefficient. Rechtschaffen and Kales standards and the American Academy of Sleep Medicine Manual (AASM) are the two most commonly used sleep criteria. Specifically, Rechtschaffen and Kales defined a spindle wave as a burst of oscillatory activity on the EEG with a frequency of 12–14 Hz that occurs during NREM sleep state 2 and lasts at least 0.5–3 s [18]. The AASM modified Rechtschaffen and Kales’ standard guidelines for sleep classification and proposed new guidelines for the terminology, recording method and scoring rules pertaining to sleep-related behaviour [19]. The AASM standard defines the sleep spindle as a sinusoidal spindle-shaped EEG signal lasting at least 0.5s, with a frequency distribution between 11–16 Hz [20]. Many current studies use the AASM standard as the gold standard for the automatic detection and evaluation of spindle events [21]. However, even with detailed rules and guidelines for detecting sleep spindles, the manual detection task is still onerous and costly. Furthermore, due to the subjective understanding of the AASM standard and the differences in experience, the annotation results of different experts may be inconsistent [21]. Therefore, to improve the reliability and objectivity of detecting spindle activity and to compensate for the limitations of the manual detection of spindle events, it is very important to explore algorithms to automatically detect sleep spindle events.

This study presents an autonomous sleep spindle detection algorithm combining MP and LSBoost [22]. Unlike previous studies that used the MP method to identify sleep spindles [23,24], this study considers the MP as a pre-detection step to search for potential sleep spindles. Then, to obtain a reliable label for the EEG segments, this study creates representative EEG characteristics and trains an ensemble learning classifier called LSBoost to eliminate the high-frequency alpha waves recognized by MP. The experiment results on the public DREAMS dataset demonstrate the effectiveness of the proposed method for the automatic detection of sleep spindles. The novelty of our work can be summarized as follows:

•   To accurately locate the possible sleep spindles from raw EEG data, we adopt the MP method as a pre-detection step.

•   We propose the MP-LSBoost scheme for automatic sleep spindle detection and validate its efficiency on the public DREAMS dataset.

The remainder of this paper is structured as follows. Section 2 describes the data and annotation criterion. It then presents the proposed method including MP and LSBoost. The experiment findings and a performance evaluation are shown in Section 3. Section 4 discusses the strengths and weaknesses of the study approach. Conclusions are presented in Section 5.

2  Related Work

Current mainstream automatic spindle detectors are based on signal processing that is, to identify the amplitude information [25] or the time-frequency information [26] of the spindle event. The detection methods that use amplitude information include Teager energy operator (TEO) [25,27] and the root mean square of amplitude [28]. Jiang et al. used the TEO with adaptive parameters to detect a large number of EEG segments containing spindle wave amplitude information and a bagging classifier to pick out the wrong sleep spindles to ensure that all detected spindles are ground truth [25]. This method achieved an F1-score of 54.5% on the open DREAMS dataset. Schimekek developed a spindle wave detector for rapid alpha activity. He compared the peak-to-peak amplitude of EEG data with the amplitude standard to screen out spindle wave segments, and then calculated the ratio of the root mean square of alpha to the root mean square of the spindle wave. If it is greater than 1.2, it is a fast alpha wave and removed, with an accuracy of 89.7% [28]. However, using amplitude information to identify spindles has several limitations. On the one hand, as the amplitude contains less spindle wave information, judgements based on it are unreliable, and often result in excessive error detection. On the other hand, it is well known that EEG is a non-stationary signal, and the amplitude of each spindle wave changes with time, which makes it difficult to accurately detect and locate the spindle wave band.

The detection methods utilizing time-frequency information include band-pass filtering [29], continuous wavelet transform decomposition [30,31], short-time Fourier transform (STFT), MP [32] and so on. Of these, the signal segment included in the event detected by short-time Fourier transform cannot be too short, otherwise it is easy to miss detection [33]. Although wavelet decomposition has advantages in detecting short-lived events, some studies have found that wavelet-based methods are prone to filter distortions, which adversely affects the analysis of short-term events such as spindles [34]. LaRocco et al. used the MP with Gabor atoms to decompose the signal and detect the spindle using parametric analysis [23]. The authors validated the performance of their algorithm on the DREAMS dataset, achieving an F1-score of 66.7%. Lachner-Piza et al. first computed features of the EEG (e.g., spectral power and amplitude) and filtered out redundant features, and then used a binary support vector machine to classify the spindles [35]. They reported a sensitivity of 53.0% and a precision of 37.0% on the DREAMS dataset. Causa et al. [36] used the Hill-Huang transform to combine the two pieces of information to detect spindles. Parekh et al. considered the EEG as the sum of transient and oscillatory components [37], and detected spindles using a bandpass filter and the TEO. The proposed method achieves an F1-score of 66.0% on the DREAMS dataset. Overall, the performance of the detection methods based on time-frequency information is generally higher than that of methods based on amplitude information. The accurate determination of the onset and offset of each spindle segment is the most important task in sleeping spindle assays. More efficient time-frequency analysis techniques should be explored to further enhance the detection efficacy of sleep spindles.

3  Method

3.1 Dataset

The DREAMS dataset [38] is a public dataset consisting of 30-min excerpts taken from clinical polysomnography (PSG) recordings on eight subjects (age range: 31–53, sex: 4F/4M). The manual scoring of the spindle in 30-s time periods is undertaken by two trained experts following the Rechtschaffen and Kales criteria. However, one expert scored the recordings for all eight subjects, but the other only expert scored six recordings. So, the study analyzed the six subjects’ data which was scored by both experts (two recordings from C3-A1, one at 50 Hz and one at 100 Hz sampling rates; four recordings from CZ-A1 at 200 Hz sampling rate).

The sleep spindle annotation characteristics from the DREAMS dataset are shown in Fig. 1, including spindle wave numbers and mean duration, where black represents the results from Expert 1, orange represents the results from Expert 2, and cyan represents the results from the Union standard, which is the union of the sleep spindle data annotated by Expert 1 and Expert 2 for the same subject. In Fig. 1a, the number of sleep spindles identified by Expert 1 and Expert 2 is quite different, and Expert 2 usually demarcates more spindles. During the detection process, relying only on the annotation of Expert 1 or Expert 2 may result in large errors. Therefore, in this paper, we combine the annotation results of two experts with the “or” criterion as the real reference value. Fig. 1b is the average time of each subject’s spindle data of Expert 1, Expert 2 and Union. It can be clearly seen that the average duration of Expert 2 and Union are relatively similar.

Figure 1: The sleep spindle annotation characteristics based on the experts’ scoring of the DREAMS dataset. (a) Number of spindles per subject. (b) Average duration of the spindles for each subject. Expert1 and Expert 2 are the two experts in the dataset respectively, and Union is the spindle wave generated when the “or criterion” is used

3.2 Data Processing

The organization of the method proposed in this paper is shown in Fig. 2, which comprises two steps. The first step is pre-detection. Band-pass filtering is used to extract the spindle band components from the original input EEG signal. The entire spectrum of sleep spindle components is covered by the bandpass filter, which has a frequency range of 11 to 16 Hz. A frequency self-increment that varies from subject to subject is then set to create a Gabor dictionary, which is combined with MP to discover all the potential sleep spindle in the input EEG. In the second step, an ensemble learning model is used to filter out the false detections in the first step from all candidate sleep spindles, resulting in the final detections.

Figure 2: The organization of the proposed detection algorithm

Prior to this, we used the EEGLAB toolbox to filter EEG data. Firstly, the raw EEG data from channel CZ-A1 or C3-A1 are filtered using a ten-order minimum phase finite impulse response (FIR) bandpass filter between 11 and 16 Hz. In addition, in the DREAMS data set, there are two subjects whose sampling frequencies are 50 and 100 Hz respectively, which need to be resampled to 200 Hz [39].

3.2.1 Pre-Detection: MP for Searching for Sleep Spindle Candidates

MP is a high-resolution time-frequency signal analysis technique [33,40] in which the waveform of a large class of functions is fitted to the local signal structure through a recursive procedure. The algorithm can reasonably represent the fluctuation and weakening of the oscillation of the characteristic wave. Using this technique, sleep spindles can be positioned on the time-frequency plane with high precision. The process is to choose the largest inner product based on the dictionary function and the signal residual, minus the function fitted in the previous iteration. In this way, the width of the analysis window is adjusted to the local characteristics of the signal. The specific calculation method is shown in Eq. (1):

{r0=yβ=|<Ij,ri−1>|ri=ri−1−Ij ⋅<Ij,ri−1>(1)

where y is the filtered EEG data, r0 is the initial residual, β is the maximum inner product of the absolute value generated by the current atom Ij and the residual ri−1, and Ij represents the jth atom in the dictionary, ri is the residual produced in the iterations, <⋅,⋅> represents the inner product of the signal, and |·| represents the absolute value.

As for dictionary atom I,this study uses the Gabor Gaussian function [41], which provides the highest time-frequency resolution [40].

I=λe−(tσi)2cos⁡(2πfit+φ)(2)

where σi is the width of the Gaussian kernel, fi is the frequency, from 11–16, gradually increasing by 0.1, φ is phase, and λ is the normalization constant.

Finally, some constraints are added to improve the reliability of sleep spindle candidates detected by the MP method. According to the AASM criteria [20], candidate waves usually last 0.5–3 s. The study established the following processing rules based on the statistics in Fig. 1. First, merge the spindles detected with a time gap less than 0.15 s. Candidate waves detected with a duration shorter than 0.5 s are rejected. The spindle with a detected duration of more than 3.0 s is set to 3.0 s and the excess part is discarded. That is, in the case of these long detection windows with fixed centers, the discarded spindle wave refers to the part 1.5 s before and 1.5 s after the detection window.

3.2.2 Enhancement: LSBoost for Identifying Real Spindles from Candidates

Generally, the sleep spindle candidates detected by the pre-detection step include a large number of false samples, i.e., a high false positive. To improve the detection accuracy, this study regards the sleep spindles previously detected from the filtered band EEG as candidate spindles, and applies an ensemble learning strategy, LSBoost which automatically identifies ground truth spindles from all candidate waves. Based on the “Fitensemble” function developed in MATLAB, the LSBoost method with a regression tree is used as the classifier. The goal of LSBoost is to reduce the mean squared error (MSE) between the target variable (Y) and the combined predictions (Ypred) of the weak learners (B) using a set of regression trees referred to as weak learners (B) [42]. The new learner is adjusted by LSBoost to the difference between the observed response and the sum of all learners previously grown at each step’s predictions. To lower its mistake rate, the algorithm repeatedly trains the weights before using those weights to determine the final outcome.

Ypred(X)=Y¯(X)+t∑m−1MρmBm(X)(3)

where ρm is the weight for model m, M is the total number of weak learners, t is the learning rate with 0<t<1.

In this study, two steps are included, namely feature extraction and classification. However, candidate EEG segments are likely to consist of ground truth and non-spindles. Since there is more ground truth in sleep spindle candidates, this research established a parameter λ as the judgement threshold of that percentage. EEG segments containing candidates exceeding the threshold ratio are regarded as ground truth.

After collecting a large amount of literature and trying all sorts of features of EEG signals, the following features were chosen to represent the feature differences of EEG segments of candidate frequency bands related to sleep spindles. The basic principle is that the identification of EEG characteristic waves is connected to the classification of various sleep stages. Furthermore, even if the duration for the sleep spindles might differ, the extracted characteristics are length independent and have the same dimension across all samples.

(1) Root mean square (RMS)

μRMS=∑i=1Nxi2N(4)

(2) Standard deviation (STD)

μstd=∑i=1N(xi−x¯)2N(5)

(3) Log root mean of sequential variations (LRM)

μLRM=log10∑i=2N(xi−xi−1)2N(6)

For each sleep spindle candidate, a 3-dimensional feature vector is created by normalizing each feature to the range [−1, 1]. This process reduces the number of false positive from all the spindle candidate waves during the first step detection. The LSBoost ensemble function was chosen because this boosting technique is suitable for regression and prediction problems, where the number of weak learners is set to 20, and the learning rate t is the result of repeated experiments, with a value of 0.9. The leave-one-subject-out (LOSO) validation strategy is then used to train the model and validate the results.

3.3 Performance Analysis

The agreement between the automated detection findings and the expert comments is the basis for the performance evaluation. In terms of sleep spindle events identification, this paper uses sample-based evaluation (SBE) and event-based evaluation (EBE) to make a comprehensive comparison.

SBE is an analysis based on each sampling point of the EEG time series with the best temporal resolution. In this study, 1 represents the spindle data segment, 0 represents the non-spindle data segment, and each binary number corresponds to each sampling point of the data. Using this binary vector, a 2 × 2 contingency table can be created to calculate the detector’s true positives (TP), false positives (FP), true negatives (TN) and false negatives (FN). These values are further used to calculate the sensitivity (Sen), precision (Pr) or positive predictive value (PPV), F1-score, accuracy (Acc), negative predictive value (NPV) and Cohen’s kappa (Kappa) value of the spindle detection algorithm. The specific definitions of these values are as follows:

Sen=TPTP+FN(7)

Pr (PPV)=TPTP+FP(8)

F1−score=2∗Sen∗PPVSen+PPV(9)

Acc=TP+TNN,N=TP+TN+FP+FN(10)

NPV=TNTN+FN(11)

Kappa=Acc−Pr(e)1−Pr(e),Pr(e)=TP+FNN∗TP+FPN+(1−TP+FNN)(1−TP+FPN)(12)

EBE is an overlap between a spindle detected automatically and a visually scored one is considered to be a TP. Specifically, if the overlap ratio ODE exceeds OT−overlap, the spindle is classified as TP; otherwise, the spindles in the binary individual expert vector are classified as FP, and the spindles in the expert group vector are classified as FN.

ODE=D∩ED∪E(13)

where ∩ represents the intersection and ∪ represents the union between D and E. E represents the Union-annotated spindle, and D is the sleep spindle detected by the automatic detection algorithm. In this study, OT−overlap are both set to 0.25. The choice of 0.25 follows the results of [43]. These values are further used to calculate recall (Recall), precision (Pr), and F1-score.

4  Result

4.1 Detection Results with Annotations from Union

Fig. 3 explains the stepwise results of the proposed detection method using Union’s annotations as ground truth in the DREAMS database. Fig. 3a shows that in the 20-s raw EEG segment, the experts marked 4 spindles. Fig. 3b shows the spindle candidate wave detected by MP after data filtering (the data in the purple rectangular area is the detected spindle wave segment). Compared with the spindle wave annotated by experts (the red rectangular area segment), eight spindle waves were detected in this step, which is equivalent to the non-spindle wave band detected by the proposed method. Fig. 3c shows the final result of LSBoost classifier recognition after extracting the features of each candidate spindle. It can be seen that the final detection is approximately consistent with the ground truth annotated by experts. Comparing the results in Figs. 3b and 3c, this research find that the pre-detection step of the MP method searches for ambiguous spindle candidates and the LSBoost identifies accurate results.

Figure 3: The detection results of each step using the proposed method. (a) Raw data and ground truth. The blue data represents a sample of 20 s raw EEG segments without filtering, where the red rectangular window refers to the Union’s spindle. (b) Filtering data, candidate waves and ground truth. The blue data represents the filtered EEG data, the purple rectangles represent the sleep spindle candidates searched for by the MP algorithm in large numbers, and the red rectangles represent the real spindles. (c) Filtering data, spindles and ground truth. The purple rectangles represent the sleep spindles identified by the LSBoost algorithm, and the red rectangles represent the ground truth

4.2 Performance Measures

Table 1 lists the overall detection performance based on the sample evaluation of the proposed MP-LSBoost method and several automatic sleep spindle detection algorithms, utilizing the Union of labels in the DREAMS dataset. The classification results show that the proposed method achieves the best performance in term of Sen, F1-score and Kappa value. Furthermore, the Acc of 94.7% is consistent with the state-of-the-art results of Spindler [23] and MUSSDET [35]. As for the indicator of Pr (PPV) and NPV, the result is only lower than that of TEO-Bag [25].

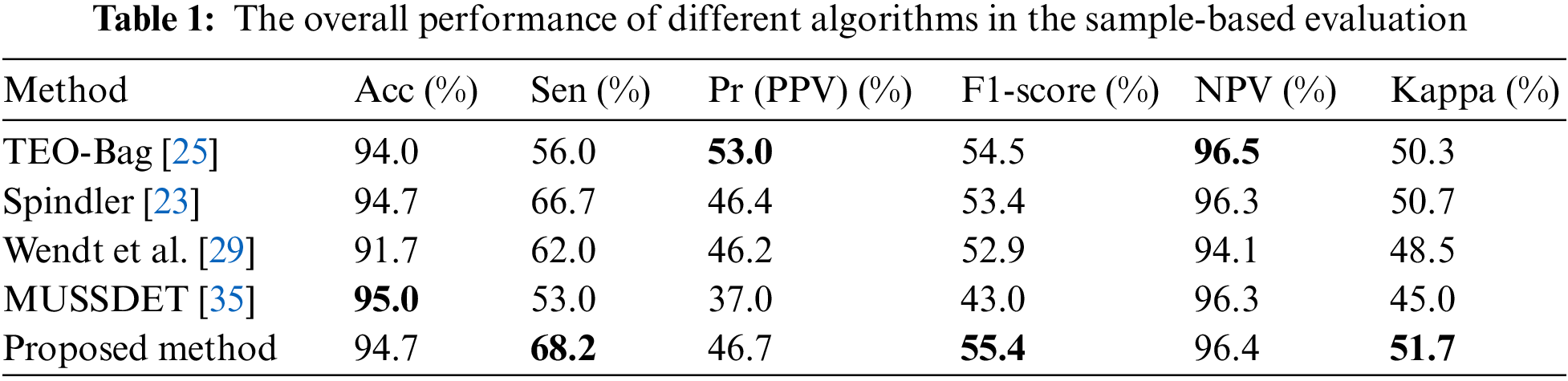
Fig. 4 shows the recall-precision plots of various methods based on event evaluation in the DREAMS dataset. Gray-blue represents the line y = x. In Fig. 4, the values of Spindler [23], Wendt et al. [29], Chen et al. [44] and MUSSDET [35] are below the line y = x, which indicates that their Pr values are high, while the Recall value is low. Spindler [23] achieves the highest Pr of 73.8%. TEO-Bag [25], SST-RUS [26] and the proposed method are at the top right of the line, and the proposed method achieves the highest recall of 83.8%. Notably, in the y-axis direction, the Recall value of the proposed method is higher than that of TEO-Bag [25] and SST-RUS [26], while in the horizontal direction, the Pr value of TEO-Bag [25] and SST-RUS [26] are slightly higher than that of the proposed method. For both the Recall value and the Pr value, this study aims to obtain a Recall and Pr value which is as high as possible, that is, at the top right of the coordinates axis, so that the experiment can obtain an ideal F1-score. This research further calculates the F1-scores of the Went et al. [29], MUSSDET [35], TEO-Bag [25], Spindler [23], Chen et al. [44], SST-RUS [26] and the proposed algorithm based on event evaluation, which are 49.7%, 54.8%, 69.0%, 64.3%, 65.8%, 62.9% and 70.8%, respectively.

Figure 4: Recall and Pr values in the event-based evaluation

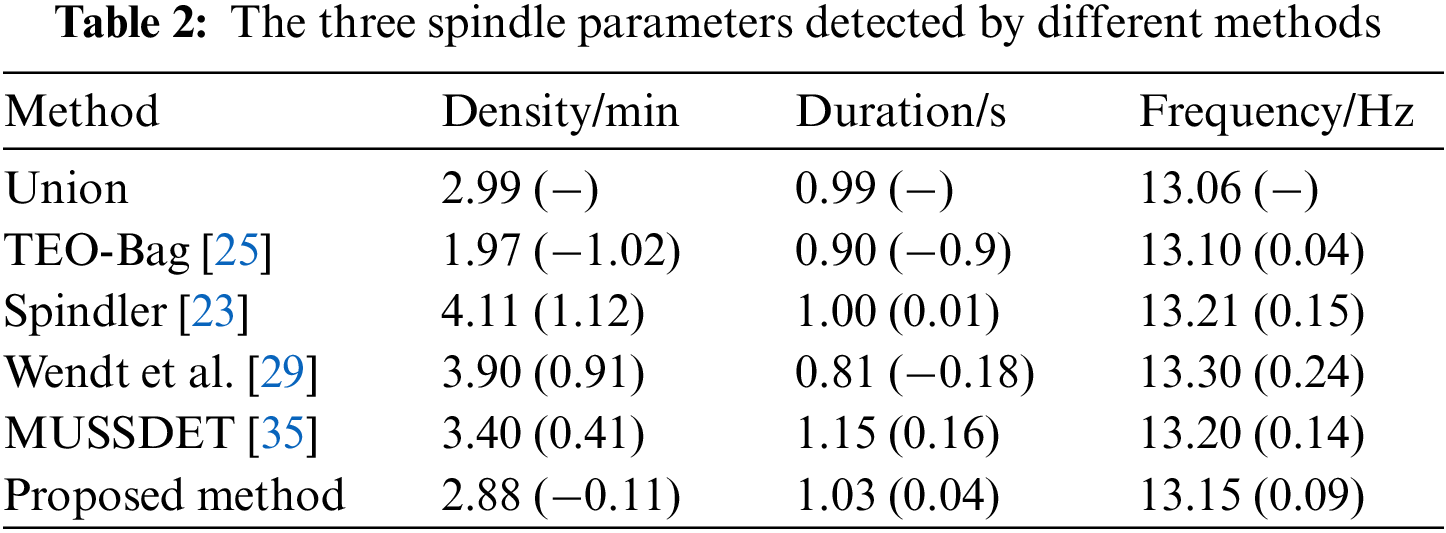
To demonstrate further the effectiveness of the automatic detector, we calculate and compare three independent sleep spindle characteristics, namely density (the numbers of sleep spindle per minute), average durations and frequency (compared to true sleep spindles) using the proposed method. Table 2 illustrates the overall numerical comparison of the three spindle parameters in the DREAMS dataset. The values in parentheses represent the difference with the Union method. Compared with Union, the duration in the Spindler [23] is the closest to Union, but the density is quite different to Union; the frequency in the TEO-Bag [25] was 13.10, which is only 0.04 different from Union, making it the closest to Union of all the detectors, but the density was also quite different to Union. The duration and frequency of the proposed method are close to Spindler [23] and TEO-Bag [25], but the density is the closest to Union. It can be seen that the three sleep spindle features obtained by the proposed approach are most consistent with the ground truth.

4.3 Comparison of Ground Truth and Spindles Detected by Different Methods

Fig. 5 illustrates spindles detected by different detectors in the same data segment using Union’s annotations as ground truth. Experts annotated four sleep spindles at 0.33, 3.605, 8.695 and 14.06 s. It can be seen that each detector has detected multiple spindle waves in the 15 s data segment. TEO-Bag [25] only detected three spindle waves; Wendt et al. [29] detected four spindles, of which only three were consistent with the spindles annotated by experts, and the spindles annotated by experts at 0.33 s were not detected; Spindle waves noted by experts were detected by Spindler [23] and the proposed method, but the spindles detected by Spindler [23] are partially different from those noted by experts in time. All spindles are detected by the proposed method. For spindles at 3.605 s, the start time of spindles detected by the proposed method is the most consistent with that of Union, compared with Wendt et al. [29] and Spindler [23].

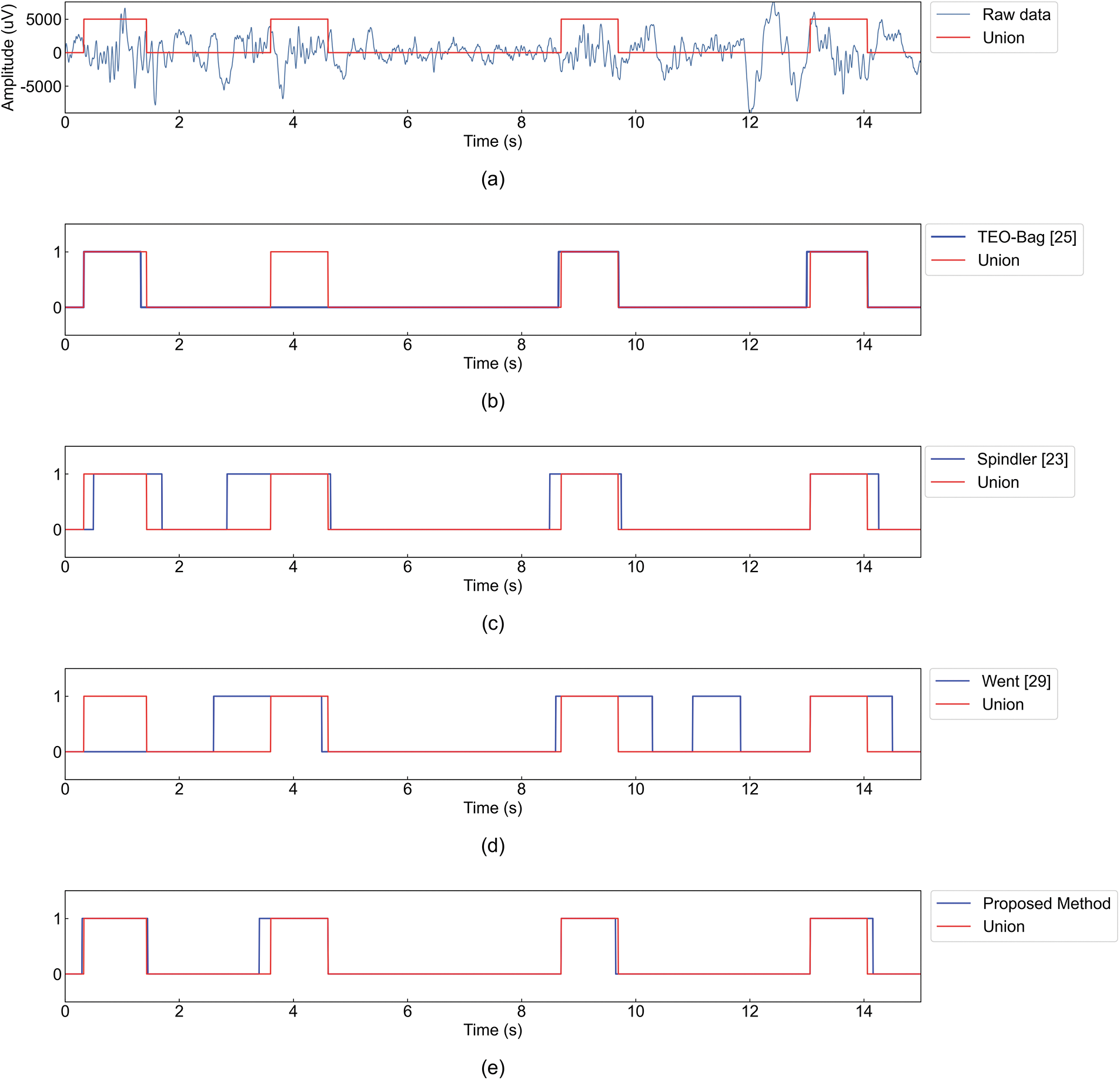
Figure 5: A display of the spindle detection by TEO-Bag [25], Spindler [23], Wendt et al. [29] and the proposed method. (a) Raw data and ground truth. (b) TEO-Bag [25] and ground truth. (c) Spindler [23] and ground truth. (d) Wendt et al. [29] and ground truth. (e) The proposed method and ground truth. In (a), the red rectangle represents the spindle under Union; blue represents an EEG segment with 15 s. In (b–e), the red rectangles represent the spindles under Union, and the blue rectangles represent the spindles detected by different detectors

4.4 Comparison of Different Classifiers

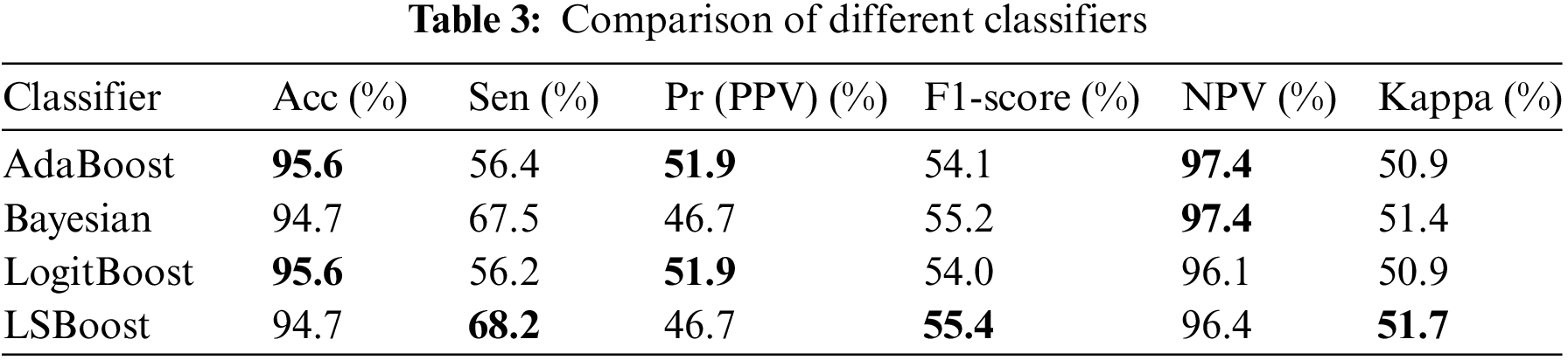
In the classification phase, this paper compares the performance of several popular classification algorithms [45] on a sample-based evaluation, as shown in Table 3. Comparisons are performed on the DREAMS dataset using LOSO validation, with Union annotations as ground truth. The input data, splits for training and testing, and all other experimental parameters are the same with the exception of the classifier. Although AdaBoost and LogitBoost have the best performance on Pr, Sen and F1-score are inferior to LSBoost. Hence, the overall classification performance using LSBoost is better than the other classifiers.

5  Discussion

In this study, a two-step MP-LSBoost algorithm is proposed to accurately identify sleep spindles. First, the MP method searches for the spindle candidates from the filtered raw EEG data. In the second step, LSBoost is designed to remove false candidates and identify real spindles. We first validated the proposed method on the DREAMS dataset, and then performed a comprehensive comparison with other prior approaches. The experiment results show that the proposed method performs extremely well, especially in the indicators of Sen, F1-score and Kappa value. Therefore, these results illustrat the stability and effectiveness of the proposed algorithm.

Over the past decade, many studies have focused on the field of sleep spindle detection and have made several achievements. Jiang et al. [25] proposed a sleep spindle detection method TEO-Bag based on a single channel EEG. Wendt et al. [29] developed an automatic sleep spindle detector using the band-pass filtering method and time-varying threshold. Lachner-Piza et al. [35] used a single channel sleep spindle detector MUSSDET based on EEG multivariate classification. LaRocco et al. [23] used MP to decompose the signal, and detected spindle waves in the fine grid of the parameter values. In the sample-based evaluation, it can be seen from Table 1 that the sensitivity, F1-score and Kappa value of the method proposed in this paper are higher than those of the previous methods. Although the Acc and Pr of the proposed method are respectively close to that of MUSSDET and TEO-Bag, the values are similar. Furthermore, the subfigures (b) and (c) of Fig. 3 also verify that the proposed method can correctly detect those spindles and maintain a very low error detection rate. This means that the proposed method is the overall optimal approach, improving the sensitivity while maintaining an appropriate specificity.

It should be noted that spindle wave activity is a micro event, which means that the performance evaluation algorithm based on sample-based evaluation is not comprehensive enough. To assess the comprehensive performance of the proposed method, this paper also adopts the event evaluation indicators. Table 2 shows the analysis of spindle wave characteristic parameters using different detectors. The Density of the proposed method is 2.88 and the Density of Union is 2.99, with a difference of 0.11. Compared with the other detectors, the proposed method is the closest to Union, which also shows that the proposed method is basically consistent with the experts’ results. It can be seen from Fig. 4 that Wendt et al. [29], Spindler [23], Chen et al. [44] and MUSSDET [35] are all on the lower right, which indicates that their Pr values are high, and their Recall values are low. TEO-Bag [25], SST-RUS [26] and the proposed method are on the upper right, and the Pr value is similar, but the Recall value of TEO-Bag [25] and SST-RUS [26] are lower than the proposed method. In this study, the Recall, Pr, and F1-score of event-based assessments were 83.8%, 61.3%, and 70.8%, respectively. Fig. 5 shows that for the same segment of data, different detectors have detected spindles annotated by experts. However, TEO-Bag [25] and Wendt et al. [29] only detected three spindles, and Wendt et al. [29] also detected a spindle wave that was not recognized by experts. Spindler [23] and the proposed method both detected four spindle waves, however, the start time of the spindle waves detected by Spindler [23] is quite different from that noted by the experts. Therefore, the performance evaluation based on events also verifies the effectiveness of this work.

Subfigures (b) and (c) in Fig. 3 show the stage-by-stage detection results of this work. By comparing these two figures, it can be found that without the second enhancement operation, there will be many false positives in the results. After using LSBoost as the classifier, these non-spindle waves are eliminated, thus ensuring the reliability of spindle wave recognition. In addition, the detection performance of LSBoost is compared with other ensemble learning methods, such as AdaBoost, LogitBoost and Bayesian. The input features and parameters are adjusted in the same way as LSBoost. Table 3 illustrates the sensitivity, accuracy and F1-score of each ensemble learner. From the perspective of F1-score and sensitivity, LSBoost performs the best of the three methods. In summary, the proposed two-step method combining MP and LSBoost achieves great performance and can be used to automatically identify sleep spindles.

6  Conclusion

This study proposes a new method for the automatic detection of sleep spindles which combines MP and LSBoost. In the proposed algorithm, MP may be used to produce a fairly equal number of sleep spindle candidates, which helps LSBoost to recognize the true spindles. In addition, LSBoost adjusts the weights through repeated training to reduce the error rate, and performs binary classification based on the iterative weights. The experimental findings of automated spindle detection on the DREAMS dataset demonstrate that the proposed approach is on par with cutting-edge approaches. The results of this study are anticipated to serve as a reference for future sleep related research. Future research might focus further on investigating sleep spindle alterations in people with a sleep disorder.

Funding Statement: This project was funded by the Guangdong Basic and Applied Basic Research Foundation (Grant Nos. 2021A1515011853 and 2020A1515110294), the National Natural Science Foundation of China (Grant Nos. 61906019 and 62076103), STI 2030-Major Projects 2022ZD0208900, Guangzhou Science and Technology Plan Project (Grant No. 202102020877) and the Guangzhou Science and Technology Plan Project Key Field R&D Project (202007030005).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. F. Abbasi, J. Ahmad, A. Tahir, M. Awais, C. Chen et al., “EEG-based neonatal sleep-wake classification using multilayer perceptron neural network,” IEEE Access, vol. 8, pp. 183025–183034, 2020. [Google Scholar]

2. M. P. St-Onge, M. A. Grandner, D. Brown, M. B. Conroy, G. Jean-Louis et al., “Sleep duration and quality: Impact on lifestyle behaviors and cardiometabolic health: A scientific statement from the American Heart Association,” Circulation, vol. 134, no. 18, pp. e367–e386, 2016. [Google Scholar] [PubMed]

3. J. A. Christensen, M. Nikolic, S. C. Warby, H. Koch, M. Zoetmulder et al., “Sleep spindle alterations in patients with Parkinson’s disease,” Frontiers in Human Neuroscience, vol. 9, 233, 2015. [Google Scholar] [PubMed]

4. A. Parekh, I. W. Selesnick, D. M. Rapoport and I. Ayappa, “Detection of K-complexes and sleep spindles (DETOKS) using sparse optimization,” Journal of Neuroscience Methods, vol. 251, no. 1, pp. 37–46, 2015. [Google Scholar] [PubMed]

5. S. M. Fogel and C. T. Smith, “Learning-dependent changes in sleep spindles and stage 2 sleep,” Journal of Sleep Research, vol. 15, no. 3, pp. 250–255, 2006. [Google Scholar] [PubMed]

6. M. P. Normand, J. Dallery and C. M. Slanzi, “Sleep spindles characteristics in insomnia sufferers and their relationship with sleep misperception,” Neural Plasticity, vol. 2016, no. 1, 6413473, 2016. [Google Scholar] [PubMed]

7. D. Ulrich, “Sleep spindles as facilitators of memory formation and learning,” Neural Plasticity, vol. 2016, no. 8, 1796715, 2016. [Google Scholar] [PubMed]

8. S. Laventure, B. Pinsard, O. Lungu, J. Carrier, S. Fogel et al., “Beyond spindles: Interactions between sleep spindles and boundary frequencies during cued reactivation of motor memory representations,” Sleep, vol. 41, no. 9, zsy142, 2018. [Google Scholar] [PubMed]

9. V. Cologan, X. Drouot, S. Parapatics, A. Delorm, G. Gruber et al., “Sleep in the unresponsive wakefulness syndrome and minimally conscious state,” Journal of Neurotrauma, vol. 30, no. 5, pp. 339–346, 2013. [Google Scholar] [PubMed]

10. V. Latreille, J. Carrier, M. Lafortune, R. B. Postuma, J. A. Bertrand et al., “Sleep spindles in Parkinson’s disease may predict the development of dementia,” Neurobiology of Aging, vol. 36, no. 2, pp. 1083–1090, 2015. [Google Scholar] [PubMed]

11. M. Gorgoni, G. Lauri, I. Truglia, S. Cordone, S. Sarasso et al., “Parietal fast sleep spindle density decrease in Alzheimer’s disease and amnesic mild cognitive impairment,” Neural Plasticity, vol. 2016, no. 8, 8376108, 2016. [Google Scholar] [PubMed]

12. K. Kam, A. Parekh, R. A. Sharma, A. Andrade, M. Lewin et al., “Sleep oscillation-specific associations with Alzheimer’s disease CSF biomarkers: Novel roles for sleep spindles and tau,” Molecular Neurodegeneration, vol. 14, no. 1, pp. 1–12, 2019. [Google Scholar]

13. E. Limoges, L. Mottron, C. Bolduc, C. Berthiaume and R. Godbout, “Atypical sleep architecture and the autism phenotype,” Brain, vol. 128, no. 5, pp. 1049–1061, 2005. [Google Scholar] [PubMed]

14. I. Merikanto, L. Kuula, T. Makkonen, L. Salmela, K. Räikkönen et al., “Autistic traits are associated with decreased activity of fast sleep spindles during adolescence,” Journal of Clinical Sleep Medicine, vol. 15, no. 3, pp. 401–407, 2019. [Google Scholar] [PubMed]

15. D. S. Manoach and R. Stickgold, “Abnormal sleep spindles, memory monsolidation, and schizophrenia,” Annual Review of Clinical Psychology, vol. 15, no. 1, pp. 451–479, 2019. [Google Scholar] [PubMed]

16. E. Serdaroğlu, F.İ. Tezer and S. Saygi, “Autoimmune epilepsy and/or limbic encephalitis can lead to changes in sleep spindles,” Archives of Neuropsychiatry, vol. 55, no. 4, pp. 320–324, 2018. [Google Scholar] [PubMed]

17. S. M. Alotaibi, Atta-ur-Rahman, M. I. Basheer and M. A. Khan, “Ensemble machine learning based identification of pediatric epilepsy,” Computers, Materials & Continua, vol. 68, no. 1, pp. 149–165, 2021. [Google Scholar]

18. T. Hori, Y. Sugita, E. Koga, S. Shirakawa, K. Inoueet et al., “Proposed supplements and amendments to ‘A manual of standardized terminology, techniques and scoring system for sleep stages of human subjects’, the Rechtschaffen & Kales (1968) standard,” Psychiatry and Clinical Neurosciences, vol. 55, no. 3, pp. 305–310, 2001. [Google Scholar] [PubMed]

19. D. Moser, P. Anderer, G. Gruber, S. Parapatics, E. Loretz et al., “Sleep classification according to AASM and Rechtschaffen & Kales: Effects on sleep scoring parameters,” Sleep, vol. 32, no. 2, pp. 139–149, 2009. [Google Scholar] [PubMed]

20. R. B. Berry, R. Brooks, C. Gamaldo, S. M. Harding, R. M. Lloyd et al., “AASM scoring manual updates for 2017 (Version 2.4),” Journal of Clinical Sleep Medicine, vol. 13, no. 5, pp. 665–666, 2017. [Google Scholar] [PubMed]

21. S. L. Wendt, P. Welinder, H. B. Sorensen, P. E. Peppard, P. Jennum et al., “Inter-expert and intra-expert reliability in sleep spindle scoring,” Clinical Neurophysiology, vol. 126, no. 8, pp. 1548–1556, 2015. [Google Scholar] [PubMed]

22. S. F. Abbasi, H. Jamil and W. Chen, “EEG-based neonatal sleep stage classification using ensemble learning,” Computers, Materials & Continua, vol. 70, no. 3, pp. 4619–4633, 2022. [Google Scholar]

23. J. LaRocco, P. J. Franaszczuk, S. Kerick and K. Robbins, “Spindler: A framework for parametric analysis and detection of spindles in EEG with application to sleep spindle,” Journal of Neural Engineering, vol. 15, no. 6, 066015, 2018. [Google Scholar] [PubMed]

24. P. J. Durka, U. Malinowska, M. Zieleniewska, C. O’Reilly, P. T. Różański et al., “Spindles in svarog: Framework and software for parametrization of EEG transients,” Frontiers in Human Neuroscience, vol. 9, 258, 2015. [Google Scholar] [PubMed]

25. D. Jiang, Y. Ma and Y. Wang, “A robust two-stage sleep spindle detection approach using single-channel EEG,” Journal of Neural Engineering, vol. 18, no. 2, 026026, 2021. [Google Scholar]

26. T. Kinoshita, K. Fujiwara, M. Kano, K. Ogawa, Y. Sumi et al., “Sleep spindle detection using RUSBoost and synchrosqueezed wavelet transform,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 28, no. 2, pp. 390–398, 2020. [Google Scholar] [PubMed]

27. S. A. Imtiaz, S. Saremi-Yarahmadi and E. Rodriguez-Villegas, “Automatic detection of sleep spindles using Teager energy and spectral edge frequency,” in 2013 IEEE Biomedical Circuits and Systems Conf., Rotterdam, Netherlands, pp. 262–265, 2013. [Google Scholar]

28. P. Schimicek, J. Zeitlhofer, P. Anderer and B. Saletu, “Automatic sleep-spindle detection procedure: Aspects of reliability and validity,” Clinical Electroencephalography, vol. 25, no. 1, pp. 26–39, 1994. [Google Scholar] [PubMed]

29. S. L. Wendt, J. A. Christensen, J. Kempfner, H. L. Leonthi, P. Jennum et al., “Validation of a novel automatic sleep spindle detector with high performance during sleep-in middle-aged subjects,” in 2012 Annual Int. Conf. of the IEEE Engineering in Medicine and Biology Society, Piscataway, NJ, USA, vol. 2012, pp. 4250–4253, 2012. [Google Scholar]

30. A. Tsanas and G. D. Clifford, “Stage-independent, single lead EEG sleep spindle detection using the continuous wavelet transform and local weighted smoothing,” Frontiers in Human Neuroscience, vol. 9, no. 910, 181, 2015. [Google Scholar] [PubMed]

31. S. Naseem, K. Javed, M. J. Khan, S. Rubab, M. A. Khan et al., “Integrated cwt-cnn for epilepsy detection using multiclass EEG dataset,” Computers, Materials & Continua, vol. 69, no. 1, pp. 471–486, 2021. [Google Scholar]

32. A. Nonclercq, C. Urbain, D. Verheulpen, C. Decaestecker, P. V. Bogaert et al., “Sleep spindle detection through amplitude-frequency normal modelling,” Journal of Neuroscience Methods, vol. 214, no. 2, pp. 192–203, 2013. [Google Scholar] [PubMed]

33. S. G. Mallat and Z. Zhang, “Matching pursuits with time-frequency dictionaries,” IEEE Transactions on Signal Processing, vol. 41, no. 12, pp. 3397–3415, 1993. [Google Scholar]

34. E. J. Wamsley, M. A. Tucker, A. K. Shinn, K. E. Ono, S. K. McKinley et al., “Reduced sleep spindles and spindle coherence in schizophrenia: Mechanisms of impaired memory consolidation?,” Biological Psychiatry, vol. 71, no. 2, pp. 154–161, 2012. [Google Scholar] [PubMed]

35. D. Lachner-Piza, N. Epitashvili, A. Schulze-Bonhage, T. Stieglitz, J. Jacobs et al., “A single channel sleep-spindle detector based on multivariate classification of EEG epochs: MUSSDET,” Journal of Neuroscience Methods, vol. 297, pp. 31–43, 2018. [Google Scholar] [PubMed]

36. L. Causa, C. M. Held, J. Causa, P. A. Estévez, C. A. Perez et al., “Automated sleep-spindle detection in healthy children polysomnograms,” IEEE Transactions on Biomedical Engineering, vol. 57, no. 9, pp. 2135–2146, 2010. [Google Scholar] [PubMed]

37. A. Parekh, I. W. Selesnick, R. S. Osorio, A. W. Varga, D. M. Rapoport et al., “Multichannel sleep spindle detection using sparse low-rank optimization,” Journal of Neuroscience Methods, vol. 288, no. 1, pp. 1–16, 2017. [Google Scholar] [PubMed]

38. S. Devuyst, T. Dutoit, P. Stenuit and M. Kerkhofs, “Automatic sleep spindles detection–overview and development of a standard proposal assessment method,” in 2011 Annual Int. Conf. of the IEEE Engineering in Medicine and Biology Society, Buenos Aires, Argentina, vol. 2011, pp. 1713–1716, 2011. [Google Scholar]

39. S. F. Abbasi, M. Awais, X. Zhao and W. Chen, “Automatic denoising and artifact removal from neonatal EEG,” in BIBE 2019; The Third Int. Conf. on Biological Information and Biomedical Engineering, Hangzhou, China, pp. 1–5, 2019. [Google Scholar]

40. T. Spustek, W. W. Jedrzejczak and K. J. Blinowska, “Matching pursuit with asymmetric functions for signal decomposition and parameterization,” PLoS One, vol. 10, no. 6, e0131007, 2015. [Google Scholar] [PubMed]

41. M. M. Hassan, H. I. Hussein, A. S. Eesa and R. J. Mstafa, “Face recognition based on gabor feature extraction followed by fastica and lda,” Computers, Materials & Continua, vol. 68, no. 2, pp. 1637–1659, 2021. [Google Scholar]

42. R. Barzegar, A. Asghari Moghaddam, J. Adamowski and B. Ozga-Zielinski, “Multi-step water quality forecasting using a boosting ensemble multi-wavelet extreme learning machine model,” Stochastic Environmental Research and Risk Assessment, vol. 32, no. 3, pp. 799–813, 2018. [Google Scholar]

43. S. C. Warby, S. L. Wendt, P. Welinder, E. G. Munk, O. Carrillo et al., “Sleep-spindle detection: Crowdsourcing and evaluating performance of experts, non-experts and automated methods,” Nature Methods, vol. 11, no. 4, pp. 385–392, 2014. [Google Scholar] [PubMed]

44. P. Chen, D. Chen, L. Zhang, Y. Tang and X. Li, “Automated sleep spindle detection with mixed EEG features,” Biomedical Signal Processing and Control, vol. 70, no. 1, 103026, 2021. [Google Scholar]

45. M. Hasnain, I. Ghani, S. R. Jeong and A. Ali, “Ensemble learning models for classification and selection of web services: A review,” Computer Systems Science and Engineering, vol. 40, no. 1, pp. 327–339, 2022. [Google Scholar]