Intermediary RRT*-PSO: A Multi-Directional Hybrid Fast Convergence Sampling-Based Path Planning Algorithm

1  Introduction

In the era of Industry 4.0, Artificial Intelligence (AI), and Robotics including Drones (Unmanned aerial vehicles) have been identified as three typical technologies [1]. Nowadays, robots and drones are serving the world in many fields, including industry, agriculture, education, and healthcare, by integrating contemporary technologies such as additive manufacturing (3D printing), open-source programming environments, artificial intelligence (AI), and the Internet of Things (IoT). Mobile robots and drones (controlled or autonomous) can be used in education and research owing to their ability to move around and interact with their surrounding environments [2]. Stationary robots, such as robotic arms, are mostly used in factories for automatic manufacturing processes, including picking and placing, welding, sorting, and painting, thus significantly reducing the use of the human workforce. Regardless of the robot type, path planning is one of the most important procedures in robotic operation. Mobile robots generate pathways to navigate safely from points A to B; stationary robots, especially robotic arms, need to plan trajectories to move their arms efficiently.

Path planning is an essential process that helps autonomous vehicles find the shortest path between predefined starting and goal positions to avoid collisions with obstacles along the way [3]. Robot path planning problems can be categorized into two major groups: graph search and sampling-based methods. In practice, graph-search-based methods, such as Dijkstra [2,3], A* [4], and laser simulator (GLS) [5], generate a discrete node graph from the mapped environment and then search the graph for the optimum path. In contrast, sampling-based methods include Probabilistic Roadmap Method (PRM) [6] and Rapidly exploring Random Tree (RRT) [7], heuristic RRT (RRT*) [8], Fast Marching Tree (FMT*) [9,10], Batch Informed Tree (BIT*) [11], Adaptively Informed Trees (AIT*) and Effort Informed Trees (EIT*) [12] use a collision checking module to determine feasible trajectories and interconnect a subset of points sampled in the free space to create an optimized path [8]. The key advantages of sampling-based methods are their ability to operate in a continuous environment and their computational efficiency when compared to the graph search-based method in a complex environment. According to [13], sampling-based path planning algorithms are asymptotically optimal, which means that they continuously find a better solution by sampling more points in the working environment. However, to approach the global optimal solution, the sampling-based methods may require a significant number of samples, which demands a significant amount of memory resources [14].

In addition to these methods, another valuable approach for global path planning is nature-inspired optimization algorithms (NIOAs), also known as metaheuristics, such as Genetic Algorithm (GA), Particle Swarm Optimization (PSO), Ant Colony Optimization (ACO), Grey Wolf Optimization (GWO), Harris Hawk Optimization (HHO), Whale Optimization (WO), Artificial Potential Field (AFP), etc. [13]. Metaheuristic methods have been developed to solve nondeterministic polynomial hard (NP-hard) problems that traditional methods cannot achieve [15]. Previous studies have confirmed that solving path planning problems using NIOAs is fast and efficient [13]. However, the issues of optimality and local minima due to environmental complexity remain, as most benchmarking environments are rather simple.

The main contribution of this research is the proposal of a new single-query hybrid multidirectional path planning algorithm called Intermediary RRT*-PSO. The method is a combination of the advantages of the prior algorithm, RRT*-connect, exploration phase, and uses the first solution as input for PSO for solution refinement. This study aims to create and evaluate the speed and accuracy of the proposed and previous methods for complex and tricky configurations.

The remainder of this paper is organized as follows. Section 2 reviews the related studies used to support the main method, including the RRTs family and metaheuristic algorithms. Section 3 introduces the proposed methodology framework for the path planning problem. The metrics, benchmarking simulation results, and analysis of Intermediary RRT*-PSO and the prior bidirectional version RRT, Informed RRT*-connect, are presented in Section 4. Finally, Section 5 presents the conclusions of the results and potential future work.

2  Background

2.1 Problem Definition

We define the problem similarly to [7,8]. Let X be a state space that contains all the possible positions of the mapped environment. Let Xobstacle be the subset of X, where there is no path that can pass and Xfree=X\Xobstacle where the robot can go through. Let Vstart∈X and Vgoal∈X be the starting and desired goal positions, respectively. Let Ti⊂Xfree be the set of all nodes of ith tree and a path to node jth of tree ith is defined as Pij⊂Ti, thus Pi1 is also the root node of the ith tree. Let Cij be the cost function of Pij.  The possible solution is Pij  where Tij=Vgoal and the optimal solution is Pij where Cij is minimized.

2.2 Related Works

RRT was published in 2001 by LaValle and Kuffner as a single-query path planning method experimented on hovercraft and satellites [7]. RRT begins to expand the tree from the starting node (Vstart). For every iteration, a sampled point Vrandom is stochastically chosen from the X set. Then, the tree is extended toward the sampling point by finding Vrandom’s nearest node, Vnearest. The added node Vnew position is calculated by using Vrandom as Vnew. Then, if the path length from Vnearest to Vrandom is greater than an extend radius (rextend) constant, its length is shortened to be equal to rextend, as shown in Fig. 1.

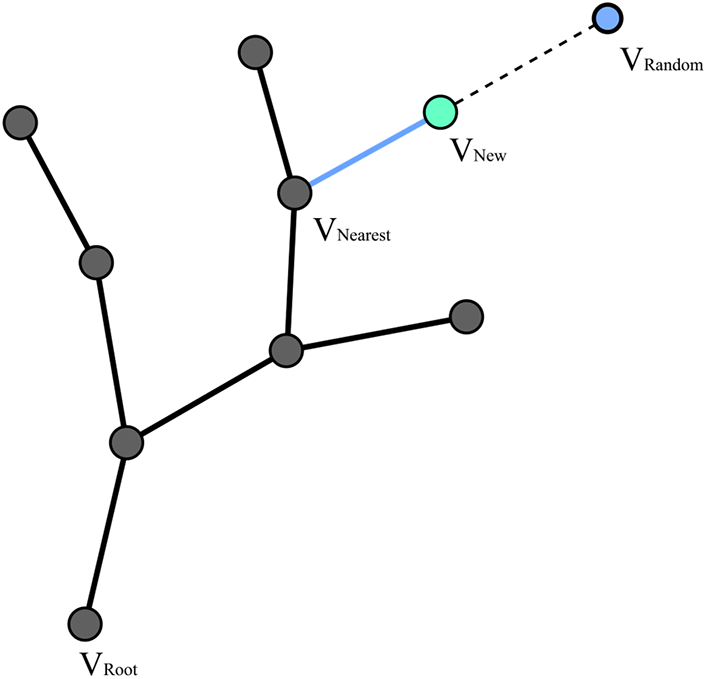
Figure 1: RRT expansion mechanism

The RRT strength explores the state space rapidly and is collision-free; however, its major weakness is its non-optimal solution [8]. To address this problem, RRT* [8] introduces a rewiring (re-branching) function after Vnew is added. Then, within a constant rewiring radius rrewire, Vnew is rewired to its best new parent node. Next, within rrewire, if the indirect path across Vnew is shorter than the path to their current parent nodes, then their parent nodes are set to be Vnew. The entire rewiring process is shown in Fig. 2.

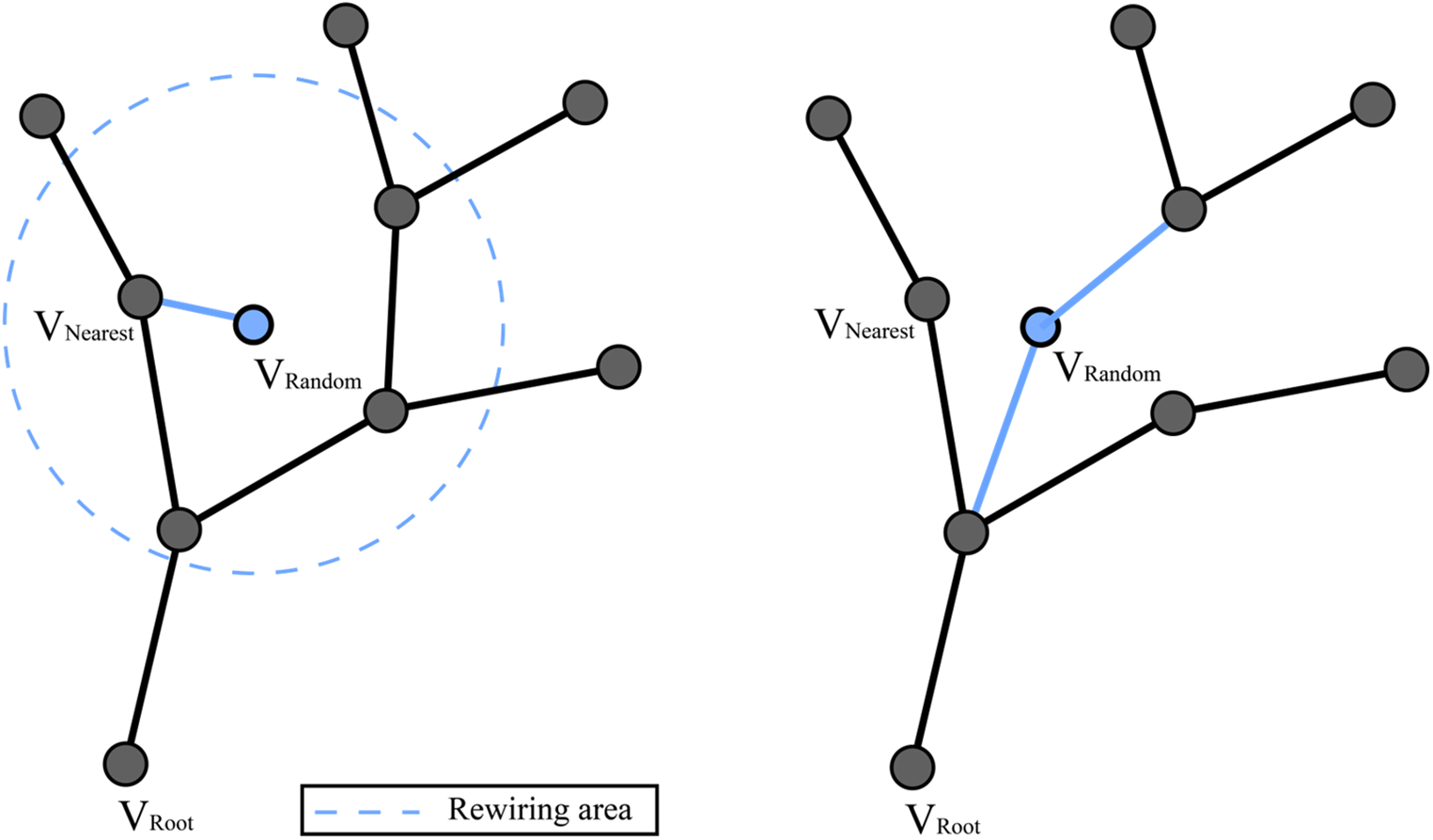
Figure 2: RRT* node rewiring mechanism. In this case, Vrandom is also VNew as the distance for Vrandom to Vnearrest is shorter than rextend

In addition to RRT and RRT*, RRT-connect [16] and RRT*-connect [17] utilize two trees expanding from both the starting node and the goal node with the aim of converging to an optimal solution faster. In each iteration, after a new node is added, a validation function is used to check whether the newly added node can be connected to any other node in the other tree. If one connection exists, the trees are connected via that node, and the path cost is calculated based on the current cost to the two nodes, plus the distance between them. The validation process is called every iteration to update the best node pair that yields the lowest cost. In 2014, Informed RRT* [18] and Informed RRT*-connect [19] were introduced to solve the convergence speed weakness. The method proposed a new sampling strategy that only samples points in the ellipsoid subset, where the starting and goal nodes are the two ellipse foci points, and the ellipse constant sum is set to be equal to the best current path length. In other words, if at least one path is shorter than the current best path, it must be a subset of the ellipsoid set. In this way, the number of sampling regions is significantly reduced, which also helps the algorithm converge faster. Reference [19] claimed Informed RRT*-connect can have up to a 90% success rate and converge faster than RRT*-connect.

In the field of natural-inspired optimization algorithms (NIOAs), many research methods have been proposed to solve path planning problems, typically Genetic Algorithm (GA), Ant Colony Optimization (ACO), Artificial Potential Field (APF) and Particle Swarm Optimization (PSO), according to [20]. The GA and PSO approaches initialize their search agents by randomly sampling a sequence of waypoints on Xfree. For each iteration in the main loop, GA approaches apply the reproduction strategy by simulating the natural selection process based on the search agent (chromosome) fitness value. The chosen chromosomes are then used to create their offspring version by crossover and mutation procedures. Recently, researchers have attempted to improve GA for path planning by introducing techniques such as parallel processing [21], elite reproduction strategy [21,22], and same-adjacency crossover [23]. PSO approaches utilize swarm intelligence to update the search agent (particle) decision variables based on three vectors: particle previous velocity, particle personal best, and swarm global best. There are path planning methods utilizing variations of PSO as the main framework, [24] proposed a path smoothing method using a high degree Bezier curve and fractional-order PSO, and [25] proposed self-adaptive learning PSO (SLPSO), which introduces four different decision variable update functions and a self-adaptive mechanism. Both proposed PSO variations were claimed to be more efficient and precise than the original version of PSO.

3  The Proposed Method

The main goal of the proposed algorithm is to take advantage of both the sampling-based method in the exploration phase and NIOA method in the exploitation phase. In the exploration phase, we utilized the RRT*-connect idea of expanding two trees from the start and goal positions, however, we added one more intermediary tree to a random unexplored position of the environment to increase the possibility of exploring the undiscovered region. The intermediary tree is merged with the two main trees if they can establish a safe connection. During the exploitation phase, PSO is used to refine the rough raw solution path of the first phase into a straight usable path.

3.1 The Undiscovered Subset

The discovered set Xdiscovered is defined as a subset of Xfree, where its elements are all the possible positions except the tree nodes. Thus, Xdiscovered=Xfree/Tij for all nodes of all trees. In contrast, the undiscovered set Xundiscovered is defined as a subset of Xfree where its element is not discovered yet, therefore Xundiscovered=Xfree/Xdiscovered.

3.2 Intermediary Tree

The first phase of Intermediary RRT* is inherited from informed RRT*-connect, which has two trees that expand from both the start and target positions. However, to improve the ability to expand to an undiscovered region or narrow passage, a new intermediary tree is added to a random undiscovered area of the environment by picking one random node in the undiscovered set (Algorithm 1). Then, all trees continued to expand until the two main trees were connected. Meanwhile, if the intermediary tree can connect to any of the 2 other trees, it merges all its nodes to that tree using Algorithm 3.

The undiscovered set is updated ever iteration by Algorithm 2 if one node is added to the tree system. Let Densexy be the sampling probability of an undiscovered region (x,y) in the current state. The Dense matrix is initialized by copying the initial configuration, which means Densexy=0 if there is an obstacle at the position (x,y), otherwise Densexy=1. After every iteration, for each added node with position (xadded, yadded), then Densexaddedyadded=0 and other surrounding positions within a constant radius r are also be marked as discovered. Dense(xadded±r),(yadded±r)=0. In this way, the number of undiscovered regions was considerably reduced, thus accelerating the sampling process for every new intermediary tree root position.

3.3 Intermediary Tree Merging Procedure

The tree merging process is activated when the newly added node of the intermediary tree can be connected to any node of any other tree (Figs. 3a and 3b). When a new node is added to a tree, it is checked to verify whether there is at least one possible connection to the nodes of any other tree. If there exists one connection, the intermediary tree nodes are transferred to the connected tree using Algorithm 3.

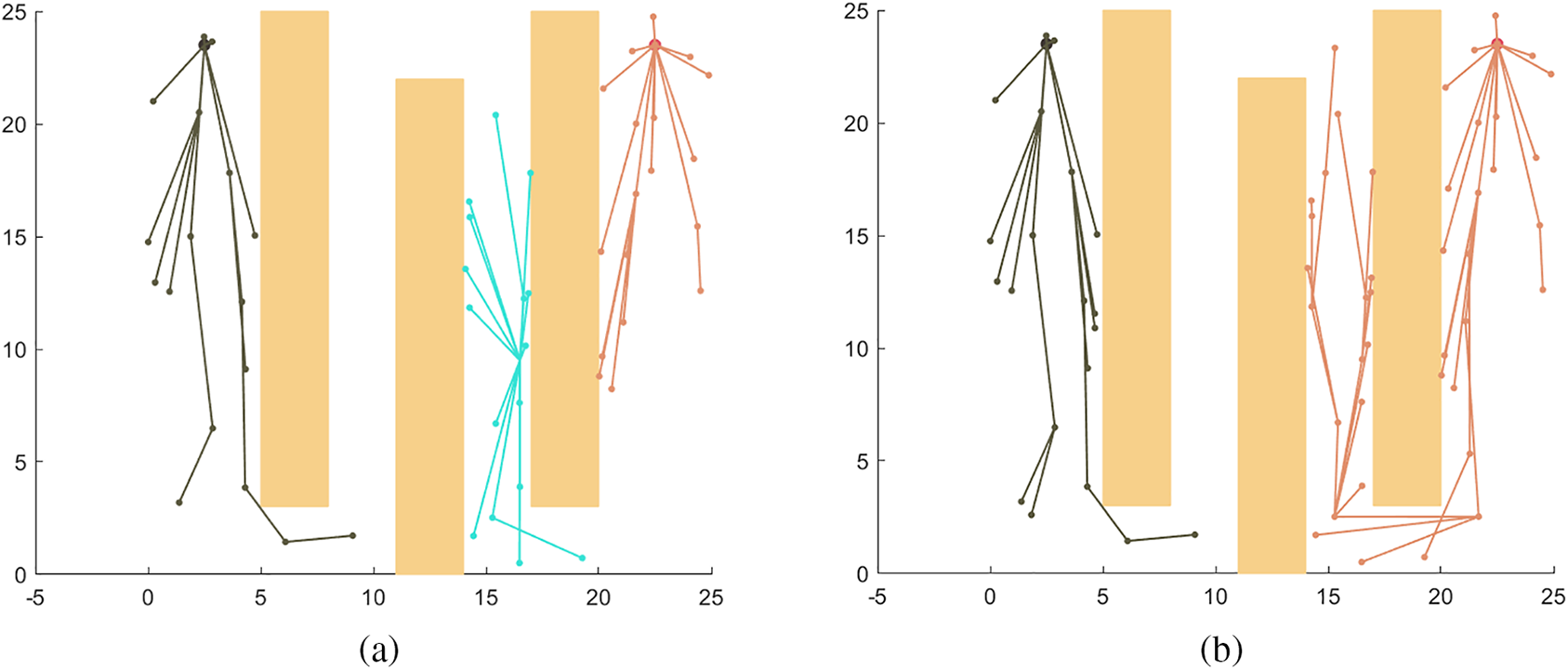
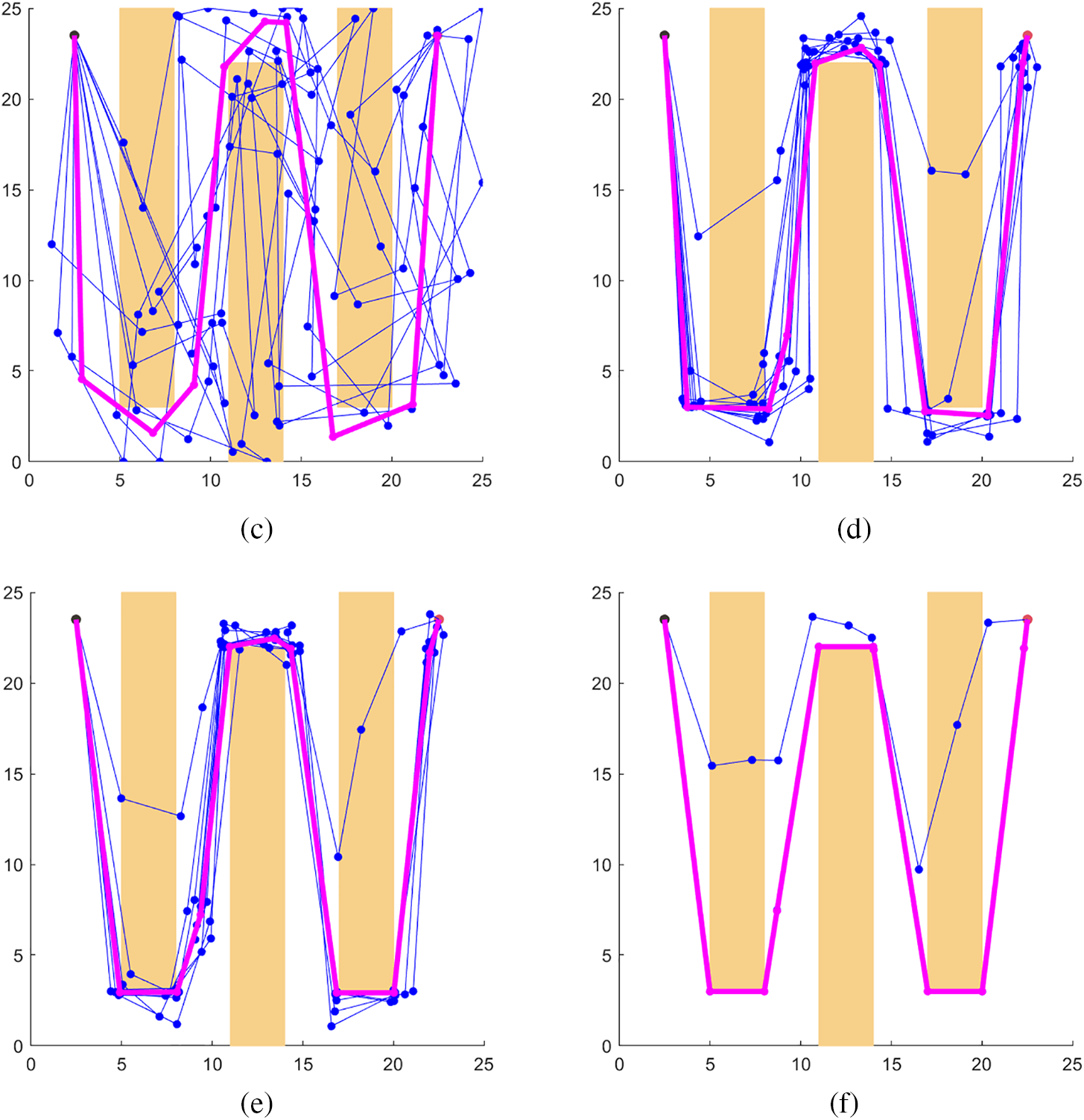
Figure 3: Intermediary RRT*-PSO in action: (a) Intermediary Tree (cyan) helped expand the tree to the undiscovered region of the map; (b) The intermediary tree found a connection and then merged with the goal tree; (c) Initial population of PSO was initialized after the goal tree met the starting tree (the magenta path is the Global best particle); (d)–(f) PSO particles continue searching the space, update their global best particle and converged to the final solution

In Algorithm 3, let T1 be the intermediary tree and T2 be the connected tree. First, all the nodes in the connected branch of T1 are added to T2 by the first while loop. Then the second for loop adds the other Tt nodes to T2 and rewires them. With this strategy, the merging process is guaranteed to transfer almost all nodes from the intermediary tree to its connected tree.

3.4 Exploration Phase Terminate Condition

At the end of every basic RRT* iteration, when the re-branching process is completed, the newly added nodes of the two main trees are checked to determine if they can be connected to any node of the other main tree. If there is existed 1 connection, then the trees are connected, and the exploration phase terminate condition is true.

3.5 Path Minimization Procedure

Traditional sampling-based motion planners have proven to be highly effective in rapidly computing paths for high dimensional systems [7,8,16–19]. However, due to the sampling process and other heuristics used during the search, the solutions from these planners may be gratuitously long. As a result, sampling-based solutions are rarely used without prior optimization [26]. There are several methods for path simplification. Post-processing methods such as path shortcutting [27] and hybridization [28] have been demonstrated to be highly effective at removing redundant motions from paths and forming a shorter solution from a combination of input paths, respectively [26].

In this study, the path minimization process was used only once during the phase transition period. The main goal of path minimization is to reduce the number of path waypoints as much as possible because RRT can generate a huge amount of nodes while PSO takes a lot of computations if the particle dimensions are large. Therefore, minimizing the path would help remove redundant nodes and accelerate PSO speed significantly. The minimization process was performed by checking two non-consecutive nodes of the solution sequence. If the edge created by these two nodes is obstacle-free, then all nodes between them are removed (Algorithm 5).

3.6 PSO Implementation

After the first solution is obtained, PSO is deployed to refine the current solution, which uses the minimized version of the RRT* result as the global best particle.

3.6.1 Particle Encoding

As the solution size of RRT* can be varied as the total number of waypoints is not fixed, PSO particle size must also be dynamic. Each PSO particle contains a sequence of waypoint positions, velocities, a personal best sequence, the current path length, and the fitness values. The fitness value of each particle is its path length plus an arbitrary large number multiple with the number of obstacles crossed.

3.6.2 PSO Population Initialization and Main Loop

At the beginning of PSO phase, the initial population is randomly initialized based on configuration of the RRT* solution. Then, after the population initialization, the RRT* solution is injected directly into the population as one of the particles. Usually, the PSO random initial population is very chaotic and mostly crosses obstacles, thus providing one rational particle to the population, which helps other particles quickly converge to the final Pareto solution.

There are three key coefficients in PSO which conquer the behavior of exploration and exploitation-w, C1 and C2–also known as “acceleration coefficient”. In this study, we set initial w value equal 1 and exponentially decrease over iterations by multiplying with a damping coefficient wdamp = 0.995, C1 and C2 were set to 2 and 1.5 as they give the best result based on our observation. For the main loop of PSO, every particle position, velocity, and personal best are updated in every iteration using Algorithm 6.

3.6.3 Opposition-Based Multi-Restart Strategy

Opposition-based learning (OBL) has been commonly used in metaheuristic algorithms [29–31]. One of the major weaknesses of PSO is the local minima trapped situation, as w (personal acceleration coefficient), has decreased in large amounts, while the global best solution has not been found. Therefore, to avoid these scenarios, we applied the theory of OBL to increase the diversity of the search agents. Whenever the optimizer does not find any significant improvement to the current best solution, the entire population is re-initialized by first randomly assigning a new position and velocity to every search agent, then creating the opposite population based on the first population.

To integrate OBL into PSO algorithm, we introduce a multi-restart strategy to the main loop of PSO. Let Dt be the population best fitness value at iteration tth, ΔDt=Dt−Dt−K (K is a constant). When t is greater than K and ΔDt<β (β is a constant), we can assume that the algorithm converges. The re-initialization process is then activated by randomly choosing one of the two re-initialize strategies mentioned above. The re-initialization process is described in Algorithm 7.

4  Method Implementation

To verify the proposed method, we used two datasets from [19] and four typical proposed datasets at four different levels of complexity. Four methods, Informed RRT*, RRT*-connect, Informed RRT*-connect, and Intermediary RRT*-PSO, were executed 100 times for each test file. All the approaches were programmed using MathWorks MATLAB 2020a. The computer that ran these configurations was equipped with the following specifications: AMD Ryzen 5 3600 (3.6 GHz), 16 GB (2600 MHz) RAM, and Windows 10 operating system.

4.1 Single Cube

The single cube dataset (Fig. 4a) originated from [18] to evaluate the influence of the informed sampling algorithm on the map size and the desired distance from Xstart to Xgoal. The dataset included only one square obstacle with a random width between [10,25] at the center, and the map size (w) was determined by the ratio between dgoal (the distance between Xstart and Xgoal) and l (the width of the configuration space). In this test, the two algorithms were executed with eight different ldgoal ratios from 1 to 4.5 until they found the first solution to verify their CPU time.

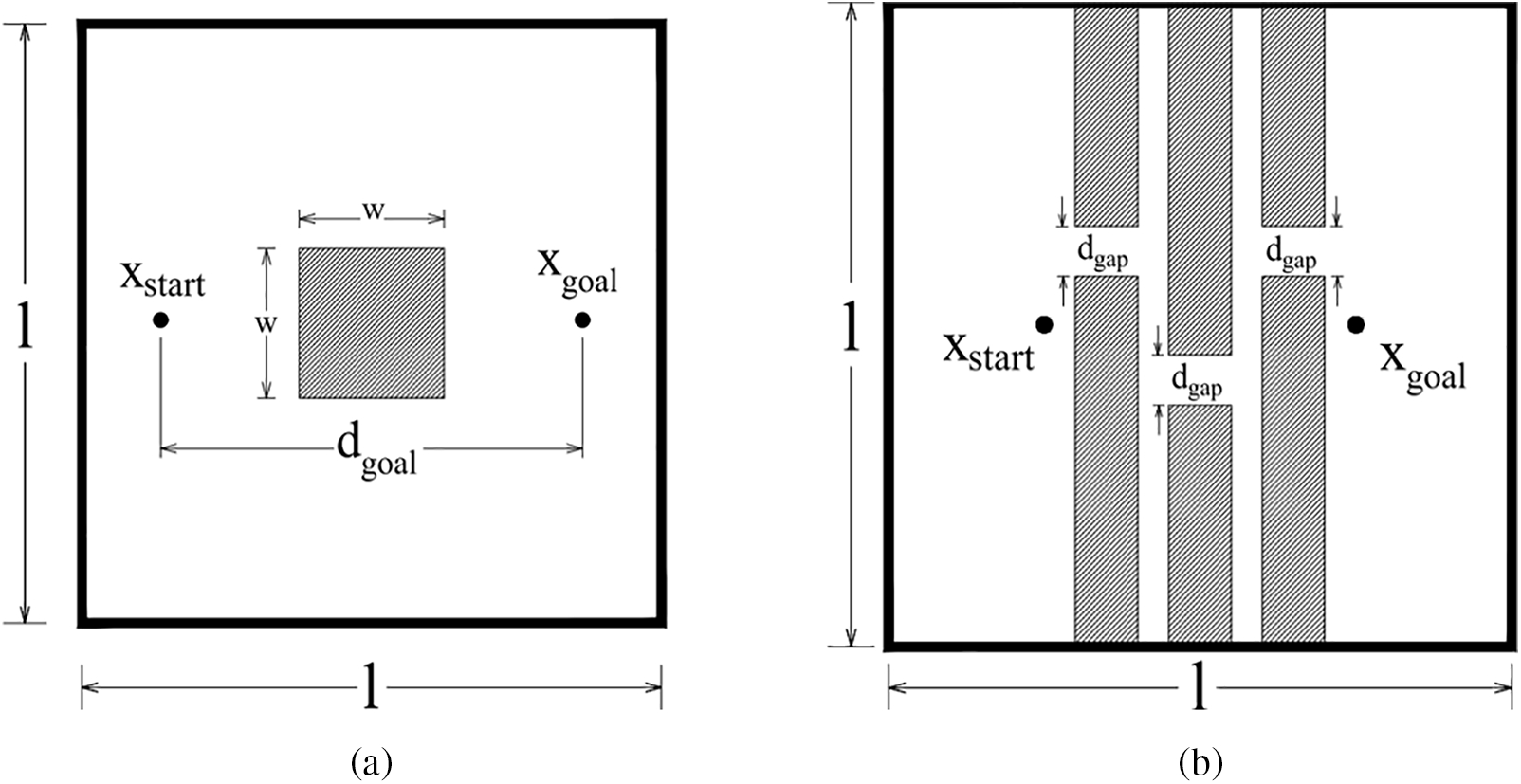
Figure 4: (a) Single cube; (b) Multiple narrow passage

Fig. 5a shows the results obtained after 100 executions, all four algorithms successfully found the solutions. In this test, RRT*-connect was slower than Informed RRT* in all cases although it mostly found the first solution earlier. Intermediary RRT*-PSO was the fastest algorithm, faster than Informed RRT*-connect 10 to 28 percent for a map size ratio larger than 2 and slower in a small ratio. The two results were almost identical for the smaller ratios. For algorithm efficiency, Fig. 6a indicates that Informed RRT*-connect can find the first solution within 22 iterations, whereas it only requires 12 iterations for Intermediary RRT*-PSO (map size = 2). For accuracy, Intermediary RRT*-PSO performed better than Informed RRT*-connect by both converging rate (within 200 iterations) and path length (2% shorter at iteration 1000th).

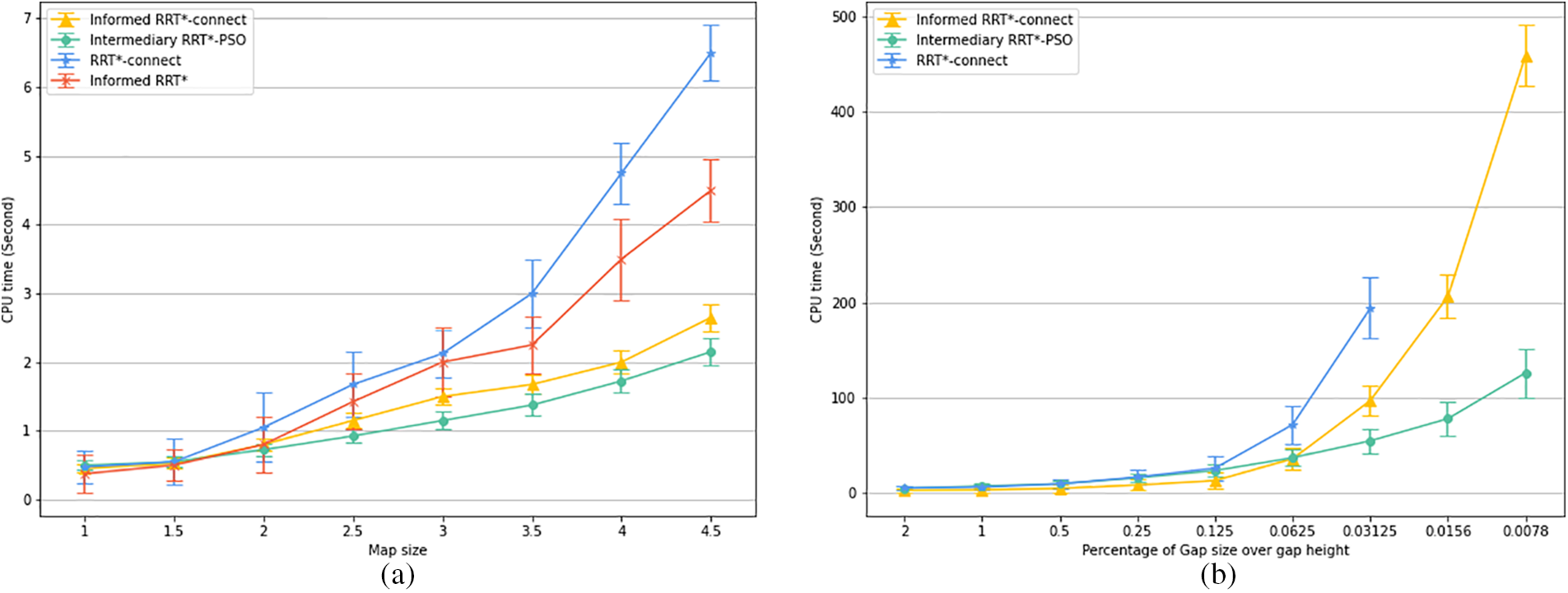
Figure 5: Median computational time required for informed RRT*-connect and Intermediary RRT*-PSO to find solutions within a 2% deviation from the ideal path length for different single cube map sizes (a) and multiple narrow passages map height (b) configurations. Error bars illustrate the non-parametric 95% confidence interval for the median path length

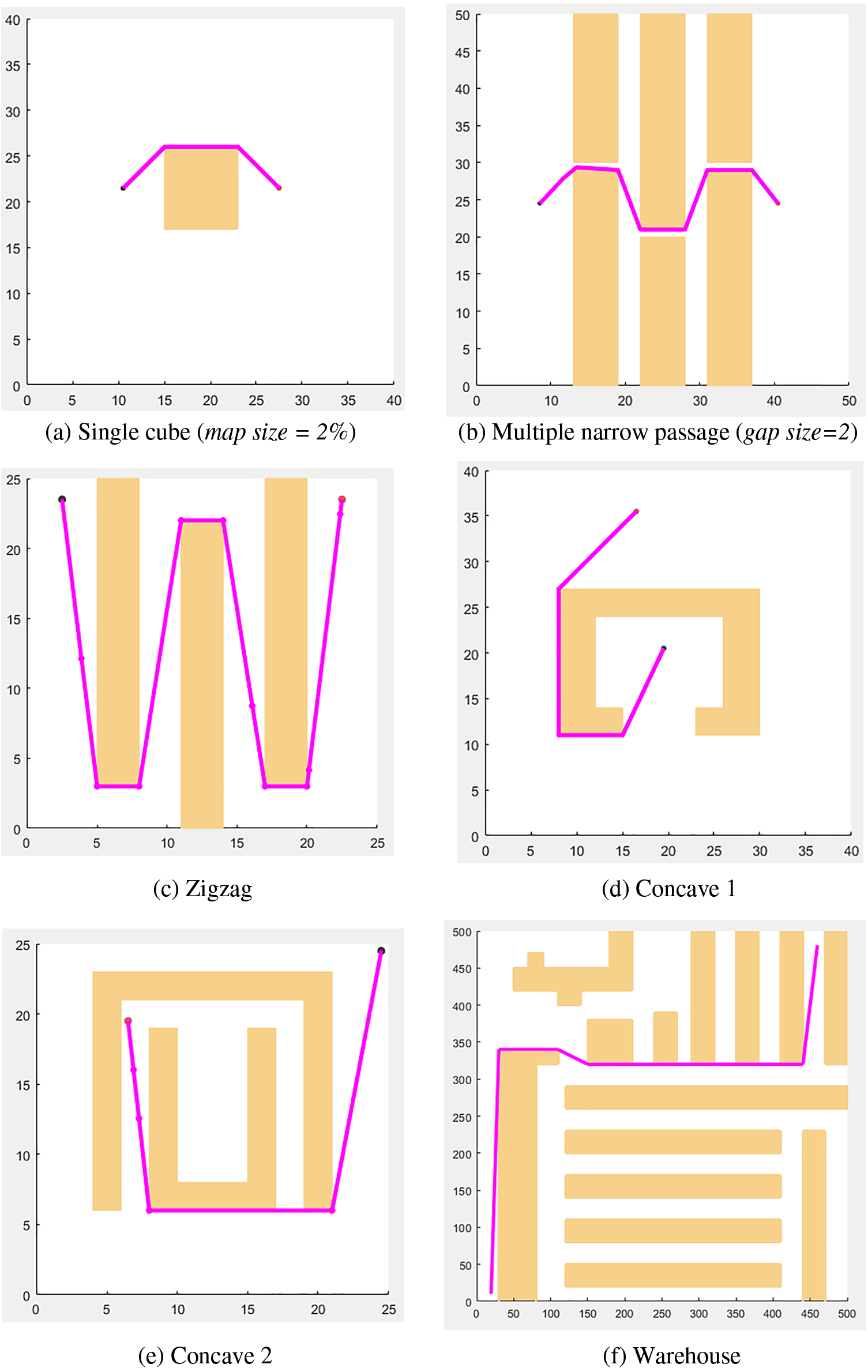
Figure 6: Benchmark environment used in this paper and the ideal solutions (magenta) solved by Intermediary RRT*-PSO

4.2 Multiple Narrow Passages

The next dataset is the Multiple Narrow Passages configuration, which is proposed by [19] to verify the planner’s ability to find paths through narrow gaps, which is also a weakness of many previous methods. In this test, six rectangular walls were used (Fig. 4b) to create 3 narrow gaps with size dgap, the planner trees must go through all three narrow gaps to complete the task. The gap heights ranged from 2 percent of the total configuration height and decreased exponentially to 1/128 percent. The algorithms were executed until they completed their exploration phase or exceeded 1000 s maximum runtime.

According to expectations, Informed RRT*, RRT*-connect and Informed RRT*-connect required more effort to sample paths through the narrow gaps. In contrast, Intermediary RRT*-PSO started to sample the gap area by creating intermediary trees in those areas after the outside regions were fully sampled.

After 100 executions, Informed RRT* could not find any feasible solution with 1000 iterations; thus, their graph did not appear. RRT*-connect was able to find solutions with a gap size greater than 1/32%; however, the time required was approximately three times greater. In the other hand, Informed RRT*-connect finished finding the solution faster than Intermediary RRT*-PSO from 5% to 42% in most cases; however, Intermediary RRT*-PSO outperformed Informed RRT*-connect for configurations with a gap size smaller than 1/16% (Fig. 5b).

In the most extreme case with a gap height of 1/128%, Intermediary RRT*-PSO is four times faster than Informed RRT*-connect. For algorithm efficiency, Intermediary RRT*-PSO found the solution within 560 iterations (2% gap height), whereas Informed RRT*-connect required 827 iterations (Fig. 8b) and RRT*-connect has. Moreover, PSO helped to refine the solution quickly within 810 iterations (Fig. 7b).

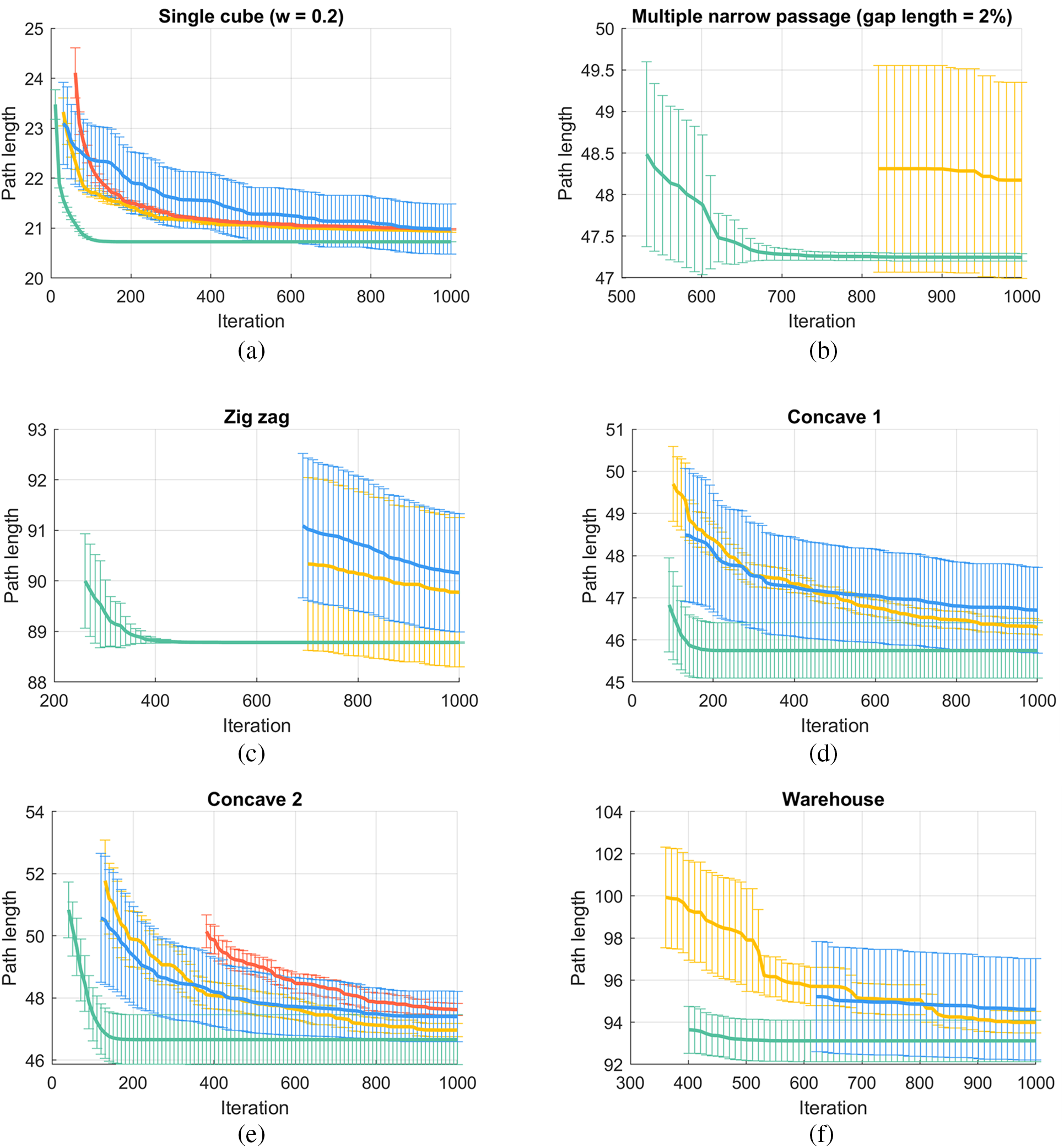
Figure 7: Path length vs. iteration number chart. Error bars illustrate the non-parametric 95% confidence interval for the mean path length

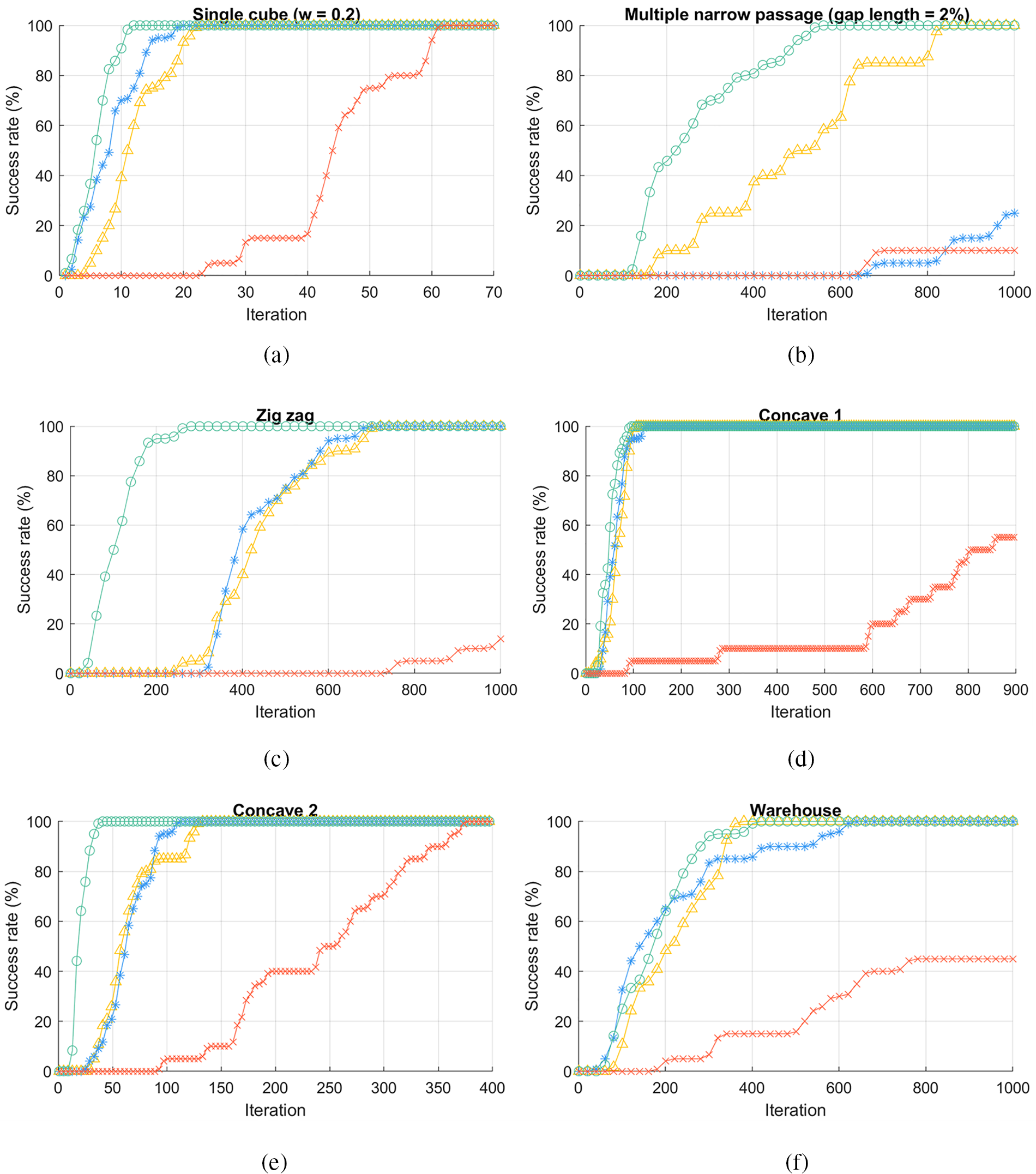
Figure 8: The success rate vs. iteration of Informed RRT*-connect and Intermediary RRT*-PSO

4.3 Zigzag

Zigzag is one of our proposed datasets, whose purpose is to test the superior exploration speed of Intermediary RRT*-PSO in an environment containing zigzag passages. The environment had three rectangular obstacles (Fig. 6c) forming a zigzag route. The middle area of the map is much larger than the side area, which means that the probability of sampling a point in the side area is much lower, making it harder for the planner to sample in the right position.

As expected, Intermediary RRT*-PSO found the first solution within 300 iterations, whereas Informed RRT*-connect and RRT*-connect struggled to find paths to the middle section of the environment. Additionally, PSO only required approximately 200 iterations to enhance the solution accuracy (Fig. 7c), and there was almost no path length variation between 100 executions.

4.4 Concave

As mentioned above, RRT family methods struggle with concave walls as they force the planner to generate an indirect path. Thus, to verify the effectiveness of the intermediary tree, we propose two Concave (Figs. 6d and 6e) datasets that contain one and two U-shaped obstacles. The test results are presented in Figs. 7d, 7e, 8d, and 8e.

As can be seen, Intermediary RRT*-PSO finds the first solution and converges faster than other algorithms in most runs. However, as the datasets have multiple possible routes, 27 percent of the time Intermediary RRT*-PSO is trapped in local minimum solutions in the Concave 1 dataset and 18% in the Concave 2 dataset. In contrast, over the long run at iteration 1000th, Informed RRT* and Informed RRT*-connect have more consistent accuracy as their ellipsoid sampling region is narrowed down considerably. However, the overall Intermediary RRT*-PSO solutions are refined rapidly within only 200 iterations and are slightly shorter than Informed RRT*-connect.

4.5 Warehouse

Warehouse (Fig. 6f) is the last dataset that replicates a practice scenario environment containing many small passages and creates many possible routes. After the simulation, as shown in Figs. 7f and 8f, both algorithms successfully found near-optimal paths; however, Intermediary RRT*-PSO was trapped in local minimum solutions 31% of the time, thus leading to higher variations in the final path length. Fig. 9 shows two cases when Intermediary RRT*-PSO failed to find the ideal path because the RRT* first obtained solutions did not lie on the ideal route, while the other scenarios were caused by oversimplification due to the minimization process deleting some key waypoints. Nevertheless, the overall refined PSO solution was acceptable for most cases and converged within 600 iterations.

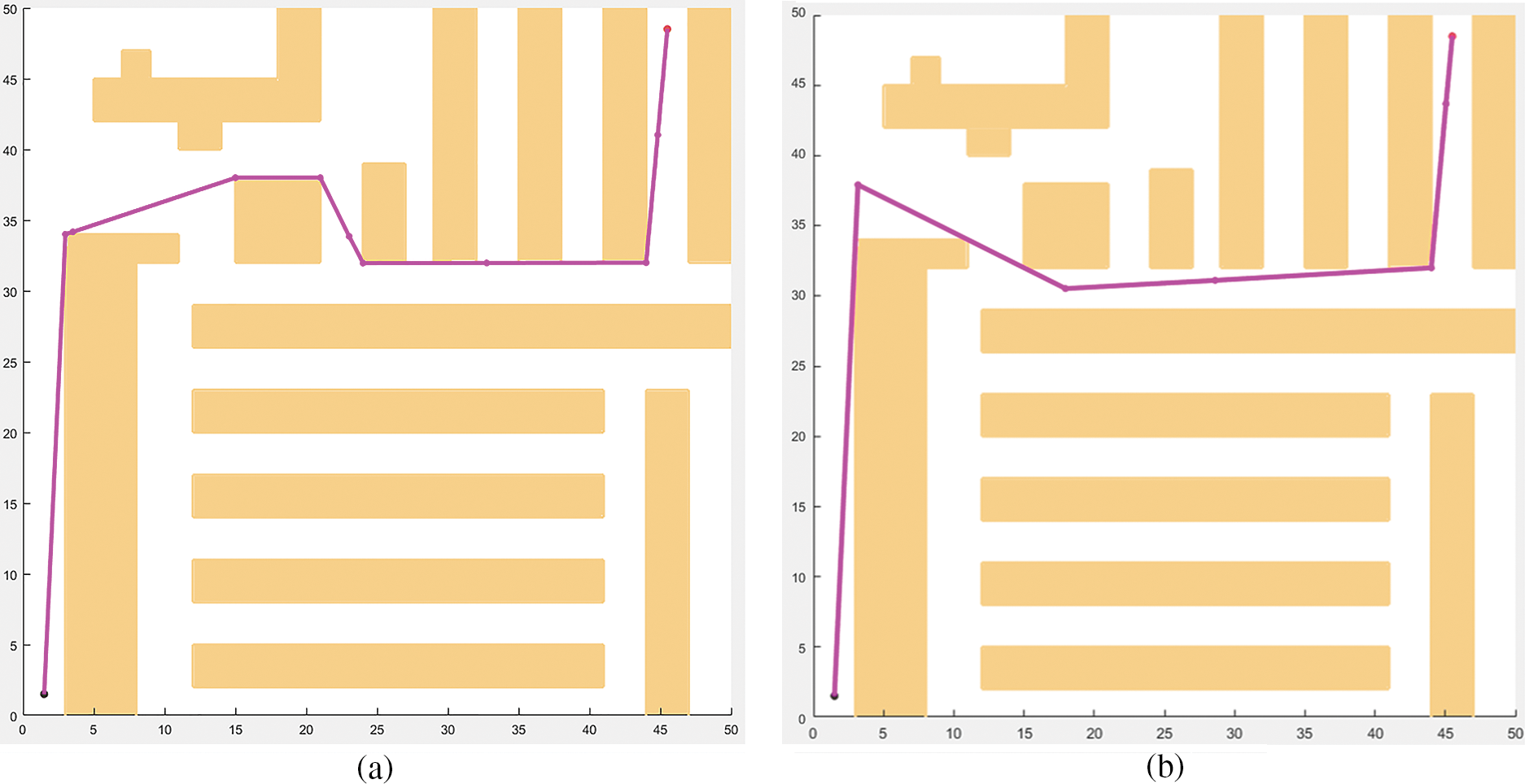
Figure 9: Intermediary RRT*-PSO trapped in the local minimum solution because the RRT* first solution did not lie on the ideal route (a) or the over-aggressive minimization process (b)

5  Discussion and Conclusion

In this paper, we present a novel hybrid sampling-based path planning approach based on creating a new intermediate tree between the start and end points, combined with the superiority of the available methods (RRT*-connect and PSO), to deliver a new method that is optimized for both speed and accuracy. After 100 executions for each dataset, the results showed that Intermediary RRT*-PSO outperformed the previous profound method (RRT*-connect, Informed RRT*, Informed RRT*-connect) in terms of both exploration speed and solution accuracy, with the same amount of computational effort. Although in some scenarios Intermediary RRT*-PSO takes a longer time to solve 1000 iterations (Fig. 10), it only requires approximately 1/4 of the total iterations to complete the task compared with other algorithms.

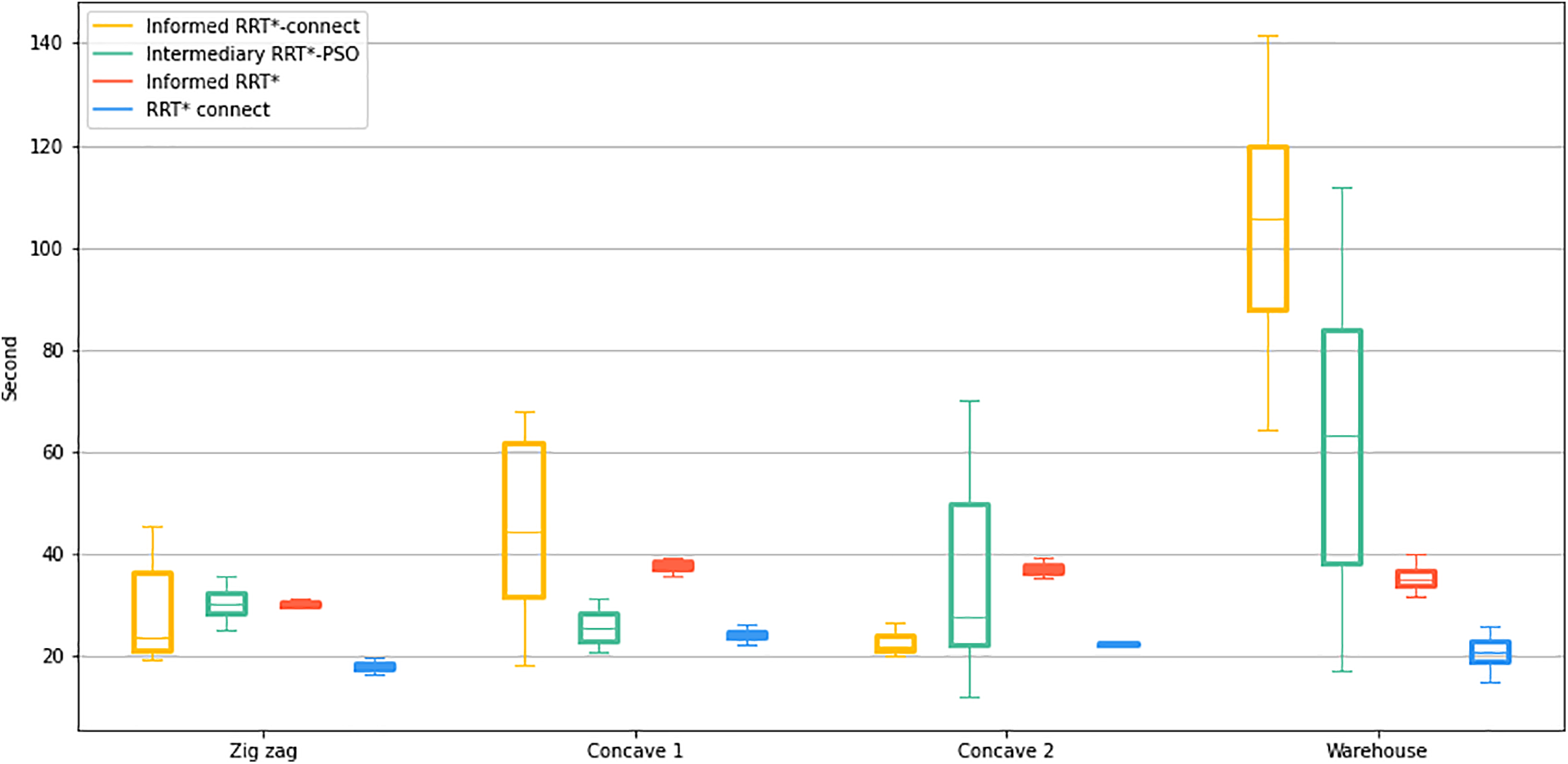
Figure 10: The algorithm computational time (1000 iterations) box plot for each dataset

As mentioned, the presentation of the intermediary tree helps Intermediary RRT*-PSO to create a considerable number of nodes simultaneously, which can easily approach the goal node in complex and large maps. Nevertheless, Intermediary RRT*-PSO sometimes tends to fall into local minimum states by approximately 14% in multiple route configurations.

For the computational complexity, at each iteration of phase 1, the complexity of Intermediary RRT*-PSO remains the same, O(n), as other RRT algorithms with n is the current number of nodes. In phase 2, the algorithm complexity is O(nm), where n is the number of search agents and m is the number of nodes carried by each search agent. Overall, the algorithm complexity of Intermediary RRT*-PSO is lower than the traditional informed sampling method.

In future research, we would like to improve on the following features:

•   Parallel computing: which means each tree is utilized on an individual processor core. Hence, there could be more than one intermediary tree, thus accelerating the algorithm’s exploration speed even more, and the exploration phase could be conducted simultaneously with the PSO phase to inject more solutions, thereby helping the planner avoid trapping in local minimum states.

•   Better metaheuristic algorithms: PSO is currently used to improve the feasible solution over time, as shown in the previous section. However, PSO is known to suffer from local traps and premature convergence [32,33]. It is possible to hybridize PSO with other local-search techniques, as shown in [19,20] to improve the exploitation and local trap escaping capabilities. Another alternative is to find more recent algorithms with a better exploration-exploitation balance, such as Harris Hawk Optimization (HHO) [34], Whale Optimization (WO) [35], etc.

•   Multi-objective optimization: In this study, PSO utilized path length as a metric to calculate particle fitness. However, in practice, there are many objectives that a planner should also need to consider, such as smoothness, obstacle safety distance, maximum steering angle (minimum corner radius), etc.

Funding Statement: This research is funded by International University, VNU-HCM under Grant Number T2021-02-IEM.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. Bai, P. Dallasega, G. Orzes and J. Sarkis, “Industry 4.0 technologies assessment: A sustainability perspective,” International Journal of Production Economics, vol. 229, pp. 107776, 2020. [Google Scholar]

2. S. Alshammrei, S. Boubaker and L. Kolsi, “Improved dijkstra algorithm for mobile robot path planning and obstacle avoidance,” Computers, Materials and Continua, vol. 72, no. 3, pp. 5939–5954, 2022. [Google Scholar]

3. E. W. Dijkstra, “A note on two problems in connexion with graphs,” Numerische Mathematik, vol. 1, no. 1, pp. 269–271, 1959. [Google Scholar]

4. P. Hart, N. Nilsson and B. Raphael, “A formal basis for the heuristic determination of minimum cost paths,” IEEE Transactions on Systems Science and Cybernetics, vol. 4, no. 2, pp. 100–107, 1968. [Google Scholar]

5. M. A. H. Ali and M. Mailah, “Laser simulator: A novel search graph-based path planning approach,” International Journal of Advanced Robotic System, vol. 15, no. 2018, pp. 1–16, 2018. [Google Scholar]

6. L. E. Kavraki, P. Svestka, J. C. Latombe and M. H. Overmars, “Probabilistic roadmaps for path planning in high-dimensional configuration spaces,” IEEE Transactions on Robotics and Automation, vol. 12, no. 4, pp. 566–580, 1996. [Google Scholar]

7. S. M. LaValle and J. J. Kuffner, “Randomized kinodynamic planning,” The International Journal of Robotics Research, vol. 20, no. 5, pp. 378–400, 2001. [Google Scholar]

8. S. Karaman and E. Frazzoli, “Sampling-based algorithms for optimal motion planning,” The International Journal of Robotics Research, vol. 30, no. 7, pp. 846–894, 2011. [Google Scholar]

9. L. Janson, E. Schmerling, A. Clark and M. Pavone, “Fast marching tree: A fast marching sampling-based method for optimal motion planning in many dimensions,” The International Journal of Robotics Research, vol. 34, no. 7, pp. 883–921, 2015. [Google Scholar] [PubMed]

10. J. Xu, K. Song, D. Zhang, H. Dong, Y. Yan et al., “Informed anytime fast marching tree for asymptotically optimal motion planning,” IEEE Transactions on Industrial Electronics, vol. 68, no. 6, pp. 5068–5077, 2021. [Google Scholar]

11. J. D. Gammell, S. S. Srinivasa and T. D. Barfoot, “Batch informed trees (BITSampling-based optimal planning via the heuristically guided search of implicit random geometric graphs,” in 2015 IEEE Int. Conf. on Robotics and Automation (ICRA), Seattle, WA, USA, pp. 3067–3074, 2015. [Google Scholar]

12. M. Strub and J. Gammell, “Adaptively informed trees (AIT*) and effort informed trees (EIT*Asymmetric bidirectional sampling-based path planning,” The International Journal of Robotics Research, vol. 41, no. 4, pp. 390–417, 2022. [Google Scholar]

13. J. Sánchez-Ibáñez, C. Pérez-del-Pulgar and A. García-Cerezo, “Path planning for autonomous mobile robots: A review,” Sensors, vol. 21, no. 23, pp. 7898, 2021. [Google Scholar]

14. I. Noreen, A. Khan and Z. Habib, “Optimal path planning using RRT* based approaches: A survey and future directions,” International Journal of Advanced Computer Science and Applications, vol. 7, no. 11, pp. 97–107, 2016. [Google Scholar]

15. M. Nazarahari, E. Khanmirza and S. Doostie, “Multi-objective multi-robot path planning in continuous environment using an enhanced genetic algorithm,” Expert Systems with Applications, vol. 115, pp. 106–120, 2019. [Google Scholar]

16. J. J. Kuffner and S. M. LaValle, “RRT-connect: An efficient approach to single-query path planning,” in IEEE Int. Conf. on Robotics and Automation. Symposia Proc., San Francisco, CA, USA, vol. 2, pp. 995–1001, 2000. [Google Scholar]

17. S. Klemm, J. Oberländer, A. Hermann, A. Roennau, T. Schamm et al., “RRT*-Connect: Faster, asymptotically optimal motion planning,” in 2015 IEEE Int. Conf. on Robotics and Biomimetics (ROBIO), Zhuhai, China, pp. 1670–1677, 2015. [Google Scholar]

18. J. D. Gammell, S. S. Srinivasa and T. D. Barfoot, “Informed RRT: Optimal sampling-based path planning focused via direct sampling of an admissible ellipsoidal heuristic,” in 2014 IEEE/RSJ Int. Conf. on Intelligent Robots and Systems, Chicago, IL, USA, pp. 2997–3004, 2014. [Google Scholar]

19. R. Mashayekhi, M. Y. I. Idris, M. H. Anisi, I. Ahmedy and I. Ali, “Informed RRT*-connect: An asymptotically optimal single-query path planning method,” IEEE Access, vol. 8, pp. 19842–19852, 2020. [Google Scholar]

20. H. Zhang, W. Lin and A. Chen, “Path planning for the mobile robot: A review,” Symmetry, vol. 10, no. 10, pp. 450, 2018. [Google Scholar]

21. C. Tsai, H. Huang and C. Chan, “Parallel elite genetic algorithm and its application to global path planning for autonomous robot navigation,” IEEE Transactions on Industrial Electronics, vol. 58, no. 10, pp. 4813–4821, 2011. [Google Scholar]

22. M. Nazarahari, E. Khanmirza and S. Doostie, “Multi-objective multi-robot path planning in a continuous environment using an enhanced genetic algorithm,” Expert Systems with Applications, vol. 115, pp. 106–120, 2019. [Google Scholar]

23. C. Lamini, S. Benhlima and A. Elbekri, “Genetic algorithm based approach for autonomous mobile robot path planning,” Procedia Computer Science, vol. 127, pp. 180–189, 2018. [Google Scholar]

24. B. Song, Z. Wang and L. Zou, “An improved PSO algorithm for smooth path planning of mobile robots using continuous high-degree Bezier curve,” Applied Soft Computing, vol. 100, pp. 106960, 2021. [Google Scholar]

25. G. Li and W. Chou, “Path planning for mobile robot using self-adaptive learning particle swarm optimization,” Science China Information Sciences, vol. 61, no. 5, pp. 052204:1–052204:18, 2017. [Google Scholar]

26. R. Luna, I. Sucan, M. Moll and L. Kavraki, “Anytime solution optimization for sampling-based motion planning,” in 2013 IEEE Int. Conf. on Robotics and Automation, Karlsruhe, Germany, pp. 5068–5074, 2013. [Google Scholar]

27. R. Geraerts and M. H. Overmars, “Creating high-quality paths for motion planning,” The International Journal of Robotics Research, vol. 26, no. 8, pp. 845–863, 2007. [Google Scholar]

28. B. Raveh, A. Enosh and D. Halperin, “A little more, a Lot better: Improving path quality by a path-merging algorithm,” IEEE Transactions on Robotics, vol. 27, no. 2, pp. 365–371, 2011. [Google Scholar]

29. Q. Kang, C. Xiong, M. Zhou and L. Meng, “Opposition-based hybrid strategy for particle swarm optimization in noisy environments,” IEEE Access, vol. 6, pp. 21888–21900, 2018. [Google Scholar]

30. S. Dhargupta, M. Ghosh, S. Mirjalili and R. Sarkar, “Selective opposition based grey wolf optimization,” Expert Systems with Applications, vol. 151, pp. 113389, 2020. [Google Scholar]

31. B. Kar, S. Nayak and C. Nayak, “Opposition-based GA learning of artificial neural networks for financial time series forecasting,” Advances in Intelligent Systems and Computing, vol. 411, pp. 405–414, 2015. [Google Scholar]

32. T. M. Le, T. N. Pham and S. V. Dao, “A novel wrapper-based feature selection for heart failure prediction using an adaptive particle swarm grey wolf optimization,” Enhanced Telemedicine and e-Health, vol. 410, pp. 315–336, 2021. [Google Scholar]

33. T. M. Le, L. V. Tran and S. V. T. Dao, “A feature selection approach for fall detection using various machine learning classifiers,” IEEE Access, vol. 9, pp. 115895–115908, 2021. [Google Scholar]

34. T. N. Pham, L. V. Tran and S. V. T. Dao, “A multi-restart dynamic harris hawk optimization algorithm for the economic load dispatch problem,” IEEE Access, vol. 9, pp. 122180–122206, 2021. [Google Scholar]

35. E. S. M. El-Kenawy, S. Mirjalili, F. Alassery, Y. Zhang, M. Eid et al., “Novel meta-heuristic algorithm for feature selection, unconstrained functions and engineering problems,” IEEE Access, vol. 10, pp. 40536–40555, 2022. [Google Scholar]